二次函数图像与性质课件PPT
合集下载
《二次函数的图像和性质》PPT课件 人教版九年级数学

2
y=20x2+40x+20③
d=
学生以小组形式讨论,并由每组代表总结.
探究新知
【分析】认真观察以上出现的三个函数解析式,
分别说出哪些是常数、自变量和函数.
函数解析式
y=6x2
自变量
函数
x
y
n
d
x
y
这些函数自变量的最高次项都是二次的!
这些函数有什
么共同点?
探究新知
二次函数的定义
一般地,形如y=ax²+bx+c(a,b,c是常数,a≠ 0)的
总结二次
函数概念
二次函数y=ax²+bx+c
(a,b,c为常数,a≠0)
确定二次函数解
析式及自变量的
取值范围
二次函数的判别:
①含未知数的代数式为整式;
②未知数最高次数为2;
③二次项系数不为0.
人教版 数学 九年级 上册
22.1 二次函数的图象和性质
22.1.2
二次函数y=ax2的
图象和性质
导入新知
探究新知
方法点拨
运用定义法判断一个函数是否为二次函数的
步骤:
(1)将函数解析式右边整理为含自变量的代
数式,左边是函数(因变量)的形式;
(2)判断右边含自变量的代数式是否是整式;
(3)判断自变量的最高次数是否是2;
(4)判断二次项系数是否不等于0.
巩固练习
下列函数中,哪些是二次函数?
(1) y=3(x-1)²+1(是)
(1) 你们喜欢打篮球吗?
(2)你们知道投篮时,篮球运动的路线是什么
曲线?怎样计算篮球达到最高点时的高度?
素养目标
y=20x2+40x+20③
d=
学生以小组形式讨论,并由每组代表总结.
探究新知
【分析】认真观察以上出现的三个函数解析式,
分别说出哪些是常数、自变量和函数.
函数解析式
y=6x2
自变量
函数
x
y
n
d
x
y
这些函数自变量的最高次项都是二次的!
这些函数有什
么共同点?
探究新知
二次函数的定义
一般地,形如y=ax²+bx+c(a,b,c是常数,a≠ 0)的
总结二次
函数概念
二次函数y=ax²+bx+c
(a,b,c为常数,a≠0)
确定二次函数解
析式及自变量的
取值范围
二次函数的判别:
①含未知数的代数式为整式;
②未知数最高次数为2;
③二次项系数不为0.
人教版 数学 九年级 上册
22.1 二次函数的图象和性质
22.1.2
二次函数y=ax2的
图象和性质
导入新知
探究新知
方法点拨
运用定义法判断一个函数是否为二次函数的
步骤:
(1)将函数解析式右边整理为含自变量的代
数式,左边是函数(因变量)的形式;
(2)判断右边含自变量的代数式是否是整式;
(3)判断自变量的最高次数是否是2;
(4)判断二次项系数是否不等于0.
巩固练习
下列函数中,哪些是二次函数?
(1) y=3(x-1)²+1(是)
(1) 你们喜欢打篮球吗?
(2)你们知道投篮时,篮球运动的路线是什么
曲线?怎样计算篮球达到最高点时的高度?
素养目标
二次函数y=ax2的图象和性质ppt课件

例4 如图, 四个二次函数的图象分别对应 ① y=ax2 ;② y=bx2;
③ y=cx2;④ y=dx2,且①与③,②与④分别关于x 轴对称.
(1)比较a,b,c,d 的大小; (2)说明a 与c,b 与d 的数量关系.
解:(1)由抛物线的开口方向,知 a > 0,b > 0,c < 0,d < 0,
由抛物线的开口大小,知 |a| > |b|,|c| > |d|, 因此a > b,c < d. ∴ a > b > d > c. (2)∵①与③,②与④分别关于x 轴对称,
∴①与③,②与④的开口大小相同,方向相反. ∴ a+c=0,b+d=0.
课堂练习
1、下列函数中,y总随x增大而减小的是( B )
归纳总结
位置开 开口向上,在x轴上方 开口向下,在x轴下方
口方向
a的绝对值越大,开口越小
对称性 顶点最值
关于y轴对称,对称轴方程是直线x=0 顶点坐标是原点(0,0)
当x=0时,y最小值=0 当x=0时,y最大值=0
增减性
在对称轴左侧递减 在对称轴左侧递增 在对称轴右侧递增 在对称轴右侧递减
1、如右图,观察函数y=( k-1)x2的图象, 则k的取值范围是 k>1 .
复习引入
1.二次函数的一般形式是怎样的? y=ax²+bx+c(a,b,c是常数,a≠ 0)
2.下列函数中,哪些是二次函数?
①
②
③
④
⑤
3.一次函数的图象是一条 直线.
4.通常怎样画一个函数的图象? 列表、描点、连线
那么,二次函数的图象会是什么样的图形呢?这节课我们 来学习最简单的二次函数y=ax2的图像
不同点: a的值越大,开口越小.
人教版数学九年级上册22.1.2二次函数y=ax2的图像与性质 课件(21张PPT)

二二次次函函数数y的=图x2象的都图是象抛是物一线条,曲线它,们它的的开形口状或类者似向于上投或篮者球向 时下球.在一空般中地所,经二过次的函路数线y,=只ax是2 +这b条x +曲c线(开a≠口0)向的上图,象这叫条做曲抛 线物叫线做y =抛a物x2线+ byx=+xc2 ,
9 6 3
-3
3
实y轴际是上抛,物每线条y抛= 物x 2线的都对有称对轴称,轴抛,物抛线物y 线= x与2 对与称它轴的的对交称点轴 叫的做交抛点物(线0,的0顶)点叫.做顶抛点物是线抛y =物x线2 的的顶最点低,点它或是最抛高物点线.y = x 2 的最低点.
交点坐标
y
求抛物线与直线的 交点坐标的方法: 两解析式联列方程
组
y=4x2 y=3x+1
O
x
1.若抛物线y=ax²与y=4x²的形状及开口方向 均相同,则a= 4
2.下列关于二次函数y=ax²(a≠0)的说法中,错误 的是( C ) A.它的图像的顶点是原点 B.当a<0,在x=0时,y取得最大值
(2)说出函数图象的顶点坐标、对称轴、
开口方向和图象的位置;
在x轴的下方
解: (1)依题意,得 (2)2 a 3
解得
a=
3 4
∴ 该函数的解析式为 y
3 4
x2
例3、y=kx2与y=kx-2(k≠ 0)在同一坐标系中, 可能是( B )
A
B
C
D
例4、求抛物线y=4x2与直线y=3x+1的
描点法
列表、描点、连线
以0为中心 选取7个x值
画最简单的二次函数 y = x2 的图象列表
二次函数 的图象和性质--PPT课件
点(h,k)坐标 Nhomakorabea对
称
x=h
轴
最 值
最小值为k
最大值为k
新知应用-----基础知识
新知应用-----拓展提高
这节课你学到了什么
图像及性质 合作、分享 类比、化归
知识 方法 思想
作业布置
• 课后习题 • 练习册
送给大家
函数是纲 纲举目张 数形结合 相得益彰
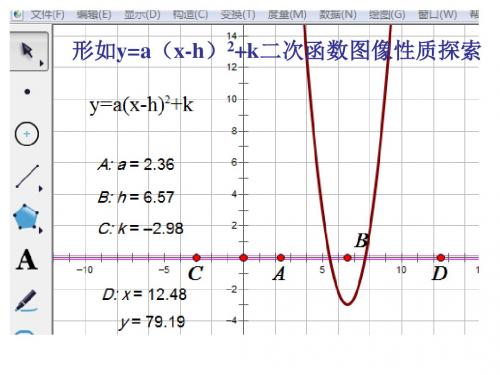
形如y=a(x-h)2+k二次函数图像性质探索
文件名
抛物 线
开口 方向
顶点 坐标
对称 轴
y=ax2(a>0) y=ax2(a<0)
向上
向下
(0,0) y轴
最值 最小值为0 最大值为0
温馨提示:鼠标拖动点A
文件名
抛物 线
开口 方向
顶点 坐标
对称 轴
y=ax2+k y=ax2+k (a>0) (a<0)
向上
向下
(0,K)
y轴
最值 最小值为k 最大值为k
文件名
抛物 线
开口 方向
顶点 坐标
对称 轴
最值
y=a(x-h)2 y=a(x-h)2
(a>0)
(a<0)
向上
向下
(h,0)
x=h
最小值为0
最大值为0
文件名
抛
物 y=a(x-h)2+k
线
(a>0)
y=a(x-h)2+k (a<0)
开
口
向上
方
向
向下
顶
二次函数的图像和性质PPT课件(共21张PPT)

相同点
相同点:开口都向下,顶点是
原点而且是抛物线的最高点,
对称轴是 y 轴.
不同点
不同点:|a|越大,抛物线的
开口越小.
x
O
y
-4 -2
2
4
-2
-4
-6
y 1 x2 2
-8
y x2
y 2x2
尝试应用
1、函数y=2x2的图象的开向口上 ,对称轴y轴 ,顶点是(0,0;)
2、函数y=-3x2的图象的开口向下 ,对称轴y轴 ,顶点是(0,0;) 3、已知抛物线y=ax2经过点A(-2,-8).
不在此抛物线上。
小结
1. 二次函数的图像都是什么图形?
2. 抛物线y=ax2的图像性质: (1) 抛物线y=ax2的对称轴是y轴,顶点是原点.
(2)当a>0时,抛物线的开口向上,顶点是抛物 线的最低点;
当a<0时,抛物线的开口向下,顶点是抛物 线的最高点;
(3)抛物线的增减性
(4)|a|越大,抛物线的开口越小;
得到y=-x2的图像.
y 1
-5 -4 -3 -2 -1-1 o 1 2 3 4 5 x
-2
-3 -4
-5
-6
y=-x2
-7
-8 -9
-10
二次函数的图像
从图像可以看出,二次函数y=x2和y=-x2的图像都是一条
曲线,它的形状类似于投篮球或投掷ห้องสมุดไป่ตู้球时球在空中所经过
的路线.
这样的曲线叫做抛物线.
y=x2的图像叫做抛物线y=x2.
解:分别填表,再画出它们的图象,如图 当a<0时,抛物线的开口向下,顶点是抛物线的最高点;
在同一直角坐标系中画出函数y=-x2、y=-2x2、y=- x2的图象,有什么共同点和不同点? -8=a(-2)2,解出a= -2,所求函数解析式为y= -2x2.
人教九年级数学上册《二次函数图像与性质》课件(共14张PPT)

(3) 二次函数的图象是什么 形 状呢?
结合图象讨论
性质是数形结合
的研究函数的重要 方法.我们得从最 简单的二次函数开 始逐步深入地讨论 一般二次函数的图 象和性质.
画最简单的二次函数 y = x2 的图象
1. 列表:在y = x2 中自变量x可以是任意实数,列表表示几组对应值:
x ··· -3 -2 -1 0
2 0.5
0 0.5 2 4.5
···
8
x
·· -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 ···
·
y 2x2 ·· 8 4.5 2 0.5 0 0.5 2 4.5 8 ···
·
y x2
y 2x2
8
6
4
y 1 x2
2
2
-4 -2
24
函数 y 1 x2 , y 2x2 的图象与函数 y=x2 的图象相比 ,有什么共同2 点和不同点?
相同点:开口:向上, 顶点:原点(0,0)——最低点 对称轴: y 轴
增减性:y 轴左侧,y随x增大而减小
y 轴右侧,y随x增大而增大
y x2
8 6
y 2x2
不同点:a 值越大,抛物线的开 口越小.
4 2 -4 -2
y 1 x2 2
24
探究
画出函数 yx2,y1x2,y2x2 的图象,并考虑这些抛物 2
1
2
3 ···
y = x2 ··· 9 4 1 0 1 4 9 ···
2. 根据表中x,y的数值在坐标平面中描点(x,y)
3.连线 如图,再用平滑曲线顺次
9
连接各点,就得到y = x2 的图象
.
6
y = x2
22.1.4二次函数的图像与性质ppt课件

2
列表、描点、连线,画出函数 y 1 x 62 3 图像.
y
1 2
x2
2 6x
21
问题:
1.怎样平移抛物线 y 1 x2
2
可以得到抛物线
●
●
5
●
●
●
●
●
(6,3)
O
5
10
y 1 x2 6x 21 ? 2
2.看图像说说抛物线 y 1 x2 6x 21
2
的增减性。
x
12
你能用前面的方法讨论二次函数 y = -2x2 - 4x +1 的 图象和性质吗?
2
9
如何将 y 1 x2 6x 21 转化成y =a(x - h)2 +k 的形
式?
2
y 1 x2 6x 21 2
= (12 x2-12x)+ 21
(提取二次项系数)
= (12 x2-12x+36-36) +21 (配方)
= 12(x – 6)2 -18+21 = 12(x - 6)2 +3
22.1.4二次函数y=ax2+bx+c 图象和性质(一)
y
o
x
1
一般地,抛物线y=a(x-h)2 +k与 y=ax2的 形状 相同, 位置 不同
y=ax2 上加下减 y=a(x-h)2 +k 左加右减
2
抛物线y=a(x-h)2+k有如下特点:
1.当a﹥0时,开口向上 , 当a﹤0时,开口 向下 ,
• (3)2x2 4x 2 (4) 2x2 3x 1
7
问题1 如何研究二次函数
y
1 x2
6x
列表、描点、连线,画出函数 y 1 x 62 3 图像.
y
1 2
x2
2 6x
21
问题:
1.怎样平移抛物线 y 1 x2
2
可以得到抛物线
●
●
5
●
●
●
●
●
(6,3)
O
5
10
y 1 x2 6x 21 ? 2
2.看图像说说抛物线 y 1 x2 6x 21
2
的增减性。
x
12
你能用前面的方法讨论二次函数 y = -2x2 - 4x +1 的 图象和性质吗?
2
9
如何将 y 1 x2 6x 21 转化成y =a(x - h)2 +k 的形
式?
2
y 1 x2 6x 21 2
= (12 x2-12x)+ 21
(提取二次项系数)
= (12 x2-12x+36-36) +21 (配方)
= 12(x – 6)2 -18+21 = 12(x - 6)2 +3
22.1.4二次函数y=ax2+bx+c 图象和性质(一)
y
o
x
1
一般地,抛物线y=a(x-h)2 +k与 y=ax2的 形状 相同, 位置 不同
y=ax2 上加下减 y=a(x-h)2 +k 左加右减
2
抛物线y=a(x-h)2+k有如下特点:
1.当a﹥0时,开口向上 , 当a﹤0时,开口 向下 ,
• (3)2x2 4x 2 (4) 2x2 3x 1
7
问题1 如何研究二次函数
y
1 x2
6x
二次函数的图像和性质PPT课件

顶点形式
二次函数的顶点形式是f(x) = a(x - h)^2 + k,其中(h, k)为顶点坐标。
二次函数图像的性质
对称轴
二次函数的对称轴是x = -最大值。
开口方向
二次函数开口向上当且仅当a > 0,开口向下当且仅当a < 0。
二次函数的变换
导数
二次函数的导数是一条直线,表示了函数的变化率。
凹性质
二次函数的凹性质取决于a的值,a > 0时函数向上凹,a < 0时函数向下凹。
凸性质
二次函数的凸性质取决于a的值,a > 0时函数向上凸,a < 0时函数向下凸。
二次函数的非负和非正性质
1 非负性质
2 非正性质
当a > 0时,二次函数的图像位于x轴以上。
建筑
物理
二次函数的图像和性质可应用 于建筑设计,优化结构和形状。
P物理实验中,二次函数可以 用于描述运动曲线和力学模型。
总结和展望
通过本课程,我们深入了解了二次函数的图像和性质,掌握了解析和图像求 解的方法,并应用于实际领域。希望你喜欢这次学习!继续思考和探索,创 造性地应用二次函数。
1
平移
平移变换可通过改变顶点来实现,横向平移表示为f(x ± h),纵向平移表示为f(x) ± k。
2
缩放
缩放变换可通过改变a的值来实现,a > 1时函数变窄,0 < a < 1时函数变宽。
3
反转
反转变换可通过改变a的符号来实现,a > 0时函数朝上,a < 0时函数朝下。
二次函数的导数和凹凸性质
二次函数的图像和性质
欢迎来到二次函数的图像和性质课程!通过本课程,您将学习二次函数的定 义和表达形式,并探索其图像的性质和变换。让我们开始吧!
二次函数的顶点形式是f(x) = a(x - h)^2 + k,其中(h, k)为顶点坐标。
二次函数图像的性质
对称轴
二次函数的对称轴是x = -最大值。
开口方向
二次函数开口向上当且仅当a > 0,开口向下当且仅当a < 0。
二次函数的变换
导数
二次函数的导数是一条直线,表示了函数的变化率。
凹性质
二次函数的凹性质取决于a的值,a > 0时函数向上凹,a < 0时函数向下凹。
凸性质
二次函数的凸性质取决于a的值,a > 0时函数向上凸,a < 0时函数向下凸。
二次函数的非负和非正性质
1 非负性质
2 非正性质
当a > 0时,二次函数的图像位于x轴以上。
建筑
物理
二次函数的图像和性质可应用 于建筑设计,优化结构和形状。
P物理实验中,二次函数可以 用于描述运动曲线和力学模型。
总结和展望
通过本课程,我们深入了解了二次函数的图像和性质,掌握了解析和图像求 解的方法,并应用于实际领域。希望你喜欢这次学习!继续思考和探索,创 造性地应用二次函数。
1
平移
平移变换可通过改变顶点来实现,横向平移表示为f(x ± h),纵向平移表示为f(x) ± k。
2
缩放
缩放变换可通过改变a的值来实现,a > 1时函数变窄,0 < a < 1时函数变宽。
3
反转
反转变换可通过改变a的符号来实现,a > 0时函数朝上,a < 0时函数朝下。
二次函数的导数和凹凸性质
二次函数的图像和性质
欢迎来到二次函数的图像和性质课程!通过本课程,您将学习二次函数的定 义和表达形式,并探索其图像的性质和变换。让我们开始吧!
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课堂互动讲练
t2-2t-7,t<1,
从而 g(t)=-8,1≤t≤2, t2-4t-4,t>2.
(2)g(t)的图象如图所示二次函数区间最 值主要有三种类型:轴定区间定,轴 定区间动和轴动区间定.
一般来说,讨论二次函数在闭区 间上的最值,主要是看区间是落在二 次函数的哪一个单调区间上,从而应 用单调性求最值.
课堂互动讲练
1.已知三个点坐标时,宜用一 般式.
2.已知抛物线的顶点坐标与对 称轴有关或与最大(小)值有关时,常 使用顶点式.
3.若已知抛物线与x轴有两个交 点,且横轴坐标已知时,选用两根式 求f(x)更方便.
课堂互动讲练
例1 已知f(x)是二次函数,且
f(0)=0,f(x+1)=f(x)+x+1,求f(x)的解析 式.
基础知识梳理
2.二次函数的图象及其性质
基础知识梳理
基础知识梳理
基础知识梳理
二次函数可以为奇函数吗? 【思考·提示】 不会为奇 函数.
三基能力强化
1.已知函数f(x)=4x2-mx+5在
区间[-2,+∞)上是增函数,则f(1)的
范围是( )
A.f(1)≥25
B.f(1)=25
C.f(1)≤25
D.f(1)>25
答案:A
三基能力强化
2.若函数f(x)=ax2+bx+c满足 f(4)=f(1),那么( )
A.f(2)>f(3) B.f(3)>f(2) C.f(3)=f(2) D.f(3)与f(2)的大小关系不确定 答案:C
三基能力强化
3.已知函数y=x2-2x+3在闭区
间[0,m]上有最大值3,最小值2,则
f(n)=3n,
-12n2-2n=0,②
10 分
由①知m=0或m=-4, 由②知n=0或n=-4.
又∵m<n≤16,
课堂互动讲练
∴取m=-4,n=0. 即存在实数m=-4,n=0使f(x) 的定义域为[-4,0],值域为[-12,0].
12分 【名师点评】 解决本题的关键 是确定n的范围,从而把定义域[m, n]“放”在增区间内,问题便可解决.
第4课时 二次函数
基础知识梳理
1.二次函数的解析式有三种常用表 达形式
(1)一般式:f(x)= ax2+bx+c(a≠0) ; (2)顶点式:f(x)=a(x-h)2+k(a≠0), (h,k)是顶点; (3)标根式(或因式分解式):f(x)=a(x -x1)(x-x2)(a≠0);其中x1,x2分别是f(x) =0的两实根.
(2)当0≤a≤1时,f(x)max=a2-a+1, ∴a2-a+1=2,∴a2-a-1=0, ∴a=1±2 5(舍). (3)当a>1时,f(x)max=f(1)=a, ∴a=2. 综上可知a=-1或a=2.
课堂互动讲练
考点三 二次函数的综合问题
二次函数常和二次方程、二次 不等式结合在一起.
三个“二次”以二次函数为核 心,通过二次函数的图象贯穿为一 体,因此,解题时通过画二次函数 的图象来探索解题思路是非常行之 有效的方法.
课堂互动讲练
【思路点拨】 (1)待定系数法.(2) 二次函数的单调性.
【解】 (1)依题意,方程f(x)=ax2 +bx=x有等根,
则有Δ=(b-1)2=0,∴b=1. 2分 又f(-x+5)=f(x-3), 故f(x)的图象关于直线x=1对称, ∴-2ba=1,解得 a=-12,
∴f(x)=-21x2+x. 5 分
课堂互动讲练
互动探究
若题目变为:已知函数f(x)=-x2+ 2ax+1-a在x∈[0,1]时有最大值2,求a的 值.
解:函数f(x)=-x2+2ax+1-a =-(x-a)2+a2-a+1 对称轴方程为x=a. (1)当a<0时,f(x)max=f(0)=1-a, ∴1-a=2,∴a=-1.
课堂互动讲练
课堂互动讲练
(2)∵f(x)=-21x2+x=-21(x-1)2+12≤21, ∴一定有 3n≤21,即 n≤16. 6 分 而抛物线 f(x)=-12x2+x 的对称轴为 x=1, ∴当 n≤16时,f(x)在[m,n]上是单调递增函 数. 8 分
课堂互动讲练
假设存在 m,n 满足要求,则有
f(m)=3m, -12m2-2m=0,①
课堂互动讲练
考点二 二次函数的最值
求二次函数的最值必须认清定 义域区间与对称轴的相对位置以及 抛物线的开口方向(即二次函数中 二次项系数的正负),然后借助于 二次函数的图象或性质求解.因 此,定义域、对称轴及二次项系数 是求二次函数的最值的三要素.
课堂互动讲练
例2 函数f(x)=x2-4x-4在闭区间 [t,t+1](t∈R)上的最小值记为g(t).
m的取值范围是( )
A.[1,+∞) B.[0,2]
C.[1,2]
D.(-∞,2]
答案:C
三基能力强化
4.抛物线y=8x2-(m-1)x+m-7 的顶点在x轴上,则m=_______. 答案:9或25
课堂互动讲练
考点一 求二次函数的解析式
利用已知条件求二次函数解析 式,常用的方法是待定系数法,但 可根据不同的条件选用适当形式求 f(x)解析式.
(1)试写出g(t)的函数表达式; (2)作g(t)的图象并写出g(t)的最 小值.
【思路点拨】 二次函数的对 称轴x=2,分情况讨论x=2是否在 区间[t,t+1]内.
课堂互动讲练
【解】 (1)f(x)=x2-4x-4 =(x-2)2-8. 当t>2时,f(x)在[t,t+1]上是增 函数, ∴g(t)=f(t)=t2-4t-4; 当t≤2≤t+1,即1≤t≤2时, g(t)=f(2)=-8; 当t+1<2,即t<1时,f(x)在[t,t +1]上是减函数, ∴g(t)=f(t+1)=t2-2t-7.
课堂互动讲练
对于通过换元可转化为二次函数 的问题,要注意中间变元的取值范 围,它是转化后二次函数的定义域.
课堂互动讲练
例3 (解题示范)(本题满分12分) 已知二次函数f(x)=ax2+bx(a,b
为常数,且a≠0)满足条件:f(-x+5) =f(x-3),且方程f(x)=x有等根.
(1)求f(x)的解析式; (2)是否存在实数m,n(m<n), 使f(x)的定义域和值域分别为[m,n]和 [3m,3n]?如果存在,求出m,n的 值;如果不存在,说明理由.
