专业标准曲线要素等计算公式表格············ ······
excel 制作标准曲线

excel 制作标准曲线在实验室的科研工作中,我们经常需要制作标准曲线来对实验数据进行分析和比较。
而在实验数据的处理中,Excel是一个非常常用的工具,它可以帮助我们快速、准确地制作标准曲线。
下面,我将向大家介绍如何在Excel中制作标准曲线。
首先,我们需要准备实验数据。
假设我们已经有了一组标准溶液的浓度和对应的吸光度数据。
接下来,我们打开Excel,将这些数据输入到Excel的工作表中。
在工作表中,我们可以将浓度数据放在一列,将吸光度数据放在另一列,以便于后续的操作。
然后,我们需要在Excel中绘制散点图。
选中浓度和吸光度的数据,点击“插入”菜单中的“散点图”按钮,选择合适的散点图样式。
Excel会自动根据我们的数据绘制出散点图,我们可以根据需要对图表进行调整,比如添加数据标签、修改坐标轴的刻度等。
接着,我们需要在散点图上添加趋势线。
选中散点图,点击“布局”菜单中的“趋势线”按钮,选择合适的趋势线类型。
Excel会自动在散点图上添加趋势线,并显示出对应的方程式和相关系数。
通过趋势线,我们可以更直观地观察出标准曲线的走势和相关性。
最后,我们可以对标准曲线进行进一步的分析和处理。
比如,我们可以利用标准曲线对未知样品的浓度进行定量分析,或者对不同条件下的实验数据进行比较和验证。
通过Excel制作的标准曲线,我们可以更加方便地进行实验数据的处理和分析,为科研工作提供更多的支持和便利。
总的来说,利用Excel制作标准曲线是一项非常实用的技能,它可以帮助我们更好地理解和利用实验数据。
希望通过本文的介绍,大家能够掌握这项技能,并在科研工作中加以运用,为实验数据的处理和分析提供更多的可能性和便利。
标准曲线r方计算公式(二)

标准曲线r方计算公式(二)标准曲线R方计算公式R方(R-squared)是一种衡量统计模型拟合优度的常用指标,用于判断模型对数据的解释程度。
在标准曲线分析中,R方是衡量回归线拟合程度的指标。
R方计算公式在标准曲线分析中,R方可以通过以下公式进行计算:R方计算公式R方计算公式其中,SSR表示回归平方和,SST表示总平方和。
回归平方和(SSR)表示数据的观测值与回归线预测值之间的差异的平方和,可以计算为:回归平方和公式回归平方和公式总平方和(SST)表示数据的观测值与数据的均值之间的差异的平方和,可以计算为:总平方和公式总平方和公式例子解释为了更好地理解标准曲线R方计算公式,我们举一个简单的例子。
假设我们有一组标准溶液数据,浓度分别为1、2、3、4、5单位,对应的吸光度分别为、、、、。
我们希望通过回归分析得到一条最佳拟合曲线,并计算R方来评估拟合程度。
首先,我们需要找到最佳拟合曲线。
假设我们通过拟合得到的回归方程为:吸光度 = * 浓度 + 。
接下来,我们可以计算回归平方和(SSR)和总平方和(SST)。
•SSR的计算:–首先,将回归方程中的吸光度代入计算预测值:•预测值1 = * 1 + =•预测值2 = * 2 + =•预测值3 = * 3 + =•预测值4 = * 4 + =•预测值5 = * 5 + =–然后,计算观测值与预测值之间的差异的平方和:•SSR = ( - )² + ( - )² + ( - )² + ( - )² + ( -)² =•SST的计算:–首先,计算吸光度的均值:•均值 = ( + + + + ) / 5 =–然后,计算观测值与均值之间的差异的平方和:•SST = ( - )² + ( - )² + ( - )² + ( - )² + ( -)² =最后,我们可以计算R方: - R方 = 1 - SSR / SST = 1 - / = 通过计算得到的R方为,可以认为拟合程度较低,模型对数据的解释程度较差。
用excel制作标准曲线

用EXCEL制作标准曲线首先,将数据整理好输入Excel,并选取完成的数据区,并点击图表向导,点击图表向导后会运行图表向导,先在图表类型中选“XY散点图”,并选了图表类型的“散点图”(第一个没有连线的)。
点击“下一步”,出现界面。
如是输入是横向列表的就不用更改,如果是纵向列表就改选“列”。
如果发现图不理想,就要仔细察看是否数据区选择有问题,如果有误,可以点击“系列”来更改。
如果是X值错了就点击它文本框右边的小图标,出现界面后,在表上选取正确的数据区域。
然后点击“下一步”出现图表选项界面,相应调整选项,以满足自己想要的效果。
点击“下一步”,一张带标准值的完整散点图就已经完成。
完成了散点图后需要根据数据进行回归分析,计算回归方程,绘制出标准曲线。
其实这很简单,先点击图上的标准值点,然后按右键,点击“添加趋势线”。
由于是线性关系,所以在类型中选“线性”,点击“确定”,标准曲线就回归并画好了。
计算回归后的方程:点击趋势线(也就是我们说的标准曲线)然后按右键,选趋势线格式,在显示公式和显示R平方值(直线相关系数)前点一下,勾上。
再点确定。
这样公式和相关系数都出来了。
用Excel电子表格中的TREND函数,将标准品的吸光度值与对应浓度进行直线拟合,然后由被测物的吸光度值返回线性回归拟合线,查询被测物的浓度,方法简便,可消除视觉差,提高实验的准确性。
方法:打开Excel电子表格,在A1∶Ai区域由低浓度依次输入标准品的浓度值;在B1∶Bi区域输入经比色(或比浊)后得到的标准品相应A值:存盘以备查询结果。
点击工具栏中的函数钮(fx),选取“统计”项中的TREND函数;点击“确定”,即出现TREND函数输入框。
在known-y′s框中输入“A1∶Ai”,在known-x′s中输入“B1∶Bi”;在new-x′s中,输入被测物的A值,其相应的浓度值立即出现在“计算结果”处。
随着计算机的普及,Excel电子表格亦被广泛应用于实验室,因此,用Excel电子表格制作标准曲线及查询测定结果准确、实用。
运用excel做标准曲线
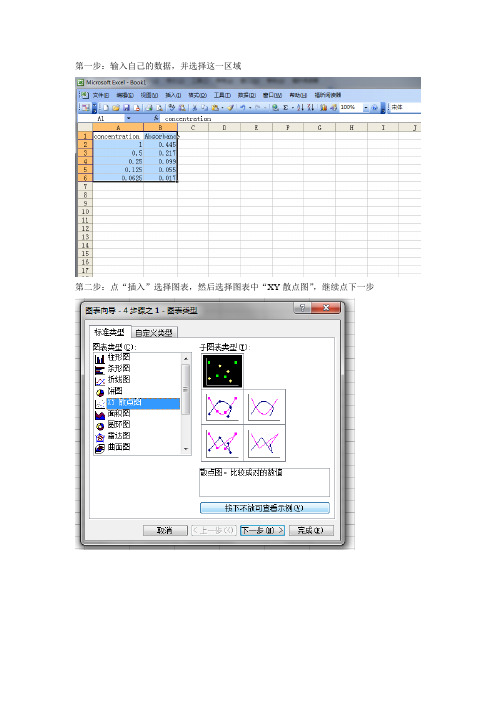
第一步:输入自己的数据,并选择这一区域
第二步:点“插入”选择图表,然后选择图表中“XY散点图”,继续点下一步
再接着点下一步,在右边图表标题、数值X轴等处写上横纵坐标,然后点下一步,出来对话框以后点完成
第三步:在坐标点上右击,选择“添加趋势线”
选择第一个线性,点确定
Hale Waihona Puke 第四步:选择直线右击,选趋势线格式
在“选项”中将显示公示和显示R平方值勾上,点确定
各种曲线计算公式

一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
Excel绘制标准曲线教程

Excel绘制标准曲线全图片教程随着计算机的日益普及,越来越多的检验工作者希望能从一些烦琐的工作中解脱出来,如:绘制标准曲线、绘制质控图、计算检测值等等。
当然借助检验科办公系统理论上是最方便的,但很多单位是没有检验科办公系统的。
其实借助Microsoft的Excel电子表格工具对检验工作也会带来很大的便利。
Excel是Microsoft offices系统的重要组成,它是界于WORD字处理软件与ACCESS数据库软件之间的电子表格工具,功能十分强大,特别适合于日常工作使用。
使用得好,完全比目前所有的检验科办公系统优秀。
现就先介绍一下如何使用Excel绘制标准曲线。
首先,将数据整理好输入Excel,并选取完成的数据区,并点击图表向导,如下图所示。
点击图表向导后会运行图表向导如下图,先在图表类型中选“XY散点图”,并选了图表类型的“散点图”(第一个没有连线的)。
点击“下一步”,出现如下图界面。
如是输入是如本例横向列表的就不用更改,如果是纵向列表就改选“列”。
如果发现图不理想,就要仔细察看是否数据区选择有问题,如果有误,可以点击“系列”来更改,如下图如果是X值错了就点击它文本框右边的小图标,结果如下图:出现上图后,如图在表上选取正确的数据区域。
然后点击“下一步”出现图表选项界面,如下图,上应调整选项,以满足自己想要的效果。
点击“下一步”,现在一张带标准值的完整散点图就已经完成,如下图。
完成了散点图,现在需要根据数据进行回归分析,计算回归方程,绘制出标准曲线。
其实这很简单,先点击图上的标准值点,然后按右键,点击“添加趋势线”。
如下图。
由于本例是线性关系,在类型中选“线性”如下图点击“确定”,标准曲线就回归并画好了。
标准曲线是画好了,可是我们怎么知道回归后的方程是什么样呢?这了简单,点击趋势线(也就是我们说的标准曲线)然后按右键,选趋势线格式,如下图:在显示公式和显示R平方值(直线相关系数)前点一下,勾上。
怎么用excel制作标准曲线

怎么用excel制作标准曲线在实验室中,我们经常需要用到标准曲线来进行定量分析。
而Excel作为一款功能强大的电子表格软件,可以帮助我们制作标准曲线,并且具有直观、方便、灵活的特点。
下面,我将向大家介绍如何用Excel制作标准曲线。
首先,打开Excel软件,创建一个新的工作表。
在工作表中,我们需要输入两列数据,一列是浓度,另一列是对应的吸光度。
这些数据通常是实验室中通过实际实验测得的,或者是根据实验设计的浓度梯度和对应吸光度计算得出的。
接下来,选中我们输入的数据,包括浓度和吸光度两列。
然后点击“插入”选项卡中的“散点图”按钮,选择“散点图”中的“散点图加线”选项,这样就可以得到散点图并连接成线条。
在得到散点图并连接成线条之后,我们需要对图表进行进一步的美化和调整。
首先,添加图表标题和坐标轴标题,使得整个图表更加清晰明了。
其次,调整坐标轴的刻度和范围,确保图表的展示效果更加直观和准确。
在制作标准曲线的过程中,我们还需要对图表进行拟合曲线的操作。
在Excel 中,可以通过添加“趋势线”来实现。
选中散点图,右键点击选择“添加趋势线”,然后选择合适的趋势线类型,比如线性、多项式、对数等,根据实际情况选择最适合的拟合曲线类型。
最后,我们需要对标准曲线进行验证和分析。
可以通过在Excel中输入待测样品的吸光度数据,然后利用拟合曲线的方程进行计算,得出样品的浓度。
这样就可以实现对待测样品浓度的定量分析。
总的来说,用Excel制作标准曲线是一个简单而又实用的方法。
通过上面的步骤,我们可以轻松地创建出清晰准确的标准曲线图表,并且可以对待测样品进行准确的定量分析。
希望以上内容对大家有所帮助,谢谢!。
标准曲线回归方程公式excel

标准曲线回归方程公式excel
标准曲线回归方程是一种常见的统计分析方法,通过对一组数据进行线性回归分析,得出一条最佳拟合直线,进而预测未知数据点的值。
在excel中,可以使用“趋势线”功能进行标准曲线回归分析,具体步骤如下:
1. 将需要分析的数据点插入到excel中,例如在A列输入自变量数据,在B列输入因变量数据。
2. 选中数据点,并点击“插入”选项卡中的“散点图”按钮,将数据点用散点图表示出来。
3. 选中散点图上的任一数据点,并右键点击,选择“添加趋势线”选项。
4. 在弹出的“趋势线”对话框中,选择“线性回归”选项,并勾选“显示方程式”和“显示R值”选项。
5. 点击“确定”按钮,即可在散点图上显示出标准曲线回归方程和相关系数R的值。
标准曲线回归方程公式excel示例如下:
y = 0.5x + 2.5
其中,y表示因变量的值,x表示自变量的值,0.5表示回归系数,2.5表示截距。
需要注意的是,在使用标准曲线回归方程进行预测时,应该对模型进行验证,以确保模型的准确性和可靠性。
同时,还应该注意避免过度拟合和欠拟合的情况。
用Excel绘制标准曲线以及求未知含量的方法

用Excel绘制标准曲线以及求未知含量的方法将数据整理好输入Excel,并选取完成的数据区,并点击图表向导,如下图:点击图表向导后会运行图表向导如下图,先在图表类型中选“XY散点图”,并选了图表类型的“散点图”(第一个没有连线的)。
点击“下一步”,出现如下图界面。
如是输入是如本例横向列表的就不用更改,如果是纵向列表就改选“列”:如果发现图不理想,就要仔细察看是否数据区选择有问题,如果有误,可以点击“系列”来更改,如下图:如果是X值错了就点击它文本框右边的小图标,结果如下图:在表上选取正确的数据区域,点击“下一步”,出现图表选项界面如下图,调整选项,以满足自己想要的效果:点击“下一步”,一张带标准值的完整散点图完成,如下图:现在要根据数据进行回归分析,计算回归方程,绘制出标准曲线:先点击图上的标准值点,然后按右键,点击“添加趋势线”。
如下图:本例是线性关系,在类型中选“线性”,如下图:点击“确定”,标准曲线回归画好:回归后的方程是什么样呢?点击趋势线(也就是标准曲线)然后按右键,选趋势线格式,如下图:在显示公式和显示R平方值(直线相关系数)前点一下,勾上。
再点确定,公式和相关系数都出来了。
如图:由此标准曲线可得出浓度:切换到“选项”标签页,选择“显示公式”,确定。
在图表中出现一个公式,即浓度对吸光度的关系。
在单元格中输入该公式(其中的X值用具体的单元格引用代替),即可根据该公式计算出样品的浓度。
有时候有的项目是成指数增加,散点图如下图:从上图看并不相关,除了最大的一个点外其余的几乎都成了直线。
这不难理解,因为对于10000000而言,10与10000都差不了多少。
因此我们平时常使用半对数坐标纸画图。
对于Excel,先点中Y坐标轴,再按右键,选“坐标轴格式”如下图:将左下方的对数刻度选中,确定。
完整的一个半对数标准曲线就做好了:利用Excel制作标准曲线,如果认真调整参数可以得到不同的效果。
绘图时最好用XY散点图。
excel做标准曲线

excel做标准曲线在科学研究和实验数据分析中,标准曲线是一种非常重要的工具,它可以用于定量分析未知样品中的成分,也可以用于监测实验条件和仪器的准确性。
而在实验数据的处理和分析中,Excel表格是一款非常常用的工具,它提供了丰富的数据处理和图表绘制功能,非常适合用来制作标准曲线。
本文将介绍如何使用Excel来制作标准曲线,希望能对大家有所帮助。
首先,我们需要准备实验数据。
在制作标准曲线之前,我们需要先进行一系列实验,得到一组已知浓度的标准溶液,并测量它们的吸光度或者其他相关的实验数据。
这些数据将会成为我们制作标准曲线的基础,因此实验的准确性和数据的可靠性非常重要。
接下来,我们将利用Excel来处理这些实验数据,并绘制标准曲线。
首先,我们需要将实验数据输入到Excel表格中。
在表格中,通常会有两列数据,一列是已知浓度的标准溶液的浓度值,另一列是对应的实验数据,比如吸光度值。
将这些数据输入到Excel表格中后,我们可以利用Excel的函数和公式来进行数据处理,比如计算吸光度与浓度的比值。
接着,我们可以利用Excel的图表功能来绘制标准曲线。
在Excel中,我们可以选择合适的图表类型,比如散点图或者折线图,然后将已知浓度和对应的实验数据绘制成图表。
在图表中,已知浓度将作为横坐标,实验数据将作为纵坐标,我们可以很直观地看到它们之间的关系,从而得到标准曲线。
在绘制标准曲线之后,我们可以对曲线进行进一步的分析和处理。
比如,我们可以利用Excel的拟合曲线功能来拟合标准曲线,从而得到一个更加精确的数学模型。
这样,我们就可以利用标准曲线来对未知样品进行定量分析,或者对实验数据进行进一步的处理和分析。
总的来说,Excel是一款非常强大的工具,它提供了丰富的数据处理和图表绘制功能,非常适合用来制作标准曲线。
通过本文的介绍,希望大家能够更加熟练地运用Excel来处理实验数据,制作标准曲线,并在科研工作中发挥更大的作用。
EXCEL曲线坐标计算公式

公式解析一.坐标转换X =A +N COSα-E SINαY =B +N SINα+E COSαN=(X-A) COSα±(Y-B)SINαE=(Y-B)COSα±(X-A)SINαA,B为施工坐标系坐标原点α为施工坐标系与北京坐标系X轴的夹角(旋转角)即大地坐标系方位角X,Y为北京坐标值 N,E为施工坐标值二.方位角计算1.直线段方位角: α=tanˉ¹ [(Yb-Ya)/(Xb-Xa)]2.交点转角角度: α=2 tanˉ¹ (T/R)计算结果①为﹢且<360,则用原数;②为﹢且>360,则减去360;③为﹣,则加上180.3.缓和曲线上切线角: α=ƟZH±90°*Lo²/(π*R* Ls)α= Lo/(2ρ)=Lo²/(2 A²)=Lo²/(2R*Ls)ρ—该点的曲率半径4.圆曲线上切线角: α=ƟHY±180°*Lo/(π*R)ƟZH—直缓点方位角, ƟHY—缓圆点方位角,注:以计算方向为准,左偏,取"﹣";右偏,取"﹢"。
左偏,则第一段缓和曲线和圆曲线上取"﹣",第二段缓和曲线上取"﹢" ;右偏,则第一段缓和曲线和圆曲线上取"﹢",第二段缓和曲线上取"﹣" .。
符号说明:A—回旋线参数(A²=R* Ls) Ls—缓和曲线长度R—曲线半径Lo—曲线长度:计算点位到特殊点(ZH、HY、YH、HZ)的长度三.坐标值计算1.直线段坐标计算公式:直线两端点A.B间距离为S;A点坐标为A(Xa, Ya);方位角为αXb= Xa+S*cosαYb= Ya+S*sinα2.缓和曲线及圆曲线坐标计算公式:①缓和曲线坐标计算公式:X=XZH+(Lo-Lo^5/(40*R^2*Ls^2)+Lo^9/(3456*R^4*Ls ^4)-Lo^13/(599040*R^6*Ls^6)+Lo^17/(175472640*R ^8*Ls^8))*cosα-(Lo^3/(6*R*Ls)-Lo^7/(336*R^3*L s^3)+Lo^11/(42240*R^5*Ls^5)-Lo^15/(9676800*R^7 *Ls^7)+Lo^19/(3530096640*R^9*Ls^9))*sinαY=YZH+(Lo-^5/(40*R^2*Ls^2)+Lo^9/(3456*R^4*Ls^4 )-Lo^13/(599040*R^6*Ls^6)+Lo^17/(175472640*R^8 *Ls^8))*sinα+(Lo^3/(6*R*Ls)-Lo^7/(336*R^3*Ls^ 3)+Lo^11/(42240*R^5*Ls^5)-Lo^15/(9676800*R^7*L s^7)+Lo^19/(3530096640*R^9*Ls^9))* cosα符号说明:XZH—直缓点X坐标值 YZH—直缓点Y坐标值 A—回旋线参数(A²=R* Ls)Lo—计算点位到特殊点的长度 Ls—缓和曲线长度R—曲线半径α—方位角注:式中,紫色部分为缓和曲线任意点的坐标增量(支距坐标)。
用Excel绘制实用标准曲线以及求未知含量地方法
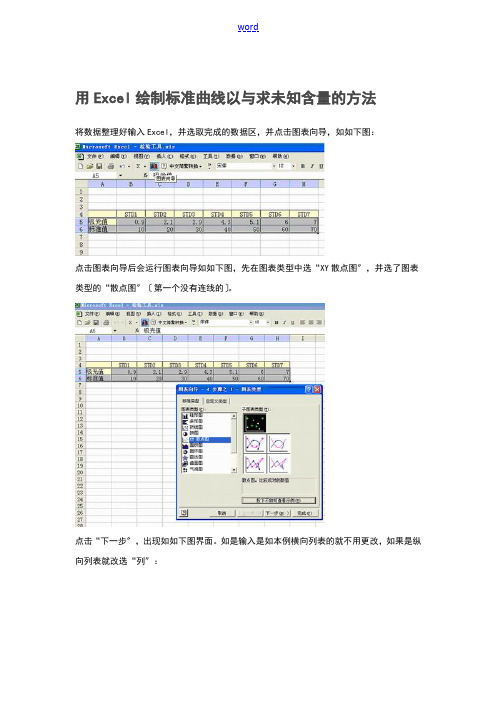
用Excel绘制标准曲线以与求未知含量的方法将数据整理好输入Excel,并选取完成的数据区,并点击图表向导,如如下图:点击图表向导后会运行图表向导如如下图,先在图表类型中选“XY散点图〞,并选了图表类型的“散点图〞〔第一个没有连线的〕。
点击“下一步〞,出现如如下图界面。
如是输入是如本例横向列表的就不用更改,如果是纵向列表就改选“列〞:如果发现图不理想,就要仔细观察是否数据区选择有问题,如果有误,可以点击“系列〞来更改,如如下图:如果是X值错了就点击它文本框右边的小图标,结果如如下图:在表上选取正确的数据区域,点击“下一步〞,出现图表选项界面如如下图,调整选项,以满足自己想要的效果:点击“下一步〞,一X带标准值的完整散点图完成,如如下图:现在要根据数据进展回归分析,计算回归方程,绘制出标准曲线:先点击图上的标准值点,然后按右键,点击“添加趋势线〞。
如如下图:本例是线性关系,在类型中选“线性〞,如如下图:点击“确定〞,标准曲线回归画好:回归后的方程是什么样呢?点击趋势线〔也就是标准曲线〕然后按右键,选趋势线格式,如如下图:在显示公式和显示R平方值〔直线相关系数〕前点一下,勾上。
再点确定,公式和相关系数都出来了。
如图:由此标准曲线可得出浓度:切换到“选项〞标签页,选择“显示公式〞,确定。
在图表中出现一个公式,即浓度对吸光度的关系。
在单元格中输入该公式〔其中的X值用具体的单元格引用代替〕,即可根据该公式计算出样品的浓度。
有时候有的项目是成指数增加,散点图如如下图:从上图看并不相关,除了最大的一个点外其余的几乎都成了直线。
这不难理解,因为对于10000000而言,10与10000都差不了多少。
因此我们平时常使用半对数坐标纸画图。
对于Excel,先点中Y坐标轴,再按右键,选“坐标轴格式〞如如下图:将左下方的对数刻度选中,确定。
完整的一个半对数标准曲线就做好了:利用Excel制作标准曲线,如果认真调整参数可以得到不同的效果。
曲线要素表中的校正值

曲线要素表中的校正值
校正值就是切曲差,即2倍的切线长减去曲线长。
前一个交点桩号减去后个交点桩号不等于两交点之间的直线长度。
设D为切曲差,L为曲线长度,T为切线长:
则D=2T-L,前一个交点桩号=前一个ZY(ZH)桩号+T,前一个YZ(HZ)桩号=前一个ZY(ZH)桩号+L,把D=2T-L带入前式,前一个YZ(HZ)桩号=前一个ZY(ZH)桩号+(D-L)/2
可以看出,前一个YZ(HZ)桩号不等于前一个交点桩号+T。
现在我们分析后个交点:
后个交点桩号=前一个YZ(HZ)桩号+中间直线长(如果中间有直线的话)+后T。
那么
后个交点桩号-前一个交点桩号=前一个YZ(HZ)桩号+中间直线长(如果中间有直线的话)+后T-(前一个ZY(ZH)桩号+前T)=中间直线长(如果中间有直线的话)+后T+L-前T,
由D=2T-L得L=2T-D,带入上式,得:
后个交点桩号-前一个交点桩号=中间直线长(如果中间有直线的话)+后T+前T-D。
测量中切曲差有什么用途?假如切曲差是D,切线长为T,圆曲线的弧长为L,那么D=2T-L,可是为什么切线交点JD=QZ+D/2?QZ是圆曲线中点,即曲中点!
D/2=(2T-L)/2=T-L/2 这就是切线长和半个曲线长的差
JD是直圆点到交点,也就是切线长
QZ是直圆点到曲中,也就是半个曲线长
这个公式不是纯为了推导各个要素之间的关系,主要是说明切线长和半个曲线长的差之后,在实际工作中,放样时一般是先放出JD点(过渡点而已),利用这个公式就可以得到QZ点,那是实际修路时要用的.。
标准曲线数据表
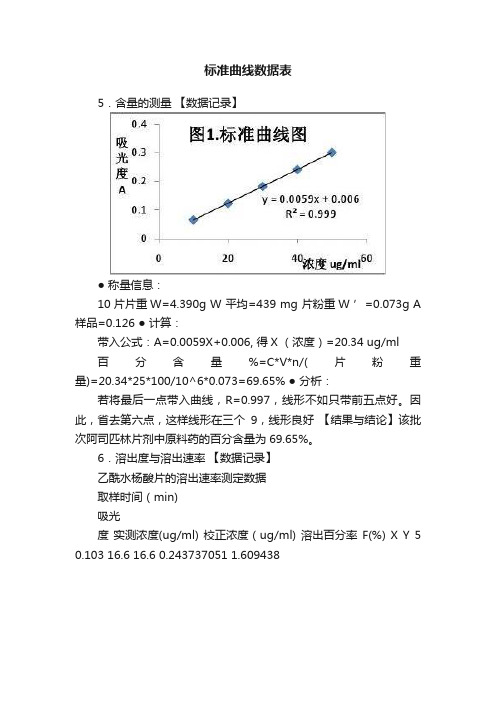
标准曲线数据表5.含量的测量【数据记录】● 称量信息:10片片重W=4.390g W 平均=439 mg 片粉重W ’=0.073g A 样品=0.126 ● 计算:带入公式:A=0.0059X+0.006, 得X (浓度)=20.34 ug/ml百分含量%=C*V*n/(片粉重量)=20.34*25*100/10^6*0.073=69.65% ● 分析:若将最后一点带入曲线,R=0.997,线形不如只带前五点好。
因此,省去第六点,这样线形在三个9,线形良好【结果与结论】该批次阿司匹林片剂中原料药的百分含量为69.65%。
6.溶出度与溶出速率【数据记录】乙酰水杨酸片的溶出速率测定数据取样时间(min)吸光度实测浓度(ug/ml) 校正浓度(ug/ml) 溶出百分率F(%) X Y 5 0.103 16.6 16.6 0.243737051 1.609438-1.27523 10 0.18 32 32.083 0.471073241 2.302585 -0.45113 15 0.244 44.8 45.043 0.661364336 2.70805 0.079578 25 0.339 63.8 64.267 0.943629461 3.218876 1.056334 35 0.38 72 72.786 1.068713553 3.555348 #NUM! 45 0.418 79.6 80.746 1.185589874 3.806662 #NUM! (1)F=50%, 带入线形公式计算得,t=10.04 min , Lnt=2.31——T50(2)F=63.2%,带入线形公式计算得,t=12.94 min ,Lnt=2.56——Td(3)m 值计算:过M 点(1,0)的直线为, y=1.426x-1.426, 所以,m=-1.426(4)溶出度测定: F(45min)= 118.6% > 70%,溶出百分率复合药典规定【结果】T50为2.31,时间10.04min ,Td 为2.56,时间为12.94min, m=-1.426, F(45min)为118.6%>70% 【结论】该片剂的溶出度符合药典规定,溶出速率符合Welbull 方程,溶出较快,较均匀。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
桩号
K718+210.000 K718+210.000 K718+210.000 K718+210.000 K718+563.833 K144+480.000 K144+481.006 K144+500.000 K144+480.300 K228+790.000 K144+539.700 K228+980.000 K229+043.000 K229+060.000 K229+080.000 K229+100.000 K229+107.000 K229+120.000 K229+130.000 K229+140.000 K229+160.000 K229+187.290 K229+280.000 K229+435.000 K229+575.230 K229+575.230 K229+592.230 K229+592.230 K229+637.770 K229+637.770 K229+654.770 K229+654.770 K229+680.000 K229+698.000 K229+720.000
3098727.564
526352.374
第二计算边缓和段 3082393.235
518297.803
K719+006.188 ################ ####################
################ ####################
################ ####################
519082.168 519082.168 519082.168 519082.168 519082.168 519082.168 519082.168
20.000 24.000
24.000 15.000 15.000 23.000
K718+210.000 K718+210.000 K718+210.000 K718+210.000 K718+210.000 K718+210.000 K718+210.000
左边桩距
15.000
20.000 2.850 22.000 25.000 20.000 24.000 29.000 29.000
23.000
27.000 14.000 19.000
23.000
24.000 23.000 20.000 23.000 20.000 8.000 8.000 20.000 20.000 23.000 22.000 14.000 13.000
右边桩距
23.000 19.000 22.000
2.850
10.150 10.150 23.000 10.150
25.000 22.000 22.000 26.000
19.000
26.000
29.000 28.000 28.000 25.000 27.000 25.000 13.000 13.000 25.000 25.000 28.000 27.000 31.000 18.000
X 3082514.444 3082529.157 3082529.157 3082529.157 3082442.953 3098859.624 3098868.449 3098853.541 3098868.047 3085003.480 3098821.160 3084875.314 3084856.847 3084828.286 3084833.136 3084820.359 3084795.095 3084796.815 3084786.585 3084794.890 3084764.409 3084764.923 3084687.907 3084592.396 3084509.158 3084506.767 3084498.877 3084508.449 3084481.041 3084471.439 3084461.235 3084458.832 3084444.525 3084440.203 3084427.911
注:红块内的数据为需要输入的数,D、E、F栏内的数据为需要输入的数,其余均为自动计算值.在计算新的里程或加桩里程坐标时,一定要先
2416.9530
交点坐标Y 518517.9709
曲线半径R 11000
曲线偏角α 4.439666667
4°
26′
22.8″
3082529.157
519082.168
K718+210.000
18.000 3082529.157 519082.168
X 3082529.157 3082529.157 3082529.157 3082529.157 圆曲线 3082462.639 K718+563.833 3098858.181 3098857.314 3098840.924 3098857.923 3085021.519 3098806.615 3084897.438 3084856.847 3084845.941 3084833.136 3084820.359 3084815.894 3084807.610 3084801.246 3084794.890 3084782.197 3084764.923 3084706.633 3084610.543 3084525.093 3084525.093 3084514.831 3084514.831 3084487.442 3084487.442 3084477.257 3084477.257 3084462.180 3084451.452 3084438.371
1003147.827
3167617.591
1232235.284
3167617.591
1232235.284
3167617.591
1232235.284
左边桩距
14.000
16.000 22.000
23.000 22.000
13.000 13.000 18.000 18.000 20.000 20.000 8.000 8.000 8.000
0.000 3178088.903 999616.825
第一计算边缓和段 3082540.105
519137.258
20.900
K718+153.833
24.000 3082519.607 519141.334
K718+153.833 3082529.157 3082529.157
519082.168 519082.168
K716+100.000 3082940.689
521151.646
0.000
K716+100.000
0.000 3082940.689 521151.646
3082940.689
521151.646
0.000
K716+100.000
0.000 3082940.689 521151.646
3082940.689
8.000 8.000 8.000 8.000
桩号
K229+800.000 K229+820.000 K229+860.000 K229+880.000 K229+900.000 K229+944.000 K229+950.000 K144+630.857 K719+006.188 K144+634.411 K144+654.331 K230+135.000 K230+157.380 K230+157.380 K230+174.380 K230+174.380 K230+214.000 K149+340.000 K719+416.188 K149+400.000 K1493+500.000 K144+770.743 K230+714.000
圆缓点桩号YH K719+006.188
缓直点桩号HZ K719+416.188
第二计算方位角A2 263.1924806
中桩坐标
X
Y
左边桩距
桩号
右边桩距
左边桩坐标
X
Y
第一计算边直线段 3082954.551
521151.646
0.000
K716+100.000
0.000 3082954.551 521151.646
25.000 26.000 28.000 27.000 20.000
3082509.539 3082505.616 3082529.157 3082505.616 3082514.444 3082514.444 3082506.597
519086.062 519086.841 519082.168 519086.841 519085.088 519085.088 519086.646
0.000 20.000
K718+210.000 K718+210.000
0.000 25.000
3082529.157 3082509.539
519082.168 519086.062
3082529.157 3082529.157 3082529.157 3082529.157 3082529.157 3082529.157 3082529.157
X
Y
3084391.106
523257.351
3084379.363
