SPSS二项Logistic回归ppt课件
《SPSS回归分析》ppt课件

.
-3.666
.002
从表中可知因变量与自变量的三次回归模型为: y=-166.430+0.029x-5.364E-7x2+5.022E-12x3
9.2 曲线估计
➢拟合效果图
从图形上看出其拟合效果非常好。
8.3 曲线估计
说明:
曲线估计是一个自变量与因变量的非线性回归过程,但 只能处理比较简单的模型。如果有多个自变量与因变量呈非 线性关系时,就需要用其他非线性模型对因变量进行拟合, SPSS 19中提供了“非线性”过程,由于涉及的模型很多,且 非线性回归分析中参数的估计通常是通过迭代方法获得的, 而且对初始值的设置也有较高的要求,如果初始值选择不合 适,即使指定的模型函数非常准确,也会导致迭代过程不收 敛,或者只得到一个局部最优值而不能得到整体最优值。
8.1 回归分析概述
(3)回归分析的一般步骤
第1步 确定回归方程中的因变量和自变量。 第2步 确定回归模型。 第3步 建立回归方程。 第4步 对回归方程进行各种检验。
➢拟合优度检验 ➢回归方程的显著性检验 ➢回归系数的显著性检验
第5步 利用回归方程进行预测。
主要内容
8.1 回归分析概述 8.2 线性回归分析 8.3 曲线估计 8.4 二元Logistic回归分析
8.3 曲线估计
(2) 统计原理
在曲线估计中,有很多的数学模型,选用哪一种形式的回 归方程才能最好地表示出一种曲线的关系往往不是一个简单的 问题,可以用数学方程来表示的各种曲线的数目几乎是没有限 量的。在可能的方程之间,以吻合度而论,也许存在着许多吻 合得同样好的曲线方程。因此,在对曲线的形式的选择上,对 采取什么形式需要有一定的理论,这些理论是由问题本质决定 的。
SPSS实验8-二项Logistic回归分析
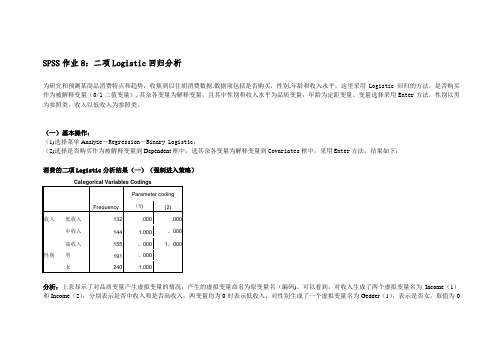
SPSS作业8:二项Logistic回归分析为研究和预测某商品消费特点和趋势,收集到以往胡消费数据.数据项包括是否购买,性别,年龄和收入水平。
这里采用Logistic回归的方法,是否购买作为被解释变量(0/1二值变量),其余各变量为解释变量,且其中性别和收入水平为品质变量,年龄为定距变量。
变量选择采用Enter方法,性别以男为参照类,收入以低收入为参照类。
(一)基本操作:(1)选择菜单Analyz e-Regression-Binary Logistic;(2)选择是否购买作为被解释变量到Dependent框中,选其余各变量为解释变量到Covariates框中,采用Enter方法,结果如下:消费的二项Logistic分析结果(一)(强制进入策略)Categorical Variables CodingsFrequency Parameter coding (1) (2)收入低收入132 .000 .000中收入144 1.000 。
000高收入155 。
000 1。
000性别男191 。
000女240 1.000分析:上表显示了对品质变量产生虚拟变量的情况,产生的虚拟变量命名为原变量名(编码)。
可以看到,对收入生成了两个虚拟变量名为Income(1)和Income(2),分别表示是否中收入和是否高收入,两变量均为0时表示低收入;对性别生成了一个虚拟变量名为Gedder(1),表示是否女,取值为0时表示为男。
消费的二项Logistic 分析结果(二)(强制进入策略)Block 0: Beginning BlockClassification Table a,bObserved Predicted是否购买 Percentage Correct不购买购买Step 0是否购买不购买 269 0 100。
购买162。
0 Overall Percentage62。
4a 。
Constant is included in the model 。
spss中的回归分析PPT课件
6、Statistics(统计)对话框 单击“Statistics”按钮,进入统计对话框如图:
第19页/共134页
Estimates(默认选择项):回归系数的估计值(B)及其标准误(Std.Error)、 常数(Constant);标准化回归系数(Beta);B的t值及其双尾显著性水平(Sig.)。
第5页/共134页
H0:1 0, 2 0,, k 0
Fα
第6页/共134页
(3)回归系数的显著性检验(t检验) 所谓回归系数的显著性检验,就是根据样 本估计的结果对总体回归系数的有关假设进行 检验。 之所以对回归系数进行显著性检验,是因 为回归方程的显著性检验只能检验所有回归系 数是否同时与零有显著性差异,它不能保证回 归方程中不包含不能较好解释说明因变量变化 的自变量。因此,可以通过回归系数显著性检 验对每个回归系数进行考察。
4、 Selection variable(选择变量):可从源变量栏中 选择一个变量,单击Rule后,通过该变量大于、小于或等于某 一数值,选择进入回归分析的观察单位。
5、Case Labels(个案标签):在左侧的源变量框中选择 一变量作为标签变量进入 Case Labels框中。
第18页/共134页
Model fit(默认选择项):列出进入或从模型中剔除的变量;显示下列拟合 优度统计量:复相关系数(R)、判定系数(R2)、调整 R2(Adjusted R Square)、 估计值的标准误以及方差分析表。
Confidence intervals:回归系数 B的 95%可信区间(95%Confidence interval for B)。
第7页/共134页
回归参数显著性检验的基本步骤。 ① 提出假设
同济医学院SPSSSPSSLogistic回归PPT课件

料或分类资料
21
SPSS哑变量设置
Indicator Simple
参照分类为0,其余为1, 即各分类与参照分类比较
Difference 除第一类分类外,各分类与
Repeated
其之前平均分类效应比较
22
2020/1/10
23
SPSS哑变量设置
Helmert
与Difference相反,各水平与其之后水平的平 均效应比较
Deviation:
除参照分类外,各水平与分类的总效应比较
Polynomial
正交多项式设置
自动设置哑变量是有缺点的
等级变量不合适
24
哑变量设置应注意的问题
参照水平最好要有实际意义,不推荐使 用其他作为参照;
14
例1
研究急性心肌梗塞(AMI)患病与饮酒 的关系, 采用横断面调查。
饮酒 不饮酒 合计
(X=1) (X=0)
患病(y=1) 55
74
129
未患病(y=0) 104663 212555 317218
合计
104718 212629 317347
15
SPSS基本操作
16
SPSS基本操作
17
SPSS基本操作
所以 -< ln(Odds) <+
对ln(Odds)引入类似多重线性回归 的表达式
ln(Odds)
ln( P 1 P
)
0
1x1
m xm
10
Logistic回归模型
记:log it(P) ln( P ) 1 P
[课件]SPSS回归分析过程详解()PPT
![[课件]SPSS回归分析过程详解()PPT](https://img.taocdn.com/s3/m/9975250eed630b1c59eeb5c4.png)
回归分析的概念
寻求有关联(相关)的变量之间的关系 主要内容:
从一组样本数据出发,确定这些变量间的定 量关系式 对这些关系式的可信度进行各种统计检验 从影响某一变量的诸多变量中,判断哪些变 量的影响显著,哪些不显著 利用求得的关系式进行预测和控制
回归分析的模型
按是否线性分:线性回归模型和非线性回归模型 按自变量个数分:简单的一元回归,多元回归 基本的步骤:利用SPSS得到模型关系式,是否 是我们所要的,要看回归方程的显著性检验(F 检验)和回归系数b的显著性检验(T检验),还要 看拟合程度R2 (相关系数的平方,一元回归用R Square,多元回归用Adjusted R Square)
我们只讲前面3个简单的(一般教科书的讲法)
10.1 线性回归(Liner)
一元线性回归方程: y=a+bx
a称为截距 b为回归直线的斜率 用R2判定系数判定一个线性回归直线的拟合程度:用来说明用自变 量解释因变量变异的程度(所占比例)
b0为常数项 b1、b2、…、bn称为y对应于x1、x2、…、xn的偏回归系数 用Adjusted R2调整判定系数判定一个多元线性回归方程的拟合程度: 用来说明用自变量解释因变量变异的程度(所占比例)
逐步回归方法的基本思想
对全部的自变量x1,x2,...,xp,按它们对Y贡献的大小进 行比较,并通过F检验法,选择偏回归平方和显著的变 量进入回归方程,每一步只引入一个变量,同时建立 一个偏回归方程。当一个变量被引入后,对原已引入 回归方程的变量,逐个检验他们的偏回归平方和。如 果由于引入新的变量而使得已进入方程的变量变为不 显著时,则及时从偏回归方程中剔除。在引入了两个 自变量以后,便开始考虑是否有需要剔除的变量。只 有当回归方程中的所有自变量对Y都有显著影响而不需 要剔除时,在考虑从未选入方程的自变量中,挑选对Y 有显著影响的新的变量进入方程。不论引入还是剔除 一个变量都称为一步。不断重复这一过程,直至无法 剔除已引入的变量,也无法再引入新的自变量时,逐 步回归过程结束。
logistic回归分析(2)幻灯片PPT

例1(成组病例对照研究) 某单位研究胸膜间皮瘤与接触石 棉的关系,资料见下表。试对其进展分析。
组别 间皮瘤病例
对照 合计
表 1 胸膜间皮瘤与接触石棉的关系
以往接触过石棉
未接触过石棉
40
36
9
67
49
103
合计 76 76 152
方法1:卡方检验 方法2:拟合logistic回归模型,即
自变量〔各种影响因素〕 :可以是分类变量,也可 以是连续型变量。
二分类资料的分析
非条件logistic模型:成组病例对照研究资料
条件logistic模型:配比病例对照研究资料
非条件logistic回归模型
l( o p ) 0 + g 1 X 1 + i 2 X = 2 t k X k
------------------------------------------------------------------------------
似然比2 =30.67,P=0.0000,因此可以认为模型有意义。
li o ( p t ) g eo x s p 0 . 6 u 2 r . 1e e 1 1 o x 1 2 s p 8 ur
Number of obs = 152 LR chi2(1) = 30.67 Prob > chi2 = 0.0000
Pseudo R2 = 0.1455
-----------------------------------------------------------------------------case | Coef. Std. Err. z P>|z| [95% Conf. Interval]
SPSS课件logistic回归分析

Logistic回归分析
Log.sav
关于考试
考试时间:下周的上课时间
每人准备一张软盘,在软盘上注明姓名、学 号
Logistic回归分析
数据背景(data13-02) 北京医科大学附属人民医院内分泌科卢纹凯教授课题。 颈总动脉中层厚度imt>0.8mm或有斑块定义为动脉硬 化,因变量type值为1;非硬化imt<0.8mm且无斑块, 因变量type值为0。糖尿病患者123例数据。研究哪 些指标可以判断糖尿病患者是否动脉硬化。自变量 AGE年龄、ALB尿白蛋白、BMI体重指数、ISI胰岛素 敏感指数、SBP收缩压、TG甘油三脂、CHO胆固醇、 DURA糖尿病程。其中尿白蛋白、甘油三脂、胆固醇 三项生化指标在回归估计过程中均使用他们的对数变 量:ALBLN、TGLN、CHOLN。
级分组资料或是计量资料,此时,可以使用logistic
回归来分析பைடு நூலகம்变量(二值变量)与自变量的关系。
三、 Logistic回归分析
Categorical 多分类变量的比较
Save 功能按钮
Option 功能按钮
Logistic回归分析
为研究急性肾衰(AFR)患者死亡的危险因素,经回顾性
调查分析,获得某医院1999~2000年中所有发生AFR的
422名患者的临床资料见数据文件logistic.sav。本资料共涉 及29个变量,分别是:sex, age, 社会支持,慢性病,手术,
肿瘤,糖尿病,动脉硬化,器官移植,cr(血肌酐),hg
(血红蛋白),肾毒性,少尿,lbp,黄疸,昏迷,辅助呼 吸,心衰,肝衰,出血,呼衰,器官衰竭,胰腺炎,dic, 败血症,感染,hbp,透析方式,死亡。其中器官衰竭、和 透析方式为多分类变量,分别有6个和4个水平,定量变量 有age,cr,hg;其余为二分类变量。
《logistic回归分析》PPT课件

第一节 非条件logistic回归
一、logistic 回归模型:
设因变量 Y 是一个二分类变量,其取值为 Y =1 和Y =0。 影响 Y 取值的 m 个自变量分别为 X1, X 2 ,, X m 。在 m 个自变量(即暴露因素)作用下阳性结果发生的条件
概率为 P P(Y 1 X1, X 2 ,, X m ) ,则 logistic 回归模
表 1 调查数据
y
x
1
0
1
a
b
0
c
d
合计 a+c b+d
表 2 对应概率
y
x
1
0
1 0 合计
p1 1- p1
1
p2 1- p2
1
9
表 1 调查数据
y
x
1
0
1
a
b
0
c
d
合计 a+c b+d
表 2 对应概率
y
x
1
0
1 0 合计
p1 1- p1
1
p2 1- p2
1
Logistic
模型为:
p1
p( y
1|
(2)多分类资料Logistic回归: 因变量为多项分类的资料,可 用多项分类Logistic回归模型或有序分类Logistic回归模型进 行分析。
2
非条件Logistic回归分析 条件Logistic回归分析 无序分类反应变量Logistic回归分析 有序多分类反应变量Logistic回归分析 Logistic回归分析应用及注意事项
21
对所拟合模型的假设检验:
概率p值均小 于0.05,说明 方程有意义。
如何用SPSS做logistic回归分析解读课件.doc

类)的情况,当Y具有两种以上的取值时,就要用多项logistic回归(M
utinomialLogisticRegression)分析了。这种分析不仅可以用于医疗领
域,也可以用于社会学、经济学、农业研究等多个领域。如不同阶段(初
一、初二、初三)学生视力下降程度,不同龋齿情况(轻度、中度、重
ECAS和NCAS三种,但现在我们仅考虑性别和年龄与ICAS的关系,
因此将分组数据ICAS、ECAS和NCAS转化为1、0分类,是ICAS赋
值为1,否赋值为0。年龄为数值变量,可直接输入到spss中,而性别
需要转化为(1、0)分类变量输入到spss当中,假设男性为1,女性为
0,但在后续分析中系统会将1,0置换(下面还会介绍),因此为方便
(Covariates)框中,在协变量下方的“方法(Method)”一栏中,共有
七个选项。采用第一种方法,即系统默认的强迫回归方法(进入“Enter)”。
接下来我们将对分类(Categorical),保存(Save),选项(Options)
按照如图1-4、1-5、1-6中所示进行设置。在“分类”对话框中,因为性
单击继续。当然也可以选择“第一类别”和“最后类别”,入选中分别表
示以最低数值或最高数值作为参考类别。其他设置与二元Logistic分析
相似,将我们要输出的项勾选即可,点击图2-5中确定,输出数据。
输出数据基本与二元Logistic分析相似,我们重点讲下最后一项“参
考估计”,如图2-7所示,其中参考类别为ICAS=1的分类情况,而其中
19、学而不思则惘,思而不学则殆。——孔子
20、读书给人以快乐、给人以光彩、给人以才干。——培根
spss课件Lecture 12 Binary Logistic__ Regression (W)

• This curve has the following form when the parameter b1 is positive, or its mirror image when the parameter is negative.
1.0 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.0
12
2
The linearity assumption is seriously violated
• This would be very dangerous to do, because of the second problem, which is that the assumptions of linear regression are violated badly in this case.
7
Example: Obtaining Abortion
• The data in the following tables were
derived from the 1997 survey, which
contains information on abortion use and
associated information. The tables and the
• This can be seen clearly in the scatterplot of the standardized residuals against the predicted values:
13
Residual plot
14
• Recall that this scatter diagram should show no pattern at all, as if a handful of stones were dropped at the centre of the diagram. On the contrary, in this case it could not show a pattern more clearly! This pattern of two lines across the diagram is caused by the fact that the dependent variable can only take two values (1 for having abortion and 0 otherwise), and the distribution of the residuals consequently has a binomial distribution, not a normal distribution.
SPSS二项Logistic回归ppt课件

b. Variable(s) entered on step 2: gender.
Variables in the Equation
S.E.
Wald
df
10.512
2
.259
.001
1
.247
7.424
1
.187
16.634
1
.209
5.824
1
11.669
2
.263
.134
1
.251
9.147
1
.240
8
回归模型的拟合优度检验
Model Summary
Cox & Snell R
Nagelkerke R
Step
-2 Log likelihood
Square
Square
1
552.208a
.042
.057
a. Estimation terminated at iteration number 4 because parameter estimates changed by less than .001.
SPSS二项Logistic回归
当被解释变量是0/1二值品质变量时,通常应采用 Logistic回归;
Logistic回归模型:
Logit P ln
P 1 P
0 i xi
1
案例分析:消费行为的logistic回归分析
背景:为研究和预测某商品消费特点和趋势,收集到以 往的消费数据。数据项包括:是否购买(PURCHASE)、性 别(Gender)、年龄(Age)和收入水平(Income)。
21.432
1
Sig.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当被解释变量是0/1二值品质变量时,通常应采用 Logistic回归;
Logistic回归模型:
Logit P ln
P 1 P
0 i xi
1
案例分析:消费行为的logistic回归分析
背景:为研究和预测某商品消费特点和趋势,收集到以 往的消费数据。数据项包括:是否购买(PURCHASE)、性 别(Gender)、年龄(Age)和收入水平(Income)。
解释变量是品质变量时,点击 ‘分类’按钮指定如何生成虚拟 变量。
分类变量的选择。
•‘更改对比(change contrast)’框中 ‘对比(contrast)’中选择参照类, 并点击‘更改’。 •其中:指示符(indicator)表示以某 个特定的类为参照类;这个类可以是品 质变量最大值对应的类(即:参考类别 (reference)中的‘最后一个 (last)’);也可以是品质变量最小值 对应的类(即:参考类别(reference) 中的‘第一个(first)’)
从上表中可知,-2倍的对上似然函数值较高;Cox & Snell R2和 Nagelkerke R2的值均接近0,说明模型的拟合优度较低。
输出风险比默认95%的置信 区间。
只输出最终的模型结果。
设置概率分界值。预测 概率值大于0.5时认为 被解释变量的分类预测 值为1,小于0.5时认为 分类预测值为0.根据需 要对预测精度的要求修 改该参数。
6
保存被解释变量取 值为1的概率值。
保存分类预测值。
一般库克距离大 于1,就可认为对应 的观察值为强影响 点。 杠杆值是指反映 了解释变量x的第i个 值与x的平均值之间 的差异;一般第i个 样本的杠杆值较高 (大于2倍或3倍的 中心化杠杆值)意 味着对应的x是一个 强影响点。 剔除第i个样本后, 观察标准化回归系 数前后变化。n标准 化回归系数变化的 绝对值大于2/ 时, 可认为第i个样本可 能是强影响点。
.001
上表中step行是本步与前一步相比的似然比卡方;Block行是本块与前一块相 比的似然比卡方;Model行是本模型与前一模型相比的似然比卡方。 本例中没有设置解释变量块且解释变量是一次性强制进入,所以三行结果相同。 模型显著性检验的零假设:各回归系数同时为0,解释变量全体与logit P的线 性关系不显著;备择假设:·······。如果显著性水平为0.05,因为概率P值0.001 小于0.05,应拒绝零假设,认为‘所有回归系数不同时为0,解释变量全体与 Logit P之间的关系显著,采用该模型是合理的’。
保存残差。
对被解释变量y中 异常值的探测。 标准化残差:根 据3σ准则,认为标 准化残差绝对值大 于3对应的观察值为 异常值。 学生化残差:适 用于存在‘异方差’ 现象时的异常值判 断。一般认为:学 生化残差大于3对应 的观察值为异常值。
利用残差分析探测样本中的异常值和强影响点。通常异常值和 强影响点是指那些远离均值的样本数据点,对回归方程的参数估 计有较大影响,应尽量找出并加以剔除。
7
强制进入策略下的回归结果: 回归模型的显著性检验
Omnibus Tests of Model Coefficients
Step 1
Step Block Model
Chi-square(似然 比卡方) Df(自由度) Sig.(显著性水平)
18.441
4
.001
18.441
4
.001
18.441
4
5
绘制被解释变量实际值和 预测分类值的关系图。
输出Hosmer-Lemeshow拟合优 度指标。(当解释变量较多 且多为定距型变量时使用) 输出各样本数据的非标准化 残差和标准化残差等指标。
输出模型建立过程中每一步 的结果。
指定解释变量进入或剔除出 模型ห้องสมุดไป่ตู้显著性水平。
设置极大似然估计的最大迭代次数。
2
此时‘女’类作为参照类。
基本操作:
选择分析(analyze)--回归(regression)--二元Logistic回归
被解释变量的选择
解释变量的选择
选择解释变量的筛选策略
条件变量的选择,只有满足条件变量
值的样本才参与回归分析
3
选择解释变量的筛选策略 (1)进入(enter):表示解释 变量全部强行进入模型; (2)向前:条件(forward: conditional)表示向前筛选变量 且变量进入模型的依据是比分检 验统计量,剔除出模型的依据是 条件参数估计原则下的似然率卡 方(首选选择使变化量变化最小 的解释变量剔除出模型); (3)向前:LR(forward: LR) 表示向前筛选变量且变量进入模 型的依据是比分检验统计量,剔 除出模型的依据是极大似然估计 原则下的似然比卡方; (4)向后:条件(backward: conditional)表示向后筛选变量 且变量剔除出模型的依据是条件 参数估计原则下的似然比卡方; (5)向后:LR( backward : LR) 表示向后筛选变量且变量剔除出 模型的依据是极大似然估计原则 下的似然比卡方; (6)向后:Wald( backward : Wald)表示向后筛选变量且变量 剔除出模型的依据是wald统4 计量;
8
回归模型的拟合优度检验
Model Summary
Cox & Snell R
Nagelkerke R
Step
-2 Log likelihood
Square
Square
1
552.208a
.042
.057
a. Estimation terminated at iteration number 4 because parameter estimates changed by less than .001.
现依据性别(Gender)、年龄(Age)和收入水平 (Income)预测判断消费者行为。
注意: 1、本例中性别属于品质型变量。品质型变量应将其转化虚拟变量后再参与回归分析。 2、虚拟变量的设置是将品质变量的各个类别分别以0/1二值变量的形式重新编码,1 表示属于该类,0表示不属于该类; 3、对于n个分类的品质变量,当确定了参照类后,只需设置n-1个虚拟变量即可。 如:性别可需只设置变量x1表示‘是否男’,取1表示男,取0表示非男即‘女’,
