运筹学习题集(第二章)
运筹学习题集

第一章线性计划1.1将下述线性计划问题化成标准形式1)min z=-3x1+ 4x2- 2x3+ 5 x44x1- x2+ 2x3-x4 =-2st. x1+ x2- x3+ 2 x4 ≤ 14-2x1+ 3x2+ x3- x4 ≥ 2x1,x2,x3≥ 0,x4 无约束2)min z = 2x1-2x2+3x3- x1+ x2+ x3= 4st. -2x1+ x2- x3≤ 6x1≤0 ,x2≥ 0,x3无约束1.2用图解法求解LP问题,并指出问题具有唯一最优解、无穷多最优解、无界解仍是无可行解。
1)min z=2x1+3x24x1+6x2≥6st2x1+2x2≥4x1,x2≥02)max z=3x1+2x22x1+x2≤2st3x1+4x2≥12x1,x2≥03)max z=3x1+5x26x1+10x2≤120st5≤x1≤103≤x2≤84)max z=5x1+6x22x1-x2≥2st-2x1+3x2≤2x1,x2≥01.3找出下述LP问题所有基解,指出哪些是基可行解,并确信最优解(1)min z=5x1-2x2+3x3+2x4x 1+2x 2+3x 3+4x 4=7 st 2x 1+2x 2+x 3 +2x 4=3 x 1,x 2,x 3,x 4≥01.4 别离用图解法与单纯形法求解以下LP 问题,并对照指出最优解所对应的极点。
1) maxz =10x 1+5x 2 3x 1+4x 2≤9 st 5x 1+2x 2≤8 x 1,x 2≥02) maxz =2x 1+x 2 3x 1+5x 2≤15 st 6x 1+2x 2≤24 x 1,x 2≥01.5 别离用大M 法与两时期法求解以下LP 问题。
1) minz =2x 1+3x 2+x 3 x 1+4x 2+2x 3≥8 st 3x 1+2x 2 ≥6 x 1,x 2 ,x 3≥02) max z =4x 1+5x 2+ x 3. 3x 1+2x 2+ x 3≥18 St. 2x 1+ x 2 ≤4x 1+ x 2- x 3=53) maxz = 5x 1+3x 2 +6x 3 x 1+2x 2 -x 3 ≤ 18 st 2x 1+x 2 -3 x 3 ≤ 16 x 1+x 2 -x 3=10 x 1,x 2 ,x 3≥01231231231231234)max 101512539561515.25,,0z x x x x x x x x x st x x x x x x =++++≤⎧⎪-++≤⎪⎨++≥⎪⎪≥⎩1.6求下表中a ~l 的值。
运筹学第二章习题答案

运筹学第二章习题答案运筹学是一门应用数学学科,旨在通过数学模型和定量方法来解决实际问题。
在运筹学的学习中,习题是必不可少的一部分,通过解答习题可以加深对知识的理解和应用。
本文将针对运筹学第二章的习题进行解答,希望能够帮助读者更好地掌握运筹学的知识。
第一题:线性规划问题的基本要素包括目标函数、约束条件和决策变量。
请问线性规划问题的目标函数通常是什么形式?为什么?答:线性规划问题的目标函数通常是线性函数的形式。
这是因为线性函数具有简单的数学性质,容易求解和分析。
此外,线性函数的图像为直线,可以通过直观的图形方法来理解问题的解。
第二题:什么是单纯形法?请简要描述单纯形法的基本思想和步骤。
答:单纯形法是一种求解线性规划问题的常用方法。
其基本思想是通过不断地移动到更优解的顶点,直到找到最优解。
单纯形法的步骤如下:1. 初始解的选择:选择一个可行解作为初始解。
初始解可以通过图形方法或其他启发式算法得到。
2. 进行迭代:通过计算目标函数的改进方向来确定下一步移动的方向。
如果目标函数不能再改进,则停止迭代,当前解即为最优解。
3. 顶点的移动:通过改变决策变量的值,将当前解移动到相邻的顶点。
移动的方向和距离由迭代步骤中计算得到。
4. 检验最优性:对移动后的顶点进行最优性检验,判断是否达到最优解。
如果达到最优解,则停止迭代,当前解即为最优解;否则,返回第2步。
第三题:什么是整数规划问题?请举一个实际应用的例子,并说明为什么需要使用整数规划方法来解决。
答:整数规划问题是线性规划问题的一种扩展形式,要求决策变量的取值为整数。
整数规划问题通常用于需要离散决策的场景,如生产调度、资源分配等。
举个例子,假设某公司有多个项目需要进行投资,每个项目的投资金额和预期收益已知。
公司希望选择一些项目进行投资,使得总投资金额不超过公司的可用资金,并最大化预期收益。
由于项目的投资金额和收益都是整数,这就是一个整数规划问题。
使用整数规划方法来解决这个问题的原因是,如果将决策变量的取值限制为整数,可以更好地符合实际情况。
运筹课后习题

第2章 习题 P 58—6、86、福安商场是个中型的百货商场,它对售货员的需求经过统计分析如表 2-15 所示:表 2-15 每日售货员的需求情况表为了保证售货人员充分休息,售货人员每周工作 5天,休息两天,并要求休息的两天是连续的。
问应该如何安排售货人员的作息,既满足工作需要,又使配备的售货人员的人数最少? 解:⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧≥≥++++≥++++≥++++≥++++≥++++≥++++≥++++++++++=0,,,,,,19252415282831..654321,,,,,,76543217432176321765217654176543654325432176543217654321x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x t s x x x x x x x f Min x x x x x x x ,日的上班人数,,,,,分别为星期设8、有1,2,3,4四种零件均可在设备A 或设备B 上加工,已知在这两种设备上分别加工一个零件的费用如表 2-16 所示。
又知设备A 或B 只要有零件加工均需要设备的启动费用,分别为100元和150元。
现要求加工1,2,3,4零件各三件。
问应如何安排使总的费用最小。
试建立线性规划模型。
解:关键问题是启动费用,因此,应有三个模型来比较结果:设 x ij ,i = 1、2、3、4;j = 1、2;分别为产品 i 在设备 j ( 1 为 A ,2 为 B )上加工的数量。
模型1 只用设备A 加工:总费用:z = (50+80+90+40)*3+100 = 880元。
模型2 只用设备B 加工:总费用:z = (30+100+50+70)*3+150 = 900元。
模型3 同时用设备A 、B 加工:.030330302,1;4,3,2,103333..25070501003040908050423222124131211142413231222112114232221241312111========⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=+=+=+=+++++++++=x x x x x x x x j i x x x x x x x x x t s x x x x x x x x f Min ij ,,,,,,,最优解总费用:z = 850元。
《运筹学教程》第二章习题答案

《运筹学教程》第二章习题答案1、(1)解:引入松弛变量x4≥0,x5≥0,化不等式为等式为:minz=2X1 +3X2+4X3s.t. X1+3X2+2X3+X4=74X1+2X2+X5=9X1,X2,X4,X5≥0化自由变量为非负,令X3=X3′-X3〞,X3′,X3〞≥0 :minz=2X1 +3X2+4X3′-4X3〞s.t. X1+3X2+2 X3′-2 X3〞+X4=74X1+2X2+X5=9X1,X2, X3′,X3〞,X4,X5 ≥0(2)解:引入松弛变量x5≥0,剩余变量X6≥0,化不等式为等式为:maxz=X1 -5X2+4X3- X4s.t. X1+2X3+X5=7X2-2X4-X6=9X1,X2,X4,X5 ,X6≥0化自由变量为非负,令X3=X3′-X3〞,X3′,X3〞≥0 :maxz=X1 -5X2+4X3′-4X3〞- X4s.t. X1+2 X3′-2 X3〞+X5=7X2-2X4-X6=9X1,X2, X3′,X3〞,X4,X5 , X6≥0化极大的目标函数为极小的目标函数:minz=-X1+5X2-4X3′+4X3〞+X4s.t. X1+2 X3′-2 X3〞+X5=7X2-2X4-X6=9X1,X2, X3′,X3〞,X4,X5 , X6≥02、(1)是不等式表示下图阴影区域,过阴影部分任意两点的直线仍在该区域内。
(2)不是不等式表示下图阴影区域,过阴影部分且通过曲线上部的直线上的点不完全在该区域内。
(3)不是 不等式表示下图阴影区域,过阴影部分且通过圆内部的直线上的点不完全在该区域内。
3、在以下问题中,指出一组基础变量,求出所有基础可行解以及最优解。
(1)123123123123m ax 2..2644,,0z x x x s t x x x x x x x x x =+-⎫⎪++≤⎪⎬+-≤⎪⎪≥⎭解:将上式化成标准形式,如下:1231234123512345m in 2..2644,,,,0p x x x s t x x x x x x x x x x x x x =--+⎫⎪+++=⎪⎬+-+=⎪⎪≥⎭从上式中可以得出系数矩阵为[]12345112101411A P P P P P ⎡⎤==⎢⎥-⎣⎦, 取基础变量为45,x x ,令非基变量123,,x x x =0,解方程组123412352644x x x x x x x x +++=+-+=得基础可行解(1)(0,0,0,6,4)T x =同理得基础解:(2)(0,6,0,0,20)T x =-,(3)(0,0,3,0,7)T x =,(4)(0,0,4,24,0)T x =-,(5)(0,1,0,5,0)Tx =,(6)1420(0,,,0,0)99Tx =,(7)(6,0,0,0,2)T x =-,(8)(4,0,0,2,0)Tx=,(9)202(,,0,0,0)33Tx =-,(10)142(,0,,0,0)33Tx =。
运筹学习题答案(第二章)

0
-5/4
(j)
第二章习题解答
2.4 给出线性规划问题 写出其对偶问题;(2)用图解法求解对偶问题;(3)利用(2)的结果及根据对偶问题性质写出原问题最优解。
最优解是:y1=-8/5,y2=1/5,目标函数值-19/5。
01
由于 y1=-8/5,y2=1/5都不等于零,原问题中的约束取等号。又上面第4个约束不等号成立,故x4=0,令x3=0就可以得到最优解: x1=8/5,x2=1/5。
3
2
5
0
0
0
CB
基
b
X1
X2
X3
X4
X5
X6
2
X2
15-7/4
1/4
1
0
0
0
1/4
5
X3
30+
3/2
0
1
0
1/2
0
0
X4
3 /2-5
-1
0
0
1
-1/2
-1/2
Cj-Zj
-7
0
0
-1
-2
0
第二章习题解答
第二章习题解答
2.14 某厂生产A,B,C三种产品,其所需劳动力、材料等有关数据见下表:
第二章习题解答
已知原问题最优解为X*=(2,2,4,0),代入原问题,第4个约束不等式成立,故y4=0。有由于x1,x2,x3大于0,上面对偶问题前3个约束取等号,故得到最优解: y1=4/5, y2,=3/5, y3=1, y4=0
第二章习题解答
2.8 已知线性规划问题A和B如下:
01
01
02
2.6 已知线性规划问题
(完整版)《运筹学》习题集

第一章线性规划1.1将下述线性规划问题化成标准形式1)min z=-3x1+4x2-2x3+5 x4-x2+2x3-x4=-24xst. x1+x2-x3+2 x4 ≤14-2x1+3x2+x3-x4 ≥2x1,x2,x3≥0,x4无约束2)min z =2x1-2x2+3x3+x2+x3=4-xst. -2x1+x2-x3≤6x1≤0 ,x2≥0,x3无约束1.2用图解法求解LP问题,并指出问题具有唯一最优解、无穷多最优解、无界解还是无可行解。
1)min z=2x1+3x24x1+6x2≥6st2x1+2x2≥4x1,x2≥02)max z=3x1+2x22x1+x2≤2st3x1+4x2≥12x1,x2≥03)max z=3x1+5x26x1+10x2≤120st5≤x1≤103≤x2≤84)max z=5x1+6x22x1-x2≥2st-2x1+3x2≤2x1,x2≥01.3找出下述LP问题所有基解,指出哪些是基可行解,并确定最优解(1)min z=5x1-2x2+3x3+2x4x1+2x2+3x3+4x4=7st2x1+2x2+x3 +2x4=3x1,x2,x3,x4≥01.4 分别用图解法与单纯形法求解下列LP 问题,并对照指出最优解所对应的顶点。
1) maxz =10x 1+5x 23x 1+4x 2≤9 st 5x 1+2x 2≤8 x 1,x 2≥02) maxz =2x 1+x 2 3x 1+5x 2≤15 st 6x 1+2x 2≤24 x 1,x 2≥01.5 分别用大M 法与两阶段法求解下列LP 问题。
1) minz =2x 1+3x 2+x 3 x 1+4x 2+2x 3≥8 st 3x 1+2x 2 ≥6 x 1,x 2 ,x 3≥02) max z =4x 1+5x 2+ x 3. 3x 1+2x 2+ x 3≥18 St. 2x 1+ x 2 ≤4x 1+ x 2- x 3=53) maxz = 5x 1+3x 2 +6x 3 x 1+2x 2 -x 3 ≤ 18 st 2x 1+x 2 -3 x 3 ≤ 16 x 1+x 2 -x 3=10 x 1,x 2 ,x 3≥01231231231231234)max 101512539561515.25,,0z x x x x x x x x x st x x x x x x =++++≤⎧⎪-++≤⎪⎨++≥⎪⎪≥⎩1.61.7某班有男生30人,女生20人,周日去植树。
运筹学习题集(第二章)

运筹学习题集(第二章)判断题判断正误,如果错误请更正第二章线形规划的对偶理论1.原问题第i个约束是<=约束,则对偶变量yi>=0.2.互为对偶问题,或则同时都有最优解,或则同时都无最优解.3.原问题有多重解,对偶问题也有多重解.4.对偶问题有可行解,原问题无可行解,则对偶问题具有无界解.5.原问题无最优解,则对偶问题无可行解.6.设X,Y分别为{minZ=CX|AX>=b,X>=0}和{maxw=Yb|YA<=C,Y>=0}的可行解,则有(1)CX<=Yb;(2)CX是w的上界;(3)当X,Y为最优解,CX=Yb;(4)当CX=Yb 时,有YXs+YsX=0;(5)X为最优解且B是最优基时,则Y=C B B-1是最优解;(6)松弛变量Ys的检验数是λs,则X=-λs是基本解,若Ys是最优解, 则X=-λs是最优解.7.原问题与对偶问题都可行,则都有最优解.8.原问题具有无界解,则对偶问题可行.9.若X,Y是原问题与对偶问题的最优解.则X=Y.10.若某种资源影子价格为0,则该资源一定有剩余.11影子价格就是资源的价格.12.原问题可行对偶问题不可行,可用对偶单纯形法计算.13.对偶单纯形法比值失效说明原问题具有无界解.14.对偶单纯形法是直接解对偶问题的一种解法.15.减少一个约束,目标值不会比原来变差.16.增加一个约束,目标值不会比原来变好.17增加一个变量, 目标值不会比原来变差.18.减少一个非基变量, 目标值不变.19.当Cj(j=1,2,3,……,n)在允许的最大范围内同时变化时,最优解不变。
选择题在下列各题中,从4个备选答案中选出一个或从5个备选答案中选出2~5个正确答案。
第二章线性规划的对偶理论1.如果决策变量数列相等的两个线规划的最优解相同,则两个线性规划A约束条件相同B目标函数相同C最优目标函数值相同D以上结论都不对2.对偶单纯形法的最小比值规则是为了保证A使原问题保持可行B 使对偶问题保持可行C逐步消除原问题不可行性D逐步消除对偶问题不可行性3.互为对偶的两个线性规划问题的解存在关系A若最优解存在,则最优解相同B原问题无可行解,则对偶问题也无可行解C对偶问题无可行解,原问题可能无可行解D一个问题无界,则另一个问题无可行解E一个问题无可行解,则另一个问题具有无界解4.已知规范形式原问题(max)的最优表中的检验数为(λ1,λ2,……λn),松弛变量的检验数为(λn+1,λn+2,……λn+m),则对偶问题的最优解为A—(λ1,λ2,……λn)B (λ1,λ2,……λn)C —(λn+1,λn+2,……λn+m)D (λn+1,λn+2,……λn+m)5.原问题与对偶问题都有可行解,则A原问题有最优解,对偶问题可能没有最优解B原问题与对偶问题可能都没有最优解C可能一个问题有最优解,另一个问题具有无界解D原问题与对偶问题都有最优解计算题线性规划问题和对偶问题2.1 对于如下的线性规划问题min z = 3x1 + 2x2 +x3s.t. x1 + x2+ x3 ≤ 15 (1)2x1 - x2+ x3≥ 9 (2)-x1 + 2x2+2x3≤ 8 (3)x1 x2x3 ≥ 01、写出题目中线性规划问题的对偶问题;2、分别求出原始问题和对偶问题的最优解(求解的次序和方法不限);解答:1、写出题目中线性规划问题的对偶问题;解:max w = 15y1 + 9y2 + 8y3s.t. y1 + 2y- y3 ≤ 3 (1)y1 - y2+ 2y3≤ 2 (2)y1 + y2+ 2y3≤ 1 (3)y1≤0、y2 ≥0、y3 ≤02、分别求出原始问题和对偶问题的最优解(求解的次序和方法不限);解:先将原问题化成以下形式,则有mi n z = 3x1 + 2x2 + x3s.t. x1 + x2+ x3+ x4= 15 (1)-2x1 + x23+ x5= -9 (2)-x1 + 2x2+2x3+x6= 8 (3)原始问题的最优解为(X 1 X 2 X 3 X 4 X 5 X 6)=(2,0,5,8,0,0),minz=11 对偶问题的最优解为(y 1 y 2 y 3 y 4 y 5 y 6)=(0,7/5,-1/5,0,19/5,0),maxw=112.2 对于以下线性规划问题max z = -x 1 - 2x 2s.t. -2x 1 + 3x 2 ≤ 12 (1) -3x 1 + x 2 ≤ 6 (2) x 1 + 3x 2 ≥ 3 (3) x 1 ≤ 0,x 2 ≥ 01、写出标准化的线性规划问题;2、用单纯形表求出这个线性规划问题的最优解和最优的目标函数值;3、写出这个(极大化)线性规划问题的对偶问题;4、求出对偶问题的最优解和最优解的目标函数值;5、第(2)个约束右端常数b 2=6在什么范围内变化,最优解保持不变。
运筹学第二章答案.
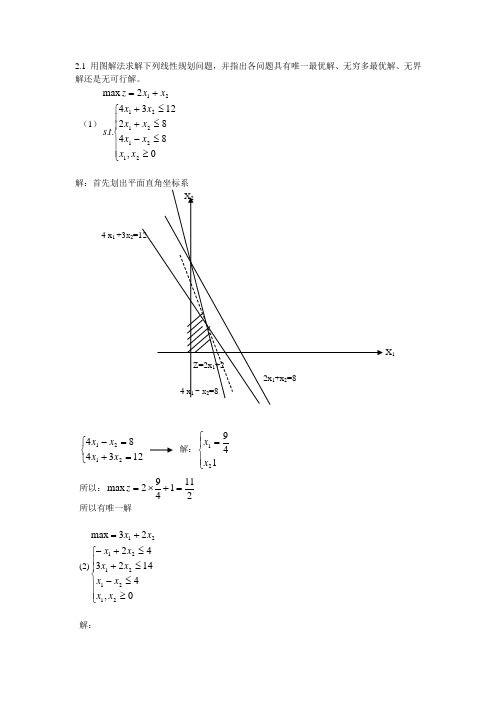
2.1 用图解法求解下列线性规划问题,并指出各问题具有唯一最优解、无穷多最优解、无界解还是无可行解。
(1)⎪⎪⎩⎪⎪⎨⎧≥≤-≤+≤++=0,84821234..2max 2121212121x x x x x x x x t s x x z解:首先划出平面直角坐标系4 x 1 +3x 2X 1⎩⎨⎧=+=-1234842121x x x x 解:⎪⎩⎪⎨⎧=14921x x 所以:2111492max =+⨯=z 所以有唯一解(2)⎪⎪⎩⎪⎪⎨⎧≥≤-≤+≤+-+=0,414234223max 2121212121x x x x x x x x x x 解:2=41⎩⎨⎧=+=+-1423422121x x x x 解得:⎪⎪⎩⎪⎪⎨⎧==4132521x x 所以:144132253max =⨯+⨯=z 因为直线02321=+x x 与直线142321=+x x 平行, 所以有无穷多最优解,max z=14(3) ⎪⎩⎪⎨⎧≥≤+-≤-+=0,432..32max 21212121x x x x x x t s x x z 解:(4)⎪⎩⎪⎨⎧≥-≤-≥-+=0,330..max 21212121x x x x x x t s x x z解:2.2将下列线性规划问题化为标准形式(1) s.t.⎪⎩⎪⎨⎧≥≤≤-+-=++-+-=无约束321321321321,0,0624322min x x x x x x x x x x x x z (2)⎪⎪⎩⎪⎪⎨⎧≤≥-=-+-≤+-≥--+=0,0232132..23min 3213213132321x x x x x x x x x x t s x x x z 无约束, 解:(1)令011≥-=x x )0'','('''33333≥-=x x x x x则上述形式可化为:)'''(32'2m ax 3321x x x x z --+=⎪⎩⎪⎨⎧≥=+--+=-++0,'',',,'6)'''('24)'''('..43321433213321x x x x x x x x x x x x x x t s(2)⎪⎪⎩⎪⎪⎨⎧≤≥-=-+-≤+-≥--+=0,0232132..23min 3213213132321x x x x x x x x x x t s x x x z 无约束, 解:令33'x x -= )0','','(322≥x x x 则上述形式可化为:')'''(23m ax 3221x x x x z ----=⎪⎪⎩⎪⎪⎨⎧≥=---=+--=+---0,,','',',2')'''(321')'''(3')'''(2..543221322153224322x x x x x x x x x x x x x x x x x x t s 2.3. 在下列线性规划问题中,找出所有基解,指出哪些是基可行解并分别代入目标函数,比较找出最优解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
判断题判断正误,如果错误请更正第二章线形规划的对偶理论1.原问题第i个约束是<=约束,则对偶变量yi>=0.2.互为对偶问题,或则同时都有最优解,或则同时都无最优解.3.原问题有多重解,对偶问题也有多重解.4.对偶问题有可行解,原问题无可行解,则对偶问题具有无界解.5.原问题无最优解,则对偶问题无可行解.6.设X,Y分别为{minZ=CX|AX>=b,X>=0}和{maxw=Yb|YA<=C,Y>=0}的可行解,则有(1)CX<=Yb;(2)CX是w的上界;(3)当X,Y为最优解,CX=Yb;(4)当CX=Yb 时,有YXs+YsX=0;(5)X为最优解且B是最优基时,则Y=CB-1是最优解;(6)松弛变量Ys的检验数是λs,则X=-λs是基本解,若Ys是最优解, 则X=-λs是最优解.7.原问题与对偶问题都可行,则都有最优解.8.原问题具有无界解,则对偶问题可行.9.若X,Y是原问题与对偶问题的最优解.则X=Y.10.若某种资源影子价格为0,则该资源一定有剩余.11影子价格就是资源的价格.12.原问题可行对偶问题不可行,可用对偶单纯形法计算.13.对偶单纯形法比值失效说明原问题具有无界解.14.对偶单纯形法是直接解对偶问题的一种解法.15.减少一个约束,目标值不会比原来变差.16.增加一个约束,目标值不会比原来变好.17增加一个变量, 目标值不会比原来变差.18.减少一个非基变量, 目标值不变.19.当Cj(j=1,2,3,……,n)在允许的最大范围内同时变化时,最优解不变。
选择题在下列各题中,从4个备选答案中选出一个或从5个备选答案中选出2~5个正确答案。
第二章线性规划的对偶理论1.如果决策变量数列相等的两个线规划的最优解相同,则两个线性规划 A约束条件相同B目标函数相同 C最优目标函数值相同 D以上结论都不对2.对偶单纯形法的最小比值规则是为了保证 A使原问题保持可行 B使对偶问题保持可行C逐步消除原问题不可行性 D逐步消除对偶问题不可行性3.互为对偶的两个线性规划问题的解存在关系 A若最优解存在,则最优解相同 B原问题无可行解,则对偶问题也无可行解 C对偶问题无可行解,原问题可能无可行解 D一个问题无界,则另一个问题无可行解 E一个问题无可行解,则另一个问题具有无界解4.已知规范形式原问题(max)的最优表中的检验数为(λ1,λ2,……λn),松弛变量的检验数为(λn+1,λn+2,……λn+m),则对偶问题的最优解为 A—(λ1,λ2,……λn) B (λ1,λ2,……λn) C —(λn+1,λn+2,……λn+m)D(λn+1,λn+2,……λn+m)5.原问题与对偶问题都有可行解,则 A原问题有最优解,对偶问题可能没有最优解B原问题与对偶问题可能都没有最优解 C可能一个问题有最优解,另一个问题具有无界解D 原问题与对偶问题都有最优解计算题线性规划问题和对偶问题对于如下的线性规划问题min z = 3x1 + 2x2+x3. x1 + x2+ x3 ≤ 15 (1)2x1 - x2+ x3≥ 9 (2)-x1 + 2x2+2x3≤ 8 (3)x1 x2x3 ≥ 01、写出题目中线性规划问题的对偶问题;2、分别求出原始问题和对偶问题的最优解(求解的次序和方法不限);解答:1、写出题目中线性规划问题的对偶问题;解:max w = 15y1 + 9y2 + 8y3. y1 + 2y2- y3 ≤ 3 (1)y1 - y2+ 2y3≤ 2 (2)y1 + y2+ 2y3≤ 1 (3)y1≤0、 y2 ≥0、y3 ≤02、分别求出原始问题和对偶问题的最优解(求解的次序和方法不限);解:先将原问题化成以下形式,则有mi n z = 3x1 + 2x2 + x3. x1 + x2+ x3+ x4= 15 (1)-2x1 + x2- x3+ x5= -9 (2)-x1 + 2x2+2x3+x6= 8 (3)x1 x2x3x4x5x6 ≥ 0原始问题的最优解为(X1 X2 X3 X4 X5 X6)=(2,0,5,8,0,0),minz=11对偶问题的最优解为(y1 y2 y3 y4 y5 y6)=(0,7/5,-1/5,0,19/5,0),maxw=11对于以下线性规划问题max z = -x1 - 2x2. -2x1 + 3x2≤ 12 (1)-3x1 + x2≤ 6 (2)x1 + 3x2≥ 3 (3)x1≤ 0, x2≥ 01、写出标准化的线性规划问题;2、用单纯形表求出这个线性规划问题的最优解和最优的目标函数值;3、写出这个(极大化)线性规划问题的对偶问题;4、求出对偶问题的最优解和最优解的目标函数值;5、第(2)个约束右端常数b2=6在什么范围内变化,最优解保持不变。
解答:1、写出标准化的线性规划问题:令x1*=- x1max z = x1*- 2x2. 2x1* + 3x2+ x3= 12 (1)3x1* + x2+ x4= 6 (2)-x1* + 3x2-x5= 3 (3)x1* x2x3x4x5≥ 02、(6分)用单纯形表求出这个线性规划问题的最优解和最优的目标函数值此时最优解为(X1、X2、X3、X4 X5)=(-3/2,3/2,9/2,0,0)maxz=-3/2 3、写出这个(极大化)线性规划问题的对偶问题;min w = 12y1 + 6y2+ 3y3. -2y1 - 3y2+ y3 ≤ -1 (1)3y1 + y2+ 3 y3≥ -2 (2)y1≥0、 y2 ≥0、y3 ≤04、求出对偶问题的最优解和最优解的目标函数值;此时最优解为(y1、y2、y3、y4 y5)=(0,1/10,-7/10,0,0)minw =-3/2 5、则有1≤b2≤11,最优解不变。
已知LP 问题:max z = x 1 + 2x 2 +3x 3 + 4x 4. x 1 + 2x 2 + 2x 3 + 3x 4 ≤ 20 (1) 2x 1 + x 2 + 3x 3 + 2x 4 ≤ 20 (2) x 1 、 x 2 、 x 3 、 x 4 ≥ 0的最优解为(0,0,4,4)T ,最优值为Z=28。
请用互补松弛定理计算其对偶问题的最优解。
解答:首先写出此LP 问题的对偶问题为:min w = 20y 1 + 20y 2. y 1 + 2y 2 ≥ 1 (1)2y 1 + y 2 ≥ 2 (2)2y 1 + 3y 2 ≥ 3 (3)3y 1 + 2y 2 ≥ 4 (4)y 1 、 y 2 、 ≥ 0将上述对偶问题的化成标准型,取松弛变量分别为v 1 、v 2、、 v 3 、v 4,则有min w = 20y 1 + 20y 2. y 1 + 2y 2 - v 1 = 1 (5)2y 1 + y 2 - v 2 = 2 (6)2y 1 + 3y 2 - v 3 = 3 (7)3y 1 + 2y 2 - v 4 = 4 (8)y 1 、 y 2 、 ≥ 0利用互补松弛定理可知:x 3 = 4 > 0 ,又有 x 3 v 3 = 0 , 所以有 v 3 = 0 代入(7)式 x 4 = 4 > 0,又有 x 4 v 4= 0 , 所以有 v 4 = 0 代入(8)式,则有2y 1 + 3y 2 = 3 (9)3y 1 + 2y 2 = 4 (10)从中可计算出y 1 = 6/5 、 y 2 = 1/5,则 w* =28一个工厂用四种原料生产三种产品,生产每种产品要消耗的各种原料数量(表中“—”表示相应的产品不需要这种原料)、各种产品的利润以及各种原料的限量如下表所示。
1、写出原料限制条件下利润最大化的线性规划模型;2、写出以上问题的对偶问题;3、已知利润最大的线性规划问题的最优解是产品A生产120件,产品B不生产,产品C生产52件,用互补松弛关系求四种原料的影子价格。
解答:一个工厂用四种原料生产三种产品,生产每种产品要消耗的各种原料数量(表中“—”表示相应的产品不需要这种原料)、各种产品的利润以及各种原料的限量如下表所示。
1.写出原料限制条件下利润最大化的线性规划模型;max z = 120x1 + 180x2+210x3. 12x1 + 8x2+10x3 ≤ 2400 (1)6x1 + 10x2+15x3 ≤ 1500 (2)15x1 + 18x2≤ 1800 (3)20x2 + 22x3≤ 2000 (4)x1≥ 0, x2≥ 0 x3≥ 0 2.写出以上问题的对偶问题;min w = 2400y 1 + 1500 y 2 +1800 y 3 +2000 y 4. 12y 1 + 6y 2 + 15y 3 ≥ 120 (1)8y 1 + 10y 2 + 18 y 3 + 20 y 4 ≥ 180 (2) 10y 1 + 15y 2 +22y 4 ≥ 210 (3) y 1≥ 0, y 2 ≥ 0 y 3 ≥ 0 y 4 ≥ 03. 已知利润最大的线性规划问题的最优解是产品A 生产120件,产品B 不生产,产品C 生产52件,用互补松弛关系求四种原料的影子价格。
max z = 120x 1 + 180 x 2 +210 x 3. 12x 1 + 8x 2 +10 x 3 +x 4 = 2400 (1) 6x 1 + 10x 2 +15 x 3 + x5 = 1500 (2) 15x 1 + 18x 2 + x 6 = 1800 (3) 20x 2 + 22x 3 + x 7 = 2000 (4) x 1≥0, x 2 ≥0 x 3 ≥0 x 4 ≥0 x 5 ≥0 x 6 ≥0 x 7 ≥0 x 4 =440 x 5 =0 x 6 =0 x 7 =856min w = 2400y 1 + 1500 y 2 +1800 y 3 +2000 y 4. 12y 1 + 6y 2 + 15y 3 - y 5 = 120 (1) 8y 1 + 10y 2 + 18 y 3 + 20 y 4 - y 6 = 180 (2) 10y 1 + 15y 2 +22y 4 - y 7 = 210 (3) y 1≥ 0, y 2 ≥0 y 3 ≥0 y 4 ≥0 y 5 ≥0 y 6 ≥0 y 7 ≥0由互补松弛关系可知,x 1 x 3 x 4 x 7≥0,得到y 5= y 7= y 1= y 4=06y 2 + 15y 3 = 12010y 2 + 18 y 3 - y 6 = 180 15y 2 = 210解得y 2=14 y 3= y 6= 原材料甲的影子价格为:0万元/吨 原材料乙的影子价格为:14万元/吨 原材料丙的影子价格为:万元/吨原材料丁的影子价格为:0万元/吨。
