考研数学三知识点总结

合集下载

数学三考研知识点总结

数学三考研知识点总结一、数学分析1. 集合与映射集合的基本概念，包括子集、并集、交集、补集等；映射的定义和性质，包括单射、满射、双射等。

2. 数列与级数数列的概念，包括常数数列、等差数列、等比数列等；级数的概念，包括收敛级数、发散级数等。

3. 函数与极限函数的定义和性质，包括连续函数、可导函数等；极限的概念，包括极限存在的条件、极限运算法则等。

4. 一元函数微分学导数的定义和性质，包括高阶导数、隐函数求导等；微分的概念和应用，包括微分中值定理、泰勒公式等。

5. 一元函数积分学不定积分的计算方法，包括分部积分、换元积分等；定积分的计算方法，包括定积分的几何意义、定积分的性质等。

6. 定积分的应用定积分在几何、物理等领域的应用，包括求曲线长度、曲线面积、体积等问题。

7. 多元函数微分学偏导数的概念和性质，包括高阶偏导数、全微分等；多元函数的极值和条件极值的判定。

8. 重积分重积分的定义和性质，包括累次积分、极坐标系下的重积分等；重积分的应用，包括质量、质心、转动惯量等问题。

9. 曲线积分与曲面积分曲线积分的概念和计算方法，包括第一类曲线积分和第二类曲线积分；曲面积分的概念和计算方法，包括第一类曲面积分和第二类曲面积分。

10. 常微分方程常微分方程的基本概念，包括初值问题、兼切性、自由度等；常微分方程的解法，包括特征方程法、常数变易法、常系数高阶线性齐次微分方程的特解法等。

11. 泛函分析线性空间和内积空间的定义和性质，包括线性子空间、正交投影等；巴拿赫空间和希尔伯特空间的概念和性质。

12. 牛顿-莱布尼茨公式牛顿-莱布尼茨公式的推导和应用，包括用它来求定积分、用它来求极限等。

二、代数与数论1. 线性代数线性代数的基本概念，包括向量空间、线性变换、矩阵等；线性方程组的解法，包括高斯消元法、矩阵的秩等。

2. 群论群的定义和性质，包括子群、正规子群、循环群等；群的同态映射和同构定理。

3. 环论环的定义和性质，包括理想、素理想、商环等；整环、域的概念和性质。

考研数学三需要掌握的重要考点

考研数学三需要掌握的重要考点考研数学三需要掌握的重要考点我们在准备数学三考研的时候，需要掌握的重要考点有很多。

店铺为大家精心准备了考研数学三需要掌握的重点，欢迎大家前来阅读。

考研数学三掌握23个重要考点(1)曲线的渐近线;(2)某点处的高阶导数;(3)化极坐标系下的二次积分为直角坐标系下的二次积分;(4)数项级数敛散性的判定;(5)向量组的线性相关性;(6)初等变换与初等矩阵;(7)二维均匀分布;(8)统计量的常见分布;(9)未定式的极限;(10)分段函数的复合函数的导数;(11)二元函数全微分的定义;(12)平面图形的面积;(13)初等变换、伴随矩阵、抽象行列式的计算;(14)随机事件的概率;(15)未定式的极限;(16)无界区域上的二重积分;(17)多元函数微分学的经济应用，条件极值;(18)函数不等式的证明;(19)微分方程、变限积分函数、拐点;(20)含参数的方程组;(21)利用正交变换化二次型为标准形;(22)二维离散型随机变量的概率、数字特征;(23)二维常见分布的随机变量函数的分布、数字特征考研数学必掌握的7个高频考点1、两个重要极限，未定式的极限、等价无穷小代换这些小的知识点在历年的考察中都比较高。

而透过我们分析，假如考极限的话，主要考的是洛必达法则加等价无穷小代换，特别针对数三的，这儿可能出大题。

2、处理连续性，可导性和可微性的关系要求掌握各种函数的求导方法。

比如隐函数求导，参数方程求导等等这一类的，还有注意一元函数的应用问题，这也是历年考试的一个重点。

数三的同学这儿结合经济类的一些试题进行考察。

3、参数估计这一点是咱们经常出大题的地方，这一块对咱们数一，数二，数三的考生来讲，包含两块知识点，一个是矩估计，一个是最大似然估计，这两个集中出大题。

4、级数问题，主要针对数一和数三这部分的重点是：一、常数项级数的性质，包括敛散性;二、牵扯到幂级数，大家要熟练掌握幂级数的收敛区间的计算，收敛半径与和函数，幂级数展开的问题，要掌握一个熟练的方法来进行计算。

考研数学三知识点整理

考研数学三知识点整理一、数学分析1.极限与连续-无穷小量与无穷大量-函数极限的定义和性质-极限运算的基本法则-函数连续的定义和性质-邻域及其性质-间断点的分类-初等函数的连续性2.一元函数微分学-导数的定义和性质-导数的几何意义-凹凸性与拐点-微分中值定理-泰勒公式及其应用-常用高阶导数的计算3.一元函数积分学-普通函数的不定积分-定积分与不定积分的关系-牛顿—莱布尼茨公式-反常积分的概念和性质-反常积分的审敛法-定积分的应用4.多元函数微分学-多元函数的极限与连续-偏导数的定义和性质-方向导数和梯度-隐函数的求导-全微分和全导数-多元函数的泰勒公式5.曲线积分与曲面积分-第一类曲线积分-第二类曲线积分-曲面积分的概念和性质-曲面积分的计算方法-散度和旋度的概念及计算二、高等代数1.行列式与矩阵-行列式的定义和性质-行列式的计算方法-矩阵的概念和运算-矩阵的秩和逆-矩阵的特征值和特征向量-对称矩阵和正定矩阵2.线性方程组与向量空间-线性方程组的解的结构-线性方程组的常用解法-向量空间的概念和性质-线性相关性和线性无关性-线性方程组与矩阵的关系-矩阵的秩与线性方程组的解3.线性变换与矩阵的相似-线性变换的概念和性质-线性变换的矩阵表示和标准形-矩阵的相似和对角化-幂零矩阵和对角化的条件-线性变换的特征值和特征子空间-正交矩阵和对称矩阵4.线性空间与线性变换-线性空间的定义和性质-基与维数-有限维线性空间的同构-线性变换的矩阵表示-基变换和坐标变换矩阵-初等变换和矩阵的相似5.内积空间-内积与内积空间的定义和性质-正交与正交补-角和长度的内积表示-柯西—施瓦茨不等式和三角不等式-格拉姆—斯密特正交化方法-正交投影和最小二乘逼近三、概率论1.随机事件与概率-随机事件和样本空间-随机事件的运算和性质-概率的定义和性质-条件概率与乘法定理-全概率公式与贝叶斯公式2.随机变量与概率分布-随机变量的概念和分类-分布函数和概率密度函数-离散型随机变量与连续型随机变量-随机变量函数的概率分布-重要离散型和连续型分布-数学期望和方差的定义和性质3.多维随机变量及其分布-多维随机变量的联合分布-边缘分布和条件分布-随机变量的独立性-随机变量函数的分布-重要的二维和多维分布-列联表和卡方检验4.随机变量的数字特征-几个重要的数字特征-方差和标准差-协方差和相关系数-强大数定律与中心极限定理-大数定律和极限定理-泊松定理和辛钦定理5.数理统计基础-总体和样本的概念-统计量及其分布-正态总体的统计推断-点估计和区间估计-参数估计的评价准则-假设检验和拒绝域以上是对考研数学三知识点的整理，内容包括数学分析、高等代数和概率论三个方面的主要知识点。

考研数三知识点总结

考研数三知识点总结一、数学基础知识1.集合与逻辑（1）集合的概念与运算（2）命题与联结词（3）命题公式与合取、析取范式（4）命题演算（5）范式和合取析取范式的相互转化（6）命题公式的永真式和等值式（7）命题逻辑的等值演算2. 代数与数论（1）复数的概念与运算（2）多项式的整除与因式分解（3）有理数的整除性（4）整数、模运算、同余（5）素数与合数（6）整数的唯一分解定理（7）不定方程的整数解3. 几何与简单的变量（1）空间几何问题与直线的方程（2）空间解析几何（3）坐标与原点（4）斜率与截距（5）直线的夹角与距离（6）点、直线、平面的位置关系（7）三角函数的概念与运算4. 极限与微积分（1）极限与无穷小（2）函数的极限（3）连续与间断（4）导数的概念与运算（5）定积分与不定积分（6）微分方程的基本概念（7）参数方程与极坐标方程二、典型题型解题技巧1. 集合与逻辑（1）对于集合的运算，要熟练掌握并运用交、并、差、补集等运算。

（2）在命题与联结词的运用中，要能够准确理解并灵活运用“非”、“或”、“与”等联结词的含义及其在逻辑命题中的应用。

（3）在命题公式的演算中，要善于利用等值演算将命题公式转化成合取或析取范式，以求解相关问题。

2. 代数与数论（1）对于复数的运算，要熟练掌握复数的加减乘除运算，并在解题过程中灵活运用复数的性质和运算规律。

（2）在多项式的整除与因式分解中，要善于运用求因式分解的方法，并能够准确判断多项式的整除性。

（3）对于素数与合数、模运算、同余等知识点，要能够理清概念，掌握相关定理，并能够灵活应用于解题过程中。

3. 几何与简单的变量（1）在直线的方程与三角函数的概念与运算中，要善于利用直线的斜率与截距，以及三角函数的相关性质，解决与直线、三角函数相关的几何问题。

（2）对于空间解析几何、坐标与原点、斜率与截距等知识点，要善于利用坐标系方法，灵活运用相关几何知识，解决几何问题。

4. 极限与微积分（1）在极限与无穷小、函数的极限等知识点中，要善于利用夹逼定理、无穷小量的性质、函数极限的计算方法，解决极限问题。

2023-2024年考研《数学》必备知识点考点汇编

考研数学公式整理1 1.等价代换的补充2.泰勒公式3.基本导数公式4.几个常用函数的高阶导数5.不定积分的基本积分公式6.定积分性质7.渐近线8.微分中值定理考研数学公式整理2 ⚫二重积分的性质⚫对称性⚫ 莱布尼茨判别法则⚫麦克劳林级数⚫狄利克雷收敛定理⚫奇偶函数的傅里叶级数⚫常用的二次曲面考研数学公式整理31.行列式的性质()()()11121311121321222321222331323331323311111212131321222331.0,0.,.,.T A A k k ka ka ka a a a a a a k a a a a a a a a a a b a b a b a a a a ==+++行列互换,其值不变,即某行列全为则行列式的值为某行列有公因子则可把提到行列式外面某行列每个元素都是两个数之和则可拆成两个行列式之和性质1 性质2 性质3 性质4 ()()()11121311121321222321222332333132333132331112131112132122231121122213313233..0..a a ab b b a a a a a a a a a a a a a a k a a a a a a a a a ka a ka a ka a a a =+=++两行列互换,行列式的值变号两行列元素相等或对应成比例,则行列式的值为某行列倍加到另一行（列）,行列式的值不变性质5 性质6 性质7 23313233a a a a +2.抽象型行列式—解法解题思路：对抽象型行列式,计算方法主要是利用行列式的性质，矩阵的性质，特征值及相似等。

主要的公式有:11112121.,2.,3.,4.5.6.,,,,7..T T n n n n A n A A A A A n kA k A A B n AB A B A n A AA n A A n A A n AB A B λλλλλλ−*−−=======L L 若是阶矩阵是的转置矩阵,则；若是阶矩阵则；若都是阶矩阵,则；若是阶矩阵,则；若是阶可逆矩阵,则；若是阶矩阵的特征值则；若阶矩阵与相似,则4.逆矩阵的性质()()111111111111;10;;.A A kA A k k AB B A AA AB A B −−−−−−−−−−−−==≠==+≠+1）（）2）（）3）（）；4）没公式特别注意:5.逆矩阵—解法()()()()111111111110,..,,,.0000.0000A A A AA E E A AB n AB E A B A B AB A A A B B BB A*−−−−−−−−−−−≠=→==+⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦若则都是阶矩阵则对型化为型.；方法一:用伴随方法二:用初等变换方法三:用定义方法四:用单位矩阵恒等变形方法五:用分块公式6.矩阵的秩定理8.具体向量组如何判定相关无关()()1212121212,,,,,,0,,,1.,,,,,,00.m m m n n x r m m n n n n ααααααααααααααα⇔=⇔<=+⇔=≠L L L L L 对具体（含参数）向量组如何判定相关无关？向量组相关（无关）齐次方程组有非零解（只有零解）（向量个数）（（向量个数））.个维向量必相关个维向量相关（无关）（）定理1推论1推论21212112121212,,,,,,,,,,,,,,,,,,,,,m m m m nm m m r m ααααααααβββααααααβββ++−⎧⎨⎩⎧⎨⎩L L L L L L L 若向量组相关,增加个数后的向量组则仍相关；对应减少向量坐标后的向量组若向量组无关,减少个数后的向量组则仍无关.对应增加向量坐标后的向量组定理29.抽象向量组如何证明无关10.特征值和特征向量的性质11.相似矩阵的性质()()111,.A B nnii ii i i A B A B r A r B E A E B a b λλλλ==⇒=⇒=⇒−=−=⇒=∑∑:（）（必要条件）；；即；()()()11112,,,,,,,.n n n n n n A B P AP B P A kE P B kE P A P B A B A kE B kE A kE B kE r A kE r B kE A B A B A PB P −−−−=+=+=+++=++=+=:::::（）如设则因此由要想到进而；由要想到进而可用相似求 12.矩阵相似对角化的条件()()11,0.n i i nTn ii i A A n A i i n r E A i A n A r A A A a λλαβ=Λ⇔⇔−−=⇐⇐==Λ⇔≠∑::有个线性无关的特征向量；的重特征值有个无关的特征向量,即；有个不同的特征值；是实对称阵.对或的矩阵注:13.正定定理()12,,,0,0000,T n T ii f x x x x Ax x x Ax A A A a A =⇔∀≠>⇔⇔≤L 二次型正定有；的特征值都大于；的全部顺序主子式大于.若的主对角线某元素则必不正定.定理4注:14.等价、相似、合同()(),.,.A B A B A B A B A B P Q PAQ B r A r B ≅⇔=⇔=两个同型矩阵与,若可经过初等变换变成称与等价,记作同型矩阵矩阵与等价存在可逆矩阵和使；判定1,,,.,,A B P P AP B A B A B A B A B A B A B A B A B −=ΛΛΛ::::两个方阵与若存在可逆矩阵使称与相似,记作若与的迹或秩或行列式或特征值不相等,则与不相似；若,但不能对角化则与不相似；若,且则与相似.判定,,,..T T T A B C C AC B A B A B A B x Ax x Bx A B =⇔⇔:两个实对称矩阵与若存在可逆矩阵使称与合同,记作实对称矩阵与合同二次型和有相同的正、负惯性指数；实对称矩阵与有相同的正、负特征值个数判定考研数学公式整理41.概率基本公式()()()()()()()()()()()()()()()()()()1.=.3.=..P A P A P A B P A P B P AB P A B C P A P B P C P AB P AC P BC P ABC P A B P A P AB P AB =−+−=++−−−+−−=U U U 正面直接求概率困难时可考虑此公式,比如涉及"至少、至多"等字眼.超过个事件的加法公式往往会有两两互斥的条件考减法公式是考试的重点；(1)逆事件的概率（2）加法公式（3）减法公式注：注：注： ()()()()()()()()()()()()0,,=.1;.P A A B P AB P B A P B A P A P B A P B A P B A P B C A P B A P BC A P BC A >=−−=−= 若称在发生的条件下,发生的概率为条件概率记为,且条件概率也是概率,满足概率的一切性质与公式,如（4）条件概率注:()()()()0,=.P A P AB P A P B A >⋅如果则（5）乘法公式()()()()121=,,1,,.,.n i j ni i i i A A A A A i j n B P B P A P B A B A B P B =Ω=Φ≤≠≤=∑U UL U I 若且则对任一事件有如果某个事件的发生总是与某些原因或前一阶段的某些结果有关则总是使用全概率公式把各种导致发生的可能性（概率）加起来求（6）全概率公式注:()()()()()()()121=,,1,0,.,,.n i j i jj niii j j A A A A A i j n P A P B A B P B P A B P A P B A B A P A B =Ω=Φ≤≠≤>=∑U UL U I 若且,则对任一事件只要则如果已知发生了去探求是某原因导致发生的可能性（概率）则总是使用贝叶斯公式看这一原因占总的原因的比例注（7）贝叶斯公式 :2. 独立与互斥、包含的关系()()01,01,,P A P B A B A B <<<<设如果与互斥或存在包含关系则与不独立.3.常见的分布{}()(){}()()()1011,0,1.0101,1,.1,0,1,,.,01,,.12,,kk n k k kn X P X k p p k X p p X B p X P X k C p p k n X n p p X B n p n X X B n p −−−==−=<<−==−=<<:L ::1.分布如果随机变量的分布律为则称服从参数为（）的分布记为2.二项分布如果随机变量的分布律为则称服从参数为（）的二项分布记为（）次伯努利试验中试验成功的次数服从二项分布；（）对最可能发生（成注:()(){}(){}()()1111.,0,1,2,!0,.1,1,2,1,.k k k n p k n p e X P X k k k X X P X P X k p p k X p p X G p X λλλλλ−−+−≤≤+===>==−=<<L:L:功）的次数满足3.泊松分布如果随机变量的分布律为则称服从参数为（）的泊松分布记为4.几何分布如果随机变量的分布律为则称服从参数为（0）的几何分布记为伯努利试验中首次成功所需的试验次数服从几何分布.注:()()()()(){}5.1,,0,0,,,,.,.1,,,,.a x b X f x b a x a x a X a b X U a b X F x a x b b a x b d cX U a b a c d b P c X d b a⎧<<⎪=−⎨⎪⎩<⎧⎪−⎪=≤<⎨−⎪≥⎪⎩−≤<≤<<=−::均匀分布如果随机变量的概率密度为其他则称服从上的均匀分布记为的分布函数为若对则注: ()()()(){}{}{}o o ,0,00,1,0..0,0,10,;2,0,.x x a e x X f x e x X X E X F x x X E a P X a e t s P X t s X s P X t λλλλλλλλ−−−⎧>=>⎨⎩⎧−≥=⎨<⎩∀>≥=∀>≥+≥=≥::6.指数分布如果随机变量的概率密度为其中为参数;其他则称服从参数为的指数分布,记为的分布函数为若则对则对则注:()()()()()()()()()()()()()222222222o 2o ,.,,,.,0,10,1;,;.1,,0,1;21,0x x x x x X f x x X X N X N x x x t dt dt X X N N x x μσμσμσμσϕϕμμσσ−−−−−∞=−∞<<+∞===−∞<<+∞Φ==−Φ−=−ΦΦ=⎰⎰::::7.正态分布如果随机变量的概率密度为:则称服从参数为的正态分布记为特别地当时称为记为概率密度分布函数若则标准化标准正态分布,注:()()o 222o 1;23,,,;4,X N aX b N a b a X Y aX bY μσμσ+++::若则若分别服从正态分布,且相互独立,则服从正态分布.4. 两个常见的二维连续型随机变量1.二维均匀()()()()(){},,1,,,0,,,,,D D GDX Y D X Y DS f x y S D S X Y D G D P X Y G S ⎧∈⎪=⎨⎪⎩⊂∈=在平面区域上服从均匀分布则，其中是的面积.其他设在区域上服从均匀分布若则；注:2.二维正态()()()()()222212121212221122,,,,;.,,,;1,1.,,,,,,,,0.X Y N EX EY DX DY X N Y N X Y aX bY X Y X Y μμσσρμμσσρμσμσρ====∈−+⇔=:::其中（1）反之不对（独立时可以）；（2）的条件分布都是正态分布；（3）服从正态分布；（4）独立不相关即注:5.期望{}()()()()()()()()()()111,2,,.,.i i i i i i i i X P X x p i Y g X X EX x p Eg X g x p X f x Y g X X EX xf x dx Eg X g x f x dx ∞∞==+∞+∞−∞−∞=========∑∑⎰⎰L 设离散型随机变量的分布律为是的函数,则；设连续型随机变量的概率密度为是的函数,则；（1）一维离散型（2）一维连续型(){}()()()()()()()()()()()()11,,,1,2,,,,,,.,,,,,,,,.i j iji j ij i j X Y P X x Y y p i j Z g X Y X Y Eg X Y g x y p X Y f x y Z g X Y X Y Eg X Y g x y f x y dxdy ∞∞==+∞+∞−∞−∞========∑∑⎰⎰L 设二维离散型随机变量的联合分布为是的函数,则设二维连续型随机变量的联合概率密度为是的函数,则（3）二维离散型（4）二维连续型()()()o o o o 1234,,.Ec c E aX c aEX c E X Y EX EY X Y E XY EX EY =+=+±=±=⋅；；；若独立则（5）性质6.方差()()222.DX E X EX EX EX =−=−（1）定义()()()()()()()()2o 2o o 2o o 2210,;20342,5,,,.DX EX EX DX Dc D aX b a DX D X Y DX DY Cov X Y X Y D X Y DX DY D XY DXDY DX EY DY EX ≥=+=+=±=+±±=+=++；；；若独立则（2）性质7.常用分布的数学期望和方差()()()()()()()()()()()o o o o 22o o 2o 22o 11,,12,,13,114,5,,212116,7,,280,11.X B p EX p DX p p X B n p EX np DX np p X P EX DX p X G p EX DX p pb a a bX U a b EX DX X E EX DX X N EX DX X N E X D X λλλλλλμσμσπ==−==−==−==−+========−::::::::如果,则；如果,则；如果,则；如果,则；如果,则；如果,则；如果,则；如果,则8.协方差()()()()()()()()()()()()()()()o oo o 121211122122,.1,,,,2,03,,,,,,,.Cov X Y E X EX Y EY E XY EX EY Cov X Y Cov Y X Cov X X DX Cov X c Cov aX bY abCov X Y Cov aX bX cY dY acCov X Y adCov X Y bcCov X Y bdCov X Y =−−=−⋅⎡⎤⎣⎦====++=+++；；；4（1）定义（2）性质9.相关系数,0,.XY XY Cov X Y X Y ρρ==如果称和不相关（1）定义{}oo o o 1123=1,11,04,1,0XY YX XX XY XY XYa b P Y aX b a Y aX b a ρρρρρρ==≤⇔=+=>⎧=+=⎨−<⎩；；1；存在使；如果则.（2）性质10.大数定律1.依概率收敛{}1212,,,,,,0,lim 1,,,,,,,.n n n Pn n X X X a P X a X X X a X a εε→∞>−<=⎯⎯→L L L L 对随机变量序列和常数如果对任意的有则称随机变量序列依概率收敛于记为2.切比雪夫大数定律1211,,,,,,,1,2,,110,lim 1.n k k k n ni i n i i X X X EX DX DX k P X EX n n εε→∞===⎧⎫>−<=⎨⎬⎩⎭∑∑L L L 设独立,期望方差都存在,方差有一致上界则对任意的有3.伯努利大数定律(),,,,0,lim 1.n X n A A p X X B n p P p n εε→∞⎧⎫>−<=⎨⎬⎩⎭:设是重伯努利试验中事件发生的次数每次试验事件发生的概率为即则对任意的有4.辛钦大数定律1211,,,,,,0,lim 1.n n k i n i X X X EX P X n μεμε→∞=⎧⎫=>−<=⎨⎬⎩⎭∑L L 设独立同分布,期望存在则对任意的有11.中心极限定理1.列维—林德伯格中心极限定理()22122,,,,,,,,lim .n k k n t i x n X X X EX DX X n x P x dt x μσμ−−∞→∞==⎧⎫−⎪⎪⎪≤==Φ⎬⎪⎪⎪⎩⎭∑⎰L L 设独立同分布期望方差都存在,则对任意的有2.拉普拉斯中心极限定理()()22,,lim .t x n X B n p x P x dt x −→∞⎧⎫⎪≤==Φ⎬⎪⎭⎰:设,则对任意的有12.三大抽样分布()()()()(){}()()()()()()()2122222222212122222222,,,01,,.01,,,2;n n n n X X X N X X X n X X X n P n n f x dx f x n n n X n EX n DX n X ααχαχχααχχαχχχαχχ+∞++++++<<>====⎰L L L :::设相互独立且都服从标准正态，则服从自由度为的分布记为对于给定的（）称满足（是的概率密度）的数为的上分位点.若则若221.χn 分布（1）定义：（2）上α分位点（3）χ分布的性质()()()221212,,,.n Y n X Y X Y n n χχ++::,且独立则()()()()(){}()()()()()()()()()()()()21201,,,,.01,,,01,1,t n X N Y n X Y n t t n P t n t n fx dx fx t n t n t n t f x t n t n n t n N t t n t F αααααχαααα+∞−<<>===−⎰:::::设，且独立，的分布对于给定的（）称满足（是的概率密度）的数为的上分位点.分布的概率密度是偶函数故,且当自由度充分大时分布近似于，；则2.t 分布（1）定义：（2）上α分位点（3）t 分布的性质().n()()()()(){}()()()()()()()122212111212221212,12121212,,,,,.01,,,,,,1,,F n n X n Y n X Y X Xn n n n F F n n Y Y n n P F n n F n n f x dx f x F n n F n n F n n F F n n F Fαααχχαααα+∞<<>==⎰:::::设且独立，则服从第一自由度为,第二自由度为的分布记为对于给定的（）称满足（是的概率密度）的数为的上分位点.若则3.F 分布（1）定义：（2）上α分位点（3）F 分布的性质()()()()211211221,1,,,.,n n F F n n F n n F n n αα−=:；若则13.矩估计的求法1222111,...11()n kk k k i i n ni ii i A X EX n X EX X EX X EX X EX X X DX n n α======⎧⎧==⎪⎪⎨⎨=−=⎪⎪⎩⎩∑∑∑：用样本矩替换总体矩——即：对一个未知参数的情形令对两个未知参数的情形令或原理步骤14.最大似然估计的求法()()()()121121.,,,;,,,,;,.ln ln .0,.ln 0,ln .i nn i i i nn i i a L x x x f x L x x x p x b Ld L c d d L L d θθθθθθθθ=====⎡⎤⎣⎦=⎡⎤⎣⎦==∏∏L L ：写出样本的似然函数取对数得求导解出即可若无解即单调,则应该用定义法找出的最大似然估计量步骤连续型离散型15.估计量的评价标准121212,.,,,.0,lim 1,,Pn E D D P θθθθθθθθθθθεθθεθθθθ∧∧∧∧∧∧∧∧∧∧∧→∞=<⎧⎫>−<=⎯⎯→⎨⎬⎩⎭若则称是的无偏估计量设都是的无偏估计量若则称比更有效若对任意的有即则称是的一致估计量.（1）无偏性（2）有效性（3）一致性16. 求置信区间的步骤{}1212,,12:,,.T a b P a T b a T b ααθθθθθθ∧∧∧∧<<=−⎛⎫<<<< ⎪⎝⎭（1）构造统计量并确定其分布；（2）给定,确定常数使得；（3）由（）反解出的范围得置信区间。

考研数学三知识点总结

重要极限 lim
x →0
sinx =1 x
1 x lim ( 1 + ) = e x x →∞
lim ( 1 + x ) =e
x →0
1 x
x 趋向于 0 时的等价无穷小
sinx ∼ x tanx ∼ x arcsinx ∼ x arctanx ∼ x 1 2 1− cosx∼ x 2
ln ( 1 + x )∼ x
n 1+ x − 1 ∼ √
log a ( x +1 )∼
x lna
e x −1∼ x
a x −1∼ xlna
x n
( 1+bx )a−1 ∼abx
导数公式 ( a x )' = a x lna ( tanx )' = sec 2 x ( arcsinx )' = 1 √1− x 2
( log a x ) =
1 2 圆锥体积 V = π r h 3
4 3 球体积 V = π r 3
交点坐标 (
p ,0) 2
准线 x =−
p 2Βιβλιοθήκη ∣ax 0+by 0+ c∣
√a 2 +b2
第一类间断点：包括可去间断点和跳跃间断点。可去间断点：间断点处左右极限存在但不等于该点函数值。 f ( x 0+ 0 )= f ( x 0− 0 )≠ f ( x 0) 跳跃间断点：间断点处左右极限存在但不相等。 f ( x 0+ 0 )≠ f ( x 0−0 ) 第二类间断点：间断点处左右极限至少有一个是∞
cos ( A+ B)=cosAcosB + sinAsinB sin ( A+ B )= sinAcosB + cosAsinB 1 sinxcosx = sin2x 2

数学三考研常见的知识点解析

知识点1：二重积分对称性问题数学三考研对于二重积分对称性问题，要弄清这个问题首先就是要解决二重积分坐标变换的问题，首先是对二重积分坐标变化的引理，也就是通过什么样的坐标变换，使得积分的值不变，以及极坐标变换中r,为什么会出现，上述公式有以下几个意思第一点经过此坐标变换积分的值不改变，第二点坐标变化应该是一对一的，只有这样才能保证积分的值不变，第三点关于极坐标变换的r,其本质是雅可比行列式的值，也可以说是.),()],(),,([),(:)3(;0),(),(),()2(),(),,()1(),(),,(:),(⎰⎰⎰⎰=→'≠∂∂='''==D D dudv v u J v u y v u x f dxdy y x f D D T v u y x v u J D D v u y v u x D xoy D uov v u y y v u x x T D xoy y x f 是一对一的，则有变换上雅可比式在；上具有一阶连续偏导数在且满足，平面上的变为平面上的闭区域将连续，变换上平面上的闭区域在设定理积分复合函数的性质，所以在做极坐标变化的题目的时候，应注意关于后缀r 的书写由上面的坐标变化我们引出对于二重积分对称性的证明，首先看第一条性质，关于函数对称性问题性质一的证明我们可以用上面来证明，说一下思路，我们可以进行坐标变换如果积分区域关于x 轴对称那么我们采用坐标变换x 的值保持不变y 值变为(-t)，那么在xot 的坐标下积分的值是不变，（用上面的坐标变换定理），所以dxdt t x f xdy y x f d p ⎰⎰⎰⎰-=21),(d ),( 又由()⎰⎰==1)-,(,1d y ,x f d y x f t y x x y 积分公式就变为了那么积分区域就变成了变换使得的奇函数，在经过坐标是关于函数由于函数是y 的奇函数所以dxdy y x f dxdy y x f dxdy y x f dxdy y x f dxdy y x f d d d d ⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰-+=+=11d 12),(),(),(),(),(所以如果y 是奇函数那么我们就能得到积分结果为零所以结论的证！知识点2：什么是自由度统计学上的自由度（degree of freedom, df ），是指当以样本的统计量来估计总体的参数时，样本中独立或能自由变化的数据的个数称为该统计量的自由度。

数学三考研常见的知识点解析

数学三考研常见的知识点解析数学三是考研数学的一部分，主要涵盖了高等数学和线性代数的内容。

下面将对数学三考研常见的知识点进行解析。

一、高等数学1.常见函数及其性质：常见函数有多项式函数、指数函数、对数函数、三角函数等。

在考研中，需要掌握这些函数的基本性质，如定义域、值域、奇偶性、单调性等。

2.极限与连续：极限是高等数学的重要概念之一、需要掌握数列极限和函数极限的求解方法，如夹逼准则、洛必达法则等。

此外，连续函数的判定与性质也是考试重点，例如连续函数与间断点、连续函数的运算性质等。

3.导数与微分：导数是函数的变化率，微分是导数的微小增量。

需要熟练掌握导数的定义和求导法则，如基本初等函数的导数、链式法则、隐函数求导等。

此外，还需要理解函数的凸凹性与极值点的求解方法。

4.定积分与不定积分：定积分是求函数在一定区间上的面积，不定积分是求函数的原函数。

需要熟练掌握定积分与不定积分的定义和性质，如牛顿-莱布尼茨公式、变量替换法、分部积分法等。

5.级数与幂级数：级数是无穷项数列的和，幂级数是形如∑(a_n*x^n)的级数。

需要掌握级数和幂级数的收敛性判定方法，如比较判别法、根值判别法、幂函数展开等。

二、线性代数1.矩阵与行列式：矩阵是二维数组，行列式是一个数。

需要了解矩阵的基本运算，如加法、乘法、转置运算等。

行列式的运算包括展开法、伴随矩阵法、逆矩阵法等。

2.向量与线性方程组：向量是有方向和大小的量，线性方程组是一组线性方程的集合。

需要掌握向量的基本运算，如加法、数量积、向量积等。

对于线性方程组，需要掌握高斯消元法、矩阵法、矩阵的秩等解法。

3.特征值与特征向量：特征值是矩阵对应的线性变换中的固有值，特征向量是与特征值对应的非零向量。

需要了解特征值与特征向量的求解方法，如特征方程的根、特征向量的求解等。

4.正交与正交对角化：正交是指向量间的垂直关系，正交矩阵满足乘积为单位阵。

正交对角化是将一个矩阵通过正交变换转化为对角矩阵。

考研数学知识点总结

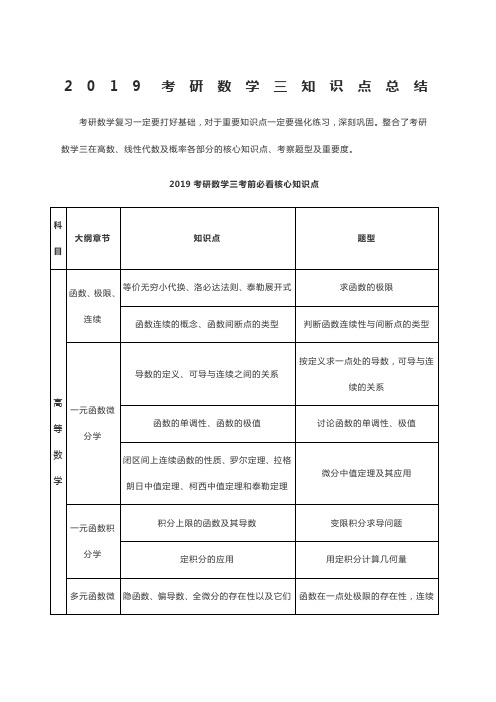
2019考研数学三知识点总结考研数学复习一定要打好基础，对于重要知识点一定要强化练习，深刻巩固。

整合了考研数学三在高数、线性代数及概率各部分的核心知识点、考察题型及重要度。

2019考研数学三考前必看核心知识点科目大纲章节知识点题型高等数学函数、极限、连续等价无穷小代换、洛必达法则、泰勒展开式求函数的极限函数连续的概念、函数间断点的类型判断函数连续性与间断点的类型一元函数微分学导数的定义、可导与连续之间的关系按定义求一点处的导数，可导与连续的关系函数的单调性、函数的极值讨论函数的单调性、极值闭区间上连续函数的性质、罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理微分中值定理及其应用一元函数积分学积分上限的函数及其导数变限积分求导问题定积分的应用用定积分计算几何量多元函数微隐函数、偏导数、全微分的存在性以及它们函数在一点处极限的存在性，连续积分学之间的因果关系性，偏导数的存在性，全微分存在性与偏导数的连续性的讨论与它们之间的因果关系二重积分的概念、性质及计算二重积分的计算及应用无穷级数级数的基本性质及收敛的必要条件，正项级数的比较判别法、比值判别法和根式判别法，交错级数的莱布尼茨判别法数项级数敛散性的判别常微分方程一阶线性微分方程、齐次方程，微分方程的简单应用用微分方程解决一些应用问题线性代数行列式行列式的运算计算抽象矩阵的行列式矩阵矩阵的运算求矩阵高次幂等矩阵的初等变换、初等矩阵与初等变换有关的命题向量向量组的线性相关及无关的有关性质及判别法向量组的线性相关性线性组合与线性表示判定向量能否由向量组线性表示线性方程组齐次线性方程组的基础解系和通解的求法求齐次线性方程组的基础解系、通解矩阵的特征值和特征向量实对称矩阵特征值和特征向量的性质，化为相似对角阵的方法有关实对称矩阵的问题相似变换、相似矩阵的概念及性质相似矩阵的判定及逆问题二次型二次型的概念求二次型的矩阵和秩合同变换与合同矩阵的概念判定合同矩阵概率论与数理统计随机事件和概率概率的加、减、乘公式事件概率的计算随机变量及其分布常见随机变量的分布及应用常见分布的逆问题多维随机变量及其分布两个随机变量函数的分布二维随机变量函数的分布随机变量的独立性和不相关性随机变量的独立性随机变量的数字特征随机变量的数学期望、方差、标准差及其性质，常用分布的数字特征有关数学期望与方差的计算大数定律和中心极限定理大数定理用大数定理估计、计算概率数理统计的常用统计量的性质求统计量的数字特征基本概念参数估计点估计、似然估计点估计与似然估计的应用知识点口诀，掌握解题技巧。

2023考研数学三

2023考研数学三引言2023年考研数学三科目是考研数学中的一门重要科目，也是考研数学中难度较大的科目之一。

本文将介绍考研数学三科目的考试内容、考试形式以及备考方法，帮助考生更好地应对2023年考研数学三科目的考试。

考试内容2023年考研数学三科目主要考察的内容包括数理统计基础知识、数理统计方法和应用以及常微分方程与动力系统。

具体来说，考试内容涵盖以下几个方面：1.概率论基础：包括事件与概率、条件概率与独立性、随机变量及其分布、数学期望和方差等基本概念。

2.数理统计基础：包括统计量、抽样分布以及点估计和区间估计等基本知识。

3.统计方法与应用：包括参数估计、假设检验、方差分析、回归分析等常用的统计方法和应用。

4.常微分方程与动力系统：包括一阶常微分方程和高阶常微分方程的解法、线性方程系统以及动力学系统等内容。

考试形式2023年考研数学三科目的考试形式将分为两个部分，分别是选择题和解答题。

选择题部分主要考察考生对基本概念和基本知识的掌握程度，以及计算和推理的能力。

该部分共包含多道选择题，每个选择题后面有四个选项，考生需要选择正确的答案。

解答题部分主要考察考生的问题解决能力和数学建模能力。

该部分共包括若干道解答题，每个问题都需要考生进行详细的解答和推理。

整个考试的时间约为120分钟，考生需要合理安排时间，以确保每道题都有足够的时间来思考和解答。

备考方法考生在备考2023年考研数学三科目时，可以参考以下几个备考方法：1.认真复习基础知识：数学三科目中的内容相对较多，因此要先确保自己对基础知识有牢固的掌握。

可以通过阅读教材、做习题集等方式来巩固基础知识。

2.多做题、多总结：选择题部分在考试中占比较大，因此要多做选择题，并及时总结错题和易错点。

解答题部分则需要多进行练习和模拟考试，以增强解答问题的能力。

3.制定合理的复习计划：考试时间有限，因此要合理安排复习时间，并将重点放在重要知识点和容易出错的地方。

可以制定每天的复习计划，并按计划进行复习。

考研数学3知识点总结

考研数学3知识点总结一、实变函数1. 极限和连续实变函数的极限是指当自变量逼近某个确定值时，函数的取值也逼近一个确定值。

极限的概念是实变函数中最为基础的概念之一，它是后续讨论的连续性、导数等概念的基础。

连续性是一个函数在某一点上的性质，如果这个函数在这一点可导，那么它在这一点也是连续的。

连续的函数具有一些良好的性质，如介值定理、零点定理等。

2. 导数和微分导数是实变函数中的一个重要概念，它描述了函数在某一点上的变化率。

导数的概念与实际问题密切相关，例如速度、加速度等概念都可以通过导数来描述。

微分是导数的几何意义，微分可以看作是对函数在某点上的局部线性逼近，这对于研究函数的增长趋势、凹凸性等问题有很大的帮助。

微分也是求解微分方程的一种工具。

3. 级数级数是一种无穷序列的和的形式，级数的收敛性和敛散性是实变函数中的一个重要问题。

级数的收敛性可以通过不同的方法来判断，比如比较法、根值法、积分法等。

4. 泰勒级数和泰勒展开泰勒级数是一个函数在某一点附近的一种无穷级数表示。

泰勒级数的性质决定了当自变量足够靠近展开点时，函数的值可以用泰勒级数来近似表示。

泰勒展开是对函数的泰勒级数的一种应用，它可以用来求解函数的近似值，研究函数的性质等。

5. 不定积分不定积分是函数积分的一种形式，它可以用来描述函数的原函数。

不定积分的计算方法有很多，比如换元法、分部积分法、积分表法等，学习不定积分需要掌握这些方法的应用。

6. 定积分定积分是函数在一个区间上的积分，它可以用来描述函数在这个区间上的累积效应，比如曲线所围成的面积、质量、能量等。

定积分有很多重要的性质，比如微积分基本定理、平均值定理等。

7. 微分方程微分方程是一种包含未知函数及其导数的方程，它在自然科学、工程技术等领域中有着广泛的应用。

微分方程的求解方法有很多，比如常数变易法、特征方程法、拉普拉斯变换法等。

二、复变函数1. 复数和复变函数复数是实数集的扩充，它具有形式为a+bi的特点，其中a和b为实数，i为虚数单位。

今年考研数学三知识点总结

今年考研数学三知识点总结一、高等数学高等数学是数学的一个重要分支，考研数学三中最基础的一个知识点，这里我们主要涵盖了微积分和线性代数两个方面的内容。

1. 微积分微积分是数学的一个重要分支，由于它在实际中具有广泛的应用，所以在考研数学中也是一个非常重要的知识点。

微积分的内容很多，包括导数、积分、微分方程等。

导数是微积分中的一个基本概念，它代表了函数在某一点的变化率。

在考研数学三中，导数的应用非常广泛，比如在求解极值、最值、曲线的凹凸性等方面都会用到导数的知识。

积分是微积分中的另一个基本概念，它代表了函数在某一区间内的累积变化量。

在考研数学三中，积分的应用也非常广泛，比如在求解面积、体积、曲线的长度等方面都会用到积分的知识。

微分方程是微积分的一个重要分支，它是用来描述变化的规律的方程。

在考研数学三中，微分方程的应用也非常广泛，比如在物理、生物、经济等领域都会用到微分方程的知识。

2. 线性代数线性代数是数学的一个重要分支，它主要涉及向量、矩阵、线性方程组等内容。

在考研数学三中，线性代数的知识点也是非常重要的。

向量是线性代数中的一个基本概念，它是用来表示空间中的方向和大小的。

在考研数学三中，向量的知识点涉及到向量的加法、数量积、向量积等内容。

矩阵是线性代数中的另一个基本概念，它是用来表示线性变换的矩形数组。

在考研数学三中，矩阵的知识点涉及到矩阵的运算、矩阵的秩、逆矩阵等内容。

线性方程组是线性代数中的一个重要概念，它是用来求解多元线性方程组的方法。

在考研数学三中，线性方程组的知识点涉及到线性方程组的解的判别、线性方程组的解的存在性和唯一性等内容。

以上是高等数学的一些基本知识点，在考研数学三中也是最为重要的内容。

二、概率统计概率统计是数学的一个重要分支，它主要涉及概率和统计两个方面的内容。

概率统计在现实中有很多应用，比如在科学、工程、经济等领域都会用到概率统计的知识。

考研数学三中，概率统计的知识点主要包括概率的基本概念、随机变量、概率分布、参数估计、假设检验等内容。

2024年考研数学知识模块大总结

2024年考研数学知识模块大总结随着每年考研的临近，考研数学成为了很多考生关注的焦点。

对于即将参加2024年考研的考生来说，了解数学知识模块的内容及重点是非常重要的。

下面是对2024年考研数学知识模块的大总结。

一、高等代数在高等代数模块中，重点关注以下几个方面的知识：1. 向量空间：- 向量空间的定义与性质- 子空间、张成空间和线性无关的概念- 基和维数- 线性映射和线性变换的概念与性质- 线性映射的矩阵表示和线性变换的标准矩阵2. 矩阵理论：- 矩阵的运算与性质- 矩阵的秩、特征值和特征向量- 矩阵的相似和对角化- 正交矩阵和正交对角化- 矩阵的特征分解和奇异值分解3. 行列式与线性方程组：- 行列式的定义和性质- 行列式的计算和性质- 矩阵的秩与线性方程组的解的关系- 线性方程组的解的存在唯一性和解的结构二、数学分析数学分析是考研数学中最重要的模块之一，重点关注以下几个方面的知识：1. 极限与连续：- 数列极限和函数极限的定义与性质- 极限的四则运算和极限存在准则- 连续函数的定义与性质- 闭区间上连续函数的性质- 极值和最值2. 导数与微分：- 导数的定义与性质- 高阶导数与高阶导数的运算- 微分的定义与性质- 高阶微分与泰勒公式- 函数的凸凹性与最值3. 积分与级数：- 不定积分和定积分的定义与性质- 积分的基本公式和换元法- 数值积分和定积分的应用- 广义积分的收敛性和计算- 级数的概念与性质- 收敛级数和判别法三、概率论与数理统计在概率论与数理统计模块中，重点关注以下几个方面的知识：1. 概率论基础：- 随机试验、样本空间和事件的概念- 概率的定义与性质- 条件概率和独立性- 事件的全概率公式和贝叶斯公式- 随机变量和分布函数的概念- 离散型和连续型随机变量的分布函数2. 数理统计基础：- 参数估计与点估计- 最大似然估计和矩估计- 区间估计和假设检验- 正态总体的参数估计与假设检验- 卡方检验和t检验的应用3. 随机过程与统计推断：- 随机过程、马尔可夫链和隐马尔可夫模型- 统计推断的基本原理和方法- 极大似然估计和贝叶斯估计- 模型检验和参数估计的统计性质- 时间序列分析和回归分析的应用四、线性规划与组合数学线性规划与组合数学是考研数学中的辅助模块，重点关注以下几个方面的知识：1. 线性规划：- 线性规划的基本概念和最优性条件- 单纯形法和对偶性理论- 整数规划和0-1整数规划- 网络流和线性规划的应用2. 图论与组合数学：- 图的基本概念和性质- 连通性和最小生成树- 图的着色和Hamilton回路- 动态规划和组合数学的基本方法以上是对2024年考研数学知识模块的大总结。

2021年考研数学三知识点总结

2021年考研数学三知识点总结考研数学复习一定要打好基础，对于重要知识点一定要强化练习，深刻巩固。

下面整合了考研数学三在高数、线性代数及概率各部分的核心知识点、考察题型及重要度，2021考生参考。

2021考研数学三考前必看核心知识点科目大纲章节知识点题型高等数学第一章函数、极限、连续等价无穷小代换、洛必达法则、泰勒展开式求函数的极限函数连续的概念、函数间断点的类型判断函数连续性与间断点的类型第二章一元函数微分学导数的定义、可导与连续之间的关系按定义求一点处的导数，可导与连续的关系函数的单调性、函数的极值讨论函数的单调性、极值闭区间上连续函数的性质、罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理微分中值定理及其应用第三章一元函数积分学积分上限的函数及其导数变限积分求导问题定积分的应用用定积分计算几何量第四章多元函数微积分学隐函数、偏导数、全微分的存在性以及它们之间的因果关系函数在一点处极限的存在性，连续性，偏导数的存在性，全微分存在性与偏导数的连续性的讨论与它们之间的因果关系二重积分的概念、性质及计算二重积分的计算及应用第五章无穷级数级数的基本性质及收敛的必要条件，正项级数的比较判别法、比值判别法和根式判别法，交错级数的莱布尼茨判别法数项级数敛散性的判别第六章常微分方程一阶线性微分方程、齐次方程，微分方程的简单应用用微分方程解决一些应用问题线性代数第一章行列式行列式的运算计算抽象矩阵的行列式第二章矩阵矩阵的运算求矩阵高次幂等矩阵的初等变换、初等矩阵与初等变换有关的命题第三章向量向量组的线性相关及无关的有关性质及判别法向量组的线性相关性线性组合与线性表示判定向量能否由向量组线性表示第四章线性方程组齐次线性方程组的基础解系和通解的求法求齐次线性方程组的基础解系、通解第五章矩阵的特征值和特征向量实对称矩阵特征值和特征向量的性质，化为相似对角阵的方法有关实对称矩阵的问题相似变换、相似矩阵的概念及性质相似矩阵的判定及逆问题第六章二次型二次型的概念求二次型的矩阵和秩合同变换与合同矩阵的概念判定合同矩阵概率论与数理统计第一章随机事件和概率概率的加、减、乘公式事件概率的计算第二章随机变量及其分布常见随机变量的分布及应用常见分布的逆问题第三章多维随机变量及其分布两个随机变量函数的分布二维随机变量函数的分布随机变量的独立性和不相关性随机变量的独立性第四章随机变量的数字特征随机变量的数学期望、方差、标准差及其性质，常用分布的数字特征有关数学期望与方差的计算第五章大数定律和中心极限定理大数定理用大数定理估计、计算概率第六章数理统计的基本概念常用统计量的性质求统计量的数字特征第七章参数估计//。

考研333知识点总结

考研333知识点总结1. 集合与函数(1) 集合的概念与基本运算(2) 函数的概念、性质及其运算(3) 极限的定义与性质(4) 无穷级数的收敛与发散2. 一元函数微分学(1) 函数的连续性与可导性(2) 隐函数与参数方程、相关变化率(3) 微分中值定理及应用(4) 高阶导数与高阶导数的应用(5) 泰勒公式及泰勒展开(6) 不定积分和定积分的概念、性质与计算方法3. 一元函数积分学(1) 不定积分和定积分的概念、性质与计算方法(2) 微积分基本定理与定积分的应用(3) 微积分基本定理的应用和数值积分法(4) 定积分与无穷积分的收敛性(5) 积分中值定理及应用(6) 函数的可积性与积分存在的条件4. 无穷级数(1) 幂级数收敛半径的求法(2) 函数项级数的收敛性(3) 幂级数的性质与收敛域的研究(4) 幂级数的运算法则(5) 一般函数项级数的收敛性5. 空间解析几何(1) 向量的基本运算(2) 空间中的直线和平面(3) 空间中的曲线和曲面方程(4) 空间曲线与曲面的切线与法平面(5) 空间直线与平面的夹角与距离6. 多元函数微分学(1) 偏导数及其应用(2) 多元函数的微分中值定理(3) 方向导数与梯度(4) 隐函数与参数方程的微分(5) 多元函数的极值与条件极值(6) 多元函数微分的应用7. 重积分(1) 重积分的概念与性质(2) 罗尔定理的应用(3) 重积分的累次积分与直角坐标系下的三种重积分(4) 重积分的换序积分与坐标变换(5) 重积分的应用8. 常微分方程(1) 微分方程的基本概念与分类(2) 常系数线性微分方程(3) 高阶线性微分方程(4) 变系数线性微分方程(5) 线性微分方程的解法(6) 微分方程的应用9. 向量场与梯度、散度、旋度(1) 向量场的概念与性质(2) 梯度、散度、旋度的概念与运算法则(3) 一些特殊函数的梯度、散度、旋度(4) 散度定理、格林公式、斯托克斯公式与应用10. 数理方程(1) 初值问题、边值问题(2) 区段延拓与解的存在唯一性(3) 解的连续依赖(4) 线性化稳定性(5) 特殊非线性方程解的存在唯一性(6) 一些特殊非线性方程的解法11.特殊函数与级数(1) 单周期与多周期函数的展开(2) 傅里叶级数与傅里叶变换(3) 第二型贝塞尔函数与欧拉积分(4) 球谐函数与柱坐标系中的拉普拉斯方程(5) 约旦霍夫积分变换(6) 几类特殊级数的收敛性12. 实分析(1) 实数系与实数轴上的点集(2) 线性空间、巴拿赫空间、希尔伯特空间与完备性(3) 紧性、连通性、上确界和下确界、区间套(4) 对于一切实数的运算性质、连续复合函数的连续性(5) 函数的一致连续性、可积性(6) 影响函数的收敛极限的紧性和绝对收敛性13. 级数收敛法则(1) 积分判别法(2) 比较判别法(3) 极限判别法(4) 商判别法(5) 根判别法(6) 柯西-庞加莱准则14. 综合题型(1) 代数方程与不等式求解(2) 固体几何问题(3) 空间向量及其运算问题(4) 微分方程的题目(5) 多元函数极值、条件极值问题(6) 重积分的题目15. 工具公式(1) 积分工具公式(2) 微积分工具公式(3) 级数收敛法则(4) 固体解析几何工具公式(5) 空间向量工具公式(6) 多元函数微分工具公式以上就是考研数学中的333个知识点的总结，希望考生能够通过学习和复习，掌握这些知识点，为考研数学的复习和应试做好充分准备。

考研数学备考：数三中常考知识点

考研数学备考：数三中常考知识点1500字考研数学备考中，数学三是一个非常重要的科目。

它涵盖了较多的知识点，需要我们进行系统的学习和复习。

下面我将介绍一些数三中常考的知识点，供大家参考。

1. 极限与连续：- 函数极限的概念和性质，如极限存在准则、函数极限的四则运算、夹逼定理等。

- 数列极限的概念和性质，如数列极限的四则运算、夹逼定理等。

- 连续函数的定义和性质，如连续函数的四则运算、连续函数的复合、连续函数的保号性等。

2. 一元函数微分学：- 函数的导数和导数的基本运算法则，如常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数等的导数计算。

- 高阶导数的计算和应用，如泰勒公式、极值、凹凸性等。

- 隐函数的导数计算，如隐函数定理等。

3. 一元函数积分学：- 积分的基本概念和性质，如定积分的定义、定积分的性质、积分中值定理等。

- 基本积分公式和换元积分法、分部积分法的应用。

- 微积分基本定理，如牛顿—莱布尼茨公式等。

4. 多元函数微分学：- 多元函数的偏导数和偏导数的应用，如多元函数的全微分、多元函数的极值、隐函数偏导数计算等。

- 多元函数的方向导数和梯度，如方向导数的计算公式、梯度的计算公式等。

5. 多元函数积分学：- 二重积分和三重积分的概念和性质，如积分的可加性、积分的线性性质等。

- 二重积分和三重积分的计算方法，如极坐标法、累次积分法等。

- 曲线积分和曲面积分的概念和计算方法，如格林公式、斯托克斯公式等。

6. 常微分方程：- 常微分方程的基本概念和性质，如初值问题、解的存在唯一性等。

- 一阶常微分方程的求解方法，如分离变量法、齐次方程法、一阶线性常微分方程法等。

- 高阶常微分方程的求解方法，如常系数齐次线性方程、常系数非齐次线性方程等。

以上是考研数学三中常考的知识点的简单介绍。

备考过程中，我们需要系统地学习这些知识点，并进行大量的练习和习题训练，以提高自己的解题能力和应试水平。

同时，要善于总结归纳，将学过的知识点整理成思维导图或笔记，方便复习时查阅和回顾。

考研数学(三)概率论与数理统计第一章复习重点总结

2018考研数学（三）：概率论与数理统计第一章复习重点总结一、第一章随机事件与概率1.重点：概率的定义与性质，条件概率与概率的乘法公式，事件之间的关系与运算，全概率公式与贝叶斯公式。

2.难点：随机事件的概率，乘法公式、全概率公式、Bayes公式以及对贝努利概型的事件的概率的计算。

3.常考题型事件、概率与独立性是本章给出的概率论中最基本、最重要的三个概念。

事件关系及其运算是本章的重点和难点，概率计算是本章的重点。

注意事件与概率之间的关系。

本章主要考查随机事件的关系和运算，概率的性质、条件概率和五大公式，注意事件的独立性。

近几年单独考查本章的试题相对较少，但是大多数考题中将本章的内容作为基本知识点来考查。

相当一部分考生对本章中的古典概型感到困难。

大纲只要求对古典概率和几何概率会计算一般难度的题型就可以。

考生不必可以去做这方面的难题，因为古典型概率和几何型概率毕竟不是重点。

应该将本章重点中的有关基本概念、基本理论和基本方法彻底理解和熟练掌握。

【评注】本题是典型的根据全概率公式及条件概率的解题的题型，这类题型一直都是考查的重点。

三、注意事项与线性代数一样，概率也比高数容易，花同样的时间复习概率也更为划算。

但与线代一样，概率也常常被忽视，有时甚至被忽略。

一般的数学考研参考书是按高数、线代、概率的顺序安排的，概率被放在最后，复习完高数和线代以后有可能时间所剩无多；而且因为前两部分分别占60%和20的分值，复习完以后多少会有点满足心理；这些因素都可能影响到概率的复习。

概率这门课如果有难点就应该是“记忆量大”。

在高数部分，公式、定理和性质虽然有很多，但其中相当大一部分都比较简单，还有很多可以借助理解来记忆；在线代部分，需要记忆的公式定理少，而需要通过推导相互联系来理解记忆的多，所以记忆量也不构成难点；但是在概率中，由大量的概念、公式、性质和定理需要记清楚，而且若靠推导来记这些点的话，不但难度大耗时多而且没有更多的用处（因为概率部分考试时对公式定理的内在推导过程及联系并没有什么要求，一般不会在更深的层次上出题）。

考研数学三知识点总结

高数三角函数变换cos(A−B)=cosAcosB+sinAsinB cos(A+B)=cosAcosB+sinAsinB sin(A−B)=sinAcosB−cosAsinB sin(A+B)=sinAcosB+cosAsinBsinAcosB=12[sin(A+B)+sin(A−B)]sinxcosx=12sin2xsinAsinB=12[cos(A−B)−cos(A+B)]sin2x=12(1−cos2x)cosAcosB=12[cos(A−B)+cos(A+B)]cos2x=12(1+cos2x)cos2x=1−tan2x1+tan2xsin2x=2tanx1+tan2xarcsinx+arccosx=π2arctanx+arccotx=π2arctanx+arctan1x=π2圆柱体积V=πr2h圆锥体积V=13πr2h球体积V=43πr3椭圆面积S=πab抛物线y2=2px交点坐标(p2,0)准线x=−p2点到直线距离ax+by+ca+b第一类间断点：包括可去间断点和跳跃间断点。

可去间断点：间断点处左右极限存在但不等于该点函数值。

f(x0+0)=f(x0−0)≠f(x0)跳跃间断点：间断点处左右极限存在但不相等。

f(x0+0)≠f(x0−0)第二类间断点：间断点处左右极限至少有一个是∞重要极限lim x→0sinxx=1limx→∞(1+1x)x=e limx→0(1+x)1x=ex趋向于0时的等价无穷小sinx∼x tanx∼x arcsinx∼x arctanx∼x1−cosx∼12x2ln (1+x )∼x log a (x +1)∼xlnae x −1∼x a x −1∼xlna n√1+x −1∼x n(1+bx )a−1∼abx 导数公式(a x )'=a x lna (log a x )'=1xlna(tanx )'=sec 2x (cotx )'=−csc 2x (secx )'=secx tanx (cscx )'=−cscx cotx (arcsinx )'√1−x (arccosx )'√1−x (arctanx )'=11+x 2 (arccotx )'=−11+x 2[sin (ax +b )](n )=a n sin (ax +b +n2π)[cos (ax +b )](n )=a n cos (ax +b +n2π)(1ax +b )(n )=(−1)n a n n !(ax +b )n +1[ln (ax +b )](n )=(−1)n −1(n −1)!a n(ax +b )n积分公式√x ±aln ∣x +√x 2±a 2∣+C dx a −xarcsin xa +C ∫dx x 2−a2=12ln ∣x −a x +a ∣+C ∫dx x 2+a2=1a arctan x a +C ∫dx a 2x 2+b2=1ab arctan axb +c ∫secxdx =ln ∣secx +tanx ∣+c∫cscxdx =ln ∣cscx −cotx ∣+c∫√a 2−x 2dx =a 22arcsin x 2+x 2√a 2−x 2+c ∫√x 2±a 2dx =x 2√x 2±a 2±a 22ln ∣x +√x 2±a 2∣+c∫0π2sin nxdx =∫0π2cos n xdx =(n −1)!!n !!π2(n 为偶数)∫0π2sin nxdx =∫0π2cos n xdx =(n −1)!!n !!(n 为奇数)∫0π2f (sinx )dx =∫0π2f (cosx )dx∫0πxf (sinx )dx =π2∫0πf (sinx )dx =π∫0π2f (sinx )dx ∣∫xf (t )dt ∣≤∫0x∣f (t )∣dt∫0af (x )dx =12∫0a[f (x )+f (−x )]dx ∫−aaf (x )dx =∫0a[f (x )+f (−x )]dxf x '(x ,y ),f y '(x ,y )在(x 0,y 0)连续⇒z =f (x ,y )在(x 0,y 0)可微⇒f (x ,y )在(x 0,y 0)连续二重积分特点积分区域D 关于x 轴对称∬D f (x ,y )d σ=0f 为y 的奇函数，即f (x ,−y )=−f (x ,y )∬Df (x ,y )d σ=2∬D 1f (x ,y )d σf 为y 的偶函数，即f (x ,−y )=f (x ,y )积分区域D 关于y 轴对称∬Df (x ,y )d σ=0f 为x 的奇函数，即f (−x ,y )=−f (x ,y )∬Df (x ,y )d σ=2∬D 1f (x ,y )d σf 为x 的偶函数，即f (−x ,y )=f (x ,y )积分区域关于原点对称∬D f (x ,y )d σ=0f 为x，y 的奇函数，即f (−x ,−y )=−f (x ,y )∬Df (x ,y )d σ=2∬D 1f (x ,y )d σf 为x，y 的偶函数，即f (−x ,−y )=f (x ,y )函数展开式e x=1+x +12!x 2+⋯+1n !x n =∑k =0nx kk !sinx =x −13!x 3+15!x 5−⋯+(−1)n −11(2n −1)!x 2n −1=∑k =0n(−1)k x 2k +1(2k +1)!cosx =1−12!x 2+14!x 4−⋯+(−1)n 1(2n )!x 2n =∑k =0n(−1)k x 2k (2k )!ln (1+x )=x −12x 2+13x 3+⋯+(−1)n −11n x n =∑k =1n (−1)k −1x kk 11+x =∑k =0n(−1)k x k11−x =∑k =0nx k多元函数极值：驻点(x0,y0)满足f x'(x0,y0)=0，f y'(x0,y0)=0且A=f xx''(x0,y0) ,B=f xy''(x0,y0),C=f yy''(x0,y0)B2−AC<0时，(x0,y0)是极值点，A>0时是最小值，A<0时是最大值。