普通高中课程标准实验教科书人教A版数学必修1第二章2.3.1 幂函数(共32张PPT).pptx
人教A版高中数学 2.3 幂函数课件 新人教A版必修1.ppt

y f (x) x3 为奇函数.
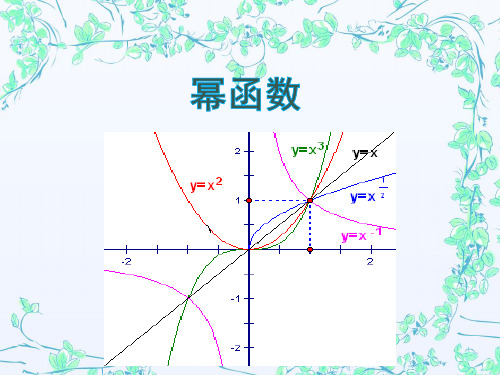
二、五个常用幂函数的图象: y x, y x2, y x1
(-2,4)
y y x3
4
y x2
(2,4)
yx
1
y x2 , y x3
3
1
2
y x2
y x1
若将它们的自变量用 x来表示,函数值用 y来表
示,则它们的函数关系式将是:
以上几个函数有什么共同特征?
(1) y x
(2) y x2
(3) y x3
1
(4) y x 2
(5) y x1
x ①底数都是自变量 ;
②指数都是常数; ③幂的系数都是1.
y ax
是不是指数 函数啊
问题
指数函数与幂函数有什么区别?
1
-4
-3
-2
-1
o
(1,1)
1
2
y x1
3
4x
(-1,-1)
-1
XX
…0
3 2
1
2 -1
1 12
02
1
3
23 14 2……
-2 yy xx123 …0-3.308.7-11 -01.13 1.041 01.1.733 1 2 3.3…8 …
-3
解析式
图象
定义 域
值域 奇偶
性 单调
性 定点
观察图象,将你发现的结论填在下表中
3、下列命题中,不正确的是( C )
(A)幂函数 y x1是奇函数
(B)幂函数 y x2 是偶函数
(C)幂函数 y x 既是奇函数,又是偶函数
人教A版高中数学必修一课件:2.3幂函数

练习
2. 在同一平面直角坐
y y x3
y x2
标系内作出幂函数
yx, yx2, yx3,
1
yx2, yx1
的图象.
O
yx
1
y x2
y x1
x
观察图象,将你发现的结论写下下表内
1
yx y x2 y x3 y x 2
y x1
定义域
R
R
R [0,+∞) {x|x≠0}
§2.3 幂 函 数
2019年10月
一、教学目标:
幂1函、数掌的握图幂像函与数性的质概;念能;利熟用悉幂a函数1, 的2, 性3, 质12, 来解1时决的一 些实际问题;
2、通过学生对情景的观察、思考、归纳、总结形成 结论,培养学生的发现问题、解决问题的能力。
二、教学重难点:
重点:幂函数的定义、图像与性质。 难点幂函数的图像与性质。
1.成为世界上经济增长速度最快的国 家,创 造了世 界经济 增长史 上的新 奇迹。 1.否定商 品经济 的存在 ,否定 市场及 价值规 律对经 济的调 节作用 。 35、生命是以时间为单位的,浪费别 人的时 间等于 谋财害 命;浪费 自己的 时间, 等于慢 性自杀 。—— 鲁迅 36、社会上崇敬名人,于是以为名人的 话就是 名言, 却忘记 了他之 所以得 名是那 一种学 问或事 业--鲁迅 38、推销员接近顾客的方式,往往决 定自己 在他们 心目中 的地位 是“接 单者” 还是“ 建议者 ”。 39、事先写出自己所要提出的每点意 见,以 合乎逻 辑的顺 序表达 出来: 言简意 骇,抓 住重点 。 2、人生的成功,不在于拿到一幅好 牌,而 是怎样 将坏牌 打好。 3、人生的路每一个人都要走一趟, 同样是 一条路 每一个 人走起 来却有 着不同 的感受 ,是好 是坏那 就要靠 几分的 机缘与 自己的 抉择。 38、推销员接近顾客的方式,往往决 定自己 在他们 心目中 的地位 是“接 单者” 还是“ 建议者 ”。
人教A版高中数学必修一教学课件2.3幂函数

7
,从而-8-8
<-1978
.
(3)-23-23 =23-23 ,-π6-32 =π6-23 .
2
函数 y=x-3 在(0,+∞)上为减函数,
数学 ·必修1(A版)
课前自主预习
课堂互动探究
课时跟踪检测
又23>π6,
所以-32-32 =23-23 <π6-23 =-π6-23 .
2
2
2
2
(4)4.15 >15 =1;0<3.8-3 <1-3 =1;
数学 ·必修1(A版)
课前自主预习
课堂互动探究
课时跟踪检测
由图象可知:(1)当 x>1 或 x<-1 时,f(x)>g(x); (2)当 x=±1 时,f(x)=g(x); (3)当-1<x<0 或 0<x<1 时,f(x)<g(x).数学 Leabharlann 必修1(A版)课前自主预习
课堂互动探究
课时跟踪检测
1.作幂函数图象的原则和方法 (1)原则:作幂函数的图象要联系函数的定义域、值域、单 调性、奇偶性等. (2)方法:首先作出幂函数在第一象限内的图象,然后根据 奇偶性就可作出幂函数在定义域内完整的图象.
课前自主预习
课堂互动探究
课时跟踪检测
奇偶
非奇
奇
偶
奇
奇
性
非偶
单调 性
x∈[0,+∞)_增__
增
增
x∈(-∞,0]_减__
x∈(0,+∞)_减__ 增
x∈(-∞,0)_减__
定点 (1,1), (1,1),(0,0) (1,1),(1,1),
(1,1)
(0,0)
(0,0) (0,0)
数学 ·必修1(A版)
人教A版数学必修一2.3幂函数课件1.pptx

幂函数:解析式,y底数为x自a 变量x,指数为常数
α,α∈R;
判一判
判断下列函数是否为幂函数.
(1)y=x4
1 (2) y x2
1
(4) y x 2
(5)y=2x
(3)y=-x2
(6)y=x3+2
下面研究幂函数 y xa .
结合图象,研究性质:定义域、值域、
单调性、奇偶性、过定点的情况等。
空白演示
在此输入您的封面副标题
第二章基本初等函数(I) 2.3幂函数
y=x (1)如果张红购买了每千克1元的蔬菜w千克,那么她需 要支付P=____w__元 __P__是__w__的函数
(2)如果正方形的边长为a,那么正方形的面积S=___a_²
__S__是__a__的函数
y=x2
(3)如果立方体的边长为a,那么立方体的体积V=__a_³_
例2.利用单调性判断下列各值的大小。
(1)5.20.8与5.30.8
(2)0.20.3与0.30.3
(3)
-2
-2
2.5 5 与 2.7 5
解:(1)y=x0.8在(0,+∞)内是增函数,
∵5.2<5.3 ∴5.20.8<5.30.8 (2)y=x0.3在(0,+∞)内是增函数
∵0.2<0.3∴0.20.3<0.30.3 (3)y=x-2/5在(0,+∞)内是减函数
-4
-2
-1
(-1,-1)
-2
2
4
6
-3
-4
(-2,4)
4
3
2
1
(-1,1)
y=x3 (2,4) y=x2
高中人教A版数学必修一课件2.3幂函数

R
值域 R
_[0_,__+__∞)
R
奇偶性
单调性
__奇____ 在 R 上是___增
在(-∞,0)上 偶 _减__函__数____;在
∞)上是增函数
__奇____ 在 R 上是_增__
y=x12 y=x-1
[0,+∞)
(-∞,0)∪ (_0_,__+__∞_)_____
__[0_,__+__∞_ )
[解析] (1)若 f(x)为正比例函数,则mm22+ +m2m-≠10=1 ,∴m=
(2)若 f(x)为反比例函数,则mm22+ +m2m-≠10=-1 ,∴m=-1.
(3)若 f(x)为二次函数,则mm22+ +m2m-≠10=2
,∴m=-1±2
13 .
(4)若 fபைடு நூலகம்x)为幂函数,则 m2+2m=1,∴m=-1± 2.
大约到15世纪,人们才意识到要用一个缩写的方式来表 的乘积.直到17世纪才开始出现在幂的符号中将指数与底数 势.
1636年苏格兰人休姆(Hume)引进了一种较好的记法,他 指数,写在底数的右上角,如“A4”写作“AⅣ”,这种记法与现 数字采用罗马数字外,其余完全一样.一年以后,法国数学家 了改进,把罗马数字改用阿拉伯数字,成了今天的样子。此后 里斯(Wallis,1616~1703)、牛顿等人分别引入负指数幂和分数指 号,从而使幂的概念及符号发展得更完备了。那么,什么是幂 么关系呢?
新课标导学
数学
必修① ·人教A版
第二章
基本初等函数(Ⅰ) 2.3 幂函数
1
自主预习
2
互动探究
3
课时作业
自主预习学案
数学史上很早就借用“幂”字,起先用于表示面积,后 方或立方.1859年中国清末大数学家李善兰(1811~1882)译成《 书,创设了不少数学专有名词,如函数、极限、微分、积分等 这个词译为“幂”.这样“幂”就转译为若干个相同数之积.
高中数学(人教版A版必修一)配套课件:第二章 2.3幂函数

MN=NA.那么αβ等于( A )
A.1
B.2
C.3
D.无法确定
解析 由条件知,M(13,23)、N(23,13),
∴13=(23)α,23=(13)β,
∴(13)αβ=[(13)β]α=(23)α=13,
∴αβ=1.故选A.
解析答案
类型三 幂函数性质的综合应用
例3
(1)探讨函数
f
x
=x
1 2
的单调性.
第二章 基本初等函数 (Ⅰ)
2.3 幂函数
学习目标
1.理解幂函数的概念; 2.学会以简单的幂函数为例研究函数性质的方法; 3.理解和掌握幂函数在第一象限的分类特征,能运用数形结合的方 法处理幂函数有关问题.
问题导学
题型探究
达标检测
问题导学
新知探究 点点落实
知识点一 幂函数的概念 思考 y=1x,y=x,y=x2 三个函数有什么共同特征? 答案 底数为x,指数为常数. 一般地, 函数y=xα 叫做幂函数,其中x是自变量,α是常数.
为啥总是听懂了, 但不会做,做不好?
高效学习模型-内外脑模型
2
内脑-思考内化
思 维 导 图 &超 级 记 忆 法 &费 曼 学 习 法
1
外脑-体系优化
知 识 体 系 &笔 记 体 系
内外脑高效学习模型
超级记忆法
超级记忆法-记忆规律
记忆前
选择记忆的黄金时段 前摄抑制:可以理解为先进入大脑的信息抑制了后进 入大脑的信息
类型一 幂函数的概念
例1 已知 y=(m2+2m-2)xm2-1+2n-3 是幂函数,求m,n的值.
m2+2m-2=1, 解 由题意得m2-1≠0,
[教案精品]新课标高中数学人教A版必修一全册教案2.3幂函数
![[教案精品]新课标高中数学人教A版必修一全册教案2.3幂函数](https://img.taocdn.com/s3/m/5078a5af2e3f5727a4e96237.png)
[教案精品]新课标高中数学人教A版必修一全册教案2.3幂函数(2.3 幂函数(一)教学目标1.知识与技能(1)理解幂函数的概念,会画幂函数y=x,y=x2,y=x3,y=x-1,y=x21的图象.(2)结合这几个幂函数的图象,理解幂函数图象的变化情况和性质.2.过程与方法(1)通过观察、总结幂函数的性质,培养学生概括抽象和识图能力.(2)使学生进一步体会数形结合的思想.3. 情感、态度、价值观(1)通过生活实例引出幂函数的概念,使学生体会到数学在实际生活中的应用,激发学生的学习兴趣.(2)利用计算机,了解幂函数图象的变化规律,使学生认识到现代技术在数学认知过程中的作用,从而激发学生的学习欲望.(二)教学重点、难点重点:常见幂函数的概念、图象和性质.难点:幂函数的单调性及比较两个幂值的大小.(三)教学方法采用师生互动的方式,由学生自我探索、自我分析,合作学习,充分发挥学生的积极性与主动性.利用实物投影仪及计算机辅助教学.(四)教学过程教学环节教学内容师生互动设计意图复习(多媒体显示以下5个问题,同时附注学生阅读、思考、交流、口答,教培养引入相关图象,每个问题的结论由学生说出,然后再在多面体屏幕上弹出)问题1:如果张红购买了每千克1元的蔬菜w千克,那么她需要付的钱数p=w元,这里p是w的函数.问题2:如果正方形的边长为a,那么正方形的面积S=a2,这里S是a的函数.问题3:如果正方体的边长为a,那么正方体的体积V=a3,这里V是a的函数.问题4:如果正方师板演.师:观察上述例子中函数模型,这几个函数表达式有什么共同特征?生:解析式的右边都是指数式,且底数都是变量. 变量在底数位置,解析式右边又都是幂的形式,我们把这种函数叫做幂函数.(引入新课,书写课题)学生的观察、归纳、概括能力,形场地的面积为S,那么正方形的边长a=S21,这里a是S的函数.问题5:如果某人t s内骑车行进了 1 km,那么他骑车的平均速度v=t-1 km/s,这里v是t的函数.形成概念幂函数的定义一般地,形如y xα=(x∈R)的函数称为幂函数,其中x是自变量,α是常数.师:请同学们举出几个具体的幂函数.生:如11234,,y x y x y x-===等都是幂函数,幂函数与指数函数,对数函数一样,都是基本初等函数.理解幂函数的定义.深化概念1.研究幂函数的图像(1)y x=(2)12y x=(3)2y x=(4)1y x-=(5)3y x=2.通过观察图像,填P86探究中的表格y x=2y x=定义域R R奇偶性奇奇引导学生用列表描点法,应用函数的性质,如奇偶性,定义域等,画出函数图像,最后,教师利用电脑软件画出以上五个数数的图像.42-2-4-6-8-10-551015让学生通过观察图像,分组讨论,探究幂函数的性质和图像探究幂函数的性质和图像y x=12y x=y=xy=x-1在第Ⅰ象限单调增减性 在第Ⅰ象限单调递增在第Ⅰ象限单调递增定点 (1,1)(1,1) 3y x=12y x=1y x -=R {}|0x x ≥ {}|0x x ≠奇非奇非偶奇在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递减(1,(1,(1,的变化规律,教师注意引导学生用类比研究指数函数,对函数的方法研究幂函数的性质.的变化规律,1)1)1)3.幂函数性质(1)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1)(原因:11x=);(2)x>0时,幂函数的图象都通过原点,并且在[0,+∞]上,是增函数(从左往右看,函数图象逐渐上升).特别地,当x>1,x>1时,x∈(0,1),2=的图象都在y x=图y x象的下方,形状向下凸越大,下凸的程度越大(你能找出原因吗?)当0<α<1时,x∈(0,1),y xα=的图象都在y x=的图象上方,形状向上凸,α越小,上凸的程度越大(你能说出原因吗?)(3)α<0时,幂函数的图象在区间(0,+∞)上是减函数.在第一家限内,当x向原点靠近时,图象在y轴的右方无限逼近y轴正半轴,当x慢慢地变大时,图象在x轴上方并无限逼近x轴的正半轴.应用举例例1 求下列幂函数的定义域,并指出其奇偶性、单调性.(1)y=x52;(2)y=x43 ;(3)y=x-2.例1分析:解决有关函数求定义域的问题时,可以从以下几个方面来考虑,列出相应不等式(组),解不等式(组)即可得到所求函数的定义域.①若函数解析式中含有分母,分母不能为0;②若函数解析式中含有根号,要注意偶次根号下非负;③0的0次幂没有意义;④若函数解析掌握幂函数知识的应用.A.幂函数的图象一定过(0,0)和(1,1) B.当α<0时,幂函数y =x α是减函数C.当α>0时,幂函数y =x α是增函数D.函数y =x 2既是二次函数,也是幂函数3.函数y =x 53的图象大致是4.幂函数f (x )=axmm 82-(m ∈Z )的图(-710)32=(107)32-,1.134-=[(1.1)2]32-=1.2132-.∵幂函数y =x32-在(0,+∞)上单调递减,且107<22<1.21, ∴(107)32->(22)32->1.2132-, 即(-710)32>(-22)32->1.134-. (3)利用幂函数和指数函数的单调性可以发现0<3.832-<1,3.952>1,备选例题例 1 已知221(22)23m y mm x n -=+-+-是幂函数,求m ,n 的值.【解析】由题意得⎪⎪⎩⎪⎪⎨⎧=-≠-=-+0320112222n m m m ,解得⎪⎩⎪⎨⎧=-=233n m , 所以23,3=-=n m . 【小结】做本题时,常常忽视m 2 + 2m – 2 = 1且2n – 3 = 0这些条件.表达式y =αx (x ∈R)的要求比较严格,系数为1,底数是x ,α∈R 为常数,如221-==x x y ,y = 1 = x 0为幂函数,而如y = 2x 2,y = (x – 1)3等都不是幂函数.例2 比例下列各组数的大小. (1)8787)91(8---和;(2)(–2)–3和(–2.5)–3; (3)(1.1)–0.1和(1.2)–0.1; (4)533252)9.1()8.3(,)1.4(--和.【解析】(1)8787)81(8-=--,函数87x y =在(0, +∞)上为增函数,又9181>,则8787)91()81(>,从而8787)91(8-<--.(2)幂函数y = x –3在(–∞, 0)和(0, +∞)上为减函数,又∵–2>–2.5,∴(–2)–3<(–2.5)–3.(3)幂函数y = x –0.1在(0, +∞)上为减函数, 又∵1.1<1.2,∴1.1–0.1>1.2–0.1. (4)52)1.4(>521= 1;0<32)8.3(-<321-= 1;53)9.1(-<0,∴53)9.1(-<32)8.3(-<52)1.4(.【小结】比较大小题,要综合考虑函数的性质,特别是单调性的应用,更善于用“搭桥”法进行分组,常数0和1是常用的“桥梁”.。
高中数学人教版必修1课件:2.3幂函数
1.通过实例了解幂函数的概念. 2.结合几个常见幂函数的图象发现幂函数的性质.
难点和重点:
学会数形结合的思想概括出幂函数的性质.
以下的函数解析式具有什么共同特征?
y=x y = x2
y xa
y = x3 y x 1
1
y x2
共同特征:函数解析式是幂的情势,且指数是常数, 底数是自变量。
(1,1)
幂函数的性质:(定义域、奇偶性、单调性,因函数
式中α的不同而各异) 1. 所有的幂函数在(0,+∞)都有定义,并且图 象都过点(1,1); 2. 当α为奇数时,幂函数为奇函数, 当α为偶数时,幂函数为偶函数.
3. 当α >0时,幂函数在区间(0,+∞)上是增函数; 当α<0时,幂函数在区间(0,+∞)上是减函数.
1
y x2
y x1
[0,+∞) ,0 (0,+) [0,+∞) ,0 (0,+)
奇偶性 奇函数 偶函数 奇函数 非奇非偶
奇函数
在(-∞,0)上 R上是 是减函数,
单调性 增函数在(0, +∞)上 是增函数
R上是 在(0,+∞) 增函数 上是增函数
在( -∞,0) 和(0, +∞)上 是减函数
公共点
练习1.
(1) 1.30.5 < 1.50.5
(2) 5.12 < 5.092
1
1
(3) 0.54 > 0.44
(4)
2
0.7 3
>
2
0.8 3
2.若m
4
1 2
3
2m
1 2
,则求m的取值范围.
解:
幂函数f
人教A版数学必修一第1部分第二章2.3幂函数

<(3-2a)
-m 3
的
a
的取值范围.
[思路点拨] 由函数在(0,+∞)上递减,及图象关于 y
轴对称求出正整数 m 的值,然后利用单调性求解.
[精解详析] ∵函数 y=x3m-9 在(0,+∞)上单调递减,
∴3m-9<0.解得 m<3.
(4 分)
又 m∈N*,∴m=1,2.
又函数图象关于 y 轴对称,
(2)依据图象确定幂指数 α 与 0,1 的大小关系,即 根据幂函数在第一象限内的图象(类似于 y=x-1 或 y= x12或 y=x3)来判断.
3.函数y=xa,y=xb与y=xc在第一象限中的图
象如图所示,则a,b,c的可能取值为( ) A.a=2,b=-1,c=12 B.a=2,b=12,c=-1 C.a=-1,b=2,c=12 D.a=12,b=-1,c=2
高中数学课件
灿若寒星整理制作
理解 教材 新知
知识点一 知识点二
第 二
2.3
把握 热点
考点一 考点二
章
考向
考点三
应用创新演练
问题1:函数y=2x,y=x3是指数函数吗? 提示:y=2x是指数函数,而y=x3不是指数函数. 问题2:函数y=x3中自变量有什么特点? 提示:自变量在底数的位置. 问题3:再举出几个这样的函数. 提示:y=x2,y=x,y=x-1.
D.y=x-2
解析:先判断在(0,+∞)上的单调性,再利用奇函 数在关于原点对称的区间上单调性相同,偶函数在 关于原点对称的区间上单调性相反判断在(-∞,0) 上的单调性. 答案:C
7.设 a=(35)25,b=(25)35,c=(25)25,则 a,b,c 的大小
人教A版数学必修一2-3-1幂函数.pptx

答:平均每年需增长11.9%.
[例4] 幂函数y=(m2-m-1)xm2-2m-3当x∈(0,+∞) 时为减函数,求实数m的值.
[例5] 判断幂函数y=x3的单调性和奇偶性. [分析] 函数单调性的判断:取值——作差——判断 符号——下结论,函数奇偶性的判断:定义域——f(-x)与 -f(x)、f(x)的关系——下结论. [解析] ∵f(-x)=(-x)3=-x3=-f(x), ∴y=x3是奇函数. 解法一:∵α=3>0,∴f(x)在(0,+∞)上为增函数, 又∵f(x)为奇函数,∴f(x)在R上为增函数. 解法二:在(-∞,+∞)上任取x1,x2,设x2>x1,
偶
∞)增
观察总结可知幂函数y=xα(α为常数)的性质: (1)所有的幂函数在(0,+∞)上都有定义,并且图象都 通过点(1,1); (2)如果α>0,则幂函数的图象过原点,并且在区间[0, +∞)上为增函数; (3)如果α<0,则幂函数在(0,+∞)上为减函数,在第 一象限内,向上与y轴无限接近,向右与x轴无限接近. (4)当α为奇数时,幂函数为奇函数,图象都过(-1,- 1)点,当α为偶数时,幂函数为偶函数、图象都过(-1,1) 点.
1
3在第一象限内是减函
数,∴53-31<43-31,∴-323<-233<53-13<43-31<150
32 <23<
2
23.
[解析] ∵y=(m2-m-1)xm2-2m-3为幂函数, ∴m2-m-1=1, 即(m-2)(m+1)=0, ∴m=2,或m=-1. 当m=-1时,m2-2m-3=0不满足题意,舍去. 当m=2时,m2-2m-3=-3满足题设条件, ∴m=2.
高中数学(人教版A版必修一)配套课件:第二章 2.3幂函数

返回
1 2
达标检测
1.已知幂函数 1 A. 2
解析
1 f(x)=k· xα 的图象过点 , 2
1
2
3
4
5
2 ,则 k+α 等于( C ) 2
B.1
3 C. 2
D.2
1 = 2
由幂函数的定义知 k=1.又 f
2 , 2
1 α 所以2 =
已知幂函数 f x =x
1 m2 m
(m N* ).
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
解 ∵m∈N*,
∴m2+m=m×(m+1)为偶数.
令 m +m=2k,k∈N ,则 f(x)=
2 *
2k
x,
∴定义域为[0,+∞),在[0,+∞)上f(x)为增函数.
解析答案
答案 底数为x,指数为常数. 一般地, 函数y=xα 叫做幂函数,其中x是自变量,α是常数.
答案
知识点二
思考
幂函数的图象与性质
1 2
如图在同一坐标系内作出函数(1)y=x; 2 y=x ; (3)y=x2;(4)y
=x-1;(5)y=x3的图象.
填写下表: y=x 定义域 值域 奇偶性 R R 奇 y=x2 R [0,+∞) 偶 在[0,+∞) 单调性 增 上 增 上 减 , 在(-∞,0] 增 增 y=x3 R R 奇
解析答案
类型三
幂函数性质的综合应用
1 2
1 2
例3 (1)探讨函数 f x =x 的单调性. 解 f x =x
的定义域为(0,+∞).
任取x1,x2∈(0,+∞),且x1<x2, 1 1 1 1 则 f(x2)-f(x1)= x2 2 x1 2 = - x2 x1 x 1- x 2 x1-x2 = = . x1x2 x1x2· x1+ x2 因为x2>x1>0,所以x1-x2<0,
人教A版数学必修一2.3.1幂函数(一).docx

幂函数(一)[自学目标]1.了解幂函数的概念2.会画出几个常见的幂函数的图象3.了解几个常见的幂函数的性质,并能简单应用 [知识要点]1. 幂函数的定义.2. y=x, y=x 2, y=x 3, xy 1=, 21x y =的图象.3 .幂函数的性质. [预习自测]例1:求下列函数的定义域,并指出它们的奇偶性。
(1)3x y = (2)21x y = (3)2-=x y (4)32-=xy变式引申: 求函数3241)2()1(-++=-x x y 的定义域。
例2:画出下列函数2x y =,3x y =,21x y =的图象例3:比较下列各组数的大小 (1)253-和251.3-(2)32)32(--和32)6(--π例4:求出函数2)3(--=x y 的定义域和单调区间.例5:已知1222)()(--+=m mx m m x f ,当m 取什么值时,(1))(x f 为正比例函数; (2))(x f 为反比例函数; (3))(x f 为幂函数。
[课内练习]1.求下列幂函数的定义域,并指出它们的奇偶性。
(1)32x y =(2)65x y =(3)54-=x y (4)23-=xy2.已知幂函数y=f(x)的图象经过(3,33),则f(x)= 3.下列函数图象中,表示函数31-=xy 的是( )4.画出函数31x y =的图象,并指出其单调区间。
5.比较下列各组数中两个值的大小: (1)212124.5,23.5(2)1127.0,26.0--(3)33)75.0(,)72.0(--[归纳反思]1.关于指数式值的比较,主要有:①同底异指,用指数函数单调性比较②异底同指,用幂函数单调性比较③异底异指,构造中间量(同底或同指)进行比较 2.性质:对于幂函数ax y =:①当a>0时,图象经过点(1,1)和(0,0),在第一象限内是增函数.②当a <0时,图象经过点(1,1),在第一象限内是减函数,并且图象向上与y 轴无限接近,向右与x 轴无限接近.[巩固提高]1.在下列函数中,定义域为R 的是( ) A 23x y = B 3xy = C x y 2= D 1-=x y2.下面给出了5个函数○112+=x y ○221-=x y ○322x y =○432-=x y ○5131+=x y ,其中是幂函数的是( )A ○1○5 B ○1○2○3 C ○2○3 D ○2○3○5 3下列命题中正确的是( )A 当m=0时,函数mx y =的图象是一条直线 B 幂函数的图象都经过(0,0),(1,1)两点 C 幂函数mx y =图象不可能在第四象限内D 若幂函数m x y =为奇函数,则mx y =是定义域内的增函数 4. 下列函数中,既是奇函数,又在),0(+∞上是减函数的是( )A x y =B x y -=2C 3x y -=D 3x y -=5.函数3x y =与函数31xy =的图象( )A 关于原点对称B 关于y 轴对称C 关于x 轴对称D 关于直线y=x 对称6.函数32x y =图象的大致形状是( )A B C D 7.如图,曲线21,C C 分别是函数mx y =和nx y =在第一象限的图象,那么一定有 A n<m<0 B m<n<0C m>n>0D n>m>08.用“〈”或“〉”连接下列各式6.032.0 5.034.0 528.0- 326.0-9.幂函数的图象过点( 2 , 41),则它的单调递增区间是 10.函数43-=xy 在区间 上是减函数11.比较下列各组数的大小(!)3232)2.1(,3.1--- (2)323132)4(,)4.2(,1.2---(3)733243)8.0(,5.2,3.6--12.函数)1()24(2241+-++++=-mx x m x mx y 的定义域是全体实数,求实数m 的取值范围?幂函数(一) 课内练习答案: 1)(1)偶函数 (2)非奇非偶函数 (3)偶函数 (4)非奇非偶函数 2) 21)(-=xx f 3) D 4)图略5) (1)212124.523.5< (2)1127.026.0-->(3)33)75.0()72.0(->- 巩固提高答案: 1) C 2) (2)(4) 3) C 4) C 5) D 6) D 7) A 8) <<; 9) )0,(-∞ 10) ),0(+∞11)(1)3232)2.1(3.1---< (2)323231)4(1.2)4.2(-<<--(3)4332736.35.2)8.0(<<--12)解:由题得 0242>+++m x mx 对x 恒成立 (1)当0>m 时,0<∆8416)2(4162<--=+-m m m m0422>-+m m得:51+->m 或51--<m 又因为0>m 51+->∴m (2)当0<m 时 不可能 (3)当0=m 时 不可能 综上所述:51+->m。
人教A版数学必修一2.3.1幂函数(二).docx

2.4 幂函数(二)[自学目标]. 进一步理解幂函数的定义、图象和性质,能熟练的运用幂函数的定义、图象和性质解决有关问题[知识要点]1幂函数的单调性2幂函数的图象[预习自测]例1:求下列各式中参数的取值范围(1)43a 435.0>(2)3232)42()2(+>-a例2:讨论函数32x y =的定义域,奇偶性,作出它的图象,并根据图象,说明函数的增减性。
例3: 已知2222)1()(----=m mx m m x f 是幂函数,且当∈x ),0(+∞时是减函数,求实数及相应的幂函数。
例4:已知函数42215x x y --=(1) 求函数的定义域,值域;(2) 判断函数的奇偶性;(3) 求函数的单调区间。
[课内练习]1.当32x x >成立时,x 的取值范围是 ( )A x<1且x ≠0B 0<x<1C x>1D x<12.函数x y x y y x3.02log ,,5.0===-的图象形状如图所示,依次大致是( )① ② ③A ○1○2○3B ○2○1○3C ○3○1○2D ○3○2○13.求函数32)1(--=x y 的单调区间。
4.若54)(x x f =,2)(-=x x g ,求函数)]([x g f 的单调区间。
O x y xyO yO y O x x x 5.已知幂函数y=f(x)的图象过点( 2 , 22), 试求出此函数的解析式,并判断奇偶性,单调性.[归纳反思]1.确定幂的范围,可根据所需值的大小关系及幂函数的单调性。
2.绘制图象与研究性质时,可先由性质,特别是奇偶性绘制出图象,再由图象观察性质,是研究函数的常用方法。
[巩固提高]1.当10<<x 时,1212)(,)(,)(-===x x h x x g x x f 的大小关系。
2.图中曲线是幂函数n x y =在第一象限的图象,已知n 取21,2±±四个值,则相对于曲线 4321,,,C C C C 的n 依次为( )3 .已知幂函数y=(x)的图象过点( 2 , 41) ,则该函数的图象( )A 关于原点对称B 关于y 轴对称C 关于x 轴对称D 关于直线y=x 对称4.如图为b ax y +=21的图象,求a ,b5.将21x y =,3x y =,2x y =,x y =,21-=xy ,31x y =,2-=x y ,1-=x y 填入对应图象的下面。
