高一数学向量的线性运算练习题

合集下载

向量的线性运算经典测试题含答案

向量的线性运算经典测试题含答案一、选择题1．化简()()AB CD BE DE -+-的结果是（）．A ．CAB ．AC C ．0D ．AE【答案】B【解析】【分析】根据三角形法则计算即可解决问题．【详解】解：原式()()AB BE CD DE =+-+AE CE =-AE EC =+ AC =，故选：B ．【点睛】本题考查平面向量、三角形法则等知识，解题的关键是灵活运用三角形法则解决问题，属于中考基础题．2．下列等式正确的是（）A ．AB +BC ＝CB +BAB ．AB ﹣BC ＝ACC ．AB +BC +CD ＝DAD ．AB +BC ﹣AC ＝0【答案】D【解析】【分析】根据三角形法则即可判断.【详解】∵AB BC AC +=，∴0AB BC AC AC AC +-=-= ，故选D ．【点睛】本题考查平面向量的三角形法则，解题的关键是熟练掌握三角形法则.3．已知a 、b 和c 都是非零向量，在下列选项中，不能判定//a b 的是( ) A ．2a b =B ．//a c ，//b cC ．||||a b =D ．12a c =，2bc = 【答案】C【解析】【分析】由方向相同或相反的非零向量叫做平行向量，对各选项分析判断．【详解】A 选项：由2a b =，可以推出//a b ．本选项不符合题意；B 选项：由//a c ，//b c ，可以推出//a b ．本选项不符合题意；C 选项：由||||a b =，不可以推出//a b ．本选项符合题意；D 选项：由12a c =，2bc =，可以推出//a b ．本选项不符合题意；故选：C ．【点睛】考查了平面向量，解题关键是熟记平行向量的定义．4．已知5AB a b =+，28BC a b =-+，()3CD a b =-，则（）．A ．A 、B 、D 三点共线B ．A 、B 、C 三点共线 C ．B 、C 、D 三点共线D ．A 、C 、D 三点共线【答案】A【解析】【分析】根据共线向量定理逐一判断即可.【详解】解：∵28BC a b =-+，()3CD a b =-，5AB a b =+∴()2835BD BC CD a b a b a b =+=-++-=+， ∴AB 、BD 是共线向量∴A 、B 、D 三点共线，故A 正确；∵5AB a b =+，28BC a b =-+∴不存在实数λ，使AB BC λ=，即AB 、BC 不是共线向量∴A 、B 、C 三点共线，故B 错误；∵28BC a b =-+，()3CD a b =-∴不存在实数λ，使BC CD λ=，即BC 、CD 不是共线向量∴B 、C 、D 三点共线，故C 错误；∵5AB a b =+，28BC a b =-+，()3CD a b =-，∴()52813AC AB BC a b a b a b =+=++-+=-+∴不存在实数λ，使AC CD λ=，即AC 、CD 不是共线向量∴A 、C 、D 三点共线，故D 错误；故选A.【点睛】此题考查的是共线向量的判定，掌握共线向量的定理是解决此题的关键.5．若点O 为平行四边形的中心，14AB m =，26BC m =，则2132m m -等于（）． A ．AOB ．BOC ．COD ．DO 【答案】B【解析】【分析】根据向量加法的平行四边形法则和平行四边形的性质逐一判断即可.【详解】解:∵在平行四边形ABCD 中, 14AB m =，26BC m =，∴1246B m C AC AB m =+=+,1246BD BA BC AC m m =+==-+,M 分别为AC 、BD 的中点, ∴122312AO AC m m =+=，故A 不符合题意； 211322BO BD m m ==-，故B 符合题意； 122312CO AC m m ==---，故C 不符合题意； 121232DO BD m m =-=-，故D 不符合题意. 故选B.【点睛】此题考查的是平行四边形的性质及向量的加、减法,掌握平行四边形的对角线互相平分和向量加法的平行四边形法则是解决此题的关键.6．已知m 、n 是实数，则在下列命题中正确命题的个数是（）．①0m <，0a ≠时，ma 与a 的方向一定相反；②0m ≠，0a ≠时，ma 与a 是平行向量；③0mn >，0a ≠时，ma 与na 的方向一定相同；④0mn <，0a ≠时，ma 与na 的方向一定相反．A ．1个B ．2个C ．3个D ．4个【答案】D【分析】根据向量关系的条件逐一判断即可.【详解】解：①因为0m <，1＞0，0a ≠，所以ma 与a 的方向一定相反，故①正确； ②因为0m ≠，1≠0，0a ≠，所以ma 与a 是平行向量，故②正确；③因为0mn >，0a ≠，所以m 和n 同号，所以ma 与na 的方向一定相同，故③正确； ④因为0mn <，0a ≠，所以m 和n 异号，所以ma 与na 的方向一定相反，故④正确．故选D.【点睛】此题考查的是共线向量，掌握共线向量定理是解决此题的关键.7．下列各式正确的是（）．A ．()22a b c a b c ++=++B ．()()330a b b a ++-= C ．2AB BA AB +=D ．3544a b a b a b ++-=- 【答案】D【解析】【分析】根据平面向量计算法则依次判断即可.【详解】 A 、()222a b c a b c ++=++，故A 选项错误；B 、()()3333+33=6a b b a a b b a b ++-=+-，故B 选项错误；C 、0AB BA +=，故C 选项错误；D 、3544a b a b a b ++-=-，故D 选项正确；故选D.【点睛】本题是对平面向量计算法则的考查，熟练掌握平面向量计算法则是解决本题的关键.8．下列结论正确的是（）．A ．2004cm 长的有向线段不可以表示单位向量B ．若AB 是单位向量，则BA 不是单位向量C ．若O 是直线l 上一点，单位长度已选定，则l 上只有两点A 、B ，使得OA 、OB 是单位向量D ．计算向量的模与单位长度无关【答案】C【解析】根据单位向量的定义及意义判断即可.【详解】A.1个单位长度取作2004cm 时，2004cm 长的有向线段才刚好表示单位向量，故选项A 不正确；B. AB 是单位向量时，1AB =，而此时1AB BA ==，即BA 也是单位向量，故选项B 不正确；C.单位长度选定以后，在l 上点O 的两侧各取一点A 、B ，使得OA 、OB 都等于这个单位长度，这时OA 、OB 都是单位向量，故选项C 正确；D.没有单位长度就等于没有度量标准，故选项D 不正确.故选C. 【点睛】本题考查单位向量，掌握单位向量的定义及意义是解题的关键.9．□ABCD 中， -+等于( ) A ．B ．C ．D ．【答案】A【解析】【分析】在平行四边形中，两对对边平行且相等，以一对对边所在的线段构成向量，得到的向量要么相等，要么是相反向量，根据本题所给的两个向量来看，它们是一对相反向量，和为零向量，得到结果．【详解】 ∵在平行四边形ABCD 中，与是一对相反向量， ∴= - ∴ -+=- +=，故选A ．【点睛】此题考查向量加减混合运算及其几何意义，解题关键在于得出与是一对相反向量.10．如图，点C 、D 在线段AB 上，AC BD =，那么下列结论中，正确的是（）A ．AC 与BD 是相等向量B ．AD 与BD 是平行向量C ．AD 与BD 是相反向量D ．AD 与BC 是相等向量【答案】B【解析】【分析】由AC=BD，可得AD=BD，即可得AD与BD是平行向量，AD BC AC BD=-=-，，继而证得结论．【详解】A、∵AC=BD，∴AC BD=-，该选项错误；B、∵点C、D是线段AB上的两个点，∴AD与BD是平行向量，该选项正确；C、∵AC=BC，∴AD≠BD，∴AD与BD不是相反向量，该选项错误；D、∵AC=BD，∴AD=BC，∴AD BC=-，，该选项错误；故选：B．【点睛】本题考查了平面向量的知识．注意掌握相等向量与相反向量的定义是解此题的关键．11．若a＝2e，向量b和向量a方向相反，且|b|＝2|a|，则下列结论中不正确的是（）A．|a|＝2 B．|b|＝4 C．b＝4e D．a＝1 2b -【答案】C【解析】【分析】根据已知条件可以得到：b＝﹣4e，由此对选项进行判断．【详解】A、由a＝2e推知|a|＝2，故本选项不符合题意．B、由b＝-4e推知|b|＝4，故本选项不符合题意．C、依题意得：b＝﹣4e，故本选项符合题意．D、依题意得：a＝-12b，故本选项不符合题意．故选C．【点睛】考查了平面向量，注意：平面向量既有大小，又有方向．12．在下列关于向量的等式中，正确的是（）A．AB BC CA=+B．AB BC AC=-C．AB CA BC=-D ．0AB BC CA ++=【答案】D【解析】【分析】根据平面向量的线性运算逐项判断即可.【详解】AB AC CB =+，故A 选项错误；AB AC BC =-，故B 、C 选项错误；0AB BC CA ++=，故D 选正确.故选：D.【点睛】本题考查向量的线性运算，熟练掌握运算法则是关键.13．如图,在平行四边形ABCD 中，设AB a =,AD b =，那么向量OC 可以表示为. ( )A ．1122a b + B ．1122a b - C ．1122a b -+ D ．1122a b -- 【答案】A【解析】【分析】利用平行四边形的性质以及平面向量的加法与减法运算法则解题即可. 【详解】由题意可得 ()()1111122222OC AC AD AB a b a b ==+=+=+ 【点睛】本题主要考察平面向量的加法与减法运算，掌握平行四边形法则是解题的关键.14．已知e 是单位向量，且2,4a e b e =-=，那么下列说法错误的是（）A ．a ∥bB ．|a |=2C ．|b |=﹣2|a |D ．a =﹣12b 【答案】C【解析】【分析】【详解】解：∵e 是单位向量，且2a e =-，4b e =，∴//a b ，2a =， 4b = ， 12a b =-，故C 选项错误，故选C.15．如图，向量OA 与OB 均为单位向量，且OA ⊥OB ，令n =OA +OB ，则||n =（）A ．1B ．2C ．3D ．2【答案】B【解析】根据向量的运算法则可得:n =()222OA OB +=,故选B.16．如图，平行四边形ABCD 的对角线AC 与BD 相交于点O ，设OA a =，OB b =，下列式子中正确的是（）A ．DC a b =+B ．DC a b =-； C ．DC a b =-+D ．DC a b =--．【答案】C【解析】【分析】由平行四边形性质，得DC AB =，由三角形法则，得到OA AB OB +=，代入计算即可得到答案.【详解】解：∵四边形ABCD 是平行四边形，∴DC AB =，∵OA a=，OB b=，在△OAB中，有OA AB OB+=，∴AB OB OA b a a b=-=-=-+，∴DC a b=-+；故选择：C.【点睛】此题考查了平面向量的知识以及平行四边形的性质．注意掌握平行四边形法则与三角形法则的应用是解此题的关键．17．已知一个单位向量e，设a、b是非零向量，那么下列等式中正确的是（）．A．1a ea=；B．e a a=；C．b e b=；D．11a ba b=．【答案】B【解析】【分析】长度不为0的向量叫做非零向量，向量包括长度及方向，而长度等于1个单位长度的向量叫做单位向量，注意单位向量只规定大小没规定方向，则可分析求解．【详解】解：A、左边得出的是a的方向不是单位向量，故错误；B、符合向量的长度及方向，正确；C、由于单位向量只限制长度，不确定方向，故错误；D、左边得出的是a的方向，右边得出的是b的方向，两者方向不一定相同，故错误．故选：B．【点睛】本题考查了向量的性质．18．设,m n为实数，那么下列结论中错误的是（）A．m na mn a（）＝（）B．m n a ma na++（）＝C．m a b ma mb+（+）＝D．若0ma=，那么0a=【答案】D【解析】【分析】空间向量的线性运算的理解：（1）空间向量的加、减、数乘运算可以像代数式的运算那样去运算；（2）注意向量的书写与代数式的书写的不同，我们书写向量的时候一定带上线头，这也是向量与字母的不同之处；（3）虽然向量的线性运算可以像代数式的运算那样去运算，但它们表示的意义不同．【详解】根据向量的运算法则，即可知A （结合律）、B 、C （乘法的分配律）是正确的，D 中的0是有方向的，而0没有，所以错误．解：∵A 、B 、C 均属于向量运算的性质，是正确的；∵D 、如果a =0，则m=0或a =0．∴错误．故选D ．【点睛】本题考查的知识点是向量的线性运算，解题关键是熟记向量的运算法则.19．已知e 是一个单位向量，a 、b 是非零向量，那么下列等式正确的是（） A ．a e a = B ．e b b = C ．1a e a = D ．11a b a b= 【答案】B【解析】【分析】长度不为0的向量叫做非零向量，向量包括长度及方向，而长度等于1个单位长度的向量叫做单位向量，注意单位向量只规定大小没规定方向，则可分析求解．【详解】A. 由于单位向量只限制长度，不确定方向，故错误；B. 符合向量的长度及方向，正确；C. 得出的是a 的方向不是单位向量，故错误；D. 左边得出的是a 的方向，右边得出的是b 的方向，两者方向不一定相同，故错误. 故答案选B.【点睛】本题考查的知识点是平面向量，解题的关键是熟练的掌握平面向量.20．对于非零向量a 、b ，如果2|a |＝3|b |，且它们的方向相同，那么用向量a 表示向量b 正确的是（）A ．b ＝32a B ．b ＝23a C ．b ＝﹣32a D ．b ＝-23a 【答案】B【解析】【分析】根据已知条件得到非零向量a 、b 的模间的数量关系，再结合它们的方向相同解题．【详解】 ∵2|a |=3|b |，∴|b |23=|a |．又∵非零向量a与b的方向相同，∴23b a ．故选B．【点睛】本题考查了平面向量的知识，即长度不为0的向量叫做非零向量，向量包括长度及方向，而长度等于1个单位长度的向量叫做单位向量，注意单位向量只规定大小没规定方向．。

向量线性运算练习题

向量线性运算练习题一、填空题：1. 若向量a = (2, 3)T，向量b = (5, -1)T，则a + b = ________。

2. 若向量c = (-3, 4)T，向量d = (2, -5)T，则c - d = ________。

3. 若向量e = (4, -2, 6)T，向量f = (1, 3, -5)T，则e · f = ________。

4. 若向量g = (2, -1, 3)T，k为标量，则2g = ________。

5. 若向量h = (3, 1)T，k为标量，则k · h = ________。

二、选择题：1. 已知向量a = (2, 1)T，向量b = (-1, -3)T，下列哪个式子成立？A. a + b = b - aB. a - b = b - aC. a + b = -b - aD. a - b = -b - a2. 已知向量c = (3, 4)T，向量d = (2, 1)T，下列哪个式子成立？A. c · d = d · cB. c + d = d + cC. c - d = d + cD. c + d = -d - c3. 若向量e = (2, 1, -3)T，向量f = (1, 2, -4)T，则下列哪个式子成立？A. e + f = f - eB. e - f = -f - eC. e · f = f · eD. 2e = -2f三、计算题：1. 已知向量a = (3, 2)T，向量b = (1, -1)T，求a + b。

2. 已知向量c = (-4, 3)T，向量d = (2, -5)T，求c - d。

3. 已知向量e = (4, -2, 1)T，向量f = (1, 3, -5)T，求e · f。

4. 已知向量g = (2, -1, 3)T，求5g。

5. 已知向量h = (3, 1)T，求-2h。

高一数学线性运算试题答案及解析

高一数学线性运算试题答案及解析1.设与是不共线向量，，若且，则实数的值为（）.A．0B．1C．D．【答案】C【解析】因为，若且，所以存在，使，即，又因为与是不共线向量，所以，解得.【考点】平面向量平行的判定.2.已知是△的外心，且，，是线段上任一点（不含端点），实数，满足，则的最小值是（）A．1B．2C．3D．4【答案】B【解析】由已知是△的外心，知，又因为，所以四边形OACB 是菱形（如图）又因为可知：；再由P、A、B三点共线及得到：，从而=，当且仅当时“=”成立，所以的最小值为2.故选B．【考点】１．向量的线性运算；２．基本不等式．3.已知点C在内部且，设，则等于（）.A．3B．C．D．【答案】A【解析】由题意得：是直角三角形，且，;延长OC交AB于D,则.在中，,,则,,,.【考点】解三角形、平面向量的线性运算.4.如果三点共线，那么的值为【答案】-9【解析】∵三点A（3，1）、B（-2，k）、C（8，11）共线，∴存在实数λ，使得【考点】三点共线的充要条件5.如图，正六边形ABCDEF中，有下列四个命题：①＋＝2②＝2＋2③·＝·④(·)＝ (·)其中真命题的序号是________．(写出所有真命题的序号)【答案】①②④【解析】，∴①对;取AD的中点O，则,，∴②对;设，则·＝×2×cos=3，·=2×1×cos=1，∴③不对；又·=·=2×1×cos=1=，·=1×1×cos=，∴④对。

故真命题的序号①②④。

【考点】平面向量的数量积，平面向量的线性计算。

点评：简单题，向量的夹角公式。

平面向量模的计算，往往“化模为方”，转化成向量的运算。

6.如图, 中,、、分别是、、上的中线，它们交于点，则下列各等式中不正确的是 ( )A．B．；C．D．【答案】B【解析】根据题意，由于有三角形的重心分各条中线为1：2得解．解：由条件可知G为△ABC的重心，由三角形重心的性质可知显然成立，故选B.对于A，，以及C.和 D. 成立，故错误的为B.【考点】三角形的重心点评：考查三角形中重心的性质．属于基础题。

高一数学苏教版四2.2向量的线性运算练习含答案

一、填空题1。

在△ABC中，已知M是BC中点，设错误!＝a，错误!＝b,则错误!＝________．(用a，b表示）2. 在四边形ABCD中，错误!＝a＋2b，错误!＝－4a－b，错误!＝－5a －3b，则四边形ABCD的形状是__________．3。

设点M是线段BC的中点，点A在直线BC外，错误!2＝64，｜AB→＋错误!｜＝|错误!－错误!|，则｜错误!|＝__________．4. 在△ABC中，错误!＝a，错误!＝b，点D满足错误!＝2错误!.若错误!＝x a＋y b（x，y是实数),则x＋y＝________．5。

在△ABC中,已知D是边AB上一点．若错误!＝2错误!,错误!＝错误!错误!＋λ错误!，则λ＝__________．6。

已知向量a和b不共线，实数x,y满足（2x－y）a＋4b＝5a ＋（x－2y）b，则x＋y的值等于________．7. 如图，设O是△ABC内部一点，且错误!＋错误!＝－2错误!,则△AOB与△AOC的面积之比为________．(第7题)（第9题)8. 已知P是△ABC所在平面内的一点P，错误!＋错误!＋错误!＝错误!。

给出关于点P的位置的下列四种说法：① P在△ABC的内部；② P 在△ABC的外部；③P在直线AB上；④ P在边AC上．其中正确的说法是____________．（填序号)9。

如图，在△ABC中，错误!＝错误!错误!,P是BN上的一点．若错误!＝m错误!＋错误!错误!，则实数m的值为________．10。

下列命题中正确的有________．（填序号）①两个向量相等，则它们的起点相同，终点相同；②若｜a|＝｜b|,则a＝b;③若错误!＝错误!,则A，B,C，D四点构成平行四边形；④在▱ABCD中，一定有AB→＝错误!；⑤若a＝b，b＝c，则a＝c;⑥若a∥b,b∥c,则a∥c。

二、解答题11. 如图，已知▱OADB的对角线交点为C，错误!＝错误!错误!,错误!＝13错误!，错误!＝a,错误!＝b，试用a,b表示错误!，错误!，错误!.12设a，b都是非零向量，且a与b不共线．（1) 若错误!＝a＋b，错误!＝2a＋8b，错误!＝3(a－b），求证：A，B，D三点共线；（2) 若k a＋b和a＋k b共线，求实数k的值．13已知O为原点,A，B，C为平面内的三点．求证：(1）若A，B,C三点共线,则存在实数α，β，且α＋β＝1，使得错误!＝α错误!＋β错误!;(2) 若存在实数α，β，且α＋β＝1,使得错误!＝α错误!＋β错误!，则A,B，C三点共线．1。

高一数学平面向量的线性运算试题

高一数学平面向量的线性运算试题1.设向量且其中是的内角．（Ⅰ）求的取值范围;（Ⅱ）试确定的取值范围.【答案】（Ⅰ）（Ⅱ）【解析】因为,所以，即又所以即（Ⅰ）=因此的取值范围是（Ⅱ）由（Ⅰ）得,所以设=,则,所以即令则由定义可证在上是单调递减函数，（此处参考答案省略定义证明过程,考生倘若用此法解题，必须写明证明过程，不可用复合函数单调性说明），所以所以取值范围为【考点】两角和与差的正弦函数；数量积表示两个向量的夹角．点评：此题考查了两角和与差的正弦函数公式，半角公式，数量积表示两向量的夹角，正弦函数的定义域与值域，以及特殊角的三角函数值，熟练掌握公式是解本题的关键．2.已知＝（2，3），＝（x，－6），若∥，则x等于A．9B．4C．－4D．－9【答案】C【解析】∵＝（2，3），＝（x，－6），且∥，∴3x=2×(-6),解得x=-4,故选C【考点】本题考查了向量共线的坐标运算点评：两个向量设=(x1，y1)，=(x2，y2)平行的充要条件是x1y2－x2y1=03.已知向量＝（1，－2），＝，若·≥0，则实数x的取值范围为A．B．C．∪D．∪【答案】C【解析】由=（1，-2），=，•=3-，根据•≥0，得出3-≥0即≥0化为x（3x-2）≥0且x≠0，解得x∈（-∞，0）∪，故选C【考点】本题考查了数量积的坐标运算点评：考查向量数量积的坐标运算，不等式的解法．本题中涉及到分式不等式求解，一般化为整式不等式求解4. .如图，在，是上的一点，若，则实数的值为（）A．B．C．D．【答案】C【解析】因为,因为B、P、N三点共线，所以.5.已知在四边形ABCD中，AB=AD=4，BC=6，CD=2，，求三角形ABC的外接圆半径R为【答案】【解析】解：因为四边形ABCD中，AB=AD=4，BC=6，CD=2，即利用勾股定理，求解AC边，然后利用正弦定理表示三角形外接圆的半径即可。

6.已知点O为△ABC外接圆的圆心，且＋＋＝0，则△ABC的内角A等于(A)．A．30°B．60°C．90°D．120°【答案】A【解析】解析:如图，∵＋＋＝0，∴＋＝，∴四边形OACB为菱形，∴OG⊥AB，∴∠CAB＝30°.7.如图在△ABC所在平面上有一点P，满足＋＋＝，则△PAB与△ABC的面积之比是()A．B．C．D．【答案】A【解析】解：∵＋＋＝，∴＋＋- =，即＋＋+ =∴＋+ =，2+ =，∴点P在线段AC上，且|AC|=2|PA|那么△PAB的面积与△ABC的面积之比是1/ 3 ．故选 A．8.已知，则（）A．A、B、D三点共线 B. A、B、C三点共线C、B、C、D三点共线D、A、C、D三点共线【答案】A【解析】解：因为故A、B、D三点共线9.在中，满足,是边上的一点.（Ⅰ）若,求向量与向量夹角的正弦值；（Ⅱ）若，=m (m为正常数) 且是边上的三等分点.，求值；（Ⅲ）若且求的最小值。

高一数学苏教版必修4同步练习：2.2 向量的线性运算

2.2 向量的线性运算1、在平行四边形ABCD 中，设,,,AB a AD b AC c BD d ====，下列等式中不正确的是（）A ．a b c +=B ．a b d -=C ．b a d -=D ．c a b -=2、给出下面四个命题：① 0AB BA +=；② AB BC AC +=；③ AB AC BC -=；④ 00AB ⋅=其中正确的个数为（）A. 1个 B ．2个 C ．3个 D ．4个3、已知点()()1,0,3,2A B ==，向量()2,1AC =，则向量BC =( )A.()0,1-B.()1,1-C.()1,0D.()1,0-4、已知ABC △是边长为1的等边三角形,点,D E 分别是边,AB BC 的中点,连接DE 并延长到点F ,使得2DE EF =,则AF BC ⋅的值为( ) A. 58- B. 18 C. 14 D. 1185、已知()()2,3,4,3A B -且2AP PB =-,则P 点的坐标为( )A. ()6,9B. (3,0)C. ()6,9-D. ()2,36、下列四式中不能化简为AD 的是( )A ．()AB CD BC ++ B ．()()AD MB BC CM +++ C ．()MB AD BM +- D ．()OC OA CD -+ 7、如图,原点O 是△ABC 内一点,顶点A 在x 上,150,90AOB BOC ∠=︒∠=︒=3,=u +λ,则u λ=( )A ．3-B ．3C ．-3D ．3 8、已知AD 、BE 分别为ABC ∆的边BC 、AC 上的中线,设AD a =,BE b =,则BC 等于( )A. 4233a b + B. 2433a b + C. 2433a b - D. 2433a b -+ 9、已知平面向量()()1,4,2,3a b →→==，则向量1255a b →→+=( ) A ．()2,1 B ．()3,5 C.()5,3 D.()1,210、设向量, (cos ,sin ),(1,2)a b θθ==，且||(1,2)a b =,则tan 4πθ（）等于( ) A ．4-3 B ．1-3 C ．13 D ．4311、已知向量()()3,2,0,1a b ==-,那么向量3b a -的坐标是__________ 12、已知向量()1,2,25,a b b a λ===且0λ<，则b = .13、已知P 为平行四边形ABCD 所在平面上任一点，且满足20PA PB PD ++=，λ0PA PB PC μ++=，则λμ＝________．14、ABC △中,5,25AB AC ==BC 上的高4AD =，且垂足D 在线段BC 上，H 为ABC △的垂心且(,R)AH xAB y AC x y =+∈，则x y=________. 15、已知向量12121223,23,29a e e b e e c e e =-=+=-其中12,e e 为两个非零不共线向量.问:是否存在这样的实数,λμ,使向量d a b λμ=+与c 共线?答案以及解析1答案及解析：答案：B解析：2答案及解析：答案：C解析：3答案及解析：答案：A解析：4答案及解析：答案：B解析：设BA a =,BC b =,∴()1122DE AC b a ==-, ()3324DF DE b a ==-,()13532444AF AD DF a b a a b =+=-+-=-+, ∴25353144848AF BC a b b ⋅=-⋅+=-+=, 故选B5答案及解析：答案：C 解析：6答案及解析：答案：C解析：由题意得A ：()AB CD BC AB CD BC AC CD AD ++=++=+=，B ：()()0AD MB BC CM AD MB BC CM AD CM CM AD AD +++=+++=++=+=， C ：()2MB AD BM MB AD MB MB AD +-=++=+，所以C 不能化简为AD ， D ：()OC OA CD OC OA CD AC CD AD -+=-+=+=，故选：C ．7答案及解析：答案：D解析：8答案及解析：答案：B解析：设AD 与BE 的交点为F ,则23AF a =,23BF b =. 由0AB BF FA ++=,得()23AB a b =-, 所以()24233BC AD AB a b =-=+.9答案及解析：答案：D解析：10答案及解析：答案：B解析：11答案及解析：答案：(3,5)--解析：12答案及解析：答案：(2,4)--解析：13答案及解析：答案：34- 解析：14答案及解析：答案：23解析：15答案及解析：答案：121212(23)(23)(22)(33)d a b e e e e e e λμλμλμμλ=+=-++=++-. 要使//c d ,则应存在实数k ,使d kc =即121212(22)(33)(29)29e e k e e ke e λμμλ++-=-==∵12,e e 不共线,∴222339k k λμλμ+=⎧⎨-+=-⎩∴,2λμ-故存在这样的实数,λμ,满足2λμ=-就能使d 与c 共线.由Ruize收集整理。

向量的线性运算基础测试题附解析

向量的线性运算基础测试题附解析一、选择题1．已知5AB a b =+u u u r r r ，28BC a b =-+u u u r r r ，()3CD a b =-u u u r r r ，则（）．A ．A 、B 、D 三点共线 B ．A 、B 、C 三点共线 C ．B 、C 、D 三点共线 D ．A 、C 、D 三点共线【答案】A 【解析】【分析】根据共线向量定理逐一判断即可. 【详解】解：∵28BC a b =-+u u u r r r ，()3CD a b =-u u u r r r ，5AB a b =+u u u r r r∴()2835BD BC CD a b a b a b =+=-++-=+u u u r u u u r u u u r r r r r r r， ∴AB u u u r 、BD u u u r是共线向量∴A 、B 、D 三点共线，故A 正确；∵5AB a b =+u u u r r r ，28BC a b =-+u u u r r r∴不存在实数λ，使AB BC λ=u u u r u u u r ，即AB u u u r 、BC uuur 不是共线向量∴A 、B 、C 三点共线，故B 错误；∵28BC a b =-+u u u r r r ，()3CD a b =-u u u r r r ∴不存在实数λ，使BC CD λ=u u u r u u u r ，即BC uuu r 、CD uuur 不是共线向量∴B 、C 、D 三点共线，故C 错误；∵5AB a b =+u u u r r r ，28BC a b =-+u u u r r r ，()3CD a b =-u u u r r r ，∴()52813AC AB BC a b a b a b =+=++-+=-+u u u r u u u r u u u r r r r r r r∴不存在实数λ，使AC CD λ=u u u r u u u r ，即AC u u u r 、CD uuur 不是共线向量∴A 、C 、D 三点共线，故D 错误；故选A. 【点睛】此题考查的是共线向量的判定，掌握共线向量的定理是解决此题的关键.2．在四边形ABCD 中，，，，其中与不共线，则四边形ABCD 是( ) A ．平行四边形 B ．矩形C ．梯形D ．菱形【答案】C 【解析】【分析】利用向量的运算法则求出，利用向量共线的充要条件判断出，得到边AD∥BC，AD=2BC，据梯形的定义得到选项.【详解】解：∵，∴，∴AD∥BC，AD=2BC.∴四边形ABCD为梯形.【点睛】本题考查向量的运算法则向量共线的充要条件、利用向量共线得到直线的关系、梯形的定义.3．若非零向量、满足｜-｜=｜｜，则( )A．｜2｜＞｜-2｜B．｜2｜＜｜-2｜C．｜2｜＞｜2-｜D．｜2｜＜｜2-｜【答案】A【解析】【分析】对非零向量、共线与否分类讨论，当两向量共线，则有，即可确定A、C满足；当两向量不共线，构造三角形，从而排除C，进而解答本题.【详解】解：若两向量共线，则由于是非零向量，且，则必有；代入可知只有A、C满足；若两向量不共线，注意到向量模的几何意义，故可以构造三角形，使其满足OB=AB=BC；令，，则，∴且；又BA+BC>AC ∴∴.故选A.【点睛】本题考查了非零向量的模，针对向量是否共线和构造三角形是解答本题的关键.4．已知向量，若与共线，则( ) A．B．C．D．或【答案】D【解析】【分析】要使与，则有=，即可得知要么为0，要么，即可完成解答.【详解】解：非零向量与共线的充要条件是当且仅当有唯一一个非零实数，使=,即；与任一向量共线.故答案为D. 【点睛】本题考查了向量的共线，即=是解答本题的关键.5．下列命题中，真命题的个数为( ) ①方向相同 ②方向相反 ③有相等的模 ④方向相同 A ．0 B ．1C ．2D ．3【答案】C 【解析】【分析】直接利用向量共线的基本性质逐一核对四个命题得答案. 【详解】解：对于①，若，则方向相同，①正确；对于②，若，则方向相反，②正确；对于③，若，则方向相反，但的模不一定，③错误；对于④，若，则能推出的方向相同，但的方向相同，得到④错误. 所以正确命题的个数是2个，故选:C. 【点睛】本题考查命题的真假判断与应用，考查了向量共线的基本性质，是基础题.6．下列等式正确的是（）A ．AB u u u r +BC uuur ＝CB u u u r +BA u u u rB ．AB u u u r﹣BC uuu r ＝AC u u u rC ．AB u u u r +BC uuur +CD uuu r ＝DA u u u r D ．AB u u u r +BC uuur ﹣AC u u u r ＝0r【答案】D 【解析】【分析】根据三角形法则即可判断. 【详解】∵AB BC AC +=u u u r u u u r u u u r ， ∴0AB BC AC AC AC +-=-=u u u u r u u u r u u u r u u u r u u u r r ，故选D ．【点睛】本题考查平面向量的三角形法则，解题的关键是熟练掌握三角形法则.7．如图，在△ABC 中，中线AD 、CE 交于点O ，设AB a,BC k ==u u u r r u u u r r，那么向量AO uuu r用向量a br r 表示为（）A ．12a b +rrB ．2133a b +r rC ．2233a b +r rD ．1124a b +r r【答案】B 【解析】【分析】利用三角形的重心性质得到： 23AO AD =；结合平面向量的三角形法则解答即可．【详解】∵在△ABC 中，AD 是中线， BC b =u u u r r，∴11BD BC b 22==u u u r u u u r r．∴1b 2AD AB BD a =+=+u u u r u u u r u u u r r r又∵点O 是△ABC 的重心， ∴23AO AD =， ∴221AO AD a b 333==+u u u r u u u r r r ．故选：B ．【点睛】此题主要考查了平面向量与重心有关知识，根据重心知识得出23AO AD =是解题的关键．8．下列判断不正确的是（）A ．如果AB CD =u u u r u u u r，那么AB CD =u u u r u u u rB ．+＝+C ．如果非零向量a b(0)k k=坠r r，那么a r 与b r平行或共线D ．AB BA 0+=u u u r u u u r【答案】D 【解析】【分析】根据模的定义，可判断A 正确；根据平面向量的交换律，可判断B 正确；根据非零向量的知识，可确定C 正确；又由0AB BA +=u u u r u u u r r可判断D 错误【详解】A 、如果AB CD =u u u r u u u r，那么AB CD =u u u v u u u v ，故此选项正确；B 、a b b a +=+r r r r，故本选项正确；C 、如果非零向量a b(0)k k =坠r r ，那么a r 与b r平行或共线，故此选项正确；D 、0AB BA +=u u u r u u u r r，故此选项错误；故选：D ．【点睛】此题考查的是平面向量的知识，掌握平面向量相关定义是关键9．已知平行四边形ABCD ，O 为平面上任意一点.设=，=，=，=，则（） A ．+++= B ．-+-= C ．+--= D ．--+=【答案】B 【解析】【分析】根据向量加法的平行四边形法则，向量减法的几何意义，以及相反向量的概念即可找出正确选项．【详解】根据向量加法的平行四边形法则及向量减法的几何意义，即可判断A,C,D 错误；；而；∴B 正确. 故选B. 【点睛】此题考查向量加减混合运算及其几何意义，解题关键在于掌握运算法则.10．已知矩形的对角线AC 、BD 相交于点O ，若BC a =u u u rr，DC b =u u u r r，则（）A ．()12BO a b =+u u u r rr ； B ．()12BO a b =-u u u r rr ；C ．()12BO b a =-+u u u r r r； D．()12BO b a =-u u u r r r ．【答案】D 【解析】1,.21(b-a)2BCD BO BD BD DC CB CB BCBO D∆==+=-=u u u r u u u r u u u r u u u r u u u r u u u r u u u ru u u r r r在中，所以故选11．如图，在△ABC 中，点D 是在边BC 上，且BD ＝2CD ，＝，＝，那么等于（）A ．＝＋B ．＝＋C ．＝－D ．＝＋【答案】D 【解析】【分析】利用平面向量的加法即可解答. 【详解】解：根据题意得＝,＋ .故选D. 【点睛】本题考查平面向量的加法及其几何意义,涉及向量的数乘,属基础题.12．化简OP QP PS SP -++u u u r u u u r u u u r u u r的结果等于（）．A ．QP uuu rB ．OQ uuu rC ．SP u u rD ．SQ u u u r【答案】B 【解析】【分析】利用向量的加减法的法则化简即可. 【详解】解：原式=+Q OP P PS SP ++u u u r u u u r u u u r u u r=Q O uuu r，故选B. 【点睛】本题主要考查两个向量的加减法的法则，以及其几何意义，难度不大.13．如图，ABCD □对角线AC 与BD 相交于点O ，如果AB m =u u u r u r ，AD n =u u u r r，那么下列选项中，与向量()12m n +ur r 相等的向量是（）.A ．OA u u u rB ．OB uuu rC ．OC u u u rD ．OD uuu r【答案】C 【解析】【分析】由四边形ABCD 是平行四边形根据平行四边形法则，可求得BC AD n ==u u u r u u u r r，然后由三角形法则，求得AC u u u r 与BD u u u r，继而求得答案．【详解】∵四边形ABCD 是平行四边形， ∴BC AD n ==u u u r u u u r r，∴AC u u u r ＝AB BC m n +=+u u u r u u u r u r r ，=BD AD AB n m -=-u u u r u u u r u u u r r u r，∴()11=-22OA AC m n =-+u u u r u u u r ur r ，()11=22OC AC m n =+u u u r u u u r u r r ()11=-22OB BD n m =--u u u r u u u r r ur ，()11=22OD BD n m =-u u u r u u u r r u r故选：C ．【点睛】此题考查了平面向量的知识以及平行四边形的性质．注意掌握三角形法则与平行四边形法则的应用是解此题的关键．14．下列说法正确的是（） A ．()0a a +-=r rB ．如果a r 和b r 都是单位向量，那么a b =r rC ．如果||||a b =r r ，那么a b =r rD ．12a b =-r r （b r为非零向量），那么//a b r r【答案】D【解析】【分析】根据向量，单位向量，平行向量的概念，性质及向量的运算逐个进行判断即可得出答案. 【详解】解：A 、()a a +-r r等于0向量，而不是0，故A 选项错误；B 、如果a r 和b r都是单位向量，说明两个向量长度相等，但是方向不一定相同，故B 选项错误；C 、如果||||a b =r r，说明两个向量长度相等，但是方向不一定相同，故C 选项错误；D 、如果12a b =-r r （b r为非零向量），可得到两个向量是共线向量，可得到//a b r r ，故D选项正确. 故选：D. 【点睛】本题考查向量的性质及运算，向量相等不仅要长度相等，还要方向相同，向量的运算要注意向量的加减结果都是一个向量.15．在矩形ABCD 中，下列结论中正确的是（）A ．AB CD =u u u r u u u rB ．AC BD =uuu r uu u rC ．AO OD =u u u r u u u rD ．BO OD =-u u u r u u u r【答案】C 【解析】【分析】根据相等向量及向量长度的概念逐一进行判断即可．【详解】相等向量：长度相等且方向相同的两个向量． A. AB CD =-u u u r u u u r，故该选项错误；B. AC BD =u u u r u u u r，但方向不同，故该选项错误；C. 根据矩形的性质可知，对角线互相平分且相等，所以AO OD =u u u r u u u r，故该选项正确； D. BO OD =u u u r u u u r，故该选项错误；故选：C ．【点睛】本题主要考查相等向量及向量的长度，掌握相等向量的概念是解题的关键．16．如图，向量OA u u u r 与OB uuu r 均为单位向量，且OA ⊥OB ，令n r =OA u u u r +OB uuu r，则||n v=（）A ．1B 2C 3D ．2【答案】B 【解析】根据向量的运算法则可得: n v ()222OA OB +=u u u v u u u v 故选B.17．已知5a b =r r，下列说法中，不正确的是（） A ．50a b -=rrB ．a r与b r方向相同 C ．//a b r rD ．||5||a b =r r【答案】A 【解析】【分析】根据平行向量以及模的定义的知识求解即可求得答案，注意掌握排除法在选择题中的应用．【详解】A 、50a b -=r rr，故该选项说法错误B 、因为5a b =r r ，所以a r 与b r的方向相同，故该选项说法正确， C 、因为5a b =r r ，所以//a b r r，故该选项说法正确，D 、因为5a b =r r ，所以||5||a b =r r ；故该选项说法正确，故选：A ．【点睛】本题考查了平面向量，注意，平面向量既有大小，又由方向，平行向量，也叫共线向量，是指方向相同或相反的非零向量．零向量和任何向量平行．18．已知a r =3，b r =5，且b r 与a r 的方向相反，用a r 表示b r 向量为（） A ．35b a =r r B ．53b a =r r C ．35b a =-r r D ．53b a =-r r【答案】D 【解析】【分析】根据a r =3，b r =5，且b r 与a r 的方向相反，即可用a r表示b r 向量.【详解】a r=3，b r =5，b r =53a r ,b r 与a r的方向相反, ∴5.3b a =-r r故选：D. 【点睛】考查了平面向量的知识，注意平面向量的正负表示的是方向.19．已知一个单位向量e v ，设a v 、b v是非零向量，那么下列等式中正确的是（）．A ．1a e a=r r r ；B ．e a a =r r r ；C ．b e b =r r r ；D ．11a b a b=r r r r ．【答案】B 【解析】【分析】长度不为0的向量叫做非零向量，向量包括长度及方向，而长度等于1个单位长度的向量叫做单位向量，注意单位向量只规定大小没规定方向，则可分析求解．【详解】解：A 、左边得出的是a 的方向不是单位向量，故错误；B 、符合向量的长度及方向，正确；C 、由于单位向量只限制长度，不确定方向，故错误；D 、左边得出的是a 的方向，右边得出的是b 的方向，两者方向不一定相同，故错误．故选：B ．【点睛】本题考查了向量的性质．20．已知a r、b r和c r都是非零向量，在下列选项中，不能判定//a b rr 的是( )A ．2a b =rrB ．//a c r r，//b c r rC ．||||a b =rrD ．12a c =r r ，2bc =r r【答案】C 【解析】【分析】由方向相同或相反的非零向量叫做平行向量，对各选项分析判断．【详解】A 选项：由2a b =r r ，可以推出//a b r r．本选项不符合题意；B 选项：由//a c r r ，//b c r r ，可以推出//a b r r ．本选项不符合题意；C 选项：由||||a b =r r ，不可以推出//a b r r ．本选项符合题意；D 选项：由12a c =r r ，2bc =r r ，可以推出//a b r r ．本选项不符合题意；故选：C ．【点睛】考查了平面向量，解题关键是熟记平行向量的定义．。

高一数学线性运算试题

高一数学线性运算试题1. A、B、D三点共线，则对任一点C，=,则λ=（）.A． B． C．- D．-【答案】C【解析】三点共线，存在实数，使,则,即，，即.【考点】平面向量的线性运算.2.已知点C在内部且，设，则等于（）.A．3B．C．D．【答案】A【解析】由题意得：是直角三角形，且，;延长OC交AB于D,则.在中，,,则,,,.【考点】解三角形、平面向量的线性运算.3.四边形OABC中，，若，，则=（）A．B．C．D．【答案】D【解析】故选D.【考点】向量的加法4.已知向量a=（1，），则与a反向的单位向量是【答案】【解析】的反向向量为,所以其单位向量为.【考点】向量的单位向量的计算.5.如图，正方形ABCD中，点E是DC的中点，CF:FB=2:1，那么＝()．A．－B．＋C．＋D．－【答案】Ｄ【解析】，所以选Ｄ【考点】向量的加法法则6.在中，，．若点满足，则（）A．B．C．D．【答案】A【解析】根据题意，由于中，，，由于，则说明点D是BC的三等分点，则可知，故选A.【考点】向量的线性表示点评：主要是考查了向量的线性表示，属于基础题。

7.已知，则与共线的向量为A．B．C．D．【答案】C【解析】因为，那么则与共线的向量要满足，那么对于选项A,分析不满足比例关系，对于选项B，由于不存在实数满足，因此不共线，同理可知选项D，也不满足，排除法只有选C.【考点】共线向量点评：主要是考查了向量共线的概念的运用，属于基础题。

8.化简A．B．C．D．【答案】B【解析】解：因为选B9.如图，已知，用表示，则A．B．C．D．【答案】B【解析】解：，用表示，则,选B10.在等边三角形ABC中,点在线段上，满足，若，则实数的值是___________．【答案】【解析】设三角形ABC的边长为a,则11.在平面直角坐标系中，若为坐标原点，则、、三点在同一直线上的等价条件为存在唯一的实数，使得成立，此时称实数为“向量关于和的终点共线分解系数”.若已知、,且向量与向量垂直,则“向量关于和的终点共线分解系数”为（）A．B．C．D．【答案】D【解析】解：由向量 OP3 是直线l：x-y+10=0的法向量得出： OP3与向量 a =（1，1）垂直，可设 OP3=(t，-t)(t≠0)，由 OP3=λ• OP1+(1-λ)• OP2得（t，-t）=λ（1，3）+（1-λ）（-1，3）=（4λ-1，3-2λ），∴ 4λ-1="t" 3-2λ=-t ，两式相加得2λ+2=0，∴λ=-1．故答案为：-1．12.已知点，，若直线与线段的交点满足，且，则实数的取值范围为（）A．B．C．D．【答案】B【解析】若直线与线段有交点，则据图得直线与直线AC重合时符合临界条件，此时斜率,又且，所以P点距A较近，最远距离为，此时斜率是C与AB中点D()的连线的斜率故实数的取值范围。

向量的线性运算专项训练及答案

向量的线性运算专项训练及答案一、选择题1．点C在线段AB上，且35AC AB=u u u r u u u r，若ACmBC=u u u r u u u r，则m的值等于（）．A ．23B ．32C．23-D．32-【答案】D【解析】【分析】根据已知条件即可得：25AC ABCB AB==-u u u r u u u r u u u r u u u r，从而得出：52AB BC=-u u u r u u u r，再代入35AC AB=u u u r u u u r中，即可求出m的值.【详解】解：∵点C在线段AB上，且35AC AB=u u u r u u u r∴25AC ABCB AB==-u u u r u u u r u u u r u u u r∴5522CBAB BC==-u u u r u u u r u u u r∴55322335BC BC A CA B⎛⎫=-⎝==-⎪⎭u u u r u u u r u u u r u u u r故选D.【点睛】此题考查的是向量的运算，掌握共线向量的加法、减法和数乘法则是解决此题的关键. 2．□ABCD中， -+等于( )A．B．C．D．【答案】A【解析】【分析】在平行四边形中，两对对边平行且相等，以一对对边所在的线段构成向量，得到的向量要么相等，要么是相反向量，根据本题所给的两个向量来看，它们是一对相反向量，和为零向量，得到结果．【详解】∵在平行四边形ABCD中，与是一对相反向量，∴ = -∴ -+=- + =，故选A．【点睛】此题考查向量加减混合运算及其几何意义，解题关键在于得出与是一对相反向量.3．若非零向量、满足｜-｜=｜｜，则( )A．｜2｜＞｜-2｜B．｜2｜＜｜-2｜C．｜2｜＞｜2-｜D．｜2｜＜｜2-｜【答案】A【解析】【分析】对非零向量、共线与否分类讨论，当两向量共线，则有，即可确定A、C满足；当两向量不共线，构造三角形，从而排除C，进而解答本题.【详解】解：若两向量共线，则由于是非零向量，且，则必有；代入可知只有A、C满足；若两向量不共线，注意到向量模的几何意义，故可以构造三角形，使其满足OB=AB=BC；令，，则，∴且；又BA+BC>AC ∴∴.故选A.【点睛】本题考查了非零向量的模，针对向量是否共线和构造三角形是解答本题的关键.4．在中，已知是边上一点，，则( ) A．B．C．D．【答案】A【解析】【分析】根据A，B，D三点共线得出入的值,即可完成解答.【详解】解：在∆ABC中，已知D是AB边上一点，若=2，，则，∴，故选A.【点睛】本题考查了平面向量的基本定理，识记定理内容并灵活应用是解答本题的关键.5．已知向量，若与共线，则( )A ．B ．C ．D ．或【答案】D 【解析】【分析】要使与，则有=，即可得知要么为0，要么，即可完成解答. 【详解】解：非零向量与共线的充要条件是当且仅当有唯一一个非零实数，使=,即；与任一向量共线.故答案为D. 【点睛】本题考查了向量的共线，即=是解答本题的关键.6．下列命题中，真命题的个数为( ) ①方向相同 ②方向相反 ③有相等的模 ④方向相同 A ．0 B ．1C ．2D ．3【答案】C 【解析】【分析】直接利用向量共线的基本性质逐一核对四个命题得答案. 【详解】解：对于①，若，则方向相同，①正确；对于②，若，则方向相反，②正确；对于③，若，则方向相反，但的模不一定，③错误；对于④，若，则能推出的方向相同，但的方向相同，得到④错误. 所以正确命题的个数是2个，故选:C. 【点睛】本题考查命题的真假判断与应用，考查了向量共线的基本性质，是基础题.7．如果向量a r 与单位向量e r方向相反，且长度为12，那么向量a r 用单位向量e r表示为（）A ．12a e =rr B ．2a e =r rC ．12a e =-rr D ．2a e =-r r【答案】C 【解析】由向量a r 与单位向量e r方向相反，且长度为12，根据向量的定义，即可求得答案．解：∵向量a r 与单位向量e r方向相反，且长度为12， ∴12a e =-rr ．故选C ．8．已知233m a b =-r r r ，1124n b a =+r r r ，那么4m n -r r等于（）A ．823a b -r rB ．443a b r r -C ．423a b -r rD ．843a b -r r【答案】A 【解析】根据向量的混合运算法则求解即可求得答案，注意解题需细心．解：∵233m a b =-r r r ，1124n b a =+r r r，∴4m n -r r =2112834()32232433a b b a a b b a a b --+=---=-rr r r r r r r r r ．故选A ．9．D 、E 、F 分别是△ABC 三边AB 、BC 、CA 的中点，则下列等式不成立的是( ) A ．+ ＝B ．++＝0C ．+＝D ．+＝【答案】C 【解析】【分析】由加法的三角形法则化简求解即可．【详解】由加法的三角形法则可得， + ＝, ++＝ , +＝,+＝故选：B.【点睛】此题考查向量的加法及其几何意义，解题关键在于掌握平面向量的加法法则.10．下列说法正确的是（）． A ．一个向量与零相乘，乘积为零 B ．向量不能与无理数相乘C ．非零向量乘以一个负数所得向量比原向量短D ．非零向量乘以一个负数所得向量与原向量方向相反【答案】D 【解析】【分析】根据平面向量的定义和性质进行判断．【详解】解：A. 一个向量与零相乘，乘积为零向量.故本选项错误； B. 向量可以与任何实数相乘.故本选项错误；C. 非零向量乘以一个负数所得向量的方向与原向量相反，但不一定更短.故本选项错误；D. 非零向量乘以一个负数所得向量与原向量方向相反.故本选项正确. 故答案是：D. 【点睛】考查了平面向量的知识，属于基础题，掌握平面向量的性质和相关运算法则即可解题．11．若a v ＝2e v，向量b v和向量a v方向相反，且|b v|＝2|a v|，则下列结论中不正确的是（）A ．|a v |＝2B ．|b v|＝4 C ．b v ＝4e vD ．a v＝12b v【答案】C 【解析】【分析】根据已知条件可以得到：b v＝﹣4e v，由此对选项进行判断．【详解】A 、由a v ＝2e v 推知|a v |＝2，故本选项不符合题意．B 、由b v ＝-4e v推知|b v |＝4，故本选项不符合题意．C 、依题意得：b v ＝﹣4e v，故本选项符合题意．D 、依题意得：a v＝-12b v，故本选项不符合题意．故选C ．【点睛】考查了平面向量，注意：平面向量既有大小，又有方向．12．若点O 为平行四边形的中心，14AB m =u u u rr，26BC m =u u u rr，则2132m m -r r等于（）． A ．AO u u u rB ．BO uuu rC ．CO uuu rD ．DO u u u r【答案】B 【解析】【分析】根据向量加法的平行四边形法则和平行四边形的性质逐一判断即可. 【详解】解:∵在平行四边形ABCD 中, 14AB m =u u u r r ，26BC m =u u u r r， ∴1246B m C AC AB m =+=+u u u r u u u r u u u r u u r u u r ,1246BD BA BC AC m m =+==-+u u u r u u u r u u u r u u u r u u r u u r,M 分别为AC 、BD 的中点,∴122312AO AC m m =+=u u u r u u u u u r r u u r，故A 不符合题意；211322BO BD m m ==-u u u r u u u r u u r u u r，故B 符合题意；122312CO AC m m ==---u u u r u u uu u r r u u r ，故C 不符合题意；121232DO BD m m =-=-u u u r u u ur u u r u u r ，故D 不符合题意.故选B.【点睛】此题考查的是平行四边形的性质及向量的加、减法,掌握平行四边形的对角线互相平分和向量加法的平行四边形法则是解决此题的关键.13．如图，ABCD □对角线AC 与BD 相交于点O ，如果AB m =u u u r u r ，AD n =u u u r r，那么下列选项中，与向量()12m n +ur r 相等的向量是（）.A ．OA u u u rB ．OB uuu rC ．OC u u u rD ．OD uuu r【答案】C 【解析】【分析】由四边形ABCD 是平行四边形根据平行四边形法则，可求得BC AD n ==u u u r u u u r r，然后由三角形法则，求得AC u u u r 与BD u u u r，继而求得答案．【详解】∵四边形ABCD 是平行四边形， ∴BC AD n ==u u u r u u u r r，∴AC u u u r ＝AB BC m n +=+u u u r u u u r u r r ，=BD AD AB n m -=-u u u r u u u r u u u r r u r，∴()11=-22OA AC m n =-+u u u r u u u r ur r ，()11=22OC AC m n =+u u u r u u u r u r r ()11=-22OB BD n m =--u u u r u u u r r ur ，()11=22OD BD n m =-u u u r u u u r r u r故选：C ．【点睛】此题考查了平面向量的知识以及平行四边形的性质．注意掌握三角形法则与平行四边形法则的应用是解此题的关键．14．如果向量a r 与单位向量e r 的方向相反，且长度为3，那么用向量e r 表示向量a r为（）A ．3a e =v vB ．3a e =-v vC ．3e a =v vD ．3e a =-v v【答案】B 【解析】【分析】根据平面向量的定义解答即可．【详解】解：∵向量e r 为单位向量，向量a r 与向量e r方向相反， ∴3a e r r =-．故选：B ．【点睛】本题考查平面向量的性质，解题的关键是灵活运用所学知识解决问题．15．下列条件中，不能判定a ∥b 的是（）．A ． //a c r r ,//b c r rB ．||3||a b =rrC ． 5a b =-r rD ．2a b =r r【答案】B 【解析】【分析】根据平面向量的性质进行逐一判定即可．【详解】解：A 、由//a c r r ,//b c r r 推知非零向量a r 、b r 、c r 的方向相同，则//a b r r，故本选项不符合题意．B 、由||3||a b =r r只能判定向量a r 、b r 的模之间的关系，不能判定向量a r 、b r 的方向是否相同，故本选项符合题意．C 、由5a b =-r r 可以判定向量a r 、b r的方向相反，则//a b r r ，故本选项不符合题意．D 、由2a b =r r可以判定向量a r 、b r 的方向相同，则//a b r r ，故本选项不符合题意．故选：B ．【点睛】本题考查的是向量中平行向量的定义，即方向相同或相反的非零向量a r 、b r叫做平行向量．16．化简()()AB CD BE DE -+-u u u r u u u r u u u r u u u r的结果是（）．A ．CA u u u rB ．AC u u u r C ．0rD ．AE u u u r【答案】B 【解析】【分析】根据三角形法则计算即可解决问题．【详解】解：原式()()AB BE CD DE =+-+u u u r u u u r u u u r u u u r AE CE =-u u u r u u u r AE EC =+u u u r u u u rAC =u u u r ，故选：B ．【点睛】本题考查平面向量、三角形法则等知识，解题的关键是灵活运用三角形法则解决问题，属于中考基础题．17．下列说法不正确的是( ) A ．设e r为单位向量，那么||1e =rB ．已知a r、b r、c r 都是非零向量，如果2a c =r r，4b c =-rr ，那么//a b rrC ．四边形ABCD 中，如果满足//AB CD ，||||AD BC =u u u r u u u r，那么这个四边形一定是平行四边形D ．平面内任意一个非零向量都可以在给定的两个不平行向量的方向上分解【答案】C 【解析】【分析】根据单位向量的定义、平行向量的定义以及平行四边形的判定进行解答即可．【详解】解：A. 设e r为单位向量，那么||1e =r，此选项说法正确；B. 已知a r、b r、c r 都是非零向量，如果2a c =r r，4b c =-rr ，那么//a b rr，此选项说法正确；C. 四边形ABCD 中，如果满足//AB CD ，||||AD BC =u u u r u u u r，即AD=BC ，不能判定这个四边形一定是平行四边形，此选项说法不正确；D. 平面内任意一个非零向量都可以在给定的两个不平行向量的方向上分解，此选项说法正确．故选：C ．【点睛】本题考查的知识点是平面向量，掌握单位向量的定义、平行向量的定义以及平行四边形的判定方法是解此题的关键．18．如图,在平行四边形ABCD 中，设AB a =rr,AD b =r r ，那么向量OC r可以表示为. ( )A ．1122a b +r rB ．1122r r a b -C ．1122a b -+rrD ．1122a b --rr【答案】A 【解析】【分析】利用平行四边形的性质以及平面向量的加法与减法运算法则解题即可.【详解】由题意可得()()1111122222OC AC AD AB a b a b ==+=+=+r rr r r r r r【点睛】本题主要考察平面向量的加法与减法运算，掌握平行四边形法则是解题的关键.19．如图，向量OA u u u r 与OB uuu r 均为单位向量，且OA ⊥OB ，令n r =OA u u u r +OB uuu r，则||n v=（）A ．1B 2C 3D ．2【答案】B 【解析】根据向量的运算法则可得: n v()222OA OB +=u u u v u u u v 故选B.20．若AB u u u r是非零向量，则下列等式正确的是（）A ．AB BA =u u u r u u u r ；B ．AB BA u u u v u u u v =；C ．0AB BA +=u u u r u u u r；D ．0AB BA +=u u u r u u u r.【答案】B 【解析】【分析】长度不为0的向量叫做非零向量,本题根据向量的长度及方向易得结果【详解】 ∵AB u u u r是非零向量, ∴AB BA =u u u v u u u v 故选B 【点睛】此题考查平面向量，难度不大。

向量数乘和线性运算精选题32道附参考答案与试题解析

向量数乘和线性运算精选题32道附参考答案与试题解析一．选择题（共12小题）1．如图，在平行四边形ABCD中，E是BC的中点，F是线段AE上靠近点A的三等分点，则＝（）A．B．C．D．2．如图，在△ABC中，，，若，则的值为（）A．﹣3B．3C．2D．﹣23．如图，若＝，＝，＝，B是线段AC靠近点C的一个四等分点，则下列等式成立的是（）A．＝﹣B．＝+C．＝﹣D．＝+4．O是平面上一定点，A、B、C是平面上不共线的三个点，动点P满足，λ∈[0，+∞），则P的轨迹一定通过△ABC的（）A．外心B．内心C．重心D．垂心5．如图所示，矩形ABCD的对角线相交于点O，E为AO的中点，若，则λ•μ等于（）A．B．C．D．6．已知点O是△ABC内部一点，满足+2＝m，＝，则实数m为（）A．2B．﹣2C．4D．﹣47．在平行四边形ABCD中，＝，＝，若E是DC的中点，则＝（）A．B．C．﹣+D．﹣+8．已知D为△ABC所在平面内一点，3＝，则＝（）A．﹣+B．+C．﹣D．+9．在△ABC中，，则＝（）A．B．C．D．10．如图，在△ABC中，，，BE和CD相交于点F，则向量等于（）A．B．C．D．11．△ABC中，AB＝6，BC＝8，AB⊥BC，M是△ABC外接圆上一动点，若＝λ+μ，则λ+μ的最大值是（）A．1B．C．D．212．设点M是线段BC的中点，点A在直线BC外，||2＝16，|+|＝|﹣|，则||＝（）A．8B．4C．2D．1二．多选题（共4小题）（多选）13．设点M是△ABC所在平面内一点，则下列说法正确的是（）A．若＝，则点M是边BC的中点B．若＝，则点M在边BC的延长线上C．若＝，则点M是△ABC的重心D．若＝，且x+y＝，则△MBC的面积是△ABC面积的（多选）14．若点O是线段BC外一点，点P是平面上任意一点，且（λ，μ∈R），则下列说法正确的有（）A．若λ+μ＝1且λ＞0，则点P在线段BC的延长线上B．若λ+μ＝1且λ＜0，则点P在线段BC的延长线上C．若λ+μ＞1，则点P在△OBC外D．若λ+μ＜1，则点P在△OBC内（多选）15．已知正方形ABCD的边长为2，向量，满足，，则（）A．B．C．D．（多选）16．下列四式可以化简为的是（）A．+（）B．（）+（）C．+D．三．填空题（共12小题）17．如图，在四边形ABCD中，∠B＝60°，AB＝3，BC＝6，且＝λ，•＝﹣，则实数λ的值为，若M，N是线段BC上的动点，且||＝1，则•的最小值为．18．已知O在△ABC内，且S△AOB：S△BOC：S△AOC＝4：3：2，，则λ+μ＝19．已知，，，，…，（k∈N*）是平面内两两互不相等的向量，满足||＝1，且|﹣|∈{1，2}（其中i＝1，2，j＝1，2，…，k），则k的最大值是．20．在△ABC中，点D，E分别在边AB，BC上，且AD＝DB，BE＝2EC，记，＝，若，则x+y的值为．21．在四边形ABCD中，AB＝6，若，则＝．22．已知△ABC的一内角，AB＝10，AC＝6，O为△ABC所在平面上一点，满足|OA|＝|OB|＝|OC|，设＝m+n，则m+3n的值为．23．在直角坐标系中，O为原点，，则x+y＝．24．已知，，，则＝．25．已知G为△ABC的重心，过点G的直线与边AB，AC分别相交于点P，Q．若＝，则当ABC与△APQ的面积之比为时，实数λ的值为．26．如图，给定单位向量和，它们的夹角为120°，点C在以O为圆心的上运动．若，其中x，y∈R，则x+2y的最大值是．27．已知点O是△ABC内部一点，并且满足，△BOC的面积为S1，△ABC 的面积为S2，则＝．28．设λ是正实数，三角形ABC所在平面上的另三点A1，B1，C1满足：＝λ（+），＝λ（+），＝λ（+），若三角形ABC与三角形A1B1C1的面积相等，则λ的值为．四．解答题（共4小题）29．如图，已知△ABC中，D为BC的中点，AE＝EC，AD，BE交于点F，设＝，＝．（1）用，分别表示向量，；（2）若＝t，求实数t的值．30．如图所示，在△ABO中，，，AD与BC相交于点M，设，．（1）试用向量，表示；（2）过点M作直线EF，分别交线段AC，BD于点E，F．记，，求证：为定值．31．如图，在平面直角坐标系中，点A（﹣，0），B（，0），锐角α的终边与单位圆O 交于点P．（Ⅰ）用α的三角函数表示点P的坐标；（Ⅱ）当•＝﹣时，求α的值；（Ⅲ）在x轴上是否存在定点M，使得||＝||恒成立？若存在，求出点M的横坐标；若不存在，请说明理由．32．已知O是△ABC所在平面内一点，D为BC边中点．（1）若点O满足，求证：；（2）已知E为AC边中点，O在线段DE上，且满足，△BOC的面积为2，求△ABC的面积．向量数乘和线性运算精选题32道参考答案与试题解析一．选择题（共12小题）1．如图，在平行四边形ABCD中，E是BC的中点，F是线段AE上靠近点A的三等分点，则＝（）A．B．C．D．【解答】解：由可知，＝﹣＝﹣＝﹣++＝，故选：C．2．如图，在△ABC中，，，若，则的值为（）A．﹣3B．3C．2D．﹣2【解答】解：∵＝+，＝＝（﹣）＝﹣＝×﹣＝﹣，∴＝+（﹣）＝+；又＝λ+μ，∴λ＝，μ＝；∴＝×＝3．故选：B．3．如图，若＝，＝，＝，B是线段AC靠近点C的一个四等分点，则下列等式成立的是（）A．＝﹣B．＝+C．＝﹣D．＝+【解答】解：＝，＝，＝，则＝+＝+＝+（﹣）＝﹣＝﹣．故选：C．4．O是平面上一定点，A、B、C是平面上不共线的三个点，动点P满足，λ∈[0，+∞），则P的轨迹一定通过△ABC的（）A．外心B．内心C．重心D．垂心【解答】解：∵、分别表示向量、方向上的单位向量∴+的方向与∠BAC的角平分线一致又∵，∴＝λ（+）∴向量的方向与∠BAC的角平分线一致∴一定通过△ABC的内心故选：B．5．如图所示，矩形ABCD的对角线相交于点O，E为AO的中点，若，则λ•μ等于（）A．B．C．D．【解答】解：由题意及图，可知：＝+＝+＝+（+）＝﹣，∴λ＝，μ＝﹣，∴λ•μ＝﹣．故选：A．6．已知点O是△ABC内部一点，满足+2＝m，＝，则实数m为（）A．2B．﹣2C．4D．﹣4【解答】解：如图所示，点O是△ABC内部一点，满足+2＝m，延长OB到D点，以OA，OD为邻边作平行四边形AODF，连接CF分别交AB，AD于E，G点．则点E是△OAD的重心．∵＝，不妨设CE＝7，则OC＝3，OE＝4，EG＝2，OF＝12．∴m＝＝﹣4，解得m＝﹣4．故选：D．7．在平行四边形ABCD中，＝，＝，若E是DC的中点，则＝（）A．B．C．﹣+D．﹣+【解答】解：如图所示，平行四边形ABCD中，＝，＝，则＝＝﹣＝﹣，又E是DC的中点，则＝+＝（﹣）+＝﹣＝﹣+．故选：C．8．已知D为△ABC所在平面内一点，3＝，则＝（）A．﹣+B．+C．﹣D．+【解答】解：因为D为△ABC所在平面内一点，3＝，所以．故选：A．9．在△ABC中，，则＝（）A．B．C．D．【解答】解：∵；∴；∴．故选：B．10．如图，在△ABC中，，，BE和CD相交于点F，则向量等于（）A．B．C．D．【解答】解：设＝k＝k（﹣）＝k（﹣），∵＝+＝k（﹣）+﹣＝（k﹣1）+（1﹣k），＝﹣＝﹣．∵∥，∴＝λ，则（k﹣1）+（1﹣k）＝λ（﹣）．∴，∴k＝，＝﹣，∴＝+＝+．故选：B．11．△ABC中，AB＝6，BC＝8，AB⊥BC，M是△ABC外接圆上一动点，若＝λ+μ，则λ+μ的最大值是（）A．1B．C．D．2【解答】解：以B为坐标原点，BC方向为X轴正方向建立直角坐标系，∴A（0，6）C（8，0），∴外接圆的方程为：（x﹣4）2+（y﹣3）2＝25，即，∴设M（4+5cosθ，3+5sinθ），∴，，∵，∴，∴，∴，故选：C．12．设点M是线段BC的中点，点A在直线BC外，||2＝16，|+|＝|﹣|，则||＝（）A．8B．4C．2D．1【解答】解：由＝16，得||＝4，∵＝||＝4，而∴＝2故选：C．二．多选题（共4小题）（多选）13．设点M是△ABC所在平面内一点，则下列说法正确的是（）A．若＝，则点M是边BC的中点B．若＝，则点M在边BC的延长线上C．若＝，则点M是△ABC的重心D．若＝，且x+y＝，则△MBC的面积是△ABC面积的【解答】解：若＝，则点M是边BC的中点，故A正确；若＝，即有﹣＝﹣，即＝，则点M在边CB的延长线上，故B错误；若＝，即++＝，则点M是△ABC的重心，故C正确；若＝，且x+y＝，可得2＝2x+2y，设＝2，由右图可得M为AN的中点，则△MBC的面积是△ABC面积的，故D正确．故选：ACD．（多选）14．若点O是线段BC外一点，点P是平面上任意一点，且（λ，μ∈R），则下列说法正确的有（）A．若λ+μ＝1且λ＞0，则点P在线段BC的延长线上B．若λ+μ＝1且λ＜0，则点P在线段BC的延长线上C．若λ+μ＞1，则点P在△OBC外D．若λ+μ＜1，则点P在△OBC内【解答】解：因为若λ+μ＝1且λ＞0，故即又λ＞0则点P在线段BC或其反向延长线上，A错误；若λ+μ＝1且λ＜0，同上可得而λ＜0则点P在线段BC的延长线上，B正确；若λ+μ＞1，，同上可得，当λ+μ＞1时，λ+μ﹣1＞0根据向量加法的平行四边形法则可以看出则点P在△OBC外，C正确；若λ+μ＜1，不防令λ＝0，μ＝﹣1则，很显然此时点P在线段CO的延长线上，不在△OBC内，D错误．故选：BC．（多选）15．已知正方形ABCD的边长为2，向量，满足，，则（）A．B．C．D．【解答】解：由条件可得：，所以，A正确；，与不垂直，B错误；，C错误；，根据正方形的性质有AC⊥BD，所以，D项正确．故选：AD．（多选）16．下列四式可以化简为的是（）A．+（）B．（）+（）C．+D．【解答】解：＝＝，A正确；+＝＝，B正确；＝，C正确；＝，D错误．故选：ABC．三．填空题（共12小题）17．如图，在四边形ABCD中，∠B＝60°，AB＝3，BC＝6，且＝λ，•＝﹣，则实数λ的值为，若M，N是线段BC上的动点，且||＝1，则•的最小值为．【解答】解：以B为原点，以BC为x轴建立如图所示的直角坐标系，∵∠B＝60°，AB＝3，∴A（，），∵BC＝6，∴C（6，0），∵＝λ，∴AD∥BC，设D（x0，），∴＝（x0﹣，0），＝（﹣，﹣），∴•＝﹣（x0﹣）+0＝﹣，解得x0＝，∴D（，），∴＝（1，0），＝（6，0），∴＝，∴λ＝，∵||＝1，设M（x，0），则N（x+1，0），其中0≤x≤5，∴＝（x﹣，﹣），＝（x﹣，﹣），∴•＝（x﹣）（x﹣）+＝x2﹣4x+＝（x﹣2）2+，当x＝2时取得最小值，最小值为，故答案为：，．18．已知O在△ABC内，且S△AOB：S△BOC：S△AOC＝4：3：2，，则λ+μ＝【解答】解：如图，根据题意不妨设△ABC的边，AB＝4，AC＝2，BC＝＝2，建立如图坐标系，则BC的方程为x+2y﹣4＝0，则3a﹣4＜0，设O点坐标为（a，a），点O在三角形内，则O到BC的距离d＝＝，则根据S△AOB：S△BOC：S△AOC＝4：3：2，得（•4a）：（2×）：（×2a），解得a＝，∴＝（，），＝（4，0），＝（0，2），由，得，解得，，所以：λ+μ＝，故填：19．已知，，，，…，（k∈N*）是平面内两两互不相等的向量，满足||＝1，且|﹣|∈{1，2}（其中i＝1，2，j＝1，2，…，k），则k的最大值是6．【解答】解：如图，设，，由||＝1，且|﹣|∈{1，2}，分别以A1，A2为圆心，以1和2为半径画圆，其中任意两圆的公共点共有6个．故满足条件的k的最大值为6．故答案为：6．20．在△ABC中，点D，E分别在边AB，BC上，且AD＝DB，BE＝2EC，记，＝，若，则x+y的值为．【解答】解：如图，∵AD＝DB，BE＝2EC；∴，＝，且；∴＝；又；∴根据平面向量基本定理得，；∴．故答案为：．21．在四边形ABCD中，AB＝6，若，则＝12．【解答】解：根据题意，如图，在AB上取一点E，使＝，则有＝+＝+＝+（﹣）＝+，又由，则有＝，四边形AECD为平行四边形，则有＝＝，又由AB＝6，则＝6×2＝12；故答案为：12．22．已知△ABC的一内角，AB＝10，AC＝6，O为△ABC所在平面上一点，满足|OA|＝|OB|＝|OC|，设＝m+n，则m+3n的值为．【解答】解：由得：||＝||＝||，则点O是△ABC的外心，则，由＝10×＝30所以，所以，所以m+3n＝，故答案为：23．在直角坐标系中，O为原点，，则x+y＝0．【解答】解：∵，∴x+y＝2（﹣），∴（x+2）+（y﹣2）＝，∴x＝﹣2，y＝2，x+y＝0，故答案为：0．24．已知，，，则＝2．【解答】解：因为，，，所以＝7，所以＝1，则2＝＝4﹣4×1+4＝4，则＝2．故答案为：2．25．已知G为△ABC的重心，过点G的直线与边AB，AC分别相交于点P，Q．若＝，则当ABC与△APQ的面积之比为时，实数λ的值为或．【解答】解：G为△ABC的重心，所以＝+，设＝μ，故＝+，因为P，G，Q三点共线，故+＝1①，所以+＝3，＝＝＝②，由①②得或，故答案为：或．26．如图，给定单位向量和，它们的夹角为120°，点C在以O为圆心的上运动．若，其中x，y∈R，则x+2y的最大值是．【解答】解：根据题意，建立如图所示的坐标系，则A（1，0），B（cos120°，sin120°），即B（﹣，）；设∠AOC＝α，则＝（cosα，sinα），∵，∴（cosα，sinα）＝（x，0）+（﹣y，y）；即cosα＝x﹣y，sinα＝y，解得：x＝sinα+cosα，y＝sinα；∴x+2y＝sinα+cosα＝sin（α+θ），其中tanθ＝；又sin（α+θ）≤1，∴x+2y≤．故答案为：．27．已知点O是△ABC内部一点，并且满足，△BOC的面积为S1，△ABC 的面积为S2，则＝．【解答】解：因为，所以，分别取AC，BC的中点D，E，则，，所以，即O，D，E三点共线且，则，因为D为AC中点，所以，所以．故答案为：．28．设λ是正实数，三角形ABC所在平面上的另三点A1，B1，C1满足：＝λ（+），＝λ（+），＝λ（+），若三角形ABC与三角形A1B1C1的面积相等，则λ的值为．【解答】解：△ABC的重心为点G，由题意可知△ABC与△A1B1C1关于中心点G对称，由，＝（+）＝λ（+），故，故答案为：．四．解答题（共4小题）29．如图，已知△ABC中，D为BC的中点，AE＝EC，AD，BE交于点F，设＝，＝．（1）用，分别表示向量，；（2）若＝t，求实数t的值．【解答】解：（1）由题意，D为BC的中点，且＝，∵+＝2，∴＝2﹣，∴＝﹣＝2﹣﹣＝﹣+2；（2）∵＝t＝t，∴＝﹣＝﹣+（2﹣t），∵＝﹣+2，，共线，∴，∴t＝．30．如图所示，在△ABO中，，，AD与BC相交于点M，设，．（1）试用向量，表示；（2）过点M作直线EF，分别交线段AC，BD于点E，F．记，，求证：为定值．【解答】解：（1）由A，M，D三点共线，可设＝，由B，M，C三点共线，可设＝，因为，不共线，所以，解得，，故．（2）因为E，M，F三点共线，设＝，由（1）知，，即，，所以，故为定值，即得证．31．如图，在平面直角坐标系中，点A（﹣，0），B（，0），锐角α的终边与单位圆O 交于点P．（Ⅰ）用α的三角函数表示点P的坐标；（Ⅱ）当•＝﹣时，求α的值；（Ⅲ）在x轴上是否存在定点M，使得||＝||恒成立？若存在，求出点M的横坐标；若不存在，请说明理由．【解答】解：锐角α的终边与单位圆O交于点P．（Ⅰ）用α的三角函数表示点P的坐标为（cosα，sinα）；（Ⅱ），，•＝﹣时，即（cos）（cos）+sin2α＝，整理得到cos，所以锐角α＝60°；（Ⅲ）在x轴上假设存在定点M，设M（x，0），，则由||＝||恒成立，得到＝，整理得2cosα（2+x）＝x2﹣4，所以存在x＝﹣2时等式恒成立，所以存在M（﹣2，0）．32．已知O是△ABC所在平面内一点，D为BC边中点．（1）若点O满足，求证：；（2）已知E为AC边中点，O在线段DE上，且满足，△BOC的面积为2，求△ABC的面积．【解答】解：（1）∵D为BC边中点；∴；∴由得，；∴；（2）如图，根据条件：＝＝；∴；∴DE＝3DO；又AB＝2DE；∴AB＝6DO；∴S△ABC＝6S△BOC＝12；即△ABC的面积为12．。

高一数学平面向量的线性运算测试

2．2．1向量加法运算及其几何意义班级学号姓名 .一、选择题1．假设C 是线段AB 的中点,那么AC BC += 〔〕 A ．ABB ．BAC ．0D ．以上均不正确2．正方形ABCD 边长为1,=AB a ,=BC b ,=AC c ,那么++a b c 的模等于A ．0B ．3C ．D 〔〕3．在四边形ABCD 中,AD AB AC +=,那么四边形是〔〕 A ．矩形 B ．菱形C ．正方形D ．平行四边形4．向量()()AB MB BO BC OM ++++化简后等于〔〕 A ．BCB ．ABC ．ACD ．AM5．a 、b 为非零向量,且+=+||||||a b a b ,那么〔〕 A ．a 与b 方向相同 B ．a =b C ．a =-b D ．a 与b 方向相反6．设+++=()()AB CD BC DA a ,而b 是一非零向量,那么以下各结论：①//a b ；②+=a b a ；③+=a b b ；④+<+a b a b ,其中正确的选项是〔〕A ．①②B ．③④C ．②④D ．①③二、填空题7．化简〔CB BA AC ++)= .8．在矩形ABCD 中,假设=||3AB ,=||4BC ,那么+=||AB AD _________. 9．==||||3OA a ,==||||3OB b ,∠AOB=60︒,那么+=||a b __________. 10．当非零向量a 和b 满足条件时,使得b a +平分a 和b 间的夹角.三、解做题+=+. 11．O是平行四边形ABCD外一点,求证：OA OC OB OD12．一汽车向北行驶3 km,然后向北偏东60︒方向行驶3 km,求汽车的位移.2．2．2向量减法运算及其几何意义班级学号姓名 .一选择题1．化简MN PN PM +-所得结果是〔〕 A ．MPB ．NPC ．0D ．MN2．在∆ABC 中,===||||||1AB BC CA ,那么-||AB AC 的值为〔〕 A ．0B ．1CD ．23．设a 和b 的长度均为6,夹角为 120︒,那么-|a b |等于〔〕 A ．36B ．12C ．6D．4．下面四个式子中不能化简成AD 的是〔〕 A ．MB DA BM -- B ．NC NA CD -+C ．-+()AB DC BCD ． -+-()()AD BM BC MC5．3．在△ABC 中,D 、E 、F 分别BC 、CA 、AB 的中点,点M 是△ABC 的重心,那么 MC MB MA -+等于〔〕 A ．OB ．MD 4C ．MF 4D ．ME 46．向量b a 与反向,以下等式中成立的是〔〕A ．||||||b a b a -=-B ．||||b a b a -=+C ．||||||b a b a -=+D ．||||||b a b a +=+ 二、填空题 7．在ABCD 中,=AB a ,=AD b ,那么________CA =,______BD =.8．在a =“向北走20km 〞,b =“向西走15km 〞,那么-a b =_________,+a b 与a 的夹角的余弦值=______________.9．如图,D 、E 、F 分别是∆ABC 边AB 、BC 、CA 上的中点,那么等式：FE C①+-=FD DA AF 0 ②+-=FD DE EF 0 ③+-=DE DA BE 0④+-=AD BE AF 0其中正确的题号是__________________ 其中正确的题号是__________________10．a 、b 是非零向量,指出以下等式成立的条件：①a b a b +=+ 成立的条件是_________________________； ②a b a b +=-成立的条件是_________________________； ③a b a b +=-成立的条件是 _________________________； ④a b a b -=-成立的条件是_________________________. 三、解做题 11．如图,O 是ABCD 的对角线AC 与BD 的交点,假设=AB a ,=BC b ,=OD c ,证实：+-=OB c a b.12．长度相等的三个非零向量a 、b 、c 满足++=a b c 0, 求每两个向量之间的夹角.2．2．3向量数乘运算及其几何意义班级学号姓名 .一选择题1．化简)]24()82(21[31b a b a --+的结果是〔〕 A ．b a -2B ．a b -2C ．a b -D ．b a -2．R λ∈,那么以下命题正确的选项是〔〕 A ．a a λλ=B ．a a λλ=C ．a a λλ=D ．0a λ>3．以下各式计算正确的有〔〕(1)(－7)6a =-42a (2)7(a +b )－8b =7a +15b(3)a －2b +a +2b =2a (4)假设a =m +n ,b =4m +4n ,那么a ∥b A ．1个 B ．2个 C ．3个 D ．4个4．E 、F 分别为四边形ABCD 的边CD 、BC 边上的中点,设AD a =,BA b =,那么EF = A ．1()2a b +B ．1()2a b -+ C ．1()2a b -- D ．1()2b a - 〔〕5．假设a b c =+化简3(2)2(3)2()a b b c a b +-+-+ 〔〕 A ．aB ．bC ．cD ．以上都不对6．四边形ABCD 是菱形,点P 在对角线AC 上〔不包括端点A 、C 〕,那么AP =〔〕A ．().(0,1)AB AD λλ+∈B ．2().AB BC λλ+∈ C ． ().(0,1)AB AD λλ-∈ D ． 2().AB BC λλ-∈ 二、填空题7．m 、n 是实数,a 、b 是向量,对于命题： ①()m a b ma mb -=-②()m n a ma na -=-③假设ma mb =,那么a b = ④假设ma na =,那么m n =其中正确命题为_____________________． 8．计算：〔1〕3(53)2(6)--+a b a b =__________；〔2〕4(35)2(368)-+---+a b c a b c =__________．9．向量a ,b ,且3()2(2)4()++---+=0x a x a x a b ,那么x =__________． 10．假设向量x 、y 满足+=-=23,32x y a x y b ,a 、b 为向量,那么x =__________； y =___________．三、解做题11．1e ,2e 是两个不共线的向量,122=-a e e ,12k =+b e e ．假设a 与b 是共线向量,求实数k 的值．12．如图,在∆ABC 中,G 是∆ABC 的重心,证实：()=+13AG AB AC。

高一数学线性运算试题

高一数学线性运算试题1.在△ABC中，N是AC边上一点，且＝，P是BN上的一点，若＝m＋，则实数m的值为().A．B．C．1D．3【答案】B【解析】, , ,则;因为＝m＋，所以.，即;是BN上的一点，,，即.【考点】平面向量的线性运算.2.如图，E、F、G、H分别是任意四边形ABCD各边中点，若，则四边形EFGH必是（）A．正方形B．梯形C．菱形D．矩形【答案】C【解析】连接,由已知得：,,故,故四边形是菱形.【考点】1.向量的加法；2.向量与平面几何的关系.3.在平行四边形ABCD中，E和F分别是边CD和BC的中点，且，其中,则 .【答案】【解析】由题知,而，∴，两式联立即可求得.【考点】向量的线性运算.4.如图,在中,,点E是BC上一点,且满足:,以A为圆心,AC的长为半径作圆交AB于D,交AE于F.若,求的值.【答案】。

【解析】【考点】平面向量的线性运算，平面向量模的计算。

点评：中档题，本题属于平面向量在平面几何中的应用，充分借助于图形的几何特征，利用平面向量的线性运算，用AC表示各个线段，较方便的解决问题。

5.如图，正六边形ABCDEF中，有下列四个命题：①＋＝2②＝2＋2③·＝·④(·)＝ (·)其中真命题的序号是________．(写出所有真命题的序号)【答案】①②④【解析】，∴①对;取AD的中点O，则,，∴②对;设，则·＝×2×cos=3，·=2×1×cos=1，∴③不对；又·=·=2×1×cos=1=，·=1×1×cos=，∴④对。

故真命题的序号①②④。

【考点】平面向量的数量积，平面向量的线性计算。

点评：简单题，向量的夹角公式。

平面向量模的计算，往往“化模为方”，转化成向量的运算。

6.已知，则与共线的向量为A．B．C．D．【答案】C【解析】因为，那么则与共线的向量要满足，那么对于选项A,分析不满足比例关系，对于选项B，由于不存在实数满足，因此不共线，同理可知选项D，也不满足，排除法只有选C.【考点】共线向量点评：主要是考查了向量共线的概念的运用，属于基础题。

向量的线性运算练习题

向量的线性运算练习题Ⅰ 一、选择题1．若C 是线段AB 的中点，则AC BC += （）A ．AB B ．BAC ．0D ．以上均不正确2．已知正方形ABCD 边长为1，=AB a ，=BC b ，=AC c ，则++a b c 的模等于A ．0B ．3C ．D （）3．在四边形ABCD 中，+=，则四边形是（）A ．矩形B ．菱形C ．正方形D ．平行四边形4．向量()()AB MB BO BC OM ++++化简后等于（）A ．BCB ．ABC ．ACD ．AM5．a 、b 为非零向量，且+=+||||||a b a b ，则（）A ．a 与b 方向相同B ．a =bC ．a =-bD ．a 与b 方向相反6．设+++=()()AB CD BC DA a ，而b 是一非零向量，则下列各结论：①//a b ；②+=a b a ；③+=a b b ；④+<+a b a b ，其中正确的是（）A ．①②B ．③④C ．②④D ．①③二、填空题 7．化简（++)= 。

8．在矩形ABCD 中，若=||3AB ，=||4BC ，则+=||AB AD _________。

9．已知==||||3OA a ，==||||3OB b ，∠AOB=60︒，则+=||a b __________。

10．当非零向量a 和b 满足条件时，使得b a +平分a 和b 间的夹角。

Ⅱ选择1．化简MN PN PM +-所得结果是（）A ．MPB ．NPC ．0D ．MN2．在∆ABC 中，===||||||1AB BC CA ，则-||AB AC 的值为（）A ．0B ．1 CD ．23．设a 和b 的长度均为6，夹角为 120︒，则-|a b |等于（）A ．36B ．12C ．6 D．4．下面四个式子中不能化简成AD 的是（）A ．MB DA BM -- B ．NC NA CD -+C ．-+()AB DC BCD ． -+-()()AD BM BC MC5．在△ABC 中，D 、E 、F 分别BC 、CA 、AB 的中点，点M 是△ABC 的重心，则 -+等于（）A ．B ．4C ．4D ．46．已知向量与反向，下列等式中成立的是（）A ．||||||-=-B ．||||-=+C ．||||||-=+D ．||||||+=+二、填空题7．在ABCD 中，=AB a ，=AD b ，则________CA =，______BD =。

高一数学平面向量线性运算限时训练专题

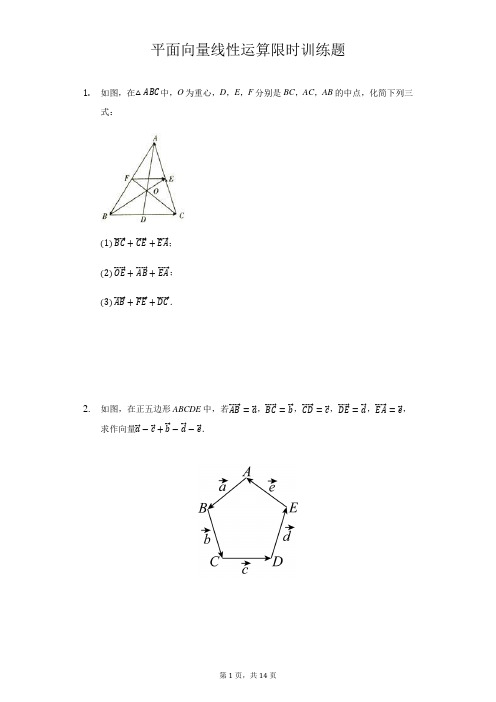
平面向量线性运算限时训练题1. 如图，在△ABC 中，O 为重心，D ，E ，F 分别是BC ，AC ，AB 的中点，化简下列三式：(1)BC ⃗⃗⃗⃗⃗ +CE ⃗⃗⃗⃗⃗ +EA ⃗⃗⃗⃗⃗ ； (2)OE ⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ +EA ⃗⃗⃗⃗⃗ ； (3)AB ⃗⃗⃗⃗⃗ +FE ⃗⃗⃗⃗⃗ +DC ⃗⃗⃗⃗⃗ ．2. 如图，在正五边形ABCDE 中，若AB ⃗⃗⃗⃗⃗ =a ⃗ ，BC ⃗⃗⃗⃗⃗ =b ⃗ ，CD ⃗⃗⃗⃗⃗ =c ⃗ ，DE ⃗⃗⃗⃗⃗⃗ =d⃗ ，EA ⃗⃗⃗⃗⃗ =e ⃗ ，求作向量a ⃗ −c ⃗ +b ⃗ −d ⃗ −e ⃗ ．3. 化简下列各式：(1)3(a ⃗ +b ⃗ )−2(a ⃗ −b ⃗ );(2)2(a ⃗ +2b ⃗ −c ⃗ )−(2c ⃗ +b ⃗ −a ⃗ );(3)25(a ⃗ −b ⃗ )−13(2a ⃗ +4b ⃗ )+215(2a ⃗ +13b ⃗ ). 4. 化简：(1)PM⃗⃗⃗⃗⃗⃗ −NQ ⃗⃗⃗⃗⃗⃗ +MQ ⃗⃗⃗⃗⃗⃗⃗ +NP ⃗⃗⃗⃗⃗⃗ ．(2)(BC ⃗⃗⃗⃗⃗ −DA ⃗⃗⃗⃗⃗ )+CD ⃗⃗⃗⃗⃗ −(BD ⃗⃗⃗⃗⃗⃗ −CA ⃗⃗⃗⃗⃗ ).5. 已知△ABC 是等腰直角三角形，∠ACB =90∘，M 是斜边AB 的中点，CM ⃗⃗⃗⃗⃗⃗ =a ⃗ ，CA ⃗⃗⃗⃗⃗ =b ⃗ ，求证：(1)|a ⃗ −b ⃗ |=|a ⃗ |;(2)|a ⃗ +(a ⃗ −b ⃗ )|=|b ⃗ |.6. 如图，在△ABC 中，AB ⃗⃗⃗⃗⃗ =a ⃗ ，BC ⃗⃗⃗⃗⃗ =b ⃗ ，AD 为边BC 上的中线，点G 在中线AD 上，且AG =2GD ，用a ，b 表示向量AD ⃗⃗⃗⃗⃗⃗ ，AG ⃗⃗⃗⃗⃗ ，GC ⃗⃗⃗⃗⃗ ，GB ⃗⃗⃗⃗⃗ ．7. (1)化简：25(a⃗ −b ⃗ )−13(2a ⃗ +4b ⃗ )+215(2a ⃗ +13b ⃗ )； (2)设两个非零向量e 1⃗⃗⃗ 与e 2⃗⃗⃗ 不共线．如果AB ⃗⃗⃗⃗⃗ =e 1⃗⃗⃗ +e 2⃗⃗⃗ ，BC ⃗⃗⃗⃗⃗ =2e 1⃗⃗⃗ +8e 2⃗⃗⃗ ，CD ⃗⃗⃗⃗⃗ =3(e 1⃗⃗⃗ −e 2⃗⃗⃗ )，求证：A 、B 、D 三点共线．8. 如图所示，在△ABC 中，AMAB =13，ANAC =14，BN 与CM 交于点P ，且AB ⃗⃗⃗⃗⃗ =a ⃗ ，AC ⃗⃗⃗⃗⃗ =b ⃗ 用a ⃗ ,b ⃗ 表示AP ⃗⃗⃗⃗⃗ ．9. 化简：(1)(AB ⃗⃗⃗⃗⃗ −CD ⃗⃗⃗⃗⃗ )−(AC ⃗⃗⃗⃗⃗ −BD⃗⃗⃗⃗⃗⃗ )； (2)(AC ⃗⃗⃗⃗⃗ +BO ⃗⃗⃗⃗⃗⃗ +OA ⃗⃗⃗⃗⃗ )−(DC ⃗⃗⃗⃗⃗ −DO ⃗⃗⃗⃗⃗⃗ −OB⃗⃗⃗⃗⃗⃗ )．10. 已知a ⃗ ，b ⃗ 是不共线的两个向量，AP ⃗⃗⃗⃗⃗ =−2a ⃗ +t b ⃗ ，BP ⃗⃗⃗⃗⃗ =2a ⃗ −b ⃗ ，BQ ⃗⃗⃗⃗⃗⃗ =3a ⃗ −3b ⃗ ．(1)若三点A 、P 、Q 共线，求实数t 的值；(2)若t =−1，当AP ⃗⃗⃗⃗⃗ =x BP ⃗⃗⃗⃗⃗ +y BQ⃗⃗⃗⃗⃗⃗ 时，求x ，y 的值．11. 如图，O 为△ABC 内一点，OA ⃗⃗⃗⃗⃗ =a ⃗ ，OB ⃗⃗⃗⃗⃗⃗ =b ⃗ ，OC ⃗⃗⃗⃗⃗=c ⃗ .求作：(1)b ⃗ +c ⃗ −a ⃗ ； (2)a ⃗ −b ⃗ −c ⃗ ．12. 在四边形ABCD 中，AB ⃗⃗⃗⃗⃗ =DC ⃗⃗⃗⃗⃗ ，AC ⊥BD ，|AC ⃗⃗⃗⃗⃗ |=6，|BD⃗⃗⃗⃗⃗⃗ |=8.求： (1)|AB⃗⃗⃗⃗⃗ |的值． (2)四边形ABCD 的面积．答案和解析1.【答案】解：(1)BC ⃗⃗⃗⃗⃗ +CE ⃗⃗⃗⃗⃗ +EA ⃗⃗⃗⃗⃗ =BE ⃗⃗⃗⃗⃗ +EA ⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ . (2)OE ⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ +EA ⃗⃗⃗⃗⃗ =(OE ⃗⃗⃗⃗⃗ +EA ⃗⃗⃗⃗⃗ )+AB ⃗⃗⃗⃗⃗ =OA →+AB →=OB →. (3)AB ⃗⃗⃗⃗⃗ +FE ⃗⃗⃗⃗⃗ +DC ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BD ⃗⃗⃗⃗⃗⃗ +DC ⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗⃗ +DC ⃗⃗⃗⃗⃗ =AC⃗⃗⃗⃗⃗ ．2.【答案】解：a ⃗ −c ⃗ +b ⃗ −d ⃗ −e ⃗ =(a ⃗ +b ⃗ )−(c ⃗ +d ⃗ +e ⃗ ) =(AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ )−(CD ⃗⃗⃗⃗⃗ +DE ⃗⃗⃗⃗⃗⃗ +EA ⃗⃗⃗⃗⃗ )=AC ⃗⃗⃗⃗⃗ −CA ⃗⃗⃗⃗⃗ =2AC ⃗⃗⃗⃗⃗ ．如图，连接AC ，并延长至点F ，使CF =AC ，则CF⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ ．∴AF ⃗⃗⃗⃗⃗ =2AC ⃗⃗⃗⃗⃗ ，即为所求作的向量a ⃗ −c ⃗ +b ⃗ −d ⃗ −e ⃗ ．【解析】本题考查向量的运算，三角形法则，属于基础题．化简a ⃗ −c ⃗ +b ⃗ −d ⃗ −e ⃗ =2AC⃗⃗⃗⃗⃗ ，作出2AC ⃗⃗⃗⃗⃗ 即可．3.【答案】解：(1)3(a ⃗ +b ⃗ )−2(a ⃗ −b ⃗ )=3a ⃗ +3b ⃗ −2a ⃗ +2b ⃗ =a ⃗ +5b ⃗ ．(2)2(a ⃗ +2b ⃗ −c ⃗ )−(2c ⃗ +b ⃗ −a ⃗ )=2a ⃗ +4b ⃗ −2c ⃗ −2c ⃗ −b ⃗ +a ⃗ =3a ⃗ +3b ⃗ −4c ⃗ ．(3)25(a ⃗ −b ⃗ )−13(2a ⃗ +4b ⃗ )+215(2a ⃗ +13b ⃗ ) =25a ⃗ −25b ⃗ −23a ⃗ −43b ⃗ +415a⃗ +2615b ⃗=(25−23+415)a ⃗ +(−25−43+2615)b ⃗=0⃗ ．4.【答案】解：(1)原式=(PM ⃗⃗⃗⃗⃗⃗ +MQ ⃗⃗⃗⃗⃗⃗⃗ )+(NP ⃗⃗⃗⃗⃗⃗ −NQ ⃗⃗⃗⃗⃗⃗ )=PQ ⃗⃗⃗⃗⃗ +QP ⃗⃗⃗⃗⃗ =0⃗ ． (2)原式=(BC ⃗⃗⃗⃗⃗ −BD ⃗⃗⃗⃗⃗⃗ )+(CA ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗⃗ )+CD ⃗⃗⃗⃗⃗ =DC ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ =CD ⃗⃗⃗⃗⃗ ．【解析】略5.【答案】解：如图，在等腰Rt △ABC 中，由M 是斜边AB 的中点，得|CM ⃗⃗⃗⃗⃗⃗ |=|AM ⃗⃗⃗⃗⃗⃗ |，|CA ⃗⃗⃗⃗⃗ |=|CB⃗⃗⃗⃗⃗ |. (1)在△ACM 中，AM ⃗⃗⃗⃗⃗⃗ =CM ⃗⃗⃗⃗⃗⃗ −CA ⃗⃗⃗⃗⃗ =a ⃗ −b ⃗ ．于是由|AM ⃗⃗⃗⃗⃗⃗ |=|CM ⃗⃗⃗⃗⃗⃗ |，得|a ⃗ −b ⃗ |=|a ⃗ |. (2)MB ⃗⃗⃗⃗⃗⃗ =AM ⃗⃗⃗⃗⃗⃗ =a ⃗ −b ⃗ ，在△MCB 中，CB ⃗⃗⃗⃗⃗ =MB ⃗⃗⃗⃗⃗⃗ −MC ⃗⃗⃗⃗⃗⃗ =a ⃗ −b ⃗ +a ⃗ =a ⃗ +(a ⃗ −b ⃗ ). 从而由|CB ⃗⃗⃗⃗⃗ |=|CA ⃗⃗⃗⃗⃗ |，得|a ⃗ +(a ⃗ −b ⃗ )|=|b ⃗ |.【解析】本题考查平面向量的减法，相等向量的概念，向量的模，属于基础题．在等腰Rt △ABC 中，由M 是斜边AB 的中点，可得|CM ⃗⃗⃗⃗⃗⃗ |=|AM ⃗⃗⃗⃗⃗⃗ |，|CA ⃗⃗⃗⃗⃗ |=|CB ⃗⃗⃗⃗⃗ |， (1)在△ACM 中，由向量减法AM ⃗⃗⃗⃗⃗⃗ =a ⃗ −b ⃗ ，结合|AM ⃗⃗⃗⃗⃗⃗|=|CM ⃗⃗⃗⃗⃗⃗ |，即可证明； (2)由相等向量及(1)，得MB ⃗⃗⃗⃗⃗⃗ =a ⃗ −b ⃗ ，△MCB 中，根据向量减法CB ⃗⃗⃗⃗⃗ =a ⃗ +(a ⃗ −b ⃗ )，结合|CB ⃗⃗⃗⃗⃗ |=|CA⃗⃗⃗⃗⃗ |，即可证明．6.【答案】解：由题D 为边BC 的中点，得到BD →=DC →=12BC →=12b →，所以AD →=AB →+BD →=AB →+12BC →=a →+12b →，因为AG =2GD所以AG →=23AD →=23a →+13b →，GC →=GD →+DC →=13AG →+12BC →=13a →+23b →GB →=GD →+DB →=13AG →−12BC →=13a →−13b →综上：AD →=a →+12b →，AG →=23a →+13b →，GC →=13a →+23b →，GB →=13a →−13b →．【解析】本题给出三角形的两条边对应的向量，求其它向量的线性表达式．着重考查了平面向量的加法法则，数乘运算等知识，属于基础题．由题D 为边BC 的中点，得到BD →=DC →=12BC →=12b →，利用向量加法法则，结合AG =2GD ，即可逐一的表达出所求向量．7.【答案】解：(1)原式=(25−23+415)a⃗ +(−25−43+2615)b ⃗ =0⋅a ⃗ +0⋅b ⃗ =0⃗ ； (2)证明：∵BD ⃗⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ =2e 1⃗⃗⃗ +8e 2⃗⃗⃗ +3(e 1⃗⃗⃗ −e 2⃗⃗⃗ )=5(e 1⃗⃗⃗ +e 2⃗⃗⃗ )=5AB ⃗⃗⃗⃗⃗ ，∴BD ⃗⃗⃗⃗⃗⃗ //AB ⃗⃗⃗⃗⃗ ，又BD⃗⃗⃗⃗⃗⃗ ,AB ⃗⃗⃗⃗⃗ 有公共点B ， ∴A ，B ，D 三点共线．【解析】(1)进行向量的数乘运算即可；(2)根据BD⃗⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ ，进行向量的数乘运算即可得出BD ⃗⃗⃗⃗⃗⃗ =5AB ⃗⃗⃗⃗⃗ ，从而得出BD ⃗⃗⃗⃗⃗⃗ ,AB ⃗⃗⃗⃗⃗ 共线，进而得出A ，B ，D 三点共线．本题考查了向量的数乘运算，向量加法的几何意义，共线向量基本定理，考查了计算能力，属于基础题．8.【答案】解：取AN 的三等分点D ，使|AD ⃗⃗⃗⃗⃗⃗ |=13|AN ⃗⃗⃗⃗⃗⃗ |，所以|AM⃗⃗⃗⃗⃗⃗⃗ ||AB ⃗⃗⃗⃗⃗⃗ |=|AD⃗⃗⃗⃗⃗⃗ ||AN⃗⃗⃗⃗⃗⃗ |=13，所以MD ⃗⃗⃗⃗⃗⃗⃗ //BN ⃗⃗⃗⃗⃗⃗ ，连结DM ，设|AD ⃗⃗⃗⃗⃗⃗ |=t ，t >0，则|AN ⃗⃗⃗⃗⃗⃗ |=3t ，又|AN ⃗⃗⃗⃗⃗⃗ |=14|AC ⃗⃗⃗⃗⃗ |，所以|AC ⃗⃗⃗⃗⃗ |=12t ，|NC ⃗⃗⃗⃗⃗⃗ |=9t ，所以|MP⃗⃗⃗⃗⃗⃗⃗ ||MC ⃗⃗⃗⃗⃗⃗ |=|DN⃗⃗⃗⃗⃗⃗ ||DC⃗⃗⃗⃗⃗⃗ |=211，∴|MP ⃗⃗⃗⃗⃗⃗ |=211|MC ⃗⃗⃗⃗⃗⃗ |，∴ AP ⃗⃗⃗⃗⃗ =AM ⃗⃗⃗⃗⃗⃗ +MP ⃗⃗⃗⃗⃗⃗ =AM ⃗⃗⃗⃗⃗⃗ +211MC ⃗⃗⃗⃗⃗⃗ =13AB ⃗⃗⃗⃗⃗ +211(MA ⃗⃗⃗⃗⃗⃗ +AC⃗⃗⃗⃗⃗ ) =13AB ⃗⃗⃗⃗⃗ +211(−13AB ⃗⃗⃗⃗⃗ +AC⃗⃗⃗⃗⃗ ) =311AB ⃗⃗⃗⃗⃗ +211AC ⃗⃗⃗⃗⃗=311a ⃗ +211b ⃗ ．【解析】本题考查平面向量的加法、减法、数乘运算，属于中档题．取AN 的三等分点D ，使|AD ⃗⃗⃗⃗⃗⃗ |=13|AN ⃗⃗⃗⃗⃗⃗ |，由题意可得MD ⃗⃗⃗⃗⃗⃗⃗ //BN ⃗⃗⃗⃗⃗⃗ ，可得|MP ⃗⃗⃗⃗⃗⃗⃗ ||MC ⃗⃗⃗⃗⃗⃗ |=|DN ⃗⃗⃗⃗⃗⃗||DC ⃗⃗⃗⃗⃗⃗ |=211，可得|MP ⃗⃗⃗⃗⃗⃗ |=211|MC ⃗⃗⃗⃗⃗⃗ |，结合AP ⃗⃗⃗⃗⃗ =AM ⃗⃗⃗⃗⃗⃗ +MP ⃗⃗⃗⃗⃗⃗ ，利用平面向量的加法、减法、数乘运算即可求解．9.【答案】解：(1)(AB ⃗⃗⃗⃗⃗ −CD ⃗⃗⃗⃗⃗ )−(AC ⃗⃗⃗⃗⃗ −BD ⃗⃗⃗⃗⃗⃗ ) =(AB ⃗⃗⃗⃗⃗ +BD ⃗⃗⃗⃗⃗⃗ )−(AC ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ )=AD ⃗⃗⃗⃗⃗⃗ −AD ⃗⃗⃗⃗⃗⃗ =0⃗ ． (2)(AC⃗⃗⃗⃗⃗ +BO ⃗⃗⃗⃗⃗⃗ +OA ⃗⃗⃗⃗⃗ )−(DC ⃗⃗⃗⃗⃗ −DO ⃗⃗⃗⃗⃗⃗ −OB ⃗⃗⃗⃗⃗⃗ ) =(AC ⃗⃗⃗⃗⃗ +BA ⃗⃗⃗⃗⃗ )−(OC ⃗⃗⃗⃗⃗ −OB ⃗⃗⃗⃗⃗⃗ )=BC ⃗⃗⃗⃗⃗ −BC ⃗⃗⃗⃗⃗ =0⃗ ．【解析】本题主要考查向量的加减计算，属于基础题． (1)根据向量的加减法求解即可； (2)根据向量的加减法求解即可．10.【答案】解：(1)PQ ⃗⃗⃗⃗⃗ =BQ ⃗⃗⃗⃗⃗⃗ −BP ⃗⃗⃗⃗⃗ =(3a ⃗ −3b ⃗ )−(2a ⃗ −b ⃗ )=a ⃗ −2b ⃗ ，因为A.P ，Q 三点共线，则存在唯一实数λ，满足AP ⃗⃗⃗⃗⃗ =λPQ ⃗⃗⃗⃗⃗ ，所以−2a ⃗ +t b ⃗ =λ(a ⃗ −2b ⃗ )=λa ⃗ −2λb ⃗ ，所以{−2=λt =−2λ，解得t =4;(2)当t =−1时，AP ⃗⃗⃗⃗⃗ =−2a ⃗ −b ⃗ =x BP ⃗⃗⃗⃗⃗ +y BQ ⃗⃗⃗⃗⃗⃗ =x(2a ⃗ −b ⃗ )+y(3a ⃗ −3b ⃗ )=(2x +3y)a ⃗ −(x +3y)b ⃗ ，所{−2=2x +3y −1=−x −3y ，解得{x =−3y =43．【解析】本题考查平面向量的加减运算及平面向量共线的充要条件，属于基础题． (1)利用平面向量的加减运算及A 、P 、Q 共线得出关系式求出t 的值； (2)将t =−1代入由AP⃗⃗⃗⃗⃗ =x BP ⃗⃗⃗⃗⃗ +y BQ ⃗⃗⃗⃗⃗⃗ 得出关系式求出x ，y 的值．11.【答案】解：(1)以OB ⃗⃗⃗⃗⃗⃗ ，OC ⃗⃗⃗⃗⃗ 为邻边作▱OBDC ，连接OD ，AD ，则OD ⃗⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ =b ⃗ +c ⃗ ，所以b ⃗ +c ⃗ −a ⃗ =OD⃗⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗⃗ ，如图所示．(2)由a ⃗ −b ⃗ −c ⃗ =a ⃗ −(b ⃗ +c ⃗ )，如图，作▱OBEC ，连接OE ，则OE ⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ =b ⃗ +c ⃗ ，连接AE ，则EA ⃗⃗⃗⃗⃗ =a ⃗ −(b ⃗ +c ⃗ )=a ⃗ −b ⃗ −c ⃗ ．【解析】本题主要考查向量的加法，减法运算，解答本题的关键是知道向量运算的法则.属于基础题．(1)以OB ⃗⃗⃗⃗⃗⃗ ，OC ⃗⃗⃗⃗⃗ 为邻边作▱OBDC ，连接OD ，AD ，则AD⃗⃗⃗⃗⃗⃗ 即为所求；(2)作▱OBEC ，连接OE ，AE ，则EA⃗⃗⃗⃗⃗ 即为所求．12.【答案】解：(1)解法一：∵BC ⃗⃗⃗⃗⃗ =BD ⃗⃗⃗⃗⃗⃗ +DC ⃗⃗⃗⃗⃗ ，BC ⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ ，∴BD ⃗⃗⃗⃗⃗⃗ +DC ⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ ，又∵AB ⃗⃗⃗⃗⃗ =DC ⃗⃗⃗⃗⃗ ，∴BD⃗⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ ， ∴2AB ⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ −BD⃗⃗⃗⃗⃗⃗ ，又∵ AC ⊥BD ，|AC ⃗⃗⃗⃗⃗ |=6，|BD⃗⃗⃗⃗⃗⃗ |=8 ∴4|AB ⃗⃗⃗⃗⃗ |2=(AC ⃗⃗⃗⃗⃗ −BD⃗⃗⃗⃗⃗⃗ )2 =AC⃗⃗⃗⃗⃗ 2+BD ⃗⃗⃗⃗⃗⃗ 2−2AC ⃗⃗⃗⃗⃗ ·BD ⃗⃗⃗⃗⃗⃗ =62+82−2×6×8×cos90°=100， ∴|AB ⃗⃗⃗⃗⃗ |=5；解法二：∵在四边形ABCD 中，AB ⃗⃗⃗⃗⃗ =DC ⃗⃗⃗⃗⃗ ， ∴AB = //DC ，∴四边形ABCD 为平行四边形， ∴AC ，BD 互相平分．又∵ AC ⊥BD ，∴四边形ABCD 为菱形，设AC ∩BD =O ，则OA ⊥OB ．∵|AC ⃗⃗⃗⃗⃗ |=6，|BD⃗⃗⃗⃗⃗⃗ |=8， ∴OA =3，OB =4，∴AB =5，即|AB ⃗⃗⃗⃗⃗ | =5；(2)同(1)的解法二，设AC ∩BD =O ， ∵ AC ⊥BD ，∴OA ⊥BD ，OC ⊥BD ．又∵|AC ⃗⃗⃗⃗⃗ |=6，|BD⃗⃗⃗⃗⃗⃗ |=8． ∴S 四边形ABCD =S △ABD +S △BCD =12|AO||BD|+12|OC||BD| =12(|AO|+|OC|)|BD|=12|AC||BD| =12×6×8=24.【解析】略。

高一数学向量的线性运算练习题

平面向量及其线性运算〔一〕根底知识：1.向量的定义: 既有_____又有_____的量叫做向量.向量的______也即向量的长度,叫做向量的_____.2.零向量: 模长为_____的向量叫做零向量,记作_______.零向量没有确定的方向.3.单位向量: 模长等于________________的向量叫做单位向量,记作_______.4.共线向量(平行向量):方向______________的非零向量叫做共线向量. 规定:_______与任意向量共线.其中模长相等方向一样的向量叫做____________;模长相等且方向相反的向量叫做___________;5.向量的运算: 加法、减法、数乘运算的运算法那么,运算率，及其几何意义.6.向量共线定理:向量b 与非零向量a 共线的充要条件是:有且只有一个实数λ,使得___________.7.平面向量根本定理: 如果21,e e 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a ,有且只有一对实数21,λλ,使a =_____________________. 8.三点共线定理:平面上三点A,B,C 共线的充要条件是:存在实数α,β,使_____________________,其中α+β=____, O 为平面内任意一点.9.①中点公式：假设M 是线段AB 的中点, O 为平面内任意一点,那么OM =__________________②在△ABC 中, 假设G 为重心,那么CA BC AB ++ =_________,GC GB GA ++ =____________. 〔二〕例题分析：1.以下命题中，正确的选项是〔〕A ．假设c b b a //,//，那么c a //B ．对于任意向量b a ,，+≥+C ．=那么b a =或b a -= D ．对于任意向量b a ,，-≥+2.O 是ABC △所在平面内一点，D 为BC 边中点，且2OA OB OC ++=0，那么〔〕Ａ．AO OD = Ｂ．2AO OD = Ｃ．3AO OD = Ｄ．2AO OD =3．在平行四边形ABCD 中，AC 与BD 交于点O ，E 是线段OD 的中点，AE 的延长线与CD 交于点F. 假设a AC =, b BD =,那么=AF 〔〕 A ．1142a b + B. 2133a b + C. 1124a b +D. 1233a b +〔三〕根底训练：1.如图，在平行四边形ABCD 中，以下结论中错误的选项是〔〕〔A 〕→--AB ＝→--DC ；〔B 〕→--AD ＋→--AB ＝→--AC 〔C 〕→--AB －→--AD ＝→--BD ；〔D 〕→--AD ＋→--CB ＝→0．2．假设O 、E 、F 是不共线的任意三点，那么以下各式中成立的是〔〕 A ．EF OF OE =+ B. EF OF OE =- C. EF OF OE =-+ D.EF OF OE =--3．四边形ABCD 是菱形，点P 在对角线AC 上〔不包括端点A 、C 〕，那么=AP 〔〕A ．)1,0(),(∈+λλAD AB B ．)22,0(),(∈+λλBC AB C ．)1,0(),(∈-λλAD ABD ．)22,0(),(∈-λλBC AB4.O ，A ，B 是平面上的三个点,直线AB 上有一点C ，满足20AC CB +=,那么OC =〔〕 A ．2OA OB -B ．2OA OB -+C ．2133OA OB -D ．1233OA OB -+5O 是平面上一定点，A B C 、、是平面上不共线的三个点，动点P 满足[)(),0,,AB AC OP OA P ABACλλ=++∈+∞则的轨迹一定通过ABC 的( )〔A 〕外心〔B 〕内心〔C 〕重心〔D 〕垂心6．点(3,1)A ，(0,0)B ，3,0)C ．设BAC ∠的平分线AE 与BC 相交于E ，那么有BC CE λ=其中λ等于( )〔A 〕２〔B 〕12〔C 〕－３〔D 〕－137．设b a ,是两个不共线的非零向量，假设向量b a k 2+与b k a +8的方向相反，那么k=__________.8.如图，在△ABC 中，点O 是BC 的中点，过点O 的直线分别交直线AB 、AC 于不同的两点M 、N ，假设AB ＝ m AM ，AC ＝n AN ，那么m ＋n 的值为．9．三角形ABC 的外接圆的圆心为O ，两条边上的高的交点为H ，)(OC OB OA m OH ++=，那么实数m =10.如图，平面内有三个向量OA 、OB 、OC ，其中OA 与OB 的夹角为120°，OA 与OC 的夹角为30°，且OA ＝OB ＝1，OC ＝22.假设OC ＝μλμλμλ+∈+则R),,(OB OA 的值为 . 11、设平面向量1a 、2a 、3a 的与1230a a a ++=。

2.2向量的线性运算(习题)

又 ∵ || = ||
∴四边形ABCD为菱形
B 能力提升
1.点是正六边形的中心, = , = ,试用向量、表示向量、、.
E
解：
D
= ; = =
∴ = + = +
C
F
OБайду номын сангаас
A
∴ = = ( + )
解：
= (, ); = (, −)
() + = (, ) + (, −)
= (, −)
() − = (, ) − (, −)
= (−, )
()( + ) = (, −)
7.根据下列条件判断四边形ABCD的形状,并证明你的结论.

() = ; () = 且|| = || ; () = 且|| = ||.

解：

() =

() =
∴ //, =

∴ //, =

∴四边形ABCD为平行四边形
∴四边形ABCD为梯形
又 ∵ || = ||
∴四边形ABCD为距形
() =
∴ //, =
∴四边形ABCD为平行四边形
4.(1)如图,向量、不共线,试比较| + |与|| + ||的大小.
(2)对于任意向量、,讨论在什么情况下,| + | = || + ||.
解：

()| + | < || + ||

()当、方向相同时, | + | = || + ||
(3) − ( + ).
解：原式= − −

向量的线性运算经典测试题及解析

【详解】
a =3， b =5，
b =5 a , 3
b 与 a 的方向相反, b 5 a.
3
故选：D. 【点睛】考查了平面向量的知识，注意平面向量的正负表示的是方向.
17．已知非零向量 a 、 b ，且有 a 2b ，下列说法中，不正确的是（）
A． | a | 2 | b | ； B． a ∥ b ；
D. BO OD ，故该选项错误；
故选：C．【点睛】本题主要考查相等向量及向量的长度，掌握相等向量的概念是解题的关键．
14．已知 a ， b 为非零向量，如果 b ＝﹣5 a ，那么向量 a 与 b 的方向关系是（）
A． a ∥ b ，并且 a 和 b 方向一致
B． a ∥ b ，并且 a 和 b 方向相反
A． a
B． a
【答案】B
C． a
D． a
【解析】【分析】按照向量之间的加减运算法则解题即可【详解】
-4a+5a=a ,
所以答案为 B 选项【点睛】本题主要考查了向量的加减法，熟练掌握相关概念方法是关键
6．如图， ABCD 中，E 是 BC 的中点，设 AB a, AD b ，那么向量 AE 用向量 a、b
C． a 和 b 方向互相垂直
【答案】B 【解析】
D． a 和 b 之间夹角的正切值为 5
【分析】
根据平行向量的性质解决问题即可．
【详解】
∵已知 a ， b 为非零向量，如果 b ＝﹣5 a ，
∴ a ∥ b ， a 与 b 的方向相反，
故选：B．【点睛】
本题考查了平面向量，熟记向量的长度和方向是解题关键．
【答案】C
【解析】
【分析】
根据题目中给的已知条件与是平行向量，可得 AB 与 CD 是平行的，且不确定与

高一数学平面向量的线性运算试题

高一数学平面向量的线性运算试题1.在四边形ABCD中，＝＋，则四边形ABCD一定是()A．矩形B．菱形C．正方形D．平行四边形【答案】D【解析】在四边形ABCD中，＝＋，又＝＋，∴＝，∴四边形ABCD是平行四边形．2.向量(＋)＋(＋)＋等于()A．B．C．D．【答案】C【解析】原式＝＋＋＋＋＝＋0＝.3.若a，b为非零向量，则下列说法中不正确的是()A．若向量a与b方向相反，且|a|>|b|，则向量a＋b与a的方向相同B．若向量a与b方向相反，且|a|<|b|，则向量a＋b与a的方向相同C．若向量a与b方向相同，则向量a＋b与a的方向相同D．若向量a与b方向相同，则向量a＋b与b的方向相同【答案】B【解析】∵a与b方向相反，|a|>|b|，∴a＋b与a的方向相反，故B不正确．4.a、b为非零向量，且|a＋b|＝|a|＋|b|，则下列说法正确的是()A．a与b方向相同B．a∥bC．a＝－bD．a与b的关系不确定【答案】A【解析】当两个非零向量a与b不共线时，a＋b的方向与a、b的方向都不相同，且|a＋b|<|a|＋|b|；向量a与b同向时，a＋b的方向与a、b的方向都相同，且|a＋b|＝|a|＋|b|；向量a与b反向且|a|<|b|时，a＋b的方向与b的方向相同(与a方向相反)，且|a＋b|＝|b|－|a|.5.在△ABC中，D、E、F分别为AB、BC、CA的中点，则＋等于()A．B．C．D．【答案】C【解析】∵D、E、F分别为AB、BC、AC中点，∴DE∥AF且DE＝AF，∴＝，∴＋＝＋＝.6.若||＝10，||＝8，则||的取值范围是______．【答案】[2,18]【解析】如图．固定，以A为起点作，则的终点C在以A为圆心，||为半径的圆上，由图可见，当C在C1处时，||取最小值2，当C在C2处时，||取最大值18.7.在四边形ABCD中，对角线AC、BD交于点O且||＝||＝1，＋＝＋＝0，cos∠DAB＝.求|＋|与|＋|.【答案】1,1【解析】∵＋＝＋＝0，∴＝，＝.∴四边形ABCD为平行四边形．又||＝||＝1，知四边形ABCD为菱形．∵cos∠DAB＝，∠DAB∈(0，π)，∴∠DAB＝，∴△ABD为正三角形．∴|＋|＝|＋|＝||＝2||＝.|＋|＝||＝||＝1.8.已知x、y是实数，向量a，b不共线，若(x＋y－1)a＋(x－y)b＝0，则x＝________，y＝________.【答案】【解析】由已知得⇒.9.点E、F分别为四边形ABCD的对角线AC、BD的中点，设＝a，＝b，试用a，b表示.【答案】＝＋＝－＋＝－a－b＝－ (a＋b)．【解析】如图所示，取AB中点P，连结EP，FP，在△ABC中，EP是与BC平行的中位线，∴＝＝a.在△ABD中，FP是与AD平行的中位线，∴＝＝－b.在△EFP中，＝＋＝－＋＝－a－b＝－ (a＋b)．10.已知▱ABCD的边BC、CD的中点分别是M、N，设＝a，＝b，试用a、b表示、.【答案】＝a－b，＝b－a.【解析】[分析]∵M、N分别为▱ABCD的边BC、CD的中点，故以、作为基向量较易表示出、，然后，解方程组即可求出、.在▱ABCD中，M、N分别是边BC、CD的中点，∴＝，＝.∴＝＋＝＋，＝＋，∴解得＝a－b，＝b－a.。

向量的线性运算技巧及练习题

向量的线性运算技巧及练习题一、选择题1．如果向量a 与单位向量e 的方向相反，且长度为3，那么用向量e 表示向量a 为（）A ．3a e =B ．3a e =-C ．3e a =D ．3e a =-2．在四边形ABCD 中，，，，其中与不共线，则四边形ABCD 是( )A ．平行四边形B ．矩形C ．梯形D ．菱形3．若非零向量、满足｜-｜=｜｜，则( )A ．｜2｜＞｜-2｜B ．｜2｜＜｜-2｜C ．｜2｜＞｜2-｜D ．｜2｜＜｜2-｜4．在矩形ABCD 中，如果AB 3BC 模长为1，则向量（AB +BC +AC ）的长度为（）A ．2B ．4C 31D 315．若AB 是非零向量，则下列等式正确的是（）A ．AB BA =；B ．AB BA =；C ．0AB BA +=；D ．0AB BA +=.6．下列判断正确的是( )A ．0a a -=B ．如果a b =，那么a b =C ．若向量a 与b 均为单位向量，那么a b =D ．对于非零向量b ，如果()0a k b k =⋅≠，那么//a b7．如图，在△ABC 中，中线AD 、CE 交于点O ，设AB a,BC k ，那么向量AO 用向量a b ⋅表示为（）A ．12ab B ．2133a b C ．2233a b D ．1124a b8．若向量a 与b 均为单位向量，则下列结论中正确的是（）．A ．a b =B ．1a =C ．1b =D ．a b =9．已知平行四边形ABCD ，O 为平面上任意一点.设=，=， =，=，则（）A ．+++=B ．-+-=C ．+--=D ．--+=10．下列各式正确的是（）．A ．()22a b c a b c ++=++B ．()()330a b b a ++-=C ．2AB BA AB +=D ．3544a b a b a b ++-=-11．已知a 、b 、c 都是非零向量，如果2a c =，2b c =-，那么下列说法中，错误的是（）A ．//a bB ．a b =C ．72BD = D ．a 与b 方向相反12．下列说法正确的是（）A ．()0a a +-=B ．如果a 和b 都是单位向量，那么a b =C ．如果||||a b =，那么a b =D ．12a b =-（b 为非零向量），那么//a b13．化简()()AB CD BE DE -+-的结果是（）． A ．CAB ．AC C ．0D ．AE14．下列有关向量的等式中，不一定成立的是（） A ．AB BA =- B ．AB BA = C ．AB BCAC D ．AB BC AB BC +=+15．已知c 为非零向量， 3a c =， 2b c =-，那么下列结论中错误的是（） A ．//a bB ．3||||2a b =C ．a 与b 方向相同D ．a 与b 方向相反16．如果a b c +=，3a b c -=，且0c ≠，下列结论正确的是 A ．=a b B ．20a b += C ．a 与b 方向相同 D ．a 与b 方向相反17．已知非零向量a 、b 和c ，下列条件中，不能判定a b 的是（） A ．2a b =-B ．a c =，3b c =C ．2a b c +=，a b c -=-D ．2a b =18．如果2a b =（a ，b 均为非零向量），那么下列结论错误的是（） A ．a //b B ．a -2b =0 C ．b =12a D ．2a b =19．已知点C 是线段AB 的中点，下列结论中，正确的是（）A ．12CA AB =B ．12CB AB =C ．0AC BC +=D ．0AC CB +=20．已知AM 是ABC △的边BC 上的中线，AB a =，AC b =，则AM 等于（）． A ．()12a b - B ．()12b a - C ．()12a b + D ．()12a b -+。