平面向量中三点共线问题
(完整版)平面向量中“三点共线定理”妙用

平面向量中“三点共线定理”妙用对平面内任意的两个向量b a b b a//),0(,≠的充要条件是:存在唯一的实数λ,使b a λ=由该定理可以得到平面内三点共线定理:三点共线定理:在平面中A 、B 、P 三点共线的充要条件是:对于该平面内任意一点的O ,存在唯一的一对实数x,y 使得:OP xOA yOB =+且1x y +=。
特别地有:当点P 在线段AB 上时,0,0x y >> 当点P 在线段AB 之外时,0xy <笔者在经过多年高三复习教学中发现,运用平面向量中三点共线定理与它的两个推广形式解决高考题,模拟题往往会使会问题的解决过程变得十分简单!本文将通过研究一些高考真题、模拟题和变式题去探究平面向量中三点共线定理与它的两个推广形式的妙用,供同行交流。
例1(06年江西高考题理科第7题)已知等差数列{a n }的前n 项和为S n ,若1200OB a OA a OC =+,且A 、B 、C 三点共线,(设直线不过点O ),则S 200=( ) A .100B .101C .200D .201解:由平面三点共线的向量式定理可知:a 1+a 200=1,∴1200200200()1002a a S +==,故选A 。
点评:本题把平面三点共线问题与等差数列求和问题巧妙地结合在一起,是一道经典的高考题。
例2 已知P 是ABC ∆的边BC 上的任一点,且满足R y x AC y AB x AP ∈+=.,,则yx 41+ 的最小值是解:点P 落在ABC 的边BC 上 ∴B ,P,C 三点共线AP xAB yAC =+ 1x y ∴+= 且x>0,y>014141444()1()()145y x y xx y x y x y x y x y x y∴+=+⨯=+⨯+=+++=++ x>0,y>040,0y xx y ∴>> 由基本不等式可知:4424y x y xx y x y+≥⨯=,取等号时4y xx y =224y x ∴=2y x ∴=±0,0x y >>2y x∴=1x y +=12,33x y ∴==,符合所以yx 41+的最小值为9 点评:本题把平面三点共线问题与二元函数求最值、基本不等式巧妙地结合在一起, 较综合考查了学生基本功.例3(湖北省2011届高三八校第一次联考理科)如图2,在△ABC 中,13AN NC =,点P 是BC 上的一点,若211AP mAB AC =+,则实数m 的值为( ) A .911 B. 511 C. 311 D. 211解:,,B P N 三点共线,又2284111111AP mAB AC mAB AN mAB AN =+=+⨯=+ 8111m ∴+= 311m ∴=,故选C 例4(07年江西高考题理科)如图3,在△ABC 中,点O 是BC 的中点,过点O 的直线分别交直线AB 、AC 于不同的两点M 、N ,若AB = m AM ,AC =n AN ,则m +n 的值为 .解:因为O 是BC 的中点,故连接AO ,如图4,由向量加法的平行四边形法则可知:1()2AO AB AC ∴=+m AB AM =,AC nAN =1()2AO mAM nAN ∴=+22m nAO AM AN ∴=+又,,M O N 三点共线,∴由平面内三点共线定理可得:122m n+= 2m n ∴+=例5(广东省2010届高三六校第三次联)如图5所示:点G 是△OAB 的重心,P 、Q 分别是边OA 、OB 上的动点,且P 、G 、Q 三点共线. 设OA x OP =,OB y OQ =,证明:yx 11+是定值; 图3图4图2证明:因为G 是OAB 的重心,211()()323OG OA OB OA OB ∴=⨯+=+1OP xOAOA OP x=∴= 1OQ yOBOB OQ y=∴=111111()()3333OG OA OB OP OQ OG OP OQ x y x y∴=+=+∴=+ 又,,P G Q 三点共线,11133x y ∴+= 113x y ∴+= 11x y∴+为定值3例6(汕头市东山中学2013届高三第二次模拟考试)如图6所示,在平行四边形ABCD 中,13AE AB =,14AF AD =,CE 与BF 相交于G 点,记AB a =,AD b =,则AG =_______A .2177a b + B. 2377a b + C. 3177a b + D. 4277a b +分析:本题是以平面几何为背景,为载体,求向量的问题,所以我们很容易联想到点F 、G 、B 以及E,G,C 三点在一条直线上,可用平面内三点共线定理求解。
平面向量补充讲义----三点共线定理(修改版)

平面向量补充讲义----三点共线定理班级:__________姓名:___________三点共线定理:若平面内,向量12,OP OP 不共线,向量12OP OP OP λμ=+,则12,,P P P 三点共线的等价条件是1λμ+=.(如图,共线时λ满足:221P P P P λ=)说明1:若12,,P P P 三点共线,设221P P P P λ=,则11OP OP PP =+,则例1.如图,在△ABC 中,13AN NC =,点P 是BN 上的一点,若211AP mAB AC =+,则实数m 的值为( ) A .911 B. 511 C. 311 D. 211练习例2.,点在边上,,设,则( )例3.如图,点是△的重心,、分别是边、上的动点,且、、三点共线.设,,求:的值推论:如图,若平面内,向量12,OP OP 不共线,点P 为直线12P P 的平行线上任意一点,且向量12OPOPOP λμ=+,则λμ+为定值.(这条平行线称为等和线)例4.已知点G 为ABC ∆重心,P 为GBC ∆内动点(不包括边界),且AP AB AC λμ=+,则λμ+的取值范围是__________________;2λμ+的取值范围是_______________________.OAB ∆P AB 3AB AP =,OA a OB b ==OP =12.33A a b +21.33B a b +.C 1233a b -.D 2133a b -G OAB P Q OA OB P G Q x =y =yx 11+212P 1例5.半径为1的扇形AOB ,120AOB ∠=,C 为圆弧AB 上任意一点,y x +=,则x y +的最大值为__________________,2x y +最大值为_______________.练习1.在平行四边形ABCD 中,13AE AB =,14AF AD =,CE 与BF 相交于G 点,记AB a =,AD b =,则AG =( )A .2177a b + B. 2377a b + C. 3177a b + D. 4277a b +2.在△ABC 中,∠A =60°,∠A 的平分线交BC 于点D ,若AB =4,且AD →=14AC →+λAB →(λ∈R ),则AD 的长为( )A .32B .33C .34D .353.若O 为△ABC 所在平面内一点,且743=++,则△OAC 和△OBC 的面积之比为__________________4.如图,OM ∥AB ,点P 由射线OM 、线段OB 及AB 的延长线围成的阴影区域内(不含边界).且y x +=,则实数对(x ,y )可以是( )A .)43,41( B. )32,32(- C. )43,41(- D. )57,51(-5.已知向量,OA OB 满足1OA OB ==,,(,,)OA OB OC OA OB R λμλμ⊥=+∈若M 为AB的中点,A并且1MC =,则λμ+的最大值是___________。
共线定理以及三点共线

共线定理以及三点共线一、向量共线定理平面向量共线定理:对平面内任意的两个向量b a b b a//),0(,≠的充要条件是:存在唯一的实数λ,使b aλ=例1.设与是两个不共线的向量,且向量与共线,则A. 0B.C.D.【解答】 解:因为向量与共线,所以存在实数x 有,则,解得故选D .例2.已知向量,,且与共线,,则 A.B.C.或D.或【解答】 解:与共线,,, , 或.故选:D .例3.若、是不共线向量,,,且,则k等于A. 8B. 3C.D.【解析】解:,是不共线向量,,,且,存在实数使得..,解得.故选D.例4.向量,,若与共线且方向相反,则______.【解答】解:,,解得,又与方向相反,.故答案为.例5.已知点P在线段AB上,且,设,则实数______.【解析】解:如图所示,点P在线段AB上,且,;又,.故答案为:.例6.已知向量______.【解析】解:,,则有,解得,故答案为.例7.已知是平面内两个不共线向量,,若A,B,D三点共线,则k的值为A. 2B.C.D. 3【解答】解:,,、B、D三点共线,与共线,存在唯一的实数,使得即解得.故选A.例8.已知、是两个不共线向量,设,,,若A,B,C三点共线,则实数的值等于A. 1B. 2C.D.【解答】解:,,,,,,B,C三点共线,不妨设,,,解得.故选C.例9.设,是两个不共线的向量,已知,,,若三点A,B,D共线,则k的值为A. B. 8 C. 6 D.【解答】解:,因为三点A,B,D共线,所以与共线,则存在实数,使得,即,由向量相等的条件得,所以.故选A.例10.设,是不共线向量,与共线,则实数k为______ .【解答】解:与共线,且,是不共线向量,存在实数满足:,且,.故答案为.例11.设向量,不平行,向量与平行,则实数________.【解答】解:向量,不平行,向量与平行,,,解得实数.故答案为.二、三点共线定理在平面中A、B、P三点共线的充要条件是:对于该平面内任意一点的O,存在唯一的一对实数x,y使得:OP xOA yOB=+且1x y+=。
“三点共线”在解平面向量问题的一些感悟

以上两 种解 法 中 , 法一 充分 考虑 了 向量 共 线 的条 件 , 利 用 ,
分 析 : 要 证 明 B E = ÷ 鲋 , 根 据 题 意 只 要 证 明 , 而 向 量 蔚, 赢
曰, C是 平 面 内三 个 点 , 且 A与 B不 重 合 , P 为共线向量, 由向量共线的条件可知菇 = A 赢, 从而求得A= 1 共 线的 一 个 方 法 。A,
于 E, 用向量方法证明: B E= — 。
先 在上 面选 取满 足结 论 的点后 , 再 证 明两点 重 合 。两 种 方法 都 选 取 两个不 共线 的向量 为基 底 , 把其 他相 关 向量 用 它们 表示 出来 。 法 一 的三点 共线 , 我 不禁想 到课 本 例题 3中判 断 三点 A , B, C
÷ , 而 = 一 , 赢= a 一 . 3 = . ・ . 菌:
3 ( - o  ̄一 - 苫 ) : ( 一 ) ,
于 是 : T 一 ( a + 3 ) = ÷ ( + s - a ) =
由 向量共线 条 件可知 ,
一
和 为共 线 向量 , 又・ . ・ O E , O D有
出 时
教
古
目
添竣 球 霹
底
D A 0
A
再
图 l
图2
二法 : 如图2 , 设E 是 线段 B A上 的 一 点 , 且B E = B A 。则
只需证 明E, E 重合即可设 0 =。 一 , D 雪=b : 则B D: ÷ ,一 o , 0 D=b+ 一
是 平面 内任 意一 点 , 若 点 C在 直线 A B上 , 则存 在 实 数 A, 使得P 即可 , 为解 决 问题方 便 , 可选 取两 个不 共 线 的 向量 , 再 把 有 关 向量 =A +( 1 一A ) 朋, 即如果 A, 曰, C三点 共 线 , 点 0在 直 线 外 , 则 用 它们 表示 出来 。 有 = A , 其中 A =1 , 反之 也成立 , 同样 此 时 ,
高中数学例题:利用平面向量基本定理证明三点共线问题

高中数学例题:利用平面向量基本定理证明三点共线问题 例3.设OA 、OB 、OP 是三个有共同起点的不共线向量,求证:它们的终点A 、B 、P 共线,当且仅当存在实数m 、n 使m+n=1且OP mOA nOB ==.
【思路点拨】本题包含两个问题:(1)A 、B 、P 共线⇒m+n=1,且OP mOA nOB ==成立;(2)上述条件成立⇒A 、B 、P 三点共线.
【证明】(1)由三点共线⇒m 、n 满足的条件.
若A 、B 、P 三点共线,则AP 与AB 共线,由向量共线的条件知存在实数λ使AP AB λ=,即()OP OA OB OA λ-=-,∴(1)OP OA OB λλ=-+. 令1m λ=-,n=λ,则OP mOA nOB =+且m+n=1.
(2)由m 、n 满足m+n=1⇒A 、B 、P 三点共线.
若OP mOA nOB =+且m+n=1,则(1)OP mOA m OB =+-.
则()OP OB m OA OB -=-,即BP mBA =.
∴BP 与BA 共线,∴A 、B 、P 三点共线.
由(1)(2)可知,原命题是成立的.
【总结升华】 本例题的结论在做选择题和填空题时,可作为定理使用,这也是证明三点共线的方法之一.
举一反三:
【变式1】设e 1,e 2是平面内的一组基底,如果124AB e e =-,12BC e e =+,1269CD e e =-,求证:A ,C ,D 三点共线.
【解析】 因为1212121(4)()233
AC AB BC e e e e e e CD =+=-++=-=,所以AC 与CD 共线.。
平面向量中的三点共线结论的应用
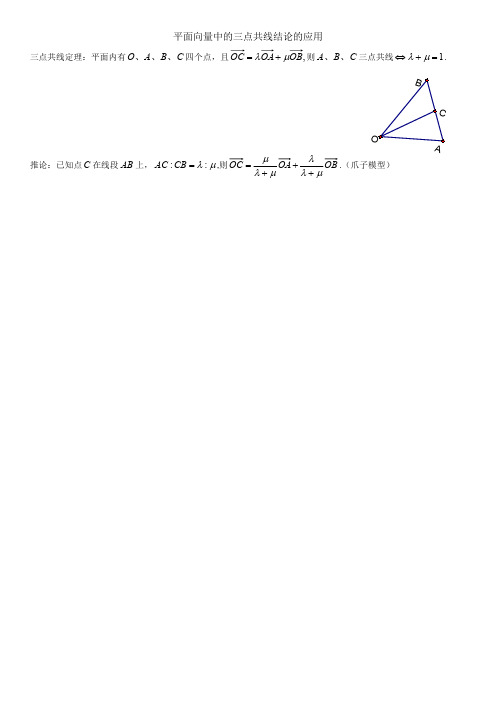
若,3.已知B 为OAC 边AC 上一点,且满足OC y OA x OB +=4,不等式222313x y m m x y +≥-++恒成立时,实数m 的最值范围为___________.巩固练习1.在ABC ∆中,4AB =,O 为三角形的外接圆的圆心,若),(R y x AC y AB x AO ∈+=且21x y +=,则ABC ∆的面积的最大值为_____.2.在P AB ∆中,,60,9,80=∠==APB PB P A 点C 满足PB y P A x PC +=,且,0,0,532≥≥=+y x y x 其中则||PC 的最大值为______,最小值为______.3.已知ABC ∆的外心为O 满足AC y AB x AO +=,若,10,6==AC AB 且,5102=+y x 则=∠BAC cos ______.例5.如图,M 为△ABC 的中线AD 的中点,过点M 的直线分别交线段AB 、AC 于点P 、Q 两点,设AP xAB =,AQ y AC =,记()y f x =,设32()32g x x a x a =++,[0,1]x ∈,若对任意11[,1]3x ∈,总存在2[0,1]x ∈,使得12()()f x g x =成立,则实数a 的取值范围为______.巩固练习2.(2022·辽宁葫芦岛·高三期末)如图,在等腰ABC 中,已知2AB AC ==,120A ∠= ,E ,F 分别是边AB ,AC 上的点,且AE AB λ= ,AF AC μ=,其中λ,R μ∈,且21λμ+=,若线段EF ,BC 的中点分别为M ,N ,则MN的最小值是()A .77B .217C .2114D .213.(2023·全国·高三专题练习)直角三角形ABC 中,P 是斜边BC 上一点,且满足2BP PC =,点M 、N 在过点P 的直线上,若AM m AB = ,AN nAC =,()0,0m n >>,则下列结论错误的是()A .12m n+为常数B .m n +的最小值为169C .2m n +的最小值为3D .m 、n 的值可以为12m =,2n =巧用杠杆原理处理三角形中的向量问题数值,各线段上得如图所示各点的标数则根据杠杆平衡原理可,已知三角形中的赋值标数法,d,cNC AN b a MB AM ==点数值乘数值等于点数值乘线段上,段数值乘积相等。
平面向量中“三点共线定理”妙用

平面向量中“三点共线定理”妙用对平面内任意的两个向量b a b b a//),0(,≠的充要条件是:存在唯一的实数λ,使b a λ=由该定理可以得到平面内三点共线定理:三点共线定理:在平面中A 、B、P三点共线的充要条件是:对于该平面内任意一点的O ,存在唯一的一对实数x ,y使得:OP xOA yOB =+且1x y +=。
特别地有:当点P在线段AB 上时,0,0x y >> 当点P 在线段A B之外时,0xy <笔者在经过多年高三复习教学中发现,运用平面向量中三点共线定理与它的两个推广形式解决高考题,模拟题往往会使会问题的解决过程变得十分简单!本文将通过研究一些高考真题、模拟题和变式题去探究平面向量中三点共线定理与它的两个推广形式的妙用,供同行交流。
例1(06年江西高考题理科第7题)已知等差数列{a n }的前n 项和为Sn,若1200OB a OA a OC =+,且A 、B 、C 三点共线,(设直线不过点O),则S 200=( ) A .100ﻩﻩﻩﻩB.101 ﻩC.200 ﻩﻩﻩD.201解:由平面三点共线的向量式定理可知:a1+a 200=1,∴1200200200()1002a a S +==,故选A。
点评:本题把平面三点共线问题与等差数列求和问题巧妙地结合在一起,是一道经典的高考题。
例2 已知P 是ABC ∆的边BC 上的任一点,且满足R y x AC y AB x AP ∈+=.,,则yx 41+ 的最小值是解:点P 落在ABC 的边BC 上 ∴B ,P,C 三点共线AP xAB yAC =+ 1x y ∴+= 且x>0,y>014141444()1()()145y x y xx y x y x y x y x y x y∴+=+⨯=+⨯+=+++=++ x>0,y>040,0y x x y ∴>> 由基本不等式可知:4424y x y x x y x y+≥⨯=,取等号时4y xx y =224y x ∴=2y x ∴=±0,0x y >>2y x∴=1x y +=12,33x y ∴==,符合所以yx 41+的最小值为9 点评:本题把平面三点共线问题与二元函数求最值、基本不等式巧妙地结合在一起, 较综合考查了学生基本功.例3(湖北省2011届高三八校第一次联考理科)如图2,在△ABC 中,13AN NC =,点P 是BC 上的一点,若211AP mAB AC =+,则实数m的值为( ) A .911 B. 511 C. 311 D. 211解:,,B P N 三点共线,又2284111111AP mAB AC mAB AN mAB AN =+=+⨯=+ 8111m ∴+= 311m ∴=,故选C 例4(07年江西高考题理科)如图3,在△ABC 中,点O 是B C的中点,过点O 的直线分别交直线AB 、AC于不同的两点M 、N,若AB = m AM ,AC =nAN ,则m +n 的值为 .解:因为O 是B C的中点,故连接AO ,如图4,由向量加法的平行四边形法则可知:1()2AO AB AC ∴=+m AB AM =,AC nAN =1()2AO mAM nAN ∴=+22m nAO AM AN ∴=+又,,M O N 三点共线,∴由平面内三点共线定理可得:122m n+= 2m n ∴+=例5(广东省2010届高三六校第三次联)如图5所示:点G 是图3图4图2△OAB 的重心,P 、Q 分别是边OA 、OB 上的动点,且P 、G 、Q 三点共线.设OA x OP =,OB y OQ =,证明:yx 11+是定值; 证明:因为G 是OAB 的重心,211()()323OG OA OB OA OB ∴=⨯+=+1OP xOAOA OP x=∴= 1OQ yOBOB OQ y=∴=111111()()3333OG OA OB OP OQ OG OP OQ x y x y∴=+=+∴=+ 又,,P G Q 三点共线,11133x y∴+= 113x y ∴+= 11x y ∴+为定值3例6(汕头市东山中学2013届高三第二次模拟考试)如图6所示,在平行四边形ABCD 中,13AE AB =,14AF AD =,CE 与B F相交于G 点,记AB a =,AD b =,则AG =_______A.2177a b +B. 2377a b +C. 3177a b + D. 4277a b + 分析:本题是以平面几何为背景,为载体,求向量的问题,所以我们很容易联想到点F 、G 、B以及E,G,C 三点在一条直线上,可用平面内三点共线定理求解。
平面向量中三点共线定理的应用

平面向量中三点共线定理的应用知识梳理(一)对平面内任意的两个向量b a b b a//),0(,≠的充要条件是:存在唯一的实数λ,使b aλ=由该定理可以得到平面内三点共线定理:(二)三点共线定理:在平面中A 、B 、P 三点共线的充要条件是:对于该平面内任意一点的O ,存在唯一的一对实数x ,y 使得:OP xO A yOB =+ 且.OP xO A yOB =+ 例题精讲例1设M 为平行四边形ABCD 对角线的交点,O 为平行四边形ABCD 所在平面内任意一点,则OA →+OB →+OC →+OD →等于()A.OM→B .2OM→C .3OM→D .4OM→例2如图,在平行四边形ABCD 中,AC ,BD 相交于点O ,E 为线段AO 的中点.若BE →=λBA →+μBD →(λ,μ∈R),则λ+μ=.例3如图所示,在平行四边形ABCD 中,13AE AB = ,14AF AD =,CE 与BF 相交于G 点,记AB a = ,AD b = ,则AG =_______例4在△ABC 中,D 是△ABC 所在平面内一点,且AD →=13AB →+12AC →,延长AD 交BC 于点E ,若AE →=λAB →+μAC →,则λ-μ的值是.练习1.如图,在三角形ABC 中,BE 是边AC 的中线,O 是BE 边的中点,若AB →=a ,AC →=b ,则AO →=()A.12a +12b B.12a +13b C.14a +12b D.12a +14b 2.(2019·济南调研)在△ABC 中,AN →=14NC →,若P 是直线BN 上的一点,且满足AP →=mAB →+25AC →,则实数m 的值为()A .-4B .-1C .1D .43.在△ABC 中,13AN NC =,点P 是BC 上的一点,若211AP mAB AC =+,则实数m 的值为()A .911B .511C .311D .2114.如图所示,在△ABC 中,点O 是BC 的中点,过点O 的直线分别交直线AB ,AC 于不同的两点M ,N ,若AB →=mAM →,AC →=nAN →,则m +n 的值为()A .1B .2C .3D .45.已知点M 是△ABC 的边BC 的中点,点E 在边AC 上,且EC →=2AE →,则向量EM →=()A .12AC →+13AB→B .12AC →+16AB→C .16AC →+12AB →D .16AC →+32AB→6.(2019·衡水中学调研)一直线l 与平行四边形ABCD 中的两边AB ,AD 分别交于点E ,F ,且交其对角线AC 于点M ,若AB →=2AE →,AD →=3AF →,AM →=λAB →-μAC →(λ,μ∈R),则52μ-λ=()A .-12B .1C.32D .-37.在平行四边形ABCD 中,E 和F 分别是CD 和BC 的中点,若AC →=λAE →+μAF →,其中λ,μ∈R,则λ+μ=________.8.在平行四边形ABCD 中,E 和F 分别是CD 和BC 的中点,若AC →=λAE →+μAF →,其中λ,μ∈R,则λ+μ=________.9.(2019·中原名校联考)如图,在△ABC 中,点M 是BC 的中点,N 在边AC 上,且AN =2NC ,AM 与BN 相交于点P ,则APPM=________.10.点G 是△OAB 的重心,P 、Q 分别是边OA 、OB 上的动点,且P 、G 、Q 三点共线.设OA x OP =,OB y OQ =,证明:yx 11+是定值;11.在三角形ABC 中,AM ﹕AB =1﹕3,AN ﹕AC =1﹕4,BN 与CM 相交于点P ,且a AB =,b AC =,试用a 、b表示AP .12.已知P 是ABC ∆的边BC 上的任一点,且满足R y x AC y AB x AP ∈+=.,,求yx 41+的最小值.PABCMN答案例1答案:D 解析:OA →+OB →+OC →+OD →=(OA →+OC →)+(OB →+OD →)=2OM →+2OM →=4OM →例2解:因为E 为线段AO 的中点,所以BE →=12BA →+12BO →=12BA →+1221(⨯BD →)=12BA →+14BD →=λBA →+μBD →,所以λ+μ=12+14=34.例3解:,,E G C 三点共线,∴由平面内三点共线定理可得:存在唯一的一对实数x 使得(1)AG xAE x AC∴=+- , 1133AE AB a == ,AC a b=+ 12(1)()(1)(1)33x AG x a x a b a x b ∴=⨯+-+=-+-…………………①又,,F G B 三点共线,∴由平面内三点共线定理可得:存在唯一的一对实数λ使得(1)AG AB AFλλ∴=+- 1144AF AD b ==,,1(1)4AG a b λλ∴=+-……………………………②由①②两式可得:213114x x λλ⎧=-⎪⎪⎨-⎪=-⎪⎩6737x λ⎧=⎪⎪∴⎨⎪=⎪⎩3177AG a b ∴=+ 例4解:设AE →=xAD →,因为AD →=13AB →+12AC →,所以AE →=x 3AB →+x2AC →.由于E ,B ,C 三点共线,所以x 3+x 2=1,解得x =65.又AE →=λAB →+μAC →.所以λ=x 3=25,μ=x 2=35,因此λ-μ=-15.练习1、答案:D 解析:因为在三角形ABC 中,BE 是AC 边上的中线,所以AE →=12AC →.因为O 是BE 边的中点,所以AO →=12(AB →+AE →)=12AB →+14AC →=12a +14b .2、答案:B解析:根据题意设BP →=nBN →(n ∈R),则AP →=AB →+BP →=AB →+nBN →=AB →+n (AN →-AB →)=AB →+-(1-n )AB →+n5AC →,又AP →=mAB →+25AC →,n =m ,=25,=2,=-1.3、答案:C 解析:,,B P N 三点共线,又2284111111AP m AB AC m AB AN m AB AN=+=+⨯=+ 8111m ∴+=311m ∴=4、答案:B 解析:因为O 为BC 的中点,所以AO →=12(AB →+AC →)=12(mAM →+nAN →)=m 2AM →+n 2AN →,因为M ,O ,N 三点共线,所以m 2+n2=1,所以m +n =2.5、答案:C 解析:如图,因为EC →=2AE →,所以EM →=EC →+CM →=23AC →+12CB →=23AC →+12(AB →-AC →)=12AB →+16AC →.6、答案:A 解析:AM →=λAB →-μAC →=λAB →-μ(AB →+AD →)=(λ-μ)AB →-μAD →=2(λ-μ)AE →-3μAF →,因此E ,M ,F 三点共线.所以2(λ-μ)+(-3μ)=1,则2λ-5μ=1.因此52μ-λ=-12.7、答案:43解析:选择AB →,AD →作为平面向量的一组基底,则AC →=AB →+AD →,AE →=12AB →+AD →,AF →=AB →+12AD →,又AC →=λAE →+μAF →=12λ+μ→+λ+12μ→,12λ+μ=1,λ+12μ=1,λ=23,μ=23,所以λ+μ=43.8、答案:43解析:选择AB →,AD →作为平面向量的一组基底,则AC →=AB →+AD →,AE →=12AB →+AD →,AF →=AB →+12AD →,又AC →=λAE →+μAF →=12λ+μ→+λ+12μ→,+μ=1,+12μ=1,=2,=23,所以λ+μ=43.9、答案:4解析:设AB →=a ,AC →=b ,因为A 、P 、M 三点共线,所以存在唯一实数λ,使得AP →=λAM →.又知M 为BC 的中点,所以AP →=12λ(a +b ).因为B 、P 、N 三点共线,所以存在唯一实数μ,使得BP →=μBN →,又AP →=AB →+BP →=AB →+μBN →=AB →+μ(AN →-AB →)=AB →+-(1-μ)a +2μb ,所以12λ(a +b )=(1-μ)a +23μb ,μ=12λ,=12λ,解得λ=45,μ=35.所以AP →=45AM →,PM →=15AM →.所以|AP →|∶|PM →|=4∶1,即APPM=4.10、证明: 因为G 是OAB 的重心,分析:211()()323OG OA OB OA OB ∴=⨯+=+1OP xOAOA OPx=∴=1OQ yOBOB y=∴= 111111()()3333OG OA OB OQ OG OP OQx y x y ∴=+=+∴=+又,,P G Q 三点共线,11133x y∴+=113x y∴+=11x y∴+为定值311、解:,,N P B 三点共线,∴由平面内三点共线定理可得:存在唯一的一对实数x,y 使得,1AP xAB y AN x y =++=,AN ﹕AC=1﹕4,b AC AN 4141==1444y y x AP xAB AC xa xa b -∴=+=+=+……①又,,C P M 三点共线,∴由平面内三点共线定理可得:存在唯一的一对实数μ,λ使得,1AP AM AC μλμλ∴=++=∵AM ﹕AB=1﹕3∴a AB AM3131==,,133AP a b a b μλλλ-∴=+=+ ……………………………②由①②两式可得:1314x x λλ-⎧=⎪⎪⎨-⎪=⎪⎩311211x λ⎧=⎪⎪∴⎨⎪=⎪⎩81,11x y y +=∴=321111AP a b∴=+12. 点P 落在ABC 的边BC 上∴B,P,C 三点共线AP xAB y AC=+ 1x y ∴+= 且x>0,y>014141444()1()()145y x y x x y x y x y x y x y x y ∴+=+⨯=+⨯+=++=++ x>0,y>040,0y xx y∴>>由基本不等式可知:44y x x y +≥=,取等号时4y xx y=224y x ∴=2y x ∴=±0,0x y >> 2y x ∴=1x y += 12,33x y ∴==,符合所以yx 41+的最小值为9。
平面向量中“三点共线定理”妙用讲解学习

平面向量中“三点共线定理”妙用对平面内任意的两个向量b a b b a//),0(,≠的充要条件是:存在唯一的实数λ,使b a λ=由该定理可以得到平面内三点共线定理:三点共线定理:在平面中A 、B 、P 三点共线的充要条件是:对于该平面内任意一点的O ,存在唯一的一对实数x,y 使得:OP xOA yOB =+且1x y +=。
特别地有:当点P 在线段AB 上时,0,0x y >> 当点P 在线段AB 之外时,0xy <笔者在经过多年高三复习教学中发现,运用平面向量中三点共线定理与它的两个推广形式解决高考题,模拟题往往会使会问题的解决过程变得十分简单!本文将通过研究一些高考真题、模拟题和变式题去探究平面向量中三点共线定理与它的两个推广形式的妙用,供同行交流。
例1(06年江西高考题理科第7题)已知等差数列{a n }的前n 项和为S n ,若1200OB a OA a OC =+,且A 、B 、C 三点共线,(设直线不过点O ),则S 200=( ) A .100B .101C .200D .201解:由平面三点共线的向量式定理可知:a 1+a 200=1,∴1200200200()1002a a S +==,故选A 。
点评:本题把平面三点共线问题与等差数列求和问题巧妙地结合在一起,是一道经典的高考题。
例2 已知P 是ABC ∆的边BC 上的任一点,且满足R y x AC y AB x AP ∈+=.,,则yx 41+ 的最小值是解:点P 落在ABC 的边BC 上 ∴B ,P,C 三点共线AP xAB yAC =+ 1x y ∴+= 且x>0,y>014141444()1()()145y x y xx y x y x y x y x y x y∴+=+⨯=+⨯+=+++=++ x>0,y>040,0y xx y ∴>> 由基本不等式可知:4424y x y xx y x y+≥⨯=,取等号时4y xx y =224y x ∴=2y x ∴=±0,0x y >>2y x∴=1x y +=12,33x y ∴==,符合所以yx 41+的最小值为9 点评:本题把平面三点共线问题与二元函数求最值、基本不等式巧妙地结合在一起, 较综合考查了学生基本功.例3(湖北省2011届高三八校第一次联考理科)如图2,在△ABC 中,13AN NC =,点P 是BC 上的一点,若211AP mAB AC =+,则实数m 的值为( ) A .911 B. 511 C. 311 D. 211解:,,B P N 三点共线,又2284111111AP mAB AC mAB AN mAB AN =+=+⨯=+ 8111m ∴+= 311m ∴=,故选C 例4(07年江西高考题理科)如图3,在△ABC 中,点O 是BC 的中点,过点O 的直线分别交直线AB 、AC 于不同的两点M 、N ,若AB = m AM ,AC =n AN ,则m +n 的值为 .解:因为O 是BC 的中点,故连接AO ,如图4,由向量加法的平行四边形法则可知:1()2AO AB AC ∴=+m AB AM =,AC nAN =1()2AO mAM nAN ∴=+22m nAO AM AN ∴=+又,,M O N 三点共线,∴由平面内三点共线定理可得:122m n+= 2m n ∴+=例5(广东省2010届高三六校第三次联)如图5所示:点G 是△OAB 的重心,P 、Q分别是边OA 、OB 上的动点,且P 、G 、Q 三点共线. 设OA x OP =,OB y OQ =,证明:yx 11+是定值; 图3图4图2证明:因为G 是OAB 的重心,211()()323OG OA OB OA OB ∴=⨯+=+1OP xOAOA OP x=∴= 1OQ yOBOB OQ y=∴=111111()()3333OG OA OB OP OQ OG OP OQ x y x y∴=+=+∴=+ 又,,P G Q 三点共线,11133x y ∴+= 113x y ∴+= 11x y∴+为定值3例6(汕头市东山中学2013届高三第二次模拟考试)如图6所示,在平行四边形ABCD 中,13AE AB =,14AF AD =,CE 与BF 相交于G 点,记AB a =,AD b =,则AG =_______A .2177a b + B. 2377a b + C. 3177a b + D. 4277a b +分析:本题是以平面几何为背景,为载体,求向量的问题,所以我们很容易联想到点F 、G 、B 以及E,G,C 三点在一条直线上,可用平面内三点共线定理求解。
平面向量中三点共线

知识梳理(一)、对平面内任意的两个向量b a b b a//),0(,≠的充要条件是:存在唯一的实数λ,使b aλ=由该定理可以得到平面内三点共线定理:(二)、三点共线定理:在平面中A 、B 、P 三点共线的充要条件是:对于该平面内任意一点的O ,存在唯一的一对实数x,y 使得:OP xOA yOB =+且OP xOA yOB =+。
特别地有:当点P 在线段AB 上时,0,0x y >>当点P 在线段AB 之外时,0xy <典例剖析例1、 已知P 是ABC ∆的边BC 上的任一点,且满足R y x AC y AB x AP ∈+=.,,则yx 41+ 的最小值是 分析:点P 落在ABC 的边BC 上 ∴B ,P,C 三点共线AP xAB yAC =+ 1x y ∴+= 且x>0,y>014141444()1()()145y x y xx y x y x y x y x y x y∴+=+⨯=+⨯+=+++=++ x>0,y>040,0y xx y ∴>> 由基本不等式可知:44y x x y +≥=,取等号时4y xx y=224y x ∴=2y x ∴=±0,0x y >>2y x∴=1x y +=12,33x y ∴==,符合所以yx 41+的最小值为9 点评:本题把平面三点共线问题与二元函数求最值、基本不等式巧妙地结合在一起, 较综合考查了学生基本功.例2、在△ABC 中,13AN NC =,点P 是BC 上的一点,若211AP mAB AC =+,则实数m 的值为( ) A .911 B. 511 C. 311 D. 211分析:,,B P N三点共线,又2284111111AP mAB AC mAB AN mAB AN =+=+⨯=+8111m ∴+=311m ∴=,故选C例3、在△ABC 中,点O 是BC 的中点,过点O 的直线分别交直线AB 、AC 于不同的两点M 、N ,若AB = m AM ,AC =n AN ,则m +n 的值为 .:因为O 是BC 的中点,故连接AO ,如图4,由向量加法的平行四边形法则可知:1()2AO AB AC ∴=+m AB AM =,AC nAN =1()2AO mAM nAN ∴=+22m nAO AM AN ∴=+ 又,,M O N 三点共线,∴由平面内三点共线定理可得:122m n+= 2m n ∴+=变式、直线l 过ABCD 的两条对角线AC 与BD 的交点O ,与AD 边交于点N,与AB 的延长线交于点M 。
平面向量中三点共线的证明及其应用

平面向量中三点共线的证明及其应用作者:高永亮来源:《考试·高考数学版》2012年第12期利用平面向量证明三点共线是一种常见的较为简单的方法(相对于用斜率、距离、直线、定比分点等的证明方法),但学生对三点共线的应用大都不太熟练,在这里做一个整理,共广大师生参考.定理1:向量a(a≠0)与b共线,当且仅当有唯一一个实数λ,使b=λa.定理2:设a=(x1,y1),b=(x2,y2),其中b≠0,当且仅当x1y2-x2y1=0时,向量a与b(b≠0)共线.推论1:设: c与d为不共线向量,若向量a=x1c+y1d(x1,y1∈R)与b=x2c+y2d(x2,y2∈R)共线,则有x1y2=x2y1=0推论2:已知不共线向量OA,O B,O C,且OC=λO A+μO B,则A,B,C三点共线的充要条件为:λ+μ=1(λ,μ∈R)一、证明三点共线例1 已知三点A(-1,-1),B(1,3),C(2,5),证明A,B,C三点共线.证明:∵A(-1,1),B(1,3),C(2,5)得A B=(2,4),A C=(3,6)又2×6=4×3 ∴ A B∥A C(由定理2),又直线AB,与直线AC有公共点A,故A,B,C三点共线例2 设A B=a+5b,B C=-2a+8b,C=3(a-b)求证:A,B,D三点共线证明:由A B=a+5b,B C=-2a+8b, C D=3(a-b)得A D=A B+BC+C D=2a+10b=2A B,故A D∥A B(由定理1)又直线AB,与直线AD有公共点A,故A,B,D三点共线二、三点共线的应用(一)题中共线条件明显,学生较为容易入手.例3 若a,b是两个不共线的向量,a与b起点相同,则当t为何值时,a,t b,13(a+b)三个向量的终点在同一条直线上?解设:O A=a,O B=t b,O C=13(a+b)则A C=O C-O A=-23a+13b,A B=O B-O A=-a+t b由于A,B,C三点共线,有-23t=-13(由推论1),即t=12因此,当t=12时,a,t b,13(a+b)三个向量的终点在同一条直线上.例4 设O A=(1,-2),O B=(a,-1),O C=(-b,0),(a>0,b>0),O 为坐标原点,若A,B,C三点共线,则1a+2b最小值为解由O A=(1,-2),O B=(a,-1),O C=(-b,0),得A B=(a-1,1),A C=(-b,-1,2),由A,B,C三点共线,得2(a-1)=-b-1(由定理2),即2a+b=1,又a>0,b>0故1a+2b=1a+2b(2a+b)=ba+4ab+4≥24+4=8,当且仅当ba=4ab,即a=14,b=12时取等号.∴1a+2b最小值为8.(二)题中共线条件不明显,学生较难入手.例5 如图,在△ABC中,A N=13N C,P是BN上的一点,若A P=m A B+211A C,则实数m的值为例5图解法1:设:A B=a,A C=b,则B P=A P-A B=(m-1)a+211b,B N=A N-A B=14A C-A B=-a+14b,由B,N,P三点共线,得14(m-1)=-211(由推论1),即m=311解法2:由A P=m A B+211A C,A N=13NC,得A P=m A B+211A C=m A B+811A N由B,N,P三点共线,得m+811=1(由推论2),即m=311说明:图中B,N,P三点共线是关键.例6 如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同两点M,N,若A B=m A M,AC=n A N,则m+n=例6图解法1:令A B=a,A C=b,则A O=12(A B+A C)=12(a+b)M O=A O-A M=12(a+b)-1m a=12-1m a+12bM N=A N-A M=-1m a+1n b由M,Q,N三点共线,得12-1m1n=12-1m(由推论1),化简得12m+12n=1mn,即m+n=2说明:图中M,O,N三点共线是关键.解法2:∵O是BC的中点,∴A O=12(A B+A C)由题意A B=m A M,A C=n A N,得A O=m2A M+n2A N又∵M,O,N三点共线,∴m2+n2=1(由推论2)即m+n=2说明:巧妙灵活地使用三点共线的结论,在解题的过程中能起到事倍功半的作用.(例5,例6的解法2)。
三点共线向量表示形式的应用举例

三点共线向量表示形式的应用举例三点共线的充要条件:已知o、a、b是不共线的三点,且存在实数x,v使得op=xoa+yob,则a、b、p三点共线的充要条件是x+y=1。
这是三点共线的一个充要条件,主要以向量形式表述,用其来解决一些与三点共线有关的问题,显得非常简便和巧妙。
举例如下:一、解决与三点共线有关的求值问题如图中△abc,an=13ac,p是bn上的一点,若ap=mab+211ac,则m的值为.解:∵an=13ac,∴ap=mab+211ac=mab+611an又b、p、n三点共线,∵m+611=1∴m=511本题直接利用三点共线的向量式中x+y=1来解决.2.△abc中,o点是bc的中点,过点o的直线分别交直线ab、ac 于不同的两点m、n。
若ab=mam,ac=nan,则m+n=.解:∵ao=12ab+12ac又ab=mam,ac=nan∴ao=m2am+n2an又o、m、n三点共线,∴m2+n2=1即m+n=23.变式:△abc中,点o是bc的中点,k为ao上一点,且ao=2ak.过点k的直线分别交直线ab、ac于不同的两点m、n。
若ab=mam,ac=nan,则m+n=.解:∵ao=12ab+12acab=mam,ac=nan∴ao=m2am+n2an,又ao=2ak∴2ak=m2am+n2an∴ak=m4am+n4an又k、m、n三点共线,∴m4+n4=1即m+n=4以上两题实质都是以ao为桥梁,利用三点共线的充要条件整体求值,体现了三点共线的向量式x+y=1中在求值问题(尤其是整体求值)中的重要作用.二、在向量的表示中的应用4.△abc中,点e在ab边上,f在边ac上,且ae=2eb,af=13fc,bf与ce交于点m,设am=xae+yaf,则x+y=.解法一:∵e、m、c三点共线,∴设am=mae+(1-m)ac又ac=4af∴am=mae+4(1-m)af①∵b、m、f三点共线∴设am=nab+(1-n)af又ab=32ae∴am=32nae=(1-n)af②又ae,af又不共线,∴32n=m1-n=4(1-m)解得m=910n=35,∴am=910ae+410af∴x+y=1310此种解法主要通过两组三点共线的向量式设定系数,用同一组基底来表示向量am,再结合平面向量基本定理求解系数。
平面向量三点共线定理和等和线定理(学生用)

平面向量三点共线定理与等和线定理(方法素养·助学培优)【考情分析】平面向量是有效连接代数和几何的桥梁,已成为高考数学命题的一个热点,向量三点共线和等和线巧妙地将代数问题转化为图形关系问题,将系数和的代数式运算转化为距离的比例运算,数形结合思想得到了有效体现。
平面向量三点共线定理和等和线定理在近些年高考及各省市的模拟考试相继出现,这类问题综合性较强,难度稍大,学生在解决此类问题大多会思路不清晰,解题繁琐,得分率不高,通过三点共线和等和线定理的研究学习为求解此类问题打开崭新的解题空间。
【考点知识回顾】1.共线向量定理向量a(a≠0)与b共线,当且仅当有唯一一个实数λ,使b=λa.2.平面向量基本定理如果e1、e2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a,有且只有一对实数λ1、λ2,使a=λ1e1+λ2e2.其中,不共线的向量e1、e2叫做表示这一平面内所有向量的一组基底.【考点探究·题型突破】▶▶▶思考1 如图所示,在平面内,已知C在直线AB上(即A,B,C三点共线),= ,若点C在线段AB 上,则。
▶▶▶引申探究,则A,B,C三点一定共线吗?★★★1.三点共线定理:已知为平面内两个不共线的向量且,是A,B,C三点共线的充要条件。
2.已知,若A,B,C三点共线且点C在线段AB 上,则(系数交叉对应)。
3.特别地:当C为AB的中点时,.☛☛☛练习1 如图,在☛ABC中,D为BC的中点,E在线段AD上,且AE=2ED,则( )▶▶▶思考2如图所示,在平面内,已知,,若点C在直线AB外,则=★★★等和线定理:平面内一组基底及任一向量,,若点C在直线AB上或者平行与AB的直线上,则且,反之也成立。
(直线AB以及直线AB平行的直线称为等和线)。
性质:(1);(2)当等和线恰为直线AB时,;(3)当等和线在O和直线AB之间时,;(4)当直线AB在点O和等和线之间时,;(5)当等和线过O点时,。
有关平面向量三点共线问题的求解

有关平面向量三点共线问题的求解
三点共线向量公式:(x2-x1)(y3-y1)=(x3-x1)(y2-y1)。
三点共线指的是三点在同一条直线上。
可以设三点为A、B、C,利用向量证明:λAB=AC(其中λ为非零实数)。
三点共线证明方法:
方法一:挑两点奠定一条直线,排序该直线的.解析式.代入第三点座标看看与否满足用户该解析式(直线与方程)。
方法二:设三点为a、b、c,利用向量证明:λab=ac(其中λ为非零实数)。
方法三:利用点差法求出来ab斜率和ac斜率,成正比即为三点共线。
方法四:用梅涅劳斯定理。
方法五:利用几何中的公理“如果两个不重合的平面存有一个公共点,那么它们存有且只有一条过该点的公共直线”.所述:如果三点同属两个平行的平面则三点共线。
方法六:运用公(定)理“过直线外一点有且只有一条直线与已知直线平行(垂直)”.其实就是同一法。
2023届高三数学一轮复习专题 平面向量的表示、三点共线研究 讲义 (解析版)

高三第一轮复习专题 平面向量表示、三点共线研究 一、平面向量基本定理:设12,e e 是同一平面内两个不共线向量,a 是这一平面内的任一向量。
在平面内任取一点O ,作12,,OA e OB e OC a ===,过C 作OB 的平行线,交直线OA 于M ;过C 作OA 的平行线,交直线OB 于N 。
因OM 与OA 共线,则存在实数1λ,使得:11OM e λ=;因ON 与OB 共线,则存在实数2λ,使得:22ON e λ=; OC OM ON =+1122a e e λλ∴=+也即,任一向量a 都可表示成1122e e λλ+的形式。
平面向量基本定理:若12,e e 是同一平面内的两个不共线向量,则对于这个平面内的任意向量a ,有且只有一对实数12,λλ,使得:1122a e e λλ∴=+。
(也可称为a 用12,e e 表示出来)不共线向量12,e e 称为表示这一平面内所有向量的一组基底,12,e e 称为基向量。
例1。
ABCD 两条对角线交于O ,AB a =,AD b =,用a 、b 表示OA 、OB 、OC 、OD 。
2e2ea解:AC AB AD a b =+=+,DB AB AD a b =-=-O ABCD 为两条对角线的交点()1122OA AC a b ∴=-=-+,()1122OC AC a b ==+()1122OB DB a b ==-, ()1122OD DB a b =-=--。
故在一个图形中,任意两个不共线向量都可以作为一组基底,其余向量都可用这一组基向量表示出来。
在具体问题中,基向量的选择十分重要,它决定了是否容易表示。
二、向量的表示:★★★★★在研究向量间关系时,常先取两个基向量作为一组基底,其余向量用这两个基向量表示出来,这样能够更清晰地找出所研究向量间的关系。
1.,其余向量用这两个基向量表示出来。
例。
在ABC 中,2BD DC =,设,AB a AC b ==,用,a b 表示AD 。
