命题逻辑和一阶逻辑
离散数学第2章一阶逻辑

2.1 一 阶 逻 辑 基 本 概 念
综上,有如下结论: (1)谓词中个体词的顺序不能随意变更。 (2)一元谓词用以描述一个个体的某种特性, 而n元谓词则用以描述n个个体之间的关系。 (3)0元谓词就是一般命题。 (4)具体命题的谓词表示形式和n元谓词是不同的, 前者是有真值的,而后者不是命题,它的 真值是不确定的。 (5)一个n元谓词不是一个命题,但将n元谓词中的 个体变项都用个体域中某个具体的个体取代后, 就成为一个命题。而且,个体变项在不同的个体域 中取不同的值对是否成为命题及命题的真值有很大 的影响。
26
2.2.1 一阶逻辑公式的语言翻译 2.1 一 阶 逻 辑 基 本 概 念
例2.2.1 用一阶逻辑符号化下述语句. (1)天下乌鸦一般黑。 (2)没有人登上过木星。 (3)在美国留学的学生未必都是亚洲人。 (4)每个实数都存在比它大的另外的实数。 (5)尽管有人很聪明,但未必一切人都聪明 (6)对任意给定的ε >0,必存在着δ >0,使 得对任意的x,只要|x-a|<δ ,就有 |f(x)-f(a)|<ε 成立。
27
2.1 一 阶 逻 辑 基 本 概 念
解: (1)设F(x):x是乌鸦;G(x,y):x与y一般黑 (x)(y)(F(x)F(y)G(x,y)) 或者 (x)(y)(F(x)F(y)G(x,y)) (2)设H(x):x是人;M(x):x登上过木星。 (x)(H(x)M(x)) 或 (x)(H(x) M(x)) (3)设H(x):是亚洲人;A(x):是在美国留学的学生。 (x)(A(x) H(x)); 或者: (x)(A(x) H(x)) (4)设R(x):x是实数;L(x,y):x小于y (x)(R(x) (y)(R(y) L(x,y))); (5)设M(x):x是人;C(x):x很聪明 (x)(M(x)C(x)) (x)((M(x) C(x)); (6)对任意给定的ε >0,必存在着δ >0,使得对任意的x,只 要|x-a|<δ ,就有|f(x)-f(a)|<ε 成立。 (ε )((ε >0)(δ )((δ >0) (x)(( |x-a|<δ (|f(x)-f(a)|<ε )))) 28
8一阶逻辑-概念公式4-14-1

4)∀x(F(g(x,a),x)→F(x,y) )
4)谓词 F(x,y): x=y
5)∀x∀y(F(f(x,a),y)→
F(f(y,a),x) )
6)∀x∀y∃z F(f(x,y),z)
例:给定解释I 1)个体域为整数集合Z 2) Z上的特定元素 a0=0,a1=1; 3)Z上的特定函数 f(x,y)=x-y, g(x,y)=x+y; 4)Z上的特定谓词 F(x,y): x < y;
任何数如果是整数则一定都是偶数--是假命题
仅有个体与谓词还不能准确表示一些逻辑问题 如:N(x):x是整数, O(x):x是偶数 所有的整数是偶数可符号化为 N(x)→ O(x) 肯定为假 其否定应为真. 但 ┑(N(x)→O(x))等值于 N(x)∧┑O(x) 即: 所有的整数且不是偶数也为假 主要原因是:没有体现整体和个别的关系 所以在描述时必须引入反映数量关系的词
4、闭式定义 设A是公式,若A中不含自由出现的个体变项则称A为封闭的
公式,简称闭式
二、公式的解释(相当于命题公式的赋值) 按合式公式的形成规则形成的符号串是F中的公式,这种公式 没有确定意义.一旦将其中的变项(项的变项,谓词变项等)用 指定的常项代替后,所得公式就具备一定意义,有时就变成命 题了
一个解释不外乎指定个体域、个体域中一些特定的元素、特定 的函数和谓词等部分. 1、公式的解释 1)定义:F的解释I的内容一般由下面4部分组成: (a)指定非空个体域DI (个体域的取值范围) (b)指定DI中一些特定元素(常量)的集合{a1,a2,…ai}. (c)给定DI上特定函数集合{fi | i ≥ 1}. 具体的函数 (d)给定DI上特定谓词的集合{ Hi | i≥1}. 具体的谓词
在解释I下的公式A中的个体变项均取值于DI. 被解释I下的公式不一定全部包含解释中的四部分
第四章 一阶逻辑命题符号化

“ x , y 等表示个体域里的所有个体; 用 ”.
用 xF ( x ), yG ( y )等分别表示个体域里所有个体 都有性质 F 和都有性质 G .
2 存在量词
日常生活和数学中所用的“存在”,“有一 个”,“有的”,“至少有一个” 等词统称为 存在量词,将它们都符号化为“”. 用 x , y 等表示个体域里有的个体;
三、量词
有了个体词和谓词之后, 有些命题还是不能准确 的符号化,原因是还缺少表示个体常项或变项之
间数量关系的词. 称表示个体常项或变项之间数
量关系的词为量词. 量词可分两种:
全称量词
存在量词
1 全称量词
日常生活和数学中所用的“一切的”,“所 有的”,“每一个”,“任意的”,“凡”,“都” 等词可统称为全称量词,将它们符号化为
表达出个体与总体的内在联系和数量关系,这就是一
阶逻辑所研究的内容. 一阶逻辑也称一阶谓词逻辑或 谓词逻辑.
第1节
一阶逻辑的符号化
一、个体词 二、谓词 三、量词
四、一阶逻辑命题符号化
个体词、谓词和量词是一阶逻辑命题符号化
的三个基本要素. 下面讨论这三个要素.
一、个体词
个体词是指所研究对象中可以独立存在的具体 的或抽象的客体. (1)将表示具体或特定的客体的个体词称作个体 常项,一般用小写英文字母a,b,c…表示; (2)而将表示抽象或泛指的个体词称为个体变项, 常用x,y,z , …表示. (3)称个体变项的取值范围为个体域(或称论域).
(3) 函数符号: f, g, h, …, fi, gi, hi,…, i≥1
(4) 谓词符号: F, G, H,…,Fi , Gi , Hi ,…,i≥1
(5) 量词符号: ,
命题逻辑与一阶逻辑的异同

命题逻辑与一阶逻辑的异同
一、命题逻辑与一阶逻辑的异同
1、定义
命题逻辑是一切形式逻辑最具有重要性的一种,它是研究并证明形而上世界和经验世界等客观事物之间的有效关系的一类抽象数理系统。
一阶逻辑是以符号语言作为基础,主要研究建立定量的、确定的、可计算的逻辑系统和知识表示语言的一种逻辑学方法。
2、目的
命题逻辑的目的是证明一系列客观事物之间的有效关系,而一阶逻辑的目的是建立可计算的逻辑系统和知识表示语言。
3、应用
命题逻辑主要用于科学中的证明,比如经济学,会计学,金融学等;一阶逻辑主要用于计算机科学中的程序设计,人工智能,数据库等。
4、证明方法
命题逻辑使用演绎证明法来证明,而一阶逻辑则使用自然语言或者形式化程序设计来证明。
5、特点
命题逻辑特别关注两类事实的内在联系与关系,把客观事实转化为语义事实,它以自然语言的表达方式完成比较重要的推理;一阶逻辑则能够提供定量的计算技巧,把物理性知识转换成信息性知识,从而实现人工智能的目的。
一阶逻辑和命题逻辑

一阶逻辑和命题逻辑
一阶逻辑(first-order logic)和命题逻辑(propositional logic)
是数理逻辑中两种不同的形式系统,用于表示和推理关于命题和谓词的逻辑语句。
命题逻辑是最简单的逻辑系统,它只涉及命题(proposition)
和逻辑连接词(如“与”、“或”、“非”等),而不涉及个体和谓词。
命题逻辑中一切复杂的语句都可以用原子命题和逻辑连接词的组合来表示。
命题逻辑的推理只关注命题之间的逻辑关系,而不关注具体命题所代表的内容。
一阶逻辑是一种更为复杂的逻辑系统,它不仅涉及命题,还涉及个体和谓词。
在一阶逻辑中,命题可以包含变量和量词,可以表示更为复杂的逻辑语句,如“对于所有”的量化语句和“存在”的量化语句。
一阶逻辑允许进行更为精确的推理,可以表
示更复杂的逻辑关系和推导。
总的来说,命题逻辑更简单,只涉及命题的逻辑关系;而一阶逻辑更复杂,除了命题的逻辑关系,还涉及个体和谓词的逻辑关系。
离散数学-第1章

练习1解答
提示: 分清复合命题与简单命题 分清相容或与排斥或 分清必要与充分条件及充分必要条件
答案: (1) 是简单命题
(2) 是合取式
(3) 是析取式(相容或)(4) 是析取式(排斥或)
设 p: 交通阻塞,q: 他迟到
(5) pq,
(6) pq或qp
(7) qp 或pq, (8) qp或pq
假命题 真命题 不是命题 不是命题
不是命题 不是命题
命题,但真值现在不知道
5
命题分类
命题分类:简单命题(也称原子命题)与复合命题 简单命题符号化
用小写英文字母 p, q, r, …, pi, qi, ri (i1)表示简单命题
用“1”表示真,用“0”表示假 例如,令
p: 2是有理数,则 p 的真值为0,
p q p pq (pq) (pq)q
00 1 1
0
0
01 1 1
0
0
10 0 0
1
0
11 0 1
0
0
成假赋值:00,01,10,11; 无成真赋值
24
公式的类型
定义1.10 (1) 若A在它的任何赋值下均为真, 则称A为重言式或永真式; (2) 若A在它的任何赋值下均为假, 则称A为矛盾式或永假式; (3) 若A不是矛盾式, 则称A是可满足式.
30
练习3解答
(1) pr(qp)
pqr
qp (qp) pr(qp)
000
1
0
0
001
1
0
0
010
0
1
0
011
0
1
0
100
1
0
0
101
第四章一阶逻辑的基本概念
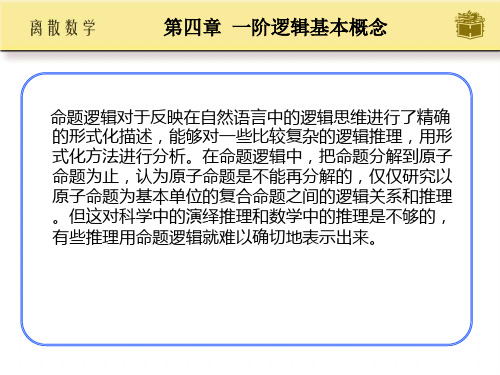
(2) 令F(x):x是无理数,G(y):y是有理数,L(x,y):x>y x(F(x)y(G(y)L(x,y) ) )
或者 xy(F(x)G(y)L(x,y))
14
实例4
例4 在一阶逻辑中将下面命题符号化 (1) 没有不呼吸的人 (2) 不是所有的人都喜欢吃糖 解 (1) M(x): x是人, G(x): x呼吸
合式公式 (4) 若A是合式公式,则xA, xA也是合式公式 (5) 只有有限次地应用(1)—(4)形成的符号串才是合式公式. 合式公式简称公式
如, F(x), F(x)G(x,y), x(F(x)G(x)) xy(F(x)G(y)L(x,y))等都是合式公式
19
量词的辖域
定义4.5 在公式 xA 和 xA 中,称x为指导变元,A为相应 量词的辖域. 在x和 x的辖域中,x的所有出现都称为约束 出现,A中不是约束出现的其他变项均称为是自由出现的.
9
(3)存在唯一量词!,用来表达“恰有一个”、“存在唯一”等词语。
“(!x)R(x)”表示命题:“在个体域中恰好有一个个体使谓词R(x)为
真”。(了解)
全称量词、存在量词统称量词。量词是由逻辑学家Fray引入的,有了量 词之后,用逻辑符号表示命题的能力大大增强。
实例1
例1 用0元谓词将命题符号化 (1) 墨西哥位于南美洲
(2) 2 是无理数仅当 3 是有理数
(3) 如果2>3,则3<4
解:在命题逻辑中: (1) p, p为墨西哥位于南美洲(真命题)
(2) p→q, 其中, p:2 是无理数, q: 3 是有理数. 是假命题
(3) pq, 其中, p:2>3, q:3<4. 是真命题
第4章_一阶逻辑

Q(1,2) = 0
Q(3,0) = 1
7
一阶逻辑基本概念
EXAMPLE 3
设R(x, y, z) 表示语句“x+y=z.”,
则R(1, 2, 3) 和R(0, 0, 1) 的真值是多少?
R(1, 2, 3)= 1
R(0, 0, 1)= 0
8
一阶逻辑基本概念
当n>1时,通常P给出了xi(i=1,2,…,n)之间的关系。 例如, P(x,y,z) 表示 x 位于 y 与 z 之间,是一个三元 谓词。当x,y,z分别用赤道、南半球、北半球代入时, 得到命题:赤道位于南半球与北半球之间,其真值 为 1 。再如,将杭州、南京、北京代入,则得到: 杭州位于南京和北京之间,真值为0。 当n=0时(即0元谓词),该谓词对应一个命题。
18
一阶逻辑基本概念
EXAMPLE 8
设P(x) 表示语句“x2>10.”,个体域 为不大于4的所有正整数。则xP(x)的 真值是多少?
xP(x) =P(1)∨P(2)∨P(3)∨P(4) =1
19
一阶逻辑基本概念
EXAMPLE 9
在一阶逻辑中将下列命题符号化: (1) 所有的狮子都是凶猛的。
x(C(x)∨y(C(y)∧F(x, y))) 其中,C(x)表示“x有一台计算机”,F(x,y)表示“x和y 是朋友”,x和y的个体域为数计学院的所有学生集合。 解答:对于数计学院的任意一个学生x来说,x有一台 计算机,或者存在一个学生y,y有一台计算机而且x和 y是好朋友。换句话说,数计学院的所有学生要么有一 台计算机,要么有一个拥有一台计算机的朋友。
从苏格拉底三段论到一阶逻辑
苏格拉底苏格拉底三段论:人都是会死的, 苏格拉底是人,所以苏格拉底会死。
离散数学命题逻辑和一阶逻辑的选择题解析

离散数学命题逻辑和一阶逻辑的选择题解析在命题逻辑中,如果P为真,Q为假,那么P ∧ Q的值为?A. 真B. 假C. 无法确定D. 与P、Q无关解析:在命题逻辑中,合取运算(∧)表示“并且”。
如果P为真,Q为假,那么“P并且Q”显然为假。
因此,答案是B。
在一阶逻辑中,如果F(x)表示“x是人”,G(x)表示“x是聪明的”,那么“存在一个聪明的人”可以表示为?A. ∀x(F(x) → G(x))B. ∃x(F(x) ∧ G(x))C. ∃x(F(x) → G(x))D. ∀x(F(x) ∧ G(x))解析:在一阶逻辑中,存在量词(∃)表示“存在”。
因此,“存在一个聪明的人”可以表示为“存在一个x,使得x是人并且x是聪明的”,即∃x(F(x) ∧ G(x))。
因此,答案是B。
在命题逻辑中,如果P → Q为真,且P为真,那么Q的值为?A. 真B. 假C. 无法确定D. 与P无关解析:在命题逻辑中,如果P → Q为真,且P为真,那么根据蕴含运算(→)的定义,“如果P则Q”,Q必然为真。
因此,答案是A。
在一阶逻辑中,全称量词(∀)表示什么?A. 存在B. 所有C. 至少一个D. 不多于一个解析:在一阶逻辑中,全称量词(∀)表示“对于所有的”。
因此,答案是B。
在命题逻辑中,如果P为假,Q为真,那么P → Q的值为?A. 真B. 假C. 无法确定D. 与P、Q的值无关解析:在命题逻辑中,即使P为假,Q为真,蕴含式P → Q仍然为真。
这是因为蕴含式的定义是“如果P为真,则Q也为真”,但这并不排除“P为假而Q为真”的情况。
因此,答案是A。
在一阶逻辑中,如果F(x)表示“x是红的”,那么“所有的东西都是红的”可以表示为?A. ∃xF(x)B. ∀xF(x)C. ∀x¬F(x)D. ∃x¬F(x)解析:在一阶逻辑中,“所有的东西都是红的”可以表示为“对于所有的x,x都是红的”,即∀xF(x)。
因此,答案是B。
3 命题逻辑的推理理论
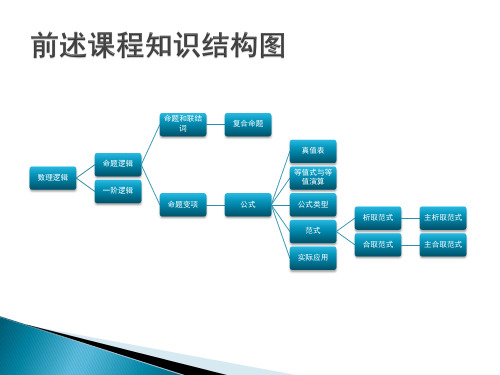
(7)拒取式规则
AB B A
(8) 假言三段论规则
AB BC AC
(9)析取三段论规则
AB B A
(10)构造性二难推理规则
AB CD AC BD
(11)破坏性二难推理规则
AB CD BD AC
(12) 合取引入规则
A B AB
证明方法: ◦ 直接证明法 ◦ 附加前提法 ◦ 归谬法(或称反证法)
(2) 联结词符号: ┐, , , , (3) 括号与逗号:( ),, 2. 合式公式(同合取联接词定义)
3. 推理规则
(1)前提引入规则 在证明的任何步骤上都可以引入前提。
(2)结论引入规则 在证明的任何步骤上所得到的结论都可以作为后继证明的前提。
(3)置换规则 在证明的任何步骤上,命题公式中的子公式都可以用与之等值的公
1、用不同的方法验证下面推理是否正确。对于正确的推理还 要在P系统中给出证明。 (1) 前提:pq, q
结论:p (2) 前提:qr, pr
结论:qp
(1)不正确。 验证答案,只需证明(pq)qp不是重言式。 方法一 等值演算
(pq)qp ((pq)q)p (pq)qp ((pq)(qq))p pq 易知10是成假赋值,故(pq)qp不是重言式,所以推理不正确。
数理逻辑
命题逻辑 一阶逻辑
命题和联结 词
命题变项
复合命题 公式
真值表 等值式与等
值演算 公式类型
范式
实际应用
析取范式 合取范式
主析取范式 主合取范式
根据下列真语句,请判断是谁谋害了张先生? (1)A、B、C三人中至少有一人。 (2)如果张先生生前未饮过麻醉剂,那不是C。 (3)如果张先生曾饮过麻醉剂,那不是A。 (4)如果是A谋害的,那么B也参加了。 (5)如果作案在落雨前,则是A谋害的。 (6)如果作案不在落雨前,张先生临死前搏斗过。 (7)张先生临死前搏斗过,就不是B谋害的。 (8)经过法医解剖化验,张先生死前曾饮过麻醉剂。
第三四讲——产生式及一阶谓词

专家系统的开发过程
专家系统是一个复杂的智能软件,与一般软件 类似,但又有不同的特点。
一般软件处理的对象是数值、文字、图形等信 息,且有固定的算法序列,而专家系统软件处理的 对象是以符号表示的知识,在运行过程中常有回溯 发生,因此专家系统的开发过程与一般软件的开发 有所不同。
专家系统的创始人费根鲍姆教授把开发专家系 统的技术称之为知识工程,即以知识获取、知识表 示、知识运用(推理)为中心。根据这个思想,可把 专家系统的开发过程分为以下几个阶段。
14
2019/12/15
例:初始状态 Start 目标状态 Goal
R冲1:突if 原P 则a:nd Q then Goal
R2:if选R取最an久d 以S 前t被he触n 发P 的或根本没有被触发的规则
R3:if如W果出an现d R“平t局he”n Q,选取R其4:中if的T第a一nd个U规则then Q
接口,完成信息适的用性和有效性密切相关的。
内部形式和人可接
间假设和中间结 果
收的形式之间进行
转换。
用
推
理
动态库
用
户
执
知识
户
界
行
获取
机
面
构
知识库
推理机根据动态库的当 前状态,利用知识库中 的知识进行推理。
包括:1与当前问题有关的数据信
解 释 息;2 一般知识和领域知识。规
机构
则、网络和过程等形式表示。
以人类专家知识为基础的专家系统的问题求解,从本质
上都可以看作是从初始状态到目标状态的推导变换过程,
因而都可用产生式系统来求解。
2019/12/15
21
2019/12/15
离散数学 第二章:一阶逻辑

(2) xF(x) G(x, y);
(3) xyR(x, y) L(y, z) xH(x, y).
2.闭式
定义6. 设A为任一公式,若A中无自由出现的个体变项,则称A是 封闭的合式公式,简记闭式.
例: xF(x) G(x),xyF(x) G(x, y) 闭式, 但 xF(x) G(x, y),zyL(x, y, z) 不是闭式.
(1)所有的人都要死的. (2)有的人活百岁以上.
全称量词:一切,所有,任意. 用 表示.
1.量词
x:表示对个体域中的所有个
xF(x)体:表. 示个体域中的所有个体都具有性质F.
存在量词:存在着,有一个,至少有一个. 用 表示.
x:表示存在个体域里的个体.
xF ( x):表示存在着个体域中的个体具有性质F.
(2)xR(x) G(x), 其中 G(x): x是整数.
3) 同2).
例3. 将下面命题符号化. (1)对所有的x ,均有 x2-1=(x+1)(x-1). (2)存在x,使得 x+5=2.
要求: 1)个体域为自然数集合. 2)个体域为实数集合.
解:1) 不用引入特性谓词.
(1)xF(x), 其中 F(x): x2-1=(x+1)(x-1). 真命题
(3) xF(x) yF(y) L(x, y),
其中 F(x): x是自然数, L(x,y): y是 x的先驱数.
§2.2 一阶逻辑合式公式及解释
一、合式公式
1.字母表 定义1.字母表如下: (1)个体常项: a,b,c,… (2)个体变项: x,y,z,… (3)函数符号: f,g,h,… (4)谓词符号: F,G,H,…
一阶逻辑导论

一阶逻辑导论1.前言简单的说,一阶逻辑是在在命题逻辑上扩展了谓词和量化。
通俗的可以把谓词看作是一个只返回真或伪的函数。
例如在命题逻辑中,语句“苏格拉底是哲学家”、“柏拉图是哲学家”为二个独立命题,在一阶逻辑中,可以通过一个谓词Phil(a)(意思为a是哲学家)来表达。
这里a是一个变量,若a 代入苏格拉底时, Phil(a)对应了第一个命题;当a 代入柏拉图时,则Phil(a)对应了第二个命题。
相对于命题逻辑,一阶逻辑是对于变量上的共享特性质(谓词)进行推论的。
例如设定谓词Phil(a)(表示a 是哲学家)和Schol(a)(表示a是学者)。
这样用公式Phil(a)→Schol(a)表示如果a 为哲学家,那么a 为学者。
这里,对于a的不同的取值公式的真值也可能不同。
如果我们使得对每个a的取值都有相同的真值(即)时,可以通过下列一阶公式来表述∀a(Phil(a)→Schol(a))(表示对于每个a,若a 为哲学家,则a 为学者)。
这里符号∀称为全局量词,强调对所有a括号内的叙述为真。
当要表达至少有一个a使得括号内叙述成立时可以用一阶逻辑的存在量词来表述。
例如∃a(Phil(a)→Schol(a))(表示存在一个a,若a 为哲学家,则a 为学者)。
简单来说,对每个a都成立的叙述,等价于至少存在一个a使得叙述不成立。
一阶逻辑有两个主要的部份:语法定义哪些符号的组合是一阶逻辑内的合法表示式,而语义则定义这些表示式之间的意义。
2.句法在一阶逻辑中的标识(signature)是函数(function constants)和谓词(predicate constants)俩种元素的集合。
元素具有一个非负的整数参数(称为变元数(arity))。
变元数为0的函数称为对象(object constants);变元数为0的谓词称为命题(propositional constants)。
对象变量(Object variables)为某些特定符号的无限序列中的元素,例如x, y, z, x1, y1, z1, . . . 等。
命题逻辑与一阶逻辑之间的区别和联系

命题逻辑与一阶逻辑之间的区别和联系
命题逻辑与一阶逻辑之间的区别和联系
命题逻辑和一阶逻辑是逻辑学中的两个重要学科,它们之间有着密切的联系,也有着明显的区别。
命题逻辑是以事实判断为基础,研究可以用事实表述的大类断言的逻辑规律及其证明规则。
它是用来判断一个命题是否为真还是假的。
命题逻辑主要关注的是逻辑性的语句及其证明,因此它所涉及的是命题的真假性。
一阶逻辑是一种研究逻辑性断言的规则系统,它主要关注的是语句的真假性,还有函数、定义和变量的概念,以及这些因素之间的关系。
一阶逻辑是对命题逻辑的推广,除了包括命题逻辑的内容外,还要考虑到语言中函数、量词和变量的概念。
一阶逻辑是研究变量的逻辑演绎判断的,它的推理不仅仅是针对常量,还可以针对变量进行判断。
命题逻辑和一阶逻辑之间有着密切的联系,他们都是研究变量的逻辑演绎判断,而且一阶逻辑也包括了命题逻辑的内容。
但是它们之间还有明显的区别,命题逻辑主要关注的是逻辑性的断言及其证明,它只考虑语句的真假性,而一阶逻辑比命题逻辑复杂,它考虑到语句的真假性、函数、定义和变量的概念,以及这些因素之间的关系。
- 1 -。
浅析逻辑代数、命题逻辑、一阶逻辑、高阶逻辑和数理逻辑

浅析逻辑代数、命题逻辑、⼀阶逻辑、⾼阶逻辑和数理逻辑1. 从逻辑代数开始逻辑代数是⼀种⽤于描述客观事物逻辑关系的数学⽅法,由英国科学家乔治·布尔 (George·Boole) 于 19 世纪中叶提出,因⽽⼜称布尔代数。
所谓逻辑代数,就是把逻辑推理过程代数化,即把逻辑推理过程符号化。
2. 从逻辑代数到命题逻辑同样的,命题逻辑是将那些具有真假意义的陈述句接着进⾏符号化,产⽣原⼦命题。
与此同时,当我们把逻辑代数中的运算符:与( · )、或( + )、⾮( - ),替换成命题逻辑中的联结词集:合取( ∧ )、析取( ∨ )、⾮( ¬ )、蕴涵( → ) 和等价( ↔ ) 之后,我们就进⼊了命题逻辑的研究领域。
需要指出的是,通常也将命题逻辑称作命题演算,后者的出现就是⽤来讨论前者的,这⾥不再区分。
它与下⾯出现的⼀阶逻辑(谓词逻辑)都是数理逻辑的⼦集(或称之为分⽀),是数理逻辑的两个最基本的也是最重要的组成部分。
有⼈可能会问,为什么不从数理逻辑开始,其实意义不⼤。
要谈数理逻辑,不可避免的下⼀个主题就是逻辑代数。
为什么这样说呢?因为数理逻辑⼀开始的诞⽣是没有意义的,它的创始⼈正是我们熟知的莱布尼茨(没错,就是⾼数中的那个⽜顿-莱布尼茨公式)。
莱布尼茨⼀开始是想要建⽴⼀套普遍的符号语⾔,从⽽将⼀些由⾃然语⾔的推理转换成⽤符号演算。
但可惜他的⼯作只是开了个头,⽽且没有太多的发表,因此影响不⼤。
⽽真正使数理逻辑这门学科迅速扩张的是开头所说的英国科学家——乔治·布尔,⽽他所做的正是将逻辑代数化。
2.1 数理逻辑与数学和逻辑学数理逻辑⼜称符号逻辑、理论逻辑,是⼀门⽤数学⽅法研究逻辑或形式逻辑的学科,这是百度词条给出的解释。
还有⼀句话⾮常拗⼝:它既是数学的⼀个分⽀,也是逻辑学的⼀个分⽀。
其研究对象是对证明和计算这两个直观概念进⾏符号化以后的形式系统。
简单来讲,数理逻辑研究的并不是数学领域,⽽是计算机科学等领域。
离散数学(第二版)第2章一阶逻辑

F表示“……是学生”; G表示“……整除……”; H表示“……位于……与……之间”。
第二章 一 阶 逻 辑
这时F、G、H表示的是具体的谓词,称为谓词常元, 否则,称为谓词变元。显然,单独的一个谓词(即使是谓词 常元)并不能构成一个完整的句子,必须以个体词取代 “……”方能构成一个句子。通常我们用小写的英文字母a、 b、c(可加下标)等表示个体。这样,“小王是学生”可符号 化为F(a),其中a表示小王。若用b表示小李,则F(b)就表示 “小李是学生”。若用c1表示2,用c2表示6,则G(c1,c2)就 表示“2整除6”。
第二章 一 阶 逻 辑
事实上,在一般的简单命题中,常有一些表示数量的词 语,诸如“所有的”、“有一些”等等,用来表示谓词中 的变量取自论域中的全体或部分个体,例如下面的两个陈 述句:
“对所有的x∈D,论断F(x)为真。” “对某些x∈D,论断F(x)为真。” 在谓词逻辑中,我们用量词把它们形式化。
x y(F(x)∧G(y)∧ H(x,y)) x(F(x)∧ y (G(y)∧ H(x,y)))
第二章 一 阶 逻 辑
(4) 本命题的意思是:对于每个x,如果x是病人,就存 在着医生y,使得x相信y。因此,本命题符号化为:
x(F(x)→ y(G(y)∧H(x,y))) 【例2.1.5】将下列命题形式化为一阶逻辑中的命题: (1) 任意一个整数x,均有另一个整数y,使得x+y等于0。 (2) 存在这样的实数x,它与任何实数y的乘积均为y。
离散数学 第三章 一阶逻辑

在引入特性谓词后, 5. 在引入特性谓词后,使用全称量词与存 在量词符号化的形式是不同的。 在量词符号化的形式是不同的。
例将命题符号化:(1) 每个自然数都是实数. (2) 有的自然数是实数. 解(1) ∀x(N(x) →R(x)) 其中特性谓词N(x):x是自然数 ; R(x):x是实数 (2) ∃x(N(x) ∧R(x)) 其中特性谓词N(x):x是自然数 ; R(x):x是实数
8
例1(续) 续
2 (2) 2 是无理数仅当 3 是有理数 2 是无理数 3 在一阶逻辑中, 是无理数, 在一阶逻辑中 设F(x): x是无理数 G(x): x是有理 是有理 数 F ( 2 ) → G( 3 )
F ( 2 ) → G( 3 ) (3) 如果2>3,则3<4 如果 ,
符号化为
在一阶逻辑中, 在一阶逻辑中 设 F(x,y):x>y,G(x,y):x<y, : , : 符号化为 F(2,3)→G(3,4) →
15
在不同的个体域中, 4. 在不同的个体域中,命题符号化的形式可能不一样 将命题符号化: 凡有理数均可表成分数, 例:将命题符号化: 凡有理数均可表成分数, 个体域是有理数集合. (1) 个体域是有理数集合. (2) 个体域是实数集合 解(1)∀xA(x) 其中A(x):x可表成分数
(2)∀x( R(x)→A(x) ) 其中 R(x):x是有理数, A(x):x可表成分数
18
一阶逻辑中命题符号化( 一阶逻辑中命题符号化(续)
例3 在一阶逻辑中将下面命题符号化 (1) 兔子比乌龟跑得快 (2) 有的兔子比所有的乌龟跑得快 (3)并不是所有的兔子都比乌龟跑得快 ) (4)不存在跑得同样快的两只兔子 )
19
第二章一阶逻辑

第二章一阶逻辑☆命题逻辑中,主要研究命题和命题演算,其基本组成单位是命题常项/变项,它们且不可再分. 例如:P: n是一个奇数;根据命题的定义,P不是命题.因为它随n的取值而定.而计算机中大多数语句使用变量.所以,必须扩展逻辑系统以包含这样的语句.☆在命题公式中也允许出现命题变项,但仅仅作为一个整体考虑其真值.第二章一阶逻辑☆也就是说, 在命题逻辑中,命题的内部结构及命题之间内在的联系,无法处理.例如:著名的“苏格拉底三段论”就无法判断其正确性:所有的人都是要死的,苏格拉底是人,所以苏格拉底是要死的.分析: 在命题逻辑中,如用P,Q,R表示上述三个命题,则(P∧Q) R,但这个命题公式不是重言式,可是凭我们的直觉可知上述论断是正确的.为此,引入一阶逻辑(也称为谓词逻辑).第二章一阶逻辑§2.1 一阶逻辑命题符号化2.1.1 个体和谓词§在原子命题(陈述句)中所描述的对象称为个体;用以描述个体性质或个体间关系的部分称为谓词;§例:1.他是三好学生§2.7是质数§3.每天早晨做广播体操是好习惯§4.5大于3§5.哥白尼指出地球绕着太阳转§2.2 一阶逻辑公式与解释§2.1.1 个体和谓词§个体常项、变项和个体域§①表示具体的或特定的个体的词称为个体常项,常用a,b,c,…小写字母表示.§②表示抽象的或泛指的个体的词称为个体变项,常用x,y,z,…小写字母表示.§③个体变项的取值范围称为个体域(或论域).个体域可以是有限事物的集合,也可以是无限事物的集合.无特别声明时,将宇宙间一切事物组成个体域称为全总个体域.§2.1.1 个体和谓词§谓词常项和谓词变项§①表示具体性质或关系的谓词称为谓词常项,用大写字母F,G,H…等表示,如F:表示是大学生§②表示抽象或泛指的谓词称为谓词变项,也用大写字母F,G,H…等表示.个体变项x具有性质F,记F(x);个体变项x,y具有关系L,记L(x,y)等.§注: F,G,H等表示谓词常项还是变项取决于上下文.§§§2.4 前束范式§2.5 一阶逻辑推理理论本章小结2.1 一阶逻辑命题符号化2.1 一阶逻辑命题符号化2.1 一阶逻辑命题符号化2.1 一阶逻辑命题符号化§2.1.2 命题函数设H是谓词“能够到达山顶”,a表示个体王华,t表示老虎,c表示汽车,则H(a), H(t),H(c)分别表示不同的命题.共同形式为H(x),当x取a,t,c时,有上述表示.同理,若L(x,y)表示“x小于y”,则L(2,3)表示一个真命题,L(5,1)表示一个假命题.2.1 一阶逻辑命题符号化§2.1.2 命题函数(续)一个原子命题用一个谓词P和n 个有序的个体变元x1 ,…,x n表示成P(x1,…,x n),它是以个体变项的个体域为定义域, 以{0,1}为值域的n元函数, 称为命题函数(或谓词命名式)简称为谓词; 谓词中个体变项的个数成为元数, P称为n 元谓词; 不带个体变项的谓词称为0元谓词.由一个或n个简单命题函数以及逻辑联结词组成的表达式称为复合命题函数.2.1 一阶逻辑命题符号化§2.1.2 命题函数(续)例1:…x是素数‟中x是个体,谓词…是素数‟记为P,则可写为P(x).其中:x 表示不确定的个体,称为个体变元.注意:①P(x)的真值随x而变,它对某些x 可能为真,对某些x可能为假.所以,P(x)是命题函数,而不是命题逻辑中要求的非真即假的命题.②n元谓词中个体的顺序是重要的,顺序变了谓词公式的含义也变了.例如, P(x,y,z)≡…x-y=z’≠…y-x=z’≡P(y,x,z)2.1 一阶逻辑命题符号化§2.1.2 命题函数(续)§谓词概念是命题概念的扩充与深化考虑谓词: P(x,y,z)≡…x-y=z‟.若定义P1(y,z)≡P(3,y,z)≡…3-y=z’;P2(z)≡P(3,2,z)≡…3-2=z’;P3≡P(3,2,1)≡…3-2=1’;则P(x,y,z),P1(y,z),P2(z)分别是3元,2元,1元谓词,它们都不是命题逻辑中的命题,而P3 是0元谓词,是命题逻辑中的命题.由此可见,谓词概念是命题概念的扩充与深化.例: 教材P56例4.12.1 一阶逻辑命题符号化§2.1.2 命题函数(续)注意: 命题函数的值取决于个体变元的取值范围, 即个体域.例1: R(x)表示“x是大学生”如果x的取值范围是大学班级里的学生, 则R(x)是永真式; 如果x的讨论范围是某中学班级里的学生, 则R(x)是永假式; 如果x的讨论范围是电影院的观众, 则对某些观众R(x)为真, 对另外一些观众R(x)为假.2.1 一阶逻辑命题符号化§2.1.2 命题函数(续)例2: (P(x,y)∧P(y,z))→P(x,z)若P(x,y)解释为“x小于y”, 当x,y,z在实数范围内取值时, 是永真式; 若P(x,y)解释为“x为y 的儿子”, 当x,y,z为人时, 则是永假式; 若P(x,y)解释为“x距离y为10米”, 如果x,y,z取地面上的房子, 则可能为真, 也可能为假.2.1 一阶逻辑命题符号化§2.1.3 量词①全称量词: ∀x, 表示并读作:…对一切x’; ∀x P(x), 表示并读作: …对一切x,P(x)是真‟ (称x被全称量化).②存在量词: ∃x, 表示并读作:…存在一个x’;∃x P(x), 表示并读作: …存在一个x,P(x)是真‟ (称x 被存在量化).例1. 当论述域为实数集R时, ∀x(x<x+1)表示对一切实数x, x<x+1为真.例2. 当论述域为实数集R时, ∃y(y=3)表示存在一个实数y, y=3为真.2.1 一阶逻辑命题符号化§2.1.3 量词例3: 令S(x,y,z)≡…x-y=z‟; M(x,y,z)≡…xy=z‟;(1)用谓词表示: …任何整数减去0, 其结果是原整数‟.解:答案为: ∀xS(x,0,x).(2)用谓词表示:…对所有x, 所有y,xy=y‟.解:答案为: ∀x∀yM(x,y,y).2.1 一阶逻辑命题符号化§2.1.3 量词§谓词F(x)变命题的两种途径①令命题变元x取定一个a值,所得F(a)是命题.②将谓词量化,如∃xF(x),∀xF(x)都是命题(可取非真即假的真值).例如F(x)≡…x是素数‟不是命题,因其真值随x而变,但∀xF(x)是命题,因它有唯一的真值…假‟;∃xF(x)也是命题,因它有唯一的真值…真‟.2.1 一阶逻辑命题符号化§2.1.3 量词§量化后所得命题的真值与论域有关,即随个体域不同而可能不同.例1.∃y(y=3)当论述域为正整数集N时为真;而当论述域为负整数集-N时为假.例2.∀x(x>0)当论述域为N时为真;而当论述域为R时为假.2.1 一阶逻辑命题符号化§2.1.4 全总个体域与特性谓词的概念★令D(x)表示x是要死的;F(x)表示x是怕死①当论域为全人类时,…人总是要死的‟译为∀xD(x),…有些人怕死‟译为∃xF(x).②当论域为全总个体域时,需引入一个新的谓词,将研究的对象分离出来,这个谓词称为特性谓词.这样它们分别译为∀x(M(x)→D(x)),∃x(M(x)∧F(x)),其中,M(x)表示x是人.苏格拉底三段论可符号化为: (∀x(M(x)→D(x))∧M(s))→D(s),其中s表示特定的一个人:苏格拉底.2.1 一阶逻辑命题符号化§2.1.4 全总个体域与特性谓词的概念§特性谓词的加入规则:①全称量词之后特性谓词作蕴涵式前件加入;②存在量词之后特性谓词作合取项加入.例如,令P(x)表示x为素数…任何两个素数之和是一个素数‟可符号化为: ∀x∀y(P(x)∧P(y)→P(x+y));…存在两个素数其和是素数‟ 可符号化为: ∃x∃y(P(x)∧P(y)∧P(x+y)).2.1 一阶逻辑命题符号化§2.1.5 一阶逻辑的翻译(符号化)把一个文字叙述的陈述句用谓词公式表示出来的过程称为一阶逻辑翻译或符号化,其步骤如下:①正确理解给定命题, 必要时可适当加以改叙使其中的原子命题的关系更明显.②把每个原子命题分解成个体、谓词和量词, 在全总个体域中讨论时要给出特性谓词.③找出适当量词, 注意∀后跟蕴涵式, ∃后跟合取式2.1 一阶逻辑命题符号化§2.1.5 一阶逻辑的翻译(符号化)(1)令T(x):x是火车; C(x):x是卡车;Q(x,y):x比y快,则…某些卡车慢于所有火车,但至少有一辆火车快于每辆卡车‟可符号化为∃y(C(y)∧∀x(T(x)→Q(x,y)))∧∃u(T(u)∧∀v(C(v)→Q(u,v))).(2)令论述域为全人类; B(x):x步行;M(x):x骑马; C(x):x乘车; K(x):x口渴; Q(x):x喝泉水. 则…所有步行的,骑马的或乘车的人,凡是口渴的都喝泉水‟可符号化为∀x(((B(x)∨M(x)∨C(x))∧(K(x))→Q(x)).2.1 一阶逻辑命题符号化§2.1.5 一阶逻辑的翻译(符号化)(3)令F(x):x是大学生;G(x):x是文科生; H(x):x是理科生。
02一阶逻辑

x约束出现2次,y约束出现2次,自由出现1次,
z自由出现1次。
(3) (x)(P(x) (x)Q(x, z)(y)R(x, y))Q(x, y) ; 解:(x)Q(x, z)中x是作用变元,的辖域为Q(x,z),
其中 x 约束出现,z自由出现;(y)R(x, y)中,y是
作用变元,的辖域为R(x, y),其中y约束出现,x自 由出现; 在(x)(P(x)(x) Q(x,z)(y)R(x, y)) 中, 作用变元为x,的作用域为(P(x)(x)Q(x, z) (y)R(x, y)), 但Q(x, z)中的x不是的作用变元,x, y 在整个公式中,x约束出现3次,自由出现1次, y约束出现1次,自由出现1次,z自由出现1次。
由原子公式、联结词、量词及括号组成的字符串,
但最外层括号可以省略。
二、谓词公式的改写 在谓词公式中,我们还用到以下概念。
指导变元及作用域
在谓词公式中,形如(x)A(x)或(x)A(x)的 部分,叫做公式的约束部分。
量词,后面的x叫做量词的作用变元,或
指导变元,A(x)叫做量词的作用域。 在作用域中,x的一切出现为约束出现,非 约束出现的其它变元叫自由出现变元。
为了在命题演算中,反映命题的内在联系, 常常要将简单命题分解成 个体词、谓词、量词 等,并对它们的形式结构及逻辑关系加以研究,总 结出正确的推理形式和规则,这就是本章一阶逻辑
要研2.1 一阶逻辑基本概念 §2.2 一阶逻辑合式公式及解释 §2.3 一阶逻辑等值式及前束范式
变项符号不同的变项符号去代替,且处处代替。
换名规则与代替规则可避免有的个体变项既 可以约束出现,又可以自由出现。
例4.试对下列公式换名或代替。
(1) (x)(P(x)(y)R (x,y)) ;
一阶逻辑

11
与谓词相关的概念 : 谓词常项:表示具体性质或关系的谓词 例如:可以用F表示“…是无理数“
谓词变项:表示抽象的或泛指的谓词
谓词常项和变项都用大写英文字母F,G, H,…表示 F,G,H…表示的是谓词常项还是谓词变项 要根据上下文而定
12
F(x): 表示x具有性质F 如F(x):x是学生 F(x,y) :表示x和y具有关系F 如F(x,y) :x和y是同学
15
谓词与命题的关系
一般说来,谓词P(x1,x2,…,xn) 不是命题,它的真值无法确定 为了使它成为命题,必须
指定某一谓词常项代替P 指定n个个体常项a1,a2,…,an分 别代替n个个体变项x1,x2,…,xn
16
例如,L(x,y)是一个2元谓词,它不 是命题 当令L(x,y)表示“x小于y”之后, 该谓词中的谓词部分便成为了常项, 但它不是命题 当取a为2,b为3时,L(a,b)才是 命题,并且是真命题 同理,当取c为2,d为1时,L(c,d) 为假命题
现在假设个体域D是全总个体域 这时,xF(x)和xG(x)不能表达原命题 的意义,因为 1. 所有的人要死的。 2. 有的人活百岁以上。 变成了 1. 所有的个体要死的。 变严格 2. 有的个体活百岁以上。 变松垮
27Leabharlann 个体域D是全总个体域时,命题应转述为 1. 所有的人要死的。 2. 有的人活百岁以上。 1. 对所有个体而言,如果它是人,则它是要死 的。 2. 存在着个体,它是人并且活百岁以上。
一阶逻辑也称谓词逻辑
4
第2章 一阶逻辑
本章学习: 一阶逻辑的基本概念 一阶逻辑合式公式及解释 一阶逻辑等值式 一阶逻辑推理理论
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
命题逻辑和一阶逻辑
逻辑学是哲学中的一个重要分支,它主要研究思维的规律,探讨
推理和证明的方法。
命题逻辑和一阶逻辑是逻辑学最基础的两种逻辑
系统,下面我们就来一一探讨。
1. 命题逻辑
命题逻辑是研究命题及其关系的逻辑系统。
命题是一个陈述性语句,可以是真、假或未知的。
命题逻辑包括命题合取、命题析取、命
题蕴含和命题等价等一系列逻辑运算符。
正是这些运算符使得我们能
够对不同的命题进行组合和推理,并得出新的结论。
例如,如果我们有两个命题p和q,它们有如下的真假情况:
p:今天是周一 => 真
q:天气晴朗 => 真
命题合取就是将这两个命题用“并且”的方式联系起来,得到新
的命题。
“今天是周一并且天气晴朗”是一个命题,它的真假情况是:p ∧ q:今天是周一并且天气晴朗 => 真
2. 一阶逻辑
一阶逻辑是研究复杂命题及其关系的逻辑系统。
它扩展了命题逻辑,引入了量词和变元等概念。
在一阶逻辑中,我们可以用变元代表
一个个体,用谓词表示个体的性质或关系,用量词表示个体的范围,
用量词的限定揭示个体之间的关系,有助于我们表达更加复杂的命题。
例如,如果我们需要表达“对于所有的人而言,如果他今天没有
打电话,那么他也没有发短信”,可以用一阶逻辑的方式表示成:∀x ( ¬Phone(x) → ¬Msg(x) )
其中,x是变元,表示一个人;Phone(x)表示x今天是否打电话;Msg(x)表示x今天是否发短信;→表示蕴含;¬表示非;∀表示全称量词。
可以看出,一阶逻辑比命题逻辑更加强大,能够灵活地表达更加
复杂的命题,因此在各个领域都有广泛的应用。
例如,在计算机科学
中,语义网、人工智能、数据库等都需要使用一阶逻辑进行描述和推理。
综上所述,命题逻辑和一阶逻辑都是逻辑学中的基础理论,其分别适用于不同的问题领域。
熟练掌握这两种逻辑系统,对于我们的推理和思考能力都有很大的帮助。
