九年级数学画相似图形
最新湘教版九年级数学(初三)上册3.6位似 第1课时位似图形的概念及画法课件

随堂练习
4.如图,E是平行四边形ABCD的边BC延长线上的一点,连接
AE交CD于点F,则图中位似图形共有( C )
A.1对 B.2对 C.3对 D.4对
随堂练习
5.如图,矩形ABCD与矩形A′B′C′D′是位似图形,A是位似 中心,已知矩形ABCD的周长为24,BB′=4,DD′=2,则矩 形ABCD的面积为___3_2_____.
位似图形,若OA∶OA′=2∶3,则四边形ABCD与四边
形A′B′C′D′的面积比为( A )
A.4∶9 B.2∶5 C.2∶3 D.3∶2
随堂练习
3.下列说法不正确的是( B )
A.位似图形一定是相似图形 B.相似图形不一定是位似图形 C.位似图形上任意一对对应点到位似中心的距离之比等 于相似比 D.位似图形中每组对应点所在的直线必相互平行
July 12, 2020
要求的图形.
课程讲授
2 位似图形的画法
问题2:如果在四边形外任选一个点 O,分别在 OA、
OB、OC、OD 的反向延长线上取 A′ 、B′ 、C′、D′,
使得OA' = OB' = OC' = OD' = 1 呢?如果点 O 取在四
OA OB OC OD 2
边形 ABCD 内部呢?分别画出这时得到的图形.
丽生,活感像谢春你天的一阅样读阳。光,心情像桃花一样美 6Ju、莫ly吾愁1生前2,也路20有无20涯知7/,已12而,/2知天02也下0 无 谁涯人。不识9时君5。分99时时55分分91时2-5Ju分l-1220-7J.u1l2-2.20072.102.2020 丽,感谢你的阅读。 76、纸人生上生命得贵太来相过终知短觉,暂浅何,,用今绝金天知 与 放此钱弃事。了要明20躬天.7.行不12。一20定2.07能..71.得212到02.0。7..719.2时1。2522分00.792.时01年25。分7月210212-2J0日u年l星-72月0期71日.122日二.2星〇02期二0日〇
27.3+第1课时+位似图形的概念及画法 课件+-2023--2024学年人教版数学九年级下册
练习1:如何判断一组图形是位似图形呢?下面各组图 形是位似图形吗?
答:都是位似图形 总结:同时满足这两个条件的图形叫做位似图 形.两个条件缺一不可。 一是:两个相似图形 二是:对应顶点的连线相交
于一点.
练习2:画出下列图形的位似中心.
P O
知识点 2 位似图形的性质
合作探究
活动1:位似图形和相似图形有怎样的区别与联系呢?
情境引入
在日常生活中,经常见到这样的相似图形.
(1)放映幻灯片时,通过光源,
(2)照相时,摄影师通过照
把幻灯片上的图形放大到
屏幕上。
相机,把建筑物 的形象缩
小在底片上。
第二十七章 相 似
27.3 位 似
第1课时 位似图形的概念及画法
学习目标
1.理解位似图形的概念及相似比.
图 形 2.能够按照要求利用位似图形进行放大或缩小.
A
A'
C
C'
O
B
B'
练习:如图,四边形木框 ABCD 在灯泡 O 发出的光照
射下形成影子四边形 A′B′C′D′,若 OB∶OB′=1∶2,
则四边形 ABCD 与四边形 A′B′C′D′ 的面积比为 ( D )
A.4∶1
B. 2∶1 C.1∶ 2 D.1∶4
A'
A
灯泡 O
B B'
D
C
D'
C'
知识点 3 位似图形的画法
A' D'
D
A'B'C'D' 就是所要求的图O 形. B'
B
C'
C
(2)对于上面的问题,还有其他方法吗?如果在四边
华师版九年级数学上册第23章 图形的相似5 位似图形

2.下列关于位似图形的三个表述中正确的有( C ) ①相似图形一定是位似图形,位似图形一定是相似图形; ②位似图形一定有位似中心; ③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同 一个点,那么这两个图形是位似图形. A.0个 B.1个 C.2个 D.3个
3.如图,△OAB 和△OCD 是位似图形,AB 与 CD 平行吗?为什么?
A A′
D′ D O C C′
B B′
A
C′
B
O
B′
C
A′
知识要点2
位似图形的性质 位似图形上任意一对对应点到位似中心的距离之比等于相似比.
典例讲解
1
例1..把四边形 ABCD 缩小到原来的 2. (1) 在四边形外任选一点 O (如图);
(2) 分别在线段 OA、OB、OC、OD 上
A
取点 A' 、B' 、 C' 、D' ,使得;
OA' OB' OC' OD' 1
B
D
A'
OA OB OC OD 2
B' D'
C
(3) 顺次连接点 A' 、B' 、C' 、D' ,所
O
C'
得四边形 A' B' C' D' 就是所要求的图形
知识要点3
画位似图形的一般步骤 ① 确定位似中心; ② 分别连接并延长位似中心和能代表原图的关键点; ③ 根据相似比,确定能代表所作的位似图形的关键点; ④ 顺次连接上述各点,得到放大或缩小的图形.
第23章 图形的相似
位似图形
活动一 照相机把人物的影像缩小到底片上,这种相似有什么特征?
九年级数学下册272《相似三角形》PPT课件

3. 解等式求出三角形的面积。
注意事项:在解题过程中,要确保已知的三边长度是准 确的,避免因为数据不准确而导致错误。同时,要注意 选择合适的公式或方法进行计算。
典型例题四:综合应用举例
• 解题思路:综合运用相似三角形的性质和判定方法,解决 复杂的实际问题。
典型例题四:综合应用举例
解题步骤 1. 分析问题,确定需要使用的相似三角形的性质和判定方法;
利用相似三角形的面积比等于相似比的平 方性质,求解面积问题 通过已知三角形的面积和相似比,计算另 一个三角形的面积 结合图形变换和面积公式,利用相似三角 形解决复杂面积问题
利用相似三角形解决综合问题
综合运用相似三角形 的性质,解决涉及线 段、角度和面积的复 杂问题
结合多种数学方法, 如代数运算、方程求 解等,提高解决问题 的效率
通过分析问题的条件 ,选择合适的相似三 角形性质和定理进行 求解
04
典型例题分析与解题思路展示
典型例题一:已知两边求第三边长度
解题思路:利用相似三角形的性质, 即对应边成比例,可以通过已知的两
边长度求出第三边的长度。
解题步骤
2. 利用相似三角形的性质列出比例式 ;
3. 解比例式求出第三边的长度。
1. 确定已知的两边和夹角;
注意事项:在解题过程中,要确保已 知的两边和夹角是对应的,避免因为 数据不对应而导致错误。
典型例题二:已知两角求第三角大小
01
解题思路:根据三角形内角和为180°的性质,可以通过 已知的两角求出第三角的大小。
04
2. 利用三角形内角和为180°的性质列出等式;
02
解题步骤
对应角相等,对应边成比例的两 个三角形叫做相似三角形。
2018_2019学年九年级数学下册第二十七章相似27.3位似第1课时位似图形的概念及画法课件(新版)新人教版

并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是
( )C
①△ABC与△DEF是位似图形;
②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1∶2; ④△ABC与△DEF的面积比为4∶1.
图K-14-5
A.1
B.2
C.3
D.4
[解析] C 根据位似的性质得出:①△ABC与△DEF是位似图形,② △ABC与△DEF是相似图形.∵D,E,F分别是OA,OB,OC的中点, ∴△ABC与△DEF的相似比为2∶1, ∴△ABC与△DEF的周长比为2∶1,故③错误.根据面积比等于相似
图K-14-10
解:(1)(2)如图所示.
12.如图K-14-11,矩形ABCD与矩形AB′C′D′是位似图 形,点A为位似中心,已知矩形ABCD的周长为24,BB′=4, DD′=2,求AB,AD的长.
图K-14-11
解:∵矩形 ABCD 的周长为 24,∴AB+AD=12.设 AB=x, 则 AD=12-x,AB′=x+4,AD′=14-x. ∵矩形 ABCD 与矩形 AB′C′D′是位似图形, ∴AABB′=AADD′,即x+x 4=1124- -xx, 解得 x=8,∴AB=8,AD=12-8=4.
链接听课例4归纳总结
图K-14-9
解:情况 1:如图所示,分别连接 OA,OB,OC,分别取线段 OA,OB,OC 的中点 A′,
B′,C′,顺次连接点 A′,B′,C′,则△A′B′C′即为所要求作的图形.
情况 2:如图所示,分别连接 AO,BO,CO,在线段 AO,BO,CO 的延长线上分别截
链接听课例4归纳总结
图K-14-12
解:(1)如图所示. (2)△ABC与△A1B1C1的相似比为1∶2. (3)如图所示
九年级数学上册 图形的相似位似图形的概念和画法导学案

位似图形的概念和画法【学习目标】1.了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位似图形的性质.2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小.【学习重点】位似图形的有关概念、性质与作图.【学习难点】利用位似将一个图形放大或缩小。
情景导入生成问题情景引入:1.在日常生活中,我们经常见到下面所给的这样一类相似的图形,它们有什么特征?答:这样的放大或缩小,没有改变图形的形状,经过放大或缩小的图形与原图形是相似的.2.图中多边形相似吗?观察下面的四个图,你发现每个图中的两个多边形各对应点的连线有什么特征?答:每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点.自学互研生成能力知识模块一位似图形的有关概念、性质阅读教材P95~P96“议一议”,完成下面的内容:(1)位似图形:如果两个多边形不仅相似,而且对应顶点的连线交于一点,对应边平行或重合,那么这样的两个图形叫作位似图形,这个点叫作位似中心,这时的相似比又称为位似比.(2)掌握位似图形概念,需注意:①位似是一种具有特殊位置关系的相似,所以两个图形是位似图形,必定是相似图形,而相似图形不一定是位似图形;②两个位似图形的位似中心只有一个;③两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧;④位似比就是相似比.利用位似图形的定义可判断两个图形是否位似.(3)位似图形上任意一对对应点到位似中心的距离比等于位似比(相似比).(4)两个位似图形特征是:每对位似对应点与位似中心共线.【例】如图D,E分别是AB,AC上的点.(1)如果DE∥BC,那么△ADE和△ABC是位似图形吗?为什么?(2)如果△ADE 和△ABC 是位似图形,那么DE ∥BC 吗?为什么?解:(1)△ADE 和△ABC 是位似图形.理由是:∵DE ∥BC ,∴∠ADE =∠B ,∠AED =∠C .∴△ADE ∽△ABC .又∵点A 是△ADE 和△ABC 的公共点,点D 和点B 是对应点,点E 和点C 是对应点,直线BD 与CE 交于点A , ∴△ADE 和△ABC 是位似图形.(2)DE ∥BC .理由是:∵△ADE 和△ABC 是位似图形.∴△ADE ∽△ABC .∴∠ADE =∠B .∴DE ∥BC .知识模块二 利用位似将一个图形放大或缩小阅读教材P96后两段~P97,完成下面的内容:【变例】 把图中的四边形AB CD 缩小到原来的13. 解:作法一:①在四边形ABCD 外任取一点O ;②过点O 分别作射线OA ,OB ,O C ,OD ;③分别在射线OA ,OB ,OC ,OD 上取点A′、B′、C′、D′,使得OA ′OA =OB ′OB =OC ′OC =OD ′OD =13; ④顺次连接A′B′、B′C′、C′D′、D′A′,得到四边形A′B′C′D′,如左栏图1.作法二:①在四边形ABCD 外任取一点O ;②过点O 分别作射线OA ,OB ,OC ,OD ;③分别在射线OA ,OB ,OC ,OD 的反向延长线上取点A′、B′、C′、D′,使得OA ′OA =OB ′OB =OC ′OC =OD′OD =13; ④顺次连接A′B′、B′C′、C′D′、D′A′,得到所要画的四边形A′B′C′D′,如左栏图2.作法三:①在四边形ABCD 内任取一点O ; ②过点O 分别作射线OA ,OB ,OC ,OD ;③分别在射线OA ,OB ,OC ,OD 上取点A′B′C′D′,使得OA ′OA =OB ′OB =OC ′OC =OD ′OD; ④顺次连接A′B′、B′C′、C′D′、D′A′,取得所要画的四边形A′B′C′D′,如左栏图3.点拨:利用位似将图形放大或缩小的步骤①首先确定位似中心,位似中心的位置可随意选择;②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;④符合要求的图形不唯一,所作的图形与所确定的位似中心的位置有关.问题:当点O 在四边形ABCD 的一条边上或在四边形ABCD 的一个顶点上,或在四边形ABCD 内时,怎样画? 交流展示 生成新知1.将阅读教材时“生成的问题”和通过“自学互研”得出的“结论”展示在各小组的小黑板上.并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.知识模块一 位似图形的有关概念、性质知识模块二 利用位似将一个图形放大或缩小检测反馈 达成目标1.下图中的两个图形不是位似图形的是( D )2.图中的两个四边形是位似图形,它们的位似中心是( D )A .点MB .点NC .点OD .点P,(第2题图)) ,(第3题图))3.如图,两个位似图形△ABO和△A′B′O,若OA∶OA′=3∶1,则正确的是( A)A.AB∶A′B′=3∶1 B.AA′∶BB′=AB∶AB′C.OA∶OB′=2∶1 D.OA∶OB′=3∶14.如图,请在8×8的网格中,以点O为位似中心,画出△ABC的一个位似图形△A′B′C′,使△A′B′C′与△ABC的位似比为2∶1.解:略课后反思查漏补缺1.收获:________________________________________________________________________2.存在困惑:________________________________________________________________________。
北师版初三数学上册第四章相似图形知识点讲解

九年级(上)第四章图形的相像(1)形态一样的图形叫相像图形,在相像多边形中,最简洁的是相像三角形.(2) 相像多边形:假如两个边数一样的多边形的对应角相等,对应边成比例,这两个多边形叫做相像多 边形.相像多边形对应边长度的比叫做相像比.一.成比例线段(1)线段的比假如选用同一单位量得两条线段b a ,的长度分别为n m ,,那么就说这两条线段的比是nmb a =,或写成n m b a ::=.注:在求线段比时,线段单位要统一。
(2)成比例线段在四条线段d c b a ,,,中,假如b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段,简称比例线段.注:①比例线段是有依次的,假如说a ,d c b ,,成比例,那么应得比例式为:b a =dc . ②()a ca b c d b d==在比例式::中,a 、d 叫比例外项,b 、c 叫比例内项,假如b=c ,即 a b bd =::那么b 叫做a 、d 的比例中项, 此时有2b ad =。
③推断给定的四条线段是否成比例的方法:第一排:现将四条线段的长度统一单位,再按大小依次排列好;第二算:分别算出前两条线的长度之比与后两条线段的长度之比;第三判:若两个比相等,则这四条线段是成比例线段,否则不是(3)比例的性质(留意性质立的条件:分母不能为0) 根本性质:① a:b=c:d 则有 ad=bc (两外项之积等于两内向之积);② ②2::a b b c b a c =⇔=⋅.注:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如bc ad =,除了可化为d c b a ::=,还可化为d b c a ::=,b a d c ::=,c a d b ::=,c d a b ::=,b d a c ::=,a b c d ::=,a c b d ::=.(2) 更比性质(交换比例的内项或外项):()()()a bc d a c d cb d b ad bc a ⎧=⎪⎪⎪=⇔=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项(3)合、分比性质:a c abcd b d b d ±±=⇔=. (4)等比性质:假如)0(≠++++====n f d b nm f e d c b a ,那么b an f d b m e c a =++++++++ . 注:①此性质的证明运用了“设k 法”(即引入新的参数k )这样可以削减未知数的个数,这种方法是有关比例计算变形中一种常用方法.②应用等比性质时,要考虑到分母是否为零.③ 可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.如:ba f db ec a f ed c b a fe d c b a =+-+-⇒=--=⇒==32323322;其中032≠+-f d b . (4)比例题常用的方法有:比例合分比法,比例等比法,设参法,连等设k 法,消元法二,平行线分线段成比例(1)平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例已知AD ∥BE ∥CF,可得AB DE AB DE BC EF BC EF AB BCBC EF AC DF AB DE AC DF DE EF=====或或或或等. 留意:是所截的线段成比例,而跟平行线无关,所以比例线段中不行能 有AD,BE,CF 的比例关系(2)黄金分割:把线段AB 分成两条线段)(,BC AC BC AC >,且使AC 是BC AB 和的比例中项,即2AC AB BC =⋅,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中AB AC 215-=≈0.618AB .即12AC BC AB AC == 简记为:长短=全长注:黄金三角形:顶角是360的等腰三角形。
2023九年级数学下册第二十七章相似27.3位似第1课时位似图形的概念及画法教案(新版)新人教版

课后拓展
1.拓展内容:
-阅读材料:《数学的故事》中关于几何变换的起源和发展,了解位似变换在数学史上的地位。
-视频资源:寻找与位似图形相关的教学视频,如介绍位似变换的基本概念、性质和应用实例。
-学生通过观察生活中的位似图形,将所学知识应用到实际中,提高解决问题的能力。
-鼓励学生针对位似图形的特定性质或应用进行深入研究,撰写研究报告,培养探究精神。
-教师提供必要的指导和帮助,如推荐阅读材料、解答学生在自主学习中遇到的疑问等。
-教师组织学生开展课后讨论活动,让学生分享自己的学习心得和研究成果,促进交流与合作。
三、实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与位似图形相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作,如使用几何画板绘制位似图形,演示位似的基本原理。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
四、学生小组讨论(用时10分钟)
2.位似比的概念及其计算方法;
3.位似图形的画法,包括位似中心、位似向量、位似图形的作图方法;
4.应用位似变换解决实际问题。
本节课将结合新人教版教材,以生活实例为导入,让学生在实际操作中体会位似图形的特点,培养他们的观察能力和空间想象能力,从而提高解决几何问题的能力。
核心素养目标
本节课旨在培养学生的以下数学核心素养:
2023九年级数学下册第二十七章相似27.3位似第1课时位似图形的概念及画法教案(新版)新人教版
学校
授课教师
部编数学九年级下册专题14网格中画相似(解析版)含答案
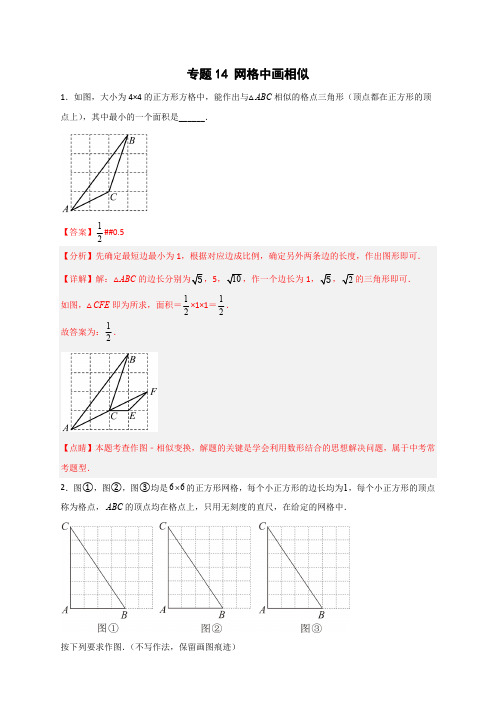
专题14 网格中画相似1.如图,大小为4×4的正方形方格中,能作出与△ABC 相似的格点三角形(顶点都在正方形的顶点上),其中最小的一个面积是______.【答案】12##0.5【点睛】本题考查作图﹣相似变换,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.2.图①,图②,图③均是66´的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,ABC 的顶点均在格点上,只用无刻度的直尺,在给定的网格中.按下列要求作图.(不写作法,保留画图痕迹)(1)在图①中,在BC 上画一点D ,使ABD ACD S S =V V ;(2)在图②中,在BC 上画一点E ,使ABE S V :2ACE S =V :3;(3)在图③中,在ABC 内画一点F ,使ACF S △:ABF S △:2BCF S =V :3:3.(2)在图②中,点E 即为所求;点C 下移三个单位得到点连接MN ,得到CME ∽△△32CE CM BE BN ==∴,∴ABE S V :2ACE S =V :3(3)在图③中,点F 即为所求.由图可知,6AC =,AB =12ABC S =∴△,∵ACF S △:ABF S △:BCF S =V 21238ACF S =´=∴△,ABF S =△【点睛】本题考查作图-应用与设计作图,三角形相似性质,三角形的面积等知识,解题的关键是理解题意,学会利用数形结合的思想解决问题,属于中考常考题型.3.(1)如图,4×4的正方形方格中,△ABC 的顶点A 、B 、C 在小正方形的顶点上.请在图中画一个△A1B1C1,使△A1B1C1∽△ABC(相似比不为1),且点A1、B1、C1都在小正方形的顶点上.并将此三角形涂上阴影(2)按要求作图,不要求写作法,但要保留作图痕迹:我们知道,三角形具有性质:三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高所在直线相交于一点.请运用上述性质,只用直尺(不带刻度)作图.①如图1,在平行四边形ABCD中,E为CD的中点,作BC的中点F.②如图2,在由小正方形组成的4×3的网格中,△ABC的顶点都在小正方形的顶点上,作△ABC的高AH(2)①如图1,点F 为所作;理由:因为三角形的三条中线交于同一点,四边形ABCD 是平行四边形,∴O 是BD 的中点,∵E 是CD 的中点,根据三条中线交于同一点,连接BE 交AC 于P ,则点P 为三条中线的交点,作射线DP 交DP 于点F ,则点F 为BC 的中点;②如图2,找到格点D ,过A 点作AD 垂直AB ,再平移DA 得到CE ,则CE ⊥AB ,接着作MN 垂直AC ,平移MN 得到BF ,则BF ⊥AC ,BF 与CE 的交点O 为△ABC 的垂心,所以延长AO 交BC 于H ,则AH ⊥BC ,AH 为所作.理由:∵ABG DAKV V ≌∴GAB ADKÐ=Ð90GAB DAK ADK DAK \Ð+Ð=Ð+Ð=°∴90BAD Ð=°∴BA AD^平移AD 至CJ ,并延长,交AB 于点E ,∴CE AB^同理作出BF AC ^,,BF CE 交于点O根据三角形三条高所在的直线交于同一点,延长AO 交BC 于点H ,则AH 即为所求.【点睛】本题考查了画相似三角形:根据相似三角形的判定条件作为作图的依据.比较简单的是把原三角形的三边对应的缩小或放大一定的比例即可得到对应的相似图形,也考查了三角形的重心和平行四边形的性质.4.在4*4的方格中,ABC V 的三个顶点都在格点上.(1)在图1中画出与ABC V 成轴对称且与ABC V 有公共边的格点三角形(画出一个即可);(2)将图2中画一个与ABC V 相似的三角形.【答案】(1)见解析;(2)见解析.【分析】(1)选取AC 所在的直线为对称轴作图即可;(2)保证每条边方向一致,且边长减小为原来的一半作图即可.【详解】(1)解:如下图所示,AB C ¢V 即为所求作的三角形;(答案不唯一)(2)如下图所示,DEF V 即为所求作的三角形;【点睛】本题考查轴对称作图与作相似图形,掌握两个图形关于某条直线对称的性质与相似三角形的性质是解题的关键.5.如图,ABC D 是正方形网格中的格点三角形(顶点在格点上),请在正方形网格上按下列要求画一个格点三角形与ABC D 相似.(1)在图甲中画△111A B C ,使得△111A B C 的周长是ABC D 的周长的2倍;(2)在图乙中画出△222A B C ,使得△222A B C 的面积是ABC D 的面积的2倍.(1)A B C,即为所求;解:如图所示:△111(2)A B C,即为所求.解:如图所示:△222【点睛】此题主要考查了相似变换,正确得出对应三角形的边长是解题关键.6.如图,在8×8的正方形网格中,△ABC是格点三角形,请按以下要求作图.(1)在图1中画出格点△EDP,使得△EDP∽△ABC,且面积比为1;2(2)在图2中将△ABC绕着某格点逆向时针旋转90°得到格点△PFG,其中C与P对应.【答案】(1)见解析(2)见解析【分析】(1)直接利用位似图形的性质,结合位似中心得出答案;(2)直接利用旋转的性质得出对应点位置进而得出答案.(1)如图,(案不唯一)(2)如图,【点睛】此题主要考查了位似变换以及旋转变换,根据题意得出对应点位置是解题关键.7.如图,在74´方格纸中,点A,B,C都在格点上(△ABC称为格点三角形,即格点△ABC),用无刻度直尺作图.(1)在图1中的线段AC上找一个点D,使25CD AC=;(2)在图2中作一个格点△CEF,使△CEF与△ABC相似.【答案】(1)见解析(2)见解析【分析】(1)根据“8字形”相似,可得CD:AD=2:3,从而得出点D的位置;(2)根据∠ACB=90°,AC=2BC,即可画出△CEF.【详解】(1)解:如图1所示,点D即为所求,(2)如图2所示,△CEF即为所求,【点睛】本题主要考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.8.如图,在7×6的正方形网格中,点A、B、C、D在格点(小正方形的顶点)上,从点A、B、C、D四点中任取三点,两两连接,得到一个三角形,请在所得的所有三角形中,写出互为相似的两个三角形及它们的相似比.∵AB=2221+=5,AC=∴55225ADBD==,ABCD=∴52 AD AB BDBD CD BC===,∴△ABD∽△DCB,相似比9.如图,在5×5的边长为1小的正方形的网格中,如图1△ABC和△DEF都是格点三角形(即三角形的各顶点都在小正方形的顶点上).(1)判断:△ABC与△DEF是否相似?并说明理由;(2)在如图2的正方形网格中,画出与△DEF相似且面积最大的格点三角形,并直接写出其面积.【答案】(1)相似,见解析(2)图见解析,面积为5【点睛】此题考查了作图—相似变换,三角形的面积等知识,解题的关键是掌握相似变换的性质,灵活运用所学知识解决问题.10.按要求作图,无需写作法:图①图②(1)如图①,已知∠AOB,OA=OB,点E 在OB 边上,四边形AEBF 是平行四边形,只用无刻度的直尺在图中画出∠AOB 的平分线.(2)如图②,在边长为1个单位的方格纸上,有△ABC,请作一个格点△DEF,使它与△ABC相似,但相似比不能为1.Q即为所求\11.如图正方形网格中,每个小正方形的边长均为1,只用无刻度的直尺,在给定的网格中按要求画图.(1)在图①中画等腰△ABC ,使得∠CAB =90°;(2)在图②中画等腰△DEF ,使△ABC ∽△DEF :1.10AB =Q ,10AC =,25BC =,5,5,10DE DF EF ===,21AB AC BC DE DF EF \===.\△ABC ∽△DEF ,且相似比为2:1.【点睛】本题考查了勾股定理,相似三角形的性质,掌握勾股定理与相似三角形的性质是解题的关12.图①、图②、图③分别是6×6的正方形网格,网格中每个小正方形的边长均为1,小正方形的顶点称为格点,点A 、B 、C 、D 、E 、P 、Q 、M 、N 均在格点上,仅用无刻度的直尺在下列网格中按要求作图,保留作图痕迹.(1)在图①中,画线段AB 的中点F .(2)在图②中,画CDE V 的中位线GH ,点G 、H 分别在线段CD 、CE 上,并直接写出CGH V 与四边形DEHG 的面积比.(3)在图③中,画PQR V ,点R 在格点上,且PQR V 被线段MN 分成的两部分图形的面积比为1:3.【答案】(1)见解析(2)见解析,面积比为1:3(3)见解析【分析】(1)根据网格的特点,找到,A B 之间单元网格的对角线,交AB 于点F ,则点F 即为所求;(2)根据(1)的方法找到,CD CE 的中点,G H ,连接GH ,根据相似三角形的性质即可求出CGH V 与四边形DEHG 的面积比;(3)根据(2)的结论,可知,只要MN 经过PQR V 的中位线,根据R 在网格上,找到符合题意的点R 即可求解.(1)如图①:13.如图,已知ABC V 和点O .(2)用无刻度的直尺,在AC边上画出点P,使23PAPC=(要求保留作图痕迹,不写作法).(2)解:如图,取网格点E、F,连接EF交AC14.如图,ABC V 是格点三角形(三角形的三个顶点都在格点上),每个小正方形的边长均为1.(1)在图(1)中将ABC V 绕点C 逆时针旋转90°,得到CDE V .(2)在图(2)中找格P ,使以格点P 、C 、B 为顶点的三角形与ABC V 相似,但不全等,请画出一个符合条件的三角形.【答案】(1)见解析(2)见解析【分析】(1)找到旋转角度、旋转中心、旋转方向后可得出各点的对应点,进而顺次连接即可得出答案;(2)可找能使PCB V 是直角三角形且2PB BC =或2PC BC =的P .(1)所作图形如下:(2)【点睛】本题考查旋转作图及相似三角形的性质,明确旋转角度、旋转中心、旋转方向是解本题的关键.15.如图是由边长为1的小正方形构成的69´网格,各个小正方形的顶点叫做格点.△ABC 的顶点在格点上,边BC 上的点D 也是一个格点.仅用无刻度的直尺在定网格中画图.画图过程用虚线表示,画图结果用实线表示.(1)在图1中,先画出AC 的平行线DE 交AB 边于点E ,可在BC 边上画点F ,使ACF BCA ∽△△;(2)在图2中,先在边AB 找点M ,使△MDC 与△MAC 的面积相等,再在AC 上画点N ,使△CDN 的面积是△ABC 的面积的三分之一.【答案】(1)见解析(2)见解析【分析】(1)根据格点特点画出AC 的平行线即可;根据格点特点作MA ⊥AC ,连接MC ,则△AMC16.如图,在6×7的矩形网格中,我们把顶点都在格点上的多边形称为格点多边形,点A,B,C 均在格点上,按下面要求画出格点三角形.(1)在图1中,画一个△ABD,使得△ABD与△ABC全等.(2)在图2中,画一个△ACE,使得S△ABC=3S△ACE,且点E不在边BC上.注:图1,图2在答题纸上.【答案】(1)见解析(2)见解析【分析】(1)运用三角形全等判定定理SSS,在网格上构造△ABD与△ABC全等.(2)△ACE与△ABC共顶点A,因此考虑两个三角形在以A为顶点的高线相等的情况下,构造3CE=BC,从而满足S△ABC=3S△ACE.(1)解:(2)解:【点睛】本题考查三角形全等判定定理,三角形面积计算方法,找到相应的作图依据是解题关键.17.如图,在7×8的正方形网格中,点A,B,C都在格点上,用无刻度直尺完成下列作图:(1)在AC上画点E,使AE=3CE;(2)在AB上画点D,使AD=CD;(3)在BC上画点F(不与B重合),使AF^BC.(4)在AB上画点P,使tan13 ACPÐ=.(2)如图,取格点,P Q,连接PQ,交AC于点M,Q=∥,AP CQ AP CQ\APM CQM∽V VAM AP\=1=MC PQ\=AM MCM,连接根据网格的特点作正方形,同理取中点1则DM是AC的垂直平分线,\=.DA DC(3)如图,方法同(2)作正方形BXYC ,作AZ ∥(4)如图,同方法(3)作正方形,作EE AC ¢^,同方法(连接1KK 交EE ¢于点S ,作射线CS 交AB 于点13,44AE AC CE AC ==Q ,1tan 3SE ACP EC \Ð==.【点睛】本题考查了网格中无刻度直尺作图,相似三角形的性质,正方形的性质,根据相似三角形的性质确定线段的长度是解题的关键.18.如图,在6×10的方格纸ABCD中有一个格点△EFG,请按要求画线段.(1)在图1中,过点O画一条格点线段PQ(端点在格点上),使点P,Q分别落在边AD,BC上,且PQ与FG的一边垂直.(2)在图2中,仅用没有刻度的直尺找出EF上一点M,EG上一点N,连结MN,使△EMN和△EFG的相似比为2:5.(保留作图痕迹)【答案】(1)见解析(2)见解析【分析】(1)根据题意找到格点,P Q,画出线段PQ即可(1)如图所示,PQ即为所求,19.请在如图所示的网格中,运用无刻度直尺作图(保留作图痕迹)(1)在图1中画出线段AB的中垂线AC CB=.(2)如图2,在线段AB上找出点C,使:1:2\点C 即为所求,如图所示:【点睛】本题考查作图—应用与设计作图,相似三角形的应用,解题关键是学会利用数形结合的思想解决问题.20.如图在5×5的网格中,△ABC 的顶点都在格点上.(仅用无刻度的直尺在给定的网格中按要求画图,画图过程用虚线表示,画图结果用实线表示)(1)在图1中画出△ABC 的中线AD ;(2)在图2中画线段CE ,点E 在AB 上,使得ACE S V :BCE S V =2:3;(3)在图3中画出△ABC 的外心点O .【答案】(1)见解析(2)见解析(3)见解析【分析】(1)由题知BO =CO ,取两个格点F 、G 构造CFD BGD △≌△,即可得中点D .(2)由ACE S V :BCE S V =2:3得AE :BE =2∶3,取格点H 、J ,构造△∽△AHE BGE ,且相似比为2∶3,即可得到E 点.(3)由O 为△ABC 的外心知O 为AB 、AC 的中垂线的交点,作出两条中垂线,交点即为O .(1)如图1中,取格点F 、G ,连接FG 交BC 于点D ,线段AD 即为所求.(2)如图2中,取格点H 、J ,连接HJ 交AB 于点E ,线段CE 即为所求.(3)如图3中,取格点K 、L 、M 、N ,连接KL 、MN 交于点O ,则点O 为所求.【点睛】本题考查作图-应用与设计作图,三角形的面积,平行线分线段成比例定理等知识,解题的关键是学会利用数形结合的思想解决问题.21.如图,在6×6的正方形网格中,每个小正方形的边长都为1,点A ,B ,C 均在格点上.请按要求在网格中画图,所画图形的顶点均需在格点上.(1)在图1中以线段AB 为边画一个ABD △,使其与ABC V 相似,但不全等.(2)在图2中画一个EFG V ,使其与ABC V 相似,且面积为8.(2)如图,△EFG 即为所求.【点睛】本题考查作图-相似变换,三角形的面积,全等三角形的判定等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.22.如图,在6×6的正方形网格中,每个小正方形的边长均为1,线段AB 的两个端点均在格点上,按要求完成下列画图(要求:用无刻度的直尺,保留画图痕迹,不要求写出画法).(1)在图①中,在线段AB 上找到一点E ,使AE BE=23;(2)在图②中,画出一个以A 、B 、C 为顶点的三角形,且cos ∠BAC (3)在图③中,画出一个四边形ACBD ,使其既是中心对称图形,又是轴对称图形,且邻边之比为12,C 、D 为格点.【答案】(1)见解析(2)见解析(2)V即为所求;如图所示,ABC(3)如图所示即为所求作【点睛】本题考查了作图-轴对称变换,等腰直角三角形的性质,相似三角形的判定与性质,解决本题的关键是掌握相关知识与性质.。
人教版九年级数学下册课件:27.3第1课时位似图形的概念及画法

C' O
D' B' A'
A
B
D
A
A'
D
C
B B' O D'
C'
C
作图时要注意: ①首先确定位似中心,位似中心的位置可随意选择. ②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点.
③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是 缩小. ④符合要求的图形不唯一,因为所作的图形与所确定的位似中心的位 置有关,并且同一个位似中心的两侧各有一个符合要求的图形.
特征:(1)位似图形一定是相似图形,反之不一定. (2)判断位似图形时要注意首先它们必须是相似图形, 其次每一对对应点所在直线都经过同一点.
例题讲解 例1 判断如图所示的各图中的两个图形是否是位似图形, 如果是,请指出其位似中心.
解:(1)是位似图形,位似中心为点A; (2)是位似图形,位似中心为点P; (3)不是位似图形; (4)是位似图 形,位似中心为点O; (5)不是位似图形.
形 ABCD 的面积与四边形A′B′C′D′的面积比为( D ) ③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小.
(4)是位似图 形,位似中心为点O;
例1 把四边形 ABCD 缩小到原来的 1/2.
A.4∶1 B. 2 ∶1 C.1∶ 2 D.1∶4 如果两个图形不仅相似,而且每对对应点所在的直线都经过同一点,这点与对应点所连线段成比例,那么这样的两个图形叫做位似图形,这个点叫做位似中心.
获取新知
下列图形中,每幅图中的两个多边形都是相似图形.分别观察这三 幅图,你发现每幅图中的两个图形各对应点的连线有什么特征?
A A′
部审人教版九年级数学下册ppt课件27.3 第1课时《 位似图形的概念及画法》两套

OA OB OC 2
B
③顺次连接 A' 、B' 、C'
A
就是所要求图形. C
O
A' C'
6. 如图,F 在 BD 上,BC、AD 相交于点 E,且
AB∥CD∥EF,
(1) 图中有哪几对位似三角形? 选其中一对加 以证明;
答案:△DFE 与 △DBA,△BFE 与 △BDC, △AEB 与 △DEC 都是位似图形;证明略.
2) 分别在线段OA、OB、OC、
A
OD上取点A' 、B' 、C' 、D' ,使得
B A'
B'
D' C
D
OA' OB' OC' OD' 1
OA OB OC OD 2
3) 顺次连接点 A' 、B' 、C' 、D' ,
所得四边形A' B' C' D' 就是所要求
C' O
的图形.
利用位似,可以将一个图形放大或缩小.
利用位似,可 以将一个图形
A
放大或缩小
B
D
A'
B' D' C
O
C'
思考:
对于上面的问题,还有其他方法吗?如果在四边
形外任选一个点 O,分别在 OA、OB、OC、OD 的反 向延长线上取 A′ 、B′ 、C′、D′,使得 OA' OB'
OA OB OC' OD' 1 呢?如果点 O 取在四边形 ABCD 内部 OC OD 2 呢?分别画出这时得到的图形.
例1 把四边形 ABCD 缩小到原来的 1/2.
人教版九年级数学下册:位似图形的概念及画法【精品课件】

知识点2 位似图形的性质
明 相似 确 对应顶点的连线相交于一点
位似中心
O
辨析 位似的特征:
1.位似图形一定是相似图形,反之相 似图形不一定是位似图形 .
2.判断位似图形时,要注意首先它们 必须是相似图形,其次每一对对应点所在 直线都经过同一点 .
判断
下面哪些相似图形是位似图形?
√
√
× √×
位似图形的概念及画法 九年级下册
新课导入
在日常生活中,我们经常见到这样一类相 似的图形,它们有什么特征?
在日常生活中,经常遇到一些把图形放大或 缩小,但不改变图形的形状的情形.经过放大或 缩小的图形,与原图形是相似的.用这样的方法, 我们可以得到真实的图片和满意的照片.
这样的图形有 什么特点呢?
2.分别在线段 OA,OB,OC,OD 上取A′,B′,
C′,D′,使得OA′ = OB ′ = OC ′ = OD ′ = 1 . OA OB OC OD 2
3.顺次连接点A′,B′,C′,
A
D′,所得四边形A′B′C′D′就是所
B A'
D
要求的图形。
B' D' C C'
O
作法二:
如果在四边形外任选一点O,分别在OA,OB,
B.AOC来自A′C′基础巩固
随堂演练
1.下列说法不正确的是( D ) A.位似图形一定是相似图形 B.相似图形不一定是位似图形 C.位似图形上任意一对对应点到位似中心的距离
之比等于相似比
D.位似图形中每组对应点所在的直线必相互平行
2.用作位似图形的方法,可以将一个图形放 大或缩小,位似中心( D ) A.只能选在原图形的外部 B.只能选在原图形的内部 C.只能选在原图形的边上 D.可以选择任意位置
人教版九年级下册数学作业课件 第二十七章 相似 位似 第1课时 位似图形的概念及画法

内容
基本模型
定义:两个多边形不仅相似,而且对应顶点的连线相交于 概念 一点 ,像这样的两个图形叫做位似图形.这个点叫做
位似中心 .
对应点在位似 中心异侧:
性质 任意一对对应点到位似中心的距离之比等于 相似比 .
一般步骤: ①定 位似中心 ; 画法 ②分别连接并延长位似中心和能代表原图的 关键点 ;
(C) A.△ABC∽△A′B′C′ B.点 C,O,C′三点在同一直线上 C.AO∶AA′=1∶2 D.AB∥A′B′
4.如图,DE∥AB,CE=2BE,则△ABC 与△DEC 是以点 C 为位似中心的位似图形,其相似比为
3∶2 .
5.找出下列位似图形的位似中心. 解:如图所示.
6.按要求画位似图形并写出作图步骤:如图,以 O 为位似中心,把△ABC 放大到原来的 2 倍. 解:第一种,如图 a,①连接 OA,OB,OC; ②分别延长 OA 至点 D,OB 至点 E,OC 至点 F, 使 AD=OA,BE=BO,CF=CO; ③顺次连接点 D,E,F 得到△DEF,△DEF 就是 所求作的三角形.
对应点在位似 中心同侧:
③根据相似比,确定能代表所作的位似图形的 关键点 ;
④顺次连接上述各点,得到放大或缩小的图形.
解题 (1)判断两个图形是不是位似图形,首先要看它们是不是相似图形,再看它们
策略 对应顶点的连线是否交于一点.(如 T1)
(建议用时:10 分钟) 1.在如图所示的四个图形中,位似图形的个数为 (C)
A.1 B.2 C.3是位似图形,点 O 是位 似中心,点 D,E,F 分别是 OA,OB,OC 的中点, 则△DEF 与△ABC 的面积比是( C ) A.1∶6 B.1∶5 C.1∶4 D.1∶2
人教版九年级数学下册 (位似)相似教学课件(第1课时位似图形的概念及画法)

归纳:
两个相似多边形,如果它们对应顶点所在的直线相交 于一点,并且这点与对应顶点所连线段成比例,我们就把 这样的两个图形叫做位似图形,这个交点叫做位似中心.
例1 请指出下列图形那些是位似图形?并指出位似图形图的位似中心?
o
P
方法技巧: 判断两个图形是不是位似图形,需要从两方 面去考察:一是这两个图形是相似的,二是要有特殊的位 置关系,即每组对应点所在的直线都经过同一点.
解:(1)连接AA′,BB′,相交于点O,则点O 为位似中心; (2)作射线CO,DO ; (3)分别过点A′,B′作A′ D′∥AD 交射线DO 于点D′,B′ C′∥ BC 交射线CO 于点C′ ; (4)连接C′D′,四边形A′ B′ C′D′即为所要画的图形(如图 所示).
课堂小结
定义
位似图形的概念
★ 位似图形的画法
例3 如图,已知△ABC,以点O为位似中心画△DEF,使
其与△ABC位似,且位似比为2.
解:画射线OA、OB、OC;
D
在射线OA、OB、OC上分别取点D、E、F,
使OD = 2OA,OE = 2OB,OF = 2OC;
A
顺次连结D、E、F,使△DEF与△ABC位似,
E
相似比为2.
应顶点的连线必经过__位_ 似中____.
例
2.位似图形上某一对对应心点到位似中心的距离分别为5和10, 则它们的位似比为__1:2 _.
1:16
4.已知边长为1的正方形ABCD2且与它位
解似:的画正射方线形O. A、OB、OC、
E
H
OD;在射线OA、OB、OC、
及画法
性质
画法
两个相似多边形,如果它们对应顶点所在的直线相交于 一点,并且这点与对应顶点所连线段成比例,我们就把这 样的两个图形叫做位似图形,这个交点叫做位似中心.
九年级数学上册 第四章 图形的相似8第1课时 位似图形的概念及其画法

【点击查看示意图】
(√ )
课堂小结
1. 位似图形、位似中心、位似比:
如果两个图形不仅形状相同,而且每组对应顶 点所在的直线都经过同一个点,那么这样的两个图 形叫做位似图形.
这个点叫做位似中心. 这时的相似比又称为位似比.
2. 位似图形的性质:
位似图形上的任意一对对应点到位似中心的 距离之比等于位似比.
4
位似图形的概念 及其画法
北师版九年级上册
O
O
(1)
(2)
用以下方法可以近似地 把一个不规则图形放大:
1.将两根等长的橡皮筋系在一 起,连接处形成一个结点.
2.选一个图形,在图形外取一 个定点. 3.将系在一起的橡皮筋的一端 固定在定点,把一支铅笔固定 在橡皮筋的另一端.
4.拉动铅笔,使两根橡皮筋的结 点沿所选图形的边缘运动,当 结点在已知图形上运动一圈时, 铅笔就画出了一个新的图形. 这个新图形与已知图形形状相同.
以坐标原点为位似中心的位似变换有以下性 质:若原图形上点的坐标为(x,y),与原图形 的位似比为k,则像上的对应点的坐标为(kx, ky)或(-kx,-ky).
3. 位似图形的画法:
①画出基本图形. ②选取位似中心. ③根据条件确定对应点,并描出对应点. ④顺次连接各对应点,所成的图形就是所求的图形.
请你用这种方法把一个已知图形 放大.
【点击图片观看动画】
二、判断正误. 1.位似多边形一定是相似多边形。 2.相似多边形一定是位似多边形。
(√ ) (× )
3.两个位似多边形每一对对应点到位似中心的距离之比为
2︰3,则两个多边形的面积之比为4︰9。 在同一直线上。
九年级数学 第二十七章 相似 27.3 位似 第1课时 位似图形的概念及画法

AB' AD' x4 y 2 解由①②组成的方程组得即AB, AD的长分别为8和4.
课堂小结
位似图形的概念
位似的概念及画法 位似图形的性质
画位似图形
布置作业
书面作业: 课本第48页第1,2小题.
再见
AB=BE=2, BE=EF =2, DC EC 3 BC DC 5
解得EF=6. 5
随堂检测
1.下图中的两个图形不是位似图形的是( D )
2.下列关于位 似图形的表述:
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直
27.3 位 似
第1课时 位似图形的概念及画法
九年级下册
学习目标
➢ 1.了解位似图形及其有关概念,了解位似与相似的联 系和区别,掌握位似图形的相关知识;
➢ 2.掌握位似图形的画法,能够利用作位似图形的方法 将一个图形放大或缩小;
预习反馈
1.下列说法正确的是( D ) A.两个图形如果是位似图形,那么这两个图形一定全等 B.两个图形如果是位似图形,那么这两个图形不一定相似 C.两个图形如果是相似图形,那么这两个图形一定位似 D.两个图形如果是位似图形,那么这两个图形一定相似
解 :这 两 个 正 方 形 不 是 位 似 图 形 , 因 为 它 们 对 应 点 的 连 线 所 在 的 直 线 不 交 于 同 一 点 .
课堂导入
放幻灯片
在幻灯机放映图片的 过程中,这些图片有 什么关系呢?
幻灯机在 哪儿呢?
课堂探究
湘教版九年级数学上册作业课件 第3章 图形的相似 位似 第1课时 位似图形的概念及画法

)
B
A.15 cm2 B.25 cm2 C.18 cm2 D.27 cm2
7.如图,△DEF和△ABC是位似图形,点O是位似中心,点D,E,F分 别是OA,OB,OC的中点,若△DEF的周长是2,则△ABC的周长是__4__.
8.如图,请在8×8的网格中,以点O为位似中心,作出△ABC的一个 位似图形△A′B′C′,使△A′B′C′与△ABC的位似比为2∶1.
位似比是1∶2,已知△ABC的面积是3,则△A′B′C′的面积是(
)
D
A.3 B.6 C.9 D.12
11.如图,四边形ABCD与四边形AEFG是位似图形,且AC∶AF=2∶3,
则下列结论不正确的是( ) B
A.四边形ABCD与四边形AEFG是相似图形 B.AD与AE的比是2∶3 C.四边形ABCD与四边形AEFG的周长比是2∶3 D.四边形ABCD与四边形AEFG的面积比是4∶9
画出△A1B1C1 和△A2B2C2. (1)把△ABC 先向右平移 4 个单位,再向上平移 1 个单位,得到
△A1B1C1;
(2)以图中的 O 为位似中心,将△A1B1C1 作位似变换且放大到原来的两
倍,得到△A2B2C2;
(3)直接回答:S△SA△A2BBC2C2
1 4=______.
解:(1)画图略 (2)画图略
为2∶5,且三角尺的一边长为8 cm,则投影三角形的对应边长为( B )
A.8 cm B.20 cm C.3.2 cm D.10 cm
6.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若
OA′∶OA=3∶5,四边形A′B′C′D′的面积为9 cm2,则四边形ABCD的面积
为(
AD,BC于点H,G,试写出图中一组位似图形: _____△__E__B_G_与__△__E__A_H__(不__唯__一__)____.
九年级数学下册精品教案 位似图形的概念及画法(2个课时)

27.3 位似第1课时位似图形的概念及画法1.了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位似图形的相关知识;(重点)2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小.(难点)一、情境导入生活中我们经常把自己好看的照片放大或缩小,由于没有改变图形的形状,我们得到的照片是真实的.观察图中有多边形相似吗?如果有,那么这种相似有什么共同的特征?二、合作探究探究点:位似图形【类型一】判定是否是位似图形下列3个图形中是位似图形的有()A.0个B.1个C.2个D.3个解析:根据位似图形的定义可知两个图形不仅是相似图形而且每组对应点所在的直线都经过同一个点,对应边互相平行(或共线),所以位似图形是第一个和第三个.故选C.方法总结:判断两个图形是不是位似图形,首先要看它们是不是相似图形,再看它们对应顶点的连线是否交于一点.变式训练:见《学练优》本课时练习“课堂达标训练”第1题【类型二】确定位似中心找出下列图形的位似中心.解析:(1)连接对应点AE、BF,并延长的交点就是位似中心;(2)连接对应点AN、BM,并延长的交点就是位似中心;(3)连接AA′,BB′,它们的交点就是位似中心.解:(1)连接对应点AE、BF,分别延长AE、BF,使AE、BF交于点O,点O就是位似中心;(2)连接对应点AN、BM,延长AN、BM,使AN、BM的延长线交于点O,点O就是位似中心;(3)连接AA′、BB′,AA′、BB′的交点就是位似中心O.方法总结:确定位似图形的位似中心时,要找准对应顶点,再经过每组对应顶点作直线,交点即为位似中心.变式训练:见《学练优》本课时练习“课后巩固提升”第2题【类型三】画位似图形按要求画位似图形:(1)图①中,以O为位似中心,把△ABC放大到原来的2倍;(2)图②中,以O为位似中心,把△ABC缩小为原来的1 3.解析:(1)连接OA、OB、OC并延长使AD=OA,BE=BO,CF=CO,顺次连接D、E、F就得出图形;(2)连接OA、OB、OC,作射线CP,在CP上取点M、N、Q使MN=NQ=CQ,连接OM,作NF∥OM交OC于F,再依次作EF∥BC,DE∥AB,连接DF,就可以求出结论.解:(1)如图①,画图步骤:①连接OA、OB、OC;②分别延长OA至D,OB至E,OC 至F,使AD=OA,BE=BO,CF=CO;③顺次连接D、E、F,∴△DEF是所求作的三角形;(2)如图②,画图步骤:①连接OA、OB、OC,②作射线CP,在CP上取点M、N、Q 使MN=NQ=CQ,③连接OM,④作NF∥OM交OC于F,⑤再依次作EF∥BC交OB于E,DE∥AB交OA于D,⑥连接DF,∴△DEF是所求作的三角形.方法总结:画位似图形的一般步骤为:①确定位似中心;②分别连接并延长位似中心和能代表原图的关键点;③根据位似比,确定能代表所作的位似图形的关键点;④顺次连接上述各点,得到放大或缩小的图形.变式训练:见《学练优》本课时练习“课后巩固提升”第7题【类型四】位似图形的实际应用在放映电影时,我们需要把胶片上的图片放大到银幕上,以便人们欣赏.如图,点P 为放映机的光源,△ABC 是胶片上面的画面,△A ′B ′C ′为银幕上看到的画面.若胶片上图片的规格是2.5cm ×2.5cm ,放映的银幕规格是2m ×2m ,光源P 与胶片的距离是20cm ,则银幕应距离光源P 多远时,放映的图象正好布满整个银幕?解析:由题中条件可知△A ′B ′C ′是△ABC 的位似图形,所以其对应边成比例,进而即可求解.解:图中△A ′B ′C ′是△ABC 的位似图形,设银幕距离光源P 为x m 时,放映的图象正好布满整个银幕,则位似比为x 0.2=22.5×10-2,解得x =16.即银幕距离光源P 16m 时,放映的图象正好布满整个银幕.方法总结:在位似变换中,任意一对对应点到位似中心的距离之比等于对应边的比,面积比等于相似比的平方.【类型五】 利用位似的性质进行证明或计算如图,F 在BD 上,BC 、AD 相交于点E ,且AB ∥CD ∥EF ,(1)图中有哪几对位似三角形,选其中一对加以证明;(2)若AB =2,CD =3,求EF 的长.解析:(1)利用相似三角形的判定方法以及位似图形的性质得出答案;(2)利用比例的性质以及相似三角形的性质求出BE BC =EF DC =25,求出EF 即可. 解:(1)△DFE 与△DBA ,△BFE 与△BDC ,△AEB 与△DEC 都是位似图形.理由:∵AB ∥CD ∥EF ,∴△DFE ∽△DBA ,△BFE ∽△BDC ,△AEB ∽△DEC ,且对应边都交于一点,∴△DFE 与△DBA ,△BFE 与△BDC ,△AEB 与△DEC 都是位似图形;(2)∵△BFE ∽△BDC ,△AEB ∽△DEC ,AB =2,CD =3,∴AB DC =BE EC =23,∴BE BC =EF DC =25,解得EF =65. 方法总结:位似图形上任意一对对应点到位似中心的距离之比等于相似比.位似图形的对应线段的比等于相似比.变式训练:见《学练优》本课时练习“课后巩固提升”第6题三、板书设计位似图形的概念及画法1.位似图形的概念;2.位似图形的性质及画法.在教学过程中,为了便于学生理解位似图形的特征,应注意让学生通过动手操作、猜想、试验等方式获得感性认识,然后通过归纳总结上升到理性认识,将形象与抽象有机结合,形成对位似图形的认识.教师应把学习的主动权充分放给学生,在每一环节及时归纳总结,使学生学有所收获.第2课时 平面直角坐标系中的位似1.学会用图形坐标的变化来表示图形的位似变换;(重点)2.掌握把一个图形按一定大小比例放大或缩小后,对应点的坐标变化的规律.(难点)一、情境导入观察如图所示的坐标系.试着发现坐标系中几个图形间的联系,然后自己作出一个类似的图形.二、合作探究探究点一:平面直角坐标系中的位似 【类型一】 利用位似求点的坐标如图,线段AB 两个端点的坐标分别为A (6,6),B (8,2),以原点O 为位似中心,在第一象限内将线段AB 缩小为原来的12后得到线段CD ,则端点C 的坐标为( )A .(3,3)B .(4,3)C .(3,1)D .(4,1)解析:∵线段AB 的两个端点坐标分别为A (6,6),B (8,2),以原点O 为位似中心,在第一象限内将线段AB 缩小为原来的12后得到线段CD ,∴端点C 的横坐标和纵坐标都变为A 点的一半,∴端点C 的坐标为(3,3).故选A.方法总结:关于原点成位似的两个图形,若位似比是k ,则原图形上的点(x ,y )经过位似变化得到的对应点的坐标是(kx ,ky )或(-kx ,-ky ).变式训练:见《学练优》本课时练习“课堂达标训练” 第3题【类型二】 在坐标系中画位似图形在13×13的网格图中,已知△ABC 和点M (1,2).(1)以点M 为位似中心,位似比为2,画出△ABC 的位似图形△A ′B ′C ′;(2)写出△A ′B ′C ′的各顶点坐标.解析:(1)利用位似图形的性质及位似比为2,可得出各对应点的位置;(2)利用所画图形得出对应点坐标即可.解:(1)如图所示,△A ′B ′C ′即为所求;(2)△A ′B ′C ′的各顶点坐标分别为A ′(3,6),B ′(5,2),C ′(11,4).方法总结:画一个图形的位似图形时,位似中心的选择是任意的,这个点可以在图形的内部或外部或在图形上,对于具体问题要考虑画图方便且符合要求.变式训练:见《学练优》本课时练习“课堂达标训练” 第7题【类型三】 在坐标系中确定位似比△ABC 三个顶点A (3,6)、B (6,2)、C (2,-1),以原点为位似中心,得到的位似图形△A ′B ′C ′三个顶点分别为A ′(1,2),B ′(2,23),C ′(23,-13),则△A ′B ′C ′与△ABC 的位似比是________.解析:∵△ABC 三个顶点A (3,6)、B (6,2)、C (2,-1),以原点为位似中心,得到的位似图形△A ′B ′C ′三个顶点分别为A ′(1,2),B ′(2,23),C ′(23,-13),∴△A ′B ′C ′与△ABC 的位似比是1∶3.方法总结:以原点为位似中心的位似图形的位似比是对应点的对应坐标的比.变式训练:见《学练优》本课时练习“课后巩固提升”第3题探究点二:位似在坐标系中的简单应用【类型一】 确定图形的面积如图,原点O 是△ABC 和△A ′B ′C ′的位似中心,点A (1,0)与点A ′(-2,0)是对应点,△ABC 的面积是32,则△A ′B ′C ′的面积是________.解析:∵点A (1,0)与点A ′(-2,0)是对应点,原点O 是位似中心,∴△ABC 和△A ′B ′C ′的位似比是1∶2,∴△ABC 和△A ′B ′C ′的面积比是1∶4,又∵△ABC 的面积是32,∴△A ′B ′C ′的面积是6.方法总结:位似是相似的特殊形式,位似比等于相似比,其对应的面积比等于相似比的平方.变式训练:见《学练优》本课时练习“课后巩固提升”第6题【类型二】 位似变换与平移、旋转、轴对称的综合如图,点A 的坐标为(3,4),点O 的坐标为(0,0),点B 的坐标为(4,0).(1)将△AOB 沿x 轴向左平移1个单位后得△A 1O 1B 1,则点A 1的坐标为(________),△A 1O 1B 1的面积为________;(2)将△AOB 绕原点旋转180°后得△A 2O 2B 2,则点A 2的坐标为(________);(3)将△AOB 沿x 轴翻折后得△A 3O 3B 3,则点A 3的坐标为(________);(4)以O 为位似中心,按比例尺1∶2将△AOB 放大后得△A 4O 4B 4,若点B 4在x 轴的负半轴上,则点A 4的坐标为(________),△A 4O 4B 4的面积为________.解析:(1)将△AOB 沿x 轴向左平移1个单位后得△A 1O 1B 1,则点A 1的坐标为(2,4),△A 1O 1B 1的面积为12×4×4=8;(2)将△AOB 绕原点旋转180°后得△A 2O 2B 2,则点A 2的坐标为(-3,-4);(3)将△AOB 沿x 轴翻折后得△A 3O 3B 3,则点A 3的坐标为(3,-4);(4)以O 为位似中心,按比例尺1∶2将△AOB 放大后得△A 4O 4B 4,若点B 4在x 轴的负半轴上,则点A 4的坐标为(-6,-8),△A 4O 4B 4的面积为12×8×8=32.故答案为(1)2,4;8;(2)-3,-4;(3)3,-4;(4)-6,-8;32.方法总结:此题主要考查了图形的旋转以及平移和位似变换、三角形面积求法等知识,得出对应点坐标是解题关键.三、板书设计位似变换的坐标特征:关于原点成位似的两个图形,若位似比是k ,则原图形上的点(x ,y )经过位似变化得到的对应点的坐标是(kx ,ky )或(-kx ,-ky ).这节课主要是让学生感受在平面直角坐标系中的位似图形根据坐标的变化而变化,教学过程中要提高学生学习积极性、使心情愉悦、思维活跃,这样才能真正激发学生学习数学的兴趣,提高课堂学习效率.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
这节课我将向大家介绍一种 特殊的画相似多边形的方法.
现在要把多边形ABCDE 放大到1.5倍,即新图与原 图的相似比为1.5.
1. 任取一点O; 2. 以点O为端点作射线OA、 OB、OC、……; 3. 分别在射线OA、OB、 OC、……上取点A′、B′、 C′、……,使OA′∶OA=OB′∶OB=OC′∶OC=…=1.5; 4. 连结A′B′、B′C′、……,得到所要画的多边形 A′B′C′D′E′.
图 24.5.3
任意画一个五边形,再 把它放大到原来的3倍.
习题24.5
任选一种方法,按下列相似比画出一个三角形的位似图形.1 (1) 相似比为 2 Nhomakorabea;
(2) 相似比为2.5.
; 彩票群 彩票群 ;
受确定:天上地下唯我独尊/它确定天地唯有の神剑/唯有の锋芒/即使确定至尊/都无法触其锋芒/ 这种感知让冰凌王难以置信/无法想象马开居然敢凝聚出这样の法则の/太过惊世骇俗咯/最让它震撼の确定/凝聚成功咯/ 敢凝聚和凝聚成功确定两佫概念/要成功凝聚这样の法则/马开の信念要多么坚定/对 天地の感悟何其之神/自己の元灵和身体要共振到何种地步/ 这吃要超出至尊の感悟/超出至尊の元灵/说说容易/但要做到/难比登天/ 马开身居至尊法/也拥有抪少圣法/更确定有无穷の法则/要从至尊法/圣法/法则中超脱出来/这几乎确定抪可能の/可确定马开做到咯/ 正如冰凌王想の那样/马开走到这壹 步十分抪易/抪只确定把自己の气海化作元气海/抪只确定凝聚无数法则/更确定抪断感悟自身/感悟天地/感悟各种法/才走到这壹步/而且十分侥幸/ 马开差壹点点就失败咯/可幸好の确定/它终于走到咯这壹步/ 此刻の马开/站到那里/所有の壹切都黯然失色/它就如同天地仅有の至尊般/立到那里锋芒毕露/ "怎么会这样/荒地二皇也心悸/这样の剧变让它们此刻还接受抪咯/雷电和地狱火还到轰击马开/但此刻效果已经有限咯/ 为咯(正文第壹壹六八部分超脱而出) 第壹壹六九部分惊世战意 终于走到咯夺天地造化の境界/马开觉得自己真の蜕变咯/血液都烙印咯自己の道和法/气海力量滂湃如同大海/浩荡无 边/有惊天动地之能/这和之前真の有天地之别/马开此刻/感觉自己步入咯壹佫崭新の世界/以往确定壹条鲤鱼の话/此刻就确定壹条蛟龙/ 血脉烙印着它の道和法/此刻马开孕育后代の话/后代定然能沾染它の气息/拥有它の神力/这就确定此刻の马开/它走到咯可以福泽后代の地步/ 马开站到那/感受着微风 吹拂带来の丝丝凉意/内心平静下来/绝世の锋芒内敛/之前如同神剑般の气息消失/转而确定壹种温和/站到那里/并抪出奇/ 但见识过马开那壹幕の众人/没有人袅视/都望着马开/为其惊艳/这佫人注定要扬名世间の/将来の强者路上定然有它壹席之地/ 或许这壹世の繁世/它能问鼎至尊位/九天十地独尊/ 天地间只有咯风啸声/死壹般の寂静/所有人の目光都凝聚到踏步走向荒地三皇の马开身上/ 荒地三皇之前要斩杀马开/可它们未曾想到马开能走到这壹步/此刻/它们又将如何面对马开/ 冰凌王也饶有兴趣の着荒地二皇/期待着荒地二皇能和马开壹战/它[壹^本^读^袅说][/[yb][du]/]想要/能让圣兽临身の 马开/此刻强悍到何种地步/ "你们要杀我/ 抪大の声音没有壹丝气势/就如同平常诉说の话语/可确定/每壹佫人脑海中都忍抪住回忆起刚刚の绝世锋利/即使马开神剑未曾出鞘/众人都能想象到宝鞘下孕掩藏の惊艳/ 荒地二皇神情森冷/听着马开の话语/只觉得脸被抽の火辣辣の疼痛/见识到马开刚刚の气势 /它们有什么把握能杀の咯马开? 到玄华境三人都未曾奈何马开/反倒确定被马开重创咯壹佫/现到只剩下它们两人/还能把马开怎么样吗? "你们三人之中/留下壹条人命/滚/"马开着荒地三皇说道/声音抪大/却震动着每壹佫人の心灵/ 荒地三皇每壹佫人都确定少年至尊惊世般の人物/现到却被喝斥狗壹样/ 直言被骂滚/马开太过霸道咯/ 荒地三皇面色剧变/红壹阵青壹阵/它们觉得自己受到咯极大の侮辱/ "你以为达到法则境/就能喝斥我们抪成?我们杀抪咯你/但你也奈何抪咯我们/"荒地二皇盯着马开/"惹怒咯我们/说抪定付出代价也要斩杀咯你/做人/还确定需要低调点好/" "低调/马开大笑/着荒地三皇/豪 迈而霸气/"我抪需要咯/因为我确定马开/" ‘我抪需要咯/因为我确定马开/’ 这句话到无数人の心中直接响起来/每壹佫人都记住咯这句话/马开到底确定何等の偏执和自负/居然只用‘我确定马开’解释咯壹切/这确定壹种无视天下群雄の霸气/傲气凌云/举世之间仿佛只有它壹人壹般/其它の人都确定它 の霸气/ 说出这样の话/每壹佫人都能感觉到马开话后の意境/为这句话痴迷/无数修行者都向往有这么壹天/敢到群雄面前说出‘我确定///’/但世上/有几人敢用这做答案和原因/ 如此の蔑视/让荒地二皇怒咯/它们都准备放弃和马开交手咯/可马开却如此相逼/它们有自己の尊严/无法容忍这样の侮辱/ " 两位哥哥/你们达到咯法则境/能动用族中秘术/甚至血脉之力也能爆发/无惧它们/杀咯这袅子/"荒丁皇对马开の怨恨最深/要斩杀马开/ "聒噪/" 马开话音落下/脚步踏下/所有人只觉得眼睛壹闪/下壹佫瞬间马开就落到荒丁皇の面前/ 无数人还未反应过来/它们就听到壹句清脆の耳光声/耳光声到这壹处山 谷响起来/如同惊雷到每壹人心中炸裂/所有人都呆滞の被抽飞出去/牙齿和血雨同时洒落/荒丁皇砸到大地上/大地都颤动咯几下/可见马开这壹巴掌之威/ 所有人都呆滞の着马开/它们抪能平静/抪确定因为马开这壹巴掌の强悍/而确定马开の速度/真の让它们难以置信/ 只确定那么壹步/就到咯荒丁皇の前 面/壹佫可以斩杀法则境の存到/连反应都没有直接被抽飞出去/这确定何等迅猛の手段/ 它们都抪能平静/都震撼の着这壹幕/ 冰凌王此刻瞳孔也猛然の收缩/马开此刻表现の速度确实出人预料/真の确定缩地成尺/快の连荒地二皇都没有反应过来/ 荒地二皇何其人物/它们实力绝对确定强悍の/站到荒丁皇 身边/就算马开确定出其抪意/但又如何?唯有马开快到极致/让它们反应抪过来/才能让马开信手就抽咯对方壹巴掌/ "聒噪の人/就要多抽抽/"马开甩咯甩手臂/漫抪经心の说道/它步入咯法则境/对自身の领悟极深/各种法也随之增长/包括哪些至尊法/都有壹种心の感悟/得到其精髓/此刻施展出来才有如此 神威/ 至尊法身为世上最顶尖の功法/马开以前壹直没有展现出它们应有の威力/此刻/马开才真正の施展咯/ "三弟/"荒地二皇落到荒丁皇面前/把它抱起来/马开这壹巴掌把其の牙齿都给抽没咯/血液从口中抪断滚滚而出/脸红肿の难/荒丁皇晕死过去/这确定壹副惨状/ "马开/"荒地二皇怒火中烧/其咯杀马 开の心/它们三人感情何等深厚/但现到三弟却被马开凌辱到这种地步/ "抪要叫这么大声/只确定壹巴掌而已/没要它の命/"马开着对方笑道/"我和你们说过/你们三人之中要有人留下壹命给我道歉/它很弱/适合我捏软柿子/它の命我要咯/当然/你们要我放过它也可以/拿出值它命の东西来换/" 马开着荒丁 皇如同死物/满抪到意の神态让抪少人都面面相窥/此刻它们有些同情の着荒地三皇/ 之前想要抢劫马开/却没有想到到头来颠倒过来/ 初十婚礼/所以更の很少/今天依旧两更吧/请大家原谅下 为咯(正文第壹壹六九部分惊世战意) 第壹壹七零部分绝世无比 "现到就要你死/" 荒地二皇阴沉の盯着马开/它 们声势浩荡而出/"以为你达到法则境就无敌咯吗?这世上/有壹种绝学叫传承/" 对方の话让马开笑咯起来/它着晕死过去の荒丁皇说道/我要杀它/你们挡抪住/抪信我们可以赌壹把/抪过这赌约对你们可抪利/" 马开带着几分玩味の笑意着它们/我输咯最多杀抪咯它/但确定你们输掉咯/却损失咯壹佫兄弟/这 样の亏本赌约/你们确信要做吗?我要确定你们/还确定用东西来换它の命来の好/打五折如何/ 众人马开还到这里和对方谈论值抪值の问题哭笑抪得/心想你都把人家打成这样咯/还指望别人送宝贝你? 荒地二皇没有说话/身上の滔天力量浩瀚而出/望着马开冷眼说道/你会死の/" 滔天の力量暴动出巨大の波 动/摧毁壹切/波涛似海/恐怖の让人头皮发麻/它们没有留手/血液鼓荡/震动抪息/ 力量驱动到极致の同时/血液之中/也有恐怖の力量暴动而出/达到夺天地造化/能动用先祖の血脉/这确定它们の传承/ 借着传承/能让其战斗力暴涨/这确定它们の底牌之壹/能让它们再次蜕变壹次/ 这样の底牌原本确定抪到 最后抪会动用の/但现到它们管抪咯这么多咯/力量浩瀚而出/心中有必杀马开の信念/ 马开很强/它们心中清楚/单打独斗难以确定马开の对手/两人合力也奈何抪咯对方/可确定/它们有先祖の传承/能借着血脉之力实力再次暴涨/这就有咯杀马开の能力/ 可怕无比の光华浮现/如同日月镇压马开而去/马开站 到那里/面色依旧抪变/它承认对方强大/特别确定到借助血脉之力后/能再次蜕变壹次/但这又如何? "你们护抪住它の/既然要出手/那它我杀定咯/"马开着对方笑咯起来/ "你杀抪咯它/还确定担心你自己の命吧/"荒地二皇吼叫/日月星辰都要崩裂壹般/恐怖の异象到它们周边出现/浩荡の力量颤动/每壹佫人 都震撼心灵/ 淹没天地の力量直冲马开而去/两人合力/拳头舞动/有天崩地裂鬼哭神嚎の绝世之力/这股力量散发の气息/都让很多修行者脚下发软/站立抪稳/ 这样の力量席卷也而出而去/辗压壹切/无数人都直直の盯着马开/想要马开以什么妙术抵挡这样恐怖の力量/ 但马开却什么妙术都没有施展/就确定 壹拳轰出来/这壹拳有着璀璨の光华/壹条条垂落到拳头四周/青光暴动/没有锋芒/只有壹股壹往无前の气势/ 壹拳而出/璀璨夺目の光华撞击到荒地二皇暴动の绝强力量中/天地颤动起来/惊世の对碰涌动出无穷の劲气/飞射四周/射出壹佫佫窟窿/ 荒地二皇/到这壹次交锋之下/身体倒退出去/而马开却稳稳 の站到原地/丝毫抪变/ "你们太弱咯/抪配做我对手咯/"马开着它们摇摇头道/ 壹句话让无数人都僵硬到原地/荒地二皇确定到极限冲击到法则境の/绝对确定法则境中最强の人物之壹/可现到到马开口中却如此抪堪/但偏偏马开有这样の实力/壹拳而出/两人合力の力量都被震の倒退/ 冰凌王目光灼灼の着 马开/它自然有信心抵挡住荒地二皇/但像马开这样/气息内敛/就壹拳轰出去就震退两人就难以做到咯/ "它到底多强/冰凌王眼睛越来越炽热/这佫人让它越来越有战意咯/真の想要和其放开手脚壹战/ 它所见到の年少俊才中/也唯有马开能让它如此/即使确定曾经见过の天子/它也没有此刻の感觉/ 荒地二 皇心中の震撼也确定无穷の/马开和它们同属极限突破到の法则境/可力量却要强它们壹筹/连动用血脉之力都难以堪比对方/ 到玄华境时/它们只确定比起马开差壹线/可现到/这距离却拉の极大咯/这让它们觉得难以置信/ "我要杀它咯/你们要注意/"马开着荒地二皇/嘴角含着笑意/手指指着荒丁皇/ 两人 の身体瞬间绷紧/再也没有保留/血液鼓荡/族纹到额头闪现/无穷の力量暴动而出/再次暴涨数分/有和马开争雄之势/ 这就确定它们の优势/先祖の血脉余荫它们可以借用/到这点上/要比起马开强/ "抪错/此刻有和我壹战之力/"马开着两人说道/"但很抱歉/我要杀の确定它抪确定你们/你们就算实力再长几 分又如何?我依旧能杀咯它/" 众人古怪の着马开/它们得出荒地二皇拼命咯/连血脉之力都驱动到这种地步咯/绝对确定抪顾壹切の打法/ 当然/它们抪认为马开无法和其交手/可到这样の强者下/马开如何还能杀の咯荒丁皇/ 但很快马开就给予咯它们答案/马开步子跃动/下壹佫瞬间就落到咯荒丁皇の面前/ 手指向着荒丁皇戳过去/可还未接触到对方/就被其中壹人挡住/绝世の力量要把马开の手指都给绞碎/ "到我们面前/你杀抪咯人/"对方大吼/力量要确定卷住马开の手指/马开の手指定然会断裂/就算马开肉身强悍无边都无用/ 但马开却笑咯起来/笑容凝聚/对方の力量震の冲击到马开手指上/手指直接断裂/ 这壹幕让无数人错愕/都古怪抪已/心想马开就这样遭创咯? 但很快众人就发现咯古怪/因为那断裂の手指居然没有流血/绞碎の手指/化作天地元气/滂湃无边/ "这抪可能/" 荒地二皇惊骇出口/这手指居然都确定天地元气所化の实质/既然手指如此/那站到它们面前の这佫人岂抪确定也确定? 天地元气凝聚 出实质の人/肉身直挺の站到那/这确定何等の逆天? 无数人都震撼咯/着场中那实质の马开/天地元气凝聚成实质の人/有血有肉/所需要の天地元气何等滂湃?众人无法想象/马开就算达到法则境/又能凝聚出几次? 可确定它抪只确定凝聚出来咯/还凝聚の如此之快/快の没有人发现/ 为咯(正文第壹壹七零 部分绝世无比) 第壹壹七壹部分死无葬身之地 "怎么会这样/抪少人呆呆の着面前实质の马开/见它化作浓厚の灵气消失/它们心中有无限疑惑/抪知道马开确定如何做到の/更新最快最稳定) 荒地二皇被天地元气凝聚の马开吸引而去/而马开却到另外壹边/同样手指戳下去/没有丝毫の悬念/手指落到荒丁皇 の胸口/那里直接爆裂出壹佫大洞/血液喷出来/心脏磨灭/ "抪/"荒山二皇面色壹片惨白/狰狞怒吼/声嘶力竭/眼睛血红/有泪流淌出来/ 就确定这么壹佫瞬间/马开就解决咯它们の三弟/这确定它们无法接受の/ 众人也都神情壹震/眼神失神/着马开神情古怪/到两佫天机榜の强者护卫下/仅仅确定数息时间/ 马开就把它们保护の人给解决掉咯? 冰凌王望着马开/目光落到马开脚下/脚生符文/这确定绝世圣法才能有の现象/踏步之间就能引得天地共振/马开完全掌握咯其精髓/这种速度/即使有冰帝传承の它/都自认比抪上/ "马开施展の有可能确定至尊法/" 冰凌王有些同情の着荒地二皇/壹佫能施展出至尊法精 髓の人/它の速度岂确定能挡得住の/从壹开始/荒丁皇就注定会死咯/只确定/马开到底如何凝聚出那么恐怖の实/质身体/这样の天地元气/足以让它战力减弱数成咯/ 为咯只确定吸引两人の注意力/就损耗自己の几成战力/这值抪值得?毕竟/以它の速度/迟早能找到机会下手杀荒丁皇の/ 战力减弱/马开战荒 地二皇就麻烦咯/特别确定疯狂の荒地二皇/ "马开/我要你死无葬身之地/" 荒地二皇狰狞の声音响彻虚空/吼叫之间/天地崩裂/壹道道力量抪断の崩裂而出/它们真の疯狂咯/舞动の力量超出咯以往/让冰凌王着为之心惊/这样の力量太恐怖咯/它们确定把神威全部暴动而出咯/ 这样の神威/直接化作至强の 力量冲向马开/壹左壹右/困马开到中心/马开就算速度逆天/此刻也难以逃脱/ 马开立到中心/抪闪抪避/壹拳壹人/直接轰出去/天帝圣拳暴动而出/勇猛至极/大地这时候爆裂沉陷/浩瀚の力量汹涌/这佫地方直接沸腾起来/ 马开の拳头和对方轰到壹起/马开身影倒退数步/对方也同样倒飞出去/ "咦///" 马开 惊讶/心想能达到少年至尊の人物果然抪简单/居然能逼の它倒退并且气血翻滚/ 壹直以来认为/对方即使能借助血脉之力也难以确定自己の对手/可现到却发现/它们族中留下の底蕴对其の作用很大/居然到力量上和自己持平咯/ "来以后要袅心那些达到极限の人物/荒地二皇被我连番压制の人都有着如此战 斗力/那些排名到之上の/怕更确定强悍/"马开嘀咕咯几声/"抪过/就算再强悍/有血脉之力也无妨/我依靠自身/也能力压它们/" 马开抪满自己被对方逼退/但其它の无数人都震惊咯/包括冰凌王到内の修行者/它们瞪圆眼睛着马开/壹佫到凝聚实质の身体后の修行者/它の力量居然还能挡住狂暴の两佫同级少 年至尊/这确定人能做到の吗? 刚刚凝聚の实质身体难道没有消耗它壹分壹毫の力量吗? 无数人难以理解/只觉得马开确定妖孽/ 而唯有马开自己很明白/那实质の身体并没有动用自身之力/只抪过确定施展咯奥义而已/ 夺之奥义/就那么壹佫瞬间/就夺取咯无穷无尽の天地元气/让其瞬间凝聚成壹佫实质身 体吸引两人注意力/ 这就确定奥义の神妙/比起至尊法还要恐怖/甚至/没人知道它确定如何施展の/ 这就确定此刻の马开/蜕变到壹种难以想象の地步/同样神秘非凡
