青岛版五四制小学五年级数学下册教案完美的图形——圆

合集下载

五四制青岛版五年级下册数学一完美的图形1圆的认识导学案设计

五年级下册数学导学案一、完美的图形1、圆的认识【学习内容】信息窗1 2—6页【学习目标】1、结合具体实物，经历认识圆，掌握圆的特征及其各部分名称。

2、会用字母表示圆心、半径、直径；理解掌握同圆或等圆中半径和直径的关系。

3、通过观察、操作、想象等活动，发展空间观念。

【学习过程】一、回顾旧知1、长方形、正方形、三角形、梯形、平行四边形有什么特征?2、硬币、车轮等，这些物体形状的平面是什么形？3、你能用自己的方法画一个圆吗？二、预习导航，探究新知1、圆的认识（1）说一说你周围哪些物体上有圆？（2）圆与我们以前学过的平面图形有什么不同？（3）你能用圆规画一个圆吗？说一说你是怎样画的？应注意什么？还有别的方法一个圆吗？2、圆各部分的名称(1)找圆心。

把圆形纸片对折，使上下两部分完全重合，打开；再换个方向对折，再打开。

反复不同的方向对折几次，观察这些折痕，你发现了什么？折痕相交的点是圆的中心，叫做，用字母表示。

（2）连接和叫做半径。

半径一般用字母表示。

（3）通过并且叫做直径。

直径一般用字母表示。

（4）请任意画一个圆，并标出各部分的名称。

3、圆的特征（1）折一折：把圆形纸片对折，能折（）次。

说明同一圆中，有（）条直径。

（2）画一画：圆内可以画（）条半径？说明同一圆中，有（）条半径。

（3）测一测：a、在同一个圆内所有直径长度有何关系？所有半径长度有何关系？b、在同一个圆内，直径的长度与半径的长度有什么关系？你能用字母表示它们的关系吗？4、想一想：用圆规随意画几个圆，（）决定圆的位置，（）决定圆的大小。

三、当堂达标（20分）1、判断：（10分）⑴圆规两脚间的距离是3厘米，所画圆的直径就是3厘米。

（）⑵两端都在圆上的线段中，直径最长。

（）⑶在同一个圆中，所有的半径的长度都相等，所有的直径的长度都相等。

（）⑷直径是该圆半径长度的2倍。

（）⑸半径能决定圆的大小，圆心能决定圆的位置。

（）2、请在下面画一个半径是2厘米的圆，并且用字母标出圆心、半径和直径。

小学数学青岛版(五四)五年级下册第一单元完美的图形——圆圆的面积-章节测试习题(9)

章节测试题1.【答题】笑笑绕着圆形花坛边缘走一圈，刚好走了62.8米.这个花坛的面积是多少平方米？（π取3.14）【答案】花坛面积是314平方米.【分析】由“圆的周长＝2πr”可得“r＝圆的周长÷2π”，于是可以求出花坛的半径，进而利用圆的面积公式即可求出花坛的面积.【解答】花坛的半径：62.8÷（2×3.14）＝10（米），花坛的面积：（平方米），答：花坛面积是314平方米.2.【答题】下图中长方形面积是40平方厘米，请你求出其他几个图形的面积.【答案】三角形的面积是40平方厘米，平行四边形的面积是32平方厘米，圆的面积是50.24平方厘米.【分析】因为平行线间的距离处处相等，所以“正方形的边长＝三角形的高＝平行四边形的高＝圆的直径”，由此解答.【解答】长方形的长：40÷5＝8（厘米），三角形的面积：10×8÷2＝40（平方厘米），平行四边形的面积：4×8＝32（平方厘米），圆的面积：（平方厘米），答：三角形的面积是40平方厘米，平行四边形的面积是32平方厘米，圆的面积是50.24平方厘米.3.【答题】求下图阴影部分的面积.（单位：厘米）【答案】阴影部分的面积是91.06平方厘米.【分析】根据图形的特点可知，阴影的面积＝大圆面积－小圆面积，由此解答.【解答】（平方厘米），答：阴影部分的面积是91.06平方厘米.4.【题文】花园里有一个半径为8米的圆形花坛，要在其周围铺设2米宽的水泥路，这条路的面积是多少平方米？【答案】113.04平方米【分析】先根据花坛的半径求出这个花坛的面积，然后再求出花坛和水泥路的面积和，最后用花坛和水泥路的面积和减去花坛的面积即可.【解答】花坛的面积是：（平方米）；水泥路的面积是：（平方米）；答：这条水泥路的面积是113.04平方米.5.【答题】圆的半径是10厘米，那么圆的面积是______平方厘米.【答案】314【分析】圆的面积，由此代入数据即可解答.【解答】（平方厘米），答：圆的面积是314平方厘米.6.【答题】半径是3厘米时，直径是______厘米，面积是______平方厘米.【答案】6,28.26【分析】根据直径公式，面积公式，即可求出圆的直径与面积.【解答】3×2＝6（厘米），（平方厘米），答：它的直径是6厘米，面积是28.26平方厘米.7.【答题】时钟的分针长6厘米，它的尖端走一圈是______厘米，其中扫过的面积是______平方厘米.【答案】37.68,113.04【分析】分针一小时正好走一圈，针尖走过的路线正好画成了一个圆，求尖端走了一圈的长度，实际是求半径是6厘米的圆的周长是多少，它走一圈扫过的面积就是半径为6厘米的圆的面积，可利用圆的周长公式、圆的面积公式解答即可.【解答】2×3.14×6＝37.68（厘米），（平方厘米），它的尖端走一圈是37.68厘米，其中扫过的面积是113.04平方厘米.8.【答题】圆的半径扩大到原来的5倍，则它的直径扩大到原来的______倍；周长扩大到原来的______倍；面积扩大到原来的______倍.【答案】5,5,25【分析】设圆的半径为，则直径＝，周长＝，面积＝，由此可得：圆的直径、周长与圆的半径成正比例，圆的面积与半径的平方成正比例，由此即可解答.【解答】设圆的半径为，则直径＝，周长＝，面积＝，则圆的半径扩大到原来的5倍时，直径就扩大到原来的5倍，周长也是扩大到原来的5倍；圆的面积就扩大到原来的25倍.9.【答题】把一个圆转化成长方形，长方形的周长是16.56厘米，圆的面积是______平方厘米.【答案】12.56【分析】把一个圆等分成若干个小扇形后拼成一个近似的长方形，周长比原来的圆的周长增加了两个圆的半径，依此可求出圆的半径，然后根据圆的面积公式解答即可.【解答】16.56÷(3.14×2＋2)＝2（厘米），（平方厘米），答：圆的面积是12.56平方厘米.10.【答题】正方形的周长是4dm，在正方形中画一个最大的圆，圆的面积是______平方分米.【答案】0.785【分析】根据题干可得这个最大圆的直径就是这个正方形的边长，根据正方形的周长公式即可求得这个正方形的边长，进而依据圆的面积公式即可求解.【解答】4÷4＝1（分米），（平方分米），答：圆的面积是0.785平方分米.11.【题文】如图，如果毎个圆的直径都是a，那么长方形的周长是多少？面积是多少？【答案】长方形的周长是6a，面积是2a2.【分析】观察图形可知，这个长方形的长是2a，宽是a，据此利用长方形的周长公式：C＝2（a＋b）和面积公式：S＝ab即可解答问题.【解答】(2a＋a)×2＝6a2a×a＝2a2答：长方形的周长是6a，面积是2a2.12.【答题】一个圆形杯垫的半径是4厘米，这个杯垫的周长是______厘米，面积是______平方厘米.【答案】25.12,50.24【分析】可利用圆的周长公式和面积公式进行计算，列式解答即可.【解答】2×3.14×4＝25.12（厘米），（平方厘米），答：这个杯垫的周长是25.12厘米，面积是50.24平方厘米.13.【答题】把一个直径是4厘米的圆分成若干等份，然后把它剪开，照图的样子拼起来，拼成的图形的周长比原来圆的周长增加______厘米.【答案】4【分析】由圆的面积推导过程可知：将圆拼成近似的长方形后，长方形的长就等于圆的周长的一半，宽就等于圆的半径，从而可知，这个长方形的周长比原来圆的周长多出了两个半径的长度，据此即可求解.【解答】因为将圆拼成近似的长方形后，长方形的长就等于圆的周长的一半，宽就等于圆的半径，所以这个长方形的周长比原来圆的周长多出了两个半径的长度，即多出了一个直径的长度，也就是4厘米.14.【答题】如图的圆的半径是6cm，它的阴影部分面积是______.【答案】41.04【分析】阴影部分的面积等于圆的面积减去正方形的面积，正方形的对角线等于圆的直径，把这个正方形分成两个完全一样的三角形，根据三角形的面积公式和圆的面积公式，把数据代入公式解答.【解答】（平方厘米），答：阴影部分的面积是41.04平方厘米.15.【答题】圆的周长总是直径的______倍.一个圆的半径扩大到原来的3倍，那么它面积也跟着扩大到原来的______倍.【答案】π,9【分析】根据同圆或等圆中半径和直径之间的关系及圆周率的含义：圆的周长总是它的直径的3倍多一些，这个固定的倍数叫做圆周率，通常用字母π表示；因为S＝πr2，所以当圆的半径扩大到原来的3倍，面积扩大原来的9倍，由此得出答案.【解答】一个圆的周长总是它直径的π倍；当圆的半径扩大到原来的3倍，面积扩大到原来的9倍.16.【答题】在绕直径为4米的圆形水池周围铺一条1米宽的小路，小路的面积是______平方米.【答案】15.7【分析】求小路的面积，实际上就是求圆环的面积，即用外圆的面积减内圆的面积即可；由题意知，内圆的直径为4米，则半径为2米；外圆的半径为2＋1＝3米，分别求出内外圆的面积，问题得解.【解答】内圆的半径：4÷2＝2（米），小路的面积：（平方米）；答：小路的面积是15.7平方米.17.【答题】如图中，直角三角形（阴影部分）的面积是12平方厘米，圆的面积是______平方厘米.【答案】75.36【分析】观察图形可知，直角三角形的两条直角边是圆的半径，设圆的半径是r厘米，则根据三角形的面积公式可得：，由此可得出，把它代入圆的面积公式中即可计算.【解答】设圆的半径是r厘米，所以，，则，把它代入圆的面积公式可得：3.14×24＝75.36（平方厘米）；答：圆的面积是75.36平方厘米.18.【答题】已知如图中三角形的面积是10平方厘米，图中圆的面积是______平方厘米.【答案】62.8【分析】根据图意可知，三角形的面积等于圆的半径2÷2，所以圆的半径2＝10×2＝20，再将这一数据代入圆的面积公式计算即可解答.【解答】3.14×（10×2）＝62.8（平方厘米），答：圆的面积是62.8平方厘米.19.【答题】一张长方形纸的长是8分米，宽是6分米，把它剪成一个最大的圆，这个圆的面积是______平方分米.【答案】28.26【分析】这个最大的圆的直径就是这个长方形的宽6分米，利用圆的面积公式即可解答.【解答】（平方分米），答：这个圆的面积是28.26平方分米.20.【答题】小圆的半径是大圆的，小圆与大圆的直径比是______，面积比是______.【答案】3:5,9:25【分析】本题主要利用圆的周长公式与圆的面积公式解决问题.由大圆与小圆的半径比是5：3，设大圆与小圆的半径分别为、，它们的周长分别是、，；它们的面积分别是、，然后求出面积比和周长比，再根据比的基本性质化简比即可.【解答】由大圆与小圆的半径比是5:3，设大圆与小圆的半径分别为、，它们的周长分别是、，；它们的面积分别是、，所以小圆与大圆的直径比是，它们的面积比是.。

(青岛版)六年级数学完美的图形——圆的认识PPT课件

最新课件
14
练习：
1 判断：
（1）在同一个圆内可以画100条直径。（2）所有的圆的直径都相等。（3）等圆的半径都相等。（4）两端都在圆上的线段叫做直径。
2 口答：
(√ )
(× )
(√ )
(× )
r (米) 0.24 0.43 1.42 0.52 d(米) 0.48 0.86 2.84 1.04
21
H
9
直径和半径的关系
r•
r
do
最新课件
10
直径和半径的关系
r r
•r do
最新课件
11
直径和半径的关系
r
• do
r r
最新课件
12
想一想：
相等的两个圆中的半径和直径又有什么关系呢？
最新课件
13
在纸上画一个圆。并在小组内交流思考。
思考： 1、用圆规画圆分哪几步？ 2、圆画在纸上的位置与什么有关？ 3、圆的大小与什么有关？
完美的图形——圆
最新课件
1
最新课件
2
1.利用手中的工具，自己动手画个圆。
·
·o
·
最新课件
3
认识半径
· · o
·r
最新课件
4
• 自己在圆上画几条半径？你又发现了什么？什么长度相等？（你怎么知道的）
• 学生汇报自己所画圆的半径（刚才不是说圆的半径是相等的吗，为什么你们的数据不一样呢？）
最新课件
a
三角形底=8 cm 高=4cm
3厘米
圆的直径= 15 cm
长方形的宽=
15
cm 最新课件
小圆直径= 3 cm 小圆半径= 1.5 cm 18

小学数学青岛版(五四)五年级下册第一单元完美的图形——圆圆的认识-章节测试习题(3)

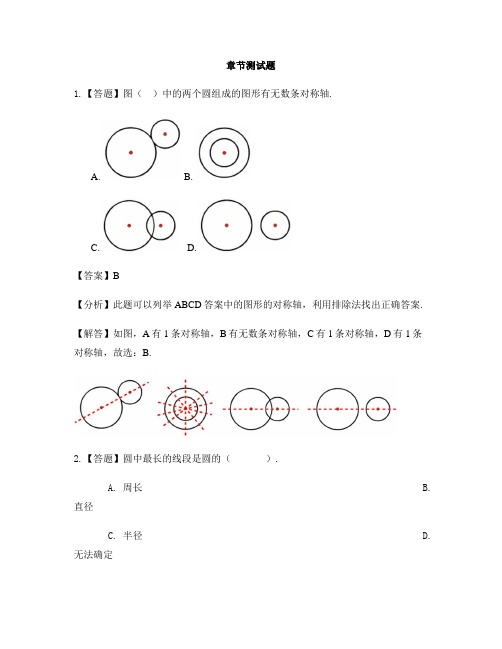
章节测试题1.【答题】图（）中的两个圆组成的图形有无数条对称轴.A. B.C. D.【答案】B【分析】此题可以列举ABCD答案中的图形的对称轴，利用排除法找出正确答案.【解答】如图，A有1条对称轴，B有无数条对称轴，C有1条对称轴，D有1条对称轴，故选：B.2.【答题】圆中最长的线段是圆的（）.A. 周长B. 直径C. 半径D. 无法确定【答案】B【分析】此题考查的是圆的认识.【解答】圆的直径是圆中最长的线段.选B.3.【答题】直径是通过圆心并且两端都在圆上的（）.A. 线段B. 直线C. 射线D. 以上都不是【答案】A【分析】此题考查的是圆的认识.【解答】通过圆心并且两端都在圆上的线段叫作直径.选A.4.【答题】圆的大小与（）有关.A.圆心B.半径C.圆周率【答案】B【分析】此题考查圆半径、圆心的作用：圆心确定圆的位置，半径决定圆的大小.【解答】圆的大小与半径有关.故选B.5.【答题】在下列图形中，（）有3条对称轴.A. 圆B. 正方形C. 长方形D. 等边三角形【答案】D【分析】依据轴对称图形的概念：将图形沿着一条直线对折，如果直线两侧的部分能够完全重合，这样的图形就是轴对称图形.折痕所在的这条直线就是这个图形的对称轴.据此解答即可.【解答】圆有无数条对称轴，正方形有4条对称轴，长方形有2条对称轴，等边三角形有3条对称轴.选D.6.【答题】下列图形中对称轴最少的是（）.A. 长方形B. 正方形C. 等腰梯形D. 圆【答案】C【分析】根据轴对称图形的概念：将图形沿着一条直线对折，如果直线两侧的部分能够完全重合，这样的图形就是轴对称图形.折痕所在的这条直线就是这个图形的对称轴.据此作答.【解答】A.长方形是轴对称图形，有2条对称轴；B.正方形是轴对称图形，有4条对称轴；C.等腰梯形是轴对称图形，有1条对称轴；D.圆形是轴对称图形，有无数条对称轴.则对称轴最少的是等腰三角形.选C.7.【答题】一张圆形纸片，至少需要折（）次，才能找到圆心.A. 1B. 2C. 3【答案】B【分析】圆中心的那个点即圆心，所有直径都相交于圆心，将一个圆形纸片最少要对折两次，才能找到两条折痕相交的那个点，即圆心.【解答】将一个圆形纸片最少要对折两次，才能找到两条折痕相交的那个点，即圆心.选B.8.【答题】圆中两端都在圆上的线段（）.A. 一定是圆的半径B. 一定是圆的直径C. 无法确定【答案】C【分析】此题考查的是圆直径的认识.通过圆心并且两端都在圆上的线段叫作直径.【解答】圆中两端都在圆上的线段无法确定是否是圆的直径.选C.9.【答题】下图中，这个圆的直径是（）.A. 11厘米B. 2.5厘米C. 3.5厘米【答案】B【分析】直径是圆内最长的线段.【解答】11－8.5=2.5（厘米），这个圆的直径是2.5厘米.选B.10.【答题】盒子内刚好放下5盒罐头（如图），每个罐头底面半径为3厘米，这个盒子的长度为（）厘米.（盒子的厚度忽略不计）A. 15B. 25C. 30【答案】C【分析】这个盒子的长度为：（罐头底面半径×2）×罐头的盒数5.【解答】(3×2)×5=30（厘米），所以这个盒子的长度是30厘米.选C.11.【答题】在长10厘米，宽8厘米的铁皮里剪一个最大的圆，圆的直径是（）.A. 10cmB. 5cmC. 16cmD. 8cm【答案】D【分析】解答此题应明确，在长方形中画一个最大的圆，圆的直径等于长方形短边的长.【解答】一个长方形的长是10厘米，宽是8厘米，在长方形内画一个最大的圆，圆的直径长是8厘米.选D.12.【答题】一个圆的直径是10厘米，则这个圆的半径是（）厘米.A. 20B. 5C. 10D. 40【答案】B【分析】根据在同一个圆中，圆的半径等于直径的一半，计算即可.【解答】10÷2=5（厘米），所以这个圆的半径是5厘米.选B.13.【答题】圆的大小与下面哪个条件无关？（）.A. 半径B. 圆心的位置C. 直径【答案】B【分析】根据圆心决定圆的位置，半径（直径）决定圆的大小，进行选择即可. 【解答】圆的大小和半径、直径有关，和圆心无关，圆心决定圆的位置.选B. 14.【答题】如图所示，线段（）.A. a是直径B. b是半径C. c是半径【答案】C【分析】此题考查的是直径、半径的概念.通过圆心并且两端都在圆上的线段叫做直径。

青岛版五四制五年级数学下册教案全册

一、完美的图形——圆单元教学内容：教科书的第2—22页，圆的认识、圆的周长和圆的面积。

单元教学目标：1、结合生活实际，通过观察、操作等活动，认识圆及圆的特征；认识半径、直径，理解同一圆中直径与半径的关系；会用圆规画圆。

2、结合具体情境，通过动手拼摆等活动，理解圆周率的意义，掌握圆周率的近似值；理解和掌握圆的周长与面积的计算公式，并能正确的计算圆的周长和面积。

3、在探索圆的周长与面积的计算公式的过程中，体会“化曲为直”、“化圆为方”的思想，建立“现实问题—数学问题—联想已有经验—寻求方法—总结归纳—解释应用”的“模型化”思想。

4、通过观察、操作、想象、图案设计等活动，发展空间观念。

5、结合具体情境，体验数学与日常生活的密切联系，能用圆的知识来解释生活中的简单现象，解决一些简单的实际问题。

6、通过了解圆周率的史料，感受数学的魅力，激发爱国的情感。

单元教学重点：理解并掌握圆的周长与面积公式，并能运用公式解决实际问题。

单元教学难点：圆的周长与面积公式的熟练运用。

教具与学具准备：多媒体课件、学具袋。

课时安排：教学过程：第一课时教学内容：教科书的第2、3页。

教学目标：1、使学生认识圆，知道圆的各部分名称。

2、使学生掌握圆的特征，理解和掌握在同一个圆里半径和直径的关系。

3、初步学会用圆规画圆，培养学生的作图能力。

4、培养学生观察、分析、抽象、概括等思维能力。

教学重点：理解和掌握圆的特征，学会用圆规画圆的方法。

教学难点：理解圆上的概念，归纳圆的特征。

教学准备：多媒体一套。

学生准备硬币等圆形物体若干；圆规一把、直尺一把、三角尺一副；小剪刀一把；红色、蓝色彩笔各一支。

教学过程；一、情景导入新课开始，老师用多媒体演示三种不同轮子（分别用三角形，长方形和圆做轮子）的汽车画面。

问：你喜欢哪种汽车，为什么？为什么车轮子一定要设计成圆形呢，你们知道这是为什么吗？今天这堂课，我们一起来探究这个问题。

（出示课题：圆的认识）师：在日常生活中，你见过哪些圆形物体？二、探索新知1、画圆：你们会画圆吗？自己尝试着画一个圆。

五四制青岛版五年级数学下册第一单元重难点题目解析

五四制青岛版五年级数学下册第一单元重难点题目解析完美的图形——圆在下面的正方形中画一个最大的圆。

思路分析：通过之前的学习，我们知道，对于一个圆来说，其圆心确定圆的位置，半径决定圆的大小。

要在这个正方形中画一个最大的圆，那这个圆的圆心就应该是正方形的中心（两条对角线的交点），圆的直径应该等于这个正方形的边长。

解答：先画出正方形的两条对角线，然后以对角线的交点为圆心，正方形边长的一半为半径画圆，所得的圆就是最大的圆。

如下图：如右图，已知长方形的长是36厘米，则圆的半径和直径分别是多少厘米？思路分析：从图中可以看出，长方形中间的完整的圆和两边的两个半圆的直径是相等的，都等于长方形的宽。

另外，两边的半圆的半径加上中间大圆的直径刚好等于长方形的长，所以长方形的长正好等于它们的半径的4倍，即用长方形的长除以4就可以求出它们的半径，再根据半径与直径的关系求出直径。

解答：24÷4=6（厘米） 6×2=12（厘米）答：圆的半径和直径分别是6厘米、12厘米。

要点提示：正方形的中心是正方形两条对角线的交点,也是最大圆的圆心。

要点提示：长方形的长正好等于圆的半径的4倍。

用两种方法把四个直径是16厘米的圆柱形木料捆扎在一起,截面如下图所示。

求这两种方法分别需要多少厘米的绳子。

图(1) 图(2),四个角上共四个思路分析：图(1)：在一个圆周上环绕的绳子长度是这个圆的周长的14圆周，正好是一个圆的周长,即3.14×16=50.24(厘米)。

四边两圆之间水平的线段,每条线段的长度正好等于两个圆的半径的和,也就是直径的长度,有4条线段,即水平线段的长度为4×16=64(厘米)。

,两边的两个圆周加起来图(2)：在一个圆周上环绕的绳子长度是这个圆的周长的12正好是一个圆的周长,即3.14×16=50.24(厘米)。

上面或下面相邻两个圆之间水平的线段,每条线段正好等于三个圆的直径的和,两条线段就是六个圆的直径的和,即6×16=96(厘米)。

小学五年级数学教案-青岛版五四制五年级数学下册教案全册

一、完美的图形——圆单元教学内容：教科书的第2—22页，圆的认识、圆的周长和圆的面积。

单元教学目标：1、结合生活实际，通过观察、操作等活动，认识圆及圆的特征；认识半径、直径，理解同一圆中直径与半径的关系；会用圆规画圆。

4、通过观察、操作、想象、图案设计等活动，发展空间观念。

5、结合具体情境，体验数学与日常生活的密切联系，能用圆的知识来解释生活中的简单现象，解决一些简单的实际问题。

6、通过了解圆周率的史料，感受数学的魅力，激发爱国的情感。

单元教学重点：理解并掌握圆的周长与面积公式，并能运用公式解决实际问题。

单元教学难点：圆的周长与面积公式的熟练运用。

教具与学具准备：多媒体课件、学具袋。

课时安排：教学过程：第一课时教学内容：教科书的第2、3页。

教学目标：1、使学生认识圆，知道圆的各部分名称。

2、使学生掌握圆的特征，理解和掌握在同一个圆里半径和直径的关系。

3、初步学会用圆规画圆，培养学生的作图能力。

4、培养学生观察、分析、抽象、概括等思维能力。

教学重点：理解和掌握圆的特征，学会用圆规画圆的方法。

教学难点：理解圆上的概念，归纳圆的特征。

教学准备：多媒体一套。

学生准备硬币等圆形物体若干；圆规一把、直尺一把、三角尺一副；小剪刀一把；红色、蓝色彩笔各一支。

教学过程；一、情景导入问：你喜欢哪种汽车，为什么？为什么车轮子一定要设计成圆形呢，你们知道这是为什么吗？今天这堂课，我们一起来探究这个问题。

（出示课题：圆的认识）师：在日常生活中，你见过哪些圆形物体？二、探索新知1、画圆：你们会画圆吗？自己尝试着画一个圆。

青岛版五四制五年级数学(下)全册备课

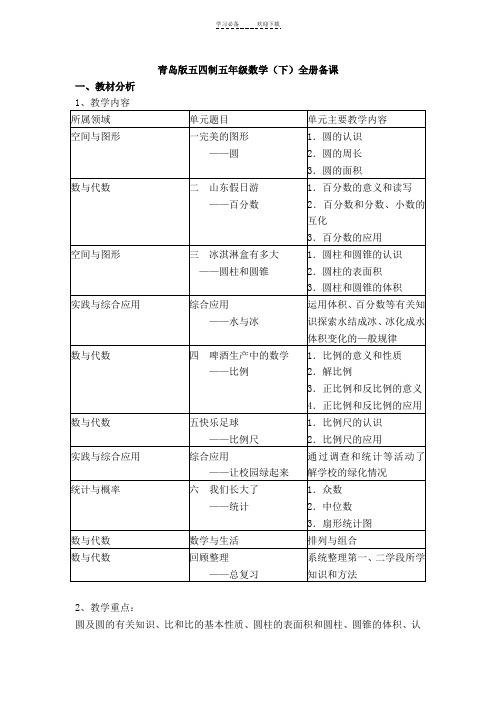
青岛版五四制五年级数学（下）全册备课一、教材分析2、教学重点：圆及圆的有关知识、比和比的基本性质、圆柱的表面积和圆柱、圆锥的体积、认识扇形统计图。

3、教学难点：圆柱和圆锥的体积计算。

解决实际问题三、改进教学的措施1．素材的选取具有现实性、科学性和时代性。

2．坚持“情境串”带动“问题串”，整合经验课程与学科课程。

3．从学生的认知规律和解决问题的需要出发，优化知识结构。

4．渗透数学思想方法，提高学生的数学素养。

5．注重数学与生活的联系，拓宽学生的视野。

四、教学中应注意的几个问题1．联系实际加强概念教学，融知识的理解于体验之中。

2．动手实践要把握好“度”，提高操作活动的有效性。

3．重视方程教学，初步建立代数观念。

4．加强探索方法的指导，提高自主探究的能力。

5．用好教材，做教材“再开发”的智者。

6．对学生学习情况的评价要全面、合理、科学。

五、学生情况分析本班有学生36人，学生学习基础教差的有8人，特别是乔永磊、赵孟超、吴韶腾、杨昆，其对基本技能的掌握特别差，学习习惯非常差，上课不能认真听讲，课后作业不能及时完成这些同学的学习习惯需要继续培养，其余大部分同学能够在班级里起到带动作用。

六、本学期打算学习的材料为了适应工作，深入开展课堂教学改革，新学期要继续学习《新课程标准》《二十一条军规》及有关心课程改革的论文，提高自身素质。

七、教学业务学习及有关的教研活动安排本学期要积极参加市、镇组织的教研活动，以及本校组织的各种教研活动，吸取校内外教师的教学经验，取长补短，提高自己的业务素质及教学成绩。

1、认真学习业务理论，大胆进行课堂教学改革。

2、加强集体备课，确定教学目标及教学重难点。

3、认真钻研教材，认真备课。

4、积极探索，引导学生自由合作学习。

的一半，宽相当于半径。

师：你能根据它们的关系，推出圆的面积公式吗？长方形的面积=长×宽圆的面积=c÷2×r=πr×r=πr2师：如果用s表示圆的面积，那么圆的面积公式可以写成：s=πr2师：黑板上的这个圆半径是10厘米，它的面积是多少？三、拓宽应用。

小学数学青岛版(五四)五年级下册第一单元完美的图形——圆圆的面积-章节测试习题(7)

章节测试题1.【答题】求图中阴影部分的面积.（单位：厘米）【答案】36.48平方厘米【分析】图中阴影部分的面积：用四个半圆即两个圆的面积减去正方形的面积即可.【解答】（平方厘米），答：图中阴影部分的面积是36.48平方厘米.2.【答题】一个圆形游乐场的周长是62.8米，扩建时，半径增加了1米，面积增加了多少平方米？【答案】65.94平方米【分析】根据题意可知，扩建时，半径增加了1米，求面积增加了多少平方米，也就是求这个环形的面积，已知内圆周长，首先求出内圆半径，根据环形面积＝外圆面积－内圆面积，由此列式解答.【解答】62.8÷3.14÷2＝10（米），10＋1＝11（米），（平方米），答：面积增加了65.94平方米.3.【答题】已知圆的面积为31.4平方厘米，求大小正方形的面积是多少平方厘米？【答案】大正方形的面积是40平方厘米；小正方形的面积是20平方厘米.【分析】由图形可知，圆的面积为31.4平方厘米，则半径的平方为：31.4÷3.14＝10，大正方形的边长等于圆的直径，根据正方形的面积公式：，即可求出大正方形的面积，小正方形的对角线的长度等于圆的直径，把小正方形沿对角线分成两个完全相同的三角形，根据三角形的面积公式：，三角形的高等于圆的半径，据此解答.【解答】解：设圆的半径为r厘米，，则（平方厘米）；大正方形的面积：（平方厘米）；小正方形的面积：（平方厘米）；答：大正方形的面积是40平方厘米，小正方形的面积是20平方厘米.4.【答题】一块边长是10米的正方形草地，在相邻的两边的中点各有一棵树，树旁各栓一只羊，羊绳子5米，两只羊都不能吃到的草地面积为多少平方米？【答案】35.75平方米【分析】根据题意，两只羊都不能吃到的草地面积为阴影部分面积，如图所示，图1、2、3的面积相等，先用半圆面积减去三角形OAB的面积即得图1与图2的面积之和，再用两个半圆面积之和（即圆面积）减去图1和2的面积，就是正方形内的空白部分面积，最后用正方形的面积减去空白部分面积，就是阴影部分面积.【解答】解：如图，（平方厘米）；（平方厘米）；（平方厘米）；答：两只羊都不能吃到的草地面积为35.75平方米.5.【答题】图形计算.（单位：厘米）（1）计算图形①中涂色部分的面积.（2）如图②中圆的周长是20厘米，如果圆的面积和长方形的面积相等，计算涂色部分的周长.【答案】（1）面积为6.88平方厘米；（2）周长25厘米【分析】（1）涂色部分的面积＝长方形的面积－半圆的面积，根据题意可知：长方形的长＝半圆的直径＝8，宽＝半圆的半径，分别计算出长方形的面积与半圆的面积，即能求出半圆的面积；（2）方法一：先根据圆的周长公式：，计算出圆的半径；再根据圆的面积公式：计算出圆的面积，即长方形的面积；根据长方形的宽＝圆的半径，计算出长方形的长；根据圆的周长计算出阴影部分中圆弧的长度；用圆弧的长度＋长方形的周长－2个半径的长度＝阴影部分的周长.这种做法因为都是四舍五入，与最精确答案有偏差，可以运用方法二比较精确：设圆的半径为r，则分别表示出圆的周长和面积，再根据圆的面积和长方形的面积相等，用r表示出阴影部分的周长，然后根据圆的周长已知，去掉r，得出阴影部分的周长.【解答】（1）8÷2＝4（厘米），（平方厘米）；（2）设圆的半径为r，则圆的周长：厘米，圆的面积：，长方形的面积：＝长×宽；根据題意：，即：＝长×宽，因为长方形的宽就是圆的半径，所以可以推出，长等于；所以涂色部分的周长是：答：图形①中涂色部分的面积是6.88平方厘米，涂色部分的周长是25厘米.6.【答题】公园里有一个直径为16米的圆形花圃，在它的周围环绕着一条2米宽的走道.现将走道也改成花圃，现在花圃的面积是多少？【答案】314平方米【分析】由题意可知：现在的花圃也是一个圆形的，其半径为16÷2＋2＝10米，从而利用圆的面积即可求出现在花圃的面积.【解答】（平方米），答：现在花圃的面积是314平方米.7.【答题】求图中阴影部分的周长和面积.【答案】阴影部分周长为18.84厘米；阴影部分的面积为2.28平方厘米.【分析】（1）阴影部分的周长可看作由下面几部分组成：大圆周长的一半、中间小圆的周长、下面两个小半圆周长的一半，并且小圆直径和两个小半圆直径都相等，根据圆的周长公式解答即可；（2）求阴影部分的面积可作几条辅助线，如图：将阴影1、2、3、4分别移到空白1、2、3、4，处，那么用大半圆的面积减去大三角形的面积即阴影部分的面积，据此解答.【解答】阴影部分周长：3.14×4÷2＋3.14×(4÷2)×2＝18.84（厘米），阴影部分的面积：3.14×(4÷2)2÷2－4×(4÷2)÷2＝2.28（平方厘米），答：阴影部分周长为18.84厘米，面积为2.28平方厘米.8.【答题】求下面阴影部分的面积.【答案】86平方厘米【分析】用正方形的面积减去一个半径是10厘米的圆的面积，就等于阴影部分的面积.【解答】（平方厘米），答：下面阴影部分的面积是86平方厘米.9.【答题】—个花坛（如下图），两端是半径为l0m的半圆，中间是长为30m的长方形.这个花坛的周长是多少米？面积是多少平方米？【答案】这个花坛的周长是122.8米，面积是914平方米.【分析】花坛的周长相当于半径为10m的圆的周长与长为30m的两条线段的长度的和；花坛的面积是一个半径为10m的圆的面积加上一个长是30m，宽是20m的长方形的面积.【解答】30×2＋3.14×2×10＝122.8（米）；30×10×2＋3.14×10×10＝914（平方米），答：这个花坛的周长是122.8米，面积是914平方米.10.【答题】求阴影部分的面积.（单位：厘米）【答案】75.36平方厘米【分析】根据环形面积公式：，把数据代入公式进行解答.【解答】（平方厘米），答：阴影部分的面积是75.36平方厘米.11.【答题】求下图中阴影部分的面积.【答案】200平方厘米【分析】认真观察图形，阴影部分和空白部分的面积相等，因此只要求出整个图形的面积再除以2就是阴影部分的面积.【解答】解：20×20÷2＝200（平方厘米），答：图中阴影部分的面积是200平方厘米.12.【答题】①画一个周长是6.28厘米的圆；②计算这个圆的面积.【答案】①如下图，②3.14平方厘米【分析】根据题意周长为6.28厘米，先计算出圆的半径，然后利用圆规画圆.再计算面积.【解答】6.28÷2÷3.14＝1（厘米）；3.14×1×1＝3.14（平方厘米），答：画图如下，这个圆的面积是3.14平方厘米.13.【答题】求下图中阴影部分的面积.（单位：厘米）【答案】2平方厘米.【分析】仔细观察图，本题不能直接计算阴影部分的面积，因此要采取减法计算.用第一个长方形与和它相邻的圆面积的和减掉空白圆的面积，剩下的就是阴影部分的面积.【解答】解：2×1＋3.14×2×2÷4－3.14×2×2÷4＝2（平方厘米），图中阴影部分的面积是2平方厘米.14.【答题】求下图阴影部分的面积.（单位：米）【答案】21.5平方米【分析】观察发现四个小扇形的面积能拼成一个圆，所以阴影部分的面积等于正方形的面积减去半径是5厘米的圆的面积.【解答】（平方米），答：图中阴影部分的面积是21.5平方米.15.【答题】计算如图中圆环（阴影部分）的面积.（R＝10厘米，r＝6厘米）【答案】200.96平方厘米【分析】根据环形面积公式，把数据代入公式进行解答.【解答】（平方厘米），答：圆环的面积是200.96平方厘米.16.【答题】一个钟表的分针长10厘米，它转一圈指针扫过的面积是多大？【答案】314平方厘米【分析】分针要走过1圈，分针走过的路程也就是一个以分针的长度10厘米为半径的圆，求分针针尖所扫过的面积就是求半径是10厘米的圆面积，由此利用圆的面积公式即可解答.【解答】（平方厘米），答：它转一圈指针扫过的积是314平方厘米.17.【答题】计算如图阴影部分的面积，已知d＝6厘米.【答案】3.87平方厘米【分析】阴影部分的面积是长6厘米，宽为6÷2＝3厘米的长方形的面积减去半径为6÷2＝3厘米的圆面积的一半，据此根据长方形的面积公式：和圆的面积公式：代入数据进行解答即可.【解答】解：（平方厘米），答：图中阴影部分的面积是3.87平方厘米.18.【答题】明明有一根长60厘米的铁丝围了一个最大的圆.亮亮说：“如果我画一个半径为10厘米的圆，肯定比你围的圆的面积大”.哪个圆的面积大呢？请你帮忙做出判断，并说明理由.【答案】亮亮画的圆的面积大.【分析】根据圆的周长公式：，求出半径为10厘米的圆的周长，与60厘米比较大小即可求解.【解答】解：3.14×10×2＝62.8（厘米），因为62.8厘米＞60厘米，所以亮亮画的圆的面积大.19.【答题】求出下列阴影部分的面积（单位：厘米）.【答案】第一个图形阴影部分的面积是（平方厘米），答：第一个图形阴影部分的面积是37.68平方厘米；第二个图形阴影部分的面积是（平方厘米），答：第二个图形阴影部分的面积是13.76平方厘米.【分析】图形一根据求圆环的面积公式求出阴影部分的面积，图形二根据用边长8厘米的正方形面积减去直径为8厘米的圆形的面积，依此进一步得解.【解答】（平方厘米），答：第一个图形阴影部分的面积是37.68平方厘米；（平方厘米），答：第二个图形阴影部分的面积是13.76平方厘米.20.【答题】计算如图阴影部分的面积，已知d＝6厘米.【答案】阴影部分的面积是3.87平方厘米【分析】阴影部分的面积是长6厘米，宽为6÷2＝3厘米的长方形的面积减去半径为6÷2＝3厘米的圆面积的一半，据此根据长方形的面积公式和圆的面积公式代入数据进行解答即可.【解答】（平方厘米），答：阴影部分的面积是3.87平方厘米.。

五四制小学青岛版数学配套练习册五下参考答案

青岛版数学配套练习册五年级下册参考答案（五·四学制）一　完美的图形———圆信息窗１练习设计４．（１）√　（２）（３）√信息窗２练习设计１．（１）（２）（３）√　２．（１）Ａ　（２）Ｃ　（３）Ａ３．６２．８ｃｍ　３１．４ｃｍ　４．１２５．６ｃｍ　４．７１ｄｍ６．１８８．４厘米　７．６２．８米　８．１２．２８米　９．１５７棵信息窗３练习设计１．７８．５ｃｍ２　１１３．０４ｃｍ２　２．（１）３．１４平方米　（２）６．２８米　３．１２．５６平方米４．２８．２６平方米　５．９４．２厘米　７０６．５平方厘米６．６２．８平方厘米　５８．８７５平方厘米　７．１５．７平方米我学会了吗？２．（１）（２）（３）√　５．（１）１５０．７２米（２）２００．９６平方米　６．５０２４平方米　２５１．２米７．３１４厘米　８．１２．５６平方米　９．５０．２４ｃｍ２　２７．８７ｃｍ２　１０．９．８５９６ｃｍ２　１２．５６ｃｍ２１１．（１）２３５．５平方米　（２）１６棵１２．（１）１８５．１２ｄｍ２　（２）５２．５６ｄｍ二　体检中的百分数———百分数（一）信息窗１练习设计６．（１）（２）（３）√　７．５４％　４６％相关链接练习设计７．科普书　８．乙工厂　信息窗２练习设计１．８０％　２．９２％　８％　５．９６％　６．９５％７．９９％　９９．２％　９９％　第二天　８．９０．９％我学会了吗？４．（１）（２）（３）（４）（５）（６）５．（１）８７．５％　（２）张华智慧广场１８张　３２张　２１２０棵　３２棵　３１５人　３５人４６只　８只　５５０张　１５０张　三　欢乐农家游———百分数（二）信息窗１练习设计１（１）２０　（２）１２０　（３）２０３４０％　４２５％　５１０％　６３３．３％　７２０％　８５５％　信息窗２练习设计１（１）６５　（２）９０　（３）１１５　（４）２５　（５）二　２甲桶２．４千克　乙桶２．８千克　３（１）２２．５元　（２）９０元　４（１）２４个　（２）１２０个　５（１）３２棵（２）２０棵　６（１）８８２千克　（２）５０００千克　７（１）４页　（２）４４页　８４４元　９８０页　１０（１）８００吨（２）８８０吨　１１（１）３００人　（２）３００人信息窗３练习设计１（１）九　（２）六六　（３）８０　９５　５０　１０　７５　５０　（４）９０　（５）４９．５　２１９６０元　３８０元４（１）能。

青岛五四学制版五年级数学下册一完美的图形——圆《信息窗三(圆的面积)》一等奖创新教案

青岛五四学制版五年级数学下册一完美的图形——圆《信息窗三（圆的面积）》一等奖创新教案圆的面积教学设计一.概述：圆的面积是教科书（青岛版五四学制）数学五年级下册，第一单元《完美的图形》第三课时的教学内容。

本节课主要是通过学生动手操作、自主探索、推导出圆的面积公式和应用圆的面积公式解决实际问题二、教学目标分析：知识与技能：1、让学生经历操作、观察、验证、讨论和归纳等数学活动的过程，探索并掌握圆的面积公式，能正确计算圆的面积，并能应用公式解决相关的简单实际问题。

2、培养学生观察、分析、归纳的能力，以及逻辑推理能力3、培养学生灵活运用公式解决实际问题的能力过程与方法：1、引导学生学会利用已有知识，运用数学思想方法，动手实践，推导、归纳出圆的面积计算公式。

2、渗透极限、转化、以直代曲等数学思想方法，发展学生的空间观念让学生进一步体会“转化”的数学思想方法，培养运用以有知识解决新问题的能力，增强空间观念，发展数学思考。

情感态度价值观：通过实例引入，让学生体验数学来源于生活，又服务于生活；向学生展示生动、活泼的数学天地，唤起学生学习数学的兴趣，使全体学生积极参与探索，在参与中体验成功的乐趣。

培养学生认真观察、深入思考的良好思维品质，体验自主发现新知的快乐，培养学生数学的兴趣。

重点：圆的面积计算公式的推导和应用三、教学准备教具：多媒体课件.自制圆形学具四、教学过程：一、情境导入出示场景——《马儿的困惑》师：同学们，你们知道马儿吃草的大小是一个什么图形呀？生：是一个圆形。

师：那么，要想知道马儿吃草的大小，就是求圆形的什么呢？生：圆的面积。

师：今天我们就一起来学习圆的面积。

（板书课题：圆的面积）师：大家看，一匹马被拴在小树上，它吃草的面积是多少？从图中，你知道了哪些信息？【设计意图：在教学过程的伊始就用这个生活中的数学问题来导入新课的学习，既可以激起学生学习的兴趣，又可以为后面圆面积的学习奠定基础，更可以让学生从课堂上涉猎生活中的数学问题，让学生体验到数学来源于生活。

青岛版五四制五年级下册数学课件圆的认识

1号
2号
是半径。因为它是连接圆心到圆上一点的线段。
3号
4号
判断：那条是圆的直径？
不是直径。因为它的另一端不在圆上
1号
不是直径。因为它两端都不在圆上。
3号
2号 4号
不是直径。因为没有经过圆心。
是直径。因为它经过圆心并且两端都在圆上。
用圆规画圆
画一个半径是2cm的圆，并用字母O，r ，d 标
3、思考：你们发现了什么？并填写记录单。
探究半径的特征：
• o
半径的在同一个圆里，有（无数）条半径，特征：它们的长度都（相等）
探究直径的特征：
• o
直径的在同一个圆里，有（无数）条直径，特征：它们的长度都（相等）
半径与直径的关系: r• r do
半径与直径的关系:
研究的问题
1、圆有几条半径？ 2、半径的长度相等吗？
3、圆有几条直径？ 4、直径的长度相等吗？
5、圆的直径和半径有什么关系？ 6、为什么？ 7、······
研究提纲
1、计划：（1）选择你感兴趣的问题进行研究。（2）想想你用哪些方法进行研究？（折一折、画一画、量一量、其它方法）
2、行动：同桌合作，用圆形纸片操作。
“圆—— 一中同长也 ” 。这个定义比希腊数学家
欧几里得给圆下定义要早 1000多年。
墨子
圆心到圆上任意一点的距离都相等。
为什么车轮要做成圆的？车轴应装在哪里？
你能用这节课所学的知识，
从数学的角度来解释一下吗？
这是利用圆心到圆上任意一点的距离都相等的特性，车轴放在圆心的位置，车轮滚动时车轴保持安稳状态，使行进的车辆也保持安稳状态。

青岛版五四制五年级数学下册《完美的图形——圆》知识点汇总

一完美的图形——圆一、圆的定义感知圆的特征:以前学过长方形、正方形、平行四边形、梯形、三角形等,都是由线段围成的平面图形,而圆是由曲线围成的一种平面图形。

二、圆的各部分名称1.圆心:用圆规画出圆以后,针尖固定的一点就是圆心,通常用字母O表示。

2.半径:连接圆心和圆上任意一点的线段叫作半径,一般用字母r表示。

把圆规两脚分开,两脚之间的距离就是圆的半径。

3.直径:通过圆心并且两端都在圆上的线段叫作直径,一般用字母d表示。

直径是一个圆内最长的线段。

三、圆的主要特征1.在同圆或等圆内,有无数条半径,有无数条直径。

所有的半径都相等,所有的直径都相等。

2.在同圆或等圆内,直径的长度是半径的2倍,半径的长度是直径的12。

用字母表示为d=2r或r=d2。

3.如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形。

圆是轴对称图形且有无数条对称轴。

4.画圆的方法:(1)用手指画圆。

以大拇指为圆心,以食指与大拇指之间的距离为半径,旋转一周所形成的图形就是圆。

(2)用线绳、图钉和笔画圆。

用图钉固定线绳的一端作圆心,将笔系在线绳的另一端,拉直绳子作半径,旋转线绳一周所形成的图形就是圆。

(3)用圆规画圆。

将圆规的一个针脚固定在本上作圆心,用圆规两脚间的距离作半径,旋转圆规一周所形成的图形就是圆。

(4)用物体的圆形面画圆。

按住物体的圆形面,用笔在物体的圆形面的圆周上画一圈,所形成的图形就是一个圆。

四、圆的周长的认识1.围成圆的曲线的长叫作圆的周长。

2.圆的周长与圆的直径有关,圆的直径越长,圆的周长就越大。

五、圆周率的意义及圆的周长公式1.圆周率实验:在圆形纸片上做个记号,与直尺0刻度线对齐,在直尺上滚动一周,求出圆的周长。

2.发现一般规律,就是圆的周长比它的直径的3圆与其他平面图形不同,圆是由曲线围成的。

直径和半径的关系只能在同圆和等圆中。

用字母表示:d=2r。

不能说直径是圆的对称轴。

因为对称轴是一条直线。

小学数学青岛版(五四)五年级下册第一单元完美的图形——圆圆的面积-章节测试习题(3)

章节测试题1.【答题】一个圆的半径是2米，它的直径是______米，周长是______米，面积是______平方米．【答案】4,12.56,12.56【分析】圆的直径是半径的2倍，所以其直径为2×2＝4（米），圆的周长公式和圆的面积公式，已知半径、周长、面积据公式求出即可.【解答】直径为2×2＝4（米）；周长为2×2×3.14＝12.56（米）；面积为3.14×2×2＝12.56（平方米）.2.【答题】在推导圆的面积计算公式时，将圆分成32等份，拼成一个近似的长方形.已知长方形的周长比圆的周长增加4分米，那么这个圆的周长是______分米，这个长方形的面积是______平方分米．【答案】12.56,12.56【分析】在推导圆的面积计算公式时，将圆分成32等份，拼成一个近似的长方形，它的周长就比圆的周长增加了圆的两个半径.求出圆的半径，然后根据周长公式求出其周长，长方形的面积等于圆的面积.据此解答.【解答】2×3.14×(4÷2)＝12.56（分米）；3.14×(4÷2)2＝12.56（平方分米）.3.【答题】把一根长6.28分米的铁丝围成一个最大的圆，它的面积是______平方分米．【答案】3.14【分析】根据圆的周长公式列出算式先求出半径，再根据圆的面积公式列出算式求解.【解答】6.28÷3.14÷2＝1（分米）；3.14×12＝3.14（平方分米）.4.【答题】一个钟表，分针长40厘米，一小时分针所扫过的面积是______平方厘米．【答案】5024【分析】此题实际上是求半径为40厘米的圆的面积，利用圆的面积公式即可求解.【解答】3.14×40×40＝5024（平方厘米）.5.【答题】一个圆的直径是10分米，它的周长是______分米，面积是______平方分米．【答案】31.4,78.5【分析】根据圆的周长公式和圆的面积公式列出算式求解.【解答】3.14×10＝31.4（分米）；3.14×(10÷2)2＝78.5（平方分米）.6.【答题】一个圆的周长是25.12厘米，这个圆的直径是______厘米，面积是______平方厘米．【答案】8,50.24【分析】先依据圆的周长公式求出圆的直径，进而再用圆的面积公式即可求解.【解答】25.12÷3.14＝8（厘米）；3.14×(8÷2)2＝50.24（平方厘米）.7.【答题】一个圆的半径是3厘米，面积是______平方厘米．【答案】28.26【分析】根据圆的面积公式列出算式求解.【解答】3.14×3×3＝28.26（平方厘米）.8.【答题】从一个边长是10分米的正方形纸里剪一个最大的圆，这个圆的周长是______分米，面积是______平方分米．【答案】31.4,78.5【分析】抓住“最大的圆就是直径等于正方形边长的圆”，利用圆的周长公式和圆的面积公式即可解决问题.【解答】3.14×10＝31.4（分米）；3.14×(10÷2)2＝78.5（平方分米）.9.【答题】图中的圆有______条对称轴，如果圆的半径是3cm，那么圆的面积是______cm2，长方形的面积是______cm2．【答案】2,28.26,72【分析】依据轴对称图形的概念，即在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能完全重合，这样的图形叫做轴对称图形，据此即可进行判断；观察图形可知，这个长方形的长是2×3×2＝12（厘米），宽是3×2＝6（厘米），根据圆的面积公式、长方形的面积公式解答即可.【解答】如图，图中有2条对称轴；圆的面积是3.14×3×3＝28.26（平方厘米）；长方形的面积是(2×3×2)×(3×2)＝72（平方厘米）.10.【答题】两个圆的周长之比是2:3，它们的半径之比是______，面积之比是______．【答案】2:3,4:9【分析】根据题意，假设圆的周长分别是和，由圆的周长公式求出大小圆的半径，再根据圆的面积公式可以求出大小圆的面积，最后根据比的意义就可以求出它们的半径的比和面积比.【解答】设大圆的周长是，小圆的周长是，由圆的周长公式可知，大圆的半径是1.5，小圆的半径是1，所以它们半径之比是1:1.5＝2:3；面积之比是(3.14×1×1):(3.14×1.5×1.5)＝4:9.11.【答题】如果大小两个圆的半径比是2:1，那么大小两个圆的面积的比是______．【答案】4:1【分析】由“大小两个圆的半径比是2:1”，设小圆的半径为r，则大圆的半径为2r，分别代入圆的面积公式，表示出各自的面积，再写出相应的比即可.【解答】设小圆的半径为r，大圆的半径为2r，则小圆的面积是，大圆的面积是，所以大小两个圆的面积之比是.12.【答题】在正方形里画一个最大的圆，正方形的边长是圆半径的______，正方形的面积与圆的面积的比是______．【答案】2倍,4:π【分析】分析题意，知道圆的直径就是正方形的边长，求它们的面积比，需要求出它们各自的面积，然后再比.因此要设圆的半径是r，正方形的边长就是2r，利用圆的面积公式和正方形的面积公式表示出来.【解答】在正方形里画一个最大的圆，正方形的边长是圆半径的2倍；设圆的半径是r，正方形的边长就是2r，圆的面积是，正方形的面积是，所以正方形的面积与圆的面积的比是.13.【答题】如果小圆的直径等于大圆的半径，那么小圆面积是大圆面积的（）A.B.C. 2倍【答案】B【分析】本题考察的知识点是圆的面积.【解答】根据圆的面积公式可得答案为B.14.【答题】要剪一个面积是12.56平方厘米的圆形纸片，至少需要面积是（）平方厘米的正方形纸片（π取3.14）．A. 12.56B. 14C. 16D. 20【答案】C【分析】本题考察的知识点是圆的面积和正方形的关系.【解答】根据圆的面积公式，求出一个半径，最后得出正方形的面积.15.【答题】圆的半径扩大4倍，这个圆的面积扩大（）A. 8B. 12C. 16【答案】C【分析】本题考察的知识点是圆的面积.【解答】根据圆的面积的计算公式圆的半径扩大4倍，那么面积扩大16倍.16.【答题】有大、小两个圆，大圆半径是5厘米，小圆半径是4厘米，小圆面积是大圆面积的（）A.B.C. 倍【答案】B【分析】本题考察的知识点是圆的面积.【解答】根据圆的面积的计算公式，可以得出答案选B.17.【答题】如图，已知正方形的面积是36cm2，那么圆的面积是（）A. 9πcm2B. 18πcm2C. 36πcm2【答案】A【分析】本题考察的知识点是圆的面积的计算.【解答】根据圆的面积计算公式，以及半径与直径的关系可以得出答案选A.18.【答题】如图，阴影部分的面积是（）平方分米.（π取3.14）A.6.28B.12.56C.25.12D.28.26【答案】B【分析】此题考查的是圆的面积计算公式.【解答】圆的面积＝πr².图中小圆的直径是4分米，半径是2分米，半圆的半径是4分米.求半圆的面积，列式计算为：求小圆的面积，列式计算为：求阴影部分的面积，用半圆的面积减去小圆的面积，列式计算为：25.12－12.56＝12.56（平方分米）.故此题选B.19.【答题】两张正方形硬纸板，一张剪去1个圆，另一张剪去4个圆（如下图）.剩下的废料相比，（）.A.剪1个圆剩下的多B.剪4个圆剩下的多C.剩下的一样多【答案】C【分析】此题考查的是圆的面积.【解答】假设正方形的边长为a，，则左边圆的半径是0.5a，左边的一个圆的面积为：π×0.5a×0.5a＝0.25πa²，右边圆的半径是0.25a，右边四个圆的面积为：4×π×0.25a×0.25a＝0.25πa²，两边剪去的图形面积相等，所以剩下的一样多.故此题选C.20.【答题】如下图，正方形ABCD的面积是60平方厘米，以A为圆心、AB为半径画一个圆.阴影部分的面积是（）平方厘米.（π取3.14）A.12.9B.13.8C.47.1【答案】A【分析】此题考查的是不规则图形的面积.【解答】由图可知，阴影部分的面积等于正方形ABCD的面积减去个圆的面积.圆的面积＝πr²，由图可知，正方形的边长是圆的半径，所以正方形的面积等于r²，即圆的面积是：3.14×60＝188.4（平方厘米）；个圆的面积是：188.4×＝47.1（平方厘米）；所以阴影部分的面积是：60-47.1＝12.9（平方厘米）.故此题选A.。

青岛版五四制五年级下册数学第一单元第2课《圆的周长》课件

祈年殿殿顶周长是100米。
你能提出什么问题？
圆的周长是什么？
围成圆的曲线的长,就是圆的周长
合作探究
祭天台上层圆台的周长是多少米？
求它的周长就是求圆的周长
圆的周长与什么有关系呢？
我猜周长与半径有关系。
可能与直径有关系。
测量几个圆的直径和周长，看它们有什么关系。
怎样测量1分硬币的周长？
方法一、用绳子绕硬币一圈，再量绳子的长度。
情景导入
你知道吗？
生活中你还见过哪些物体的形状是圆形的？与同学交流一下。
圆被誉为最完美的图形。我们在生活和生产中，随处都能见到圆的踪影，感受到圆的魅力。
美丽的天坛
天坛主要是由圜丘和祈谷（祈年殿）两坛组成。
圜丘坛俗称祭天台。共有三层，上层圆台的直径是 30米，中层直径是50米，下层直径是70米。
上层圆台的直径是30米，中层直径是50米，下层直径是70米。
解题思路：
易错题型祈年殿殿顶的直径是多少米？
易错提醒：
方法一：用方程解。
解：设祈年殿殿顶的直径是x米。
x x 3.14 = 100
x x 3.14 ÷3.14 = 100 ÷ 3.14。 d＝c÷ π ＝100÷ 3.14
学以致用
1、求下面各圆的周长。
3.14×20=62.8(cm) 3.14×4×2=25.12(dm)
学以致用
2、请将下面的表格补充完整。（单位：米）
圆的半径 2 5 10
圆的直径 4 10
20
圆的周长 12.56 31.4 62.8
(1)今天我学习了圆周长的知识。我知道圆
课堂小结周率是( 周长)和( 直径)的比值，它用字母
除不尽时，得数一般保留两位小数。

青岛版五四制小学五年级数学下册全套教案

完美的图形——圆【教学目标】知识与技能：认识圆，知道各部分的名称，掌握圆的特征，知道同一圆内半径、直径的特征，理解在同一个圆里直径与半径的关系，初步学会用圆规画圆。

过程与方法：培养学生的观察、分析、抽象、概括等思维能力和初步的空间观念，使学生初步学会用数学知识解释、解决生活中的实际问题。

情感态度价值观：通过学生自己动手操作探究圆的简单特征，激发学生学习的兴趣，通过折、量、比、算等方式让学生体会合作学习的乐趣。

【教学重点】圆的各部分名称及直径与半径之间的关系。

【教学难点】用圆规按要求画圆。

【教学准备】课件，圆规。

学具准备：长方形纸、圆规、直尺、三角板等。

【教学过程】（一）创设情境，导入新知。

师：同学们，今年的里约奥运会你们看了吗？奥林匹克的标志是什么你们注意了吗？（学生齐说“奥运五环”）那它是由什么组成的呢？是由五个圆环组成的。

那么我们生活中还有什么是圆形的呢？哪位同学来说一下？生1：井盖，硬币，妈妈的戒指，蛋糕。

生2：车轮，风扇。

师：圆形的物体无时无刻不存在于我们的生活中，现在就让我们一起来认识一下圆。

（板书）（二）启发诱导，领会新知。

师：请同学们自由发挥画一个圆。

学生独立画圆。

师：大家都画完圆了吗？哪位同学能和同学分享一下你是怎么画的圆吗？生1：用圆形的瓶盖画的圆。

生2：自己随手画的圆。

师：比较一下，以前学过的平面直线图形，与你刚才画的圆有什么不同呢？（学生积极回答）师：圆是平面上的一种曲线图形。

师：怎样才能画出一个规范的圆呢？给大家介绍一种画圆的仪器——圆规。

请大家拿出圆规我们一起来认识一下它，圆规由三部分组成，一部分是有铅笔的一脚，一部分是有针尖的一脚，最后一部分是手柄。

师：现在请大家尝试用圆规画一个圆，然后和同桌交流你是怎么画的。

学生独立用圆规画圆。

师：哪位同学愿意起来展示一下你画的圆和你用圆规画圆的方法。

生：用圆规画圆时，先把圆规的两脚分开，定好两脚之间的距离，再把有针尖的一脚固定在一点上，把有铅笔的一脚旋转一周。