等差数列与等比数列知识总结
小学等差等比数列知识点归纳总结

小学等差等比数列知识点归纳总结【小学等差等比数列知识点归纳总结】数列是数学中一个重要的概念,它由一系列按照特定规律排列的数所组成。
在小学阶段,学生们将接触到两种常见的数列,即等差数列和等比数列。
本文将对小学等差等比数列的知识点进行归纳总结。
一、等差数列(Arithmetic Progression)等差数列是指数列中相邻两项之差相等的一种数列。
等差数列的通项公式为:an = a1 + (n - 1)d,其中an表示第n项,a1表示首项,d表示公差。
1. 公差等差数列中,相邻两项之差称为公差。
公差可以是正数、负数或零。
2. 首项等差数列中的第一项称为首项,通常表示为a1。
3. 通项公式等差数列中的通项公式可以通过首项和公差来计算任意一项的值。
4. 前n项和公式等差数列的前n项和公式为Sn = (n/2)(a1 + an),其中Sn表示前n项和。
二、等比数列(Geometric Progression)等比数列是指数列中相邻两项之比相等的一种数列。
等比数列的通项公式为:an = a1 * r^(n-1),其中an表示第n项,a1表示首项,r表示公比。
1. 公比等比数列中,相邻两项之比称为公比。
公比可以是正数或负数,但不能为零。
2. 首项等比数列中的第一项称为首项,通常表示为a1。
3. 通项公式等比数列中的通项公式可以通过首项和公比来计算任意一项的值。
4. 前n项和公式等比数列的前n项和公式为Sn = (a1 * (r^n - 1))/(r - 1),其中Sn表示前n项和。
三、等差数列与等比数列的关系等差数列和等比数列都是数学中常见的数列形式。
它们之间存在一定的联系。
1. 等差数列的前n项和与等差数列的平均数等差数列的前n项和可以表示为Sn = n * (a1 + an)/2,其中an表示第n项。
而等差数列的平均数可以表示为(a1 + an)/2,即首项与末项的平均值。
2. 等差数列的前n项和与等比数列的前n项和之比当等比数列的公比为1时,等比数列变为等差数列。
(完整版)高考等差等比数列知识点总结

1高考数列知识点等差数列1.等差数列的定义:d aa n n=--1(d 为常数)(2≥n );2.等差数列通项公式:*11(1)()n a a n d dn a d n N =+-=+-∈ , 首项首项首项::1a ,公差,公差:d :d :d,末项,末项,末项::n a推广: d m n a a m n )(-+=. 从而mn a a d m n --=; 3.等差中项(1)如果a ,A ,b 成等差数列,那么A 叫做a 与b 的等差中项.即:2ba A +=或b a A +=2(2)等差中项:数列{}n a 是等差数列)2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a4.等差数列的前n 项和公式:1()2n n n a a S +=1(1)2n n na d -=+211()22dn a d n =+-2An Bn =+(其中(其中A A 、B 是常数,所以当是常数,所以当d d ≠0时,时,S S n 是关于是关于n n 的二次式且常数项为的二次式且常数项为00) 特别地()()()12121121212n n n n a a S n a +++++==+5.等差数列的判定方法(1) 定义法:若d a a n n=--1或d a an n =-+1(常数*∈N n )⇔ {}n a 是等差数列.是等差数列. (2) 等差中项:数列{}na 是等差数列)2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a .(3) 数列{}n a 是等差数列⇔b kn a n +=(其中b k ,是常数)。
是常数)。
(4) 数列{}n a 是等差数列⇔2n S An Bn =+,(其中(其中A A 、B 是常数)6.等差数列的证明方法定义法:若d a a n n=--1或d a an n =-+1(常数*∈N n )⇔ {}n a 是等差数列7.等差数列的性质: (1)当公差0d ≠时,等差数列的通项公式11(1)n a a n d dn a d =+-=+-是关于n 的一次函的一次函 数,数,且斜率为公差d ;前n 和211(1)()222n n n d d S na d n a n -=+=+-是关于n 的二次函数且常数项为0. (2)若公差0d >,则为递增等差数列,若公差0d <,则为递减等差数列,若公差0d =,则为常数列。
等差、等比数列公式总结

一、等差数列1.定义:)(1常数d a a n n =-+2.通项公式:d n a )1(a 1n -+=3.变式:d m n a m n )(a -+= m n a a d m n --=4.前n 项和:2)(1n a a S n n += 或 d n n n a S n 2)1(1-+= 5.几何意义:①d dn a d n a a n -+=-+=11)1(即q pn a n += 类似 q px y += ②n d a n d S n )2(212-+= 即 Bn An S n +=2 类似 Bx Ax y +=2 6.}{n a 等差d a a a a a Bn An S q pn a n n n n n n n =-⇔+=⇔+=⇔+=⇔++-11122 7.性质① q p n m +=+则 q p n m a a a a +=+② p n m 2=+ 则 p n m a a a 2=+③ Λ=+=+=+--23121n n n a a a a a a④ m S 、m -m 2S 、2m -m 3S 等差⑤ }{n a 等差,有12+n 项,则n S S 1n +=偶奇 ⑥ 1212-=-n S a n n 二、等比数列1.定义:常数)(a 1q a n n =+ 2.通项公式:11a -=n n q a3.变式: m n m n q a -=a m n mn q a a -= 4. ⎪⎩⎪⎨⎧≠--==)1( 1)1()1( 11q qq a q na S n n 前n 项和:n a S n 1= )1(=q 或 qq a S n n --=11()1 )1(≠q5.变式:mn m n q q S S --=11 )1(≠q 6.性质:① r p n m +=+则 r p n m a a a a ⋅=⋅② p n m 2=+ 则 2p n m a a a =⋅③ Λ=⋅=⋅=⋅--23121n n n a a a a a a④ m S 、m -m 2S 、2m -m 3S 等比⑤ }{n a 等比,有12+n 项偶奇qS a a a a q a a a a S n n +=++++=++++=+1242112531)(a ΛΛ三、等差与等比的类比{}n a 等差{}n b 等差 和积 差商 系数指数 “0”“1”1.分组求和 本数列的和公式求和.进行拆分,分别利用基,则可或等比数列的和的形式数列,但通项是由等差通项虽不是等差或等比项的和:前如求n n n )}1({+)2)(1(31 )1(21)12)(1(61 )321()321( )()22()11(])1(22222222++=++++=++++++++=++++++=∴+=+n n n n n n n n n n n n S n n n n n ΛΛΛΘ).11(11}{1 111+++-=⋅⋅n n n n n n n a a d a a a n a a 为等差数列,项和,其中的前项为用于通从而计算和的方法,适别裂开后,消去一部分把数列和式中的各项分).2()7(!)!1(!)6()5()(11)4(])2)(1(1)1(1[21)2)(1(1)3()121121(21)12)(12(1)2(111)1(1)1(111≥-=-+=⋅-=--=+++-+=+++--=+-+-=+-+-n S S a n n n n C C C b a b a ba n n n n n n n n n n n n n n n n n n m n m n m n ;;;;;;列的求和.数列对应项相乘所得数列和一个等比可解决形如一个等差数的推导方法求解,一般利用等比数列求和公式 项和公式的推导:前如:等比数列n a n }{11132321)1(++-=-⇒⎩⎨⎧++++=++++=n n n n n n n a a S q a a a a qS a a a a S ΛΛ.)1(11)1()1( 111⎪⎩⎪⎨⎧≠--=--=⇒q q q a a qq a q na n n THANKS !!!致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求欢迎您的下载,资料仅供参考。
等差与等比数列知识与方法总结
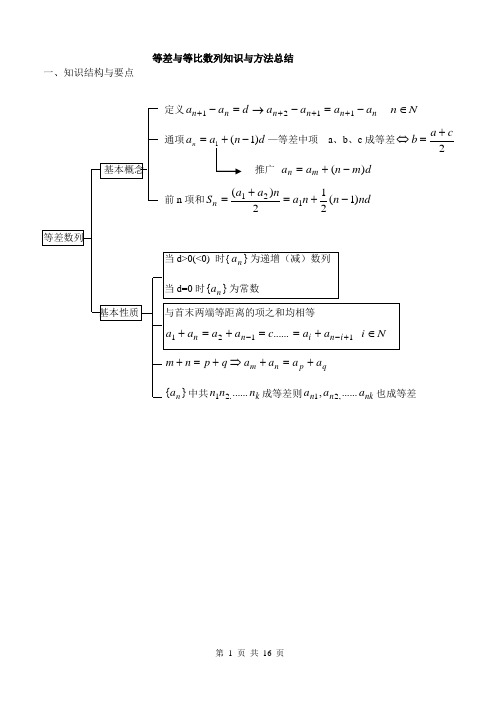
等差与等比数列知识与方法总结一、知识结构与要点N2cab+=定义:nn n n n n a a a a q a a 1121+++-=→= N n ∈通项 →⋅=-1n q a a 等比中项:a b c 成等比数列ac b =⇒2基本概念推广m n m n q a a -⋅= 前n 项和=n S )1(11)1()1(111≠--=--=q qq a a qq a q n a n n等比数列与首末两端等距离的两项之积相等1121......+--⋅===i n i n n a a a a a a q p n m a a a a q p n m ⋅=⋅⇒+=+}{n a 成等比,若k n n n ,...,21 成等差则nk n a a a ,...,21成等比基本性质 当101>>q a 或1001<<<q a 时 {}n a 为递增数列当101><q a 或1001<<>q a 时 {}n a 为递减数列当 q<0时 {}n a 为摆动数列 当 q=1时 {}n a 为常数数列二、等差数列、等比数列基础知识与方法概括 (一).一般数列数列的定义及表示方法;数列的项与项数;有穷数列与无穷数列;递增(减)、摆动、循环数列;数列{a n }的通项公式a n ;数列的前n 项和公式S n ;一般数列的通项a n 与前n 项和S n 的关系:⎩⎨⎧≥-===-)2()1(111n S S n S a a n n n(二)等差数列 1.等差数列的概念[定义]如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母d 表示。
即:成等比数列}{)0,0,2(1n n n n a q a n d a a ⇔≠≠≥=--2.等差数列的判定方法(1)定义法:对于数列{}n a ,若d a a n n =-+1(常数),则数列{}n a 是等差数列。
等比等差数列公式总结

等比等差数列公式总结数列是数学中一个非常重要的概念。
在数列中,等差数列和等比数列是最为常见和基础的两种形式。
它们具有简单明了的规律性,用简洁的公式能够表达出来。
本文将对等差数列和等比数列的公式进行总结,希望可以帮助到对数列感兴趣的读者。
一、等差数列公式总结等差数列是指数列中相邻两项之间的差值保持相等的数列。
比如,1,3,5,7,9,11...就是一个等差数列,它的公差为2。
对于等差数列,我们可以通过以下公式进行总结。
1. 通项公式等差数列的通项公式可以用来求出数列中的任意一项。
设等差数列的首项为a₁,公差为d,第n项为aₙ,则通项公式可以表示为:aₙ = a₁ + (n-1)d 。
这个公式的原理是通过每一项之间的差值与公差之间的关系来确定每一项的值。
2. 前n项和公式在等差数列中,我们经常需要求出前n项和的值。
这可以通过前n项和公式来实现。
设等差数列的首项为a₁,公差为d,则前n项和公式可以表示为:Sₙ = n/2(2a₁ + (n-1)d) 。
这个公式的原理是通过将数列拆分成两个相同的递增序列,然后对每一项求和来计算前n项和的值。
二、等比数列公式总结等比数列是指数列中相邻两项之间的比值保持相等的数列。
比如,1,2,4,8,16...就是一个等比数列,它的公比为2。
对于等比数列,我们可以通过以下公式进行总结。
1. 通项公式等比数列的通项公式可以用来求出数列中的任意一项。
设等比数列的首项为a₁,公比为q,第n项为aₙ,则通项公式可以表示为:aₙ = a₁ * qⁿ⁻¹。
这个公式的原理是通过每一项与首项之间的比值与公比之间的关系来确定每一项的值。
2. 前n项和公式在等比数列中,我们同样需要求出前n项和的值。
这可以通过前n项和公式来实现。
设等比数列的首项为a₁,公比为q,则前n项和公式可以表示为:Sₙ = a₁(1-qⁿ)/ (1-q) 。
这个公式的原理是通过将数列拆分成n个相同的递增序列,然后对每一项求和来计算前n项和的值。
(完整版)等差等比数列知识点总结

1.等差数列:一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数d ,那么这个数列就叫做等差数列,这个常数d 叫做等差数列的公差,即d a a n n =--1(d 为常数)(2≥n );.2.等差中项:(1)如果a ,A ,b 成等差数列,那么A 叫做a 与b 的等差中项.即:2ba A +=或b a A +=2 (2)等差中项:数列{}n a 是等差数列)2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a3.等差数列的通项公式:一般地,如果等差数列{}n a 的首项是1a ,公差是d ,可以得到等差数列的通项公式为:()d n a a n 11-+=推广: d m n a a m n )(-+=. 从而mn a a d mn --=; 4.等差数列的前n 项和公式:1()2n n n a a S +=1(1)2n n na d -=+211()22d n a d n =+-2An Bn =+ (其中A 、B 是常数,所以当d ≠0时,S n 是关于n 的二次式且常数项为0) 5.等差数列的判定方法(1) 定义法:若d a a n n =--1或d a a n n =-+1(常数*∈N n )⇔ {}n a 是等差数列. (2) 等差中项:数列{}n a 是等差数列)2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a .(3) 数列{}n a 是等差数列⇔b kn a n +=(其中b k ,是常数)。
(4) 数列{}n a 是等差数列⇔2n S An Bn =+,(其中A 、B 是常数)。
6.等差数列的证明方法定义法:若d a a n n =--1或d a a n n =-+1(常数*∈N n )⇔ {}n a 是等差数列.(1)当m n p q +=+时,则有q p n m a a a a +=+,特别地,当2m n p +=时,则有2m n p a a a +=.(2) 若{n a }是等差数列,则232,,n n n n n S S S S S -- ,…也成等差数列(3)设数列{}n a 是等差数列,d 为公差,奇S 是奇数项的和,偶S 是偶数项项的和,n S 是前n 项的和 1.当项数为偶数n 2时,()121135212n n n n a a S a a a a na --+=+++⋅⋅⋅+==奇 ()22246212n n n n a a S a a a a na ++=+++⋅⋅⋅+==偶 ()11=n n n n S S na na n a a nd ++-=-=-偶奇 11n n n n S na a S na a ++==奇偶2、当项数为奇数12+n 时,则21(21)(1)1n S S S n a S n a S n S S a S na S n +⎧=+=+=+⎧+⎪⎪⇒⇒=⎨⎨-==⎪⎪⎩⎩n+1n+1奇偶奇奇n+1n+1奇偶偶偶 (其中a n+1是项数为2n+1的等差数列的中间项). 1、等比数列的定义:()()*12,nn a q q n n N a -=≠≥∈0且,q 称为公比 2、通项公式:()11110,0n nn n a a a q q A B a q A B q-===⋅⋅≠⋅≠,首项:1a ;公比:q推广:n m n m n n n m m a a a q q q a --=⇔=⇔=3、等比中项:(1)如果,,a A b 成等比数列,那么A 叫做a 与b 的等差中项,即:2A ab =或A = 注意:同号的两个数才有等比中项,并且它们的等比中项有两个(两个等比中项互为相反数)(2)数列{}n a 是等比数列211n n n a a a -+⇔=⋅ 4、等比数列的前n 项和n S 公式:(1)当1q =时,1n S na = (2)当1q ≠时,()11111n n n a q a a qS qq--==-- 11''11n n n a aq A A B A B A q q=-=-⋅=---(,,','A B A B 为常数)5、等比数列的判定方法:(1)用定义:对任意的n ,都有11(0){}n n n n n na a qa q q a a a ++==≠⇔或为常数,为等比数列(2)等比中项:21111(0){}n n n n n n a a a a a a +-+-=≠⇔为等比数列 (3)通项公式:()0{}n n n a A B A B a =⋅⋅≠⇔为等比数列 6、等比数列的证明方法:依据定义:若()()*12,nn a q q n n N a -=≠≥∈0且或1{}n n n a qa a +=⇔为等比数列 7、等比数列的性质:(1)若*(,,,)m n s t m n s t N +=+∈,则n m s t a a a a ⋅=⋅。
常见数列知识点总结归纳

常见数列知识点总结归纳数列是数学中常见的概念,它由一系列按照一定规律排列的数所组成。
数列的研究在数学中具有广泛的应用,涉及到多个领域。
本文将对常见数列的相关知识点进行总结和归纳。
一、等差数列等差数列是最基础也是最常见的数列类型之一。
它的特点是数列中的每一项与前一项之间的差值都是相等的。
1. 通项公式等差数列的通项公式为an = a1 + (n-1)d,其中an为第n项,a1为首项,d为公差。
2. 前n项和公式等差数列的前n项和公式为Sn = n/2 * (a1 + an),其中Sn为前n项的和。
3. 性质与运算等差数列具有多个性质和运算规则,例如:任意两项之和等于其间项数乘以公差、删除相同项后,剩下的数列仍然是等差数列等。
二、等比数列等比数列是另一种常见的数列类型,它的特点是数列中的每一项与前一项之比都是相等的。
1. 通项公式等比数列的通项公式为an = a1 * r^(n-1),其中an为第n项,a1为首项,r为公比。
2. 前n项和公式等比数列的前n项和公式为Sn = a1 * (1 - r^n) / (1 - r),其中Sn为前n项的和。
3. 性质与运算等比数列也有多个性质和运算规则,例如:相邻两项之商等于公比、删除相同项后,剩下的数列仍然是等比数列等。
三、斐波那契数列斐波那契数列是一种特殊的数列,它的前两项为1,从第三项开始,每一项都等于前两项之和。
斐波那契数列的通项公式为an = an-1 + an-2,其中an为第n项,an-1为第n-1项,an-2为第n-2项。
斐波那契数列具有独特的性质,例如:相邻两项之比逐渐接近黄金分割比、在数列中,某一项与它之后的项之商趋近于黄金分割比等。
四、几何数列几何数列是一种特殊的数列,它的前一项与后一项之比都是相等的。
几何数列的通项公式为an = a1 * r^(n-1),其中an为第n项,a1为首项,r为公比。
几何数列的前n项和公式为Sn = a1 * (1 - r^n) / (1 - r),其中Sn为前n项的和。
等比数列与等差数列知识点

=
.
第 7页(共 13页)
2.等比数列前 n 项和的性质 公比不为﹣1 的等比数列{an}的前 n 项和为 Sn,则 Sn,S2n﹣Sn,S3n﹣S2n 仍成等比数列,
其公比为 qn. 8.数列的求和 【知识点的知识】 就是求出这个数列所有项的和,一般来说要求的数列为等差数列、等比数列、等差等比数列 等等,常用的方法包括: (1)公式法: ①等差数列前 n 项和公式:Sn=na1+ n(n﹣1)d 或 Sn= ②等比数列前 n 项和公式:
③几个常用数列的求和公式:
(2)错位相减法:
适用于求数列{an×bn}的前 n 项和,其中{an}{bn}分别是等差数列和等比数列. (3)裂项相消法:
,
∴=
,
=1, =
,=
,
∵数列{ }也为等差数列,
∴
=+,
∴
=1+
,
解得 d=2.
∴Sn+10=(n+10)2,
=(2n﹣1)2,
∴
=
=
,
由于
为单调递减数列,
∴
≤ =112=121,
故选:D. 2.等差数列的性质 【等差数列】
第 2页(共 13页)
如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差
∴an=
,
把 n=1 代入 2n﹣1 可得 1≠2, ∴{an}不是等差数列
考察了对概念的理解,除掉第一项这个数列是等差数列,但如果把首项放进去的话就不是 等差数列,题中 an 的求法是数列当中常用到的方式,大家可以熟记一下. eg2:已知等差数列{an}的前三项分别为 a﹣1,2a+1,a+7 则这个数列的通项公式为 解:∵等差数列{an}的前三项分别为 a﹣1,2a+1,a+7, ∴2(2a+1)=a﹣1+a+7, 解得 a=2. ∴a1=2﹣1=1,a2=2×2+1=5,a3=2+7=9, ∴数列 an 是以 1 为首项,4 为公差的等差数列, ∴an=1+(n﹣1)×4=4n﹣3.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.中项法
证明一个数列为等比数列的方法:
1.定义法
2.中项法
设元技巧
三数等差:
四数等差:
三数等比:
四数等比:
联系
真数等比,对数等差;指数等差,幂值等比。
等差数列与等比数列知识梳理
等差数列与等比数列
等差数列
等比数列
定义
( 为常数, )
递推公式
( )
( )
通项公式
( )
中项
(要性质
②
③从等差数列中抽取等距离的项组成的数列是一个等差数列。
如: (下标成等差数列)
②
③从等比数列中抽取等距离的项组成的数列是一个等比数列。
如: (下标成等差数列)
证明方法
证明一个数列为等差数列的方法:
