第7章-正交试验设计的极差分析汇总
正交试验设计极差分析方法

1.1极差分析法特点 (1)极差分析法直观形象、简单易懂。 (2)通过非常简便的计算和判断就可以求得试验的优化成 果——主次因素、优水平、优搭配及最优组合。能比较圆 满迅速地达到一般试验的要求。它在试验误差不大、精度 要求不高的各种场合中,在筛选因素的初步试验中,在寻求最 优生产条件、最佳工艺、最好配方的科研生产实际中都能 得到广泛的应用。 (3)极差分析法是正交设计中常用的方法之一。但是,由 于极差分析法不能充分利用试验数据所提供的信息,因此,其 应用还受到一定的限制。
针对上机操作内容讲解具体实例2个
1.以“正交试验设计”为关键词查询20052006年度《食品科学》期刊上发表的论文10 篇; 2.对其极差分析过程进行上机计算,求R; 3.分析所查阅论文在优水平、主次因素、最 优组合的分析与讨论的阐述内容; 4. 独立L9(34)设计方案并模拟进行极差分 析。
1.3 2005-2006食品研究正交试验设计极差 分析具体实例讲解(1)
1.1极差分析法特点 (4)极差分析法不能估计试验误差。实际上,任何 试验都不可避免地存在着试验误差,而极差分析法 却不能估计这种试验误差的大小,无法区分某因素 各水平所对应的试验指标平均值间的差异究竟有多 少是由因素水平不同引起的,又有多少是由试验误 差引起的。 (5)对于误差较大或精度要求较高的试验,若用极 差法分析试验结果而不考虑试验误差的影响,就会 给准确分析带来困难,影响获得正确的结论。 (6)极差法无法确定试验的优化成果的可信度,也 不能应用于回归分析与回归设计。
1.3 2005-2006食品研究正交试验设计极差 分析具体实例讲解(5)
转谷氨酰胺酶、复合磷酸盐、卡拉胶、酪蛋白对鸡肉肠质硬度 的影响.PDF
1.2极差分析步骤:
1.2试验结果直观分析
正交试验结果的极差分析法
正交试验结果的极差分析法正交试验方法能得到科技工作者的重视,在实践中得到广泛的应用,原因之一是不仅试验的次数减少,而且用相应的方法对试验结果进行分析可以引出许多有价值的结论。
因此,在正交试验中,如果不对试验结果进行认真的分析,并明确地引出应该引出的结论,那就失去用正交试验法的意义和价值。
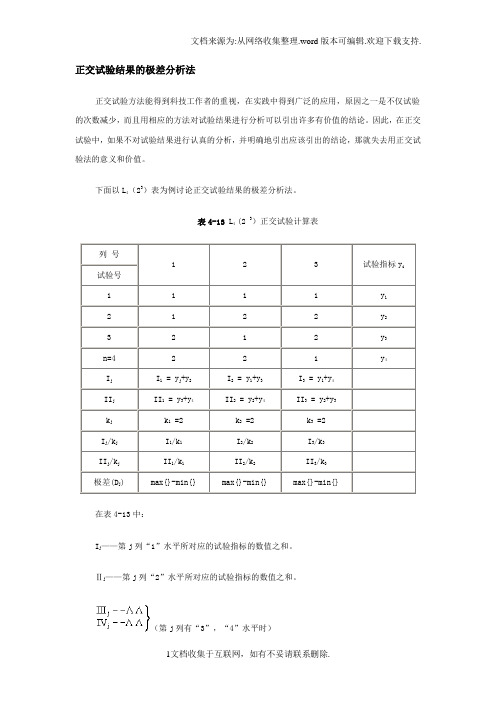
下面以L4(23)表为例讨论正交试验结果的极差分析法。
表4-13 L4 (2 3)正交试验计算表列号1 2 3 试验指标y i试验号1 1 1 1 y12 1 2 2 y23 2 1 2 y3n=4 2 2 1 y4I j I1 = y j+y2I2 = y1+y3I3 = y1+y4II j II1 = y3+y4II2 = y2+y4II3 = y2+y3k j k1 =2 k2 =2 k3 =2I j/k j I1/k1I2/k2I3/k3II j/k j II1/k1II2/k2II3/k3极差(D j) max{}-min{} max{}-min{} max{}-min{}在表4-13中:I j——第j列“1”水平所对应的试验指标的数值之和。
Ⅱj——第j列“2”水平所对应的试验指标的数值之和。
(第j列有“3”,“4”水平时)k j——第j列同一水平出现的次数。
等于试验的次数(n)除以第j列的水平数。
——第j列“1”水平所对应的试验指标的平均值。
——第j列“2”水平所对应的试验指标的平均值。
D j——第j列的极差。
等于第j列各水平对应的试验指标平均值中的最大值减最小值,即用极差法分析正交试验结果应引出以下几个结论:①在试验范围内,各列对试验指标的影响从大到小的排队。
某列的极差最大,表示该列的数值在试验范围内变化时,使试验指标数值的变化最大。
所以各列对试验指标的影响从大到小的排队,就是各列极差D的数值从大到小的排队。
②试验指标随各因素的变化趋势。
③使试验指标最好的适宜的操作条件(适宜的因素水平搭配)。
④对所得结论和进一步研究方向的讨论。
(完整版)第7章正交试验设计的极差分析汇总,推荐文档
第7章 正交试验设计的极差分析正交试验设计和分析方法大致分为二种:一种是极差分析法(又称直观分析法),另一种是方差分析法(又称统计分析法)。
本章介绍极差分析法,它简单易懂,实用性强,在工农业生产中广泛应用。
7.1 单指标正交试验设计及其极差分析极差分析法简称R 法。
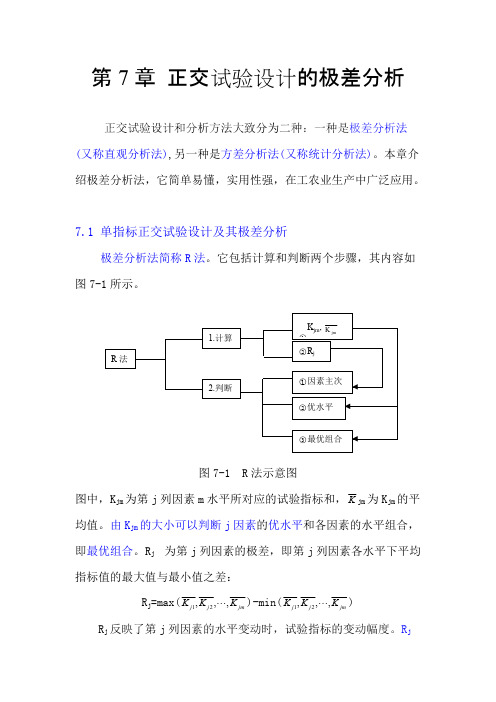
它包括计算和判断两个步骤,其内容如图7-1所示。
图7-1 R 法示意图图中,K jm 为第j 列因素m 水平所对应的试验指标和,jm 为K jm 的平K 均值。
由K jm 的大小可以判断j 因素的优水平和各因素的水平组合,即最优组合。
R j 为第j 列因素的极差,即第j 列因素各水平下平均指标值的最大值与最小值之差:R j =max()-min()jm j j K K K ,,,21 jm j j K K K ,,,21 R j 反映了第j 列因素的水平变动时,试验指标的变动幅度。
R j越大,说明该因素对试验指标的影响越大,因此也就越重要。
于是依据R j的大小,就可以判断因素的主次。
极差分析法的计算与判断,可直接在试验结果分析表上进行,现以例6-2来说明单指标正交试验结果的极差分析方法。
一、确定因素的优水平和最优水平组合例6-2 为提高山楂原料的利用率,某研究组研究了酶法液化工艺制造山楂精汁。
拟通过正交试验寻找酶法液化工艺的最佳工艺条件。
在例6-2中,不考虑因素间的交互作用(因例6-2是四因素三水平试验,故选用L9(34)正交表),表头设计如表6-5所示,试验方案则示于表6-6中。
试验结果的极差分析过程,如表7-1所示.表6-4 因素水平表水平因素加水量(ml/100g)A加酶量(ml/100g)B酶解温度( C)C酶解时间(h)D1 2 31050901472035501.52.53.5表6-6 试验方案及结果因素试验号A B C D试验结果液化率(%)1 2 31(10)111(1)2(4)3(7)1(20)2(35)3(50)1(1.5)2(2.5)3(3.5)0.0017.024.04567892(50)223(90)3312312323131231223112.047.028.01.0018.042.0试验指标为液化率,用y i 表示,列于表6-6和表7-1的最后一列。
正交试验结果的极差分析法

正交试验结果的极差分析法正交试验方法能得到科技工作者的重视,在实践中得到广泛的应用,原因之一是不仅试验的次数减少,而且用相应的方法对试验结果进行分析可以引出许多有价值的结论。
因此,在正交试验中,如果不对试验结果进行认真的分析,并明确地引出应该引出的结论,那就失去用正交试验法的意义和价值。
下面以L4(23)表为例讨论正交试验结果的极差分析法。
表4-13 L4 (2 3)正交试验计算表在表4-13中:I j——第j列“1”水平所对应的试验指标的数值之和。
Ⅱj——第j列“2”水平所对应的试验指标的数值之和。
(第j列有“3”,“4”水平时)k j——第j列同一水平出现的次数。
等于试验的次数(n)除以第j列的水平数。
——第j列“1”水平所对应的试验指标的平均值。
——第j列“2”水平所对应的试验指标的平均值。
D j——第j列的极差。
等于第j列各水平对应的试验指标平均值中的最大值减最小值,即用极差法分析正交试验结果应引出以下几个结论:①在试验范围内,各列对试验指标的影响从大到小的排队。
某列的极差最大,表示该列的数值在试验范围内变化时,使试验指标数值的变化最大。
所以各列对试验指标的影响从大到小的排队,就是各列极差D的数值从大到小的排队。
②试验指标随各因素的变化趋势。
③使试验指标最好的适宜的操作条件(适宜的因素水平搭配)。
④对所得结论和进一步研究方向的讨论。
例4-5要求对例4-4的试验问题,写出应用正交试验设计方法的全过程,用极差法分析正交实验的结果。
解:试验目的:提高磺化反应的乙酰胺苯的收率。
试验指标:乙酰胺苯的收率表4-14因素水平表应考虑的交互作用:A×B,A×C选择的正交表:L8(27),表头设计及计算结果均见表4-15。
应该引出的四个结论如下:1.各列对试验指标影响大小的排队问题。
因为极差D3=D4=4.75最大,依次是D1=2.75,D2=D7=2.25,D6=1.75,最小是D5=0.75。
正交试验结果的极差分析与方差分析

实验报告实验三:正交试验结果的极差分析与方差分析课程名称考查学期姓名学号专业成绩任课教师实验三:正交试验结果的极差分析与方差分析一、实验目标熟练使用Excel和SPSS软件进行正交试验设计和结果分析二、实验要求按照1人/组的样式,所有成员都应该根据实验内容完成相应的任务。
三、仪器设备笔记本电脑与数据分析软件Excel、SPSS。
四、实验内容1. 正交试验数据的极差分析(Excel)大枣的微波干燥工艺研究,试验因素选取A微波功率(W)、B干燥时间(min)、C载样量(kg/m2),以干燥大枣中总黄酮的含量为指标(越高越好),试选出最优工艺条件。
表3-1. 因素水平表水平试验因素A(微波功率/W)B(干燥时间/min)C(载样量/kg/m2)1150105 22501510 33502015表3-2. 干燥大枣中的总黄酮含量试验号微波功率A干燥时间B空列载样量C总黄酮含量1(mg/g)总黄酮含量2(mg/g)11111272.6 278.9 21222251.7 250.331333245.2 247.2 42123289.7 279.6 52231275.8 268.8 62312258.7 257.7 73132246.6 246.2 83213231.4 232.1 93321222.1 228.6表3-3 干燥大枣中的总黄酮含量极差分析试验号列号重复试样指标和1 2 3 41 2A B C1 1 1 1 1 272.6 278.9 551.52 1 2 2 2 251.7 250.3 5023 1 3 3 3 245.2 247.2 492.44 2 1 2 3 289.7 279.6 569.35 2 2 3 1 275.8 268.8 544.66 2 3 1 2 258.7 257.7 516.47 3 1 3 2 246.6 246.2 492.88 3 2 1 3 231.4 232.1 463.59 3 3 2 1 222.1 228.6 450.7K11545.9 1613.6 1531.4 1546.8K21630.3 1510.1 1522.0 1511.2K31407.0 1459.5 1529.8 1525.2k1257.650 268.933 255.233 257.800k2271.717 251.683 253.667 251.867k3234.500 243.250 254.967 254.200R 37.217 25.683 1.567 5.933较优水平A2B1C1因为指标越大越好,所以为因素A的2水平,即A2较好。
正交检验的极差分析和方差分析教材

正交检验的极差分析和方差分析教材正交检验的极差分析和方差分析引言:正交检验的极差分析和方差分析是统计学中常用的两种分析方法。
它们被广泛应用于实验设计和数据分析中,可以帮助我们判断变量之间的差异是否显著,并且确定是哪些因素对变量影响最为显著。
本文将重点介绍正交检验的极差分析和方差分析的基本原理和应用方法。
一、正交检验的极差分析1.1 基本原理正交检验的极差分析是通过观察不同水平的自变量对因变量的影响,推断不同水平之间的差异是否显著的一种方法。
它基于方差分析的原理,通过计算不同水平之间的平均差和标准差,判断不同水平之间的差异是否超过了预期的随机误差范围,从而得出结论。
1.2 应用方法首先,确定研究的自变量和因变量,并确定自变量的水平。
然后,通过随机抽样的方式获取样本数据,并计算每个水平下的极差。
接下来,计算整体样本数据的均值和方差,以及不同水平之间的平均差和标准差。
最后,使用统计方法,比较差异是否显著,并进一步推断不同水平之间的差异。
1.3 实例分析以某品牌洗衣机的不同水平温度对洗涤效果(洗涤时间)为例,通过极差分析探究不同水平温度下洗涤效果是否存在显著差异。
首先,选择3个不同水平的温度:40℃、60℃和80℃。
然后,使用这3个水平的温度进行多次洗涤实验,每次实验记录洗涤时间。
接下来,计算每个水平下的极差,并计算整体样本数据的均值和方差。
最后,使用正交检验的极差分析方法,比较不同水平之间的差异是否显著。
二、方差分析2.1 基本原理方差分析是通过比较不同组之间的方差大小,来判断不同组之间的差异是否显著的一种方法。
它基于总体方差和组内方差之间的关系,通过计算F统计量来比较差异是否显著。
2.2 应用方法首先,确定研究的自变量和因变量,并确定不同组别。
然后,通过随机抽样的方式获取样本数据,并计算每个组别的均值和方差。
接下来,计算总体样本数据的均值和方差,以及组内方差和组间方差。
最后,使用统计方法,计算F统计量,并比较差异是否显著。
正交试验设计(内容详尽)

偏差大小,通常用 V 表示:
V S2 / f
存在期望值时:
V
1 n
n
( xi
i 1
)2
不存在期望值时:
V
1 n1
n
( xi
i 1
x)2
均方差也称为准偏差或标准差,定义为方差的平方根,
通常用 表示,即
存在期望值时:
V
1 n
n i 1
( xi
)2
不存在期望值时:
V
1 n
1
n i 1
正交试验设计
7.1.5 试验的主要步骤(阶段)
● 试验设计阶段——选题、设计试验方案、准备试 验材料及设备、安排试验环境等;
● 试验实施阶段——按计划进行试验(包括试验操 作、收集试验数据等);
● 试验分析阶段——核查试验数据、进行统计分析、 解释试验结果、获取试验结论等。
正交试验设计
7.1.6 试验设计的基本原则(费歇尔三原则)
● 重复原则——利用重复观测减小试验误差,提高试 验精度;
● 随机化原则——目的是为了消除或减小人为因素引 起的系统误差的影响;
● 局部控制原则——该原则也称为区组控制原则,指 的是把比较的水平设置在差异较小的区组内,其目的也是 为了消除或减小试验中系统误差的影响。例如,按机器设 备、班次、原料批号、操作人员划分区组。
其他:
★ 标示因素
★ 区组因素
★ 信号因素
★ 误差因素
正交试验设计
⑷ 因素的水平 试验中因素变化的状态和条件称为因素的水平或位数,
简称水平。水平用数字(1,2,3…)表示。 试验中设计过程中水平的选取原则是:
◆ 宜选用三水平,以有利于实验结果的分析; ◆ 水平通常取等间隔,特殊情况下取对数间隔; ◆ 水平应该具体。水平应该是可控的,其变化对试验指 标有影响。
正交试验极差方差及单因素分析结果
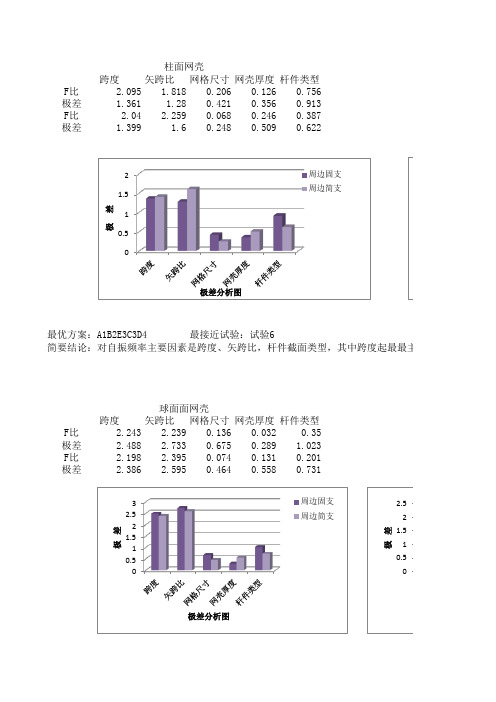
跨度矢跨比网格尺寸网壳厚度杆件类型F比 2.095 1.8180.2060.1260.756极差 1.361 1.280.4210.3560.913F比 2.04 2.2590.0680.2460.387极差1.3991.60.2480.5090.622跨度矢跨比网格尺寸网壳厚度杆件类型F比 2.243 2.2390.1360.0320.35极差 2.488 2.7330.6750.289 1.023F比 2.198 2.3950.0740.1310.201极差2.3862.5950.4640.5580.731简要结论:对自振频率主要因素是跨度、矢跨比,杆件截面类型,其中跨度起最最主要柱面网壳球面面网壳最优方案:A1B2E3C3D4最接近试验:试验60.5 1 1.5 2 极 差极差分析图周边固支 周边简支0.5 1 1.5 2 2.5 3 极 差极差分析图周边固支 周边简支0.5 1 1.5 2 2.5 极 差跨度矢跨比网格尺寸网壳厚度杆件类型F比4.0140.3170.2310.0860.351极差5 1.349 1.0720.745 1.376F比 4.0410.2850.2080.1280.338极差4.8981.224 1.0160.908 1.352单因素分析球面网壳矢跨比刚度比阶数1/31/41/51/70.51 1.9104 2.4817 2.8727 3.3385 2.3752 1.9105 2.4818 2.8727 3.3386 2.37513 2.3345 2.8474 3.1617 3.4956 2.86184 5.3839 6.44867.09477.7783 6.20625 5.5045 6.63647.34198.1125 6.20636 5.5048 6.63657.34238.1127 6.48297 6.90978.25149.03469.60727.61828 6.91038.2529.03489.60757.618898.22619.674910.42910.618.9255108.22649.674910.42910.618.9255118.537110.20411.21311.2689.8891128.819410.56311.59111.2699.8895138.819510.56311.59211.57510.185最优方案:A1E3B2C4D4最接近试验:试验6双曲网壳简要结论:对自振频率主要因素是矢跨比、跨度、杆件截面类型,其中矢跨比起最主要简要结论:对自振频率主要因素是矢跨比、跨度、杆件截面类型,其中跨度是最显著因最优方案:B1A1E4C2D3最接近试验:试验51 23 4 5 极 差极差分析图周边固支 周边简支149.4910.99611.63311.57610.185 159.490310.99711.63311.59710.26 169.611511.10411.65812.28110.367 179.612111.10511.65912.62210.368 1810.72912.25512.66212.62311.419 1910.72912.25612.66312.66811.419 2010.82512.28212.80612.66911.478网格尺寸网壳厚度阶数182********1 2.4817 2.5556 2.6151 2.6648 2.26542 2.4818 2.5556 2.6151 2.6649 2.26563 2.8474 2.9725 3.0828 3.1814 2.95074 6.4486 6.74427.00717.2435 6.38295 6.6364 6.91197.14517.3452 6.38326 6.6365 6.91227.14527.3457 6.686778.25148.56038.82559.05228.080888.2528.56078.82579.05278.08199.674910.01410.30510.5519.6806109.674910.01410.30510.5529.6807 1110.20410.66811.0811.4510.588 1210.56311.05911.48911.86810.67 1310.56311.0611.48911.86810.67 1410.99611.35311.65811.91111.229 1510.99711.35411.65811.91111.229 1611.10411.43811.69911.91211.317 1711.10511.43811.69911.91211.318 1812.25512.59512.83913.04112.637 1912.25612.59512.8413.04112.638 2012.28212.62312.93313.1912.699单因素分析双曲网壳矢跨比刚度比阶数1/41/51/61/80.51 3.6083 3.9952 4.2635 4.5818 3.42862 4.6255 5.2058 5.5698 5.9443 4.36593 4.6256 5.2058 5.5699 5.9445 4.3664 5.7013 6.3387 6.73867.1346 5.31045 6.57947.33657.83158.3905 6.17776 6.72717.40437.86178.3913 6.273677.33358.15148.67799.2318 6.793987.33388.15188.67799.232 6.794297.99488.85199.3339.49637.526107.99498.85259.33319.49637.526118.75689.661110.20510.5278.0887128.77999.716210.33610.68.1206138.96439.829310.34411.0438.3281149.908910.92311.40911.3269.1858159.909110.92311.40911.3279.18591610.15511.23611.92412.1589.53591710.27811.29911.92512.1589.63721810.68911.59711.94812.4159.9981910.68911.59811.98312.5459.99932010.86811.90212.60712.75110.318网格尺寸网壳厚度阶数161820224001 3.3486 3.6083 3.8165 4.0256 3.15992 4.2943 4.6255 4.8818 5.1377 4.09113 4.2947 4.6256 4.8821 5.1383 4.09134 5.2939 5.7013 6.0167 6.3301 4.95685 6.0542 6.57947.00537.4332 6.1326 6.1884 6.72717.16947.612 6.28257 6.78677.33357.76428.1886 6.71638 6.7877.33387.76478.1891 6.717697.39457.99488.45998.90987.7799107.39497.99498.468.9117.7809118.0918.75689.28539.81218.216128.10148.77999.32579.87338.3556138.27198.96439.522610.0778.4758149.20729.908910.42510.9049.5678159.20769.909110.42510.9059.5686169.302510.15510.85811.56410.186179.407110.27811.00111.72210.309189.89410.68911.19811.72310.63199.894110.68911.19811.73110.632010.2110.86811.52212.22210.927单因素分析柱面网壳矢跨比刚度比阶数1/21/31/41/70.510.88982 1.2484 1.4487 1.6845 1.455120.97008 1.6762 2.1783 2.8843 2.01853 1.1539 1.7933 2.2705 2.9672 2.12414 1.9096 2.5832 2.9693 3.4269 2.96935 2.0831 2.797 3.138 3.6598 2.98496 2.1356 3.1931 3.876 4.6833 3.56417 2.3397 3.2652 3.9681 4.8101 3.66558 2.8132 3.8599 4.4557 4.9311 4.1879 2.8859 3.8679 4.505 5.1587 4.258310 3.3391 4.2056 4.506 5.2819 4.454111 3.3816 4.9433 5.5488 6.2301 5.161312 3.7268 4.9962 5.9204 6.5012 5.413513 3.786 5.001 5.9245 6.943 5.549914 3.9408 5.2452 6.08267.1367 5.712615 4.1347 5.5061 6.1387.3314 5.963516 4.4927 5.7664 6.4867.5527 6.017917 4.5367 6.3621 6.92347.7131 6.410418 4.7917 6.4117.26378.1497 6.702919 4.9462 6.48257.57188.41947.002420 5.0166 6.49547.64248.82377.1666网格尺寸网壳厚度阶数182********1 1.4487 1.5152 1.5745 1.6275 1.47962 2.1783 2.2238 2.2539 2.2745 2.01343 2.2705 2.3283 2.3699 2.4013 2.12224 2.9693 3.0996 3.2157 3.3192 2.85235 3.138 3.2285 3.3012 3.3627 3.00846 3.876 3.9946 4.0944 4.1694 3.70117 3.9681 4.0979 4.2077 4.2919 3.80768 4.4557 4.6399 4.7537 4.8529 4.19959 4.505 4.6469 4.7684 4.8644 4.222110 4.506 4.6497 4.8224 4.9766 4.523511 5.5488 5.7146 5.8587 5.9777 5.216412 5.9204 6.1498 6.3444 6.5041 5.856713 5.9245 6.1776 6.3996 6.5532 5.890814 6.0826 6.2614 6.4165 6.5904 5.99115 6.138 6.3851 6.5998 6.7852 6.165316 6.486 6.7385 6.95517.136 6.393817 6.92347.11897.28997.4348 6.6456187.26377.52817.75717.95137.1094197.57187.89268.14318.3187.6547207.64247.94488.17768.43147.7421最主要作用1 2 3F 比方差分析图周边固支 周边简支方差分析图周边固支 周边简支1.02.03.02.4817 2.5691 2.56912.4818 2.5692 2.56922.8474 2.7369 2.73696.4486 6.1883 6.18836.6364 6.9956 6.99566.6365 6.9956 6.99568.25148.84628.84628.2528.84688.84689.67499.7789.7789.674910.38610.38610.20410.38710.38710.56311.11311.11310.56311.11311.113最主要作用显著因素1 2 3 4 5 极 差方差分析图周边固支 周边简支10.99611.73111.73110.99711.73211.73211.10411.74711.74711.10511.74711.74712.25512.9712.97 12.25612.9712.97 12.28212.99312.9937009001200 2.4032 2.4817 2.513 2.4033 2.4818 2.5132 2.8979 2.8474 2.7735 6.5654 6.4486 6.2767 6.6289 6.6364 6.4563 6.6293 6.6365 6.4567 8.32128.25147.93328.32178.2527.93339.84079.67499.23599.84079.67499.237410.39310.2049.9213 10.73410.56310.16210.73410.56310.16211.26110.99610.456 11.26210.99710.457 11.36211.10410.56211.36311.10510.56412.60612.25511.629 12.60612.25611.63 12.6212.28211.637 1233.6083 3.7393 3.79974.6255 4.805 4.86974.6256 4.8051 4.86985.7013 5.97076.06176.5794 6.8597 6.95316.72717.05077.16557.33357.71687.85517.33387.71717.85547.99488.31428.41227.99498.31448.41248.75689.23949.41518.77999.25399.42428.96439.40589.54589.908910.4110.5839.909110.41110.58310.15510.58110.710.27810.72310.85110.68911.07311.18110.68911.07411.18210.86811.36511.533 60090012003.4358 3.6083 3.59394.4615 4.6255 4.54444.462 4.6256 4.54455.4945 5.7013 5.56446.5399 6.5794 6.35566.7176 6.7271 6.46687.27347.33357.04847.27387.33387.04858.11187.99487.65138.11287.99497.65138.79918.75688.3438.84858.77998.39139.01288.96438.579510.0959.90899.390710.0969.90919.390810.43810.1559.666110.5710.2789.780911.00310.68910.11811.00510.68910.11811.3510.86810.29 1231.4487 1.4235 1.3942.1783 2.307 2.37022.2705 2.3771 2.41812.9693 2.9348 2.89033.138 3.2353 3.26013.8764.0982 4.14793.96814.1475 4.16454.4557 4.4224 4.39344.505 4.6611 4.68824.506 4.7168 4.76435.5488 5.808 5.73675.9204 5.8572 5.86225.92456.2947 6.37226.0826 6.3264 6.41136.138 6.4769 6.58416.486 6.8596 6.96016.92347.27447.28747.26377.44597.35477.57187.66247.7637.64248.03968.102 900120015001.4487 1.4177 1.38762.1783 2.2027 2.15592.2705 2.2837 2.2322.9693 2.9164 2.8573.138 3.2476 3.24713.876 3.8051 3.65693.9681 3.8883 3.73674.4557 4.3651 4.26824.505 4.5118 4.4074.506 4.5303 4.43315.5488 5.5103 5.3385.9204 5.6903 5.41135.9245 5.7489 5.50736.0826 5.9446 5.76696.138 6.0125 5.84436.486 6.2936 6.03346.9234 6.8065 6.57227.26377.0597 6.76347.57187.2963 6.91987.64247.36917.0545。
正交试验设计(内容详尽)
示。
存在期望值时:
n
S 2 ( xi )2 i 1
不存在期望值时:
n
S 2 ( xi x)2 i 1
自由度指的是关系式中独立数据的个数,通常用 f 表示。
例如,在计算偏差平方和的过程中,若表达式中使用
的是期望值 ,则 f n;若表达式中使用的是平均值 x ,
n
则因为存在约束条件 ( xi x) 0 而使独立数据的个数少 i 1
其他:
★ 标示因素
★ 区组因素
★ 信号因素
★ 误差因素
正交试验设计
⑷ 因素的水平 试验中因素变化的状态和条件称为因素的水平或位数,
简称水平。水平用数字(1,2,3…)表示。 试验中设计过程中水平的选取原则是:
◆ 宜选用三水平,以有利于实验结果的分析; ◆ 水平通常取等间隔,特殊情况下取对数间隔; ◆ 水平应该具体。水平应该是可控的,其变化对试验指 标有影响。
◆ 确定出各因素对试验指标的影响规律,得知哪些因素的 影响是主要的、哪些因素的影响是次要的、哪些因素之间 存在相互影响; ◆ 选出各因素的一个水平组合来确定最佳生产条件。
正交试验设计的基础是正交表。
7.1.3 基本概念
■ 过程或系统
人、机器、实验条件等资源的组合。
正交试验设计
可控因素
x1 x2
xp
通常用 表示,即
存在期望值时:
V
1 n
n i 1
( xi
)2
不存在期望值时:
V
1 n1
n i 1
( xi
x)2
正交试验设计
7.2.2 样本及其分布
■ 总体、个体与样本 总体(population):被研究对象的全体。 个体(individual):组成总体的每个单元。
第7章-正交试验设计的极差分析

第7章正交试验设计的极差分析正交试验设计和分析方法大致分为二种:一种是极差分析法(又称直观分析法),另一种是方差分析法(又称统计分析法)。
本章介绍极差分析法,它简单易懂,实用性强,在工农业生产中广泛应用。
7.1单指标正交试验设计及其极差分析极差分析法简称R法。
它包括计算和判断两个步骤,其内容如图7-1所示。
图7-1 R法示意图图中,K m为第j列因素m水平所对应的试验指标和,K jm为K m的平均值。
由K m 的大小可以判断j因素的优水平和各因素的水平组合,即最优组合。
R为第j 列因素的极差,即第j列因素各水平下平均指标值的最大值与最小值之差:R二max(心,耳,,爲)-min(心,兀,,爲)R反映了第j列因素的水平变动时,试验指标的变动幅度。
R越大,说明该因素对试验指标的影响越大,因此也就越重要。
于是依据R j的大小,就可以判断因素的主次。
极差分析法的计算与判断,可直接在试验结果分析表上进行,现以例6 - 2来说明单指标正交试验结果的极差分析方法。
一、确定因素的优水平和最优水平组合例6-2为提高山楂原料的利用率,某研究组研究了酶法液化工艺制造山楂精汁。
拟通过正交试验寻找酶法液化工艺的最佳工艺条件。
在例6 -2中,不考虑因素间的交互作用(因例6 - 2是四因素三水平试验,故选用L9(34)正交表),表头设计如表6 - 5所示,试验方案则示于表6 - 6中。
试验结果的极差分析过程,如表7 - 1所示.表6-4 因素水平表表6-6 试验方案及结果试验指标为液化率,用y表示,列于表6 - 6和表7 - 1的最后一一表7-1试验方案及结果分析计算示例:因素A的第1水平A i所对应的试验指标之和及其平均值分别为:1K\i=y i+y2+y3=0+17+24=41, K AI = — K Ai=13.73同理,对因素A的第2水平A和第3水平A,有1K A2=y4+y5+y6=12+47+28=87 K A2=-K A2=2931K A3=y7+y8+y9=1 + 18+42=61 , K A3K A3=20.33由表7 - 1或表6 - 6可以看出,考察因素A进行的三组试验中(A,A2,A3), B、C D各水平都只出现了一次,且由于B C、D间无交互作用,所以B、C D因素的各水平的不同组合对试验指标无影响,因此,对A、A和A来说,三组试验的试验条件是完全一样的。
正交试验设计(极差分析)

正交试验设计适用于多因素多水平的情况,对于非等水平的情况可能不适用; 同时,正交试验设计要求因素之间相互独立,如果有交互作用则无法准确反映 各因素对试验结果的影响。
ห้องสมุดไป่ตู้
02 极差分析方法
极差的概念与计算
极差的概念
极差是指一组数据中最大值与最 小值之差,用于描述数据的波动 范围。
极差的计算
极差 = 最大值 - 最小值,通过计 算极差可以了解数据的变化范围 。
05 正交试验设计软件介绍
正交试验设计软件的功能与特点
自动化试验设计
软件可以根据用户需求,自动生 成正交试验方案,大大提高了试
验效率。
数据分析与可视化
软件内置强大的数据分析功能,可 以将试验结果进行极差分析、方差 分析等,并生成各种可视化图表。
多因素分析
支持多因素、多水平的试验设计, 能够全面评估各因素对试验结果的 影响。
折线图
通过折线图展示各因素与试验结果的 关系,可以更直观地看出各因素对试 验结果的影响趋势。
03 正交试验设计的应用场景
工业生产优化
01
02
03
生产工艺优化
通过正交试验设计,对生 产工艺参数进行优化,提 高产品质量和生产效率。
设备性能测试
通过正交试验设计,测试 设备的性能参数,找出最 佳工作条件,延长设备使 用寿命。
详细描述
在机械制造过程中,工艺参数如温度、压力、时间等对产品质量和生产效率有重要影响。通过正交试 验设计,可以确定最佳的工艺参数组合,从而提高产品质量和生产效率。
案例三:农业生产中的肥料配比实验
总结词
通过正交试验设计,优化肥料配比,提 高农作物产量和品质。
VS
正交试验设计(内容详尽)讲解
水平 1
因素
A 回火温度(℃)
440
B 保温时间(min)
3
C 工件重量(kg)
7.5
2
470
4
9.0
3
500
5
10.5
正交试验设计
7.1.4 试验设计的作用
通过合理、科学的试验设计,可以显著提高产品的设 计、开发质量,找出最佳的工艺条件,从而提高产品最终 的质量。
田口认为,设计质量(包括产品设计和工艺设计)对 整个产品质量的贡献约为60%~70%。
◆ 观测值与平均值 x 之差 vi xi x(i 1,2,, n)
由于期望值通常是未知的,因此试验中常使用后者, 前者只用于理论分析中。
注意:
n
n
vi (xi x) 0
i 1
i 1
正交试验设计
■ 偏差平方和与自由度
偏差平方和用来表示一组数据的离散程度,通常用 表S 2
次设计、回归试验设计、完全随机化试验设计、随机区组试验设计、 拉丁方试验设计、正交拉丁方试验设计、均匀试验设计等。
正交试验设计
7.2 试验设计的统计学基础
7.2.1 常用统计量
■ 极差 极差指的是一组数据中的最大值与最小值之差,也称
为变异幅。
R xmax xmin
极差反映了一组数据的最大离散程度。
示。
存在期望值时:
n
S 2 ( xi )2 i 1
不存在期望值时:
n
S 2 ( xi x)2 i 1
自由度指的是关系式中独立数据的个数,通常用 f 表示。
例如,在计算偏差平方和的过程中,若表达式中使用
的是期望值 ,则 f n;若表达式中使用的是平均值 x ,
实用干货!正交试验设计及极差分析步骤总结!

实⽤⼲货!正交试验设计及极差分析步骤总结!⼀、研究背景当前有⼀项研究,研究⼤⾖出油率分别与3个因素的关系情况,分别是萃取液,温度和处理时间。
需要设计⼀个三因素三⽔平的正交试验表,并收集试验数据后进⾏分析,希望找出3个因素时各⽔平的最佳⼤⾖出油率组合。
⼆、正交实验设计进⼊SPSSAU系统,选择[实验/医学研究]--[]。
确定因⼦个数及⽔平数,点击[开始分析]。
得到正交表L9.3.4,总共进⾏9次试验。
三、数据收集确定选⽤的正交表后,把表中各列因⼦下的数字“1”、“2”、“3”,分别换成各因⼦在试验中的⽔平值,并根据此表格安排试验⽅案。
下⼀步按照试验⽅案进⾏试验,将对应数据收集填⼊表中。
本案例数据如下表:表格中⽔平数量使⽤数字表⽰,⽐如因⼦2(温度)⾥⾯的数字1表⽰20度,数字2表⽰35度。
四、数据分析上传数据,对试验数据进⾏分析。
选择[实验/医学研究]--[]。
放置分析项操作如下:SPSSAU输出结果如下:极差分析可⽤于研究正交试验数据,包括因素间的优势或因素间具体⽔平的优劣。
表格中各指标含义说明如下:极差分析表格中可知:从3个因素来看,结合R值(因素极差值)的⼤⼩对⽐可知,因⼦2温度是最优因素,其次是因⼦1萃取液量,最后是因⼦3处理时间。
因⽽3个因素的优劣排序为:因⼦2(温度)>因⼦1(萃取液量)>因⼦3(处理时间)。
具体结合各因⼦的最佳⽔平可知,因⼦1萃取液量时第2个⽔平即50时最优,因⼦2温度以第3个⽔平即50度最优,因⼦3处理时间以第3个⽔平即3.5⼩时最优。
综合上述分析可知:最优因⼦为温度。
最优组合为“温度50度,萃取液量50,处理时间3.5⼩时”。
通过图形也可直观查看:「更多内容登录了解」。
第7章-正交试验设计的极差分析汇总

第7章-正交试验设计的极差分析汇总第7章正交试验设计的极差分析正交试验设计和分析方法大致分为二种:一种是极差分析法(又称直观分析法),另一种是方差分析法(又称统计分析法)。
本章介绍极差分析法,它简单易懂,实用性强,在工农业生产中广泛应用。
7.1单指标正交试验设计及其极差分析极差分析法简称R法。
它包括计算和判断两个步骤,其内容如图7-1所示。
图中,K m为第j列因素m水平所对应的试验指标和,K jm为K m的平均值。
由K m的大小可以判断j因素的优水平和各因素的水平组合,即最优组合。
R为第j列因素的极差,即第j列因素各水平下平均指标值的最大值与最小值之差:R j=max(K~i,K~2, ,K jm)-min(心,兀,,K~)R反映了第j列因素的水平变动时,试验指标的变动幅度。
R 越大,说明该因素对试验指标的影响越大,因此也就越重要。
于是依据R j的大小,就可以判断因素的主次极差分析法的计算与判断,可直接在试验结果分析表上进行,现以例6 - 2来说明单指标正交试验结果的极差分析方法。
一、确定因素的优水平和最优水平组合例6-2为提高山楂原料的利用率,某研究组研究了酶法液化工艺制造山楂精汁。
拟通过正交试验寻找酶法液化工艺的最佳工艺条件。
在例6 -2中,不考虑因素间的交互作用(因例6 - 2是四因素三水平试验,故选用L9(34)正交表),表头设计如表6 - 5所示,试验方案则示于表6 - 6中。
试验结果的极差分析过程,如表7 - 1所示.表6-4 因素水平表表6-6 试验方案及结果试验指标为液化率,用y i表示,列于表6 - 6和表7 - 1的最后一一计算示例:因素A的第1水平A i所对应的试验指标之和及其平均值分别为:K AI二y i+y2+y3=0+17+24=41, K A1同理,对因素A的第2水平A和第3水平A,有-K AI=13.7 31K A2=y4+y5+y6=12+47+28=87 K A2 K A2=2931K A3=y7+y8+y9=1 + 18+42=61 , K A3K A3=20.33由表7 - 1或表6 - 6可以看出,考察因素A进行的三组试验中(A,A2,A3),B、C D各水平都只出现了一次,且由于B、C D间无交互作用,所以B、C D因素的各水平的不同组合对试验指标无影响,因此,对A、A2和A s来说,三组试验的试验条件是完全一样的。
正交试验结果的极差分析法

正交试验结果的极差分析法正交试验方法能得到科技工作者的重视,在实践中得到广泛的应用,原因之一是不仅试验的次数减少,而且用相应的方法对试验结果进行分析可以引出许多有价值的结论。
因此,在正交试验中,如果不对试验结果进行认真的分析,并明确地引出应该引出的结论,那就失去用正交试验法的意义和价值。
下面以L4(23)表为例讨论正交试验结果的极差分析法。
表4-13 L4 (2 3)正交试验计算表列号1 2 3 试验指标y i试验号1 1 1 1 y12 1 2 2 y23 2 1 2 y3n=4 2 2 1 y4I j I1 = y j+y2I2 = y1+y3I3 = y1+y4II j II1 = y3+y4II2 = y2+y4II3 = y2+y3k j k1 =2 k2 =2 k3 =2I j/k j I1/k1I2/k2I3/k3II j/k j II1/k1II2/k2II3/k3极差(D j) max{}-min{} max{}-min{} max{}-min{}在表4-13中:I j——第j列“1”水平所对应的试验指标的数值之和。
Ⅱj——第j列“2”水平所对应的试验指标的数值之和。
(第j列有“3”,“4”水平时)k j——第j列同一水平出现的次数。
等于试验的次数(n)除以第j列的水平数。
——第j列“1”水平所对应的试验指标的平均值。
——第j列“2”水平所对应的试验指标的平均值。
D j——第j列的极差。
等于第j列各水平对应的试验指标平均值中的最大值减最小值,即用极差法分析正交试验结果应引出以下几个结论:①在试验范围内,各列对试验指标的影响从大到小的排队。
某列的极差最大,表示该列的数值在试验范围内变化时,使试验指标数值的变化最大。
所以各列对试验指标的影响从大到小的排队,就是各列极差D的数值从大到小的排队。
②试验指标随各因素的变化趋势。
③使试验指标最好的适宜的操作条件(适宜的因素水平搭配)。
④对所得结论和进一步研究方向的讨论。
第7章 正交试验设计的极差分析资料

第7章正交试验设计的极差分析第7章 正交试验设计的极差分析正交试验设计和分析方法大致分为二种:一种是极差分析法(又称直观分析法),另一种是方差分析法(又称统计分析法)。
本章介绍极差分析法,它简单易懂,实用性强,在工农业生产中广泛应用。
7.1 单指标正交试验设计及其极差分析极差分析法简称R 法。
它包括计算和判断两个步骤,其内容如图7-1所示。
图7-1 R 法示意图图中,K jm 为第j 列因素m 水平所对应的试验指标和,K jm 为K jm 的平均值。
由K jm 的大小可以判断j 因素的优水平和各因素的水平组合,即最优组合。
R j 为第j 列因素的极差,即第j 列因素各水平下平均指标值的最大值与最小值之差:R j =max(jm j j K K K ,,,21 )-min(jm j j K K K ,,,21 )R j反映了第j列因素的水平变动时,试验指标的变动幅度。
R j 越大,说明该因素对试验指标的影响越大,因此也就越重要。
于是依据R j的大小,就可以判断因素的主次。
极差分析法的计算与判断,可直接在试验结果分析表上进行,现以例6-2来说明单指标正交试验结果的极差分析方法。
一、确定因素的优水平和最优水平组合例6-2 为提高山楂原料的利用率,某研究组研究了酶法液化工艺制造山楂精汁。
拟通过正交试验寻找酶法液化工艺的最佳工艺条件。
在例6-2中,不考虑因素间的交互作用(因例6-2是四因素三水平试验,故选用L9(34)正交表),表头设计如表6-5所示,试验方案则示于表6-6中。
试验结果的极差分析过程,如表7-1所示.表6-4 因素水平表表6-6 试验方案及结果试验指标为液化率,用y i表示,列于表6-6和表7-1的最后一列。
表7-1 试验方案及结果分析计算示例:因素A 的第1水平A 1所对应的试验指标之和及其平均值分别为:K A1=y 1+y 2+y 3=0+17+24=41, 1A K 31K A1=13.7同理,对因素A 的第2水平A 2和第3水平A 3,有K A2=y 4+y 5+y 6=12+47+28=87, 2A K 31K A2=29 K A3=y 7+y 8+y 9=1+18+42=61, 3A K 31K A3=20.3由表7-1或表6-6可以看出,考察因素A 进行的三组试验中(A 1,A 2,A 3),B 、C 、D 各水平都只出现了一次,且由于B 、C 、D 间无交互作用,所以B 、C 、D 因素的各水平的不同组合对试验指标无影响,因此,对A 1、A 2和A 3来说,三组试验的试验条件是完全一样的。
第七章 正交试验设计与分析

例如,要考察增稠剂用量、pH值和杀菌温度对豆奶稳
定性的影响。每个因素设置3个水平进行试验 。 A因素是增稠剂用量,设A1、A2、A3 3个水平;B因 素是pH值,设B1、B2、B3 3个水平;C因素为杀菌温度, 设C1、C2、C3 3个水平。这是一个3因素3水平的试验,各
因素的水平之间全部可能组合有27种 。
1.3.2 正交表的基本性质
1.3.2.1 正交性 (1)任一列中,各水平都出现,且出现的次数相等 例如L8(27)中不同数字只有1和2,它们各出现4次; L9(34)中不同数字有1、2和3,它们各出现3次 。
上一张 下一张 主 页
退 出
(2)任两列之间各种不同水平的所有可能组 合都出现,且出现的次数相等
(2) 选因素、定水平,列因素水平表
根据专业知识、以往的研究结论和经验,从影响试验指标的
诸多因素中,通过因果分析筛选出需要考察的试验因素。一般确
定试验因素时,应以对试验指标影响大的因素、尚未考察过的因
素、尚未完全掌握其规律的因素为先。试验因素选定后,根据所
掌握的信息资料和相关知识,确定每个因素的水平,一般以2-4
素自由度+交互作用自由度+误差自由度。
此例有4个3水平因素,可以选用L9(34)或
L27(313) ;因本试验仅考察四个因素对液化率的影
响效果,不考察因素间的交互作用,故宜选用 L 9
( 3 4 )正交表。若要考察交互作用,则应选用
4-3 因素水平表
试验因素
水平
加水量 (mL/100g) A
10 50 90
加酶量 (mL/100g) B
1 4 7
酶解温度 (℃) C
20 35 50
酶解时间 (h) D
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
\第7章 正交试验设计的极差分析正交试验设计和分析方法大致分为二种:一种是极差分析法(又称直观分析法),另一种是方差分析法(又称统计分析法)。
本章介绍极差分析法,它简单易懂,实用性强,在工农业生产中广泛应用。
单指标正交试验设计及其极差分析极差分析法简称R 法。
它包括计算和判断两个步骤,其内容如图7-1所示。
&图7-1 R 法示意图—图中,K jm 为第j 列因素m 水平所对应的试验指标和,K jm 为K jm 的平均值。
由K jm 的大小可以判断j 因素的优水平和各因素的水平组合,即最优组合。
R j 为第j 列因素的极差,即第j 列因素各水平下平均指标值的最大值与最小值之差:R j =max(jm j j K K K ,,,21 )-min(jm j j K K K ,,,21 )R j反映了第j列因素的水平变动时,试验指标的变动幅度。
R j越大,说明该因素对试验指标的影响越大,因此也就越重要。
于是依据R j的大小,就可以判断因素的主次。
极差分析法的计算与判断,可直接在试验结果分析表上进行,现以例6-2来说明单指标正交试验结果的极差分析方法。
一、确定因素的优水平和最优水平组合例6-2 为提高山楂原料的利用率,某研究组研究了酶法液化工艺制造山楂精汁。
拟通过正交试验寻找酶法液化工艺的最佳工艺条件。
在例6-2中,不考虑因素间的交互作用(因例6-2是四因素三水平试验,故选用L9(34)正交表),表头设计如表6-5所示,试验方案则示于表6-6中。
试验结果的极差分析过程,如表7-1所示.(表6-4 因素水平表酶解温度(C)(C表6-6 试验方案及结果试验指标为液化率,用y i表示,列于表6-6和表7-1的最后一列。
表7-1 试验方案及结果分析=}计算示例:因素A 的第1水平A 1所对应的试验指标之和及其平均值分别为:K A1=y 1+y 2+y 3=0+17+24=41,=1A K 31K A1=同理,对因素A 的第2水平A 2和第3水平A 3,有K A2=y 4+y 5+y 6=12+47+28=87,=2A K 31K A2=29K A3=y 7+y 8+y 9=1+18+42=61,=3A K 31K A3=由表7-1或表6-6可以看出,考察因素A 进行的三组试验中(A 1,A 2,A 3),B 、C 、D 各水平都只出现了一次,且由于B 、C 、D 间无交互作用,所以B 、C 、D 因素的各水平的不同组合对试验指标无影响,因此,对A 1、A 2和A 3来说,三组试验的试验条件是完全一样的。
假如因素A 对试验指标无影响,那么321,,A A A K K K 应该相等,但由上面的计标可知,321,,A A A K K K 实际上并不相等,显然,这是由于因素A 的水平变化引起的,因此,321,,A A A K K K 的大小反映了A 1、A 2和A 3对试验指标影响的大小。
由于液化率y 越大越好,而132A A A K K K >>,所以可判断A 2为因素A 的优水平。
同理,可判断因素B 、C 、D 的优水平分别为B 3、C 3、D 1。
所以,优水平组合为A 2B 3C 3D 1,即最优工艺条件为加水量A 2=50ml/100g 、加酶量B 3=7ml/100g 、酶解温度C 3=50。
C 和酶解时间D 1=小时。
二、确定因素主次顺序极差R j 按定义计算,如3.157.130.2912=-=-=A A A K K R ,0.273.43.3113=-=-=B B B K K R同理可求出R C 和R D . 计算结果列于表7-1中。
比较R j 值可知R B >R A >R D >R C ,所以试验因素对试验指标的影响的主次顺序为BADC 。
即加酶量影响最大,其次是加水量和酶解时间,而酶解温度的影响最小。
三、绘制因素与指标趋势图、为了更直观地反映因素对试验指标的影响规律和趋势,用因素的水平作横坐标,试验指标的平均值(j K )作纵坐标,画出因素与指标的关系图(即趋势图),如图7-2所示. (p137)趋势图可为进一步试验时选择因素水平指明方向.如对因素A,由图7-2可见,A 2水平时,指标最高,但若能在A 2附近再取一些水平(如40、60)作进一步试验,则有可能取得更高的指标;对D 因素,若能取一些比D 1更小的水平(如和作进一步试验,也有可能得到更好的结果.以上三个步骤即为极差分析的基本程序与方法.四、说明与讨论1、计算结果的检验: 每一列的K j 之和应等于全部试验结果(即指标值)之和, 即∑∑===nj j mj j y K 11,m 为水平数,n 为试验总实施次数.2.因素的最优水平组合,在实际处理中是灵活的,即对于主要因素,一定要选最优水平;而对次要因素,则应权衡利弊,综合考虑其它条件进行水平选取,从而得到最符合实际生产的最优或较优生产工艺条件.3.例6-2的最优工艺条件A 2B 3C 3D 1并不在实施的9个试验之中.这表明优化结果不仅反映了已做的试验信息,而且反映了全面试验信息.因此,正交试验设计的部分实施方案反映了全面试验信息.~4.例6-2得出的最优工艺条件,只有在试验所考察的范围内才有意义,超出这个范围,情况就可能发生变化。
另外,只能说是“较优工艺条件”,而不能说是“最优工艺条件”.最好能根据趋势图做进一步试验,找出最靠近最优的工艺条件.5.对已确定的最优工艺条件(如例6-2的A 2B 3C 3D 1)进行重复试验,验证其试验指标是否最优.多指标正交试验设计及其极差分析在实际生产和科研试验中,所要考察的指标往往不止一个,这一类的试验设计叫做多指标试验设计.在多指标试验设计中,各指标之间可能存在一定的矛盾,如何兼顾各个指标,找出使每个试验都尽可能好的试验条件呢换言之,应如何分析多指标试验设计的结果呢常用的有两种方法:综合平衡法和综合评分法.下面举例说明综合平衡法的分析方法.这种方法在试验方案安排和各指标计算分析方法上,与单指标试验完全一样.其步骤是先分别找出各个指标最优或较优的生产条件,然后将这些生产条件综合平衡,找出兼顾每个指标都尽可能好的生产条件.例7-1 在油炸方便面的生产中,主要原料质量和主要工艺参数对产品的质量有影响。
今欲通过正交试验确定最佳生产条件。
;一. 试验方案设计1.确定试验指标评价方便面质量好坏的主要指标是: 脂肪含量(越低越好),水分含量(越高越好)和复水时间(越短越好)。
2.挑因素,选水平,列出因素水平表根据专业知识和实际经验,确定试验因素和水平,如表7-2所示。
表7-2 因素水平表油炸温度(C)D3.选正交表,设计表头,编制试验方案…本试验是四因素三水平试验,不考虑因素间的交互作用,因此,可应选L9(34)安排试验,表头设计和试验方案见表7-3(p140)。
按上述方案实施后,将每一项试验指标都记录下来,见表7-3。
注:对极差分析可以这样选正交表,但对方差分析应留有空列,以便估计试验误差.表7-3 试验方案及结果分析=,==二.试验结果分析1.计算每列各水平下每种试验指标的数据和(K 1,K 2,K 3),及其平均值(321K ,K ,K ),并计算极差R ,填入表7-3中。
2.画出因素与各种指标的趋势图,如图7-3所示(p140)。
3.按极差大小列出各指标下各因素主次顺序:|各因素主次顺序表主--次4.初选最优工艺条件根据各指标下的平均数据和321,,K K K ,初步确定各因素的最优水平组合为:对脂肪含量(%):A 3B 3C 1D 2 (脂肪含量越低越好) 对水分含量(%):A 1B 2C 1D 1 (水分含量越高越好)对复水时间(s ):A 2B 2C 2D 3 (复水时间越短越好):5.综合平衡....确定最优工艺条件(难点)!由于三个指标单独分析出来的最优条件并不一致,所以必须根据因素对三个指标影响的主次顺序,综合考虑,确定出最优条件。
首先,把水平选取上没有矛盾的因素的水平定下来,即如果对三个指标影响都重要的某一因素,都是取某一水平时最好,则该因素就是选这一水平。
在本试验中无这样的因素,因此我们只能逐个考察每一因素。
对因素A :从主次顺序来看,对脂肪含量和复水时间的影响都排在第一位为主要因素,而对水分含量的影响则排在第三位,属次要因素,因此,应以主要因素为主选因素的水平。
从初选的最优水平组合中可以看出,对脂肪含量选A3为好,而对复水时间,则选A2为好。
因为二者不一致,所以还须根据试验结果分析确定选A2还是A3。
从表7-3可知,当取A2时,复水时间比取A3时缩短%(有利),即[,而脂肪含量只比取A3时增加%(不利),即 [,且从水分含量指标来看,取A2也比取A3时更好,因此,应选取A2水平。
注:当取A3时,脂肪含量比取A2时降低%(有利),即复水时间比取A2时增加%(不利),即()/×100%=%。
综合平衡∴对“有利”部分,A2>A3;对“不利”部分,A2<A3,故应选A2!:对因素B:从主次顺序表中可见,对脂肪含量和水分含量的影响均排在最后,属次要因素;对复水时间的影响排在第三位,所以,应以复水时间这一指标来考虑。
再从初选最优水平组合中可知,对复水时间选B2为好,故B应取B2。
对因素C:从主次顺序表中和初选最优水平中可知,C对水分含量的影响排在第一位,对脂肪含量的影响排在第二位,且都是取C1为好;而对复水时间的影响则排在最后一位,属次要因素,故C应取C 1。
对因素D :对水分含量和复水时间的影响均排在第二位;而对脂肪含量的影响则排在第三位,属次要因素。
对复水时间而言,选D 3较好;而对水分含量而言,则选D 1为好。
所以,D 应选D 1或D 3。
但取D 1时,从表7-3可见,虽然水分含量最高,但复水时间最长,并且脂肪含量最高,而D 对这两项指标的影响也是比较主要的(在主次顺序表中排在第二、三位),综合考虑,D 应选D 3。
〔此时,复水时间最短,脂肪含量接近(K 3与K 2很接近),对这两个指标都有利;但水分含量此时低,不利〕---这是书上的解释方法!!! 以上分析方法称为综合平衡法.....。
所以,本试验的较优工艺条件为3122D C B A 。
由因素水平可知,此时湿面筋值为32%,改良剂用量为%,油炸时间为70s,油炸温度为C 160.最后,应在该条件下,进行验证试验,看其指标是否在所有试验中为最优.讨论:上述对选D 1还是选D 3的讨论,侧重于定性.下面,从完全定量..的角度讨论如何选D 的水平.。
选D 1与选D 3优缺点的比较. 综合平衡○1选D 1时 水分含量: %3.30%10097.207.297.2=⨯-(有利) 复水时间:%4.20%10043.373.243.3=⨯-(不利)脂肪含量:%6.3%1003.225.213.22=⨯-(不利) ○2选D 3时 水分含量: %5.43%10007.297.207.2-=⨯-(不利) 复水时间: %6.25%10073.243.373.2-=⨯- (有利)脂肪含量: %7.3%1005.213.225.21-=⨯-(有利)由此可见,选D 1时,“有利”>“不利”;选D 3时,“不利”>“有利”.并且D 1 (有利)>D 3(有利之和绝对值),D 1 (不利之和)< D 3(不利绝对值).因此,从定量分析来看,D 应取D 1,而不是取D 3.那么,究竟如何决定D 的水平呢最后,应该再进行A 2B 2C 1D 1和A 2B 2C 1D 3两次试验,由试验结果决定D 1好还是D 3好!实践是检验真理的唯一标准!】混合型正交表的试验设计极差分析前面讨论的都是水平数)(k n m L 相同的正交试验设计.但在实际工作中,有些试验受到设备、原材料和生产条件等限制.某些因素的水平选择受到制约,或者在有些试验中,要重点考察某个(或某些)因素需要多取几个水平,这时就会遇到水平数不同的正交试验设计.在这种情况下,通常有三种解决方法:一是直接选用合适的混合型正交表;二是采用拟水平法;三是采用拟因素法.我们现在只讨论第一种方法,即使用混合型正交表)(2121k k n m m L ⨯进行正交试验设计.例7-2 某油炸膨化食品的体积与油温、物料含水量及油炸时间有关,为确保产品质量,提出工艺要求。
