数学建模与数学实验 第4讲 线性规划
数学建模实验报告线性规划.doc

数学建模实验报告线性规划数学建模实验报告姓名:霍妮娜班级:计算机95学号:09055093指导老师:戴永红提交日期:5月15日一.线性规划问题描述:某厂生产甲乙两种口味的饮料,每百箱甲饮料需用原料6千克,工人10名,可获利10万元;每百箱乙饮料需用原料5千克,工人级大学生正在从若干个招聘单位中挑选合适的工作岗位,他考虑的主要因素包括发展前景、经济收入、单位信誉、地理位置等,试建立模型给他提出决策建议。
问题分析首先经过对问题的具体情况了解后,建立层次结构模型,进而进行决策分析。
下面我建立这样一个层次结构模型:某岗位综合分数发展前景x1经济收入x2家庭因素x3地理位置x4这是一个比较简单的层次结构模型,经过如下步骤就可以将问题解决。
1.成对比较从x1,x2,x3,x4中任取xi和xj,对他们对于y贡献的大小,按照以下标度给xi/xj赋值:xi/xj=1,认为前者与后者贡献程度相同;xi/xj=3,前者比后者的贡献程度略大;xi/xj=5,前者比后者的贡献程度大;xi/xj=7,前者比后者的贡献大很多;xi/xj=9,前者的贡献非常大,以至于后者根本不能和它相提并论;xi/xj=2n,n=1,2,3,4,认为xi/xj介于2n-1和2n+1直接。
xj/xi=1/n,n=1,2,…,9,当且仅当xi/xj=n。
2.建立逆对称矩阵记已得所有xi/xj,i,j=1,2,3,4,建立n阶方阵1135A=11351/31/3131/51/51/313.迭代e0=(1/n,1/n,1/n,1/n)Tek=Aek-1一直迭代直达到极限e=(a1,a2,…,a4)T则权系数可取Wi=ai 解:首先通过迭代法计算得x1,x2,x3,x4的权数分别为:0.278,0.278,0.235,0.209.假设对所有的xi都采用十分制,现假设有三家招聘公司,它们的个指标如下所示:x1x2x3x4甲8579乙7966丙5798按公式分别求出甲、乙、丙三家公司的综合指数为7.144,7.112和7.123.由此可以看出,应该选择甲公司。
数学建模教案--线性规划PPT课件

在满足约束条件下尽可能的给最左上角的变量最大值.
销地
产地
B1
B2
B3
B4 产量
4
12
4
11
A1 8
8
16
2
10
3
9
A2
64
10
8
5
11
6
A3
8
14
22
销量
8
14
12
14
48
所以,初始基可行解为:……目标函数值Z=372
表上作业法
1、初始基可行解--沃格尔法
最小元素法,有时按某一最小单位运价优先安排 物品调运时,却可能导致不得不采用运费很高的其他 供销点,从而使整个运输费用增加。
ai b j
mn
min z
Cij xij
i1 j1
n
xij ai
i 1,2,...m
j 1
m
(Ⅰ ) xij bj
j 1,2,...n
i 1
xij 0
i 1,2,..., m; j 1,2,..., n
其中ai , b j Cij 0
运输问题及其数学模型
该模型是一个线性规划模型,可以用单纯形法 求解。但是变量数目非常多。如3个产地,4个销地。 变量数目会有19个之多。
(3)所有结构约束条件都是等式约束; (4)各产地产量之和等于各销地销量之和。 秩 ( A) =m+n-1 运输问题的基可行解中应包含m+n-1个基变量.
表上作业法
表上作业法是一种迭代法,迭代步骤为: 1、先按某种规则找出一个初始解(初始调运方案); 2、再对现行解作最优性判别; 3、若这个解不是最优解,就在运输表上对它进行调整 改进,得出—个新解; 4、再判别,再改进; 5、直至得到运输问题的最优解为止。 迭代过程中得出的所有解都要求是运输问题的基可行解。
数学建模之线性规划

第一章 线性规划§1 线性规划在人们的生产实践中,经常会遇到如何利用现有资源来安排生产,以取得最大经济效益的问题。
此类问题构成了运筹学的一个重要分支—数学规划,而线性规划(Linear Programming 简记LP)则是数学规划的一个重要分支。
自从1947年G. B. Dantzig 提出求解线性规划的单纯形方法以来,线性规划在理论上趋向成熟,在实用中日益广泛与深入。
特别是在计算机能处理成千上万个约束条件和决策变量的线性规划问题之后,线性规划的适用领域更为广泛了,已成为现代管理中经常采用的基本方法之一。
1.1 线性规划的实例与定义例1某机床厂生产甲、乙两种机床,每台销售后的利润分别为4000元与3000元。
生产甲机床需用B A 、机器加工,加工时间分别为每台2小时和1小时;生产乙机床需用C B A 、、三种机器加工,加工时间为每台各一小时。
若每天可用于加工的机器时数分别为A 机器10小时、B 机器8小时和C 机器7小时,问该厂应生产甲、乙机床各几台,才能使总利润最大?上述问题的数学模型:设该厂生产1x 台甲机床和2x 乙机床时总利润最大,则21,x x 应满足(目标函数)2134m ax x x z += (1)s.t.(约束条件)⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0,781022122121x x x x x x x (2)这里变量21,x x 称之为决策变量,(1)式被称为问题的目标函数,(2)中的几个不等式是问题的约束条件,记为s.t.(即subject to)。
由于上面的目标函数及约束条件均为线性函数,故被称为线性规划问题。
总之,线性规划问题是在一组线性约束条件的限制下,求一线性目标函数最大或最小的问题。
在解决实际问题时,把问题归结成一个线性规划数学模型是很重要的一步,但往往也是困难的一步,模型建立得是否恰当,直接影响到求解。
而选适当的决策变量,是我们建立有效模型的关键之一。
1.2 线性规划的Matlab 标准形式线性规划的目标函数可以是求最大值,也可以是求最小值,约束条件的不等号可以是小于号也可以是大于号。
数学建模线性规划

线性规划1.简介:线性规划是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支,它是辅助人们进行科学管理的一种数学方法.在经济管理、交通运输、工农业生产等经济活动中,提高经济效果是人们不可缺少的要求,而提高经济效果一般通过两种途径:一是技术方面的改进,例如改善生产工艺,使用新设备和新型原材料.二是生产组织与计划的改进,即合理安排人力物力资源.线性规划所研究的是:在一定条件下,合理安排人力物力等资源,使经济效果达到最好.规划问题。
一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性线性约束条件的解叫做可行解,由所有可行解组成的集合叫做可行域。
在优化模型中,如果目标函数f(x)和约束条件中的gi(x)都是线性函数,则该模型称为线性规划。
2.线性规划的3个基本要素(1)决策变量(2)目标函数f(x)(3)约束条件(gi(x)≤0称为约束条件)3.建立线性规划的模型(1)找出待定的未知变量(决策变量),并用袋鼠符号表示他们。
(2)找出问题中所有的限制或者约束,写出未知变量的线性方程或线性不等式。
(3)找到模型的目标或判据,写成决策变量的线性函数,以便求出其最大值或最小值。
以下题为例,来了解一下如何将线性规划用与实际的解题与生活中。
生产计划问题某工厂生产甲乙两种产品,每单位产品消耗和获得的利润如表试拟订生产计划,使该厂获得利润最大解答:根据解题的三个基本步骤(1)找出未知变量,用符号表示:设甲乙两种产品的生产量分别为x1与x2吨,利润为z万元。
(2)确定约束条件:在这道题目当中约束条件都分别为:钢材,电力,工作日以及生产量不能为负的限制钢材:9x 1+5 x 2≤360,电力:4x 1+5 x 2≤200,工作日:3x 1+10 x 2≤300,x 1 ≥0 ,x 2 ≥0,(3)确定目标函数:Z=7x 1+12 x 2所以综合上面这三步可知,这个生产组合问题的线性规划的数学模型为:max Z=7x 1+12 x 2s.t.⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥≤+≤+≤+00300103200543605921212121x x x x x x x x4.使用MATLAB 解决线性规划问题依旧是以上题为例,将其用MATLAB 来表示出来1.将目标函数用矩阵的乘法来表示max Z=(7 12)⎪⎪⎭⎫ ⎝⎛21x x 2.将约束条件也用矩阵的乘法表示s.t.⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎭⎫ ⎝⎛≤⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛≤⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛2121003002003601035459x x x x 编写MATLAB 的程序如下:c=[-7 -12]; (由于是max 函数,因此将目标函数的系数全部变为负数)A=[9,5;4,5;3,10];b=[360;200;300];Aeq=[];beq=[];vlb=[0;0];vub=[];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)其运行结果显示如下:x =20.000024.0000fval =-428.00005.MATLAB 求解线性规划的语句(1)c=[ ] 表示目标函数的各个决策变量的系数(2)A=[ ] 表示约束条件中≥或≤的式子中的各个决策变量的系数。
数学建模-线性规划实验

3 线性规划实验3.1实验目的与要求●学会建立线性规划模型●学会LINGO软件的基本使用方法,求解线性规划问题●学会对线性规划问题进行灵敏度分析,以及影子价格的意义3.2基本实验1.生产计划安排与灵敏度分析解:(1)假设最后总生产得到的Ⅰ型产品为x1kg,Ⅱ型产品为x2kg,那么它们必须同时满足以下条件:Max Z=130x1+400x2-100(x1+x2/0.33)x1+(x2)/0.33≤902x1+3(x2)/0.33≤200x2≤40LINGO程序:Max =130*x1+400*x2-100*(x1+x2/0.33);x1+x2/0.33<=90;2*x1+3*x2/0.33<=200;x2<=40;结果:Global optimal solution found.Objective value: 2740.000Infeasibilities: 0.000000Total solver iterations: 3Model Class: LPTotal variables: 2Nonlinear variables: 0Integer variables: 0Total constraints: 4Nonlinear constraints: 0Total nonzeros: 7Nonlinear nonzeros: 0Variable Value Reduced CostX1 70.00000 0.000000X2 6.600000 0.000000Row Slack or Surplus Dual Price1 2740.000 1.0000002 0.000000 26.000003 0.000000 2.0000004 33.40000 0.000000即:最优的方案是Ⅰ型产品为70kg,Ⅱ型产品为6.6kg。
(2)Max Z=130x1+400x2-100(x1+x2/0.33)x1+(x2)/0.33≤872x1+3(x2)/0.33≤200x2≤40LINGO程序:Max =130*x1+400*x2-100*(x1+x2/0.33);x1+x2/0.33<=87;2*x1+3*x2/0.33<=200;x2<=40;结果:Variable Value Reduced CostX1 61.00000 0.000000X2 8.580000 0.000000Row Slack or Surplus Dual Price1 2662.000 1.0000002 0.000000 26.000003 0.000000 2.0000004 31.42000 0.000000那么公司得到的利润为:2662元(3)如果产品Ⅱ的销售价格变为395元/千克,最优解没有变化。
数学建模第4讲线性规划

解 编写M文件xxgh1.m如下:
c=[-0.4 -0.28 -0.32 -0.72 -0.64 -0.6];
A=[0.01 0.01 0.01 0.03 0.03 0.03;0.02 0 0 0.05 0 0;0 0.02 0 0 0.05 0;0 0 0.03 0 0 0.08];
b=[850;700;100;900]; Aeq=[]; beq=[];
8 4 x1 8 3 x2 32 x1 24 x2
因检验员错检而造成的损失为:
(8 25 2% x1 8 15 5% x2 ) 2 8x1 12 x2
2024/8/3
数学建模
故目标函数为:
min z (32 x1 24 x2) (8x1 12 x2 ) 40 x1 36 x2
0 0 0 0.5 1.2 1.3];
b = [800; 900];
Aeq=[1 0 0 1 0 0
010010
0 0 1 0 0 1]; beq=[400 600 500];
To MATLAB (xxgh3)
vlb = zeros(6,1);
vub=[];
[x,fval] = linprog(f,A,b,Aeq,beq,vlb,vub)
解: 编写M文件xxgh2.m如下:
x1
min z (6
3
4)
x2
x3
s.t.
1
0
1 1
1 0
x1 x2 x3
120
50
30 0 20
x1 x2 x3
c=[6 3 4];
A=[0 1 0];
b=[50];
Aeq=[1 1 1];
beq=[120]; vlb=[30,0,20];
第4讲 线性规划

当目标函数该边后,等值线的方向会发生改变, 如果等值线与某个约束对应的函数直线平行, 则该函数值线上的所有可行解都是最优解
最优解(1,4)
2 x 1 x 2 2
x1 2 x 2 2
x1 x 2 5
注 释
可能出现的情况: • 可行域是空集
• 可行域无界无最优解 • 最优解存在且唯一,则一定在顶点上达到 • 最优解存在且不唯一,一定存在顶点是最优 解
m 定义 2.2.2: B 是秩为 设
基本可行解,这时对应的基阵 为可行基。 B 1 b 0 如果 则称该基可行解为非退化的,如果一个线 性规划的所有基可行解都是非退化的则称该规划为非退化 的。
B
例 考虑问题:
min z x 1 x 2 2 x 1 x 2 x 3 2 x1 2 x 2 x 4 2 s .t . x1 x 2 x 5 5 x j 0; j 1,2,3,4,5
或
a i 1 x 1 a i 2 x 2 a in x n bi a i 1 x 1 a i 2 x 2 a in x n bi
例2.1.3 把问题转化为标准
形式
max z x1 x 2 2 x 1 x 2 2 x1 2 x 2 2 s .t . x1 x 2 5 x1 0
基本可行解与基本 定理
• 定义 • 基本定理 • 问题
基本可行解定 义
令 A ( B , N ) , x =( x B , x N )。
Ax b
分块 左乘B
xN
1
Bx B Nx N b
x B B 1 Nx N B 1 b
《数学建模与数学实验》实验报告实验五:线性规划模型实验
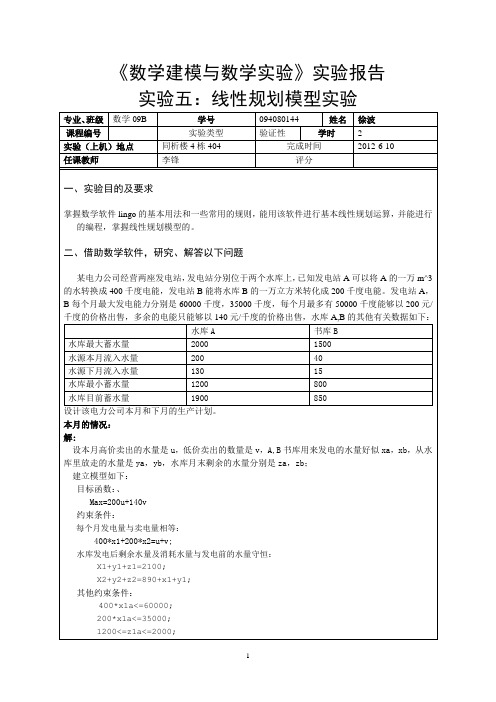
《数学建模与数学实验》实验报告实验五:线性规划模型实验专业、班级数学09B 学号094080144 姓名徐波课程编号实验类型验证性学时 2实验(上机)地点同析楼4栋404 完成时间2012-6-10任课教师李锋评分一、实验目的及要求掌握数学软件lingo的基本用法和一些常用的规则,能用该软件进行基本线性规划运算,并能进行的编程,掌握线性规划模型的。
二、借助数学软件,研究、解答以下问题某电力公司经营两座发电站,发电站分别位于两个水库上,已知发电站A可以将A的一万m^3 的水转换成400千度电能,发电站B能将水库B的一万立方米转化成200千度电能。
发电站A,B每个月最大发电能力分别是60000千度,35000千度,每个月最多有50000千度能够以200元/千度的价格出售,多余的电能只能够以140元/千度的价格出售,水库A,B的其他有关数据如下:水库A 书库B水库最大蓄水量2000 1500水源本月流入水量200 40水源下月流入水量130 15水库最小蓄水量1200 800水库目前蓄水量1900 850设计该电力公司本月和下月的生产计划。
本月的情况:解:设本月高价卖出的水量是u,低价卖出的数量是v,A,B书库用来发电的水量好似xa,xb,从水库里放走的水量是ya,yb,水库月末剩余的水量分别是za,zb;建立模型如下:目标函数:、Max=200u+140v约束条件:每个月发电量与卖电量相等:400*x1+200*x2=u+v;水库发电后剩余水量及消耗水量与发电前的水量守恒:X1+y1+z1=2100;X2+y2+z2=890+x1+y1;其他约束条件:400*x1a<=60000;200*x1a<=35000;1200<=z1a<=2000;800<=z2a<=1500;u1<=50000;现在进行两个月同时计算:设本月和下月高价卖出的水量是u1,u2,低价卖出的水量是v1,v2,A,B水库用来发电的水量是xa1,xa2,xb1,xb2,从水库直接放走的水量分别是ya1,ya2,yb1,yb2,水库月末剩余水量分别是za1,za2,zb1,zb2.建立模型如下:目标函数:Max=200*(u1+u2)+140*(v1+v2)约束条件:每个月发电量与卖电量相等:400*xa1+200*xb1=u1+v1;400*xa2+200*xb2=u2+v2;水库发电后剩余水量及消耗水量与发电前的水量守恒:xa1+ya1+za1=2100;xb1+yb1+zb1=890+xa1+ya1;xb2+yb2+zb2=zb2+15+xa2+ya2;xa2+ya2+za2=za1+130;其他约束条件:400*xa1<=60000;400*xa2<=60000;200*xb1<=35000;200*xb2<=35000;1200<=za1<=2000;1200<=za2<=2000;800<=zb1<=1500;800<=zb2<=1500;u1<=50000;u2<=50000;编程实现如下:model:max=200*u+140*v;400*x1+200*x2=u+v;X1+y1+z1=2100;X2+y2+z2=890+x1+y1;400*x1<=60000;200*x2<=35000;Z1>=1200;Z1<=2000;Z2>=800;Z2<=1500;u<=50000;end解得:Global optimal solution found.Objective value: 0.1630000E+08Total solver iterations: 5Variable Value Reduced Cost U 50000.00 0.000000V 45000.00 0.000000X1 150.0000 0.000000 X2 175.0000 0.000000 Y1 0.000000 0.000000 Z1 1950.000 0.000000 Y2 0.000000 0.000000 Z2 865.0000 0.000000Row Slack or Surplus Dual Price1 0.1630000E+08 1.0000002 0.000000 -140.00003 0.000000 0.0000004 0.000000 0.0000005 0.000000 140.00006 0.000000 140.00007 750.0000 0.0000008 50.00000 0.0000009 65.00000 0.00000010 635.0000 0.00000011 0.000000 60.000000编程实现如下:model:max=200*(u1+u2)+140*(v1+v2);400*x1a+200*x2a-u1+v1=0;400*x1b+200*x2b=u2+v2;X1a+y1a+z1a=2100;X2b+y2b+z2b=zb2+15+x1b+y1b;X2a+y2a+z2a=890+x1a+y1a;X1a+y1b+z1b=z1a+130;400*x1a<=60000;400*x1b<=60000;200*x2a<=35000;200*x2b<=35000;Z1a<=2000;Z1a>=1200;Z1b<=2000;Z1a>=1200;Z2a<=1500;Z2a>=800;Z2b>=800;Z2b<=1500;u1<=50000;u2<=50000;end解得:Global optimal solution found.Objective value: 0.3330000E+08Total solver iterations: 0Variable Value Reduced Cost U1 50000.00 0.000000 U2 50000.00 0.000000 V1 50000.00 0.000000 V2 45000.00 0.000000 X1A 0.000000 56000.00 X2A 0.000000 28000.00 X1B 150.0000 0.000000 X2B 175.0000 0.000000 Y1A 900.0000 0.000000 Z1A 1200.000 0.000000 Y2B 0.000000 0.000000 Z2B 800.0000 0.000000 ZB2 810.0000 0.000000 Y1B 0.000000 0.000000 Y2A 990.0000 0.000000 Z2A 800.0000 0.000000 Z1B 1330.000 0.000000Row Slack or Surplus Dual Price1 0.3330000E+08 1.0000002 0.000000 140.00003 0.000000 -140.00004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 60000.00 0.0000009 0.000000 140.000010 35000.00 0.00000011 0.000000 140.000012 800.0000 0.00000013 0.000000 0.00000014 670.0000 0.00000015 0.000000 0.00000016 700.0000 0.00000017 0.000000 0.00000018 0.000000 0.00000019 700.0000 0.00000020 0.000000 340.000021 0.000000 60.00000由上可知,最大值是0.3260000E+08,每月A,B厂发电用水量是150,175,150,175三、本次实验的难点分析实验过程中遇到了一些问题:对掌握lingo的基本用法有所欠缺,本实验中存在偏差。
线性规划模型

(1)模型中常数数据不精确
(2)模型中常数数据可能发生变化
价值变动
min z cx s.t. Ax b x0
11/43
资源总量变动
敏感性分析
max z 60d 30t 20c 8d + 6t + c <=48 4d + 2t + 1.5c <= 20 d + 1.5t + 0.5c <=8 t <= 5
mn
满足约束条件的解称为可行解,所有可行解的集合 称为可行域 ,满足最优目标的解称为最优解 决策变量为整数时,称为整数线性规划
决策变量取0或1时,称为0-1线性规划
7/43
线性规划问题的解
线性规划问题的可行域是一个凸多边形;
线性规划问题如果存在最优解,则最优解必在可行域的
顶点处达到。
单纯形法:
约束条件右端变化一个单位时目标函数变化量,只对紧约 决策变量改变一个单位时目标函数的改变量,只有非基变 量有值 束有值
12/43
敏感性分析
Objective Coefficient Ranges Current Allowable Allowable Coefficient Increase Decrease 60.00000 0.0 8.000000 30.00000 60.00000 0.0 20.00000 2.500000 INFINITY Righthand Side Ranges Current Allowable Allowable RHS Increase Decrease 48.00000 INFINITY 2.000000 20.00000 1.333333 8.000000 8.000000 1.000000 3.000000 5.000000 INFINITY 2.000000
整数线性规划数学建模与数学实验

280x1+250x2+400x3<60000
end
IP 结果输出
gin 3
OBJECTIVE FUNCTION VALUE VARIABLE VALUE REDUCED COST
X3
0.000000 -4.000000
“gin 3”表示“前3个变量 为整数”,等价于: gin x1 gin x2 gin x3
最优值比界坏
舍弃 边界
最优解为整数 最优值比界好
最优解为非整 数最优值比界好
分支
分支
分支的方法
0
N
I
B1N
cBB1b
B 1b
xr br Z
brxrbr
min c x
Ax b
s .t .
x
0,
x 为整. x r
b r
x
0,
x 为整数
min c x
Ax b
模型求解 整数规划(Integer Programming,简记IP)
Mz a 2 x 1 3 x 2 4 x 3
IP可用LINDO直接求解
s.t. 1.5x13x25x3600
max 2x1+3x2+4x3
st
28x10 25x20 40x30 600010 .5x1+3x2+5x3<600
x1, x2, x3为非负整数
一般整数变量:GIN <Variable> 0-1整数变量: INT <Variable>
LinGo
一般整数变量: @GIN( variable_name); 0-1整数变量:@BIN( variable_name);
《数学建模》课程教案

《数学建模》课程教案教学文档一、教学内容本节课选自《数学建模》教材第四章:线性规划及其应用。
详细内容包括线性规划的基本概念、线性规划模型的建立、单纯形方法及其应用。
二、教学目标1. 理解线性规划的基本概念,掌握线性规划模型的建立方法。
2. 学会运用单纯形方法求解线性规划问题,并能将其应用于实际问题。
3. 培养学生的数学建模能力,提高解决实际问题的能力。
三、教学难点与重点难点:线性规划模型的建立、单纯形方法的运用。
重点:线性规划的基本概念、线性规划模型的求解。
四、教具与学具准备教具:黑板、粉笔、PPT课件。
学具:教材、笔记本、计算器。
五、教学过程1. 导入:通过一个实际情景,引出线性规划问题。
实践情景:某工厂生产两种产品,产品A和产品B。
生产每个产品A需要2小时工时和3平方米厂房面积,生产每个产品B需要4小时工时和1平方米厂房面积。
工厂每天有8小时工时和6平方米厂房面积可用。
如何分配生产时间和厂房面积,使得工厂每天的生产利润最大?2. 知识讲解:1) 线性规划的基本概念。
2) 线性规划模型的建立。
3) 单纯形方法及其应用。
3. 例题讲解:例题1:求解导入环节提出的实际线性规划问题。
例题2:求解一个标准形式的线性规划问题。
4. 随堂练习:让学生独立求解一个线性规划问题,并给出解答。
六、板书设计1. 线性规划基本概念2. 线性规划模型的建立3. 单纯形方法4. 例题解答七、作业设计1. 作业题目:习题4.1:求解线性规划问题。
习题4.2:应用单纯形方法求解实际问题。
2. 答案:八、课后反思及拓展延伸1. 反思:本节课学生对线性规划的基本概念和求解方法掌握程度,以及对实际问题的建模能力。
2. 拓展延伸:探讨线性规划的其他求解方法,如内点法、对偶问题等。
引导学生关注线性规划在实际问题中的应用,如物流、生产计划等。
重点和难点解析1. 线性规划模型的建立。
2. 单纯形方法的运用。
3. 例题讲解与随堂练习的设置。
数学建模-线性规划

x2
P1
P2 P3 P4 P5
M
O点 Q点 R点 P点
B [P P 1 3 B [P 2 P 3
P ] x (0,1, 3, 0,16) 5 P ] x (4,1, 5, 0, 0) 3
T
T
R
P Q
B [P P 1 2
0
x1
最优解
数学建模之线性规划
单纯形算法举例
m in s .t z = -2 x 1 -3 x 2 -x 1 + x 2 2 x1 +2x 2 10 3x1 +x 2 15 x1, x 2 0
min z min( z ) max z C X
(2)约束条件为不等式:对于不等号“≤(≥)”的约束 条件,则可在“≤(≥)”的左端加上(或减去)一个非 负变量(称为松弛变量)使其变为等式; (3)对于无约束的决策变量:譬如 x (, ,则令 )
x x x,使得 x, x 0 ,代入模型即可。
n
,称之为决策变量, B j 产量为 x j ( j 1, 2, , n)
所得的利润为 z ,则要解决的问题的目标是使得总利润
函数
z c j x 有最大值。决策变量所受的约束条件为 j
j 1
数学建模之线性规划
aij x j bi (i 1,2, , m) j 1 x 0( j 1,2, , n) j
数学建模
线性规划问题
数信学院 任俊峰
2012-7-9
数学建模之线性规划
线性规划方法
最优化问题是求使问题的某一项指标“最优”的 方案,这里的“最优”包括“最好”、“最大”、 “最小”、“最高”、“最低”、“最多”等等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结果为: x= 9.0000 0.0000 fval =360 即只需聘用9个一级检验员。
注:本问题应还有一个约束条件:x1、x2取整数。故 它是一个整数线性规划问题。这里把它当成一个线性规 划来解,求得其最优解刚好是整数:x1=9,x2=0,故它 就是该整数规划的最优解。若用线性规划解法求得的最 优解不是整数,将其取整后不一定是相应整数规划的最 优解,这样的整数规划应用专门的方法求解。
解 编写M文件xxgh2.m如下: c=[-0.4 -0.28 -0.32 -0.72 -0.64 -0.6]; A=[0.01 0.01 0.01 0.03 0.03 0.03;0.02 0 0 0.05 0 0;0 0.02 0 0 0.05 0;0 0 0.03 0 0 0.08]; b=[850;700;100;900]; To Matlab (xxgh2) Aeq=[]; beq=[]; vlb=[0;0;0;0;0;0]; vub=[]; [x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)
返 回
解答
线性规划模型的一般形式
目标函数和所有的约束条件都是设计变量 的线性函数。
min u ci xi
i 1
n
矩阵形式: min u cx n aik xk bi , i 1,2,...,n. Ax b s.t. k 1 s.t. vlb x vub x 0, i 1,2,...,n. i
例1
பைடு நூலகம்
加工奶制品的生产计划 12小时
8小时 3公斤A1 4公斤A2 获利24元/公斤
1桶 牛奶 或
获利16元/公斤
每天: 50桶牛奶
时间480小时 至多加工100公斤A1
制订生产计划,使每天获利最大
• 35元可买到1桶牛奶,买吗?若买,每天最多买多少?
• 可聘用临时工人,付出的工资最多是每小时几元? • A1的获利增加到 30元/公斤,应否改变生产计划?
x1 min z (6 3 4) x2 x 3 x1 1 2 3 80 0 1 0 x2 50 x3 x1 s.t. 1 1 1 x2 120 x 3 30 x1 0 x2 20 x 3
(2) 对简单的LINGO程序
•LINGO也可以LINDO一样编程
•但LINGO与LINDO语法有差异
2.Lingo软件包使用
1)安装
2)特点:优化模型、易学、程序与模型非常类似; 3)Lingo软件包简单编程方法: 注意: 程序: 1)等号 模型: min=7*x1+3*x2; Min f=7x1+3x2 2)乘号 x1+x2>=345.5; x1+x2>=345.5 3)分号 x1>=98; x1>=98 2*x1+x2<=600; 4)说明 2*x1+x2<=600 @gin(x1); @gin(x2); x1,x2 为整数 end
数学建模与数学实验
第4讲 线性规划
实验目的
1、了解线性规划的基本内容。
2、掌握用数学软件包求解线性规划问题。
实验内容
1、两个引例。 2、用数学软件包matlab求解线性规划问题。
3、用数学软件包lindo、lingo求解线性规划问题。 4、建模案例:投资的收益与风险
5、实验作业。
两个引例
问题一 : 任务分配问题:某车间有甲、乙两台机床,可用 于加工三种工件。假定这两台车床的可用台时数分别为800和 900,三种工件的数量分别为400、600和500,且已知用三种 不同车床加工单位数量不同工件所需的台时数和加工费用如 下表。问怎样分配车床的加工任务,才能既满足加工工件的 要求,又使加工费用最低?
返 回
用LINGO优化工具箱解线性规划
LINGO软件能求解的优化模型
优化模型
连续优化
整数规划(IP)
线性规划 (LP)
二次规划 (QP)
非线性规划 (NLP) LINGO
LINDO
1. LINGO软件简介
(1) LINGO模型的优点
•包含了LINDO的全部功能 •提供了灵活的编程语言(矩阵生成器)
问题
x1 min z 40 36 x 2 x1 s.t. 5 3 x (45) 2
编写M文件xxgh4.m如下: c = [40;36]; A=[-5 -3]; b=[-45]; Aeq=[]; To Matlab (xxgh4) beq=[]; vlb = zeros(2,1); vub=[9;15]; %调用linprog函数: [x,fval] = linprog(c,A,b,Aeq,beq,vlb,vub)
解答
问题二: 某厂每日8小时的产量不低于1800件。为了进行质量 控制,计划聘请两种不同水平的检验员。一级检验员的标准为: 速度25件/小时,正确率98%,计时工资4元/小时;二级检验员 的标准为:速度15小时/件,正确率95%,计时工资3元/小时。 检验员每错检一次,工厂要损失2元。为使总检验费用最省, 该工厂应聘一级、二级检验员各几名? 解 设需要一级和二级检验员的人数分别为x1、x2人, 则应付检验员的工资为:
优化模型的分类
实际问题中 Min (或Max ) z f ( x ), x ( x1 , x n )T 的优化模型 s.t. g i ( x) 0, i 1,2, m x~决策变量 线性规划(LP) 二次规划(QP) 非线性规划(NLP) f(x)~目标函数 数学规划 0-1整数规划 一般整数规划 纯整数规划(PIP) 混合整数规划(MIP) gi(x)0~约束条件
连续规划
整数规划(IP)
用MATLAB优化工具箱解线性规划
1、模型: min z=cX s.t. AX b 命令:x=linprog(c,A,b) 2、模型:min z=cX s.t. AX b Aeq X beq 命令:x=linprog(c,A,b,Aeq,beq)
或 或
x=linprog(c,A,b,Aeq,beq,x0) [x,fval]=linprog(c,A,b,Aeq,beq)
3. lingo软件包的变量界定 变量界定函数实现对变量取值范围的限制,共4种: •@bin(x) 限制x 为0 或1; •@bnd(L,x,U) 限制L≤x≤U; •@free(x) 取消对变量x 的默认下界为0 的限制, 即x 可以取任意实数; •@gin(x) 限制x 为整数. •在默认情况下,LINGO 规定变量是非负的,也 就是说下界为0,上界为+∞。
8 4 x1 8 3 x2 32 x1 24 x2
因检验员错检而造成的损失为:
(8 25 2% x1 8 15 5% x2 ) 2 8x1 12 x2
故目标函数为:
min z (32 x1 24 x2 ) (8x1 12 x2 ) 40 x1 36 x2
约束条件为:
8 25 x1 8 15 x2 1800 8 25 x 1800 1 8 15 x2 1800 x1 0, x2 0
线性规划模型:
min z 40 x1 36 x2
5 x1 3 x2 45 x 9 1 s.t. x 15 2 x1 0, x2 0
x5、x6。可建立以下线性规划模型:
min z 13x1 9x2 10x3 11x4 12x5 8x6
x 1 x 4 400 x x 600 5 2 x3 x6 500 s.t. 0.4 x1 1.1x 2 x3 800 0.5 x 4 1.2 x5 1.3x6 900 xi 0, i 1,2,,6
计算结果:
x= 0.0000 600.0000 0.0000 400.0000 0.0000 500.0000 fval =1.3800e+004
即在甲机床上加工600个工件2,在乙机床上加 工400个工件1、500个工件3,可在满足条件的情 况下使总加工费最小为13800。
例2 问题二的解答
改写为:
车床 类 型 甲 乙 单位工件所需加工台时数 工件 1 0.4 0.5 工件 2 1.1 1.2 工件 3 1.0 1.3 单位工件的加工费用 工件 1 13 11 工件 2 9 12 工件 3 10 8 可用台 时数 800 900
解
设在甲车床上加工工件1、2、3的数量分别为x1、
x2、x3,在乙车床上加工工件1、2、3的数量分别为x4、
min z 6 x1 3 x 2 4 x 3
例1
x1 2 x2 3 x3 80 x1 x2 x3 120 s.t. x1 30 0 x2 50 x3 20
解: 编写M文件xxgh1.m如下: c=[6 3 4]; A=[1,2,-3;0 1 0]; b=[80;50]; Aeq=[1 1 1]; beq=[120]; vlb=[30,0,20]; vub=[]; [x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)
To Matlab (xxgh1)
例2
max
z 0.4 x1 0.28 x 2 0.32 x3 0.72 x4 0.64 x5 0.6 x6 s.t. 0.01x1 0.01x2 0.01x3 0.03x4 0.03x5 0.03x6 850
0.02 x1 0.05x 4 700 0.02 x 2 0.05 x5 100 0.03x3 0.08 x6 900 xj 0 j 1,2, 6
