09 非条件Logistic 回归分析
logistic回归分析精选PPT课件
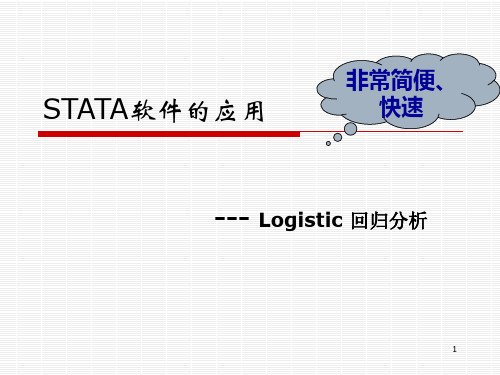
Number of obs =
LR chi2(1)
=
Prob > chi2
=
Pseudo R2
=
152 30.67 0.0000 0.1455
------------------------------------------------------------------------------
case |
Coef. Std. Err.
z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
exposure | 2.112829 .4228578 5.00 0.000 1.284043 2.941615
2
二分类资料的分析
非条件logistic模型:成组病例对照研究资料 条件logistic模型:配比病例对照研究资料3源自非条件logistic回归模型
lo ( p ) g 0 + i 1 X 1 + t = 2 X 2 k X k
01X1+ 2X2+ + kXk
p1ee01X12X2 kXk 1
|------------------------+----------------------
Odds ratio |
8.271605
| 3.4193 21.33091 (exact)
Attr. frac. ex. |
.8791045
| .7075425 .9531197 (exact)
Attr. frac. pop |
.4626866
非条件Logistic回归实例解析

学习要点:
1.了解Logistic回归分析的基本思想; 2.了解Logistic回归分析的医学应用; 3.熟悉非条件Logistic回归分析在SPSS19.0 中操作演练及统计结果解释;
4.了解非条件Logistic回归分析的注 意事项。
OR值定义及其意义
OR值=(病例中暴露的比例/病例中非暴露的 比例)/(对照中暴露的比例/对照中非暴露的 比例)
OR值=2,说明病例中暴露于某个危险因素的 比例为对照组的2倍,说明该因素可能与疾病 发生有关。
统计结果解释
结果显示:最终引入模型的变量及常数项的偏 回归系数值B,标准误(SE),Wald卡方值 (Wals),自由度(df),P值(Sig),及其 OR值(ExpB)和OR的95%CI。
4.了解非条件Logistic回归分析的注 意事项。
三、SPSS19.0实例应用与解析
1、自变量进入模型的方法:
一般分为:进入法(enter)、前进法(forward) 和后退法(backward)3种,后两种方法还可 以分为条件(conditional)、偏拟然比(LR) 和Wald检验3种。如果变量较少,通常采用进入 法,如果变量太多,则选用前进LR,前进LR相 当于多重线性回归分析中的逐步回归,本例当中 采用进入法。
学习要点:
1.了解Logistic回归分析的基本思想; 2.了解Logistic回归分析的医学应用; 3.熟悉非条件Logistic回归分析在SPSS19.0 中操作演练及统计结果解释;
4.了解非条件Logististic回归分析的基本思想
多重线性回归模型适用于分析一个连续型因变 量与一组自变量之间的关系,但如果因变量为 分类变量,那么因变量与自变量之间就丧失了 线性关系,则不适用线性回归分析来解决,但 经过Logit变化后,就可以将模型转变为线性 关系,这就产生了Logistic回归模型。
医学统计学:Logistic回归分析

析包含某个或某几个变量的模型是否有统计学意义。
模型s的对数似然函数
模型s的对数似然函数 大样本
G = -2 ( ln Ls- ln LP ) ~ 2 ( p -s)
模型s嵌套 于模型p内
LS :包含s个回归系数的模型的似然函数对数值; LP:包含p个回归系数的模型的似然函数对数值,p > s ;
• G值的大小反映增加某个或某几个自变量的模型拟合优度提高的程度。 • s=0时,是对模型的整体检验;p=s+1时,是对某个自变量的检验。
包括:多元线性回归模型,logistic回归模型,Probit回归模型,
Poisson回归模型,负二项回归模型
2
当因变量是分类变量时,其自变量与因变量更多的是 非线性关系,严重违背了线性回归模型的假设条件。 故直接应用线性回归分析不合理;
不能直接分析 y 与 x 的关系 y=f(x) ,因y仅取有 限的几个值
23
2019/6/6
Logistic回归模型的统计推断 • Logistic回归方程(系数)的假设检验 • Logistic回归模型的拟合优度检验 • Logistic回归模型预测准确度的检验
22
(1) 似然比检验(likelihood ratio test)
通过比较两个相嵌套模型的对数似然函数统计量G (又称Deviance):来分
对数似然 ln L a(0 1) a ln[1 exp(0 1)] b ln[1 exp(0 1)] c0 c ln[1 exp(0)] d ln[1 exp(0 )]
求一非阶线偏性导迭,代并方令法一阶偏导数=0 ——Newton-Raphson迭代法
最大似然估计
ˆ0
ln
c d
非条件Logistic 回归分析

非条件前言zzz原理z原理z原理z对概率进行转换,可建立线性回归模型–––原理zzz基本语句zzzzProc logistic zzMODELz关于变量选择:––––MODEL zMODELz两个协变量的例2:研究性别、疾病的严重程度对疾病疗效的影响,得数据如下拟合回归方程程序datainput sex degree effect count @@;cards;0 0 1 21 0 0 0 6 0 1 1 9 0 1 0 91 0 1 8 1 0 0 10 1 1 1 4 1 1 0 11;procfreq count;model effect=sex degree/scale=none aggregate; /*模型的拟合优度检验run;输出Deviance and Pearson Goodness-of-Fit StatisticsCriterion DF Value Value/DF Chi-Square Deviance 1 0.2141 0.2141Pearson 1 0.2155 0.2155z-输出Model Fitting Information and Testing Global Null Hypothesis BETA=0 Criterion Only Covariates-2LOGLScorez模型检验:z似然比的卡方=量的-df=2(可以认为两个协变量的回归系数至少有一个不为认为模型有意义输出Variable DF Estimate Error Chi-Square Chi-SquareINTERCPT 1 1.1568 0.4036 8.2167 0.0042 .SEX 1 -1.2770 0.4980 6.5750 0.0103 -0.350072 0.279 DEGREE 1 -1.0545 0.4980 4.4844 0.0342 -0.289086 0.348回归系数检验:Wald 卡方:大样本时近似标准正态分布,小样本时可能不如似然比检验输出z回归方程:logit[p/(1-p)]= 1.1568-1.2770sex -z男性治愈与未愈的比值为z女性治愈与未愈的比值为z两个比值的比各子组的模型预测的有效概率和基于有效水平的SEX1多分类无序自变量的z n需转变成(z例否影响。
LOGISTIC回归分析

LOGISTIC回归分析前⾯的博客有介绍过对连续的变量进⾏线性回归分析,从⽽达到对因变量的预测或者解释作⽤。
那么如果因变量是离散变量呢?在做⾏为预测的时候通常只有“做”与“不做的区别”、“0”与“1”的区别,这是我们就要⽤到logistic分析(逻辑回归分析,⾮线性模型)。
参数解释(对变量的评价)发⽣⽐(odds): ODDS=事件发⽣概率/事件不发⽣的概率=P/(1-P)发⽣⽐率(odds ratio):odds ratio=odds B/odds A (组B相对于组A更容易发⽣的⽐率)注:odds ratio⼤于1或者⼩于1都有意义,代表⾃变量的两个分组有差异性,对因变量的发⽣概率有作⽤。
若等于1的话,该组变量对事件发⽣概率没有任何作⽤。
参数估计⽅法线性回归中,主要是采⽤最⼩⼆乘法进⾏参数估计,使其残差平⽅和最⼩。
同时在线性回归中最⼤似然估计和最⼩⼆乘发估计结果是⼀致的,但不同的是极⼤似然法可以⽤于⾮线性模型,⼜因为逻辑回归是⾮线性模型,所以逻辑回归最常⽤的估计⽅法是极⼤似然法。
极⼤似然公式:L(Θ)=P(Y1)P(Y2)...p(Y N) P为事件发⽣概率P I=1/(1+E-(α+βX I))在样本较⼤时,极⼤似然估计满⾜相合性、渐进有效性、渐进正太性。
但是在样本观测少于100时,估计的风险会⽐较⼤,⼤于100可以介绍⼤于500则更加充分。
模型评价这⾥介绍拟合优度的评价的两个标准:AIC准则和SC准则,两统计量越⼩说明模型拟合的越好,越可信。
若事件发⽣的观测有n条,时间不发⽣的观测有M条,则称该数据有n*m个观测数据对,在⼀个观测数据对中,P>1-P,则为和谐对(concordant)。
P<1-P,则为不和谐对(discordant)。
P=1-P,则称为结。
在预测准确性有⼀个统计量C=(NC-0.5ND+0.5T)/T,其中NC为和谐对数,ND为不和谐对数,这⾥我们就可以根据C统计量来表明模型的区分度,例如C=0.68,则表⽰事件发⽣的概率⽐不发⽣的概率⼤的可能性为0.68。
logit分析

类
型
条件Logistic回归与非条件Logistic回归,两 者根本的差别在于:构造回归模型时,前者使用 了条件概率。
条件 Logistic回归主要用于配对或配比资料 的分析;而非条件Logistic回归主要用于成组设 计的资料分析。
非条件logistic回归分析
如: Brown(1980)在术前检查了53例前列腺癌患者: 观察年龄(AGE )、酸性磷酸酯酶(ACID)、术前探针活检 病理分级(GRADE)、 X射线(X_RAY) 、直肠指检肿瘤的大小
例2: 某北方城市研究喉癌发病的危险因素,用1:2配对的 病例对照研究方法进行了调查。选取了6个可能的危险因 素。试作条件logistic逐步回归分析。
应用及其注意事项
应变量为(二项)分类的资料
(预测、判别、危险因素分析等等)
分类自变量的编码
为了便于解释,对二项分类变量一 般按0、1编码,一般以0表示阴性或较轻 情况,而1表示阳性或较严重情况。
其检验假设为: H0:模型1与模型2拟合效果相同 H1:模型1与模型2拟合效果不同 在H0成立的条件下,G服从相应自由度 (为增加的自变量个数)的2分布。 若P﹤0.05,说明引入自变量后模型拟合优
度的改善有统计学意义,引入后模型2比模型1
预测效果好。
统计量G=244.346-222.616=21.73,自由度 为增加的变量个数=3,P=0.000。拒绝H0。 有统计学意义,模型2比模型1回归效果好。
Wald检验 ——偏回归系数的假设检验
优势比的区间估计
logistic回归模型的回归系数的区间估计与
பைடு நூலகம்线性回归系数的区间估计相似,可以根据正
态分布理论做估计。
注意:在分析病例对照资料时,由
回归原理

Logistic 回归原理解析临床评价中心:白文静2006-1-9内容序论之序—相关与回归概述非条件Logistic回归条件Logistic回归分析步骤应用及注意一、序论之序—变量间的联系相关与回归、关联eg1、身高与体重?eg2、肺癌与吸烟?eg3、啤酒与尿布?相关:两个变量或者多个变量之间是否存在关系和关系的密切程度;回归:研究变量之间联系的形式;关联:要寻找出各项目(Item)之间相互的关联性,从资料库中寻找出现频率较高的样型(Pattern),然後再利用這些样型分析出关联规则,解释变量间的关系。
一、序论之序—变量间的联系且方差相等;平均数在一条直线上,即线性。
7654321x拟合值真实值一、序论之序—变量间的联系;22110i Ki K i i i X B X B X B B Y ε++…+++=多元线性回归模型假定现实需求医学数据的复杂、多样—连续型和离散型数据;医学研究中疾病的复杂性—一种疾病可能有多种致病因素或与多种危险因素有关;疾病转归的影响因素也可能多种多样;临床治疗结局的综合性;一、序论之序—变量间的联系 应对方法:Χ+…+Χ+=βββP 式1二、概述参数估计最大似然估计法;假设检验(似然比检验;ROC)利用最大似然估计得到一套回归系数;计算得到对数似然度lnL( );假定第K个变量不存在,重新得到和lnL ( );计算统计量αββˆβˆ)(ˆk −β)(ˆk −β[]{})ˆ(ln ˆln 2)(2ββχL L k −−=−0:0=k H β0:n 20==βββ…==k H三、非条件Logistic 回归26例冠心病病人和28例对照者进行病例−对照研究data disease;input y x freq;cards ;1 1 101 0 20 1 400 0 80;proc logistic data=disease;model y=x;weight freq ;run ;三、非条件Logistic 回归SAS 程序再现三、非条件Logistic 回归)]1/(/[]p 1/p [p p −′−′)(2χ2χ-比数比(OR )如果发病率或死亡率不高,例如<<10%,则比数比可以近似估计相对危险度(RR)因为上述数据是四格表资料,如果用也可以分析行变量和列变量间的独立性,即疾病和暴露是否有联系。
统计学中的Logistic回归分析

统计学中的Logistic回归分析Logistic回归是一种常用的统计学方法,用于建立并探索自变量与二分类因变量之间的关系。
它在医学、社会科学、市场营销等领域得到广泛应用,能够帮助研究者理解和预测特定事件发生的概率。
本文将介绍Logistic回归的基本原理、应用领域以及模型评估方法。
一、Logistic回归的基本原理Logistic回归是一种广义线性回归模型,通过对数据的处理,将线性回归模型的预测结果转化为概率值。
其基本原理在于将一个线性函数与一个非线性函数进行组合,以适应因变量概率为S形曲线的特性。
该非线性函数被称为logit函数,可以将概率转化为对数几率。
Logistic回归模型的表达式如下:\[P(Y=1|X) = \frac{1}{1+e^{-(\beta_0+\beta_1X_1+...+\beta_pX_p)}}\]其中,P(Y=1|X)表示在给定自变量X的条件下,因变量为1的概率。
而\(\beta_0\)、\(\beta_1\)、...\(\beta_p\)则是待估计的参数。
二、Logistic回归的应用领域1. 医学领域Logistic回归在医学领域中具有重要的应用。
例如,研究者可以使用Logistic回归分析,探索某种疾病与一系列潜在风险因素之间的关系。
通过对患病和非患病个体的数据进行回归分析,可以估计各个风险因素对疾病患病的影响程度,进而预测某个个体患病的概率。
2. 社会科学领域在社会科学研究中,研究者常常使用Logistic回归来探索特定变量对于某种行为、态度或事件发生的影响程度。
例如,研究者可能想要了解不同性别、教育程度、收入水平对于选民投票行为的影响。
通过Logistic回归分析,可以对不同自变量对于投票行为的作用进行量化,进而预测某个选民投票候选人的概率。
3. 市场营销领域在市场营销中,Logistic回归也被广泛应用于客户分类、市场细分以及产品销量预测等方面。
通过分析客户的个人特征、购买习惯和消费行为等因素,可以建立Logistic回归模型,预测不同客户购买某一产品的概率,以便制定个性化的市场营销策略。
多因素非条件logistic回归

多因素非条件logistic回归多因素非条件logistic回归是一种常用的统计分析方法,用于研究多个自变量对于二分类结果的影响程度。
本文将介绍多因素非条件logistic回归的基本原理、应用场景以及步骤。
一、基本原理多因素非条件logistic回归是一种广义线性模型,用于建立自变量与二分类结果之间的关系。
它基于logistic函数(也称为S型函数),通过将自变量的线性组合映射到[0,1]的范围内,来描述自变量与二分类结果之间的概率关系。
二、应用场景多因素非条件logistic回归广泛应用于医学、社会科学、市场营销等领域的研究中。
例如,在医学领域,研究人员可以使用多因素非条件logistic回归来分析各种因素对于患病与否的影响程度,以便预测和预防疾病的发生。
三、步骤进行多因素非条件logistic回归分析时,通常需要以下步骤:1. 收集数据:收集包括自变量和二分类结果在内的相关数据。
2. 数据预处理:对数据进行清洗、缺失值处理、异常值处理等预处理工作。
3. 变量选择:根据领域知识和统计方法,选择与二分类结果相关的自变量进行分析。
4. 模型拟合:将选定的自变量输入logistic回归模型,拟合出模型参数。
5. 模型评估:通过各种指标(如AIC、BIC、似然比检验等)评估模型的拟合效果。
6. 结果解释:根据模型参数的正负和大小,解释自变量对于二分类结果的影响程度。
7. 预测与应用:根据已建立的模型,进行未知样本的预测,或者根据模型结果制定相应的决策。
多因素非条件logistic回归的优点是可以考虑多个自变量的影响,更贴近实际情况。
然而,它也有一些限制,比如对于样本量较小或者自变量之间存在共线性的情况,可能会导致模型参数的不准确性。
多因素非条件logistic回归是一种重要的统计分析方法,可以应用于各种领域的研究。
通过充分利用多个自变量,我们可以更全面地了解自变量对于二分类结果的影响,从而做出科学合理的预测和决策。
非条件Logistic回归分析

由于非条件Logistic回归分析采用最大似然估计法进行参数估计,因 此对异常值较为敏感,可能导致模型精度下降。
无法处理多分类问题
非条件Logistic回归分析只能处理二分类问题,对于多分类问题需要 进行额外的处理或使用其他算法。
对自变量间的交互项处理不足
非条件Logistic回归分析在模型中未考虑自变量间的交互项,对于存 在复杂交互关系的自变量无法准确建模。
究方向
01
引言
背景介绍
统计学在数据分析中的重要性
统计学是数据分析的重要基础,Logistic回归分析作为统计学中的一种方法,在 多个领域都有广泛的应用。
非条件Logistic回归的起源与发展
非条件Logistic回归分析最初由英国统计学家David Cox在20世纪70年代提出, 经过多年的研究和发展,该方法在理论和应用方面都取得了显著的进展。
范围
适用于数据量较大、样本间相互独立 的情况,且因变量和自变量之间存在 线性关系。
模型假设
无多重共线性
自变量之间不存在多重共线性, 即各自对因变量的影响是独立 的。
正态分布
误差项服从正态分布,即均值 为0,方差为常数。
线性关系
自变量与Logit P之间存在线性 关系,即 P=11+eXPfrac{1}{1+e^{x}}P 1+eX1。
无自相关
样本之间相互独立,不存在自 相关。
无异常值
数据中无异常值或离群点。
03
非条件Logistic回归模型 的建立
数据准备和处理
数据清洗
去除异常值、缺失值和重复值,确保数据质量。
数据转换
对分类变量进行编码,连续变量进行适当转换, 以满足模型需求。
非条件logistic回归模型

(一)53例接受手术的前列腺癌患者情况
(二)26例冠心病病人和28例对照进 行病例对照研究
26例冠心病病人和28例对照者进行 病例对照研究
队列研究
• 设有m个因素(包括研究因素与混杂因 素),第i个因素取值为xi(xi可以是计量的; 也可以是等级变量;也可以是二分类或 多分类变量,后者要经过数量化处理)。 m个因素的取值用向量X表示 X=(xl,x2,…,xm) 当m个变量取值为X时的发病概率为P(D|X)
MAX ln L
MAX
k j 1
m i0
i xij
n
ln
1
exp
j1
m i0
i xij
病例对照研究
• 设从病例及对照人群总体中,各按抽样比例 π1及π2分别抽取一部分病例和对照,组成一 个随机样本。
• 一个具有因素变量为X的个体是病例,且被 抽到样本中的概率为 P D | X 1
表示A型血 表示B型血 表示AB型血 表示O型血
ln
P 1 P
0
1x1
2 x2
3 x3
– exp(1) 表示B与A比之OR; – exp( 2) 表示AB与A比之OR; – exp( 3) 表示O与A比之OR。
令
1 吸烟
1 肺癌
X=
y=
0 不吸
0 非肺癌
若求得: β= 1, OR=e
表明:吸烟个体 患肺癌的危险性是不吸烟 个体的2.71828倍。
回归系数的解释
• 多分类变量:指示变量
– x1=0, x2=0, x3=0 – x1=1, x2=0, x3=0 – x1=0, x2=1, x3=0 – x1=0, x2=0, x3=1
m xm
非条件逻辑回归

非条件逻辑回归一、什么是逻辑回归逻辑回归是一种用于建立分类模型的统计学方法,常用于解决二分类问题。
逻辑回归的目标是根据给定的自变量,估计二分类输出变量的概率。
二、逻辑回归的基本原理逻辑回归基于逻辑函数(又称为Sigmoid函数)来建立模型。
逻辑函数的公式为:ℎ(z)=11+e−z其中,h(z)是概率估计值,z是自变量的线性组合。
逻辑回归的模型可以表示为:P(y=1|x)=ℎ(z)=11+e−zP(y=0|x)=1−ℎ(z)=1−11+e−z其中,P(y=1|x)表示给定自变量x情况下y=1的概率,P(y=0|x)表示给定自变量x 情况下y=0的概率。
三、非条件逻辑回归的意义在逻辑回归中,通常基于条件概率进行建模。
即使用自变量x条件下y=1的概率和y=0的概率来建立模型。
而非条件逻辑回归则是不考虑自变量x的条件,直接估计y=1和y=0的概率,从而得到分类结果。
非条件逻辑回归主要用于以下两个方面: ### 1. 独立分布的样本当样本独立分布时,即样本的生成过程与自变量无关,可以使用非条件逻辑回归进行建模。
在这种情况下,非条件逻辑回归可以提供更简单、更高效的分类模型。
2. 缺乏自变量信息有时候,我们可能只有因变量的标签,却缺乏与自变量的相关信息。
此时,非条件逻辑回归可以直接估计出分类的概率,从而得到分类结果。
四、非条件逻辑回归的建模方法非条件逻辑回归可以使用最大似然估计来估计模型参数。
最大似然估计的目标是找到模型参数,使得给定样本的出现概率最大。
步骤如下: 1. 初始化模型参数。
可以使用随机数来初始化模型参数。
2. 计算逻辑回归的似然函数。
3. 对似然函数进行求导,得到模型参数的梯度。
4. 使用梯度下降法更新模型参数。
5. 重复步骤2-4,直到收敛或达到最大迭代次数。
五、非条件逻辑回归的优缺点非条件逻辑回归相比于条件逻辑回归有一些优点和缺点。
优点:1.简单易用:非条件逻辑回归不需要考虑自变量x的条件,只需要估计y=1和y=0的概率即可,因此模型更加简单易用。
logistic回归分析8个知识点整理,建议收藏

Pearson χ2、偏差 (deviance) 主要用于自变量不多且为分类变量的情况,当自变量增多且含有连续型变量时,用 HL 指标则更为恰当。
以下为线性回归方程判断依据,可用于 logistic 回归分析
① 决定系数 (R2) 和校正决定系数,可以用来评价回归方程的优劣。R2 随着自变量个数的增加而增加,所以需要校正;
校正决定系数越大,方程越优。但亦有研究指出 R方 是多元线性回归中经常用到的一个指标,表示的是因变量的变动中由模型中自变量所解释的百分比,并不涉及预测值与观测值之间差别的问题,因此在 logistic 回归中不适合。
Pearson χ2、偏差 (deviance)、Hosmer- Lemeshow (HL) 指标值均服从χ2 分布,χ2 检验无统计学意义 (P>0.05) 表示模型拟合的较好,χ2 检验有统计学意义 (P ≤ 0.05) 则表示模型拟合的较差。AIC 和 SC 指标还可用于比较模型的优劣,当拟合多个模型时,可以将不同模型按其 AIC 和 SC 指标值排序,AIC 和 SC 值较小者一般认为拟合得更好。
③在逐步回归的时可根据需要放宽或限制进入方程的标准,或硬性将最感兴趣的研究变量选入方程;
④ 强影响点记录的选择:从理论上讲,每一个样本点对回归模型的影响应该是同等的,实际并非如此。有些样本点(记录)对回归模型影响很大。对由过失或错误造成的点应删去,没有错误的强影响点可能和自变量与应变量的相关有关,不可轻易删除。
可以采用双向筛选技术:
《logistic回归分析》PPT课件

第一节 非条件logistic回归
一、logistic 回归模型:
设因变量 Y 是一个二分类变量,其取值为 Y =1 和Y =0。 影响 Y 取值的 m 个自变量分别为 X1, X 2 ,, X m 。在 m 个自变量(即暴露因素)作用下阳性结果发生的条件
概率为 P P(Y 1 X1, X 2 ,, X m ) ,则 logistic 回归模
表 1 调查数据
y
x
1
0
1
a
b
0
c
d
合计 a+c b+d
表 2 对应概率
y
x
1
0
1 0 合计
p1 1- p1
1
p2 1- p2
1
9
表 1 调查数据
y
x
1
0
1
a
b
0
c
d
合计 a+c b+d
表 2 对应概率
y
x
1
0
1 0 合计
p1 1- p1
1
p2 1- p2
1
Logistic
模型为:
p1
p( y
1|
(2)多分类资料Logistic回归: 因变量为多项分类的资料,可 用多项分类Logistic回归模型或有序分类Logistic回归模型进 行分析。
2
非条件Logistic回归分析 条件Logistic回归分析 无序分类反应变量Logistic回归分析 有序多分类反应变量Logistic回归分析 Logistic回归分析应用及注意事项
21
对所拟合模型的假设检验:
概率p值均小 于0.05,说明 方程有意义。
心肺复苏自主循环恢复患者预后预测的非条件Logistic回归分析

T e ̄co i h p si l r dc uc me fCP —ROS r ay e y sn l a tra a y i a d mu t a it n y i r ・ h tr whc o sb yp e ito to s o R — s C we e a lz d b i ge f co l ssn l v rae a a ss e n n i l ・ s e f ey Re u t Ag , b s cd s a e s e o a d a re tc ud p e itt e o to fp t ns w t R —ROS p c vl. s l i s e a i i s , i f r i c ar s o l n t r dc u c me o a e t i CP e t c h i h C; b t u
—
y e N u —n i Dp r etfcrioyo hnhnScn o i l hnhn5 80 ,C i u ,W GX e v. eat n ado g e m o l fSeze eodH s t ,Seze 10 0 hn pa a
【 btat O jcie oepi th r iin ̄ tr o rtr f pnaeu i ua o R S A s c】 r bet T x litepe c o c s f e no ot o s r lin( O C)ae adou- v c dt o u s n cc t f r ripl tc
Logistic回归分析报告结果解读分析-logit回归解读

Logistic回归分析报告结果解读分析Logistic回归常用于分析二分类因变量(如存活与死亡、患病与未患病等)与多个自变量得关系。
比较常用得情形就是分析危险因素与就是否发生某疾病相关联。
例如,若探讨胃癌得危险因素,可以选择两组人群,一组就是胃癌组,一组就是非胃癌组,两组人群有不同得临床表现与生活方式等,因变量就为有或无胃癌,即“就是”或“否”,为二分类变量,自变量包括年龄、性别、饮食习惯、就是否幽门螺杆菌感染等。
自变量既可以就是连续变量,也可以为分类变量。
通过Logistic回归分析,就可以大致了解胃癌得危险因素。
Logistic回归与多元线性回归有很多相同之处,但最大得区别就在于她们得因变量不同。
多元线性回归得因变量为连续变量;Logistic回归得因变量为二分类变量或多分类变量,但二分类变量更常用,也更加容易解释。
1、Logistic回归得用法一般而言,Logistic回归有两大用途,首先就是寻找危险因素,如上文得例子,找出与胃癌相关得危险因素;其次就是用于预测,我们可以根据建立得Logistic 回归模型,预测在不同得自变量情况下,发生某病或某种情况得概率(包括风险评分得建立)。
2、用Logistic回归估计危险度所谓相对危险度(risk ratio,RR)就是用来描述某一因素不同状态发生疾病(或其它结局)危险程度得比值。
Logistic回归给出得OR(odds ratio)值与相对危险度类似,常用来表示相对于某一人群,另一人群发生终点事件得风险超出或减少得程度。
如不同性别得胃癌发生危险不同,通过Logistic回归可以求出危险度得具体数值,例如1、7,这样就表示,男性发生胃癌得风险就是女性得1、7倍。
这里要注意估计得方向问题,以女性作为参照,男性患胃癌得OR就是1、7。
如果以男性作为参照,算出得OR将会就是0、588(1/1、7),表示女性发生胃癌得风险就是男性得0、588倍,或者说,就是男性得58、8%。
非条件logistic 回归结果解读

非条件logistic 回归结果解读
非条件logistic回归是一种用于预测二分类问题的回归分析方法。
对于非条件logistic回归的结果进行解读,可以从以下几
个方面进行分析:
1. 回归系数:非条件logistic回归模型的回归系数表示自变量
对因变量的影响程度。
如果回归系数为正,表示该自变量与因变量呈正相关关系,即自变量增加时,因变量的概率也会增加;如果回归系数为负,表示该自变量与因变量呈负相关关系。
回归系数的大小可以用来判断自变量对因变量的重要程度,绝对值越大表示影响越大。
2. 模型拟合度:非条件logistic回归模型的拟合度可以通过R
方(R-squared)或者对数似然比(log-likelihood)来评估。
R
方的取值范围为0到1,越接近1表示模型的拟合度越好;而
对数似然比越大表示模型的拟合度越好。
需要注意的是,拟合度高并不一定意味着模型预测准确度高,还需要考虑其他评估指标。
3. p值:非条件logistic回归模型的p值可以用来判断自变量
的显著性。
p值越小,表示该自变量对因变量的影响越显著。
通常,p值小于0.05被认为是显著的。
如果p值超过设定的显
著性水平,就需要谨慎解释该自变量对因变量的影响。
4. 假设检验:非条件logistic回归模型通常会进行一些假设检验,如对模型的合理性、模型参数的正态分布等。
如果假设检验不通过,就需要重新考虑模型的建立和解释。
需要注意的是,非条件logistic回归模型的结果解读还需要考虑实际问题和数据的背景。
同时,还需要结合其他统计学方法和领域知识来对结果进行综合分析和解释。
Logistic回归分析(重点、难点)

1
p2 p2
,通通常常在在流流行行病病研研究究中中p1
为病例
p1为组病的暴例露组率的,暴p露2 是率指,对p2照为组对的照暴组露的率暴。露率。
对发病对率发较病低率的较疾低的病疾,病一,般一有般R有R≈RORR OR 。
比数比
病例对照研究
暴露 未暴露
病例 a b
对照 c
d
OR a/(ab) / c/(cd) b/(ab) d/(cd)
理解 非条件Logistic回归和条件Logistic回归的 区别
1. Logistic回归分析结果及解释 掌握 2. Logistic回归变量筛选方法
3. Logistic回归系数的流行病学意义 4. Logistic回归的应用及注意事项
几个重要的流行病学概念
病因分析(预后分析)的目的:找出影响疾 病发生(或预后好坏)的影响因素及其影响的强 度。
ORj 1无作用
则有ORj expj, j >0,ORj 1 危险因子
0,ORj 1 保护因子
模型参数的意义
当 P 1 , 则 有 O RP 1/(1P 1) R R P 0/(1P 0)
由 于 Oj值 R 与 模 型 中 的 常 数 项 0α 无 关 ,
α0在 危 险 因 素 分 析 中 通 常 视 其 为 无 效 参 数 。
实例分析
❖ Analyze ▪ Regression
• Binary Logistic
实例分析
❖ 应变量编码Depen dent Variabl e Enco din g
Original ValuIenternal Value
.00
0
1.00
1
❖ 模型拟合结果
《Logistic回归》PPT课件

常量 -20.207 4.652 18.866
1 .000
.000
a. 在步骤 1 中输入的变量: 性别, 年龄, 学历, 体重指数, 家族史, 吸烟, 血压, 总胆 固醇, 甘油三脂, 高密度脂蛋白, 低密度脂蛋白.
七、变量筛选
从所用的方法看,有强迫法、前进法、后退 法和逐步法。在这些方法中,筛选变量的过 程与线性回归过程的完全一样。但其中所用 的统计量不再是线性回归分析中的F统计量, 而是以上介绍的参数检验方法中的三种统计 量之一。
八、logistic 回归模型拟合优度检验和预 测准确度检验
(一)拟合优度检验:
Logistic回归模型的拟合优度检验是通过比较模型 预测的与实际观测的事件发生与不发生的频数有无差 别来进行检验。如果预测的值与实际观测的值越接近, 说明模型的拟合效果越好。
·模型的拟合优度检验方法有偏差检验(Deviance)、 皮尔逊(pearson)检验、统计量(Homser-Lemeshow), 分别计算统计量X2D、X2 P、X2HL值。统计量值越小, 对应的概率越大。无效假设H0:模型的拟合效果好。
第九章 Logistic回归
(非条件Logistic回归)
第一节 Logistic回归概述
一、Logistic回归目的: Logistic回归通常以离散 型的分类变量(疾病的死亡、痊愈等)发生结果的 概率为因变量,以影响疾病发生和预后的因素为自 变量建立模型。研究分类变量(因变量)与影响因 素(自变量)之间关系的研究方法。属于概率型非 线性回归方法。
本例模型的似然比检验结果:
X2=-2(ln Lp-ln Lk)=95.497
模 型 系数 的 综 合检 验
步骤 1
步骤 块 模型
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
È Ê ± ý ± È Odds Ratio . 6.000
2 . 8 9 0 4
1 .7 9 1 8
两个协变量的Logistic回归模型
例2:研究性别、疾病 有效(effect=1) 无效(effect=0) 合计 不严重(degree=0) 21 6 27 女(sex=0) 严重(degree=1) 9 9 18 不严重(degree=0) 8 10 18 男(sex=1) 严重(degree=1) 4 11 15 性别
e 1 (1 e 1 ) e 1 2 (1 e 1 2 )
Odds of (effect=1)
e
e 2
1
0 1
e 1
e 1 2
多分类无序自变量的Logistic回归模型
n分类无序自变量在logistic回归模型中需转变
输出
模型检验: H0:1=2=0 vs H1:1,2不全为0 似然比的卡方=(无协变量的-2LOGL值)-(有两个协变量
的-2LOGL值)=107.669-95.9=11.769,自由度df=2(模型 中的协变量个数),相应的P值=0.0028,因此可以认为两个 协变量的回归系数至少有一个不为0。即:认为模型有意义
两个比值的比
p P 1 . 277 OR e 0 . 279 1 p1 P
各子组的模型预测的有效概率和基于有效水平的 Odds(P/1-P)
SEX 0
DEGREE Pr(effect=1) 0 1
e (1 e ) e 2 (1 e 2 )
当反应变量为离散型变量时,如研究不同治疗
方法对某病治疗的效果,反应变量疗效Y的值 为1(治愈)和0(未愈),要研究的是某种事 件(如治愈)发生的可能与自变量(治疗方法) 的关系,反应变量为事件发生的概率P (Y=1)。
对概率进行转换,可建立线性回归模型
P ln x x ... x X 1 1 2 2 n n 1 P
拟合回归方程
L o g i t ( P ) s e x d e g r e e 1 2
程序9-2:
data a1; input sex degree effect count @@; cards; 0 0 1 21 0 0 0 6 0 1 1 9 0 1 0 9 1 0 1 8 1 0 0 10 1 1 1 4 1 1 0 11 ; proc logistic descending; freq count; model effect=sex degree/scale=none aggregate; /*模型的拟合优度 检验*/ run;
两分类反应变量的logistic回归
例1:不同治疗方法对某病疗效的影响研究
Ö Î « ´ Â Ð Ï º Á × Æ é ± ð ³ × Í é (treat=1) ¨× · é (treat=2) Æ ¼ Ó Ð Ð §(effect=1) 16(25%) 40(66.67%) 56 Î Ð Þ §(effect=0) 48(75%) 20(33.33%) 68 º ¼ Ï Æ 64 60 124
H0:=0的似然比检验: 似然比的卡方值=(无协变量的-2LOGL值)-(有两个协变量的- 2LOGL值)=170.737-148.361=22.376,自由度df为1,p值= 0.0001,因此可以认为模型有意义。
输出
² Ê Î ý × î ´ ó Ë Æ È » ¹ À ¼ Æ µ Ä Í ³ ¼ Æ · Ö Î ö Analysis of Maximum Likelihood Estimates Ø é » ¹ Ï µ Ê ý ê × ± ¼ Î ó Wald¿ ¨· ½ PÖ µ ê » ± ¯ µ Ï Ê ý À ¼ ¹ Æ Parameter Standard Wald Pr> Standardized Variable DF Estimate Error Chi-Square Chi-Square Estimate INTERCPT 1 -2.8904 0.6390 20.4594 0.0001 . TREAT 1 1.7918 0.3979 20.2762 0.0001 0.495670
t r e a t e 可用logistic回归模型 P ( e f f e c t 1 |t r e a t ) t r e a t 1 e 拟合,即
l o g i tp () t r e a t
程序9-1
data a; input treat effect count@@; cards; 1 1 16 1 0 48 2 1 40 2 0 20 ; proc logistic order=data; /*规定按数据集建立时反应变量水平出现 的先后次序进行运算,按照p=Pr(effect=1|x)来拟合模型*/ freq count; model effect=treat; run;
p1=p2 ,则可得两个比数相等Odds1=Odds2 ;
因此我们可以把两个患病率大小的比较转化为两个
Odds大小的比较。并引入比数比(Odds Ratio,OR)
p 2 2 O d d s2 1 p e 2 O R e p O d d s e 1 1 1 p 1
两分类反应变量(proc logistic) 多分类有序反应变量(proc logistic) 多分类无序反应变量( proc catmod)
原理
Y x x ... x X 多元线性回归模型: 1 1 2 2 n n 是参数向量,X是自变量向量。 其中是截距, 表示n个自变量x与反应变量Y间的关系,Y为任 意实数 ,属于连续变量
输出
Deviance and Pearson Goodness-of-Fit Statistics Pr > Criterion DF Value Value/DF Chi-Square Deviance 1 0.2141 0.2141 0.6436 Pearson 1 0.2155 0.2155 0.6425 两种拟合优度检验的结果均显示:P值=0.64>>0.05,因此可以认 为当前模型与拟合最好的模型比较,差别无统计意义。因此没有 必要对模型作进一步改进
MODEL语句的选项
参数估计和预测
alpha= 设置可信区间的置信度 cl 要求估计要求估计所有参数的可信区间 plrl 对自变量估计比数比的可信区间 ctable 和pprob= 以pprob=指定的概率值为分 割点,输出根据最后模型预测的Y的分类表 (ctable的作用),ctable选项仅对两分类变量 起作用。
输出
Analysis of Maximum Likelihood Estimates Parameter Standard Wald Variable DF Estimate Error Chi-Square INTERCPT 1 1.1568 0.4036 8.2167 SEX 1 -1.2770 0.4980 6.5750 DEGREE 1 -1.0545 0.4980 4.4844 Pr > Standardized Chi-Square Estimate 0.0042 . 0.0103 -0.350072 0.0342 -0.289086 Odds Ratio . 0.279 0.348
非条件Logistic 回归分析
2019/2/6
前言
Logistic回归模型是适用于反应变量(因变量为
分类变量的回归分析 按设计类型:
条件Logistic回归:配对设计(proc phreg) 非条件Logistic回归:未配对(proc logistic)
按变量类型:
基本语句
Proc logistic [options]; Model 反应变量=自变量[/options];
/*建立
模型*/ [freq 变量名;] run;
/*指定频数变量*/
MODEL语句的选项
关于模型拟和优度
Aggregate 和scale=n|p|d 计算偏差和pearson卡方拟和优度统计量 n 对离差参数不进行校正 p 规定离差参数的估计为pearson卡方统计量 除以自由度 d 规定离差参数的估计为偏差除以自由度
成(n-1)个哑变量进行分析 例3:研究性别和不同疗法对某病治愈与否影 响。数据如下
治疗方法(treat) 有效(response=1) 无效 response=0 合计 A 78 28 106 男(sex=1) B 101 11 112 C 68 46 114 A 40 5 54 女(sex=0) B 54 5 59 C 34 6 40 性别
男性治愈与未愈的比值为 女性治愈与未愈的比值为
P 1 P
x x 1 . 277 1 x 1 1 2 2 2 2 e e
x x 1 . 277 0 x 1 1 2 2 2 2 e e
P 1 P
由于治疗方式是3水平,而且是无序的,必须引入两个
