第八章 绕流运动
第八章绕流运动

x
y
在以上二式中均取积分常数为零,这对流动的计算并无影响。
一 均匀流
设均匀流的速度为与 x 轴平行,那么
ux x y a
uy
y
x
0
求速度势函数: d uxdx uydy adx ax c
令 c=0, ax
求流函数 d uydx uxdy ady ay c 令 c=0, ay
得证。
§8.2 平面无旋流动
1 流网的性质
(2)流网中每一网格的边长之比等于和 的增值之比
若取 =,则流网网格为正方形网格。
/
证明:如右图所示,取相邻两线间的差 值为ΔC,流线间隔为Δn ,等势线间隔 为Δs。
us
q A
n
C n
且
us
s
s
C s
所以 C n,则流网网格为正方形网格。
§8.2 平面无旋流动
仍为
Γ
ur r 0, u r 2 r
由以上关系式知,r 0 时,u ,所以涡点为奇点,该式仅 适用于 r>0 区域。由此式可见, 只是 的函数。
故有
d
u rd
2
d
积分得
2
速度和流函数的关系为
ur
1 r
0,
u r
r 上式表明 只是 的函数,所以
d
u dr
Γ 2 r
dr
点涡
上式积分得
Γ ln r 2
由上可知,点涡流场的等势线为不同极角的径线,即 =常数;流线为不同半径的同心圆
数。与点源(或点汇)相反。点涡的强度即沿围绕点涡的速度环量 Γ >0 时,环流为逆时针方
0,环流为顺时针方向。由斯托克斯定理知,点涡的强度 Γ 取决于旋涡的强度。
第五版 流体力学习题答案完整版

《流体力学》答案1-6.当空气温度从00C 增加至020C 时,ν值增加15%,容重减少10%,问此时μ值增加多少?⎡⎤⎣⎦解0000000000(115%90%)()()0.035 3.5%gggγγννμμρνρνμρνγν⨯---====1-7.图示为一水平方向运动的木板,其速度为1m s ,平板浮在油面上,油深 1mm δ=,油的0.09807Pa s μ=,求作用于平板单位面积上的阻力?⎡⎤⎣⎦解10.0980798.070.001du Pa dy τμ==⨯= 1-9.一底面积为4045cm ⨯,高为1cm 的木板,质量为5kg ,沿着涂有润滑油的斜面等速向下运动,已知1m v s =,1mm δ=,求润滑油的动力粘滞系数?⎡⎤⎣⎦解0T GSin α-= 55255131313T GSin G g g α==⋅=⨯⨯=所以 10.400.451800.001du T A dy μμμ==⨯=但 259.8070.10513180Pa s μ⨯==⋅⨯所以1-10.一个圆锥体绕其铅直中心轴等速旋转,锥体与固定壁的间距为δ=1mm ,全部为润滑油充满,μ=0.1Pa.s ,当旋转角速度ω=16s -1,锥体底部半径R =0.3m,高H =0.5m 时,求:作用于圆锥的阻力矩。
解: 取微元体, 微元面积:阻力矩为:阻力: 阻力矩51213GVδ22cos 0dhdA r dl r du r dy dT dA dM dT rππθωτμμδτ=⋅=⋅-====⋅0333012cos 12()cos 12cos HHHM dM rdT r dAr r dh r dh r tg h tg h dhττπθωμπθδθωμπθδθ====⋅⋅=⋅⋅⋅=⋅=⋅⋅⋅⋅⎰⎰⎰⎰⎰⎰1-14.图示为一采暖系统图,由于水温升高引起水的体积膨胀,为了防止管道及暖气片胀裂,特在顶部设置一膨胀水箱,使水的体积有自由膨胀的余地,若系统内水的总体积38V m =,加热前后温度差050t C =,水的热胀系数0.0005α=,求膨胀水箱的最小容积?⎡⎤⎣⎦解因为 dV V dt α=所以 30.00058500.2dV Vdt m α==⨯⨯=2-2.在封闭管端完全真空的情况下,水银柱差250Z mm =,求盛水容器液面绝对压强1p 及测压管中水面高度1Z ?⎡⎤⎣⎦解312013.6109.80.056664a p Z p γ=+=⨯⨯⨯=11 6.6640.686809.8p Z m mm γ==== 2-6.封闭容器水面的绝对压强20107.7KNp m =,当地大气压强298.07a KNp m =,试求(1)水深0.8h m =的A 点的绝对压强和相对压强?(2)若容器水面距基准面高度5Z m =,求A 点的测压管高度和测压管水头。
第8章 边界层理论基础及绕流运动

ux
∂ux ∂x
+ uy
∂ux ∂y
=
−
1 ρ
∂p ∂x
+
ν
∂ 2u x ∂y 2
∂ux ∂x
+
∂uy ∂y
=
0
边界条件: y =∞(或y = δ),ux = U0 y = 0,ux = 0, uy = 0
其中 U0 = U0(x) =边界层外界限上外部流动的流速 且 p = p(x) = 边界层外界限上外部流动的压强
=
1 2
δ
∫ ∫ δ2 =
δ 0
ux u0
⎜⎜⎝⎛1 −
ux u0
⎟⎟⎠⎞dy
=
δ
1η(1− η)dη = 1 δ
0
6
∫ ∫ ( ) δ3 =
δ 0
ux u0
⎜⎜⎝⎛1 −
ux 2 u0 2
⎟⎟⎠⎞dy
=
δ
1η 1− η2
0
dη = 1 δ 4
10
8.2 边界层微分方程
——利用边界层的性质对粘性流体基本方程(纳维-斯托克斯方 程)的简化。
⎟⎠⎞
=
−δ
dp dx
− τ0
其中: dp/dx和u0应由外部流动求出 → 三个未知量:τ0、δ、ux
应用动量积分方程求解边界层问题的步骤: (1) 补充 ux (x, y)、τ0(δ)关系式,积分方程转变为δ的常微分方程
(2)求解方程 → δ(x) →τ0(x) → 总阻力→ 计算位移厚度等其他 参数。
∫ ∫∫ ∑ 积分形式的动量方程
∂ ∂t
ρurdV
cv
+
cs
ρurundA
08.圆柱绕流

流体力学实验 I ——圆柱绕流
§2.3 两种流态
发生“阻力微机”前后的两种典型流态
亚临界(Re < Rec): CD≈1.2,层流附面层分离,分离点约78 ° ; 超临界(Re > Rec): CD≈0.3,湍流附面层分离,分离点约130 °。
流体力学实验室 14-6
流体力学实验 I ——圆柱绕流
流体力学实验室
14-12
流体力学实验 I ——圆柱绕流
§4 旋涡脱落频率的测量
流体力学实验室
14-13
流体力学实验 I ——圆柱绕流
通知
实验地点:风洞实验室 时间安排: 组号 1 圆柱表面压力分布 5月24日 13:30~13:45
2
3 4 5 6 7 8
流体力学实验室
5月24日 13:45~14:00
理想流体绕流圆柱
流体力学实验室
粘性流体绕流圆柱
14-4
流体力学实验 I ——圆柱绕流
§2.2 阻力曲线
曲线左端属于小Re数情况(Stokes流动),阻力全来自于摩擦阻力, 阻力系数与Re数成反比; 当102 < Re < 2.5×105,阻力曲线变化缓慢,阻力主要来自于压差阻力;
在Rec≈2× 105,阻力系数由1.2突然下降到0.3,出现“阻力危机”。 阻力下降的原因是由层流分离转变为湍流分离。
其中D为阻力,S为圆柱体在垂直于流动方向的投影面积。对无限长等直 径圆柱,有S=1×d=d,d为圆柱直径。
单位宽度圆柱体所受压差阻力和圆柱的阻力系数分别为:
d d 2 p cos d ( p p ) cos d 0 2 2 0 d 2 0 ( p p ) cos d 1 2 p p D 1 2 2 CD cos d C p cos d 1 2 1 2 2 0 1 v2 2 0 v d v d 2 2 2 D 1
流体力学(平时的作业题)

第一章 绪论1-6.图示为一水平方向运动的木板,其速度为1m s,平板浮在油面上,油深 1mm δ=,油的0.09807Pa s μ=,求作用于平板单位面积上的阻力?⎡⎤⎣⎦解10.0980798.070.001du Pa dy τμ==⨯= 1-7. 温度为20℃的空气,在直径为2.5cm 管中流动,距管壁上1mm 处的空气速度为3cm/s 。
求作用于单位长度管壁上的粘滞切应力为多少? 解: f=m N dyduA/103.410/1031105.2100183.053223-----⨯=⨯⨯⨯⨯⨯⨯=πμ 1-8.一底面积为4045cm ⨯,高为1cm 的木板,质量为5kg ,沿着涂有润滑油的斜面等速向下运动,已知1m v s=,1mm δ=,求润滑油的动力黏度?⎡⎤⎣⎦解0T GSin α-= 55255131313T GSin G g g α==⋅=⨯⨯=所以 10.400.451800.001du T A dy μμμ==⨯=但 259.8070.10513180Pa s μ⨯==⋅⨯所以5第二章 流体静力学2-6.封闭容器水面的绝对压强20107.7KNp m=,当地大气压强298.07a KNp m =,试求(1)水深0.8h m =的A 点的绝对压强和相对压强?(2)若容器水面距基准面高度5Z m =,求A 点的测压管高度和测压管水头。
并图示容器内液体各点的测压管水头线;(3)压力表M 和酒精(27.944KNm γ=)测压计h 的读数值?hh 1AM p 0⎡⎤⎣⎦解(1)201107.79.8070.8115.55A KN p p h m γ'=+=+⨯= 2115.5598.0717.48A A a KN p p p m '=-=-=(2)217.481.789.807Ap h m γ=== 25 1.78 6.78n A H Z h m =+=+=(3)20107.798.079.63M a KNp p p m =-=-=9.631.217.944Mp h m γ=== 2-16. 已知水箱真空表M 的读数为0.98kPa ,水箱与油箱的液面差H =1.5m ,水银柱差m 2.02=h ,3m /kg 800=油ρ,求1h 为多少米?解:取等压面1-1,则()()()()()12122211332800.29809800 1.50.2 5.610008009.8a a Hg Hg P P g H h h P gh gh gh P g H h h gmρρρρρρρ-+++=+++-+=-⨯+-⨯+==-⨯油油2-20.图为倾斜水管上测定压差的装置,已知cm 20=z ,压差计液面之差cm 12=h ,求当(1)31kg/m 920=ρ的油时;(2)1ρ为空气时;A 、B 两点的压差分别为多少?解:(1)取等压面1-1 PaghgZ gh P P ghgZ P gh P A B B A 92.1865)12.02.0(980012.08.992011=-⨯+⨯⨯=-+=---=-ρρρρρρ(2)同题(1)可得Pagh gZ P P gZP gh P A B B A 784)12.02.0(9800=-⨯=-=--=-ρρρρ2-36.有一圆滚门,长度10l m =,直径4D m =,上游水深14H m =,下游水深22H m =,求水作用于圆滚门上的水平和铅直分压力?⎡⎤⎣⎦解2212121()2x x x p p p l H H γ=-=- 2219.80710(42)5902KN =⨯⨯⨯-=23439.8074109204z p V Al R lKN γγγππ==∙==⨯⨯⨯=2-44. 一洒水车以等加速度2/98.0s m a =在平地上行驶,水车静止时,B 点位置m x 5.11=,m h 1=,求运动后该点的静水压强。
流体力学第八章 绕流运动

由此得 24 Cd Re
(8-70)
二、悬浮速度 设在上升的气流中,小球的密度为 m,大于气体的密 度 , 即 m 。小球受力情况如下。 方向向上的力有: u 0 2 1 2 2 F C A C d u 绕流阻力 d d 0 1 3 D 2 8 FB d g 浮力 6 方向向下的力有: 1 重力 G d 3 m g
绕流物体的摩擦阻力作用,主要表现在附面层 内流速的降低,引起动量的变化。
附面层的动量方程为 d d dp 2 u x dy U u x dy 0 dx 0 dx 0 dx
、 p、 u x、 U 和 0。 附面层动量方程有五个未知数: dp 其中U可以用理想流体的势流理论求得, 可
u y
为平面无旋流动。
u x x y
平面无旋流动的速度势函数为 d u x dx u y dy 并满足拉普拉斯方程:
2 2 2 0 2 x y
义一个函数 , 令u x ,uy y x 满足上式的函数称为流函数。
由不可压缩流体平面流动的连续性方程可以定
第八章 绕流运动
第一节 无旋流动 第二节 平面无旋流动 第三节 几种简单的平面无旋运动 第四节 势流叠加 第五节 绕流运动与附面层基本概念 第六节 附面层动量方程 第七节 平板上层流附面层的近似计算 第八节 平板上紊流附面层的近似计算 第九节 曲面附面层的分离现象与卡门涡街 第十节 绕流阻力和升力
因此,无旋流动的前提条件是
u z u y y z u x u z z x u y u x x y 由不可压缩流体的连续性方程 u x u y u z 0 x y z 得出拉普拉斯方程 2 2 2 2 2 0 2 x z y
绕流运动

绕流运动(2)1.在管径d =100mm 的管道中,试分别计算层流和紊流时的入口段长度(层流按Re=2000计算)。
解:层流时,根据dX E=0.028Re ,有X E =0.028Re d =5.6m 紊流时,根据dX E=50可知:入口段长度X E =50d =50×0.1=5m2有一宽为2.5m ,长为 30m 的平板在静水中以5m/s 的速度等速拖曳,水温为 20℃, 求平板的总阻力。
解:取 Re xk =5×105,则根据υkxkXu 0Re=(查表知 t=20ºC ,sm /10007.16-⨯=υ)X k =0Reu xkυ⋅=0.1m <30m可认为是紊流附面层:Re=υXu 0=1.49×108采用58.2)(lg 445.0e fR C=,则:fC=1.963×10-3根据D =ACf22u ρ(其中3/2.998,305.22m kg A =⨯⨯=ρ)平板总阻力:D =3680 N3.光滑平板宽1.2m ,长3m 潜没在静水中以速度u =1.2m/s 沿水平方向拖曳,水温为10℃求:(1)层流附面层的长度;(2)平板末端的附面层厚度;(3)所需水平拖曳力。
(5105Re⨯=xk)解:(1)由查表知:t =10℃, υ=1.308×sm /1026-根据=xkReυkX u 0,知X k =0.55m(2)根据:δ=0.3751)(0xu υx ,知δ=0.0572m=57.2mm(3) 根据:Re=υvx 知Re =2.75×106. 则:fC =Re1700Re074.051-=3.196×10-3根据:fDfC=A22u ρ3/17.999,32.12mkg A =⨯⨯=ρfD=16.57N4.在渐缩管中会不会产生附面层的分离?为什么? 答:不会,因为在增速减压区。
5.若球形尘粒的密度m ρ=2500kg/ m 3,空气温度为 20℃ 求允许采用斯托克斯公式计算尘粒在空气中悬浮速度的最大粒径(相当于Re =1)解:由查表知:=t 20℃,μ=0.0183×10-3Pa.sυ=15.7×10-6m 2/s ,ρ=1.205kg/m 3由Re=υud及u =μρρ18)(2gd m - 可得dυRe =μρρ18)(2gd m -d =6×10-2mm6.某气力输送管路,要求风速 u 0为砂粒悬浮速度u 的5倍,已知砂粒粒径mm d 3.0=,密度ρm =2650kg/m 3 空气温度为20℃,求风速u 0 值。
第八章 绕流运动

2、形状阻力:
流体绕经物体时,物体受到流体所给予的阻力主要包括两部分 即摩擦阻力和形状阻力(或称压差阻力,尾涡阻力),这两部分之和称 绕流阻力。其中的形状阻力大小取决于漩涡区的大小,即分离点的 位置。
分离点后移,漩涡区减小,则形状阻力减少,摩擦阻力增大;在高 Re时形状阻力比摩擦阻力大许多。因此,工程上减少了形状阻力便 减少了绕流阻力。
c 取不同值,得不同的势函数等值线,称为等势线 c 同理
c 取不同值,得不同的流函数等值线,即流线
对比二函数与流速的关系
ux x y
二式交叉相乘
uy y x
等势线与流线正交
0 x x y y
0
2 ux dy dx
微元体三个面上的平均压强
固体壁面对流体的切力
p pCD p dx x 1 p pAC p dx 2 x
TBD 0dx
pAB p
各表面力在 x 方向的合力
p 1 p p dx d + p dx ds sin 0dx Fsx p x 2 x
汇流流动与源流相反,势函数与流函数则均取负值 Q 称为源(汇)流强度
□ 8.3.3 环流(势涡) 速度环量
y
r θ
2 ru
分速度
ur 0 u 2 r
势函数
x
ur dr u rd 2
流函数
ur rd udr ln r 2
z
将速度势函数带入不可压缩流体的连续性方程:
ux u y uz 0 x y z
2 2 2 2 2 0 2 x y z
工程流体力学+第八章粘性流体绕物体的流动

(8-13)
三、纳维-斯托克斯方程(简称N-S方程)
如果质量力只有重力作用,用 g 代表重力加速度,不可压缩
粘性流体的运动方程的矢量形式为:
DV g - p 2 v Dt
(8-14)
右端第一项表示单位质量的质量力;第二项代表作用于 单位质量流体的压强梯度力;第三项代表黏性变形应力。
◇作用于微元体个面上的Y、Z轴方向的应力
同理,表面力在y方向的分量为:
y y
zy z
xy x
dxdydz
表面力在z方向的分量为:
z xz yz z x y
dxdydz
★作用在微元体上的表面力
如果用 Px ,
Py 和 Pz
表示单位体积的表面力,则:
上式称纳维-斯托克斯(Naver-Stokes)方程,是粘性 流体运动微分方程的又一种形式。
三、纳维-斯托克斯方程(简称N-S方程)
对于不可压流体,其连续方程为: v x v y v z 0 x y z 对于不可压缩粘性流体,粘性体膨胀应力为零,其运动方
程为:
2vx 2vx 2vx Dvx p Fx 2 2 2 x Dt x y z 2 v y 2 v y 2 v y Dv y p Fy 2 2 x 2 Dt y y z 2vz 2vz 2vz Dvz p Fz 2 2 2 x Dt z y z
(8-22)
(8-23)
而切应力的最大值,发生在C( =90°)为:
c 3V / 2r0
流体力学(第二版) 龙天渝 第八章 绕流运动习题答案
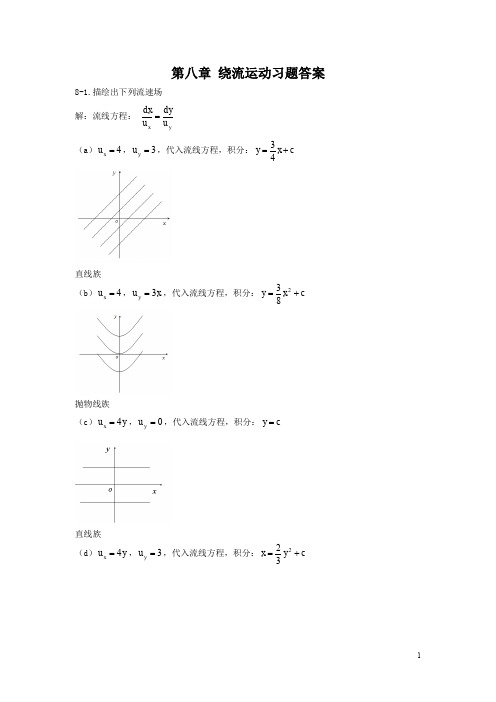
直线族 (d) u x 4 y , u y 3 ,代入流线方程,积分: x
2 2 y c 3
1
抛物线族 (e) u x 4 y , u y 3x ,代入流线方程,积分: 3x 2 4 y 2 c
椭圆族 (f) u x 4 y , u y 4 x ,代入流线方程,积分: x 2 y 2 c
5
u0 X k
(查表知 t=20ºC, 1.007 106 m / s )
Xk=
Re xk =0.1m<30m u0
可认为是紊流附面层:Re= 采用 C f
u0 X
=1.49×10
8
0.445 -3 ,则: C f =1.963×10 2.58 (lg Re )
2 u 0
u0 X k
,知
Xk=0.55m
8
(2)根据: =0.37 (
u0 x
) x,知 =0.0572m=57.2mm
1 5
(3) 根据:Re= 则: C f =
vx 6 知 Re =2.75×10 .
0.074 1700 -3 =3.196×10 1 Re Re 5
2 u 0
根据: D f C f A
解:叠加前
ux
Q y y (arctg arctg ) 2 xa xa
Q xa xa ( ) y 2 y 2 ( x a) 2 y 2 ( x a) 2 Q y y ( 2 2 ) 2 x 2 y ( x a) y ( x a) 2 uy Qy (y2 a2 )
Q y y (arctg arctg ) 2 xa xa
绕流运动详解

来流速度v∞平行于平板。由于平板极薄,边界层外部 的流动不受平板的影响,因此边界层外边界上流速处
处边界相上等压,强等p于也来处流处速相度等v,∞。ddpx 由0 于。流对速于不不变可,压边缩界流层体,外 平板绕流边界层动量方程可写成:
vd dx0vxd yd dx0vx2dy 0
(1)
该方程适用于层流和紊流边界层。
图7-3
一 平板层流边界层的计算
设定平板上为层流边界层,首先补充边界层流速分布
关系式,假定层流边界层内的流速分布与管流中的层流
速度分布相同,即
r2 v vmax(1 r02 )
应用于层流边界层,流速分布为
vx
y2
v[1 2 ]
或
vx
2v
(yy2)
2
(2)
补充第二个关系式,由牛顿内摩擦定律,求平板上的切
应力
0 d dx|v y y 0 d d[2 y v (y 2 y 2)|y ] 0 2 v
上式中负号表示切应力和x轴的方向相反,用其绝对值
0
2v
(3)
把(2)、(3)代入(1)
v d d0 x 2 v (y 2 y 2)d y d d0 x [2 v (y 2 y 2)2 d ] y 2v
设平板固定不动,来流的速度为 V ,方向与板面方向一 致。当流体流过平板时,根据固壁无滑移条件,板面上流体 质点的速度为零,在与板面垂直的方向上存在很大的速度梯 度,因此存在很大的摩擦应力,它将阻滞邻近的流体质点的 运动。在边界层区域以外,速度基本均匀,保持和来流速度 基本相同的大小和方向。绕流边界层在平板的前缘开始形成, 随着流动向下游发展,受摩擦应力的影响,越来越多的流体 质点受到阻滞,边界层的厚度也随之增加。在平板的前部边 界层呈层流状态,随着流程的增加,边界层的厚度也在增加, 层流变为不稳定状态,流体的质点运动变得不规则,最终发 展为紊流,这一变化发生在一段很短的长度范围,称之为转 类区,转类区的开始点称为转类点。转类区下游边界层内的 流动为紊流状态。如图所示,由于紊流边界层内的流体质点 更容易和外部主流区的流动进行动量交换,因此紊流区域边 界层厚度的增加比层流增加的更快。在转类区和紊流区的壁 面附近,由于流体的质点的随机脉动受到平板壁面的限制, 因此在靠近壁面的更薄的区域内,流动仍保持为层流状态, 称为粘性底层。
第八章 绕流问题

u
环流的速度分布规律
说明,纯环流中,任一包围原点的速度 环量等于常数。并称Γ为环流强度。
u rd
2
0
c rd 2c r
7
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
(8-5)
(8-4)
式(8-5)称为拉普拉斯方程。满足拉普拉斯方程的函数称 为调和函数
3
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
8.1.1 势函数和流函数
1 w v x 2 y z 1 u w y 2 z x 1 v u z 2 x y
在圆柱坐标系中,势函数为,且有:
2、源流和汇流 设想流体在单位时间内从源泉 点流出体积为 Q 的流体。如 果流体在间距为 1的平行平板 间向四周均匀扩散,这种流动 就称为源流。点称为源点,如 图所示。反过来,若流体从四 周向某汇合点集中,这种流动 称为汇流流动。点称为汇点。 由于流动是连续且对称的,任意点的速度为:
源流的势函数为 :
8.1.2 几种简单的平面势流 1、平行流(均匀直线流) 流场中各点的速度大小和方向都相同的流动称为平行流。 设x,y方向的速度分量分别为
8.1.2 几种简单的平面势流
显然,流线是一簇与轴成角的平行线,如 下图所示的实线。图中虚线为等势线,流 线和等势线正交。
ay bx ax by
y
2d
v
b dxc
dy
《流体力学》第八章绕流运动

这时速度势函数全微分为:
duxdxuydy
对应的拉普拉斯方程为: 2 2 0
H
x2 y2
8
在平面流动中,流线微分方程为:
dx dy ux uy
uxdy(uydx)0
二元流动 连续性方程为:
ux x
u y y
0
ux x
(uy ) y
由全微分理论,由于存在条件 ux (u y )
x y
则 uxdy(uydx) 必是某函数的全微分,即:
Q 2
环
流
ur =0
u
2 r
ln x2 y2 2
ln r 2
势流叠加演示 H
Q ln x2 y2 2 Q ln x2 y2 2
arctg y 2 x
Q ln r 2 Q ln r 2
2
15
第六节 绕流运动与附面层基本概念
在绕流中,流体作用在物体的力可分为两分量: ➢ 升力:垂直于来流方向的作用力。 ➢ 阻力:平行于来流方向的作用力。
本章主要讨论绕流阻力
摩擦阻力:空气、水等粘性小的流体在绕过物体 运动时,其摩擦阻力主要发生在附面层内(紧靠物 体表面的流速梯度很大的流体薄层)。
形状阻力:流体绕曲面体或具有锐缘棱角的物体
流动时,附面层要发生分离,从而产生涡旋所造成
的阻力。
H
16
u
u
u 紊流边界层
层流边界层
xx l
δ δ
附 层流底层 面
流函数存在的条件则是不可压缩流体,以 及流动是平面问题,与流动是否无旋,是 否恒定和是否具有粘性无关。当流动又是 无旋时,则流函数也满足拉普拉斯方程。
H
13
第三节 几种简单的平面无旋流动
流体力学 第八章 绕流运动

第八章绕流运动一、应用背景1、问题的广泛存在性:在自然界和工程实际中,存在着大量的流体绕物体的流动问题(绕流问题),如:飞机在空气中的飞行、河水流过桥墩、大型建筑物周围的空气流动、植物护岸(消浪,船行波),粉尘颗粒在空气中的飞扬和沉降,水处理中固体颗粒污染物在水中的运动。
(一种:流体运动;另外一种:物体运动),我们研究,将坐标系固结于物体上,将物体看成静止的,讨论流体相对于物体的运动。
2、问题的复杂性上一章的内容中可以看出,流体力学的问题可以归结为求解在一定边界条件和初始条件下偏微分方程组的求解。
但描述液体运动的方程式非常复杂的:一方面,是方程的非线性性质,造成方程求解的困难;另一方面,复杂的边界条件和初始条件都给求解流体力学造成了很多麻烦。
迄今为止,只有很少数的问题得到了解决。
平面泊萧叶流动,圆管coutte流动等等。
而我们所要解决的绕流问题正是有着非常复杂的边界条件。
3、问题的简化及其合理性流体力学对此的简化则是,简化原方程,建立研究理想液体的势流理论。
实际液体满足势流运动的条件:粘性不占主导地位,或者粘性还没有开始起作用。
正例:远离边界层的流体绕流运动、地下水运动、波浪运动、物体落入静止水体中,水的运动规律研究。
反例:研究阻力规律、能量损失、内能转换等等。
圆柱绕流(经典之一)半无限长平板绕流(经典之二)分成两个区域:一个区域是远离边界的地方,此区域剪切作用不明显,而且流体惯性力的影响远远大于粘性力的影响(理想液体)(引导n-s方程);另一个是靠近边界的地方(附面层,粘性底层),此区域有很强烈的剪切作用,粘性力的影响超强,据现代流体力学的研究表明,此区域是产生湍流的重要区域,有强烈的剪切涡结构,但此区域只有非常薄的厚度。
此区域对绕流物体的阻力、能量耗损、扩散、传热传质都产生重要影响。
4、本章的主要研究内容(1) 外部:理想液体,(简化方法,求解方式)、(2) 内部:附面层理论,(简化方法,求解方式,求解内容,现象描述) (3) 两者的衔接。
8第八章 边界层理论基础和绕流运动

第八章 边界层理论基础和绕流运动8—1 设有一静止光滑平板宽b =1m ,长L =1m ,顺流放置在均匀流u =1m/s 的水流中,如图所示,平板长边与水流方向一致,水温t =20℃。
试按层流边界层求边界层厚度的最大值δmax 和平板两侧所受的总摩擦阻力F f 。
解:20℃水的运动粘度ν=1.003⨯10-6 m 2/s 密度3998.2/kg m ρ=6119970091.00310ν-⨯===⨯L uLRe因为 56310997009310⨯<=<⨯L Re按层流边界层计算。
max 1/25.4470.0055m Re L L δ===3f 1/21.46 1.4610-===⨯L C Re 223998.2122 1.461011N 1.46N 22f ff u F C A ρ-⨯==⨯⨯⨯⨯⨯= 8—2 设有极薄的静止正方形光滑平板,边长为a ,顺流按水平和铅垂方向分别置放于二维恒定均速u 的水流中,试问:按层流边界层计算,平板两种置放分别所受的总摩擦阻力是否相等,为什么?解:因为两种置放情况的物理模型和数学模型及其分析、推导所得计算公式是相同的,所以两种情况平板所受的总摩擦阻力相等。
8—3 设有一静止光滑平板,如图所示,边长1m,上宽0.88m,下宽0.38m,顺流铅垂放置在均匀流速u =0.6m/s 的水流中,水温t =15℃。
试求作用在平板两侧的总摩擦阻力F f 。
注:若为层流边界层,C f 按式(8—24)计算。
解:由表1—1查得,15℃时水的密度ρ=999.13/kg m ,运动粘度ν=1.139×10-6m 2/s 。
首先判别流态,计算平板上宽雷诺数560.60.884635655101.13910ν-⨯===<⨯⨯L uLRe ,按层流边界层计算。
设z 轴铅垂向上,平板宽度x 为0.38+0.5z ,阻力系数C f 按式(8-24)计算,即12f 60.6(0.380.5)1.328 1.13910--⨯+⎡⎤==⨯⎢⎥⨯⎣⎦z C1521.328 5.2677810(0.380.5)z -轾=创?犏臌总摩擦阻力F f 按式(8—20)计算,f f1212(0.380.5)d 2F C u z z r =?ò115202 1.328 5.2677810(0.380.5)z -轾=创创+犏臌ò21999.10.6(0.380.5)d 2z z 创创+ 1120.658(0.380.5)d z z =?ò。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
管流附面层
从入口到形成充分发展的管流的长度称 入口段长度,以Xe表示。Xe以后为充分发展 管流
曲面附面层分离现象
1.减压加速区 2.增压减速区 分离点发生在增压减速区 附面层分离后,物体后部形成许多无规则的旋涡,
由此产生形状阻力
解释流线型能减小形状阻力
卡门涡街
物体后面形成有规则的交错排列的旋涡组合
uz dz
流函数
一切不可压缩流体的平面流动,无论有 旋流动或是无旋流动都存在流函数.
函数Ψ称为流函数,则
d
x
dx
y
dy
u y dx ux dy
求流函数
课堂练习
(07港航)假设不可压缩流体平面流场为
ux 2xy x,uy y2 y x2 ,检验此为何种流动?
(A)无此种流动 (B)有旋流动
总摩擦力
Df
C
f
A
u
2 0
2
此时
Cf
0.074 1700 Re0.2 Re
(短板)
长板选用P245的式8-9-7或8-9-8
平板附面层厚度计算
平板层流附面层厚度
5.477 x
u0
平板紊流附面层厚度
1
0.37
u0
x
5
x
曲面绕流阻力计算
绕流阻力包括摩擦阻力和形状阻力,可
用斯托克斯公式计算:
D
无旋流动
流动场中各点旋转角速度等于零的运 动,称为无旋流动 x y z 0
x
1 2
( uz y
u y z
)
y
1 (uz 2 z
uz x
)
z
1 ( uy 2 x
ux y
)
势函数
无旋流动一定有势函数,反之有势则无旋. 函数Φ称为速度势函数,则
d
x
dx
y
dy
z
dz
u x dx
u y dy
gd
系数 Cd 随 Re 而变的值
如果 Re 1
,则
Cd
24 Re
代入得
u
1
18
d
2 m
g
如果 Re 10 ~ 103 则 Cd
13 Re
如果 Re 103 ~ 2 105 则 Cd 0.48
Re 为其它值 Cd 可查下图
升力计算
绕流升力计算
L
CL
A
u
2 0
2
升力系数由实验确定
第八章 绕流运动
本章主要论述理想不可压缩流体平面 无旋运动,以及有关附面层(边界层)的基本 概念和阻力计算. 作为专业的应用之一, 对 固体颗粒在空气中的升降的临界速度----悬 浮速度也进行了分析与讨论.
1.无旋运动 2.绕流运动与附面层基本概念 3.附面层分离及卡门涡街 4.阻力计算 5.悬浮速度 6.升力计算
涡街振动频率计算
斯特洛哈尔公式
fd 0.1981 19.7
u0
Re
Re 250 ~ 2 105
f 为振动频率 解释产生横向振动对工程破坏力
平板层流附面层总摩擦力计算
此时只有摩擦阻力而无形状阻力
总摩擦力
Df
C
f
A
u
2 0
2
此时
Cf
1.46 Re
平板紊流附面层总摩擦力计算
此时也只有摩擦阻力而无形状阻力
悬浮速度分析及计算
绕流阻力 微粒浮力
D
Cd
AuBiblioteka 2 021 8
C d d
2 u02
B 1 d 3g 6
微粒重力 G
1 d 6
3m
g
当D+B>G时,微粒随气流上升
当D+B<G时,微粒随气流沉降
当D+B=G时,微粒处于悬浮状态,此时
1 8
Cd d
2 u 2
1 6
d
3 g
1 6
d
3m g
u
4 3Cd
m
Cd
A
u02
2
D 物体所受的绕流阻力
Cd 无因次的阻力系数
A 物体面积
u0 未受干扰时的来流速度
流体密度
悬浮速度
为了研究在气力输送中,固体颗粒在何 种条件下才能被气体带走;在除尘室中,尘粒 在何种条件下才能沉降;在燃烧技术中,都要 研究固体颗粒或液体颗粒在气流中的运动 条件,这就提出了悬浮速度这个概念.
附面层形成及其性质
平板附面层 二个流区,速度0.99U0处作为两区分界 1.附面区:粘性流体有旋流动 2.势流区:理想流体无旋流体
附面层厚度δ沿流向逐渐增加,层流附 面层转化为紊流附面层临界雷诺数为
Re xk
u0 xk
3.5 ~ 5.0105
附面层意义:将流场划分为两个计算
方法不同区域,即势流区和附面层
(C)平面势流
(D)非定常流动
绕流运动所受的力
在绕流中,流体作用在物体上的力可 以分为两个分量: 1.垂直于来流方向的作 用力,叫做升力;2.另一平行于来流方向 的作用力,叫做阻力
绕流阻力可分为:摩擦阻力与形状阻力。
1.摩擦阻力发生在紧贴物体表面流速梯度很 大的薄层内,这薄层叫附面层或边界层。
2.形状阻力是流体绕曲面等物体时,附面层 发生分离,从而产生漩涡所造成的阻力。 这种阻力与物体形状有关,故称形状阻力。 也叫压差阻力。
