3.4 简单的图案设计
北师大版数学八年级下册:3.4《简单的图案设计》课时练习含答案解析

北师大版数学八年级下册第三章第四节简单的图案设计课时练习一、选择题(共10题)1.如图,是四家银行行标,不可以先设计出一半来通过对折来完成的是( )A.①③B.②④C.②D.④答案:D解析:解答:根据轴对称图形的定义可以判断④不是轴对称图形;故答案是D选项分析:考查如何通过轴对称设计图案2.图画上大风车的叶片可以看作一个叶片通过怎样的运动得到()A.平移B.旋转C.平移和旋转D.对折答案:B解析:解答:大风车上的叶片可以看作由一个叶片旋转得到;故答案是B选项分析:考查利用旋转设计图案3.利用电脑,在同一页面对某图形进行复制,得到一组图案,这一组图案可以看作一个基本图形通过()得到的A.旋转B.平移和旋转C.平移D.拉伸答案:C解析:解答:复制就是把一个平移到另一个位置,所以答案是C选项分析:考查平移设计图案4.如图是一个风筝的图案,它是轴对称图形,若∠B=30︒,那么∠E=( )A. 20︒B. 60︒C. 30︒D. 45︒答案:C解析:解答:因为设计的风筝是轴对称图形,所以对应角相等,故答案是C选项分析:注意中心对称和轴对称的特点5.广告设计人员在设计图案的时候经常用到的方法是()A.旋转B.平移C.轴对称D.以上都是答案:D解析:解答:在设计图案的时候经常用到的是旋转、平移、轴对称,故答案是D选项分析:考查图案的设计方法6. 如图,将△ABC绕点O旋转一定的角度得到△A′B′C′,下列结论中不成立的是( )A.OC=OC′B.OA=OA′C.BC=B′C′D.∠ABC=∠A′C′B′答案:D解析:解答:旋转前后的图形全等,而且对应角相等,D选项中不是对应角分析:考查旋转前后的图形全等的问题7.一个长方形绕一点旋转一周所形成的图形可能是( )A.圆B.长方形C.圆环D.正方形答案:C解析:解答:长方形绕一点旋转一周时所形成的图形是圆环,故答案是C选项分析:注意成简单的图案设计方法8.五星红旗上的四个小五角星可以看作一个基本图案经过怎样的运动得到的()A.旋转B.平移C.对折D.旋转和平移答案:D解析:解答:五星红旗上的四个小五角星可以看作一个基本图案经过平移和旋转得到,故答案是D分析:注意对中心对称图形的理解9. 小丽制作了一个对面图案均相同的正方体礼品盒(如图所示),则这个正方体礼品盒的平面展开图可能是( )答案:A解析:解答:此题需有一定空间想象能力,可以实际动手操作一下,以自己能辩认的简单图案代表各图案.,故答案是A选项10.下列几种图案是车的标志,问其中是轴对称图形的有( )A.2个B.3个C.4个D.1个答案:A解析:解答:根据轴对称图形的定义可知奥迪和大众这两个车标是轴对称图形,所以答案是A分析:考查轴对称图形二、填空题(共10题)11.如图的雪花有______条对称轴答案:3解析:解答:依据轴对称图形的意义,沿着对称轴所在的直线对折,对折后的两部分能够完全重合,所以雪花有3条对称轴分析:考查对称轴的多少12.起重机将重物垂直提起,这可以看作为数学上的_____________答案:平移解析:解答:起重机将重物垂直提起,可以看成平移现象分析:注意分清平移的特点13.关于轴对称的两个图形,沿对称轴折叠后答案:重合解析:解答:关于轴对称的两个图形,沿对称轴折叠后重合分析:注意对称点的连线一定经过对称中心14.轴对称图形只有一条对称轴_______(判断对错)答案:错误解析:解答:有的轴对称图形不止有一条对称轴,如圆、正方形等分析:考查轴对称图形的对称轴的数目15.广告设计人员进行图案设计,经常将一个基本图案进行轴对称、平移和_______等答案:旋转解析:解答:图案设计的时候经常用到的是行轴对称、平移和旋转等16. 将点A 绕另一个点O 旋转一周,点A 在旋转过程中所经过的路线是_______ 答案:圆解析:解答:利用旋转一周可以得到的图形是圆分析:考查利用旋转设计图案17. 利用电脑,在同一页面上对某图形进行复制,得到一组图案,这一组图案可以看作是一个基本图形通过_______得到的答案:平移解析:解答:利用平移可以得到一些相同的图案分析:考查简单的图案设计18. 利用平移、旋转和对称变换可以设计出美丽的镶嵌图案;这种说法_____________ 答案:正确解析:解答:构成一个镶嵌图形的基本单元是多边形或是类似的常规图形,利用平移、旋转和对称变换可以设计出美丽的镶嵌图案分析:考查简单图形的设计方法19. 国际奥委会会旗上的五环图案可以看作一个基本图案圆环经过______运动得到 答案:平移解析:解答:一个圆环经过平移运动可以得到五环图案分析:考查简单的图案设计20.木工师傅在设计拉动抽屉时,参考的数学原理是 _____答案:平移解析:解答:在拉动抽屉时候前后移动而抽屉不发生改变,这是平移的原理分析:注意旋转的要点三、解答题(共5题)21. 从8:55到9:15,钟表的分针转动的角度是?答案:120°解答:分针60分钟转一周,时针十二小时转一周.从8:55到9:15经过了20分钟,所以,分针转动的角度是6020×360°=120° 解析:分析:注意钟表分针旋转一周的角度22. 从5:55到6:15,时针转动的角度是?答案:10°解答:从5:55到6:15经过了31小时,所以,时针转动的角度是31×121×360°=10°.解析:分析:注意钟表上时针一小时走过的角度 23. 如图,王虎使一长为4 cm ,宽为3 cm 的长方形木板,在桌面上做无滑动地翻滚(顺时针方向),木板上点A 位置变化为A →A 1→A 2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A 翻滚到A 2位置时共走过的路径长为?答案:27πcm 解答::第一次翻滚可以看成是以B 为圆心,以AB 为半径的弧,且可求得∠ABA 1=90°,∴第一次翻滚走过的路径为41×2×5π=25π,第二次翻滚可看成是以C 为圆心,以A 1C 为半径的弧,且∠A 1CA 2=60°,∴第二次翻滚走过的路径为61×2×3π=π.总共路径=25π+π=27π cm. 解析:分析:考查旋转问题,关键是找准对应点24.请你设计一个只有两条对称轴的优美图案答案:解答:解析:分析:注意轴对称图形的特点25. 在图案设计中常用的作图工具有?答案:解答:在图案设计中常用的作图工具有直尺,圆规,三角尺解析:分析:考查简单的图案设计。
【四清导航】2015春八年级数学下册 3.4 简单的图案设计课件 (新版)北师大版

图案的设计 1.(4分)下列四个图案中,只能用平移来分析的图案是( A )
2.(4分)在下列图形中,既是中心对称图形又是轴对称图形的是(C )
3.(4分)观察下列图案,在A,B,C,D四幅图案中,能通过 图案①逆时针旋转90°得到的是( D )
4.(4分)如图,经过平移或旋转,不可能将甲图案 变成乙图案的是( )
二、填空题(每小题5分,共10分)
15.如图是小亮设计地板砖图案的过程:方法一:由图①到图② 采用的是 轴对称 ____ 方法,由图②到图③也是采 轴对称方法设计的. 用 ____ 方法二:由图①到图②采用的是__ 旋转 __ 方法, 的中心 旋转中心是正方形__ __ ,由图②到图③也是 旋转方法,顺时针旋转____ 90 度. 采用____
13.由图中左侧三角形仅经过一次平移、旋转或轴对称变换, 不能得到的图形是( B )
14.(2014·荆门)如图,在4×4的正方形网格中,每个小正方 形的顶点称为格点,左上角阴影部分是一个以格点为顶点的 正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影, 使这两个格点正方形无重叠面积,且组成的图形是轴对称图形, 又是中心对称图形,则这个格点正方形的作法共有( C ) A.2种 B.3种 C .4种 D.5 种
5.(4分)下列几何图形中,对称性与其他图形不同的是(
)
6.(4分)如图是某药业公司商品标志图案,则下列说法中, 正确的个数有( ) ①图案是按照轴对称设计的;②图案是按照旋转设计的; ③图案的外层“S”是按照旋转设计的; ④图案的内层“A”是按照轴对称设计的. A.1个 B .2个 C.3 个 D.4个
7.(4分)永州市新田县的龙家大院至今已有930多年历史, 因该村拥有保存完好的“三堂九井二十四巷四十八栋”明 清建筑而申报为中国历史文化名村.如图是龙家大院的一 个窗花图案,它具有很好的对称美,这个图案是由: ①正六边形(平面内,内角都相等、各边都相等的六边形 叫做正六边形);②等边三角形;③等腰梯形; ④直角梯形等几何图形构成.在这四种几何图形中既是 轴对称图形又是中心对称图形的是____.(填序号) 8.(4分)如图所示为某煤气公司的商业标志图案,外层可 视为利用图形的 ____ 设计;内层可以视为利用图形 的 ____ 设计,既形象又美观.
北师大版八年级数学下学期《3.4 简单的图案设计 》 同步练习 包含答案

3.4 简单的图案设计一.选择题(共10小题)1.将如图方格纸中的图形绕O点顺时针旋转90°得到的图形是()A.B.C.D.2.在以下绿色食品、回收、节能、节水四个标志中,是由某个基本图形经过旋转得到的是()A.B.C.D.3.如图绕中心旋转180°,所得到的图形是()A.B.C.D.4.如图,下列四个图形都可以分别看作是一个“基本图案”经过旋转所形成,则它们的旋转角相同的图形为()A.(1)(2)B.(1)(4)C.(2)(3)D.(3)(4)5.如下左图所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的一个是()A.B.C.D.6.如图,△DEF是△ABC经过某种变换后得到的图形.△ABC内任意一点M的坐标为(x,y),点M经过这种变换后得到点N,点N的坐标是()A.(﹣y,﹣x)B.(﹣x,﹣y)C.(﹣x,y)D.(x,﹣y)7.如图,在平面直角坐标系xOy中,△AOB可以看作是由△OCD经过两次图形的变化(平移、轴对称、旋转)得到的,这个变化过程不可能是()A.先平移,再轴对称B.先轴对称,再旋转C.先旋转,再平移D.先轴对称,再平移8.如图,把图中的△ABC经过一定的变换得到△A′B′C′,如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为()A.(a﹣3,b)B.(a+3,b)C.(3﹣a,﹣b)D.(a﹣3,﹣b)9.如图,在9×6的方格纸中,小树从位置A经过平移旋转后到达位置B,下列说法中正确的是()A.先向右平移6格,再绕点B顺时针旋转45°B.先向右平移6格,再绕点B逆时针旋转45°C.先向右平移6格,再绕点B顺时针旋转90°D.先向右平移6格,再绕点B逆时针旋转90°10.如图,对△ABC分别作下列变换:①先以x轴为对称轴作轴对称图形,然后再向左平移4个单位;②以点O为中心顺时针旋转180°,然后再向左平移2个单位;③先以y 轴为对称轴作对称图形,然后再向下平移3个单位;其中能使△ABC变成△DEF的是()A.①B.②C.②或③D.①或③二.填空题(共5小题)11.在下图方框中设计一个美丽的中心对称图形并使它成为正方体的一种侧面展开图.12.在中国的园林建筑中,很多建筑图形具有对称性.如图是一个破损花窗的图形,请把它补画成中心对称图形..13.下面图案中,可以由一个基本图案连续旋转45°得到的是(填序号).14.如图,在平面直角坐标系xOy中,点A、B的坐标分别为(﹣4,1)、(﹣1,3),在经过两次变化(平移、轴对称、旋转)得到对应点A''、B''的坐标分别为(1,0)、(3,﹣3),则由线段AB得到线段A'B'的过程是:,由线段A'B'得到线段A''B''的过程是:.15.如图是用围棋棋子在6×6的正方形网格中摆出的图案,棋子的位置用有序实数对表示,如A点为(5,1),若再摆一黑一白两枚棋子,使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是(请填写正确答案的序号)①黑(1,5),白(5,5)②黑(3,2),白(3,3)③黑(3,3),白(3,1)④黑(3,1),白(3,3)三.解答题(共6小题)16.如图,是由2个白色正方形和2个黑色正方形组成的“L”型图形,按下列要求画图:(1)在图1中,添1个白色或黑色正方形,使它成轴对称图形;(2)在图2中,以点O为旋转中心,将图形顺时针旋转90°.17.(1)图1是4×4的正方形网格,请在其中选取一个白色的正方形并涂上阴影,使图中阴影部分是一个中心对称图形.(2)如图2,在正方形网格中,以点A为旋转中心,将△ABC按逆时针方向旋转90°,画出旋转后的△AB1C1.18.课堂上,老师给出了如下一道探究题:“如图,在边长为1的正方形组成的6×8的方格中,△ABC和△A1B1C1的顶点都在格点上,且△ABC≌△A1B1C1.请利用平移或旋转变换,设计一种方案,使得△ABC通过一次或两次变换后与△A1B1C1完全重合.”(1)小明的方案是:“先将△ABC向右平移两个单位得到△A2B2C2,再通过旋转得到△A1B1C1”.请根据小明的方案画出△A2B2C2,并描述旋转过程;(2)小红通过研究发现,△ABC只要通过一次旋转就能得到△A1B1C1.请在图中标出小红方案中的旋转中心P,并简要说明你是如何确定的.19.如图,是3×3的正方形网格,将其中两个方格涂黑,使得涂黑后的整个图案是轴对称图形.请在以下备用网格中画出四个不同的图案(如果绕正方形的中心旋转,能重合的图案视为同一种,例如,下列四个图形就属于同一种).20.在平面直角坐标系中,如图所示A(﹣2,1),B(﹣4,1),C(﹣1,4).(1)△ABC向上平移一个单位,再向左平移一个单位得到△A1B1C1,那么C的对应点C1的坐标为;P点到△ABC三个顶点的距离相等,点P的坐标为;(2)△ABC关于第一象限角平分线所在的直线作轴对称变换得到△A2B2C2,那么点B 的对应点B2的坐标为;(3)△A3B3C3是△ABC绕坐标平面内的Q点顺时针旋转得到的,且A3(1,0),B3(1,2),C3(4,﹣1),点Q的坐标为.21.如图,在平面直角坐标系xOy中,点A的坐标为(﹣2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.(1)△AOC沿x轴向右平移可得到△OBD,则平移的距离是个单位长度;△AOC 与△BOD关于某直线对称,则对称轴是;△AOC绕原点O顺时针旋转可得到△DOB,则旋转角至少是°.(2)连接AD,交OC于点E,求∠AEO的度数.参考答案一.选择题(共10小题)1.D.2.B.3.C.4.D.5.B.6.B.7.C.8.C.9.B.10.A.二.填空题(共5小题)11.解:12.解:13.(2).14.向右平移4个单位长度;绕原点顺时针旋转90°.15.④.三.解答题(共6小题)16.解:(1)如图1所示:(2)如图2所示:17.解:(1)如图1所示:此阴影部分是中心对称图形;(2)如图2所示:△AB1C1,即为所求.18.解:(1)如图所示,△A2B2C2即为所求,将△A2B2C2绕着点B1顺时针旋转90°,即可得到△A1B1C1.(2)如图所示,连接CC1,BB1,作CC1的垂直平分线,BB1的垂直平分线,交于点P,则点P即为旋转中心.19.解:符合要求的正方形如图所示:20.解:(1)如图,△A1B1C1即为所求,那么C的对应点C1的坐标为(﹣2,5)P,点P 的坐标为(﹣3,3).故答案为(﹣2,5),(﹣3,3).(2)△A2B2C2如图所示,那么点B的对应点B2的坐标为(1,﹣4).故答案为(1,﹣4).(3)△A3B3C3即为所求,Q(﹣1,﹣1),故答案为(﹣1,1).21.解:(1)∵点A的坐标为(﹣2,0),∴△AOC沿x轴向右平移2个单位得到△OBD;∴△AOC与△BOD关于y轴对称;∵△AOC为等边三角形,∴∠AOC=∠BOD=60°,∴∠AOD=120°,∴△AOC绕原点O顺时针旋转120°得到△DOB.(2)如图,∵等边△AOC绕原点O顺时针旋转120°得到△DOB,∴OA=OD,∵∠AOC=∠BOD=60°,∴∠DOC=60°,即OE为等腰△AOD的顶角的平分线,∴OE垂直平分AD,∴∠AEO=90°.故答案为;2;y轴;120.。
简单的图案设计 导学案

3.4简单的图案设计一、学习准备:什么是平移?什么是旋转?它们的性质是什么?二、学习目标:1.了解图案最常见的构图方式:轴对称、平移、旋转……,理解简单图案设计的意图。
2.经历收集、欣赏、分析、操作和设计的过程,培养学生收集和整理信息的能力,分析和解决问题的能力,合作和交流的能力以及创新能力。
3.经历对典型图案设计意图的分析,进一步发展学生的空间观念,增强审美意识,培养学生积极进取的生活态度。
三、学习提示:1、自主探究:(1).分析课本85页课前引例。
(2).欣赏课本85页图3—27的图案,并分析这个图案形成过程。
理解:图案是密铺图案的代表,旨在通过对典型图案的分析欣赏,逐步能够进行图案设计,同时了解轴对称、平移、旋转变换是图案制作的基本手段。
解答的关键是确定“基本图案”,然后再运用平移、旋转关系加以说明,注意旋转中心可以为图形上某一特征的点。
(3).利用下面提供的基本图形,用平移、旋转、轴对称、中心对称等方法进行图案设计,并简要说明自己的设计意图。
(4).考虑分析课本85-86页做一做和议一议。
2、合作探究:(1).请利用旋转分析下列图案,请设计一个你所喜欢的徽标.2.下列四幅图是怎样利用旋转、平移或轴对称进行设计的?你能仿照其中的一个自己设计一个图案吗?3、练习:在现实生活中,我们经常见到一些美丽的图案.(1)请用平移、旋轴、轴对称分析各图案的形成过程?(2)哪几个图案可以经过平移得到?哪几个图案可以经过旋转得到?哪几个图案可以经过轴对称得到?四、学习小结:你有哪些收获?五、夯实基础: 选择题1.国旗上的四个小五角星,通过怎样的移动可以相互得到( )A.轴对称B.平移C.旋转D.平移和旋转 2.起重机将重物垂直提起,这可以看作为数学上的( )A.轴对称B.平移C.旋转D.变形 填空题3.广告设计人员进行图案设计,经常将一个基本图案进行轴对称、平移和_______等。
4.将点A 绕另一个点O 旋转一周,点A 在旋转过程中所经过的路线是_______。
北师大版八年级下册数学《3.4 简单的图案设计》PPT课件

第三章 图形的平移与旋转
3.4 简单的图案设计
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.利用旋转、轴对称或平移进行简单的图案设计. (重点) 2.认识和欣赏平移、旋转在现实生活中的应用. 3.灵活运用平移与旋转组合的方式进行一些图案设 计.(难点)
导入新课
问题:经过一波三折,东京奥组公布了2020年东 京夏季奥运会新会徽,名为“组合市松纹”的方 案最终胜出.据称, 该方案的设计灵感源自在日本 江户时代颇为流行的西洋跳棋黑白棋盘格,加入 了日本传统的靛蓝色彩,体现出精致又优雅的日 式风情.说一说图案中的奥运 五环可以通过其中一个圆怎样变化而得到?
(1)
(2)
(3)
(4)
分析图案的形成过程
基本图案
图案的形成过程
分析图案的形成过程
基本图案
图案的形成过程
方法归纳
图形的变换可以通过选择不同的变换方式得 到,可能需要旋转、轴对称、平移等多种变换组 合才能得到完美的图案,希望同学们认真分析, 精心设计出漂亮的图案来.
三 图案的设计
例3 下面花边中的图案以正方形为基础,由圆弧、 圆或线段构成.仿照例图,请你为班级的板报设计一条 花边.要求:(1)只要画出组成花边的一个图案;(2)以所 给的正方形为基础,用圆弧、圆或线段画出;(3)图案 应有美感.
讲授新课
一 分析构成图案的基本图形
典例精析 例1 试说出构成下列图形的基本图形.
(1) (1)
(2) (2)
(3) (3) (4)
基本图形
(4)
想一想:看成 轴对称时基本 图形是什么?
方法归纳
对于这三种图形变换一般从定义区分即可.分清 图形变换的几个最基本概念是解题的关键.
3.4简单的图案设计课件北师大版

3/31/2014 5:48:20 AM
3/31/2014 5:48:20 AM
(1)仿照上图中的某个标志,每个小组设计一个 图案. (2)你设计的图案是如何形成的?要表现什么?
3/31/2014 5:48:20 AM
• 利用
• 来设计一个图案。大 家下去有没有思考呢?
3/31/2014 5:48:20 AM
这节课我们通过对一些图案的观察、分析,并进行了简单的 图案设计,进一步理解了平移、旋转及轴对称,同学们以后 要能灵活应用这些性质.
生活中还有哪些图案用到了平 移或旋转?分析其中的一个,并 与同伴交流.
3/31/2014 5:48:20 AM
3/31/2014 5:48:20 AM
例 题 解 析
例 1 欣赏图 3—24 的图案 , 并分析这个图案形 的过程。
3/31/2014 5:48:20 AM
分析
基本图案有几个? 三种不同颜色的“爬虫”(绿、白、黑), 形状、大小完全相同。 分析同色“爬虫”、异色“爬虫”之间的关系。 若为旋转关系,必须先指出“旋转中心”。
3/31/2014 5:48:20 AM
用“平移”“旋转”“轴对称”来分析图案的形成过程
基本图案
图案的形成过程
3/31/2014 5:48:20 AM
用“平移”“旋转”“轴对称”来分析图案的形成过程
基本 图案
图案 的形 成过 程 3/31/2014 5:48:20 AM
下图的图案,并分析这个图案形成的过程.
3/31/2014 5:48:20 AM
练习 下图是由12个全等三角形组成的, 利用平移、轴对称或旋转分析这个图案 的形成过程。
3/31/2014 5:48:20 AM
3 4 简单的图案设计 同步练习题 (无答案)北师大版八年级数学下册
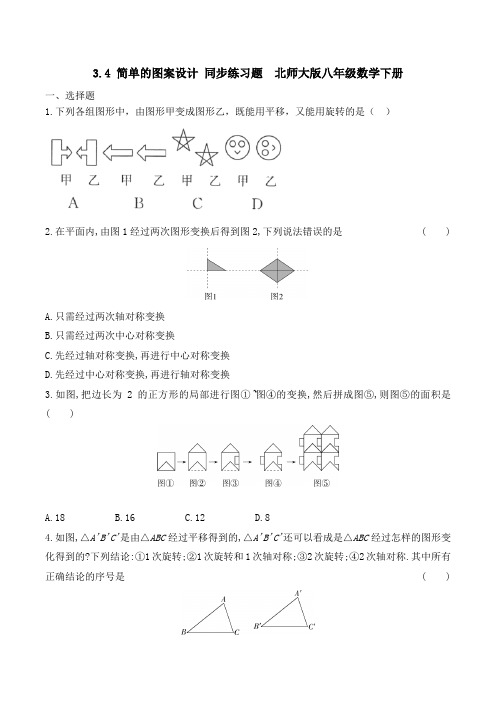
3.4 简单的图案设计同步练习题北师大版八年级数学下册一、选择题1.下列各组图形中,由图形甲变成图形乙,既能用平移,又能用旋转的是()2.在平面内,由图1经过两次图形变换后得到图2,下列说法错误的是( )A.只需经过两次轴对称变换B.只需经过两次中心对称变换C.先经过轴对称变换,再进行中心对称变换D.先经过中心对称变换,再进行轴对称变换3.如图,把边长为2的正方形的局部进行图①~图④的变换,然后拼成图⑤,则图⑤的面积是( )A.18B.16C.12D.84.如图,△A'B'C'是由△ABC经过平移得到的,△A'B'C'还可以看成是△ABC经过怎样的图形变化得到的?下列结论:①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是( )A.①④B.②③C.②④D.③④5.下列图案分别是三菱、宝马、奥迪、奔驰汽车的车标,其中形成过程不是同类型的是( )6.按图中第一、二两行图形的平移、轴对称及旋转等变换规律,填入第三行“?”处的图形应是( )二、填空题7.利用电脑,在同一页面上对某图形进行复制,得到一组图案,这一组图案可以看作是一个“基本图案”通过______得到的.8.如图所示的4个图案中,由基本图形经过平移得到的是①②,由基本图形经过旋转得到的是______.(填序号)9.点O是正五边形ABCDE的中心,分别以各边为直径向正五边形的外部作半圆,组成了一幅美丽的图案(如图),这个图案绕点O旋转一定度数后能与原来的图案互相重合,至少应该旋转的度数为.10.如图,在平移,轴对称,旋转三种图形变换中,该图案不包含的变换是.11.如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合.若每个叶片的面积为4 cm2,∠AOB=120°,则图中阴影部分的面积之和为cm2.三、解答题12.如图所示,已知每个网格中小正方形的边长都是1,图1中的阴影图案是由三段以格点为圆心,半径分别为1和2的圆弧围成的.请你在图2中以图1为基本图案,借助轴对称平移或旋转设计两个完整的花边图案,(要求至少含有两种图形变换)13.请你分别在如图所示的三个网格(两相邻隔点的距离均为1)中,各设计一个图案,要求所设计的图案既是轴对称图形又是中童心对称图形,每个图案的面积都等于23,并且各图案都不相同,将你设计的图案用铅笔涂黑。
北师大版八年级数学下册精品教案 3.4 简单的图案设计

3.4简单的图案设计1.利用旋转、轴对称或平移进行简单的图案设计.2.认识和欣赏平移、旋转在现实生活中的应用,并灵活运用平移与旋转组合的方式进行一些图案设计.一、情境导入2016年里约热内卢奥运会会徽是由三人牵手相连的标志,代表巴西的著名景点“面包山”作为图形的基础,融合充满激情的卡里奥克舞,并且呼应了巴西国旗的绿黄蓝三色.标志象征着团结、转变、激情及活力.在和谐动感中共同协力,同时也体现了里约的特色和这座城市多样的文化,展示了热情友好的里约人和这座美丽的上帝之城.二、合作探究探究点一:分析图案的形成过程【类型一】分析构成图案的基本图形分析下列图形的形成过程.解析:仔细观察图案,分析构成的基本图形,再分析图形变换的过程和方式.是通过平移、轴对称、旋转中的一种变换还是其中的几种变换的组合,另外要注意图形形成不是唯一的,即基本图形也不唯一,要全面思考,认真分析.解:仔细观察会发现这四个图形分别是由以下的基本图形构成的.第一个是由基本图形旋转十次后得到的,第二个是由基本图形平移两次后得到的,第三个是由基本图形旋转五次后得到的,第四个是由基本图形旋转五次后得到的.因为图形的变换不唯一还可以有其他的变换方式,如(1)、(4)可以由图2(a)、2(b)通过轴对称变换得到.方法总结:对于这四种图形变换一般从定义区分即可.分清图形变换的几个最基本概念是解题的关键.【类型二】分析图案的形成过程分析左边的树形图案,经过怎样的图形变换就可得到右边的树形图案.解析:根据左右两图形的位置关系可知,若要由左图得到右图,可以通过以下两种途径:(1)把左图绕点A 沿顺时针方向旋转一个角度,使左边的树形图案与直线垂直,然后再作轴对称变换(要注意对称轴的正确选择),即可得到右边的树形图案.(2)把左图先做轴对称变换(要注意对称轴的正确选择),使左边的树形图案与直线垂直,然后再作平移变换,即可得到右边的树形图案.方法总结:图形的变换可以通过选择不同的变换方式得到,可能需要旋转、轴对称、平移等多种变换组合才能得到完美的图案.探究点二:利用平移、旋转、轴对称等方式设计图案用四块如图①所示的正方形卡片拼成一个新的正方形,使拼成的图案是一个轴对称图形,请你在图②、图③、图④中各画出一种拼法(要求三种画法各不相同,且其中至少有一个既是轴对称图形,又是中心对称图形).解:解法不唯一.例如:方法总结:求解时只要符合题意即可,另外,在平时的学习生活中一定要留意身边的各种形状的图案,这样才能在具体求解问题时如鱼得水,一蹴而就.三、板书设计1.分析图案的形成过程(1)分析构成图案的基本图形;(2)分析图案的形成过程.2.利用平移、旋转、轴对称等方式设计图案教学过程中,强调学生自主探索和合作交流,经历运用平移、旋转、轴对称的组合进行简单的图案设计过程,体会图案的欣赏与设计过程.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.4简单的图案设计
1.利用旋转、轴对称或平移进行简单
的图案设计.
2.认识和欣赏平移、旋转在现实生活
中的应用,并灵活运用平移与旋转组合的方
式进行一些图案设计.
一、情境导入
2016年里约热内卢奥运会会徽是由三
人牵手相连的标志,代表巴西的著名景点
“面包山”作为图形的基础,融合充满激情
的卡里奥克舞,并且呼应了巴西国旗的绿黄
蓝三色.标志象征着团结、转变、激情及活
力.在和谐动感中共同协力,同时也体现了
里约的特色和这座城市多样的文化,展示了
热情友好的里约人和这座美丽的上帝之城.
二、合作探究
探究点一:分析图案的形成过程
【类型一】分析构成图案的基本图形
分析下列图形的形成过程.
解析:仔细观察图案,分析构成的基本
图形,再分析图形变换的过程和方式.是通
过平移、轴对称、旋转中的一种变换还是其
中的几种变换的组合,另外要注意图形形成
不是唯一的,即基本图形也不唯一,要全面
思考,认真分析.
解:仔细观察会发现这四个图形分别是
由以下的基本图形构成的.第一个是由基本
图形旋转十次后得到的,第二个是由基
本图形平移两次后得到的,第三个是由
基本图形旋转五次后得到的,第四个
是由基本图形旋转五次后得到的.因
为图形的变换不唯一还可以有其他的变换
方式,如(1)、(4)可以由图2(a)、2(b)通过轴
对称变换得到.
方法总结:对于这四种图形变换一般从
定义区分即可.分清图形变换的几个最基本
概念是解题的关键.
【类型二】分析图案的形成过程
分析左边的树形图案,经过怎样
的图形变换就可得到右边的树形图案.
解析:根据左右两图形的位置关系可
知,若要由左图得到右图,可以通过以下两
种途径:
(1)把左图绕点A沿顺时针方向旋转一
个角度,使左边的树形图案与直线垂直,然后再作轴对称变换(要注意对称轴的正确选择),即可得到右边的树形图案.
(2)把左图先做轴对称变换(要注意对称轴的正确选择),使左边的树形图案与直线垂直,然后再作平移变换,即可得到右边的树形图案.
方法总结:图形的变换可以通过选择不同的变换方式得到,可能需要旋转、轴对称、平移等多种变换组合才能得到完美的图案.探究点二:利用平移、旋转、轴对称等方式设计图案
用四块如图①所示的正方形卡片
拼成一个新的正方形,使拼成的图案是一个轴对称图形,请你在图②、图③、图④中各画出一种拼法(要求三种画法各不相同,且其中至少有一个既是轴对称图形,又是中心对称图形).
解:解法不唯一.例如:
方法总结:求解时只要符合题意即可,另外,在平时的学习生活中一定要留意身边的各种形状的图案,这样才能在具体求解问题时如鱼得水,一蹴而就.
三、板书设计
1.分析图案的形成过程
(1)分析构成图案的基本图形;
(2)分析图案的形成过程.
2.利用平移、旋转、轴对称等方式设计图案
教学过程中,强调学生自主探索和合作交流,经历运用平移、旋转、轴对称的组合进行简单的图案设计过程,体会图案的欣赏与设计过程.。
