计算全息实验一
光的全息实验报告

#### 实验目的1. 理解全息照相的基本原理和过程。
2. 掌握全息照相的实验技术和操作方法。
3. 通过实验观察全息图像的记录和再现,了解全息图像的特点。
#### 实验时间2023年10月25日#### 实验地点光学实验室#### 实验器材1. 防震光学平台2. 氦氖激光器3. 分束器4. 反射镜5. 扩束镜6. 载物台7. 被摄物体8. 全息干板9. 显影液10. 定影液11. 暗房设备#### 实验原理全息照相是一种利用光的干涉和衍射原理来记录和再现物体的三维图像的技术。
其基本原理是利用激光作为光源,通过分束器将激光束分为物光束和参考光束。
物光束照射到被摄物体上,反射的光波与参考光束发生干涉,产生干涉条纹。
这些干涉条纹被记录在感光材料(全息干板)上,形成全息图。
当全息图受到适当的光照射时,通过衍射原理,再现出被摄物体的三维图像。
#### 实验步骤1. 设置实验装置:将全息干板固定在载物台上,调整反射镜和分束器,使激光束能够照射到全息干板上。
2. 选择被摄物体:选择一个合适的被摄物体,如小物体或图案,确保其表面平整且具有一定的纹理。
3. 记录全息图:- 打开激光器,调整激光强度和光路,使物光束和参考光束的相对角度适中。
- 将被摄物体放置在物光束的路径上,确保物体与全息干板的距离适中。
- 按下快门,记录干涉条纹。
4. 冲洗全息干板:- 将记录有干涉条纹的全息干板放入显影液中,按照规定时间进行显影。
- 显影后,将干板放入定影液中,按照规定时间进行定影。
5. 观察再现图像:- 将定影后的全息干板置于观察位置,用激光照射全息干板。
- 通过观察,可以看到被摄物体的三维图像。
#### 实验结果与分析实验成功记录了被摄物体的全息图像,并在激光照射下成功再现了三维图像。
观察结果显示,全息图像具有以下特点:1. 立体感:全息图像具有强烈的立体感,可以从不同角度观察到被摄物体的不同侧面。
2. 细节丰富:全息图像能够记录物体的细微纹理,使得再现图像更加真实。
全息术体积和计算全息综述
kr
q1 q q2
ko.
z
R
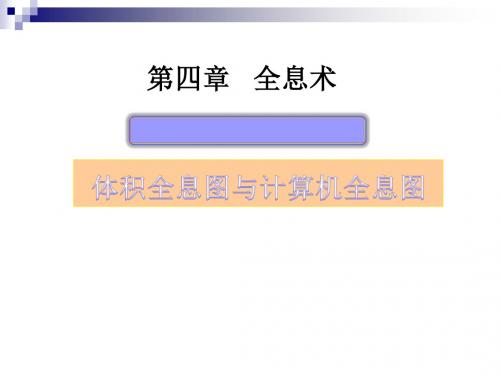
d 这是一个周期为Lkg的正弦型图样, d 形成等间距的平面族结构,其等强度面垂直于光栅矢量kg。 用感光材料将干涉图样记录下来成为厚衍射光栅, 或体全息图。
体光栅的条纹面与两束光的夹角θ 应满足关系式
x
θ = (θ
参考光在介质 内的入射角
1
- θ 2 )/2
光学全息 1.真实存在的物体 2.干涉条纹位置强度和 反衬度实现编码
计算全息 1.非物理实在的物体 2.编码方式多样
计算全息图理论基础
一般计算全息的制作过程分为五步
(1)抽样(2)计算(3)编码(4)绘制和缩小(5)再现
以下是傅里叶变换全息图的制作流程
数学函数
抽样得离散 样点分布
离散傅里叶变换
离散傅里叶变 换谱
1.2、体积全息图:再现条件
再现时,把条纹面看作反射镜面,则只有当相邻条纹面的 反射光均满足同相相加的条件(光程差等于一个波长)时, 才能使衍射光达到极强——布拉格条件。 单个条纹面上的衍射主极大出现在反射方向
2Λ sinf =λc
再现光与条纹 平面的夹角
布拉格条件 再现光在介质 内的波长
f
L
2Λ sinθ = λ
物光在介质 内的入射角
O
L
q1 q q2
z
kg
体光栅常数Λ 满足关系式: 2Λ sinθ = λ 记录光波在介 质内的波长
R d d
记录光与条纹平面的夹角
体光栅常数Λ 满足关系式:
2Λ sinθ = λ
参考波指向z方向,而物波与z轴夹角为2q
x
z
q
L d
kg
实验报告 全息术

实验报告勾天杭 pb05210273题目:全息光栅,三维全息目的:初步了解全息术的基本原理,并拍摄物体的三维全息图和制作全息光栅。
原理:预习报告和下面思考题(二)已述,不再重复思考题:一 把拍摄好的全息光栅用一束细光束垂直入射,测出L,x,计算光栅常数d 及两光束夹角φ并与测量值比较6328A λ= ,并测得/2 6.9x cm = 15.1L cm = 28ϕ=︒由光栅方程 sin d m θλ= (此处m=1)及sin θ=求得光栅常数 1.52d m μ= 由12sin (/2)242sin 2d d λϕλϕ-=⇒==︒测量值与计算值有一些偏差.因为我们拍出来的光栅不太好,只能同时看到两个点(+1和-1级不同时出现, 得把干板稍微转一个小角度才能看到+1或-1级光点),零级亮斑的光强也比较弱.所以只测量了1级光点与零级光点的距离,记为x/2.这可能会给光栅常数的计算带来误差,导致算出来的φ与测出来的φ有差距.二 简述全息术的两步成像方法,利用什么原理实现1.波前记录(双光束干涉)双光束干涉原理表明,干涉光强分布包含着干涉光束的振幅信息和位相信息,这就构成波前记录的基础. 从双光束干涉到全息记录,只需在干涉光束中用物光束替换其中的一束光. 全息干板上记录到的就是物光束O 与参考光束R 的双光束干涉条纹. 曝光后的全息干板经显影、定影处理,成为一张记录着干涉条纹的干板,称为全息图或全息照片. 这样以干涉条纹的形式记录了物光相对于参考光的振幅分布和位相分布,振幅分布表现为条纹的衬比度,位相分布表现为条纹的位置、形状和疏密.波前记录称得上是用参考光波对物光波进行的编码记录,在同一张全息干板上,就可以用不同的编码实现对不同波前的记录,这就是波前记录的多重性.考虑通常全息记录的是来自同一光源的相干波的干涉, 物体发出(透射或散射) 的光波即物光波在记录面上的光场分布为00(,)(,)exp[(,)]O x y O x y i x y =Φ,参考光在此平面上的光场分布为0(,)(,)exp[(,)]R R x y R x y i x y =Φ,记录面上某点记录的光强为)cos(2****)*)((0002020R R O R O RO OR RR OO R O R O I Φ-Φ++=+++=++=上述光强分布表明,波前记录面上每一点的光强依赖于物光波的振幅和位相, 即波前记录面上每一个点域均记录着物光波前的全部信息.在线性记录的条件下, tI H H ββββτ+=+=00t 为曝光时间,I 为总光强,β0和β为常数。
12计算全息

J −1 2
K −1 2
m、n、j、k均取值为 的幂,采用快速傅立叶变换可大大缩短计算时间。 、 、 、 均取值为 的幂,采用快速傅立叶变换可大大缩短计算时间。 均取值为2的幂 提取计算出来的F(m,n)的振幅 的振幅A(m,n)和相位Φ(m,n), 和相位Φ 提取计算出来的 的振幅 和相位 , 如果在MATLAB软件中,可以用函数库中的函数直接计算振幅和相位: 软件中,可以用函数库中的函数直接计算振幅和相位: 如果在 软件中
物光波和参考光波产生干涉条纹, 物光波和参考光波产生干涉条纹,其强度分布为
I ( x , y ) = f ( x , y ) + R( x , y )
线性记录条件下, 线性记录条件下,忽略常数因子
2
β ,τ
等,全息图的透过率函数为
2
= R 2 + A 2 ( x , y ) + 2 RA( x , y ) cos[2παx − φ ( x , y )]
π 3 3 各部分的相位分别 0, , π (− π ), π − π 2 2 . 2 是
x
全息图上待记录的一个样点的复振幅分布可以分解为4个正交分量 全息图上待记录的一个样点的复振幅分布可以分解为 个正交分量: 个正交分量
f (m , n ) = f1 (m , n )r + + f 2 (m , n ) j + + f 3 (m , n )r − + f 4 (m , n ) j −
δx
δyBiblioteka 11 21 31 4112 22 32 42
13 23 33 43
14 24 34 44
左图是第mn单元的编码 左图是第 单元的编码. 单元的编码
第6章 计算全息

b(
x x
)com
b(
y y
)
F
(
,
)
xycomb(x )comb(y) F( ,)
( n , m ) F ( ,)
n m
x y
F ( n , m )
n m
x y
它是由 函数的阵列构成
fs
(
x,
y)
comb(
x x
)comb(
y y
)
f
(
x,Βιβλιοθήκη y) x y f (n x, m y) ( x n x, y m y) n m
§6-1计算全息原理
利用卷积定理得抽样函数的频谱
Fs ( ,)
com
计算全息的主要应用范围:
① 二维和三维物体像的显示
② 在光学信息处理中用计算全息制作各种空间滤波器
③产生特定波面用于全息干涉计量 ④ 激光扫描器 ⑤ 数据存贮
计算全息图的制作和再现过程的主要步骤:
① 抽样:得到物体或波面在离散样点上的值 ② 计算:计算物光波在全息平面上的光场分布 ③ 编码:把全息平面上光波的复振幅分布编码成全息图的透过率
第六章 计算全息
第六章 计算全息
概述
什么叫计算全息
借助参考光,利用光的干涉原理,可以将物光的复振幅 (振幅和相位)以干涉条纹的形式记录下来。我们可以称之 为光学编码的方法。
如果不用光学的方法而是用人工的方法进行编码制作全息 图,这就是计算全息图(Computer-generated Hologram)。
11
x 2 x
空间域 的抽样间隔是 x 和 y ,空间频谱被重复的频谱中
实验数字全息及实时光学再现实验

无透镜傅里叶变换全息的优点 记录光路结构简单; 能够充分利用CCD的有限带宽 ; 允许的最小记录距离与被测量物体的大小成正比; 强度再现像准确、重建速度快;
实验内容与步骤
本实验系统对全息技术做出了全面地展示,具体有一定前沿性和综合性。如果 从全息角度区分,实验内容包括计算机模拟全息、数字全息、可视数字全息、 实时传统全息。如果从记录方式和光学再现方式的角度区分,实验内容可分为 数字记录,数字再现;光学记录,数字再现;数字记录,光学再现;光学记录 、光学再现。图—给出了实验内容的整体规划示意图。
北京工大
实验目的
1、 理解数字记录、光学记录、数字再现、光学实时再现 2、 理解计算模拟全息原理,实现数字记录,数字再现 3、 理解可视数字全息原理,在空间光调制器上加载计算模拟全 息图,利用再现光路恢复物信息,实现数字记录,光学再现 4、 理解实时传统全息实验原理,了解与传统全息之间的异同, 通过空间光调制器再现全息图,完成光学记录,光学再现 5、 探究数字全息在测量方面的应用
实共轭像复振幅
u1(xi ,
yi
)
exp
jk
2
z0
( xi
xr
)2
( yi
yr
)2
J1(xi ,
yi )
J1(xi , yi )
O ( fx ,
jk
f
y
)
R0
exp
2
z0
( xr2
yr2
)
exp
jk z0
O (
fx,
f y )R0
计算全息图的制作及数字再现

计算全息图的制作及其数字再现物理科学与工程技术学院作者姓名:杨煦、杨康明指导老师:蔡志岗教授摘要:计算机制全息图是制作全息图的一种新技术,它是利用数字计算机来综合的全息图,它不需要物体的实际存在,而是把物波的数学描述输入计算机处理后,控制绘图仪输出或显示器显示二制成的全息图。
计算全息图的数字再现是利用计算机模拟光学全息的光路,仿真菲涅尔衍射、透镜傅里叶变换等光学过程从而在虚拟的观察屏上得到全息再现像。
关键词:计算全息数字再现一、引言:早在1965年,Kozman和Kelly就提出了计算机生成全息图(Computer Generated Holography,简称CGH)的概念,那时受计算机速度、容量和显示器分辨率等因素的约束,直到80年代中期以前计算机全息图的研究一直未取得大的进展。
国内对全息技术的研究主要集中在物理光学领域。
而目前由于计算机技术的发展以及计算机硬件的进步,已经可以制作空间带宽积很大的计算全息图,但是由于输出设备的精度问题,难以制作质量很高的全息图。
因此我们将以此为研究重点,希望从编码方法上有所突破,解决这个问题。
二、实验原理计算全息图的制作和再现过程主要分为以下几个步骤:1、抽样,得到物体或波面在离散样点上的值;2、计算,计算物光波在全息平面上的光场分布;3、编码,把全息平面上光波的复振幅分布编码成为全息图的透过率变化;4、成图,在计算机控制下,将全息图的透过率变化绘制成图,如果绘图设备分辨率不够,则绘制一个较大的图,再缩版到得到使用的全息图;5、再现,这一步骤与光学全息图的再现没有什么区别。
制作一个傅立叶变换全息图的典型流程如下:(一)、抽样抽样包括对输入图像的抽样和对全息图的抽样。
实际上,输入图像和全息图像的信号都是连续的。
而计算机只能对离散的数据进行处理,所以必须对物光和全息图像进行离散化,即抽样处理。
由空间带宽积的传递不变性可以知道,在全息图平面上的空间带宽积SW 应该和物体的空间带宽积SW 相等。
第六章计算全息(1)教材

6·1·4时域信号和空域信号的调制与解调
在第五章我们已经知道,在光学全息中, 由于记录介质只能记录光场强度分布, 对波前(复振幅分布)的记录必须通过 与参考光干涉形成干涉花样(强度分布) 才有可能。再现过程中,通过照明光照 射全息图产生的衍射效应,又将干涉花 样(强度分布)还原成所需要的波前 (复振幅分布)。
例如:连续函数f(t)和序列f(n)之间满足:
直观上,抽样间隔越小,则抽样序列越 准确地反映原来的连续函数,但是抽样 间隔越小,对于信息检测、传送、存贮 和处理都提出了更高的要求。
问题:那么如何选择一个合理的抽样间 隔,以便做到既不丢失信息,又不对检 测、处理等过程提出过分的要求,并由 这样的抽样值恢复一个连续函数呢?
通常
称为奈魁斯特(Nyquist)间隔,
奈魁斯特抽样定理又可表述为:
一个有限带宽的函数,它没有频率在Bx和By以 上的频谱分量,则该函数可以由一系列间隔小
于
的抽样值唯一地确定。
2·函数的复原
将抽样函数作为输入,加到一个低通滤波器上, 只要抽样函数的频谱不产生混叠,总可以选择 一个适当的滤波函数,使 的项无畸变通过,而滤除其它各项,这时滤波 器的输出就是复原的原函数。
6·1 计算全息的理论基础
6·1·1概述 光学全息图是直接用光学干涉法在记录介质上记
录物光波和参考光波叠加后形成的干涉图样。 假如物体并不存在,而只知道光波的数学描述,
也可以利用电子计算机,并通过计算机控制绘图仪 或其它记录装置(例如阴极射线管、电子束扫描器 等)将模拟的干涉图样绘制和复制在透明胶片上, 这种计算机合成的全息图称为计算全息图。
全息光学实验

空间滤波一、实验目的1.观察各种光栅、图片的付里叶频谱,加深对频谱概念的理解.2.由观察到的频谱判断输入图像的根本特征,理解物分布与其频谱函数间的对应关系,进而了解频谱分析的根本原理、方法与各种应用。
3.掌握空间滤波的根本原理,理解成像过程中“分频〞与“合成〞作用4. 掌握方向滤波、高通滤波、低通滤波等滤波技术,观察各种滤波器产生的滤波效果,加深对光学信息处理实质的认识.二、实验原理1、付立叶频谱。
设二维函数g(x,y),其空间频谱G(ξ,η)为g(x,y)的付里叶变换,即而g〔x, y〕如此为G(ξ,η)的傅立叶逆变换,即用光学的方法可以很方便地获得二维图像g(x,y)的空间频谱G(ξ,η).只要在一付里叶透镜的前焦面上放置一幅透射率为g(x,y)的图像,并以相干平行光束垂直照射图像,如此根据透镜的付里叶变换性质,在透镜后焦面上得到的光复振幅分布将是g(x,y)的付里叶变换G(ξ,η),即空间频谱G(x f/λf,y f/λf).其中λ为光波波长,f为透镜焦距,x f、y f为后焦面(即频谱面)上任意一点的位置坐标.显然.点(x f,y f)对应的空间频率为因此,在后焦面上放置毛玻璃屏,在其后通过放大镜观察频谱,或者在后焦面上放置全息干板将频谱记录下来,如果有条件,在后焦面上装置电视摄像机,并将其与电视显示器联结,在荧光屏上就可显示出图像的付里叶频谱。
如果输入图像很小,衍射屏幕和图像之间距离很远,如此在近似满足夫琅和费条件下,也可以不用透镜而直接在屏幕上得到图像的空间频谱G(x f/λz,y f/λz),其中z为图像至屏幕的距离。
由于频谱面上的频谱函数G(ξ,η)是物函数g〔x,y)的付里叶变换,因而从实验上得到频谱函数G(ξ,η)后.即可反过来求出图像的复振幅分布g(x,y)。
据此,对图像进展简单分类.也可用于分析图像的结构比如在森林资源的考察中,根据图像的频谱可以判断哪些地区已绿化,哪些目前还是荒地,以利更好地规划.2、空间滤波空间滤波是光学信息处理的一种重要技术。
XXGX第6章 计算全息

看看一维信号的例子对函数f (x ,y )进行傅立叶变换:(,)(,)f x y F u v →:2Bu 带宽为对抽样函数做傅立叶变换:(,)(,)s s f x y F u v →(,){(,)}(,)s s n m n mF u v f x y F u v x y ∞∞=−∞=−∞==−−ΔΔ∑∑F 函数在空间域被抽样,导致函数频谱F (u ,v )在空间频域的周期复现,频谱F (u ,v )的中心间隔为1/,1/x yΔΔ假定f (x ,y )是有限带宽函数,频谱在空间频域的一个有限区间上不为零,假设2Bx 和2B y 是这个有限区域在u ,v 方向上的宽度,即:(,){(,)}0F u v f x y ⎧=⎨⎩F ,x x y yB u B B v B −≤≤−≤≤这样就能用滤波的方法,分离出F (u ,v ),进而恢复出原函数二、函数的复原:只要抽样时满足抽样定理,其抽样后的函数fs (x,y)的频谱F s(u,v)就不会交叠,就可以选择一个合适的低通滤波器(如矩形函数),通过滤波操作、再经逆傅立叶变换复原原函数f(x,y)。
脉冲幅度调制(PAM)脉冲宽度调制(PWM)脉冲位置调制(PPM)二值化,具有很强的抗干扰和抗噪声能力。
事实上、3π/2,与复平面上的实轴和虚轴所表示的在复平面上,可用四个基矢表示一个复矢量uu vvf1、f2和f3是实非负数将每一个抽样单元沿应在小单元中用开孔大小或灰度等级来表示振幅(b) 物光波的频谱(,){(,)}=FF u v f x yα≥u6.3 计算傅立叶变换全息制作过程:6.3 计算傅立叶变换全息1 26.3.1 抽样包含对物波函数和全息图的抽样物面的抽样点数:f ( x, y ) = a ( x, y ) exp[ jφ ( x, y )],X ,Y需要:δ x ≤1 1 ,δ y ≤ 2uB 2v BF (u , v) = A(u, v) exp[ jψ (u , v)], uB , vB ; 2u B , 2vB所需抽样点数为:J K =频谱面的抽样点数:需要:δ u ≤ 1 1 ,δ v ≤ X YX Yδxδy= XY 2u B 2vB = SW所需抽样点数为:M N =(a) 物光波函数 抽样:确定物面和频谱面上的抽样点数32u B 2vB = XY 2uB 2vB = SW δu δv(b) 物光波的频谱函数F (u , v) = F { f ( x, y )}可见:都刚好满足抽样定理时,物面和谱面的抽样点数相等,都 等于空间带宽积。
CGH计算全息

信息光学课程设计报告题目:基于迂回相位编码的CGH及其实现专业班级:时间:组员:指导教师:完成日期:基于迂回相位编码的CGH及其实现摘要计算全息作为一种灵活的、全新的全息方式已经得到了极为广泛的研究和发展,在诸多的领域中都有广泛的应用。
计算全息是将通信编码技术引入到光学全息中,利用计算的方法对物光的复振幅进行编码,实现全息的制作。
光学全息采用干涉的方法,将复振幅的相位信息编码为干涉光场光强的分布,实现复函数到实函数的转换。
计算全息则采用编码的方式将复函数转换为实函数。
编码的方法有两种,一种是利用二维脉冲编码方式分别对振幅和相位进行编码,得到两个实函数;另一种则是仿照光学全息,引入离轴参考光,计算干涉光场的强度分布,再记录该光场达到转换的目的。
我们这里采用的第一种方式。
首先对待记录的图像进行傅立叶变换,再利用迂回相位编码法分别对振幅和相位进行编码,得到二元的二维全息图。
模拟再现时则仿照光学全息再现,对全息图进行傅立叶逆变换,得到再现图像。
关键词:计算全息光学全息编码Detour phase encoding and its implementation based CGHAbstract:new holographic approach has been very extensive research and development in many fields have a wide range of applications. CGH is a communication coding technology into optical holography, using the method of calculation of the complex amplitude of the object beam is encoded achieve holographic production. Optical holographic interferometry method using the phase information coding for the complex amplitude of the interference field intensity distribution of light to achieve a complex function to convert real function. CGH coding method is used to convert the complex function of a real function. Coding methods are two, one is the use of two-dimensional coding scheme pulse amplitude and phase respectively encode get two real functions; another is modeled optical holography, off-axis reference beam is introduced to calculate the interference light field intensity distribution, and then record the light field to achieve conversion purposes.The first way we used here. Treatment of the image recording of the first Fourier transform, and then use the detour phase coding method, respectively, the amplitude and phase encoding to obtain a binary two-dimensional hologram. The modeled analog reproducing optical holographic reproduction of hologram inverse Fourier transform to obtain a reproduced image.Key word: solography Computer-Generated Hologram coding1引言本设计目的在于帮助掌握光学全息记录及再现原理,掌握CGH的编码方法和实现过程。
激光全息实验

Two-Step Rainbow Holography 二步彩虹全息
第二步
制作彩虹全息图 H2 以 H1的共轭实像为“物”,
通过狭缝 S 记录彩虹全息图 H2
记录
H2
S
R1*
O’
R2
H1
再现
彩虹全息图的单色光再现
Two-Step Rainbow Holography 二步彩虹全息
用单色光再现(共轭光)
• 调整M2的位置,使参考光程和物光光程相 等。
• 参考光与物光的光强比在3:1—6:1间选择。
(3)关闭光开关,在干板架上放上全息干板, 稳定1min后利用曝光定时器控制光开关曝 光。
(4)将曝光后的全息干板在暗示进行常规的 显影、定影、水洗、干燥等处理,得一张 一张彩虹全息图。
(5)用白光源再现彩虹全息像,照明方向与 原参考光的方向一致,沿水平方向改变观 察位置,全息像的颜色将变化。垂直方向 改变观察位置,全息像将有立体感。
全反镜
物光
光程差=物光程-参考光程 物 体 全息干板
(3)使物光和参考光的光程大致相等
(4)调节物体位置,使物光和参考光的夹 角在30o~60o之间。
θ
θ=30o ~60o
移 动 物 体
(5)调节参考光与物光在全息干 版上照度比为3:1~7:1。
2、曝光
(1)遮光 (2)在盒中取出全息干(注意不要曝光)
(3)取下白屏换上全息干版,注意药膜面对着光。
(4)安静等待1到2分钟,等到整个系统稳定后,打 开曝光计时器开关进行曝光,曝光时间为数秒。
3、全息干版的冲洗
在照相暗室中,可在暗绿灯下操 作,整个过程不能用手触摸全息干版 的表面。
显影液
实验一全息照相

实验一 全息照相[实验目的]了解全息照相的基本原理,学习拍摄全息图与再现立体图像的方法。
[实验原理]全息照相是一种新型的照相技术。
早在1948 年伽柏(D . Gabor )就提出了全息原理。
60 年代初激光的发明使全息技术得到迅速的发展,并在许多领域得到了广泛的应用。
无论从基木原理上,还是从拍摄和观察方法上,全息照相与普通照相都有本质的区别。
普通照相基于几何光学的透镜成像原理,它所记录的是物通过透镜成像后,像平面上的光强分布,而失掉了光波的另一个信息——位相,因而只能呈现一个平面图像,而失去了立体感。
全息照相是基于干涉、衍射的原理。
它的关键是引入一束相干的参考光波,使其和来自物体的物光波在个全息干板处相干涉,底片上以干涉条纹的形式记录下物光波的全部信息—— 强度和位相,这就是全息照相名称的由来。
经过显影定影等暗室处理后,底片上形成明暗相间的复杂的干涉条纹,这就是全息图。
若用与参考光相同的光束以同样的角度照射全息图,全息、图上密密的干涉条纹相当于一块复杂的光栅,在光栅的衍射光中,会出现原来的物光波,能形成原物体的立体像。
因此,全息照像可分为全息记录和波前重现两个基本过程,它们的本质就是干涉和衍射。
(一).投射式全息照相透射式全息照相是指重现时所观察的是全息图透射光的成像。
下面对平面全息图的情况做具体的数学描述。
1.全息记录 设来自物体的单色光波在全息干板平面(平面)上的复振幅分布为:称为物光波。
同一波长的参考光波在于平板平面上的复振幅分布为:称为参考光波。
平板上总的复振幅分布为:干板上的光强分布为:适当控制曝光量和冲洗条件,可以使全息图的振幅透过率t ( x , y )与曝光量E (与光强I 成正比)成线性关系,α,β为常数。
这就是全息图的记录过程。
由上面的描述可知,底片上干涉条纹的反衬度为:干涉条纹的间距则决定于(ΨR -ΨO )随位置变化的快慢。
对一定的ΨR ,АR 来说,干涉条纹的明暗对比反映了物光波的振幅大小,即强度因子,干涉条纹的形状间隔反映了物光波的位相分布。
全息术实验报告

4+4+全息术By 金秀儒物理三班Pb052062182. 波前再现设再现用的照相光波在Oxy 平面上的分布为此再现光波经过全息图后衍射波的复振幅分布为考察式第二项(由于第一项较小,大多数情况下可以忽略),可以认为:为全息照相的基本公式,式中第一项代表直射光,第二项代表原始像,第三项代表共轭像。
对有许多物点组成的物体,式(9)中...321+++=O O O O ,所以容易知道这叫做晕轮光,当物体较小时它的空间频率不高,在拍摄全息图时,取稍大一些的参考光与物光的夹角就可以避开它的影响,观察到清晰的原始图。
原始数据记录:布置好光路,并在干板上曝光进行冲洗后进行重现,可以看到明亮的小鸡的虚像,但实验中并没有观察到明显的实像…34.29’球面光波都照亮整个底片并且与参考光波在整个底片上发生干涉,因此整个底片上都留下了该物点的全部信息。
所以,任意一小块都能再现处全息像。
另一方面,当然由于受光面积减小,相应的,成像光束强度减弱,成像的衬比度下降,还会引起色差、像差,致使再现的画质下降。
4. 分析两次实验拍摄的结果。
答:1、全息光栅:在布置光路时,我们采用了很对称的分布使得50%的分束镜恰好平分到达干板的两束光,ϕ);同时测量两支光路的距离是光程差尽量小;这样为了是干涉条纹有较好(其夹角为=35.0的衬比度;但由于实验中激光器不稳定,(尤其在拍摄时有闪烁),加之透镜表面可能不大干净(建议实验室定期擦一下),影响了拍摄的效果;冲洗时,定影之后没有在水里冲洗,致使难以吹干,底片上留有颗粒;,这与实验中拿量角器在实验中测得L=20.00cm,x=14.60cm,由此计算出=34.29粗测结果35.0大致相等。
2、三维全息:本次实验注意了上次没有注意的地方,以及老师强调的内容;因此实验结果好于前一次,实验中可以看到比较清晰的虚像;但并没有观察到实像,分析原因,一方面是由于实验中的参考光较强而物光相对较弱,另一方面是由于激光器仍旧不稳定。
全息术体积和计算全息
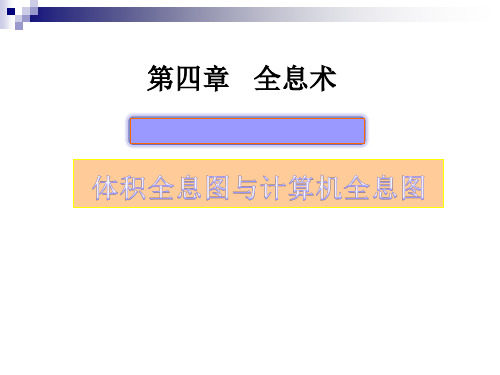
1.1、体积全息图的记录
在相对厚的介质中记录的全息图
简单情形: 物波和参考波是波矢量为ko和kr的平面波, x L 记录介质的前后两表面是z = 0和 z =d
干涉图样是x, y和z的函数: I(x, y, z) = | Ir1/2exp(j kr.r) + Io1/2exp(j ko.r)|2 = Ir+ Io+ 2(IrIo) 1/2cos(ko.r - kr.r) = Ir+ Io+ 2(IrIo) 1/2cos(kg.r) 式中kg = kr - ko.
物光在介质 内的入射角
O
L
q1 q q2
z
kg
体光栅常数Λ 满足关系式: 2Λ sinθ = λ 记录光波在介 质内的波长
R d d
记录光与条纹平面的夹角
体光栅常数Λ 满足关系式:
2Λ sinθ = λ
参考波指向z方向,而物波与z轴夹角为2q
x
z
2q
L d
kg
kr
q q
ko
kg=2ksinq
O kg
kr
q1 q q2
ko.
z
R
d 这是一个周期为L2kg的正弦型图样, d 形成等间距的平面族结构,其等强度面垂直于光栅矢量kg。 用感光材料将干涉图样记录下来成为厚衍射光栅, 或体全息图。
体光栅的条纹面与两束光的夹角θ 应满足关系式
x
θ = (θ
参考光在介质 内的入射角
1
- θ 2 )/2
参考波照明全息图,被厚全息图布拉格反射 再现出物波
体积全息图可以用白光再现吗?为什么?
布喇格条件保证了体积全息图的波长选择性; 尽管记录过程必须用单色光完成,再现却可以用白光
计算全息

计算全息图的制作步骤
对物光信息的采集:对于实际存在的物体,可利用激 对物光信息的采集 光扫描仪或数字摄像机进行数据采集。而对于那些实 际不存在的物体,可将其函数形式直接输入计算机 处理:用抽样定理将物函数离散化,取抽样单元数不 处理 超过物的空间带宽积,计算物波在全息平面上的光场 分布 编码:将所得的光场分布编码成全息图的透过率变化 编码 存储:用计算机绘图仪直接画在纸上,然后用精密照 存储 相翻拍在照相底片上,适当放大或缩小到合适的尺寸
罗曼型计算全息图的制作及再 现
在全息图的抽样单元中放置一个矩形通光孔径,矩形孔的宽度形取为定值(一般 取抽样单元宽度的一半),波面中的幅值通过矩形孔的高度进行调制(相当于改变 矩形孔的面积),波面的位相通过改变矩形孔中心距抽样单元中心的位置来调制。 选择的编码参数为: 矩孔高度: 矩孔中心偏离距抽样单元中心距离:
物信息的采集
物光信息的采集是指确定物光信息的函数形式,一般表现为复振幅 透射率函数(或反射率函数) 对于实际存在的物体,可利用激光扫描仪或数字摄像机进行采集 对于那些实际不存在的物体,可将其函数形式直接输入计算机 物函数需要离散化,一般取抽样单元数不超过物的空间带宽积,即 满足关系式 M·N ≤ Δx·Δy·Δfx·Δfy 式中M、N分别为X方向和Y方向的抽样单元数,Δx和Δy为物体的空 间宽度,Δfx和Δfy为物的频带宽度
谢谢各位老师!
迂回位相效应
在 衍射角方向上相邻光线的光程差为 当光栅某一部分的栅距有一错位量P时,则 栅距由d变为d+p,这时,栅距加大处 的衍射光波光程差变为:
故在衍射方向上的平面波分量将会产生如下的延迟量:
相应的位相延迟为:
迂回相位效应的讨论
由上式可以看出,迂回位相值和入射波的倾斜角度和入射波的波长无关, 但和错位量P成正比,只要连续改变P值的大小,就可在特定的衍射方向 上得到连续的位相变化。 用迂回位相效应对复数物函数的位相进行编码,制成迂回位相型计算全 息图。从物理光学的角度看,一张全息图由很多抽样单元组成,每个单 元中有错位量不同的矩形开孔,这就是一个不规则光栅。在观察全息图 的再现时,在某个特定的衍射级上,就可以得到我们所需要的相位移。
第六章 计算全息(2-3)

这一过程是采用计算机,并基于快速傅 里叶变换算法(FFT)完成的.对于连续函 数的傅里叶变换可表示为
而计算机完成傅里叶变换必须采用离散 傅里时变换的形式,二维序列f(j,k)的 离散傅里叶变换定义为
直接用上面公式作二维离散傅里叶变换, 涉及极大的计算量,1965年库列-图基 (Cooley-Tukey)提出矩阵分解的新算法, 也就是快速傅里叶变换算法,大大缩短 了计算时间,才使二维图形的离散傅里 叶变换在实际上成为可能。 F(m,n)通常是复数,记为 式中:
于是总的抽样点数就降低为原来的1/4,这时 计算全息图的频谱如图6.2.5(e)所示。 应该指出,载频在全息图上的表现形式是余弦 型条纹的间距,这与光学全息是相同的,但光 学离轴全息函数与我们所构造的全息函数的频 域结构不同,因此载频也不同.选取载频的目 的是保证全息函数在频域个各结构分量不混 叠.对全息函数进行抽样是制作计算全息的要 求,抽样间隔必须保证全息函数的整体频谱 (包含各个结构分量)不混叠,这两个概念不可 混淆.
在这种全息图中,被记录的复数波面是物波函 数的傅里叶变换.由于这种全息图再现的是物 波函数的傅里叶谱,所以要得到物波函数本身, 必须通过变换透镜再进行一次逆变换,这与光 学傅里叶变换全息图的基本原理是一致的.对 复数波面进行编码可以采用上节介绍的两种方 法.一种是迂回相位编码方法,直接对抽样点 上复数波面的振幅和相位进行编码。另一种是 修正离轴参考光编码方法,将全息函数造成实 的非负函数.从而只对振幅进行编码.
图6.3.1(a)是迂回相位编码的计算傅里叶变换 全息图的原图
6· 3· 5 再现
计算全息的再现方法与光学全息相似,仅在某 个特定的衍射级次上才能再现我们所期望的波 前.图6.3.2是计算傅里叶变换全息图的再 现光路,当用平行光垂直照明全息图时,在透 射光场中沿某一特定衍射方向的分量波将再现 物光波的傅里叶变换,而直接透过分量具有平 面波前,并且另一侧的衍射分量将再现物谱的 共轭光波.于是经透镜L进行逆傅里叶变换后, 输出平面中心是一个亮点,两边是正、负一级 像和高级次的像,如图6.3.1(b)所示.
计算全息实验一

1、实验目的:
1. 2. 通过设计制作一计算全息图、利用高分辨液晶空间光调制器(LCD)实时再现 该计算全息图、观察再现结果、并利用 CCD 记录再现像等实验内容; 掌握计算全息图的编码原理,加深对光全息原理, 光的干涉和衍射特性的 认识; 训练使用空间滤波器、空间光调制器(LCD) 、CCD 图像采集等重要 的现代光学实验装置进行数字光学实验的能力。 同时初步了解 Matlab 语言在光学中的应用。
(1)
其傅里叶变换(空间频谱)为
F (u, v ) = A(u, v ) exp[iφ (u, v )] ,
(2)
为满足抽样定理 (见附录) 的要求, 物波函数及其空间频谱函数必须是带限函数, 即
f ( x, y ) = 0 F ( u, v ) = 0 x ≥ u≥
∆x 2 ∆u 2
, ,
y ≥ v ≥
实验过程中要切记以上注意事项。如 有违犯,将严重影响你的实验成绩!
1 鲁东大学物理与光电工程学院 朱林伟---内部资料禁止外传
2015 年光电信息科学与工程专业综合实验-信息光学专题实验
ቤተ መጻሕፍቲ ባይዱ计算全息(一) 罗曼迂回相位编码与李氏四阶迂回相位编码
计算全息是利用计算机设计制作全息图或衍射光学元件的技术。从原理上, 计算全息和光学全息没有什么本质差别,所不同的是产生全息图的方法。光学全 息是直接利用光的干涉特性, 通过物波和一束相干参考波的干涉将物波的振幅和 位相信息转化成一幅干涉条纹的强度分布图,即全息图。光学全息记录的物体必 须是实际存在的。 而计算全息则是利用计算机程序对被记录物波的数学描述或离 散数据进行处理,形成一种可以光学再现的编码图案,即计算全息图。他不需要 被记录物体的实际存在。由于计算全息图编码的多样性和波面变换的灵活性,以 及近年来计算机技术的飞速发展,计算全息技术已经在三维显示、图像识别、干 涉计量、激光扫描、激光束整形等研究领域得到应用。最近计算全息领域的新进 展是利用高分辨位相空间光调制器实现了计算全息图的实时再现, 这种实时动态 计算全息技术已经在原子光学、光学微操纵、微加工、软物质自组织过程的控制 等领域得到成功的应用,显示了计算全息技术的巨大应用发展前景。 计算全息除了其在工业和科学研究方面的应用价值, 也是一个非常好的教学 工具。要做好一个计算全息图,既要熟悉衍射光学、光全息学等物理知识,还要 了解抽样理论、快速傅里叶变换、调制技术和计算机编程方面的知识。这些知识 对于物理类和光电信息技术类专业的学生和研究人员都是不可缺少的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d
图2
4 鲁东大学物理与光电工程学院 朱林伟---内部资料禁止外传
2015 年光电信息科学与工程专业综合实验-信息光学专题实验
如图 2 所示,当用一束平面波垂直照明一栅距 d 恒定的平面光栅时,产生 的各级衍射光仍为平面波,等相位面为垂直于相应衍射方向的平面。根据光栅方 程,光栅的任意两条相邻狭缝在第 K 级衍射方向的光程差为 2π (8) = ∆ϕ = d sin θ k 2π K , 是等相位的。如果某一点的狭缝位置有偏差,如栅距增大了 Δ,则该处在第 K 级 ′ ( d + ∆ )sin θ K ,从而导致一附加相移: 衍射方向的衍射光的光程差变为 L= ∆ 2π φ K = ∆ sin θ K = 2π K 。 λ d
3.
2、实验原理
本实验以经典的迂回相位型计算全息图设计制作过程为例, 介绍计算全息的 基本原理。一般说来,计算全息图的制作大致可分成下述五个步骤: 1.选择物体或波面,给初其数学描述或离散数据。 2.计算物波在全息图面上的光场分布。 3.把上述光场分布编码成全息图的透过率变化。 4.输出:光学缩版或微加工。 5.光学再现。
物体 抽样 离散物 函数 计算 傅立叶 频谱 编码 再现像 光学再现 CGH 输出 CGH 原 图
ห้องสมุดไป่ตู้
图1
2.1 物面和全息图面的抽样 数字计算机通常只能对离散的数字信号进行处理,并以离散的形式输出。因 此,制作计算全息图的第一步是对物波函数进行抽样。设待记录的物波函数为
f ( x, y ) = a ( x, y ) exp[iϕ ( x, y )] ,
FFT → = f ( m, n ) F ( j, k ) Fr ( j, k ) + iFi ( j, k ) ,
(6)
其振幅和位相可分别表示为:
A( j, k ) = Fr2 ( j, k ) + Fi 2 ( j, k ),
φ ( j, k ) = tan −1 ( i
F ( j, k ) ). Fr ( j, k )
(13)
f1
f2
f3
f4
图4
把全息图上每个抽样单元细分为四个子单元 , 并使他们的透过率或开孔面 积分别正比于 f1 、 f 2 、 f3 和 f 4 ,如图 4 所示。由于 4 个子单元的相对位移产生 的迂回相位刚好依次为 0、 exp(iπ / 2) 、 exp(iπ ) 和 exp(i3π / 2) ,因此该单元的+1 级衍射光的复振幅刚好就是(16)式所表示的物波在该抽样点的复振幅。
6 鲁东大学物理与光电工程学院 朱林伟---内部资料禁止外传
(7)
2.3 编码 编码的目的就是将计算出的全息图面上的复振幅函数转化成实值函数。从编 码函数构造的角度来说,计算全息技术主要有两大类:纯计算编码型和光学模拟 型。二者的主要差别是,前者的编码函数是人为构造出来的,后经数学证明和实 验验证,可以再现物光。因此这一类全息图是计算全息术所特有的,没有传统的 光学全息图与之对应。而后者呢,顾名思义,其编码函数是在研究传统光学全息 图透过率函数的基础之上构建起来的, 可以说是用计算机来模拟光学记录过程绘 制全息图。当然,这不是简单地模拟,而是以原全息图透过率函数为出发点,仔 细研究其物理数学本质,进而构造出既便于计算处理又不损失信息的编码函数。 下面首先介绍 Lohmann 等人提出的迂回相位型计算全息图的编码方法。 2.3.1 Lohmann 型二元迂回相位编码 一般说来,对于光波的振幅进行编码比较容易,例如可以通过控制全息图上 抽样单元的透过率或开孔大小来实现。但是,对于光场的相位信息进行编码则相 对比较困难。 虽然从原理上可以通过改变抽样单元的厚度或折射率来实现相位调 制,但实际制作非常困难。美国科学家 Lohmann(1966 年)巧妙的利用了不规 则光栅的衍射效应,提出了迂回相位编码方法。
实验过程中要切记以上注意事项。如 有违犯,将严重影响你的实验成绩!
1 鲁东大学物理与光电工程学院 朱林伟---内部资料禁止外传
2015 年光电信息科学与工程专业综合实验-信息光学专题实验
计算全息(一) 罗曼迂回相位编码与李氏四阶迂回相位编码
计算全息是利用计算机设计制作全息图或衍射光学元件的技术。从原理上, 计算全息和光学全息没有什么本质差别,所不同的是产生全息图的方法。光学全 息是直接利用光的干涉特性, 通过物波和一束相干参考波的干涉将物波的振幅和 位相信息转化成一幅干涉条纹的强度分布图,即全息图。光学全息记录的物体必 须是实际存在的。 而计算全息则是利用计算机程序对被记录物波的数学描述或离 散数据进行处理,形成一种可以光学再现的编码图案,即计算全息图。他不需要 被记录物体的实际存在。由于计算全息图编码的多样性和波面变换的灵活性,以 及近年来计算机技术的飞速发展,计算全息技术已经在三维显示、图像识别、干 涉计量、激光扫描、激光束整形等研究领域得到应用。最近计算全息领域的新进 展是利用高分辨位相空间光调制器实现了计算全息图的实时再现, 这种实时动态 计算全息技术已经在原子光学、光学微操纵、微加工、软物质自组织过程的控制 等领域得到成功的应用,显示了计算全息技术的巨大应用发展前景。 计算全息除了其在工业和科学研究方面的应用价值, 也是一个非常好的教学 工具。要做好一个计算全息图,既要熟悉衍射光学、光全息学等物理知识,还要 了解抽样理论、快速傅里叶变换、调制技术和计算机编程方面的知识。这些知识 对于物理类和光电信息技术类专业的学生和研究人员都是不可缺少的。
1、实验目的:
1. 2. 通过设计制作一计算全息图、利用高分辨液晶空间光调制器(LCD)实时再现 该计算全息图、观察再现结果、并利用 CCD 记录再现像等实验内容; 掌握计算全息图的编码原理,加深对光全息原理, 光的干涉和衍射特性的 认识; 训练使用空间滤波器、空间光调制器(LCD) 、CCD 图像采集等重要 的现代光学实验装置进行数字光学实验的能力。 同时初步了解 Matlab 语言在光学中的应用。
3 鲁东大学物理与光电工程学院 朱林伟---内部资料禁止外传
2015 年光电信息科学与工程专业综合实验-信息光学专题实验
= F ( j, k )
m= − M n= − N 2 2
∑ ∑
M 2
−1
N −1 2
f ( m, n ) exp[ −i 2π (
jm kn + ). M N
(5)
为了减少运算时间,通常采用快速傅里叶变换(FFT)算法。计算结果一般为复 数:
(1)
其傅里叶变换(空间频谱)为
F (u, v ) = A(u, v ) exp[iφ (u, v )] ,
(2)
为满足抽样定理 (见附录) 的要求, 物波函数及其空间频谱函数必须是带限函数, 即
f ( x, y ) = 0 F ( u, v ) = 0 x ≥ u≥
∆x 2 ∆u 2
, ,
y ≥ v ≥
2 鲁东大学物理与光电工程学院 朱林伟---内部资料禁止外传
2015 年光电信息科学与工程专业综合实验-信息光学专题实验
制作一张傅里叶变换计算全息图的典型流程如图 1 所示。 对于用高分辨空间 光调制器实时再现的情况,上述第 4 步的照相缩版或微加工步骤可以省去。下面 我们就对迂回相位型计算全息图的制作过程进行详细地介绍。
y
δx
Wδ x
nδ y
≈ ≈
mδ x
图3
Lm ,nδ y δ y
Pm ,nδ x
x
光孔径中心距抽样单元中心的位置来实现光场相位的编码。 通光孔径的形状可以 是多种多样的,可根据实际情况来选取。图 3 所示是采用矩形通光孔径编码的计 算全息图的一个抽样单元的示意图。 图中, δx 和 δy 为抽样单元的抽样间隔, Wδx 为开孔的宽度,Lmnδy 为开孔的高度,Pmnδx 为开孔中心到抽样单元中心的距离。 我们可以选取矩形孔的宽度参数 W 为定值,用高度参数 Lmn 和位置参数 Pmn 来 分别编码光波场的振幅和位相。设待记录光波场的归一化复振幅分布函数为: f mn = Amn exp( jφmn ) , 则孔径参数和复振幅函数的编码关系为:
5 鲁东大学物理与光电工程学院 朱林伟---内部资料禁止外传
2015 年光电信息科学与工程专业综合实验-信息光学专题实验
2.3.2 李(Lee)氏四阶迂回相位编码 由于在 Lohmann 型迂回相位编码计算全息图的实际制作中各单元开孔存在 较大的定位误差, 这种全息图存在较大的再现噪声。 美国科学家李威汉 (W.H.Lee) 在 1970 年提出了提出了一种改进的迂回相位编码技术。该方法把全息图上每个 抽样点细分为四个子单元, 用这四个子单元的开孔大小或透过率变化来编码该抽 样点的任意复数波前,故称为四阶迂回相位编码方法。它的基本原理是,将(1) 式所表示的物波复振幅改写成以下形式:
(9)
λ
Lohmann 称这种位相为迂回位相。 迂回位相的值与相对偏移量 Δ/d 和衍射级次 K 成正比,与入射光波的波长无关。迂回相位效应表明,通过局部改变狭缝或开孔 位置, 可以在某个衍射方向得到所需要的位相调制。 Lohmann 正是基于这一原理 提出了迂回相位编码方法。其基本思想是,在全息图的每个抽样单元中,放置一 个通光孔径,通过改变通光孔径的面积来实现光波场的振幅调制,而通过改变通
, Pmn Lmn A = = mn
(10)
φmn 。 (11) 2π K 利用这种方法编码的计算全息图的透过率只有 0、1 两个值,故制作简单,抗干 扰能力强,对记录介质的非线性效应不敏感,可多次复制而不失真,因而应用较 为广泛。在上述编码中,根据实际情况的需要,也可以固定孔径的面积不变,而 通过改变开孔的透过率来编码光波的振幅信息。
∆y 2 ∆v 2
.
.
(3)
在此条件下,根据抽样定理,对物函数及其频谱函数的抽样间隔应为: 1 1 , δy≤ ∆u ∆v . 1 1 , δv ≤ . δu ≤ ∆x ∆y
