信号与系统第一章
信号与系统第一章(重点)

-1
图 1.2-1 连续时间信号
离散时间信号:亦称序列, 其自变量n是离散的, 通常为整数。 若是时间信号 (可为非时间信号), 它只在某些不连续的、 规定的瞬时给出确定的函数值, 其它 时间没有定义, 其幅值可以是连续的也可以是离散的, 如图1.2-2所示。
x1(n) 2
1
只能取-1,0,1,2
0
t
-1
6. 单位冲激偶函数δ′(t)
单位冲激函数的导数。
(t)
1 lim
0
u(t
)
2
u(t
2)
(t)
d(t)
dt
1 lim
0
(t
)
2
(t
2)
(1.3-30) (1.3-31)
式(1.3-31)取极限后是两个强度为无限大的冲激函数,
0
t
-k
3. 复指数信号
f(t)=kest
s=σ+jω为复数, σ为实部系数, ω为虚部系数。 借用欧拉公式: kest=ke(σ+jω)t=keσt e jωt=keσt cosωt+jkeσt sinωt 复指数信号可分解为实部与虚部。 实部为振幅随时间变化的余弦函数, 虚部为振幅随时间变化的正弦函数。
第1章 信号与系统
1.1 信号与系统概述 1.2 信号及其分类 1.3 典型信号 1.4 连续信号的运算 1.5 连续信号的分解 1.6 系统及其响应 1.7 系统的分类 1.8 LTI系统分析方法
1.1 信号与系统概述
人们每天都与载有信息的信号密切接触:
听广播、看电视是接收带有信息的消息; 发短信、打电话是传送带有信息的消息。
《信号与系统》第一章知识要点+典型例题

y() 表示系统的输出。
1、线性系统与非线性系统 若系统满足下列线性性质: (1)可分解性 全响应 y () 可分解为零输入响应 y zi () 与零状态响应 y zs () 之和,即
y() y zi () y zs ()
(2)齐次性 零输入响应 y zi () 满足齐次性,零状态响应 y zs () 满足齐次性,即
( t ) 、 ( t ) 的重要性质
1
( t )dt 1 ,
t
( t )dt 0 , ( t )dt ( t ) ( k ) (k )
f ( k ) ( k ) f (0) ( k ) f ( k ) ( k k 0 ) f ( k 0 ) ( k k 0 )
f ( t ) ( t a )dt f (a )
k
f ( k ) ( k ) f (0)
(at )
5
1 (t ) a
1 b (at b) ( t ) a a f ( t ) ( t ) f (0) ( t ) f (0) ( t ) f ( t ) ( t ) f (0) ( t ) f (0) ( t )
2
。
而对离散的正弦(或余弦)序列 sin( k ) [或 cos( k ) ]( 称为数字角频率,单位为 rad ), 只有当
2
为有理数时才是周期序列,其周期 N M
2
, M 取使 N 为整数的最小整数。
如对信号 cos(6 k ) ,由于
2
2 1 为有理数,因此它是周期序列,其周期 N 1 。 6 3
信号与系统绪论第一章

= −
1 a
δ(t)dt
证毕。
1 1 1 ∴ 2δ ( t + ) = 2δ [ ( t + 1 )] = 4δ ( t + 1 ) 2 2 2
作业 2t+ 的波形。 1、信号f(t)的波形如图所示。画出信号f(-2t+4)的波形。 信号f(t)的波形如图所示。画出信号f f(t)的波形如图所示
f (t )
意义:在同样起始条件 下,系统的响应与激励 输入的时刻无关。
t0
t0 +T
t
0
t0
t
波形不变,仅延时 t0
1.3 系统的描述与分类
例3:判断以下系统是否为非时变系统。
(1) r (t ) = T [e(t )] = ate(t ). (2) r (t ) = T [e(tቤተ መጻሕፍቲ ባይዱ)] = ae(t )
f (t + t 0 )
左移 1
− t0 − 2 − t0 − t0 + 1
0
f (−t + t 0 )
反转
1
0
f (t )
1
t0 − 1 t0
t0 + 2 t
-2
0 1
t
f (t − t 0 )
1 右移 t0 − 2 t0 t 0 + 1 t
− t0 − 1 − t0 − t0 + 2
f (−t − t 0 )
= k1 [ ae1 ( t ) + b ] + k 2 [ ae2 ( t ) + b ] = a [ k1e1 ( t ) + k 2 e2 ( t )] + bk1 + bk 2
显然 T [ k1e1 ( t ) + k 2 e2 ( t )] ≠ k1r1 ( t ) + k 2 r2 ( t ) 故系统为非线性系统。
信号与系统第一章(1.2 1.3)系统的描述

,k 0
式中a,b为常数, x 0 为初始状态,在t=0或k=0时接入 激励 f 。上述系统是否为线性的,时不变的
解:(1)系统的零输入响应和零状态响应分别为
y x ( t ) ax(0) y f ( t ) b f d
t 0
,t 0
符合分 解特性
显然,无论激励是何种形式的序列,只要它是有界的, y f也是有界的,因而该系统是稳定的。 (k ) 那么
例2: y f (t ) 0 f ( x )dx, t 0 是否稳定? 若 f (t ) (t ) ,则
t
y f (t ) f ( x )dx ( x )dx t , t 0
当 f1 t f t t 0 时
所以,该系统为时不变系统。
2 y f t f t cos t
当 f1 t f t t 0 时
y f 1 t f t t 0 cos t y f t t 0
所以,该系统为时变系统。
y x (t ) 、 y f (t ) 满足零输入线性和零状态线性,
因而该系统是线性的。
设
f1 ( t ) f ( t t 0 ), t t 0 , 其零状态响应
令 x t 0 ,则
y f1 (t ) b f ( t 0 )d
0
t
, t t0
dx d,代入上式,相应的积分
0 0
t
t
它随时间t无限增长,故系统是不稳定的。
1.2.3 系统的描述
建立描述系统基本特性的数学模型 分析一个系统 用数学方法求出它的解 对所得的结果赋予实际的含义
1、系统的数学模型
《信号与系统》第一章

学习目标
1
掌握信号与系统的基本概念、性质和分类,理解 信号与系统在信息传输、处理和应用中的重要地 位和作用。
2
掌握信号的描述和分析方法,包括时域和频域分 析,理括线性时不变系 统和线性时变系统,理解系统的基本特性、分析 和设计方法。
02
系统的基本概念和分类
阐述了系统的基本概念,系统分类(如线性时不变系统、非线性系统 、离散系统等),以及系统的描述方法。
信号与系统在通信工程中的应用
讨论了信号与系统在通信工程中的重要性,如调制解调、频分复用等 。
信号与系统在控制工程中的应用
探讨了信号与系统在控制工程中的应用,如PID控制器、控制系统稳 定性分析等。
下章预告
傅里叶变换
介绍傅里叶变换的定义、性质 及其在信号处理中的应用。
系统的状态变量分析
通过状态变量法对线性时不变系统 进行分析,包括状态方程的建立、 解法以及系统的稳定性分析。
拉普拉斯变换与Z变换
介绍拉普拉斯变换和Z变换的定 义、性质及其在连续系统和离 散系统分析中的应用。
系统的能控性和能观性
介绍能控性和能观性的概念、 判据以及其在控制系统设计中 的应用。
02
在实际应用中,需要根据具体需求和场景,选择合适的系统和信号处理方法, 以达到最佳的处理效果。
03
深入研究和理解信号与系统之间的相互作用关系,有助于更好地应用信号处理 技术,推动相关领域的发展和创新。
05
CATALOGUE
总结与展望
本章总结
信号的基本概念和分类
介绍了信号的基本概念、信号的分类(如连续信号、离散信号、周期 信号、非周期信号等)以及信号的表示方法。
CATALOGUE
信号的基本概念
信号与系统第1章总结

第一章:信号与系统的基本概念1.1 信号的基本概念一、什么是信号信号是信息的表现形式。
例如,光信号、声信号和电信号等。
二、信号的分类1、确定性信号和随机信号()f t 确定性信号有确定的函数表达式2、周期信号和非周期信号f(t)=f(t+kT) k=1,2,3...周期信号3、连续时间信号和非连续时间信号时间t 连续的是连续时间信号,时间变量t 只取特定值的为离散时间信号4、有始信号和无始信号0t t <若,0()0,f t t =为起始点三、典型的连续时间信号1、正旋信号21()cos(),,,2f t A wt T f w f w T πϕπ=+===AMFMPM A w ϕ不为常数,调幅信号不为常数,调频信号不为常数,调相信号欧拉公式:cos 2sin 2j j e e j j ee jθθθθθθ-+--=⎧⎪⎪⎨⎪⎪⎩=2、指数信号为实数αα,)(t ke t f =3、复指数信号(一种数学模型)(),st f t ke s jw δ==+4、抽样信号sin (),a ts t t t =-∞<<∞性质1、偶函数,随着t 的增大,幅值减小0sin 2()lim 1a x tt t →==性质:t=0,s3sin 0,1, 2...t t k k π=⇒==±±性质:过零点1.2 信号的运算一、信号的时域变换1、平移(时移)000()()()()()()f t f t t f t f t t f t f t t =±→-→+右移,左移2、反转以纵轴为中心,左右反转()()f t f t =-t 3、展缩{011,()(),a a f t f at <<>=,扩展压缩二、信号的相加、相乘、微分和积分1、相加:对应点相加2、相乘:主要用于信号的截取3、微分:t 4∞、积分:指(-,0)上积分t-(),f d t ττ∞⎰为变量t<0()0t 1()t>1()1t t t f d f d tf d ττττττ-∞-∞-∞=<<==⎰⎰⎰当时,当0时,当时,1.3 奇异信号----------------------------------------------------一种数学模型信号的取值或导数出现了奇异值(极大),趋于无穷一、单位阶跃信号{0,01,0()t t t ε<>=t因果信号{0,0(),0()()t f t t f t t ε<>=二、单位冲击信号----------------也是一种数学模型作用时间极短,但幅值极大{()0,0()1,1t t t dt δδ+∞-∞=∀≠=⎰即冲激强度为性质1:抽样性0000001.()()(0)()2.()()(0)()3.()()(0)()(0)4.()()()()()t t t t f t t f t f t t t f t t f t t d f t d f f t t t d f t t t d f t δδδδδδδδ+∞+∞-∞-∞+∞+∞-∞-∞=-=-==-=-=⎰⎰⎰⎰性质2:卷积特性1212()()()()()f t f t f t f f t d τττ+∞-∞=*=-⎰0005.()()()()()6.()()()()()f t t f t d f t f t t t f t t d f t t ττδτδτδτδτ+∞-∞+∞-∞*=-=*-=--=-⎰⎰注:一个信号与冲激信号的卷积就是信号本身三、阶跃、冲激信号的关系 {0,01,0()()()()t t t d t d t t dt δττεεδ<-∞>===⎧⎰⎨⎩注:阶跃信号求导即为冲激信号1.4 信号分解为冲激信号的叠加1.5系统及分类一、分类1.连续时间系统:微分方程离散时间系统:差分方程2.线性系统:叠加性、齐次性f(t)→系统→y(t) kf(t)→系统 →ky(t)f1(t)+f2(t)→系统→y1(t)+y2(t)当齐次和叠加只要有一个不满足则是非线性的3.因果系统:响应不早于激励非因果系统4.时变系统是不变系统:输入输出都做相应的变化,并不随时间变化二、线性时不变系统(LTI 系统)性质1:线性、齐次性、叠加性Yzi(t):零输入响应,外部激励为0,仅在初始状态作用下的响应 Yzs(t):零状态响应,仅在外部激励作用下的响应性质2:是不变性性质3:微分、积分性f(t)→系统→y(t)()y ()f t t ''→→系统t -()()tf t dt y t dt-∞∞→→⎰⎰系统 性质4:因果性。
信号与系统第一章

m 0
n
m
令 k n பைடு நூலகம்,则 n
k
k
n
上式的正确性在于 k 仅在 k 0时为1,其余 k时取为0, n时,求和式为 0 所以当 时,求和式为零,而当 n0 1。
T
2t
2
e 4T lim T 2
所以该信既非能量信号又非功率信号
1.2 基本的连续时间和离散时间信号
1.2.1 单位阶跃信号(unit step function)与单位冲激信 号(unit impulse function) 阶跃函数和冲激函数不同于普通函数,称为奇异函 数。研究奇异函数的性质要用到广义函数(或分配函数) 的理论。这里将直观地引出阶跃函数和冲激函数。
一、阶跃函数
下面采用求函数序列极限 的方法定义阶跃函数。 选定一个函数序列γn(t)如图所示。
若阶跃幅度为 A ,则可记为 A t
若单位阶跃函数跃变点在 t t 0处,则称为延迟单位阶 跃函数
1, t t0 0, t t0 t t0
阶跃函数性质: (1)可以方便地表示某些信号 f(t) = 2ε (t)- 3ε (t-1) +ε (t-2) (2)用阶跃函数表示信号的作用区间
3.信号(signal) 信号是信息的载体,通过信号传递信息。 为了有效的传播和利用信息,常常需要将信息转 换成便于传输和处理的信号。 信号于我们并不陌生,如刚才的铃声——声信号, 表示该上课了; 十字路口的红路灯——光信号,指挥交通; 电视机天线接收的电视信号——电信号; 日常生活中的文字信号,图像信号,生物电信号 等,都属于信号。
信号与系统第一章

62
第1章 信号与系统的基本概念
1.14 设某地区人口的正常出生率和死亡率分别为α和β, 第k年从外地迁入的人口为f(k)。若令该地区第k年的人口为y(k), 写出y(k)的差分方程。 解 设第(k-1)年的总人口数为y(k-1),经一年后净增人口 数为(α-β)y(k-1), 第k年迁入的人口数为f(k), 故第k年的总
利润回报率稳定在β%。试建立预测若干年后该经济开发区拥
有的资金总额的数学模型。
64
第1章 信号与系统的基本概念
解 设k年后开发区拥有资金总额为y(k), 第k年投入资金 为f(k)。按题意,第(k-1)年投入资金f(k-1)在第k年度增长为
(1+α)f(k-1), 而资金y(k-2)在第k年度增长为(1+β)y(k-2)。因
人口数为上述三部分之和,即
y(k)=y(k-1)+(α-β)y(k-1)+f(k)
整理得
y(k)-(1+α-β)y(k-1)=f(k)
这是一个一阶差分方程。
63
第1章 信号与系统的基本概念
1.15 某经济开发区计划每年投入一定资金,设这批资金 在投入后第二年度的利润回报率为α%,第三年度开始年度的
号。因sint的周期T1=2π s, sin2t的周期T2=π s,且T1/T2=2为有 cosπt的周期T2=2 s, 且T1/T2=π/2 理数, 故f1(t)是周期信号,它的周期为2π s。 (2) 因sin2t的周期T1=π s, 为无理数, 故f2(t)是非周期信号。
(3) 因cost的周期为T1=2π s,
(10) x(t+1) ·y(t-1)。
15
第1章 信号与系统的基本概念
信号与系统第一章

.-
第 1 章 信号与系统的基本概念
图 1 3 1 连 续 信 号 的 相 加 和 相 乘
第 1 章 信号与系统的基f1(k) 本概念
1
- 3- 2- 10 1 2 3 4 5 6
k
图
f2(k )
1
1
.-
- 3- 2- 1
3
0 12345
k
2
-1
离
f1(k )+f2(k )
散
2
信
号
1
的
- 3- 2- 1
如果信号是时间的随机函数,事先将无法预知它的变化 规律,这种信号称为不确定信号或随机信号。
第 1 章 信号与系统的基本概念 图 1.1-1 噪声和干扰信号
第 1 章 信号与系统的基本概念
2. 连续信号与离散信号
一个信号,如果在某个时间区间内除有限个间断点外都有 定义, 就称该信号在此区间内为连续时间信号,简称连续信
时间轴展缩(尺度变换)而成的一个新的信号函数或波形。 在信号f(at)中,a为常数,|a|>1时表示f(t)沿时间轴压
缩;|a|<1时表示f(t)沿时间轴展宽。例如图1.3-5分别表示 f(t)、f(2t)、f(t/2)的波形。
信号展缩的一个例子是:如果f(t)表示录制在磁带上 的语音信号,则f(2t)表示放音速度要比原来录制的高一 倍;f(t/2)表示放音速度要比原来录制的慢一倍。
序列f(k)的数学表示式可以写成闭式,也可以直接列出序 列值或者写成序列值的集合。例如,图1.1-3(a)所示的正弦序 列可表示为
f1(k )Asin 4k
第 1 章 信号与系统的基本概念
f1(k )
… -2
-8 -6 -4
信号与系统概论第一章

2)冲激函数定义 (多种方式演变) ①单位冲激函数(狄拉克函数)
( ※ 0时刻取不定值,面积为1。为广义函数)
1.5 奇异信号及其基本特性(续)
◆ t=t0时刻的单位冲激函数:
②矩形脉冲定义的单位冲激函数
( ※ 面积为冲激强度,强度为1时为单位冲激)
1.5 奇异信号及其基本特性(续)
※ 对于冲激偶函数可继续二次求导。(如双边指数脉冲等)
冲激函数
冲激偶函数
强度无穷大
(单向面积:1/τ)
1.5 奇异信号及其基本特性(续)
2)冲激偶函数的性质 ①
推导:
0
性质
1.5 奇异信号及其基本特性(续)
②面积为零:
③冲激偶函数与普通函数乘积的性质: (证:两边取积分)
-f’(0)
0
-f’(0)
1.4 信号的基本运算及波形变换(续)
② 若以变量 at+b 代替 t,可得沿时间轴伸缩平移的 新信号 f(at+b)。 a>0时:信号沿时间轴伸缩、平移。
(a>1, a<1)
a<0时:信号沿时间轴伸缩、平移、反褶。(a>-1,a<-1) ◆特点:
所有运算都是自变量t的变换,且变换前后端点函数值不变。
③其他函数形式定义的单位冲激函数
1.5 奇异信号及其基本特性(续)
1.5 奇异信号及其基本特性(续)
3)冲激函数的性质 ①抽样性质(筛选特性)
1.5 奇异信号及其基本特性(续)
冲激函数与普通函数乘积的积分可将普通 函数在冲激出现时刻的函数值抽取出来!
1.5 奇异信号及其基本特性(续)
②偶函数性质: ③与阶跃函数的关系: ◆冲激函数的积分是阶跃函数: δ(t) = δ(-t)
信号与系统第1章

速率越慢。 指数信号的一个重要特性是其对时间的微 分和积分仍然是指数信号。 实际上, 用得较多的是单边指数信号, 其表达式为
0, f (t ) e 1 t, K t0 t0
(1.5)
第一章 信号与系统的基本概念
当a为复数时, f(t)为复指数信号, 其数学表达式为
第一章 信号与系统的基本概念
除此以外, 抽样信号还具有以下性质:
Sa (t )dt 2
0
(1.9)
Sa(t )dt
(1.10)
第一章 信号与系统的基本概念
图 1.7 抽样信号
第一章 信号与系统的基本概念
1.2.3 阶跃信号与冲激信号
1. 单位阶跃信号 单位阶跃信号ε(t)的数学表达式为
第一章 信号与系统的基本概念
第一章
信号与系统的基本概念
1.1 信号的概念与分类 1.2 基本的连续时间信号 1.3 信号的运算与变换
1.4 系统的描述与分类
1.5 线性时不变系统的基本性质 1.6 连续时不变系统分析方法综述 1.7 信号变换与运算及系统判断的 MATLAB实现
第一章 信号与系统的基本概念
描述信号的基本方法是写出它的数学表达式, 此表达式
是时间的函数, 依据函数绘出的图像称为信号的波形。 为方便讨论, 本书中将信号与函数两名词通用。 除了用 数学表达式和波形进行描述外, 随着问题的深入, 还引用 了频谱分析、 各种变换等方式来描述和研究信号。
第一章 信号与系统的基本概念
1.1.2 信号的分类
g 2 (t ) (t ) e(t ) 2 2
(1.13b)
第一章 信号与系统的基本概念
信号与系统第1章-信号与系统的基本概念

1 0
1
t
1 0
2
一半语速信号
4 t
正常语速信号
2倍语速信号
若
a 1 ,波形在t 轴上扩展 1 a 倍。
若 a 1 ,波形在t 轴上压缩1/
a 倍。
信号与系统
SIGNALS & SYSTEMS
第一章 信号与系统的基本概念
前言
§1.1 信号的描述与分类 §1.2 连续时间信号的基本运算与变换 §1.3 系统的描述与分类 §1.4 系统分析方法
♣ 连续时间信号的基本运算主要包括
相加(减)、相乘(除)、微分、积分
♣ 信号波形变换主要指
波形的翻转、平移和展缩 通常是通过对自变量的代换实现
信号与系统
SIGNALS & SYSTEMS
一.信号的相加减
f1(t) 1 0 1
1
f ( t )=f1 ( t )+f2 ( t )
2 1
1
f2 (t)
f1 (t ) f2 (t )
信号与系统
SIGNALS & SYSTEMS
六.信号的时移(波形平移)
连续时间信号的时移定义为
y(t ) f (t t0 )
f (t )
f (t b)
t0为时移量
t t t0
f (t b)
-1
b1
t
(-1+b)
1 (1+b) t
(-1-b)
(1-b)
t
t0>0时右移
t0<0时左移
出现冲激, 其冲激强度 为该处的跳 变量
0
1 2 3
t
0 1
-2
3 (2)
t
信号与系统 第一章

§1.4
系统的概念
一、系统(Systems)的定义
一般而言,系统是一个由若干相互关联的事物构成的, 用以达到某些特定目的的有机整体。 本课主要讨论电路系统。 电路系统 ———— 处理信号的电路之组合。
系统与网络、电路的区别:主要在于分析问 题的着眼点,而不在于组成的复杂程度。
•系统 ——— 着重在输入输出间的关系, 或者运算功能上。
t t
4.抽样函数sampling
sin t f (t ) Sa(t ) t
Sa(t ) 是偶函数, t , 2 , Sa(t ) 具有以下性质:
0
f (t )
t
时,函数值为0。
Sa (t ) dt
2
Sa(t )dt
另一种类似的表示形式为
3.从信号特性上划分continuous-time,discrete连续时间系统 ——— 激励信号与响应信号都 是连续时间信号。 离散时间系统 ——— 激励信号与响应信号 都是离散时间信号。
系统还可划分为集总参数系统和分布参数 系统等。
三、系统的数学模型
方程:equation
线性系统 ———— 线性方程 非线性系统 ———— 非线性方程 时变系统 ———— 变参数方程 非时变系统———— 常参数方程
•Variable-coefficient •Constant- coefficient 连续时间系统———— 微分方程differential 离散时间系统———— 差分方程difference
四、基本系统性质(1.6节) 1.记忆系统与无记忆系统(systems with and without memory)
t
2. 从时间取值的连续性划分 在某一时间间隔内,对于一切时 间值,除了若干不连续点外,函 (continuous-time signals) 数都能给出确定的函数值。 离散时间信号——— 只在某些不连续的规定瞬时给出 函数值,其它时间没有定义的信 (discrete-time signals) 号。 连续时间信号———
信号与系统第一章
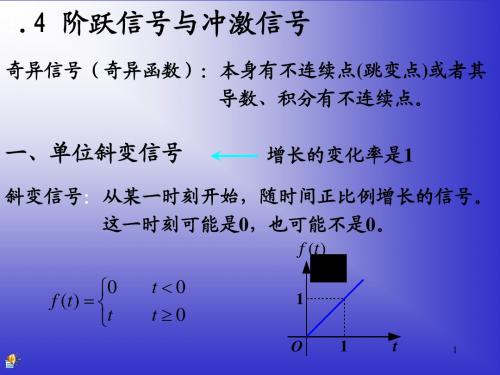
t
1
f (t )
R( t )
延迟的单位斜变信 号 f (t t 0 )
R( t t 0 )
1
1 t
0 f (t ) t
t 0 t 0
1
O
O
t t0 0 f (t t0 ) t t0 t t0 三角形脉冲可用单位斜变信号表示:
f1 (t ) f (t )
冲激强度为1
(1) t
6
o
(t )
(1) t
o
(t t0 )
延时的单位冲激信号
(1)
o
t0
t
只在 t 0 有一个“单位冲激”,在 处,信号值 t0 都为 0,单位冲激的强度为 1。若矩形脉冲面积为 A,则冲 激强度为A。 三角形脉冲、双边指数脉冲、钟形信号、抽样信号等 取极限,都可以得到冲激信号。
f 2 (t ) e t u(t ) u(t t 0 )
0
t0
t
1
sgnt
• 可用阶跃信号表示符号函数。
1 sgn(t ) 1 t 0 t 0
O
-1
t
sgn(t ) u(t ) u(t ) 2u(t ) 1
1 u (t ) [sgn( t ) 1] 2 5
0
t
同样,对于电感电路,由于
当i L (t )为阶跃信号时,v L (t )为冲激信号,说明由于冲激 电压的出现,允许电感电流在无限短时间内产生跳变。
12
四、冲激偶信号
冲激信号求导,称为冲激偶信号。是正、负极性的一 对冲激,强度均为无限大。
s( t )
1
《信号与系统》第一章课件

x(t)
x[n]
时间t连续取值
序号 n 取零和整数
信号的描述:
连续时间信号 x(t ) x(t1, t2 )..... 离散时间信号 x[n] x[n1, n2 ]....
鸟鸣声的时域波形,其幅值是时间的一元函数
心电图 —— 幅值是时间的一元函数
C(m, n)
图片上: (m, n) 是像素的位置 C是 {R,G, B}的函数
二. 周期信号与非周期信号:
周期信号:x(t ) = x(t + T ) x[n] = x[n + N ]
满足此关系的正实数(正整数)中最小的一个,
称为信号的基波周期 T0( N0 )。
x(t ) = C 可视为周期信号,但基波周期没有
确定的定义。
x[n] = C 可以视为周期信号,基波周期 N0 =1
−T
•离散时间情况下:
∑ P∞
=
lim
N →∞
1 2N +1
N x[n] 2
n=−N
三类重要信号:
1. 能量信号—总能量有限:
E∞ < ∞, P∞ = 0
2. 功率信号—总能量无限平均功率有限:
E∞ = ∞, 0 < P∞ < ∞
3. 信号的总能量和平均功率都是无限的:
E∞ = ∞, P∞ = ∞
对复信号而言:
x(t) = x[n] =
x*(−t) x*[−n]
则称该信号为共轭偶信号
x(t) x[n]
= =
− −
x* (−t ) x*[−n]
则称为共轭奇信号
任何信号都能分解成一个偶信号与 一个奇信号之和
对实信号有: x(t ) = xo (t ) + xe(t )
信号与系统第一章

0 t ≠ 0 δ (t) = 和 ∞ t = 0
∫
∞
∞
δ (t)dt =1
3. 复指数信号(complex exponential signal)
f (t) = est
s = σ + jω 为复数,称复频率.
由于复指数信号能概括多种情况,所以可利用它来描述多种 基本信号,如直流信号,指数信号,等幅,增幅或减幅正弦 或余弦信号,因此,它是信号与系统分析中经常遇到的重要 信号. 上面我们介绍了几种最基本的信号,接着来介绍有关信号的 各种运算. 1.2 信号的运算 1.2.1 信号的相加与相乘 两个信号相加(相乘)可得到一个新的信号,它在任意时刻 的值等于两个信号在该时刻的值之和(积).信号相加与相 乘运算可以通过信号的波形 ( 或信号的表达式 ) 进行.
信号的特性可以从两个方面来描述,即时间特性和频率特性. 信号可写成数学表达式,即是时间 t 的函数,它具有一定的 波形,因而表现出一定波形的时间特性,如出现时间的先后, 持续时间的长短,重复周期的大小及随时间变化的快慢等. 另一方面,任意信号在一定条件下总可以分解为许多不同频 率的正弦分量,即具有一定的频率成份,因而表现为一定波 形的频率特性,如含有大小不同频率分量,主要频率分量占 有不同的范围等. 信号的形式所以不同,就因为它们各自有不同的时间特性和 频率特性,而信号的时间特性和频率特性有着对应的关系, 不同的时间特性将导致不同的频率特性的出现. 1.1.2 信号的分类 对于各种信号,可以从不同的角度进行分类. 1.确定信号和随机信号
信号与系统
沈元隆 周井泉
第一章
第1章 信号与系统的基本概念 1.1 信号的描述及分类 1.2 信号的运算 1.3 系统的数学模型及其分类 1.4 系统的模拟 1.5 线性时不变系统分析方法概述 习题1
信号与系统第一章__绪论

• 系统对激励的的响应称为冲激响应函数 h(t)
• 对激励的响应是激励函数与系统冲激响 应函数的卷积
频域分析
• 作为时间函数的激励和响应,可通过傅立叶 变换将时间变量变换为频率变量去进行分析, 这种利用信号频率特性的方法称为频域分析 法。频域是最常用的一种变换域。
• 时域分析 –信号时域分析(线性系统叠加原理) –卷积积分的应用及其数学描述
• 频域分析 –周期信号的频域分析(三角与指数傅立叶级 数) –非周期信号的频域分析(傅立叶积分) –信号在频域与时域之间的变换(正反傅立 叶变换式) –频谱与时间函数的关系
时域分析
• 系统的输入信号称为激励,输出称为响应 • 激励与响应都是时间的函数
– 频带:复杂信号频谱中各分量的频率理论上可扩展至无限, 但因原始信号的能量一般集中在频率较低范围内,在工程 应用上一般忽略高于某一频率的分量。频谱中该有效频率 范围称为该信号的频带。
• 以频谱描述信号的图象称为频域图,在频域上分析信号称为 频域分析。
4.偶信号与奇信号
偶信号:
x t x t
– 如果时间间隔趋于无穷大,将产生两种情况。
• 信号总能量为有限值而信号平均功率为零,称为能量信号; 考察信号能量在时域和频域中的表达式,非周期的单脉冲信 号就是常见的能量信号;信号平均功率为大于零的有限值而 信号总能量为无穷大,称为功率信号,考察信号功率在时域 和频域中的表达式。周期信号就是常见的功率信号。
• 例:周期性脉冲信号的重复周期的倒数就是该 信号的基波频率,周期的大或小分别对应着低 的或高的基波和谐波频率;
• 信号分析中将进一步揭示两者的关系。
不同频率信号的时域图和频域图
信号与系统 第一章_绪论(青岛大学)小白发布

∫
∞
−∞ ∞
Sa (t )dt = π Sa 2 (t )dt = π
∫
−∞
另外一个类似的函数:
sin π t sinc( t ) = πt
§1.3 信号的运算
(一)对自变量进行的运算: 移位、反褶与尺度 对自变量进行的运算: 移位、 1. 移位: f (t ) → f (t ± t0 ) 移位:
t
t
t
sin (Ωt ) + sin (8 Ωt )
× sin ( Ωt ) sin (8 Ωt )
t
t
反相点
§1.4 阶跃信号与冲激信号 奇异信号: 奇异信号:
(一)单位斜变信号tu(t) (二)单位阶跃信号 u(t) (三)单位冲激信号δ (t) (四)冲激偶信号δ ' (t)
(一)单位斜变信号tu(t)
(3) cos(3n − )
当 当
2π
2π
π
ω0
为有理数时, 为周期序列; 为有理数时,sin(ω0n) 为周期序列; 为无理数时, 为非周期序列。 为无理数时,sin(ω0n) 为非周期序列。
2π 为无理数, 为无理数, 3
非周期序列
4
ω0
4.能量(有限)信号与功率(有限)信号 能量(有限)信号与功率(有限)
2.信号的传输、 2.信号的传输、交换和处理 信号的传输
信号传输(Transmission)
——古代烽火传送边疆警报 ——击鼓、信鸽、旗语等 击鼓、信鸽、 ——电信号传输(19世纪开始): 电信号传输( 世纪开始 世纪开始):
1837年莫尔斯发明了电报 年莫尔斯发明了电报 1876年贝尔发明了电话 年
信号与系统第一章总结

信号与系统第一章总结1、信号的分类(1)周期信号和非周期信号两个周期信号x(t),y(t)的周期分别为T 1和T 2,若其周期之比T 1/T 2为有理数,则其和信号x(t)+y(t)仍然是周期信号,其周期为T 1和T 2的最小公倍数。
(2)连续信号和离散信号连续时间信号:信号存在的时间范围内,任意时刻都有定义。
用t 表示连续时间变量。
离散时间信号:在时间上是离散的,只在某些不连续的规定瞬时给出函数值, 用n 表示。
(3)模拟信号,抽样信号,数字信号 模拟信号:时间和幅值均为连续的信号。
抽样信号:时间离散,幅值连续的信号。
数字信号:时间和幅值均为离散的信号。
(4)按照信号能量特点分类:能量受限信号:若信号f (t)的能量有界,即E<∞ ,则称其为能量有限信号,简称能量信号,此时P = 0。
功率受限信号:若信号f(t)的功率有界,即P<∞ ,则称为功率有限信号,简称功率信号,此时E = ∞。
PS :时限信号为能量信号;周期信号属于功率信号。
2、典型的确定性信号(1)指数信号: , α=0 直流(常数);α<0 指数衰减;α>0指数增长。
通常把称为指数信号的时间常数,记作τ ,代表信号衰减速度,具有时间的量纲。
对时间的微分和积分仍然是指数形式(2)正弦信号:,振幅K ,周期T=ωπ2 ,初相衰减正弦信号:对时间的微分和积分仍然是同频率的正弦信号 (3)复指数信号:α1θdt t f E 2)(⎰∞∞-∆=⎰-∞→=222|)(|1lim T T T dt t f T P t K t f αe )(=)sin()(θω+=t K t f ()0sin e )(>⎩⎨⎧<≥=-αωαt t t K t f t()()t K t K t K t f t t stωωσσsin e j cos e )( e )(+=∞<<-∞=为复数,称为复频率j ωσ+=s rad/s的量纲为 ,/s 1 的量纲为 ωσ振荡衰减增幅等幅⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≠<≠>≠= 0 ,0 0 ,0 0 ,0ωσωσωσ⎪⎩⎪⎨⎧=<=>==衰减指数信号升指数信号直流 0 ,0 0 ,0 0 ,0ωσωσωσ(4)抽样信号(重点): 性质:1. 偶函数2. 3. 4.5. 6.(5)钟形信号(高斯函数):3、信号的平移,反褶,展缩(1)平移:左加右减(注意符号)(2)反褶:关于y 轴对称(3)展缩:f(t)到f(at),图形变换(1/a)倍变换方法: 1. 先展缩:a>1,压缩a 倍; a<1,扩展1/a 倍 2. 后平移:+,左移b/a 单位;-,右移b/a 单位 3. 加上倒置:4、阶跃信号和冲激信号(1)单位阶跃信号(通常以u (t )表示)门函数:符号函数:ttt sin )Sa(=)Sa(lim ,即1)Sa(,00===→t t t t 3,2,1π,0)Sa(=±==n n t t ,⎰⎰∞∞-∞==πd sin ,2πd sin 0t t t t t t 0)Sa(lim=±∞→t t ()()t t t ππsin )sinc(=2e )(⎪⎭⎫ ⎝⎛-=τt E tf ()()()[]()0 >±=±→a a b t a f b at f t f 设()()[]a b t a f b at f -=±-()[(/)]f t f a t b a →±()()f t f at →210 0100)(点无定义或⎩⎨⎧><=t t t u ()⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛+=22ττt u t u t f ⎩⎨⎧<->=0101)sgn(t t t(2)单位冲激信号:①定义:狄拉克函数 只在t=0时,函数值不为0;积分面积为1;t =0 时,为无界函数。
