管管相交相贯线公式
机械制图相贯线

机械制图相贯线简介在机械制图中,相贯线是指两个或多个图形的交集,它通常用于确定零件之间的相对位置以及其运动轨迹。
相贯线在机械设计和制造过程中具有重要的作用,在设计阶段就能够精确地确定各个零件的相对位置关系,从而确保整个机械系统的正常运行。
相贯线的计算方法相贯线的计算方法主要依赖于图形的几何属性和运动规律。
下面介绍几种常见的相贯线计算方法。
1. 直线与直线的相贯线当两条直线相交时,它们的相贯线就是它们的交点。
如果两条直线不相交,则它们没有相贯线。
如上图所示,直线A和直线B相交于点O,因此它们的相贯线为点O。
2. 圆与直线的相贯线当一个圆与一条直线相交时,它们的相贯线可以是一个或两个交点。
相贯线的计算方法如下:•首先,确定圆心和半径。
•其次,确定直线的方程。
•然后,将直线方程代入圆的方程,求解相交点的坐标。
上图中,圆C与直线D相交于点E和点F,因此它们的相贯线为点E和点F。
3. 圆与圆的相贯线当两个圆相交时,它们的相贯线可以是一个或两个交点。
相贯线的计算方法如下:•首先,确定两个圆的圆心和半径。
•其次,根据两个圆的几何关系,列出它们的方程。
•然后,解方程得到相交点的坐标。
上图中,圆G与圆H相交于点I和点J,因此它们的相贯线为点I 和点J。
相贯线的应用相贯线在机械制图中具有广泛的应用,以下列举几个常见的应用场景。
1. 齿轮传动在齿轮传动中,相贯线用于确定齿轮之间的啮合关系。
通过计算齿轮的相贯线,可以确定齿轮的模数、齿数和啮合角等参数,从而确保齿轮传动的正常运转。
2. 运动机构相贯线在运动机构设计中起着重要的作用。
通过计算运动机构各个零件的相贯线,可以确定它们的相对运动轨迹,从而实现机构的运动控制。
3. 机械零件组装在机械零件组装过程中,相贯线被用于确定零件之间的相对位置关系。
直管弯管相贯线放样计算模型
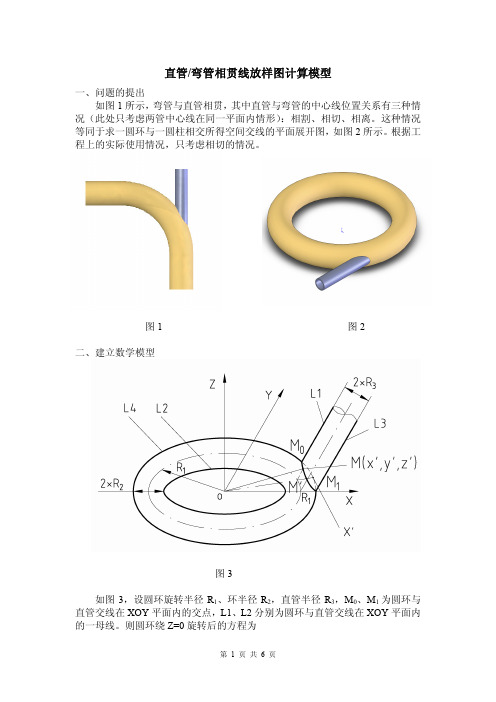
直管/弯管相贯线放样图计算模型一、问题的提出如图1所示,弯管与直管相贯,其中直管与弯管的中心线位置关系有三种情况(此处只考虑两管中心线在同一平面内情形):相割、相切、相离。
这种情况等同于求一圆环与一圆柱相交所得空间交线的平面展开图,如图2所示。
根据工程上的实际使用情况,只考虑相切的情况。
图1 图2二、建立数学模型图3如图3,设圆环旋转半径R1、环半径R2,直管半径R3,M0、M1为圆环与直管交线在XOY平面内的交点,L1、L2分别为圆环与直管交线在XOY平面内的一母线。
则圆环绕Z=0旋转后的方程为()22212R zR −+=……………………… ①或2222212x y R z R R +++−=± (注:圆环关于XOY 平面对称) 直管圆柱面方程为()22213x R z R −+=……………………… ②联立①②,则得圆环与直管的交线(即相贯线)方程()()2221222213R z R x R z R ⎧+=⎪⎨⎪−+=⎩……………………… ③ 为便于求解,只求第一象限的交线,则定义域为1313122300{,}R R x R R y R R z MAX R R −≤≤+⎧⎪≤≤+⎨⎪≤≤⎩三、求解直管沿母线L1剪切展开后的图形大致类似于图4,圆环沿母线L2剪切展开后的图形大致类似于图5。
图4 图5在图3任取一动点M(x’,y’,z’),当点 M(x’,y’,z’)沿方程③运动时,对应于图4、图5中点M(x,y)的运动轨迹即为所求。
从图3和方程组③中可以得知,图4、图5的曲线是关于y 轴对称的,所以只需研究图3第一象限上半部分的曲线展开方程,即图4、图5中的第二象限部分曲线方程。
1、直管相贯线展开方程X =-(图3中直管上的截面圆上点M 到M 1所在母线L3的一段弧长) Y =图3中M 的Y 坐标值-图3中M 1的Y坐标值第 3 页 共 6 页X 的具体求解方法为:将直管投影在XOZ 平面上(见图6)。
[理学]11[1]相贯线
![[理学]11[1]相贯线](https://img.taocdn.com/s3/m/8176bfea7375a417876f8f02.png)
答案
(二)辅助截面法
例2:圆柱与圆锥相贯,求其相贯线的投影。
●
●
★辅助截面法
PW
P
●
●
●
●
水平面P截两立体,与圆锥面的交线为圆,与圆柱面的交线为两条直线, 圆与两直线的交点即为相贯线上的点。
作图
● ●
● ●
●
●
●
●
●
●
●
●
●
●
●
步骤:
★ 求特殊点
★ 用辅助平面法求 一般点
★ 光滑连接各点
答案
(一)表面取点法
例1:二不等直径圆柱正交,求其相贯线。
●
●
●
●
●
●
● ●
● ●
●
●
●
●● ●
大圆柱轴线垂直于W面,侧面投影
积聚空为圆间,及相投贯线影的分侧析面投:影应积聚 在该求圆相上贯,为线两的圆柱投面影共:有的一段圆
弧。
利用积聚性,采用表 面取点法。 平投☆分影析积找:聚特小为圆圆殊柱,点轴根线据垂相直贯于线H的面共,有水 性,☆相贯补线充的一水平般投点影积聚在该圆上 。☆ 光滑连接
2008-2009
现代机械 工程图学
(11)
相贯线
(教材P88-97) 一、相贯线概述 二、相贯线的求作方法 三、相贯线的特殊情况 四、小结 五、截交与相贯综合题分析
一、相贯线概述
概念: 两立体表面相交产生的交线 分类:全贯、互贯
全贯
互贯
相贯线的主要性质
★ 是立体表面的交线 ★ 一般是封闭的空间曲线 ★ 是两立体表面的共有线
选择正 平面P 为辅助 截平面
(3)求相贯点
如图,I、II是最左、 最右点,III、IV是最前 点、最后点。V、VI是 球的V投影转向轮廓线 上点,而最高、最低点 E、F的H投影应是在H 投影中圆柱和球中心连 线与圆周相交的点e、f。 以上各点的V投影由它 们已知的H投影和通过 作正平面P为辅助平面 的方法求得。
TKY 管节点焊缝的超声检测

TKY 管节点焊缝的超声检测简添福;潘文超;陆铭慧;郑志忠【摘要】TKY 管节点结构及其类似机构在钢结构及海洋平台中的广泛应用,对无损检测技术提出了严峻的挑战。
对于其焊缝部分复杂的空间结构的检测,经过不断地研究、开发和完善,目前超声检测已成为最主要的检测方法。
随着新技术的发展,一些新的无损检测技术和方法也逐步应用于该场合,尤其是超声相控阵技术。
综述了 TKY 管节点焊缝超声检测的发展概况,介绍了适用于 TKY管节点焊缝超声检测的各种方法,并对 TKY 管节点焊缝无损检测技术的发展方向进行了展望。
%TKY tubular joints and similar structure is widely used in steel structure and marine platform,which presents a severe challenge to nondestructive testing technology.For the specific and complicated welding part,UT (ultrasonic testing)is the most useful method so far.With the scientific development and application of new technology,some new nondestructive testing methods and means have gradually applied,such as phased array ultrasonic technology.The context not only reviewed the development condition of UT,but also recommended methods that were appropriate for the TKY tubular joints.Finally, it intended to make prospects for the nondestructive detecting technology in the respect.【期刊名称】《无损检测》【年(卷),期】2015(000)005【总页数】4页(P60-62,67)【关键词】TKY 管节点;焊缝;超声检测;相控阵【作者】简添福;潘文超;陆铭慧;郑志忠【作者单位】福建省锅炉压力容器检验研究院漳州分院,漳州 363000;南昌航空大学无损检测技术教育部重点实验室,南昌 330063;南昌航空大学无损检测技术教育部重点实验室,南昌 330063;福建省锅炉压力容器检验研究院漳州分院,漳州 363000【正文语种】中文【中图分类】TG115.28钢结构由于其具有强度高、韧性好、刚度大、占地空间少、外观优美等优点,在建筑行业及海洋工程领域得到了广泛应用。
常见组合构件相贯线的计算公式

常见组合构件相贯线的计算公式《常见组合构件相贯线的计算公式》
随着科技的发展,组合构件越来越多地应用于当今的计算技术。
它能够产生新
的结构,并为用户提供更强大的功能。
相贯线是组合构件的主要功能,是实现其功能的关键要素之一。
在结构分析和设计中,经常要计算组合构件的相贯线。
计算可以使用公式方法,而这些公式如果使用正确,可以很好地评估不同结构的组合构件的相贯性。
常见的组合构件固定杆件或板材的相贯线计算公式基本如下:
∆Y=L-R1-R2
其中,"L"是固定杆件或板材的长度,"R1"是受影响组件的抗压力系数,"R2"
是力向补偿系数。
另外,由于组合构件的性质,常见的3种组件的相贯线计算公式如下:
∆Y=L-2R;
∆Y=L-2R1-R2;
∆Y=L-2R1-2R2-R3。
其中,R1,R2和R3是每个受影响组件的抗压力系数,L是固定杆件或的板材的
长度,"R"代表系数的力向补偿。
以上就是关于常见组合构件相贯线的计算公式的介绍,希望能够给大家带来帮助。
资深结构规划师了解不同类型和构件的相贯线计算公式,在计算结构力学上给出理性的判断,它可以为计算机技术的发展起到重要的作用。
3-3相贯线

[例五]求两偏交圆柱的交线。 例五]求两偏交圆柱的交线。 投影分析 两圆柱面分别垂直于水平 作图方法 面和侧面, 面和侧面,所以交线水平投影 积聚在小圆柱的水平投影上, 积聚在小圆柱的水平投影上, 辅助平面法。 辅助平面法。取一正平面 交线的侧面积聚在大圆柱的侧 为辅助平面, 为辅助平面,此辅助平面切此 面投影圆弧上( 面投影圆弧上(即在小圆柱轮 。 模型的交线都是圆柱的素线。 模型的交线都是圆柱的素线 廓线之间的一段圆弧)。 廓线之间的一段圆弧)。 这些素线的交点即为相贯线上 的点。 的点。
QH
PW
作图步骤
1. 求特殊位置点。 求特殊位置点。 2. 用辅助平面法求一般位置点。 用辅助平面法求一般位置点。 用光滑曲线连线,并判别可见性。 3. 用光滑曲线连线,并判别可见性。
PH
擦除多余作图线后的结果
例八] [例八]求作两曲面体的交线。
作图方法 辅助球面法— 辅助球面法 同心球面法。 同心球面法。其基本原 理:若一回转面与一球 心在其回转轴上的球面 相交, 相交,则其交线一定是 圆。 投影分析 同心球面法适 同心球面法适 轴线为铅垂线的直立回 用于当两个曲面都是回 转体的水平投影有积聚性。 转面时, 转面时,且它们的轴线 倾斜圆柱的轴线为正平线, 相交并平行于投影面。 相交并平行于投影面 其正面投影有积聚性。 。
相贯线为椭圆
(1)两等直径圆柱正交或斜交,相贯线为两个椭圆。 两等直径圆柱正交或斜交,相贯线为两个椭圆。
(2)圆柱与圆锥、圆锥与圆锥相交,若它们能公切 2 圆柱与圆锥、圆锥与圆锥相交, 一个球面,则相贯线为两个椭圆。 一个球面,则相贯线为两个椭圆。
(四)组合相贯线
[例九] 补画主视图 例九] 作图步骤 形体分析
作图方法
相贯线及画法举例

一、概述两立体表面的交线称为相贯线,见图5-14a和b所示的三通管和盖。
三通管是由水平横放的圆筒与垂直竖放的带孔圆锥台组合而成。
盖是由水平横放的圆筒与垂直竖放的带孔圆锥台、圆筒组合而成。
它们的表面(外表面或表面)相交,均出现了箭头所指的相贯线,在画该类零件的投影图时,必然涉及绘制相贯线的投影问题。
讨论两立体相交的问题,主要是讨论如何求相贯线。
工程图上画出两立体相贯线的意义,在于用它来完善、清晰地表达出零件各部分的形状和相对位置,为准确地制造该零件提供条件。
(一)相贯线的性质由于组成相贯体的各立体的形状、大小和相对位置的不同,相贯线也表现为不同的形状,但任何两立体表面相交的相贯线都具有下列基本性质:1.共有性相贯线是两相交立体表面的共有线,也是两立体表面的分界线,相贯线上的点一定是两相交立体表面的共有点。
2.封闭性由于形体具有一定的空间围,所以相贯线一般都是封闭的。
在特殊情况下还可能是不封闭的,如图5-15c所示。
3.相贯线的形状平面立体与平面立体相交,其相贯线为封闭的空间折线或平面折线。
平面立体与曲面立体相交,其相贯线为由若干平面曲线或平面曲线和直线结合而成的封闭的空间的几何形。
应该指出:由于平面立体与平面立体相交或平面立体与曲面立体相交,都可以理解为平面与平面立体或平面与曲面立体相交的截交情况,因此,相贯的主要形式是曲面立体与曲面立体相交。
最常见的曲面立体是回转体。
两回转体相交,其相贯线一般情况下是封闭的空间曲线(如图5-15a),特殊情况下是平面曲线(如图5-15 b)或由直线和平面曲线组成(如图5-15c ).(二)求相贯线的方法、步骤求画两回转体的相贯线,就是要求出相贯线上一系列的共有点。
求共有点的方法有:面上取点法、辅助平面法和辅助同心球面法。
具体作图步骤为:(1)找出一系列的特殊点(特殊点包括:极限位置点、转向点、可见性分界点);(2)求出一般点;(3)判别可见性;(4)顺次连接各点的同面投影;(5)整理轮廓线。
第九章相贯线

⒉ 作图
当相贯线的投影为非圆曲线时,其作图步 骤为: ⑴ 找点 ☆ 先找特殊点 特殊点包括:最上点、最下点、最左点、 最右点、最前点、最后点、 轮廓线上的点等。 ☆ 补充若干中间点 ⑵连线 ⑶检查、加深 尤其注意检查回转体轮廓素线的投影。
P
假想用水平面P截切立体,P面与圆柱 体的截交线为两条直线,与圆锥面的交线 为圆,圆与两直线的交点即为交线上的点。
例 :圆柱与圆锥相贯,求其相贯线的投影。
● ● ● ● ●
● ● ●
●
●
● ●
●
解题步骤: ★ 求特殊点 ★ 用辅助平面法求 中间点 ★ 光滑连接各点
3′ 2′ a′ 1′ a′ 2′ 3′
同心球面法
使用条件: • 两立体均为回 转体 • 两回转体的轴 线相交
最大球 最小球
最内点
Pv o′
辅助球球心
注意: 不是最内点! •两回转体轴线所确定平面//某投影面 最大球! 最小球! •辅助球球心位于二轴线交点处 最小球? •过二轮廓线最远交点的球为最大球 •两内切球中大者为最小球 o′ •俯视图的交线利用面上找点法完成 •特殊点(最高、最内…)可用: 辅助平面法、辅助球面法、换面法及 最内点 面上找点法求得 无法直 若不能直接求得,则应保证二投影对正 接求得。
1′ b′
最内点!
b〞 4〞 a〞 3〞 1〞 b〞 2〞 a〞 QW PW
注意: 辅助面法找点, 辅助面的位置: 平行圆柱的轴线, 垂直圆锥的轴线。
2′4′ a′ 3′
RW
a 3
4
b
a
1 b 2
重点: • 找到相贯线的已知投影 • 想出相贯线的空间形状 • 找点的方法(辅助面的确定)
圆柱与圆锥相交
求两曲面体相交相贯线常用的方法

在几何学中,两曲面体相交相贯线的求解是一个重要且复杂的问题。
相交相贯线是指两个曲面体相交所形成的曲线或曲线的一部分。
这个问题在工程、建筑、地质学和日常生活中都有广泛的应用,因此其求解方法也变得极为重要。
要求解两曲面体的相交相贯线,我们可以采用多种方法,下面我将简要介绍一些常用的方法。
1. 几何绘图法- 通过几何绘图的方式,我们可以将两个曲面体的截面绘制出来,从而求解它们的相交相贯线。
这种方法相对直观和易于理解,但对于复杂的曲面体,会需要较大的绘图工作量。
2. 解析几何法- 利用解析几何的知识,我们可以通过方程来描述两个曲面体,然后求解它们的交点或交线。
这种方法需要实时计算和分析,对于数学功底较好的人来说比较合适。
3. 数值计算法- 在计算机辅助设计和工程领域,我们可以利用数值计算方法,通过算法和程序来求解曲面体的相交相贯线。
这种方法可以适用于复杂的曲面体,并且计算精度高,但需要具备一定的编程和数值计算能力。
在实际的应用中,以上三种方法可能会结合使用,以求得更为准确和高效的结果。
另外,在具体问题的求解中,我们还需要考虑曲面体的方程形式、曲率、位置关系等因素,从而选择合适的求解方法。
求解两曲面体相交相贯线的方法有很多种,而每种方法都有其适用的场景和优劣势。
在实际操作中,我们需要根据具体问题的要求和条件来选择合适的方法,同时也需要不断学习和探索,以提高求解问题的能力和水平。
个人观点上,我认为在解决任何问题时,都需要全面理解问题的内涵和现状,多角度思考,并结合适当的求解方法来推动问题的解决。
也需要不断学习和积累经验,提升自己的解决问题的能力。
对于求解两曲面体相交相贯线的问题,同样如此。
在实际的工程设计中,常常会遇到需要求解两个曲面体的相交相贯线的问题。
这种问题在建筑设计、机械制造、地质勘探和其他领域都有着重要的应用价值。
掌握求解曲面体相交相贯线的方法,对于工程技术人员来说是十分关键的。
在工程设计中,曲面体的相交相贯线问题通常涉及到不同曲面体之间的连接、交界处的处理、材料切割等。
第六讲 相贯线求法、相贯线应用

一、相贯线的概念和性质 二、相贯的种类
三、两圆柱相贯的三种基本形式
四、相贯线的求法、相贯线应用举例
一、 相贯线的概念和性质
1.概念
一、 相贯线的概念和性质
相贯线为两立体表面的交线。 2.性封闭曲线,两立体表面的共有点的集合; ⑶ 相贯线要画在两个立体的公共部分,若超出一个立体 之外肯定错误; ⑷ 当两个圆柱相贯时,相贯线的形状取决于圆柱的大小、 轴线的相对位置。
两圆柱相贯线的变化趋势(二)
当圆柱的相对位置相对变化时,相贯线的变化趋势
四、相贯线求法、相贯线应用举 1. 实心圆柱×实心圆柱 例
例题 1
四、相贯线求法、相贯线应用举例
2. 实心圆柱×空心圆柱
例题 2 3. 空心圆柱×空心圆柱 例题 3 例题4
4. 截交、相贯在组合体中的应用
例题 5
5. 组合体常见简单结构
[例题1] 求两圆柱的相贯线
a' d' c' e' b'
(实×实)
a" b" d" e" c" 解题步骤 (逐点相连法)
1 分析 相贯线的水平投 影和侧面投影已知,只需 补画主视图;可利用表面 取点法求共有点; 2 求出相贯线上的特殊点 A、B、 C; 3 求出若干个一般点D、E ;
y
y
4 光滑且顺次地连接各点 ,作出相贯线; 5 整理轮廓线。
二、相贯的种类
1. 平面立体与平面立体相贯
2. 平面立体与曲面立体相贯
3. 曲面立体与曲面立体相贯
三、两圆柱相贯的三种基本形式
1. 两外表面相交; 2. 外表面与内表面相交;
3. 两内表面相交。
§4.3 两立体相交求相贯线

共有性——相贯线是两立体表面的共有线,相关线上
的点是相贯两立体表面上的共有点。
作图实质:找两立体表面的若干共有点的投影。
相贯线的形状由两立体的形状和它们的相对位置所确 定。当一个立体全部贯穿另一个立体时,称为全贯,有两 组相贯线;但当一个立体全部穿进另一立体后,不穿出来 了,虽属全贯,便只有一组相贯线。当两个立体互相贯穿
[解]
①作未开孔时的 三棱锥的侧面投 影
②作前后两组孔 口线的水平投影 和侧面投影 ③画出孔壁交线 的投影,补全水 平投影和侧面投 影 (完成作图) (b)解题分析 (c) (d) 作图过程和结果 清理图面后的投影图 (a)已知条件 图2.187 补全具有三棱柱孔的三棱锥的投影
二、平面立体与曲面立体相交
【例】如图a所示,求作三棱柱与三棱锥的相贯线,并补 全相贯体的水平投影和侧面投影。
[解]
①作诸棱线的贯 穿点和两立体的 相贯线
②补全相贯体的 水平投影和侧面 投影 (完成作图)
(c) (d) 作图过程和结果 清理图面后的投影图 (a)已知条件
(b)解题分析
【例】如图a所示,三棱锥被前后穿通了一个正三棱柱形状 的贯通孔,求作孔口线的水平投影,补全这个具有三棱柱贯 通孔的三棱锥的水平投影,并作出它的侧面投影。
空间分析: 具有同坡屋面屋顶的楼房。
同坡屋面屋顶立体图。
平脊 斜脊 屋面交线交点 屋檐多边形
斜沟
同坡屋面特点:
(1)坡屋面如前后檐口线平行
且等高时,前后坡面必相交成 水平的屋脊线,屋脊线的H投影, 必平行于檐口线的H 投影,且与檐口线等距。 ( 2 )同坡屋面的正投影和侧面投影中斜脊线和斜沟线与 水平线的角度反映出同坡屋面和地面的坡度。 (3)三个相交的坡面的三条交线必交于一点。 作同坡屋面的投影图,可根据同坡屋面的投影特点, 直接求得水平投影,再根据各坡面与水平面的倾角求得 V 面投影以及W 面投影。
管道相交线画法

管道相交线画法第四讲圆柱相贯线1.知识要点(1)外圆柱面和外圆柱面相贯:实实相贯(2)内圆柱面和内圆柱面相贯:空空相贯(3)内圆柱面和外圆柱面相贯:空实相贯(4)直径相等的圆柱面相贯(5)相贯线的近似画法2.教学设计:外与外、外与内、内与内圆柱面相交产生的交线性质是相同的,画法原理也是相同的,只是在可见性上有点不同。
教学中要强调相贯线的三个投影,不要只注意相贯线投影为曲线的那个投影,要强调特殊点的三面投影。
结合具体示例讲解相贯线的画法规律。
3.课前准备准备教具4.教学内容(1)圆柱体正交的三种情况(电子挂图配仿真模型,注意相贯线的三个投影和特殊点的投影)表4-4圆柱相贯线[例1]外圆柱面和外圆柱面相交(仿真模型)【作图步骤】如图4-11所示1)首先画出两个圆柱轮廓线的三视图,确定两个圆柱的相对位置;2)求特殊点的正面投影。
所谓特殊点,就是两个柱面转向轮廓线上的点和表示相贯线空间极限范围的点,本例中的A、B、C、D即为柱面对V面和H面转向轮廓线上的点,也是空间曲线最高点、最低点、最后点和最前点。
3)求一般点的投影。
如M和N点,可先确定其水平投影,根据宽相等求出其侧面投影,最后求出正面投影。
4)根据点在空间的连接顺序,用曲线板连接成光滑曲线。
图4-11圆柱相贯线画法[例2]直径相等的两个外圆柱面相交(用动画演示)上例中假想大圆柱的直径不变,而小圆柱的直径变大,D点的V面投影将向右移动,A点V面投影将向上移动。
当两个圆柱的直径相等时,相贯线将由空间曲线变为平面曲线椭圆,若竖直放置的圆柱面只有左半个柱面参与相贯,则相贯线的空间形状为两段椭圆弧,且椭圆平面和V面处于垂直位置,所以,相贯线的V面投影为两段直线。
【分析】若两个直径相等的柱面互相贯穿,则相贯线为两个完整的椭圆,两个椭圆在柱面不反映圆的视图上,聚积成直线。
如图4-12所示。
图4-12直径相等的两个柱面相交[例3]外圆柱面和内圆柱面相交(仿真模型,本例的目的是介绍近似画法)【分析】外圆柱面和内圆柱面相交、内圆柱面和内圆柱面相交时,相贯线的形状和外圆柱面与外圆柱面相交时相贯线的形状相同,画法也完全一样。
主管支管相交计算公式

主管支管相交计算公式
主管与分支管相交计算公式的推导基于流体力学基本原理,其中涉及
到流量、速度、管道直径、流速、摩阻等参数。
这些参数的计算公式主要
有以下几个:
1.流量计算公式:
流量Q=A*v
其中,Q为流量,单位为立方米/秒;A为断面积,单位为平方米;v
为平均流速,单位为米/秒。
2.流速计算公式:
流速v=Q/A
其中,v为平均流速,单位为米/秒;Q为流量,单位为立方米/秒;A
为断面积,单位为平方米。
3.流体压力计算公式:
p=ρ*g*h
其中,p为压力,单位为帕斯卡;ρ为流体的密度,单位为千克/立
方米;g为重力加速度,单位为米/秒的平方;h为流体的高度,单位为米。
4.流体速度计算公式:
v=√(2*g*h)
其中,v为速度,单位为米/秒;g为重力加速度,单位为米/秒的平方;h为流体的高度,单位为米。
5.摩擦损失计算公式:
hf = (f * L * v^2) / (2 * g * D)
其中,hf为摩擦损失,单位为米;f为摩擦系数;L为流体流动的管
道长度,单位为米;v为流速,单位为米/秒;g为重力加速度,单位为米
/秒的平方;D为管道的直径,单位为米。
这些公式是主管支管相交计算的基本公式,通过代入相关参数的数值,可以得出主管与分支管相交时的压力、流量、流速、摩擦损失等信息,以
指导管网设计与施工。
在实际应用中,还需考虑管道的材料、细节设计等
因素,以获得更精确的结果。
圆管相贯线三维坐标方程的推导

圆管相贯线三维坐标方程的推导在采用数控机床加工零件时,往往会遇到零件形状是由复杂的空间曲线构成。
已知条件是曲线的方程,这些方程可能是直接得到的,或者是通过轮廓形状上的一些关键点,通过拟合的方法得到近似的曲线方程。
特别在起重机、锅炉制造等行业经常有不同管径的圆管交叉连接。
其中两管相贯线的确定和精确切割加工是一个难点。
常用的方法是在知道管的相对位置等条件下,经过计算手工制出模板,用模板画线,手工切割。
其过程十分烦琐,且切割精度也无法保证。
数控加工的目的在于按照已知的曲线方程加工零件,因此将曲线转换为数控加工需要的数控代码是很重要的一个环节。
如果用手工编程,则效率低、可靠性差,不能充分发挥机床的功能和性能。
随着CAD/CAM技术的发展,国外许多高档的CAD软件都具有相应的CAM模块。
例如美国SRDC公司的I_DEAS、PTC公司的Pro/E、UG、SolidWork等性能良好的CAM模块。
利用其三维实体数据生成数控加工代码,通过通讯接口传输到数控机床的数控系统。
也有一些第三方开发的CAM模块,可与CAD软件无缝集成,完成数控代码的生成。
然而,这些软件相对来说要求高,价格昂贵。
且没有配置专用的后置处理器,或者只配置了通用的后置处理器而没有根据数控机床的特点进行二次开发,由此产生的代码还需要做大量的手工修改。
本文以Autodesk公司的AutoCAD2000为平台,利用其内嵌的ARX编程工具,针对生产现场的数控切割机床加工两管的相贯线,开发了一套能够计算并自动获得相贯线数控加工代码的系统。
通过设置刀具路径等工艺参数和后置处理,最后生成NC代码,供数控机床加工零件。
此过程可以节省大量的人力和时间。
并且最大限度的减少人为和系统因素的影响,使管缝切割精度高,保证焊接质量更加稳定可靠。
在一定程度上弥补了零件制造从设计到成型的薄弱环节。
1.数学模型的建立两个圆管的相交形式多样。
但都是两个相同或者不同直径的圆柱面以一定的角度相交形成的空间曲线。
