5常用概率分布3
概率论与数理统计公式整理

概率论与数理统计公式整理在现代数学中,概率论与数理统计是两个重要的分支。
其中概率论是研究随机事件发生的可能性或概率的科学。
而数理统计则是利用概率论的方法,对已经发生的随机事件进行统计分析和推断。
本文将整理概率论与数理统计中常用的公式。
一、基本概率公式1.概率:$P(A)=\frac{n(A)}{n(S)}$其中,$P(A)$表示事件$A$发生的概率,$n(A)$表示事件$A$所包含的基本事件的个数,$n(S)$表示所有基本事件的个数。
2.加法原理:$P(A\cup B)=P(A)+P(B)-P(A\cap B)$其中,$A$和$B$是两个事件,$A\cup B$表示事件$A$和事件$B$中至少有一个发生的概率,$A\cap B$表示两个事件同时发生的概率。
3.条件概率:$P(B|A)=\frac{P(A\cap B)}{P(A)}$其中,$P(B|A)$表示在事件$A$发生的条件下,事件$B$发生的概率。
4.乘法定理:$P(A\cap B)=P(A)P(B|A)$其中,$P(A\cap B)$表示两个事件同时发生的概率,$P(B|A)$表示在事件$A$发生的条件下,事件$B$发生的概率。
二、概率分布1.离散随机变量的概率分布律:$\sum\limits_{i=1}^{+\infty}{p(x_i)}=1$其中,$p(x_i)$表示离散随机变量取值为$x_i$的概率。
2.连续随机变量的概率密度函数:$\int_{-\infty}^{+\infty}{f(x)}\mathrm{d}x=1$其中,$f(x)$表示连续随机变量在$x$处的概率密度。
3.数学期望:$E(x)=\sum\limits_{i=1}^{+\infty}{x_ip(x_i)}$或$E(x)=\int_{-\infty}^{+\infty}{xf(x)}\mathrm{d}x$其中,$E(x)$表示随机变量$x$的数学期望,$p(x_i)$表示$x_i$这一离散随机变量取到的带权概率。
16种常见概率分布概率密度函数、意义及其应用

目录1. 均匀分布 (1)2. 正态分布(高斯分布) (2)3. 指数分布 (2)4. Beta分布(:分布) (2)5. Gamm 分布 (3)6. 倒Gamm分布 (4)7. 威布尔分布(Weibull分布、韦伯分布、韦布尔分布) (5)8. Pareto 分布 (6)9. Cauchy分布(柯西分布、柯西-洛伦兹分布) (7)210. 分布(卡方分布) (7)8 11. t分布................................................9 12. F分布 ...............................................10 13. 二项分布............................................10 14. 泊松分布(Poisson 分布).............................11 15. 对数正态分布........................................1. 均匀分布均匀分布X ~U(a,b)是无信息的,可作为无信息变量的先验分布。
2. 正态分布(高斯分布)当影响一个变量的因素众多,且影响微弱、都不占据主导地位时,这个变量 很可能服从正态分布,记作X~N (」f 2)。
正态分布为方差已知的正态分布N (*2)的参数」的共轭先验分布。
1 空f (x ): —— e 2-J2 兀 o'E(X), Var(X) _ c 23. 指数分布指数分布X ~Exp ( )是指要等到一个随机事件发生,需要经历多久时间。
其 中,.0为尺度参数。
指数分布的无记忆性:Plx s t|X = P{X t}。
f (X )二 y oiE(X) 一4. Beta 分布(一:分布)f (X )二 E(X)Var(X)=(b-a)2 12Var(X)二1~2Beta 分布记为X 〜Be(a,b),其中Beta(1,1)等于均匀分布,其概率密度函数 可凸也可凹。
第三章 常用概率分布之正态分布

图4.13 离均差的绝对值≤1 , 2 和3 的概率值
随机变量x在区间( μ – kσ, μ + kσ )外取值的概率P ( x<μ – kσ ) + P( x>μ + kσ )为两尾概率,记为α P ( x<μ – kσ ) + P( x>μ + kσ )=α P ( x<μ – kσ ) = P( x>μ + kσ )=α/2 两尾分位数Uα
=0.0227
0.020
fN (x)
0.020
fN (x)
0.016
0.016
0.012
0.012
0.008
P( y 40) 0.9773
P( y 26) 0.2119
0.008
0.004
0.004
0.000 10 15 20 25 30 35 40 45
0.000 10 15 20 25 30 35 40 45
第三章
常用概率分布
第一节 事件与概率 第二节 概率分布 第三节 二项式分布 第四节 正态分布 第五节 样本平均数抽样分布与标准误 第六节 t分布,x2分布和F分布
第三章
常用概率分布
第一节 事件与概率 第二节 概率分布 第三节 二项式分布 第四节 正态分布 第五节 样本平均数抽样分布与标准误 第六节 t分布,x2分布和F分布
首先计算:
查附表2,当u=-0.8时,FN(26)=0.2119,说明这 一分布从-∞到26范围内的变量数占全部变量数的 21.19%,或者说,y≤26概率为0.2119. 同理可得: FN(40)=0.9773
所以:P(26<y≤40)=FN(40)-FN(26)=0.9773-0.2119
概率统计方法

第七章概率统计方法概率分布及数字特征;样本与统计量;参数估计法;案例分析:足球门的危险区域问题;案例分析:最优评卷问题。
1.一维随机变量与分布函数一.概率分布与数字特征随机变量:用数值表示的随机事件的函数。
分布函数:设ξ为一随机变量,对任意的实数x 有函数)()()(x P x P x F ≤=≤<-∞=ξξ称为随机变量ξ的分布函数。
对任意两个实数)(,2121x x x x <,则有)()()(1221x F x F x x P -=≤<ξ如果随机变量ξ所有取值有限个或可列无穷个数值,则这种随机变量为离散型随机变量。
非离散型的随机变量,则称为连续型的随机变量。
如果ξ为离散型随机变量,所有的取值为 ,2,1,=k x k ,则称 ,2,1,)(===k p x P k k ξ为随机变量ξ的分布列,其相应的分布函数为∑≤=x x k k px F )(。
如果ξ为连续型随机变量,则分布函数定义为 ⎰∞-=xdx x f x F )()(,其中)(x f 为一个非负可积函数,称之为随机变量ξ的分布密度,或密度函数。
具有下列性质: (1)0)(≥x f ; (2)1)(=⎰+∞∞-dx x f ;(3)dx x f a F b F b a P ba ⎰=-=≤<)()()()(ξ;(4)当)(x f 为连续函数时有)()(x f x F ='。
(1)数学期望设ξ为离散型随机变量,其分布列为 ,2,1,)(===k p x P k k ξ,如果级数∑∞=1k k k p x收敛,则称∑∞=1k k k p x 为随机变量ξ的数学期望,记为ξE ,即∑∞==1k k k p xE ξ。
2. 随机变量的数学期望与方差一.概率分布与数字特征设ξ为连续型随机变量,其分布密度函数为 )(x f ,如果dx x f x ⎰+∞∞-)(收敛,则称dx x xf ⎰+∞∞-)(为随机变量ξ的数学期望,记为ξE ,即dx x xf E ⎰+∞∞-=)(ξ。
概率论 常用统计分布

由中心极限定理得
n
lim P {
n
2 n n
2n
x}
x
lim P{ i 1
n
2 X i n
n
x}
1 2
t2 e 2 dt
即 2分布的极限分布是正态 分布,也即当 n
很大时,
2 n n
2n
2 服从N (0,1), 进而 n N ( n,2n).
Y12
Y22
~ 2 ( 2)
则C1 1 2 , C2 1 4 .
2. t 分布 历史上,正态分布由于其广泛的应用背景 和良好的性质,曾一度被看作是“万能分布”, 在这样的背景下,十九世纪初英国一位年轻 的酿酒化学技师Cosset. WS, 他在酒厂从事试验 数据分析工作,对数据误差有着大量感性的认 识,我们知道在总体均值和方差已知情况下, 样本均值的分布将随样本量 增大而接近正态分布,
n
x
1 2
e dt .
t2
2
2 证 由假设和定义5.6, n X i2 , 其中X 1 , X 2 ,, X n i 1
2 2 2 独立且每个X i ~ N (0,1),因而X1 , X2 ,, X n 独立同分布,
且
E( X i2 ) 1, D( X i2 ) 2 (i 1,2,, n)
(3) T的数字特征
E (T ) 0,
n D(T ) n2
( n 2).
例3 设总体X和Y相互独立, 且都服从N(0,9)
X 1 , X 2 ,, X 9和Y1 ,Y2 ,,Y9来自总体X ,Y的样本,
求统计量T的分布,其中
T Xi /
16种常见概率分布概率密度函数、意义及其应用

目录1. 均匀分布 ...................................................................................................... 1 2. 正态分布(高斯分布) ........................................................................... 2 3. 指数分布 ...................................................................................................... 2 4. Beta 分布(β分布) ............................................................................. 2 5. Gamma 分布 .................................................................................................. 3 6. 倒Gamma 分布 ............................................................................................. 4 7. 威布尔分布(Weibull 分布、韦伯分布、韦布尔分布) ................. 5 8. Pareto 分布 ................................................................................................ 6 9. Cauchy 分布(柯西分布、柯西-洛伦兹分布) . (7)10. 2χ分布(卡方分布) (7)11. t 分布 ........................................................................................................ 8 12. F 分布 ........................................................................................................ 9 13. 二项分布 ................................................................................................ 10 14. 泊松分布(Poisson 分布) ............................................................. 10 15.对数正态分布 .......................................................................................111. 均匀分布均匀分布~(,)X U a b 是无信息的,可作为无信息变量的先验分布。
常见概率分布期望方差以及分布图汇总
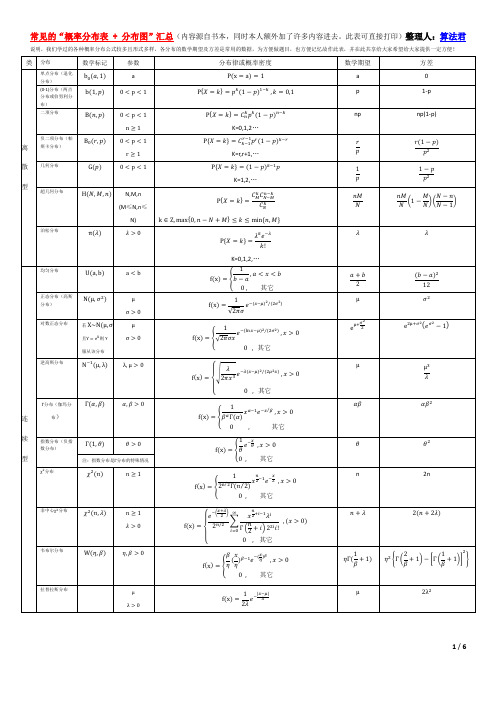
������������
������������ 2
指数分布(负指 数分布)
Γ(1, ������)
������ > 0
������
������ 2
注:指数分布是Γ分布的特殊情况 χ2 分布
������2 (������)
������ ≥ 1
负二项分布(帕
离 散 型
斯卡分布)
B0 (������, ������)
0<p<1 r≥1
K=r,r+1,… P{������ = ������} = (1 − ������)������−1 ������ K=1,2,…
������ ������ 1 ������ ������������ ������
������ 2 ∞ ������⁄ 2
0,n>1
������ , ������ > 2 ������ − 2
非中心 t 分布
������(������, ������)
������ ������ ≥ 1
������ − 1 ������Γ ( ) ������ 2 √ ������ 2 Γ( ) 2 (n>1)
常见的“概率分布表 + 分布图”汇总(内容源自书本,同时本人额外加了许多内容进去。此表可直接打印)整理人:算法君
说明,我们学过的各种概率分布公式较多且形式多样,各分布的数学期望及方差是常用的数据,为方便做题目,也方便记忆故作此表,并在此共享给大家希望给大家提供一定方便!
类
分布
单点分布(退化 分布) (0-1)分布(两点 分布或伯努利分 布) 二项分布
数学期望 a p np
常用概率分布间简介

其中 c 为常数,解方程(1)得
f ( ) c f ( )
f
(
)
k
e
1 2
c
2
,
k
为常数.
为使 f ( ) 为概率密度函数,
f
( )d
1,
即
k
e
1 2
c
2
dy
1
故必须 c 0 ,不妨令 c 1 ( 0 ),代入(2)解得 2
k 1 , 2 Biblioteka 于是f ( ) 1
2
e2 2 , R ,
2
这是均值为 0,方差为 2 的正态分布的概率密度函数.
.
X
~
N(0, 2)
,
则Y
X2
~
Ga(
1 2
,
1 2
2
)
.
(1) (2)
Ga( n , 1) 2(n) . 22
m
Xi ~ N(0,1) , i 1,2,,n 且相互独立 , 则 X
X
2 i
~
2(n) .
i 1
⒊ 相当误差(比率)的概率分布
m
设
Xi
~
N(0, 2 ) ,i
1,2,, m,m 1,,m n且相互独立,则
i 1
二、随机误差的概率分布
⒈ 高斯随机误差模型 随机变量的高斯分解
可观测的指标
X
不可观测的随机干扰
指标的标准值(生产控制参数,理论均值)
原始测量误差的概率分布
由棣莫弗提出,高斯推证,拉普拉斯再证,原始测量误差的概率分布为:
~ N (0 , 2 )
高斯的推证要点如下:
设测量误差 X 的密度函数为 f ( ) ,由“最大后验概率”的原则得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P(x) 0.5 0.4 0.3 0.2 0.1 0
0 1 2 3 4 5 6 7 8
150
1 [8.471010 1.90108 ]
1
9 10 11 12 13 14 15
n=10,π =0.3
x
Poisson分布 (Poisson Distribution)
Siméon-Denis Poisson
二项分布的定义
总体阳性率 样本含量 n 在总体率为 的总体中随机抽样,抽取样本含量 为n的样本,有X例为阳性的概率:
P( X ) CnX X (1 ) n X
称X服从二项分布,记为:X~B(n,)
n! C X !(n X )!
X n
n! n( n 1 )( n 2 )1
Poisson分布(Poisson Distribution) 正态分布(Normal Distribution)
二项分布 (Binomial Distribution)
二项分布
0.20 1 0.80
n3
X
0
概率
0.8×0.8×0.8 0.2×0.8×0.8 0.8×0.2×0.8 0.8×0.8×0.2
150 ! P(10) 0.1310 0.87140 0.0055 10!(150 10)!
6 7 8 9 10 11 12 13 14 15
n=10,π =0.3
x
二项分布累计概率计算
二项分布出现阳性的次数至多为k次的概率为:
P( X k ) P( X ) p(0) p(1) ... p(k )
Poisson分布的定义
可以证明: 很小,n很大时,单位(面积、容 积、时间等)内某稀有事件发生数X的概率
P( X ) CnX X (1 ) n X
P( X ) e
X
X!
n
称X服从Poisson分布,记作X~Poisson( ) X=0,1,2,……。
21 June 1781 (Pitviers) - 25 Apr 1840 (Paris)
很小,n很大,
总体
0.0001 0.9999
X为单位(面积、容积、时间 等)内某稀有事件发生数。
10万(单位人口)人中某恶性 肿瘤的发生数;
1ml(单位体积)水中大肠杆菌 数;
1h(单位时间)内放射物质的 放射次数; 显微镜中1个视野(单位面积) 内血细胞的计数; 1cm3(单位体积)空气中粉尘 的计数; ……
二项分布的均数和标准差
如果每次试验出现阳性结果的概率均为π,进行n 次独立重复试验,出现X次阳性结果,则X的 总体均数: 总体方差:
X n n 1
2 X X
P(x) 0.5 0.4 0.3 0.2 0.1 0
0 1 2 3 4 5 6 7 8
总体标准差:
0.512
1
1 C3 0.21 (1 0.2) 2
0.384
2
P( X ) CnX X (1 ) n X
C 0.2 (1 0.2)
2 3 2
1
3
0.096 3 C3 0.23 (1 0.2) 0 0.008
0
1
2
3
0.512 0.384 0.096 0.008 (0.2 0.8)3 1
Poisson分布的应用条件
观察结果是二分类变量,如阳性与阴性、治愈与 未愈、生存与死亡等; 每个观察对象发生阳性结果的概率为,发生阴性 结果的概率为1- ; 各个观察对象的结果是相互独立的; 接近0或1。
某地20年间共出生肢短畸形儿10名,现随机抽取1年, 这1年中出生肢短畸形儿的人数为X,则X分别为0,1, 2,……的概率为?
n 总体标准差: (1 ) p n
6 7 8 9 10 11 12 13 14 15
n=10,π =0.3
x
实例:已知钩虫感染率为6.7%,如果随机 抽查某地150人,记样本钩虫感染率为p , 求 p 的标准差(抽样误差) p 。
p
(1 )
n
0.067(1 0.067) 0.96
P( X 4) P( X ) p(0) p(1) p(2) p(3) p(4)
X 0 4
e 0.96 0.960 e 0.96 0.961 e 0.96 0.962 e 0.96 0.963 e 0.96 0.964 0! 1! 2! 3! 4! 0.997
二项分布的应用条件
观察结果是二分类变量,如阳性与阴性、治愈与未 愈、生存与死亡等; 每个观察对象发生阳性结果的概率为,发生阴性 结果的概率为1- ; 各个观察对象的结果是相互独立的。
二项分布的图形(见pdf.sas)
P(x) 0.5 0.4 0.3 0.2 0.1 0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
X 0
k
P(x) 0.5 0.4 0.3 0.2 0.1 0
0 1 2
出现阳性的次数至少为k次的概率为:
P( X k ) P( X ) 1 p( X k 1)
X k
n
或p(k ) p(k 1) ... p(n)
3
4
5
6
7
8
9 10 11 12 13 14 15
X 0 X 0
P(x) 0.4 0.3 0.2 0.1 0
0 2 4 6 8 10 12 14 16 18 20 22
X
X!
至少为k次的概率为:
P( X k ) 1 P( X )
X 0
k 1
或p(k ) p(k 1) ... p(n)
λ =3
x
例4-8:如果某地新生儿先天性心脏病的发病概率 为8‰,那么该地120名新生儿中至多有4人患先天 性心脏病的概率有多大?
P( X ) e
X
X!
表4-2 某地每年出生肢短畸形儿概率分布
X P(X)
0 0.607
1 0.303
2 0.076
3 0.013
4 0.002
5 0.000
表4-2 某地每年出生肢短畸形儿概率分布
X P(X)
P(X)
0 0.607
1 0.303
2 0.076
3 0.013
4 0.002
n 120 0.008 0.96
P( X 4) e
X
e 0.96 0.964 0.014 X! 4!
λ =3
x
Poisson分布累计概率
如果稀有事件发生次数的总体均数为λ,那么该稀 有事件发生次数X至多为k次的概率为 :
k k
P( X k ) P( X ) e
n 1
9 10 11 12 13 14 15
n=10,π =0.3
x
二项分布的均数和标准差
X 如果出现阳性结果的频率为 p ,则p的 n
总体均数: 总体方差:
p
p
2
(1 )
P(x) 0.5 0.4 0.3 0.2 0.1 0
0 1 2 3 4 5
λ =1
P(x) 0.4 0.3 0.2 0.1 0
0 2 4 6 8 10 12 14 16
x
P(x) 0.4 0.3 0.2 0.1 0
18 20 22
0 2 4 6
λ =3
x
8
10
12
14
16
18
20
22
λ =6
x
λ =10
x
Poisson分布的图形特征
离散型分布 Poisson分布的图形与 有关。 愈小,分布 愈偏,随着 增大,分布趋于对称。
x
9 10 11 12 13 14 15
0
1
2
3
4
5
6
7
8
9 10 11 12 13 14 15
n=10,π =0.3
x
n=20,π =0.3
x
图4-2 π=0.3时, 不同n值对应的二项分布
二项分布的图形
图4-1 π=0.5时,不同n值对应的二项分布
二项分布的图形特征
离散型分布
二项分布图的形态取决于n与,高峰在=n处 当接近0.5时,图形对称;离0.5愈远,对称性愈差, 但随着n的增大,分布趋于对称。 当n→∞时,只要不太靠近0或1, 二项分布近似于正 态分布。
P(x) 0.5 0.4 0.3 0.2 0.1 0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
n=3,π =0.3
P(x) 0.5 0.4 0.3 0.2 0.1 0
0 1 2 3 4 5 6 7 8
x
n=6,π =0.3
P(x) 0.5 0.4 0.3 0.2 0.1 0
10
1.9010 2.1110
8
7
2.31107
9 10 11 12 13 14 15
n=10,π =0.3
x
例4-6:某地钩虫感染率为13%,随机抽查当地150人,其中至少 有2名感染钩虫的概率有多大?
P( X 2) P( X ) 1 [ p(0) p(1)]
二项分布概率估计
例4-5 :如果某地钩虫感染率为13%,随机观察当 地150人,其中有10人感染钩虫的概率有多大?
