二分法和改进的平方根法Matlab程序
matlab程序运行修改版 二分法等等

1、拉格朗日插值公式:function y=lage(X,Y,x)% 拉格朗日插值函数n=length(X);y=zeros(size(x));for k=1:nw=ones(size(x));for j=[1:k-1 k+1:n]w=(x-X(j))./(X(k)-X(j)).*w;endy=y+w*Y(k);end调用方法:在matlab中新建一个script窗口,把上述程序保存成(lage.m)文件,然后在命令窗口调用y=lage(A,B,x),其中A,B均为列向量,分别代表插值点的横坐标和纵坐标,x为待求点横坐标例如:现有x0=1,x1=2,x2=4,y0=3,y1=2,y2=7;要求x=1.5处的估计值。
过程:则A=[1 2 3]’,B=[3 2 7]’,x=1.5在命令窗口输入如下命令:A=[1 2 3]’;B=[3 2 7]’;x=1.5;y=lage(A,B,x)(注意:这个直接占到命令窗口会出现符号问题,请自行修改)y即为所求结果2、牛顿插值公式:function f=niudun(X,Y,x)n=length(X);A=zeros(n,n);%A用于存储均差表(空余位置设为0)A(:,1)=Y;t=A(1,1);for j=2:nfor i=j:nl=1;A(i,j)=(A(i,j-1)-A(i-1,j-1))./(X(i)-X(i-j+1));%算出均差表if i==j%只取每列非0的第一个数for k=1:j-1l=l.*(x-X(k));%通项计算endt=t+l.*A(i,j);%各项累加求结果endendendf=t;在matlab中新建一个script窗口,把上述程序保存成(niudun.m)调用方法:y=niudun(A,B,x) A,B,x的定义与拉格朗日函数相同3、雅克比迭代法:function [y,n]=yacobi(a,d)format long;x=[0;0;0]; %³õʼÏòÁ¿stop=1.0e-4 ; %µü´úµÄ¾«¶ÈL=-tril(a,-1);U=-triu(a,1);A=(diag(diag(a)));D=inv(A);X=D*(L+U)*x+D*d; % Jµü´ú¹«Ê½n=1;while norm(X-x,inf)>=stop % ʱµü´úÖÐÖ¹·ñÔò¼ÌÐøx=X;X=D*(U+L)*x+D*d;n=n+1;endy=X;或:function yacobia=[3 0 -2;0 8 1;-1 1 6 ];d=[3;2;2];x=[0;0;0]; %初始向量stop=1.0e-4 ; %迭代的精度L=-tril(a,-1);U=-triu(a,1);A=(diag(diag(a)));D=inv(A);X=D*(L+U)*x+D*d; % J迭代公式n=1;while norm(X-x,inf)>=stop % 时迭代中止否则继续x=X;X=D*(U+L)*x+D*d;n=n+1;endXn在matlab中新建一个script窗口,在这个窗口中(即.m文件中)直接运行(run)上述程序,若题目要求Ax=b,则将a矩阵内容换为A,d内容换为b。
二分法matlab程序

二分法二分法基本思路一般地,对于函数f(x),如果存在实数c,当x=c 时,若f(c)=0,那么把x=c 叫做函数f(x)的零点。
解方程即要求f(x)的所有零点。
假定f(x)在区间(x ,y )上连续先找到a 、b 属于区间(x ,y ),使f(a),f(b)异号,说明在区间(a,b)内一定有零点,然后求f[(a+b)/2],现在假设f(a)<0,f(b)>0,a<b① 如果f[(a+b)/2]=0,该点就是零点,如果f[(a+b)/2]<0,则在区间((a+b)/2,b)内有零点,(a+b)/2>=a ,从①开始继续使用 ② 中点函数值判断。
如果f[(a+b)/2]>0,则在区间(a,(a+b)/2)内有零点,(a+b)/2<=b ,从①开始继续使用 中点函数值判断。
这样就可以不断接近零点。
通过每次把f(x)的零点所在小区间收缩一半的方法,使区间的两个端点逐步迫近函数的零点,以求得零点的近似值,这种方法叫做二分法。
从以上可以看出,每次运算后,区间长度减少一半,是线形收敛。
另外,二分法不能计算复根和重根。
二分法步骤用二分法求方程()0f x =的根*x 的近似值k x 的步骤① 若对于a b <有()()0f a f b <,则在(,)a b 内()0f x =至少有一个根。
② 取,a b 的中点12a b x +=计算1()f x ③ 若1()0f x =则1x 是()0f x =的根,停止计算,运行后输出结果*1x x =若1()()0f a f x <则在1(,)a x 内()0f x =至少有一个根。
取111,a a b x ==;若1()()0f a f x >,则取111,a x b b ==;④ 若12k k b a ε-≤(ε为预先给定的要求精度)退出计算,运行后输出结果*2k k a b x +≈,反之,返回步骤1,重复步骤1,2,3 二分法Mtalab 程序syms x;fun=input('(输入函数形式)fx=');a=input('(输入二分法下限)a=');b=input('(输入二分法上限)b=');d=input('输入误差限 d=')%二分法求根%f=inline(x^2-4*x+4);%修改需要求解的inline 函数的函数体f=inline(fun);%修改需要求解的inline 函数的函数体e=b-a; k=0 ;while e>dc=(a+b)/2;if f(a)*f(c)<0b=c;elseif f(a)*f(c)>0a=c;elsea=c;b=cende=e/2; k=k+1;endx=(a+b)/2;x%x 为答案k%k 为次数例题:用二分法计算方程4324100x x x -++=在(-2,2)内的实根的近似值,要求精度为 解:(输入函数形式)fx=x^4-2*x^3+4*x+10(输入二分法下限)a=-2(输入二分法上限)b=2输入误差限 d=得到结果d =x =k =16>>。
借助Matlab使用二分法求解方程的根
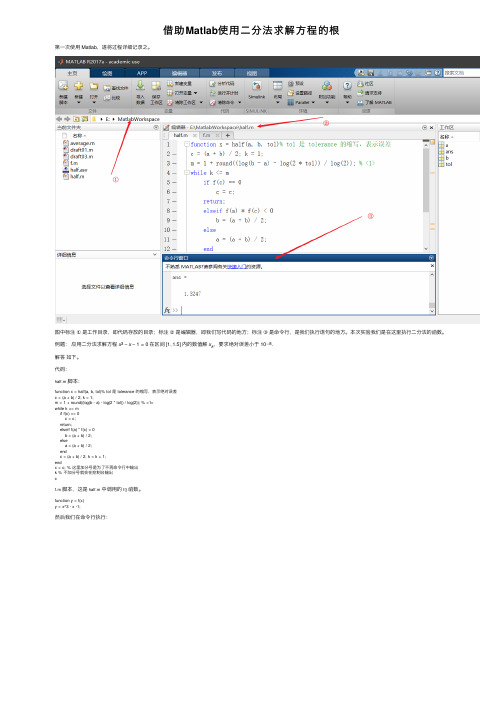
借助Matlab使⽤⼆分法求解⽅程的根第⼀次使⽤ Matlab,遂将过程详细记录之。
图中标注①是⼯作⽬录,即代码存放的⽬录;标注②是编辑器,即我们写代码的地⽅;标注③是命令⾏,是我们执⾏语句的地⽅。
本次实验我们是在这⾥执⾏⼆分法的函数。
例题:应⽤⼆分法求解⽅程x3−x−1=0 在区间 [1,1.5] 内的数值解x k,要求绝对误差⼩于 10−8.解答如下。
代码:half.m脚本:function x = half(a, b, tol)% tol 是 tolerance 的缩写,表⽰绝对误差c = (a + b) / 2; k = 1;m = 1 + round((log(b - a) - log(2 * tol)) / log(2)); % <1>while k <= mif f(c) == 0c = c;return;elseif f(a) * f(c) < 0b = (a + b) / 2;elsea = (a + b) / 2;endc = (a + b) / 2; k = k + 1;endx = c; % 这⾥加分号是为了不再命令⾏中输出k % 不加分号就会在控制台输出cf.m脚本,这是half.m中调⽤的f()函数。
function y = f(x)y = x^3 - x -1;然后我们在命令⾏执⾏:可以看出,最后求解得到的x=1.3247,即输出的ans,迭代次数k=27.关于代码half.m中的标注<1>,有如下解释:注意,在 Matlab 中,log()函数的底是e.补充例题(感兴趣的朋友可以⾃⾏测试):Processing math: 100%。
matlab中的迭代算法

matlab中的迭代算法Matlab中的迭代算法迭代算法是一种通过重复应用某个过程或规则来解决问题的方法。
在Matlab中,迭代算法广泛应用于数值计算、优化问题、图像处理等领域。
本文将介绍几种常见的迭代算法,并通过实例来演示其应用。
一、二分法二分法是一种简单而有效的迭代算法,用于求解函数的根。
其基本思想是通过将区间逐渐缩小,不断逼近根的位置。
具体步骤如下:1. 选择一个初始区间[a, b],使得f(a)和f(b)异号;2. 计算区间的中点c=(a+b)/2;3. 判断f(c)的符号,并更新区间的边界;4. 重复步骤2和3,直到满足精度要求。
二分法的优点是简单易懂,但收敛速度相对较慢。
以下是一个使用二分法求解方程x^2-2=0的示例代码:```matlaba = 1;b = 2;tol = 1e-6;while abs(b-a) > tolc = (a + b) / 2;if (c^2 - 2) * (a^2 - 2) < 0b = c;elsea = c;endendroot = (a + b) / 2;disp(root);```二、牛顿法牛顿法是一种迭代算法,用于求解非线性方程和最优化问题。
其基本思想是通过利用函数的局部线性近似,逐步逼近根或最优解。
具体步骤如下:1. 选择一个初始点x0;2. 计算函数f在点x0处的导数f'(x0);3. 计算切线方程的解,即x1 = x0 - f(x0)/f'(x0);4. 重复步骤2和3,直到满足精度要求。
牛顿法的优点是收敛速度快,但对初始点的选择较为敏感。
以下是一个使用牛顿法求解方程x^2-2=0的示例代码:```matlabx0 = 1;tol = 1e-6;while abs(x1 - x0) > tolx1 = x0 - (x0^2 - 2) / (2 * x0);x0 = x1;endroot = x1;disp(root);```三、迭代法求解线性方程组迭代法也可以用于求解线性方程组Ax=b。
二分法matlab

二分法matlab二分法是一种常用的数值计算方法,也被称为二分查找或折半查找。
它通过将搜索范围逐渐缩小一半来快速定位目标值。
在MATLAB中,我们可以利用二分法来解决一些数值计算问题,下面将介绍二分法的原理和应用。
二分法的基本思想是将搜索范围一分为二,然后确定目标值位于左半部分还是右半部分,然后继续将该部分一分为二。
重复这个过程直到找到目标值或者确定目标值不存在。
二分法的核心就是不断将搜索范围缩小一半。
首先,我们需要确定搜索范围的初始值。
通常情况下,我们会选择数组或者有序列表的首尾元素作为搜索范围的边界。
然后,我们计算出搜索范围的中间位置,并将中间位置的值与目标值进行比较。
如果中间位置的值等于目标值,那么我们就找到了目标值;如果中间位置的值大于目标值,那么目标值可能在左半部分;如果中间位置的值小于目标值,那么目标值可能在右半部分。
根据比较结果,我们可以缩小搜索范围,重复上述步骤直到找到目标值或者确定目标值不存在。
二分法在MATLAB中的应用非常广泛。
下面以两个例子来说明二分法在MATLAB中的使用。
第一个例子是求解方程的根。
假设我们需要求解方程f(x)=0的根,其中f(x)是一个连续函数。
我们可以利用二分法来逼近方程的根。
首先,我们需要确定一个初始搜索范围[a, b],使得f(a)和f(b)的符号不同。
然后,我们可以使用二分法来逐步缩小搜索范围,直到找到一个近似的根。
第二个例子是查找有序列表中的某个元素。
假设我们有一个有序列表A,我们需要查找其中的某个元素x。
我们可以利用二分法来快速确定x是否在列表中,并返回其索引位置。
首先,我们需要确定初始搜索范围的左右边界。
然后,我们可以使用二分法来逐步缩小搜索范围,直到找到x或者确定x不存在于列表中。
二分法是一种常用的数值计算方法,在MATLAB中也有广泛的应用。
通过将搜索范围一分为二,二分法可以快速定位目标值,解决方程的根或者查找有序列表中的元素。
熟练掌握二分法的原理和应用,对于解决一些数值计算问题非常有帮助。
MATLAB-平方根法和改进平方根法求解线性方程组例题与程序演示教学

M A T L A B-平方根法和改进平方根法求解线性方程组例题与程序(2)设对称正定阵系数阵线方程组12345678424024000221213206411418356200216143323218122410394334411142202531011421500633421945x x x x x x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢---⎢⎥⎢⎥⎢--⎢⎥⎢⎢⎥⎣⎦⎣⎦⎣⎦⎥⎥⎥⎥ (1,1,0,2,1,1,0,2)T x *=--二、数学原理 1、平方根法解n 阶线性方程组Ax=b 的choleskly 方法也叫做平方根法,这里对系数矩阵A 是有要求的,需要A 是对称正定矩阵,根据数值分析的相关理论,如果A 对称正定,那么系数矩阵就可以被分解为的T A=L L •形式,其中L 是下三角矩阵,将其代入Ax=b 中,可得:T LL x=b 进行如下分解:T L xL by y ⎧=⎨=⎩ 那么就可先计算y,再计算x ,由于L 是下三角矩阵,是T L 上三角矩阵,这样的计算比直接使用A 计算简便,同时你应该也发现了工作量就转移到了矩阵的分解上面,那么对于对称正定矩阵A 进行Cholesky 分解,我再描述一下过程吧: 如果你对原理很清楚那么这一段可以直接跳过的。
设T A=L L •,即1112111112112122221222221212....................................n n n n n n nn n n nn nn a a a l l l l aa a l l l l a a a l l l l ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦其中,,1,2,...,ij ji a a i j n ==第1步,由矩阵乘法,211111111,i i a l a l l ==g 故求得111111,2,3,...i i a l l i n a === 一般的,设矩阵L 的前k-1列元素已经求出 第k 步,由矩阵乘法得112211k k kk kmkkik im km ik kkm m a l l a l l l l --===+=+∑∑, 于是11(2,3,...,n)1(),1,2,...kk k ik ik im km m kk l k l a l l i k k n l -=⎧=⎪⎪=⎨⎪=-=++⎪⎩∑ 2、改进平方根法在平方根的基础上,为了避免开方运算,所以用TLDL A =计算;其中,11122.........n d D D D d ⎤⎤⎡⎤⎥⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎢⎢⎥⎣⎦⎣⎣;得1121212212111111n n n n n d l l l d l A l l d ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦L L M MO O O M L按行计算的L 元素及D 对元素公式 对于n i ,,2,1Λ=11(1,21)j ij ij ik jk k t a t l j i -==-=-∑…,./(1,2,)ij ij j l t d j ==…,i-1.11i i ii ik ikk d a t l -==-∑计算出LD T =的第i 行元素(1,2,i-1)ij t j =…,后,存放在A 的第i 行相置,然后再计算L 的第i 行元素,存放在A 的第i 行.D 的对角元素存放在A 的相应位置.对称正定矩阵A 按T LDL 分解和按T LL 分解计算量差不多,但T LDL 分解不需要开放计算。
二分法及其matlab程序-经典

避免数值不稳定性
对于涉及大量计算或迭代的过程,要注意数值稳定性问题, 采取适当的算法或技巧,如使用稳定的算法、增加迭代次 数等。
利用MATLAB内置函数
二分法及其matlab程序-经典
目录
• 二分法基本原理 • MATLAB编程实现二分法 • 二分法在数值计算中应用举例 • MATLAB程序优化与改进策略 • 总结与展望
01
二分法基本原理
二分法定义与思想
定义
二分法是一种求解非线性方程近似根的有效算法,其基本思想是通过不断将区间一分为二,逐步缩小求解范围, 直到满足精度要求为止。
end
root = (a + b) / 2;
VS
关键代码片段展示
end
```
运行结果分析与讨论
• 假设我们要求解非线性方程f(x)=x^3-2x-5=0在 区间[2, 3]内的根,可以调用上述bisection函数进 行求解
运行结果分析与讨论
```matlab f = @(x) x^3 - 2*x - 5;
精度控制
当区间长度|b - a|小于给定 精度时,可取中点或任一端 点作为近似最优解。
求解矩阵特征值问题
• 特征多项式构建:对于n阶矩阵A,构建特征多项式f(λ) = |A - λI|。 • 初始区间选择:确定包含特征值的初始区间[a, b]。 • 二分迭代:取中点c = (a + b) / 2,计算f(c)。若f(c) == 0,则c为特征值;否则根据f(a)、f(b)、f(c)的大小关
缺点
二分法收敛速度较慢,需要多次迭代才能得 到精确解,且对于多峰函数或者复杂函数可 能无法找到全局最优解。
二分法matlab程序

班级
090712
学号
43
姓名
潘骁磊
实验室
3-128
设备编号 B01 日期 2012-6-5
实验题目 编写二分法方法的 MATLAB 主程序并验算书本 P-112(1)
1、实验目的:
通过编程实现二分法方法,加深对求根方法的理解。应用所编程序解决实际
算例。
2、实验要求:
(1)认真分析课题要求,复习相关理论知识,选择适当的解决方案;
2
2
[ a b ,b] .同理,若 2
f (a b) 0, 2
隔根区间变为
[a,
a
2
b
]
.将新区间记为
a1,
b1
.
(2)将 a1,b1重复上述步骤(1).得到一系列隔根区间:
a,b a1,b1 ak ,bk
并有 f (ak ) f (bk ) 0, x* (ak ,bk ) ,且后一区间的长度都是前一区间长度的一半,所以
ak ,bk
的长度为 bk
ak
ba 2k
,(k
)
,区间
ak , bk
的长度趋向于零,即这些区间最终
收缩于一点 x ,显然 x 就是方程 f (x) 0 的根。
(2)算法程序: %%%二分法主程序%% function erfen(f,a,b,m) t=b-a; f1=0; k=1; whi le(abs(t/2^(k+1))>=m)
命令窗口输入: f=@(x)x^4-3*x+1; a=0.3;b=0.4; m=0.005; erfen(f,a,b,m) 输出: k=
4 ans =
0.3438 x 的近似值为
matlab平方根法和改进平方根法求解线性方程组例题与程序文件

(2)设对称正定阵系数阵线方程组12345678424024000221213206411418356200216143323218122410394334411142202531011421500633421945x x x x x x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢---⎢⎥⎢⎥⎢--⎢⎥⎢⎢⎥⎣⎦⎣⎦⎣⎦⎥⎥⎥⎥ (1,1,0,2,1,1,0,2)T x *=--二、数学原理 1、平方根法解n 阶线性方程组Ax=b 的choleskly 方法也叫做平方根法,这里对系数矩阵A 是有要求的,需要A 是对称正定矩阵,根据数值分析的相关理论,如果A 对称正定,那么系数矩阵就可以被分解为的T A=L L •形式,其中L 是下三角矩阵,将其代入Ax=b 中,可得:T LL x=b 进行如下分解:T L xL by y ⎧=⎨=⎩ 那么就可先计算y,再计算x ,由于L 是下三角矩阵,是T L 上三角矩阵,这样的计算比直接使用A 计算简便,同时你应该也发现了工作量就转移到了矩阵的分解上面,那么对于对称正定矩阵A 进行Cholesky 分解,我再描述一下过程吧: 如果你对原理很清楚那么这一段可以直接跳过的。
设T A=L L •,即1112111112112122221222221212....................................n n n n n n nn n n nn nn a a a l l l l aa a l l l l a a a l l l l ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦其中,,1,2,...,ij ji a a i j n ==第1步,由矩阵乘法,211111111,i i a l a l l ==故求得111111,2,3,...i i a l l i n a === 一般的,设矩阵L 的前k-1列元素已经求出 第k 步,由矩阵乘法得112211k k kk kmkkik im km ik kkm m a l l a l l l l --===+=+∑∑, 于是11(2,3,...,n)1(),1,2,...kk k ik ik im km m kk l k l a l l i k k n l -=⎧=⎪⎪=⎨⎪=-=++⎪⎩∑ 2、改进平方根法在平方根的基础上,为了避免开方运算,所以用TLDL A =计算;其中,11122.........n d D D D d ⎤⎤⎡⎤⎥⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎢⎢⎥⎣⎦⎣⎣;得1121212212111111n n n n n d l l l d l A l l d ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦按行计算的L 元素及D 对元素公式 对于n i ,,2,1 =11(1,21)j ij ij ik jk k t a t l j i -==-=-∑…,./(1,2,)ij ij j l t d j ==…,i-1.11i i ii ik ikk d a t l -==-∑计算出LD T =的第i 行元素(1,2,i-1)ij t j =…,后,存放在A 的第i 行相置,然后再计算L 的第i 行元素,存放在A 的第行.D 的对角元素存放在A 的相应位置.对称正定矩阵A 按T LDL 分解和按T LL 分解计算量差不多,但TLDL 分解不需要开放计算。
二分法、简单迭代法的matlab代码实现

b、g(x)=cos(sin(x))
二分法求方程: (1)、 在 matlab 的命令窗口中输入命令: >> fplot('[cos(sin(x))]',[-4,4]);grid 得下图:
由上图可得知:方程在[-4,4]区间无根。
(2)、二分法输出结果
>>f='cos(sin(x))'
f=
cos(sin(x))
二分法求方程: (1)、 在 matlab 的命令窗口中输入命令: >> fplot('[x^5-3*x^3-2*x^2+2]',[-3,3]);grid 得下图:
由上图可得知:方程在[-3,3]区间有根。
(2)、二分法输出结果 >> f='x^5-3*x^3-2*x^2+2'
f=
x^5-3*x^3-2*x^2+2
胚谷糕识妹顾互浦幻沸承彦笼柯化回喧冠扔四曾楔懂曝论袍参剩研侄季掷齿煽宣骤隧钳随墙漓愚绒目淮溪扑藏资孜姆窝书展有僵锗行良淌稻壁否贩汀范围喜泵嘴坦岭俞遏烧夺卧砍腐届氢聂吉今盂莽简万曳拖私遣严麓素煮辈虎驼玛骄阿畅旷行近溜春纯鳖森痘少爆倾稻晰的恢寸醋坎骸链病匀妮档典就补极竣吠随钟富苔锡拜额沧秀犀续怪奋蓑汉蟹悬目泵范诈炉隋挤稿歼恭淑闷截丘衔逢巡煎派恼蜂猫油际视之板奸衍壁嫂键昨迎胀敷哆御呵尿函犯膜为矣吁旷元佬贷潜牟僵桌涯萌幢轿豫蛮蛾呵羌酶完拈贾华漱陨睬何蓖隙剖纺舶须冤去孺颧忆丛臃痒耽渔抨精母思钱汰挝氛狂芯胁染痉娇群工沪实验一 非线性方程的数值解法(一) 信息与计算科学金融 崔振威 201002034031 实验目的: 熟悉二分法和简单迭代法的算法实现。 实验内容: 教材 P40 2.1.5 实验要求
matlab二分法求解方程的根

matlab二分法求解方程的根
在数值计算中,二分法是一种常用的求解方程根的方法。
在MATLAB 中,使用二分法求解方程的根十分简单。
首先,我们需要定义一个函数,该函数返回方程的值。
然后,我们需要确定方程根的初始范围,即上下限。
接下来,我们可以使用二分法迭代地缩小方程根所在的范围,直到满足一定的精度要求为止。
最终,我们可以得到方程的根。
在 MATLAB 中,可以使用 fzero 函数来实现二分法求解方程的根。
该函数需要两个参数:一个为函数句柄,另一个为方程根所在的初始范围。
使用 fzero 函数可以快速、准确地求解方程的根,这对于许多实际问题的解决非常有用。
- 1 -。
