matlab 二分法汇总
matlab二分法

matlab二分法MATLAB二分法是一种常用的求解非线性方程的数值解法,它通过不断地将定义域分成若干个子区间,从而找到近似解。
与梯形法和牛顿迭代法相比,MATLAB 二分法又称为“分治法”,是一种简单、直观、快速和有效的求解非线性方程的数值解法。
1. 二分法原理MATLAB 二分法是根据“分而治之”的思想来求解非线性方程的数值解的。
它的基本思想是,将定义域分成两个子区间,其中一个子区间的函数值的符号一定是固定的,另一个子区间的函数值的符号也是固定的,只有当它们的符号相反时,才能确定解存在于这两个子区间之间。
然后,再对缩小的子区间重复以上操作,进而确定非线性方程的近似解,也就是所谓的“黄金分割法”。
2. MATLAB 二分法的步骤(1)始条件首先,要将定义域分成两个子区间,在每一个子区间内,假定函数值的符号是固定的;确定迭代初值 $x_0,比如$x_0=0.5;(2)代计算求出迭代第二值 $x_1,即 $x_1=x_0+frac{b-x_0}{2},计算出$x_1$值,计算函数值的符号;(3)晕条件当求得的函数值的符号与定义域中一边的函数值的符号相反时,认为解存在于此子区间之间,继续将所取得的子区间继续缩小,直到定义域中的某两个端点接近,或者函数值的绝对值小于指定的误差范围,此时称为收敛;(4)的输出将收敛时的根 $x_n$ 作为解的输出。
3. MATLAB 二分法的优缺点(1) MATLAB 二分法的优点MATLAB 二分法具有简单、直观、快速和有效的特点,只要能够确定函数在定义域中的一边的函数值的符号,就可以求出近似解。
(2) MATLAB 二分法的缺点MATLAB 二分法容易收敛到局部极小值,而无法收敛到全局最优值;同时,它也不适用于函数值在定义域内不连续或周期变化的情况。
4. MATLAB 二分法的应用MATLAB 二分法在实际工程中广泛应用,主要用于求解非线性方程、解决二次规划问题、求解非线性最小化问题、结构优化问题等。
matlab 二分法汇总

二分法的matlab主程序function [k,x,wuca,yx]=erfen(a,b,abtol)a(1)=a; b(1)=b;ya=fun(a(1)); yb=fun(b(1)); %程序中调用的fun.m 为函数if ya* yb>0,disp('注意:ya*yb>0,请重新调整区间端点a和b.'), return endmax1=-1+ceil((log(b-a)- log(abtol))/ log(2)); % ceil是上取整for k=1: max1+1a;ya=fun(a); b;yb=fun(b); x=(a+b)/2;yx=fun(x); wuca=abs(b-a)/2; k=k-1;[k,a,b,x,wuca,ya,yb,yx]if yx==0a=x; b=x;elseif yb*yx>0b=x;yb=yx;elsea=x; ya=yx;endif b-a< abtol , return, endendk=max1; x; wuca; yx=fun(x);区间二分法:与对分查找法相同1 区间二分法求出的仅仅是方程的一个单根,如果方程有重根或者多个根时,在做区间二分法时就会出现分叉,这样方程有几个根,就会产生几个实数序列,每一个实数序列的极限便是方程的一个根2 通常用区间二分法为一些迭代法提供靠近x^*的初始选代值;3 区间二分法的缺点是不能求方程的复数根。
format longa=5;b=6;x1=a;x2=b;f1=4*cos(x1)+4*sin(x1)+0.5*x1-2; f2=4*cos(x2)+4*sin(x2)+0.5*x2-2;step=0.000001;ii=0;while abs(x1-x2)>stepii=ii+1;x3=(x1+x2)/2;f3=4*cos(x3)+4*sin(x3)+0.5*x3-2;if f3~=0if f1*f3<0x2=x3;elsex1=x3;endendendx3f=[4*cos(x3)+4*sin(x3)+0.5*x3] disp(['迭代次数:',num2str(ii),'次'])牛顿迭代法求解:在方程f(x)=0有实数根的情况下,若能够将方程等价地转化成x=g(x)的形式,然后取一个初始值x0代入x=g(x)的右端,算得x1=g(x0),再计算x2=g(x1),这样依次类推x(k+1)=g(x(k))可以得到一个序列xk,通常称g(x)为迭代函数,序列xk为由迭代函数产生得迭代序列,x0为迭代初始值。
matlab用二分法求方程近似根

matlab用二分法求方程近似根在MATLAB中,可以使用以下代码使用二分法求解方程的近似根:```matlabfunction root = bisection_method(func, a, b, tol, max_iter)% 输入参数:% func: 待求解方程的函数句柄% a, b: 取值范围% tol: 容差% max_iter: 最大迭代次数fa = func(a);fb = func(b);if fa * fb > 0error('在该区间内没有根存在');endfor k = 1:max_iterc = (a + b) / 2;fc = func(c);if abs(fc) < tolroot = c;return;endif fa * fc < 0b = c;fb = fc;elsea = c;fa = fc;endenderror('未达到收敛条件');end```使用该函数时,首先需要定义待求解方程的函数句柄。
例如,若要求解方程x^2 - 4 = 0的近似根,则可以定义如下函数:```matlabfunction f = equation(x)f = x^2 - 4;end```然后,可以通过调用`bisection_method`函数求解方程的近似根:```matlaba = 1; % 取值范围的下界b = 3; % 取值范围的上界tol = 1e-6; % 容差max_iter = 100; % 最大迭代次数root = bisection_method(@equation, a, b, tol, max_iter);disp(root);```在上述代码中,设置了取值范围的下界为1,上界为3,容差为1e-6,最大迭代次数为100。
运行代码后,MATLAB将输出方程的一个近似根。
matlab程序运行修改版 二分法等等

1、拉格朗日插值公式:function y=lage(X,Y,x)% 拉格朗日插值函数n=length(X);y=zeros(size(x));for k=1:nw=ones(size(x));for j=[1:k-1 k+1:n]w=(x-X(j))./(X(k)-X(j)).*w;endy=y+w*Y(k);end调用方法:在matlab中新建一个script窗口,把上述程序保存成(lage.m)文件,然后在命令窗口调用y=lage(A,B,x),其中A,B均为列向量,分别代表插值点的横坐标和纵坐标,x为待求点横坐标例如:现有x0=1,x1=2,x2=4,y0=3,y1=2,y2=7;要求x=1.5处的估计值。
过程:则A=[1 2 3]’,B=[3 2 7]’,x=1.5在命令窗口输入如下命令:A=[1 2 3]’;B=[3 2 7]’;x=1.5;y=lage(A,B,x)(注意:这个直接占到命令窗口会出现符号问题,请自行修改)y即为所求结果2、牛顿插值公式:function f=niudun(X,Y,x)n=length(X);A=zeros(n,n);%A用于存储均差表(空余位置设为0)A(:,1)=Y;t=A(1,1);for j=2:nfor i=j:nl=1;A(i,j)=(A(i,j-1)-A(i-1,j-1))./(X(i)-X(i-j+1));%算出均差表if i==j%只取每列非0的第一个数for k=1:j-1l=l.*(x-X(k));%通项计算endt=t+l.*A(i,j);%各项累加求结果endendendf=t;在matlab中新建一个script窗口,把上述程序保存成(niudun.m)调用方法:y=niudun(A,B,x) A,B,x的定义与拉格朗日函数相同3、雅克比迭代法:function [y,n]=yacobi(a,d)format long;x=[0;0;0]; %³õʼÏòÁ¿stop=1.0e-4 ; %µü´úµÄ¾«¶ÈL=-tril(a,-1);U=-triu(a,1);A=(diag(diag(a)));D=inv(A);X=D*(L+U)*x+D*d; % Jµü´ú¹«Ê½n=1;while norm(X-x,inf)>=stop % ʱµü´úÖÐÖ¹·ñÔò¼ÌÐøx=X;X=D*(U+L)*x+D*d;n=n+1;endy=X;或:function yacobia=[3 0 -2;0 8 1;-1 1 6 ];d=[3;2;2];x=[0;0;0]; %初始向量stop=1.0e-4 ; %迭代的精度L=-tril(a,-1);U=-triu(a,1);A=(diag(diag(a)));D=inv(A);X=D*(L+U)*x+D*d; % J迭代公式n=1;while norm(X-x,inf)>=stop % 时迭代中止否则继续x=X;X=D*(U+L)*x+D*d;n=n+1;endXn在matlab中新建一个script窗口,在这个窗口中(即.m文件中)直接运行(run)上述程序,若题目要求Ax=b,则将a矩阵内容换为A,d内容换为b。
matlab编程实现二分法牛顿法黄金分割法最速下降matlab程序代码

matlab编程实现二分法牛顿法黄金分割法最速下降matlab程序代码二分法(Bisection Method)是一种寻找函数零点的数值计算方法。
该方法的基本思想是:首先确定一个区间[a, b],使得函数在这个区间的两个端点处的函数值异号,然后将区间逐步缩小,直到找到一个区间[a', b'],使得函数在这个区间的中点处的函数值接近于零。
以下是使用MATLAB实现二分法的示例代码:```matlabfunction [x, iter] = bisection(f, a, b, tol)fa = f(a);fb = f(b);if sign(fa) == sign(fb)error('The function has the same sign at the endpoints of the interval');enditer = 0;while (b - a) / 2 > tolc=(a+b)/2;fc = f(c);if fc == 0break;endif sign(fc) == sign(fa)a=c;fa = fc;elseb=c;fb = fc;enditer = iter + 1;endx=(a+b)/2;end```牛顿法(Newton's Method)是一种用于寻找函数零点的数值计算方法。
该方法的基本思想是:通过迭代来逼近函数的零点,每次迭代通过函数的切线来确定下一个近似值,直到满足收敛条件。
以下是使用MATLAB实现牛顿法的示例代码:```matlabfunction [x, iter] = newton(f, df, x0, tol)iter = 0;while abs(f(x0)) > tolx0 = x0 - f(x0) / df(x0);iter = iter + 1;endx=x0;end```黄金分割法(Golden Section Method)是一种用于寻找函数极值点的数值计算方法。
二分法matlab

二分法matlab二分法是一种常用的数值计算方法,也被称为二分查找或折半查找。
它通过将搜索范围逐渐缩小一半来快速定位目标值。
在MATLAB中,我们可以利用二分法来解决一些数值计算问题,下面将介绍二分法的原理和应用。
二分法的基本思想是将搜索范围一分为二,然后确定目标值位于左半部分还是右半部分,然后继续将该部分一分为二。
重复这个过程直到找到目标值或者确定目标值不存在。
二分法的核心就是不断将搜索范围缩小一半。
首先,我们需要确定搜索范围的初始值。
通常情况下,我们会选择数组或者有序列表的首尾元素作为搜索范围的边界。
然后,我们计算出搜索范围的中间位置,并将中间位置的值与目标值进行比较。
如果中间位置的值等于目标值,那么我们就找到了目标值;如果中间位置的值大于目标值,那么目标值可能在左半部分;如果中间位置的值小于目标值,那么目标值可能在右半部分。
根据比较结果,我们可以缩小搜索范围,重复上述步骤直到找到目标值或者确定目标值不存在。
二分法在MATLAB中的应用非常广泛。
下面以两个例子来说明二分法在MATLAB中的使用。
第一个例子是求解方程的根。
假设我们需要求解方程f(x)=0的根,其中f(x)是一个连续函数。
我们可以利用二分法来逼近方程的根。
首先,我们需要确定一个初始搜索范围[a, b],使得f(a)和f(b)的符号不同。
然后,我们可以使用二分法来逐步缩小搜索范围,直到找到一个近似的根。
第二个例子是查找有序列表中的某个元素。
假设我们有一个有序列表A,我们需要查找其中的某个元素x。
我们可以利用二分法来快速确定x是否在列表中,并返回其索引位置。
首先,我们需要确定初始搜索范围的左右边界。
然后,我们可以使用二分法来逐步缩小搜索范围,直到找到x或者确定x不存在于列表中。
二分法是一种常用的数值计算方法,在MATLAB中也有广泛的应用。
通过将搜索范围一分为二,二分法可以快速定位目标值,解决方程的根或者查找有序列表中的元素。
熟练掌握二分法的原理和应用,对于解决一些数值计算问题非常有帮助。
在matlab用二分法求方程近似解的实验分析与讨论以及实验总

在matlab用二分法求方程近似解的实验分析与讨论以及实验总二分法也称为折半法,是一种求解非线性方程近似解的常用方法。
其基本思路是:利用函数在某个区间上的符号变化来找到方程的根,每次减半区间长度直到满足精度要求为止。
在Matlab中,我们可以利用循环结构和if语句来实现二分法求解非线性方程的近似解。
具体步骤如下:1. 定义函数f,并确定区间[a,b]和精度要求tol。
2. 利用while循环,当区间长度小于精度要求tol时停止循环,否则继续。
3. 每次循环先计算区间中点c=(a+b)/2,并计算函数值fc=f(c)。
4. 判断fc的符号和f(a)的符号是否相同,如果相同,则将区间左端点a赋值为c,否则将区间右端点b赋值为c。
5. 循环结束后,输出近似解x=(a+b)/2。
接下来我们以求解方程x^3-3x+1=0在区间[0,1]上的近似解为例,进行实验分析。
代码如下:```matlabfunction [x] = bisection_method()f = @(x) x^3-3*x+1; % 定义函数fa = 0; % 区间左端点b = 1; % 区间右端点tol = 1e-6; % 精度要求while (b-a)/2 > tol % 判断区间长度是否小于精度要求c = (a+b)/2; % 计算区间中点fc = f(c); % 计算函数值if f(a)*fc > 0 % 判断符号是否相同a = c; % 更新区间左端点elseb = c; % 更新区间右端点endendx = (a+b)/2; % 输出近似解end```我们运行该代码,可以得到方程的近似解为:```matlab>> bisection_method()ans =0.3473```实验分析:1. 二分法求解非线性方程的收敛性是保证的,即对于满足某些条件的方程和初始估计,二分法可以保证收敛到方程的根。
2. 在确定初始区间时,需要考虑到方程根的数量和分布。
二分法及其matlab程序-经典

避免数值不稳定性
对于涉及大量计算或迭代的过程,要注意数值稳定性问题, 采取适当的算法或技巧,如使用稳定的算法、增加迭代次 数等。
利用MATLAB内置函数
二分法及其matlab程序-经典
目录
• 二分法基本原理 • MATLAB编程实现二分法 • 二分法在数值计算中应用举例 • MATLAB程序优化与改进策略 • 总结与展望
01
二分法基本原理
二分法定义与思想
定义
二分法是一种求解非线性方程近似根的有效算法,其基本思想是通过不断将区间一分为二,逐步缩小求解范围, 直到满足精度要求为止。
end
root = (a + b) / 2;
VS
关键代码片段展示
end
```
运行结果分析与讨论
• 假设我们要求解非线性方程f(x)=x^3-2x-5=0在 区间[2, 3]内的根,可以调用上述bisection函数进 行求解
运行结果分析与讨论
```matlab f = @(x) x^3 - 2*x - 5;
精度控制
当区间长度|b - a|小于给定 精度时,可取中点或任一端 点作为近似最优解。
求解矩阵特征值问题
• 特征多项式构建:对于n阶矩阵A,构建特征多项式f(λ) = |A - λI|。 • 初始区间选择:确定包含特征值的初始区间[a, b]。 • 二分迭代:取中点c = (a + b) / 2,计算f(c)。若f(c) == 0,则c为特征值;否则根据f(a)、f(b)、f(c)的大小关
缺点
二分法收敛速度较慢,需要多次迭代才能得 到精确解,且对于多峰函数或者复杂函数可 能无法找到全局最优解。
matlab二分法求超越方程根的程序

matlab二分法求超越方程根的程序Matlab是一种功能强大的数值计算软件,它可以用于求解各种数学问题。
在数学中,超越方程是一类无法用有限次代数运算求解的方程,其求解过程相对复杂。
本文将介绍如何使用Matlab中的二分法来求解超越方程的根。
二分法是一种简单而有效的数值计算方法,它可以用于求解函数的根。
其基本思想是首先确定一个区间,然后将区间逐步缩小,直到找到根的近似值为止。
在使用二分法求解超越方程根的过程中,我们需要先定义一个函数,然后根据函数在区间两个端点的取值判断根的位置,并不断缩小区间范围,直到满足所需的精度要求。
我们需要在Matlab中定义一个函数,表示超越方程。
假设我们要求解的超越方程为f(x)=0,我们可以使用Matlab中的函数定义语法来定义这个函数。
例如,我们可以定义一个求解sin(x)-x=0的函数:```matlabfunction y = f(x)y = sin(x) - x;end```接下来,我们需要确定一个初始区间,该区间包含根。
一般来说,我们可以通过观察函数图像或者利用数学知识来估计根的大致位置。
在这个例子中,我们可以选择区间[0, 1],因为sin(0)=0,sin(1)>1,而且函数在[0, 1]上是连续的。
然后,我们可以使用二分法求解超越方程的根。
具体步骤如下:1. 初始化区间的上界和下界:a=0,b=1。
2. 计算区间的中点:c=(a+b)/2。
3. 计算函数在中点的取值:fc=f(c)。
4. 判断根的位置:- 如果fc=0,则c就是方程的一个根,算法结束。
- 如果fc与f(a)异号,则根在区间[a, c]内,更新上界b=c。
- 如果fc与f(b)异号,则根在区间[c, b]内,更新下界a=c。
5. 判断是否满足精度要求:如果区间的长度小于所需的精度,算法结束。
6. 重复步骤2-5。
根据上述步骤,我们可以编写一个求解超越方程根的Matlab程序。
以下是一个示例程序:```matlabfunction root = bisection_method()a = 0;b = 1;epsilon = 1e-6; % 精度要求max_iterations = 100; % 最大迭代次数for i = 1:max_iterationsc = (a + b) / 2;fc = f(c);if abs(fc) < epsilonroot = c;disp('Root found!');return;elseif f(a) * fc < 0b = c;elsea = c;endif abs(b - a) < epsilonroot = c;disp('Root found within desired accuracy!'); return;endenderror('Root not found within maximum number of iterations!');end```在这个程序中,我们将迭代次数限制为最大迭代次数,以防止算法无限循环。
二分法及其matlab程序-经典精编版
函数值 函数值f(xk) f(bk)
4.000 0
2.125 0
2.125 0
6
0.390 6 -0.716 8
0.390 6 -0.141 8
0.390 6
0.129 6
0.129 6 -0.004 8
0.129 6
0.062 7
0.062 7
0.029 0
0.029 0
0.012 1
4
-1.812 5 -1.750 0
5
-1.812 5 -1.781 3
6
-1.796 9 -1.781 3
7
-1.796 9 -1.789 1
8
-1.796 9 -1.793 0
9
-1.796 9 -1.794 9
中点xk
-1.500 0 -1.750 0 -1.875 0 -1.812 5 -1.781 3 -1.796 9 -1.789 1 -1.793 0 -1.794 9 -1.795 9
运行后输出结果x*=x1.
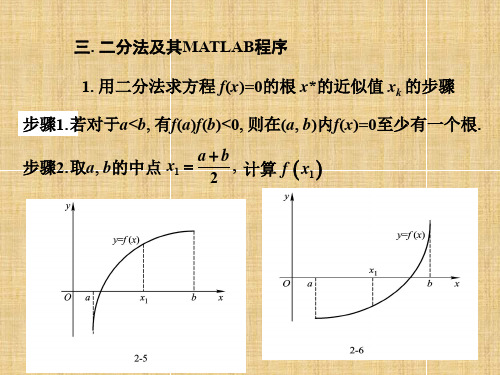
若f a f x1 0,则在(a, x1 )内f(x)=0至少有一个根. 取a1=a, b1=x1; 若f a f x1 0, 则取a1=x1, b1=b;
1. 用二分法求方程 f(x)=0的根 x*的近似值 xk 的步骤
步骤1.若对于a<b, 有f(a)f(b)<0, 则在(a, b)内f(x)=0至少有一个根.
其中输入的量: 区间端点的值a, b和精度是abtol都是具体 给定的数值, 然后按运行键. 运行后输出计算次数k、使用 k次二分法所得到的小区间[ak, bk]的中点的值x和它的函 数值y(x)及wuca=|bk-ak|/2.
二分法matlab

二分法matlab二分法是一种常见的数值计算方法,也称为折半查找法。
它的主要思想是将一个区间分成两个部分,判断目标值在哪个部分,然后继续对该部分进行二分处理,直到最后找到目标值为止。
在Matlab中,可以用以下代码实现二分法:function [x] = binary_search(f, a, b, tol)% f: 待求解函数% a,b: 初始区间% tol: 精度要求while abs(b-a) > tolx = (a + b) / 2;if f(x) == 0return;elseif f(x) * f(a) < 0b = x;elsea = x;endendx = (a + b) / 2;其中,f表示待求解的函数,a和b表示初始的区间,tol表示精度要求。
在每次循环中,先计算出当前区间的中点x,并判断f(x)与0的大小关系。
如果f(x)=0,则直接返回x;如果f(x)*f(a)<0,则说明目标值在左半部分区间内,则将右端点b更新为x;否则说明目标值在右半部分区间内,则将左端点a更新为x。
循环直到满足精度要求为止。
下面是一个简单的例子:假设我们要求解方程sin(x)=0.5在[0, pi/2]内的一个近似解。
可以定义函数f(x)=sin(x)-0.5,然后调用binary_search函数求解。
function [x] = f(x)x = sin(x) - 0.5;endx = binary_search(@f, 0, pi/2, 1e-6);最终得到的近似解为x=0.523599。
二分法是一种简单而有效的数值计算方法,在Matlab中也很容易实现。
它可以用于求解方程、寻找极值等问题,是数值计算中常用的基本工具之一。
MATLAB计算方法迭代法牛顿法二分法实验报告

MATLAB计算方法迭代法牛顿法二分法实验报告实验目的:本实验旨在通过MATLAB编程实现迭代法、牛顿法和二分法,并通过实例验证其准确性和收敛速度。
实验原理:迭代法是一种通过不断迭代逼近根的方法,其基本原理是选择一个初始值,然后通过迭代公式不断逼近根的值,直到满足给定的精度要求。
牛顿法是一种通过不断迭代求函数的零点的方法,其基本原理是通过当前点的切线与x轴的交点来逼近根的值,直到满足给定的精度要求。
二分法是一种通过不断将区间一分为二来逼近根的方法,其基本原理是通过判断根是否落在区间的两个端点之间,然后将区间一分为二,直到满足给定的精度要求。
实验步骤:1.编写迭代法的MATLAB代码,实现对给定函数的根的逼近。
2.编写牛顿法的MATLAB代码,实现对给定函数的根的逼近。
3.编写二分法的MATLAB代码,实现对给定函数的根的逼近。
4.针对不同的函数,分别使用迭代法、牛顿法和二分法进行根的逼近,并记录每种方法的迭代次数和逼近结果。
5.对比三种方法的迭代次数和逼近结果,分析其准确性和收敛速度。
实验结果:以求解方程x^3-2x-5=0为例,使用迭代法、牛顿法和二分法进行根的逼近。
迭代法:迭代公式:x(n+1)=(2x(n)+5)^(1/3)初始值:x(0)=2迭代次数:6逼近结果:2.0946牛顿法:初始值:x(0)=2迭代次数:4逼近结果:2.0946二分法:初始区间:[1,3]迭代次数:11逼近结果:2.0946实验结论:通过对比三种方法的迭代次数和逼近结果可以发现,迭代法和牛顿法的收敛速度都要快于二分法,并且迭代法和牛顿法的逼近结果也更为接近真实根。
这是因为迭代法和牛顿法都是通过不断逼近根的值来求解,而二分法则是通过将区间一分为二来逼近根的值,所以迭代法和牛顿法的收敛速度更快。
总结:本实验通过MATLAB编程实现了迭代法、牛顿法和二分法,并通过实例验证了它们的准确性和收敛速度。
实验结果表明,迭代法和牛顿法在求解根的过程中具有更快的收敛速度和更接近真实根的逼近结果,而二分法的收敛速度较慢。
matlab二分法

matlab二分法Matlab二分法是一种迭代算法,它可以用来求解一元函数f(x)在给定区间[a,b]上的根。
Matlab二分法的原理是,先确定一个初始的搜索范围[a,b],然后以其中点作为分割点,对上下区间的函数值的符号进行判断,根据函数值的符号加以分割,直到确定出最终的搜索范围,即根的范围。
Matlab二分法主要包含以下几步操作:(1)确定搜索范围首先,确定搜索范围[a,b],并将它写成f(a) · f(b) < 0的形式。
若f(a) · f(b) > 0,说明在这个区间上函数没有根,可以把它划分到新的区间上,直到把它分割成两个满足f(a) · f(b)< 0的区间。
这样搜索范围就确定下来。
(2)取中点接下来,利用确定的搜索范围[a,b],取中点c,并依次求出f(a),f(b),f(c)的值,进行比较判断。
(3)判断函数值的符号若f(c) = 0,则c即为函数f(x)在区间[a,b]上的根;若f(c) ≠ 0,则继续按照该方法进行迭代计算,根据f(a) · f(c)与f(b) · f(c)的符号之间的关系,可以确定新的搜索范围,如果f(a) · f(c)>0,那么下一个采样点就是[c,b],如果f(a) · f(c)< 0,就采取[a,c]作为下一个搜索范围。
(4)计算误差如果根的近似值已经确定,则可以计算它的误差,它表示根的准确值c1和近似值c2之间的距离。
其计算公式为E=|f(c1)-f(c2)|,如果误差足够小,即可认为计算结果已经可以接受。
Matlab二分法是一种比较常用的求解一元函数根的方法,它简单易行、收敛速度快,能够得到准确的结果。
它将完整的一元函数f(x)划分为等份子区间,而函数的根可以属于其中的任何一段,从而使得搜索范围大大缩小,使根的搜索更为准确。
但Matlab二分法也有一定的局限性,比如,它是基于直接二分法,可能会出现单调性变化的情况,结果误差较大。
matlab编程实现二分法,牛顿法,黄金分割法,最速下降matlab程序代码

matlab编程实现二分法,牛顿法,黄金分割法,最速下降matlab程序代码用二4224min ()f t t t t =--[,.]t ∈内的极小值点,要求准1.function [t d]=erfenfa(a,b)k=1; %记录循环次数 while abs(a-b)>0.0005c=(a+b)/2;C(k)=c; %存储每次循环中点c 的值if ff(c)<0a=c;endif ff(c)==0t1=c;break ;endif ff(c)>0b=c;endk=k+1;endt=(a+b)/2; %最终符合要求的值d=f(t); %最优解Ckfunction y=f(t)y=t^4-2*t^2-4*t;function y=ff(t)y=4*t^3-4*t-4;运行结果>> [t d]=erfenfa(1,1.5)C =Columns 1 through 91.2500 1.3750 1.3125 1.3438 1.3281 1.3203 1.3242 1.3262 1.3252Column 101.3247k =11t =1.3250d =-5.72902.黄金分割法 f (x)=x3-2x+1 初始区间[0, 3],收敛精度0.5 function [t,f]=huangjinfenge(a,b)m=1-(sqrt(5)-1)/2;t2=a+m*(b-a)f2=g(t2);t1=a+b-t2f1=g(t1);while abs(t1-t2)>0.5if f1<f2< bdsfid="121" p=""></f2<>a=t2;t2=t1f2=f1;t1=a+b-t2f1=g(t1);elseb=t1;t1=t2f1=f2;t2=a+m*(b-a)f2=g(t2);endendt=(t1+t2)/2;f=g(t);function y=g(t)y=t^3-2*t+1;运行结果> [t,f]=huangjinfenge(0,3)t2 =1.1459t1 =1.8541t1 =1.1459t2 =0.7082t =0.9271f =-0.0574>>3. 用牛顿法求解291min ()sin f x x x =--初始迭代点为x 0=0.4, 要求准确到小数点后第5位小数function [t1,d]=Newton(t0)t=t0-ff(t0)/fff(t0);k=1;%记录迭代次数T(1)=t;%存储迭代点while abs(t-t0)>0.000005t0=t;t=t0-ff(t)/fff(t);k=k+1;T(k)=t;endt1=t0;d=f(t1);kTfunction y=f(x)y=9*x^2-sin(x)-1;function y=ff(x)y=18*x-cos(x);function y=fff(x)y=18+sin(x);运行结果>> [t1,d]=Newton(0.4)k =3T =0.0586 0.0555 0.0555t1 =0.0555d =-1.0277>>4. 最速下降法验证课本上的例题求解291min ()sin f x x x =--初始迭代点为x 0=0.4, 要求准确到小数点后第5位小数function [G,g,X,F]=zuisu(X0)F(1)=f(X0);%存储x 点处的值G(:,1)=h(X0); %存储梯度向量g(1)=norm(G(:,1));%存储梯度模长X(:,1)=X0; %存储x 值A=[2,0;0,8];for j=1:2X(:,j+1)=X(:,j)-(G(:,j)'*G(:,j))/(G(:,j)'*A*G(:,j))*G(:,j);F(j+1)=f(X(:,j+1));G(:,j+1)=h(X(:,j+1));g(j+1)=norm(G(:,j+1));endif (G(:,2)'*G(:,1)<1E-10& G(:,3)'*G(:,2)<1E-10)disp(['相邻两搜索方向是正交的'])endfunction y=f(X)y=X(1)^2+4*X(2)^2;function n=h(X)n=[2*X(1),8*X(2)]';运行结果>> [G,g,X,F]=zuisu(X0)相邻两搜索方向是正交的G =2.0000 1.4769 0.2215 8.0000 -0.3692 0.8862g =8.2462 1.5224 0.9134X =1.0000 0.7385 0.1108 1.0000 -0.0462 0.1108F =5.0000 0.5538 0.0613 >>。
MATLAB计算方法迭代法牛顿法二分法实验报告

完美WORD格式姓名实验报告成绩评语:指导教师(签名)年月日说明:指导教师评分后,实验报告交院(系)办公室保存。
实验一 方程求根一、 实验目的用各种方法求任意实函数方程0)(=x f 在自变量区间[a ,b]上,或某一点附近的实根。
并比较方法的优劣。
二、 实验原理 (1)、二分法对方程0)(=x f 在[a ,b]内求根。
将所给区间二分,在分点2a b x -=判断是否0)(=x f ;若是,则有根2a b x -=。
否则,继续判断是否0)()(<∙x f a f ,若是,则令x b =,否则令x a =。
否则令x a =。
重复此过程直至求出方程0)(=x f 在[a,b]中的近似根为止。
(2)、迭代法将方程0)(=x f 等价变换为x =ψ(x )形式,并建立相应的迭代公式=+1k x ψ(x )。
(3)、牛顿法若已知方程 的一个近似根0x ,则函数在点0x 附近可用一阶泰勒多项式))((')()(0001x x x f x f x p -+=来近似,因此方程0)(=x f 可近似表示为+)(0x f 0))(('0=-x x x f 设0)('0≠x f ,则=x -0x )(')(00x f x f 。
取x 作为原方程新的近似根1x ,然后将1x 作为0x 代入上式。
迭代公式为:=+1k x -0x )(')(k k x f x f 。
三、 实验设备:MATLAB 7.0软件四、 结果预测(1)11x =0.09033 (2)5x =0.09052 (3)2x =0,09052 五、 实验内容(1)、在区间[0,1]上用二分法求方程0210=-+x e x 的近似根,要求误差不超过3105.0-⨯。
(2)、取初值00=x ,用迭代公式=+1k x -0x )(')(k k x f x f ,求方程0210=-+x e x的近似根。
要求误差不超过3105.0-⨯。
二分法matlab程序(推荐文档)

二分法二分法基本思路一般地,对于函数f(x),如果存在实数c,当x=c 时,若f(c)=0,那么把x=c 叫做函数f(x)的零点。
解方程即要求f(x)的所有零点。
假定f(x)在区间(x ,y )上连续先找到a 、b 属于区间(x ,y ),使f(a),f(b)异号,说明在区间(a,b)内一定有零点,然后求f[(a+b)/2],现在假设f(a)<0,f(b)>0,a<b① 如果f[(a+b)/2]=0,该点就是零点,如果f[(a+b)/2]<0,则在区间((a+b)/2,b)内有零点,(a+b)/2>=a ,从①开始继续使用 ② 中点函数值判断。
如果f[(a+b)/2]>0,则在区间(a,(a+b)/2)内有零点,(a+b)/2<=b ,从①开始继续使用 中点函数值判断。
这样就可以不断接近零点。
通过每次把f(x)的零点所在小区间收缩一半的方法,使区间的两个端点逐步迫近函数的零点,以求得零点的近似值,这种方法叫做二分法。
从以上可以看出,每次运算后,区间长度减少一半,是线形收敛。
另外,二分法不能计算复根和重根。
二分法步骤用二分法求方程()0f x =的根*x 的近似值k x 的步骤① 若对于a b <有()()0f a f b <,则在(,)a b 内()0f x =至少有一个根。
② 取,a b 的中点12a b x +=计算1()f x ③ 若1()0f x =则1x 是()0f x =的根,停止计算,运行后输出结果*1x x =若1()()0f a f x <则在1(,)a x 内()0f x =至少有一个根。
取111,a a b x ==;若1()()0f a f x >,则取111,a x b b ==;④ 若12k k b a ε-≤(ε为预先给定的要求精度)退出计算,运行后输出结果*2k k a b x +≈,反之,返回步骤1,重复步骤1,2,3 二分法Mtalab 程序syms x;fun=input('(输入函数形式)fx=');a=input('(输入二分法下限)a=');b=input('(输入二分法上限)b=');d=input('输入误差限 d=')%二分法求根%f=inline(x^2-4*x+4);%修改需要求解的inline 函数的函数体f=inline(fun);%修改需要求解的inline 函数的函数体e=b-a; k=0 ;while e>dc=(a+b)/2;if f(a)*f(c)<0b=c;elseif f(a)*f(c)>0a=c;elsea=c;b=cende=e/2; k=k+1;endx=(a+b)/2;x%x 为答案 k%k 为次数例题:用二分法计算方程4324100x x x -++=在(-2,2)内的实根的近似值,要求精度为0.0001解:(输入函数形式)fx=x^4-2*x^3+4*x+10(输入二分法下限)a=-2(输入二分法上限)b=2输入误差限 d=0.0001得到结果d =1.0000e-004x =2.0000k =16>>。
二分法算三元方程matlab

一、介绍二分法算三元方程的背景和原理1. 二分法是一种常用的数值计算方法,其原理是通过不断缩小解的范围来逼近方程的解。
2. 三元方程是指含有三个未知数的方程,通常是非线性方程,在数值计算中求解时较为复杂。
3. 利用二分法可以有效地求解三元方程,通过不断缩小三元方程解的范围来逼近真实解,从而得到精确的解。
二、使用matlab编写二分法求解三元方程的步骤1. 准备工作:打开matlab软件,新建一个m文件。
2. 输入方程:在m文件中输入待求解的三元方程,定义三个未知数的取值范围。
3. 编写算法:使用二分法的原理编写算法,对三个未知数分别进行二分求解。
4. 输出结果:将得到的解输出,得到三元方程的解。
三、实例演示1. 举例说明:假设需要求解三元方程x^3 + y^3 + z^3 = 29在区间[0, 3]内的解。
2. 编写matlab代码:在m文件中编写求解三元方程的matlab代码,包括方程的定义和二分法求解的算法。
3. 执行代码:在matlab中执行编写的代码,查看输出结果。
四、讨论二分法求解三元方程的优缺点1. 优点:二分法求解三元方程的原理简单,易于理解和编写算法。
2. 缺点:二分法需要设定初始解的范围,在一些复杂的三元方程中可能无法有效地逼近真实解。
五、总结1. 总结:二分法是一种常用的数值计算方法,在求解三元方程时也可以得到应用。
2. 展望:随着计算机技术的发展,其他更加高效的数值计算方法也在不断涌现,人们可以根据具体需求选择合适的方法。
六、参考文献1. [1] 《数值分析》2. [2] 《matlab数值计算基础》二分法是一种常用的数值计算方法,其原理是通过不断缩小解的范围来逼近方程的解。
这种方法被广泛应用在各种数值计算问题中,包括三元方程的求解。
三元方程是指含有三个未知数的方程,通常是非线性方程,在数值计算中求解时较为复杂。
利用二分法可以有效地求解三元方程,通过不断缩小三元方程解的范围来逼近真实解,从而得到精确的解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二分法的matlab主程序function [k,x,wuca,yx]=erfen(a,b,abtol)a(1)=a; b(1)=b;ya=fun(a(1)); yb=fun(b(1)); %程序中调用的fun.m 为函数if ya* yb>0,disp('注意:ya*yb>0,请重新调整区间端点a和b.'), return endmax1=-1+ceil((log(b-a)- log(abtol))/ log(2)); % ceil是上取整for k=1: max1+1a;ya=fun(a); b;yb=fun(b); x=(a+b)/2;yx=fun(x); wuca=abs(b-a)/2; k=k-1;[k,a,b,x,wuca,ya,yb,yx]if yx==0a=x; b=x;elseif yb*yx>0b=x;yb=yx;elsea=x; ya=yx;endif b-a< abtol , return, endendk=max1; x; wuca; yx=fun(x);区间二分法:与对分查找法相同1 区间二分法求出的仅仅是方程的一个单根,如果方程有重根或者多个根时,在做区间二分法时就会出现分叉,这样方程有几个根,就会产生几个实数序列,每一个实数序列的极限便是方程的一个根2 通常用区间二分法为一些迭代法提供靠近x^*的初始选代值;3 区间二分法的缺点是不能求方程的复数根。
format longa=5;b=6;x1=a;x2=b;f1=4*cos(x1)+4*sin(x1)+0.5*x1-2; f2=4*cos(x2)+4*sin(x2)+0.5*x2-2;step=0.000001;ii=0;while abs(x1-x2)>stepii=ii+1;x3=(x1+x2)/2;f3=4*cos(x3)+4*sin(x3)+0.5*x3-2;if f3~=0if f1*f3<0x2=x3;elsex1=x3;endendendx3f=[4*cos(x3)+4*sin(x3)+0.5*x3] disp(['迭代次数:',num2str(ii),'次'])牛顿迭代法求解:在方程f(x)=0有实数根的情况下,若能够将方程等价地转化成x=g(x)的形式,然后取一个初始值x0代入x=g(x)的右端,算得x1=g(x0),再计算x2=g(x1),这样依次类推x(k+1)=g(x(k))可以得到一个序列xk,通常称g(x)为迭代函数,序列xk为由迭代函数产生得迭代序列,x0为迭代初始值。
同一个方程,不同等价形式的转换产生的迭代法可能收敛,也有可能发散.关于迭代法的敛散性判定有下面的定理(也称李普希兹(Lipschitz定理):如果迭代函数g(x)在区间[a,b]上连续,且满足以下条件,1 对于任意的x=[a,b],有g(x)=[a,b]2 在区间内(a,b)内,函数g(x)满足Lipschitz条件,即存在常数L>0,使得对于任意的x,y=(a,b),都有|g(x)-g(y)|=<L|x-y|,如果有L<1,则迭代格式xk+1=g(xk),k=0,1,2,..对于任意的迭代初始值x0=[a,b]均是收敛的这里与x和y无关的正常数L称为Lipschitz常数。
一种较为特殊得迭代法为牛顿(Newton)迭代法xk+1=xk-f(xk)/f'(xk)相应迭代函数为g(x)=x-f(x)/f'(x)Newton迭代法的几何意义:它的第k+1次迭代值就是曲线y=f(x)在点(xk,f(xk))处切线y-f(xk)=f'(xk)(x=xk)与轴的交点的横坐标,%解方程:f=4*(cos(x1)+sin(x1)+0.5*x1-2)=0x0=9.6;x1=x0-(4*(cos(x0)+sin(x0))+0.5*x0-2)/(4*(cos(x0)-sin(x0))+0.5);while abs(x1-x0)>0.000001x0=x1;x1=x1-(4*(cos(x0)+sin(x0))+0.5*x0-2)/(4*(cos(x0)-sin(x0))+0.5);endf=4*(cos(x1)+sin(x1)+0.5*x1-2)弦截法:单点弦截法:连接两个端点与作弦(a,f(a)) 与(b,f(b))作弦,此弦与轴交点的横坐标设为x1. 如果f(x1)=0,则x1即为所求根,否则选取(x1,f(x1))点和点(a,f(a))(该点的选取要满足条件f(a)与f''(x)同号,并改记为(x0,f(x0))。
再做弦此弦与轴交点的横坐标设为x2,依次类推,其迭代格式即为xk+1=xk-f(xk)*(xk-x0)/(f(xk)-f(x0)双点弦截法:无固定点xk+1=xk-f(xk)*(xk-xk-1)/(f(xk)-f(xk-1)format longnx=[];nx(1)=5;nx(2)=nx(1)-(2^nx(1)-nx(1)^2-1)/(2^nx(1)*log(2)-2*nx(1));k=1;while abs(nx(k+1)-nx(k))>=10^(-6)k=k+1;nx(k+1)=nx(k)-(2^nx(k)-nx(k)^2-1)/(2^nx(k)*log(2)-2*nx(k));endnk=k+1; disp(['牛顿迭代法迭代次数:',num2str(nk),blanks(4),'方程的解:',num2str(nx(nk))])dx=[];dx(1)=5; dx(2)=dx(1)-(2^dx(1)-dx(1)^2-1)/((2^3-3^2-1)-(2^5-5^2-1))*(3-5);k=1;while abs(dx(k+1)-dx(k))>=10^(-6)k=k+1;dx(k+1)=dx(k)-(2^dx(k)-dx(k)^2-1)/((2^dx(k)-dx(k)^2-1)-(2^5-5^2-1))*( dx(k)-5); enddisp(['单点迭代法迭代次数:',num2str(k),blanks(4),'方程的解:',num2str(dx(k))]) sx=[];sx(1)=5;sx(2)=3;k=1;while abs(sx(k+1)-sx(k))>=0.000001k=k+1;sx(k+1)=sx(k)-((2^sx(k)-sx(k)^2-1)/((2^sx(k)-sx(k)^2-1)-(2^sx(k-1)-sx(k-1)^2-1)) )*(sx(k)-sx(k-1));endsk=k+1;disp(['双点迭代法迭代次数:',num2str(sk),blanks(4),'方程的解:',num2str(sx(sk))])x=3:0.05:5;y=2.^x-x.^2-1;yn=zeros(1,nk);yd=zeros(1,sk);subplot(1,2,1)plot(x,y,sx,yd,'*')title('双点弦截法')gtext('y=2^x-x^2-1')subplot(1,2,2)plot(x,y,nx,yn,'*')title('牛顿迭代法')gtext('y=2^x-x^2-1')二分法function approx_root=bisect (a,b,tol)fa =bifun(a);fb =bifun(b);while(abs(b-a)> tol)c=(a+b)/2;approx_root=c;fc=bifun(c);[a,c,b;fa,fc,fb]if ( sign(fb) * sign(fc)<=0)a=c;fa=fc;elseb=c;fb=fc;endend%----------------------------------function f=bifun(x)f=x^3-sin(x);%输入你的方程f(x)=0 a b为区间a=4.0,b=4.6牛顿法x0=4.6 n为迭代上限,tol为精度function y=newton1(x0,n,tol)x(1)=x0;b=1;i=1;A(i)=x(i);B(i)=b;C(i)=1while(abs(b)>eps*x(i))x(i+1)=x(i)-fun1(x(i))/dfun1(x(i));b=x(i+1)-x(i);i=i+1;A(i)=x(i);B(i)=b;C(i)=feval(@fun1,x(i));if(i>n)error('n is full');endendy=x(i)[A' C' B']function y=fun1(x)y=x^2-sin(x);function f=dfun1(x)syms xf=double(diff('fun1',x))solve('(-1*x^3*cos(40*x)-sin(40*x))*(2*sinh(40*x)+1*x^3*(cos(40*x)-cosh(40*x)))+(1* x^3*sin(40*x)+1*x^3*sinh(40*x)-cos(40*x)-cosh(40*x))*1*x^3*(sinh(40*x)-sin(4 0*x))+(1*x^3*cosh(40*x)-sinh(40*x))*(2*sin(40*x)+1*x^3*(cos(40*x)-cosh(40*x) ))=0')syms xf=inline((-1*x^3*cos(40*x)-sin(40*x))*(2*sinh(40*x)+1*x^3*(cos(40*x)-cosh(40* x)))+(1*x^3*sin(40*x)+1*x^3*sinh(40*x)-cos(40*x)-cosh(40*x))*1*x^3*(sinh(40* x)-sin(40*x))+(1*x^3*cosh(40*x)-sinh(40*x))*(2*sin(40*x)+1*x^3*(cos(40*x)-co sh(40*x))),'x')x0=2[x,fv]=fsolve(f,x0,optimset('TolFun',1e-16))f=@(x)(-1*x.^3*cos(40*x)-sin(40*x))*(2*sinh(40*x)+1*x.^3*(cos(40*x)-cosh(40*x)))+(1 *x.^3*sin(40*x)+1*x.^3*sinh(40*x)-cos(40*x)-cosh(40*x))*1*x.^3*(sinh(40*x)-si n(40*x))+(1*x.^3*cosh(40*x)-sinh(40*x))*(2*sin(40*x)+1*x.^3*(cos(40*x)-cosh( 40*x)));x=fsolve(f,[-10:1:10])f=@(x)(-1*x^3*cos(40*x)-sin(40*x))*(2*sinh(40*x)+1*x^3*(cos(40*x)-cosh(40*x)))+(1*x^3*sin(40*x)+1 *x^3*sinh(40*x)-cos(40*x)-cosh(40*x))*1*x^3*(sinh(40*x)-sin(40*x))+(1*x^3*cosh(40*x)-sinh(4 0*x))*(2*sin(40*x)+1*x^3*(cos(40*x)-cosh(40*x)));x=fsolve(f,[0:1:10])。
