matlab二分法求根例题
matlab 二分法汇总

二分法的matlab主程序function [k,x,wuca,yx]=erfen(a,b,abtol)a(1)=a; b(1)=b;ya=fun(a(1)); yb=fun(b(1)); %程序中调用的fun.m 为函数if ya* yb>0,disp('注意:ya*yb>0,请重新调整区间端点a和b.'), return endmax1=-1+ceil((log(b-a)- log(abtol))/ log(2)); % ceil是上取整for k=1: max1+1a;ya=fun(a); b;yb=fun(b); x=(a+b)/2;yx=fun(x); wuca=abs(b-a)/2; k=k-1;[k,a,b,x,wuca,ya,yb,yx]if yx==0a=x; b=x;elseif yb*yx>0b=x;yb=yx;elsea=x; ya=yx;endif b-a< abtol , return, endendk=max1; x; wuca; yx=fun(x);区间二分法:与对分查找法相同1 区间二分法求出的仅仅是方程的一个单根,如果方程有重根或者多个根时,在做区间二分法时就会出现分叉,这样方程有几个根,就会产生几个实数序列,每一个实数序列的极限便是方程的一个根2 通常用区间二分法为一些迭代法提供靠近x^*的初始选代值;3 区间二分法的缺点是不能求方程的复数根。
format longa=5;b=6;x1=a;x2=b;f1=4*cos(x1)+4*sin(x1)+0.5*x1-2; f2=4*cos(x2)+4*sin(x2)+0.5*x2-2;step=0.000001;ii=0;while abs(x1-x2)>stepii=ii+1;x3=(x1+x2)/2;f3=4*cos(x3)+4*sin(x3)+0.5*x3-2;if f3~=0if f1*f3<0x2=x3;elsex1=x3;endendendx3f=[4*cos(x3)+4*sin(x3)+0.5*x3] disp(['迭代次数:',num2str(ii),'次'])牛顿迭代法求解:在方程f(x)=0有实数根的情况下,若能够将方程等价地转化成x=g(x)的形式,然后取一个初始值x0代入x=g(x)的右端,算得x1=g(x0),再计算x2=g(x1),这样依次类推x(k+1)=g(x(k))可以得到一个序列xk,通常称g(x)为迭代函数,序列xk为由迭代函数产生得迭代序列,x0为迭代初始值。
数值计算作业

数值计算作业1:方程求根的二分法第一步:在MATLAB 软件中,建立一个实现二分法的MATLAB 函数文件xy01.m 如下: function [x_star,k]=xy01(fun,a,b,e) if nargin<4;endfa=feval(fun,a);fb=feval(fun,b);if fa*fb>0 x_star=[fa,fb];k=0;return;end k=1;while abs(b-a)/2>ex=(a+b)/2;fx=feval(fun,x); if fx*fa<0b=x;fb=fx; elsea=x;fa=fx; end k=k+1; endx_star=(a+b)/2; 第二步:(1)在MATLAB 命令窗口求解方程sinx+9x-2=0在自变量区间[0,1]上的近似实根,并使误差不超过0.5×10−3。
输入并得到结果如下图即结果为0.1997,二分次数为11次。
(2)改变输入参数,计算误差不超过100.510-⨯的近似实根,并给出二分的次数,输入并得到结果如下图:即结果为0.2001,二分次数为35次。
实验分析与结论:由上面二分法的实验结果,我们可以得出这样的结论:二分法要循环k=11次,才能达到精度为0.5×10−3的要求。
要循环35次,才能达到精度为0.5×10−10的要求。
作业2:方程求根的迭代法第一步:在MATLAB软件中,建立一个实现二分法的MATLAB函数文件xy02.m如下:function [z,k]=xy02(fun,x0,ep,Nmax)if nargin<4Nmax=500;endif nargin<3ep=1e-5;endx=x0;x0=x+2*ep;k=0;while abs(x0-x)>ep&k<Nmaxx0=x;x=feval(fun,x0)k=k+1endz=x;if k==Nmax waring;end第二步:(1)在MATLAB命令窗口求解方程sinx+9x-2=0在自变量区间[0,1]上的近似实根,并使误差不超过0.5×10−3。
计算方法 实验一 方程求根

实验一方程求根(1)二分法
1、实验程序
实现二分法的MATLAB函数文件agui_bisect.m
2. 在MATLAB命令窗口输入及实验结果及操作界面
(2)迭代法
1、实验程序
实现二分法的MATLAB函数文件agui_iterative.m
2、在MATLAB命令窗口输入及实验结果及操作界面
(3)牛顿法
1、实验程序
实现二分法的MATLAB函数文件agui_newton.m
2、在MATLAB命令窗口输入及实验结果及操作界面
结果分析:
由上面的对二分法、迭代法、牛顿法三种方法的三次实验结果,我们可以得出这样的结论:
二分法要循环k=10次,迭代法要迭代k=4次,牛顿法要迭代k=2次才能达到精度为0.5*10^-3的要求,而且方程0210=-+x e x
的精确解经计算,为0.0905250,由此可知,牛顿法和迭代法的精确度要优越于二分法。
而这三种方法中,牛顿法不仅计算量少,而且精确度高。
从而可知牛顿迭代法收敛速度明显加快,但由所学的内容可知,其收敛性与初值有关,它是局部收敛的。
二分法收敛虽然是速度最慢,但也常用于求精度不高的近似根。
而迭代法是逐次逼近的方法,原理简单,但存在收敛性和收敛速度的问题。
总之各种方法都各有优劣,适用于不同的情况中,须具体情况具体分析。
matlab方程求解实例

方程求根一、二分法1.用二分法求方程[]5.1,1013在区间=--x x 内的一个实根,要求两次近似值之间的误差不超过0.001。
解:用MA TLAB 求解:function rtn=bisection(fx,xa,xb,n,delta)x=xa;fa=eval(fx);x=xb;fb=eval(fx);disp(' [ n xaxb xc fc ]'); for i=1:nxc=(xa+xb)/2;x=xc;fc=eval(fx);X=[i,xa,xb,xc,fc];disp(X),if fc*fa<0xb=xc;else xa=xc;endif (xb-xa)<delta,break,endend输入:f='x^3-x-1';bisection(f,1,1.5,20,10^(-3))运行得:x0 =144 169 225y0 =12 13 15y =13.2302[ n xa xbxc fc ] 1.0000 1.0000 1.50001.2500 -0.29692.0000 1.2500 1.50001.3750 0.22463.0000 1.2500 1.37501.3125 -0.05154.0000 1.3125 1.37501.3438 0.08265.0000 1.3125 1.34381.3281 0.01466.0000 1.3125 1.3281 1.3203 -0.01877.0000 1.3203 1.3281 1.3242 -0.00218.0000 1.3242 1.3281 1.3262 0.00629.0000 1.3242 1.3262 1.3252 0.00202.求方程01)(3=--=x x x f 在区间[1,2]内的根,取精度510-=ε。
解:MATBLE 编程:function [x_star,it]=bisect(fun,a,b,ep)%%fun 为求根函数%%ep 为精度要求%%a ,b 为初始区间端点if nargin<4 ep=1e-5;endfa=feval(fun,a);fb=feval(fun,b);if fa*fb>0errorendk=0while abs(b-a)/2>=epx=(a+b)/2;fx=feval(fun,x);if fx==0breakendif fx*fa<0b=x;fb=fxelsea=x;fa=fxendk=k+1endx_star=(a+b)/2it=k输入:fun =@(x)(x^3-x-1);[x_star,it]=bisect(fun,1,2)运行得:x_star=1.3274It=16二、迭代法1.一般迭代法求解方程:.105.101)(5-03===--=ε附近的根,取精度在x x x x f 解:MATBLE 编程:function [x_star,it]=iterate(phi, x, ep, it_max) %% phi ()为迭代函数, %%x 为起始点, %%ep 为精度要求, %%it_max 为最大迭代次数。
数值计算方法matlab 第二章 求根

1第二章作业问题描述:不同温度的两种流体进入混合器混合,流出时具有相同的温度。
流体A 和B 的热容(单位:cal/(mol ·K))分别为:2623.381 1.80410 4.30010pA c T T --=+⨯-⨯ 1528.592 1.29010 4.07810pB c T T --=+⨯-⨯焓变(单位:cal/mol )为21T p T H c dT ∆=⎰。
A 进入混合器的温度为400℃,B 进入混合器的温度为700℃,A 的量(mol )是B 的量(mol )的两倍,试确定流体离开混合器的温度。
问题分析: 初始情况下,气体A 的温度比气体B 的温度低,故在混合过程中,气体A 温度升高,气体B 温度降低。
由于没有外界加热或者做功,混合气体整体的焓变应该为零。
设A 有2mol ,B 有1mol ,根据焓变公式计算得到:21-262400-22632= 6.762+3.608108.60010)6.762 1.80410 2.867105407.712T TA pA T H c dT T T dTT T T --∆=⨯-⨯=+⨯-⨯-⎰⎰(21-152700-1253=+1.29010 4.07810)0.64510 1.3591032958.030T TB pB T H c dT T T dTT T T --∆=⨯-⨯=+⨯-⨯-⎰⎰(8.5928.592而0A B H H ∆+∆=,故该问题最后变成求解方程2263()15.3548.2541016.4571038365.742f T T T T --=+⨯-⨯-的根的问题。
接下来将采用二分法、试位法以及牛顿法进行改方程的求解。
方程保存为f.m ,可在压缩文件中找到。
一、 二分法二分法的基本思想为,确定有根区间,然后不断将区间二等分,通过判断f(x)的符号,逐步将区间缩小,直到有根区间足够小,便可满足精度要求的近似根。
本例中,可以清楚的得到有根区间为(400,700)。
数值分析作业MATLAB

1.用二分法解方程 x-lnx=2 在区间【2 ,4】内的根方法: 二分法算法:f=inline('x-2-log(x)');a=2;b=4;er=b-a; ya=f(a);er0=.00001;while er>er0x0=.5*(a+b);y0=f(x0);if ya*y0<0b=x0;elsea=x0;ya=y0;enddisp([a,b]);er=b-a;k=k+1;end求解结果:>> answer13 43.0000 3.50003.0000 3.25003.1250 3.25003.1250 3.18753.1250 3.15633.1406 3.15633.1406 3.14843.1445 3.1484 3.1445 3.1465 3.1455 3.1465 3.1460 3.1465 3.1460 3.1462 3.1461 3.1462 3.1462 3.14623.1462 3.1462 3.1462 3.1462 3.1462 3.1462 最终结果为: 3.14622.试编写MATLAB 函数实现Newton 插值,要求能输出插值多项式。
对函数141)(2+=x x f 在区间[-5,5]上实现10次多项式插值。
Matlab 程序代码如下:%此函数实现y=1/(1+4*x^2)的n 次Newton 插值,n 由调用函数时指定 %函数输出为插值结果的系数向量(行向量)和插值多项式 算法:function [t y]=func5(n) x0=linspace(-5,5,n+1)'; y0=1./(1.+4.*x0.^2); b=zeros(1,n+1); for i=1:n+1 s=0; for j=1:i t=1; for k=1:iif k~=jt=(x0(j)-x0(k))*t;end;end;s=s+y0(j)/t;end;b(i)=s;end;t=linspace(0,0,n+1);for i=1:ns=linspace(0,0,n+1);s(n+1-i:n+1)=b(i+1).*poly(x0(1:i));t=t+s;end;t(n+1)=t(n+1)+b(1);y=poly2sym(t);10次插值运行结果:[b Y]=func5(10)b =Columns 1 through 4-0.0000 0.0000 0.0027 -0.0000Columns 5 through 8-0.0514 -0.0000 0.3920 -0.0000Columns 9 through 11-1.1433 0.0000 1.0000Y =- (7319042784910035*x^10)/147573952589676412928 + x^9/18446744073709551616 + (256*x^8)/93425 -x^7/1152921504606846976 -(28947735013693*x^6)/562949953421312 -(3*x^5)/72057594037927936 + (36624*x^4)/93425 -(5*x^3)/36028797018963968 -(5148893614132311*x^2)/4503599627370496 +(7*x)/36028797018963968 + 1b为插值多项式系数向量,Y为插值多项式。
二分法matlab程序(推荐文档)

二分法二分法基本思路一般地,对于函数f(x),如果存在实数c,当x=c 时,若f(c)=0,那么把x=c 叫做函数f(x)的零点。
解方程即要求f(x)的所有零点。
假定f(x)在区间(x ,y )上连续先找到a 、b 属于区间(x ,y ),使f(a),f(b)异号,说明在区间(a,b)内一定有零点,然后求f[(a+b)/2],现在假设f(a)<0,f(b)>0,a<b① 如果f[(a+b)/2]=0,该点就是零点,如果f[(a+b)/2]<0,则在区间((a+b)/2,b)内有零点,(a+b)/2>=a ,从①开始继续使用 ② 中点函数值判断。
如果f[(a+b)/2]>0,则在区间(a,(a+b)/2)内有零点,(a+b)/2<=b ,从①开始继续使用 中点函数值判断。
这样就可以不断接近零点。
通过每次把f(x)的零点所在小区间收缩一半的方法,使区间的两个端点逐步迫近函数的零点,以求得零点的近似值,这种方法叫做二分法。
从以上可以看出,每次运算后,区间长度减少一半,是线形收敛。
另外,二分法不能计算复根和重根。
二分法步骤用二分法求方程()0f x =的根*x 的近似值k x 的步骤① 若对于a b <有()()0f a f b <,则在(,)a b 内()0f x =至少有一个根。
② 取,a b 的中点12a b x +=计算1()f x ③ 若1()0f x =则1x 是()0f x =的根,停止计算,运行后输出结果*1x x =若1()()0f a f x <则在1(,)a x 内()0f x =至少有一个根。
取111,a a b x ==;若1()()0f a f x >,则取111,a x b b ==;④ 若12k k b a ε-≤(ε为预先给定的要求精度)退出计算,运行后输出结果*2k k a b x +≈,反之,返回步骤1,重复步骤1,2,3 二分法Mtalab 程序syms x;fun=input('(输入函数形式)fx=');a=input('(输入二分法下限)a=');b=input('(输入二分法上限)b=');d=input('输入误差限 d=')%二分法求根%f=inline(x^2-4*x+4);%修改需要求解的inline 函数的函数体f=inline(fun);%修改需要求解的inline 函数的函数体e=b-a; k=0 ;while e>dc=(a+b)/2;if f(a)*f(c)<0b=c;elseif f(a)*f(c)>0a=c;elsea=c;b=cende=e/2; k=k+1;endx=(a+b)/2;x%x 为答案 k%k 为次数例题:用二分法计算方程4324100x x x -++=在(-2,2)内的实根的近似值,要求精度为0.0001解:(输入函数形式)fx=x^4-2*x^3+4*x+10(输入二分法下限)a=-2(输入二分法上限)b=2输入误差限 d=0.0001得到结果d =1.0000e-004x =2.0000k =16>>。
借助Matlab使用二分法求解方程的根
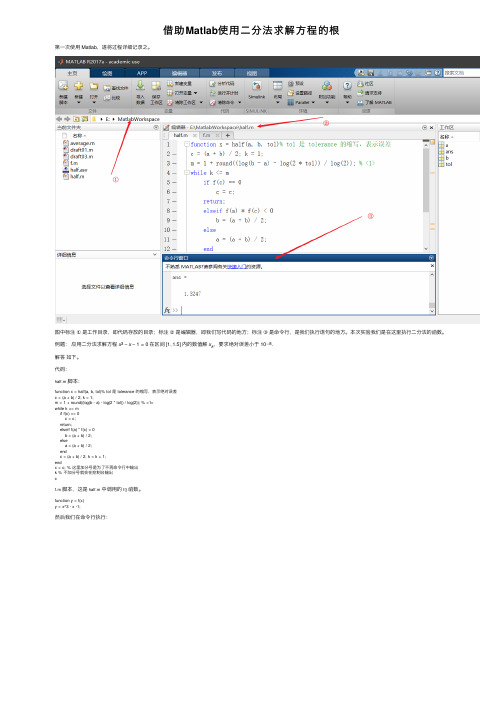
借助Matlab使⽤⼆分法求解⽅程的根第⼀次使⽤ Matlab,遂将过程详细记录之。
图中标注①是⼯作⽬录,即代码存放的⽬录;标注②是编辑器,即我们写代码的地⽅;标注③是命令⾏,是我们执⾏语句的地⽅。
本次实验我们是在这⾥执⾏⼆分法的函数。
例题:应⽤⼆分法求解⽅程x3−x−1=0 在区间 [1,1.5] 内的数值解x k,要求绝对误差⼩于 10−8.解答如下。
代码:half.m脚本:function x = half(a, b, tol)% tol 是 tolerance 的缩写,表⽰绝对误差c = (a + b) / 2; k = 1;m = 1 + round((log(b - a) - log(2 * tol)) / log(2)); % <1>while k <= mif f(c) == 0c = c;return;elseif f(a) * f(c) < 0b = (a + b) / 2;elsea = (a + b) / 2;endc = (a + b) / 2; k = k + 1;endx = c; % 这⾥加分号是为了不再命令⾏中输出k % 不加分号就会在控制台输出cf.m脚本,这是half.m中调⽤的f()函数。
function y = f(x)y = x^3 - x -1;然后我们在命令⾏执⾏:可以看出,最后求解得到的x=1.3247,即输出的ans,迭代次数k=27.关于代码half.m中的标注<1>,有如下解释:注意,在 Matlab 中,log()函数的底是e.补充例题(感兴趣的朋友可以⾃⾏测试):Processing math: 100%。
二分法及其matlab程序-经典

避免数值不稳定性
对于涉及大量计算或迭代的过程,要注意数值稳定性问题, 采取适当的算法或技巧,如使用稳定的算法、增加迭代次 数等。
利用MATLAB内置函数
二分法及其matlab程序-经典
目录
• 二分法基本原理 • MATLAB编程实现二分法 • 二分法在数值计算中应用举例 • MATLAB程序优化与改进策略 • 总结与展望
01
二分法基本原理
二分法定义与思想
定义
二分法是一种求解非线性方程近似根的有效算法,其基本思想是通过不断将区间一分为二,逐步缩小求解范围, 直到满足精度要求为止。
end
root = (a + b) / 2;
VS
关键代码片段展示
end
```
运行结果分析与讨论
• 假设我们要求解非线性方程f(x)=x^3-2x-5=0在 区间[2, 3]内的根,可以调用上述bisection函数进 行求解
运行结果分析与讨论
```matlab f = @(x) x^3 - 2*x - 5;
精度控制
当区间长度|b - a|小于给定 精度时,可取中点或任一端 点作为近似最优解。
求解矩阵特征值问题
• 特征多项式构建:对于n阶矩阵A,构建特征多项式f(λ) = |A - λI|。 • 初始区间选择:确定包含特征值的初始区间[a, b]。 • 二分迭代:取中点c = (a + b) / 2,计算f(c)。若f(c) == 0,则c为特征值;否则根据f(a)、f(b)、f(c)的大小关
缺点
二分法收敛速度较慢,需要多次迭代才能得 到精确解,且对于多峰函数或者复杂函数可 能无法找到全局最优解。
数学实验项目-使用二分法对非线性方程求根

end 程序输出
n=01,当前有根区间是[0.000000,0.500000],近似根为 0.500000,wucha=0.500000 n=02,当前有根区间是[0.250000,0.500000],近似根为 0.250000,wucha=0.250000 n=03,当前有根区间是[0.250000,0.375000],近似根为 0.375000,wucha=0.125000 n=04,当前有根区间是[0.250000,0.312500],近似根为 0.312500,wucha=0.062500 n=05,当前有根区间是[0.250000,0.281250],近似根为 0.281250,wucha=0.031250 n=06,当前有根区间是[0.265625,0.281250],近似根为 0.265625,wucha=0.015625 n=07,当前有根区间是[0.265625,0.273438],近似根为 0.273438,wucha=0.007813 n=08,当前有根区间是[0.265625,0.269531],近似根为 0.269531,wucha=0.003906 n=09,当前有根区间是[0.265625,0.267578],近似根为 0.267578,wucha=0.001953 n=10,当前有根区间是[0.265625,0.266602],近似根为 0.266602,wucha=0.000977 n=11,当前有根区间是[0.266113,0.266602],近似根为 0.266113,wucha=0.000488 n=12,当前有根区间是[0.266113,0.266357],近似根为 0.266357,wucha=0.000244 n=13,当前有根区间是[0.266235,0.266357],近似根为 0.266235,wucha=0.000122 n=14,当前有根区间是[0.266235,0.266296],近似根为 0.266296,wucha=0.000061 n=15,当前有根区间是[0.266235,0.266266],近似根为 0.266266,wucha=0.000031 n=16,当前有根区间是[0.266235,0.266251],近似根为 0.266251,wucha=0.000015 n=17,当前有根区间是[0.266243,0.266251],近似根为 0.266243,wucha=0.000008 n=18,当前有根区间是[0.266247,0.266251],近似根为 0.266247,wucha=0.000004 n=19,当前有根区间是[0.266247,0.266249],近似根为 0.266249,wucha=0.000002 n=20,当前有根区间是[0.266248,0.266249],近似根为 0.266248,wucha=0.000001
二分法matlab程序

班级
090712
学号
43
姓名
潘骁磊
实验室
3-128
设备编号 B01 日期 2012-6-5
实验题目 编写二分法方法的 MATLAB 主程序并验算书本 P-112(1)
1、实验目的:
通过编程实现二分法方法,加深对求根方法的理解。应用所编程序解决实际
算例。
2、实验要求:
(1)认真分析课题要求,复习相关理论知识,选择适当的解决方案;
2
2
[ a b ,b] .同理,若 2
f (a b) 0, 2
隔根区间变为
[a,
a
2
b
]
.将新区间记为
a1,
b1
.
(2)将 a1,b1重复上述步骤(1).得到一系列隔根区间:
a,b a1,b1 ak ,bk
并有 f (ak ) f (bk ) 0, x* (ak ,bk ) ,且后一区间的长度都是前一区间长度的一半,所以
ak ,bk
的长度为 bk
ak
ba 2k
,(k
)
,区间
ak , bk
的长度趋向于零,即这些区间最终
收缩于一点 x ,显然 x 就是方程 f (x) 0 的根。
(2)算法程序: %%%二分法主程序%% function erfen(f,a,b,m) t=b-a; f1=0; k=1; whi le(abs(t/2^(k+1))>=m)
命令窗口输入: f=@(x)x^4-3*x+1; a=0.3;b=0.4; m=0.005; erfen(f,a,b,m) 输出: k=
4 ans =
0.3438 x 的近似值为
MATLAB-平方根法和改进平方根法求解线性方程组例题与程序

(2)设对称正定阵系数阵线方程组12345678424024000221213206411418356200216143323218122410394334411142202531011421500633421945x x x x x x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢---⎢⎥⎢⎥⎢--⎢⎥⎢⎢⎥⎣⎦⎣⎦⎣⎦⎥⎥⎥⎥ (1,1,0,2,1,1,0,2)T x *=--二、数学原理 1、平方根法解n 阶线性方程组Ax=b 的choleskly 方法也叫做平方根法,这里对系数矩阵A 是有要求的,需要A 是对称正定矩阵,根据数值分析的相关理论,如果A 对称正定,那么系数矩阵就可以被分解为的T A=L L ∙形式,其中L 是下三角矩阵,将其代入Ax=b 中,可得:T LL x=b 进行如下分解:T L xL by y ⎧=⎨=⎩ 那么就可先计算y,再计算x ,由于L 是下三角矩阵,是T L 上三角矩阵,这样的计算比直接使用A 计算简便,同时你应该也发现了工作量就转移到了矩阵的分解上面,那么对于对称正定矩阵A 进行Cholesky 分解,我再描述一下过程吧: 如果你对原理很清楚那么这一段可以直接跳过的。
设T A=L L ∙,即1112111112112122221222221212....................................n n n n n n nn n n nn nn a a a l l l l aa a l l l l a a a l l l l ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦其中,,1,2,...,ij ji a a i j n ==第1步,由矩阵乘法,211111111,i i a l a l l == 故求得111111,2,3,...i i a l l i n a === 一般的,设矩阵L 的前k-1列元素已经求出 第k 步,由矩阵乘法得112211k k kk kmkkik im km ik kkm m a l l a l l l l --===+=+∑∑, 于是11(2,3,...,n)1(),1,2,...kk k ik ik im km m kk l k l a l l i k k n l -=⎧=⎪⎪=⎨⎪=-=++⎪⎩∑ 2、改进平方根法在平方根的基础上,为了避免开方运算,所以用TLDL A =计算;其中,11122.........n d D D D d ⎤⎤⎡⎤⎥⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎢⎢⎥⎣⎦⎣⎣;得1121212212111111n n n n n d l l l d l A l l d ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦按行计算的L 元素及D 对元素公式 对于n i ,,2,1 =11(1,21)j ij ij ik jk k t a t l j i -==-=-∑…,./(1,2,)ij ij j l t d j ==…,i-1.11i i ii ik ikk d a t l -==-∑计算出LD T =的第i 行元素(1,2,i-1)ij t j =…,后,存放在A 的第i 行相置,然后再计算L 的第i 行元素,存放在A 的第i 行.D 的对角元素存放在A 的相应位置.对称正定矩阵A 按T LDL 分解和按TLL 分解计算量差不多,但T LDL 分解不需要开放计算。
《Matlab软件与基础数学实验》程序(部分)

《Matlab软件与基础数学实验》程序(部分)追击问题:⼀敌舰在某海域内以椭圆轨迹航⾏,其在时间t时刻的坐标为:x(t)=10+20costy(t)=20+5sint我⽅战舰恰位于原点处,我战舰向敌舰发射制导鱼雷,鱼雷的速率为20,其运⾏⽅向始终指向敌舰,试问敌舰航⾏在何处将被击中?2. 若敌舰的运⾏轨迹变为x(t)=10+20costy(t)=20+20sint试问敌舰航⾏在何处将被击中?(⽆法击中)3. 若敌舰的运⾏轨迹变为x(t)=10+20costy(t)=20+20sint鱼雷速率提⾼⾄21,结果如何?%Matlab程序:clear;clch=0.01;%时间步长k=1;t(1)=0;x(1)=0;y(1)=0;%初始值r=10;while r>=0.05 % k<=250 %m=(20+5*sin(t(k))-y(k))/(10+20*cos(t(k))-x(k) +1.e-10)+1.e-10;if 10+20*cos(t(k))-x(k)>=0x(k+1)=x(k)+20*h/sqrt(1+m^2);elsex(k+1)=x(k)-20*h/sqrt(1+m^2);endif 20+5*sin(t(k))-y(k)>=0y(k+1)=y(k)+20*h/sqrt(1+1/m/m);elsey(k+1)=y(k)-20*h/sqrt(1+1/m/m);endr=(x(k)-10-20*cos(t(k)))^2+(y(k)-20-5*sin(t(k)))^2; r=sqrt(r); t(k+1)=h*k;k=k+1;plot(10+20*cos(t(k)),20+5*sin(t(k)), 'r*')hold onaxis([-10 32 -3 30]);plot(x,y, 'o')pause(0.02)endt=t(end),x=x(end),y=y(end)t =2.6300x =-7.1780y =22.5627第⼆问:速度相同⽆法击中第三问:t =4.4100 x =4.0221 y =0.9141%Matlab程序:clear;clch=0.01;%时间步长k=1;t(1)=0;x(1)=0;y(1)=0;%初始值r=10;while r>=0.05 % k<=250 %m=(20+20*sin(t(k))-y(k))/(10+20*cos(t(k))-x(k) +1.e-10)+1.e-10; if 10+20*cos(t(k))-x(k)>=0x(k+1)=x(k)+22*h/sqrt(1+m^2);elsex(k+1)=x(k)-22*h/sqrt(1+m^2);endif 20+20*sin(t(k))-y(k)>=0y(k+1)=y(k)+22*h/sqrt(1+1/m/m);elsey(k+1)=y(k)-22*h/sqrt(1+1/m/m);endr=(x(k)-10-20*cos(t(k)))^2+(y(k)-20-20*sin(t(k)))^2;r=sqrt(r);t(k+1)=h*k;k=k+1;plot(10+20*cos(t(k)),20+20*sin(t(k)), 'r*')hold onaxis([-12 32 -2 42]);plot(x,y, 'o')pause(0.02)endt=t(end),x=x(end),y=y(end)课本P811. 某农夫有⼀个半径10⽶的圆形⽜栏,长满了草.他要将⼀头⽜栓在⽜栏边界的栏桩上,但只让⽜吃到⼀半草,问栓⽜⿐的绳⼦应为多长?设拴⽜的绳⼦长为r, 以圆形⽜栏C1 的圆⼼为原点建⽴直⾓坐标系, 见图1, 不妨设拴⽜的栏桩为图1中圆形⽜栏C1 上的B 点, 其坐标为(10,0), 则所求问题转化为: 求出r,使得以B 点为圆⼼, 半径为r 的圆C2 与圆C1 相交部分的⾯积是圆C1 ⾯积的⼀半。
matlab二分法求根例题程序

matlab二分法求根例题程序二分法是一种常用的数值计算方法,用于求解方程的根。
其基本思想是通过不断缩小求解区间来逼近方程的根。
下面是一个使用MATLAB编写的二分法求根的例题程序:```MATLABfunction root = bisectionMethod(f, a, b, tol)fa = f(a);fb = f(b);if fa*fb >= 0error('The function has no root in the given interval'); endwhile (b-a)/2 > tolc = (a + b)/2;fc = f(c);if fc == 0break;elseif fa*fc < 0b = c;fb = fc;elsea = c;fa = fc;endendroot = (a + b)/2;end```使用该程序,可以求解一元函数在给定区间内的根。
其中,`f`代表待求解的一元函数,`a`和`b`是求解区间的端点,`tol`是收敛精度。
程序首先对给定的区间端点求函数值,如果这两个函数值的乘积大于等于零,则说明函数在该区间内没有根。
接下来,程序使用一个循环来不断缩小求解区间,直到满足收敛精度为止。
在每一次循环中,程序计算求解区间的中点,并求出中点处的函数值。
根据中点处的函数值与区间端点处函数值的乘积,可以判断根的位置,并相应地更新求解区间的端点。
最后,程序返回求得的根。
使用该程序,可以对不同的函数进行求根。
只需将待求解的函数作为参数传入,并指定求解区间的端点和收敛精度。
例如,我们可以使用该程序求解方程sin(x) = 0在区间[0, pi]内的根:```MATLABf = @(x) sin(x);a = 0;b = pi;tol = 1e-6;root = bisectionMethod(f, a, b, tol);disp(root);```以上程序中,我们定义了一个匿名函数`f`,然后指定求解区间的端点和收敛精度。
数值分析作业MATLAB

1.用二分法解方程 x-lnx=2 在区间【2 ,4】内的根方法: 二分法算法:f=inline('x-2-log(x)');a=2;b=4;er=b-a; ya=f(a);er0=.00001;while er>er0x0=.5*(a+b);y0=f(x0);if ya*y0<0b=x0;elsea=x0;ya=y0;enddisp([a,b]);er=b-a;k=k+1;end求解结果:>> answer13 43.0000 3.50003.0000 3.25003.1250 3.25003.1250 3.18753.1250 3.15633.1406 3.15633.1406 3.14843.1445 3.1484 3.1445 3.1465 3.1455 3.1465 3.1460 3.1465 3.1460 3.1462 3.1461 3.1462 3.1462 3.1462 3.1462 3.1462 3.1462 3.1462 3.1462 3.1462 最终结果为: 3.14622.试编写MATLAB 函数实现Newton 插值,要求能输出插值多项式。
对函数141)(2+=x x f 在区间[-5,5]上实现10次多项式插值。
Matlab 程序代码如下:%此函数实现y=1/(1+4*x^2)的n 次Newton 插值,n 由调用函数时指定 %函数输出为插值结果的系数向量(行向量)和插值多项式 算法:function [t y]=func5(n) x0=linspace(-5,5,n+1)'; y0=1./(1.+4.*x0.^2); b=zeros(1,n+1); for i=1:n+1 s=0; for j=1:i t=1; for k=1:i if k~=jt=(x0(j)-x0(k))*t;end;end;s=s+y0(j)/t;end;b(i)=s;end;t=linspace(0,0,n+1);for i=1:ns=linspace(0,0,n+1);s(n+1-i:n+1)=b(i+1).*poly(x0(1:i));t=t+s;end;t(n+1)=t(n+1)+b(1);y=poly2sym(t);10次插值运行结果:[b Y]=func5(10)b =Columns 1 through 4-0.0000 0.0000 0.0027 -0.0000Columns 5 through 8-0.0514 -0.0000 0.3920 -0.0000Columns 9 through 11-1.1433 0.0000 1.0000Y =- (*x^10)/12928 + x^9/0616 + (256*x^8)/93425 - x^7/076 - (013693*x^6)/3421312 - (3*x^5)/0 + (36624*x^4)/93425 - (5*x^3)/0 - (*x^2)/ + (7*x)/0 + 1b为插值多项式系数向量,Y为插值多项式。
不同方法求方程的根matlab代码

不同方法求方程的根matlab代码1、%使用二分法找到方程 600 x^4 -550 x^3 +200 x^2 -20 x -1 =0 在区间[0.1,1]上的根,%误差限为 e=10^-4disp('二分法')a=0.2;b=0.26;tol=0.0001;n0=10;fa=600*(a.^4)-550*(a.^3)+200*(a.^2)-20*a-1;for i=1:n0p=(a+b)/2;fp=600*(p.^4)-550*(p.^3)+200*(p.^2)-20*p-1;if fp==0||(abs((b-a)/2)<tol)< p="">disp('用二分法求得方程的根p=')disp(p)disp('二分迭代次数为:')disp(i)break;endif fa*fp>0a=p;else b=p;endendif i==n0&&~(fp==0||(abs((b-a)/2)<tol))< p="">disp(n0)disp('次二分迭代后没有求出方程的根')end2、%使用牛顿法找到方程 600 x^4 -550 x^3 +200 x^2 -20 x -1 =0 在区间[0.1,1]上的根,%误差限为 e=10^-4disp('牛顿法')p0=0.3;for i=1:n0p=p0-(600*(p0.^4)-550*(p0.^3)+200*(p0.^2)-20*p0-1)./(2400*(p0.^3) -1650*p0.^2+400*p0-20);if(abs(p-p0)<tol)< p="">disp('用牛顿法求得方程的根p=')disp(p)disp('牛顿迭代次数为:')disp(i)break;endp0=p;endif i==n0&&~(abs(p-p0)<tol)< p="">disp(n0)disp('次牛顿迭代后没有求出方程的根')end3、%使用割线法找到方程 600 x^4 -550 x^3 +200 x^2 -20 x -1 =0 在区间[0.1,1]上的根,%误差限为 e=10^-4disp('割线法')p0=0.2;p1=0.25;q0=600*(p0.^4)-550*(p0.^3)+200*(p0.^2)-20*p0-1;q1=600*(p1.^4)-550*(p1.^3)+200*(p1.^2)-20*p1-1;for i=2:n0p=p1-q1*(p1-p0)/(q1-q0);if abs(p-p1)<tol< p="">disp('用割线法求得方程的根p=')disp(p)disp('割线法迭代次数为:')disp(i)break;endp0=p1;q0=q1;pp=p1;p1=p;q1=600*(p.^4)-550*(p.^3)+200*(p.^2)-20*p-1;endif i==n0&&~(abs(p-pp)<tol)< p="">disp(n0)disp('次割线法迭代后没有求出方程的根')end4、%使用试位法找到方程 600 x^4 -550 x^3 +200 x^2 -20 x -1 =0 在区间[0.1,1]上的根,%误差限为 e=10^-4disp('试位法')p0=0.2;p1=0.25;q0=600*(p0.^4)-550*(p0.^3)+200*(p0.^2)-20*p0-1;q1=600*(p1.^4)-550*(p1.^3)+200*(p1.^2)-20*p1-1;for i=2:n0p=p1-q1*(p1-p0)/(q1-q0);if abs(p-p1)<tol< p="">disp('用试位法求得方程的根p=')disp(p)disp('试位法迭代次数为:')disp(i)break;endq=600*(p.^4)-550*(p.^3)+200*(p.^2)-20*p-1;if q*q1<0p0=p1;q0=q1;endpp=p1;p1=p;q1=q;endif i==n0&&~(abs(p-pp)<tol)< p="">disp(n0)disp('次试位法迭代后没有求出方程的根')end5、%使用muller方法找到方程 600 x^4 -550 x^3 +200 x^2 -20 x -1 =0 在区间[0.1,1]上的根,%误差限为 e=10^-4disp('muller法')x0=0.1;x1=0.2;x2=0.25;h1=x1-x0;h2=x2-x1;d1=((600*(x1.^4)-550*(x1.^3)+200*(x1.^2)-20*x1-1)-(600*(x0.^4)-55 0*(x0.^3)+200*(x0.^2)-20*x0-1))/h1;d2=((600*(x2.^4)-550*(x2.^3)+200*(x2.^2)-20*x2-1)-(600*(x1.^4)-55 0*(x1.^3)+200*(x1.^2)-20*x1-1))/h2;d=(d2-d1)/(h2+h1);for i=3:n0b=d2+h2*d;D=(b*b-4*(600*(x2.^4)-550*(x2.^3)+200*(x2.^2)-20*x2-1)*d)^0.5;if(abs(d-D)<abs(d+d))< p="">E=b+D;else E=b-D;endh=-2*(600*(x2.^4)-550*(x2.^3)+200*(x2.^2)-20*x2-1)/E;p=x2+h;if abs(h)<tol< p="">disp('用muller方法求得方程的根p=')disp(p)disp('muller方法迭代次数为:')disp(i)break;endx0=x1;x1=x2;x2=p;h1=x1-x0;h2=x2-x1;d1=((600*(x1.^4)-550*(x1.^3)+200*(x1.^2)-20*x1-1)-(600*(x0.^4)-55 0*(x0.^3)+200*(x0.^2)-20*x0-1))/h1;d2=((600*(x2.^4)-550*(x2.^3)+200*(x2.^2)-20*x2-1)-(600*(x1.^4)-55 0*(x1.^3)+200*(x1.^2)-20*x1-1))/h2;d=(d2-d1)/(h2+h1);endif i==n0%条件有待商榷?!disp(n0)disp('次muller方法迭代后没有求出方程的根') end</tol<></abs(d+d))<></tol)<></tol<></tol)<></tol<></tol)<></tol)<></tol))<></tol)<>。
实验5非线性方程求根及其MATLAB实现

实验5非线性方程求根及其MATLAB实现实验要求:1.掌握二分法、牛顿迭代法和二次迭代法等求根方法;2.能够通过MATLAB实现非线性方程求根算法。
实验背景:非线性方程求根是数值计算中的一个重要问题。
对于一般的非线性方程,往往无法用解析的方法得到根的精确值。
因此,需要采用数值计算的方法来逼近方程的根。
本实验将介绍三种常用的非线性方程求根算法:二分法、牛顿迭代法和二次迭代法,并通过MATLAB实现这些算法。
一、二分法二分法是一种简单直观的求根方法。
它的基本思想是:通过对函数值的符号变化情况进行判断,将方程的根所在的区间逐渐减小,直至满足精度要求。
具体实现过程如下:1.选择一个区间[a,b],使得f(a)和f(b)异号,即f(a)f(b)<0;2.确定区间的中点c=(a+b)/2,并计算f(c);3.如果f(c)为0,说明c就是方程的根。
如果不为0,再判断f(c)和f(a)的符号,如果异号,则根位于[a,c]区间;如果同号,则根位于[c,b]区间;4.根据上一步的判断,缩小区间,重复2和3步骤,直至满足精度要求。
二、牛顿迭代法牛顿迭代法利用导数与函数近似线性关系的思想,通过迭代不断逼近方程的根。
具体实现过程如下:1.选择一个初始值x0,计算f(x0)和f'(x0);2.根据一阶泰勒展开公式,得到下一个近似值x1=x0-f(x0)/f'(x0);3.计算f(x1)的绝对值,如果小于给定的精度要求,则x1是方程的近似根;否则,x1成为新的初始值,重复2和3步骤,直至满足精度要求。
三、二次迭代法二次迭代法也是一种常用的求根方法。
它通过构建二次复合函数并对其进行迭代,逐步逼近方程的根。
具体实现过程如下:1.选择一个初始点x0,计算f(x0)和f'(x0);2.利用初始点和导数构建二次复合函数g(x)=x-f(x)/f'(x),即g(x)=x0-f(x0)/f'(x0)+f''(x0)(x-x0)^2/2;3.将g(x)视为新的非线性方程,利用牛顿迭代法计算出下一个近似值y1;4.利用y1和x0计算原方程的下一个近似值x1=y1+f(x0)/f'(x0);5.计算f(x1)的绝对值,如果小于给定的精度要求,则x1是方程的近似根;否则,x1成为新的初始值,重复3到5步骤,直至满足精度要求。
实验5 非线性方程求根及其MATLAB实现

等价于 f (a) = 0
a就是方程f (x) = 0的根。
.
收敛的迭代: y=x
f(x0)
x0x2= f(x1) x
f(x1)
x1= f(x0)
.
y=f(x)
发散的迭代:
x0
.
2.不动点迭代
例2 求方程 x2x14 0
在 x = 3附近的近似实根。
解:可将方程写成下三种形式: x = 14 – x 2 ,
a+ b
ac2
b
x
f(a)
f((a+b)/2) 程序:fastbisect.m
.
2.不动点迭代
称满足方程 f(x)=x的点x为函数f的不动点.
求函数f的不动点。可以从一个初始点x0出发, 以格式 xn+1=f(xn)进行迭代;
x1 =f(x0),x2 =f(x1),…,xk+1 =f(xk),… 得到x0,x1,x2,……,xn,….. 如果该数列是收敛的,则
0 0
y=x M
0.2
0.4
0.6
0.8
1
高级例子iterexample2.m 请同学们自己消化 .
3.牛顿迭代法
记[a, b]为方程 f (x) = 0的根的存在区间, f (a)与f (b)异号,且对于每个x∈[a, b], f '(x)≠0,f "(x)保持符号不变。
取x0∈[a, b],对f (x)用微分中值定理,近似地,
1首先观测图形作fxezplot函数表达式plotlinewidty1zerossizeplotlinewidtbisectm关于此程序的解释见方程求根的代码解释一文2按两分法的思想进行迭代求根
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
matlab二分法求根例题
标题: MATLAB二分法求根例题
正文:
二分法是解决函数零点问题的一种常用方法。
在MATLAB中,可以使用
`root()`函数进行二分法求根。
下面是一个示例:
假设我们有一个函数`f(x)`,它在[-1,1]上零点为`(-1,0)`,现在我们希望使用二分法找到一个根。
我们可以使用以下步骤:
1. 使用二分法求导数,得到二分点的斜率`k`。
2. 计算二分点的横坐标`x_2`,满足`f(x_2) = f(x_1) + k`。
3. 使用二分法求导数,得到二分点的斜率`k`。
4. 计算二分点的横坐标`x_2`,满足`f(x_2) = f(x_1) + k`。
5. 重复步骤3和步骤4,直到求出的根不再重复。
下面是MATLAB代码实现:
```matlab
% 定义函数
f = -1 : 1 : 2;
% 求二分点
x_1 = min(f);
x_2 = max(f);
% 计算斜率
k = f(x_2) - f(x_1);
% 计算根
root = x_2 - (1 / k);
% 输出结果
disp(["二分法求根结果:" num2str(root)]);
```
在上面的代码中,我们首先定义了一个包含零点的函数`f(x)`,然后使用二分法求导数得到二分点的斜率`k`。
接着,我们计算二分点的横坐标`x_2`,并满足`f(x_2) = f(x_1) + k`。
最后,我们使用二分法求导数,得到二分点的斜率`k`,并计算二分点的横坐标`x_2`,满足`f(x_2) = f(x_1) + k`。
最后,我们重复步骤3和步骤4,直到求出的根不再重复,并输出结果。
需要注意的是,二分法求根可能会遇到无穷级数的情况。
这种情况下,我们需要使用一些技巧来避免无限递归。
具体来说,可以使用二分法求解函数的局部零点,或者使用二分法求解函数的极值点,然后在此基础上继续求根。
