用回溯法分析着色问题
回溯法实验(图的m着色问题)
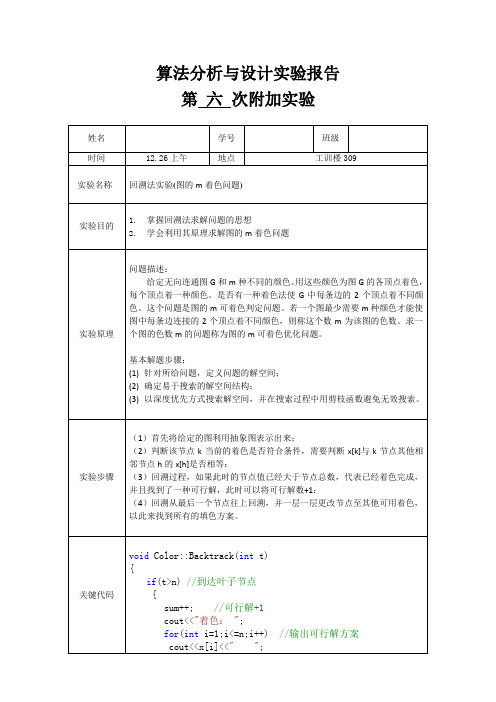
算法分析与设计实验报告第六次附加实验cout<<endl;}elsefor(int i=1;i<=m;i++){x[t]=i;if(ok(t)) Backtrack(t+1);//回溯，继续寻找下一层x[t]=0;//回到最初状态，使x[1]继续尝试其他填色的可能解}}测试结果当输入图如下时：结果如下：12435只要输入边即可当输入的图如下时：结果如下：附录：完整代码（回溯法）//图的m着色问题回溯法求解#include<iostream>using namespace std;class Color{friend void mColoring(int,int,int **);private:bool ok(int k);void Backtrack(int t);int n, //图的顶点个数m, //可用颜色数**a, //图的邻接矩阵*x; //当前解long sum; //当前已找到的可m着色的方案数};bool Color::ok(int k) //检查颜色可用性{for(int j=1;j<=n;j++)if((a[k][j]==1)&&(x[j]==x[k])) //两个点之间有约束且颜色相同return false;return true;}void Color::Backtrack(int t){if(t>n) //到达叶子节点{sum++; //可行解+1cout<<"着色： ";for(int i=1;i<=n;i++) //输出可行解方案cout<<x[i]<<" ";cout<<endl;}elsefor(int i=1;i<=m;i++){x[t]=i;if(ok(t)) Backtrack(t+1);//回溯，继续寻找下一层x[t]=0;//回到最初状态，使x[1]继续尝试其他填色的可能解 }}void mColoring(int n,int m,int **a){Color X;//初始化XX.n=n;X.m=m;X.a=a;X.sum=0;int *p=new int[n+1];for(int i=0;i<=n;i++)p[i]=0;X.x=p;cout<<"顶点： ";for(int i=1;i<=n;i++) //用于输出结果cout<<i<<" " ;cout<<endl;X.Backtrack(1); //从顶点1开始回溯delete []p;cout<<"解法个数："<<X.sum<<endl;}int main(){int n;int m;cout<<"please input number of node:";cin>>n;cout<<"please input number of color:";cin>>m;int **a=new int*[n+1];for(int i=0;i<=n;i++)a[i]=new int[n+1];for(int i=0;i<=n;i++) //利用抽象图实现图的邻接矩阵for(int j=0;j<=n;j++)a[i][j]=0;int edge;cout<<"please input adjacent edge number:";cin>>edge;int v,w;cout<<"please inout adjacent edge:"<<endl; //只要输入边即可for(int i=0;i<edge;i++){cin>>v>>w; //由于是无向图，所以对应的邻接矩阵对应的边都有，即v->m,m->v都有边a[v][w]=1;a[w][v]=1;}mColoring(n,m,a);system("pause");return 0;}。
图的着色问题--C++实现(含详细注释)
图的着色问题一、题目简述(1) 图的m-着色判定问题给定一个无向连通图 G 和 m 种不同的颜色。
用这些颜色为图 G 的各顶点着色，每个顶点着一种颜色，是否有一种着色法使 G 中任意相邻的两个顶点着不同颜色？(2) 图的m-着色优化问题若一个图最少需要 m 种颜色才能使图中任意相邻的两个顶点着不同颜色，则称这个数 m 为该图的色数。
求一个图的最小色数 m 的问题称为m-着色优化问题。
二、算法思想1. m-着色判定问题总体思想：通过回溯的方法，不断为每一个节点着色，每个点的颜色由一个数字代表，初始值为1。
在对前面 step - 1 个节点都合法的着色之后，开始对第 step 个节点进行着色。
如果 n 个点均合法，且颜色数没有达到 m 种，则代表存在一种着色法使 G中任意相邻的两个顶点着不同颜色。
具体步骤：1. 对每个点 step ，有 m 种着色可能性，初始颜色值为1。
2. 检查第 step 个节点颜色的可行性，若与某个已着色的点相连且颜色相同，则不选择这种着色方案，并让颜色值加1，继续检查该点下一种颜色的可行性。
3. 如果第 step 点颜色值小于等于 m ，且未到达最后一个点，则进行对第 step + 1 点的判断。
4. 如果第 step 点颜色值大于 m ，代表该点找不到合适的分配方法。
此时算法进行回溯，首先令第 step 节点的颜色值为0，并对第 step - 1 个点的颜色值+1后重新判断。
5. 如果找到一种颜色使得第 step 个节点能够着色，说明 m 种颜色的方案是可行的。
6. 重复步骤2至5，如果最终 step 为0则代表无解。
2. m-着色优化问题基于问题1，对于一个无向图 G ，从1开始枚举染色数，上限为顶点数，第一个满足条件的颜色数即为所求解。
三、实现过程（附代码）1. m-着色判定问题#include<iostream>using namespace std;int color[100]; // 每个点的颜色int mp[100][100]; // 图的邻接矩阵int n, m, x; // n顶点，m种颜色方案，x条边bool check(int step) {// 判断与step点相邻的点，颜色是否与step点相同，若相同则返回falsefor (int i=1; i<=n; i++) {if (mp[step][i] ==1&&color[i] ==color[step]) {return false;}}return true;}bool Solve(int m) {// 求解是否可以找到一种可行的染色方案int step=1; // step指示当前节点while (step>=1) {color[step] +=1; // 假定颜色值从1开始，若为回溯，选择下一种方案while (color[step] <=m) { // 按照问题条件选择第step点颜色if (check(step)) {break;} else {color[step]++; // 搜索下一个颜色}}if (color[step] <=m&&step==n) { // 如果找完n个点，且染色方法小于等于m种 return true;} else if (color[step] <=m&&step<n) {step++; // 求解下一个顶点} else { // 如果染色数大于m个，回溯color[step] =0; // 回溯，该点找不到合适的分配方法，对上一点进行分析step--;}}// 如果step退到0，则代表无解return false;}int main() {int i, j;bool ans=false;cout<<"输入顶点数n和着色数m"<<endl;cin>>n>>m;cout<<"输入边数"<<endl;cin>>x;cout<<"具体输入每条边"<<endl;for (int p=0; p<x; p++) { // 以无向邻接矩阵存储边cin>>i>>j;mp[i][j] =1;mp[j][i] =1;}if (Solve(m)) {cout<<"有解";} else {cout<<"无解";}return0;}2. m-着色优化问题#include<iostream>using namespace std;int color[100]; // 每个点的颜色int mp[100][100]; // 图的邻接矩阵int n, m, x; // n顶点，m种颜色方案，x条边bool check(int step) {// 判断与step点相邻的点，颜色是否与step点相同，若相同则返回falsefor (int i=1; i<=n; i++) {if (mp[step][i] ==1&&color[i] ==color[step]) {return false;}}return true;}bool Solve(int m) {// 求解是否可以找到一种可行的染色方案int step=1; // step指示当前节点while (step>=1) {color[step] +=1; // 假定颜色值从1开始，若为回溯，选择下一种方案while (color[step] <=m) { // 按照问题条件选择第step点颜色if (check(step)) {break;} else {color[step]++; // 搜索下一个颜色}}if (color[step] <=m&&step==n) { // 如果找完n个点，且染色方法小于等于m种 return true;} else if (color[step] <=m&&step<n) {step++; // 求解下一个顶点} else { // 如果染色数大于m个，回溯color[step] =0; // 回溯，该点找不到合适的分配方法，对上一点进行分析step--;}}// 如果step退到0，则代表无解return false;}int main() {int i, j;bool ans=false;cout<<"输入顶点数n"<<endl;cin>>n;cout<<"输入边数"<<endl;cin>>x;cout<<"具体输入每条边"<<endl;for (int p=0; p<x; p++) { // 以无向图邻接矩阵存储边 cin>>i>>j;mp[i][j] =1;mp[j][i] =1;}for (m=1; m<=n; m++) { // 从小到大枚举着色数mif (Solve(m)) { // 如果有解，输出答案并跳出循环cout<<"最小色数m为 "<<m;break;}}return0;}四、结果及分析问题1测试用例：问题2测试用例：经检验，最少着色数的范围为2-4，意味着使 G 中任意相邻的两个顶点着不同颜色最多需要4种颜色。
涂色问题的常见解法及策略
涂色问题的常见解法及策略涂色问题是在给定一定数量的图形或区域的情况下，选择不同的颜色对它们进行涂色，使得相邻的区域具有不同的颜色。
这个问题在计算机图像处理、地图着色、图论等领域都有广泛的应用。
本文将介绍常见的涂色问题解法及策略。
1. 回溯法回溯法是一种常见的解决涂色问题的策略。
其基本思想是尝试在每个区域上涂上一种颜色，并检查该颜色是否符合要求。
如果符合要求，则继续涂色下一个区域；如果不符合要求，则回溯到上一个区域重新选择颜色。
回溯法的算法步骤如下：1.选择一个起始区域。
2.在该区域上选择一种颜色，并检查是否与相邻区域的颜色冲突。
3.如果颜色冲突，则选择另一种颜色，并重新检查。
4.如果所有颜色都冲突，则回溯到上一个区域重新选择颜色。
5.重复步骤2-4，直到所有区域都被涂色。
回溯法的优点是简单易懂，容易实现。
但对于复杂的问题，可能会产生大量的重复计算，效率较低。
为了提高效率，可以采用剪枝或启发式搜索等技巧进行优化。
2. 图着色算法涂色问题可以看作是图着色问题的特例，其中每个区域可以看作是一个节点，相邻的区域之间有一条边。
因此，可以借用图着色算法来解决涂色问题。
图着色算法的基本思想是为每个节点选择一个颜色，并确保相邻节点具有不同的颜色。
常见的图着色算法有贪心算法、回溯法、禁忌搜索等。
其中，贪心算法是一种简单且高效的图着色算法。
其基本思想是每次选择一个颜色，并将其分配给当前节点，然后继续处理下一个节点。
在选择颜色时，优先选择与当前节点相邻节点颜色不同的颜色。
贪心算法的流程如下：1.对节点进行排序，按照节点的度从大到小排序。
2.依次处理每个节点，选择一个颜色，并将其分配给当前节点。
3.检查相邻节点的颜色，如果与当前节点的颜色相同，则选择另一种颜色，并重新检查。
4.重复步骤2-3，直到所有节点都被着色。
贪心算法的优点是简单高效，适用于大规模的问题。
然而，由于贪心算法的局部最优性，可能无法得到全局最优解。
3. 深度优先搜索深度优先搜索是一种常见的解决涂色问题的策略。
五个回路溯源分析
五个回路溯源分析
1. 回溯法的基本概念
用回溯法求解问题时，应明确问题的解空间，问题的解空间至少应包含问题的一个最优解，确定了解空间的组织结构后，回溯法从开始结点（根结点）出发，以深度优先方式搜索整个解空间，这个开始结点成为活结点，同时成为当前的扩展结点，在当前扩展结点处，如果在当前扩展结点处不能在向纵深方向移动，则当前扩展结点就成为死结点，此时应往回移动（回溯）至最近的一个活结点处，并让这个活结点成为当前的扩展结点，回溯法以这种工作方式递归的在解空间中搜索，直至找到所要求的的解或解空间中已无活结点时为止
2. 回溯法搜索空间树时，通常采用两种策略来避免无效的搜索，提高回溯法的搜索效率
是用约束函数在扩展结点剪去不满足约束的子树
是用限界函数剪去得不到最优解的子树，这两类函数称之为剪枝函数
3. 回溯法的基本算法框架
递归回溯
迭代回溯
子集树算法框架
排列树算法框架
5. 采用回溯法解决的经典问题
转载问题
批处理作业二调度问题
符号三角形问题
n后问题
0-1背包问题
最大团问题
图的m着色问题
旅行售货员问题
圆排列问题
电路板排列问题
连续邮资问题。
图节点着色问题中的禁忌搜索算法
图节点着色问题中的禁忌搜索算法09-03-25 作者：编辑：校方人员图节点着色问题是组合最优化中典型的非确定多项式(NP)完全问题，也是图论中研究得最久的一类问题。
目前解决该问题的算法很多，如回溯算法、分支界定法、Welsh-Powell算法、神经网络、遗传算法以及模拟退火算法等。
综合比较各种算法，前两种算法是精确算法，但时间复杂性太大；后三种属于近似算法，虽然时间复杂性可接受，能够得到较好的近似解，但算法本身过于复杂，算法效率难以保证。
本文采用禁忌搜索算法，它同时拥有高效性和鲁棒性。
禁忌搜索是一种全局逐步寻优的人工智能算法，它常能有效的应用于一些典型NP问题，如TSP。
但禁忌搜索存在一些参数较难设置，这也是应用于通信系统时研究的热点。
本文提出针对着色问题的禁忌搜索的具体设计方案，较好的设置了参数，并优化了数据结构，通过实验比较得到了较好的效果。
最后提出通过领域简单的变化，禁忌搜索能较好的用于一般算法难以实现的List着色问题。
1图节点着色问题图的着色问题可分为边着色、顶点着色、List着色和全着色，其中最主要的给定一个无向图G=(V,E)，其中V是节点集V={1,2,…n}，E是边集，其中(i,j)表示有连接(i,j)的一条边。
若，且V i内部的任何两个节点没有E中的边直接相连，则称(V1,V2,…,V n)为V的一个划分。
图的节点着色问题可以描述为：求一个最小的k，使得(V1,V2,…,V n)为V的一个划分。
通常的解决着色问题的算法采用蛮力法、贪婪法、深度优先或广度优先等思想可以得到最优解，但时间复杂性太大，如回溯法，其计算时间复杂性为指数阶的；有的在多项式时间内能得到可行解，但不是最优解，如Welsh-Powell算法和贪婪算法。
Welsh-Powell算法只能保证最多使用(为图中顶点的最大度)种颜色给一个图正常着色，而由Brooks定理，对于既不是完全图又不是奇圈的简单连通图，所需的颜色数。
图的着色问题
问题来源
图的着色
通常所说的着色问题是指下述两类问题： 通常所说的着色问题是指下述两类问题： 1．给定无环图G=(V,E)，用m种颜色为图中 的每条边着色，要求每条边着一种颜色， 的每条边着色，要求每条边着一种颜色，并 使相邻两条边有着不同的颜色， 使相邻两条边有着不同的颜色，这个问题称 为图的边着色问题。 为图的边着色问题。 2．给定无向图G=(V,E)，用m种颜色为图中 的每个顶点着色，要求每个顶点着一种颜色， 的每个顶点着色，要求每个顶点着一种颜色， 并使相邻两顶点之间有着不同的颜色， 并使相邻两顶点之间有着不同的颜色，这个 问题称为图的顶着色问题。 问题称为图的顶着色问题。
化简得
( a + bd )(b + aceg )(c + bdef )( d + aceg )(e + bcdf )( f + ceg )( g + bdf )
求极小覆盖法－ 求极小覆盖法－布尔代数法
Step3：从中挑选所用极大独立集个数最小者， Step3：从中挑选所用极大独立集个数最小者， 即为X 即为X（G） 但上述子集的颜色数都不是X ），正确的应 但上述子集的颜色数都不是X（G），正确的应 该是X =3，该子集为： {b,d,f}中的 该是X（G）=3，该子集为：给{b,d,f}中的 b,d,f涂颜色 涂颜色1 {a,e,g}中a,e,g涂颜色 涂颜色2 b,d,f涂颜色1，为{a,e,g}中a,e,g涂颜色2为 {a,c,g}中的 涂颜色3 中的c {a,c,g}中的c涂颜色3。 由此可见， 由此可见，求色数其需要求极大独立集以 及一切若干极大独立集的和含所有顶点的子 对于大图， 集，对于大图，因为图计算量过大而成为实 际上难以凑效的算法，所以不是一个好算法， 际上难以凑效的算法，所以不是一个好算法， 一般我们采用贪心法等近似算法来求解 。
实验四 回溯法(图着色问题)
01 234 001 1 01 1 1 01 01 21 1 01 0 3001 01 41 1 01 0
class MGraph { public:
MGraph(int v,int s); void mColoring(int m,int *x); //一维数组x，存放1~n个顶点的颜色 ~MGraph(); private: void NextValue(int k,int m,int *x); void mColoring (int k,int m,int *x); int **a; //二维数组a，存储图的邻接矩阵 int n,e; //n表示图的顶点数，e表示边数 };
无向图G
【实验内容与要求】
图的着色问题：设G=(V,E)是一连通无向图，有3 种颜色，用这些颜色为G的各顶点着色，每个顶点着 一种颜色，且相邻顶点颜色不同。试用回溯法设计一 个算法，找出所有可能满足上述条件的着色法。
无向图G
无向图G
对应这个无向图的状态空间树应该是怎样的？
是一个完全3叉树，共6层
实验四 回溯法 — 图的着色问题
图的着色问题是由地图的着色问题引申而来的： 用m种颜色为地图着色，使得地图上的每一个 区域着一种颜色，且相邻区域颜色不同。
问题处理：如果把每一个区域收缩为一个顶点， 把相邻两个区域用一条边相连接，就可以把一
个区域图抽象为一个平面图。
地图（map）中地区的相邻关系，在图（graph ）中用边表示。
//若(i, j)是图的边，且相邻结点k和j颜色相同 //发生冲突，选下一种颜色
if (j==k) return; //成功选择一种颜色返回 }while (1); //循环尝试颜色 }
运行结果：
五大常见算法策略之——回溯策略
五⼤常见算法策略之——回溯策略回溯策略欢迎⼤家访问我的个⼈搭建的博客回溯是五⼤常⽤算法策略之⼀，它的核⼼思想其实就是将解空间看作是⼀棵树的结构，从树根到其中⼀个叶⼦节点的路径就是⼀个可能的解，根据约束条件，即可得到满⾜要求的解。
求解问题时，发现到某个节点⽽不满⾜求解的条件时，就“回溯”返回，尝试别的路径。
回溯法是⼀种选优搜索法，按选优条件向前搜索，以达到⽬标。
下⾯通过⼏个例⼦来讨论这个算法策略。
货郎问题有⼀个推销员，要到n个城市推销商品，他要找出⼀个包含所有n个城市的具有最短路程的环路。
（最后回到原来的城市），也就是说给⼀个⽆向带权图G<V,E>,⽤⼀个邻接矩阵来存储两城市之间的距离（即权值），要求⼀个最短的路径。
我们设置⼀组数据如下：4个城市，之间距离如下图所⽰，默认从0号城市出发由此我们可以画出⼀棵解空间树：（只画了⼀部分，右边同理）按照这个解空间树，对其进⾏深度优先搜索，通过⽐较即可得到最优结果（即最短路径）package BackTrack;//解法默认从第0个城市出发，减⼩了问题难度，主要⽬的在于理解回溯策略思想public class Saleman {//货郎问题的回溯解法static int[][] map = {{ 0,10,5,9},{10,0,6,9},{ 5,6,0,3},{ 9,9,3,0}}; //邻接矩阵public static final int N = 4; //城市数量static int Min = 10000; //记录最短的长度static int[] city = {1,0,0,0}; //默认第0个城市已经⾛过static int[] road = new int[N]; //路线，road[i] = j表⽰第i个城市是第j个经过的/**** @param city 保存城市是否被经过，0表⽰未被⾛过，1表⽰已经⾛过* @param j 上⼀层⾛的是第⼏个城市* @param len 此时在当前城市⾛过的距离总和* @param level 当前所在的层数，即第⼏个城市*/public static void travel(int[] city, int j, int len, int level) {if(level == N - 1) { //到达最后⼀个城市/*do something*/if(len+map[j][0] < Min) {Min = len + map[j][0];for (int i = 0; i < city.length; i++) {road[i] = city[i];}}return;}for(int i = 0; i < N; i++) {if(city[i] == 0 && map[j][i] != 0) { //第i个城市未被访问过，且上⼀层访问的城市并不是此城市city[i] = level+2; //将此城市置为已访问travel(city, i, len+map[j][i], level+1);city[i] = 0; //尝试完上⼀层的路径后，将城市⼜置为未访问，以免影响后⾯的尝试情况，避免了clone数组的情况，节省内存开销}}}public static void main(String[] args) {travel(city,0,0,0);System.out.println(Min);for (int i = 0; i < N; i++) {System.out.print(road[i]+" ");}System.out.println("1");}}⼋皇后问题要在n*n的国际象棋棋盘中放n个皇后，使任意两个皇后都不能互相吃掉。
第8节图论应用实例_图着色问题
第8节图论应用实例_图着色问题预备知识_回溯法回溯法:在实际生活中，有些问题是不能用数学公式去解决的，它需要通过一个过程，此过程要经过若干个步骤才能完成，每一个步骤又分为若干种可能;同时，为了完成任务，还必须遵守一些规则，但这些规则无法用数学公式表示，对于这样一类问题，一般采用搜索的方法来解决，回溯法就是搜索算法(广度优先、深度优先等)中的一种控制策略，它能够解决许多搜索中问题。
回溯法基本思想:试探法，撞了南墙就回头。
(一般采用深度优先搜索策略) 搜索策略:深度优先(不撞南墙不回头)。
在搜索过程中，如果求解失败，则返回搜索步骤中的上一点，去寻找新的路径，以求得答案。
要返回搜索，前进中的某些状态必须保存，才能使得退回到某种状态后能继续向前。
白话搜索:如果用数组存放搜索信息，i表示数组下标(当前状态)， ++i表示往前走(下一个状态)，--i表示回溯(往回退，返回上一次状态)。
第8节图论应用实例_图着色(graph coloring)问题数学定义:给定一个无向图G=(V, E)，其中V为顶点集合，E为边集合，图着色问题即为将V分为k个颜色组(k为颜色数)，每个组形成一个独立集，即其中没有相邻的顶点。
其优化版本是希望获得最小的k值。
典型应用:地图的着色、调度问题等。
k-着色判定问题:给定无向连通图G和k种不同的颜色。
用这些颜色为图G的各顶点着色，每个顶点着一种颜色，是否有一种着色法使G中任意相邻的2个顶点着不同颜色,例四色问题。
设有如图1的地图，每个区域代表一个省，区域中的数字表示省的编号，现在要求给每个省涂上红、蓝、黄、白四种颜色之一，同时使相邻的省份以不同的颜色区分。
课外拓展:搜索“四色问题”，了解四色问题相关知识。
5674231图1问题分析:(1)属于图的搜索问题。
将问题简化:将每个省抽象为一个点，省之间的联系看为一条边，可以得到图2。
16751432图2(2)用邻接矩阵表示各省之间的相邻关系，二维数组实现:1 表示省i与省j相邻, ,,ri,j,,0 表示省i与省j不相邻,由图2可以得到如下矩阵:(对称矩阵)1 2 3 4 5 6 71 0 1 0 0 0 0 12 1 0 1 1 1 1 13 0 1 0 1 0 0 04 0 1 1 0 1 0 05 0 1 0 1 0 1 06 0 1 0 0 1 0 17 1 1 0 0 0 1 0 为一对称矩阵。
《计算机算法设计与分析》课程设计
《计算机算法设计与分析》课程设计用分治法解决快速排序问题及用动态规划法解决最优二叉搜索树问题及用回溯法解决图的着色问题一、课程设计目的：《计算机算法设计与分析》这门课程是一门实践性非常强的课程，要求我们能够将所学的算法应用到实际中，灵活解决实际问题。
通过这次课程设计，能够培养我们独立思考、综合分析与动手的能力，并能加深对课堂所学理论和概念的理解，可以训练我们算法设计的思维和培养算法的分析能力。
二、课程设计内容：1、分治法：（2）快速排序；2、动态规划：（4）最优二叉搜索树；3、回溯法：（2）图的着色。
三、概要设计：分治法—快速排序：分治法的基本思想是将一个规模为n的问题分解为k个规模较小的子问题，这些子问题互相独立且与原问题相同。
递归地解这些子问题，然后将各个子问题的解合并得到原问题的解。
分治法的条件：（1) 该问题的规模缩小到一定的程度就可以容易地解决；（2) 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质；（3) 利用该问题分解出的子问题的解可以合并为该问题的解；（4) 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。
抽象的讲，分治法有两个重要步骤：（1）将问题拆开；（2）将答案合并；动态规划—最优二叉搜索树：动态规划的基本思想是将问题分解为若干个小问题，解子问题，然后从子问题得到原问题的解。
设计动态规划法的步骤：（1）找出最优解的性质，并刻画其结构特征；（2）递归地定义最优值（写出动态规划方程）；（3）以自底向上的方式计算出最优值；（4）根据计算最优值时得到的信息，构造一个最优解。
●回溯法—图的着色回溯法的基本思想是确定了解空间的组织结构后，回溯法就是从开始节点（根结点）出发，以深度优先的方式搜索整个解空间。
这个开始节点就成为一个活结点，同时也成为当前的扩展结点。
在当前的扩展结点处，搜索向纵深方向移至一个新结点。
这个新结点就成为一个新的或节点，并成为当前扩展结点。
回溯法解决图着色问题
回溯法解决图着色问题回溯法解决图着色问题2010-05-20 20：151回溯算法也叫试探法，它是一种系统地搜索问题的解的方法。
回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。
用回溯算法解决问题的一般步骤为：一、定义一个解空间，它包含问题的解。
二、利用适于搜索的方法组织解空间。
三、利用深度优先法搜索解空间。
四、利用限界函数避免移动到不可能产生解的子空间。
问题的解空间通常是在搜索问题的解的过程中动态产生的，这是回溯算法的一个重要特性。
回溯法是一个既带有系统性又带有跳跃性的的搜索算法。
它在包含问题的所有解的解空间树中，按照深度优先的策略，从根结点出发搜索解空间树。
算法搜索至解空间树的任一结点时，总是先判断该结点是否肯定不包含问题的解。
如果肯定不包含，则跳过对以该结点为根的子树的系统搜索，逐层向其祖先结点回溯。
否则，进入该子树，继续按深度优先的策略进行搜索。
回溯法在用来求问题的所有解时，要回溯到根，且根结点的所有子树都已被搜索遍才结束。
而回溯法在用来求问题的任一解时，只要搜索到问题的一个解就可以结束。
这种以深度优先的方式系统地搜索问题的解的算法称为回溯法，它适用于解一些组合数较大的问题.递归回溯：由于回溯法是对解空间的深度优先搜索，因此在一般情况下可用递归函数来实现回溯法如下：procedure try(i：integer)；var begin if in then输出结果else for j：=下界to上界do begin x：=h[j]；if可行{满足限界函数和约束条件}then begin置值；try(i+1)；end；end；end；说明：i是递归深度；n是深度控制，即解空间树的的高度；可行性判断有两方面的内容：不满约束条件则剪去相应子树；若限界函数越界，也剪去相应子树；两者均满足则进入下一层；搜索：全面访问所有可能的情况，分为两种：不考虑给定问题的特有性质，按事先顶好的顺序，依次运用规则，即盲目搜索的方法；另一种则考虑问题给定的特有性质，选用合适的规则，提高搜索的效率，即启发式的搜索。
着色问题与排队论
12.1.1
顶点着色问题
一、基本定义 对图 G=(V,E)，设 S 是 V 的一个子集，若 S 中任意两个顶点在 G 中均不相邻，则称 S 为 G 的一个独立集，如果 G 不包含适合|S'|＞|S|的独立集 S'，则称 S 为 G 的最大独立集。 设 K 是 G 的一个独立集，并且对于 V\K 的任一顶点 v，K+v 都不是 G 的独立集，则 称 K 是 G 的一个极大覆盖。极大独立集的补集称为极小覆盖， V 的子集 K 是 G 的极小覆 盖当且仅当：对于每个顶点 v 或者 r 属于 K，或者 v 的所有邻点属于 K（但两者不同时成 立） 。 G 的一个 k 顶点着色是指 k 种颜色 1,2,…,k 对于 G 各顶点的一个分配，如果任意两个 相邻顶点都分配到不同的颜色，则称着色是正常的。换句话说，无环图 G 的一个正常 k 顶 点着色是把 V 分成 k 个（可能有空的）独立集的一个分类 (V1,V2,„,Vk)。当 G 有一个正常 k 顶点着色时，就成 G 是 k 顶点可着色的。 G 的色数 X（G）是指 G 为 k 可着色的 k 的最小值，若 X（G）=k，则称 G 是 k 色的。 ·160·
涂色问题的常见解法及策略
涂色问题的常见解法及策略涂色问题是数学中一个常见的问题，涉及到给定一定数量的区域，并使用有限数量的颜色对这些区域进行染色。
在这篇文章中，我将介绍一些常见的解法和策略，以及我对涂色问题的观点和理解。
在解决涂色问题时，最基本的策略之一是使用“回溯法”。
回溯法是一种通过不断尝试不同的选择，并撤销不合适的选择的方法。
在涂色问题中，我们可以从一个区域开始，选择一个颜色将其染色，然后递归地对相邻的区域进行染色。
如果在染色过程中发现无法继续染色，则回溯到上一个选择，并选择另一种颜色。
另一种常见的解法是使用“图论”的方法。
将涂色问题抽象成图论中的图模型，其中图的每个节点代表一个区域，边表示两个相邻区域之间的连接。
然后，我们可以使用图染色算法，如“图的着色问题算法”来解决涂色问题。
这些算法使用一系列的规则和策略来确定每个节点应该染哪种颜色，以确保相邻节点不具有相同的颜色。
除了这些基本的解法之外，还有许多高级的策略可供选择。
例如，“最小割算法”可以将复杂的涂色问题转化为图的最小割问题，并使用最小割算法来解决。
此外，还可以使用“启发式搜索”技术，通过估计每个选择的优先级来指导搜索过程。
这些策略通常需要更多的计算资源和算法知识，但在处理复杂的问题时可能会获得更好的结果。
从简单到复杂，由浅入深的方式来探讨涂色问题，可以帮助我们建立对问题的深刻理解。
我们可以从最基本的回溯法开始，逐渐引入图论的概念和算法。
了解不同解法的优缺点，并能够根据问题的具体情况选择合适的解法，这对于解决涂色问题至关重要。
总结起来，涂色问题是一个常见的数学问题，涉及到给定一定数量的区域，并使用有限数量的颜色对这些区域进行染色。
常见的解法和策略包括回溯法、图论算法、最小割算法和启发式搜索技术。
通过从简单到复杂的方式来探讨涂色问题，我们可以建立对问题的深刻理解，并能够灵活选择适合的解法。
用回溯法求解图的m着色问题
实验二用回溯法求解图的m着色问题一、实验目的12、使用回溯法编程求解图的m着色问题。
二、实验原理回溯法是一个既带有系统性又带有跳跃性的的搜索算法。
回溯法在包含问题的所有解的解空间树中，按照深度优先的策略，从根结点出发搜索解空间树。
算法搜索至解空间树的任何一个结点时，总是先判断该结点是否肯定不包含问题的解，如果肯定不包含，则跳过对以该结点为根的子树搜索。
否则，进入该子树，继续按深度优先的策略进行搜索。
回溯法在用来求问题的所有解时，要回溯到根，且根结点的所有子树都已被搜索遍才结束。
而回溯法在用来求问题的任一解时，只要搜索到问题的一个解就可结束。
回溯法从开始结点(根结点)出发，以深度优先搜索的方式搜索整个解空间。
这个开始结点就成为一个活结点，同时也成为当前的扩展结点。
在当前的扩展结点处，搜索向纵深方向移至一个新结点。
这个新结点就成为一个新的活结点，并成为当前扩展结点。
如果在当前的扩展结点处不能再向纵深方向移动，则当前的扩展结点就成为死结点。
此时，应往回移动(回溯)至最近的一个活结点处，并使这个活结点成为当前的扩展结点。
回溯法即以这种工作方式递归地在解空间中搜索，直至找到所要求的解或解空间中已无活结点时为止。
三、问题描述给定一个无向连通图G和m种不同的颜色。
用这些颜色为图G的各顶点着色，每个顶点着一种颜色。
若一个图最少需要m种颜色才能使图中任何一条边连接的2个顶点着有不同的颜色，则称这个数m为该图的色数。
求一个图的色数m的问题称为图的m可着色优化问题。
设计一个算法，找出用m种颜色对一个图进行着色的不同方案。
四、算法设计与分析用邻接矩阵a来表示一个无向连通图G=(V,E)。
用整数1,2,…,m来表示m 种不同的颜色。
x[i]表示顶点i所着的颜色来，则问题的解向量可以表示为n元组x[1:n]。
问题的解空间可表示一棵高度为n+1的完全m叉树。
解空间树的第i层中每一结点都有m个儿子，每个儿子相应于x[i]的m个可能的着色之一，第n+1层结点均为叶结点。
图论中的图的着色与染色问题
图论中的图的着色与染色问题在图论中，图的着色与染色问题是一类经典的问题。
图的着色是指给图的每个顶点赋予一个颜色，要求相邻的顶点不能有相同的颜色；而图的染色是指给图的边赋予一个颜色，要求相邻的边不能有相同的颜色。
一、图的顶点着色图的顶点着色问题是图论中的经典问题之一。
给定一个无向图，要求为每个顶点分配一个颜色，使得任意两个相邻的顶点颜色不同。
这个问题的本质是将相邻的顶点划分到不同的颜色集合中。
解决图的顶点着色问题有多种算法，其中较为简单和常用的是贪心算法。
贪心算法按照某种规则为图的顶点逐个着色，每次着色时选择当前可用颜色的最小编号。
贪心算法的时间复杂度为O(n^2)，其中n 为图的顶点数。
二、图的边染色图的边染色问题是另一个经典的图论问题。
给定一个无向图，要求给每条边分配一个颜色，使得任意两条相邻的边颜色不同。
这个问题的目标是将相邻的边划分到不同的颜色集合中。
解决图的边染色问题的算法有多种，其中常用的是基于回溯法和深度优先搜索的算法。
回溯法通过递归地尝试为每条边分配颜色，并根据约束条件进行回溯，直到找到可行的解或者穷尽所有可能。
深度优先搜索则通过遍历图的边，逐个给边染色，当发现某条边与相邻边颜色相同时，回溯到前一条边重新选择颜色。
三、特殊图的着色与染色问题除了一般的图的着色与染色问题，还存在一些特殊类型的图，对应着特殊的着色与染色问题。
1. 树的着色与染色：在树中，任意两个顶点之间都只有一条路径，因此树的着色与染色问题可以简化为树的边染色问题。
树的边染色问题可以使用贪心算法解决，每次为某条边选择一个未使用的颜色，直到所有边都被染色。
2. 平面图的着色与染色：平面图是指可以画在平面上，且任意两条边最多只有一个公共顶点的图。
平面图的着色与染色问题是在满足平面图约束条件下对图进行着色或染色。
对于平面图的着色与染色问题，使用四色定理可以得到解，即任何平面图最多只需要四种颜色来着色或染色。
四、应用领域图的着色与染色问题在实际应用中具有广泛的应用。
图着色问题论述
图着色问题论述在包含问题的所有解的解空间树中，按照深度优先搜索的策略，从根结点出发深度探索解空间树。
若用回溯法求问题的所有解时，要回溯到根，且根结点的所有可行的子树都要已被搜索遍才结束。
而若使用回溯法求任一个解时，只要搜索到问题的一个解就可以结束。
贪心法它适用于解一些组合数较大的问题。
根据当前已有的信息就做出选择，而且一旦做出了选择，不管将来有什么结果，这个选择都不会改变。
换言之，贪心法并不是从整体最优考虑，它所做出的选择只是在某种意义上的局部最优。
【关键词】图着色回溯法贪心法1 图着色问题的分类1.1 回溯法回溯法是一种系统地搜索问题解的搜索算法。
它在包含问题的所有解的解空间树中，按照深度优先的策略，从根结点出发搜索解空间树。
算法搜索至解空间树的任一结点时，总是先判断该结点是否肯定不包含问题的解。
如果肯定不包含，则跳过对以该结点为根的子树的系统搜索，逐层向其祖先结点回溯。
否则，进入该子树，继续按深度优先的策略进行搜索。
用回溯法解题的一般步骤：（1）描述解的形式，定义一个解空间，它包含问题的所有解。
（2）构造状态空间树。
（3）构造约束函数（用于杀死节点）。
1.2 贪心算法贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。
不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解，但对一些问题它能产生整体最优解或者是整体最优解的近似解。
贪心算法没有固定的算法框架，算法设计的关键是贪婪策略的选择。
一定要注意，选择的贪婪策略要具有无后向性，即某阶段状态一旦确定以后，不受这个状态以后的策略影响，也就是说某个状态以后的过程不会影响以前的状态，只与当前状态有关，也称为这种特性为无后效性。
因此，适应用贪婪策略解决的问题类型较少，对所采用的贪婪策略一定要仔细分析其是否满足无后效性。
图的着色问题是由地图的着色问题引申而来的：用m 种颜色为地图着色，使得地图上的每一个区域着一种颜色，且相邻区域颜色不同。
图的着色问题
顶点着色－基本概念
• K可着色：G的一个k顶点着色是指k种颜色1,2,…,k对于G各顶点的 可着色： 的一个k顶点着色是指k种颜色1,2,…,k对于G 1,2, 对于 一个分配，如果任意两个相邻顶点都分配到不同的颜色， 一个分配，如果任意两个相邻顶点都分配到不同的颜色，则称着 色是正常的。换句话说，无环图G的一个正常k顶点着色是把V 色是正常的。换句话说，无环图G的一个正常k顶点着色是把V分成 可能有空的）独立集的一个分类( 2,… k个（可能有空的）独立集的一个分类(V1,V2,…,Vk)。当G有一个 正常k顶点着色时，就成G 顶点可着色的。 正常k顶点着色时，就成G是k顶点可着色的。 • G的色数X（G）是指G为k可着色的k的最小值，若X（G）=k，则称G 的色数X 是指G 可着色的k的最小值， =k，则称G 色的。 是k色的。 • 事实上，如果我们将同色的顶点列入一个顶点子集，那么求X（G） 事实上，如果我们将同色的顶点列入一个顶点子集，那么求X 就转为求满足下列条件的最少子集数k 就转为求满足下列条件的最少子集数k： 两两子集中的顶点不同； （1）两两子集中的顶点不同； 子集中的两两顶点不相邻。 （2）子集中的两两顶点不相邻。 显然有： 为平凡图， =1； 显然有： （i）若G为平凡图，则X（G）=1； ii） 为偶图， （ii）若G为偶图，则X（G）=2 iii）对任意图G Δ+1（这里Δ （iii）对任意图G，有X（G）≤Δ+1（这里Δ表示为顶点 数最大值） 数最大值）
问题来源
图的着色
• 通常所说的着色问题是指下述两类问题： 通常所说的着色问题是指下述两类问题： • 1．给定无环图G=(V,E)，用m种颜色为图中 的每条边着色，要求每条边着一种颜色， 的每条边着色，要求每条边着一种颜色，并 使相邻两条边有着不同的颜色， 使相邻两条边有着不同的颜色，这个问题称 为图的边着色问题。 为图的边着色问题。 • 2．给定无向图G=(V,E)，用m种颜色为图中 的每个顶点着色，要求每个顶点着一种颜色， 的每个顶点着色，要求每个顶点着一种颜色， 并使相邻两顶点之间有着不同的颜色， 并使相邻两顶点之间有着不同的颜色，这个 问题称为图的顶着色问题。 问题称为图的顶着色问题。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
算法设计与分析课程设计题目：用回溯法分析着色问题学院：理学院专业：信息与计算科学班级：09信科二班姓名：***学号: 200910010207用回溯法分析着色问题目录1 回溯法 (3)1.1回溯法的概述 (3)1.2 回溯法的基本思想 (3)1.3 回溯法的一般步骤 (3)2 图的m着色问题 (3)2.1图的着色问题的来源 (3)2.2通常所说的着色问题 (3)2.3图的着色问题描述 (3)2.4回溯法求解图着色问题 (5)2.5图的m可着色问题的回溯算法描述 (6)2.5.1回溯算法 (6)2.5.2 m着色回溯法递归 (8)2.5.3 m着色回溯法迭代 (9)2.5.4例题利用回溯法给图着色 (11)2.6复杂度分析着色回溯法迭代 (12)§1 回溯法1.1回溯法的概述回溯法是一种系统地搜索问题解的搜索算法。
它在包含问题的所有解的解空间树中，按照深度优先的策略，从根结点出发搜索解空间树。
算法搜索至解空间树的任一结点时，总是先判断该结点是否肯定不包含问题的解。
如果肯定不包含，则跳过对以该结点为根的子树的系统搜索，逐层向其祖先结点回溯。
否则，进入该子树，继续按深度优先的策略进行搜索。
回溯法在用来求问题的所有解时，要回溯到根，且根结点的所有子树都已被搜索遍才结束。
而回溯法在用来求问题的任一解时，只要搜索到问题的一个解就可以结束。
这种以深度优先的方式系统地搜索问题的解的算法称为回溯法，它适用于解一些组合数较大的问题。
1.2回溯法的基本思想回溯法的基本思想是，在确定了解空间的组织结构后，回溯法就从开始结点（根结点）出发，以深度优先的方式搜索整个解空间。
这个开始结点就成为一个活结点，同时也成为当前的扩展结点。
在当前的扩展结点处，搜索向纵深方向移至一个新结点。
这个新结点就成为一个新的活结点，并成为当前扩展结点。
如果在当前的扩展结点处不能再向纵深方向移动，则当前扩展结点就成为死结点。
换句话说，这个结点不再是一个活结点。
此时，应往回移动（回溯）至最近的一个活结点处，并使这个活结点成为当前的扩展结点。
回溯法即以这种工作方式递归地在解空间中搜索，直至找到所要求的解或解空间中已没有活结点时为止。
1.3回溯法的一般步骤用回溯法解题的一般步骤：（1）针对所给问题，定义问题的解空间；（2）确定易于搜索的解空间结构；（3）以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索。
§2 图的m着色问题2.1图的着色问题的来源图的着色问题是由地图的着色问题引申而来的：用m种颜色为地图着色，使得地图上的每一个区域着一种颜色，且相邻区域颜色不同。
问题处理：如果把每一个区域收缩为一个顶点，把相邻两个区域用一条边相连接，就可以把一个区域图抽象为一个平面图。
例如,（a）所示的区域图可抽象为（b）所表示的平面图。
19世纪50年代，英国学者提出了任何地图都可以4中颜色来着色的4色猜想问题。
过了100多年，这个问题才由美国学者在计算机上予以证明，这就是著名的四色定理。
例如，在图（b）中，区域用城市名表示，颜色用数字表示，则图中表示了不同区域的不同着色问题。
2.2通常所说的着色问题是指下述两类问题：a)给定无环图G=(V,E)，用m种颜色为图中的每条边着色，要求每条边着一种颜色，并使相邻两条边有着不同的颜色，这个问题称为图的边着色问题。
b)给定无向图G=(V,E)，用m种颜色为图中的每个顶点着色，要求每个顶点着一种颜色，并使相邻两顶点之间有着不同的颜色，这个问题称为图的顶着色问题。
2.3图的着色问题描述给定无向连通图G和m种不同的颜色。
用这些颜色为图G的各顶点着色，每个顶点着一种颜色。
是否有一种着色法使G中每条边的2个顶点着不同颜色。
这个问题是图的m可着色判定问题。
若一个图最少需要m种颜色才能使图中每条边连接的2个顶点着不同颜色，则称这个数m为该图的色数。
求一个图的色数m的问题称为图的m可着色优化问题。
四色问题是m图着色问题的一个特例，根据四色原理，证明平面或球面上的任何地图的所有区域都至多可用四种、颜色来着色，并使任何两个有一段公共边界的相邻区域没有相同的颜色。
这个问题可转换成对一平面图的４－着色判定问题(平面图是一个能画于平面上而边无任何交叉的图)。
将地图的每个区域变成一个结点，若两个区域相邻，则相应的结点用一条边连接起来。
多年来，虽然已证明用5种颜色足以对任一幅地图着色，但是一直找不到一定要求多于4种颜色的地图。
直到1976年这个问题才由爱普尔，黑肯和考西利用电子计算机的帮助得以解决。
他们证明了4种颜色足以对任何地图着色。
2.4回溯法求解图着色问题首先把所有顶点的颜色初始化为0，然后依次为每个顶点着色。
如果其中i个顶点已经着色，并且相邻两个顶点的颜色都不一样，就称当前的着色是有效的局部着色；否则，就称为无效的着色。
如果由根节点到当前节点路径上的着色，对应于一个有效着色，并且路径的长度小于n，那么相应的着色是有效的局部着色。
这时，就从当前节点出发，继续探索它的儿子节点，并把儿子结点标记为当前结点。
在另一方面，如果在相应路径上搜索不到有效的着色，就把当前结点标记为死结点，并把控制转移去搜索对应于另一种颜色的兄弟结点。
如果对所有m个兄弟结点，都搜索不到一种有效的着色，就回溯到它的父亲结点，并把父亲结点标记为死结点，转移去搜索父亲结点的兄弟结点。
这种搜索过程一直进行，直到根结点变为死结点，或者搜索路径长度等于n，并找到了一个有效的着色为止。
由于用m种颜色为无向图G=(V,E)着色，其中，V的顶点个数为n，可以用一个n元组C=(c1,c2,…,cn)来描述图的一种可能着色，其中，ci∈{1, 2, …, m}，(1≤i≤n)表示赋予顶点i的颜色。
例如，5元组(1, 2, 2, 3, 1)表示对具有5个顶点的无向图（a）的一种着色，顶点A着颜色1，顶点B着颜色2，顶点C着颜色2，如此等等。
如果在n元组C中，所有相邻顶点都不会着相同颜色，就称此n元组为可行解，否则为无效解。
容易看出，每个顶点可着颜色有m种选择，n个顶点就有m n种不同的着色方案，问题的解空间是一棵高度为n的完全m叉树，这里树高度的定义为从根节点到叶子节点的路径的长度。
每个分支结点，都有m个儿子结点。
最底层有m n个叶子结点。
例如，表示用3种颜色为3个顶点的图着色的状态空间树。
如图所示，对第i（i>=1）层上的每个顶点，从其父节点到该节点的边上的标号表示顶点i着色的颜色编号。
2.5图的m可着色问题的回溯算法描述2.5.1回溯算法假定图的n个顶点集合用{0,1,2,….,n-1}，颜色集合用{1,2,3,…,m}。
用数组x[n]存放n个顶点的着色，用邻接矩阵c[n][n]来表示图中顶点的邻接关系，若顶点i 与顶点j之间存在关联边，则元素c[i,j]为1否则为0。
所用的数据结构如下：var n,m:integer;//表示顶点数，颜色数x:array[1..n] of integer;//顶点的着色c:array[1..n,1..n] of integer;//表示图的邻接矩阵此外，用ok函数来判断当前顶点的着色是否为有效着色，如果是有效着色，返回1，否则返回0。
Function ok(k:integer):integer;Var I;BeginOk:=1;For I:=0 to k doIf ((c[k,I]=1)and(x[I]=x[k])) ThenBeginOk:=0;Break;End;End;Ok函数假定0~k-1顶点的着色是有效着色，在此基础上判断0~k顶点的着色是否有效。
如果顶点k与顶点I是相邻接的顶点，0≤i≤k-1,而顶点k的颜色与顶点I的颜色相同，就是无效颜色，即返回0，否则返回1。
有了Ok函数之后，图的m着色问题可描述如下：算法:用m种颜色给图着色输入：输入图的顶点数n,颜色数m,图的邻接矩阵c[][]输出：n个顶点的着色x[]procedure m_coloring()var I,k:integer;beginfor I:=0 to n do x[I]:=0; //解向量初始化为0k:=0;while(k>=0) dobeginx[k]:=x[k]+1; //使当前的颜色加1while((x[k]<=m)and(ok(k)=0) do //当前颜色是否有效x[k]:=x[k]+1; //无效,继续搜索下一种颜色 if (x[k]<=m) Then //搜索成功否？If (k=n-1) then break //是最后一个顶点，完成搜索Else k:=k+1; //不是，处理下一个顶点Else //搜索失败，回溯到上一个顶点 BeginX[k]:=0;K:=k-1;End;End;End.2.5.2 m着色回溯法递归//输入n为顶点个数，颜色数m，图的邻接矩阵c[][]//输出n个顶点的着色x[]//递归方法求解#include <iostream>using namespace std;bool c[6][6];int x[6];int m=3;int n=5;bool ok(int k) //判断对顶点k着色以后是否合法着色{int i;for(i = 1; i < k; i++)if((c[k][i]==1 && x[k] == x[i]))return false;return true;}void output(int x[]){cout<<"The feasible result is:"<<endl;for(int i=1;i<=n;i++)cout<<x[i]<<' ';cout<<endl;return;}void backtrack (int t){if (t>n) output(x);elsefor (int i=1;i<=m;i++) {x[t]=i;if (ok(t)) backtrack(t+1);x[t]=0;}}int main(){int i, j;for(i = 1; i < 5; i++)for(j = 1; j < 5; j++)c[i][j] = false;c[1][2] = true;c[1][3] = true;c[2][3] = true;c[2][4] = true;c[2][5] = true;c[3][5] = true;c[4][5] = true;c[2][1] = true;c[3][1] = true;c[3][2] = true;c[4][2] = true;c[5][2] = true;c[5][3] = true;c[5][4] = true;backtrack(1);cout << endl;return 0;}2.5.3 m着色回溯法迭代//输入n为顶点个数，颜色数m，图的邻接矩阵c[][]//输出n个顶点的着色x[]//第一个结点也可以有m种着色方案#include <iostream>using namespace std;bool c[6][6];int x[6];int m=3;int n=5;bool ok(int k) //判断对顶点k着色以后是否合法着色{int i;for(i = 1; i < k; i++)if((c[k][i]==1 && x[k] == x[i]))return false;return true;}void m_coloring(int n, int m){int i, k;for(i = 1; i <= n; i++)x[i] = 0;k =1;while(k >=1){x[k]++;while(x[k] <= m)i f( ok(k)==1) break;e lse x[k]++;if(x[k] <= m && k==n){ for(i=1;i<=n;i++) cout<<x[i]<<" ";cout<<endl;k--;//return; 如果只需要一个解可以将上两句去掉，加入返回语句}e lse if (x[k]<=m &&k<n)k++;e lse{x[k]=0;k--;}}}int main(){int i, j;for(i = 1; i < 5; i++)for(j = 1; j < 5; j++)c[i][j] = false;c[1][2] = true;c[1][3] = true;c[2][3] = true;c[2][4] = true;c[2][5] = true;c[3][5] = true;c[4][5] = true;c[2][1] = true;c[3][1] = true;c[3][2] = true;c[4][2] = true;c[5][2] = true;c[5][3] = true;c[5][4] = true;m_coloring(5, 3);cout << endl;return 0;}2.5.4例：利用回溯法给下图（a）着色。