信号与线性系统分析习题答案 (吴大正 第四版 高等教育出版社)
信号与线性系统分析_(吴大正_第四版)习题答案12264精编版
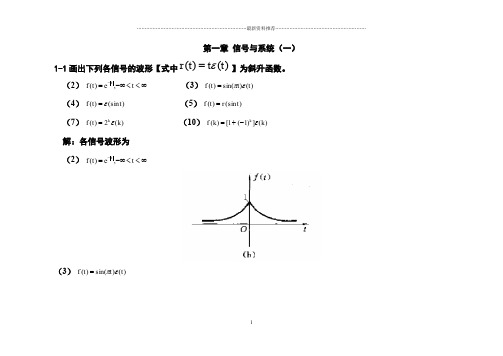
第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析吴大正:第四版习题答案

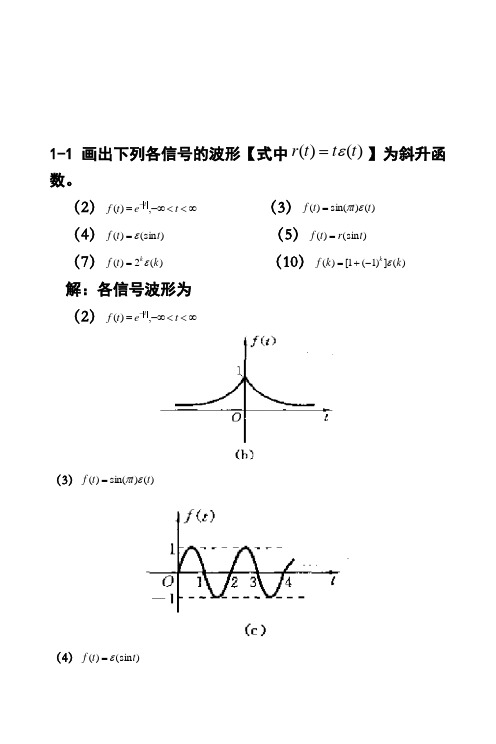
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f =(7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为(2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))(sin )(t r t f =(7))(2)(k t f k ε=(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
信与线性系统分析吴大正第四版习题答案
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))rt f=)(t(sin(7))(t f kε)(k2=(10))(])1kf kε(k)(1[=-+1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析习题答案_(吴大正_第四版__高等教育出版社)

第一章 信号与系统(二)之马矢奏春创作1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f =(7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+=解:各信号波形为(2)∞<<-∞=-t e t f t,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε=(10))(])1(1[)(k k f kε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
信号与线性系统分析吴大正第四版习题答案第四章

第四章习题4.6 求下列周期信号的基波角频率Ω和周期T 。
(1)t j e 100 (2))]3(2cos[-t π(3))4sin()2cos(t t + (4))5cos()3cos()2cos(t t t πππ++ (5))4sin()2cos(t t ππ+ (6))5cos()3cos()2cos(t t t πππ++ 4.7 用直接计算傅里叶系数的方法,求图4-15所示周期函数的傅里叶系数(三角形式或指数形式)。
图4-154.10 利用奇偶性判断图4-18示各周期信号的傅里叶系数中所含有的频率分量。
图4-184-11 某1Ω电阻两端的电压)(t u 如图4-19所示,(1)求)(t u 的三角形式傅里叶系数。
(2)利用(1)的结果和1)21(=u ,求下列无穷级数之和(3)求1Ω电阻上的平均功率和电压有效值。
(4)利用(3)的结果求下列无穷级数之和图4-194.17 根据傅里叶变换对称性求下列函数的傅里叶变换(1)∞<<-∞--=t t t t f ,)2()]2(2sin[)(ππ(2)∞<<-∞+=t t t f ,2)(22αα(3)∞<<-∞⎥⎦⎤⎢⎣⎡=t t t t f ,2)2sin()(2ππ4.18 求下列信号的傅里叶变换(1))2()(-=-t e t f jt δ (2))1(')()1(3-=--t e t f t δ(3))9sgn()(2-=t t f (4))1()(2+=-t e t f t ε(5))12()(-=tt f ε4.19 试用时域微积分性质,求图4-23示信号的频谱。
图4-234.20 若已知)(j ])([ωF t f F =,试求下列函数的频谱:(1))2(t tf (3)dt t df t )( (5))-1(t)-(1t f(8))2-3(t f e jt (9)t dt t df π1*)(4.21 求下列函数的傅里叶变换(1)⎩⎨⎧><=000,1,)(j ωωωωωF(3))(3cos 2)(j ωω=F(5)ωωωω1)(2n -20sin 2)(j +=∑=j n e F4.23 试用下列方式求图4-25示信号的频谱函数(1)利用延时和线性性质(门函数的频谱可利用已知结果)。
线性系统分析_(吴大正_第四版)习题答案

专业课习题解析课程西安电子科技大学844信号与系统专业课习题解析课程第1讲第一章信号与系统(一)专业课习题解析课程第2讲第一章信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
信与线性系统分析吴大正第四版习题答案

1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))rt f=)(t(sin(7))(t f kε)(k2=(10))(])1kf kε(k)(1[=-+1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析-(吴大正-第四版)习题答案第二章

第二章2-1 已知描述系统的微分方程和初始状态如下,试求其零输入响应。
(1)1)0(',1)0(),()(6)('5)(''-===++-y y t f t y t y t y(4)0)0(',2)0(),()()(''===+-y y t f t y t y2-2 已知描述系统的微分方程和初始状态如下,试求其+0值)0(+y 和)0('+y 。
(2))()(,1)0(',1)0(),('')(8)('6)(''t t f y y t f t y t y t y δ====++--(4))()(,2)0(',1)0(),(')(5)('4)(''2t e t f y y t f t y t y t y t ε====++--解:2-4 已知描述系统的微分方程和初始状态如下,试求其零输入响应、零状态响应和全响应。
(2))()(,2)0(',1)0(),(3)(')(4)('4)(''t e t f y y t f t f t y t y t y t ε---===+=++解:2-8 如图2-4所示的电路,若以)(t i S 为输入,)(t u R 为输出,试列出其微分方程,并求出冲激响应和阶跃响应。
2-12 如图2-6所示的电路,以电容电压)(tuC为响应,试求其冲激响应和阶跃响应。
2-16 各函数波形如图2-8所示,图2-8(b)、(c)、(d)均为单位冲激函数,试求下列卷积,并画出波形图。
(1))(*)(21t f t f (2))(*)(31t f t f (3))(*)(41t f t f(4))(*)(*)(221t f t f t f (5))3()(2[*)(341--t f t f t f波形图如图2-9(a)所示。
信号与线性系统分析_(吴大正_第四版)习题答案第六章

. 学习参考. 第六章6.4 根据下列象函数及所标注的收敛域,求其所对应的原序列。
(1)1)(=z F ,全z 平面(2)∞<=z z z F ,)(3(3)0,)(1>=-z z z F(4)∞<<-+=-z z z z F 0,12)(2(5)a z az z F >-=-,11)(1(6)a z az z F <-=-,11)(1. 学习参考.6.5 已知1)(↔k δ,az z k a k -↔)(ε,2)1()(-↔z z k k ε,试利用z 变换的性质求下列序列的z 变换并注明收敛域。
. 学习参考 .(1))(])1(1[21k k ε-+ (3))()1(k k k ε-(5))1()1(--k k k ε (7))]4()([--k k k εε(9))()2cos()21(k k k επ. 学习参考.6.8 若因果序列的z 变换)(z F 如下,能否应用终值定理?如果能,求出)(lim k f k ∞→。
(1))31)(21(1)(2+-+=z z z z F (3))2)(1()(2--=z z z z F. 学习参考.6.10 求下列象函数的双边逆z 变换。
(1)31,)31)(21(1)(2<--+=z z z z z F (2)21,)31)(21()(2>--=z z z z z F (3)21,)1()21()(23<--=z z z z z F. 学习参考 .(4)2131,)1()21()(23<<--=z z z z z F. 学习参考.. 学习参考.. 学习参考.. 学习参考.6.11 求下列象函数的逆z 变换。
(1)1,11)(2>+=z z z F (2)1,)1)(1()(22>+--+=z z z z z z z F (5)1,)1)(1()(2>--=z z z z z F (6)a z a z az z z F >-+=,)()(32. 学习参考.. 学习参考.. 学习参考.6.13 如因果序列)()(z F k f ,试求下列序列的z 变换。
信号与线性系统分析-(吴大正-第四版)习题答案

信号与系统习题解析C1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f(5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
(完整版)信号与线性系统分析_(吴大正_第四版)习题答案

1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t (7))t(k=f kε)(2(10))f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析-(吴大正-第四版)第三章习题答案

第三章习题3.1、试求序列k 01(k)=2f ⎧⎪⎛⎫⎨ ⎪⎪⎝⎭⎩,的差分(k)f ∆、(k)f ∇和i=-(i)kf ∞∑。
3.6、求以下差分方程所描述的LTI 离散系统的零输入相应、零状态响应和全响应。
1〕()-2(-1)(),()2(),(-1)-1y k y k f k f k k y ε===3〕()2(-1)(),()(34)(),(-1)-1y k y k f k f k k k y ε+==+= 5〕1()2(-1)(-2)(),()3()(),(-1)3,(-2)-52k y k y k y k f k f k k y y ε++====3.8、求以下差分方程所描述的离散系统的单位序列响应。
2〕()-(-2)()=y k y k f k5〕()-4(-1)8(-2)()+=y k y k y k f k3.9、求图所示各系统的单位序列响应。
〔a〕〔c〕3.10、求图所示系统的单位序列响应。
3.11、各序列的图形如下图,求以下卷积和。
〔1〕12()()f k f k *〔2〕23()()f k f k *〔3〕34()()f k f k *〔4〕[]213()-()()f k f k f k *3.13、求题3.9图所示各系统的阶跃响应。
3.14、求图所示系统的单位序列响应和阶跃响应。
3.15、假设LTI 离散系统的阶跃响应()()()0.5k g k k ε=,求其单位序列响应。
3.16、如下图系统,试求当鼓励分别为〔1〕()()f k k ε= 〔2〕()()0.5()kf k k ε=时的零状态响应。
3.18、如下图的离散系统由两个子系统级联组成,()1=2cos4k h k π,()()2=k h k k a ε,鼓励()()()=--1f k k a k δδ,求该系统的零状态响应()zs k y 。
〔提示:利用卷积和的结合律和交换律,可以简化运算。
〕3.22、如下图的复合系统有三个子系统组成,它们的单位序列响应分别为()()1=h k k ε,()()2=-5h k k ε,求复合系统的单位序列响应。
信号与线性系统分析_(吴大正_第四版)习题答案第六章

第六章6.4 根据下列象函数及所标注的收敛域,求其所对应的原序列。
(1)1)(=z F ,全z 平面(2)∞<=z z z F ,)(3(3)0,)(1>=-z z z F(4)∞<<-+=-z z z z F 0,12)(2(5)a z azz F >-=-,11)(1 (6)a z az z F <-=-,11)(16.5 已知1)(↔k δ,a z z k a k -↔)(ε,2)1()(-↔z z k k ε,试利用z 变换的性质求下列序列的z 变换并注明收敛域。
(1))(])1(1[21k k ε-+ (3))()1(k k k ε-(5))1()1(--k k k ε (7))]4()([--k k k εε(9))()2cos()21(k k k επ6.8 若因果序列的z 变换)(z F 如下,能否应用终值定理?如果能,求出)(lim k f k ∞→。
(1))31)(21(1)(2+-+=z z z z F (3))2)(1()(2--=z z z z F6.10 求下列象函数的双边逆z 变换。
(1)31,)31)(21(1)(2<--+=z z z z z F (2)21,)31)(21()(2>--=z z z z z F (3)21,)1()21()(23<--=z z z z z F(4)2131,)1()21()(23<<--=z z z z z F6.11 求下列象函数的逆z 变换。
(1)1,11)(2>+=z z z F (2)1,)1)(1()(22>+--+=z z z z z z z F (5)1,)1)(1()(2>--=z z z z z F (6)a z a z az z z F >-+=,)()(326.13 如因果序列)(f ,试求下列序列的z变换。
k)(zF(1))(0i f a ki i ∑= (2)∑=ki ki f a)(6.15 用z变换法解下列齐次差分方程。
信号与线性系统分析_(吴大正_第四版)第一章习题答案

专业课习题解析课程第1讲第一章信号与系统(一)专业课习题解析课程第2讲第一章信号与系统(二)1-1画出下列各信号的波形【式中r(t) = t; (t)】为斜升函数。
(2)f(t) t ::二(3)f(t)=sin「t);(t)(5) f(t)=r(s int) (10) f (k )=[1 (T )k ]"k)(4)f(t) = ;(Si nt) (7) f(t) =2k ;(k)解:各信号波形为(2) f (t) = e刊,—:: ::t ::::(3)f(t) =si n(p;(t)∕ω(4)f(t) _ ;(Sint)(5) f(t)=r(sint)/(/)—4 兀—3 Tt 一2κ —n O K 2κ 3 Ji t<e)(7) f(t) =2k;(k)(10) f(k)=[1 (_1)k];(k)/(»2・k彳__________ A i_____________I Λ-■0t 2 3 4 5(iCJ)1—2画出下列各信号的波形[式中r(t) = L(t)为斜升函数].(1) f(t) = 2 (t 1) - 3 (t T) (t — 2)(2) f (tp r(t) - 2r(t - 1) r(t -2)解:各信号波形为(1)f(t )= 2(t 1)— 3 (t - 1) (t — 2)(a ) (2) f (tp r (t ) 2r (t1) r (t 2)(5) f(t)τ(2t) (2-t) k 兀 (11) f(k) =sin( )[ (k)- ;(k-7)] 6 (8) f(k)= k[ (k)- (k-5)] (12) f (k 「2k [ (3- k)- (k)](8)f (k ). k[ (k ) -(k (5) f (t)= r (2t) (2 — t) (e )— 5)]I ∖fg1丁 ■ ~ι丨FrIΛI ∖。
d1 2 1L 5 S ⅛(k )(11)f(k)5(K2W7)]k(12)f(k)= 2k[ (3 - k)- (k)]Ifa)4∙J. A.,. JO∣ 1 2(I)1-3写出图1-3所示各波形的表达式(a) ∕(∕) = 2ε(Z + 1) —ε(∕ — 1)—ε(f— 2)(b) ∕(r)= (f÷l)ε(f÷l) - 2(z - l)ε(f — 1) + (f — 3)ε(z—3)(C)fit) = IoSin(T:/)_E(Z)-E(Z - 1)](d)∕(r) = 1 十2(r + 2)_E(I + 2) — E(r + 1)_ +(1 — l),(r +1) - E(T— 1)_1-4写出图仁4所示各序列的闭合形式表达式解图示各序列的闭合形式表示式分别为;(a)∕(⅛) = ε(⅛ + 2) (b)∕(⅛)= ε(⅛— 3) -ξ(k— 7)(c)∕(⅛) = e(-⅛ + 2) (d)∕(⅛) = (― l)*e(⅛)1—5判别下列各序列是否为周期性的.如果是,确定其周期解:⑵该序列的周期应为込(響 +于)和Cw(即+寺)的最小公倍数8 CoS⑸该序列不是周期的JX前的周期为2π,sin(πf)的周期为2,若序列周期为「则丁是2的整数倍厂也是%的整数彳氛这不成立…:不是周期的勺(2)3兀f2(k) = cos(-4πJEjlk ? C o S g k 6 (5) f5(tp 3cost 2si n( t)A该序列的周期为24.1—6已知信号f (t)的波形如图1-5所示,画出下列各函数的波形解:各信号波形为(1) f(t —1) (t )(1) f (t —1) (t )df(t )⑺—dT(2)⑹ f (0∙5t 2)t (8) 「f (χ)dx(2) f(t - 1) (t - 1)(5)f(12t)4■ /2IIO 1 3〈a)Cb)(6)f(0∙5t-2)df(t)⑺ dtI Iy(I- 2⅛)_ I _____ —11 3 ⅛2 2 2(E)t⑻“ f(x)dxJ 一 F/(Λ-2)KΛ)(Co—乂 二 二(9)(2 =);) (2-工r (逢(L2r (2 +>l ’4 (9)H寸 —〉1):0)I E4〉] 3∣2r1 2 3 4 5 6〈O/(Λ-2)KΛ) /(-⅛÷2⅛(—Λ÷J)/(Λ-2)KΛ)1—9已知信号的波形如图的波形解:由图1—11知,f(3-t)的波形如图1-12(a)所示(f(3-t)波形是由对f(3- 2t)的波形展宽为原来的两倍而得)。
(完整版)信号与线性系统分析_(吴大正_第四版)第一章习题答案

专业课习题解析课程第1讲第一章信号与系统(一)专业课习题解析课程第2讲第一章 信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))tf=r)(sin(t(7))f kε=t)(2(k(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=kkkkfεεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
信号与线性系统分析_(吴大正_第四版)第一章习题答案

专业课习题解析课程第1讲第一章信号与系统(一). 学习参考.专业课习题解析课程第2讲. 学习参考.. 学习参考 .第一章 信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)(. 学习参考.(3))()sin()(t t t f επ=(4))(sin )(t t f ε=. 学习参考.(5))(sin )(t r t f =(7))(2)(k t f k ε=. 学习参考.(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f. 学习参考 .(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f. 学习参考.(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε. 学习参考.(11))]7()()[6sin()(--=k k k k f εεπ. 学习参考 .(12))]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。
信号与线性系统分析-(吴大正-第四版)习题答案第二章

第二章2-1已知描述系统的微分方程和初始状态如下,试求其零输入响应。
(1)y''(t) 5y'(t) 6y(t) f (t), y(0) 1, y'(0 ) 1(4)y''(t) y(t) f(t), y(0) 2, y'(0 ) 0解(l)已知方程的特征方程为A2+ 5A + 6 = 0 其特征根为初=-2"? =-36澈分方程的齐次解为央⑴=CL十C代7 由于y(0_) = Kj/70_) =- 1,且激励为零•故有比(0 十〉=y^(0-) = y(O-)= 1 必(0+)=y x(o_)= y(o_)=—i 即并d= G十G = 1 y\(O~) ——2Ci —3G =—1 由上式解得C\ =2,C =-l则系统的零输入响应为y z(n= 2厂孫—色一常d $ 0(4)已知方程的特征方程为A2 -H 1 = 0 其特征根为和=人兀=—人微分方程的齐次解为片(D = Cicos/ + Cg sin/ 由于激励为零,故有>7 (0-r )=力(。
一)=y(0-)= 2 心(0 十)== y(O-)= 0 即划(0_)= Ci = 23/上(0一)= C?2 = 0则系统的零输人响应为几(f)= 2cosz^ 02-2已知描述系统的微分方程和初始状态如下,试求其0值y(0 )和y'(0 )(2)y''(t) 6y'(t) 8y(t) f''(t),y(0 ) 1, y'(0 ) 1, f(t) (t)(4)y''(t) 4y'(t) 5y(t) f'(t),y(0 ) 1,y'(0 ) 2, f (t) e2t (t)解:⑵ y (7)+ 6『⑺一 8了⑺=©"(/) 设/(/> =力一处‘仃)+必(“ +儿(门 则有 丿⑺=必‘(r 〉+处(了)一兀(r )•f/! (r ) = a : (r ) + /0(r )d^同理 y(/) = u (5(z)—人(r) y 2 (r) = /as(r) + 兀(r)dz■ —X 整理得 力"(C + (6u + 6)y (r) + (8a + 6〃 + Cd(r) +L8/2(r)+671(r) + 70(r)]=『⑴<a = 1 = 1・ J 6a 十 Z> = 0=> J )=— 6 丨 8Q + 6〃 + c = 0c = 28r o ・••有 J(O-) - J(O-)= 飞'(r)dr — 6 - Jo. J 0_ =—6 ・:y(0-) = y(0_) — 6 =— 5 (J(r)dr + /i (r)dr J O- ro y Z (0+ ) — y(0_ ) = 8 ( t)dt — 6 8 (/) dz + o_ 0. =28 ■・・y'(0J = 295(/)d/ + Jo. YQ (t)dt(4) /(/) +□></) =-2c_?£(f) + 肮。
信号与线性系统分析 (吴大正 第四版)第四章习题答案(完整资料).doc

【最新整理,下载后即可编辑】 第四章习题 4.6 求下列周期信号的基波角频率Ω和周期T 。
(1)t j e 100 (2))]3(2cos[-t π (3))4sin()2cos(t t + (4))5cos()3cos()2cos(t t t πππ++(5))4sin()2cos(t t ππ+ (6))5cos()3cos()2cos(t t t πππ++ 4.7 用直接计算傅里叶系数的方法,求图4-15所示周期函数的傅里叶系数(三角形式或指数形式)。
图4-154.10 利用奇偶性判断图4-18示各周期信号的傅里叶系数中所含有的频率分量。
图4-184-11 某1Ω电阻两端的电压)(t u 如图4-19所示,(1)求)(t u 的三角形式傅里叶系数。
(2)利用(1)的结果和1)21(=u ,求下列无穷级数之和 ......7151311+-+-=S (3)求1Ω电阻上的平均功率和电压有效值。
(4)利用(3)的结果求下列无穷级数之和 (7)151311222++++=S图4-194.17 根据傅里叶变换对称性求下列函数的傅里叶变换(1)∞<<-∞--=t t t t f ,)2()]2(2sin[)(ππ(2)∞<<-∞+=t t t f ,2)(22αα (3)∞<<-∞⎥⎦⎤⎢⎣⎡=t t t t f ,2)2sin()(2ππ4.18 求下列信号的傅里叶变换(1))2()(-=-t e t f jt δ (2))1(')()1(3-=--t e t f t δ(3))9sgn()(2-=t t f (4))1()(2+=-t e t f t ε(5))12()(-=tt f ε4.19 试用时域微积分性质,求图4-23示信号的频谱。
图4-234.20 若已知)(j ])([ωF t f F =,试求下列函数的频谱:(1))2(t tf (3)dt t df t )( (5))-1(t)-(1t f (8))2-3(t f e jt (9)tdt t df π1*)(4.21 求下列函数的傅里叶变换(1)⎩⎨⎧><=0,1,)(jωωωωωF(3))(3cos2)(jωω=F(5)ωωωω1)(2n-2sin2)(j+=∑=jneF4.23 试用下列方式求图4-25示信号的频谱函数(1)利用延时和线性性质(门函数的频谱可利用已知结果)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 信号与系统(二)
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e
t f t
,)( (3))()sin()(t t t f επ=
(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k
ε= (10))(])1(1[)(k k f k
ε-+=
解:各信号波形为 (2)∞<<-∞=-t e
t f t
,)(
(3))()sin()(t t t f επ=
(4))(sin )(t t f ε=
(5))
t
f=
r
)
(sin
(t
(7))
f kε
=
t
)
(
2
(k
(10))(])1(1[)(k k f k ε-+=
1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f
(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11)
)]7()()[6
sin(
)(--=k k k k f εεπ
(12)
)]()3([2)(k k k f k
---=εε 解:各信号波形为
(1))2()1(3)1(2)(-+--+=t t t t f εεε
(2)
)2()1(2)()(-+--=t r t r t r t f
(5)
)2()2()(t t r t f -=ε
(8)
)]5()([)(--=k k k k f εε
(11)
)]
7
(
)
(
)[
6
sin(
)
(-
-
=k
k
k
k
fε
ε
π
(12)
)]
(
)
3(
[
2
)
(k
k
k
f k-
-
-
=ε
ε
1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))6
3cos()443cos()(2π
πππ+++=k k k f
(5))sin(2cos 3)(5t t t f π+=
解:
1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
(1))()1(t t f ε- (2))1()1(--t t f ε (5)
)21(t f - (6))25.0(-t f
(7)dt
t df )
( (8)dx x f t ⎰∞-)(
解:各信号波形为 (1))()1(t t f ε-
(2)
)1()1(--t t f ε
(5)
)21(t f -
(6)
)25.0( t f
(7)dt t df )(
(8)
dx
x
f
t
⎰∞-)(
1-7 已知序列)(k f 的图形如图1-7所示,画出下列各序列的图形。
(1))()2(k k f ε- (2))2()2(--k k f ε
(3))]4()()[2(---k k k f εε (4))2(--k f (5)
)1()2(+-+-k k f ε (6))3()(--k f k f
解:
1-9 已知信号的波形如图1-11所示,分别画出)(t f
和dt t df )
(的波形。
解:由图1-11知,)3(t f -的波形如图1-12(a)所示()3(t f -波形是由对)23(t f -的波形展宽为原来的两倍而得)。
将)3(t f -的波形反转而得到)3(+t f 的波形,如图1-12(b)所示。
再将)3(+t f 的波形右移3个单位,就得到了)(t f ,如图1-12(c)所示。
dt
t df )
(的波形如图1-12(d)所示。
1-10 计算下列各题。
(1)[]{})()2sin(cos 22
t t t dt
d ε+ (2))]([)1(t
e dt d t t δ--
(5)
dt t t
t )2()]4
sin([2
++⎰
∞
∞-δπ (8)
dx x x t
)(')1(δ⎰
∞
--
1-12 如图1-13所示的电路,写出 (1)以)(t u C 为响应的微分方程。
(2)以)(t i L 为响应的微分方程。
1-20 写出图1-18各系统的微分或差分方程。
1-23 设系统的初始状态为)0(x ,激励为)(⋅f ,各系统的全响应)(⋅y 与激励和初始状态的关系如下,试分析各系统是否是线性的。
(1)⎰+=-t t
dx x xf x e t y 0)(sin )0()( (2)⎰+=t
dx x f x t f t y 0)()0()()(
(3)⎰+=t
dx x f t x t y 0)(])0(sin[)( (4))2()()0()5.0()(-+=k f k f x k y k
(5)∑=+
=k
j j f kx k y 0
)()0()(
1-25 设激励为)(⋅f ,下列是各系统的零状态响应)(⋅zs y 。
判断各系统是否是线性的、时不变的、因果的、稳定的?
(1)dt t df
t y zs )()(= (2))()(t f t y zs = (3))2cos()()(t t f t y zs π= (4))()(t f t y zs -= (5))1()()(-=k f k f k y zs
(
6))()2()(k f k k y zs -= (7)∑==k
j zs j f k y 0)()( (8))1()(k f k y zs -=
1-28 某一阶LTI离散系统,其初始状态为)0(x。
已知当激励为)(
)
(
1k
k
yε
=时,其全响应为
若初始状态不变,当激励为)(k f-时,其全响应为)(]1
)5.0(2[
)
(
2k
k
y kε
-
=
若初始状态为)0(2x,当激励为)(
4k
f时,求其全响应。
第二章
2-1 已知描述系统的微分方程和初始状态如下,试求其零输入响应。
(1)1)0(',1)0(),()(6)('5)(''-===++-y y t f t y t y t y
(4)0)0(',2)0(),()()(''===+-y y t f t y t y
2-2 已知描述系统的微分方程和初始状态如下,试求其+0值)0(+y 和)0('+y 。
(2))()(,1)0(',1)0(),('')(8)('6)(''t t f y y t f t y t y t y δ====++--
(4))()(,2)0(',1)0(),(')(5)('4)(''2t e t f y y t f t y t y t y t ε====++--
解:
2-4 已知描述系统的微分方程和初始状态如下,试求其零输入响应、零状态响应和全响应。
(2))()(,2)0(',1)0(),(3)(')(4)('4)(''t e t f y y t f t f t y t y t y t ε---===+=++
解:
2-8 如图2-4所示的电路,若以)(t i S 为输入,)(t u R 为输出,试列出其微分方程,并求出冲激响应和阶跃响应。
2-12 如图2-6所示的电路,以电容电压)(t u C 为响应,试求其冲激响应和阶跃响应。
2-16 各函数波形如图2-8所示,图2-8(b)、(c)、(d)均为单位冲激函数,试求下列卷积,并画出波形图。
(1))(*)(21t f t f (2))(*)(31t f t f (3))(*)(41t f t f
(4))(*)(*)(221t f t f t f (5))3()(2[*)(341--t f t f t f
波形图如图2-9(a)所示。
波形图如图2-9(b)所示。
波形图如图2-9(c)所示。
