高中数学必修3课件全册人教A版ppt课件
合集下载
高中数学人教A版 选择性必修第三册 超几何分布 课件

P( X
1)
1-
C30C2170 C10
30
0.7192.
例题
例3.袋中有8个白球,2个黑球,从中随机地连续抽取3次,每次取1个球. (1)若每次抽取后都放回,设取到黑球的个数为X,求X的分布列. (2)若每次抽取后都不放回,设取到黑球的个数为Y,求Y的分布列.
例题
例3.袋中有8个白球,2个黑球,从中随机地连续抽取3次,每次取1个球.
(1)若每次抽取后都放回,设取到黑球的个数为X,求X的分布列. 解.若每次抽取后都放回,则每次抽到黑球的概率均为 1 .
5
并且3次取球是3次独立重复试验,则X ~ B(3, 1), 5
则P( X
k)
C3k
(1)k 5
( 4)3k , k 5
0,1, 2,3.
则X的分布列为
例题
例3.袋中有8个白球,2个黑球,从中随机地连续抽取3次,每次取1个球.
此时称随机变量X 服从二项分布,记作X ~ B(n, p).
例题
例1.判断下列随机变量是否服从超几何分布
(1)已知有125个孩子,其中男孩62个,从这些孩子中随机抽取10个,
√ 设抽到男孩的个数位X;
(2)学校要从3名男教师和4名女教师中随机抽取3人去支教,设抽取
√ 的人中男教师的人数为X;
(3)现在共有10个球,其中4个红球,6个白球,有放回的依次抽取4
(2)若每次抽取后都不放回,设取到黑球的个数为Y,求Y的分布列. 解.若每次抽取后都不放回,则X 服从超几何分布,
且N 10, M 2, n 3.
则P( X
k)
C2k
C 3-k 8
C130
,k
0,1, 2.
则X的分布列为
人教版高中数学必修3(A版) 用样本的频率分布估计总体分布 PPT课件

0.16
0.08 0.12 0.08 0.04 0.3 0.5 0.44
有数无形欠直观, 在频率直 有形无数难入微 方图中,
0.28
12%
3.5 4 4.5
0 .1
0
各小矩形 的面积的 总和等于1
0.5
1
1.5
2
2 .5
3
88%
月均用水量/t
探究:
同样一组数据,如果组距不同,横轴、纵轴的单位 不同,得到的图的形状也会不同。不同的形状给人以不 同的印象,这种印象有时会影响我们对总体的判断。观 察分别以1和0.1为组距的图象,谈谈你对图的印象。
0.036 0.032 0.028 0.024 0.020 0.016 0.012 0.008 0.004 o 90 100 110 120 130 140 150
次数
频率= 频数
第二小组频数 12 样本容量 150 样本容量 第二小组频率 0.08
频率分布折线图.
频率/组距 (取各小长方形上端中点, 并连线 )
0.6 0.5 0.4 0.3
0.3
0.16 0.12 0.08 0.04 0.28 0.5 0.44
0.2
0.1 0.08 0 0.5 1 1.5 2 2.5 3
3.5 4
4.5
月均用水量/t
利用样本频分布对总体分布进行相应估计 用样本分布直方图去估计相应的总体分布时, (1)样本容量越大,这种估计越精确。 一般样本容量越大,频率分布直方图就会越接 (2)当样本容量无限增大,组距无限缩小,那么相应的 近总体密度曲线,就越精确地反映了总体的分 频率折线图会无限接近于一条光滑曲线 ———总体密度曲线 布规律,即越精确地反映了总体在各个范围内 取值百分比。 (3)总体密度曲线反映了总体在各个范围内取值的百
0.08 0.12 0.08 0.04 0.3 0.5 0.44
有数无形欠直观, 在频率直 有形无数难入微 方图中,
0.28
12%
3.5 4 4.5
0 .1
0
各小矩形 的面积的 总和等于1
0.5
1
1.5
2
2 .5
3
88%
月均用水量/t
探究:
同样一组数据,如果组距不同,横轴、纵轴的单位 不同,得到的图的形状也会不同。不同的形状给人以不 同的印象,这种印象有时会影响我们对总体的判断。观 察分别以1和0.1为组距的图象,谈谈你对图的印象。
0.036 0.032 0.028 0.024 0.020 0.016 0.012 0.008 0.004 o 90 100 110 120 130 140 150
次数
频率= 频数
第二小组频数 12 样本容量 150 样本容量 第二小组频率 0.08
频率分布折线图.
频率/组距 (取各小长方形上端中点, 并连线 )
0.6 0.5 0.4 0.3
0.3
0.16 0.12 0.08 0.04 0.28 0.5 0.44
0.2
0.1 0.08 0 0.5 1 1.5 2 2.5 3
3.5 4
4.5
月均用水量/t
利用样本频分布对总体分布进行相应估计 用样本分布直方图去估计相应的总体分布时, (1)样本容量越大,这种估计越精确。 一般样本容量越大,频率分布直方图就会越接 (2)当样本容量无限增大,组距无限缩小,那么相应的 近总体密度曲线,就越精确地反映了总体的分 频率折线图会无限接近于一条光滑曲线 ———总体密度曲线 布规律,即越精确地反映了总体在各个范围内 取值百分比。 (3)总体密度曲线反映了总体在各个范围内取值的百
人教A版高中数学选择性必修第三册6.2.3_组合课件

解析答案
类型二 组合的列举问题 例2 从5个不同元素a,b,c,d,e中取出2个,列出所有组合为_a_b_,__a_c_,_ _a_d_,__a_e_,__b_c_,__b_d_,__b_e_,__cd_,__c_e_,__d_e_. 解析 要想列出所有组合,做到不重不漏,先将元素按照一定顺序排好, 然后按顺序用图示的方法将各个组合逐个地标示出来.如图所示.
类型三 组合数公式及应用 角度1 有关组合数的计算与证明 例 3 (1)计算 C410-C37·A33; 解 原式=C410-A37=140××39××28××17-7×6×5=210-210=0. (2)证明:mCnm=nCmn--11. 解 mCmn =m·m!nn! -m!=m-n1·n!-n1-!m! =n·m-1n!-1n-!m!=nCmn--11.
反思与感悟 解析答案
跟踪训练 3 (1)计算 C34+C35+C36+…+C32 015的值为( C )
A.C42 015 C.C42 016-1
B.C52 015 D.C52 015-1
解析 C34+C35+C36+…+C32 015 =C44+C34+C35+C36+…+C32 015-C44
解析答案
返回
达标检测
1234
1.下列问题中,组合问题的个数是( B ) ①从全班50人中选出5人组成班委会;②从全班50人中选出5人分别担负班
长、副班长、团支部书记、学习委员、生活委员;③从1,2,3,…,9中任
取出两个数求积;④从1,2,3,…,9中任取出两个数求差或商.
A.1
B.2 C.3 D.4
=C45+C35+…+C32 015-1=…=C42 015+C32 015-1=C42 016-1
(2)计算:C37+C47+C58+C89=_2_1_0__.
类型二 组合的列举问题 例2 从5个不同元素a,b,c,d,e中取出2个,列出所有组合为_a_b_,__a_c_,_ _a_d_,__a_e_,__b_c_,__b_d_,__b_e_,__cd_,__c_e_,__d_e_. 解析 要想列出所有组合,做到不重不漏,先将元素按照一定顺序排好, 然后按顺序用图示的方法将各个组合逐个地标示出来.如图所示.
类型三 组合数公式及应用 角度1 有关组合数的计算与证明 例 3 (1)计算 C410-C37·A33; 解 原式=C410-A37=140××39××28××17-7×6×5=210-210=0. (2)证明:mCnm=nCmn--11. 解 mCmn =m·m!nn! -m!=m-n1·n!-n1-!m! =n·m-1n!-1n-!m!=nCmn--11.
反思与感悟 解析答案
跟踪训练 3 (1)计算 C34+C35+C36+…+C32 015的值为( C )
A.C42 015 C.C42 016-1
B.C52 015 D.C52 015-1
解析 C34+C35+C36+…+C32 015 =C44+C34+C35+C36+…+C32 015-C44
解析答案
返回
达标检测
1234
1.下列问题中,组合问题的个数是( B ) ①从全班50人中选出5人组成班委会;②从全班50人中选出5人分别担负班
长、副班长、团支部书记、学习委员、生活委员;③从1,2,3,…,9中任
取出两个数求积;④从1,2,3,…,9中任取出两个数求差或商.
A.1
B.2 C.3 D.4
=C45+C35+…+C32 015-1=…=C42 015+C32 015-1=C42 016-1
(2)计算:C37+C47+C58+C89=_2_1_0__.
高中数学 132 进位制课件 新人教A版必修3

最大公约数是( )
A.57
B.3
C.19
D.34
[答案] C
第十一页,共69页。
4.用秦九韶算法求多项式f(x)=2+0.35x+1.8x2-3.66x3 +6x4-5.2x5+x6在x=-1.3时的值时,令v0=a6;v1=v0x+ a5;…;v6=v5x+a0时,v3的值为( )
A.-9.8205 B.14.25 C.-22.445 D.30.9785 [答案] C
24005(7)=2×74+4×73+0×72+0×71+5=2401, 故七进制数24005(7)化成十进制数为2401.
第三十六页,共69页。
把十进制数化为k进制数 学法指导 十进制数化为k进制数(除k取余法)的步骤:
第三十七页,共69页。
(1)把十进制数89化为二进制数. (2)将十进制数21化为五进制数.
[答案] 111111(2)
第四十九页,共69页。
[解析] 将题中四个数化为十进制数. 85(9)=8×91+6×90=72+6=78; 211(6)=2×62+1×6+1=72+7=79; 1000(4)=1×43=64; 111111(2)=25+24+23+22+21+20=63.
第五十页,共69页。
[破疑点] 教材中的算法案例进一步体现了编写程序的 基本过程:
①算法分析,将解决实际问题的过程以步骤的形式用文 字语言表述出来.
②画程序框图,把算法分析用程序框和流程线的形式表 达出来.
③编写程序,将程序框图转化为算法语句即程序.
第二十四页,共69页。
以下各数有可能是五进制数的是( ) A.15 B.106 C.731 D.21340 [答案] D
第七页,共69页。
人教版高中数学必修3(A版) 几何概型 PPT课件

2 5
1 6
第二种三块区域圆心 角之比为1:2:3;
1 4
第三种圆盘两圆的半 径之比为1:2
[情境二] 问题1:在区间[0,9]上任取一个整数,恰 好取在区间[0,3]上的概率为多少? 2
5
问题2:在区间[0,9]上任取一个实数,恰 好取在区间[0,3]上的概率为多少? 1
3
探究:
请问飞镖射中靶心A(看成一个点)的 概率是多少?
中国刑法第三百零三条规定:以营利为目的,聚众 赌博或者以赌博为业的,处三年以下有期徒刑、拘役 或者管制,并处罚金;“开设赌场的,处三年以下有期徒 刑、拘役或者管制,并处罚金;情节严重的,处三年以 上十年以下有期徒刑,并处罚金.
复习提问:
1、古典概型的两个特点: (1)试验中所有可能出现的基本事件只有 有限个. (2)每个基本事件出现的可能性相等. 2、计算古典概型的公式:
几何概型的概率计算公式:
构成事件A的测度(长度、弧度、 角度、面积、体积) P( A) 全部结果的测度(长度 构成事件A的测度(长度、弧度、 角度、面积、体积) P( A) 全部结果的测度(长度 、弧度、角度、面积、 体积)
例1:取一根长度为60cm的绳子,拉直后在任意
A包含基本事件的个数 公式:P( A) 基本事件的总数
创设情境:
情境一:摸球游戏:袋子中有分别写有1 号、2号、3号、4号、5号的5个球, 问题:随机抽取一个抽到1号的概率是多 1 少? 5 上述情景改为如图所示,问 1 5 题:圆盘中指针指到到1号的 4 2 概率是多少? 3
注:五个扇形区域面 积相同;
解:设A={等待的时间不多于10分钟}. 所求的事件A恰好是打开收音机时的 时刻位于[50,60]时间段内。 因此由几何概型的概率公式得
人教A版 高中数学 必修3 第一章 1.1.2 循环结构的程序框图课件(共16张PPT)
巩固提高
1、设计一算法,求 积:1×2×3×…×100, 画出流程图
思考:该流程图与前面 的例1中求和的流程图有 何不同?
开始 i=0,S=1
i=i+1 S=S*i 否 i>=100?
是 输出S 结束
巩固提高
2、设计一算法输出1~1000以内能被3整除的整数
开始
算法:
i=0
S1:确定i的初始值为0;
开始 i=0,S=0
否 i<100? 是 i=i+1 S=S+ i
输出S 结束
思考:将步骤A和步骤B交换位 置,结果会怎样?能达到预期结果 吗?为什么?要达到预期结果,还 需要做怎样的修改?
步骤A
步骤B 答:达不到预期结果;
当i = 100时,退出循环,i 的值未能加入到S中;修 改的方法是将判断条件改 为i<101
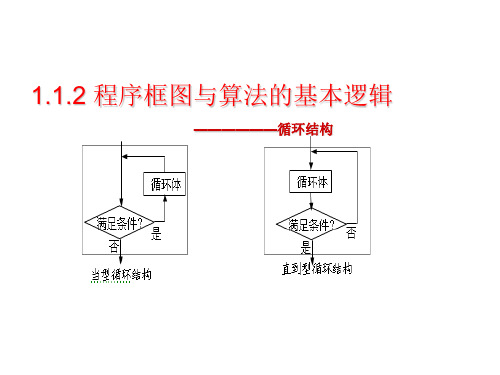
1.1.2 程序框图与算法的基本逻辑
——————循环结构
复习回顾
1、程序框图(流程图)的概念: 2、算法的三种逻辑结构: 3、顺序结构的概念及其程序框图: 4、条件结构的概念及其程序框图:
复习回顾
i) 顺序结构
ii) 条件结构
Yp N A
A
B
B
循环结构
循环结构:在一些算法中,也经常会出现从某处开始,
小结:
4.画循环结构流程图前: ①确定循环变量和初始条件; ②确定算法中反复执行的部分,即循环体; ③确定循环的转向位置; ④确定循环的终止条件.
循环结构的三要素:
循环变量,循环体、循环的终止条件。
其中顺序结构是最简单的结构,也是最基 本的结构,循环结构必然包含条件结构,所以 这三种基本逻辑结构是相互支撑的,无论怎样 复杂的逻辑结构,都可以通过这三种结构来表 达。
高中数学人教A版必修3课件:第三章3.1 3.1.1

解析: 949÷1 006≈0.943 34,1 430÷1 500≈0.953 33,1 917 ÷2 015≈0.951 36, 2 890÷3 050≈0.947 54, 4 940÷5 200=0.95. 都稳定于 0.95,故所求概率约为 0.95.
பைடு நூலகம்
探究点一
事件类型的判断
指出下列事件是必然事件、 不可能事件, 还是随机事件. (1)2012 年奥运会在英国伦敦举行; (2)甲同学今年已经上高一,三年后他被北大自主招生录取; (3)A 地区在“十三五”规划期间会有 6 条高速公路通车; (4)在标准大气压下且温度低于 0 ℃时,冰融化. [解] (1)是必然事件,因事件已经发生.
能再连任下届总统,是不可能事件,④是必然事件.
3. 某出版公司对发行的三百多种教辅用书实行跟踪式问卷调查, 连续五年的调查结果如表所示: 发送问卷数 返回问卷数 1 006 949 1 500 1 430 2 015 1 917 3 050 2 890 5 200 4 940
则本公司问卷返回的概率约为( A ) A.0.95 C.0.93 B.0.94 D.0.92
(2)(3)是随机事件,其事件的结果在各自的条件下不确定. (4)是不可能事件,在本条件下,事件不会发生.
对事件分类的两个关键点 (1)条件:在条件 S 下事件发生与否是与条件相对而言的,没有 条件,就无法判断事件是否发生; (2)结果发生与否:有时结果较复杂,要准确理解结果包含的各 种情况.
1.(1)下面的事件: ①在标准大气压下, 水加热到 80℃时会沸腾; ②a, b∈R, 则 ab=ba; ③一枚硬币连掷两次, 两次都出现正面向上.其中是不可能事件的为( B A.② C.①② B.① D.③ )
人教A版高中数学必修三课件:1-2-3

新课标导 学
数 学
必修③ ·人教 A版
第一章
算法初步
1.2 基本算法语句
1.2. 3 循环语句
1 2 3
自主预习 学 案 互动探究 学 案 课时作业 学 案
自主预习学案
• 循环是计算机解题的一个重要特征.由于 计算机运算速度快,最适宜做重复性质的 工作,所以当我们在进行程序设计时,总 是要把复杂的、不易理解的求解过程转换 为容易理解的、可操作的、多次重复的求 解过程.这样一方面降低了问题的复杂程 度,另一方面也减少了程序书写及输入的 工作量,同时也可以充分发挥计算机运算 速度快且可自动执行程序的优势.
[ 解析] 程序如下: S=1 i=2 DO S=S*i i=i+2 LOOP UNTIL i>100 PRINT S END
• 『规律总结』 UNTIL语句的适用类型及 执行方式
〔跟踪练习1〕 导学号 93750192 下面为一个求20个数的平均数的程序,在横线上应填充的语句为( A.i>20 C.i>=20 B.i<20 D.i<=20
[ 错解] 程序如下: S=5 000 i =0 WHILE S<40 000 S=S*1+0.1 i=i+1 WEND PRINT i END
• [辨析] 错解中的循环求出的S不是总销量
,而是每年的年销量.
• 用“m=m*(1+0. 1)”表示累乘,求出每
m=5000 年销量;用 “S=S+m”表示累加,求出 S=0 i=0 总销量. WHILE S<40000 S=S+ [正解 ]m 程序如下: m=m*1+0.1 i=i+1 WEND PRINT i END
[ 解析] 程序如下: i=2 p=0 DO p=p+i i=i+2 LOOP UNTIL i>99 PRINT P END
数 学
必修③ ·人教 A版
第一章
算法初步
1.2 基本算法语句
1.2. 3 循环语句
1 2 3
自主预习 学 案 互动探究 学 案 课时作业 学 案
自主预习学案
• 循环是计算机解题的一个重要特征.由于 计算机运算速度快,最适宜做重复性质的 工作,所以当我们在进行程序设计时,总 是要把复杂的、不易理解的求解过程转换 为容易理解的、可操作的、多次重复的求 解过程.这样一方面降低了问题的复杂程 度,另一方面也减少了程序书写及输入的 工作量,同时也可以充分发挥计算机运算 速度快且可自动执行程序的优势.
[ 解析] 程序如下: S=1 i=2 DO S=S*i i=i+2 LOOP UNTIL i>100 PRINT S END
• 『规律总结』 UNTIL语句的适用类型及 执行方式
〔跟踪练习1〕 导学号 93750192 下面为一个求20个数的平均数的程序,在横线上应填充的语句为( A.i>20 C.i>=20 B.i<20 D.i<=20
[ 错解] 程序如下: S=5 000 i =0 WHILE S<40 000 S=S*1+0.1 i=i+1 WEND PRINT i END
• [辨析] 错解中的循环求出的S不是总销量
,而是每年的年销量.
• 用“m=m*(1+0. 1)”表示累乘,求出每
m=5000 年销量;用 “S=S+m”表示累加,求出 S=0 i=0 总销量. WHILE S<40000 S=S+ [正解 ]m 程序如下: m=m*1+0.1 i=i+1 WEND PRINT i END
[ 解析] 程序如下: i=2 p=0 DO p=p+i i=i+2 LOOP UNTIL i>99 PRINT P END
人教A版高中数学选择性必修第三册7.4.2超几何分布课件

率均为15,3 次取球可以看成 3 次独立重复试验,则 X~B3,15, X 的分布列如下
X
0
1
2
3
P
64 125
48 125
12 125
1 125
P(X=k)=Ck3×15k×453-k,k=0,1,2.
此时,E(X)=np=3×15=35.
[方法总结] 解答此类问题的关键是先准确区分超几何散布和二项散布,再根据题意采用相 应的知识求解.
2.袋中有 10 个球,其中 7 个是红球,3 个是白球,任意取出 3 个,这 3 个都是
红球的概率是
()
A.1120
B.274
C.170
D.37
答案 解析
B P=CC37·31C0 03=274.
3.从3台甲型彩电和2台乙型彩电中任取2台,若设X表示所取的2台彩电中甲型 彩电的台数,则P(X=1)=____________.
__n__件(不放回),用 X 表示抽取的__n__件产品中的次品数,则 X 的分布列为 CkMCnN--kM
P(X=k)=______C__nN_____,k=m,m+1,m+2,…,r, 其中 n,M,N∈N*,M≤N ,n≤N ,m=max{0, n-N+M},r=minM,n. 如果随机变量 X 的分布列具有上式的形式,那么称随机变量 X 服从超几何分布.
计
算
公
式
可
知
P
X=k
=
CkMCCnNnN--kM.
袋中有8个球,其中5个黑球,3个红球,从 袋中任取3个球,求取出的红球数X的散布列,并求至少有一个红球的概率.
解 由已知可得 X 的取值为 0,1,2,3, X=0 表示取出的 3 个球全是黑球,P(X=0)=CC3538=1506=258, 同理 P(X=1)=CC13·C38 25=3506=1258,P(X=2)=CC23·C38 15=1556,P(X=3)=CC3338=516. ∴X 的分布列为
高中数学 新人教A版选择性必修第三册 第七章 7.1.1条件概率 课件

【解析】选C.设A为“某人检验呈阳性”,B为“此人患病”.则“某人检验呈阳性时 他确实患病”为B|A,
又P(B|A) =PP((AAB)) =99%0.×20%.1% =49.5%.
2.气象资料表明,某地区每年七月份刮台风的概率为35 ,在刮台风的条件下, 下大雨的概率为190 ,则该地区七月份既刮台风又下大雨的概率为( ) A.23 B.2570 C.190 D.130
1.若P(A∩B)=35 ,P(A)=34 ,则P(B|A)=( ) A.54 B.45 C.53 D.43
2.下列式子成立的是( A.P(A|B)=P(B|A) C.P(AB)=P(B|A)·P(A)
) B.0<P(B|A)<1 D.P(AB|A)=P(B)
【解析】选C.由P(B|A)=PP((AAB)) 得P(AB)=P(B|A)·P(A),而P(A|B)=PP((ABB)) 知 A不正确,C正确;当P(B)为零时知P(B|A)=0,所以B不正确;D选项应是P(AB|A) =P(B|A),故D不正确.
第七章 随机变量及其分布 7.1 条件概率与全概率公式
7.1.1 条 件 概 率
基础预习初探
主题1 条件概率的概念及性质 3张奖券中只有1张能中奖,现分别由3名同学无放回地抽取.
(1)问最后一名同学抽到中奖奖券的概率是否比其他同学小?
提示:由古典概型可知,最后一名同学抽到中奖奖券的概率为 1 ,与其他同学
(2)设“点数a,b之和不大于5”为事件B, 包含(1,1),(1,2),(1,3),(1,4),(2,1), (2,2),(2,3),(3,1),(3,2),(4,1),共10个基本事件; 设“a,b中至少有一个为2”为事件C, 包含(1,2),(2,1),(2,2),(2,3),(3,2),共5个基本事件,故“在点数a,b 之和不大于5的条件下,a,b中至少有一个为2”的概率:P=nn((BBC)) =150 =12 .
最新人教版高中数学必修三课件PPT

C.流程线无论什么方向,总要按箭头的指向执行
D.流程线是带有箭头的线,它可以画成折线
【2】具有判断条件是否成立的程序框是( C )
2021/10/31
画程序框图时应注意:
用框图表示算法比较直观、形象,容易理解,通常说
“一图胜万言”,所以用程序框图能更清楚地展现算法
的逻辑结构,在画程序框图时必须注意:
则,返回第三步.
2021/10/31
当d=0.005时,按照以上算法,可得下面表和图.
a
b
|a-b|
1
2
1
1
1.5
0.5
1.25
1.5
0.25
1.375
1.5
0.125
1.375
1.437 5
0.062 5
1.406 25
1.437 5
0.031 25
1.406 25
1.421 875
0.015 625
- 5)两点连线的方程可
先求MN的斜率,再利用点斜式方程求得。
A.1个
2021/10/31
B.2个
C.3个
D.0个
例题剖析1
设计一个算法判断7是否为质数.
第一步, 用2除7,得到余数1.因为余数不为0,
所以2不能整除7.
第二步, 用3除7,得到余数1.因为余数不为0,
所以3不能整除7.
第三步, 用4除7,得到余数3.因为余数不为0,
算法步骤:
第一步,输入三角形三条边的边长 a,b,c.
a+b+c
第二步,计算 p= 2 .
第三步,计算 S= p(pa)(pb.)(pc)
第四步,输出S.
2021/10/31
新课探究
D.流程线是带有箭头的线,它可以画成折线
【2】具有判断条件是否成立的程序框是( C )
2021/10/31
画程序框图时应注意:
用框图表示算法比较直观、形象,容易理解,通常说
“一图胜万言”,所以用程序框图能更清楚地展现算法
的逻辑结构,在画程序框图时必须注意:
则,返回第三步.
2021/10/31
当d=0.005时,按照以上算法,可得下面表和图.
a
b
|a-b|
1
2
1
1
1.5
0.5
1.25
1.5
0.25
1.375
1.5
0.125
1.375
1.437 5
0.062 5
1.406 25
1.437 5
0.031 25
1.406 25
1.421 875
0.015 625
- 5)两点连线的方程可
先求MN的斜率,再利用点斜式方程求得。
A.1个
2021/10/31
B.2个
C.3个
D.0个
例题剖析1
设计一个算法判断7是否为质数.
第一步, 用2除7,得到余数1.因为余数不为0,
所以2不能整除7.
第二步, 用3除7,得到余数1.因为余数不为0,
所以3不能整除7.
第三步, 用4除7,得到余数3.因为余数不为0,
算法步骤:
第一步,输入三角形三条边的边长 a,b,c.
a+b+c
第二步,计算 p= 2 .
第三步,计算 S= p(pa)(pb.)(pc)
第四步,输出S.
2021/10/31
新课探究
高中数学(人教版A版必修三)配套课件:3.1.1随机事件的概率

答案
返回
题型探究
重点难点 个个击破
类型一 必然事件、不可能事件和随机事件的判定
例1 在下列事件中,哪些是必然事件?哪些是不可能事件?哪些是随机 事件?
(1)如果a,b都是实数,那么a+b=b+a; (2)从分别标有1,2,3,4,5,6的6张号签中任取一张,得到4号签; (3)铁球浮在水中; (4)某电话总机在60秒内接到至少15次传呼; (5)在标准大气压下,水的温度达到50 ℃时沸腾; (6)同性电荷,相互排斥.
人教版七年级上册Unit4 Where‘s my backpack?
超级记忆法-记忆方法
TIP1:在使用场景记忆法时,我们可以多使用自己熟悉的场景(如日常自己的 卧室、平时上课的教室等等),这样记忆起来更加轻松; TIP2:在场景中记忆时,可以适当采用一些顺序,比如上面例子中从上到下、 从左到右、从远到近等顺序记忆会比杂乱无序乱记效果更好。
答案
不可能事件:在条件S下,一定不会发生的
事件,叫做相对于条件S的不可能事件.
事件确定事件必叫 然事 做件 相: 对在 于条 条件 件SS下 的, 必然一事定件会.发生 的事件,
随机事件:在条件S下, 可能发生也可能不发生
的事件,叫做相对于条件S的随机事件.
答案
知识点二 频数与频率 思考 抛掷一枚硬币10次,正面向上出现了3次,则在这10次试验中, 正面向上的频数与频率分别是多少? 答案 频数为3,频率为130. 在相同的条件S下重复n次试验,观察某一事件A是否出现,称n次试验中 事件A出现的次数nA 为事件A出现的频数,称事件A出现的比例fn(A)=nnA为 事件A出现的频率.
第三章 § 3.1 随机事件的概率
3.1.1 随机事件的概率
人教A版高中数学必修三课件高一第三章概率.pptx

“甲抽到判断题,乙抽到选择题”的情况有:(p1,x1), (p1,x2),(p1,x3),(p2,x1),(p2,x2),(p2,x3),共6种;
“甲、乙都抽到选择题”的情况有:(x1,x2),(x1,x3), (x2,x1),(x2,x3),(x3,x1),(x3,x2),共6种;“甲、乙都抽 到判断题”的情况有:(p1,p2),(p1,p1),共2种.
专题4 几何概型问题
若试验同时具有基本事件的无限性和每个事件发生的等
可能性两个特征,则此试验为几何概型,由于基本事件的个
数和结果的无限性,其概率就不能应用P(A)=
m n
求解,因此
需转化为几何度量(如长度、面积、体积等)的比值求解.
几何概型是新增内容,在高考中很少考查随机模拟,主 要涉及几何概型的概率求解问题,难度不会太大,题型可能 较灵活,涉及面可能较广.几何概型的三种类型分别为长度 型、面积型和体积型,在解题时要准确把握,要把实际问题 作合理的转化;要注意古典概型和几何概型的区别,正确地 选用几何概型解题.
(2)设身高为176 cm的同学被抽中为事件A. 从乙班10名同学中抽中两名身高不低于173cm的同学 有: (181,173),(181,176),(181,178),(181,179), (179,173),(179,176),(179,178),(178,173),(178,176), (176,173)共10个基本事件. 而事件A含有4个基本事件:(181,176),(179,176), (178,176),(176,173),所以P(A)=140=25.
[解析] (1)第二组的频率为1-(0.04+0.04+0.03+0.02 +0.01)×5=0.3,所以高为05.3=0.06.频率直方图如下:
“甲、乙都抽到选择题”的情况有:(x1,x2),(x1,x3), (x2,x1),(x2,x3),(x3,x1),(x3,x2),共6种;“甲、乙都抽 到判断题”的情况有:(p1,p2),(p1,p1),共2种.
专题4 几何概型问题
若试验同时具有基本事件的无限性和每个事件发生的等
可能性两个特征,则此试验为几何概型,由于基本事件的个
数和结果的无限性,其概率就不能应用P(A)=
m n
求解,因此
需转化为几何度量(如长度、面积、体积等)的比值求解.
几何概型是新增内容,在高考中很少考查随机模拟,主 要涉及几何概型的概率求解问题,难度不会太大,题型可能 较灵活,涉及面可能较广.几何概型的三种类型分别为长度 型、面积型和体积型,在解题时要准确把握,要把实际问题 作合理的转化;要注意古典概型和几何概型的区别,正确地 选用几何概型解题.
(2)设身高为176 cm的同学被抽中为事件A. 从乙班10名同学中抽中两名身高不低于173cm的同学 有: (181,173),(181,176),(181,178),(181,179), (179,173),(179,176),(179,178),(178,173),(178,176), (176,173)共10个基本事件. 而事件A含有4个基本事件:(181,176),(179,176), (178,176),(176,173),所以P(A)=140=25.
[解析] (1)第二组的频率为1-(0.04+0.04+0.03+0.02 +0.01)×5=0.3,所以高为05.3=0.06.频率直方图如下:
高中数学人教A版必修三第一章.3进位制-算法案例ppt课件

1.3算法案例
进位制
十进制数3721中的3表示3个千,7表示7个百,2表示2个 十,1表示1个一,从而它可以写成下面的形式:
3721=3×103+7×102+2×101+1×100.
同理: 3421(5)= 3×53+4×52+2×51+1×50.
每一位上的数都是整数.
按照十进制数的运算规则计算出结果, 结果就是十进制下该数的大小了.
89 余数
=81+18+6+1=106.
44
1
0
3
11
0
解:第一步:先把三进制数化为十进制数:
按照十进制数的运算规则计算出结果,
1
0
22
0
结果就是十进制下该数的大小了.
∴ 89=324(5)
2
1
=81+18+6+1=106. 第二步:再把十进制数化为二进制数:
106=1101010(2). ∴10221(3)=106=1101010(2).
课堂小结
1.几进制的基数就是几,基数都是大于1的数.
89=1011001(2)
11
0
17
4
∴ 89=324(5)
十进制数3721中的3表示3个千,7表示7个百,2表示2个十,1表示1个一,从而它可以写成下面的形式:
把89化为五进制的数.
5 89 5 17 53
0
余数
4 2 3
∴ 89=324(5)
练习:把3282化为16进制的数.
10
11
12
13
14
15
ABຫໍສະໝຸດ CDEF
思考 你会把三进制数10221(3)化为二进制数吗?
进位制
十进制数3721中的3表示3个千,7表示7个百,2表示2个 十,1表示1个一,从而它可以写成下面的形式:
3721=3×103+7×102+2×101+1×100.
同理: 3421(5)= 3×53+4×52+2×51+1×50.
每一位上的数都是整数.
按照十进制数的运算规则计算出结果, 结果就是十进制下该数的大小了.
89 余数
=81+18+6+1=106.
44
1
0
3
11
0
解:第一步:先把三进制数化为十进制数:
按照十进制数的运算规则计算出结果,
1
0
22
0
结果就是十进制下该数的大小了.
∴ 89=324(5)
2
1
=81+18+6+1=106. 第二步:再把十进制数化为二进制数:
106=1101010(2). ∴10221(3)=106=1101010(2).
课堂小结
1.几进制的基数就是几,基数都是大于1的数.
89=1011001(2)
11
0
17
4
∴ 89=324(5)
十进制数3721中的3表示3个千,7表示7个百,2表示2个十,1表示1个一,从而它可以写成下面的形式:
把89化为五进制的数.
5 89 5 17 53
0
余数
4 2 3
∴ 89=324(5)
练习:把3282化为16进制的数.
10
11
12
13
14
15
ABຫໍສະໝຸດ CDEF
思考 你会把三进制数10221(3)化为二进制数吗?
高中数学《古典概型》(47张) 新人教A版必修3PPT课件

n
我们把可以作古典概型计算的概率称为古典概率.
注: A即是一次随机试验的样本空间的一个子集, 而m是这个子集里面的元素个数;n即是一次随机 试验的样本空间的元素个数.
古典概率
3、概率的性质 (1) 随机事件A的概率满足
0<P(A)<1
(2)必然事件的概率是1,不可能的事件的概率是0,
即
P(Ω) =1 , P(Φ) =0.
• (1)试问:一共有多少种不同的结果?请
•思维点拨:用空间坐标(a,b,c)的形式列出 所有可能结果,再把事件“3次摸球所得总分 为5分”的个数列出,根据古典概型概率公式 可求. •解答:(1)一共有8种不同的结果,列举如下: •(红、红、红)、(红、红、黑)、(红、黑、红)、
• 思维点拨:用空间坐标(a,b,c)的形式列 出所有可能结果,再把事件“3次摸球所得 总分为5分”的个数列出,根据古典概型概 率公式可求.
【答题模板】
•解析:基本事件有20个,只要通过枚举的方法 找到随机事件“卡片上两个数的各位 •数字之和不小于14”所包含的基本事件的个数, 再按照等可能性事件的概率公式计 •算.大于14的点数的情况通过列举可得,有5
【分析点评】
• 1. 本题中,当两个数字k,k+1是一位数时, 只有k≥7时,才会使两个数的各位数字之和 不小于14;当k,k+1是两位数时,只有当 第一个两位数的数字之和不小于7才有可 能.这类题目也曾出现在高考中,如2008年 江西卷中:电子钟一天显示的时间是从
(1)两枚硬币都出现正面的概率是 0.25 (2)一枚出现正面,一枚出现反面的概率是 0.5
4、在一次问题抢答的游戏,要求答题者在问题所列出的 4个答案中找出唯一正确答案。某抢答者不知道正确答案 便随意说出其中的一个答案,则这个答案恰好是正确答
我们把可以作古典概型计算的概率称为古典概率.
注: A即是一次随机试验的样本空间的一个子集, 而m是这个子集里面的元素个数;n即是一次随机 试验的样本空间的元素个数.
古典概率
3、概率的性质 (1) 随机事件A的概率满足
0<P(A)<1
(2)必然事件的概率是1,不可能的事件的概率是0,
即
P(Ω) =1 , P(Φ) =0.
• (1)试问:一共有多少种不同的结果?请
•思维点拨:用空间坐标(a,b,c)的形式列出 所有可能结果,再把事件“3次摸球所得总分 为5分”的个数列出,根据古典概型概率公式 可求. •解答:(1)一共有8种不同的结果,列举如下: •(红、红、红)、(红、红、黑)、(红、黑、红)、
• 思维点拨:用空间坐标(a,b,c)的形式列 出所有可能结果,再把事件“3次摸球所得 总分为5分”的个数列出,根据古典概型概 率公式可求.
【答题模板】
•解析:基本事件有20个,只要通过枚举的方法 找到随机事件“卡片上两个数的各位 •数字之和不小于14”所包含的基本事件的个数, 再按照等可能性事件的概率公式计 •算.大于14的点数的情况通过列举可得,有5
【分析点评】
• 1. 本题中,当两个数字k,k+1是一位数时, 只有k≥7时,才会使两个数的各位数字之和 不小于14;当k,k+1是两位数时,只有当 第一个两位数的数字之和不小于7才有可 能.这类题目也曾出现在高考中,如2008年 江西卷中:电子钟一天显示的时间是从
(1)两枚硬币都出现正面的概率是 0.25 (2)一枚出现正面,一枚出现反面的概率是 0.5
4、在一次问题抢答的游戏,要求答题者在问题所列出的 4个答案中找出唯一正确答案。某抢答者不知道正确答案 便随意说出其中的一个答案,则这个答案恰好是正确答
人教版高中数学必修3(A版) 古典概型 PPT课件

基本事件
“正面朝上” 两个基本事件 1 “反面朝上” 的概率都是 2 “1点”、“2 六个基本事件 有限性 点” 1 “3点”、“4 的概率都是 6 点” 只有有限个 (1) 试验中所有可能出现的基本事件的个数 “5点”、“6 点” 相等 (2) 每个基本事件出现的可能性 等可能性
试 验 1 试 验 2
任何事件(除不可能事件)都可以表示成基本事件的和
一次试验可能出现的每一个结果 称为一个 基本事件
例1 从字母a、b、c、d任意取出两个不同字母的试
验中,有哪些基本事件? b c b d c d c d
a
树状图
解:所求的基本事件共有6个:
A {a, b} B {a, c} C {a, d } D {b, c} E {b, d } F {c, d }
1号骰子 2号骰子
1
2
3
4
5
6
1 2 3 4 5 6
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6) (2,1) (2,2) (2,3) (2,4) (2,5) (2,6) (3,1) (3,2) (3,3) (3,4) (3,5) (3,6) (4,1) (4,2) (4,3) (4,4) (4,5) (4,6) (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
有限性
等可能性
问题5:某同学随机地向一靶心进行射击,这一试验 的结果有:“命中10环”、“命中9环”、“命中8 环”、“命中7环”、“命中6环”、“命中5环”和 “不中环”。 5 你认为这是古典概型吗? 6 为什么? 7 8 9 有限性 5 6 7 8 9 10 9 8 7 6 5 9 等可能性 8 7 6 5 问题6:你能举出几个生活中的古典概型的例子吗?
“正面朝上” 两个基本事件 1 “反面朝上” 的概率都是 2 “1点”、“2 六个基本事件 有限性 点” 1 “3点”、“4 的概率都是 6 点” 只有有限个 (1) 试验中所有可能出现的基本事件的个数 “5点”、“6 点” 相等 (2) 每个基本事件出现的可能性 等可能性
试 验 1 试 验 2
任何事件(除不可能事件)都可以表示成基本事件的和
一次试验可能出现的每一个结果 称为一个 基本事件
例1 从字母a、b、c、d任意取出两个不同字母的试
验中,有哪些基本事件? b c b d c d c d
a
树状图
解:所求的基本事件共有6个:
A {a, b} B {a, c} C {a, d } D {b, c} E {b, d } F {c, d }
1号骰子 2号骰子
1
2
3
4
5
6
1 2 3 4 5 6
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6) (2,1) (2,2) (2,3) (2,4) (2,5) (2,6) (3,1) (3,2) (3,3) (3,4) (3,5) (3,6) (4,1) (4,2) (4,3) (4,4) (4,5) (4,6) (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
有限性
等可能性
问题5:某同学随机地向一靶心进行射击,这一试验 的结果有:“命中10环”、“命中9环”、“命中8 环”、“命中7环”、“命中6环”、“命中5环”和 “不中环”。 5 你认为这是古典概型吗? 6 为什么? 7 8 9 有限性 5 6 7 8 9 10 9 8 7 6 5 9 等可能性 8 7 6 5 问题6:你能举出几个生活中的古典概型的例子吗?
人教A版高中数学选择性必修第三册 组合与组合数 (课件)

(1)以其中2个点为端点的有向线段共有多少条?
(2)以其中2个点为端点的线段共有多少条?
分析:(1)确定一条有向线段,不仅要确定两个端点,还要考虑他们的顺序是排列问题;
(2)确定一条线段,只需确定两个端点,而不需要考虑它们的顺序是组合问题.
解:(1)一条有向线段的两个端点,要分起点和终点,以平面内4个点中的2个为端
概念辨析
1.校门口停放着9辆共享自行车,其中黄色、红色和绿色的各有3辆,下面的问题是排列
问题,还是组合问题?
(1)从中选3辆,有多少种不同的方法?
(2)从中选2辆给3位同学有多少种不同的方法?
(1)与顺序无关,是组合问题;
(2)选出2辆给3位同学是有顺序的,是排列问题。
典例解析
例5.平面内有A,B,C,D共4个点.
跟踪训练
98
199
跟踪训练 1. (1)计算:①3C83 -2C52 + C88 ;②C100
+ C200
.
+1
(2)求证:C+1 + C-1 +2C = C+2
m!
=
n!
,这里 n,m∈N*,
m!(n-m)!
典例解析
例6.计算:
3
10
0
7
(1)10
;(2)10
;(3)10
;(4)10
.
解:根据组合数公式,可得
3
(1) C10
7
(2) C10
(3)
10
C10
=
A310
A33
=
10!
7! 10−7 !
=
A10
10
A10
10
人教A版高中数学选择性必修第三册6.2排列与组合_教学课件

(4)某商场有四个大门,若从一个大门进去,购买物品后,再从另一个大门出 来,不同的出入方式有多少种? (5)有红球、黄球、白球各一个,现从这三个小球中任取两个,分别放入甲、乙 两个盒子里,有多少种不同的放法? 【思维导引】与“顺序”有关是排列问题,与“顺序”无关不是排列问题.
【解析】(1)不是.加法运算满足交换律,所以选出的2个元素做加法时,与两个 元素的位置无关,所以不是排列问题. (2)是.由于取出的两数组成的点的坐标与哪一个数为横坐标,哪一个数为纵坐 标的顺序有关,所以这是一个排列问题. (3)不是.因为任何一种从10名同学中抽取2名同学去学校开座谈会的方式不需要 考虑两个人的顺序,所以这不是排列问题.
3.书架上原来并排放着5本不同的书,现要再插入3本不同的书,那么不同的插 法共有________种(请用数字作答). 【解析】我们可以一本一本插入,先插入一本可以在原来5本书形成的6个空隙中 插入,共有6种插入方法;同理再插入第二本共有7种插入方法,插入第三本共有 8种插入方法,所以共有6×7×8=336(种)不同的插法. 答案:336
课堂素养达标
1.从2,3,5,7四个数中任选两个分别相除,则得到的结果有( ) A.6个 B.10个 C.12个 D.16个 【解析】选C.从2,3,5,7四个数中任选两个数分别相除,被除数有4种不同选 法,除数有3种不同选法,所以共有4×3=12个.
2.由1,2,3,4,5组成没有重复数字且1,2都不与5相邻的五位数的个数是 ________. 【解析】先排3,4有2种排法,再插空排5有3种排法,再插空排1有2种排法,插 空排2有3种排法,所以共有2×3×2×3=36个. 答案:36
(3)第一问不是排列问题,第二问是排列问题.从5个数中取3个数,与顺序无 关;若这3个数字组成不同的三位数,则与顺序有关.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
输入、输出 表示算法的输入和输出的信
框
息
处理框(执 赋值、计算 行框)
判断框
判断一个条件是否成立,用 “是”、“否”或“Y”、 “N”标明
6
二、程序框图
1、顺序结构
步骤n 步骤n+1
2、条件结构
先做后判, 否去循环
满足条件? 否 是
步骤A
步骤B
满足条件? 否
先判是 后做, 步是骤去A 循环
3、循环结构
S Si
i i1
i 100?
是
输出S
直到型循环语句 S=S+i
否
i=i+1
LOOP UNTIL i>100
PRINT S
结束
END
循环体
否
条件
是
DO
循环体
LOOP UNTIL 条件
20
结束Βιβλιοθήκη END17练:编写一程序,求实数X的绝对值。
开始
程序:
输入X 条件结构: INPUT X 条件语句:
X≥0 N
Y 输出X
输出-X
IF X>=0 THEN PRINT X
ELSE PRINT -X
END IF
结束
END
18
当型循环语句
练:设计一算法,求和1+2+3+ … +100。
程序框图: 程序语句:
程序框图如下:
开始
当型循环结构
i=1
循环体
条件 是
否
s=0
i<=100? 否 输出s
结束
i=i+1 是 s=s+i
12
三.五种基本算法语句
语句
一般格式
1.输入 语句
INPUT “提示内容”;变量
主要功能
可对程序中 的变量赋值
说明
(1)提示内容和它后面 的“;”可以省略 (2)一个语句可以给多个变
量赋值,中间用“,”分隔
循环体
满足条件? 是
循环体
否
满足条件? 是
否
7
二、程序框图
1、顺序结构
设计一算法,求和1+2+3+ … +100, 并画出程序框图。
算法:
第一步:取n=100; 第二步:计算 n(n 1);
2
第三步:输出结果。
开始 输入n=100 s=(n+1)n/2
输出s 结束
8
二、程序框图
2、条件结构
循环体
开始
i 1
S 0 当型循环结构
i=1 S=0
WHILE i<=100
i i1
SSi i 100? 是
否 输出S
S=S+i 当型循环语句 i=i+1
WEND
PRINT S
结束
END
条件 是
否
WHILE 条件 循环体
WEND
19
开始
i 1
i=1
S 0
直到型循环结构
S=0
DO
②UNTIL语句
DO 循环体 LOOP UNTIL 条 件
满足条件? 否
循环体 是
循环体
满足条件? 是
否
15
两种循环结构有什么差别?
While(当型)循环
A P 成立
不成立
先判断 后执行
先判断指定的条件是否为真, 若条件为真,执行循环条件, 条件为假时退出循环。
Until(直到型)循环
A P 不成立
4
二、程序框图
用程序框、流程线及文字说明来表示算 法的图形称为程序框图,它使算法步骤显得 直观、清晰、简明.
○
终端框 输入、 处理框 (起止框) 输出框 (执行框) 判断框 流程线 连接点
5
程序框图又称流程图,是一种用规定的图形,指向线及 文字说明来准确、直观地表示算法的图形。
程序框
名称
功能
终端框(起 表示一个算法的起始和结束 止框)
设计一个算法,求数x的绝对值,并画出程序框图。
算法分析:实数X的绝对值
x (x 0) x x (x 0)
算法: 第一步:输入x; 第二步:如果x≥0; 则输出x;否则输出 -x。
开始
输入x
N
x≥0
Y
输出x
输出-x
结束
9
二、程序框图
3、循环结构
直到型循环结构
当型循环结构
A
A
否
2.输出 PRINT “提示内容”;表达式 语句
3.赋值 语句
变量=表达式
(3)无计算功能
(1)表达式可以是变量,
可输出表达式 的值,计算
计算公式,或系统信息 (2)一个语句可以输入多
个表达式,中间用“,”分隔 (3)有计算功能
(1)“=”的右侧必须是表达
可对程序中 式,左侧必须是变量
的变量赋值, 计算
第一章 算法初步
1
算法知识结构:
基本概念 表示方法
自然语言 程序框图
输入、输出语句 赋值语句
算 法
基本结构
基本算法语句
顺序结构 条件结构 循环结构
条件语句 循环语句
应用
辗转相除法和更相减损数 秦九韶算法 进位制
2
算法的定义:
通常指可以用计算机来解决的某一类 问题的程序或步骤,这些程序或步骤必 须是明确和有效的,而且能够在有限步 之内完成。 算法最重要的特征: 1.有序性 2.确定性 3.有限性
P
是
是
P
否
(A)
(B)
直到型循环结构对应的程序框图是 当型循环结构对应的程序框图是
A
P否
是
(C) A D
A P是
否
(D)
10
设计一个计算1+2+3+……+100的值的算法,并画出程序框图。
算法:
程序框图如下:
第一步:令i=1,s=0;
第二步:s=s+i
第三步:i=i+1;
第四步: 直到i>100时,输出S,
3
算法的基本特点
1、有限性
一个算法应包括有限的操作步骤,能在执 行有穷的操作步骤之后结束。
2、确定性 算法的计算规则及相应的计算步骤必须是唯 一确定的,既不能含糊其词,也不能有二义 性。
3、有序性 算法中的每一个步骤都是有顺序的,前一步 是后一步的前提,只有执行完前一步后,才 能执行后一步,有着很强逻辑性的步骤序列。
成立
先执行 后判断
先执行循环体,然后再检查条 件是否成立,如果不成立就重 复执行循环体,直到条件成立 退出循环。
16
编写程序,求和1+2+3+ … +n。
顺序结构:
开始
程序语句:
输入n s=(n+1)n/2
输出s
输入语句 赋值语句 输出语句
INPUT n
变量=表达式
s=(n+1) * n/2
PRINT “S=” ; S
结束算法,否则返回第二步。
开始 i=1 s=0
循环结构
s=s+i
循环体
否
条件
是
直到型循环结构
i=i+1
i>100? 是
输出s
结束
11
设计一个计算1+2+3+……+100的值的算法,并画出程序框图。
算法:
第一步:令i=1,s=0; 第二步:若i<=100成立,则执行第三步;否则,输出s,结束算法; 第三步:s=s+i; 第四步:i=i+1,返回第二步。
(2)一个语句只能给一个 变量赋
(3)有计算功能
13
IF-THEN-ELSE格式
IF 条件 语句1
ELSE 语句2
END IF
THEN
IF-THEN格式
IF 条件 THEN 语句 END IF
满足条件? 是
语句1
否 语句2
满足条件? 否
是 语句
14
①WHILE语句
WHILE 条件 循环体 WEND
