同角三角函数的化简与证明
同角三角函数的基本关系式课件

行化简。
转换函数形式
通过同角三角函数的关系式,可 以实现三角函数的转换,如正弦 与余弦、正切与余切之间的转换。
证明恒等式
利用同角三角函数的基本关系式, 可以证明各种三角恒等式。
在解决实际问题中的应用
物理问题求解
在物理问题中,经常需要用到三角函数的知识,同角三角函数的 基本关系式是解决这类问题的重要工具。
03
代数证明法
通过代数运算和恒等变换, 利用已知的三角恒等式推 导出同角三角函数的基本 关系式。
几何证明法
利用单位圆的性质和三角 形的相似性质,通过几何 图形和角度关系证明同角 三角函数的基本关系式。
向量证明法
利用向量的数量积和向量 模的性质,通过向量的运 算证明同角三角函数的基 本关系式。
证明过程
证明结果
同角三角函数的基本关系式
sin^2θ + cos^2θ = 1,tanθ = sinθ/cosθ,cotθ = cosθ/sinθ等。
证明结果的应用
同角三角函数的基本关系式在解三角形、求三角函数的值、 判断三角函数的单调性等方面有广泛的应用。
பைடு நூலகம்
04
同角三角函数的基本关系式应用
在解三角形中的应用
代数证明过程
通过三角恒等式的变换,将同角 三角函数的基本关系式化简为已 知的三角恒等式或基本的代数恒
等式。
几何证明过程
利用单位圆的性质,将三角函数的 角度转化为单位圆上的弧长,再利 用三角形相似性质推导出同角三角 函数的基本关系式。
向量证明过程
利用向量的数量积和向量模的性质, 将同角三角函数的基本关系式转化 为向量的运算,通过向量的运算证 明。
同角三角函数的基本关系

课题:§3.1.2 同角三角函数的基本关系(2)
学习目标:
1、通过三角函数的定义导出同角三角函数的基本关系式;
2、能运用同角三角函数的基本关系式进行三角函数的求值、化简、证明.
学习重点:同角三角函数的基本关系式的推导与证明.
学习难点:能运用同角三角函数的基本关系式进行三角函数的求值、化简、证明.
【自主学习】预习教材第115~116页,完成下列问题.
1.同角三角函数的基本关系
(1)平方关系:sin2α+cos2α=1 变形公式:sin2α=;cos2α=;
(2)商数关系:tan α=sin α
cos α变形:sin α=;cos α=.
2. (sin α+cos α)2=;(sin α-cos α)2=.
3、若设sin α+cos α=t,则sin αcos α=;
若设sin α-cos α=t,则sin αcos α=.
【预习自测】首先完成课本第115页练习第1、2、3、4题,再完成下面的问题.
【合作探究】
探究1. 已知√1+sinα
1−sinα−√1−sinα
1+sinα
=−2tanα,试确定使等式成立的角α的集合。
探究2.已知sinα=−3
5
,且α是第四象限角,求tanα[cos(3π−α)−sin(5π+α)]的值。
探究4.证明:2(sinα−cosα)1+sinα+cosα=cosα
1+sinα−sinα1+cosα .
【基础检测】
1. 已知α是第二象限角,则√1−cos 2α+2√1−sin 2αcosα
=。
(完整版)三角函数化简求值证明技巧
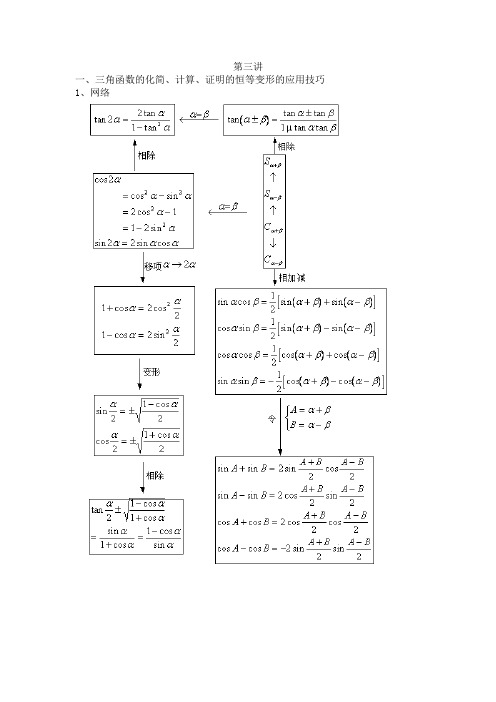
第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结(1)变换函数名对于含同角的三角函数式,通常利用同角三角函数间的基本关系式及诱导公式,通过“切割化弦”,“切割互化”,“正余互化”等途径来减少或统一所需变换的式子中函数的种类,这就是变换函数名法.它实质上是“归一”思想,通过同一和化归以有利于问题的解决或发现解题途径。
【例1】已知θ同时满足和,且a、b 均不为0,求a、b的关系。
练习:已知sin(α+β)=,cos(α-β)=,求的值。
2)变换角的形式对于含不同角的三角函数式,通常利用各种角之间的数值关系,将它们互相表示,改变原角的形式,从而运用有关的公式进行变形,这种方法主要是角的拆变.它应用广泛,方式灵活,如α可变为(α+β)-β;2α可变为(α+β)+(α-β);2α-β可变为(α-β)+α;α/2可看作α/4的倍角;(45°+α)可看成(90°+2α)的半角等等。
【例2】求sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值。
练习已知,求的值【例3】已知sinα=Asin(α+β)(其中cosβ≠A),试证明:tan(α+β)=提示:sin[(α+β)-β]=Asin (α+β)(3)以式代值利用特殊角的三角函数值以及含有1的三角公式,将原式中的1或其他特殊值用式子代换,往往有助于问题得到简便地解决。
这其中以“1”的变换为最常见且最灵活。
“1”可以看作是sin2x+cos2x, sec2x-tan2x, csc2x -cot2x,tanxcotx, secxcosx, tan45°等,根据解题的需要,适时地将“1”作某种变形,常能获得较理想的解题方法。
【例4】化简:(4)和积互化积与和差的互化往往可以使问题得到解决,升幂和降次实际上就是和积互化的特殊情形。
这往往用到倍、半角公式。
同角三角函数的基本关系

1.2.2 同角三角函数的基本关系 学习目标 1.能通过三角函数的定义推导出同角三角函数的基本关系式.2.理解同角三角函数的基本关系式.3.能运用同角三角函数的基本关系式进行三角函数式的化简、求值和证明.知识点 同角三角函数的基本关系式1.同角三角函数的基本关系式(1)平方关系:sin 2α+cos 2α=1.(2)商数关系:tan α=sin αcos α ⎝⎛⎭⎫α≠k π+π2,k ∈Z . 2.同角三角函数基本关系式的变形(1)sin 2α+cos 2α=1的变形公式sin 2α=1-cos 2α;cos 2α=1-sin 2α.(2)tan α=sin αcos α⎝⎛⎭⎫α≠k π+π2,k ∈Z 的变形公式 sin α=cos αtan α;cos α=sin αtan α.1.sin 2α+cos 2β=1.( × )提示 在同角三角函数的基本关系式中要注意是“同角”才成立,即sin 2α+cos 2α=1.2.sin 2θ2+cos 2θ2=1.( √ ) 提示 在sin 2α+cos 2α=1中,令α=θ2可得sin 2θ2+cos 2θ2=1. 3.对任意的角α,都有tan α=sin αcos α成立.( × ) 提示 当α=π2+k π,k ∈Z 时就不成立. 4.若cos α=0,则sin α=1.( × )题型一 利用同角三角函数的关系式求值命题角度1 已知角α的某一三角函数值及α所在象限,求角α的其余三角函数值例1 (1)若sin α=-513,且α为第四象限角,则tan α的值为( ) A.125 B .-125 C.512 D .-512考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值答案 D解析 ∵sin α=-513,且α为第四象限角,∴cos α=1213, ∴tan α=sin αcos α=-512,故选D. (2)已知sin α+cos α=713,α∈(0,π),则tan α= . 考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值答案 -125解析 ∵sin α+cos α=713, ∴(sin α+cos α)2=49169, 即2sin αcos α=-120169<0, 又α∈(0,π),则sin α>0,cos α<0,∴α∈⎝⎛⎭⎫π2,π,故sin α-cos α=(sin α+cos α)2-4sin αcos α=1713, 可得sin α=1213,cos α=-513,tan α=-125. 反思感悟 (1)同角三角函数的关系揭示了同角三角函数之间的基本关系,其常用的用途是“知一求二”,即在sin α,cos α,tan α三个值之间,知道其中一个可以求其余两个.解题时要注意角α的象限,从而判断三角函数值的正负.(2)已知三角函数值之间的关系式求其它三角函数值的问题,我们可利用平方关系或商数关系求解,其关键在于运用方程的思想及(sin α±cos α)2=1±2sin αcos α的等价转化,找到解决问题的突破口.跟踪训练1 已知tan α=43,且α是第三象限角,求sin α,cos α的值. 考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值解 由tan α=sin αcos α=43,得sin α=43cos α.① 又sin 2α+cos 2α=1,②由①②得169cos 2α+cos 2α=1,即cos 2α=925. 又α是第三象限角,∴cos α=-35,sin α=43cos α=-45. 命题角度2 已知角α的某一三角函数值,未给出α所在象限,求角α的其余三角函数值例2 已知cos α=-817,求sin α,tan α的值. 考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值解 ∵cos α=-817<0,且cos α≠-1, ∴α是第二或第三象限角.(1)当α是第二象限角时,则sin α=1-cos 2α=1-⎝⎛⎭⎫-8172=1517, tan α=sin αcos α=1517-817=-158. (2)当α是第三象限角时,则sin α=-1-cos 2α=-1517,tan α=158. 反思感悟 利用同角三角函数关系式求值时,若没有给出角α是第几象限角,则应分类讨论,先由已知三角函数的值推出α的终边可能在的象限,再分类求解.跟踪训练2 已知cos α=-45,求sin α和tan α. 考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值解 sin 2α=1-cos 2α=1-⎝⎛⎭⎫-452=925, 因为cos α=-45<0, 所以α是第二或第三象限角,当α是第二象限角时,sin α=35, tan α=sin αcos α=-34; 当α是第三象限角时,sin α=-35, tan α=sin αcos α=34. 题型二 齐次式求值问题例3 已知tan α=2,求下列代数式的值.(1)4sin α-2cos α5cos α+3sin α;(2)14sin 2α+13sin αcos α+12cos 2α. 考点 运用基本关系式化简和证明题点 运用基本关系式化简、求值解 (1)原式=4tan α-25+3tan α=611. (2)原式=14sin 2α+13sin αcos α+12cos 2αsin 2α+cos 2α=14tan 2α+13tan α+12tan 2α+1=14×4+13×2+125=1330. 反思感悟 (1)关于sin α,cos α的齐次式,可以通过分子、分母同除以cos α或cos 2α转化为关于tan α的式子后再求值.(2)假如代数式中不含分母,可以视分母为1,灵活地进行“1”的代换,由1=sin 2α+cos 2α代换后,再同除以cos 2α,构造出关于tan α的代数式.跟踪训练3 已知sin α+cos αsin α-cos α=2,计算下列各式的值. (1)3sin α-cos α2sin α+3cos α; (2)sin 2α-2sin αcos α+1.考点 运用基本关系式化简和证明题点 运用基本关系式化简、求三角函数值解 由sin α+cos αsin α-cos α=2,化简,得sin α=3cos α, 所以tan α=3.(1)原式=3×3cos α-cos α2×3cos α+3cos α=8cos α9cos α=89. (2)原式=sin 2α-2sin αcos αsin 2α+cos 2α+1 =tan 2α-2tan αtan 2α+1+1=32-2×332+1+1=1310. 三角函数式的化简与证明典例 (1)化简:sin 2αtan α+cos 2αtan α+2sin αcos α. 考点 运用基本关系式化简和证明题点 运用基本关系式化简解 原式=sin 2α·sin αcos α+cos 2α·cos αsin α+2sin αcos α =sin 4α+cos 4α+2sin 2αcos 2αsin αcos α=(sin 2α+cos 2α)2sin αcos α=1sin αcos α. (2)求证:tan αsin αtan α-sin α=tan α+sin αtan αsin α. 考点 运用基本关系式化简和证明题点 运用基本关系式证明证明 ∵右边=tan 2α-sin 2α(tan α-sin α)tan αsin α=tan 2α-tan 2αcos 2α(tan α-sin α)tan αsin α=tan 2α(1-cos 2α)(tan α-sin α)tan αsin α =tan 2αsin 2α(tan α-sin α)tan αsin α=tan αsin αtan α-sin α=左边, ∴原等式成立.[素养评析] (1)三角函数式的化简技巧①化切为弦,即把正切函数都化为正弦、余弦函数,从而减少函数名称,达到化繁为简的目的.②对于含有根号的,常把根号里面的部分化成完全平方式,然后去根号达到化简的目的. ③对于化简含高次的三角函数式,往往借助于因式分解,或构造sin 2α+cos 2α=1,以降低函数次数,达到化简的目的.(2)证明三角恒等式的过程,实质上是化异为同的过程,证明恒等式常用以下方法: ①证明一边等于另一边,一般是由繁到简.②证明左、右两边等于同一个式子(左、右归一).③比较法:即证左边-右边=0或左边右边=1(右边≠0). ④证明与已知等式等价的另一个式子成立,从而推出原式成立.(3)掌握逻辑推理的基本形式,学会有逻辑地思考问题;形成重论据、有条理、合乎逻辑的思维品质,提升逻辑推理的数学核心素养.1.若sin α=45,且α是第二象限角,则tan α的值为( ) A .-43 B.34 C .±34 D .±43考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值答案 A解析 ∵α为第二象限角,sin α=45, ∴cos α=-35,tan α=-43. 2.已知sin α=55,则sin 4α-cos 4α的值为( ) A .-35 B .-15 C.15 D.35考点 运用基本关系式求三角函数值题点 运用基本关系式化简、求三角函数值答案 A解析 sin 4α-cos 4α=(sin 2α+cos 2α)(sin 2α-cos 2α)=sin 2α-(1-sin 2α)=2sin 2α-1=2×⎝⎛⎭⎫552-1=-35. 3.(2018·江西上高第二中学高二期末)若α为第三象限角,则cos α1-sin 2α+2sin α1-cos 2α的值为( )A .3B .-3C .1D .-1考点 运用基本关系式化简和证明题点 运用基本关系式化简答案 B解析 ∵α为第三象限角,∴cos α<0,sin α<0,∴原式=-cos αcos α-2sin αsin α=-3. 4.已知tan x =-12,则sin 2x +3sin x cos x -1的值为( ) A.13B .2C .-2或2D .-2考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值答案 D5.已知:tan αtan α-1=-1,则sin α-3cos αsin α+cos α= . 答案 -53解析 由已知得:tan α=12, ∴sin α-3cos αsin α+cos α=tan α-3tan α+1=-53.1.利用同角三角函数的基本关系式,可以由一个角的一个三角函数值,求出这个角的其他三角函数值.2.利用同角三角函数的关系式可以进行三角函数式的化简,结果要求:(1)项数尽量少;(2)次数尽量低;(3)分母、根式中尽量不含三角函数;(4)能求值的尽可能求值.3.在三角函数的变换求值中,已知sin α+cos α,sin αcos α,sin α-cos α中的一个,可以利用方程思想,求出另外两个的值.4.在进行三角函数式的化简或求值时,细心观察题目的特征,灵活、恰当地选用公式,统一角、统一函数、降低次数是三角函数关系式变形的出发点.利用同角三角函数的基本关系主要是统一函数,要掌握“切化弦”和“弦化切”的方法.5.在化简或恒等式证明时,注意方法的灵活运用,常用技巧:(1)“1”的代换;(2)减少三角函数名的个数(化切为弦、化弦为切等);(3)多项式运算技巧的应用(如因式分解、整体思想等);(4)对条件或结论的重新整理、变形,以便于应用同角三角函数关系来求解.一、选择题1.已知α是第二象限角,tan α=-12,则cos α等于( ) A .-55 B .-15C .-255D .-45考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值答案 C解析 ∵α是第二象限角,∴cos α<0.又sin 2α+cos 2α=1,tan α=sin αcos α=-12,∴cos α=-255.2.下列四个结论中可能成立的是( )A .sin α=12且cos α=12B .sin α=0且cos α=-1C .tan α=1且cos α=-1D .α是第二象限角时,tan α=-sin αcos α考点 同角三角函数基本关系题点 运用基本关系式求值答案 B3.已知cos ⎝⎛⎭⎫α+π4=13,0<α<π2,则sin ⎝⎛⎭⎫α+π4等于( )A .-223 B .-23 C.23 D.223考点 运用基本关系式求值题点 运用基本关系式求值答案 D解析 ∵0<α<π2,∴π4<α+π4<3π4,∴sin ⎝⎛⎭⎫α+π4= 1-⎝⎛⎭⎫132=223.4.已知α是锐角,且tan α是方程4x 2+x -3=0的根,则sin α等于() A.45 B.35 C.25 D.15考点 同角三角函数基本关系题点 运用基本关系式求值答案 B解析 由4x 2+x -3=0得x =-1或x =34.又∵α是锐角,∴tan α>0,sin α>0, ∴tan α=34.又∵tan α=sin αcos α=34,且sin 2α+cos 2α=1,∴sin 2α+⎝⎛⎭⎫43sin α2=1,解得sin α=35.5.已知θ是第三象限角,且sin 4θ+cos 4θ=59,则sin θcos θ的值为() A.23 B .-23 C.13 D .-13考点 运用基本关系式化简、求值题点 运用基本关系式化简、求值答案 A解析 由sin 4θ+cos 4θ=59,得(sin 2θ+cos 2θ)2-2sin 2θcos 2θ=59,∴sin 2θcos 2θ=29,∵θ是第三象限角,∴sin θ<0,cos θ<0, ∴sin θcos θ=23.6.已知sin θ+cos θsin θ-cos θ=2,则sin θcos θ的值是( ) A.34 B .±310 C.310 D .-310考点 运用基本关系式化简、求值题点 运用基本关系式化简、求值答案 C解析 由条件得sin θ+cos θ=2sin θ-2cos θ, 即3cos θ=sin θ,tan θ=3,∴sin θcos θ=sin θcos θsin 2θ+cos 2θ=tan θ1+tan 2θ=31+32=310. 7.若α为第二象限角,化简tan α·1sin 2α-1等于( ) A .1 B .2 C .-1 D.12考点 运用基本关系式化简题点 运用基本关系式化简答案 C解析 tan α·1sin 2α-1=tan α·1-sin 2αsin 2α=sin αcos α·|cos α||sin α|. 因为α为第二象限的角,所以cos α<0,sin α>0,原式=sin αcos α·-cos αsin α=-1. 二、填空题8.已知tan α=-12,则1+2sin αcos αsin 2α-cos 2α= . 考点 运用基本关系式化简、求值 题点 运用基本关系式化简、求值答案 -13解析 1+2sin αcos αsin 2α-cos 2α=(sin α+cos α)2sin 2α-cos 2α=sin α+cos αsin α-cos α=tan α+1tan α-1=-12+1-12-1=12-32=-13. 9.已知α为第二象限角,则cos α·1+tan 2α+sin α·1+1tan 2α= . 考点 运用基本关系式化简题点 运用基本关系式化简答案 0解析 原式=cos αsin 2α+cos 2αcos 2α+sin αsin 2α+cos 2αsin 2α=cos α·1|cos α|+sin α·1|sin α|. 因为α是第二象限角,所以sin α>0,cos α<0,所以cos α·1|cos α|+sin α·1|sin α|=-1+1=0,即原式=0.10.(2018·九江高一检测)若sin α+cos α=2,则tan α+1tan α的值为 . 考点 运用基本关系式化简、求值题点 运用基本关系式化简、求值答案 2 11.在△ABC 中,2sin A = 3cos A ,则角A = .考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值答案 π3解析 由题意知cos A >0,即A 为锐角.将2sin A =3cos A 两边平方得2sin 2A =3cos A .∴2cos 2A +3cos A -2=0,解得cos A =12或cos A =-2(舍去), ∴A =π3. 三、解答题12.化简:1-2sin α2cos α2+1+2sin α2cos α2⎝⎛⎭⎫0<α<π2. 考点 运用基本关系式化简和证明题点 运用基本关系式化简解 原式=sin 2α2-2sin α2cos α2+cos 2α2+sin 2α2+2sin α2cos α2+cos 2α2 =⎝⎛⎭⎫cos α2-sin α22+⎝⎛⎭⎫cos α2+sin α22=⎪⎪⎪⎪cos α2-sin α2+⎪⎪⎪⎪cos α2+sin α2. ∵α∈⎝⎛⎭⎫0,π2,∴α2∈⎝⎛⎭⎫0,π4, ∴cos α2-sin α2>0,cos α2+sin α2>0, ∴原式=cos α2-sin α2+cos α2+sin α2=2cos α2. 13.已知tan 2α=2tan 2β+1,求证:sin 2β=2sin 2α-1.考点 运用基本关系式化简和证明题点 运用基本关系式化简证明 因为tan 2α=2tan 2β+1,所以tan 2α+1=2tan 2β+2,所以sin 2αcos 2α+1=2⎝⎛⎭⎫sin 2βcos 2β+1, 所以1cos 2α=2cos 2β,即cos 2β=2cos 2α, 所以1-sin 2β=2(1-sin 2α),即sin 2β=2sin 2α-1.14.若sin α+cos α=1,则sin n α+cos n α(n ∈N *)的值为 . 考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值答案 1解析 ∵sin α+cos α=1,∴(sin α+cos α)2=1,又sin 2α+cos 2α=1,∴sin αcos α=0,∴sin α=0或cos α=0.当sin α=0时,cos α=1,此时有sin n α+cos n α=1;当cos α=0时,sin α=1,也有sin n α+cos n α=1,∴sin n α+cos n α=1.15.已知sin α,cos α为方程4x 2-4mx +2m -1=0的两个实根,α∈⎝⎛⎭⎫-π2,0,求m 及α的值.考点 运用基本关系式求三角函数值 题点 运用基本关系式求三角函数值 解 因为sin α,cos α为方程4x 2-4mx +2m -1=0的两个实根, 所以Δ=16(m 2-2m +1)≥0且sin α+cos α=m ,sin αcos α=2m -14. 代入(sin α+cos α)2=1+2sin αcos α,解得m =1±32. 又因为α∈⎝⎛⎭⎫-π2,0, 所以sin α·cos α=2m -14<0,m <12, 所以sin α+cos α=m =1-32, 所以sin α=-32,cos α=12. 又因为α∈⎝⎛⎭⎫-π2,0,所以α=-π3. 所以m =1-32,α=-π3.。
同角三角函数基本关系式、三角函数的诱导公式

一、知识概述1、同角三角函数的基本关系式同角三角函数基本关系可概括为平方关系,商数关系和倒数关系,如考虑sinα,cos α,tanα,cotα与secα,cscα六个函数,还可借助如下图表形象记忆:(1)对角线上两个函数的积为1(倒数关系)(2)任一顶点的函数等于与其相邻两个顶点的函数的积(商数关系)(3)阴影部分,顶角两个函数的平方和等于底角函数的平方(平方关系)由此图可得出公式的变形形式或其他同角函数关系式.平方关系:sin2α+cos2α=1,sec2α=1+tan2α,csc2α=1+cot2α.商数关系:倒数关系:tanα·cotα=1,sinα·cscα=1,cosα·secα=1.注:课本上只介绍了其中两个重要的关系式,事实上,掌握好其余的五个关系式能在有关解题中节省过程,带来方便.2、三角函数的诱导公式公式一:sin(α+k·)=sinαcos(α+k·)=cosαtan(α+k·)=tanα其中k∈Z.公式二:sin(+α)=-sinαcos(+α)=-cosαtan(+α)=tanα公式三:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanα公式四:sin(-α)=sinαcos(-α)=-cosαtan(-α)=-tanα总结:α+k·2(k∈Z),-α,±α的三角函数,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号。
公式五:sin(-α)=cosαcos(-α)=sinα公式六:sin(+α)=cosαcos(+α)=-sinα总结:±α的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成锐角时原函数值的符号.二、重、难点知识归纳及讲解(一)利用诱导公式可以把任意角的三角函数转化为锐角三角函数,即:例1、求值:.分析:运用诱导公式,对于cot,可先求出sin,cos,然后由商数关系可求出cot.解:原式例2、设的值为()A.B.C.-1 D.1分析:利用诱导公式将条件等式和欲求式都化到α的同名三角函数上去,再利用同角三角函数基本关系式求解.解答:(二)同角三角函数关系式在求值、化简、证明中的应用.1、已知角α的某一三角函数值,可求出α的其余三角函数值.例3、已知tanα=2,求2sin2α-3sinαcosα-2cos2α的值.分析:由平方关系知1=sin2α+cos2α,可把式子的分母看成sin2α+cos2α,然后分子分母同除以cos2α,可得.解:2、利用同角三角函数关系式进行化简:化简结果的基本要求:(1)函数个数尽可能少;(2)次数尽可能低;(3)项数尽可能少;(4)尽可能地去掉根号;(5)尽可能地不含分母;(6)能求出值的要求出值来.例4、若sinαcosα<0,sinαtanα<0,化简:.分析:要想去掉根号,就应考虑将被开方数配成完全平方的形式.解:∵sinαcosα<0,sinαtanα<0.∴α是第二象限角.故是第一或第三象限角.原式若是第一象限角,此时1±sin>0,cos>0. 原式=若是第三象限角,此时1±sin>0,cos<0. 原式=.3、利用同角关系式进行三角恒等式的证明.证明三角恒等式的方法较多,既可由一边证向另一边,也可先证得另一个等式成立,从而得出要证的等式,还可用比较法证明等,关键是要依题而定。
同角三角函数化简求值

同角三角函数化简求值同角三角函数是指角度相同的三角函数,包括正弦、余弦、正切、余切、正割、余割等。
在化简和求值过程中,经常需要利用同角三角函数的性质进行变形和简化。
例如,常用的同角三角函数公式包括:1. 余角公式:sin(90°-x)=cos(x),cos(90°-x)=sin(x)2. 倍角公式:sin(2x)=2sin(x)cos(x),cos(2x)=cos^2(x)-sin^2(x)3. 和差角公式:sin(x±y)=sin(x)cos(y)±cos(x)sin(y),cos(x±y)=cos(x)cos(y)sin(x)sin(y)利用这些公式,可以化简和求解许多三角函数的式子和值。
例如,如果要求sin(120°),可以利用三角函数的周期性和正弦函数的奇偶性:sin(120°)=sin(120°-360°)=-sin(-240°)=-sin(240°) 再利用余角公式,得到:sin(240°)=cos(90°-240°)=-cos(150°)最后,利用正弦和余弦函数的周期性和奇偶性,得到:cos(150°)=cos(360°-150°)=cos(210°)因此,sin(120°)=-cos(150°)=-cos(360°-150°)=-cos(210°)这样,我们就成功地化简求解了sin(120°)的值。
除了以上的公式外,还有一些特殊角的三角函数值也需要掌握,例如30°、45°、60°等角度的正弦、余弦、正切值。
通过熟悉这些特殊角的值和同角三角函数的公式,我们可以更加轻松地进行三角函数的化简和求值。
三角函数中同角三角函数关系的推导过程

三角函数中同角三角函数关系的推导过程三角函数是数学中重要的概念之一,它描述了角度与其对应的三角比之间的关系。
在三角函数的研究中,同角三角函数关系是其中一个重要的推导过程。
本文将详细介绍同角三角函数关系的推导过程。
在开始推导之前,先明确一些基本概念。
在平面直角坐标系中,设有一个角度θ,该角度的终边与单位圆交于点P(x, y),其中x和y分别表示P点的横坐标和纵坐标。
根据三角函数定义,我们可以得到以下三个关系式:1. 正弦函数(Sine Function):sin(θ) = y2. 余弦函数(Cosine Function):cos(θ) = x3. 正切函数(Tangent Function):tan(θ) = y / x接下来,我们将推导出其他同角三角函数关系。
1. 同角余弦函数推导:我们已知余弦函数的定义为cos(θ) = x,可以将此式改写为:cos(θ) = 1 / sec(θ)其中sec(θ)为函数secant(θ),表示θ角的余割。
因此,同角余弦函数推导为:cos(θ) = 1 / sec(θ)2. 同角正切函数推导:我们已知正切函数的定义为tan(θ) = y / x,可以将此式改写为:tan(θ) = sin(θ) / cos(θ)其中sin(θ)和cos(θ)分别表示θ角的正弦和余弦。
因此,同角正切函数推导为:tan(θ) = sin(θ) / cos(θ)3. 同角余切函数推导:我们已知余切函数的定义为cot(θ) = 1 / tan(θ),可以将此式改写为:cot(θ) = cos(θ) / sin(θ)其中cos(θ)和sin(θ)分别表示θ角的余弦和正弦。
因此,同角余切函数推导为:cot(θ) = cos(θ) / sin(θ)4. 同角正割函数推导:我们已知正割函数的定义为sec(θ) = 1 / cos(θ),可以将此式改写为:sec(θ) = 1 / cos(θ)其中cos(θ)表示θ角的余弦。
高一数学同角三角函数的基本关系式知识精讲

高一数学同角三角函数的基本关系式【本讲主要内容】同角三角函数的基本关系式【知识掌握】 【知识点精析】1. 同角三角函数的基本关系式(1)平方关系:sin cos tan sec cot csc 222222111αααααα+=+=+=,, (2)商数关系:tan sin cos cot cos sin αααααα==, (3)倒数关系:tan cot cos sec sin csc αααααα⋅=⋅=⋅=111,,应用公式时需注意:①同角三角函数的基本关系式揭示了“同角不同名”的三角函数的运算规律,等式中涉及的角是同一个角,如sin cos 22331αα+=,tan()cot()-⋅-=1001001,而sin cos 221αβ+=就不一定成立。
②利用平方关系进行开方运算,要注意结果的符号,必要时,要进行分类讨论。
③这些关系式是对使它们有意义的那些角而言的。
如:tan sin cos ααα=是当αππ≠+∈k k z 2()时才有意义。
④在计算、化简、证明三角函数式时常用技巧有:i )“1”的代换。
根据需要,常将算式中的“1”用“sin cos 22αα+”;“sec tan 22αα-”;“sin csc αα⋅”;“tan cot αα⋅”代换。
ii )切化弦。
利用商数把正切、余切化为正弦、余弦函数。
iii )整体代换。
将算式适当变形使条件可以整体代入或将条件适当变形找出与算式之间的关系。
⑤公式应用非常广泛,因此除牢记公式原型外,还应注意公式的逆用,变形用。
如:cos sin 221αα=-,sin tan cos ααα=⋅,sin cos (sin cos )αααα⋅=+-212等等。
2. 同角三角函数基本关系式的应用(1)已知一个角的某个三角函数值,求它的其他三角函数值。
①尽可能地确定α所在的象限,以便确定三角函数值的符号。
②尽量避免使用平方关系(在一般情况下只能使用一次)。
同角三角函数的基本关系

探究四
利用平方关系求值
【典例】若sinA= ,且A是三角形的一个内角,求 的值.
【变式训练】已知sinα+cosα= ,α∈(0,π),则tanα=.
三、巩固诊断
1.已知角α是第二象限角,则下列各式成立的是()
《
一、学习目标
1.能通过三角函数的定义推导出同角三角函数的基本关系.
2.理解同角三角函数的基本关系.
3.能运用同角三角函数的基本关系进行三角函数式的化简、求值和证明.
4.体会逻辑推理的过程,加强数学运算能力的培养.
二、思维导图
关Байду номын сангаас式
文字表述
平方
关系
sin2α+cos2α=1
同一个角α的正弦、余弦的平方和等于1
②sinα=;cosα=
4.想一想:“同角”一词的含义是什么?
课堂探究
二、sinα+cosα,sinα-cosα,sinαcosα之间的关系
1.(sinα±cosα)2=1±2sinαcosα.2.(sinα+cosα)2+(sinα-cosα)2=2.
探究一利用同角三角函数的基本关系求值
【例1】(1)若sinα=- ,且角α是第三象限角,求cosα,tanα的值;
(2)若cosα= ,求tanα的值;
(3)若tanα=- ,求sinα的值.
【变式训练1】已知sinθ= ,求cosθ,tanθ的值.
探究二
化简或证明三角恒等式
【例2】(1)化简: ;(2)求证: .
【变式训练2】(1)已知sinα·tanα<0,化简: .(2)求证: .
第一章 1.2.3同角三角函数的基本关系式(二)

填一填·知识要点、记下疑难点
1.2.3(二)
本 课 时 栏 目 开 关
1.同角三角函数的基本关系 2 2 2 cos2α ;1 (1)平方关系: sin α+cos α =1.变形:1-sin α= 2 -cos2α= sin α . sin α cos (2)商数关系:tan α= .变形:sin α= tan α· α ;cos α cos α sin α = tan α . 2.(sin α+cos α)2= 1+2sin αcos α ; (sin α-cos α)2= 1-2sin αcos α . t2-1 3.若设 sin α+cos α=t,则 sin αcos α= 2 ; 1-t2 若设 sin α-cos α=t,则 sin αcos α= 2 .
=左边.
tan α· α sin sin α 方法二 左边= = , tan α-tan αcos α 1-cos α tan α+tan αcos α 1+cos α 右边= = tan αsin α sin α 1-cos2α sin2α sin α = = = . sin α1-cos α sin α1-cos α 1-cos α ∴左边=右边,原等式成立.
研一研·问题探究、课堂更高效
1-cos4α-sin4α 跟踪训练 1 化简: . 1-cos6α-sin6α
1-cos4α-sin4α 解 原式= 1-cos6α-sin6α 1-cos2α1+cos2α-sin4α = 1-cos2α1+cos2α+cos4α-sin6α sin2α1+cos2α-sin4α = 2 sin α1+cos2α+cos4α-sin6α 1+cos2α-sin2α = 1+cos2α+cos4α-sin4α 2cos2α = 1+cos2α+cos2α+sin2αcos2α-sin2α 2cos2α 2cos2α 2 = = 2 = . 1+cos2α+cos2α-sin2α 3cos α 3
同角三角函数基本关系式xiangxi

解:
由sin2 cos2 1得
4 3 cos 1 sin2 1 ( ) 2 5 5
因 为是 第 二 象 限 角 , cos 0, 所 以
3 cos 5
tan sin 4 5 4 ( ) ( ) cos 5 3 3
y
温故知新
问题1. 如图1,设 是一个任意角, 它的 终边 与单位圆交于 P( x, y ),那么由三 角函数的定义可知:
(x,y) 1
M
P
A (1, 0 )
x
O
T
图1
sin
y ; cos x
MP ;余弦线
y ( x 0) ; tan x
AT .
问题2. 图1中的三角函数线是: 正弦线
[错因分析]
[ 思路分析 ]
该解法忽略了角θ的取值范围.根据0<θ<π这
在已知 sinθcosθ 的值求 sinθ + cosθ 或 sinθ -
一条件,可以确定sinθ-cosθ的符号. cosθ的值时需开方,因此要根据角的范围确定正负号的选择. 1 1 2 [ 正解 ] ∵ sinθ + cosθ = 5 , ∴ (sinθ + cosθ) = 25 ,解得
M
y
1、探究同角正弦、余弦之间的关系
O x
图2
问题⑵
当角的终边在坐标轴上时,关系式是否还成立?
当角 的终边在 x 轴上时,
当角
sin 2 co s 2 0 1 1 sin 2 co s 2 1 0 1
平方关系
的终边在 y轴上时,
结论:对于任意角 ( R),都有 sin2 α cos2 α 1
同角三角函数关系

1.2.2 同角三角函数的基本关系同角三角函数的基本关系式 1.公式(1)平方关系: sin 2α+cos 2α=1. (2)商数关系: sin αcos α=tan α. 2.公式推导如图,以正弦线MP 、余弦线OM 和半径OP 的长作为直角三角形三边长,而且OP =1.由勾股定理,得OM 2+MP 2=1,因此x 2+y 2=1, 即sin 2α+cos 2α=1.根据三角函数的定义,当α≠k π+π2(k ∈Z )时,有sin αcos α=tan α.这就是说,同一个角α的正弦、余弦的平方和等于1,商等于角α的正切. [知识点拨]对同角三角函数基本关系式的理解(1)注意“同角”,这里“同角”有两层含义,一是“角相同”,二是对“任意”一个角(在使函数有意义的前提下)关系式都成立,即与角的表达形式无关,如sin 23α+cos 23α=1成立,但是sin 2α+cos 2β=1就不一定成立.(2)sin 2α是(sin α)2的简写,读作“sin α的平方”,不能将sin 2α写成sin α2,前者是α的正弦的平方,后者是α2的正弦,两者是不同的,要弄清它们的区别,并能正确书写.(3)同角三角函数的基本关系式是针对使三角函数有意义的角而言的,sin 2α+cos 2α=1对一切α∈R 恒成立,而tan α=sin αcos α仅对α≠π2+k π(k ∈Z )成立.3.常用的等价变形sin 2α+cos 2α=1⇒⎩⎪⎨⎪⎧sin 2α=1-cos 2α,cos 2α=1-sin 2α,sin α=±1-cos 2α,cos α=±1-sin 2α;tan α=sin αcos α⇒⎩⎪⎨⎪⎧sin α=tan αcos α,cos α=sin αtan α.[拓展]变形公式的应用要注意哪些方面?(1)使用变形公式sin α=±1-cos 2α,cos α=±1-sin 2α时,“±”号是由α的终边所在的象限确定的,而对于其他形式的变形公式就不必考虑符号问题.(2)对这些关系式不仅要牢牢掌握,还要能灵活运用(正用、逆用、变形应用). Y 预习自测u xi zi ce1.已知sin α=78,cos α=158,则tan α等于( D )A .78B .158C .157D .715152.(2015·福建文)若sin α=-513,且α为第四象限角,则tan α的值等于( D ) A .125B .-125C .512D .-5123.化简1-sin 2440°=__cos80°__.4.化简sin 2α+sin 2β-sin 2αsin 2β+cos 2αcos 2β=__1__.H 互动探究解疑u dong tan jiu jie yi命题方向1 ⇨根据同角三角函数关系求值 典例1 (1)已知sin α=15,求cos α,tan α的值;(2)已知cos α=-35,求sin α,tan α的值.[解析] (1)∵sin α=15>0,∴α是第一或第二象限角.当α为第一象限角时,cos α=1-sin 2α=1-125=265,tan α=sin αcos α=612;当α为第二象限角时,cos α=-265,tan α=-612.(2)∵cos α=-35<0,∴α是第二或第三象限角.当α是第二象限角时,sin α>0,tan α<0, ∴sin α=1-cos 2α=1-(-35)2=45,tan α=sin αcos α=-43;当α是第三象限角时,sin α<0,tan α>0,∴sin α=-1-cos 2α=-1-(-35)2=-45,tan α=sin αcos α=43.『规律总结』 在使用开平方关系sin α=±1-cos 2α和cos α=±1-sin 2α时,一定要注意正负号的选取,确定正负号的依据是角α所在的象限,如果角α所在的象限是已知的,则按三角函数在各个象限的符号来确定正负号;如果角α所在的象限是未知的,则需要按象限进行讨论.〔跟踪练习1〕已知sin α=-45,并且α是第三象限的角,求cos α、tan α的值.[解析] ∵sin 2α+cos 2α=1, ∴cos 2α=1-sin 2α=1-(-45)2=925.又∵α是第三象限角,∴cos α<0 即cos α=-925=-35, ∴tan α=sin αcos α=(-45)×(-53)=43.命题方向2 ⇨弦化切求值 典例2 已知tan α=3. (1)求sin α和cos α的值; (2)求3sin α-cos α2cos α+sin α的值;(3)求sin 2α-3sin αcos α+1的值.[思路分析] tan α=3,即sin α=3cos α,结合sin 2α+cos 2α=1,解方程组可求出sin α和cos α;对于(2),注意到分子分母都是sin α与cos α的一次式,可分子分母同除以cos α化为tan α的表达式;对于(3),如果把分母视作1,进行1的代换,1=sin 2α+cos 2α然后运用(2)的方法,分子分母同除以cos 2α可化为tan α的表达式,也可以将sin α=3cos α代入sin 2α+cos 2α=1中求出cos 2α,把待求式消去sin α,也化为cos 2α的表达式求解.[解析] (1)tan α=3=sin αcos α>0,∴α是第一或第三象限角.当α是第一象限角时,结合sin 2α+cos 2α=1,有 ⎩⎨⎧sin α=31010cos α=1010.当α是第三象限角时,结合sin 2α+cos 2α=1,有⎩⎨⎧sin α=-31010cos α=-1010.(2)∵tan α=3,∴3sin α-cos α2cos α+sin α=3tan α-12+tan α=85.(3)∵tan α=3,sin 2α+cos 2α=1, ∴原式=sin 2α-3sin αcos α+11=2sin 2α-3sin α·cos α+cos 2αsin 2α+cos 2α=2tan 2α-3tan α+11+tan 2α=2×32-3×3+11+32=1.『规律总结』 1.若已知tan α=m ,求形如a sin α+b cos αc sin α+d cos α(或a sin 2α+b cos 2αc sin 2α+d cos 2α)的值,其方法是将分子、分母同除以cos α(或cos 2α)转化为tan α的代数式,再求值,如果先求出sin α和cos α的值再代入,那么运算量会很大,问题的解决就会变得繁琐.2.形如a sin 2α+b sin αcos α+c cos 2α通常把分母看作1,然后用sin 2α+cos 2α代换,分子、分母同除以cos 2α再求解.〔跟踪练习2〕已知tan α=-12,求下列各式的值:(1)sin α+2cos α; (2)cos α-5sin α3cos α+sin α; (3)sin 2α-sin αcos α-3cos 2α5sin αcos α+sin 2α+1;(4)2sin 2α-sin αcos α+cos 2α.[解析] (1)tan α=sin αcos α=-12,∴cos α=-2sin α又sin 2α+cos 2α=1,∴sin 2α+4sin 2α=1 ∴sin 2α=15,∴sin α=±55当α为第二象限角时,sin α=55,cos α=-255, sin α+2cos α=-355,当α为第四象限角时,cos α=255,sin α=-55,sin α+2cos α=355.(2)cos α-5sin α3cos α+sin α=1-5tan α3+tan α=1-5×(-12)3-12=75.(3)sin 2α-sincos α-3cos 2α5sincos α+sin 2α+1=sin 2α-sin αcos α-3cos 2α5sin αcos α+2sin 2α+cos 2α=tan 2α-tan α-32tan 2α+5tan α+1=(-12)2-(-12)-32(-12)2+5(-12)+1=94. (4)2sin 2α-sin αcos α+cos 2α=2sin 2α-sin αcos α+cos 2αsin 2α+cos 2α=2tan 2α-tan α+1tan 2α+1=85.命题方向3 ⇨化简三角函数式典例3 (1)1-2sin10°cos10°sin10°-1-sin 210°;(2)1-cos 4α-sin 4α1-cos 6α-sin 6α.[思路分析] (1)把二次根式中的被开方式化为完全平方式.(2)中所含角α的三角函数次数相对较高,且分子、分母含常数“1”.解答本题中的(1)、(2)时应充分利用“sin 2α+cos 2α=1”这一条件.[解析] (1)原式=(cos10°-sin10°)2sin10°-cos 210°=|cos10°-sin10°|sin10°-cos10°=cos10°-sin10°sin10°-cos10°=-1.(2)解法一:原式=(cos 2α+sin 2α)2-cos 4α-sin 4α(cos 2α+sin 2α)3-cos 6α-sin 6α=2cos 2α·sin 2α3cos 2α·sin 2α(cos 2α+sin 2α)=23. 解法二:原式=1-(cos 4α+sin 4α)1-(cos 6α+sin 6α)=1-[(cos 2α+sin 2α)2-2sin 2αcos 2α]1-(cos 2α+sin 2α)(cos 4α-cos 2αsin 2α+sin 4α) =1-1+2cos 2αsin 2α1-[(cos 2α+sin 2α)2-3cos 2αsin 2α] =2cos 2αsin 2α3cos 2αsin 2α=23. 『规律总结』 三角函数式的化简过程中常用的方法:(1)化切为弦,即把非正弦、非余弦的函数都化成正弦、余弦函数,从而减少函数名称,达到化简的目的.(2)对于含有根号的,常把根号下式子化成完全平方式,然后去根号,达到化简的目的. (3)对于化简含高次的三角函数式,往往借助于因式分解,或构造sin 2α+cos 2α=1,以降低函数次数,达到化简的目的.〔跟踪练习3〕已知α是第三象限角,化简:1+sin α1-sin α-1-sin α1+sin α.[解析] 1+sin α1-sin α-1-sin α1+sin α=(1+sin α)2cos 2α-(1-sin α)2cos 2α=1+sin α|cos α|-1-sin α|cos α|=2sin α|cos α|. ∵α是第三象限角,∴|cos α|=-cos α. 原式=2sin α-cos α=-2tan α, 故1+sin α1-sin α-1-sin α1+sin α=-2tan α.命题方向4 ⇨三角恒等式的证明 典例4 求证:tan αsin αtan α-sin α=tan α+sin αtan αsin α.[思路分析] 思路一右式分子分母同乘以tan α-sin α→由右式向左式转化思路二 左右两式切化弦→整理化简得证[解析] 方法一:∵右边=tan 2α-sin 2α(tan α-sin α)tan αsin α=tan 2α-tan 2αcos 2α(tan α-sin α)tan αsin α=tan 2α(1-cos 2α)(tan α-sin α)tan αsin α=tan 2αsin 2α(tan α-sin α)tan αsin α=tan αsin αtan α-sin α=左边,∴原等式成立.方法二:∵左边=tan αsin αtan α-tan αcos α=sin α1-cos α,右边=tan α+tan αcos αtan αsin α=1+cos αsin α=1-cos 2αsin α(1-cos α)=sin 2αsin α(1-cos α)=sin α1-cos α,∴左边=右边,原等式成立.『规律总结』 利用同角三角函数的基本关系证明三角恒等式 三角恒等式的证明方法非常多,其主要方法有: (1)从左向右推导或从右向左推导,一般由繁到简; (2)左右归一,即证明左右两边都等于同一个式子;(3)化异为同法,即针对题设与结论间的差异,有针对地变形,以消除差异; (4)变更命题法,如要证明a b =c d ,可证ad =bc 或证d b =ca等;(5)比较法,即设法证明“左边-右边=0”或“左边右边=1”.〔跟踪练习4〕证明下列三角恒等式: 2sin x cos x(sin x +cos x -1)(sin x -cos x +1)=1+cos x sin x .[解析] 左边=2sin x cos x[sin x +(cos x -1)][sin x -(cos x -1)]=2sin x cos x sin 2x -(cos x -1)2=sin x1-cos x =sin x (1+cos x )1-cos 2x=1+cos xsin x=右边,所以原等式成立. X 学科核心素养ue ke he xin su yang sin θ±cos θ,sin θ·cos θ三者的关系及方程思想的运用 sin θ±cos θ,sin θ·cos θ三者的关系:(1)对于三角函数式sin θ±cos θ,sin θ·cos θ之间的关系,可以通过(sin θ±cos θ)2=1±2sin θ·cos θ进行转化.(2)若已知sin θ±cos θ,sin θ·cos θ中三者之一,利用方程思想进一步可以求得sin θ,cos θ的值,从而求出其余的三角函数值.典例5 已知sin θ+cos θ=15,θ∈(0,π),求sin θ,cos θ,sin θ-cos θ,tan θ,sin 3θ+cos 3θ的值.[解析] 本题考查已知三角函数的关系式,求其他三角函数式的值.解题时先根据已知关系式求出角的范围和三角函数值,进而解决问题.∵sin θ+cos θ=15,θ∈(0,π),∴1+2sin θ·cos θ=125,∴2sin θ·cos θ=-2425<0.又θ∈(0,π),sin θ>0,∴cos θ<0,∴θ∈(π2,π).∴sin θ-cos θ>0.∵(sin θ-cos θ)2=1-2sin θ·cos θ=1+2425=4925,∴sin θ-cos θ=75,∴⎩⎨⎧sin θ+cos θ=15,sin θ-cos θ=75⇒⎩⎨⎧sin θ=45,cos θ=-35,∴tan θ=sin θcos θ=45-35=-43,sin 3θ+cos 3θ=37125.『规律总结』 在解三角函数问题时要注意题目中的隐含条件,本题就是灵活运用了平方关系,列方程求出sin θ,cos θ,使问题得解.〔跟踪练习5〕已知sin θ、cos θ是方程4x 2-4mx +2m -1=0的两个根,3π2<θ<2π,求角θ.[解析]∵⎩⎪⎨⎪⎧sin θ+cos θ=m ,sin θ·cos θ=2m -14,Δ=16(m 2-2m +1)≥0,代入(sin θ+cos θ)2=1+2sin θ·cos θ,得m =1±32.又∵3π2<θ<2π.∴sin θ·cos θ=2m -14<0,sin θ+cos θ=m =1-32,∴sin θ=-32,cos θ=12.又∵3π2<θ<2π,∴θ=5π3.Y 易混易错警示i hun yi cuo jing shi典例6 已知θ∈(0,π),sin θ+cos θ=3-12,则tan θ的值为__________. [错解] 将sin θ+cos θ=3-12两边平方,得1+2sin θcos θ=1-32,即sin θcos θ=-34,易知θ≠π2.故sin θcos θ=sin θcos θsin 2θ+cos 2θ=tan θ1+tan 2θ=-34,解得tan θ=-3或tan θ=-33. [错因分析] 题设条件sin θ+cos θ=3-12隐含sin θ>-cos θ这一条件,结合所得sin θcos θ=-34<0可进一步得到θ的范围,错解忽略了这一点,从而造成增解. [正解] 同错解,解得tan θ=-3或tan θ=-33. ∵θ∈(0,π),sin θcos θ=-34<0,∴θ∈(π2,π),由sin θ+cos θ=3-12>0可得sin θ>-cos θ,即|sin θ|>|cos θ|,故θ∈(π2,3π4),则tan θ<-1,∴tan θ=-3.[点评] 有些关于三角函数的条件求值问题,表面上角的范围不受条件限制,实际上只要对已知式稍加变形,就会推出三角函数值间的限制关系,这种限制关系本身就隐含了角的取值范围.解题时,同学们如果忽略了对已知条件中三角函数值间限制关系的挖掘,就很可能出错.〔跟踪练习6〕已知sin αcos α=18,且π<α<5π4,则cos α-sin α的值为 -2 .[解析] ∵(cos α-sin α)2=1-2sin αcos α=1-2×18=34,且π<α<5π4,∴cos α<sin α,∴cos α-sin α<0, ∴cos α-sin α=-34=-32. K 课堂达标验收e tang da biao yan shou 1.化简1-sin 23π5的结果是( C )A .cos 3π5B .sin 3π5C .-cos 3π5D .-sin 3π52.已知tan α=12,0<α<π,则sin α-cos α= -5.. [解析] 由tan α=12>0,知α为锐角,所以sin α=55,cos α=255,∴sin α-cos α=-55.3.(2016·四川资阳阳安中学月考)已知tan α=-43,则sin α+cos αsin α-cos α等于( A )A .17B .-17C .-7D .74.化简:(1sin α+1tan α)(1-cos α)=__sin α__.A 级 基础巩固一、选择题1.α是第四象限角,cos α=1213,则sin α等于( B ) A .513B .-513C .512D .-512[解析] ∵α是第四象限角,∴sin α<0. ∵⎩⎪⎨⎪⎧cos α=1213,sin 2α+cos 2α=1,∴sin α=-513.2.已知cos α=23,则sin 2α等于( A )A .59B .±59C .53D .±53[解析] sin 2α=1-cos 2α=59.3.已知α是第四象限角,tan α=-512,则sin α=( D )A .15B .-15C .513D .-513[解析] 不妨设α对应的锐角为α′,tan α′=512,构造直角三角形如图,则|sin α|=sin α′=513, ∵α为第四象限角,∴sin α<0,∴sin α=-513.4.化简:(1+tan 2α)·cos 2α等于( C ) A .-1 B .0 C .1D .2[解析] 原式=(1+sin 2αcos 2α)·cos 2α=cos 2α+sin 2α=1.5.已知sin α-3cos α=0,则sin 2α+sin αcos α值为( B ) A .95B .65C .3D .4[解析] 由sin α-3cos α=0,∴tan α=3, 又sin 2α+sin αcos α=sin 2α+sin αcod αsin 2α+cos 2α=tan 2α+tan α1+tan 2α=1210=65.6.已知α是三角形的一个内角,且sin α+cos α=23,那么这个三角形的形状为( B )A .锐角三角形B .钝角三角形C .等边三角形D .等腰直角三角形[解析] (sin α+cos α)2=49,∴2sin αcos α=-59<0,又∵α∈(0,π),sin α>0.∴cos α<0,∴α为钝角. 二、填空题7.在△ABC 中,2sin A =3cos A ,则∠A =__60°__.[解析] ∵2sin 2A =3cos A ,∴2(1-cos 2A )=3cos A ,即(2cos A -1)(cos A +2)=0,∴cos A =12,cos A =-2(舍去),∴A =60°.8.已知tan α=cos α,那么sin α= 2. [解析] 由于tan α=sin αcos α=cos α,则sin α=cos 2α,所以sin α=1-sin 2α,解得sin α=-1±52. 又sin α=cos 2α≥0,所以sin α=-1+52.三、解答题9.求证:sin α(1+tan α)+cos α(1+1tan α)=1sin α+1cos α. [证明] 左边=sin α(1+sin αcos α)+cos α(1+cos αsin α)=sin α+sin 2αcos α+cos α+cos 2αsin α=sin 2α+cos 2αsin α+sin 2α+cos 2αcos α=1sin α+1cos α=右边. 即原等式成立.10.已知tan α=7,求下列各式的值. (1)sin α+cos α2sin α-cos α;(2)sin 2α+sin αcos α+3cos 2α.[解析] (1)sin α+cos α2sin α-cos α=sin α+cos αcos α2sin α-cos αcos α=tan α+12tan α-1=7+12×7-1=813.(2)sin 2α+sin αcos α+3cos 2α=sin 2α+sin αcos α+3cos 2αsin 2α+cos 2α=sin 2α+sin αcos α+3cos 2αcos 2αsin 2α+cos 2αcos 2α=tan 2α+tan α+3tan 2α+1=49+7+349+1=5950. B 级 素养提升一、选择题1.已知sin α-cos α=-54,则sin α·cos α等于( C )A .74B .-916C .-932D .932[解析] 将所给等式两边平方,得1-2sin αcos α=2516,故sin αcos α=-932.2.若π<α<3π2,1-cos α1+cos α+1+cos α1-cos α的化简结果为( D )A .2tan αB .-2tan αC .2sin αD .-2sin α[解析] 原式=(1-cos α)21-cos 2α+(1+cos α)21-cos 2α=1-cos α|sin α|+1+cos α|sin α|=2|sin α|∵π<α<3π2,∴原式=-2sin α.3.若sin θ+2cos θsin θ-cos θ=2,则sin θ·cos θ=( D )A .-417B .45C .±417D .417[解析] 由sin θ+2cos θsin θ-cos θ=2,得tan θ=4,sin θcos θ=sin θcos θsin 2θ+cos 2θ=tan θ1+tan 2θ=417. 4.如果sin x +cos x =15,且0<x <π,那么tan x 的值是( A )A .-43B .-43或-34C .-34D .43或-34[解析] 将所给等式两边平方,得sin x cos x =-1225,∵0<x <π,∴sin x >0,cos x <0, ∴sin x =45,cos x =-35,∴tan x =-43.二、填空题5.已知sin θ=m -3m +5,cos θ=4-2m m +5,则tan θ= -34或-512 .[解析] 由sin 2θ+cos 2θ=1得,m =0或8. m =0时,sin θ=-35,cos θ=45,tan θ=-34;m =8时,sin θ=513,cos =-1213,tan θ=-512.6.在△ABC 中,若tan A =23,则sin A = 11. [解析] 因为tan A =23>0,则∠A 是锐角,则sin A >0,解方程组⎩⎪⎨⎪⎧sin 2A +cos 2A =1,sin A cos A =23,得sin A =2211. 7.已知tan 2α=2tan 2β+1,求证:sin 2β=2sin 2α-1. [解析] 由tan 2α=2tan 2β+1,可得tan 2β=12(tan 2α-1),即sin 2βcos 2β=12(sin 2αcos 2α-1),故有sin 2β1-sin 2β=12(sin 2α1-sin 2α-1)=12×2sin 2α-11-sin 2α,整理得sin 2β1-sin 2β=sin 2α-121-sin 2α,即sin 2β(1-sin 2α)=(1-sin 2β)(sin 2α-12),展开得12sin 2β=sin 2α-12,即sin 2β=2sin 2α-1.8.化简下列式子.(1)cos 6α+sin 6α+3sin 2αcos 2α; (2)若x 是第二象限角,化简sin x1-cos x·tan x -sin xtan x +sin x.[解析] (1)原式=(cos 2α+sin 2α)(cos 4α-cos 2αsin 2α+sin 4α)+3sin 2α·cos 2α=cos 4α+2sin 2αcos 2α+sin 4α=(sin 2α+cos 2α)2=1.(2)原式=sin x 1-cos x·sin x -sin x cos x sin x +sin x cos x=sin x 1-cos x·1-cos x 1+cos x=sin x 1-cos x·(1+cos x )(1-cos x )(1+cos x )2=sin x 1-cos x ·|sin x |1+cos x.∵x 为第二象限角,∴sin x >0,∴原式=sin 2x1-cos 2x=1.C 级 能力拔高设A 是三角形的内角,且sin A 和cos A 是关于x 的方程25x 2-5ax -12a =0的两个根. (1)求a 的值; (2)求tan A 的值.[解析] (1)∵sin A 和cos A 是关于x 的方程25x 2-5ax -12a =0的两个根,∴由韦达定理得 ⎩⎨⎧sin A +cos A =15a ,①sin A ·cos A =-1225a ,②将①两边分别平方得sin 2A +2sin A cos A +cos 2A =125a 2,即1-2425a =a 225,解得a =-25或a =1.当a =-25时,sin A +cos A =-5不合题意,故a =1.(2)由⎩⎨⎧sin A +cos A =a5,sin A cos A =-1225a ,得sin A >0,cos A <0,∴sin A =45,cos A =-35.∴tan A =sin Acos A=-43.。
同角三角函数基本关系式

1弧度等于180/π度,可以利用这个公式将角度转换为弧度, 反之亦然。
三角函数和反三角函数的关系
正弦、余弦、正切的定义
正弦、余弦、正切是三角函数的基本形式,它们分别对应于直角三角形中的边的比值。
反三角函数的定义
反正弦、反余弦、反正切是反三角函数的基本形式,它们分别表示的是正弦、余弦、正切函数的反函数。
符号和表示
正弦函数sin(x)表示一个角度x的正弦值,余弦函数cos(x) 表示x的余弦值,正切函数tan(x)表示x的正切值。
对于角度的正弦、余弦和正切值,分别记为sin(x)、cos(x) 和tan(x)。
三角函数的概念和性质
三角函数是函数的一种,其定义是将一个角度作为自变量,将该角度的正弦、余弦和正切值作为因变 量。
同角三角函数基本关系式的应用和发展
应用
同角三角函数基本关系式是三角函数计算、化简、证明 的重要依据,也是三角函数图像分析的基础。在物理、 数学、工程等众多领域都有广泛的应用。
发展
同角三角函数基本关系式是三角函数理论的基础,它为 后续的三角函数学习提供了重要的基础。同时,它也是 连接初等数学和高等数学的重要纽带之一,为数学的学 习提供了重要的帮助。
三角函数在圆和椭圆中的应
用
圆和椭圆是常见的曲线形状,利用三角函数可以方便 地对其进行解析表达和性质研究。
三角函数在物理学中的应用
三角函数在力学中的应用
在研究物体的运动和受力时,可以将时间、位移等物理 量用三角函数表示,从而利用三角函数的性质得到物体 运动规律。
三角函数在电磁学中的应用
电磁学中,交流电的电压、电流等物理量可以用三角函 数表示,从而可以利用三角函数的性质得到交流电的规 律和性质。
三角函数和解三角公式总结

sin 2 cos 2
sin 2 − , cos 2 −
tan 2 −
− cos
sin 2
− sin , cos 2
sin 2 − cos 2 −
tan 2
− cos
sin .
sin 2 cos 2
3.两角和与差公式:
①cos −
cos cos sin sin ;③sin −
sin cos − cos sin ;
⋯
2 2sin(
).( ,
)
①其中辅助角 是方程 tan
在( , )内的解;【提取系数 2 2是关键】
2
② : : 或 : 或 : 时要熟练;
③必要时可化为余弦形式.
④显然,
sin
cos 的值域为[ − 2 2, 2 2 .
7.若函数
sin cos 的图象关于直线
对称,则
①
( − ); ② 2
( ); ③
tan
tan 2 −
)
− sin sin − cos , cos − − tan tan −
− sin cos ; − tan
一全正↕,
二正弦↕,
三正切↕,
四余弦↕,
四余弦↑
sin 2 − ⑵ cos 2 −
tan 2 −
cos
sin 2
sin , cos 2
sin 2− cos 2−
tan 2
cos
三角函数和解三角公式总结
1.同角三角函数的基本关系式:(用于求值、化简、证明;变形运用、1 的代换、齐次化切.)
⑴平方关系:sin2 cos2
;
⑶三角完全平方公式:① sin cos 2
高一数学同角三角函数的基本关系式及诱导公式

同角三角函数的基本关系式及诱导公式一、基本知识:(1)同角三角函数的基本关系式:平方关系:sin 2α+cos 2α=1,1tan sec 22=-αα,1cot csc 22=-αα,商式关系:sin α cos α=tan α, αααcot sin cos =, 倒数关系:tan αcot α=1,ααcos 1sec = ααsin 1csc =(2)诱导公式:函数名称不变,符号看象限。
二、例题分析:例1 化简 sin(2π-α)tan(π+α)cot(-α-π) cos(π-α)tan(3π-α). 解 原式=(-sin α)tan α[-cot(α+π) ] (-cos α)tan(π-α)= (-sin α)tan α(-cot α) (-cos α)(-tan α) = sin α·cos α sin α cos α=1 . 例2 若sin θcos θ= 18 ,θ∈(π4 ,π2),求cos θ-sin θ的值.解 (cos θ-sin θ)2=cos 2θ+sin 2θ-2sin θcos θ=1- 14 = 34. ∵θ∈(π4 ,π2),∴ cos θ<sin θ. ∴cos θ-sin θ= - 32. 变式1 条件同例, 求cos θ+sin θ的值.变式2 已知cos θ-sin θ= -32 , 求sin θcos θ,sin θ+cos θ的值.例3 已知tan θ=3.求(1)ααααsin 3cos 5cos 2sin 4+-;(2)cos 2θ+sin θcos θ的值.例4、证明:1+2sin αcos α cos 2α-sin 2α=1+ tan α 1-tan α例5、(1)化简:2cos 2sin 212cos 2sin 21αααα++-,⎪⎭⎫ ⎝⎛<<20πα (2)已知α是第三象限角,求ααααcos 1cos 1cos 1cos 1-+++-的值。
同角三角函数的基本关系

今日作业:
1.课本:练习题1、4、5, 做在书上
2.课本:习题 A组10∽13,
变式1:已知:tanA=2
,
求
2Sin2 4Sin2
A A
3Cos2 9Cos2
A的值 A
变式2:已知:tanA=2 , 求 :Sin2A+3SinACosA+1的值
例4.已知:Sinα+Cosα= 1 ,试求:
2
(1)Sin3α+Cos3α (4)Sin4α+Cos4α
变式1:化简并求值:1 Sin4 A Cos4 A
Cos2α= 1— sin2α= 16
又∵π<α<
π3
25
,∴ Cosα<0
∴Cosα= 4 2 tanα= sin 3
5
cos 4
变式1: 将上题的条件中α范围改为:
α为第三象限角,所求内容不变,应如 何解答?
变式2:将上题条件中的α范围去
掉,所求内容不变,又将如何解答?
变式3:已知 tan 3, 求sin, cos的值.
引题:一般说来,如果我们需要求解一
个未知数,就需要一个方程, 因此, 如 果已知了Sinx = 0.6 , 我们应该怎样去 求 Cosx 呢?
思路一:我们可以这样想:Sinx=0.6 → x →Cosx 思路二:我们能不能这样考虑:直接由Sinx=0.6→Cosx
如果要实现思路二,那么就需要我们能找到Sinx与Cosx之 间的联系,这正是我们今天要研究的课题
例2.化简: 1 — Sin2 4000
变式1:化简: 1 — 2Sin100Cos100 Sin100 — 1 — Sin2100
变式2:已知:sin 2 x + sin x=1 , 求: cos 4 x+ cos 2 x 的值.
同角三角函数的基本关系(基础知识+基本题型)(含解析)

5.2.2 同角三角函数的基本关系(基础知识+基本题型)知识点一 同角三角函数的基本关系式利用单位圆中的三角函数线以及勾股定理,我们可以得到同一个角的三个三角函数之间的两种关系:(1)根据三角函数的定义,当,2k k Z παπ=+∈时,sin tan cos ααα=不成立. (2)2sin α是()2sin α的简写,不能将2sin α写成2sin α,前者是α的正弦的平方,而后者是α平方的正弦.(3)利用平方关系,得sin α=,cos α=,“±”号由α的终边所在象限决定.(4)“同角”有两层含义,一是“角相同”,二是对“任意”一个角(在使函数有意义的前提下)关系式都成立,与角的表达形式无关,如22sin 3cos 31αα+=等.知识点二 同角三角函数关系式的应用同角三角函数的基本关系式主要用于:(1)已知某角的一个三角函数值,求它的其余各三角函数值;(2)化简三角函数式;(3)证明三角恒等式.常用的等价变形有:sin α=, cos α=,22sin 1cos αα=-,22cos 1sin αα=-,sin tan cos ααα=,sin cos tan ααα=. 【提示】 已知某角的一个三角函数值,在使用22sin cos 1αα+=求它的其余三角函数值时,要注意角的终边所在的象限.求解过程中一般有以下三种情况:①如果已知三角函数值,且角所在的象限已知,那么只有一组解;②如果已知三角函数值,但没有指定角在哪个象限,那么先由已知三角函数值的正负确定角可能在的象限,再求解,这种情况一般有两组解;③如果所给的三角函数值是由字母给出的,且没有指明角在哪个象限,那么就需要进行讨论.考点一应用同角三角函数关系式求值【例1】已知()1sin cos05αααπ+=<<,求tanα.解:方法1:由1sin cos5αα+=两边平方.得221sin2sin cos cos25αααα++=,即112sin cos25αα+=.所以12sin cos025αα=-<,又因为0απ<<,所以sin0α>,cos0α<,所以sin cos0αα->.所以7sin cos5αα-====.所以4sin5α=,3cos5α=-.所以sin4tancos3ααα==-.方法2:由221sin cos5sin cos1αααα⎧+=⎪⎨⎪+=⎩,联立消去cosα,得221sin sin15αα⎛⎫+-=⎪⎝⎭,即225sin5sin120αα--=,解得4sin5α=或3sin5α=-(舍去).所以3cos5α=-,所以sin4tancos3ααα==-.(1)在sin cosαα+,sin cosαα-,sin cosαα三个式子中,已知其中一个,可以求其他两个,即“知一求二”,它们之间的关系是()2sin cos12sin cosαααα±=±.(2)设sin cos tαα+=,由三角函数线,知当02πα<<时,1t>;当324ππα<<时,01t<<;当34παπ<<时,10t-<<;当32ππα<<时,1t <-; 当3724ππα<<时,10t -<<; 当724παπ<<时,01t <<. 依据以上结论,已知sin cos αα+的值时,可进一步得出α的范围.【例2】已知tan 2α=,则(1)2sin 3cos 4sin 9cos αααα-=-______; (2)224sin 3sin cos 5cos αααα--=______.解:(1):2sin 3cos 2tan 34sin 9cos 4tan 9αααααα--=-- 2231429⨯-==-⨯-. (2)2222224sin 3sin cos 5cos 4sin 3sin cos 5cos sin cos αααααααααα----=+. 224tan 3tan 5tan 1ααα--=+. 44325141⨯-⨯-==+. 答案:(1)-1 (2)1本题是一个在已知tan m α=的条件,求关于sin ,cos αα的齐次式的整体代入的问题.解决这类问题,需注意以下两点;(1)一定是关于sin ,cos αα的齐次式(或能化为齐次式,如第(2)问)的三角函数式;(2)cos 0α≠,这样分子、分母才能都除以()*cos n n N α∈.先将被求式化为关于tan α的表达式,再将tan m α=代入,从而使问题获得求解.考点二 三角函数式的化简【例3】 化简tan α是第二象限角. 分析:先由角α是第二象限角确定出sin ,cos αα的符号,利用22sin cos 1αα+=对含根号的式子化简,结合sin ,cos αα的符号去掉根号,再由sin tan cos ααα=把式子化简. 解:因为α是第二象限角,所以sin 0α>,cos 0α<.故tan tan tan ==sin cos sin cos cos sin cos sin αααααααα-=⋅=⋅. =1.化简三角函数式的一般要求:(1)函数种类最少;(2)项数最少;(3)函数次数最低;(4)能求值的求出值;(5)尽量使分母不含三角函数;(6)尽量使分母不含根式.考点三 三角恒等式的证明【例4】 求证:tan sin tan sin tan sin tan sin αααααααα⋅+=-⋅. 证明:左边=tan sin tan tan cos ααααα⋅-⋅. ()tan sin sin tan 1cos 1cos αααααα⋅==--. 右边=tan tan cos tan sin ααααα+⋅⋅ =()tan 1cos 1cos tan sin sin αααααα++=⋅=()21cos sin 1cos ααα-- =()2sin sin sin 1cos 1cos ααααα=-- 所以左边=右边,即原等式成立.(1)利用同角三角函数关系式证明时,要熟悉公式.方法有从左至右、从右至左或从两侧证明等于同一式,还可用比较法.(2)注意切化弦、弦化切及平方关系的应用.。
高中数学例题:利用同角关系化简三角函数式

高中数学例题:利用同角关系化简三角函数式例.化简:(1(2)若322παπ<< 【思路点拨】把根号下面的式子化成完全平方式,开方去掉根号。
【解析】 (1)原式=|cos10sin10|cos10sin101sin10cos10sin10cos10︒-︒︒-︒===-︒-︒︒-︒。
(2)∵322παπ<<,∴sin α<0,∴原式==|1cos ||1cos ||sin ||sin |αααα-+=+ ∵sin α<0, ∴原式1cos 1cos 2sin sin sin ααααα-+=--=-。
【总结升华】解答此题目常用的方法有:(1)化切为弦,即把非正弦、余弦的函数都化成正弦函数、余弦函数,从而减少函数名称,达到化简的目的。
(2)对于含有根号的,常把根号下的式子化成完全平方式,然后去根号达到化简的目的。
(3)对于化简含高次的三角函数式,往往借助于因式分解,或构造sin 2α+cos 2α=1,以降低函数次数,达到化简的目的。
举一反三:【变式1】化简(12,22k k k Z πθππ⎛⎫∈-∈ ⎪⎝⎭;(2【答案】(1)-1(2)cos2sin 2--【解析】(1)原式|sin cos |1sin cos θθθθ-==--(2)原式|cos2||sin 2|cos2sin 2=-=--类型四:利用同角关系证明三角恒等式例5.求证:(1)111sin (1tan )cos (1)tan sin cos θθθθθθ+++=+; (2)cos sin 2(cos sin )1sin 1cos 1sin cos αααααααα--=++++。
【思路点拨】利用同角三角函数关系式对式子的左边或右边进行化简,使之与式子的另一边相同。
【证明】(1)左边222sin cos sin cos sin 1cos 1sin cos cos sin cos sin θθθθθθθθθθθθ⎛⎫⎛⎫=+++=+++ ⎪ ⎪⎝⎭⎝⎭2222sin cos sin cos 11sin cos sin cos θθθθθθθθ++=+=+=右边, ∴原等式成立。
第八课 同角三角函数关系(2)

第八课 同角三角函数关系(2)学习目标:1、能够应用同角三角函数基本关系式化简三角函数式;2、证明简单的三角恒等式。
重、难点分析:本节的重点是应用公式化简求值,证明简单的三角恒等式。
难点是对三角函数式化简时化简到什么程度学生不易掌握;在证明恒等式时,选择适当的推理途径是本小节的另一个难点。
学习内容:知识回顾:同角三角函数的两个基本关系式:① ② 回答:⑴2sin 2α+2cos 2α=⑵2sin +αβ()+()2cos αβ+=平方关系式可以有如下的变形:22sin 1cos (1cos )(1cos )αααα=-=+-据此证明:sin 1cos 1cos sin αααα-=+你还能推导出另一个与此类似的等式吗?从上面的问题中可以看到,三角函数公式的应用,在角的处理和公式的变形上,都体现了三角公式的灵活性。
利用公式,不仅可以证明三角恒等式,还可以进行求值或化简。
看下面的问题:例1、 化简下列各式:(1)cos θtan θ (2)()221+tan cos αα练习:证明(1)2222tan sin tan sin αααα=-(2)4422sin cos 12sin cos αααα+=-例2、 化简66441sin cos 1sin cos x x x x----例3、 (关于含二次根式的三角函数式的化简问题)化简下列各式:⑵ ⑶tan α是第二象限角。
例4、 (关于sin α,cos α的其次式问题) 已知sin 2cos 3cos sin θθθθ+=-,求222sin cos θθ-的值。
课后作业: 姓名1、化简:sin 4=2=3、已知0<x <2π,且sin x cos x =12,则11+sin x +11+cos x 的值为 4、设x 为三角形的一个内角,且sin x +cos x =1,则该三角形的形状是5、已知θcos sin 22θθ=-,则2θ是第 象限角.67、证明等式:2212sin cos 1tan cos sin 1tan x x x x x x--=-+8、已知2tan x =-,求x 的取值范围。
