初中一次函数的图像专项练习30题有答案
初中数学一次函数的图像专项练习30题(有答案)ok之欧阳史创编

一次函数的图像专项练习30题(有答案)时间:2021.02.10 创作:欧阳史1.函数y=ax+b与y=bx+a的图象在同一坐标系内的大致位置正确的是()A.B.C.D.2.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x>2时,y2>y1,其中正确的个数是()A.0B.1C.2D.33.一次函数y=kx+b,y随x的增大而减小,且kb>0,则在直角坐标系内它的大致图象是()A.B.C.D.4.下列函数图象不可能是一次函数y=ax﹣(a﹣2)图象的是()5.如图所示,如果k•b<0,且k <0,那么函数y=kx+b 的图象大致是( )A .B .C .D .6.如图,直线l1:y=x+1与直线l2:y=﹣x ﹣把平面直角坐标系分成四个部分,则点(,)在( ) A . 第一部分 B . 第二部分 C . 第三部分D . 第四部分 7.已知正比例函数y=﹣kx 和一次函数y=kx ﹣2(x 为自变量),它们在同一坐标系内的图象大致是( )A .B .C .D .8.函数y=2x+3的图象是( )A . 过点(0,3),(0,﹣)的直线B . 过点(1,5),(0,﹣)的直线C . 过点(﹣1,﹣1),(﹣,0)的直线D . 过点(0,3),(﹣,0)的直线 9.下列图象中,与关系式y=﹣x ﹣1表示的是同一个一次函数的图象是( )10.函数kx﹣y=2中,y随x的增大而减小,则它的图象是下图中的()A.B.C.D.11.已知直线y1=k1x+b1,y2=k2x+b2,满足b1<b2,且k1k2<0,两直线的图象是()A.B.C.D.12.如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是()A.B.C.D.13.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若该水库的蓄水量V(万米3)与降雨的时间t(天)的关系如图所示,则下列说法正确的是()A.降雨后,蓄水量每天减少5万米3 B.降雨后,蓄水量每天增加5万米3C.降雨开始时,蓄水量为20万米3 D.降雨第6天,蓄水量增加40万米3 14.拖拉机开始行驶时,油箱中有油4升,如果每小时耗油0.5升,那么油箱中余油y(升)与它工作的时间t(时)之间的函数关系的图象是()A.B.C.D.15.已知正比例函数y=kx的图象经过第一、三象限,则y=kx﹣k的大致图象可能是下图的()A.B.C.D.16.一次函数y=kx+b的图象如图所示,当x _________ 时,y>2.17.一次函数的图象如图所示,根据图象可知,当x_________ 时,有y<0.18.如图,直线l是一次函数y=kx+b的图象,当x _________时,y>0.19.一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x=3时,y1=y2;④当x>3时,y1<y2中,正确的判断是_________ .20.如图,已知函数y1=ax+b和y2=kx的图象交于点P,则根据图象可得,当x _________ 时,y1>y2.21.已知一次函数y=kx+b的图象如图所示,当y<0时,x 的取值范围是_________ .22.在平面直角坐标系中画出函数的图象.(1)在图象上标出横坐标为﹣4的点A,并写出它的坐标;(2)在图象上标出和y轴的距离是2个单位长度的点,并写出它的坐标.23.作函数y=2x﹣4的图象,并根据图象回答下列问题.(1)当﹣2≤x≤4,求函数y的取值范围.(2)当x取何值时,y<0?y=0?y>0?24.如图是一次函数y=﹣x+5图象的一部分,利用图象回答下列问题:(1)求自变量的取值范围.(2)在(1)在条件下,y是否有最小值?如果有就求出最小值;如果没有,请说明理由.25.已知函数y1=﹣x+和y2=2x﹣1.(1)在同一个平面直角坐标系中画出这两个函数的图象;(2)根据图象,写出它们的交点坐标;(3)根据图象,试说明当x取什么值时,y1>y2?26.作出函数y=3﹣3x的图象,并根据图象回答下列问题:(1)y的值随x的增大而_________ ;(2)图象与x轴的交点坐标是_________ ;与y轴的交点坐标是_________ ;(3)当x _________ 时,y≥0;(4)函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是多少?27.已知函数y=2x﹣1.(1)在直角坐标系中画出这函数的图象;(2)判断点A(﹣2.5,﹣4),B(2.5,4)是否在函数y=2x ﹣1的图象上;(3)当x取什么值时,y≤0.28.已知函数y=﹣2x﹣6.(1)求当x=﹣4时,y的值,当y=﹣2时,x的值.(2)画出函数图象.(3)如果y的取值范围﹣4≤y≤2,求x的取值范围.29.已知一次函数的图象经过点A(﹣3,0),B(﹣1,1)两点.(1)画出图象;(2)x为何值时,y>0,y=0,y<0?30.已知一次函数y=﹣2x+2,(1)在所给的平面直角坐标系中画出它的图象;(2)根据图象回答问题:①图象与x轴的交点坐标是_________ ,与y轴的交点坐标是_________ ;②当x _________ 时,y>0.参考答案:1.分四种情况:①当a>0,b>0时,y=ax+b的图象经过第一、二、三象限,y=bx+a的图象经过第一、二、三象限,无选项符合;②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a的图象经过第一、二、四象限,C选项符合;③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a的图象经过第一、三、四象限,无选项符合;④当a<0,b<0时,y=ax+b的图象经过第二、三、四象限;y=bx+a的图象经过第二、三、四象限,无选项符合.故选C2.由一次函数y1=kx+b与y2=x+a的图象可知k<0,a<0,当x>2时,y2>y1,①③正确.故选C3.∵一次函数y=kx+b,y随x的增大而减小,∴k<0,又∵kb>0,∴b<0,∴函数的图象经过第二、三、四象限.故选C4.根据图象知:A、a>0,﹣(a﹣2)>0.解得0<a<2,所以有可能;B、a<0,﹣(a﹣2)<0.解得两不等式没有公共部分,所以不可能;C、a<0,﹣(a﹣2)>0.解得a<0,所以有可能;D、a>0,﹣(a﹣2)<0.解得a>2,所以有可能.故选B5.∵k•b<0,且k<0,∴b>0,k<0,∴函数y=kx+b的图象经过第一、二、四象限,故选D6.由题意可得,解得,故点(,)应在交点的上方,即第二部分.故选B.7.分两种情况:(1)当k>0时,正比例函数y=﹣kx的图象过原点、第一、三象限,一次函数y=kx﹣2的图象经过第一、三、四象限,选项A符合;(2)当k<0时,正比例函数y=﹣kx的图象过原点、第二、四象限,一次函数y=kx﹣2的图象经过第二、三、四象限,无选项符合.故选A.8.A、把x=0代入函数关系式得2×0+3=3,故函数图象过点(0,3),不过(0,﹣),故错误;B、由A知函数图象不过点(0,﹣),故错误;C、把x=﹣1代入函数关系式得,2×(﹣1)+3=1,故(﹣1,﹣1)不在函数图象上,故错误;D、分别令x=0,y=0,此函数成立,故正确.故选D9.函数y=﹣x﹣1是一次函数,其图象是一条直线.当x=0时,y=﹣1,所以直线与y轴的交点坐标是(0,﹣1);当y=0时,x=﹣1,所以直线与x轴的交点坐标是(﹣1,0).由两点确定一条直线,连接这两点就可得到y=﹣x﹣1的图象.故选D10.整理为y=kx﹣2∵y随x的增大而减小∴k<0又因为图象过2,4,3象限故选D.11.k1k2<0,则k1与k2异号,因而两个函数一个y随x的增大而增大,另一个y随x的增大而减小,因而A是错误的;b1<b2,则y1与y轴的交点在y2与y轴的交点的下边,因而B、C都是错误的.故选D.12.①当ab>0,正比例函数y=abx过第一、三象限;a与b 同号,同正时y=ax+b过第一、二、三象限,故D错误;同负时过第二、三、四象限,故B错误;②当ab<0时,正比例函数y=abx过第二、四象限;a与b 异号,a>0,b<0时y=ax+b过第一、三、四象限,故C错误;a<0,b>0时过第一、二、四象限.故选A13.A、根据图象知,水库的蓄水量因该随着降雨的时间的增加而增多;故本选项错误;B、本图象的直线,所以每天的降雨量是相等的,所以,蓄水库每天的增加的水的量是(40﹣10)÷6=5;故本选项正确;C、根据图示知,降雨开始时,蓄水量为10万米3,故本选项错误;D、根据图示知,降雨第6天,蓄水量增加了40万米3﹣30万米3=10万米3,故本选项错误;故选B14.根据题意列出关系式为:y=40﹣5t,考虑实际情况:拖拉机开始工作时,油箱中有油4升,即开始时,函数图象与y轴交于点(0,40),如果每小时耗油0.5升,且8小时,耗完油,故函数图象为一条线段.故选D15.∵正比例函数y=kx的图象经过第一、三象限,∴k>0,∴﹣k<0,∴y=kx﹣k的大致图象经过一、三、四象限,故选:B.16.由图形可知,该函数过点(0,2),(3,0),故斜率k==,所以解析式为y=,令y>2,即>2,解之得:x<017.根据题意,要求y<0时,x的范围,即:x+3<0,解可得:x<﹣2,故答案为x<﹣218.根据题意,观察图象,可得直线l过点(2,0),且y随x的增大而增大,分析可得,当x>2时,有y>0 19.根据图示及数据可知:①一次函数y1=kx+b的图象经过第二、四象限,则k<0正确;②y2=x+a的图象经与y轴交与负半轴,则a>0错误;③一次函数y1=kx+b与y2=x+a的图象交点的横坐标是3,所以当x=3时,y1=y2正确;④当x>3时,y1<y2正确;故正确的判断是①,③,④20.根据图示可知点P的坐标是(﹣4,2),所以y1>y2即直线1在直线2的上方,则x<﹣4.21.根据图象和数据可知,当y<0即图象在x轴下侧,x<1.故答案为x<122.函数与坐标轴的交点的坐标为(0,3),(6,0).(1)点A的坐标(﹣4,5);(2)和y轴的距离是2个单位长度的点的坐标M(2,2),N (﹣2,4)23.当x=0时,y=﹣4;当y=0时,2x﹣4=0,解得x=2,∴函数图象与两坐标轴的交点为(0,﹣4)(2,0).图象如下:(1)x=﹣2时,y=2×(﹣2)﹣4=﹣8,x=4时,y=2×4﹣4=4,∵k=2>0,∴y随x的增大而增大,∴﹣8≤y≤4;(2)x<2时,y<0;x=2时,y=0;x>2时,y>0.24.(1)由图象可看出当y=2.5时,x=5,因此x的取值范围应该是0<x≤5(y轴上的点是空心圆,因此x≠0);(2)由图象可看出,当x=5时,函数的值最小,是y=2.5 25.(1)如图所示:(2)由(1)中两函数图象可知,其交点坐标为(1,1);(3)由(1)中两函数图象可知,当x>1时,y1>y2.26.如图.(1)因为一次项系数是﹣3<0,所以y的值随x的增大而减小;(2)当y=0时,x=1,所以图象与x轴的交点坐标是(1,0);当x=0时,y=3,所以图象与y轴的交点坐标是(0,3);(3)由图象知,在A点左边,图象在x轴上方,函数值大于0.所以x≤1时,y≥0.(4)∵OA=1,OB=3,∴函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是S△AOB=×1×3=.27.(1)函数y=2x﹣1与坐标轴的坐标为(0,﹣1)(,0),描点即可,如图所示;(2)将A、B的坐标代入函数式中,可得出A点不在直线y=2x ﹣1的图象上,B点在直线y=2x﹣1的图象上,A代入函数后发现﹣2.5×2﹣1=﹣6≠﹣4,因此A点不在函数y=2x﹣1的图象上,然后用同样的方法判定B是否在函数的图象上;(3)当y≤0时,2x﹣1≤0,因此x≤.28.(1)当x=﹣4时,y=2;当y=﹣2时,x=﹣2;(2)由(1)可知函数图象过(﹣4,2)、(﹣2,﹣2),由此可画出函数的图象,如下图所示:(3)∵y=﹣2x﹣6,﹣4≤y≤2∴﹣4≤﹣2x﹣6≤22≤﹣2x≤8﹣4≤x≤﹣129.(1)图象如图:(2)观察图象可得,当x>﹣3时,y>0;当x=﹣3时,y=0;当x<﹣3时,y<0.30.(1)列表:x 0 1y 2 0描点,连线(如图)…(也可以写成过点(0,2)和(1,0)画直线)(2)①(1,0);(0,2)②<1。
初中数学一次函数的图像专项练习30题有答案
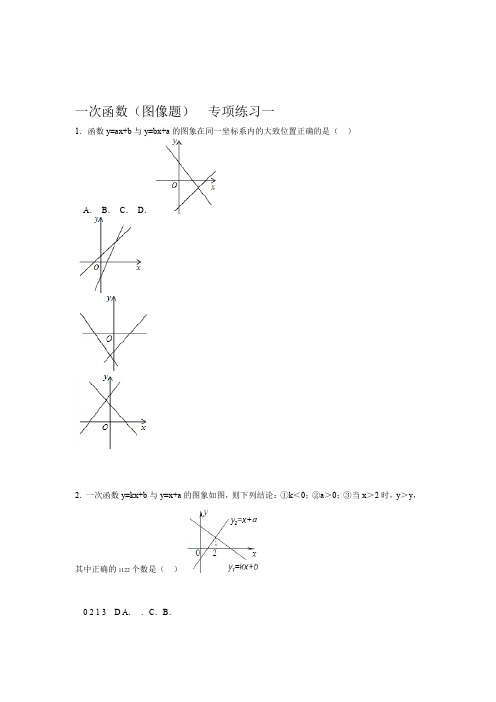
一次函数(图像题)专项练习一1.函数y=ax+b与y=bx+a的图象在同一坐标系内的大致位置正确的是()A.B.C.D.2.一次函数y=kx+b与y=x+a的图象如图,则下列结论:①k<0;②a>0;③当x>2时,y>y,其中正确的1122个数是()0 2 1 3 D A..C.B.3.一次函数y=kx+b,y随x的增大而减小,且kb>0,则在直角坐标系内它的大致图象是()A.B.C.D.4.下列函数图象不可能是一次函数y=ax﹣(a﹣2)图象的是()5.如图所示,如果k?b<0,且k<0,那么函数y=kx+b的图象大致是()A.B.C.D.6.如图,直线l:y=x+1与直线l:y=﹣x﹣把平面直角坐标系分成四个部分,则点(,)在()21A.第一部分B.第二部分C.第三部分D.第四部分7.已知正比例函数y=﹣kx和一次函数y=kx﹣2(x为自变量),它们在同一坐标系内的图象大致是()A.B.C.D.8.函数y=2x+3的图象是()A.B.过点(1,5),(0,﹣)的直线0过点(0,3),(,﹣)的直线DC..过点(﹣1,﹣1),(﹣,0)的直线,过点(0,3)(﹣,0)的直线9.下列图象中,与关系式y=﹣x﹣1表示的是同一个一次函数的图象是()A.B.C.D.10.函数kx﹣y=2中,y随x的增大而减小,则它的图象是下图中的()A.B.C.D.1.已知直=x+=x+,满,,两直线的图象是()12.如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是()A.B.C.D.313.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若该水库的蓄水量V(万米)与降雨的时间t(天))的关系如图所示,则下列说法正确的是(.33A.B.降雨后,蓄水量每天减少5万米降雨后,蓄水量每天增加5万米33C.D.降雨开始时,蓄水量为20万米降雨第6天,蓄水量增加40万米14.拖拉机开始行驶时,油箱中有油4升,如果每小时耗油0.5升,那么油箱中余油y(升)与它工作的时间t(时)之间的函数关系的图象是()A.B.C.D.15.已知正比例函数y=kx的图象经过第一、三象限,则y=kx﹣k的大致图象可能是下图的().DCA.B..2.x_________时,y>y=kx+b16.一次函数的图象如图所示,当._________时,有y<0x17.一次函数的图象如图所示,根据图象可知,当0>.的图象,当是一次函数y=kx+bx_________时,y.如图,直线18l 的图象如图所示,则下列结论:与19.一次函数y=kx+by=x+a21 yy<中,时,>当;=yyx=3③0a;<①k0②>;当时,④x32211正确的判断是_________.20.如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,当x_________时,y>y.212121.已知一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是_________..在平面直角坐标系中画出函数的图象.22(1)在图象上标出横坐标为﹣4的点A,并写出它的坐标;(2)在图象上标出和y轴的距离是2个单位长度的点,并写出它的坐标.23.作函数y=2x﹣4的图象,并根据图象回答下列问题.(1)当﹣2≤x≤4,求函数y的取值范围.(2)当x取何值时,y<0?y=0?y>0?﹣x+5图象的一部分,利用图象回答下列问题:24.如图是一次函数y=(1)求自变量的取值范围.(2)在(1)在条件下,y是否有最小值?如果有就求出最小值;如果没有,请说明理由..﹣y=2x1.已知函数25y=﹣和x+21)在同一个平面直角坐标系中画出这两个函数的图象;(1 2)根据图象,写出它们的交点坐标;(y>取什么值时,)根据图象,试说明当(3xy?21.26.作出函数y=3﹣3x的图象,并根据图象回答下列问题:(1)y的值随x的增大而_________;(2)图象与x轴的交点坐标是_________;与y轴的交点坐标是_________;(3)当x_________时,y≥0;(4)函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是多少?27.已知函数y=2x﹣1.(1)在直角坐标系中画出这函数的图象;(2)判断点A(﹣2.5,﹣4),B(2.5,4)是否在函数y=2x﹣1的图象上;(3)当x取什么值时,y≤0.28.已知函数y=﹣2x﹣6.(1)求当x=﹣4时,y的值,当y=﹣2时,x的值.(2)画出函数图象.(3)如果y的取值范围﹣4≤y≤2,求x的取值范围.)两点.,1),B(﹣1029.已知一次函数的图象经过点A(﹣3,)画出图象;(1 0?y=0,y<)(2x为何值时,y>0,,y=﹣2x+230.已知一次函数)在所给的平面直角坐标系中画出它的图象;(1 )根据图象回答问题:(2 ;_________y_________图象与①x轴的交点坐标是,与轴的交点坐标是.0y_________x②当时,>参考答案:1.分四种情况:①当a>0,b>0时,y=ax+b的图象经过第一、二、三象限,y=bx+a的图象经过第一、二、三象限,无选项符合;②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a的图象经过第一、二、四象限,C选项符合;③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a的图象经过第一、三、四象限,无选项符合;④当a<0,b<0时,y=ax+b的图象经过第二、三、四象限;y=bx+a的图象经过第二、三、四象限,无选项符合.故选C2.由一次函数y=kx+b与y=x+a的图象可知k<0,a<0,当x>2时,y>y,①③正确.故选C 11223.∵一次函数y=kx+b,y随x的增大而减小,∴k<0,又∵kb>0,∴b<0,∴函数的图象经过第二、三、四象限.故选C4.根据图象知:A、a>0,﹣(a﹣2)>0.解得0<a<2,所以有可能;B、a<0,﹣(a﹣2)<0.解得两不等式没有公共部分,所以不可能;C、a<0,﹣(a﹣2)>0.解得a<0,所以有可能;D、a>0,﹣(a﹣2)<0.解得a>2,所以有可能.故选B5.∵k?b<0,且k<0,∴b>0,k<0,∴函数y=kx+b的图象经过第一、二、四象限,故选D.由题意可得,6,)应在交点的上方,即第二部分.故选B,故点(.解得7.分两种情况:(1)当k>0时,正比例函数y=﹣kx的图象过原点、第一、三象限,一次函数y=kx﹣2的图象经过第一、三、四象限,选项A符合;(2)当k<0时,正比例函数y=﹣kx的图象过原点、第二、四象限,一次函数y=kx﹣2的图象经过第二、三、四象限,无选项符合.故选A.,﹣)0,故错误;0,3),不过(、把8.Ax=0代入函数关系式得2×0+3=3,故函数图象过点(,﹣),故错误;B、由A知函数图象不过点(0C、把x=﹣1代入函数关系式得,2×(﹣1)+3=1,故(﹣1,﹣1)不在函数图象上,故错误;D、分别令x=0,y=0,此函数成立,故正确.故选D9.函数y=﹣x﹣1是一次函数,其图象是一条直线.当x=0时,y=﹣1,所以直线与y轴的交点坐标是(0,﹣1);当y=0时,x=﹣1,所以直线与x轴的交点坐标是(﹣1,0).由两点确定一条直线,连接这两点就可得到y=﹣x﹣1的图象.故选D10.整理为y=kx﹣2∵y随x的增大而减小∴k<0又因为图象过2,4,3象限故选D.11.kk<0,则k与k异号,2121因而两个函数一个y随x的增大而增大,另一个y随x的增大而减小,因而A是错误的;b<b,则y与y轴的交点在y与y轴的交点的下边,因而B、C都是错误的.2121.D故选.12.①当ab>0,正比例函数y=abx过第一、三象限;a与b同号,同正时y=ax+b过第一、二、三象限,故D错误;同负时过第二、三、四象限,故B错误;②当ab<0时,正比例函数y=abx过第二、四象限;a与b异号,a>0,b<0时y=ax+b过第一、三、四象限,故C错误;a<0,b>0时过第一、二、四象限.故选A13.A、根据图象知,水库的蓄水量因该随着降雨的时间的增加而增多;故本选项错误;B、本图象的直线,所以每天的降雨量是相等的,所以,蓄水库每天的增加的水的量是(40﹣10)÷6=5;故本选项正确;3C、根据图示知,降雨开始时,蓄水量为10万米,故本选项错误;333D、根据图示知,降雨第6天,蓄水量增加了40万米﹣30万米=10万米,故本选项错误;故选B14.根据题意列出关系式为:y=40﹣5t,考虑实际情况:拖拉机开始工作时,油箱中有油4升,即开始时,函数图象与y轴交于点(0,40),如果每小时耗油0.5升,且8小时,耗完油,故函数图象为一条线段.故选D15.∵正比例函数y=kx的图象经过第一、三象限,∴k>0,∴﹣k<0,∴y=kx﹣k的大致图象经过一、三、四象限,故选:B.=,k=,故斜率3,0)16.由图形可知,该函数过点(0,2),(,,即>2所以解析式为,令y=y>20<解之得:x,故答案为x<﹣2时,17.根据题意,要求y<0x的范围,即:x+3<0,解可得:x<﹣2 >0218.根据题意,观察图象,可得直线l过点(2,0),且y随x的增大而增大,分析可得,当x>时,有y 0正确;<19.根据图示及数据可知:①一次函数y=kx+b的图象经过第二、四象限,则k1 0错误;②y=x+a的图象经与y轴交与负半轴,则a>2 =y③一次函数y=kx+b与y=x+a的图象交点的横坐标是3,所以当x=3时,y正确;2211④当x>3时,y<y 正确;21,④①,③故正确的判断是<﹣4.在直线y即直线12的上方,则x,所以20.根据图示可知点P的坐标是(﹣4,2)y>21 1<1.故答案为x<x21.根据图象和数据可知,当y<0即图象在x轴下侧,6,0).22).函数与坐标轴的交点的坐标为(0,3,((1)点A的坐标(﹣4,5);(2)和y轴的距离是2个单位长度的点的坐标M(2,2),N(﹣2,4)23.当x=0时,y=﹣4;当y=0时,2x﹣4=0,解得x=2,∴函数图象与两坐标轴的交点为(0,﹣4)(2,0).图象如下:(1)x=﹣2时,y=2×(﹣2)﹣4=﹣8,x=4时,y=2×4﹣4=4,∵k=2>0,∴y随x的增大而增大,∴﹣8≤y≤4;.0>y时,2>x;y=0时,x=2;0<y时,2<x)2(.24.(1)由图象可看出当y=2.5时,x=5,因此x的取值范围应该是0<x≤5(y轴上的点是空心圆,因此x≠0);(2)由图象可看出,当x=5时,函数的值最小,是y=2.525.(1)如图所示:(2)由(1)中两函数图象可知,其交点坐标为(1,1);(3)由(1)中两函数图象可知,当x>1时,y>y.2126.如图.(1)因为一次项系数是﹣3<0,所以y的值随x的增大而减小;(2)当y=0时,x=1,所以图象与x轴的交点坐标是(1,0);当x=0时,y=3,所以图象与y轴的交点坐标是(0,3);(3)由图象知,在A点左边,图象在x轴上方,函数值大于0.所以x≤1时,y≥0.3=.1×﹣3x的图象与坐标轴所围成的三角形的面积是S=×OB=3(4)∵OA=1,,∴函数y=3AOB △(,0),﹣1),描点即可,如图所示;)函数27.(1y=2x﹣1与坐标轴的坐标为(0(2)将A、B的坐标代入函数式中,可得出A点不在直线y=2x﹣1的图象上,B点在直线y=2x﹣1的图象上,A代入函数后发现﹣2.5×2﹣1=﹣6≠﹣4,因此A点不在函数y=2x﹣1的图象上,然后用同样的方法判定B是否在函数的图象上;≤.x012x0y3()当≤时,﹣≤,因此28.(1)当x=﹣4时,y=2;当y=﹣2时,x=﹣2;(2)由(1)可知函数图象过(﹣4,2)、(﹣2,﹣2),由此可画出函数的图象,如下图所示:(3)∵y=﹣2x﹣6,﹣4≤y≤2∴﹣4≤﹣2x﹣6≤22≤﹣2x≤8﹣4≤x≤﹣129.(1)图象如图:(2)观察图象可得,当x>﹣3时,y>0;当x=﹣3时,y=0;当x<﹣3时,y<0.30.(1)列表:x 0 1y 2 0描点,连线(如图)…(也可以写成过点(0,2)和(1,0)画直线)(2)①(1,0);(0,2)②<1。
初中数学一次函数的图像专项练习30题(有标准答案)ok

一次函数(图像题)专项练习一1.函数y=ax+b与y=bx+a的图象在同一坐标系内的大致位置正确的是()A.B.C.D.2.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x>2时,y2>y1,其中正确的个数是()A.0B.1C.2D.33.一次函数y=kx+b,y随x的增大而减小,且kb>0,则在直角坐标系内它的大致图象是()A.B.C.D.4.下列函数图象不可能是一次函数y=ax﹣(a﹣2)图象的是()A.B.C.D.5.如图所示,如果k?b<0,且k<0,那么函数y=kx+b的图象大致是()A.B.C.D.6.如图,直线l1:y=x+1与直线l2:y=﹣x﹣把平面直角坐标系分成四个部分,则点(,)在()A.第一部分B.第二部分C.第三部分D.第四部分7.已知正比例函数y=﹣kx和一次函数y=kx﹣2(x为自变量),它们在同一坐标系内的图象大致是()A.B.C.D.8.函数y=2x+3的图象是()A.过点(0,3),(0,﹣)的直线B.过点(1,5),(0,﹣)的直线C.过点(﹣1,﹣1),(﹣,0)的直线D.过点(0,3),(﹣,0)的直线9.下列图象中,与关系式y=﹣x﹣1表示的是同一个一次函数的图象是()A.B.C.D.10.函数kx﹣y=2中,y随x的增大而减小,则它的图象是下图中的()A.B.C.D.11.已知直线y1=k1x+b1,y2=k2x+b2,满足b1<b2,且k1k2<0,两直线的图象是()A.B.C.D.12.如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是()A.B.C.D.13.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若该水库的蓄水量V(万米3)与降雨的时间t(天)的关系如图所示,则下列说法正确的是()A.降雨后,蓄水量每天减少5万米3B.降雨后,蓄水量每天增加5万米3C.降雨开始时,蓄水量为20万米3D.降雨第6天,蓄水量增加40万米314.拖拉机开始行驶时,油箱中有油4升,如果每小时耗油0.5升,那么油箱中余油y(升)与它工作的时间t(时)之间的函数关系的图象是()A.B.C.D.15.已知正比例函数y=kx的图象经过第一、三象限,则y=kx﹣k的大致图象可能是下图的()A.B.C.D.16.一次函数y=kx+b的图象如图所示,当x_________时,y>2.17.一次函数的图象如图所示,根据图象可知,当x_________时,有y<0.18.如图,直线l是一次函数y=kx+b的图象,当x_________时,y>0.19.一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x=3时,y1=y2;④当x>3时,y1<y2中,正确的判断是_________.20.如图,已知函数y1=ax+b和y2=kx的图象交于点P,则根据图象可得,当x_________时,y1>y2.21.已知一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是_________.22.在平面直角坐标系中画出函数的图象.(1)在图象上标出横坐标为﹣4的点A,并写出它的坐标;(2)在图象上标出和y轴的距离是2个单位长度的点,并写出它的坐标.23.作函数y=2x﹣4的图象,并根据图象回答下列问题.(1)当﹣2≤x≤4,求函数y的取值范围.(2)当x取何值时,y<0?y=0?y>0?24.如图是一次函数y=﹣x+5图象的一部分,利用图象回答下列问题:(1)求自变量的取值范围.(2)在(1)在条件下,y是否有最小值?如果有就求出最小值;如果没有,请说明理由.25.已知函数y1=﹣x+和y2=2x﹣1.(1)在同一个平面直角坐标系中画出这两个函数的图象;(2)根据图象,写出它们的交点坐标;(3)根据图象,试说明当x取什么值时,y1>y2?26.作出函数y=3﹣3x的图象,并根据图象回答下列问题:(1)y的值随x的增大而_________;(2)图象与x轴的交点坐标是_________;与y轴的交点坐标是_________;(3)当x_________时,y≥0;(4)函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是多少?27.已知函数y=2x﹣1.(1)在直角坐标系中画出这函数的图象;(2)判断点A(﹣2.5,﹣4),B(2.5,4)是否在函数y=2x﹣1的图象上;(3)当x取什么值时,y≤0.28.已知函数y=﹣2x﹣6.(1)求当x=﹣4时,y的值,当y=﹣2时,x的值.(2)画出函数图象.(3)如果y的取值范围﹣4≤y≤2,求x的取值范围.29.已知一次函数的图象经过点A(﹣3,0),B(﹣1,1)两点.(1)画出图象;(2)x为何值时,y>0,y=0,y<0?30.已知一次函数y=﹣2x+2,(1)在所给的平面直角坐标系中画出它的图象;(2)根据图象回答问题:①图象与x轴的交点坐标是_________,与y轴的交点坐标是_________;②当x_________时,y>0.参考答案:1.分四种情况:①当a>0,b>0时,y=ax+b的图象经过第一、二、三象限,y=bx+a的图象经过第一、二、三象限,无选项符合;②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a的图象经过第一、二、四象限,C选项符合;③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a的图象经过第一、三、四象限,无选项符合;④当a<0,b<0时,y=ax+b的图象经过第二、三、四象限;y=bx+a的图象经过第二、三、四象限,无选项符合.故选C2.由一次函数y1=kx+b与y2=x+a的图象可知k<0,a<0,当x>2时,y2>y1,①③正确.故选 C3.∵一次函数y=kx+b,y随x的增大而减小,∴k<0,又∵kb>0,∴b<0,∴函数的图象经过第二、三、四象限.故选 C4.根据图象知:A、a>0,﹣(a﹣2)>0.解得0<a<2,所以有可能;B、a<0,﹣(a﹣2)<0.解得两不等式没有公共部分,所以不可能;C、a<0,﹣(a﹣2)>0.解得a<0,所以有可能;D、a>0,﹣(a﹣2)<0.解得a>2,所以有可能.故选B5.∵k?b<0,且k<0,∴b>0,k<0,∴函数y=kx+b的图象经过第一、二、四象限,故选 D6.由题意可得,解得,故点(,)应在交点的上方,即第二部分.故选B.7.分两种情况:(1)当k>0时,正比例函数y=﹣kx的图象过原点、第一、三象限,一次函数y=kx﹣2的图象经过第一、三、四象限,选项A符合;(2)当k<0时,正比例函数y=﹣kx的图象过原点、第二、四象限,一次函数y=kx﹣2的图象经过第二、三、四象限,无选项符合.故选A.8.A、把x=0代入函数关系式得2×0+3=3,故函数图象过点(0,3),不过(0,﹣),故错误;B、由A知函数图象不过点(0,﹣),故错误;C、把x=﹣1代入函数关系式得,2×(﹣1)+3=1,故(﹣1,﹣1)不在函数图象上,故错误;D、分别令x=0,y=0,此函数成立,故正确.故选 D9.函数y=﹣x﹣1是一次函数,其图象是一条直线.当x=0时,y=﹣1,所以直线与y轴的交点坐标是(0,﹣1);当y=0时,x=﹣1,所以直线与x轴的交点坐标是(﹣1,0).由两点确定一条直线,连接这两点就可得到y=﹣x﹣1的图象.故选 D10.整理为y=kx﹣2∵y随x的增大而减小∴k<0又因为图象过2,4,3象限故选D.11.k1k2<0,则k1与k2异号,因而两个函数一个y随x的增大而增大,另一个y随x的增大而减小,因而A是错误的;b1<b2,则y1与y轴的交点在y2与y轴的交点的下边,因而B、C都是错误的.故选D.12.①当ab>0,正比例函数y=abx过第一、三象限;a与b同号,同正时y=ax+b过第一、二、三象限,故D错误;同负时过第二、三、四象限,故B错误;②当ab<0时,正比例函数y=abx过第二、四象限;a与b异号,a>0,b<0时y=ax+b过第一、三、四象限,故C错误;a<0,b>0时过第一、二、四象限.故选A13.A、根据图象知,水库的蓄水量因该随着降雨的时间的增加而增多;故本选项错误;B、本图象的直线,所以每天的降雨量是相等的,所以,蓄水库每天的增加的水的量是(40﹣10)÷6=5;故本选项正确;C、根据图示知,降雨开始时,蓄水量为10万米3,故本选项错误;D、根据图示知,降雨第6天,蓄水量增加了40万米3﹣30万米3=10万米3,故本选项错误;故选B14.根据题意列出关系式为:y=40﹣5t,考虑实际情况:拖拉机开始工作时,油箱中有油4升,即开始时,函数图象与y轴交于点(0,40),如果每小时耗油0.5升,且8小时,耗完油,故函数图象为一条线段.故选D15.∵正比例函数y=kx的图象经过第一、三象限,∴k>0,∴﹣k<0,∴y=kx﹣k的大致图象经过一、三、四象限,故选:B.16.由图形可知,该函数过点(0,2),(3,0),故斜率k==,所以解析式为y=,令y>2,即>2,解之得:x<017.根据题意,要求y<0时,x的范围,即:x+3<0,解可得:x<﹣2,故答案为x<﹣218.根据题意,观察图象,可得直线l过点(2,0),且y随x的增大而增大,分析可得,当x>2时,有y>0 19.根据图示及数据可知:①一次函数y1=kx+b的图象经过第二、四象限,则k<0正确;②y2=x+a的图象经与y轴交与负半轴,则a>0错误;③一次函数y1=kx+b与y2=x+a的图象交点的横坐标是3,所以当x=3时,y1=y2正确;④当x>3时,y1<y2正确;故正确的判断是①,③,④20.根据图示可知点P的坐标是(﹣4,2),所以y1>y2即直线1在直线2的上方,则x<﹣4.21.根据图象和数据可知,当y<0即图象在x轴下侧,x<1.故答案为x<122.函数与坐标轴的交点的坐标为(0,3),(6,0).(1)点A的坐标(﹣4,5);(2)和y轴的距离是2个单位长度的点的坐标M(2,2),N(﹣2,4)23.当x=0时,y=﹣4;当y=0时,2x﹣4=0,解得x=2,∴函数图象与两坐标轴的交点为(0,﹣4)(2,0).图象如下:(1)x=﹣2时,y=2×(﹣2)﹣4=﹣8,x=4时,y=2×4﹣4=4,∵k=2>0,∴y随x的增大而增大,∴﹣8≤y≤4;(2)x<2时,y<0;x=2时,y=0;x>2时,y>0.24.(1)由图象可看出当y=2.5时,x=5,因此x的取值范围应该是0<x≤5(y轴上的点是空心圆,因此x≠0);(2)由图象可看出,当x=5时,函数的值最小,是y=2.525.(1)如图所示:(2)由(1)中两函数图象可知,其交点坐标为(1,1);(3)由(1)中两函数图象可知,当x>1时,y1>y2.26.如图.(1)因为一次项系数是﹣3<0,所以y的值随x的增大而减小;(2)当y=0时,x=1,所以图象与x轴的交点坐标是(1,0);当x=0时,y=3,所以图象与y轴的交点坐标是(0,3);(3)由图象知,在A点左边,图象在x轴上方,函数值大于0.所以x≤1时,y≥0.(4)∵OA=1,OB=3,∴函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是S△AOB=×1×3=.27.(1)函数y=2x﹣1与坐标轴的坐标为(0,﹣1)(,0),描点即可,如图所示;(2)将A、B的坐标代入函数式中,可得出A点不在直线y=2x﹣1的图象上,B点在直线y=2x﹣1的图象上,A代入函数后发现﹣ 2.5×2﹣1=﹣6≠﹣4,因此A点不在函数y=2x﹣1的图象上,然后用同样的方法判定B是否在函数的图象上;(3)当y≤0时,2x﹣1≤0,因此x≤.28.(1)当x=﹣4时,y=2;当y=﹣2时,x=﹣2;(2)由(1)可知函数图象过(﹣4,2)、(﹣2,﹣2),由此可画出函数的图象,如下图所示:(3)∵y=﹣2x﹣6,﹣4≤y≤2∴﹣4≤﹣2x﹣6≤22≤﹣2x≤8﹣4≤x≤﹣129.(1)图象如图:(2)观察图象可得,当x>﹣3时,y>0;当x=﹣3时,y=0;当x<﹣3时,y<0.30.(1)列表:x 0 1y 2 0描点,连线(如图)…(也可以写成过点(0,2)和(1,0)画直线)(2)①(1,0);(0,2)②<1。
初中数学一次函数的图像专项练习30题(有答案)ok之欧阳德创编

一次函数的图像专项练习30题(有答案)时间:2021.03.07 创作:欧阳德1.函数y=ax+b与y=bx+a的图象在同一坐标系内的大致位置正确的是()A.B.C.D.2.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x>2时,y2>y1,其中正确的个数是()A.0B.1C.2D.33.一次函数y=kx+b,y随x的增大而减小,且kb>0,则在直角坐标系内它的大致图象是()A.B.C.D.4.下列函数图象不可能是一次函数y=ax﹣(a﹣2)图象的是()A .B .C .D .5.如图所示,如果k•b<0,且k <0,那么函数y=kx+b的图象大致是( )A .B .C .D .6.如图,直线l1:y=x+1与直线l2:y=﹣x ﹣把平面直角坐标系分成四个部分,则点(,)在( ) A . 第一部分 B . 第二部分 C . 第三部分D . 第四部分 7.已知正比例函数y=﹣kx 和一次函数y=kx ﹣2(x 为自变量),它们在同一坐标系内的图象大致是( )A .B .C .D .8.函数y=2x+3的图象是( )A . 过点(0,3),(0,﹣)的直线B . 过点(1,5),(0,﹣)的直线C . 过点(﹣1,﹣1),(﹣,0)的直线D . 过点(0,3),(﹣,0)的直线 9.下列图象中,与关系式y=﹣x ﹣1表示的是同一个一次函数的图象是( )A.B.C.D.10.函数kx﹣y=2中,y随x的增大而减小,则它的图象是下图中的()A.B.C.D.11.已知直线y1=k1x+b1,y2=k2x+b2,满足b1<b2,且k1k2<0,两直线的图象是()A.B.C.D.12.如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是()A.B.C.D.13.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若该水库的蓄水量V(万米3)与降雨的时间t(天)的关系如图所示,则下列说法正确的是()A.降雨后,蓄水量每天减少5万米3 B.降雨后,蓄水量每天增加5万米3 C.降雨开始时,蓄水量为20万米3 D.降雨第6天,蓄水量增加40万米3 14.拖拉机开始行驶时,油箱中有油4升,如果每小时耗油0.5升,那么油箱中余油y(升)与它工作的时间t(时)之间的函数关系的图象是()A.B.C.D.15.已知正比例函数y=kx的图象经过第一、三象限,则y=kx﹣k的大致图象可能是下图的()A.B.C.D.16.一次函数y=kx+b的图象如图所示,当x_________ 时,y>2.17.一次函数的图象如图所示,根据图象可知,当x _________ 时,有y<0.18.如图,直线l是一次函数y=kx+b的图象,当x_________ 时,y>0.19.一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x=3时,y1=y2;④当x>3时,y1<y2中,正确的判断是_________ .20.如图,已知函数y1=ax+b和y2=kx的图象交于点P,则根据图象可得,当x _________ 时,y1>y2.21.已知一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是_________ .22.在平面直角坐标系中画出函数的图象.(1)在图象上标出横坐标为﹣4的点A,并写出它的坐标;(2)在图象上标出和y轴的距离是2个单位长度的点,并写出它的坐标.23.作函数y=2x﹣4的图象,并根据图象回答下列问题.(1)当﹣2≤x≤4,求函数y的取值范围.(2)当x取何值时,y<0?y=0?y>0?24.如图是一次函数y=﹣x+5图象的一部分,利用图象回答下列问题:(1)求自变量的取值范围.(2)在(1)在条件下,y是否有最小值?如果有就求出最小值;如果没有,请说明理由.25.已知函数y1=﹣x+和y2=2x﹣1.(1)在同一个平面直角坐标系中画出这两个函数的图象;(2)根据图象,写出它们的交点坐标;(3)根据图象,试说明当x取什么值时,y1>y2?26.作出函数y=3﹣3x的图象,并根据图象回答下列问题:(1)y的值随x的增大而_________ ;(2)图象与x轴的交点坐标是_________ ;与y轴的交点坐标是_________ ;(3)当x _________ 时,y≥0;(4)函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是多少?27.已知函数y=2x﹣1.(1)在直角坐标系中画出这函数的图象;(2)判断点A(﹣2.5,﹣4),B(2.5,4)是否在函数y=2x﹣1的图象上;(3)当x取什么值时,y≤0.28.已知函数y=﹣2x﹣6.(1)求当x=﹣4时,y的值,当y=﹣2时,x的值.(2)画出函数图象.(3)如果y的取值范围﹣4≤y≤2,求x的取值范围.29.已知一次函数的图象经过点A(﹣3,0),B(﹣1,1)两点.(1)画出图象;(2)x为何值时,y>0,y=0,y<0?30.已知一次函数y=﹣2x+2,(1)在所给的平面直角坐标系中画出它的图象;(2)根据图象回答问题:①图象与x轴的交点坐标是_________ ,与y轴的交点坐标是_________ ;②当x _________ 时,y>0.参考答案:1.分四种情况:①当a>0,b>0时,y=ax+b的图象经过第一、二、三象限,y=bx+a的图象经过第一、二、三象限,无选项符合;②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a的图象经过第一、二、四象限,C选项符合;③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a的图象经过第一、三、四象限,无选项符合;④当a<0,b<0时,y=ax+b的图象经过第二、三、四象限;y=bx+a的图象经过第二、三、四象限,无选项符合.故选C2.由一次函数y1=kx+b与y2=x+a的图象可知k<0,a<0,当x>2时,y2>y1,①③正确.故选C 3.∵一次函数y=kx+b,y随x的增大而减小,∴k<0,又∵kb>0,∴b<0,∴函数的图象经过第二、三、四象限.故选C4.根据图象知:A、a>0,﹣(a﹣2)>0.解得0<a<2,所以有可能;B、a<0,﹣(a﹣2)<0.解得两不等式没有公共部分,所以不可能;C、a<0,﹣(a﹣2)>0.解得a<0,所以有可能;D、a>0,﹣(a﹣2)<0.解得a>2,所以有可能.故选B5.∵k•b<0,且k<0,∴b>0,k<0,∴函数y=kx+b 的图象经过第一、二、四象限,故选D6.由题意可得,解得,故点(,)应在交点的上方,即第二部分.故选B.7.分两种情况:(1)当k>0时,正比例函数y=﹣kx 的图象过原点、第一、三象限,一次函数y=kx﹣2的图象经过第一、三、四象限,选项A符合;(2)当k<0时,正比例函数y=﹣kx的图象过原点、第二、四象限,一次函数y=kx﹣2的图象经过第二、三、四象限,无选项符合.故选A.8.A、把x=0代入函数关系式得2×0+3=3,故函数图象过点(0,3),不过(0,﹣),故错误;B、由A知函数图象不过点(0,﹣),故错误;C、把x=﹣1代入函数关系式得,2×(﹣1)+3=1,故(﹣1,﹣1)不在函数图象上,故错误;D、分别令x=0,y=0,此函数成立,故正确.故选D 9.函数y=﹣x﹣1是一次函数,其图象是一条直线.当x=0时,y=﹣1,所以直线与y轴的交点坐标是(0,﹣1);当y=0时,x=﹣1,所以直线与x轴的交点坐标是(﹣1,0).由两点确定一条直线,连接这两点就可得到y=﹣x﹣1的图象.故选D10.整理为y=kx﹣2∵y随x的增大而减小∴k<0又因为图象过2,4,3象限故选D.11.k1k2<0,则k1与k2异号,因而两个函数一个y随x的增大而增大,另一个y随x 的增大而减小,因而A是错误的;b1<b2,则y1与y轴的交点在y2与y轴的交点的下边,因而B、C都是错误的.故选D.12.①当ab>0,正比例函数y=abx过第一、三象限;a与b同号,同正时y=ax+b过第一、二、三象限,故D错误;同负时过第二、三、四象限,故B错误;②当ab<0时,正比例函数y=abx过第二、四象限;a与b异号,a>0,b<0时y=ax+b过第一、三、四象限,故C错误;a<0,b>0时过第一、二、四象限.故选A13.A、根据图象知,水库的蓄水量因该随着降雨的时间的增加而增多;故本选项错误;B、本图象的直线,所以每天的降雨量是相等的,所以,蓄水库每天的增加的水的量是(40﹣10)÷6=5;故本选项正确;C、根据图示知,降雨开始时,蓄水量为10万米3,故本选项错误;D、根据图示知,降雨第6天,蓄水量增加了40万米3﹣30万米3=10万米3,故本选项错误;故选B 14.根据题意列出关系式为:y=40﹣5t,考虑实际情况:拖拉机开始工作时,油箱中有油4升,即开始时,函数图象与y轴交于点(0,40),如果每小时耗油0.5升,且8小时,耗完油,故函数图象为一条线段.故选D15.∵正比例函数y=kx的图象经过第一、三象限,∴k >0,∴﹣k<0,∴y=kx﹣k的大致图象经过一、三、四象限,故选:B.16.由图形可知,该函数过点(0,2),(3,0),故斜率k==,所以解析式为y=,令y>2,即>2,解之得:x<017.根据题意,要求y<0时,x的范围,即:x+3<0,解可得:x<﹣2,故答案为x<﹣218.根据题意,观察图象,可得直线l过点(2,0),且y随x的增大而增大,分析可得,当x>2时,有y >019.根据图示及数据可知:①一次函数y1=kx+b的图象经过第二、四象限,则k<0正确;②y2=x+a的图象经与y轴交与负半轴,则a>0错误;③一次函数y1=kx+b与y2=x+a的图象交点的横坐标是3,所以当x=3时,y1=y2正确;④当x>3时,y1<y2正确;故正确的判断是①,③,④20.根据图示可知点P的坐标是(﹣4,2),所以y1>y2即直线1在直线2的上方,则x<﹣4.21.根据图象和数据可知,当y<0即图象在x轴下侧,x<1.故答案为x<122.函数与坐标轴的交点的坐标为(0,3),(6,0).(1)点A的坐标(﹣4,5);(2)和y轴的距离是2个单位长度的点的坐标M(2,2),N(﹣2,4)23.当x=0时,y=﹣4;当y=0时,2x﹣4=0,解得x=2,∴函数图象与两坐标轴的交点为(0,﹣4)(2,0).图象如下:(1)x=﹣2时,y=2×(﹣2)﹣4=﹣8,x=4时,y=2×4﹣4=4,∵k=2>0,∴y随x的增大而增大,∴﹣8≤y≤4;(2)x<2时,y<0;x=2时,y=0;x>2时,y>0.24.(1)由图象可看出当y=2.5时,x=5,因此x的取值范围应该是0<x≤5(y轴上的点是空心圆,因此x≠0);(2)由图象可看出,当x=5时,函数的值最小,是y=2.5 25.(1)如图所示:(2)由(1)中两函数图象可知,其交点坐标为(1,1);(3)由(1)中两函数图象可知,当x>1时,y1>y2.26.如图.(1)因为一次项系数是﹣3<0,所以y的值随x的增大而减小;(2)当y=0时,x=1,所以图象与x轴的交点坐标是(1,0);当x=0时,y=3,所以图象与y轴的交点坐标是(0,3);(3)由图象知,在A点左边,图象在x轴上方,函数值大于0.所以x≤1时,y≥0.(4)∵OA=1,OB=3,∴函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是S△AOB=×1×3=.27.(1)函数y=2x﹣1与坐标轴的坐标为(0,﹣1)(,0),描点即可,如图所示;(2)将A、B的坐标代入函数式中,可得出A点不在直线y=2x﹣1的图象上,B点在直线y=2x﹣1的图象上,A代入函数后发现﹣2.5×2﹣1=﹣6≠﹣4,因此A点不在函数y=2x﹣1的图象上,然后用同样的方法判定B 是否在函数的图象上;(3)当y≤0时,2x﹣1≤0,因此x≤.28.(1)当x=﹣4时,y=2;当y=﹣2时,x=﹣2;(2)由(1)可知函数图象过(﹣4,2)、(﹣2,﹣2),由此可画出函数的图象,如下图所示:(3)∵y=﹣2x﹣6,﹣4≤y≤2∴﹣4≤﹣2x﹣6≤22≤﹣2x≤8﹣4≤x≤﹣129.(1)图象如图:(2)观察图象可得,当x>﹣3时,y>0;当x=﹣3时,y=0;当x<﹣3时,y<0.30.(1)列表:x 0 1y 2 0描点,连线(如图)…(也可以写成过点(0,2)和(1,0)画直线)(2)①(1,0);(0,2)②<1。
(2021年整理)初中数学一次函数的图像专项练习30题(有答案)ok

初中数学一次函数的图像专项练习30题(有答案)ok编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(初中数学一次函数的图像专项练习30题(有答案)ok)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为初中数学一次函数的图像专项练习30题(有答案)ok的全部内容。
一次函数的图像专项练习30题(有答案)1.函数y=ax+b与y=bx+a的图象在同一坐标系内的大致位置正确的是()A.B.C.D.2.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x>2时,y2>y1,其中正确的个数是( )A.0B.1C.2D.33.一次函数y=kx+b,y随x的增大而减小,且kb>0,则在直角坐标系内它的大致图象是()A.B.C.D.4.下列函数图象不可能是一次函数y=ax﹣(a﹣2)图象的是()A.B.C.D.5.如图所示,如果k•b<0,且k<0,那么函数y=kx+b的图象大致是()6.如图,直线l1:y=x+1与直线l2:y=﹣x ﹣把平面直角坐标系分成四个部分,则点(,)在( )A.第一部分B.第二部分C.第三部分D.第四部分7.已知正比例函数y=﹣kx和一次函数y=kx﹣2(x为自变量),它们在同一坐标系内的图象大致是()A.B.C.D.8.函数y=2x+3的图象是()A.过点(0,3),(0,﹣)的直线B.过点(1,5),(0,﹣)的直线C.过点(﹣1,﹣1),(﹣,0)的直线D.过点(0,3),(﹣,0)的直线9.下列图象中,与关系式y=﹣x﹣1表示的是同一个一次函数的图象是( )10.函数kx﹣y=2中,y随x的增大而减小,则它的图象是下图中的()A.B.C.D.11.已知直线y1=k1x+b1,y2=k2x+b2,满足b1<b2,且k1k2<0,两直线的图象是() A.B.C.D.12.如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是()A.B.C.D.13.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若该水库的蓄水量V(万米3)与降雨的时间t(天)的关系如图所示,则下列说法正确的是()A.降雨后,蓄水量每天减少5万米3B.降雨后,蓄水量每天增加5万米3C.降雨开始时,蓄水量为20万米3D.降雨第6天,蓄水量增加40万米314.拖拉机开始行驶时,油箱中有油4升,如果每小时耗油0。
八年级数学:一次函数的图像练习(含解析)

八年级数学:一次函数的图像练习(含解析)1.一次函数y=x+2的图像大致是下图中的( A )解析:根据直线y=x+2与y轴和x轴的交点分别是(0,2)和(-2,0),观察得到选项A.故选A.2.若一次函数y=3x+k的图像过点(1,2),则函数y=kx+2的图像大致为下图中的( A )解析:把(1,2)代入y=3x+k,得k=-1,则y=kx+2为y=-x+2,故图像为A.故选A.3.直线y=kx-1一定经过点( D )A.(1,0) B.(1,k) C.(0,k) D.(0,-1)解析:当x=0时,y=-1.故选D.4.(2017·沈阳)在平面直角坐标系中,一次函数y=x-1的图像是( B )解析:一次函数y=x-1,其中k=1,b=-1,其图像为,故选B.5.若k≠0,b<0,则y=kx+b的图像可能是( B )解析:一次函数,k≠0,不可能与x轴平行,排除D选项;b<0,说明图像过第三、四象限,排除A,C选项.故选B.6.已知一条直线y=kx+b,其中k+b=-5,kb=6,那么该直线经过( D )A.第二、四象限B.第一、二、三象限C.第一、三象限D.第二、三、四象限解析:由kb=6,k+b=-5.知k<0,b<0,∴图像经过第二、三、四象限.故选D.7.如图,表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)的图像是( A )解析:由A中正比例函数图像可知mn<0,∴m与n异号.由一次函数可知m<0,n>0,∴A 选项中图像与描述一致,故选A.8.如图,是一个正比例函数的图像,把该图像向左平移一个单位长度,得到的函数图像的表达式为y=-2x-2.解析:正比例函数为y=-2x,图像向左平移一个单位长度则x+1,即y=-2(x+1)=-2x-2.9.一次函数y=3x-6的图像与坐标轴围成的三角形的面积是6.解析:y=3x-6与x轴交于(2,0),与y轴交于(0,-6),∴S=12×2×6=6.10.已知y+1与2-x成正比,且当x=-1时,y=5,则y与x的函数关系式是y=-2x+3.解析:设y+1=k(2-x)(k≠0),把x=-1,y=5代入得5+1=k(2+1),解得k=2,则y+1=2(2-x),即y=-2x+3.11.已知一次函数y=kx+2的图像经过A(-1,1).(1)求此一次函数的表达式;(2)求这个一次函数图像与x轴的交点B的坐标,画出函数图像;(3)求△AOB的面积.解:(1)将A(-1,1)的坐标代入一次函数y=kx+2,解得k=1,故其表达式为y=x+2.(2)令y=0,解得x=-2,故该一次函数的图像与x轴交于点B(-2,0).函数图像如图.(3)过A作AC⊥x轴于点C,△AOB的面积=12OB·AC=12×2×1=1.12.在同一平面直角坐标系中画出一次函数y=32x与y=32x+3的图像,并根据图像回答:(1)两个函数的图像有什么位置关系?你是怎样看出的?(2)其中一个函数图像能否通过平移得到另一个函数图像?若能,说出你的平移方法.解:对于y=32x,当x=0时,y=0;当x=2时,y=3.对于y=32x+3,当x=0时,y=3;当y=0时,解得x=-2.过点(0,0)与(2,3)画直线,则得到y=32x的图像;过点(-2,0)与(0,3)画直线,则得到y=32x+3的图像,如图所示.(1)两个函数图像互相平行.理由为:因为点A与B的纵坐标相同、横坐标相差2,点O与C的纵坐标相同、横坐标相差2,所以两个函数图像互相平行.(2)能.平移方法不唯一,如:把函数y=32x的图像向左平移2个单位长度则得到函数y=32x+3的图像.。
(最新整理)初中数学一次函数的图像专项练习30题(有答案)ok

初中数学一次函数的图像专项练习30题(有答案)ok编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(初中数学一次函数的图像专项练习30题(有答案)ok)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为初中数学一次函数的图像专项练习30题(有答案)ok的全部内容。
.B.C.D..B.C.D..B.C.D.y=﹣x﹣把平面直角坐标系分成四个部分,则点(,) .B.C.D.,﹣)的直线),(0,﹣),(﹣,(﹣,.B.C.D..B.C.D..B.C.D..B.C.D..B.C.D..一次函数的图象如图所示,根据图象可知,当18.如图,直线l是一次函数y=kx+b的图象,当x _________ 时,y>0.19.一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x=3时,y1=y2;④当x>3时,y1<y2中,正确的判断是 _________ .20.如图,已知函数y1=ax+b和y2=kx的图象交于点P,则根据图象可得,当x _________ 时,y1>y2.21.已知一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是 _________ .22.在平面直角坐标系中画出函数的图象.(1)在图象上标出横坐标为﹣4的点A,并写出它的坐标;(2)在图象上标出和y轴的距离是2个单位长度的点,并写出它的坐标.23.作函数y=2x﹣4的图象,并根据图象回答下列问题.(1)当﹣2≤x≤4,求函数y的取值范围.(2)当x取何值时,y<0?y=0?y>0?24.如图是一次函数y=﹣x+5图象的一部分,利用图象回答下列问题:(1)求自变量的取值范围.(2)在(1)在条件下,y是否有最小值?如果有就求出最小值;如果没有,请说明理由.25.已知函数y1=﹣x+和y2=2x﹣1.(1)在同一个平面直角坐标系中画出这两个函数的图象;(2)根据图象,写出它们的交点坐标;(3)根据图象,试说明当x取什么值时,y1>y2?26.作出函数y=3﹣3x的图象,并根据图象回答下列问题:(1)y的值随x的增大而 _________ ;(2)图象与x轴的交点坐标是 _________ ;与y轴的交点坐标是 _________ ;(3)当x _________ 时,y≥0;(4)函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是多少?27.已知函数y=2x﹣1.(1)在直角坐标系中画出这函数的图象;(2)判断点A(﹣2。
初中数学一次函数的图像专项练习30题(有答案解析)ok
参考答案ax+b的图象经过第一、二、三象限,y=bx+a的图象经过第一、二、三象限,无选项符合;
②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a的图象经过第一、二、四象限,C选项符合;
③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a的图象经过第一、三、四象限,无选项符合;
9.函数y=﹣x﹣1是一次函数,其图象是一条直线.
当x=0时,y=﹣1,所以直线与y轴的交点坐标是(0,﹣1);
当y=0时,x=﹣1,所以直线与x轴的交点坐标是(﹣1,0).
由两点确定一条直线,连接这两点就可得到y=﹣x﹣1的图象.故选D
10.整理为y=kx﹣2∵y随x的增大而减小∴k<0又因为图象过2,4,3象限故选D.
(3)由(1)中两函数图象可知,当x>1时,y1>y2.
26.如图.
(1)因为一次项系数是﹣3<0,所以y的值随x的增大而减小;
(2)当y=0时,x=1,所以图象与x轴的交点坐标是(1,0);
当x=0时,y=3,所以图象与y轴的交点坐标是(0,3);
(3)由图象知,在A点左边,图象在x轴上方,函数值大于0.所以x≤1时,y≥0.
C、根据图示知,降雨开始时,蓄水量为10万米3,故本选项错误;
D、根据图示知,降雨第6天,蓄水量增加了40万米3﹣30万米3=10万米3,故本选项错误;故选B
14.根据题意列出关系式为:y=40﹣5t,考虑实际情况:
拖拉机开始工作时,油箱中有油4升,即开始时,函数图象与y轴交于点(0,40),
如果每小时耗油0.5升,且8小时,耗完油,故函数图象为一条线段.故选D
八年级数学一次函数图象性质 专项练习题(含答案)

参考答案 1、B 2、C ; 3、A 4、C 5、C 6、B 7、A 8、C 9、A 10、C 11、A 12、D 13、B 14、A 15、A 16、A 17、A 18、C 19、D 20、A 21、 22、y=23、答案为 1. 24、-3 25、一、二、三. 26、2 . 27、3 28、答案是:3. 29、答案为 y=3x+4. 30、(0,-1) ;
m313将直线ykx1向上平移2个单位长度可得直线的解析式为aykx3bykx1cykx3dykx114直线y2xb与x轴的交点坐标是20则关于x的方程2xb0的解是ax2bx4cx8dx1015如图直线ykxb与x轴y轴分别相交于点a30b02则不等式kxb0的解集是ax3bx3cx2dx216同一直角坐标系中一次函数y1k1xb与正比例函数y2k2x的图象如图所示则满足y1y2的x取值范围是ax2bx2cx2dx217点ax1y1点bx2y2是一次函数y2x4图象上的两点且x1x2则y1与y2的大小关系是ay1y2by1y20cy1y2dy1y218已知a320则一次函数yaxb的图象不经过6)在 y=k1x 上∴﹣6=3k1∴k1=﹣2 ∵点 P(3,﹣6)在 y=k2x﹣9 上∴﹣6=3k2﹣9∴k2=1; (2)∵k2=1,∴y=x﹣9∵一次函数 y=x﹣9 与 x 轴交于点 A 又∵当 y=0 时,x=9∴A(9,0). 33、(1) ;(2)23;
八年级数学一次函数图象性质 专项练习题
一、选择题: 1、下列函数(1)y=3πx;(2)y=8x-6;(3)y= ( ) A.4 个 2、函数 A.(3,5); B.3 个 C.2 个 D.1 个
1 ;(4)y= -8x;(5)y=5x2-4x+1 中,是一次函数的有 x
初中数学一次函数图像专项练习30题(有答案)ok

)))))))))一次函数的图像专项练习30题(有答案)1.函数y=ax+b与y=bx+a的图象在同一坐标系内的大致位置正确的是()2.一次函数y=kx+b与y=x+a的图象如图,则下列结论:①k<0;②a>0;③当x>2时,y>y,其中正确的1212个数是()0 2 1 3 D.A.C.B.3.一次函数y=kx+b,y随x的增大而减小,且kb>0,则在直角坐标系内它的大致图象是()A.B.C.D.4.下列函数图象不可能是一次函数y=ax﹣(a﹣2)图象的是()A.B.C.D.5.如图所示,如果k?b<0,且k<0,那么函数y=kx+b的图象大致是()A.B.C.D.6.如图,直线l:y=x+1与直线l:y=﹣x﹣把平面直角坐标系分成四个部分,则点(,)在()21)))))))))).)))))))))二部分B.第第三部分D.第四部分A.第一部分C.)(x为自变量),它们在同一坐标系内的图象大致是(﹣7.已知正比例函数y=﹣kx和一次函数y=kx2 .C.DA.B.)y=2x+3的图象是(8.函数..BA 0(,﹣)的直线过点(1,,﹣过点(0,3),(0)的直线5),D.C.,0)的直线,3,),(﹣0)的直线),(﹣过点(0过点(﹣1,﹣1)x﹣1表示的是同一个一次函数的图象是(9.下列图象中,与关系式y=﹣.D C.A.B.)x的增大而减小,则它的图象是下图中的(10.函数kx﹣y=2中,y随D.C.B..A),两直线的图象是(0b=kyx+b,满足b<,且kk<,=k11.已知直线yx+b2221122111D.B.C.A.)ab是常数,且≠0)的图象是(bay=abxy=ax+b12.如图所示,表示一次函数与正比例函数(,)))))))))).)))))))))D.B.C.A.3(天)t)V(万米与降雨的时间13.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若该水库的蓄水量)的关系如图所示,则下列说法正确的是(33B.A.降雨后,蓄水量每天减少5降雨后,蓄水量每天增加5万米万米33.C D.降雨开始时,蓄水量为20万米40降雨第6天,蓄水量增加万米(时)14.拖拉机开始行驶时,油箱中有油(升)与它工作的时间ty4升,如果每小时耗油0.5升,那么油箱中余油)之间的函数关系的图象是(D....A B C)的大致图象可能是下图的(15.已知正比例函数y=kx的图象经过第一、三象限,则y=kx ﹣k...A B.C D.>2y.一次函数16y=kx+b的图象如图所示,当x_________时,时,有.y<0的图象如图所示,根据图象可知,当17.一次函数x_________)))))))))).)))))))))0.时,y>18.如图,直线l是一次函数y=kx+b的图象,当x_________的图象如图所示,则下列结论:与y=kx+by=x+a19.一次函数21<yy中,④当x>3时,;③<①k0;②a>0;当x=3时,y=y2211 _________.正确的判断是y._________时,y>=kx.如图,已知函数y=ax+b和y的图象交于点P,则根据图象可得,当x202121._________y<0时,x的取值范围是的图象如图所示,当21.已知一次函数y=kx+b.在平面直角坐标系中画出函数22的图象.,并写出它的坐标;4)在图象上标出横坐标为﹣的点A(1 2个单位长度的点,并写出它的坐标.y(2)在图象上标出和轴的距离是)))))))))).)))))))))4的图象,并根据图象回答下列问题.23.作函数y=2x﹣y的取值范围.≤4,求函数(1)当﹣2≤x ?y>0y<0?y=0?x(2)当取何值时,图象的一部分,利用图象回答下列问题:﹣24.如图是一次函数y=x+5 )求自变量的取值范围.(1 y是否有最小值?如果有就求出最小值;如果没有,请说明理由.)在((21)在条件下,.﹣1﹣=2xx+和y=25.已知函数y21)在同一个平面直角坐标系中画出这两个函数的图象;(1 2)根据图象,写出它们的交点坐标;(?y>yx(3)根据图象,试说明当取什么值时,21)))))))))).)))))))))26.作出函数y=3﹣3x的图象,并根据图象回答下列问题:(1)y的值随x的增大而_________;(2)图象与x轴的交点坐标是_________;与y轴的交点坐标是_________;(3)当x_________时,y≥0;(4)函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是多少?27.已知函数y=2x﹣1.(1)在直角坐标系中画出这函数的图象;(2)判断点A(﹣2.5,﹣4),B(2.5,4)是否在函数y=2x﹣1的图象上;(3)当x取什么值时,y≤0.28.已知函数y=﹣2x﹣6.(1)求当x=﹣4时,y的值,当y=﹣2时,x的值.(2)画出函数图象.(3)如果y的取值范围﹣4≤y≤2,求x的取值范围.29.已知一次函数的图象经过点A(﹣3,0),B(﹣1,1)两点.(1)画出图象;(2)x为何值时,y>0,y=0,y<0?)))))))))).)))))))))30.已知一次函数y=﹣2x+2,(1)在所给的平面直角坐标系中画出它的图象;(2)根据图象回答问题:①图象与x轴的交点坐标是_________,与y轴的交点坐标是_________;②当x_________时,y>0.)))))))))).)))))))))参考答案:1.分四种情况:①当a>0,b>0时,y=ax+b的图象经过第一、二、三象限,y=bx+a的图象经过第一、二、三象限,无选项符合;②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a的图象经过第一、二、四象限,C选项符合;③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a的图象经过第一、三、四象限,无选项符合;④当a<0,b<0时,y=ax+b的图象经过第二、三、四象限;y=bx+a的图象经过第二、三、四象限,无选项符合.故选C2.由一次函数y=kx+b与y=x+a的图象可知k<0,a<0,当x>2时,y>y,①③正确.故选C 12123.∵一次函数y=kx+b,y随x的增大而减小,∴k<0,又∵kb>0,∴b<0,∴函数的图象经过第二、三、四象限.故选C4.根据图象知:A、a>0,﹣(a﹣2)>0.解得0<a<2,所以有可能;B、a<0,﹣(a﹣2)<0.解得两不等式没有公共部分,所以不可能;C、a<0,﹣(a﹣2)>0.解得a<0,所以有可能;D、a>0,﹣(a﹣2)<0.解得a>2,所以有可能.故选B5.∵k?b<0,且k<0,∴b>0,k<0,∴函数y=kx+b的图象经过第一、二、四象限,故选D.由题意可得,6,)应在交点的上方,即第二部分.故选B,故点(.解得7.分两种情况:(1)当k>0时,正比例函数y=﹣kx的图象过原点、第一、三象限,一次函数y=kx﹣2的图象经过第一、三、四象限,选项A符合;(2)当k<0时,正比例函数y=﹣kx的图象过原点、第二、四象限,一次函数y=kx﹣2的图象经过第二、三、四象限,无选项符合.故选A.,﹣)0,故错误;,故函数图象过点(0,3),不过(8.A、把x=0代入函数关系式得2×0+3=3,﹣)0,故错误;B、由A知函数图象不过点(C、把x=﹣1代入函数关系式得,2×(﹣1)+3=1,故(﹣1,﹣1)不在函数图象上,故错误;D、分别令x=0,y=0,此函数成立,故正确.故选D9.函数y=﹣x﹣1是一次函数,其图象是一条直线.当x=0时,y=﹣1,所以直线与y轴的交点坐标是(0,﹣1);当y=0时,x=﹣1,所以直线与x轴的交点坐标是(﹣1,0).由两点确定一条直线,连接这两点就可得到y=﹣x﹣1的图象.故选D10.整理为y=kx﹣2∵y随x的增大而减小∴k<0又因为图象过2,4,3象限故选D.11.kk<0,则k与k异号,2211因而两个函数一个y随x的增大而增大,另一个y随x的增大而减小,因而A是错误的;b<b,则y与y轴的交点在y与y轴的交点的下边,因而B、C都是错误的.2112故选D.)))))))))).)))))))))12.①当ab>0,正比例函数y=abx过第一、三象限;a与b同号,同正时y=ax+b过第一、二、三象限,故D错误;同负时过第二、三、四象限,故B错误;②当ab<0时,正比例函数y=abx过第二、四象限;a与b异号,a>0,b<0时y=ax+b过第一、三、四象限,故C错误;a<0,b>0时过第一、二、四象限.故选A13.A、根据图象知,水库的蓄水量因该随着降雨的时间的增加而增多;故本选项错误;B、本图象的直线,所以每天的降雨量是相等的,所以,蓄水库每天的增加的水的量是(40﹣10)÷6=5;故本选项正确;3C、根据图示知,降雨开始时,蓄水量为10万米,故本选项错误;333D、根据图示知,降雨第6天,蓄水量增加了40万米﹣30万米=10万米,故本选项错误;故选B14.根据题意列出关系式为:y=40﹣5t,考虑实际情况:拖拉机开始工作时,油箱中有油4升,即开始时,函数图象与y轴交于点(0,40),如果每小时耗油0.5升,且8小时,耗完油,故函数图象为一条线段.故选D15.∵正比例函数y=kx的图象经过第一、三象限,∴k>0,∴﹣k<0,∴y=kx﹣k的大致图象经过一、三、四象限,故选:B.=,k= 3,0),故斜率16.由图形可知,该函数过点(0,2),(2,,即>2所以解析式为,令y=y>0x<解之得:,故答案为2x<﹣217.根据题意,要求y<0时,x的范围,即:x+3<0,解可得:x<﹣y>0随18.根据题意,观察图象,可得直线l过点(2,0),且yx的增大而增大,分析可得,当x>2时,有正确;<0y19.根据图示及数据可知:①一次函数=kx+b的图象经过第二、四象限,则k1 0错误;a②y=x+a的图象经与y轴交与负半轴,则>2正确;,所以当③一次函数y=kx+b与y=x+a的图象交点的横坐标是3x=3时,y=y2112<④当x>3时,yy正确;21故正确的判断是①,③,④.x的上方,则<﹣4y>y即直线1在直线2的坐标是(﹣20.根据图示可知点P4,2),所以21 1.故答案为轴下侧,x<1x<<21.根据图象和数据可知,当y0即图象在x.6,(,0)22.函数与坐标轴的交点的坐标为(0,3)(1)点A的坐标(﹣4,5);(2)和y轴的距离是2个单位长度的点的坐标M(2,2),N(﹣2,4)23.当x=0时,y=﹣4;当y=0时,2x﹣4=0,解得x=2,∴函数图象与两坐标轴的交点为(0,﹣4)(2,0).图象如下:(1)x=﹣2时,y=2×(﹣2)﹣4=﹣8,x=4时,y=2×4﹣4=4,∵k=2>0,∴y随x的增大而增大,∴﹣8≤y≤4;(2)x<2时,y<0;x=2时,y=0;x>2时,y>0.)))))))))).))))))))));轴上的点是空心圆,因此x≠00<x≤5(yx=524.(1)由图象可看出当y=2.5时,,因此x 的取值范围应该是y=2.5 x=5时,函数的值最小,是(2)由图象可看出,当1)如图所示:25.();1,1(2)由(1)中两函数图象可知,其交点坐标为(.y>y1)由(1)中两函数图象可知,当x>时,(321.如图.26 的增大而减小;y的值随x1)因为一次项系数是﹣3<0,所以(;0),所以图象与x=1x轴的交点坐标是(1,(2)当y=0时,;3),所以图象与y轴的交点坐标是(0,当x=0时,y=3 0.1时,y≥≤3)由图象知,在A点左边,图象在x轴上方,函数值大于0.所以x(3=1×﹣y=33x的图象与坐标轴所围成的三角形的面积是S.=×(4)∵OA=1,OB=3,∴函数AOB△,描点即可,如图所示;0),﹣1),(127.(1)函数y=2x﹣与坐标轴的坐标为(0 1的图象上,B点在直线y=2x﹣1A)将、B的坐标代入函数式中,可得出A点不在直线y=2x﹣的图象上,(2是否在函B的图象上,然后用同样的方法判定点不在函数因此Ay=2x﹣14﹣×A代入函数后发现﹣2.52﹣1=6≠﹣,数的图象上;≤.≤2x﹣10,因此x时,≤)当(3y0 )))))))))).)))))))))2;2时,x=﹣﹣4时,y=2;当y=﹣28.(1)当x= ),由此可画出函数的图象,如下图所示:2,﹣2)可知函数图象过(﹣4,2)、(﹣(2)由(12 ≤2x﹣6≤2∴﹣4≤﹣,﹣(3)∵y=﹣2x﹣64≤y8 ≤﹣2x 2≤1 ≤﹣4≤x ﹣1)图象如图:29.(0.3时,y<<﹣;当y>0x=﹣3时,y=0;当x时,)观察图象可得,当(2x>﹣3 1)列表:30.( 1 x 0y 2)画直线)1,0…描点,连线(如图)(也可以写成过点(0,2)和(),(02;12()①(,0)1 ②<)))))))))).)))))))))精品文档考试教学资料施工组织设计方案)))))))))).。
初中数学一次函数的图像专项练习30题(有答案)

初中数学一次函数的图像专项练习30题(有答案)1.本题为选择题,无需改写。
2.在图中,当x>2时,y2>y1,因此结论③正确。
由于y1=kx+b与y2=x+a的图象相交于第三象限,因此a<0,结论②也正确。
而k<0,因此结论①错误。
因此选项C正确。
3.根据题目中的条件,k<0,b>0,因此函数的图象是下降的直线,截距为正数,应该是选项A。
4.本题为选择题,无需改写。
5.根据题目中的条件,k<0,b>0,因此函数的图象是下降的直线,截距为正数,斜率的绝对值小于1,应该是选项B。
6.将直线l1和直线l2的方程化简可得y=2x+1和y=-x-1,因此直线l1的斜率为2,直线l2的斜率为-1.由于x+y=0,因此该点在第三部分。
因此选项C正确。
7.根据两个函数的表达式可知它们的图象分别是斜率为负数的直线和斜率为正数的直线,应该是选项B。
8.函数y=2x+3的斜率为2,截距为3,应该是选项A。
9.根据图象可知,选项C表示的是y=-x-1的图象,因此选项C正确。
10.将函数kx-y=2化简可得y=kx-2,因此函数的图象是斜率为正数的直线,截距为-2,应该是选项C。
11.由于b1<b2,因此直线y1在直线y2的下方。
由于k1k2<0,因此直线y1和直线y2的斜率异号,相交于第二象限。
因此选项B正确。
12.根据图象可知,选项D表示的是y=abx的图象,因此选项D正确。
13.根据图象可知,降雨后,蓄水量每天增加5万立方米,因此选项B正确。
14.本题为选择题,无需改写。
15.将y=kx代入y=kx-k可得y=k(x-1),因此函数的图象是斜率为正数的直线,截距为-k,应该是选项C。
16.当x增加时,y的值也会增加,且当x大于某个值时,y会大于2.17.当x增加时,y的值也会增加,但当x大于某个值时,y会小于某个值。
18.当x增加时,y的值也会增加,且当x大于某个值时,y会大于某个值。
19.正确的判断是:①k0;③当x=3时,y1=y2;④当03时,y1>y2.20.当x增加时,y1的值也会增加,且当x大于某个值时,y1会大于y2.21.当y小于某个值时,x的取值范围是一定的,具体取值范围需要根据具体函数图象来确定。
初中数学一次函数的图像专项练习30题(有答案)
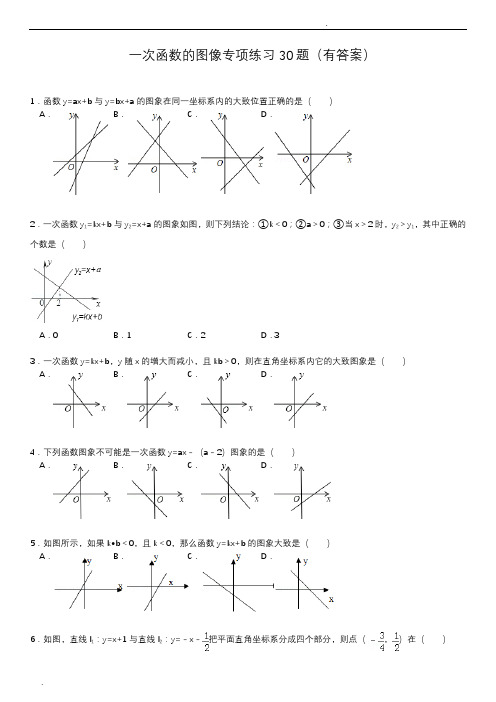
.一次函数的图像专项练习30题(有答案)1.函数y=ax+b与y=bx+a的图象在同一坐标系内的大致位置正确的是()A.B.C.D.2.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a >0;③当x>2时,y2>y1,其中正确的个数是()A.0B .1C .2D .33.一次函数y=kx+b,y随x的增大而减小,且kb>0,则在直角坐标系内它的大致图象是()A.B.C.D.4.下列函数图象不可能是一次函数y=ax﹣(a﹣2)图象的是()A.B.C.D.5.如图所示,如果k•b<0,且k<0,那么函数y=kx+b的图象大致是()A.B.C.D.6.如图,直线l1:y=x+1与直线l2:y=﹣x﹣把平面直角坐标系分成四个部分,则点(,)在()A . 第一部分B . 第二部分C . 第三部分D . 第四部分7.已知正比例函数y=﹣kx 和一次函数y=kx ﹣2(x 为自变量),它们在同一坐标系内的图象大致是( )A .B .C .D .8.函数y=2x+3的图象是( )A . 过点(0,3),(0,﹣)的直线B . 过点(1,5),(0,﹣)的直线C . 过点(﹣1,﹣1),(﹣,0)的直线D . 过点(0,3),(﹣,0)的直线9.下列图象中,与关系式y=﹣x ﹣1表示的是同一个一次函数的图象是( )A .B .C .D .10.函数kx ﹣y=2中,y 随x 的增大而减小,则它的图象是下图中的( )A .B .C .D .11.已知直线y 1=k 1x+b 1,y 2=k 2x+b 2,满足b 1<b 2,且k 1k 2<0,两直线的图象是( )A .B .C .D .12.如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是()A.B.C.D.13.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若该水库的蓄水量V(万米3)与降雨的时间t(天)的关系如图所示,则下列说法正确的是()A.降雨后,蓄水量每天减少5万米3B.降雨后,蓄水量每天增加5万米3C.降雨开始时,蓄水量为20万米3D.降雨第6天,蓄水量增加40万米314.拖拉机开始行驶时,油箱中有油4升,如果每小时耗油0.5升,那么油箱中余油y(升)与它工作的时间t(时)之间的函数关系的图象是()A.B.C.D.15.已知正比例函数y=kx的图象经过第一、三象限,则y=kx﹣k的大致图象可能是下图的()A.B.C.D.16.一次函数y=kx+b的图象如图所示,当x _________ 时,y>2.17.一次函数的图象如图所示,根据图象可知,当x _________ 时,有y<0.18.如图,直线l是一次函数y=kx+b的图象,当x _________ 时,y>0.19.一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x=3时,y1=y2;④当x>3时,y1<y2中,正确的判断是_________ .20.如图,已知函数y1=ax+b和y2=kx的图象交于点P,则根据图象可得,当x _________ 时,y1>y2.21.已知一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是_________ .22.在平面直角坐标系中画出函数的图象.(1)在图象上标出横坐标为﹣4的点A,并写出它的坐标;(2)在图象上标出和y轴的距离是2个单位长度的点,并写出它的坐标.23.作函数y=2x﹣4的图象,并根据图象回答下列问题.(1)当﹣2≤x≤4,求函数y的取值范围.(2)当x取何值时,y<0?y=0?y>0?24.如图是一次函数y=﹣x+5图象的一部分,利用图象回答下列问题:(1)求自变量的取值范围.(2)在(1)在条件下,y是否有最小值?如果有就求出最小值;如果没有,请说明理由.25.已知函数y1=﹣x+和y2=2x﹣1.(1)在同一个平面直角坐标系中画出这两个函数的图象;(2)根据图象,写出它们的交点坐标;(3)根据图象,试说明当x取什么值时,y1>y2?26.作出函数y=3﹣3x的图象,并根据图象回答下列问题:(1)y的值随x的增大而_________ ;(2)图象与x轴的交点坐标是_________ ;与y轴的交点坐标是_________ ;(3)当x _________ 时,y≥0;(4)函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是多少?27.已知函数y=2x﹣1.(1)在直角坐标系中画出这函数的图象;(2)判断点A(﹣2.5,﹣4),B(2.5,4)是否在函数y=2x﹣1的图象上;(3)当x取什么值时,y≤0.28.已知函数y=﹣2x﹣6.(1)求当x=﹣4时,y的值,当y=﹣2时,x的值.(2)画出函数图象.(3)如果y的取值范围﹣4≤y≤2,求x的取值范围.29.已知一次函数的图象经过点A(﹣3,0),B(﹣1,1)两点.(1)画出图象;(2)x为何值时,y>0,y=0,y<0?30.已知一次函数y=﹣2x+2,(1)在所给的平面直角坐标系中画出它的图象;(2)根据图象回答问题:①图象与x轴的交点坐标是_________ ,与y轴的交点坐标是_________ ;②当x _________ 时,y>0.参考答案:1.分四种情况:①当a>0,b>0时,y=ax+b的图象经过第一、二、三象限,y=bx+a的图象经过第一、二、三象限,无选项符合;②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a的图象经过第一、二、四象限,C选项符合;③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a的图象经过第一、三、四象限,无选项符合;④当a<0,b<0时,y=ax+b的图象经过第二、三、四象限;y=bx+a的图象经过第二、三、四象限,无选项符合.故选C2.由一次函数y1=kx+b与y2=x+a的图象可知k<0,a<0,当x>2时,y2>y1,①③正确.故选C3.∵一次函数y=kx+b,y随x的增大而减小,∴k<0,又∵kb>0,∴b<0,∴函数的图象经过第二、三、四象限.故选C4.根据图象知:A、a>0,﹣(a﹣2)>0.解得0<a<2,所以有可能;B、a<0,﹣(a﹣2)<0.解得两不等式没有公共部分,所以不可能;C、a<0,﹣(a﹣2)>0.解得a<0,所以有可能;D、a>0,﹣(a﹣2)<0.解得a>2,所以有可能.故选B5.∵k•b<0,且k<0,∴b>0,k<0,∴函数y=kx+b的图象经过第一、二、四象限,故选D6.由题意可得,解得,故点(,)应在交点的上方,即第二部分.故选B.7.分两种情况:(1)当k>0时,正比例函数y=﹣kx的图象过原点、第一、三象限,一次函数y=kx﹣2的图象经过第一、三、四象限,选项A符合;(2)当k<0时,正比例函数y=﹣kx的图象过原点、第二、四象限,一次函数y=kx﹣2的图象经过第二、三、四象限,无选项符合.故选A.8.A、把x=0代入函数关系式得2×0+3=3,故函数图象过点(0,3),不过(0,﹣),故错误;B、由A知函数图象不过点(0,﹣),故错误;C、把x=﹣1代入函数关系式得,2×(﹣1)+3=1,故(﹣1,﹣1)不在函数图象上,故错误;D、分别令x=0,y=0,此函数成立,故正确.故选D9.函数y=﹣x﹣1是一次函数,其图象是一条直线.当x=0时,y=﹣1,所以直线与y轴的交点坐标是(0,﹣1);当y=0时,x=﹣1,所以直线与x轴的交点坐标是(﹣1,0).由两点确定一条直线,连接这两点就可得到y=﹣x﹣1的图象.故选D10.整理为y=kx﹣2∵y随x的增大而减小∴k<0又因为图象过2,4,3象限故选D.11.k1k2<0,则k1与k2异号,因而两个函数一个y随x的增大而增大,另一个y随x的增大而减小,因而A是错误的;b1<b2,则y1与y轴的交点在y2与y轴的交点的下边,因而B、C都是错误的.故选D.12.①当ab>0,正比例函数y=abx过第一、三象限;a与b同号,同正时y=ax+b过第一、二、三象限,故D错误;同负时过第二、三、四象限,故B错误;②当ab<0时,正比例函数y=abx过第二、四象限;a与b异号,a>0,b<0时y=ax+b过第一、三、四象限,故C错误;a<0,b>0时过第一、二、四象限.故选A13.A、根据图象知,水库的蓄水量因该随着降雨的时间的增加而增多;故本选项错误;B、本图象的直线,所以每天的降雨量是相等的,所以,蓄水库每天的增加的水的量是(40﹣10)÷6=5;故本选项正确;C、根据图示知,降雨开始时,蓄水量为10万米3,故本选项错误;D、根据图示知,降雨第6天,蓄水量增加了40万米3﹣30万米3=10万米3,故本选项错误;故选B14.根据题意列出关系式为:y=40﹣5t,考虑实际情况:拖拉机开始工作时,油箱中有油4升,即开始时,函数图象与y轴交于点(0,40),如果每小时耗油0.5升,且8小时,耗完油,故函数图象为一条线段.故选D15.∵正比例函数y=kx的图象经过第一、三象限,∴k>0,∴﹣k<0,∴y=kx﹣k的大致图象经过一、三、四象限,故选:B.16.由图形可知,该函数过点(0,2),(3,0),故斜率k==,所以解析式为y=,令y>2,即>2,解之得:x<017.根据题意,要求y<0时,x的范围,即:x+3<0,解可得:x<﹣2,故答案为x<﹣218.根据题意,观察图象,可得直线l过点(2,0),且y随x的增大而增大,分析可得,当x>2时,有y>019.根据图示及数据可知:①一次函数y1=kx+b的图象经过第二、四象限,则k<0正确;②y2=x+a的图象经与y轴交与负半轴,则a>0错误;③一次函数y1=kx+b与y2=x+a的图象交点的横坐标是3,所以当x=3时,y1=y2正确;④当x>3时,y1<y2正确;故正确的判断是①,③,④20.根据图示可知点P的坐标是(﹣4,2),所以y1>y2即直线1在直线2的上方,则x<﹣4.21.根据图象和数据可知,当y<0即图象在x轴下侧,x<1.故答案为x<122.函数与坐标轴的交点的坐标为(0,3),(6,0).(1)点A的坐标(﹣4,5);(2)和y轴的距离是2个单位长度的点的坐标M(2,2),N(﹣2,4)23.当x=0时,y=﹣4;当y=0时,2x﹣4=0,解得x=2,∴函数图象与两坐标轴的交点为(0,﹣4)(2,0).图象如下:(1)x=﹣2时,y=2×(﹣2)﹣4=﹣8,x=4时,y=2×4﹣4=4,∵k=2>0,∴y随x的增大而增大,∴﹣8≤y≤4;(2)x<2时,y<0;x=2时,y=0;x>2时,y>0.24.(1)由图象可看出当y=2.5时,x=5,因此x的取值范围应该是0<x≤5(y轴上的点是空心圆,因此x≠0);(2)由图象可看出,当x=5时,函数的值最小,是y=2.525.(1)如图所示:(2)由(1)中两函数图象可知,其交点坐标为(1,1);(3)由(1)中两函数图象可知,当x>1时,y1>y2.26.如图.(1)因为一次项系数是﹣3<0,所以y的值随x的增大而减小;(2)当y=0时,x=1,所以图象与x轴的交点坐标是(1,0);当x=0时,y=3,所以图象与y轴的交点坐标是(0,3);(3)由图象知,在A点左边,图象在x轴上方,函数值大于0.所以x≤1时,y≥0.(4)∵OA=1,OB=3,∴函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是S△AOB=×1×3=.27.(1)函数y=2x﹣1与坐标轴的坐标为(0,﹣1)(,0),描点即可,如图所示;(2)将A、B的坐标代入函数式中,可得出A点不在直线y=2x﹣1的图象上,B点在直线y=2x﹣1的图象上,A代入函数后发现﹣2.5×2﹣1=﹣6≠﹣4,因此A点不在函数y=2x﹣1的图象上,然后用同样的方法判定B是否在函数的图象上;(3)当y≤0时,2x﹣1≤0,因此x≤.28.(1)当x=﹣4时,y=2;当y=﹣2时,x=﹣2;(2)由(1)可知函数图象过(﹣4,2)、(﹣2,﹣2),由此可画出函数的图象,如下图所示:(3)∵y=﹣2x﹣6,﹣4≤y≤2∴﹣4≤﹣2x﹣6≤22≤﹣2x≤8﹣4≤x≤﹣129.(1)图象如图:(2)观察图象可得,当x>﹣3时,y>0;当x=﹣3时,y=0;当x<﹣3时,y<0.30.(1)列表:x 0 1y 2 0描点,连线(如图)…(也可以写成过点(0,2)和(1,0)画直线)(2)①(1,0);(0,2)②<1。
初中数学专题一次函数的图像(含答案)

7.4 一次函数的图像(一)课内同步训练1.正比例函数的图像过点A (1,2),B (-2,m-1),则m 的值是________.2.一次函数的图像过点A (-1,2),B (0,2),则它的解析式是________.3.在同一坐标系内画出下列函数的图像,并说出它们有什么关系:(1)y=32x ;(2)y=32x+24.一次函数y 1=k 1x +b 1,利y 2=k 1x+b 2的图像交于y 轴上的同一点,则必有( )A .k 1=k 2B .b 1=b 2C .k 1=b 2D .k 2=b 15.一次函数y=ax+b 中,a>0,b<0,则它的图像可能是( )6.在直线y=3x-4上求出到y 轴的距离等于12的点的坐标.7.已知直线y=kx+b与x轴交于点(1,0),与直线y=2x-3和y轴交于同一点,•求出这条直线的解析式.课外延伸训练1.一次函数y1=k1x1+b1与y2=k2x2+b2交于x轴上同一点,则必有________.2.y=2x+b与两坐标轴围成的三角形面积为4,则b=________.3.(1)在直角坐标系中作出函数y=2x的图像,再分别将它向上平移4•个单位和向左平移2个单位,得到两个函数的图像.你发现了什么?能否结合函数的解析式给予说明?(2)如果要平移直线y=3x-6,使平移后的直线经过点(4,0),你能设计出几种方案?4.在同一坐标平面内,如果2个一次函数的图像相交,交点可能在象限内,也可能在坐标轴上.(1)若常数k、b、m、n均是正数且各不相等,试说明函数y=kx+b利y=mx+n的图像必相交,但交点不可能在第四象限内;(2)在问题(1)中,就交点在第一、第二、第三象限和坐标轴上的情况,各举出一例,并探索交点在坐标轴上的位置;(3)在问题(1)的2个函数中,若有k=n,b=m,k≠b,则交点在第几象限内?试说明不论k、b取何值,交点都在同一条直线上,并找出这条直线.7.4 一次函数的图像(一)(答案)[课内同步训练]1.5 2.y=-4x-23.图像略,2条直线互相平行4.B 5.B 6.(0.5,-2.5)(提示:点到y轴的距离等于这个点横坐标的绝对值)7.y=3x-3[课外延伸训练]1.b1k2=b2k1 2.±43.(1)平移以后两个函数的图像是同一条直线,设平移后的函数解析式为y=2x+k,向上平移4个单位过点(0,4),向左平移2个单位过点(-2,0),用待定系数法求得k=4(2)可将直线向下平移6个单位,也可以将直线向右平移2•个单位4.(1)因为k≠m,所以两直线必相交;因为字母都是正数,两直线都不经过第四象限,所以交点不可能在第四象限内(2)略,交点在坐标轴上时只能在x轴的负方向(3)满足本题条件的两直线方程为:y=kx+b,y=bx+k,它们的交点在第一象限内,坐标是(1,k+b),所以不论k、b取何值,交点都在经过点(1,0)且垂直于x轴的直线上.一次函数的图像(二)课内同步训练1.正比例函数y=•kx•的图像经过(•-•2,•4)•,•那么这个正比例函数的关系式是________,它的图象经过第_______象限,y 随x 的增大而________.2.正比例函数y=(k+1)23k x 的图像过第二、第四象限,则k=________.3.若一次函数y=mx+(m 2+m-4)的图像过点(0,8),且y 随x 的增大而减小,则m=____.4.一次函数y=kx+b 的图象经过第一、第二、第三象限,则下列结论成立的有(• )A .k>0,b>0B .k>0,b<0C .k<0,b<0D .k<0,b>05.正比例函数y=0.3x ,y=-3x ,y=(a 2+1)x 中,y 随x 增大而增大的个数是( )A .0B .1C .2D .36.某市为节约用水,实行价格调控,限定每户每月用水不超过6t 时,每t•价格为2元;当用水量超过6t 时,超过部分每吨价格为3元,则每户每月的水费y (元)•与用水量x (t )之间的函数图像是( )7.已知正比例函数y=-(k 2+1)x ,点(-2,y 1)、(-3,y 2)、(1,y 3)在它的图像上,则( )A .y 2<y 1<y 3B .y 2>y 1>y 3C .y 2>y 3>y 1D .y 3<y 2<y 18.在直角坐标系中作出一次函数y 1=-x+5与y 2=2x-2的图像,•并借助图像回答下列问题(1)当x 为何值时,y 1=1?此时y 2的值为多少?(2)当x 为何值时,y 1=y 2;(3)当x 为何值时,y 1>y 2.课外延伸训练1.一个游泳池的容积为Am3,进水管每分钟进水P m3,出水管每分钟放水qm3(P>q),一天对空池进行灌水5min后察觉未将水管堵上.随时将出水管堵上,继续灌水.•下图中能反映池内水量v(m3)与灌水时间t(min)之间函数关系的是()2.某地出租车的收费标准如下:里程不超过3km时收起步价8元;里程勃勃3km时,超过部分增收1.2元/km.试写出车费y(元)与里程x(km)的函数关系式,•并画出这个函数的图像.3.已知一次函数y=2x-3(1)当x取何值时,函数y的值在-1与2之间变化?(2)当x从-2到3变化时,函数y的最小值和最大值各是多少?4.点P(x,y)在第一象限,且x+y=8,点A的坐标为(6,0),设△OPA的面积为S.(1)用含x的解析式表示S,写出x的取值范围,画出函数S的图像.(2)当点P的横坐标为5时,△OPA的面积为多少?(3)△OPA的面积能大于24吗?为什么?5.已知点A(-3,y1),B(1,y2)在直线y=-23x+4上.(1)比较y1和y2的大小;(2)若另有一个正比例函数的图像过点B,•设在这个正比例函数中使函数值等于y1和y2的自变量分别为x1和x2,试比较x1和x2的大小.7.4 一次函数的图像(二)(答案)[课内同步训练]1.y=2x,一、三,增大 2.-3 3.-4 4.D 5.C 6.B 7.B8.(1)x=4,•此时y=6 (2)x=73(3)x<73[课外延伸训练]1.B 2.y=8(03) 1.2 4.4(3)xx x<≤⎧⎨+>⎩3.(1)12<x<2 (2)y的最小值是-3,最大值是74.(1)S=-3x+24•其中0<x<8 (2)9 (3)不能5.(1)y1>y2x1>x2。
实用文库汇编之初中数学一次函数的图像专项练习30题(有答案)ok

*作者:角狂风*作品编号:1547510232155GZ579202创作日期:2020年12月20日实用文库汇编之一次函数的图像专项练习30题(有答案)1.函数y=ax+b与y=bx+a的图象在同一坐标系内的大致位置正确的是()A .B.C.D.2.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x>2时,y2>y1,其中正确的个数是()A .0 B.1 C.2 D.33.一次函数y=kx+b,y随x的增大而减小,且kb>0,则在直角坐标系内它的大致图象是()A .B.C.D.4.下列函数图象不可能是一次函数y=ax﹣(a﹣2)图象的是()A .B.C.D.5.如图所示,如果k•b<0,且k<0,那么函数y=kx+b的图象大致是()A .B.C.D.6.如图,直线l1:y=x+1与直线l2:y=﹣x ﹣把平面直角坐标系分成四个部分,则点(,)在()A .第一部分B.第二部分C.第三部分D.第四部分7.已知正比例函数y=﹣kx和一次函数y=kx﹣2(x为自变量),它们在同一坐标系内的图象大致是()A .B.C.D.8.函数y=2x+3的图象是()A.过点(0,3),(0,﹣)的直线B.过点(1,5),(0,﹣)的直线C.过点(﹣1,﹣1),(﹣,0)的直线D.过点(0,3),(﹣,0)的直线作者:角狂风作品编号:1547510232155GZ579202创作日期:2020年12月20日9.下列图象中,与关系式y=﹣x﹣1表示的是同一个一次函数的图象是()A .B.C.D.10.函数kx﹣y=2中,y随x的增大而减小,则它的图象是下图中的()A .B.C.D.11.已知直线y1=k1x+b1,y2=k2x+b2,满足b1<b2,且k1k2<0,两直线的图象是()A .B.C.D.12.如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是()A .B.C.D.13.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若该水库的蓄水量V(万米3)与降雨的时间t(天)的关系如图所示,则下列说法正确的是()A.降雨后,蓄水量每天减少5万米3B.降雨后,蓄水量每天增加5万米3 C.降雨开始时,蓄水量为20万米3D.降雨第6天,蓄水量增加40万米314.拖拉机开始行驶时,油箱中有油4升,如果每小时耗油0.5升,那么油箱中余油y(升)与它工作的时间t(时)之间的函数关系的图象是()A .B.C.D.15.已知正比例函数y=kx的图象经过第一、三象限,则y=kx﹣k的大致图象可能是下图的()A .B.C.D.16.一次函数y=kx+b的图象如图所示,当x _________ 时,y>2.17.一次函数的图象如图所示,根据图象可知,当x _________ 时,有y<0.18.如图,直线l是一次函数y=kx+b的图象,当x _________时,y>0.19.一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x=3时,y1=y2;④当x>3时,y1<y2中,正确的判断是_________ .20.如图,已知函数y1=ax+b和y2=kx的图象交于点P,则根据图象可得,当x _________ 时,y1>y2.21.已知一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是_________ .22.在平面直角坐标系中画出函数的图象.(1)在图象上标出横坐标为﹣4的点A,并写出它的坐标;作者:角狂风作品编号:1547510232155GZ579202创作日期:2020年12月20日(2)在图象上标出和y轴的距离是2个单位长度的点,并写出它的坐标.23.作函数y=2x﹣4的图象,并根据图象回答下列问题.(1)当﹣2≤x≤4,求函数y的取值范围.(2)当x取何值时,y<0?y=0?y>0?24.如图是一次函数y=﹣x+5图象的一部分,利用图象回答下列问题:(1)求自变量的取值范围.(2)在(1)在条件下,y是否有最小值?如果有就求出最小值;如果没有,请说明理由.25.已知函数y1=﹣x+和y2=2x﹣1.(1)在同一个平面直角坐标系中画出这两个函数的图象;(2)根据图象,写出它们的交点坐标;(3)根据图象,试说明当x取什么值时,y1>y2?26.作出函数y=3﹣3x的图象,并根据图象回答下列问题:(1)y的值随x的增大而_________ ;(2)图象与x轴的交点坐标是_________ ;与y轴的交点坐标是_________ ;(3)当x _________ 时,y≥0;(4)函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是多少?27.已知函数y=2x﹣1.(1)在直角坐标系中画出这函数的图象;(2)判断点A(﹣2.5,﹣4),B(2.5,4)是否在函数y=2x﹣1的图象上;(3)当x取什么值时,y≤0.28.已知函数y=﹣2x﹣6.(1)求当x=﹣4时,y的值,当y=﹣2时,x的值.(2)画出函数图象.(3)如果y的取值范围﹣4≤y≤2,求x的取值范围.29.已知一次函数的图象经过点A(﹣3,0),B(﹣1,1)两点.(1)画出图象;(2)x为何值时,y>0,y=0,y<0?30.已知一次函数y=﹣2x+2,(1)在所给的平面直角坐标系中画出它的图象;(2)根据图象回答问题:①图象与x轴的交点坐标是_________ ,与y轴的交点坐标是_________ ;②当x _________ 时,y>0.参考答案:1.分四种情况:①当a>0,b>0时,y=ax+b的图象经过第一、二、三象限,y=bx+a的图象经过第一、二、三象限,无选项符合;②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a的图象经过第一、二、四象限,C选项符合;③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a的图象经过第一、三、四象限,无选项符合;④当a<0,b<0时,y=ax+b的图象经过第二、三、四象限;y=bx+a的图象经过第二、三、四象限,无选项符合.故选C2.由一次函数y1=kx+b与y2=x+a的图象可知k<0,a<0,当x>2时,y2>y1,①③正确.故选C3.∵一次函数y=kx+b,y随x的增大而减小,∴k<0,又∵kb>0,∴b<0,∴函数的图象经过第二、三、四象限.故选C4.根据图象知:A、a>0,﹣(a﹣2)>0.解得0<a<2,所以有可能;B、a<0,﹣(a﹣2)<0.解得两不等式没有公共部分,所以不可能;C、a<0,﹣(a﹣2)>0.解得a<0,所以有可能;D、a>0,﹣(a﹣2)<0.解得a>2,所以有可能.故选B5.∵k•b<0,且k<0,∴b>0,k<0,∴函数y=kx+b的图象经过第一、二、四象限,故选D6.由题意可得,解得,故点(,)应在交点的上方,即第二部分.故选B.7.分两种情况:(1)当k>0时,正比例函数y=﹣kx的图象过原点、第一、三象限,一次函数y=kx﹣2的图象经过第一、三、四象限,选项A符合;(2)当k<0时,正比例函数y=﹣kx的图象过原点、第二、四象限,一次函数y =kx﹣2的图象经过第二、三、四象限,无选项符合.故选A.8.A、把x=0代入函数关系式得2×0+3=3,故函数图象过点(0,3),不过(0,﹣),故错误;B、由A知函数图象不过点(0,﹣),故错误;C、把x=﹣1代入函数关系式得,2×(﹣1)+3=1,故(﹣1,﹣1)不在函数图象上,故错误;D、分别令x=0,y=0,此函数成立,故正确.故选D9.函数y=﹣x﹣1是一次函数,其图象是一条直线.当x=0时,y=﹣1,所以直线与y轴的交点坐标是(0,﹣1);当y=0时,x=﹣1,所以直线与x轴的交点坐标是(﹣1,0).由两点确定一条直线,连接这两点就可得到y=﹣x﹣1的图象.故选D10.整理为y=kx﹣2∵y随x的增大而减小∴k<0又因为图象过2,4,3象限故选D.11.k1k2<0,则k1与k2异号,因而两个函数一个y随x的增大而增大,另一个y随x的增大而减小,因而A是错误的;b1<b2,则y1与y轴的交点在y2与y轴的交点的下边,因而B、C都是错误的.故选D.12.①当ab>0,正比例函数y=abx过第一、三象限;a与b同号,同正时y=ax+b 过第一、二、三象限,故D错误;同负时过第二、三、四象限,故B错误;②当ab<0时,正比例函数y=abx过第二、四象限;a与b异号,a>0,b<0时y= ax+b过第一、三、四象限,故C错误;a<0,b>0时过第一、二、四象限.故选A13.A、根据图象知,水库的蓄水量因该随着降雨的时间的增加而增多;故本选项错误;B、本图象的直线,所以每天的降雨量是相等的,所以,蓄水库每天的增加的水的量是(40﹣10)÷6=5;故本选项正确;C、根据图示知,降雨开始时,蓄水量为10万米3,故本选项错误;D、根据图示知,降雨第6天,蓄水量增加了40万米3﹣30万米3=10万米3,故本选项错误;故选B14.根据题意列出关系式为:y=40﹣5t,考虑实际情况:拖拉机开始工作时,油箱中有油4升,即开始时,函数图象与y轴交于点(0,4 0),如果每小时耗油0.5升,且8小时,耗完油,故函数图象为一条线段.故选D 15.∵正比例函数y=kx的图象经过第一、三象限,∴k>0,∴﹣k<0,∴y=kx﹣k的大致图象经过一、三、四象限,故选:B.16.由图形可知,该函数过点(0,2),(3,0),故斜率k==,所以解析式为y=,令y>2,即>2,解之得:x<017.根据题意,要求y<0时,x的范围,即:x+3<0,解可得:x<﹣2,故答案为x<﹣218.根据题意,观察图象,可得直线l过点(2,0),且y随x的增大而增大,分析可得,当x>2时,有y>019.根据图示及数据可知:①一次函数y1=kx+b的图象经过第二、四象限,则k <0正确;②y2=x+a的图象经与y轴交与负半轴,则a>0错误;③一次函数y1=kx+b与y2=x+a的图象交点的横坐标是3,所以当x=3时,y1=y2正确;④当x>3时,y1<y2正确;故正确的判断是①,③,④20.根据图示可知点P的坐标是(﹣4,2),所以y1>y2即直线1在直线2的上方,则x<﹣4.21.根据图象和数据可知,当y<0即图象在x轴下侧,x<1.故答案为x<1 22.函数与坐标轴的交点的坐标为(0,3),(6,0).(1)点A的坐标(﹣4,5);(2)和y轴的距离是2个单位长度的点的坐标M(2,2),N(﹣2,4)23.当x=0时,y=﹣4;当y=0时,2x﹣4=0,解得x=2,∴函数图象与两坐标轴的交点为(0,﹣4)(2,0).图象如下:(1)x=﹣2时,y=2×(﹣2)﹣4=﹣8,x=4时,y=2×4﹣4=4,∵k=2>0,∴y随x的增大而增大,∴﹣8≤y≤4;(2)x<2时,y<0;x=2时,y=0;x>2时,y>0.24.(1)由图象可看出当y=2.5时,x=5,因此x的取值范围应该是0<x≤5(y 轴上的点是空心圆,因此x≠0);(2)由图象可看出,当x=5时,函数的值最小,是y=2.525.(1)如图所示:(2)由(1)中两函数图象可知,其交点坐标为(1,1);(3)由(1)中两函数图象可知,当x>1时,y1>y2.26.如图.(1)因为一次项系数是﹣3<0,所以y的值随x的增大而减小;(2)当y=0时,x=1,所以图象与x轴的交点坐标是(1,0);当x=0时,y=3,所以图象与y轴的交点坐标是(0,3);(3)由图象知,在A点左边,图象在x轴上方,函数值大于0.所以x≤1时,y≥0.(4)∵OA=1,OB=3,∴函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是S△AOB=×1×3=.27.(1)函数y=2x﹣1与坐标轴的坐标为(0,﹣1)(,0),描点即可,如图所示;(2)将A、B的坐标代入函数式中,可得出A点不在直线y=2x﹣1的图象上,B 点在直线y=2x﹣1的图象上,A代入函数后发现﹣2.5×2﹣1=﹣6≠﹣4,因此A点不在函数y=2x﹣1的图象上,然后用同样的方法判定B是否在函数的图象上;(3)当y≤0时,2x﹣1≤0,因此x≤.28.(1)当x=﹣4时,y=2;当y=﹣2时,x=﹣2;(2)由(1)可知函数图象过(﹣4,2)、(﹣2,﹣2),由此可画出函数的图象,如下图所示:(3)∵y=﹣2x﹣6,﹣4≤y≤2∴﹣4≤﹣2x﹣6≤22≤﹣2x≤8﹣4≤x≤﹣129.(1)图象如图:(2)观察图象可得,当x>﹣3时,y>0;当x=﹣3时,y=0;当x<﹣3时,y<0.30.(1)列表:x 0 1y 2 0描点,连线(如图)…(也可以写成过点(0,2)和(1,0)画直线)(2)①(1,0);(0,2)②<1作者:角狂风作品编号:1547510232155GZ579202 创作日期:2020年12月20日。
初中数学一次函数的图像专项练习30题ok

一次函数的图像专项练习30题(有答案)1.函数y=ax+b与y=bx+a的图象在同一坐标系内的大致位置正确的是()A.B.C.D.2.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x>2时,y2>y1,其中正确的个数是()A.0B.1C.2D.33.一次函数y=kx+b,y随x的增大而减小,且kb>0,则在直角坐标系内它的大致图象是()A.B.C.D.4.下列函数图象不可能是一次函数y=ax﹣(a﹣2)图象的是()A.B.C.D.5.如图所示,如果k•b<0,且k<0,那么函数y=kx+b的图象大致是()A.B.C.D.6.如图,直线l1:y=x+1与直线l2:y=﹣x﹣把平面直角坐标系分成四个部分,则点(,)在()A.第一部分B.第二部分C.第三部分D.第四部分7.已知正比例函数y=﹣kx和一次函数y=kx﹣2(x 为自变量),它们在同一坐标系内的图象大致是()A.B.C.D.8.函数y=2x+3的图象是()A.过点(0,3),(0,﹣)的直线B.过点(1,5),(0,﹣)的直线C . 过点(﹣1,﹣1),(﹣,0)的直线D . 过点(0,3),(﹣,0)的直线9.下列图象中,与关系式y=﹣x ﹣1表示的是同一个一次函数的图象是( ) A . B . C . D .10.函数kx ﹣y=2xx ,y 随x 的增大而减小,则它的图象是下图xx 的( ) A .B .C .D .11.已知直线y1=k1x+b1,y2=k2x+b2,满足b1<b2,且k1k2<0,两直线的图象是( ) A .B .C .D .12.如图所示,表示一次函数y=ax+b 与正比例函数y=abx (a ,b 是常数,且ab≠0)的图象是( )A.B.C.D.13.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若该水库的蓄水量V(万米3)与降雨的时间t(天)的关系如图所示,则下列说法正确的是()A.降雨后,蓄水量每天减少5万米3B.降雨后,蓄水量每天增加5万米3C.降雨开始时,蓄水量为20万米3D.降雨第6天,蓄水量增加40万米314.拖拉机开始行驶时,油箱中有油4升,如果每小时耗油0.5升,那么油箱xx 油y(升)与它工作的时间t(时)之间的函数关系的图象是()A.B.C.D.15.已知正比例函数y=kx的图象经过第一、三象限,则y=kx﹣k的大致图象可能是下图的()A.B.C.D.16.一次函数y=kx+b的图象如图所示,当x _________ 时,y>2.17.一次函数的图象如图所示,根据图象可知,当x _________ 时,有y<0.18.如图,直线l是一次函数y=kx+b的图象,当x _________ 时,y>0.19.一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x=3时,y1=y2;④当x>3时,y1<y2xx,正确的判断是_________ .20.如图,已知函数y1=ax+b和y2=kx的图象交于点P,则根据图象可得,当x _________ 时,y1>y2.21.已知一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是_________ .22.在平面直角坐标系中画出函数的图象.(1)在图象上标出横坐标为﹣4的点A,并写出它的坐标;(2)在图象上标出和y轴的距离是2个单位xx的点,并写出它的坐标.23.作函数y=2x﹣4的图象,并根据图象回答下列问题.(1)当﹣2≤x≤4,求函数y的取值范围.(2)当x取何值时,y<0?y=0?y>0?24.如图是一次函数y=﹣x+5图象的一部分,利用图象回答下列问题:(1)求自变量的取值范围.(2)在(1)在条件下,y是否有最小值?如果有就求出最小值;如果没有,请说明理由.25.已知函数y1=﹣x+和y2=2x﹣1.(1)在同一个平面直角坐标系中画出这两个函数的图象;(2)根据图象,写出它们的交点坐标;(3)根据图象,试说明当x取什么值时,y1>y2?26.作出函数y=3﹣3x的图象,并根据图象回答下列问题:(1)y的值随x的增大而_________ ;(2)图象与x轴的交点坐标是_________ ;与y轴的交点坐标是_________ ;(3)当x _________ 时,y≥0;(4)函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是多少?27.已知函数y=2x﹣1.(1)在直角坐标系中画出这函数的图象;(2)判断点A(﹣2.5,﹣4),B(2.5,4)是否在函数y=2x﹣1的图象上;(3)当x取什么值时,y≤0.28.已知函数y=﹣2x﹣6.(1)求当x=﹣4时,y的值,当y=﹣2时,x的值.(2)画出函数图象.(3)如果y的取值范围﹣4≤y≤2,求x的取值范围.29.已知一次函数的图象经过点A(﹣3,0),B(﹣1,1)两点.(1)画出图象;(2)x为何值时,y>0,y=0,y<0?30.已知一次函数y=﹣2x+2,(1)在所给的平面直角坐标系中画出它的图象;(2)根据图象回答问题:①图象与x轴的交点坐标是_________ ,与y轴的交点坐标是_________ ;②当x _________ 时,y>0.参考答案:1.分四种情况:①当a>0,b>0时,y=ax+b的图象经过第一、二、三象限,y=bx+a的图象经过第一、二、三象限,无选项符合;②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a的图象经过第一、二、四象限,C选项符合;③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a的图象经过第一、三、四象限,无选项符合;④当a<0,b<0时,y=ax+b的图象经过第二、三、四象限;y=bx+a的图象经过第二、三、四象限,无选项符合.故选C2.由一次函数y1=kx+b与y2=x+a的图象可知k<0,a<0,当x>2时,y2>y1,①③正确.故选C3.∵一次函数y=kx+b,y随x的增大而减小,∴k<0,又∵kb>0,∴b<0,∴函数的图象经过第二、三、四象限.故选C4.根据图象知:A、a>0,﹣(a﹣2)>0.解得0<a<2,所以有可能;B、a<0,﹣(a﹣2)<0.解得两不等式没有公共部分,所以不可能;C、a<0,﹣(a﹣2)>0.解得a<0,所以有可能;D、a>0,﹣(a﹣2)<0.解得a>2,所以有可能.故选B5.∵k•b<0,且k<0,∴b>0,k<0,∴函数y=kx+b的图象经过第一、二、四象限,故选D6.由题意可得,解得,故点(,)应在交点的上方,即第二部分.故选B.7.分两种情况:(1)当k>0时,正比例函数y=﹣kx的图象过原点、第一、三象限,一次函数y=kx﹣2的图象经过第一、三、四象限,选项A符合;(2)当k<0时,正比例函数y=﹣kx的图象过原点、第二、四象限,一次函数y=kx ﹣2的图象经过第二、三、四象限,无选项符合.故选A.8.A、把x=0代入函数关系式得2×0+3=3,故函数图象过点(0,3),不过(0,﹣),故错误;B、由A知函数图象不过点(0,﹣),故错误;C、把x=﹣1代入函数关系式得,2×(﹣1)+3=1,故(﹣1,﹣1)不在函数图象上,故错误;D、分别令x=0,y=0,此函数成立,故正确.故选D9.函数y=﹣x﹣1是一次函数,其图象是一条直线.当x=0时,y=﹣1,所以直线与y轴的交点坐标是(0,﹣1);当y=0时,x=﹣1,所以直线与x轴的交点坐标是(﹣1,0).由两点确定一条直线,连接这两点就可得到y=﹣x﹣1的图象.故选D10.整理为y=kx﹣2∵y随x的增大而减小∴k<0又因为图象过2,4,3象限故选D.11.k1k2<0,则k1与k2异号,因而两个函数一个y随x的增大而增大,另一个y随x的增大而减小,因而A是错误的;b1<b2,则y1与y轴的交点在y2与y轴的交点的下边,因而B、C都是错误的.故选D.12.①当ab>0,正比例函数y=abx过第一、三象限;a与b同号,同正时y=ax+b 过第一、二、三象限,故D错误;同负时过第二、三、四象限,故B错误;②当ab<0时,正比例函数y=abx过第二、四象限;a与b异号,a>0,b<0时y=ax+b过第一、三、四象限,故C错误;a<0,b>0时过第一、二、四象限.故选A13.A、根据图象知,水库的蓄水量因该随着降雨的时间的增加而增多;故本选项错误;B、本图象的直线,所以每天的降雨量是相等的,所以,蓄水库每天的增加的水的量是(40﹣10)÷6=5;故本选项正确;C、根据图示知,降雨开始时,蓄水量为10万米3,故本选项错误;D、根据图示知,降雨第6天,蓄水量增加了40万米3﹣30万米3=10万米3,故本选项错误;故选B14.根据题意列出关系式为:y=40﹣5t,考虑实际情况:拖拉机开始工作时,油箱中有油4升,即开始时,函数图象与y轴交于点(0,40),如果每小时耗油0.5升,且8小时,耗完油,故函数图象为一条线段.故选D 15.∵正比例函数y=kx的图象经过第一、三象限,∴k>0,∴﹣k<0,∴y=kx﹣k的大致图象经过一、三、四象限,故选:B.16.由图形可知,该函数过点(0,2),(3,0),故斜率k==,所以解析式为y=,令y>2,即>2,解之得:x<017.根据题意,要求y<0时,x的范围,即:x+3<0,解可得:x<﹣2,故答案为x<﹣218.根据题意,观察图象,可得直线l过点(2,0),且y随x的增大而增大,分析可得,当x>2时,有y>019.根据图示及数据可知:①一次函数y1=kx+b的图象经过第二、四象限,则k <0正确;②y2=x+a的图象经与y轴交与负半轴,则a>0错误;③一次函数y1=kx+b与y2=x+a的图象交点的横坐标是3,所以当x=3时,y1=y2正确;④当x>3时,y1<y2正确;故正确的判断是①,③,④20.根据图示可知点P的坐标是(﹣4,2),所以y1>y2即直线1在直线2的上方,则x<﹣4.21.根据图象和数据可知,当y<0即图象在x轴下侧,x<1.故答案为x<1 22.函数与坐标轴的交点的坐标为(0,3),(6,0).(1)点A的坐标(﹣4,5);(2)和y轴的距离是2个单位xx的点的坐标M(2,2),N(﹣2,4)23.当x=0时,y=﹣4;当y=0时,2x﹣4=0,解得x=2,∴函数图象与两坐标轴的交点为(0,﹣4)(2,0).图象如下:(1)x=﹣2时,y=2×(﹣2)﹣4=﹣8,x=4时,y=2×4﹣4=4,∵k=2>0,∴y随x的增大而增大,∴﹣8≤y≤4;(2)x<2时,y<0;x=2时,y=0;x>2时,y>0.24.(1)由图象可看出当y=2.5时,x=5,因此x的取值范围应该是0<x≤5(y 轴上的点是空心圆,因此x≠0);(2)由图象可看出,当x=5时,函数的值最小,是y=2.525.(1)如图所示:(2)由(1)中两函数图象可知,其交点坐标为(1,1);(3)由(1)中两函数图象可知,当x>1时,y1>y2.26.如图.(1)因为一次项系数是﹣3<0,所以y的值随x的增大而减小;(2)当y=0时,x=1,所以图象与x轴的交点坐标是(1,0);当x=0时,y=3,所以图象与y轴的交点坐标是(0,3);(3)由图象知,在A点左边,图象在x轴上方,函数值大于0.所以x≤1时,y≥0.(4)∵OA=1,OB=3,∴函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是S△AOB=×1×3=.27.(1)函数y=2x﹣1与坐标轴的坐标为(0,﹣1)(,0),描点即可,如图所示;(2)将A、B的坐标代入函数式中,可得出A点不在直线y=2x﹣1的图象上,B点在直线y=2x﹣1的图象上,A代入函数后发现﹣2.5×2﹣1=﹣6≠﹣4,因此A点不在函数y=2x﹣1的图象上,然后用同样的方法判定B是否在函数的图象上;(3)当y≤0时,2x﹣1≤0,因此x≤.28.(1)当x=﹣4时,y=2;当y=﹣2时,x=﹣2;(2)由(1)可知函数图象过(﹣4,2)、(﹣2,﹣2),由此可画出函数的图象,如下图所示:(3)∵y=﹣2x﹣6,﹣4≤y≤2∴﹣4≤﹣2x﹣6≤22≤﹣2x≤8﹣4≤x≤﹣129.(1)图象如图:(2)观察图象可得,当x>﹣3时,y>0;当x=﹣3时,y=0;当x<﹣3时,y<0.30.(1)列表:x 0 1y 2 0描点,连线(如图)…(也可以写成过点(0,2)和(1,0)画直线)(2)①(1,0);(0,2)②<1。
初中数学一次函数的图像专项练习30题(有答案解析)ok

WORD 格式整理版一次函数(图像题) 专项练习一 1.函数y=ax+b 与y=bx+a 的图象在同一坐标系内的大致位置正确的是( )A .B .C .D .2.一次函数y 1=kx+b 与y 2=x+a 的图象如图,则下列结论:①k <0;②a >0;③当x >2时,y 2>y 1,其中正确的个数是( )A . 0B . 1C . 2D . 33.一次函数y=kx+b ,y 随x 的增大而减小,且kb >0,则在直角坐标系内它的大致图象是( )A .B .C .D .4.下列函数图象不可能是一次函数y=ax ﹣(a ﹣2)图象的是( )A .B .C .D .5.如图所示,如果k •b <0,且k <0,那么函数y=kx+b 的图象大致是( )A .B .C .D .6.如图,直线l 1:y=x+1与直线l 2:y=﹣x ﹣把平面直角坐标系分成四个部分,则点(,)在( )A . 第一部分B . 第二部分C . 第三部分D . 第四部分7.已知正比例函数y=﹣kx 和一次函数y=kx ﹣2(x 为自变量),它们在同一坐标系内的图象大致是( ) A . B . C . D .8.函数y=2x+3的图象是( )A . 过点(0,3),(0,﹣)的直线B . 过点(1,5),(0,﹣)的直线C . 过点(﹣1,﹣1),(﹣,0)的直线D . 过点(0,3),(﹣,0)的直线9.下列图象中,与关系式y=﹣x ﹣1表示的是同一个一次函数的图象是( )A .B .C .D .10.函数kx ﹣y=2中,y 随x 的增大而减小,则它的图象是下图中的( )A .B .C .D .11.已知直线y 1=k 1x+b 1,y 2=k 2x+b 2,满足b 1<b 2,且k 1k 2<0,两直线的图象是( )A .B .C .D .12.如图所示,表示一次函数y=ax+b 与正比例函数y=abx (a ,b 是常数,且ab ≠0)的图象是( )A .B .C .D .13.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若该水库的蓄水量V (万米3)与降雨的时间t (天)的关系如图所示,则下列说法正确的是( )A.降雨后,蓄水量每天减少5万米3B.降雨后,蓄水量每天增加5万米3C.降雨开始时,蓄水量为20万米3D.降雨第6天,蓄水量增加40万米314.拖拉机开始行驶时,油箱中有油4升,如果每小时耗油0.5升,那么油箱中余油y(升)与它工作的时间t(时)之间的函数关系的图象是()A.B.C.D.15.已知正比例函数y=kx的图象经过第一、三象限,则y=kx﹣k的大致图象可能是下图的()A.B.C.D.16.一次函数y=kx+b的图象如图所示,当x_________时,y>2.17.一次函数的图象如图所示,根据图象可知,当x_________时,有y<0.18.如图,直线l是一次函数y=kx+b的图象,当x_________时,y>0.19.一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x=3时,y1=y2;④当x>3时,y1<y2中,正确的判断是_________.20.如图,已知函数y1=ax+b和y2=kx的图象交于点P,则根据图象可得,当x_________时,y1>y2.21.已知一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是_________.22.在平面直角坐标系中画出函数的图象.(1)在图象上标出横坐标为﹣4的点A,并写出它的坐标;(2)在图象上标出和y轴的距离是2个单位长度的点,并写出它的坐标.23.作函数y=2x﹣4的图象,并根据图象回答下列问题.(1)当﹣2≤x≤4,求函数y的取值范围.(2)当x取何值时,y<0?y=0?y>0?24.如图是一次函数y=﹣x+5图象的一部分,利用图象回答下列问题:(1)求自变量的取值范围.(2)在(1)在条件下,y是否有最小值?如果有就求出最小值;如果没有,请说明理由.25.已知函数y1=﹣x+和y2=2x﹣1.(1)在同一个平面直角坐标系中画出这两个函数的图象;(2)根据图象,写出它们的交点坐标;(3)根据图象,试说明当x取什么值时,y1>y2?26.作出函数y=3﹣3x的图象,并根据图象回答下列问题:(1)y的值随x的增大而_________;(2)图象与x轴的交点坐标是_________;与y轴的交点坐标是_________;(3)当x_________时,y≥0;(4)函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是多少?27.已知函数y=2x﹣1.(1)在直角坐标系中画出这函数的图象;(2)判断点A(﹣2.5,﹣4),B(2.5,4)是否在函数y=2x﹣1的图象上;(3)当x取什么值时,y≤0.28.已知函数y=﹣2x﹣6.(1)求当x=﹣4时,y的值,当y=﹣2时,x的值.(2)画出函数图象.(3)如果y的取值范围﹣4≤y≤2,求x的取值范围.29.已知一次函数的图象经过点A(﹣3,0),B(﹣1,1)两点.(1)画出图象;(2)x为何值时,y>0,y=0,y<0?30.已知一次函数y=﹣2x+2,(1)在所给的平面直角坐标系中画出它的图象;(2)根据图象回答问题:①图象与x轴的交点坐标是_________,与y轴的交点坐标是_________;②当x_________时,y>0.参考答案:1.分四种情况:①当a>0,b>0时,y=ax+b的图象经过第一、二、三象限,y=bx+a的图象经过第一、二、三象限,无选项符合;②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a的图象经过第一、二、四象限,C选项符合;③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a的图象经过第一、三、四象限,无选项符合;④当a<0,b<0时,y=ax+b的图象经过第二、三、四象限;y=bx+a的图象经过第二、三、四象限,无选项符合.故选C2.由一次函数y1=kx+b与y2=x+a的图象可知k<0,a<0,当x>2时,y2>y1,①③正确.故选C3.∵一次函数y=kx+b,y随x的增大而减小,∴k<0,又∵kb>0,∴b<0,∴函数的图象经过第二、三、四象限.故选C4.根据图象知:A、a>0,﹣(a﹣2)>0.解得0<a<2,所以有可能;B、a<0,﹣(a﹣2)<0.解得两不等式没有公共部分,所以不可能;C、a<0,﹣(a﹣2)>0.解得a<0,所以有可能;D、a>0,﹣(a﹣2)<0.解得a>2,所以有可能.故选B5.∵k•b<0,且k<0,∴b>0,k<0,∴函数y=kx+b的图象经过第一、二、四象限,故选D6.由题意可得,解得,故点(,)应在交点的上方,即第二部分.故选B.7.分两种情况:(1)当k>0时,正比例函数y=﹣kx的图象过原点、第一、三象限,一次函数y=kx﹣2的图象经过第一、三、四象限,选项A符合;(2)当k<0时,正比例函数y=﹣kx的图象过原点、第二、四象限,一次函数y=kx﹣2的图象经过第二、三、四象限,无选项符合.故选A.8.A、把x=0代入函数关系式得2×0+3=3,故函数图象过点(0,3),不过(0,﹣),故错误;B、由A知函数图象不过点(0,﹣),故错误;C、把x=﹣1代入函数关系式得,2×(﹣1)+3=1,故(﹣1,﹣1)不在函数图象上,故错误;D、分别令x=0,y=0,此函数成立,故正确.故选D9.函数y=﹣x﹣1是一次函数,其图象是一条直线.当x=0时,y=﹣1,所以直线与y轴的交点坐标是(0,﹣1);当y=0时,x=﹣1,所以直线与x轴的交点坐标是(﹣1,0).由两点确定一条直线,连接这两点就可得到y=﹣x﹣1的图象.故选D10.整理为y=kx﹣2∵y随x的增大而减小∴k<0又因为图象过2,4,3象限故选D.11.k1k2<0,则k1与k2异号,因而两个函数一个y随x的增大而增大,另一个y随x的增大而减小,因而A是错误的;b1<b2,则y1与y轴的交点在y2与y轴的交点的下边,因而B、C都是错误的.故选D.12.①当ab>0,正比例函数y=abx过第一、三象限;a与b同号,同正时y=ax+b过第一、二、三象限,故D错误;同负时过第二、三、四象限,故B错误;②当ab<0时,正比例函数y=abx过第二、四象限;a与b异号,a>0,b<0时y=ax+b过第一、三、四象限,故C错误;a<0,b>0时过第一、二、四象限.故选A13.A、根据图象知,水库的蓄水量因该随着降雨的时间的增加而增多;故本选项错误;B、本图象的直线,所以每天的降雨量是相等的,所以,蓄水库每天的增加的水的量是(40﹣10)÷6=5;故本选项正确;C、根据图示知,降雨开始时,蓄水量为10万米3,故本选项错误;D、根据图示知,降雨第6天,蓄水量增加了40万米3﹣30万米3=10万米3,故本选项错误;故选B14.根据题意列出关系式为:y=40﹣5t,考虑实际情况:拖拉机开始工作时,油箱中有油4升,即开始时,函数图象与y轴交于点(0,40),如果每小时耗油0.5升,且8小时,耗完油,故函数图象为一条线段.故选D15.∵正比例函数y=kx的图象经过第一、三象限,∴k>0,∴﹣k<0,∴y=kx﹣k的大致图象经过一、三、四象限,故选:B.16.由图形可知,该函数过点(0,2),(3,0),故斜率k==,所以解析式为y=,令y>2,即>2,解之得:x<017.根据题意,要求y<0时,x的范围,即:x+3<0,解可得:x<﹣2,故答案为x<﹣218.根据题意,观察图象,可得直线l过点(2,0),且y随x的增大而增大,分析可得,当x>2时,有y>0 19.根据图示及数据可知:①一次函数y1=kx+b的图象经过第二、四象限,则k<0正确;②y2=x+a的图象经与y轴交与负半轴,则a>0错误;③一次函数y1=kx+b与y2=x+a的图象交点的横坐标是3,所以当x=3时,y1=y2正确;④当x>3时,y1<y2正确;故正确的判断是①,③,④20.根据图示可知点P的坐标是(﹣4,2),所以y1>y2即直线1在直线2的上方,则x<﹣4.21.根据图象和数据可知,当y<0即图象在x轴下侧,x<1.故答案为x<122.函数与坐标轴的交点的坐标为(0,3),(6,0).(1)点A的坐标(﹣4,5);(2)和y轴的距离是2个单位长度的点的坐标M(2,2),N(﹣2,4)23.当x=0时,y=﹣4;当y=0时,2x﹣4=0,解得x=2,∴函数图象与两坐标轴的交点为(0,﹣4)(2,0).图象如下:(1)x=﹣2时,y=2×(﹣2)﹣4=﹣8,x=4时,y=2×4﹣4=4,∵k=2>0,∴y随x的增大而增大,∴﹣8≤y≤4;(2)x<2时,y<0;x=2时,y=0;x>2时,y>0.24.(1)由图象可看出当y=2.5时,x=5,因此x的取值范围应该是0<x≤5(y轴上的点是空心圆,因此x≠0);(2)由图象可看出,当x=5时,函数的值最小,是y=2.525.(1)如图所示:(2)由(1)中两函数图象可知,其交点坐标为(1,1);(3)由(1)中两函数图象可知,当x>1时,y1>y2.26.如图.(1)因为一次项系数是﹣3<0,所以y的值随x的增大而减小;(2)当y=0时,x=1,所以图象与x轴的交点坐标是(1,0);当x=0时,y=3,所以图象与y轴的交点坐标是(0,3);(3)由图象知,在A点左边,图象在x轴上方,函数值大于0.所以x≤1时,y≥0.(4)∵OA=1,OB=3,∴函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是S△AOB=×1×3=.27.(1)函数y=2x﹣1与坐标轴的坐标为(0,﹣1)(,0),描点即可,如图所示;(2)将A、B的坐标代入函数式中,可得出A点不在直线y=2x﹣1的图象上,B点在直线y=2x﹣1的图象上,A代入函数后发现﹣2.5×2﹣1=﹣6≠﹣4,因此A点不在函数y=2x﹣1的图象上,然后用同样的方法判定B是否在函数的图象上;(3)当y≤0时,2x﹣1≤0,因此x≤.28.(1)当x=﹣4时,y=2;当y=﹣2时,x=﹣2;(2)由(1)可知函数图象过(﹣4,2)、(﹣2,﹣2),由此可画出函数的图象,如下图所示:(3)∵y=﹣2x﹣6,﹣4≤y≤2∴﹣4≤﹣2x﹣6≤22≤﹣2x≤8﹣4≤x≤﹣129.(1)图象如图:(2)观察图象可得,当x>﹣3时,y>0;当x=﹣3时,y=0;当x<﹣3时,y<0.30.(1)列表:x 0 1y 2 0描点,连线(如图)…(也可以写成过点(0,2)和(1,0)画直线)(2)①(1,0);(0,2)②<1。
初中数学一次函数的图像专项练习30题(有答案)ok之欧阳育创编

一次函数的图像专项练习30题(有答案)时间:2021.02.04 创作:欧阳育1.函数y=ax+b与y=bx+a的图象在同一坐标系内的大致位置正确的是()A.B.C.D.2.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k <0;②a>0;③当x>2时,y2>y1,其中正确的个数是()A .0B .1C.2D .33.一次函数y=kx+b,y随x的增大而减小,且kb>0,则在直角坐标系内它的大致图象是()A.B.C.D.4.下列函数图象不可能是一次函数y=ax﹣(a﹣2)图象的是()A.B.C.D.5.如图所示,如果k•b<0,且k <0,那么函数y=kx+b 的图象大致是( )A .B .C .D .6.如图,直线l1:y=x+1与直线l2:y=﹣x ﹣把平面直角坐标系分成四个部分,则点(,)在( ) A . 第一部分 B . 第二部分 C . 第三部分 D . 第四部分7.已知正比例函数y=﹣kx 和一次函数y=kx ﹣2(x 为自变量),它们在同一坐标系内的图象大致是( )A .B .C .D .8.函数y=2x+3的图象是( )A . 过点(0,3),(0,﹣)的直线B . 过点(1,5),(0,﹣)的直线C . 过点(﹣1,﹣1),(﹣,0)的直线D . 过点(0,3),(﹣,0)的直线 9.下列图象中,与关系式y=﹣x ﹣1表示的是同一个一次函数的图象是( )A .B .C .D .10.函数kx﹣y=2中,y随x的增大而减小,则它的图象是下图中的()A.B.C.D.11.已知直线y1=k1x+b1,y2=k2x+b2,满足b1<b2,且k1k2<0,两直线的图象是()A.B.C.D.12.如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是()A.B.C.D.13.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若该水库的蓄水量V(万米3)与降雨的时间t(天)的关系如图所示,则下列说法正确的是()A.降雨后,蓄水量每天减少5万米3 B.降雨后,蓄水量每天增加5万米3 C.降雨开始时,蓄水量为20万米3 D.降雨第6天,蓄水量增加40万米314.拖拉机开始行驶时,油箱中有油4升,如果每小时耗油0.5升,那么油箱中余油y(升)与它工作的时间t(时)之间的函数关系的图象是()A.B.C.D.15.已知正比例函数y=kx的图象经过第一、三象限,则y=kx﹣k的大致图象可能是下图的()A.B.C.D.16.一次函数y=kx+b的图象如图所示,当x _________ 时,y >2.17.一次函数的图象如图所示,根据图象可知,当x_________ 时,有y<0.18.如图,直线l是一次函数y=kx+b的图象,当x _________时,y>0.19.一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x=3时,y1=y2;④当x>3时,y1<y2中,正确的判断是_________ .20.如图,已知函数y1=ax+b和y2=kx的图象交于点P,则根据图象可得,当x _________ 时,y1>y2.21.已知一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是_________ .22.在平面直角坐标系中画出函数的图象.(1)在图象上标出横坐标为﹣4的点A,并写出它的坐标;(2)在图象上标出和y轴的距离是2个单位长度的点,并写出它的坐标.23.作函数y=2x﹣4的图象,并根据图象回答下列问题.(1)当﹣2≤x≤4,求函数y的取值范围.(2)当x取何值时,y<0?y=0?y>0?24.如图是一次函数y=﹣x+5图象的一部分,利用图象回答下列问题:(1)求自变量的取值范围.(2)在(1)在条件下,y是否有最小值?如果有就求出最小值;如果没有,请说明理由.25.已知函数y1=﹣x+和y2=2x﹣1.(1)在同一个平面直角坐标系中画出这两个函数的图象;(2)根据图象,写出它们的交点坐标;(3)根据图象,试说明当x取什么值时,y1>y2?26.作出函数y=3﹣3x的图象,并根据图象回答下列问题:(1)y的值随x的增大而_________ ;(2)图象与x轴的交点坐标是_________ ;与y轴的交点坐标是_________ ;(3)当x _________ 时,y≥0;(4)函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是多少?27.已知函数y=2x﹣1.(1)在直角坐标系中画出这函数的图象;(2)判断点A(﹣2.5,﹣4),B(2.5,4)是否在函数y=2x﹣1的图象上;(3)当x取什么值时,y≤0.28.已知函数y=﹣2x﹣6.(1)求当x=﹣4时,y的值,当y=﹣2时,x的值.(2)画出函数图象.(3)如果y的取值范围﹣4≤y≤2,求x的取值范围.29.已知一次函数的图象经过点A(﹣3,0),B(﹣1,1)两点.(1)画出图象;(2)x为何值时,y>0,y=0,y<0?30.已知一次函数y=﹣2x+2,(1)在所给的平面直角坐标系中画出它的图象;(2)根据图象回答问题:①图象与x轴的交点坐标是_________ ,与y轴的交点坐标是_________ ;②当x _________ 时,y>0.参考答案:1.分四种情况:①当a>0,b>0时,y=ax+b的图象经过第一、二、三象限,y=bx+a 的图象经过第一、二、三象限,无选项符合;②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a 的图象经过第一、二、四象限,C选项符合;③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a 的图象经过第一、三、四象限,无选项符合;④当a<0,b<0时,y=ax+b的图象经过第二、三、四象限;y=bx+a 的图象经过第二、三、四象限,无选项符合.故选C2.由一次函数y1=kx+b与y2=x+a的图象可知k<0,a<0,当x>2时,y2>y1,①③正确.故选C3.∵一次函数y=kx+b,y随x的增大而减小,∴k<0,又∵kb>0,∴b<0,∴函数的图象经过第二、三、四象限.故选C4.根据图象知:A、a>0,﹣(a﹣2)>0.解得0<a<2,所以有可能;B、a<0,﹣(a﹣2)<0.解得两不等式没有公共部分,所以不可能;C、a<0,﹣(a﹣2)>0.解得a<0,所以有可能;D、a>0,﹣(a﹣2)<0.解得a>2,所以有可能.故选B5.∵k•b<0,且k<0,∴b>0,k<0,∴函数y=kx+b的图象经过第一、二、四象限,故选D6.由题意可得,解得,故点(,)应在交点的上方,即第二部分.故选B.7.分两种情况:(1)当k>0时,正比例函数y=﹣kx的图象过原点、第一、三象限,一次函数y=kx﹣2的图象经过第一、三、四象限,选项A符合;(2)当k<0时,正比例函数y=﹣kx的图象过原点、第二、四象限,一次函数y=kx﹣2的图象经过第二、三、四象限,无选项符合.故选A.8.A、把x=0代入函数关系式得2×0+3=3,故函数图象过点(0,3),不过(0,﹣),故错误;B、由A知函数图象不过点(0,﹣),故错误;C、把x=﹣1代入函数关系式得,2×(﹣1)+3=1,故(﹣1,﹣1)不在函数图象上,故错误;D、分别令x=0,y=0,此函数成立,故正确.故选D9.函数y=﹣x﹣1是一次函数,其图象是一条直线.当x=0时,y=﹣1,所以直线与y轴的交点坐标是(0,﹣1);当y=0时,x=﹣1,所以直线与x轴的交点坐标是(﹣1,0).由两点确定一条直线,连接这两点就可得到y=﹣x﹣1的图象.故选D10.整理为y=kx﹣2∵y随x的增大而减小∴k<0又因为图象过2,4,3象限故选D.11.k1k2<0,则k1与k2异号,因而两个函数一个y随x的增大而增大,另一个y随x的增大而减小,因而A是错误的;b1<b2,则y1与y轴的交点在y2与y轴的交点的下边,因而B、C都是错误的.故选D.12.①当ab>0,正比例函数y=abx过第一、三象限;a与b同号,同正时y=ax+b过第一、二、三象限,故D错误;同负时过第二、三、四象限,故B错误;②当ab<0时,正比例函数y=abx过第二、四象限;a与b异号,a>0,b<0时y=ax+b过第一、三、四象限,故C错误;a<0,b>0时过第一、二、四象限.故选A13.A、根据图象知,水库的蓄水量因该随着降雨的时间的增加而增多;故本选项错误;B、本图象的直线,所以每天的降雨量是相等的,所以,蓄水库每天的增加的水的量是(40﹣10)÷6=5;故本选项正确;C、根据图示知,降雨开始时,蓄水量为10万米3,故本选项错误;D、根据图示知,降雨第6天,蓄水量增加了40万米3﹣30万米3=10万米3,故本选项错误;故选B14.根据题意列出关系式为:y=40﹣5t,考虑实际情况:拖拉机开始工作时,油箱中有油4升,即开始时,函数图象与y 轴交于点(0,40),如果每小时耗油0.5升,且8小时,耗完油,故函数图象为一条线段.故选D15.∵正比例函数y=kx的图象经过第一、三象限,∴k>0,∴﹣k<0,∴y=kx﹣k的大致图象经过一、三、四象限,故选:B.16.由图形可知,该函数过点(0,2),(3,0),故斜率k==,所以解析式为y=,令y>2,即>2,解之得:x<017.根据题意,要求y<0时,x的范围,即:x+3<0,解可得:x<﹣2,故答案为x<﹣218.根据题意,观察图象,可得直线l过点(2,0),且y随x的增大而增大,分析可得,当x>2时,有y>019.根据图示及数据可知:①一次函数y1=kx+b的图象经过第二、四象限,则k<0正确;②y2=x+a的图象经与y轴交与负半轴,则a>0错误;③一次函数y1=kx+b与y2=x+a的图象交点的横坐标是3,所以当x=3时,y1=y2正确;④当x>3时,y1<y2正确;故正确的判断是①,③,④20.根据图示可知点P的坐标是(﹣4,2),所以y1>y2即直线1在直线2的上方,则x<﹣4.21.根据图象和数据可知,当y<0即图象在x轴下侧,x<1.故答案为x<122.函数与坐标轴的交点的坐标为(0,3),(6,0).(1)点A的坐标(﹣4,5);(2)和y轴的距离是2个单位长度的点的坐标M(2,2),N(﹣2,4)23.当x=0时,y=﹣4;当y=0时,2x﹣4=0,解得x=2,∴函数图象与两坐标轴的交点为(0,﹣4)(2,0).图象如下:(1)x=﹣2时,y=2×(﹣2)﹣4=﹣8,x=4时,y=2×4﹣4=4,∵k=2>0,∴y随x的增大而增大,∴﹣8≤y≤4;(2)x<2时,y<0;x=2时,y=0;x>2时,y>0.24.(1)由图象可看出当y=2.5时,x=5,因此x的取值范围应该是0<x≤5(y轴上的点是空心圆,因此x≠0);(2)由图象可看出,当x=5时,函数的值最小,是y=2.525.(1)如图所示:(2)由(1)中两函数图象可知,其交点坐标为(1,1);(3)由(1)中两函数图象可知,当x>1时,y1>y2.26.如图.(1)因为一次项系数是﹣3<0,所以y的值随x的增大而减小;(2)当y=0时,x=1,所以图象与x轴的交点坐标是(1,0);当x=0时,y=3,所以图象与y轴的交点坐标是(0,3);(3)由图象知,在A点左边,图象在x轴上方,函数值大于0.所以x≤1时,y≥0.(4)∵OA=1,OB=3,∴函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是S△AOB=×1×3=.27.(1)函数y=2x﹣1与坐标轴的坐标为(0,﹣1)(,0),描点即可,如图所示;(2)将A、B的坐标代入函数式中,可得出A点不在直线y=2x ﹣1的图象上,B点在直线y=2x﹣1的图象上,A代入函数后发现﹣2.5×2﹣1=﹣6≠﹣4,因此A点不在函数y=2x﹣1的图象上,然后用同样的方法判定B是否在函数的图象上;(3)当y≤0时,2x﹣1≤0,因此x≤.28.(1)当x=﹣4时,y=2;当y=﹣2时,x=﹣2;(2)由(1)可知函数图象过(﹣4,2)、(﹣2,﹣2),由此可画出函数的图象,如下图所示:(3)∵y=﹣2x﹣6,﹣4≤y≤2∴﹣4≤﹣2x﹣6≤22≤﹣2x≤8﹣4≤x≤﹣129.(1)图象如图:(2)观察图象可得,当x>﹣3时,y>0;当x=﹣3时,y=0;当x<﹣3时,y<0.30.(1)列表:x 0 1y 2 0描点,连线(如图)…(也可以写成过点(0,2)和(1,0)画直线)(2)①(1,0);(0,2)②<1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.一次函数的图像专项练习30题1.函数y=ax+b与y=bx+a的图象在同一坐标系的大致位置正确的是()A .B.C.D.2.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x>2时,y2>y1,其中正确的个数是()A.0 B.1 C.2 D.33.一次函数y=kx+b,y随x的增大而减小,且kb>0,则在直角坐标系它的大致图象是()A.B.C.D.4.下列函数图象不可能是一次函数y=ax﹣(a﹣2)图象的是()A.B.C.D.5.如图所示,如果k•b<0,且k<0,那么函数y=kx+b的图象大致是()A.B.C.D.6.如图,直线l1:y=x+1与直线l2:y=﹣x﹣把平面直角坐标系分成四个部分,则点(,)在()A .第一部分B.第二部分C.第三部分D.第四部分7.已知正比例函数y=﹣kx和一次函数y=kx﹣2(x为自变量),它们在同一坐标系的图象大致是()A .B.C.D.8.函数y=2x+3的图象是()A.过点(0,3),(0,﹣)的直线B.过点(1,5),(0,﹣)的直线C.过点(﹣1,﹣1),(﹣,0)的直线D.过点(0,3),(﹣,0)的直线9.下列图象中,与关系式y=﹣x﹣1表示的是同一个一次函数的图象是()A .B.C.D.10.函数kx﹣y=2中,y随x的增大而减小,则它的图象是下图中的()A .B.C.D.11.已知直线y1=k1x+b1,y2=k2x+b2,满足b1<b2,且k1k2<0,两直线的图象是()A .B.C.D.12.如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是()A .B.C.D.13.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若该水库的蓄水量V(万米3)与降雨的时间t(天)的关系如图所示,则下列说确的是()A.降雨后,蓄水量每天减少5万米3B.降雨后,蓄水量每天增加5万米3C.降雨开始时,蓄水量为20万米3D.降雨第6天,蓄水量增加40万米314.拖拉机开始行驶时,油箱中有油4升,如果每小时耗油0.5升,那么油箱中余油y(升)与它工作的时间t(时)之间的函数关系的图象是()A.B.C.D.15.已知正比例函数y=kx的图象经过第一、三象限,则y=kx﹣k的大致图象可能是下图的()A.B.C.D.16.一次函数y=kx+b的图象如图所示,当x _________ 时,y>2.17.一次函数的图象如图所示,根据图象可知,当x _________ 时,有y<0.18.如图,直线l是一次函数y=kx+b的图象,当x _________ 时,y>0.19.一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x=3时,y1=y2;④当x>3时,y1<y2中,正确的判断是_________ .20.如图,已知函数y1=ax+b和y2=kx的图象交于点P,则根据图象可得,当x _________ 时,y1>y2.21.已知一次函数y=kx+b的图象如图所示,当y<0时,x的取值围是_________ .22.在平面直角坐标系中画出函数的图象.(1)在图象上标出横坐标为﹣4的点A,并写出它的坐标;(2)在图象上标出和y轴的距离是2个单位长度的点,并写出它的坐标.23.作函数y=2x﹣4的图象,并根据图象回答下列问题.(1)当﹣2≤x≤4,求函数y的取值围.(2)当x取何值时,y<0?y=0?y>0?24.如图是一次函数y=﹣x+5图象的一部分,利用图象回答下列问题:(1)求自变量的取值围.(2)在(1)在条件下,y是否有最小值?如果有就求出最小值;如果没有,请说明理由.25.已知函数y1=﹣x+和y2=2x﹣1.(1)在同一个平面直角坐标系中画出这两个函数的图象;(2)根据图象,写出它们的交点坐标;(3)根据图象,试说明当x取什么值时,y1>y2?26.作出函数y=3﹣3x的图象,并根据图象回答下列问题:(1)y的值随x的增大而_________ ;(2)图象与x轴的交点坐标是_________ ;与y轴的交点坐标是_________ ;(3)当x _________ 时,y≥0;(4)函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是多少?27.已知函数y=2x﹣1.(1)在直角坐标系中画出这函数的图象;(2)判断点A(﹣2.5,﹣4),B(2.5,4)是否在函数y=2x﹣1的图象上;(3)当x取什么值时,y≤0.28.已知函数y=﹣2x﹣6.(1)求当x=﹣4时,y的值,当y=﹣2时,x的值.(2)画出函数图象.(3)如果y的取值围﹣4≤y≤2,求x的取值围.29.已知一次函数的图象经过点A(﹣3,0),B(﹣1,1)两点.(1)画出图象;(2)x为何值时,y>0,y=0,y<0?30.已知一次函数y=﹣2x+2,(1)在所给的平面直角坐标系中画出它的图象;(2)根据图象回答问题:①图象与x轴的交点坐标是_________ ,与y轴的交点坐标是_________ ;②当x _________ 时,y>0.一次函数的图像30题参考答案:1.分四种情况:①当a>0,b>0时,y=ax+b的图象经过第一、二、三象限,y=bx+a的图象经过第一、二、三象限,无选项符合;②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a的图象经过第一、二、四象限,C选项符合;③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a的图象经过第一、三、四象限,无选项符合;④当a<0,b<0时,y=ax+b的图象经过第二、三、四象限;y=bx+a的图象经过第二、三、四象限,无选项符合.故选C2.由一次函数y1=kx+b与y2=x+a的图象可知k<0,a<0,当x>2时,y2>y1,①③正确.故选C3.∵一次函数y=kx+b,y随x的增大而减小,∴k<0,又∵kb>0,∴b<0,∴函数的图象经过第二、三、四象限.故选C4.根据图象知:A、a>0,﹣(a﹣2)>0.解得0<a<2,所以有可能;B、a<0,﹣(a﹣2)<0.解得两不等式没有公共部分,所以不可能;C、a<0,﹣(a﹣2)>0.解得a<0,所以有可能;D、a>0,﹣(a﹣2)<0.解得a>2,所以有可能.故选B5.∵k•b<0,且k<0,∴b>0,k<0,∴函数y=kx+b的图象经过第一、二、四象限,故选D6.由题意可得,解得,故点(,)应在交点的上方,即第二部分.故选B.7.分两种情况:(1)当k>0时,正比例函数y=﹣kx的图象过原点、第一、三象限,一次函数y=kx﹣2的图象经过第一、三、四象限,选项A符合;(2)当k<0时,正比例函数y=﹣kx的图象过原点、第二、四象限,一次函数y=kx﹣2的图象经过第二、三、四象限,无选项符合.故选A.8.A、把x=0代入函数关系式得2×0+3=3,故函数图象过点(0,3),不过(0,﹣),故错误;B、由A知函数图象不过点(0,﹣),故错误;C、把x=﹣1代入函数关系式得,2×(﹣1)+3=1,故(﹣1,﹣1)不在函数图象上,故错误;D、分别令x=0,y=0,此函数成立,故正确.故选D9.函数y=﹣x﹣1是一次函数,其图象是一条直线.当x=0时,y=﹣1,所以直线与y轴的交点坐标是(0,﹣1);当y=0时,x=﹣1,所以直线与x轴的交点坐标是(﹣1,0).由两点确定一条直线,连接这两点就可得到y=﹣x﹣1的图象.故选D10.整理为y=kx﹣2∵y随x的增大而减小∴k<0又因为图象过2,4,3象限故选D.11.k1k2<0,则k1与k2异号,因而两个函数一个y随x的增大而增大,另一个y随x的增大而减小,因而A是错误的;b1<b2,则y1与y轴的交点在y2与y轴的交点的下边,因而B、C都是错误的.故选D.12.①当ab>0,正比例函数y=abx过第一、三象限;a与b同号,同正时y=ax+b过第一、二、三象限,故D错误;同负时过第二、三、四象限,故B错误;②当ab<0时,正比例函数y=abx过第二、四象限;a与b异号,a>0,b<0时y=ax+b过第一、三、四象限,故C错误;a<0,b>0时过第一、二、四象限.故选A13.A、根据图象知,水库的蓄水量因该随着降雨的时间的增加而增多;故本选项错误;B、本图象的直线,所以每天的降雨量是相等的,所以,蓄水库每天的增加的水的量是(40﹣10)÷6=5;故本选项正确;C、根据图示知,降雨开始时,蓄水量为10万米3,故本选项错误;D、根据图示知,降雨第6天,蓄水量增加了40万米3﹣30万米3=10万米3,故本选项错误;故选B14.根据题意列出关系式为:y=40﹣5t,考虑实际情况:拖拉机开始工作时,油箱中有油4升,即开始时,函数图象与y轴交于点(0,40),如果每小时耗油0.5升,且8小时,耗完油,故函数图象为一条线段.故选D15.∵正比例函数y=kx的图象经过第一、三象限,∴k>0,∴﹣k<0,∴y=kx﹣k的大致图象经过一、三、四象限,故选:B.16.由图形可知,该函数过点(0,2),(3,0),故斜率k==,所以解析式为y=,令y>2,即>2,解之得:x<017.根据题意,要求y<0时,x的围,即:x+3<0,解可得:x<﹣2,故答案为x<﹣218.根据题意,观察图象,可得直线l过点(2,0),且y随x的增大而增大,分析可得,当x>2时,有y>019.根据图示及数据可知:①一次函数y1=kx+b的图象经过第二、四象限,则k<0正确;②y2=x+a的图象经与y轴交与负半轴,则a>0错误;③一次函数y1=kx+b与y2=x+a的图象交点的横坐标是3,所以当x=3时,y1=y2正确;④当x>3时,y1<y2正确;故正确的判断是①,③,④20.根据图示可知点P的坐标是(﹣4,2),所以y1>y2即直线1在直线2的上方,则x<﹣4.21.根据图象和数据可知,当y<0即图象在x轴下侧,x<1.故答案为x<122.函数与坐标轴的交点的坐标为(0,3),(6,0).(1)点A的坐标(﹣4,5);(2)和y轴的距离是2个单位长度的点的坐标M(2,2),N(﹣2,4)23.当x=0时,y=﹣4;当y=0时,2x﹣4=0,解得x=2,∴函数图象与两坐标轴的交点为(0,﹣4)(2,0).图象如下:(1)x=﹣2时,y=2×(﹣2)﹣4=﹣8,x=4时,y=2×4﹣4=4,∵k=2>0,∴y随x的增大而增大,∴﹣8≤y≤4;(2)x<2时,y<0;x=2时,y=0;x>2时,y>0.24.(1)由图象可看出当y=2.5时,x=5,因此x的取值围应该是0<x≤5(y轴上的点是空心圆,因此x≠0);(2)由图象可看出,当x=5时,函数的值最小,是y=2.525.(1)如图所示:(2)由(1)中两函数图象可知,其交点坐标为(1,1);(3)由(1)中两函数图象可知,当x>1时,y1>y2.26.如图.(1)因为一次项系数是﹣3<0,所以y的值随x的增大而减小;(2)当y=0时,x=1,所以图象与x轴的交点坐标是(1,0);当x=0时,y=3,所以图象与y轴的交点坐标是(0,3);(3)由图象知,在A点左边,图象在x轴上方,函数值大于0.所以x≤1时,y≥0.(4)∵OA=1,OB=3,∴函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是S△AOB=×1×3=.27.(1)函数y=2x﹣1与坐标轴的坐标为(0,﹣1)(,0),描点即可,如图所示;(2)将A、B的坐标代入函数式中,可得出A点不在直线y=2x﹣1的图象上,B点在直线y=2x﹣1的图象上,A代入函数后发现﹣2.5×2﹣1=﹣6≠﹣4,因此A点不在函数y=2x﹣1的图象上,然后用同样的方法判定B是否在函数的图象上;(3)当y≤0时,2x﹣1≤0,因此x≤.28.(1)当x=﹣4时,y=2;当y=﹣2时,x=﹣2;(2)由(1)可知函数图象过(﹣4,2)、(﹣2,﹣2),由此可画出函数的图象,如下图所示:(3)∵y=﹣2x﹣6,﹣4≤y≤2∴﹣4≤﹣2x﹣6≤22≤﹣2x≤8﹣4≤x≤﹣129.(1)图象如图:(2)观察图象可得,当x>﹣3时,y>0;当x=﹣3时,y=0;当x<﹣3时,y<0.30.(1)列表:x 0 1y 2 0描点,连线(如图)…(也可以写成过点(0,2)和(1,0)画直线)(2)①(1,0);(0,2)②<1。
