瞬时频率和讲义复信号

复数信号探讨

号是信息的载体，实际的信号总是实的，但在实际应用中采用复信号却可以带来很大好处，由于实信号具有共轭对称的频谱，从信息的角度来看，其负频谱部分是冗余的，将实信号的负频谱部分去掉，只保留正频谱部分的信号，其频谱不存在共轭对称性，所对应的时域信号应为复信号。

通信一般具有载波，早期通信的载波为正弦波，通过调制传输信息，发射和接收的都是实信号，接收后要把调制信号从载波里提取出来，通常的做法是将载频变频到零（通称为零中频）。

我们知道，通常的变频相当于将载频下移，早期的调幅接收机将下移到较低的中频，其目的是方便选择信号和放大，然后通过幅度检波（调幅信号的载波只有幅度受调制）得到所需的低频信号，现代通信信号有各种调制方式，为便于处理，需要将频带内的信号的谱结构原封不动的下移到零中频(统称为基带信号)。

很显然，将接收到的实信号直接变到零中频是不行的，因为实信号存在共轭对称的双边谱，随着载频的下移，正、负相互接近，到中频小于信号频带一半时，两部分谱就会发生混叠，当中频为零时混叠最严重，使原信号无法恢复，这时应在变频中注意避免正、负谱分量的混叠，正确的获取基带信号。

实际表示复数变量使用实部和虚部两个分量。

复信号也一样，必须用实部和虚部两路信号来表示它，两路信号传输会带来麻烦，实际信号的传输总是用实信号，而在信号处理中则用复信号。

《通信信号处理》张贤达国防工业出版社对于虚数的难于理解，一定程度上是由于难以想像它究竟是个什么东西，就像4维以上的空间，难以在脑子里建立其形象的影像一样。

对于j，这个-1的平方根，容易产生一种直觉的排斥，除了掌握能够解出数学题目的运算规则以外，一般人都不会去琢磨它有没有实际意义，有什么实际意义。

在“达芬奇的密码”里，Langdon关于科学家对j的信仰以及教徒对宗教的信仰的类比，是对j之虚无缥缈和其重要性的绝妙诠释。

但是，对于一个搞通信或是信号处理的人来说，由于quadrature signal 的引入，j被赋予了确确实实的物理含义。

基于WVD的雷达信号瞬时频率提取方法研究

第１期
张静，等：基于ＷＶＤ的雷达信号瞬时频率提取方法研究
３９
Ｊ一∞ Ｊ一∞
ＩＩｏ－（ｘ，ｙ）ａ（一）ｅｆ２。ｄｙｄｘ
Ｃ
∞ Ｊ一∞ Ｃ
多不同类型的时频分布．虽然Ｗｉｇｎｅｒ — Ｖｉｌｌｅ分布具有许多期望的优良数学性质而倍受学界推崇，
之一．
雷达回波中的多普勒频率是目标的重要信息，它描述了目标径向运动的情况．瞬时频率可以
更好地反映信号频率随时间的变化情况，本文分析了噪声情况下多普勒信号的能量谱分布，将ＷＶＤ用于雷达回波信号的瞬时频率提取，并比较
鲁东大学学报（自然科学版）
ＬｕｄｏｎｇＵｎｉｖｅｒｓｉｔｙＪｏｕｎａｒｌ（ＮａｔｕｒａｌＳｃｉｅｎｃｅＥｄｉｔｉｏｎ）
基于ＷＶＤ的雷达信号瞬时频率提取方法研究
信号由于呈现较强的非平稳特性，传统方法对其难以实现有效的信噪分离．时频分析是近年来兴起的用于非平稳信号分
速．由于实际目标不可能是单独的理想点，通常把尺寸远小于脉冲宽度所对应长度的目标近似为 “ 点”目标．实际目标可视为众多散射点的集合，因而接收信号应为多个子回波的叠加．由于子回波问的延迟时间差远小于脉冲包络的宽度，因而接收信号可以近似看成具有相同包络的载波叠加ｊ．假设目标为二维的，目标的散射分布函数为Ｏｒ（，Ｙ），雷达射线与轴重合，则在距离处，一小段Ａｘ（设Ａｘ一０）的目标切片散射系数

瞬时频率取平均

瞬时频率取平均全文共四篇示例，供读者参考第一篇示例：瞬时频率取平均是信号处理中的一种重要方法，它能够帮助我们更好地理解信号的特性，从而取得更精确的数据分析结果。

本文将从瞬时频率的定义、瞬时频率取平均的意义和方法、在实际应用中的作用等方面进行详细的介绍。

瞬时频率是指信号在任意时刻的瞬时频率，它可以用来描述信号在不同时间点上的频率特性。

在信号处理领域，瞬时频率通常是通过信号的瞬时相位求导得到的。

瞬时相位可以反映信号的周期性和变化趋势，而瞬时频率则可以帮助我们了解信号的局部频率变化情况。

瞬时频率取平均是将信号在一段时间内的瞬时频率求平均值，这样可以得到一个更加稳定和准确的频率值，避免了信号局部频率变化的影响。

瞬时频率取平均不仅可以帮助我们更好地分析信号的频率特性，还可以在一些实际应用中提高数据处理的精度和效率。

在实际的数据处理中，瞬时频率取平均有多种方法和算法。

其中比较常见的有STFT（Short-Time Fourier Transform，短时傅立叶变换）、Hilbert Huang变换（Hilbert-Huang Transform）等。

STFT 是一种常用的瞬时频率取平均方法，它将信号分成多个小片段进行傅里叶变换，然后得到每个时间点上的频率信息。

Hilbert Huang变换则是将信号分解为一系列固有模态函数（Intrinsic Mode Functions，IMF）并计算每个IMF的瞬时频率，最后取平均值得到最终结果。

瞬时频率取平均在很多领域都有广泛的应用，比如音频信号处理、生物医学信号分析、地震信号处理等。

在音频领域，瞬时频率取平均可以帮助我们更好地理解音乐的节奏和旋律；在生物医学领域，瞬时频率取平均可以帮助我们检测心电图和脑电图中的异常信号；在地震信号处理中，瞬时频率取平均可以帮助我们更精确地识别地震信号的频率成分，从而提高地震监测的准确性。

瞬时频率取平均是一种重要的信号处理方法，它可以帮助我们更好地理解信号的特性，提高数据分析的精度和效率。

通信原理三套复习题.

复习题1一．填空题（共7小题，每空1分，共10分）1、均值为0，双边带功率谱密度为02n 的高斯白噪声通过传输函数为K ，中心频率为c f ，带宽为B ，满足c f B 的理想带通滤波器后，输出噪声包络的一维概率密度服从分布，相位服从分布，自相关函数为，平均功率为。

2、某随参信道的最大多径时延差为1ms ，为避免频率选择型衰落，工程上认为在该信道上传输QPSK 信号的传信率不应该超过比特/秒。

3、某4ASK 信号4个幅度的取值分别为0,1,2,3，其中幅度0出现的概率为1/4,则该4ASK 信号幅度所携带的最大平均信息量为。

4、某部分响应系统带宽为2000Hz ，传输16进制基带信号，则能实现无码间干扰传输的最大信息速率为比特/秒。

5、时域均衡的目的是。

6、移相法实现单边带调制的难点是。

7、循环码生成多项式为()431g x x x x =+++，则其能纠正位错码。

二、简答题（共4小题，每小题5分，共20分）1、简述随参信道的特点，通信信号通过随参信道后会产生哪些类型的衰落？如何减小这些衰落？2、什么是码间串扰？造成码间串扰的主要原因是什么？采用何种措施可以降低码间干扰？3、对于有噪声连续信道，写出信道容量的计算公式。

并简述由该公式得出的主要结论。

4、画出7位长巴克码（即1110010）识别器的原理框图，若识别器允许巴克码至多有一位错码，其判决电平为多大？为了减小漏同步概率，识别器判决门限应如何变化？为什么？三、综合题（共45分）1.（8分）设某信道具有均匀的单边带功率谱密度()710n P f W Hz -=，在该信道中传输振幅调制信号，并设调制信号带宽限制在20KHz ，而载波频率100KHz ，每个边带功率为1W ，载波功率为6W 。

若接收机的输入信号先经过一个合适的带通滤波器，然后再加至包络检波器进行解调。

求：（1）写出该带通滤波器的表达式并画图表示；（2）画出AM 系统框图（3）解调器输入端的信噪功率比；（4）解调器输出端的信噪功率比；（5）制度增益。

随机信号4.1

∧
ω0 +∆ω / 2
−ω0 +∆ω / 2
令 ω = ω −ω0 ,ω = ω +ω0 则有
' ''
∧ ∆ω / 2
'
j jω0t j − jω0t j ' jω t ' '' jω''t '' x(t) = − e ∫/A(ω )e dω + 2 e −∆∫/ 2 2 A(ω )e dω = 2 −∆ω 2 ω j jω0t j − jω0t − e a(t) + e a(t) = a(t) sin ω0t 2 2
1
∞
π −∞
∫
x(t −τ )
∧
τ
dτ =
∞
π −∞
∫
x(t +τ )
∧
τ
dτ
x(t)的希尔伯特变换为的希尔伯特变换为x(t)与1/πt的卷积的卷积. 的希尔伯特变换为与的卷积因此，因此，可以把希尔伯特变换看作是信号通过一个冲激响应为h(t)= 1/πt的线性时不变网络。的线性时不变网络。激响应为的线性时不变网络
一. 希尔伯特变换 ∧ 设有实信号x(t),它的希尔伯特变换记作x(t)或H[x(t)] 设有实信号它的希尔伯特变换记作并定义为 ∞
x(t) x(t) = H[x(t)] = ∫ dτ π −∞t −τ 1
∞ ∧
∧
反变换为
1 x(t) ∧ −1 x(t) = H x(t) = − ∫ dτ π −∞t −τ
R∧ ( ) = RXT ( ) τ τ
XT
XT
τ =0
R∧ (0) = RXT (0)

基于HVD和RDT的工作模态识别

基于HVD和RDT的工作模态识别涂文戈;邹小兵【摘要】应用希尔伯特振动分解(HVD)和随机减量技术(RDT)建立了环境激励下结构工作模态参数的识别方法.基于环境激励下结构的单点振动响应信号作为分析信号,应用希尔伯特振动分解将分析信号分解为若干个包含结构模态信息的信号,再利用随机减量技术提取自由衰减信号,应用最小二乘复指数法获得各阶模态频率和阻尼比.应用该方法对5自由度剪切模型以及12层混凝土框架地震台模型的顶点地震响应作为分析信号进行了结构工作模态参数的识别,并将识别结果与其他方法识别结果进行对比.结果表明该方法识别模态频率是可靠的;对平稳结构响应信号模态阻尼比的识别有好的精度,而对非平稳响应信号有较满意的精度.%An operational modal parameter identification method for structures under ambient excitations based on Hilbert vibration decomposition (HVD) and random decrement technique (RDT) is proposed. Operational modal frequencies and damping ratios are identified by the least squares method with free-vibration decay signals which are obtained by RDT from modal signal components and extracted by HVD from dynamic response signals of structures under ambient excitation. Operational modal parameters of both a 5-dofs shearing model and a reinforced concrete 12-story frame experimental structure are identified by the proposed method,and are compared with other identifying methods. Results show that the modal frequencies identified are reliable, the damping ratios for stationary response signals have high degree of accuracy, and the non-stationary response signals have acceptable degree of accuracy.【期刊名称】《广西大学学报（自然科学版）》【年(卷),期】2018(043)001【总页数】9页(P132-140)【关键词】模态参数识别;希尔伯特振动分解;同步解调;随机减量;最小二乘复指数法【作者】涂文戈;邹小兵【作者单位】湖南大学土木工程学院,湖南长沙410082;湖南大学土木工程学院,湖南长沙410082【正文语种】中文【中图分类】TB122;TU311.3环境激励下结构的工作模态参数识别是国内外研究的热点之一[1-2]。

时频表示及时频分布

时频表示：使用时间和频率的联合函数来表示信号。

时频分布：能够描述信号的能量密度分布的二次型时频表示。

2.1.1 解析信号与基带信号定义(解析信号)：与实信号s(t)对应的解析信号z(t)定义为z(t)=s(t)+jH[s(t)]，其中H[s(t)]是s(t)的Hilbert 变换。

物理意义：保留信号的正频部分并将幅度加倍，同时剔除负频部分。

命题：若调幅-调频信号s(t)=a(t)cos Φ(t)满足条件：A(f)= ℑ{a(t)}完全位于区域|f|<f 0，且频谱ℑ{ cos Φ(t)}只存在该区域以外，则s(t)的解析信号z(t)具有z(t)=a(t)e j Φ(t)的形式。

命题的物理意义：基于Hilbert 变换的解析信号生成器是一种高频率选择器。

基带信号：解析信号的复包络，它是复信号，是解析信号的频移形式。

实际应用：直接接受或观测到的总是实信号，需要经过加工处理，才能得到它的解析信号或基带信号。

解析信号实际得到它是困难的，因为具有理想阶跃频率特性的滤波器无法实现。

基带信号则容易得到，先将实信号频谱左移，然后用低通滤波器滤出基带分量即可。

基带信号和解析信号均适用时频分析。

2.1.2 瞬时频率和群延迟定义(瞬时频率)：解析信号相位的导数。

物理意义：把解析信号z(t)表示为复平面的向量，那么瞬时频率就表示向量幅角的转速。

定义(群延迟)：频谱Z(f)中频率为f 的各个分量的延迟。

物理意义：设零相位的信号加一线性相位，则信号做不失真的延迟，其延迟时间为该线性相位特性的负斜率。

2.1.3 不确定性原理定义：z(t)是一个具有有限能量的零均值复信号，其时宽t ∆和带宽f ∆分别定义为22222|()|()|()|t z t dt T t z t dt∞-∞∞-∞=∆=⎰⎰22222|()|()|()|f Z f dfB f Z f df∞-∞∞-∞=∆=⎰⎰物理意义：时宽t ∆和带宽f ∆分别为时间分辨率和频率分辨率，它们表示的是两时间点和两频率点间信号的区分能力。

复信号时频变换-概述说明以及解释

复信号时频变换-概述说明以及解释1.引言1.1 概述复信号时频变换是指对复信号在时域和频域上进行变换和分析的方法。

复信号具有实部和虚部两个分量，包含了相位和振幅信息，可以描述振荡信号的时变特性。

时频变换是分析信号在时域和频域上的变化规律的一种重要工具，可以提取信号的时频特征，揭示信号的时频结构。

复信号时频变换结合了复信号的特点和时频变换的优势，具有广泛的应用价值。

本文旨在介绍复信号时频变换的定义、特点、方法和算法，并探讨其应用和意义。

首先，我们将给出复信号的定义和特点，阐述复信号在时域和频域上的表示以及相位和振幅的重要性。

然后，我们将介绍时频变换的基本概念和原理，包括短时傅里叶变换（STFT）和连续小波变换（CWT）等常用方法。

接着，我们将详细讨论复信号时频变换的方法和算法，包括窗函数的选择、重叠和加权方法等。

最后，我们将探讨复信号时频变换在信号处理、通信系统和生物医学等领域的应用和意义，并做出总结和展望。

通过本文的阅读，读者将能够全面了解复信号时频变换的基本概念和原理，掌握常用的时频变换方法和算法，并能够应用于实际问题中。

复信号时频变换在信号处理与分析领域具有重要的研究价值和应用前景。

希望本文能够对相关领域的研究人员提供参考和启发，推动复信号时频变换的进一步发展和应用。

1.2文章结构文章结构简介：本文主要介绍了复信号时频变换的概念、原理、方法和算法，并探讨了其应用和意义。

文章分为引言、正文和结论三个部分。

1. 引言部分：在引言部分中，我们将对复信号时频变换的背景和意义进行简要概述。

首先介绍复信号的基本定义和特点，包括复数表示、幅度和相位表示等。

然后讨论时频变换的概念和原理，包括时域和频域的关系，以及复信号在时频域上的表现形式。

2. 正文部分：正文部分将详细介绍复信号时频变换的方法和算法。

首先介绍基于傅里叶变换的时频变换方法，包括连续时间傅里叶变换（CTFT）和离散时间傅里叶变换（DTFT），以及它们在复信号中的应用和计算方法。

线性调频脉冲_chirp_信号扫频--------------------------GOOD3

数据要做 FFT 运算 ,因此 N 不宜过大。设适合由普通
微机计算的最大采样点数为 Nmax ,则可得到
Δt = t2 - t1 = π( f h - f l) /β = Nmax/ fs
(3) 频率特性的计算。
根据
H ( jω)
=
R (jω) E (jω)
, 将响应信号的频谱
R (jω)
与激励信号的频谱 E (jω) 相除 ,即可得到所测量网络
式符合得较好。
4 扫频方法的改进
当所扫描的频带较宽 ,频带上限 f h 为下限 f l 的数倍甚至数十倍时 ,若仅仅根据 f h 来设置采样频率 ,那么在采集信号的低频部分时 ,会出现采集的数据点过多的情况。这对于 FFT 运算来说是所不希望的 ,因为
线性调频脉冲 (chirp) 信号扫频
时频率的范围是 [2πf l i , 2πf hi ] ,采集过程中对应的时
ω0 + 2βt1 = 2πfl
《测控技术》2003 年第 22 卷第 8 期
ω0 + 2βt2 = 2πf h
如果输出通道在时间范围 [ t1 , t2 ]内一共输出了 N 个点 ,那么 N 和输出通道的更新速率 f s′之间的关系便为
Δt = t2 - t1 = π( f h - fl) /β = N/ f s′
分布为
W ( t ,ω) = 2π A 2δ(ω - βt - ω0)
可见 , s ( t) 是一个单频率信号 ,任一时刻的瞬时功率都完全集中在瞬时频率 2βt + ω0 这点上。因此如果任意抽取一个时间片段[ t1 , t2 ]的 s ( t) 变换到频域 , 那么相应的频谱能量便集中在 [2βt1 + ω0 ,2βt2 + ω0 ] ,且在该频带范围内频谱的幅度相等。

高频------(杨霓清)答案(2)

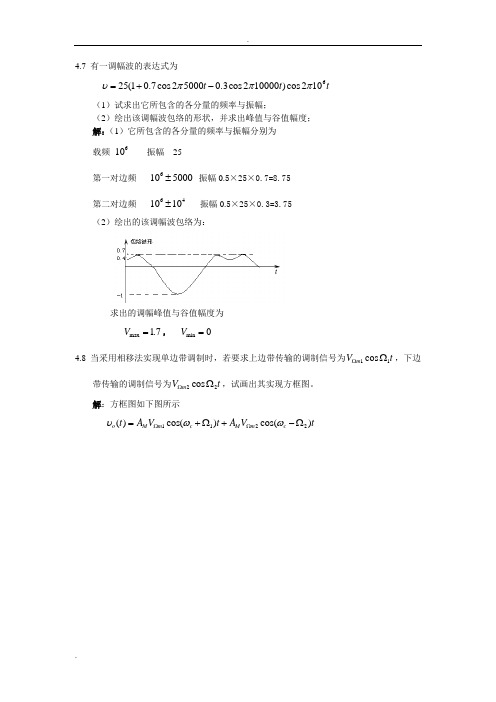
4.7 有一调幅波的表达式为625(10.7cos 250000.3cos 210000)cos 210t t t υπππ=+-（1）试求出它所包含的各分量的频率与振幅；（2）绘出该调幅波包络的形状，并求出峰值与谷值幅度；解：（1）它所包含的各分量的频率与振幅分别为载频 610 振幅 25第一对边频 6105000± 振幅0.5×25×0.7=8.75 第二对边频 641010± 振幅0.5×25×0.3=3.75 （2）绘出的该调幅波包络为：求出的调幅峰值与谷值幅度为 max 1.7V =， min 0V =4.8 当采用相移法实现单边带调制时，若要求上边带传输的调制信号为11cos m V t ΩΩ，下边带传输的调制信号为22cos m V t ΩΩ，试画出其实现方框图。

解：方框图如下图所示1122()cos()cos()o M m c M m c t A V t A V t υωωΩΩ=+Ω+-Ω4.9 电视图像传输系统如题4.9图，设输入的图像信号频谱在0～6MHz 范围内是均匀的，试画出（A ～H ）各点的频谱图，证明系统输出信号o υ不失真地重现输入图像信号1υ频谱。

题4.9图解：各点频谱如下图所示4.10 何谓过调幅？为什么双边带调制信号和单边带调制信号均不会产生过调幅？答：调制信号振幅大于载波信号振幅的情况称为过调幅。

因为双边带和单边带调制信号已经将载波信号抑制，故均不会产生过调幅。

4.11 一非线性器件的伏安特性为(0)0(0)D g i υυυ>⎧=⎨≤⎩式中 121122cos cos Q Q m m V V V t V t υυυωω=++=++。

若 2m V 很小，满足线性时变条件，则在1/2Q m V V =-、0、1m V 三种情况下，画出1()g υ波形，并求出时变增量电导1()g υ的表达式，分析该器件在什么条件下能实现振幅调制、解调和混频等频谱搬移功能。

信号瞬时频率的估算的开题报告

信号瞬时频率的估算的开题报告一、研究背景及意义信号的频率是指信号中所包含的周期性波动的次数，可以对信号进行分类、分析和处理。

对于周期性变化较快的信号，在短时间内的频率变化很大，此时需要研究信号的瞬时频率。

同时，瞬时频率也是信号处理与分析中一项重要的基础任务，例如语音和图像处理中的模式识别、噪声滤除、自适应滤波等都需要获取信号的瞬时频率信息。

因此，研究信号瞬时频率的估算具有实际意义和重要性。

二、研究内容本研究将针对信号的瞬时频率估算问题进行分析和研究，主要研究内容包括以下几方面：1. 研究信号的瞬时频率定义和计算方法，如瞬时频率的定义、瞬时频率的计算方法、瞬时频率与瞬时相位的关系等。

2. 研究不同信号的瞬时频率估算方法，如单纯余弦频率估计法、希尔伯特变换法、自适应滤波法等，对于不同信号进行分析和比较。

3. 在研究瞬时频率估算方法的基础上，提出一种基于新型算法的瞬时频率估算方法。

4. 对所提出的瞬时频率估算方法进行仿真和实验验证，并通过实验结果对所提出的方法进行评价和改进。

三、研究方法及技术路线该研究采用理论分析与计算机仿真相结合的方法，主要技术路线如下：1. 研究信号瞬时频率的理论定义和计算方法，包括多种不同的定义和计算方法，例如希尔伯特变换、自适应滤波等。

2. 通过计算机仿真与实验验证进行对这些方法的比较以及对其中一个或几个方法的改进。

3. 在基于现有算法的基础上，提出一种基于新型算法的瞬时频率估算方法，并对方法的准确性和实际应用性能进行评估和验证。

四、预期结果1. 系统地探讨了信号瞬时频率的概念、定义和计算方法，并对常见的方法进行了详细比较。

2. 提出并验证了一种基于新型算法的瞬时频率估算方法，通过仿真和实验验证，该方法能够有效提高估算准确度、抗噪声的能力以及实时性。

3. 针对所提出的方法的性能进行分析和评价，并对其进行改进和优化。

五、可行性分析本研究对于提高信号处理的精度和效率具有重要意义，研究成果有望在语音和信号处理、图像处理、雷达信号处理等领域应用，具有广泛应用前景。

基于LMD的信号瞬时频率求取方法及实验

第43卷第3期2009年3月浙　江　大　学　学　报(工学版)Journal o f Z hejiang U niv ersity (Engineering Science )Vol .43No .3M ar .2009收稿日期:2007-09-29.浙江大学学报(工学版)网址:w w w .journals .z ju .edu .cn /eng基金项目:国家自然科学基金资助项目(50675194);宁波市自然科学基金资助项目(2007A610014).作者简介:任达千(1974-),男,浙江嵊州人,博士生,从事机械故障诊断方面的研究.E -mail :bookw orm02@gmail .com通讯联系人:杨世锡,男,教授.E -mail :yangsx @z ju .edu .cnDOI :10.3785/j .issn .1008-973X .2009.03.024基于LMD 的信号瞬时频率求取方法及实验任达千,杨世锡,吴昭同,严拱标(浙江大学机械与能源工程学院,浙江杭州310027)摘　要:研究了调频信号瞬时频率的直接求取法,提出了纯调频信号的瞬时频率直接求取法的适用条件,并用数学方法证明了该适用条件.针对极值点附近瞬时频率的畸变情况引进平滑处理改进了瞬时频率求取法.应用局域均值分解(L M D )和经验模态分解(EM D )求取仿真信号和汽轮机转子振动信号的瞬时频率.结果表明,由L M D 方法求取信号瞬时频率时,不会出现难以解释物理意义的负频率现象.关键词:时频分析;局域均值分解;瞬时频率;适用条件中图分类号:T P206;T H 113.1;T H165.3 文献标识码:A 文章编号:1008-973X (2009)03-0523-06Instantaneous frequency extraction method and experiment based LMDREN Da -qian ,YANG Shi -xi ,WU Zhao -tong ,YA N G ong -biao(College of Mechanical and Ener gy Engineering ,Z he jiang University ,Hangz hou 310027,China )A bstract :A new time -frequency analy sis method called local mean deco mposition (LM D )w as introduced .The results of LMD are a serial of AM -FM sig nals ,and the instantaneous frequency can be calculated by arc cosine functio n .The direct metho d of instantaneous frequency e xtraction w as studied .A n applicable condition w as given and proved by mathema tical metho ds .Considering the aberration near the extreme points ,the moving smoo th w as applied to develo p the instantaneous frequency ex traction pro cess .LMD and empirical m ode decomposition (EMD )w ere applied to ex tract the instantaneous frequency o f the simu -lation sig nal and vibratio n sig nal o f a turbine rotor .The results sho wed that the LM D instantaneous fre -quency w as alw ays positive Key wor ds :time -frequency analysis ;local mean decomposition ;instantaneous frequency ;applicable condition Sm ith [1]于2005年提出了局域均值分解方法(local mean decomposition ,LM D ),这种新的时频分析方法将复杂的多分量信号分解为若干个乘积函数(productio n function ,PF )的线性组合,每一PF 分量由一个包络信号和一个调频信号相乘得到,包络信号就是该PF 的瞬时幅值,而PF 的瞬时频率可以由调频信号求出.进一步将所有PF 分量的瞬时频率和瞬时幅值相组合,即可得到原始信号的时频分布.Smith [1]首先将LM D 应用于脑电图(EEG )的信号处理.LMD 算法和经验模态分解(empirical mo dedecomposition ,EM D )方法类似,基于极值点来定义局域均值函数和局域包络函数,但是用滑动平均代替三次样条插值.EM D 分解的最终结果是一系列本征模函数;而LM D 的结果是一系列乘积函数,可以用反余弦函数直接求得瞬时频率.该方法不会出现难以解释物理意义的负频率现象.LM D 的端点效应相比较EMD ,在程度上轻得多,作用范围也比较小.本文提出并证明了“直接法”求取信号瞬时频率的适用条件,与经验模态分解法进行仿真与实验对比研究,表明局域均值分解有显著特点.目前,基于LMD 的时频分析方法虽未在机械故障诊断领域得到应用,但因一些优良的性质:分解过程可避免过包络、欠包络现象,没有严重的端点效应,求得的瞬时频率在任何时刻均是正的,基于LM D 的时频分析方法有望在机械故障诊断领域占一席之地.1　局域均值分解方法局域均值分解的基本思想和步骤如下:首先确定原始信号x (t )所有的局部极值点,分别由局部极值点形成局域均值函数m 11(t )和局域包络函数a 11(t ).原信号如图1(a )所示;找出信号的极值点之后,任意2个相邻极值点之平均值即定义为局域均值,如图1(b )虚线所示.第i 段的局域均值函数由下式给出:m i =(n i +n i +1)/2.(1)式中:n i 和n i +1为相邻极值点.图1　局域均值函数和局域包络函数Fig .1　Local mean function and lo ca l envelo p function同样,第i 段局域包络函数为相邻两极值点差值的1/2,如图1(c )虚线所示.第i 段局域包络函数由下式给出:a i =n i -n i +1/2.(2)然后在此基础上,用同样的算法对局域均值函数和局域包络函数分别作滑动平均.据文献[1]的附件,滑动平均的跨度取最长相邻极值点距离的1/3.设原来序列为y (i ),i =1,2,…,n ,则滑动平均的公式为y s (i )=12N +1(y (i +N )+y (i +N -1)+…+y (i -N )).(3)式中:2N +1即为滑动跨度,滑动跨度必须为奇数,如果是偶数则减去1.在边界附近,减小跨度,以不超过序列的端点为限.如果在滑动平均之后,尚有相邻点的值相等,则再次做滑动平均,直到任何相邻点不相等,如图1(b )和(c )中的实线所示.在计算得到局域均值函数和局域包络函数之后,将滑动平均后的局域均值函数m 11(t )从原始信号x (t )中分离出来,得到h 11(t )=x (t )-m 11(t ).再用h 11(t )除以滑动平均后的局域包络函数a 11(t ),以对h 11(t )进行解调,得到s 11(t )=h 11(t )/a 11(t ).如果s 11(t )相对应的局域包络函数a 12(t )=1,则已经是一个调频信号.如果a 12(t )≠1,则将s 11(t )作为原始数据重复以上迭代过程,直到s 1n (t )为一个调频信号,即-1≤s 1n (t )≤1,它的局域包络函数a 1(n +1)(t )=1.最后把迭代过程中产生的所有局域包络函数相乘便可以得到PF 的包络信号a 1(t )=a 11(t )a 12(t )…a 1n (t )=∏nq =1a1q(t ),该包络信号即PF 分量的瞬时幅值.将包络信号a 1(t )和调频信号s 1n (t )相乘便可得到原始信号的第一个PF 分量Y PF1(t )=a 1(t )s 1n (t ),它包含了原始信号中最高的频率成分,是一个单分量的调频-调幅信号,其瞬时幅值就是包络信号a 1(t ),其瞬时频率f 1(t )则可由调频信号s 1n (t )求出.将x (t )减去Y PF1(t )即得到一个新的信号u 1(t ),将u 1(t )作为原始数据重复以上步骤,循环k 次,直到u 1(t )为一个单调函数为止,这样便可以将x (t )分解为k 个PF 分量和一个单调函数u k 之和,即x (t )=∑kn =1YPF n(t )+u k (t ).2　“直接法”求取调频的瞬时频率LMD 分解得到的PF 是一单分量的调频调幅信号,其瞬时幅值就是包络信号a (t ),其瞬时频率f (t )则可由调频信号s (t )=co s φ(t )求出,即φ(t )=arcco s (s (t )).(4)将φ(t )展开然后求导,即可求得s (t )的瞬时频率,也就是PF 的瞬时频率,即524浙　江　大　学　学　报(工学版) 第43卷　ω(t )=d φ(t )/d t .(5)特别需要指出的是,必须保证-1≤s (t )≤1,s (t )的极点应等于±1,如果不等于而接近于±1,则可设置成±1.上述求取瞬时频率的方法显得简单和直接,称之为“直接法”.“直接法”的一个优点是计算得到的瞬时频率都是正的,不会出现难以解释物理意义的负频率.下面结合实例来说明“直接法”求取瞬时频率的计算过程.例1　调频信号,波形如图2所示,幅值无物理单位,表达式为s (t )=co s (50t +40t 2);0<t ≤1.(6) 因反余弦函数的值域为[0,π],将式(6)代入式(4)计算得到的相位如图3(a )所示;相位展开成可导的单调递增函数,如图3(b )所示.相位展开后再对求其导数,可得到瞬时频率.为方便后续处理,ω(t )乘以1/(2π),得f (t )=12πω(t )=12π×d φ(t )d t.(7)图3(c )即为计算所得的瞬时频率.可以看到图中有一些明显的毛刺,出现的位置是在s (t )=±1附近.将式(4)代入式(7),可得f (t )=-12π1-s 2(t )s ′(t ).(8)当s (t )=±1时,式(8)的分母等于0.因此这是一个不定式,s ′(t )的误差将被放大.在s (t )=±1的一个邻域内,式(8)并不能得到可靠的计算结果,这就是图3(c )所示的瞬时频率计算结果出现明显毛刺的原因.因此,必须作一些处理,将这一些点去除.以邻近点的平均值代替或作平滑处理,得到的瞬时频率如图4所示.图4　平滑处理后瞬时频率Fig .4　Smo othed instantaneous f requency3　“直接法”适用条件“直接法”求瞬时频率,原始信号经LM D 分解得到的调频信号s (t )应满足一定的适用条件.Smith [1]提出信号必须在[-1,1]的范围内,这是因为arcco s 函数的定义域即为[-1,1].从瞬时频率的概念出发,为得到正的瞬时频率,调频信号s (t )必须满足更苛刻的条件.应用“直接法”求取信号的瞬时频率,信号必须满足如下条件:信号的极大值等于1,信号的极小值等于-1.证明:为保证瞬时频率ω(t )=d φ(t )/d t 有定义,φ(t )必须是可导的,为了使ω(t )>0,相位φ(t )必须是连续单调递增函数.根据d φ(t )/d t 的符号和三角函数的性质[3]:co s φ(t )=co s (φ(t )+2m π),co s φ(t )=co s (-φ(t )+2n π).(9)式中:m 、n 为任意整数.以φ(t )的极值点为界将原相位函数分段,重新定义一相位函数,得Υ(t )=φ(t )+2n π,d φ/d t >0;-φ(t )+2m π,d φ/d t <0;未定义,其他.(10)如果Υ(t )可以构成一连续单调递增函数,即φ(t )的极值点是Υ(t )的可去间断点,那么φ(t )即是可以展开的,如例1的图3(b ).Υ(t )的连续性,即由间断点的特性决定.在φ(t )的极大值点处,左导数φ′-(t )>0,右导数φ′+(t )<0,那么Υ(t )的左右极限为525第3期任达千,等:基于LM D 的信号瞬时频率求取方法及实验Υ(t -)=φ(t )+2n π,Υ(t +)=-φ(t )+2m π.(11)Υ(t )在φ(t )的极大值点处连续的充要条件为Υ(t -)=Υ(t +),因此有φ(t )=0,n =m .(12)或φ(t )=π,n =m -1.(13)为此信号的极大值点可用下式表示:s (t )=co s (φ(t ))=±1.(14)当φ(t )为极小值点时,可以得到同样的结论,即信号的极值点必须是±1.“直接法”的适用条件,有如下意义:1)给出了信号应用“直接法”求取瞬时频率必须满足的条件,为进一步研究调频信号的判据提供了理论基础.2)说明瞬时频率不仅仅是局部的概念,为了计算某一时刻的瞬时频率,至少需要知道信号的全部极值点.4　“直接法”的仿真研究以下例子可以说明”直接法”的适用条件.例2　仿真信号波形如图5所示,幅值无物理单位,信号表达式为x (t )=cos (at 2+bt +c ).(15)式中:a =1,b =-10,c =10.在t =5处,信号有一极小点,其值为-0.7597.信号的相位表达式为图5　仿真信号Fig .5　Simula ted sig nalφ(t )=at 2+bt +c .(16)信号的瞬时频率表达式为ω(t )=d φ(t )/d t =2at +b .(17)但是“直接法”不能计算此信号的瞬时频率,按式(4)计算得到的相位如图6(a )所示.因为信号在t =5处有一极小值点不等于-1,不满足“直接法”的适用条件,相位连续展开后Υ(t )在t =5处有一间断点,所以不能得到有物理意义的瞬时频率,如图6(b )所示.若以此仿真信号作为原始信号,经LM D 分解结果如图7(a )、(b )和(c )所示,图中信号的幅值无物理单位.再进一步用“直接法”可求得瞬时频率,如图7(d )所示.图6　“直接法”计算所得相位F ig .6　Phase g ene rated by direct metho d5　与经验模态分解的实验对比5.1　经验模态分解简介H uang 等人[2]提出了一种被称为H ilbe rt -H uang 变换(简称H H T )的信号分析方法,其核心内容是经验模态分解(empirical m ode decom po si -tion ,EM D ),将信号分解成若干个本征模函数(in -trinsic mode function ,IM F ).对各IM F 做Hilbert 变换,可以得到信号的瞬时频率,并进一步计算信号的时频分布和边缘谱.为了得到有物理意义的瞬时频率,H uang 等人[6]提出了归一化H ilbert 变换.从EMD 分解得到的IM F 出发,首先找出IMF 的所有极大值点,对这些极大值点样条插值得到包络线E (t );再将IMF 除以E (t )即得到归一化的IMF ;然后对归一化的IMF 进行H ilbert 变换求瞬时频率.Huang 认为归一化Hilbert 变换的结果是令人满意的,但并非所有IMF 都可以求得有物理意义的瞬时频率.5.2　仿真信号对比LMD 方法的分解过程可以得到一系列的PF 分量,PF 分量由包络信号和调频信号相乘得到,从调频信号计算得到的瞬时频率是正的、连续的、具有物理意义的.而EM D 方法先得到IMF 分量,再对IMF 分量进行H ilbert 变换求得瞬时频率和瞬时幅值,则可能产生无法解释的负频率.以图8所示信号为例,信号的幅值无物理单位,表达式为526浙　江　大　学　学　报(工学版) 第43卷　图7　仿真信号LMD分解结果及瞬时频率Fig.7　LM D result fr om simula ted sig nal and in-stantaneo us frequencyx(t)=cos(2π×5t),0≤t<0.63;-1.02x+1.2354,0.63≤t<0.6357; cos(2π×5t-0.2),0.6357≤t≤1.(18)信号前后两段均为余弦信号,在0.63s附近信号的相位有一个突变,前后信号相位差0.2rad,在连接处,用一段直线过渡.这个函数既符合IMF的定义,可以用Hilbert变换求取瞬时频率,也符合“直接法”的适用条件,可以用“直接法”求取瞬时频率.该信号经H ilbert变换得到的瞬时频率在函数图8　仿真信号F ig.8　Simulated signal的过渡处出现波动,还出现负的瞬时频率值,并无法解释其物理意义,如图9所示.图10所示为应用“直接法”求取的瞬时频率,与H ilbert变换最大的不同是瞬时频率总是正的,没有出现无法解释的负频率.负频率现象不仅是一个理论问题[4-5],而且在分析实际信号时也是经常出现的,成为瞬时频率估计的一个重要的误差来源.5.3　振动信号对比如图11所示,这是一段从汽轮机上采集到的转子振动信号,EMD分解的结果见图12,信号幅值的物理单位是m V.可以看到总共有9个IM F和一个趋势项,因端点效应的影响IMF9和趋势项的幅值远超出了原信号,部分信号无法显示.图13显示了IMF1的瞬时频率,可以清楚地看到负频率现象.图14为振动信号的LMD分解结果,信号幅值527第3期任达千,等:基于LM D的信号瞬时频率求取方法及实验的物理单位是m V .图15是用“直接法”求取PF1的瞬时频率,可以看到用“直接法”求得瞬时频率总是正的,不会出现难以解释物理意义的负频率现象.6　结　论局域均值分解是一种新出现的时频分析方法,所求得的瞬时频率不会出现难以解释物理意义的负频率.本文的分析研究有以下几方面的意义:(1)给出了信号应用“直接法”求取瞬时频率必须满足的条件,为进一步研究调频信号的判据提供了理论基础.(2)针对极值点附近畸变情况引进平滑处理改进了该算法.(3)与经验模态分解法进行了实验对比,表明局域均值分解法具有避免出现负频率现象的显著特点.参考文献(References ):[1]SM I T H J S .T he local mean deco mpo sitio n and its a p -plica tion to EEG per ceptio n data [J ].Jo urnal of The Royal Society Interface ,2005,2(5):443-454.[2]H UA N G N E ,SH EN Z ,LON G S R ,et al .The empir -ical mode decom po sition and the Hilber t spectr um for no nlinear and no n -stationary time serie s analysis [J ].Proceedings of the Royal Society A ,1998,454(1971):903-995.[3]中国矿业大学数学教研室.数学手册[M ].北京:科学出版社,1990:73-95.[4]科恩L .时-频分析:理论与应用[M ].白居宪,译.西安:西安交通大学出版社,1998:22-33.[5]BO ASH AS H B .Estimating and interpre ting the insta n -taneous frequency of a sig nal -part 1:fundamentals [J ].Proceedings of the IEEE ,1992,80(4):520-538.[6]H U A NG N E ,A T T O H -OK IN E N O .The Hilbert -Huang transform in engineering [M ].Boca Rato n :T ay lo r &Fra ncis G roup ,2005.528浙　江　大　学　学　报(工学版) 第43卷　。

通信原理(陈启兴版)第4章课后习题答案

第四章模拟调制4.1 学习指导要点模拟调制的要点主要包括幅度调制、频率调制和相位调制的工作原理。

1. 幅度调制幅度调制是用调制信号去控制载波信号的幅度，使之随调制信号作线性变化的过程。

在时域上，已调信号的振幅随基带信号的规律成正比变化；在频谱结构上，它的频谱是基带信号频谱在频域内的简单平移。

由于这种平移是线性的，因此，振幅调制通常又被称为线性调制。

但是，这里的“线性”并不是已调信号与调制信号之间符合线性变换关系。

事实上，任何调制过程都是一种非线性的变换过程。

幅度调制包括标准调幅（简称调幅）、双边带调幅、单边带调幅和残留边带调幅。

如果调制信号m (t )的直流分量为0，则将其与一个直流量A 0相叠加后，再与载波信号相乘，就得到了调幅信号，其时域表达式为[]()()()AM 0c 0c c ()()cos cos ()cos (4 - 1)s t A m t t A t m t t ωωω=+=+ 如果调制信号m (t )的频谱为M (ω)，则调幅信号的频谱为[][]AM 0c c c c 1()π()()()() (4 - 2)2S A M M ωδωωδωωωωωω=++-+++- 调幅信号的频谱包括载波份量和上下两个边带。

上边带的频谱结构与原调制信号的频谱结构相同，下边带是上边带的镜像。

由波形可以看出，当满足条件|m (t )| ≤ A 0 (4-3)时，其包络与调制信号波形相同，因此可以用包络检波法很容易恢复出原始调制信号。

否则，出现“过调幅”现象。

这时用包络检波将发生失真，可以采用其他的解调方法，如同步检波。

调幅信号的一个重要参数是调幅度m ，其定义为[][][][]00max min 00max min()() (4 - 4)()()A m t A m t m A m t A m t +-+=+++ AM 信号带宽B AM 是基带信号最高频率分量f H 的两倍。

AM 信号可以采用相干解调方法实现解调。

一种分量数时变的水声信号瞬时频率估计方法[发明专利]

专利名称：一种分量数时变的水声信号瞬时频率估计方法专利类型：发明专利
发明人：苗永春,屈磊,吴军
申请号：CN202210292661.0
申请日：20220324
公开号：CN114674410A
公开日：
20220628
专利内容由知识产权出版社提供
摘要：本发明涉及一种分量数时变的水声信号瞬时频率估计方法，包括：输入多分量水声信号
s(t)，利用扩展的同步压缩变换ESST得到多分量水声信号s(t)的时频谱T(t，ω)；利用自动脊线提取AREA，追踪到时频谱T(t，ω)中所有可能的脊线，然后利用脊线融合标准，融合脊线；对得到的脊线用傅里叶级数展开，用Tikhonov正则化对脊线的傅里叶系数重构，得到重构的瞬时频率。

本发明是对自动脊线提取，与传统重叠分量的瞬时频率估计相比，本发明能够处理分量数随时间变化的信号；本发明结合分数时频谱，采用扩展同步压缩变换提取高能量集中度的时频谱，能够克服噪声干扰影响水声信号瞬时频率估计的精度；本发明方法能够准确的估计水声信号的瞬时频率。

申请人：安徽大学
地址：230601 安徽省合肥市经济技术开发区九龙路111号
国籍：CN
代理机构：合肥国和专利代理事务所(普通合伙)
代理人：张祥骞
更多信息请下载全文后查看。

探地雷达数据采集与解释

探地雷达数据采集以及解释山东大学岩土中心第1章．探地雷达简介1．1工作基本原理探地雷达（Ground Penetrating Radar，简称GPR）是利用频率介于106～109Hz的无线电波来确定地下介质的一种地球物理探测仪器。

随着微电子技术和信号处理技术的不断发展，探地雷达技术被广泛应用于工程地质勘察、建筑结构调查、公路工程质量检测、地下管线探测等众多领域。

探地雷达的基本原理如图1所示。

发射天线将高频短脉冲电磁波定向送入地下，电磁波在传播过程中遇到存在电性差异的地层或目标体就会发生反射和透射，接收天线收到反射波信号并将其数字化，然后由电脑以反射波波形的形式记录下来。

对所采集的数据进行相应的处理后，可根据反射波的旅行时间、幅度和波形，判断地下目标体的空间位置、结构及其分布。

探地雷达是在对反射波形特性分析的基础上来判断地下目标体的，所以其探测效果主要取决于地下目标体与周围介质的电性差异、电磁波的衰减程度、目标体的埋深以及外部干扰的强弱等。

其中，目标体与介质间的电性差异越大，二者的界面就越清晰，表现在雷达剖面图上就是同相轴不连续。

可以说，目标体与周围介质之间的电性差异是探地雷达探测的基本条件。

图1 探地雷达基本原理1．2电磁波传播特征探地雷达的电磁脉冲在介质中的传播速度为：v=其中c为电磁波在空气中的传播速度，ε为介质的介电常数，常见介质的介电常数如表1所示。

材质相对介电常数材质相对介电常数粉质粘土 6 水81干砂3～5 灰岩4～8湿砂20～30 花岗岩4～7金属300 砂岩 6PVC塑料 3.3 页岩5～15混凝土 6.4 淤泥5～30空气 1 海水80粘土5～40表1各种常见介质的介电常数电磁波脉冲在地质界面上的反射系数为：k=根据电磁脉冲的传播规律，在地质界面上如果反射系数为负，则相位与发射脉冲相反，若反射系数为正，则相位与反射脉冲一致。

如图2和图3，可以清除看到反射波相位的变化规律。

图2图31．3雷达的分辨率对于地质雷达的探测方式．它的分辨率也是一个必须了解的内容．地质雷达的分辨率包括垂直分辨率和水平分辨率。

信号理论(总结)

更精确的不确定原理：
ˆ( ) L2 , 则：设s (t ) L2 , 且满足：ts (t ), s
2 1 s sˆ 1 4Covt 2
第二章

信号空间 --------信号理论的数学基础
集合论基础
集合:
具有某种特定性质的事物的总体。
信号的集合表示：

正弦信号周期信号能量有限信号带宽有限信号
总能量： E
2 | s ( t ) | dt 信号波形的时域特征：平均时间（时间中心）：
<t>= t | s(t ) | dt

2
持续时间(时宽）：
= (t <t>) | s(t ) | dt
2 t 2
2
任意时间函数的平均值：
<g(t )>= g (t ) | s(t ) | dt
f n ( x) f 0 ( x) , a.e
即：A {x f n ( x)不收敛与f 0 ( x)}是一个零测集。

控制收敛定理
假定f n ( x) f ( x)几乎处处, 如果 f n ( x) g ( x) 对于所有的n成立，那么f ( x)可积，并且
f ( x)dx lim f

2 ˆ M n Sx ˆ xx , x M n} x { x L ； xx ˆ

投影定理：
ˆ a1e1 x ˆ, e1 ) 0 (x x
ˆ ( x, e1 )e1 x

2
ˆ x ( x, e1 )e1 min x x xx
表示唯一。即 x V
线性空间的基不是唯一的。