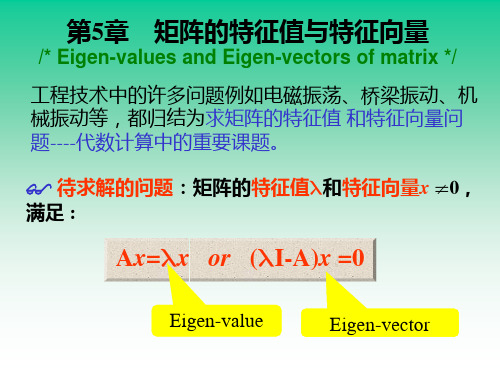
第五章矩阵特征问题的求解

第五章 矩阵特征问题的求解5.1 引言 在科学技术的应用领域中，许多问题都归为求解一个特征系统。

如动力学系统和结构系统中的振动问题，求系统的频率与振型；物理学中的某些临界值的确定等等。

设A 为n 阶方阵，n n ij R a A ⨯∈=)(，若)0(≠∈x R x n ，有数λ使Ax= λx （5.1） 则称λ为A 的特征值，x 为相应于λ的特征向量。

因此，特征问题的求解包括两方面： 1．求特征值λ，满足 0)det()(=-=I A λλϕ （5.2） 2．求特征向量)0(≠∈x R x n ，满足齐方程组0)(=-x I A λ （5.3）称ϕ（λ）为A 的特征多项式，它是关于λ的n 次代数方程。

关于矩阵的特征值，有下列代数理论，定义1 设矩阵A, B ∈R n ⨯n ，若有可逆阵P ，使AP P B 1-= 则称A 与B 相似。

定理1 若矩阵A, B ∈R n ⨯n 且相似，则 （1）A 与B 的特征值完全相同； （2）若x 是B 的特征向量，则Px 便为A 的特征向量。

定理2 设A ∈R n ⨯n 具有完全的特征向量系，即存在n 个线性无关的特征向量构成R n 的一组基底，则经相似变换可化A 为对角阵，即有可逆阵P ，使⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==-n D AP P λλλO 211其中λi 为A 的特征值，P 的各列为相应于λi 的特征向量。

定理3 A ∈R n ⨯n ，λ1, …, λn 为A 的特征值，则 （1）A 的迹数等于特征值之积，即∑∑===≡ni in i ii a A tr 11)(λ（2）A 的行列式值等于全体特征值之积，即n A λλλΛ21)det(=定理4 设A ∈R n ⨯n 为对称矩阵，其特征值λ1≥λ2≥…≥λn ，则（1）对任A ∈R n ，x ≠0，1),(),(λλ≤≤x x x Ax n（2）),(),(minx x x Ax x n ≠=λ（3）),(),(max1x x x Ax x ≠=λ 定理5 （Gerschgorin 圆盘定理） 设A ∈R n ⨯n ，则 （1）A 的每一个特征值必属于下述某个圆盘之中，n i aa z nij j ijii ,,2,1,1Λ=≤-∑≠=（5.4）（5.4）式表示以a ii 为中心，以半径为∑≠=nij j ija1的复平面上的n 个圆盘。

（2）如果矩阵A 的m 个圆盘组成的并集S （连通的）与其余n – m 个圆盘不连接，则S 内恰包含m 个A 的特征值。

定理4及定理5给出了矩阵特征值的估计方法及界。

例1 设有⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=411101014A估计A 的特征值的范围。

解 由圆盘定理，A 的3个圆盘为图5.1 D 1: 14≤-z D 2: 20≤-z D 3: 24≤+z见图5.1。

D 2为弧立圆盘且包含A 的一个实特征值λ1（因为虚根成对出现的原理），则3≤λ1≤5。

而λ2，λ3∈D 1∪D 2，则6max )(≤=i A λρ，即6)(3≤≤A ρ5.2 乘幂法与反幂法 在实际工程应用中，如大型结构的振动系统中，往往要计算振动系统的最低频率（或前几个最低频率）及相应的振型，相应的数学问题便为求解矩阵的按模最大或前几个按模最大特征值及相应的特征向量问题，或称为求主特征值问题。

5.2.1 乘幂法 乘幂法是用于求大型稀疏矩阵的主特征值的迭代方法，其特点是公式简单，易于上机实现。

乘幂法的计算公式为： 设A ∈R n ⨯n ，取初始向量x (0)∈R n ，令x (1) = Ax (0)，x (2) = Ax (1)，…，一般有)1()(-=k k Ax x（5.5）形成迭代向量序列{x (k)}。

由递推公式（5.5），有)0()1(2)2()()(x A x A Ax A x k k k k ====--Λ （5.6）这表明x (k )是用A 的k 次幂左乘x (0)得到的，因此称此方法为乘幂法，（5.5）或（5.6）式称为乘幂公式，{x (k )}称为迭代序列。

下面分析乘幂过程，即讨论当k →∞时，{x (k )}与矩阵A 的主特征值及相应特征向量的关系。

设A = (a ij )n ⨯n 有完全的特征向量系，且λ1, λ2,…, λn 为A 的n 个特征值，满足n λλλ≥≥≥Λ21v 1, v 2,…, v n 为相应的特征向量且线性无关，从而构成R n 上的一组基底。

对任取初始向量x (0) ∈ R n ，可由这组基底展开表示为∑==+++=nj jj nn v v v v x 12211)0(ααααΛ （5.7）其中α1, α2,…, αn 为展开系数。

将x (0)的展开式（5.7）代入乘幂公式（5.6）中，得)(11)(j knj j jn j j kk v Av Ax∑∑====αα（5.8）利用j k j j k v v A λ=（5.8）式为jkjnj j k vxλα∑==1)( （5.9）（1）如果A 有唯一的主特征值，即Λ≥>21λλ，设λ1 ≠ 0，且由（5.9）式，有()k kj kjnj j kk v v v x εαλλλααλ+=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+=∑=11112111)( 其中jki jnj j k v ⎪⎪⎭⎫⎝⎛=∑=λλαε2，由于n j j ,,3,2,11Λ=<λλ，故当k 充分大时，ε k ≈ 0，此时111)(v x kk αλ≈（5.10）对i = 1, 2, …, n ，若(α1v 1)i ≠ 0，考虑相邻迭代向量的对应分量比值，111111)1(1)()1()()(λαλαλ=≈++ikik k i k i v v x x （5.11）即对i = 1, …, n1)()1(lim λ=+∞→k ik i k x x （5.12）这表明主特征值λ1可由（5.11）或（5.12）式得到。

由于迭代序列x (k )，当k 充分大时，（5.10）式成立，x (k )与v 1只相差一个常数因子，故可取x (k )作为相应于主特征值λ1的特征向量的近似值。

迭代序列x (k )的收敛速度取决于12λλ的大小。

（2）如果A 的主特征值不唯一，且Λ≥>=321λλλ可分三种情况讨论： a ）λ1 = λ2；b ）λ1 = - λ2；c ）21λλ=情况a ）当λ1 = λ2时，A 的主特征值为二重根，根据（5.9）式)(221111322111)(k kj kjnj j kk v v v v v x εααλλλαααλ++=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++=∑= 当k 充分小时，由于11<λλj，j = 3,…, n ，ε k ≈ 0，则)(22111)(v v x kk ααλ+≈对i = 1, 2, …, n ，如果0)(2211≠+i v v αα，则1)()1(lim λ=+∞→k ik i k x x （主特征值） 且x (k )收敛到相应于λ1 (=λ2)的特征向量的近似值。

这种重主特征值的情况，可推广到A 的r 重主特征值的情况，即当r λλλ===Λ21 且11+>r λλ时，上述讨论的结论仍然成立。

情况b ）当λ1 = - λ2时，A 的主特征值为相反数，（5.9）式为))1(()1()1(22111132211132121113222111)(k k kj kjnj j k knj jk jj k kk nj jk jj k k k v v v v v vv v vv v xεααλλλαααλλαλαλαλαλαλα+-+=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-+=+-+=++=∑∑∑===当k 充分大时，11<λλj，j = 3, 4, …, n , ε k ≈ 0，则))1((22111)(v v x k kk ααλ-+≈（5.13）由于（5.13）式中出现因子(-1) k ，则当k 变化时，x (k )出现振荡、摆动现象，不收敛，利用(-1) k 的特点，连续迭代两步，得))1(())1((2211)2(122211)2(1)1(v v v v x kk k k k ααλααλ-+=-+≈++++从而，对i = 1, 2, …, n ，若0))1((2211≠-+i k v v αα，则21)()2(lim λ=+∞→k ik i k x x （5.14）开方之后，便得到A 的以上主特征值λ1, λ2 = - λ1。

为计算相应于λ1, λ2的特征向量，采取组合方式，1111)1(1)(1)1(2v C v x x k k k k =≈+++αλλ（5.15） 2222)1(11)(1)1(2)1(v C v x x k k k k k =-≈-+++αλλ（5.16）可见2211,v C v C k k分别为相应于λ1与λ2的特征向量。

情况c ）当21λλ=时，A 的主特征值为共轭复根。

因A 为实矩阵，A A =，于是由111v Av λ=有1211v v A Av λ==即21v v =（v 1与v 2为互为共轭向量）。

设θρλi e =1，θρλi e -=2，对任取x (0) ∈R n ，展开式（5.7）可为∑=++=nj jj vv v x31111)0(ααα （5.17）将（5.17）式代入（5.9）式，j kj nj j kik k i ik k jk jnj j k kk v v e v e vv v x⎪⎪⎭⎫⎝⎛++=++=∑∑=-=ρλαρραραλαλαλαθθ32113121111)(同理，当k 充分大时)(1111)(θθααρik ik k k e v e v x -+≈（5.18）对j = 1, 2,…, n ，设复数表示ϕϕααi j j i j j e r v e r v -==)(,)(1111则（5.18）式的复数表示可为)()()()(θϕθϕρk i j k i j k k j e r e r x +-++≈连续迭代，得⎪⎪⎩⎪⎪⎨⎧++≈++≈+≈++++))2(cos(2))1(cos(2)cos(22)2(1)1()(θϕρθϕρθϕρk r x k r x k r x j k k jj k k jj k k j （5.19）利用三角函数运算性质及λ1、λ2的复数表示，不难验证。

0)(21)1(21)2(≈++-++k j k j k j x x x λλλλ令2121,)(λλλλ=+-=q p（5.20）解方程（j = 1, 2, …, n ）0)()1()2(=++++k j k j k j qx px x（5.21）求出p, q 后，再解出主特征值λ1、λ2，得⎪⎪⎩⎪⎪⎨⎧⎪⎭⎫ ⎝⎛---=⎪⎭⎫ ⎝⎛-+-=22212222p q i p p q i p λλ（5.22）同样，采取组合方式求相应于λ1、λ2的特征向量。