电子技术基础数字部分(第五版)康光华主编第二章习题答案(可编辑修改word版)
数电课后答案解析康华光第五版(完整)

第一章数字逻辑习题1.1数字电路与数字信号1.1.2 图形代表的二进制数0101101001.1.4一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2数制2 1.2.2将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于4(2)127 (4)2.718解:(2)(127)D=72-1=(10000000)B-1=(1111111)B=(177)O=(7F)H(4)(2.718)D=(10.1011)B=(2.54)O=(2.B)H1.4二进制代码1.4.1将下列十进制数转换为8421BCD码:(1)43 (3)254.25解:(43)D=(01000011)BCD1.4.3试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,331.6逻辑函数及其表示方法1.6.1在图题1. 6.1中,已知输入信号A,B`的波形,画出各门电路输出L的波形。
解: (a)为与非, (b)为同或非,即异或第二章 逻辑代数 习题解答2.1.1 用真值表证明下列恒等式 (3)A B AB AB ⊕=+(A ⊕B )=AB+AB 解:真值表如下A B A B ⊕ABAB A B ⊕AB +AB0 0 0 1 0 1 1 0 1 1 0 0 0 0 1 0 1 0 0 0 0 11111由最右边2栏可知,A B ⊕与AB +AB 的真值表完全相同。
《数字电子技术基础(数字部分)》康华光第五版答案

环境下的门电路。
表题 3.1.1 逻辑门电路的技术参数表
V / V OH (min)
V /V OL(max)
V / V IH (min)
V / V IL(max)
逻辑门 A
2.4
0.4
2
0.8
逻辑门 B
3.5
0.2
2.5
0.6
逻辑门 C
4.2
0.2
3.2
0.8
解:根据表题 3.1.1 所示逻辑门的参数,以及式(3.1.1)和式(3.1.2),计算出逻辑门 A 的
课后答案网
2.2.4 已知逻辑函数 L = AB + BC + C A ,试用真值表,卡诺图和逻辑图(限用非门和与非
门)表示
解:1>由逻辑函数写出真值表
A
B
C
L
0
0
0
0
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
0
2>由真值表画出卡诺图
3>由卡诺图,得逻辑表达式 L = AB + BC + AC
课后答案网
www.khd课后a答w案.网com
第一章 数字逻辑习题
1.1 数字电路与数字信号 1.1.2 图形代表的二进制数
010110100 1.1.4 一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例
MSB
LSB
012
11 12 (ms)
电子技术基础数字部分第五版康光华主编第1~6章章节详细习题答案

第一章习题答案一周期性信号的波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比0121112(ms)图题1.1.4解: 周期T=10ms 频率f=1/T=100Hz占空比q=t w /T ×100%=1ms/10ms ×100%=10%将下列十进制数转换为二进制数、八进制数和十六进制数,要求误差不大于2-4:(1)43(2)127(3)(4)解:1. 转换为二进制数:(1)将十进制数43转换为二进制数,采用“短除法”,其过程如下:2 43 ………………………余1……b 02 21 ………………………余1……b 12 1 ………………………余1……b 52 2 ………………………余0……b 42 5 ………………………余1……b 32 10 ………………………余0……b 2高位低位从高位到低位写出二进制数,可得(43)D =(101011)B(2)将十进制数127转换为二进制数,除可用“短除法”外,还可用“拆分比较法”较为简单: 因为27=128,因此(127)D =128-1=27-1=(1000 0000)B -1=(111 1111)B(3)将十进制数转换为二进制数,整数部分(254)D =256-2=28-2=(1 0000 0000)B -2=(1111 1110)B 小数部分()D =()B()D=(1111 )B(4)将十进制数转换为二进制数整数部分(2)D=(10)B小数部分()D=()B演算过程如下:0.718×2=1.436……1……b-1 0.436×2=0.872……0……b-2 0.872×2=1.744……1……b-3 0.744×2=1.488……1……b-4 0.488×2=0.976……0……b-5 0.976×2=1.952……1……b-6高位低位要求转换误差小于2-4,只要保留小数点后4位即可,这里算到6位是为了方便转换为8进制数。
数电第五版_部分课后答案(清晰pdf康光华主编).txt

解:由图知该电路属于漏极开路门的线与输出
L E L4 E L1 L2 L3 E AB BC D
3.1.9 图题 3.1.9 表示三态门作总线传输的示意图,图中 n 个三态门的输出接到数据传 输总线,D1、D2、…、Dn 为数据输入端,CS1、CS2、…、CSn 为片选信号输入端。试问: (1)CS 信号如何进行控制,以便数据 D1、D2、…、Dn 通过该总线进行正常传输;(2)CS 信 号能否有两个或两个以上同时有效?如果 CS 出现两个或两个以上有效,可能发生什么情 况?(3)如果所有 CS 信号均无效,总线处在什么状态?
2 / 31
(3) A ABC ACD (C D) E A CD E
A ABC ACD (C D) E A(1 BC ) ACD (C D) E A(1 CD) ACD CDE A CD CDE A CD(1 E ) CDE A CD E
解: L ACD BCD ABCD ACD( B B) ( A A) BCD ABCD
ABCD ABCD ABCD ABCD ABCD m13 m9 m10 m 2 m15
(2) L A( B C )
L A( B C ) A ( B C ) A( BC BC ) BC ABC ABC BC ( A A) ABC A( B C ) ABC ABC ABC ABC ABC AB (C C ) AC ( B B ) ABC ABC ABC ABC ABC ABC ABC ABC ABC ABC ABC ABC m 7 m 5 m1 m 4 m 6
《电子技术基础》第五版高教康华光版部分课后答案

第一章数字逻辑习题1.1数字电路与数字信号1.1.2 图形代表的二进制数0101101001.1.4一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2数制2 1.2.2将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于4(2)127 (4)2.718解:(2)(127)D=72-1=(10000000)B-1=(1111111)B=(177)O=(7F)H(4)(2.718)D=(10.1011)B=(2.54)O=(2.B)H1.4二进制代码1.4.1将下列十进制数转换为8421BCD码:(1)43 (3)254.25解:(43)D=(01000011)BCD1.4.3试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,331.6逻辑函数及其表示方法1.6.1在图题1. 6.1中,已知输入信号A,B`的波形,画出各门电路输出L的波形。
解: (a)为与非, (b)为同或非,即异或第二章 逻辑代数 习题解答2.1.1 用真值表证明下列恒等式 (3)A B AB AB ⊕=+(A ⊕B )=AB+AB 解:真值表如下A B A B ⊕ABAB A B ⊕AB +AB0 0 0 1 0 1 1 0 1 1 0 0 0 0 1 0 1 0 0 0 0 11111由最右边2栏可知,A B ⊕与AB +AB 的真值表完全相同。
数字电路第五版(康华光)课后答案

第一章数字逻辑习题1.1 数字电路与数字信号1.1.2 图形代表的二进制数0101101001.1.4 一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2 数制1.2.2 将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于2−4(2)127 (4)2.718解:(2)(127)D= 27 -1=(10000000)B-1=(1111111)B=(177)O=(7F)H(4)(2.718)D=(10.1011)B=(2.54)O=(2.B)H1.4 二进制代码1.4.1 将下列十进制数转换为8421BCD 码:(1)43 (3)254.25 解:(43)D=(01000011)BCD1.4.3 试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you 的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43 的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,331.6 逻辑函数及其表示方法1.6.1 在图题1. 6.1 中,已知输入信号A,B`的波形,画出各门电路输出L 的波形。
解: (a)为与非, (b)为同或非,即异或第二章逻辑代数习题解答2.1.1 用真值表证明下列恒等式(3)A⊕ =B AB AB+ (A⊕B)=AB+AB解:真值表如下由最右边2栏可知,A⊕B与AB+AB的真值表完全相同。
《电子技术基础》康华光第五版模电课后问答题答案

第二章运算放大器2.1 集成电路运算放大器2.1.1答;通常由输入级,中间级,输出级单元组成,输入级由差分式放大电路组成,可以提高整个电路的性能。
中间级由一级或多级放大电路组成,主要是可以提高电压增益。
输出级电压增益为1,可以为负载提供一定的功率。
2.1.2答:集成运放的电压传输曲线由线性区和非线性区组成,线性区的直线的斜率即Vvo 很大,直线几乎成垂直直线。
非线性区由两条水平线组成,此时的Vo达到极值,等于V+或者V-。
理想情况下输出电压+Vom=V+,-Vom=V-。
2.1.3答:集成运算放大器的输入电阻r约为10^6欧姆,输出电阻r约为100欧姆,开环电压增益Avo约为10^6欧姆。
2.2 理想运算放大器2.2.1答:将集成运放的参数理想化的条件是:1.输入电阻很高,接近无穷大。
2.输出电阻很小,接近零。
3.运放的开环电压增益很大。
2.2.2答:近似电路的运放和理想运放的电路模型参考书P27。
2.3 基本线性运放电路2.3.1答:1.同相放大电路中,输出通过负反馈的作用,是使Vn自动的跟从Vp,使Vp≈Vn,或Vid=Vp-Vn≈0的现象称为虚短。
2.由于同相和反相两输入端之间出现虚短现象,而运放的输入电阻的阻值又很高,因而流经两输入端之间Ip=In≈0,这种现象称为虚断。
3.输入电压Vi通过R1作用于运放的反相端,R2跨接在运放的输出端和反相端之间,同相端接地。
由虚短的概念可知,Vn≈Vp=0,因而反相输入端的电位接近于地电位,称为虚地。
虚短和虚地概念的不同:虚短是由于负反馈的作用而使Vp≈Vn,但是这两个值不一定趋向于零,而虚地Vp,Vn接近是零。
2.3.2答:由于净输入电压Vid=Vi-Vf=Vp-Vm,由于是正相端输入,所以Vo为正值,Vo等于R1和R2的电压之和,所以有了负反馈电阻后,Vn增大了,Vp不变,所以Vid变小了,Vo 变小了,电压增益Av=Vo/Vi变小了。
由上述电路的负反馈作用,可知Vp≈Vn,也即虚短。
康华光第五版数电答案数电课后答案康华光第五版(完整)

康华光第五版数电答案数电课后答案康华光第五版(完整)第一章数字逻辑习题1.1数字电路与数字信号1.1.2 图形代表的二进制数 0001.1.4一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSBLSB 0121112(ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0.01s=100HZ 占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2数制1.2.2将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于(2)127 (4)2.718 解:(2)(127)D=-1=(10000000)B-1=(1111111)B=(177)O=(7F)H(4)(2.718)D=(10.1)B=(2.54)O=(2.B)H1.4二进制代码1.4.1将下列十进制数转换为8421BCD码:(1)43(3)254.25 解:(43)D=(01000011)BCD1.4.3试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+(2)@ (3)you (4)43 解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为0011,则(00011)B=(2B)H(2)@的ASCⅡ码为1000000,(01000000)B=(40)H (3)you的ASCⅡ码为本1111001,1111,1101,对应的十六进制数分别为79,6F,75 (4)43的ASCⅡ码为0100,0110011,对应的十六紧张数分别为34,331.6逻辑函数及其表示方法1.6.1在图题1.6.1中,已知输入信号A,B`的波形,画出各门电路输出L的波形。
解: (a)为与非, (b)为同或非,即异或第二章逻辑代数习题解答2.1.1 用真值表证明下列恒等式 (3)(A⊕B)=AB+AB 解:真值表如下 A B AB +AB 0 0 01 011 011 0 0 0 01 01 0 0 0 011 0 0111 由最右边2栏可知,与+AB的真值表完全相同。
电子技术基础(数字部分)第五版答案

第一章数字逻辑习题1.1数字电路与数字信号1.1.2 图形代表的二进制数0101101001.1.4一周期性数字波形如图题所示,试计算:〔1〕周期;〔2〕频率;〔3〕占空比例MSBLSB0 1 2 11 12 〔ms〕解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2数制1.2.2将以下十进制数转换为二进制数,八进制数和十六进制数〔要求转换误差不大于 42. 〔2〕127 〔4〕2.718解:〔2〕〔127〕D=-1=〔10000000〕B-1=〔1111111〕B=〔177〕O=〔7F〕H 72〔4〕〔2.718〕D=(10.1011)B=(2.54)O=(2.B)H1.4二进制代码1.4.1将以下十进制数转换为8421BCD码:〔1〕43 〔3〕254.25解:〔43〕D=〔01000011〕BCD1.4.3试用十六进制写书以下字符繁荣ASCⅡ码的表示:P28〔1〕+ 〔2〕@ 〔3〕you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
〔1〕“+〞的ASCⅡ码为0101011,那么〔00101011〕B=〔2B〕H〔2〕@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,331.6逻辑函数及其表示方法1.6.1在图题1. 6.1中,输入信号A,B`的波形,画出各门电路输出L的波形。
解: (a)为与非, (b)为同或非,即异或第二章逻辑代数习题解答2.1.1 用真值表证明以下恒等式(3)ABABAB⊕=+〔A⊕B〕=AB+AB 解:真值表如下ABAB⊕ABABAB⊕AB+AB111111111111由最右边2栏可知,与AB+AB的真值表完全相同。
电子技术基础 数字 康华光 课后答案

电子技术基础康华光课后习题答案(完整版)第一章数字逻辑1.1数字电路与数字信号1.1.2 图形代表的二进制数0101101001.1.4一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2数制1.2.2将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于42(2)127 (4)2.718解:(2)(127)D=72-1=(10000000)B-1=(1111111)B=(177)O=(7F)H (4)(2.718)D=(10.1011)B=(2.54)O=(2.B)H1.4二进制代码1.4.1将下列十进制数转换为8421BCD码:(1)43 (3)254.25解:(43)D=(01000011)BCD1.4.3试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,331.6逻辑函数及其表示方法1.6.1在图题1. 6.1中,已知输入信号A,B`的波形,画出各门电路输出L的波形。
解: (a)为与非, (b)为同或非,即异或第二章 逻辑代数2.1.1 用真值表证明下列恒等式 (3)A B AB AB ⊕=+(A ⊕B )=AB+AB 解:真值表如下A B A B ⊕ABAB A B ⊕ AB +AB0 0 0 1 0 1 1 0 1 1 0 0 0 0 1 0 1 0 0 0 0 110 0 111由最右边2栏可知,A B ⊕与AB +AB 的真值表完全相同。
电子技术基础数字部分(第五版)康光华主编第二章习题答案
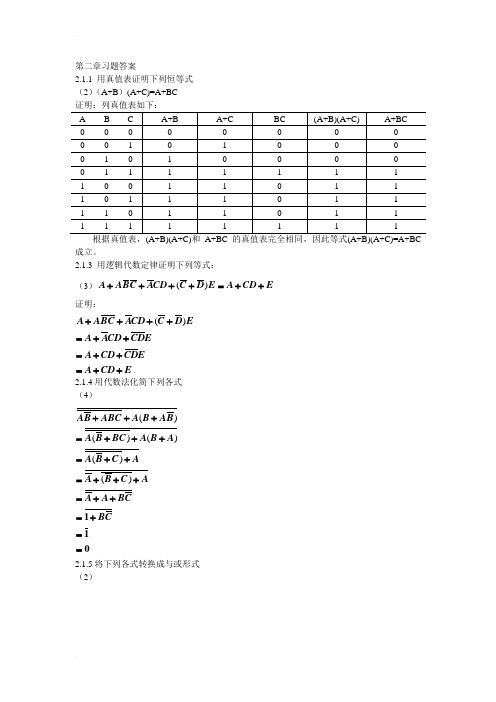
第二章习题答案2.1.1 用真值表证明下列恒等式 (2)(A+B )(A+C)=A+BC 证明:列真值表如下:成立。
2.1.3 用逻辑代数定律证明下列等式:(3)()A ABC ACD C D E A CD E ++++=++ 证明:()A ABC ACD C D E A ACD CDE A CD CDE A CD E++++=++=++=++2.1.4用代数法化简下列各式 (4)()()()()()110AB ABC A B AB A B BC A B A A B C A A B C A A A BC BC +++=+++=++=+++=++=+==2.1.5将下列各式转换成与或形式 (2)()()()()A B C D C D A DA B C D C D A D AC AD BC BD AC CD AD D AC BC AD BD CD D AC BC D+++++++=+++++=+++++++=+++++=++2.1.7 画出实现下列逻辑表达式的逻辑电路图,限使用非门和二输入与非门。
(1)L=AB+AC解:先将逻辑表达式化为与非-与非式:L AB AC AB AC AB AC =+=+=根据与非-与非表达式,画出逻辑图如下:LA B C2.1.8 已知逻辑函数表达式为L AB AC =+,画出实现该式的逻辑电路图,限使用非门和二输入或非门。
解:先将逻辑函数化为或非—或非表达式L AB A C AB A C A B A C =+=+=+++根据或非—或非表达式,画出逻辑图如下:A B CL另一种做法:用卡诺图化简变换为最简或与式A+B()()()()L A C A B A C A B A C A B =++=++=+++根据或非—或非表达式,画出逻辑图如下:AC BL2.2.1将下列函数展开为最小项表达式 (1)()()(,,,,)29101315L ACD BC D ABCD A B B CD ABCD A A BC D ABCD ABCD ABCD ABC D ABC D ABCD m =++=+++++=++++=∑(2)()L A B C =+()()()(,,)023L A B C AB AC AB C C A B B CABC ABC ABC ABC ABC ABC ABC m =+=+=+++=+++=++=∑(,,,,)14567L L m ==∑2.2.3用卡诺图化简下列各式(1) ABCD ABCD AB AD ABC ++++ 解:由逻辑表达式作卡诺图如下:ABAD由卡诺图得到最简与或表达式如下:L AB AC AD =++(5)(,,,)(,,,,,,,,,)0125689101314L A B C D m =∑解:由逻辑表达式作卡诺图如下:由卡诺图得到最简与或表达式如下:(,,,)L A B C D BD CD C D =++(7) (,,,)(,,,)(,,,,,)013141512391011L A B C D m d =+∑∑解:由逻辑表达式作卡诺图如下:A BAD AC由卡诺图得到最简与或表达式如下:=++(,,,)L A B C D AB AC AD。
电子技术基础数电部分课后答案(第五版康华光

I
T1
T2
输入全有为低高电电平 深倒饱置和使用的放大 截饱止和
平(0.2(3V.)6V)
状态
T4 截放止大
T3 饱截和止
O
低高电平 (03.26V)
2. TTL或非门
若A、B均为低电平:
T2A和T2B均将截止, T3截止。 T4和D饱和, 输出为高电平。
若A、B中有一个为高电平:
T2A或T2B将饱和, T3饱和,T4截止, 输出为低电平。
可变
很小,约为数 百欧,相当于 开关闭合
2. BJT的开关时间
BJT饱和与截止两种状态的相 互转换需要一定的时间才能完成。 从截止到导通 开通时间ton(=td+tr) 从导通到截止 关闭时间toff(= ts+tf)
3.2.2基本BJT反相器的动态性能
若带电容负载 CL的充、放电过程均需经历一定 的时间,必然会增加输出电压O波 形的上升时间和下降时间,导致基 本的BJT反相器的开关速度不高。
3.2 TTL逻辑门
3.2.1 BJT的开关特性
vI=0V时: iB0,iC0,vO=VCE≈VCC,c、e极之间近似于开路, vI=5V时: iB0,iC0,vO=VCE≈0.2V,c、e极之间近似于短路,
BJT的开关条件
工作状态 条件
截止 iB≈0
放大
0 < iB <
I CS
饱和 iB > ICS
输入 低电平
T1
T2
饱和 截止
T3
D4
截止 导通
T4 导通
输出
高电平
(2)当输入为高电平(I = 3.6 V) T2、T3饱和导通
T1:倒置的放大状态。 T4和D截止。
(完整word版)数字电子技术基础-康华光第五版答案
第一章数字逻辑习题1.1 数字电路与数字信号1。
1.2 图形代表的二进制数0101101001.1.4 一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0。
01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2 数制1.2.2 将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于2−4(2)127 (4)2。
718 解:(2)(127)D= 27 —1=(10000000)B—1=(1111111)B=(177)O=(7F)H(4)(2。
718)D=(10.1011)B=(2.54)O=(2。
B)H1。
4 二进制代码1。
4。
1 将下列十进制数转换为 8421BCD 码:(1)43 (3)254。
25 解:(43)D=(01000011)BCD1.4.3 试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@(3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示.(1)“+”的ASCⅡ码为 0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为 1000000,(01000000)B=(40)H(3)you 的ASCⅡ码为本 1111001,1101111,1110101,对应的十六进制数分别为 79,6F,75(4)43 的ASCⅡ码为 0110100,0110011,对应的十六紧张数分别为 34,331.6 逻辑函数及其表示方法1。
6。
1 在图题 1. 6.1 中,已知输入信号 A,B`的波形,画出各门电路输出 L 的波形。
解: (a)为与非, (b)为同或非,即异或第二章逻辑代数习题解答2.1.1 用真值表证明下列恒等式(3)A⊕ =B AB AB+(A⊕B)=AB+AB解:真值表如下由最右边2栏可知,A⊕B与AB+AB的真值表完全相同。
电子技术基础(第五版)康华光02 运算放大器

vS2 vS1
R2 iI R1
N P
Rf
– +
vO
v ( v v ) o S 1 S 2
输出再接一级反相电路
v S 2 v S 1 R 1 R 2 i I
N P – +
R f v O 1 R
R
– +
v O
可得 v v v o S 1 S 2
27
2.4.4 积分电路和微分电路
一、积分电路
根据虚短、虚断,并列 N点的KCL方程,得:
vI1
vO
vn vp 0 v i1 - v n v i2 - v n v n - v o R2 Rf R1
若 R R R 1 2 f
R R f f -v v v o i1 i2 R R 1 2
( v v ) 则有 v o i 1 i 2
(3)输出电阻Ro Ro→0
20
2.4 同相输入和反相输入 放大电路的其他应用
2.4.1 求差电路 2.4.2 仪用放大器
2.4.3 求和电路
2.4.4 积分电路和微分电路
21
2.4.1 求差电路
利用差分式电路以实现求差运算 利用叠加原理: 当 vi1 单独作用时, 可看作是反相放大电路 R4 ' vo vi1 R1
当 vi2 单独作用时, 可看作是同相放大电路
R4 R R 3 4 v (1 )vp ( 1 ) v i2 R1 R R R 1 2 3
'' o
R R R R 3 1 4 4 v ( )( ) v v O i2 i1 R R R R 1 2 3 1
22
R R R R 3 1 4 4 v ( )( ) v v O i2 i1 R R R R 1 2 3 1 R R R 当 4 3 , 则 vo 4 (vi2 vi1) R R1 R 2 1
数字电子技术基础-康华光第五版

第一章数字逻辑习题1.1 数字电路与数字信号1.1.2 图形代表的二进制数0101101001.1.4 一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2 数制1.2.2 将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于2−4(2)127 (4)2.718 解:(2)(127)D= 27 -1=(10000000)B-1=(1111111)B=(177)O=(7F)H(4)(2.718)D=(10.1011)B=(2.54)O=(2.B)H1.4 二进制代码1.4.1 将下列十进制数转换为 8421BCD 码:(1)43 (3)254.25 解:(43)D=(01000011)BCD1.4.3 试用十六进制写书下列字符繁荣 ASCⅡ码的表示:P28(1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的 ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的 ASCⅡ码为 0101011,则(00101011)B=(2B)H(2)@的 ASCⅡ码为 1000000,(01000000)B=(40)H(3)you 的 ASCⅡ码为本 1111001,1101111,1110101,对应的十六进制数分别为 79,6F,75(4)43 的 ASCⅡ码为 0110100,0110011,对应的十六紧张数分别为 34,331.6 逻辑函数及其表示方法1.6.1 在图题 1. 6.1 中,已知输入信号 A,B`的波形,画出各门电路输出 L 的波形。
解: (a)为与非, (b)为同或非,即异或第二章逻辑代数习题解答2.1.1 用真值表证明下列恒等式(3)A⊕ =B AB AB+ (A⊕B)=AB+AB解:真值表如下由最右边2栏可知,A⊕B与AB+AB的真值表完全相同。
《电子技术基础》第五版(数字部分) 高教(康华光)版 课后答案

第一章 数字逻辑习题1.1数字电路与数字信号 1.1.2 图形代表的二进制数0101101001.1.4一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例 MSB LSB0 1 2 11 12 (ms )解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10% 1.2数制1.2.2将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于 42−(2)127 (4)2.718解:(2)(127)D=-1=(10000000)B-1=(1111111)B =(177)O=(7F )H 72(4)(2.718)D=(10.1011)B=(2.54)O=(2.B)H1.4二进制代码1.4.1将下列十进制数转换为8421BCD 码: (1)43 (3)254.25 解:(43)D=(01000011)BCD1.4.3试用十六进制写书下列字符繁荣ASC Ⅱ码的表示:P28 (1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的ASC Ⅱ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASC Ⅱ码为0101011,则(00101011)B=(2B )H (2)@的ASC Ⅱ码为1000000,(01000000)B=(40)H(3)you 的ASC Ⅱ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75 (4)43的ASC Ⅱ码为0110100,0110011,对应的十六紧张数分别为34,33 1.6逻辑函数及其表示方法1.6.1在图题1. 6.1中,已知输入信号A ,B`的波形,画出各门电路输出L 的波形。
解: (a)为与非, (b)为同或非,即异或第二章 逻辑代数 习题解答2.1.1 用真值表证明下列恒等式 (3)A B AB AB ⊕=+(A⊕B)=AB+AB 解:真值表如下由最右边2栏可知,A B ⊕与AB +AB 的真值表完全相同。
(完整word版)《电子技术基础》第五版课后答案

解:图解3.1.7所示电路中L1= ,L2= ,L3= ,L4实现与功能,即L4=L1 L2 L3,而L= ,所以输出逻辑表达式为L=
3.1.9图题3.1.9表示三态门作总线传输的示意图,图中n个三态门的输出接到数据传输总线,D1,D2,……Dn为数据输入端,CS1,CS2……CSn为片选信号输入端.试问:
= — =0.8V—0.4V=0.4V
同理分别求出逻辑门B和C的噪声容限分别为:
=1V
=0.4V
=1V
=0.6V
电路的噪声容限愈大,其抗干扰能力愈强,综合考虑选择逻辑门C
3.1.3根据表题3.1.3所列的三种门电路的技术参数,计算出它们的延时-功耗积,并确定哪一种逻辑门性能最好
表题3.1.3逻辑门电路的技术参数表
逻辑门A
1
1.216Biblioteka 逻辑门B56
8
逻辑门C
10
10
1
解:延时-功耗积为传输延长时间与功耗的乘积,即
DP=tpdPD
根据上式可以计算出各逻辑门的延时-功耗分别为
= = *16mw=17.6* J=17.6PJ
同理得出: =44PJ =10PJ,逻辑门的DP值愈小,表明它的特性愈好,所以逻辑门C的性能最好.
3.1.5为什么说74HC系列CMOS与非门在+5V电源工作时,输入端在以下四种接法下都属于逻辑0: (1)输入端接地; (2)输入端接低于1.5V的电源; (3)输入端接同类与非门的输出低电压0.1V; (4)输入端接10kΩ的电阻到地.
解:对于74HC系列CMOS门电路来说,输出和输入低电平的标准电压值为:
《电子技术基础》数字部分第五版课后答案

第一章数字逻辑习题1.1数字电路与数字信号1.1.2图形代表的二进制数0101101001.1.4一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0121112(ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2数制2−1.2.2将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于4(2)127(4)2.718解:(2)(127)D=72-1=(10000000)B-1=(1111111)B=(177)O=(7F)H(4)(2.718)D=(10.1011)B=(2.54)O=(2.B)H1.4二进制代码1.4.1将下列十进制数转换为8421BCD码:(1)43(3)254.25解:(43)D=(01000011)BCD1.4.3试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+(2)@(3)you(4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,331.6逻辑函数及其表示方法1.6.1在图题1.6.1中,已知输入信号A,B`的波形,画出各门电路输出L的波形。
解:(a)为与非,(b)为同或非,即异或第二章逻辑代数习题解答2.1.1用真值表证明下列恒等式(3)A B AB AB ⊕=+(A⊕B)=AB+AB 解:真值表如下A B A B⊕ABAB A B⊕AB +AB00010110110000101000011111由最右边2栏可知,A B ⊕与AB +AB 的真值表完全相同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章习题答案
2.1.1 用真值表证明下列恒等式
(2)(A+B)(A+C)=A+BC
A B C A+B A+C BC (A+B)(A+C) A+BC
0 0 0 0 0 0 0 0
0 0 1 0 1 0 0 0
0 1 0 1 0 0 0 0
0 1 1 1 1 1 1 1
1 0 0 1 1 0 1 1
1 0 1 1 1 0 1 1
1 1 0 1 1 0 1 1
1 1 1 1 1 1 1 1
根据真值表,(A+B)(A+C)和A+BC 的真值表完全相同,因此等式(A+B)(A+C)=A+BC 成立。
2.1.3用逻辑代数定律证明下列等式:
(3)A ABC ACD (C D)E A CD E
证明:
A ABC ACD (C D)E
A ACD CDE
A CD CDE
A CD E
2.1.4用代数法化简下列各式
(4)
AB ABC A(B AB)
A(B BC ) A(B A)
A(B C ) A
A (
B
C ) A
A A BC
1 BC
1
2.1.5 将下列各式转换成与或形式
(2)
& &
&
A B C D C D A D
( A B )(C D ) (C D )( A D )
AC AD BC BD AC CD AD D
AC BC AD BD CD D
AC BC D
2.1.7 画出实现下列逻辑表达式的逻辑电路图,限使用非门和二输入与非门。
(1) L=AB+AC
解:先将逻辑表达式化为与非-与非式:
L AB AC AB AC AB AC
根据与非-与非表达式,画出逻辑图如下:
B
A
L
C
2.1.8 已知逻辑函数表达式为 L
AB AC ,画出实现该式的逻辑电路图,限使用非门和
二输入或非门。
解:先将逻辑函数化为或非—或非表达式
L AB AC AB AC A B A C
根据或非—或非表达式,画出逻辑图如下:
B A L
C
另一种做法:用卡诺图化简变换为最简或与式
1
≥1
≥1
≥1
1
1
L
BC A
00 0 A+C
A+B
L
( A C )( A B ) ( A C )( A B ) A C A B
根据或非—或非表达式,画出逻辑图如下:
C A
L
B
2.2.1 将下列函数展开为最小项表达式 (1)
L ACD BC D ABCD A (B B )CD ABCD ( A A )BC D ABCD ABCD
ABCD ABC D ABC D ABCD
m (2, 9,10,13,15)
(2) L
A (
B
C )
L A (B
C )
AB
AC
AB (C
C )
A (B
B )C
ABC ABC ABC ABC ABC ABC ABC
m (0,2, 3)
L L
m (1, 4, 5, 6, 7) 2.2.3 用卡诺图化简下列各式
(1) ABCD
ABCD AB AD ABC
解:由逻辑表达式作卡诺图如下:
1 ≥1
≥1
≥1
1
1
0 1 1 0 1 1 0 0
AD
AB
由卡诺图得到最简与或表达式如下:
L AB AC AD (5) L ( A , B , C , D )
m (0,1, 2, 5, 6, 8, 9,10,13,14)
解:由逻辑表达式作卡诺图如下:
B D
CD
由卡诺图得到最简与或表达式如下:
L ( A , B , C , D ) BD CD C D
(7) L ( A , B , C , D )
m (0,13,14,15)
d (1, 2, 3, 9,10,11)
解:由逻辑表达式作卡诺图如下:
L
CD
L
CD
AB 00 01 11 10
00 0 0 0 0 01 0 0 0 0 11 1 1 0 1
AC 10 1 1 1 1
AB 00 01 11 10 00 1 1 0 1 01 0 1 0 1 11 0 1 0 1
CD 10 1 1 0 1
1 L
CD
A
B 00 01 11 10 00 ╳ ╳ ╳ A B
01 0 0 0 0 11 0 1 1 1 10 0
╳ ╳ ╳
AD AC
由卡诺图得到最简与或表达式如下:
L ( A , B , C , D ) AB AC AD。
