数理逻辑.ppt
合集下载
数理逻辑PPT课件
.
4
数理逻辑
正如著名的计算机软件大师 戴克斯特拉 (E.W.Dijkstra)曾经说过：我 现在年纪大了，搞了这么多年软件，错误 不知犯了多少，现在觉悟了。我想，假如 我早在数理逻辑上好好下点功夫的话，我 就不会犯这么多错误。不少东西逻辑学家 早就说过了，可是我不知道。要是我能年 轻20岁的话，我就会回去学逻辑。
P∧Q的真值为真，当且 T T T
仅当P和Q的真值均为真。
.
11
命题逻辑
• 或者“∨”（析取）
表示“或者”，“或者”有二义性，看下面 两个例子：
例1. 灯泡或者线路有故障。 例2. 第一节课上数学或者上英语。
例1中的或者是可兼取的或。即或者“∨”
例2中的或者是不可兼取的或，也称之为异或、 排斥或。即“ ”.
.
12
命题逻辑
P：灯泡有故障。 Q：线路有故障。 例1中的复合命题可 表示为：P∨Q，读 成P或者Q，P∨Q的 真值为F，当且仅当 P与Q均为F。
P Q P∨Q FF F FT T TF T
TT T
.
13
命题逻辑
P：第一节上数学。
Q：第一节上英语。
P Q P Q
例2中的复合命题
可写成P Q，读 成P异或Q。
P Q的真值为F，
FF F FT T TF T
TT F
当且仅当P与Q的真值相同。
.
14
命题逻辑
• 蕴含(条件)“”
表示“如果… 则 …”，“当...则...”,“若... 那么...”，“假如...那么...”
例如： P表示：缺少水分。
Q表示：植物会死亡。
PQ：如果缺少水分，植物就会死亡。
PQ：也称之为蕴含式，读成“如果P则
离散数学配套课件PPT(第5版)第一部分 数理逻辑联结词全功能集
3
复合联结词
与非式: pq(pq) 或非式: pq(pq)
和与, ∧,∨有下述关系: p(p∧p)pp p∧q( p∧q)(pq)(pq)(pq) p∨q(p∧q)(p)(q)(pp)(qq)
4
复合联结词(续)
ppp p∧q(pp)(qq) p∨q(pq)(pq)
13
例ቤተ መጻሕፍቲ ባይዱ续)
解 编号
极小项
角码 标记
1 x1∧x2∧x3∧x4 2 x1∧x2∧x3∧x4 3 x1∧x2∧x3∧x4
1110 * 1011 * 0111 *
4 x1∧x2∧x3∧x4 1010 * 5 x1∧x2∧x3∧x4 0101 * 6 x1∧x2∧x3∧x4 0011 *
1.5 联结词全功能集
联结词全功能集 与非联结词,或非联结词
1
联结词的全功能集
定义 设S是一个联结词集合，如果任何n(n1) 元 真值函数都可以由仅含S中的联结词构成的公式表 示，则称S是联结词全功能集.
说明：若S是联结词全功能集，则任何命题公式都 可用S中的联结词表示.
设S1, S2是两个联结词集合，且S1 S2. 若S1是全
x y
x∧y x y
x∨y x
x
与门
或门
非门
8
组合电路的例子
(x∨y)∧x的组合电路
x y
x y
第一种画法
x 第二种画法
9
例
例 楼梯的灯由上下2个开关控制, 要求按动任何一个 开关都能打开或关闭灯. 试设计一个这样的线路. 解 x,y:开关的状态, F:灯的状态, 打开为1, 关闭为0. 不妨设当2个开关都为0时灯是打开的.
(5,7) x1∧x3∧x4 001 *
复合联结词
与非式: pq(pq) 或非式: pq(pq)
和与, ∧,∨有下述关系: p(p∧p)pp p∧q( p∧q)(pq)(pq)(pq) p∨q(p∧q)(p)(q)(pp)(qq)
4
复合联结词(续)
ppp p∧q(pp)(qq) p∨q(pq)(pq)
13
例ቤተ መጻሕፍቲ ባይዱ续)
解 编号
极小项
角码 标记
1 x1∧x2∧x3∧x4 2 x1∧x2∧x3∧x4 3 x1∧x2∧x3∧x4
1110 * 1011 * 0111 *
4 x1∧x2∧x3∧x4 1010 * 5 x1∧x2∧x3∧x4 0101 * 6 x1∧x2∧x3∧x4 0011 *
1.5 联结词全功能集
联结词全功能集 与非联结词,或非联结词
1
联结词的全功能集
定义 设S是一个联结词集合，如果任何n(n1) 元 真值函数都可以由仅含S中的联结词构成的公式表 示，则称S是联结词全功能集.
说明：若S是联结词全功能集，则任何命题公式都 可用S中的联结词表示.
设S1, S2是两个联结词集合，且S1 S2. 若S1是全
x y
x∧y x y
x∨y x
x
与门
或门
非门
8
组合电路的例子
(x∨y)∧x的组合电路
x y
x y
第一种画法
x 第二种画法
9
例
例 楼梯的灯由上下2个开关控制, 要求按动任何一个 开关都能打开或关闭灯. 试设计一个这样的线路. 解 x,y:开关的状态, F:灯的状态, 打开为1, 关闭为0. 不妨设当2个开关都为0时灯是打开的.
(5,7) x1∧x3∧x4 001 *
《高级数理逻辑》课件
介绍基于高级数理逻辑研究的智 能推理算法，让计算机更高效地 进行推理和判断。
多值逻辑及其应用
多值逻辑概述
介绍多值逻辑的概念、基本原理以及与二值逻 辑的区别。
多值逻辑在人工智能中的应用
深入研究多值逻辑在自然语言处理、机器学习 和智能系统中的应用，以提高其智能水平。
多值逻辑在计算机科学中的应用
探索多值逻辑在计算机编程、信息理论和密码 学等方面的应用。
模型检验方法
介绍基于多值逻辑的模型检验方法及其应用， 以确保系统或软件的正确性。
模态逻辑理论及扩展
1
经典模态逻辑
2
探讨经典模态逻辑的语法、语义、推理
规则及其应用。
3
非经典模态逻辑
4
介绍非经典模态逻辑，如增长逻辑、其 他模态逻辑和拓扑逻辑等，并探讨其应
用。
模态逻辑概述
介绍模态逻辑的基本概念、语言和语义。
二阶逻辑理论及应用
1 二阶逻辑概述
介绍二阶逻辑中的语法、 语义和推理规则。
Hale Waihona Puke 2 二阶逻辑的应用探讨二阶逻辑在模型论、 计算机科学和数学中的应 用。
3 高维逻辑
介绍高维逻辑的概念、语 言和语义，以及它在数学、 物理学和哲学中的应用。
可计算论概述及相关定理
可计算性理论
介绍可计算性理论和计算模型， 如图灵机、λ演算和递归函数等。
动态模态逻辑
研究模态逻辑中时间、知识和行动等概 念的语义和推理规则。
一阶逻辑及其扩展
概述
介绍一阶逻辑中的语法、语义和 推理规则。
一阶逻辑扩展
研究一阶逻辑的拓展，如高阶逻 辑、无限值逻辑和时态逻辑等， 并探讨其应用。
程序语言理论
介绍一阶逻辑在程序语言理论中 的应用，包括程序设计、程序分 析和验证等。
代数结构与数理逻辑-代数扩域
❖ (3)p(x)是唯一的。
❖ 证明: (1)p(x)不可约.设p(x)0,degp(x)1. ❖ 若degp(x)=1,p(x)当然不可约. ❖ 对于degp(x)>1,若p(x)可约, ❖ 则存在g(x),q(x)F(x),使得p(x)=g(x)q(x) ❖ 且1≤degg(x),degq(x)<degp(x)
❖ 引理15.2:f(x)F(x),是f(x)的根,则是f(x) 的重根,当且仅当在f(x)根域上(x-)|f'(x), 其中f'(x)是f(x)的形式微商。
❖ 引理15.3:Zp[x]中的多项式xq-x(这里q=pn) 在其根域N上分解为q个不同的一次因式 之积。
❖ 定理15.15:设p为素数,n1为自然数,q=pn, 则多项式xq-x在Zp上的根域是一个阶为pn 的伽罗瓦域。
❖ 0=p()=g()q(). ❖ F()是域,无零因子, ❖ 因此或者g()=0,或者q()=0. ❖ 与p(x)为极小多项式矛盾.
❖ (2)若f(x)F[x],f()=0则p(x)|f(x)。
❖ 因为f(x)=p(x)q(x)+r(x),
❖ q(x),r(x)F(x),r(x)=0或者degr(x)<degp(x)
二、给定素数p和正整数m,有阶pm的域
❖ 定义:设f(x)=a0+a1x++anxn是域F上的多 项 式 , 构 造 多 项 式 a1+2a2x++nanxn-1, 称
f(x)的形式微商, 记为f'(x)。
❖ 定理:(af(x))'=af'(x),
(f(x)+g(x))'= f'(x)+g'(x) (f(x)g(x))'= f'(x)g(x)+f(x)g'(x)。
❖ 证明: (1)p(x)不可约.设p(x)0,degp(x)1. ❖ 若degp(x)=1,p(x)当然不可约. ❖ 对于degp(x)>1,若p(x)可约, ❖ 则存在g(x),q(x)F(x),使得p(x)=g(x)q(x) ❖ 且1≤degg(x),degq(x)<degp(x)
❖ 引理15.2:f(x)F(x),是f(x)的根,则是f(x) 的重根,当且仅当在f(x)根域上(x-)|f'(x), 其中f'(x)是f(x)的形式微商。
❖ 引理15.3:Zp[x]中的多项式xq-x(这里q=pn) 在其根域N上分解为q个不同的一次因式 之积。
❖ 定理15.15:设p为素数,n1为自然数,q=pn, 则多项式xq-x在Zp上的根域是一个阶为pn 的伽罗瓦域。
❖ 0=p()=g()q(). ❖ F()是域,无零因子, ❖ 因此或者g()=0,或者q()=0. ❖ 与p(x)为极小多项式矛盾.
❖ (2)若f(x)F[x],f()=0则p(x)|f(x)。
❖ 因为f(x)=p(x)q(x)+r(x),
❖ q(x),r(x)F(x),r(x)=0或者degr(x)<degp(x)
二、给定素数p和正整数m,有阶pm的域
❖ 定义:设f(x)=a0+a1x++anxn是域F上的多 项 式 , 构 造 多 项 式 a1+2a2x++nanxn-1, 称
f(x)的形式微商, 记为f'(x)。
❖ 定理:(af(x))'=af'(x),
(f(x)+g(x))'= f'(x)+g'(x) (f(x)g(x))'= f'(x)g(x)+f(x)g'(x)。
《逻辑和证明》PPT课件
解 ：有许多方法翻译这个句子为逻辑表达式。尽管可以 用一个命题变量，如q来表示这一句子，但在分析其含义或 用其作推理时，这种表示不会有什么作用。
我们的办法是用命题变量表示其中的每一个句子成分， 并找出期间合适的逻辑联结词。具体的说，令a，c和f分别 表示“你可以从校园内访问因特网”、“你主修计算机科学” 和“你是个新生”。注意到“只有……才”是表达蕴含的一 种方式，上述句子可以译为：
7
❖例 太阳从西方升起，则2+2=4。 ❖联结词（运算符）的优先级：，，，，
减少所需的括号数目
❖例 p q s ❖命题符号化是命题演算的基础，符号化过程：
找出命题中的原子命题，分别用小写英文字母表示它 们 将原子命题用适当的联结词联结起来
a
8
❖ 例8 怎样把下面的句子翻译成逻辑表达式？ “只有你主修计算机科学或不是新生，才可以从校园内访问 因特网。”
(5)定义6 双蕴涵（等价）联结词 ， p q ：p与q的等价
a
6
❖ 真值表：给出命题真值之间的关系
❖ 含有n(n>0)个命题变量的命题公式的真值表有2n行
❖ 在数理逻辑中，组成一个复合命题的原子命题在语义可以没 有任何联系 数理逻辑关心复合命题的结构，其真值由组成它的原子命题 的真值唯一确定
பைடு நூலகம்
a
假命题 真命题 真命题 不是命题 不是命题 不是命题 不是命题 不是命题 假命题 不是命题
a
3
❖命命题题（符p、号q化、：r、用s字）母来表示命题，常用小写字母表示原子
❖比较：代数中用字母表示变量
❖例 p：2+4=8 q：水是液体
❖命题的真值：命题的真假性
真命题的真值为真，表示为T 假命题的真值为假，表示为F 比较：命题变量的真值与代数变量的值
我们的办法是用命题变量表示其中的每一个句子成分， 并找出期间合适的逻辑联结词。具体的说，令a，c和f分别 表示“你可以从校园内访问因特网”、“你主修计算机科学” 和“你是个新生”。注意到“只有……才”是表达蕴含的一 种方式，上述句子可以译为：
7
❖例 太阳从西方升起，则2+2=4。 ❖联结词（运算符）的优先级：，，，，
减少所需的括号数目
❖例 p q s ❖命题符号化是命题演算的基础，符号化过程：
找出命题中的原子命题，分别用小写英文字母表示它 们 将原子命题用适当的联结词联结起来
a
8
❖ 例8 怎样把下面的句子翻译成逻辑表达式？ “只有你主修计算机科学或不是新生，才可以从校园内访问 因特网。”
(5)定义6 双蕴涵（等价）联结词 ， p q ：p与q的等价
a
6
❖ 真值表：给出命题真值之间的关系
❖ 含有n(n>0)个命题变量的命题公式的真值表有2n行
❖ 在数理逻辑中，组成一个复合命题的原子命题在语义可以没 有任何联系 数理逻辑关心复合命题的结构，其真值由组成它的原子命题 的真值唯一确定
பைடு நூலகம்
a
假命题 真命题 真命题 不是命题 不是命题 不是命题 不是命题 不是命题 假命题 不是命题
a
3
❖命命题题（符p、号q化、：r、用s字）母来表示命题，常用小写字母表示原子
❖比较：代数中用字母表示变量
❖例 p：2+4=8 q：水是液体
❖命题的真值：命题的真假性
真命题的真值为真，表示为T 假命题的真值为假，表示为F 比较：命题变量的真值与代数变量的值
交大数理逻辑课件2-3 命题逻辑的等值和推理演算
9. Q (PQ) PBiblioteka 拒取式基本的推理公式
10. (PQ)(QR) PR 假言三段论 11.(PQ)(QR) P R 等价三段论 12. (PR)(QR) (PQ) R 13. (PQ)(RS)(PR) QS 构造性二难 14. (PQ)(RS)( QS) (PR) 破坏性二难 15. (QR) ((PQ) (PR)) 16. (QR) ((PQ) (PR))
附加前提证明法 ——举例
例如：证明下列推理。 前提： P(QR)，S∨P, Q 结论： S R 证明：(1) S P 前提 (2) S 附加前提引入 (3) P (1)(2) 析取三段论 (4) P (Q R) 前提 (5) Q R (3)(4) 假言推理 (6) Q 前提 (7) R (5)(6) 假言推理
((PQP Q
例：判断下面推理是否正确
（1）若天气凉快，小王就不去游泳。天气凉快，所 以小王没去游泳。 ③判断 ((PQ)P) Q是否为重言式 方法3：主析取范式法 ((PQ)P) Q = ((PQ)P)Q = (PQ) P Q = m11m0xmx0 = m11m00m01m00m10 = (0,1,2,3) = T ((PQP Q
(PQ(RS(PRQS 构造性二难
写出对应下面推理的证明
在大城市球赛中，如果北京队第三，那么如果上海队第 二，则天津队第四；沈阳队不是第一或北京队第三，上海队第 二。从而知：如果沈阳队第一，那么天津队第四。 解：设 (1) P (Q R) 前提 P：北京队第三 Q：上海队第二 (2) Q (P R) (1)置换 R：天津队第四 (3) Q 前提 S：沈阳队第一 (4) P R (2)(3)假言推理 前提：
P(QR)，S∨P, Q 结论： S R
数理逻辑简介.ppt课件
14、等价否定等值式 A B A B
15、归谬论 (A B) (A B) A
三、等值演算。
置换定理：如果 A B，则 ( A) (B)。
例2、验证下列等值式。
(1) p (q r) ( p q) r
(2) p (q r) p (q r) q r (3) q (p q) p 1
q (q p)
q (q p)
(q q) p
1 p 1
分配律 矛盾律 同一律 德摩根律 结合律 排中律 零律
考虑问题:能否利用等值式来化简，或判断 公式的类型(重言，矛盾，可满足)。
判断一个公式是否重言式，矛盾式，可满足 式，或者判断两个命题公式是否等值。有两种方 法，即真值表法和等值演算法。
内容：等值关系，24个重要等值式，等值演算。 重点：(1) 掌握两公式等值的定义。
(2) 掌握24个重要等值式，并能利用 其进行等值演算。
一、两命题公式间的等值关系。
1、定义：设 A, B为两命题公式，若等价式 A B 是重言式，则称 A与B是等值的，记作 A B 。
2、判定 。
判断两公式 A, B是否等值，即判断 A B
例2、 p p q r p r
为_5__层公式。
3、真值表。
公式 A 的解释或赋值
赋值
成真赋值 成假赋值
（使A为真的赋值） （使A为假的赋值）
如公式 A ( p q) r ，110( p 1, q 1, r 0 ，
按字典序)为 A 的成假赋值，111，011，010……
等是 A 的成真赋值。
2、结合律 (A B) C A (B C)， (A B) C A (B C)
3、分配律 A (B C) (A B) (A C) ， A (B C) (A B) (A C)
交大数理逻辑课件11-1函数
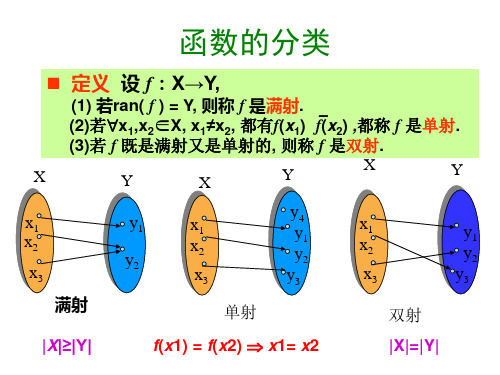
定义函数如图， 则 f∘g(a1)=c1, f∘g(a2)=c2
A
B
C
g
f
a1
b1
c1
b2
c2
a2
b3
11.2.2 函数的逆
任给函数 f, 它的逆f 1不一定是函数, 是二元关系. 实例：
f ={<a,b>,<c,b>}， f 1 ={<b,a>,<b,c>}
定理11.2.6
设 f：A→B是双射函数，则 f 的逆关系f 1 是B到 A的双 射函数。
令 f：A→B,
f()=f0,
f({1})=f1, f({2})=f2, f({3})=f3,
f({1,2})=f4, f({1,3})=f5, f({2,3})=f6, f({1,2,3})=f7
构造从A到B的双射函数（续）
二、实数区间之间构造双射
构造方法：直线方程
例 A=[0,1]
B=[1/4,1/2] 构造双射 f :A→B
一、有穷集之间的构造
例 A=P({1,2,3}), B={0,1}{1,2,3} 解： A={,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}.
B={ f0, f1, … , f7 }, 其中 f0={<1,0>,<2,0>,<3,0>}, f1={<1,0>,<2,0>,<3,1>}, f2={<1,0>,<2,1>,<3,0>}, f3={<1,0>,<2,1>,<3,1>}, f4={<1,1>,<2,0>,<3,0>}, f5={<1,1>,<2,0>,<3,1>}, f6={<1,1>,<2,1>,<3,0>}, f7={<1,1>,<2,1>,<3,1>}.
第1章 数理逻辑-命题逻辑
题 例：“张三学英语和李四学日语”
两个特殊的命题词
命题常量
T：永远表示真命题 F：永远表示假命题
T和F的两种含义
命题常量 命题的真值
数理逻辑不关心内容
具体的陈述句的真值究竟为什么或在什么环境
下是真还是假
数理逻辑只关心形式
命题可以被赋予真或假这样的可能性，以及规
一个陈述语句
命题
命题是一个非真即假(不可兼)的断言 如果命题是真
命题的真值（Truth Values）为真 真命题 大写字母“T”(1)表示
如果命题是假
命题的真值是假 假命题 大写字母“F”(0)表示
例1:
今天下雪
3+3=6
是偶数而 3 是奇数 1+101=110 明年的今天会下雨 较大的偶数都可表为两个质数之和
命题变元（命题词）
P表示任一命题时，P就称为命题变元（命题词）
命题词不是命题
命题指具体的陈述句，是有确定的真值 命题变元的真值不定，只当将某个具体命题代入命题
变元时，命题变元化为命题，方可确定其真值
复合命题(Compound proposition)
一个或几个简单命题用联结词联结所构成的命
设P表示命题, 那么“P不真”是另一命题, 表示为┐P, 叫做 P的否定, 读做“非P”。 如果P是假, 则┐P是真, 反之亦然。
P
F T
┐P
T F
真值表（Truth Table)
与自然语言中的“不”，“否”，“非”，“没有”，“未必 类似
例4
交大数理逻辑课件数理逻辑和集合论复习提纲23页PPT
答疑安排：
18周星期三(12月29日)，3:00-5:00 答疑地点：31号楼3楼教师休息室
《数理逻辑》样卷
一、单选题（共10分）
1．下列命题公式中，是重言式的 是____________。
A． (p q) q B. (p q) (p q) C. p∧q D. p q
2．设A、B、C、D为任意集合， 下面命题为真的是 ____________。
《数理逻辑与集合论》
复习提纲
第1章 命题逻辑的基本概念
1.1 命题 1.2 命题联结词及真值表 1.3 合式公式 1.4 重言式（三类公式的关系：P8） 1.5 命题形式化 1.6 波兰表达式
第2章 命题逻辑的等值和推理演算
2.1 等值定理 会运用等值式证明两个公式是否相等、判断公式的类型
2.2 等值公式
五. 证明题（20%）
证明 A=B C=D AC=BD 证： 任取<x,y>
<x,y>AC xA yC xB yD <x,y>BD
《数理逻辑》试题样卷
六.应用题：（20%）
证明苏格拉底三段论: “人都是要死的, 苏格拉底是人，所 以苏格拉底是要死的.”
令 F(x): x是人, G(x): x是要死的, a: 苏格拉底
前提：x(F(x)G(x))，F(a)
结论：G(a)
证明： ① F(a)
前提引入
② x(F(x)G(x)) 前提引入
③ F(a)G(a)
②UI
④ G(a)
①③假言推理
考试和答疑安排
考试时间：
18周星期五(12月31日)，8:00-10:00AM 考试地点：340402
2．符号化下面命题，并用谓词逻辑构造其推证结论的过程： 乌鸦都不是白色的. 北京鸭是白色的. 因此，北京鸭不是乌 鸦.
18周星期三(12月29日)，3:00-5:00 答疑地点：31号楼3楼教师休息室
《数理逻辑》样卷
一、单选题（共10分）
1．下列命题公式中，是重言式的 是____________。
A． (p q) q B. (p q) (p q) C. p∧q D. p q
2．设A、B、C、D为任意集合， 下面命题为真的是 ____________。
《数理逻辑与集合论》
复习提纲
第1章 命题逻辑的基本概念
1.1 命题 1.2 命题联结词及真值表 1.3 合式公式 1.4 重言式（三类公式的关系：P8） 1.5 命题形式化 1.6 波兰表达式
第2章 命题逻辑的等值和推理演算
2.1 等值定理 会运用等值式证明两个公式是否相等、判断公式的类型
2.2 等值公式
五. 证明题（20%）
证明 A=B C=D AC=BD 证： 任取<x,y>
<x,y>AC xA yC xB yD <x,y>BD
《数理逻辑》试题样卷
六.应用题：（20%）
证明苏格拉底三段论: “人都是要死的, 苏格拉底是人，所 以苏格拉底是要死的.”
令 F(x): x是人, G(x): x是要死的, a: 苏格拉底
前提：x(F(x)G(x))，F(a)
结论：G(a)
证明： ① F(a)
前提引入
② x(F(x)G(x)) 前提引入
③ F(a)G(a)
②UI
④ G(a)
①③假言推理
考试和答疑安排
考试时间：
18周星期五(12月31日)，8:00-10:00AM 考试地点：340402
2．符号化下面命题，并用谓词逻辑构造其推证结论的过程： 乌鸦都不是白色的. 北京鸭是白色的. 因此，北京鸭不是乌 鸦.
逻辑学全部ppt课件
逻辑学全部ppt课件CONTENTS •逻辑学概述•形式逻辑•辩证逻辑•数理逻辑初步•归纳逻辑与演绎逻辑•逻辑谬误与批判性思维逻辑学概述01逻辑学的定义与研究对象逻辑学的定义逻辑学是研究推理和论证的学科，旨在分析、评估和改进人们的思维方式和表达方法。
研究对象逻辑学的研究对象包括概念、命题、推理、论证等思维形式和规律。
起源于古希腊，代表人物有亚里士多德等，主要研究三段论等演绎推理方法。
19世纪末至20世纪初，数理逻辑得到快速发展，代表人物有弗雷格、罗素等，将数学方法应用于逻辑学研究。
随着计算机科学、人工智能等领域的发展，逻辑学在多个领域得到广泛应用，形成了多个分支学科。
古典逻辑学近现代逻辑学当代逻辑学逻辑学的发展历程03辩证思维方法在分析和评估论证过程中，运用辩证思维方法来揭示论证中的矛盾和问题，提出改进意见。
01形式化方法通过符号和公式来表示概念、命题和推理，运用形式化系统进行推导和证明。
02语义分析方法研究语言表达式与客观世界之间的关系，分析表达式的意义和真值条件。
逻辑学的研究方法形式逻辑02概念与范畴概念的定义与分类解释概念的含义，探讨概念的种类及其之间的关系。
范畴的划分与特性阐述范畴的概念，分析范畴的划分标准及其特性。
概念与范畴的关系探讨概念与范畴之间的联系与区别，以及它们在逻辑学中的地位和作用。
判断与推理判断的构成与种类分析判断的基本要素，介绍判断的种类及其逻辑特征。
推理的形式与规则阐述推理的含义，探讨推理的形式和规则，包括演绎推理和归纳推理等。
判断与推理的关系探讨判断与推理之间的联系与区别，以及它们在逻辑学中的地位和作用。
形式化方法形式化语言与符号系统介绍形式化语言的概念，阐述符号系统的构建原则和方法。
形式化证明与演算探讨形式化证明的方法和技巧，包括自然演绎、公理化方法等，以及形式化演算的基本规则和步骤。
形式化方法的应用阐述形式化方法在逻辑学、数学、计算机科学等领域的应用及其意义。
辩证逻辑03整体性辩证思维强调从整体上把握事物，注重事物之间的相互联系和相互作用。
交大数理逻辑课件11-1 函数共30页
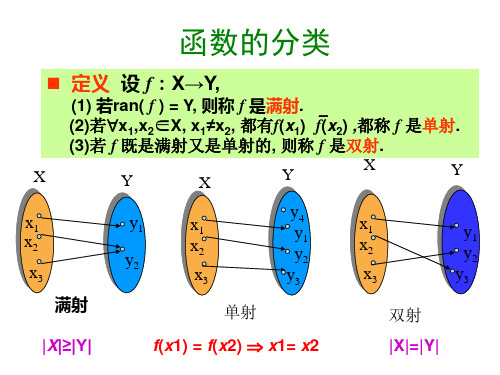
一、有穷集之间的构造
例 A=P({1,2,3}), B={0,1}{1,2,3} 解： A={,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}.
B={ f0, f1, … , f7 }, 其中 f0={<1,0>,<2,0>,<3,0>}, f1={<1,0>,<2,0>,<3,1>}, f2={<1,0>,<2,1>,<3,0>}, f3={<1,0>,<2,1>,<3,1>}, f4={<1,1>,<2,0>,<3,0>}, f5={<1,1>,<2,0>,<3,1>}, f6={<1,1>,<2,1>,<3,0>}, f7={<1,1>,<2,1>,<3,1>}.
令 f：A→B,
f()=f0,
f({1})=f1, f({2})=f2, f({3})=f3,
f({1,2})=f4, f({1,3})=f5, f({2,3})=f6, f({1,2,3})=f7
构造从A到B的双射函数（续）
二、实数区间之间构造双射
构造方法：直线方程
例 A=[0,1]
B=[1/4,1/2] 构造双射 f :A→B
T(x) 1 0 1 0 0 1 1 1
自然映射
5. 设 R 是 A 上的等价关系, 令 g：A→A/R g(a) = [a], a∈A 称 g 是从 A 到商集 A/R 的自然映射.
➢ 恒等关系确定的自然映射是双射, 其他的自然映射一 般来说是满射.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
设Ｐ、Ｑ为二个命题，则Ｐ∨Ｑ称作Ｐ与Ｑ的析取，读作:Ｐ
或Ｑ。
定义 由真值表给出，如左图。
P Q P∨ Q
F/0 F/0 F/0
当且仅当Ｐ、Ｑ均为“Ｆ”时， （Ｐ∨Ｑ）为“Ｆ”。否则，其 真值为“Ｔ”。
F/0 T/1 T/1 T/1 F/0 T/1 T/1 T/1 T/1
§1.1.2.命题联结词
区分“可兼或”与“不可兼或” ，异或，排斥或）
§ 1.1.1 命题
命题符号表示：常用大写２６个英文字母表示命题。用Ａ,Ｂ, Ｃ…Ｚ表示（命题变元）。命题中所有的”真”用Ｔ表示，命 题中所有的”假”用Ｆ表示 （命题常元）。
命题分类
原子命题（基本命题、本原命题）：一个命题，不能分解成为更 简单的命题。
例1 P: 我是一位学生。 分子命题（复合命题）：若干个原子命题使用适当的联结词 所组成的新命题
➢ 析取词∨为可兼或 即:P和Q均为T时(P∨Q)为T
例：1. 灯泡有故障或开关有故障。
2. 今晚写字或看书。
3. 今天下雨或打雷。
➢ 异或不可兼或 即 P和Q均为T时(P Q)为F
例： 1. 他通过电视看杂技或到剧场看杂技。
2. 他乘火车去北京或乘飞机去北京。
此处的“或”不完全等同于汉语中意思
讨论： 1. 只有确定真假值，才有研究的价值。 2. 判断本身只关心真、假。（二值逻辑）
例1：命题的例子 (1) 今天下雨。 (3) 别的星球上有生物。 (5) 上海是一个村庄。
(2) 明天下雨。 (4) 十是整数。
§ 1.1.1 命题
例2 不是命题的例子 命令句，感叹句，疑问句均不是命题。 （1）把门关上！ （2）你到哪里去？ 悖论 语句既为真，同时又包含假的不是命题， （1）我正在说谎。 其他一些情况 （1）x + y > 4 （2）1 +101 = 110
• 基本内容
– 从实际生活中的逻辑关系入手，通过引入符号体系 （命题符号、联结符号）将所研究的问题转换成为符 号串（命题公式）。
– 从数学角度：运算、求值、相互间关系，给出一些基 本性质。
– 符号表达式的规范化。 – 推理理论：从前提条件，根据基本的规则，推出逻辑
结论的方法。
§1.1.1 命题
命题 具有确定真值，或真或假而不能两者都是 的陈述句叫命题。
第一篇 数理逻辑
逻辑学：研究推理的科学。 逻辑学分为二类：
辩证逻辑：是研究事物发展的客观规律。 形式逻辑：对思维的形式结构和规律进行研究。
数理逻辑
是用数学的方法研究概念、判断和推理的科学， 显然数理逻辑是属于形式逻辑的范畴。
第一篇 数理逻辑
数理逻辑 用数学的方法是指引进一套符号体 系，将所研究的问题符号化，并给出理论和规 则来研究概念、判断和推理。即对符号进行判 断和推理。
例2 Q: 我是一位学生和他是一位工人。
§1.1.2 命题联结词
在命题演算中也有类似的日常生活中的联结词称做： “命题联结词”，命题联结词就是命题演算中的运算符。
下面先介绍五个常用的命题联结词：
➢ （否定词） ➢ ∧（合取词）, ∨（析取词）, （蕴含词）, （等值 词）
另外还有一些如 ：
➢ （与非词）, （或非）等。
例：
1. 他做了20或30道题。 （表示约数）
§1.1.2.命题联结词
不可兼或中当P和Q 均为“T”时，则P异 或Q为“F”。
异或用“”表示
P
Q
F
F
F
T
T
F
T
T
P
Q
F
F
F
T
T
F
T
T
P∨Q F T T T
PQ F T T F
§1.1.2.命题联结词
4. 蕴含词
符号: “”
设Ｐ、Ｑ为二个命题,Ｐ→Ｑ为新的命题,称作如果Ｐ则Ｑ,Ｐ蕴
T/1 T/1 T/1
§1.1.2.命题联结词
例1 P: 我拿起一本书 Q: 我一口气读完了这本书 PQ: 如果我拿起一本书，则我一口气读完了这本书。
通常称为形式蕴含, 即前提和结果有某种形式和内容上 的联系。
例2 P: 月亮出来了 Q: 3×3=9 P Q: 如果月亮出来了, 则3×3=9。
例2 P: 我们去种树。 Q: 房间里有一台电视机。 则ＰΛＱ: 我们去种树与房间里有一台电视机。
例3 P: 今天下大雨 Q: 3+3=6 则ＰΛＱ: 今天下大雨和3+3=6。
例4 P: 王大和王二是亲兄弟。 Q: 他打开箱子然后（而后）拿出一件衣服来。
§1.1.2.命题联结词
3. 析取词
符号: ”∨”
F/0
F/0
F/0
F/0
则，其真值为Ｆ。
F/0 T/1 F/0 F/0
注意：Ｐ和Ｑ是互为独立的，地位 是平等的，Ｐ和Ｑ的位置可以交换 而不会影响ＰΛＱ的结果。
T/1 F/0 F/0 F/0 T/1 T/1 T/1 T/1
§1.1.2.命题联结词
例1 P: 王华的成绩很好。 Q: 王华的品德很好。 则ＰΛＱ: 王华的成绩很好并且品德很好。
含Ｑ,Ｐ仅当Ｑ,Ｑ当且Ｐ,Ｐ是Ｑ的充分条件。
定义 由真值表给出，如左图。
P
Q P→Q
Ｐ:称为前件、条件、前提、假设。 F/0
F/0
T/1
Ｑ:称为后件、结论。
F/0 T/1 T/1
当Ｐ为Ｔ,Ｑ为Ｆ时，则Ｐ→Ｑ为
Ｆ,否则Ｐ→Ｑ均为Ｔ。
T/1 F/0 F/0
Q→P逆命题, ¬P→¬Q 反命题, ¬P→¬Q 逆反命题
现代数理逻辑分为四大分支：证明论、模型论、 递归论和公理集合论。我们这里介绍的是属于 四大分支的共同基础 — (命题逻辑和谓词逻辑)。
第一章 数理逻辑
§1.1命题 §1.2.重言式 §1.3.范 式
§1.1 命题
• 命题逻辑是数理逻辑的基础，通过对它的学习， 我们将了解如何用数学的手段进行逻辑研究。
这里¬Ｑ不能讲成“每一种生物都不是动物”，为假命题了。
§1.1.2.命题联结词
2. 合取词
符号: “Λ”
设Ｐ,Ｑ为两个命题，则ＰΛＱ称Ｐ与Ｑ的合取，读作: ”Ｐ与Ｑ”、”
Ｐ与Ｑ的合取”、”Ｐ并且Ｑ”等。
定义 由真值表给出，如左图。
P Q PΛ QΛP
Q
即：当且仅当Ｐ和Ｑ的真值均为Ｔ， 则（ＰΛＱ）的真值为“Ｔ”。否
§1.1.2 命题联结词
1. 否定词
符号: “¬”
设命题为Ｐ，则在Ｐ的前面加否定词¬ ，变成¬Ｐ， ¬Ｐ读做
“Ｐ的否定”或“非Ｐ”。
P ¬P
定义：由真值表定义，如左图。
例1 Ｐ：北京是一座城市。
T/1 F/0
¬Ｐ：北京不是一座城市。 例2 Ｑ：每一种生物均是动物。F
F/0 T/1
Байду номын сангаас
¬Ｑ：有一些生物不是动物。T