利用线性规划求最值

合集下载

线性规划最值问题

线性规划最值问题什么是线性规划线性规划是一种数学优化方法，用于解决一类最值问题。

在线性规划中，我们试图找到一组变量的值，使得目标函数取得最大（或最小）值，同时满足一组线性等式或不等式约束条件。

线性规划问题的一般形式线性规划问题可以用下列一般形式来表示：$$\max (或 \min) c^T x$$$$s.t.\quad Ax \leq b$$其中，$x$是变量向量，$c$是目标函数系数向量，$A$是约束条件系数矩阵，$b$是约束条件右侧常数向量。

求解线性规划最值问题的步骤求解线性规划最值问题的一般步骤如下：1. 确定目标函数：根据问题要求确定目标函数的系数向量$c$和优化目标（最大化或最小化）。

2. 设置约束条件：根据问题要求确定约束条件的系数矩阵$A$和右侧常数向量$b$。

3. 求解最值：应用线性规划算法，求解线性规划问题，找到使目标函数取得最大（或最小）值的变量向量$x$。

4. 解释结果：将最值代入目标函数，得到最终的最值结果，并解释其含义。

线性规划最值问题的应用线性规划最值问题在实际应用中具有广泛的应用，例如：- 产品混合问题：决定不同产品的生产数量，以最大化收益或最小化成本。

- 运输问题：确定不同货物在不同运输路线上的分配方案，以最小化运输成本。

- 资源分配问题：决定资源的最优分配，以最大化效益或实现平衡。

总结线性规划最值问题是一种在实际应用中常见的问题求解方法。

通过确定目标函数和约束条件，并应用线性规划算法，我们可以找到使目标函数取得最大（或最小）值的变量向量。

该方法可以应用于多个领域，帮助优化决策和资源分配。

线性规划求最值问题

(2)若z=2x-y,求z的最值.
Zmax 2 5 2 8,
x
Zmin 2 1 4.4 2.4.
y
(3)若z=x2+y2,求z的最值.
( x 2 y 2 )min 12 12 2, ( x y )max 52 22 29,
2 2
5
C
注意：目标函数化为斜截式后，分析斜率大小；z的系数符号。
x 0 1. x , y满足 x 2 y 3 2 x y 3
求z=x-y的最值
解：z x y化为y x z，与直线y x平行,纵截距为-z
直线过点 A 时z值最大; 过点 B 时z值最小.
4 2 2 1 1 10
x 4 y ≤ 3, 例1.已知x、y满足 3 x 5 y ≤ 25. x ≥ 1. y
C
x-4y+3=0
A B
1 x=1 5
3x+5y-25=0
O
x
x 4 y ≤ 3, 例1.已知x、y满足 3 x 5 y ≤ 25. x ≥ 1.
其实，世上最温暖的语言，“ 不是我爱你，而是在一起。” 所以懂得才是最美的相遇！只有彼此以诚相待，彼此尊重，相互包容，相互懂得，才能走的更远。相遇是缘，相守是爱。缘是多么的妙不可言，而懂得又是多么的难能可贵。否则就会错过一时，错过一世！择一人深爱，陪一人到老。一路相扶相持，一路心手相牵，一路笑对风雨。在平凡的世界，不求爱的轰轰烈烈；不求誓言多么美丽；唯愿简单的相处，真心地付出，平淡地相守，才不负最美的人生；不负善良的自己。人海茫茫，不求人人都能刻骨铭心，但求对人对己问心无愧，无怨无悔足矣。大千世界，与万千人中遇见，只是相识的开始，只有彼此真心付出，以心交心，以情换情，相知相惜，才能相伴美好的一生，一路同行。然而，生活不仅是诗和远方，更要面对现实。如果曾经的拥有，不能天长地久，那么就要学会华丽地转身，学会忘记。忘记该忘记的人，忘记该忘记的事儿，忘记苦乐年华的悲喜交集。人有悲欢离合，月有阴晴圆缺。对于离开的人，不必折磨自己脆弱的生命，虚度了美好的朝夕；不必让心灵痛苦不堪，弄丢了快乐的自己。擦汗眼泪，告诉自己，日子还得继续，谁都不是谁的唯一，相信最美的风景一直在路上。人生，就是一场修行。你路过我，我忘记你；你有情，他无意。谁都希望在正确的时间遇见对的人，然而事与愿违时，你越渴望的东西，也许越是无情无义地弃你而去。所以美好的愿望，就会像肥皂泡一样破灭，只能在错误的时间遇到错的人。岁月匆匆像一阵风，有多少故事留下感动。愿曾经的相遇，无论是锦上添花，还是追悔莫及；无论是青涩年华的懵懂赏识，还是成长岁月无法躲避的经历……愿曾经的过往，依然如花芬芳四溢，永远无悔岁月赐予的美好相遇。其实，人生之路的每一段相遇，都是一笔财富，尤其亲情、友情和爱情。在漫长的旅途上，他们都会丰富你的生命，使你的生命更充实，更真实；丰盈你的内心，使你的内心更慈悲，更善良。所以生活的美好，缘于一颗善良的心，愿我们都能善待自己和他人。一路走来，愿相亲相爱的人，相濡以沫，同甘共苦，百年好合。愿有情有意的人，不离不弃，相惜相守，共度人生的每一个朝夕……直到老得哪也去不了，依然是彼此手心里的宝，感恩一路有你！

线性目标函数最优解的求解方法

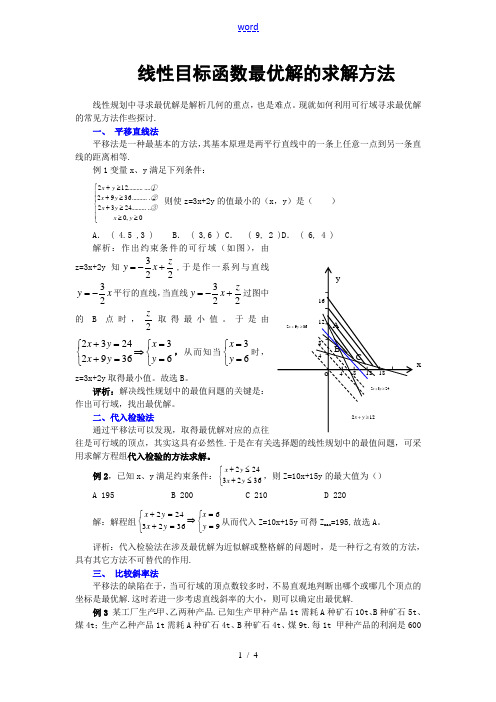
线性目标函数最优解的求解方法线性规划中寻求最优解是解析几何的重点，也是难点。

现就如何利用可行域寻求最优解的常见方法作些探讨.一、平移直线法平移法是一种最基本的方法，其基本原理是两平行直线中的一条上任意一点到另一条直线的距离相等.例1变量x 、y 满足下列条件：⎪⎪⎩⎪⎪⎨⎧≥≥≥+≥+≥+0,0............2432...........3692..............122y x ③y x ②y x ①y x 则使z=3x+2y 的值最小的（x ，y ）是（）A ． ( 4.5 ,3 )B ． ( 3,6 )C ． ( 9, 2 )D ． ( 6, 4 ) 解析：作出约束条件的可行域（如图），由z=3x+2y 知223zx y +-=,于是作一系列与直线x y 23-=平行的直线，当直线223zx y +-=过图中的B 点时，2z取得最小值。

于是由⎩⎨⎧==⇒⎩⎨⎧=+=+6336922432y x y x y x ，从而知当⎩⎨⎧==63y x 时，z=3x+2y 取得最小值。

故选B 。

评析：解决线性规划中的最值问题的关键是：作出可行域，找出最优解。

二、代入检验法通过平移法可以发现，取得最优解对应的点往往是可行域的顶点，其实这具有必然性.于是在有关选择题的线性规划中的最值问题，可采用求解方程组代入检验的方法求解。

例2，已知x 、y 满足约束条件：⎩⎨⎧≤+≤+3623242y x y x ，则Z=10x+15y 的最大值为（）A 195B 200C 210D 220解：解程组⎩⎨⎧==⇒⎩⎨⎧=+=+963623242y x y x y x 从而代入Z=10x+15y 可得Z max =195,故选A 。

评析：代入检验法在涉及最优解为近似解或整格解的问题时，是一种行之有效的方法，具有其它方法不可替代的作用.三、比较斜率法平移法的缺陷在于，当可行域的顶点数较多时，不易直观地判断出哪个或哪几个顶点的坐标是最优解.这时若进一步考虑直线斜率的大小，则可以确定出最优解.例3 某工厂生产甲、乙两种产品.已知生产甲种产品1t 需耗A 种矿石10t 、B 种矿石5t 、煤4t ；生产乙种产品1t 需耗A 种矿石4t 、B 种矿石4t 、煤9t.每1t 甲种产品的利润是600元，每1t 乙种产品的利润是1000元.工厂在生产这两种产品的计划中要求消耗A 种矿石不超过300t 、B 种矿石不超过200t 、煤不超过360t .甲、乙两种产品应各生产多少（精确到0.1t ），能使利润总额达到最大？解：设生产甲、乙两种产品分别为xt 、yt ，利润总额为z 元，那么⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+≤+0,0360942004515025y x y x y x y x 且Z=600x+1000y 作出约束条件所表示的平面区域（如左图），即可行域. 作直线l ：600x+1000y=0,即直线l ：3x+5y=0.因为94534525-<-<-<-，即k EN <k MN <k l <k FN ，所以把直线l 向上方移至m 的位置，直线经过可行域上的点M ，此时Z=600x+1000y 取最大值.解方程组⎩⎨⎧=+=+3609420045x x y x 得M 的坐标x=29360=12.3，y=291000=34.5，代入计算得Z max =291216000．答：应生产甲产品约12.3t,乙产品34.5t ，能使利润总额达到最大.评析：这是高中新教材第二册上册第七章，“简单的线性规划”一节中的例3（P62～63）,确定了直线斜率的大小，实质是确定了直线在向上平移的过程中，在经过可行域X 围内时，即可确定最优解。

线性规划求最值

线性规划求最值线性规划（Linear Programming）是一种优化问题的数学方法，通过建立线性模型来求解最大或最小值。

线性规划的目标是在给定的限制条件下，找到一个最优解，使得目标函数取得最大（或最小）值。

线性规划的数学模型可以表示为：目标函数：max（min）Z = c₁x₁ + c₂x₂ + … + cₙxₙ约束条件：a₁₁x₁ + a₁₂x₂ + … + a₁ₙxₙ ≤ b₁a₂₁x₁ + a₂₂x₂ + … + a₂ₙxₙ ≤ b₂…aₙ₁x₁ + aₙ₂x₂ + … + aₙₙxₙ ≤ bₙ其中x₁, x₂, …, xₙ为决策变量，c₁, c₂, …, cₙ为目标函数的系数，a₁₁, a₁₂, …, a₈ₙ为约束条件中的系数，b₁, b₂, …,bₙ为约束条件的常数。

解线性规划问题的过程可以分为以下几个步骤：1. 建立数学模型：根据实际问题，确定目标函数以及约束条件。

2. 线性规划的几何表示：将目标函数和约束条件用图形表示，目标函数是一个线性函数，而约束条件则是一组线性不等式。

3. 求解可行解：通过图形方法，找到目标函数与所有约束条件的交点，得到一组可行解。

4. 求解最优解：在可行解中，通过计算目标函数在每个可行解点的函数值，找到使目标函数取得最大（或最小）值的可行解，即为最优解。

5. 检验最优解的可行性：将最优解代入到原始线性规划问题中，检验是否满足所有约束条件。

如果不满足，则需要重新调整模型。

线性规划在实际应用中广泛使用，例如生产计划、资源分配、运输调度等领域。

通过线性规划，可以有效地进行决策，并找到最优解，提高效率，节约资源。

然而，线性规划也有一些局限性，如对问题的要求较高，不能解决非线性的问题等。

总之，线性规划是一种数学方法，通过建立线性模型，在给定的约束条件下求解最大或最小值，可以在各种实际问题中应用，并得到最优解。

通过线性规划，可以优化决策，提高效率，实现最大化利益。

不等式简单的线性规划问题利用简单的线性规划求最值

线性规划问题的应用
生产计划
如何安排各种资源（如人力、原材料、设备等）以生产出最大利润或最小成本的产品。
货物运输
如何安排车辆或船只运输货物，使得运输成本最低或运输时间最短。
资源分配
如何将有限的资源分配给不同的项目或任务，以获得最大的效益。
配料问题
如何在满足一定质量要求的条件下，使用最少的原料或以最小的成本配制出所需的产品。
引入人工变量
对于不等式约束条件，可以引入人工变量来扩展变量的维度，将不等式约束条件转换为等式约束条件。
不等式约束条件下线性规划问题的求解方法
将不等式约束条件加入目标函数中
将不等式约束条件加入目标函数中，并求解目标函数的最小值或最大值。
利用线性规划求解
对于不等式约束条件下线性规划问题，可以利用线性规划的求解方法，如单纯形法、椭球法等来求解目标函数的最小值或最大值。
数据科学
1. 研究大数据分析中的优化问题；2. 探索高效的数据处理和特征提取方法；3. 提高数据分析和处理的精度和效率。
THANKS
谢谢您的观看
迭代法
通过不断迭代，逼近最优解。
优化问题的实际应用
资源分配问题
如何分配有限资源，使得产出最大化或成本最小化。
运输问题
如何制定最优运输计划，使得运输成本最低且满足需求。
选址问题
如何在多个候选地点中选择最优地点，使得某项业务运营成本最低或收益最大。
06
总结与展望
不等式简单的线性规问题求解方法的优缺点
05
利用简单的线性规划解决优化问题
优化问题的定义与分类
定义
优化问题是在一定约束条件下，寻求一个或多个自变量取何值时，使得目标函数取得极值（极大值或极小值）。

线性规划求最值问题

线性规划求最值问题角度(一) 截距型1．(2017·全国卷Ⅲ)设x ，y 满足约束条件⎩⎪⎨⎪⎧3x ＋2y －6≤0，x ≥0，y ≥0，则z ＝x －y 的取值范围是( )A ．[－3,0]B ．[－3,2]C ．[0,2]D ．[0,3]2．(2017·全国卷Ⅰ)设x ，y 满足约束条件⎩⎪⎨⎪⎧x ＋2y ≤1，2x ＋y ≥－1，x －y ≤0，则z ＝3x －2y 的最小值为________．角度(二) 求非线性目标函数的最值一、距离型3．(2018·太原模拟)已知实数x ，y 满足约束条件⎩⎪⎨⎪⎧3x ＋y ＋3≥0，2x －y ＋2≤0，x ＋2y －4≤0，则z ＝x 2＋y 2的取值范围为( )A ．[1,13]B ．[1,4]二、斜率型4．(2018·成都一诊)若实数x ，y 满足约束条件⎩⎪⎨⎪⎧2x ＋y －4≤0，x －2y －2≤0，x －1≥0，则y －1x 的最小值为________．变式训练1、若x ，y 满足约束条件⎩⎪⎨⎪⎧x －1≥0，x －y ≤0，x ＋y －4≤0，则yx 的最大值为________．[题型技法] 常见的2种非线性目标函数及其意义(1)点到点的距离型：形如z ＝(x －a )2＋(y －b )2，表示区域内的动点(x ，y )与定点(a ，b )的距离的平方；(2)斜率型：形如z ＝y －bx －a ，表示区域内的动点(x ，y )与定点(a ，b )连线的斜率．角度(三) 线性规划中的参数问题5．(2018·郑州质检)已知x ，y 满足约束条件⎩⎪⎨⎪⎧x ≥2，x ＋y ≤4，2x －y －m ≤0.若目标函数z ＝3x ＋y 的最大值为10，则z 的最小值为________．变式训练2.(2018·惠州调研)已知实数x ，y 满足：⎩⎪⎨⎪⎧x ＋3y ＋5≥0，x ＋y －1≤0，x ＋a ≥0，若z ＝x ＋2y 的最小值为－4，则实数a 的值为________．[题型技法] 求解线性规划中含参问题的基本方法(1)把参数当成常数用，根据线性规划问题的求解方法求出最优解，代入目标函数确定最值，通过构造方程或不等式求解参数的值或取值范围．(2)先分离含有参数的式子，通过观察的方法确定含参的式子所满足的条件，确定最优解的位置，从而求出参数．作业：1．变量x ，y 满足⎩⎪⎨⎪⎧x －4y ＋3≤0，3x ＋5y －25≤0，x ≥1.(1)设z 1＝4x －3y ，求z 1的最大值； (2)设z 2＝yx ，求z 2的最小值； (3)设z 3＝x 2＋y 2，求z 3的取值范围．。

陕西省榆林市一中2025届高考数学模拟考试试卷理含解析

陕西省榆林市一中2025届高考数学模拟考试试卷理（含解析）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1.若（）与互为共轭复数，则的值为（）A. B. C. D.【答案】A【解析】【分析】利用复数代数形式的乘除运算化简，再由复数相等的条件求得a，b的值，则答案可求．【详解】，又与互为共轭复数，，，则.故选A.【点睛】本题考查复数代数形式的乘除运算，考查共轭复数的基本概念，是基础的计算题．2.已知集合，，则（）A. B.C. D.【答案】C【解析】【分析】先分别求出集合A和B，利用交集定义能求出A∩B．【详解】∵集合，∴A＝{x|}，B＝{x|x＜﹣1或x＞2}，∴A∩B＝{x|}．故选：C．【点睛】本题考查交集的求法，考查交集、不等式性质等基础学问，考查运算求解实力，考查函数与方程思想，是基础题．3.的部分图像大致为（）A. B.C. D.【答案】B【解析】【分析】推断函数的奇偶性以及对称性，结合函数值的符号是否一样进行解除即可．【详解】f（﹣x）＝f（x），则函数f（x）是偶函数，图象关于y轴对称，解除A，D，f（π）＝lnπ﹣cosπ＝lnπ+1＞0，解除C，故选：B．【点睛】本题主要考查函数图象的识别和推断，利用函数的对称性以及特别值的符号进行解除是解决本题的关键．4.已知向量，满意，，，则（）A. 2B.C.D.【答案】A【解析】【分析】依据向量点积运算得到，再得到.【详解】依据题意得又，故选:A．【点睛】这个题目考查了向量的点积运算以及向量的模长的计算，题目较为简洁基础.5.以双曲线的焦点为顶点，且渐近线相互垂直的双曲线的标准方程为（）A. B.C. D.【答案】D【解析】【分析】由题可知，所求双曲线的顶点坐标为，又由双曲线的渐近线相互垂直，所以，进而可求解双曲线的方程，得到答案。

【详解】由题可知，所求双曲线的顶点坐标为，又因为双曲线的渐近线相互垂直，所以，则该双曲线的方程为.【点睛】本题主要考查了双曲线的标准方程及其简洁的几何性质的应用，其中解答中熟记双曲线的标准方程和简洁的几何性质，合理、精确运算是解答的关键，着重考查了推理与运算实力，属于基础题。

初探与线性规划有关的最值问题的求法

米【Ｅ，１０９１－６收稿ｌ２０－０１￣【作者简介】刘颖（９８５）女，１７．一，安徽宿州人，现为宿城一中数学教师。
７２
第１卷・３期３第
宿州教育学院学报
ｄＯＵｎｏｚｈｕＥｃａｉｎｓ１ｔｒａ１ｆＳｕｏｄｕｔＩｔＯｎｔｕｅ
、
截距型
例ｌ已知实数ｘｙ满足线性约束条件，｛ｘ３－２０求Ｚ４一ｙ的最大值和最小值。４一ｙ１＜，＝ｘ３￣
＋ｙ＞０２－３￣
例２若实数ｘ满足ｆ一ｙ５：＋，ｙ ‘ （２≤ 则ｚｘｙ）一
ｌ２ｙ￣ｘ，
Ｉ２７０ｘｙ￣－＋＞
由ｄ２２１－－１＋－１－
．
ｚ雌即为可行域中的＝
Ｘ—ｌ
点与点Ｐ１一）（、２连线的斜率
・
．．
２１年６月第１００３卷・３期第
宿州教育学院学报
初探与线性规划有关的最值问题的求法
刘颖（城一中数学组宿
【摘
安徽・宿州
２４０３００）
要】线性规划的基本思想，是在一定的约束条件下，过数形结合求函数的最值。本文将从线性规通
为最小．ｍｘ一ｂ１；・ａ＝３＝２．Ｚ
（或可用由图知，圆心为Ａ中点亦得点Ａ坐标）Ｏ所以Ｚｘｙ的最大值为６＝＋。
点评：对于非线性约束条件中常出现的非一次

线性规划求最大值或最小值

线性规划求最大值或最小值linprog2011-09-03 18:43:17| 分类：Matlab | 标签：最优值最优解最大值最小值linprog |字号大中小订阅函数格式:linprog(f,a,b,a1,b1,xstart,xend)f:求解最小函数的表达式系数矩阵是m*1的矩阵a:≤不等式条件约束矩阵其均为形式b:a对应不等式右边的常数项a1:=等式条件约束矩阵b1:a1对应不等式右边的常数项xstart:x的取值范围的最小值的系数矩阵为n*1的矩阵xend:x的取值范围的最大值的系数矩阵为n*1的矩阵函数说明:不存在的项填写[]即可函数功能:线性规划求最优值.例子1:求f=3*x1+6*x2+2*x3的最大值满足的条件是3*x1+4*x2+x3≤2x1+3*x2+2*x3≤1且x1、x2、x3均大于等于0Matlab求解如下a =[ 3 4 11 32 ]b =[ 21 ]f=[ -3-6-2 ]%这里为什么会是负数,因为Matlab求的是f的最小值,要求最大值则取要求系数的相反数即可. x=[ 00 ]linprog(f,a,b,[],[],x,[])%执行的matlab命令后输出的如下内容.注意这里的[]表示那一项不存在.当然最后那一个[]也可以不要即linprog(f,a,b,[],[],x)Optimization terminated.ans =0.40000.20000.0000%即x1=0.4,x2=0.2,x3=0为最优解.带回原式我可以知道f的最大值=3*0.4+6*0.2=2.4例子2:求f=-2*x1-3*x2-x3的最小值满足的条件是x1+x2+x3≤3x1+4*x2+7*x3+x4=9且x1、x2、x3、x4均大于等于0Matlab求解如下原题等价于求f=-2*x1-3*x2-x3+0*x4的最小值其条件等价于x1+x2+x3+0*x4≤3x1+4*x2+7*x3+x4=9则在Matlab输入如下内容a=[1 1 1 0]b=[3]a1=[1 4 7 1]b1=[9]x=[ 00]f=[ -2-3-10]linprog(f,a,b,a1,b1,x)%执行命令或者输入linprog(f,a,b,a1,b1,x,[])Optimization terminated.ans =1.00002.00000.00000.0000%说明x1=1,x2=2,x3=0,x4=0取得最小值说明:任何线性规划问题都可以转化为上面的问题求解.细节问题请Google线性规划标准形式1、当目标函数求最大值时,例如求f=a1*x1+a2*x2+……+an*xn的最大值时这个时候等价于求f=-a1*x1-a2*x2-……-an*xn的最小值2、当约束条件为a1*x1+a2*x2+……+an*xn≥b这种形式的时候其约束等价于a1*x1+a2*x2+……+an*xn-xnn=b即多了一个xnn(xnn≥0)变量3、当一个变量比如x1是无约束的变量时,其实等价于x1=x2-x3即把一个变量x1分解成2个变量x2与x3之差(x2、x3≥0)把是x1的地方替换为(x2-x3)即可求解线性规划问题：线性规划问题其中，f, x, b, beq, lb, ub为向量, A, Aeq为矩阵。

线性规划--距离式、斜率式求最值

x y 3 0 x 2y 3 0 满足约束条件，则实数 m 的最大值为（ x m
）
1 A． 2
B．1
3 C． 2
D．2
.6（2012 届山东实验中学第一次诊断考试）设 x、y 满足约束条件
【答案】A
，若目标
a 0, b 0 【解析】解：如图所示，线性规划区域为三角形 ABC，而目标函数的斜率为 k <0，
2x－y＋2≥0， 7. 如果点 P 在平面区域x＋y－2≤0，上，点 Q 在曲线 x2＋(y＋2)2 2y－1≥0
＝1 上，那么|PQ|的最小值为( 3 A. 2 4 B. －1 5 ) C．2 2－1 D. 2－1
1 解析：如图，当 P 取点0，2，Q 取点(0，－1)时，
距离式、斜率式求最值
安徽省灵璧中学康永攀 2013.4.
一、截距式回顾
2．线性规划线性目标函数在线性约束条件下，最值问题的讨论．基本概念名称意义线性约由 x，y 的一次不等式(或方程)组成的不等式组，束条件是对 x，y 的约束条件 2 2 目标函数关于 x，y 的解析式，如 z＝2x＋y，z＝x ＋y 等
2 2
2y＋1 (3)z＝的取值范围. x＋1
解作出可行域如图，并求出顶点的坐标A(1,3)、 B(3,1)、C(7,9)． (1) 易知可行域内各点均在直线x＋2y－4＝0的上方， (2) 故x＋2y－4>0，将C(7,9)代入z得最大值为21. (2)z＝x2＋(y－5)2表示可行域内任一点(x，y)到定点M(0,5)的距离的平方， 9 过M作直线AC的垂线，易知垂足N在线段AC上，故z的最小值为|MN|2＝2. 1 y－－2 1 (3)z＝2· 表示可行域内任一点(x，y)与定点Q －1，－2 连线的斜率 x－－1 7 3 的两倍，且kQA＝4，kQB＝8， 3 7 所以z的取值范围为4，2.

线性规划求最值的常见题型

④综上,z最大值为3；z最小值为-3.
y
x+y=1 x-y=0
1
C
0ቤተ መጻሕፍቲ ባይዱ
x
1
y=-1
B(-1,-1)
��0（2，-1）A
[类题通法] 解线性规划问题的关键是准确地作出可行域，正确理解z的几何意义，对一个封闭图形而言，最优解一般在可行域的边界上取得．在解题中也可由此快速找到最大值点或最小值点．
(2)�� = ��++31的最值.
从目标函数的几何意义思考
非线性目标函数
（1）�� = (�� + 3)2+(�� + 1)2的最大值和最小值
可求得��可��目��9��行标��,��域8函��中数.=的��的��点几��到��何��P2意=点义=的��可��距2��表��离22示的5=为平654
线性规划求最值的常见题型
龙海一中徐艺凤
线性规划求最值常见的题型有
一、求线性目标函数的最值问题二、求非线性目标函数的最值问题三、实际问题中的最值问题
题型一、求线性目标函数的最值
x-y≥0 例1.设x,y满足约束条件： x+y-1 ≤ 0
y ≥ -1
线性目标函数
求z=2x+y最大值与最小值。
在这里甲、乙两个电视台的广告时间为主要变量，公司的收益为两个电视台获得的收益总和，故可设两个电视台的广告时间,列出不等式组
和建立目标函数。
间，才能使公司的收益最大，最大收益是多少万元？ [解] 设公司在甲电视台和乙电视台做广告的时间分别

线性规划最值问题

1
C 1,1
1
0
x1
x
x 4y 3 0 例:变量x,y满足 3 x 5 y 25 0， x 1 (1)设z=4x-3y,求z的最大值； y (2)设z= ，求z的最小值；
x
y
5
22 A 1, 5
y y0 ( 2) z x x0 z的值是可行域中的点与原点O连线的斜率。
y1 (其中k为小于零的常数)时，的最小值为2， x
能力提升
则实数k的值是________． -3
解析：不等式组所表示的可行域如图所示，点P(x，y)为可行域内的点时
k 1 y1 3 有＝kBP≥kBA＝＝2， x k 3 解得k＝－3.
一个半平面内的点的坐标适合不等式 Ax＋By＋C＞0 , 而另一个半平面内的点的坐标适合不等式Ax＋By＋C＜0 , 即直线Ax＋By＋C＝0划分平面所成两个半平面的点,分别由不等式Ax＋By＋C＞0与Ax＋By＋C＜0决定.因此, 如同前面所学平面内的直线可以视为二元一次方程的几何表示一样,半平面就是二元一次不等式的几何表示．
B 5,2
1
C 1,1
1
观察可知zmin kOB
x
2 5
0
x 4y 3 0 例:变量x,y满足 3 x 5 y 25 0， x 1 (3)设z= x 2 y 2 ,求z的取值范围.
( 3) z x 2 y 2的几何意义是可行域中的点到原点 O
基础自查
(2)判断不等式Ax＋By＋C＞0所表示的平面区域,可在直线Ax＋By＋C＝0的某一侧的半平面内选取一个特殊点，如选原点或坐标轴上的点来验证 Ax＋By＋C 的符号的正负．当C≠0时，常选用原点． 2．二元一次不等式Ax＋By＋C＞0在平面直角坐标系中，表示平面区域，直线l应画成虚线，画不等式 Ax＋By＋C≥0所表示的区域时,应把边界画成实线．

计算最优值的算法

计算最优值的算法1. 线性规划线性规划是一种优化问题的数学建模方法，其目标是在一系列线性约束条件下，找到使目标函数最大或最小的数值。

线性规划的基本形式可以表示为：\[Max \quad c^Tx\]\[subject \quad to \quad Ax ≤ b\]其中，c是一个n维列向量，x是一个n维变量向量，A是一个m×n的矩阵，b是一个m 维列向量。

上述形式称为标准形式。

线性规划问题的最优值就是目标函数c^Tx的最大或最小值。

线性规划通常用于工程规划、资源分配等领域。

在解决线性规划问题时，可以使用单纯形法、对偶单纯形法、内点法等算法。

这些算法都是基于线性规划的特殊性质来设计的，具有高效的计算性能和很好的稳定性。

2. 动态规划动态规划是一种通过拆分问题为更小的子问题来解决优化问题的方法。

动态规划通常用于解决多阶段决策问题、最短路径问题、最优切割问题等。

动态规划的基本思想是将原问题分解为若干个较小的相似的子问题，然后通过求解子问题来得到原问题的解。

动态规划算法包括自底向上法和自顶向下法。

自底向上法是一种迭代求解的方法，其思想是从最小的子问题开始，逐步推导出较大的子问题的解。

自顶向下法则是一种递归求解的方法，其思想是将原问题分解为若干个子问题，然后递归地求解这些子问题。

动态规划算法在实际应用中有很多成功的案例，例如0/1背包问题、最长公共子序列问题、最短路径问题等。

这些问题都可以通过动态规划算法来求解，并得到最优值。

3. 贪心算法贪心算法是一种通过每一步选择局部最优解，最终得到全局最优解的方法。

贪心算法是一种简单而有效的算法，它通常适用于一些特殊的优化问题，例如最小生成树问题、Dijkstra最短路径算法等。

在贪心算法中，每一步都选择当前最优的解，然后继续下一步。

贪心算法的关键在于确定何时选择局部最优解和何时放弃之前的选择。

如果能够确定好这些条件，就可以保证最终得到全局最优解。

贪心算法在实际应用中有很多成功的案例，例如霍夫曼编码、最小生成树、最短路径等。

线性规划最大值最小值怎么看

线性规划最大值最小值怎么看
线性规划比如求z=2x+y的最优解，显然x大y大为最大值方向，向右上平移到可行域的最远顶点，就是最大值。

最小值相反。

线性规划的主要概念有两个：一是判断二元一次不等式所表示的区域；二是求目标函数的最优解。

它们都涉及判断方向。

用x、y的方向判断。

比如判断不等式2x-y-4≤0的平面区域，正变量小负变量大即可，即x小y大，为直线的左上区域。

总结就是：不等式是大于零，正变量大负变量小；不等式是小于零，正变量小负变量大。

根据这个原理来判断平面区域的方向。

左上、右上、左下、右下。

其实我们判断x＞2的区域，也不是取点判断，而是根据变量的方向判断。

同理，我们判断x+y-1≥0，也可以根据变量的方向判断，正变量大负变量小，即x大y大，在直线的右上方。

而教材必修五求目标函数的最优解的根据是，目标函数的最大值与最小值总是在区域边界交点处取得，如有四个交点，它全算出来，然后比较大小。

显然没有必要。