2011年同济大学等九校(卓越联盟)自主招生数学试题及答案
2011年自主招生华约数学试题解析

2011年华约试题解析一、 选择题(1) 设复数z 满足|z|<1且15||2z z+=则|z| = ( )4321A B C D 5432解:由15||2z z +=得25||1||2z z +=,已经转化为一个实数的方程。
解得|z| =2(舍去),12。
(2) 在正四棱锥P-ABCD 中,M 、N 分别为PA 、PB 的中点,且。
则异面直线DM 与AN 所成角的余弦为( ) 1111A B C D 36812[分析]本题有许多条件,可以用“求解法”,即假设题中的一部分要素为已知,利用这些条件来确定其余的要素。
本题中可假设底面边长为已知(不妨设为2),利用侧面与底面所成二面角可确定其他要素,如正四棱锥的高等。
然后我们用两种方法,一种是建立坐标系,另一种是平移其中一条线段与另一条在一起。
解法一:如图,设底面边长为2,则由侧面与底面所成二面角。
如图建立坐标系,则A(1,-1,0),B(1,1,0),C(-1,1,0),D(-1,-1,0),P(0,0),则11112(,,),,,)222222 M N-,31213(,,),(,,222222DM AN=-=-。
设所成的角为θ,则1c o s6D M A ND M A Nθ==。
解法二:如图,设底面边长为2,则由侧面与底面所成二面角。
平移DM与AN在一起。
即M移到N,D移到CD的中点Q。
于是QN = DM = AN。
而PA = PB = AB = 2,所以QN = AN = ,而AQ = ,容易算出等腰ΔAQN的顶角1cos6ANQ∠=。
解法三:也可以平移AN与DM在一起。
即A移到M,N移到PN的中点Q。
以下略。
(3)过点(-1, 1)的直线l 与曲线相切,且(-1, 1)不是切点,则直线l 的斜率为 ( )A 2B1C 1D 2 - -此题有误,原题丢了,待重新找找。
(4)若222cos cos 3A B A B π+=+,则的最小值和最大值分别为 ( ) 3131A1,B ,C1,1D ,122222222--+ + [分析]首先尽可能化简结论中的表达式22cos cos A B +,沿着两个方向:①降次:把三角函数的平方去掉;②去角:原来含两个角,去掉一个。
卓越联盟自主招生试题及答案 缺答案

卓越联盟自主招生试题及答案新一轮卓越联盟自主招生开始了,小编整理卓越联盟自主招生试题及答案供大家分享学习语文英语1.完型填空是乔布斯,这篇完型填空是作者以一名“果粉”的身份,表达了对乔布斯的怀恋,比较抒情。
2.阅读短文三篇第一篇阅读讲小镇居民对树的感情,思想性比较强。
第二篇阅读材料的内容是及“有机食品的研究”,主要讲的是有机食品问题,包括有机食品和常规食品的优缺点比较等第三篇阅读材料与“关于科学发展对教育的影响和作用”。
阅读内容偏向于社会时事。
3.完形填空的文章,谈到现代技术对教育的影响。
4..英语作文题的大意为“回顾过去与展望未来一样重要”。
英语写作内容与“回忆过去,展望未来”有关,并根据自己的理解进行写作,其字数要求120字左右。
数学1.数学6道填空题2.6道大题,涉及平面几何、立体几何、抛物线、等比数列、抛物线,导数等知识点。
化学则都是大题1.一道说明题要求考生比较碳元素和硅元素的差异2.大题为根据铁元素的性质,进行沉淀实验验证。
3.一道辩证推理题.4.最难的一道有机题.物理1.大题涉及到速度与电路问题。
2013年卓越联盟自主招生笔试试题16日上午9点,卓越联盟自主招生笔试结束,以下为考生对自主招生试题的回忆记录,供参考!语文作文题目:小作文,35分400到500字:是否认可煎饼人,煎饼人是指掌握多个领域的技能和知识的人,有人说煎饼人“面面会,面面松”,有人说煎饼人是复合型人才,谈谈对此的观点。
物理实验:力学方面数学题型有数列,平面几何2013年卓越联盟自主招生家长考生心态好上周末,“华约”、“北约”和“卓越”三大自主招生联盟同时进行了笔试,这引起了考生、家长和社会的广泛关注。
本报记者分赴三个联盟考点进行采访,通过与考生的直接交流获悉,今年三大联盟笔试试题争相“瘦身”,同时又各有特色。
“卓越”联盟家长考生心态好看重经历检验实力参加了北京理工大学等9所高校“卓越”联盟自主招生笔试后,考生表示,参考“瘦身”后的自主招生笔试没有太大压力。
2011、2012、2013年卓越联盟自主招生物理部分真题及答案详解-免费下载
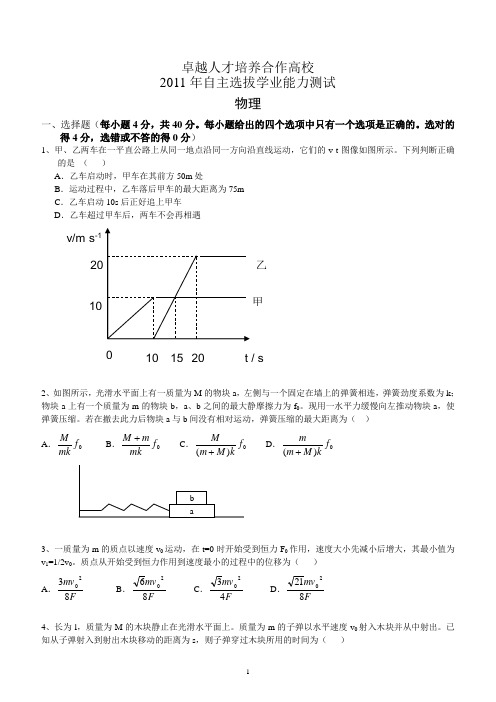
卓越人才培养合作高校 2011年自主选拔学业能力测试物理一、选择题(每小题4分,共40分。
每小题给出的四个选项中只有一个选项是正确的。
选对的得4分,选错或不答的得0分)1、甲、乙两车在一平直公路上从同一地点沿同一方向沿直线运动,它们的v-t 图像如图所示。
下列判断正确的是 ( )A .乙车启动时,甲车在其前方50m 处B .运动过程中,乙车落后甲车的最大距离为75mC .乙车启动10s 后正好追上甲车D .乙车超过甲车后,两车不会再相遇2、如图所示,光滑水平面上有一质量为M 的物块a ,左侧与一个固定在墙上的弹簧相连,弹簧劲度系数为k ;物块a 上有一个质量为m的物块b ,a 、b 之间的最大静摩擦力为f 0。
现用一水平力缓慢向左推动物块a ,使弹簧压缩。
若在撤去此力后物块a 与b 间没有相对运动,弹簧压缩的最大距离为( ) A .0f mk M B .0f mkmM + C .0)(f k M m M + D .0)(f k M m m +3、一质量为m 的质点以速度v 0运动,在t=0时开始受到恒力F 0作用,速度大小先减小后增大,其最小值为v 1=1/2v 0。
质点从开始受到恒力作用到速度最小的过程中的位移为( )A .F mv 8320B .F mv 8620C .F mv 4320D .Fmv 82124、长为l ,质量为M 的木块静止在光滑水平面上。
质量为m 的子弹以水平速度v 0射入木块并从中射出。
已知从子弹射入到射出木块移动的距离为s ,则子弹穿过木块所用的时间为( )0 10 15 20 t / s 甲 乙 v/m·s -1A .0v sl + B .⎥⎦⎤⎢⎣⎡++s m M l v )1(10 C .⎥⎦⎤⎢⎣⎡++s M m l v )1(1D .⎥⎦⎤⎢⎣⎡++s l m M v )1(105、如图,两段不可伸长细绳的一端分别系于两竖直杆上的A 、B 两点,另一端与质量为m 的小球D 相连。
大学自招数学试题及答案

大学自招数学试题及答案一、选择题(每题5分,共20分)1. 若函数f(x) = x^2 - 4x + 3,则f(2)的值为:A. 1B. 3C. -1D. 52. 以下哪个选项是不等式x^2 - 5x + 6 < 0的解集?A. (1, 6)B. (2, 3)C. (-∞, 2) ∪ (3, +∞)D. (2, 3)3. 已知向量a = (3, -1),向量b = (2, 2),则向量a与向量b的点积为:A. 4B. 2C. -2D. 04. 若复数z满足z^2 = 1 + i,则z的值是:A. 1B. -1C. iD. -i二、填空题(每题5分,共20分)5. 计算极限lim(x→0) (sin(x)/x) 的值为 _______。
6. 已知等比数列{a_n}的首项a_1 = 2,公比q = 3,求第5项a_5的值为 _______。
7. 计算定积分∫(0 to π) sin(x) dx 的值为 _______。
8. 若矩阵A = [[1, 2], [3, 4]],则矩阵A的行列式det(A)的值为_______。
三、解答题(每题15分,共40分)9. 证明:若x > 0,y > 0,则x + y ≥ 2√(xy)。
证明:由基本不等式可知,对于任意正数x和y,有x/y + y/x ≥ 2。
将不等式两边同时乘以xy,得到x^2 + y^2 ≥ 2xy。
由于x和y都是正数,所以x + y ≥ 2√(xy)。
10. 解方程组:\[\begin{cases}x + y = 5 \\2x - y = 1\end{cases}\]解:将第一个方程乘以2,得到2x + 2y = 10。
将第二个方程加到第一个方程上,得到3x = 11,所以x = 11/3。
将x的值代入第一个方程,得到y = 5 - 11/3 = 4/3。
因此,方程组的解为x = 11/3,y =4/3。
四、综合题(20分)11. 已知函数f(x) = x^3 - 3x^2 + 2,求f(x)的单调区间,并证明。
2015年《高校自主招生考试》数学真题分类解析之7、解析几何

专题之7、解析几何一、选择题。
1.(2009年复旦大学)设△ABC三条边之比AB∶BC∶CA=3∶2∶4,已知顶点A的坐标是(0,0),B的坐标是(a,b),则C的坐标一定是2.(2009年复旦大学)平面上三条直线x−2y+2=0,x−2=0,x+ky=0,如果这三条直线将平面划分成六个部分,则k可能的取值情况是A.只有唯一值B.可取二个不同值C.可取三个不同值D.可取无穷多个值3.(2010年复旦大学)已知常数k1,k2满足0<k1<k2,k1k2=1.设C1和C2分别是以y=±k1(x−1)+1和y=±k2(x−1)+1为渐近线且通过原点的双曲线,则C1和C2的离心率之比等于5.(2011年复旦大学)A.ρsin θ=1B.ρcos θ=−1C.ρcos θ=1D.ρsin θ=−1 6.(2011年复旦大学)设直线L过点M(2,1),且与抛物线y2=2x相交于A,B两点,满足|MA|=|MB|,即点M(2,1)是A,B的连接线段的中点,则直线L的方程是A.y=x−1B.y=−x+3C.2y=3x−4D.3y=−x+5 7.(2011年复旦大学)设有直线族和椭圆族分别为x=t,y=mt+b(m,b为实数,t为参数)和(a是非零实数),若对于所有的m,直线都与椭圆相交,则a,b应满足A.a2(1−b2)≥1B.a2(1−b2)>1C.a2(1−b2)<1D.a2(1−b2)≤1 8.(2011年复旦大学)极坐标表示的下列曲线中不是圆的是A.ρ2+2ρ(cos θ+sin θ)=5B.ρ2−6ρcos θ−4ρsin θ=0C.ρ2−ρcos θ=1D.ρ2cos 2θ+2ρ(cos θ+sin θ)=19.10.(2012年复旦大学)B.抛物线或双曲C.双曲线或椭圆D.抛物线或椭圆A.圆或直线线11.(2011年同济大学等九校联考)已知抛物线的顶点在原点,焦点在x轴上,△ABC的三个顶点都在抛物线上,且△ABC的重心为抛物线的焦点,若BC边所在直线的方程为4x+y−20=0,则抛物线方程为A.y2=16xB.y2=8xC.y2=−16xD.y2=−8xA.2B.2C.4D.413.(2011年清华大学等七校联考)AB为过抛物线y2=4x焦点F的弦,O为坐标原点,且∠OFA=135°,C为抛物线准线与x轴的交点,则∠ACB的正切值为14.(2012年清华大学等七校联考)椭圆长轴长为4,左顶点在圆(x−4)2+(y−1)2=4上,左准线为y 轴,则此椭圆离心率的取值范围是二、解答题。
2011全国重点高中自主招生考试数学试卷大全

2011年浙江省象山中学提前招生数学试题一、选择题(本题共6小题,每小题5分,共30分)1.一个布袋中装有10个相同的球,其中9个红球,1个黄球,从中任意摸取一个,那么( ) (A)一定摸到红球 (B)一定摸到黄球(C)不可能摸到黄球 (D)很有可能摸到红球2.为解决四个村庄用电问题,政府投资在已建电厂与这四个村庄之间架设输电线路.现已知这四个村庄及电厂之间的距离如图所示(距离单位:公里),则能把电力输送到这四个村庄的输电线路的最短总长度应该是( ).(A)19.5 (B)20.5 (C)21.5 (D)25.53.若等腰△ABC 的三边长都是方程x 2-6x+8=0的根,则△ABC 的周长是( ) (A)10或8 (B)1O (C)12或6 (D)6或10或124.A 、B 、C 、D 四人参加某一期的体育彩票兑奖活动,现已知:如果A 中奖,那么B 也中奖: 如果B 中奖,那么C 中奖或A 不中奖:如果D 不中奖,那么A 中奖,C 不中奖: 如果D 中奖,那么A 也中奖 则这四个人中,中奖的人数是( ) (A)1 (B)2 (C)3 (D)45.已知三条抛物线y 1=x 2-x+m ,y 2=x 2+2mx+4,y 3=mx 2+mx+m-1中至少有一条与x 轴相交,则实数m 的取值范围是( )(A)4/3<m<2 (B)m≤3/4且m≠0 (C)m≥2 (D)m≤3/4且m≠0或m≥26.如图,在正ABC 中,D 为AC 上一点,E 为AB 上一点,BD 、CE 交于P ,若四边形ADPE 与△BPC 面积相等,则∠BPE 的度数为( ) (A)60° (B)45° (C)7 5° (D)50° 二、填空题(本题共6小题,每小题5分,共30分)7.在△ABC 中,∠C=90°,若∠B=2∠A ,则tanB= . 8.已知|x|=4,|y|=1/2,且xy<0,则x/y 的值等于 。
自主招生数学试题及答案-word文档

自主招生数学试题及答案同学们都在忙碌地复习自己的功课,为了帮助大家能够在考前对自己多学的知识点有所巩固,下文整理了这篇数学试题及答案,希望可以帮助到大家!2019年清华等五校自主招生英语试题及答案1.以和为两根的有理系数多项式的次数最小是多少?A.2B.3C.5D.6解析:显然为满足要求的多项式,其次数为5.若存在次有理系数多项式以和为两根,则必含有因式,即最小次数为5.故选C.2.在的棋盘中停放着3个红色車和3个黑色車,每一行、每一列都只有一个車,共有多少种停放方法?A.720B.20C.518400D.14400解析:先排3个红色車,从6行中任取3行,有种取法;在选定的3行中第一行有6种停法,第一行选定后第二行有5种停法,第二行选定后第三行有4种停法;红車放定后,黑車只有6种停法.故停放方法共种.故选D.3.已知,求的值.解析:∵又由,有或当时,有当时,4.如图,△ABC中,AD为BC边上的中线,DM、DN分别为ADB、ADC的角平分线,试比较BM+CN与MN的大小关系,并说明理由.解析:延长ND至E,使ND=ED,连结BE、ME,则△BED≌△CND,△MED≌△MND,ME=MN,由BM+BEEM,得BM+CNMN.5.设数列满足,前项和为,求解析:∵由,有时,,于是特征方程有重根2,可设将代入上式,得于是6.模长为1的复数满足,求解析:取,便能得到=1.下面给出证明,=1.7.最多有多少个两两不等的正整数,满足其中任意三数之和都为素数.解析:设满足条件的正整数为个.考虑模3的同余类,共三类,记为则这个正整数需同时满足①不能三类都有;②同一类中不能有3个和超过3个.否则都会出现三数之和为3的倍数.故当时,取1,3,7,9,其任意三数之和为11,13,17,19均为素数,满足题意,所以满足要求的正整数最多有4个.8.已知为2019个实数,满足,且,求证解析:设若,则于是,进而若这2019个数去掉绝对值号后只能取和两值,又即这2019个数去掉绝对值号后取和两值的个数相同,这不可能.9.对于任意的,求的值.解析:各式相加,得10.已知有个实数,排列成阶数阵,记作使得数阵的每一行从左到右都是递增的,即对任意的,当时,有;现将的每一列原有的各数按照从上到下递增的顺序排列,形成一个新的阶数阵,记作,即对任意的,当时,有,试判断中每一行的各数的大小关系,并加以证明.解析:数阵中的中每一行的各数仍是递增的.下面用反证法给出证明. 若在第行存在,令,其中,则当时,即在第列中至少有个数小于,也就是在数阵中的第列中至少排在第行,这与排在第行矛盾.所以数阵中的中每一行的各数仍是递增的.这篇数学试题及答案就为大家分享到这里了。
2011年卓越联盟自主招生数学试题及答案.pdf

2011年同济等九校(卓越联盟)自主招生数学试题(1)向量a ,b 均为非零向量,(a -2b )⊥a ,(b -2a )⊥b ,则a ,b 的夹角为(A )6π(B )3π(C )23π (D )56π (2)已知sin2(α+γ)=n sin2β,则tan()tan()αβγαβγ++-+22等于 (A )11n n -+ (B )1n n + (C )1n n - (D )11n n +- (3)在正方体ABCD —A 1B 1C 1D 1中,E 为棱AA 1的中点,F 是棱A 1B 1上的点,且A 1F :FB 1=1:3,则异面直线EF 与BC 1所成角的正弦值为 (A )153 (B )155 (C )53 (D )55(4)i 为虚数单位,设复数z 满足|z |=1,则2221z z z i-+-+的最大值为 (A )2-1 (B )2-2 (C )2+1 (D )2+2(5)已知抛物线的顶点在原点,焦点在x 轴上,△ABC 三个顶点都在抛物线上,且△ABC 的重心为抛物线的焦点,若BC 边所在直线的方程为4x +y -20=0,则抛物线方程为(A )y 2=16x (B )y 2=8x (C )y 2=-16x (D )y 2=-8x(6)在三棱锥ABC —A 1B 1C 1中,底面边长与侧棱长均等于2,且E 为CC 1的中点,则点C 1到平面AB 1E 的距离为(A )3 (B )2 (C )32 (D )22(7)若关于x 的方程||4x x +=kx 2有四个不同的实数解,则k 的取值范围为( ) (A )(0,1) (B )(14,1) (C )(14,+∞) (D )(1,+∞) (8)如图,△ABC 内接于⊙O ,过BC 中点D 作平行于AC 的直线l ,l 交AB 于E ,交⊙O 于G 、F ,交⊙O 在A 点的切线于P ,若PE =3,ED =2,EF =3,则PA 的长为(A )5 (B )6(C )7(D )22 (9)数列{a n }共有11项,a 1=0,a 11=4,且|a k +1-a k |=1,k =1,2,…,10.满足这种条件的不同数列的个数为( )(A )100 (B )120 (C )140 (D )160(10)设σ是坐标平面按顺时针方向绕原点做角度为27π的旋转,τ表示坐标平面关于y 轴的镜面反射.用τσ表示变换的复合,先做τ,再做σ,用σk 表示连续k 次的变换,则στσ2τσ3τσ4是( ) (A )σ4 (B )σ5 (C )σ2τ(D )τσ2 (11)设数列{a n }满足a 1=a ,a 2=b ,2a n +2=a n +1+a n .(Ⅰ)设b n=a n+1-a n,证明:若a≠b,则{b n}是等比数列;(a1+a2+…+a n)=4,求a,b的值.(Ⅱ)若limn1)考察数列定义2)a1+a2+a3+...+a n=a n-a n-1+2(a n-1-a n-2)+3(a n-2-a n-3)+...+(n-1)(a2-a1)+na1=b n+2b n-1+3b n-3+...+b1+na(错位相减,可得a,b的值)(12)在△ABC中,AB=2AC,AD是A的角平分线,且AD=kAC.(Ⅰ)求k的取值范围;(Ⅱ)若S△ABC=1,问k为何值时,BC最短?(13)已知椭圆的两个焦点为F1(-1,0),F2(1,0),且椭圆与直线y=x-3相切.(Ⅰ)求椭圆的方程;(Ⅱ)过F1作两条互相垂直的直线l1,l2,与椭圆分别交于P,Q及M,N,求四边形PMQN面积的最大值与最小值.(14)一袋中有a个白球和b个黑球.从中任取一球,如果取出白球,则把它放回袋中;如果取出黑球,则该黑球不再放回,另补一个白球放到袋中.在重复n次这样的操作后,记袋中白球的个数为X n.(Ⅰ)求EX1;(Ⅱ)设P(X n=a+k)=p k,求P(X n+1=a+k),k=0,1,…,b;(Ⅲ)证明:EX n+1=(1-1a b+)EX n+1.(15)(Ⅰ)设f(x)=x ln x,求f′(x);(Ⅱ)设0<a<b,求常数C,使得1|ln|bax C dxb a--⎰取得最小值;(Ⅲ)记(Ⅱ)中的最小值为m a,b,证明:m a,b<ln2.。
【中考数学】历年各校自招数学真题及参考答案

1 1 10.定义 min a, b, c 表示实数 a, b, c 中的最小值,若 x, y 是任意正实数,则 M min x, , y 的最大 x y
值是 .
二、计算题(20 分) (10 分) 11.四个不同的三位整数的首位数字相同,并且它们的和能被它们中的三个数整除,求这些数.
12.如图,已知 PA 切 O 于 A , APO 30 , AH PO 于 H ,任作割线 PBC 交 O 于点 B 、 C ,计算
HC HB 的值.(10 分) BC
2.定义①1*1=1,②(n+1)*1=n*1+1,求 n*1=_________;
3. f ( x)
(a 1) x 2 (a 3) x 2a 8 的定义域为 D, f ( x)>0 在定义域 D 内恒成立,求 a 的取值范围? (2a 1) x 2 (a 1) x a 4
3 3 3
.
3.若有理数 a, b 满足
21 3 3 a b ,则 a b 4
.
4.如图, △ABC 中,AC=3,BC=4,AB=5,线段 DE⊥AB,且 △BDE 的面积是 △ABC 面积的三分之一, 那么,线段 BD 长为 。
5.二次函数 y ax 2 bx c 的图像与 x 轴有两个交点 M,N,顶点为 R,若 △MNR 恰好是等边三角形, 则 b 2 4ac 。
7.如图所示,正方形 ABCD 的面积设为 1, E 和 F 分别是 AB 和 BC 的中点,则图中阴影部分的面积 是 .
自招真题合集
8.在直角梯形 ABCD 中, ABC BAD 90o , AB 16 ,对角线 AC 与交 BD 于点 E ,过 E 作 EF AB 于点 F , O 为边 AB 的中点,且 FE EO 8 ,则 AD BC 的值为 .
2013年“卓越联盟”自主招生数学试卷评析

2 0 1 4 年第 1 、 2 期
福建 中学数 学
9
坐标变为原来的去 倍, 纵坐标不变
C.先 向左平 移 个单 位长 度 ,再 将所 得 点 的横
参考 .
1
解 析 由 1 + 壶 …老 < 2 ( 一
1
,
+ + … +
及 对 数 函数 性 质 ,易 得 l o g 6>1 ,
.
0< l o g 6 < 1,l o g a < 0
D
故有 l 0 g a<l o g 臼 <l o g b,
D
行, 这意味着考试时间将与两大联盟“ 北约” 、 “ 华约” 再 一次 撞车 . 对于 占据“ 半壁江 山” 的数学学科而言 , 三大联盟 的考查方式则显得颇有些耐人寻味 . “ 华约” 不分文理 科, “ 北约” 文理 仅 一题 不 同 ,而“ 卓越 ” 则相 当于 文理 分科 ,同题一 般不 超过 四题 . 本 文将 就 2 0 1 3年“ 卓越 联 盟” 自主 招 生数 学试 卷作 相 关评析 ,仅 供 广大 师 生
答 案为 A. 评 析 本 题 主 要 考 查 考 生对 于 函 数 基 本 性 质 的 灵 活 运 用 ,突 出数 形 结合 思 想 .此类 题 型 是 考 生平
题 1( 理科) 已 知S ( x ) 是定义在 R上的偶函数,
且在 区间 ( 0 , + o 。 ) 上是增 函数,则 ( )
.
的 图 象 经 过 点 B c 一 詈 , 。 ) , 且 , ( x ) 的 相 邻 两 个 零 点 的
象 上所 有 的点 ( ) A.先 向右平 移 个 单位 长 度 ,再 将 所得 点 的横
历年《高校自主招生考试》数学真题专题分类解析Word版含答案及解斩(共九大专题)

历年《高校自主招生考试》数学真题专题分类解析(共九大专题)目录:专题一:不等式 01~11页专题二:复数、平面向量 12~20页专题三:三角函数 21~27页专题四:创新与综合题 28~33页专题五:概率 34~43页专题六:数列与极限 44~55页专题七:解析几何 56~74页专题八:平面几何 75~83页专题九:排列、组合与二项式定理 84~88页历年《高校自主招生考试》数学真题分类解析专题一:不等式一、选择题。
1.(复旦大学)若实数x满足对任意实数a>0,均有x2<1+a,则x的取值范围是( )A.(-1,1)B.[-1,1]C.(-,)D.不能确定【答案】B【解析】对任意实数a>0,函数f(a)=1+a的值域是(1,+∞),因此只要x2≤1即可.由x2≤1,解得x∈[-1,1].2.(复旦大学)已知点A(-2,0),B(1,0),C(0,1),如果直线y=kx将△ABC分割为两个部分,则当k= 时,这两个部分的面积之积最大. ( )A.-B.-C.-D.-【答案】A【解析】3.(复旦大学)将同时满足不等式x-ky-2≤0(k>0),2x+3y-6≥0,x+6y-10≤0的点(x,y)组成的集合D称为可行域,将函数z=称为目标函数,所谓规划问题就是求解可行域内的点(x,y),使目标函数达到在可行域内的最小值.如果这个规划问题有无穷多个解,则( ) A.k≥1 B.k≤2 C.k=2 D.k=1【答案】C【解析】可行域如图中阴影部分所示,目标函数z=的几何意义是可行域内的点与点(0,-1)连线的斜率,如果要使其取得最小值的点有无穷多个,则直线x-ky-2=0必过点(0,-1),即k=2.选C. 在解含有参数的平面区域问题时要注意含有参数的直线系的特点,本题的突破点是直线系x-ky-2=0过定点(2,0).4.(复旦大学)设n是一个正整数,则函数y=x+在正实半轴上的最小值是( )A. B. C. D.【答案】C【解析】题中函数为非常规函数,可利用导数求其最值.因为y=x+=x+x-n,所以y'=1-x-n-1=1-,令y'=0得x=1,且函数y在(0,1)上递减,在(1,+∞)上递增,故函数y在正实半轴上的最小值为1+=.5.(复旦大学)若对一切实数x,都有|x-5|+|x-7|>a,则实数a的取值范围是( )A.a<12B.a<7C.a<5D.a<2【答案】D【解析】可先求出函数y=|x-5|+|x-7|的最小值,然后根据不等式恒成立的条件求得a的取值范围.由于|x-5|+|x-7|≥|5-7|=2,即函数y=|x-5|+|x-7|的最小值等于2,所以要使|x-5|+|x-7|>a恒成立,应有a<2.6.(2011年清华大学等七校联考)已知向量a=(0,1),b=(-,-),c=(,-),xa+yb+zc=(1,1),则x2+y2+z2的最小值为( )A.1B.C.D.2【答案】B 【解析】方法二∵xa+yb+zc=(1,1),∴-y+z=1,x-y-z=1,∴-y+z=,y+z=2x-2,∴z=+x-1,y=-+x-1,∴x2+(-+x-1)2+(+x-1)2=3x2-2(+1)x+(+1)2+2(-1)x+(-1)2=3x2-4x++2=3(x2-x+)++2-=3(x-)2+≥,当且仅当x=,z=,y=时等号成立.二、填空题。
2010-2011年度高数I试题A答案(经院内招生用)(同济版)

2010-2011年度高数I试题A答案(经院内招生用)(同济版)暨 南 大 学 考 试 试 卷一、填空题(将题目的正确答案填写在相应题目划线空白处。
共8小题,每小题2分,共16分)暨南大学《高等数学I 》试卷A 答案及评分(经济学院内招生用)1.2cos limx x tdt x→=⎰2.x →∞-= 03. 极限lim 2sin2n nn x→+∞=x(0x 为不为的常数)4. 函数20 1()2 1 121 2x f x x x x x <⎧⎪=+≤<⎨⎪+≤⎩的间断点是1x =5.设x y a =,则函数的n 阶导数()n y =(ln )n x a a ;6.若21()11x x f x ax x ⎧≤=⎨->⎩ 当a = 2 时,函数)f x ( 在1x =处可导. 7.已知某工厂生产某种商品,该产品的边际成本函数()3C x '=+,其固定成本为2000(元)则总成本为()20003C x x =++(元), 8. 1sin dx x =⎰ln csc cot x x c -+二、单选题(在每小题的备选答案中选出一个正确的答案,并将正确答案的号码填在题干的括号内。
共8小题,每小题2分,共16分)1.下列数列中收敛的是( C )(A) {}(1)n n - (B) 1n n ⎧⎫-⎨⎬⎩⎭(C)212n ⎧⎫+⎨⎬⎩⎭ (D) {}(1)n -2.若1lim(21)1x x →-=,则对于任意给定的0ε>,存在(B )当01x δ<-<时总有(21)1x ε--<成立(A) δε= (B) 2εδ=(C) 3δε= (D) 4δε=解:31232lim lim 12112xx x x x x x x →∞→∞⎛⎫+ ⎪+⎛⎫= ⎪ ⎪+⎝⎭ ⎪+⎝⎭ …………2分 312lim 112xx x x x →∞⎛⎫+ ⎪⎝⎭=⎛⎫+ ⎪⎝⎭……………………3分 32123lim 121lim 12xx xx e x e e x →∞→∞⎛⎫+ ⎪⎝⎭===⎛⎫+ ⎪⎝⎭……………………5分2.(1ln lim xx x →+∞+解:()(11ln ln ln 1x xxx e++=……………………………1分而((ln 1lim ln lim lim1ln ln x x x x x x xx→+∞→+∞→+∞+===…………4分于是()1ln 1lim xx x e e →+∞+==………………………………5分3.sin 0x x x-→解:sin x x x -→03sin lim12x x x x →-= ………………………………………………2分21cos lim32x x x →-= ………………………………………………4分sin 1lim33x x x →== ………………………………………5分4.确定常数 a , b ,的值, 使 02 sin 1lim.2ln(1)d xx ba x xt t→-=+⎰解0sin 0x ax x →-→时,0.b ∴=………………………………2分原式=0022sin sin lim lim ln(1)d ln(1)d x x x x ba x x a x x t t t t →→--=++⎰⎰…………………………3分002200cos cos 1limlim ln(1)2x x a x a x x x →→--===+() ………………………4分故lim cos x a x →-()=0,从而1a = ………………………5分四、计算题(共4小题,每题6分,共24分)1.由方程1y y xe =+确定的函数()y f x =可导,求y '及 1x y =-''。
高校自招数学试题及答案

高校自招数学试题及答案一、选择题(每题5分,共20分)1. 若函数f(x) = ax^2 + bx + c(a ≠ 0)的图像经过点(1, 2)和(2,3),则下列哪个选项是正确的?A. a + b + c = 2B. 4a + 2b + c = 3C. a + 2b + c = 3D. 4a + b + c = 5答案:C2. 已知数列{an}是等差数列,且a1 + a2 + a3 = 12,a2 + a3 + a4 = 18,则a1 + a5的值是多少?A. 18B. 20C. 24D. 26答案:B3. 若复数z满足|z - 1| = |z + i|,则z对应的点在复平面上位于哪个象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案:B4. 已知函数f(x) = ln(x) + 1/x,若f(x)在区间(0, +∞)上单调递增,则实数k的取值范围是?A. k > 0B. k ≥ 1C. k ≤ -1D. k ≤ 0答案:B二、填空题(每题5分,共20分)5. 若一个圆的直径为10,则该圆的面积为_______。
答案:25π6. 已知向量a = (3, -1),b = (2, 4),则向量a与向量b的数量积为_______。
答案:57. 若函数f(x) = x^3 - 3x^2 + 2在区间[1, 2]上单调递增,则实数k的取值范围是_______。
答案:k ≤ -18. 已知等比数列{an}的前三项分别为1,2,4,则该数列的通项公式为an = _______。
答案:2^(n-1)三、解答题(每题15分,共40分)9. 已知函数f(x) = x^2 - 4x + 3,求f(x)的单调区间,并说明理由。
答案:函数f(x)的单调递增区间为[2, +∞),单调递减区间为(-∞, 2)。
理由是f(x)的导数为f'(x) = 2x - 4,令f'(x) > 0得x > 2,令f'(x) < 0得x < 2。
历年自主招生考试数学试题大全-2012年卓越联盟自主招生数学试题Word版

2012年名牌大学自主招生考试数学试题适用高校:北京理工大学、同济大学等十三校一、选择题1.正四面体的4个而上分别写若l ,2,3,4,将4个这样的均匀正四面体投掷于桌而上,与桌面接触的4个面上的4个数的乘积被4整除的概率是( )(A )18 (B )964 (C )116 (D )13162.设a>0,b >0,c >0,且a+b+c=1,则22a b c 的最大值为( )(A )613 (B )43123 (C )34123 (D )6123.已知F 1、F 2分别为双曲线22221x y a b-=的左、右焦点,P 为双曲线左支上的任意一点, 若221||||PF PF 的最小值为8a , 则双曲线的离心率的取值范围为( ) (A )(l ,+∞)(B )(0,3] (C )(1,2](D )(1,3]4.如果关于x 的方程2x 2+3a x +a 2−a =0至少有一个根等于l 的根,那么实数a 的值( )(A )不存在(B )有一个 (C )有三个 (D )有四个5.5个顶点不共面的五边形叫空间五边形,空间五边形的5条边所在直线中,互相垂直的直线对至多有( )(A )5对 (B )6对 (C )7对 (D )8对 6.已知定义在实数集R 上的函数f (x ),其值域也是R ,井且时任意x 、y ∈R ,都有f [xf (y )]=xy ,则|f (2007)等于( )(A )0(B )1 (C )20072 (D )20077.若k 是正位数,且0242401020054010401040104010333C C C C +⨯+⨯++⨯能被2k 整除,则k 的最大值为( )(A )2004(B )2005 (C )2006 (D )20088.已知非零向量AB 与AC 满足0||||AB AC BC AB AC ⎛⎫+= ⎪⎝⎭,且12||||A B A C A B A C =则ABC ∆为( )(A )三边均为不相等的三角形(B )直角三角形 (C )等腰非等边三角形 (D )等边三角形9.关于x 、y 、z 的方程组333(6),(6),(6),y x z y x z -=-=-=的实数解的组数有( )(A )有一组解 (B )有两组解(C )有无穷多组解 (D )无法确定10.在欧非杯排球赛中,欧洲的参赛队伍比非洲的参赛队伍多9支,每两支球队赛一场,胜者得1分,败者得0分,若欧洲球队所得总分为非洲球队所得总分的9倍,则非洲球队的各支球队中得分的最大可能值是( )(A )8(B )9 (C )10 (D )11二、解答题11.在m (m ≥2)个不同数的排列P 1 P 2 ⋯P m 中, 若1≤i<j≤m 时P i >P j (即前面某数大于后面某数),则称P i 与P j 构成一个逆序.一个排列的全部逆序的总数称为该排列的逆序数.记排列(n +1)n (n −1)⋯321的逆序数为a n ,如排列21的逆序数a 1=l ,排列4321的逆序数a 3=6.(1)求a 4、a 5,并写出a n 的表达式;(2)令b n =11n n n n a a a a +++,求证:2n <12n b b b +++ <2n +3,n =1,2,…。
2015年《高校自主招生考试》数学真题分类解析之4、创新与综合题

专题之4、创新与综合题一、选择题。
1、(2011年复旦大学)设正整数n可以等于4个不同的正整数的倒数之和,则这样的n的个数是A.1B.2C.3D.42、(2011年同济大学等九校联考)设σ是坐标平面按顺时针方向绕原点做角度为的旋转,τ表示坐标平面关于y轴的镜面反射,用τσ表示变换的复合,先做τ,再做σ,用σk表示连续做k 次σ的变换,则στσ2τσ3τσ4是A.σ4B.σ5C.σ2τD.τσ2二、解答题。
3、(2009年南京大学)求所有满足tan A+tan B+ta n C≤[tan A]+[tan B]+[tan C]的非直角三角形.4、(2010年浙江大学)如图,一条公路两边有六个村庄,要建一个车站,要求到六个村庄的距离之和最小,应该建在哪里最合适?如果再在边上增加一个村庄呢?5、(2009年清华大学)A、B两人玩一个游戏,A选择n枚硬币,B根据自己的策略将这些硬币全部摆放在位点上,之后A选取一个至少有2枚硬币的位点,取走一枚硬币,再将另一枚硬币移动到相邻位点,A若在有限步内根据规则在指定点P处放上一个硬币则获胜.问在一条有5个位点的线段和7个位点的圆环上,A分别至少选择多少枚硬币时,无论点P的位置如何均可保证获胜?6、(2009年清华大学)有64匹马,每匹马的速度保持不变且各不相同,现通过比赛来完成排名,若每场比赛最多只能有8匹马参赛,问理想状态下能否在50场比赛内完成排名?7、(2009年清华大学)有100个集装箱,每个集装箱装有两件货物.在取出来的过程中货物的顺序被打乱了,现在按一定的规则将货物依次放入集装箱中.集装箱的体积都是1,且每个集装箱最多放两件货物,若装了一件货物后装不下第二件货物,那么就将这个集装箱密封,把第二件货物装到下一个集装箱中.问在最坏情况下需要多少个集装箱?8、(2009年清华大学)请写出一个整系数多项式f(x),使得+是其一根.9、(2010年清华大学)将长为n的棒锯开,要求锯成的每段长都是整数,且任意时刻,锯成的所有棒中最长的一根严格小于最短的一根的2倍,如6只能锯一次,6=3+3,而7能锯2次,7=4+3,4又能锯为2+2,问长为30的棒最多能锯成几段?若a,b,c中没有1,则a≥2,b≥2,c≥2,a+b+c=abc化为++=1,而1=++≤++=,显然不成立.∴三角形三内角的正切值分别为1,2,3.即满足三内角的正切值分别为1,2,3的三角形,即为所求.【解析】无4.1.首先设六个村庄到达公路的距离之和为S0,车站P到六个村庄的距离之和为S,下面我们根据车站所建的位置来讨论它到六个村庄的距离之和.(1)建在A、B之间(包括端点A),则S=AP+2PB+PC+PD+PE+S0=AE+BC+BD+S0+4PB.(2)建在B、C之间(包括两端点B、C),则S=PA+2PB+PC+PD+PE+S0=AE+BC+BD+S0.(3)建在C、D之间(包括端点D),则S=PA+2PB+PC+PD+PE+S0=AE+BC+BD+S0+2PC.(4)建在D、E之间(包括端点E),则S=PA+2PB+PC+PD+PE+S0=AE+BC+BD+S0+2PC+2PD.(5)建在A的左侧或E的右侧,则S均比情况(2)中的大.综合以上各种情况,我们可以发现:当车站建在B、C之间(包括端点B、C)时最合适.币.于是由结论①可知A可获胜.③对于4个位点线段的情况,A只要选择8枚硬币,不妨设点P为P1,P2,P3三点中的一点,并设点P 4处有硬币S枚,则点P4处的硬币尽可能移到点P3处后,点P1,P2与P3处共有:8−S+[]≥4②左半环内有7枚硬币.a.若这7枚硬币全在点P7处,则看右半环内的4枚硬币,若点P1处有2枚,则将其移动到点P7处后,点P7处就有8枚硬币,就能保证通过左半环的通路移动硬币,最终让点P处有硬币;若点P1处仅有1枚或没有硬币,则可将点P7处的硬币移动3枚到点P1处,再将点P1处的硬币移动到点P2处后,点P2与点P3处的硬币就不少于4枚.这样,通过右半环的通路,最终可将至少1枚硬币移动到点P4处.b.若这7枚硬币不全在点P7处,则将点P7处的硬币移到点P6处后,在点P5与点P6两处的硬币就不少于4枚.于是通过左半环的通路,最终也可保证有硬币移动到点P4处.③左半环有6枚硬币,则右半环就有5枚硬币.a.左半环内的6枚硬币全在点P7处,将它们移动到点P1处后,右半环内就有了8枚硬币,则通过右半环的通路,可最终保证至少移动1枚硬币到点P4处.b.左半环内的6枚硬币,点P7处有5枚,则再看点P1处,若点P1处的硬币数不足2枚,则在点P2与点P3处就有4枚硬币,则从右半环的通路,就能移动硬币到点P4;若点P1处的硬币数有2枚或2枚以上,则至少可从点P1处移动1枚硬币到点P7处.这样,点P7处就有6枚硬币,于是可移3枚到点P6处.这样点P5与点P6处就有4枚硬币,通过左半环可移动硬币到点P4处.c.左半环内的6枚硬币,点P7处有4枚或不足4枚,则在点P6与点P5处就有2枚或2枚以上,则将点P7处的硬币移动到点P6处以后,在点P6与点P5处的硬币数就不少于4枚,于是通过左半环可移动硬币到点P4处.④若左半环内的硬币数不足6枚,则右半环内的硬币就在6枚或6枚以上,则对右半环内硬币的分布情况进行相同的讨论,亦可发现必可将硬币移动到点P4处.各自的前4名,共8匹马进行一场比赛.这8匹马中的前4名,就是A组与B组32匹马中的前4名;接下来,又在A组与B组中分别扣除32匹马中的前4名后,再分别按照A组与B组中的排名,再各取4匹马,这8匹马进行一场比赛,它们中的前4名,就是A组与B组32匹马中的第5名到第8名;重复上述过程,又可分别确定第9名到第12名;……;最后留下的8匹马,只需进行一场比赛,就能确定第25名到第32名的排名.这样进行了7场比赛,就将A组与B组中的32匹马进行了排名.同理进行7场比赛,又可将C组与D组中的32匹马进行排名.这样第三步共进行14场比赛.第四步:要来完成AB组的32匹马与CD组的32匹马(它们各自内部的排名已经完成)共计64匹马的排名.采用第三步中的方法,每次分别选择AB组与CD组中留下的前4名进行一场比赛,都能确定其中4匹马在总体中的排名,这样14场比赛后,就确定了前56匹马的排名,最后留下的8匹马,只需进行一场比赛,就确定了第57名到第64名的排名.因此,只需15场比赛就能完成这两大组64匹马的排名.综观以上四个步骤,一共进行:8+12+14+15=49(场).所以,可以在50场比赛内完成排名.【解析】无7.由题意知共有200件货物.设a1≤a2≤…≤a99≤a100,b1≥b2≥…≥b99≥b100,令a i+b i=1,a i≥b i,则将它们按如下顺序排列:a1,a2,b1,a3,b2,a4,b3,…,a99,b98,a100,b99,b100,则a 1+a2>1,a2+b1>1,b1+a3>1,…,a100+b99>1,+<1,a1到a100,b1到b98各在一个箱中,b99,b100在一个箱子中,则在最坏情况下需要199个箱子.换个角度考虑,无论200件货物如何排列,体积最小的货物总能与它前面的或后面的货物合装进一个集装箱的,故有199个集装箱就一定能将200件货物全部装下.【解析】无8.设x=+,则(x)3=3,即x3−3x2·+3x·2−2=3,∴x3+6x−3=(3x2+2)·,∴(x3+6x−3)2=2·(3x2+2)2,整理得:x6−6x4−6x3+12x2−36x+1=0,则f(x)=x6−6x4−6x3+12x2−36x+1即为所求的一个整系数多项式.【解析】无9.首先,由题意可知:当我们锯了若干次之后,产生若干根棒,它们中有长度相等与仅差一个单位的棒(例如:7,8,9;6,6,7;5,5,6,6等),这些棒除了2k−2,2k−1,2k与2k−1,2k−1,2k这两种情况,其他无论锯开哪一根,均不能符合最长的一根严格小于最短一根的2倍,有了这样的认识,我们就可以用枚举法来解本题了.(1)30=11+19=11+7+12=11+7+6+6=5+6+7+6+6,。
同济大学_自主招生_数学_真题

同济大学2010年暨保送生考试数学试题一、填空题1.f (x )是周期为2的函数,在区间[-1,1]上,f (x )=|x |,则3(2)2f m +=___(m 为整数). 2.函数y =cos2x -2cos x ,x ∈[0,2π]的单调区间是__________________. 3.函数2y =__________________.4.5.函数y =f (x ),f (x +1)-f (x )称为f (x )在x 处的一阶差分,记作△y ,对于△y 在x 处的一阶差分,称为f (x )在x 处的二阶差分△2y ,则y =f (x )=3x ·x 在x 处的二阶差分△2y =____________. 6.7.从1~100这100个自然数中取2个数,它们的和小于等于50的概率是__________. 8.正四面体ABCD ,如图建立直角坐标系,O 为A 在底面的投影,则M 点坐标是_________,CN 与DM 所成角是_________. 9.双曲线x 2-y 2=1上一点P 与左右焦点所围成三角形的面积___________.10.椭圆22143x y +=在第一象限上一点P (x 0,y 0),若过P 的切线与坐标轴所围成的三角形的面积是_________. 二、解答题11.不等式22222log 0364x kx kx x ++<++对于任意x ∈R 都成立,求k 的取值范围. 12.不动点,()bx c f x x a +=+.(1) 12,3为不动点,求a ,b ,c 的关系;(2) 若1(1)2f =,求f (x )的解析式;(3) 13.已知sin cos ([0,2))2sin cos y θθθπθθ⋅=∈++,(1) 求y 的最小值;(2) 求取得最小值时的θ.14.正三棱柱ABC -A 1B 1C 1,|AA 1|=h ,|BB 1|=a ,点E 从A 1出发沿棱A 1A 运动,后沿AD 运动,∠A 1D 1E =θ,求过EB 1C 1的平面截三棱柱所得的截面面积S 与θ的函数关系式. 15.已知数列{a n }满足112n n n a a a -++=. (1) 若b n =a n -a n -1(n=2,3,…), 求b n ;(2) 求1ni i b =∑;(3) 求lim nn a→∞.16.抛物线y 2=2px ,(1) 过焦点的直线斜率为k ,交抛物线与A ,B ,求|AB |.(2) 是否存在正方形ABCD ,使C 在抛物线上,D 在抛物线内,若存在,求这样的k ,正方形ABCD 有什么特点?同济大学2010年自主招生优秀考生文化测试数学试卷BAC D A 1D 1 C 1 B1一、填空题(本大题共有8题,只要求直接填写结果,每题答对得5分,否则一律得零分,本大题满分40分) 1.函数12()log (sin cos )f x x x =+的单调递增区间是_______________________.2.如图所示,为某质点在20秒内作直线运动时,速度函数()v v t =的图象,则该质点运动的总路程s =_____(厘米).3.设a 与b 是两条非相互垂直的异面直线,α与β分别是过直线a 与b 的平面,有以下4个结论:(1) b //α,(2) b ⊥α,(3) β//α,(4) β⊥α,则其中不可能出现的结论的序号为__________.4.设某地于某日午后2时达到最高水位,为3.20米,下一个最高水位恰在12小时后达到,而最低水位为0.20米。
高考自招题库-卓越联盟历年自主招生真题及模拟题

华南理工大学2009年保送生、自主招生选拔试题《理科数学》试题A一.选择题1)已知复数,且的幅角主值是,则满足的幅角主值的取值范围是() A 、B 、C 、D 、2)是函数在单调的()A 、充分而不必要条件B 、必要而不充分条件C 、充分必要条件D 、既不充分也不必要条件3)已知,,则的最小值为()A 、B 、C 、D 、4)在的展开式中,的系数为()A 、B 、C 、D 、5)已知圆,点是圆内一点。
过点的圆的最短的弦在直线上,直线的方程为,那么()A 、,且与圆相交B 、,且与圆相切0z x i =+()20x i +2π02z z -=z 5,1212ππ⎛⎫⎪⎝⎭,63ππ⎛⎫ ⎪⎝⎭37,1212ππ⎛⎫ ⎪⎝⎭59,1212ππ⎛⎫⎪⎝⎭0b>()2f x x bx c =++[0,)+∞,ab R ∈2226a b +=a b +-3-3-72-()()()221111nn nn x x x x x -++++++nx ()()21!!1!n n n ++()2n+1!n!n!()2n+2!!!n n ()()22!!1!n n n ++222:O x y r +=(),,0P a b ab ≠O P O 1l 2l 2bx ayr -=12//l l 2l O 12l l ⊥2l OC 、,且与圆相离D 、,且与圆相离6)已知,函数的值域为()A 、B 、C 、D 、7)在三角形中,向量,则下列结论一定成立的是()A 、向量一定与向量平行B 、向量一定与向量平行C 、向量一定与向量平行D 、向量一定与向量平行8)已知是椭圆的半焦距,则的取值范围是()A 、B 、C 、D 、 二.填空题9)已知是某球面上不共面的四点,且,,,则此球的表面积等于 。
10)已知双曲线右焦点为,右准线与两条渐近线分别交于两点。
若是直角三角形,则双曲线的离心率。
11)已知函数是定义在上的增函数,且满足,,12//l l 2l O 12l l ⊥2l O 02x π≤≤()2cos cos 1f x x x x =++[]3,1-[]3,2-[]1,3-[]2,3-ABC ,38,4a AB AC b AB AC BC c CB BA =+=++=+a c +b b c +a a b +c a b -c c ()222210x y a b a b+=>>22b ca +1,2⎛⎫+∞⎪⎝⎭1(,1]21(,21(,2,,,A B CD AB BC AD ===2BD AC ==BC AD ⊥()0,012222>>=-b a by a x Fl Q P ,PQF ∆=e ()f x ()0,+∞()31f =()()(),0,0f xy f x f y x y =+>>则不等式的解集为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年同济大学等九校(卓越联盟)自主招生数学试题分值: 分 时量: 分钟一、选择题,1.已知向量,a b 为非零向量,(2),(2),a b a b a b -⊥-⊥则,a b 夹角为( )A.6π B.3π C.32π D.65π2.已知sin 2()sin 2,r n αβ+=则tan()tan()αβγαβγ++=-+( )A. 11n n -+ B. 1n n + C .1n n - D.11n n +-3.在正方体1111ABCD A B C D -中,E 为棱1AA 的中点,F 是棱11A B 上的点,且11:1:3A F FB =,则异面直线EF 与1BC 所成角的正弦值为( )A.3B.5C.3D.54.i 为虚数单位,设复数z 满足||1z =,则2221z z z i-+-+的最大值为( )A. 1B. 2-C. 1+D. 2+5.已知抛物线的顶点在原点,焦点在x 轴上,ABC ∆三个顶点都在抛物线上,且ABC ∆的重心为抛物线的焦点,若B C 边所在的直线方程为4200x y +-=,则抛物线方程为( ) A.. 216y x = B. 28y x = C. 216y x =- D. 28y x =-6.在三棱柱111ABC A B C -中,底面边长与侧棱长均不等于2,且E 为1CC 的中点,则点1C 到平面1AB E 的距离为( )A.B.C.2D.27.若关于x 的方程2||4x kx x =+有四个不同的实数解,则k 的取值范围为( )A. (0,1)B. 1(,1)4C.1(,)4+∞ D. (1,)+∞8.如图,内接于O ,过中点作平行于的直线,l l 交于,交O 于,交O10.设σ是坐标平面按顺时针方向绕原点做角度为27π的旋转,τ表示坐标平面关于y 轴的镜面反射.用τσ表示变换的复合,先做τ,再做σ.用k σ表示连续k 次σ的变换,则234στστστσ是( ) A. 4σ B. 5σ C.2στ D.2τσ 二、解答题11.设数列{}n a 满足1221,,2n n n a a a b a a a ++===+. (1)设1n n n b a a +=-,证明:若a b ≠,则{}n b 是等比数列; (2)若12lim ()4,n n a a a →∞+++= 求,a b 的值;12.在ABC ∆中,2,A B A C A D =是角A 的平分线,且AD kAC =. (1)求k 的取值范围;(2)若1ABC S ∆=,问k 为何值时,B C 最短?13.已知椭圆的两个焦点为12(1,0),(1,0)F F -,且椭圆与直线y x =-. (1)求椭圆的方程;(2)过1F 作两条互相垂直的直线12,l l ,与椭圆分别交于,P Q 及,M N ,求四边形PMQN 面积的最大值与最小值.14.一袋中有a 个白球和b 个黑球.从中任取一球,如果取出白球,则把它放回袋中;如果取出黑球,则该黑球不再放回,另补一个白球放到袋中.在重复n 次这样的操作后,记袋中白球的个数为n X . (1)求1EX ;(2)设()n k P X a k p =+=,求1(),0,1,,;n P X a k k b +=+= (3)证明:11(1) 1.n n EX EX a b+=-++15.设()ln f x x x =. (1)求()f x ';(2)设0,a b <<求常数c ,使得1|ln |b ax c dx b a--⎰取得最小值;(3)记(2)中的最小值为,M a b ,证明,ln 2M a b <.参考答案: 一.选择题1. 2. 3. 4. 5. 6.7.8.9.10.B D B C A D C B BD二.解答题11.【解】(1)证:由1221,,2n n n a a a b a a a ++===+,得2112()().n n n n a a a a +++-=-- 令1,n n n b a a +=-则112n n b b +=-,所以{}n b 是以b a -为首项,以12-为公比的等比数列;(2)由(1) 可知1*11()(()2n n n n b a a b a n N -+=-=--∈,所以由累加法得1111(2(),11()2nn a a b a +---=---即121()[1()],32nn a a b a +=+---也所以有121()[1(](2),132n n a a b a n n -=+---≥=时,1a a =也适合该式;所以1*21()[1(]()32n n a a b a n N -=+---∈也所以1211()224412()[]()()()()13399212nnn a a a na b a n na b a n b a b a --+++=+--=+---+--+由于12lim ()4,n n a a a →∞+++= 所以24()0,()4,39a b a b a +-=--=解得6,3a b ==-.12.【解】(1)过B 作直线BE AC ,交AD 延长线于E ,如图右. 所以,2,BD AB C DAC == 也所以有2D E BE BD ADACD C===,即2,3.B E A C A E B D ==在ABE ∆中,有2222cos .AE AB BE AB BE EBA =+-⋅∠ 即222(3)(2)(2)2(22)cos AD AC AC AC AC A =++⋅⋅ 所以,2229()88cos ,kAC AC AC A =+⋅即2816(1cos )(0,)99k A =+∈所以403k <<.(2)因为21sin sin 12ABC S AB AC A AC A ∆=⋅⋅==在ABC ∆中,有2222254cos 2cos 54cos sin A BC AB AC AB AC A AC AC A A-=+-⋅=-=记54cos sin A y A-=,则sin 4cos )5y A A A ϕ+=+=当sin()1A ϕ+=时,53y =⇒=此时y 取最小值,此时3cos 5A =.故当15k =时,B C13.【解】设椭圆方程为22221(0)x y a b ab+=>>,因为它与直线y x =-,所以方程组22221,x ya b y x ⎧+=⎪⎨⎪=-⎩只有一解,整理得2222222()30a b x x a a b +-+-=.所以2222222()4((3)0,a b a a b =--+-= 得223a b +=.又因为焦点为12(1,0),(1,0)F F -,所以221,a b -=联立上式解得222,1a b == 所以椭圆方程为2212xy +=.(2)若PQ 斜率不存在(或为0)时,则||||222PM Q N PQ M N S ⋅===四边形.若PQ 斜率存在时,设为(0)k k ≠,则M N 为1k-.所以直线PQ 方程为y kx k =+.设PQ 与椭圆交点坐标为1122(,),(,)P x y Q x y联立方程221,2.x y y kx k ⎧+=⎪⎨⎪=+⎩化简得2222(21)4220k x k x k +++-=.则22121222422,2121kk x x x x k k --+==++所以12|||21PQ x x k =-==+同理可得||M N =所以222422242421||||(1)21124444()2(2)(21)2522252PM QN kPQ M N k k k S k k k k k k ⋅+++====-++++++四边形 24221114()4()12410424410kk k k =-=-++++因为22144101018k k++≥=(当且仅当21k =时取等号)所以,2211(0,],1184410k k∈++也所以2211164()[,2]1294410k k-∈++所以综上所述,PM QN S 四边形的面积的最小值为169,最大值为2.14.【解】(1)1n =时,袋中的白球的个数可能为a 个(即取出的是白球),概率为a a b+;也可能为1a +个(即取出的是黑球),概率为b a b+,故21(1)a b a ab b EX a a a ba ba b++=⋅++⋅=+++.(2)首先,10(0);n aP X a P a b+=+=⋅+1k ≥时,第1n +次取出来有a k +个白球的可能性有两种;第n 次袋中有a k +个白球,显然每次取出球后,球的总数保持不变,即a b +个白球(故此时黑球有b k -个),第1n +次取出来的也是白球,这种情况发生的概率为;k a k P a b+⋅+第n 次袋中有1a k +-个白球,第1n +次取出来的是黑球,由于每次球的总数为a b +个,故此时黑球的个数为1b k -+.这种情况发生的概率为11(1)k b k P k a b--+⋅≥+.故111()(1).n k k a k b k P X a k P P k a ba b+-+-+=+=⋅+⋅≥++(3)第1n +次白球的个数的数学期望分为两类:第n 次白球个数的数学期望,即n EX .由于白球和黑球的总个数为a b +,第1n +次取出来的是白球,这种情况发生的概率是n EX a b+;第1n +次取出来的是黑球,这种情况发生的概率是na b EX a b+-+,此时白球的个数是 1.n EX + 故21()(1)(1)(1)n nn n n n n n EX a b EX EX EX EX EX EX EX a ba b a b a b++-=+⋅+=+-+++++22()())11(1)1n n n n n EX EX EX EX EX a ba ba ba b=+-+-=-+++++15.(1)1()ln ln 1f x x x x x'=+⋅=+;(2)若ln ,c a ≤则|ln |ln ,x c x c -=-显然,当ln ,ln c a x c =-取最小; 若ln ,c b ≤则|ln |ln ,x c c x -=-当ln ,ln c b c x =-取最小. 故ln ln .a c b ≤≤11|ln |[(ln )(ln )]ccb eb aaex c dx x c dx c x dx b ab a-=-+---⎰⎰⎰1{[(ln 1)(1)][(1)(ln 1)]}ceb xc dx c x dx =+-+++-+⎰⎰由(1)知[(ln 1)(1)]ln |(1)()ccee caax c dx x x c e a +-+=-+-⎰ [(1)(ln 1)](1)()ln |c cb c be ec x dx c e a x x +-+=+--⎰所以,11|ln |(ln ln 2)()b cax c dx a a b b e a b ac bc b ab a-=---+++-*--⎰记()2()ln ln ,c g c e a b c a a b b a b =-++--++ 则令()20c g c e a b '=-++=,得2a b c +=即2a b c +=时,1|ln |b ax C dx b a--⎰取最小值.(3)将2a b c +=代入()*式右边,1,[ln ln ()ln]ln 22a b M a b a a b b a b b a+=--++<-等价于()ln ln ln ()ln 2()ln()ln ln 2ln 22a b a b a a b b b a a b a b a a b b b ++--<-⇔+⋅+<++ln()ln ln()ln 2ln 2ln(1)ln(1)2ln 2.b a a a b a a b a b b b b a b b a b⇔+-++-<⇔+++< 由于0,12a a b b<<+<时,ln(1)ln 2.a b b b+<所以下面只须证明ln(1)ln 2b a b a+<即可.又ln(1)ln 2ln(1)ln 2.b a b a b a b a+<⇔+<令(0,1)a t b=∈,则11ln(1)ln(1)ln(1)t a bt b a t t +=+=+,注意到函数1ln(1)tt +是单调递增的,且 1.t < 所以111ln(1)ln(1)ln 21t t+<+=.得证.。
