中考数学压轴题:特殊四边形存在性问题
二次函数背景下的特殊四边形存在性判定(解析版)

备战2020年中考数学压轴题之二次函数专题06 二次函数背景下的特殊四边形存在性判定【方法综述】知识准备:特殊四边形包括平行四边形、菱形、矩形和正方形。
它们的判定方法如下:平行四边形的判定方法:两组对边分别平行的四边形是平行四边形;两组对角分别相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形两条对角线互相平分的四边形是平行四边形;矩形判的定方法有一个角是直角的平行四边形是矩形;对角线相等的平行四边形是矩形有三个角是直角的四边形是矩形菱形判定方法有一组邻边相等的平行四边形是菱形;对角线互相垂直的平行四边形是菱形四条边相等的四边形是矩形正方形的判定方法平行四边形+矩形的特性;平行四边形+菱形的特性解答时常用的技巧:(1).根据平行四边形的对角线互相平分这条性质,应用中点坐标公式,可以采用如下方法:已知点A、B、C三点坐标已知,点P在某函数图像上,是否存在以点A、B、C、P为顶点的四边形为平行四边形,求点P的坐标。
如,当AP、BC为平行四边形对角线时,由中点坐标公式,可得a+m=c+e,n+b=d+f则m= c+e-a;n= d+f-b,点P坐标可知,将其带入到函数关系式进行验证,如果满足函数关系式,即为所求P点,同理,根据分类讨论可以得到其它情况的解答方法。
(2).菱形在折叠的情况下,可以看成是等腰三角形以底边所在直线折叠所得,因此,菱形的存在性讨论,亦可以看做等腰三角形的存在性讨论。
(3).矩形中的直角证明出来常规直角的探究外,还有主要是否由隐形圆的直径所对圆周角得到。
【典例示范】类型一平行四边形的存在性探究例1:如图,在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.(1)求抛物线的解析式;(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S,求S关于m的函数关系式,并求出S的最大值;(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P,Q,B,O为顶点的四边形为平行四边形(要求PQ∥OB),直接写出相应的点Q的坐标.【答案】(1)y=12x2+x-4;(2)当m=-2时,S有最大值,S最大=4;(3)满足题意的Q点的坐标有三个,分别是(-2+2-,(-2-2+,(-4,4).【思路引导】(1)已知抛物线与x轴的两个交点的横坐标,一般选用两点式,利用待定系数法求解即可;(2)利用抛物线的解析式表示出点M 的纵坐标,从而得到点M 到x 轴的距离,然后根据三角形面积公式表示并整理即可得解,根据抛物线的性质求出第三象限内二次函数的最值,然后即可得解;(3)利用直线与抛物线的解析式表示出点P 、Q 的坐标,然后求出PQ 的长度,再根据平行四边形的对边相等列出算式,然后解关于x 的一元二次方程即可得解.【解析】(1)设抛物线的解析式为y=a (x+4)(x -2),把B (0,-4)代入得,-4=a×(0+4)(0-2),解得a=12, ∴抛物线的解析式为:y=12(x+4)(x -2),即y=12x 2+x -4; (2)过点M 作MD ⊥x 轴于点D ,设M 点的坐标为(m ,n ), 则AD=m+4,MD=-n ,n=12m 2+m -4, ∴S=S △AMD +S 梯形DMBO -S △ABO =111(4)()(4)()44222m n n m +-+-+--⨯⨯= -2n -2m -8=-2×(12m 2+m -4)-2m -8=-m 2-4m =-(m+2)2+4(-4<m <0);∴S 最大值=4.(3)设P (x ,12x 2+x -4). ①如图1,当OB 为边时,根据平行四边形的性质知PQ ∥OB ,∴Q 的横坐标等于P 的横坐标,又∵直线的解析式为y=-x ,则Q (x ,-x ).由PQ=OB ,得|-x -(12x 2+x -4)|=4,解得x=0,-4,-x=0不合题意,舍去.由此可得Q (-4,4)或(-2--2-;②如图2,当BO 为对角线时,知A 与P 应该重合,OP=4.四边形PBQO 为平行四边形则BQ=OP=4,Q 横坐标为4,代入y=-x 得出Q 为(4,-4).故满足题意的Q 点的坐标有四个,分别是(-4,4),(4,-4),(-,2-,(-2-.【方法总结】本题是二次函数综合题,交点式求解析式,二次函数与三角形面积最值问题的公共底的辅助线的做法要注意,二次函数中存在平行四边形的方法,要分别对已知边的分别为平行四边形的边或是对角线进行分类讨论.针对训练1.如图,二次函数的图象与x 轴交于A 、B 两点,与y 轴交于点C ,已知点A (﹣4,0).(1)求抛物线与直线AC 的函数解析式;(2)若点D (m ,n )是抛物线在第二象限的部分上的一动点,四边形OCDA 的面积为S ,求S 关于m 的函数关系式;(3)若点E 为抛物线上任意一点,点F 为x 轴上任意一点,当以A 、C 、E 、F 为顶点的四边形是平行四边形时,请求出满足条件的所有点E 的坐标.【答案】(1)(2)S=﹣m 2﹣4m+4(﹣4<m <0)(3)(﹣3,2)、(,﹣2)、(,﹣2)【解析】 (1)∵A (﹣4,0)在二次函数y=ax 2﹣x+2(a≠0)的图象上, ∴0=16a+6+2,解得a=﹣, ∴抛物线的函数解析式为y=﹣x 2﹣x+2; ∴点C 的坐标为(0,2),设直线AC 的解析式为y=kx+b ,则, 232(0)2y ax x a =-+≠122y x =+32--32-3212123204{2k b b=-+=解得,∴直线AC 的函数解析式为:;(2)∵点D (m ,n )是抛物线在第二象限的部分上的一动点,∴D (m ,﹣m 2﹣m+2),过点D 作DH ⊥x 轴于点H ,则DH=﹣m 2﹣m+2,AH=m+4,HO=﹣m ,∵四边形OCDA 的面积=△ADH 的面积+四边形OCDH 的面积,∴S=(m+4)×(﹣m 2﹣m+2)+(﹣m 2﹣m+2+2)×(﹣m ),化简,得S=﹣m 2﹣4m+4(﹣4<m <0);(3)①若AC 为平行四边形的一边,则C 、E 到AF 的距离相等,∴|y E |=|y C |=2,∴y E =±2.当y E =2时,解方程﹣x 2﹣x+2=2得,x 1=0,x 2=﹣3,∴点E 的坐标为(﹣3,2);当y E =﹣2时,解方程﹣x 2﹣x+2=﹣2得,x 1=,x 2=,∴点E 的坐标为(,﹣2)或(,﹣2);②若AC 为平行四边形的一条对角线,则CE ∥AF ,∴y E =y C =2,∴点E 的坐标为(﹣3,2).综上所述,满足条件的点E 的坐标为(﹣3,2)、(,﹣2)、(,﹣2).1{22k b ==122y x =+123212321212321212321232123232-32-+32-32-32--32-+2.(云南省弥勒市2019届九年级上学期期末考试数学试题)如图,抛物线y =x 2−2x −3与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2.(1)求A 、B 两点的坐标及直线AC 的函数表达式;(2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE 长度的最大值;(3)点G 是抛物线上的动点,在x 轴上是否存在点F ,使A 、C 、F 、G 四个点为顶点的四边形是平行四边形?如果存在,写出所有满足条件的F 点坐标(请直接写出点的坐标,不要求写过程);如果不存在,请说明理由.【答案】(1)A(−1,0),B(3,0),y =−x −1。
专题08 二次函数中特殊四边形存在性问题的四种考法(原卷版)-2024年常考压轴题攻略(9上人教版)

专题08二次函数中特殊四边形存在性问题的四种考法类型一、平行四边形存在性问题例.已知抛物线2y x bx c =-++与x 轴交于()1,0A -,()3,0B 两点,与轴交于C 点,点P 是抛物线上在第一象限内的一个动点,且点P 的横坐标为t .(1)求抛物线的表达式;(2)如图1,连接BC ,PB ,PC ,设PBC 的面积为S .①求S 关于t 的函数表达式;②求P 点到直线BC 的距离的最大值,并求出此时点P 的坐标.(3)如图2,设抛物线的对称轴为l ,l 与x 轴的交点为D ,在直线l 上是否存在点M ,使得四边形CDPM 是平行四边形?若存在,直接写出点M 的坐标;若不存在,请说明理由.【变式训练1】如图,在平面直角坐标系中,二次函数2=23y x x --与x 轴交于A 、B 两点(A 点在B 点的左侧),直线y x m =+与抛物线交于A 、C 两点.(1)求点C 的坐标;(2)点P 为直线AC 下方抛物线上一点,过点P 作y 轴平行线交AC 于E 点,当EP 最长时求此时点P 的坐标;(3)抛物线顶点为M ,在平面内是否存在点N ,使以,,,A B M N 为顶点的四边形为平行四边形?若存在请求出N 点坐标并在备用图中画出图形;若不存在,请说明理由.(1)求此拋物线的解析式;(2)在抛物线的对称轴上有一点P,使得PA PC+值最小,求最小值;(3)点M为x轴上一动点,在拋物线上是否存在一点N,使以边形为平行四边形?若存在,直接写出点N的坐标;若不存在,请说明理由.【变式训练3】综合与实践如图,抛物线23y ax x c=++与x轴交于A,B两点(点A在点(1)求抛物线的解析式:(2)在抛物线的对称轴上是否存在点P,使PCD是以CD为腰的等腰三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;(3)点E在x轴上运动,点F在抛物线上运动,当以点B,C,E,F为顶点的四边形是平行四边形,直接写出点E的坐标.类型二、菱形存在性问题(1)求抛物线的表达式;(2)若点E 在第一象限内对称右侧的抛物线上,四边形ODEB 的面积为(3)在(2)的条件下,若点F 是对称轴上一点,点H 是坐标平面内一点,在对称轴右侧的抛物线上是否存在点G ,使以E ,F ,G ,H 为顶点的四边形是菱形,且存在,请直接写出点G 的坐标;如果不存在,请说明理由.【变式训练1】如图1,抛物线23y ax bx =++交x 轴于点()30A ,和点(1)求抛物线的表达式;(2)若点D 是直线AC 上方拋物线上一动点,连接BC ,AD ADM △的面积为1S ,BCM 的面积为2S ,当121S S -=时,求点(3)如图2,若点P 是抛物线上一动点,过点P 作PQ x ⊥轴交直线上是否存在点E ,使以P ,Q ,E ,C 为顶点的四边形是菱形,若存在,请直接写出点坐标;若不存在,请说明理由(1)求ABC 的面积;(2)点P 为直线AC 上方抛物线上的任意一点,过点P 作PD y ∥轴交直线22PD CD +的最大值及此时点P 的坐标;(3)如图2,将抛物线沿着水平方向向右平移2个单位长度得到新的抛物线,点与平移后的抛物线的交点,点M 为平移后的抛物线对称轴上的一动点,点的一点,直接写出所有使得以点B E M N 、、、为顶点的四边形是菱形的点求其中一个点N 的坐标的求解过程写出来.类型三、矩形存在性问题例.已知抛物线()240y ax bx a =+-≠交x 轴于点()4,0A 和点()2,0B -,交y 轴于点C .(1)求抛物线的解析式;(2)如图,点P 是抛物线上位于直线AC 下方的动点,过点P 分别作x 轴、y 轴的平行线,交直线AC 于点D ,交x 轴于点E ,当PD PE +取最大值时,求点P 的坐标及PD PE +最大值.(3)在抛物线上是否存在点M ,对于平面内任意点N ,使得以A 、C 、M 、N 为顶点且AC 为一条边的四边形为矩形,若存在,请直接写出M 、N 的坐标,不存在,请说明理由.(1)求点A、B、C的坐标;(2)将抛物线L向右平移1个单位,得到新抛物线对称轴l上是否存在点D,使得以点D的坐标;若不存在,请说明理由.(1)求抛物线的表达式;的面积为S,求S (2)若点P为第一象限内抛物线上的一点,设PBC坐标;(3)已知M是抛物线对称轴上一点,在平面内是否存在点N,使以B的四边形是矩形?若存在,直接写出N点坐标;若不存在,请说明理由.类型四、正方形存在性问题例.如图,在平面直角坐标系xOy 中,直线4y x =+与x 轴交于点A ,与y 轴交于点B ,抛物线2y x bx c =-++经过,A B 两点,P 是位于对称轴左侧的抛物线上的一个动点.(1)求抛物线的对称轴方程;(2)若点P 满足PAB PBA ∠=∠,求点P 的坐标;(3)设M 是抛物线的对称轴上一点,N 是坐标平面内一点,若四边形AMPN 是正方形,求此正方形的面积.【变式训练1】如图,二次函数223y x x =-++的图象与x 轴交于A ,B 两点(点A 在点B 左侧),与y 轴交于点C .连接BC .点P 是抛物线第一象限内的一个动点,设点P 的横坐标为m ,过点P 作直线PD x ⊥轴于点D .交BC 于点E .过点P 作BC 的平行线,交y 轴于点M .(1)求A ,B ,C 三点的坐标,并直接写出直线BC 的函数表达式;(2)在点P 的运动过程中,求使四边形CEPM 为菱形时,m 的值;(3)点N 为平面内任意一点,在(2)的条件下,直线PM 上是否存在点Q 使得以P ,E ,Q ,N 为顶点的四边形是正方形?若存在,请直接写出点Q 的坐标;若不存在,请说明理由.(1)求抛物线的解析式;(2)点E 在第一象限内,过点E 作EF y ∥轴,交BC 于点F ,作EH 点H 在点E 的左侧,以线段,EF EH 为邻边作矩形EFGH ,当矩形求线段EH 的长;(3)点M 在直线AC 上,点N 在平面内,当四边形OENM 是正方形时,请直接写出点标.课后训练1.如图1,抛物线()230y ax bx a =+-≠与x 轴交于()1,0A -,()3,0B ,与y 轴交于点C .(1)求抛物线的解析式;(2)如图2,点P 、Q 为直线BC 下方抛物线上的两点,点Q 的横坐标比点P 的横坐标大1,过点P 作PM y ∥轴交BC 于点M ,过点Q 作QN y ∥轴交BC 于点N ,求PM QN +的最大值及此时点Q 的坐标;(3)如图3,将抛物线()230y ax bx a =+-≠先向右平移1个单位长度,再向下平移1个单位长度得到新的抛物线y ',在y '的对称轴上有一点D ,坐标平面内有一点E ,使得以点B 、C 、D 、E 为顶点的四边形是矩形,请直接写出所有满足条件的点E 的坐标.(1)求该抛物线的函数表达式;(2)点D 为直线y x =上的动点,当点P 在第四象限时,求四边形PBDC 点P 的坐标;(3)已知点E 为x 轴上一动点,点Q 为平面内任意一点,是否存在以点P 的四边形是以PC 为对角线的正方形,若存在,请直接写出点Q 的坐标,若不存在,请说明理由.3.如图,抛物线212y x bx c =++与x 轴交于()4,0A ,()1,0B -两点,直线物线交于A 、D 两点,与y 轴交于点E .(1)求出抛物线与直线的解析式;(2)已知点K 为线段AD 上一动点,过点K 作y 轴的平行线交抛物线于点求AHD 的最大面积;(3)若点M 是x 轴上的一动点,点N 是抛物线上一动点,当以点E 、B 的四边形是平行四边形时,请你直接写出符合条件的点N 的坐标.4.在平面直角坐标系中,抛物线2y ax bx c =++(0a ≠)经过点(1,0)-,(3,0)和()0,3.(1)求抛物线的表达式;(2)若直线x m =与x 轴交于点N ,在第一象限内与抛物线交于点M ,当AN MN +有最大值时,求出抛物线上点M 的坐标;。
2022年中考数学复习之二次函数压轴题40个问题

中考复习之二次函数压轴40个问题主要题型:1.二次函数之面积问题2.二次函数之特殊三角形的存在性问题3.二次函数之特殊四边形的存在性问题4.二次函数之线段最值问题5.二次函数之角度问题题目:如图,抛物线与x轴交于A、B两点,与y轴交于点C,OB=OC=3,OA=1,顶点为D第1问.如图,抛物线与x轴交于A、B两点,与y轴交于点C,OB=OC=3,OA=1,顶点为D.求二次函数的解析式;解:设:设二次函数解为y=a(x+1)(x-3)将(0,3)代入得a=-1,故二次函数解析式为y=-x2+2x +3第2问.如图,抛物线与x轴交于A、B两点,与y轴交于点C,OB=OC=3,OA=1.顶点为D1.判断∆BCD的形状;解:D(1,4),B(3,0),C(0,3),方法一:BC=32,CD=2,BD=25,BC2+CD2=BD2,故∆BCD是直角三角形;方法二:KCD =1,KBC=-1,KCD∙KBC=-1,故CD⊥CB,所以∆BCD是直角三角形;yxBCAODyxBCAODyxBCAODyxBCAOD第3问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于点C,OB=OC=3,OA=1.顶点为D, 2. 四边形ABDC 的面积解:BC:y =-x +3,铅垂法:E(1,2)DE=2,S BCD ∆=21∙2∙3=3 S ABDC 四=21∙4∙3+3=9第4问:如图,抛物线与x 轴交于A 、B 两点,与y 交于点C,OB=OC=3,OA=1,顶点为D, 1. P 为直线BC 上方抛物线上一点,求∆PBC 面积最大值及P 点坐标;解:方法一:设P(m,-m+2m+3)S PBC ∆=21∙3∙[-m 2+2m+3-(m+3)] =23(-m 2+3m),当m=23时,S 有最大值,此时P(23,415)S m ax =827 方法二:平移BC 至抛物线相切时,面积可取最大值设切线为y =-x +n,与抛物线y =-x 2+2x+3联立得x2-3x +n -3=0,∆=0,n=23,y =415,故P(23,415)S m ax =827y xBCAODy xBCAODEy xBCAOD第5问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D5点M 为BC 上方抛物线上一点,过点M 作y 轴的平行线交BC 于点N,求MN 的最大值;解:设点M(m,-m 2+2m+3),BC:y =-x +3,则点N(m,-m+3)MN=-m 2+2m+3-(-m+3)=-m 2+3m 当m=23时,MN m ax =49第6问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于点C,OC=3,OA=1,顶点为D, 6. 在对称轴上找一点P,使∆ACP 的周长最小,并求出最小值解:点A 、B 关于对称轴对称,连接BP,则BP=AP,PA+PC=PB+PC,当点B 、P 、C 三点共线时,可取最小值,此时P(1,2),∆ACP 周长的最小值为10+32第7问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于点C,OB=OC=3,OA=1,顶点为D 1. 在y 轴上找一点E,使∆BDE 为直角三角形,求出E 点坐标, 方法一:y xBCAOPDy xBCAODy xNBCAODMy xBCAOD P1.DE ⊥BE 时,设E(0,m)易知∆DEF~∆EBO,OE DF =BO EF ,即m 1=34m-,m=3或1,故E 1(0,1)、E 2(0,3)2. DE ⊥DB 时,设E(0,m)易知∆DEN~∆BDM,BM DN =DM EN ,即m 1=34m -,m=27故E ;(0,27)3. DB ⊥BE 时,设E(0,m),易知∆DBF~∆BEG,BG DF =EG BF ,即m -2=34,m=-23,故E 4(0,-23)第8问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1. 在y 轴上找一点F,使∆BDF 为等腰三角形,求出F 点坐标;2. BD=DF,设F(0,m),22)4()01(m -+-=25,m=4+9 或4-19,F 1(0,4+19);F 2(0,4-19)yxFBCAODExyN MBCAODExy GFEBCAODxy BCAODF2.BD=BF,设F(0,m),22)0()03(m -+-=25,m=±11,F 1(0,11),F 2(0,-11)3.DF=BF,设F(0,m),22)0()03(m -+-=22)4()01(m -+-,m=1,F 4(0,1)第9问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于点C,OB=OC=3,OA=1,顶点为D 1. 求抛物线上一点N,使S ABN ∆=S ABC ∆;解:设N 点的坐标(m,n),则∆ABC 与∆ABN 底相同,故n=±3,-m 2+2m+3=3或者-m 2+2m+3=3得m 1=0,m 2=2,m 3=1-7,m 4=1+7,N(0,3),(2,3),(1-7,-3),(1+7,-3)第10问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于点C,OB=OC=3,OA=1,顶点为D, 1. 在抛物线上找一点Q,使S BDQ ∆=S AOC ∆解:设Q(m,-m 2+2m+3),S AOC ∆=23,BD :y =-2x +6,铅垂高QS=|-m 2+2m+3-(-2m+6)| S BDQ ∆=|-m 2+2m+3-(-2m+6)|∙21∙1=23得m=0或4Q(0,3),(4,-5),xBCAODFBCAOD FBCAODFBCAODN第11问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.在抛物线上找一点E,使BE 平分∆ABC 的面积; 解:BE 平分∆ABC 的面积,故BE 经过AC 的中点,AC 中点(-21,23),BE:y =-73x +79; 与抛物线联立得-x 2+2x +3=-73+79x =-74或722,E(-74;4919)或(722;491849)第12问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA =1,顶点为D 1.在对称轴上找一点M,使|MB -MC|取最大值,并求出最大值;解:点B 关于对称轴对称的点A,连接MA,则MB=MA,MA -MC<AC, 当点A 、C 、M 共线时,|MB -MA|m ax =AC=10, AC:y =3x x +3,M(1,6)第13问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.M 、N 为对称轴上的两点(M 在N 点上方),且MN=1,求四边形ACNM 周长的最小值; 解:A 关于对称轴对称的点B,连接BN,则BN=AN,将点向下平移1个单位得C’、N,则C’N=CM, 故CM+BN=C’N+BN,当C’、N 、B 共线时,取最小值(CM+BN)m in =13,故ACNM 周长得最小值为1+10+13BCAODQABCODEABCODM第14问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.E 在抛物线对称轴上,在抛物线上找一点F,使得点四边形ACFE 为平行四边形; 解:设E(1,m)F(n,-n 2+2n+3),A(-1,0),C(0,3),A 平行至点C 与E 平移至点F, n=1+1=2,m+3=-n 2+2n+3,m=0,故E(1,0)F(2,3)第15问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.M 为y 轴上一点,在坐标平面内找一点N,使A 、C 、M 、N 为顶点的四边形为菱形; 解:当 ACM 为等腰三角形时,问题转化为等腰三角形问题 1.ACNM 为菱形时,M(0,3),N(1,0),2.AMCN 为菱形时,M(0,34),N(-1,35),3.ACMN 为菱形时,M(0,3+10),N(-1,10)ABCODMNABCODM NC'ABCODEFABCODMN ABCONDM4.ACMN 为菱形时,M(0,3-10),N(-1,-10)第16问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.E 为x 轴上一点,以BE 为边的正方形BEFG ; 另一点G 在抛物线上,求点F 坐标;设E(m,0)则EF=|-m 2+2m+3|由EF=EB 得3-m=|-m 2+2m+3|,m=0或m=-2故F(0,3)或F(-2,-5)第17问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.P 是抛物线上任意一点,过点P 作PE ⊥y 轴于点E,交直线BC 于点G ;过点G 作GF ⊥x 轴,连接EF,求EF 的最小值;连接OG,则OG=EF,当OG ⊥BC 时,OG 最小,即EF 最小,故EF m in =233x C,OB=OC=3,OA=1,顶点为D1.M 在抛物线上CB 上方一点过点M 作y 轴的平行线,交BC 于点E,则ME 的最大值是多少? 解:设M(m,-m 2+2m+3),BC :y =-x +3,E(m,3-m),ME=-m 2+2m+3-(3-m)=-m 2+3m,当m=23ABCONDMABCNODMGCABO EFF CABOE GFEGCABOPFEGCABOP时,ME m ax =49第19问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.求一点P,使∠POC=∠PCO ; 解:点P 在OC 得垂直平分线上,-x2+2x +3=23,x =1±210P 1(1-210,23)P 2(1+210,23)第20问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D1.E(2,-2),M 为x 轴上一点,且∠EMO=∠CMO ; 1.M 在右侧时,易知∆CMO~∆EMG,设M(m,0)则有2-m m =23,m=6 2.M 在左侧时,同理易知∆CMO~∆EMG ,m m --2=23,m=6(舍) 第21问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.P 是直线y =x 上的动点,当直接y =x 平分∠APB 时,求点P 的坐标; 如图,∆PAO ≅∆PEO,此时OE=OA=1,故E(0,-1),EB :y =31x -1,与y =x 得x =-23,P(-23,-23) ECABOMPPCABOCABOEMG第22问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.点P 在抛物线上,且∠ABP=∠CBD,求P 坐标;解:C(0,3)D(1,4)B(3,0)tan ∠CBD=31,故tan ∠PBO=31,OE=1或者OF=1,PB :y =-31x +1或y 且=31x -1,联立可得P 1(-32,911)P 2(-23,-23)第23问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D1.在抛物线上找一点P,使∠ACP=450;方法1:∠OCB=∠ACP=450,得∠ACO=∠ECB,故tan ∠ECB=31,作EH ⊥BC,设BH=m,则EH=m;CH=3m,故4m=32,m=423,E(23,0)故CE:y =-2x +3,联立得P(4,-5) 方法2:由12345模型得tan ∠ECO=21得E(23,0)第24问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.P 在抛物线上,∠DBP=450; 由tan ∠CBD=31,∠CBD+∠CBP=450,而∠PBO+∠CBP=450,故tan ∠PBO=31,BP:y =-31x +1,P(-32,911) ECABOPPEFCABODPPHECABOPDP第25问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.点P 在抛物线上,∠PCB=150,求点P 的坐标;解:由∠BCO=450得∠PCO=30或∠PCO=600,故PC:y =-3x +3或y =-33x +3联立得P(2+3,-23)P(2+33,3328-)第26问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D1.直线y =31x -1与y 轴交于点E,求∠EBC -∠CBD ; 由tan ∠DBC=tan ∠EBO=31,故∠EBC -∠CBD=450第27问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.过点P(3,0)作直线与抛物线交于F 、G 、FM 、GN 分别垂直于x 轴,求PM,PN ;设F(1x ,1y )G(2x ,2y ),直线y =k (x +3)与抛物线y =-2x +2x +3联立得2x +(k -2)x +3k -3=0;1x +2x =2-k ,1x •2x =3k -3,PM •PN=(1x +3)(2x +3)=1x •2x +3(1x +2x )+9=12CABOPDPPF CABODPEECABODENMGFCABOPD第28问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为DP 是第一象限抛物线上,PE ⊥AB,求BEAE的值,若PE 2=AE •BE,求P 点坐标 设P(m,-m 2+2m+3),AE=m+1,BE=3-m,BE AE =mm -+31,(m+1)(3-m)=(-m 2+2m+3)2得m=1+3,P(1+3,1)第29问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D M 为直线y =33x 3上的点,N(0,-1),求23BM+MN 的最小值, 过点B 作I ⊥x 轴,MH ⊥I,∠MBH=600,MH=23BM,23BM+MN=MH+MN,当N 、M 、H 共线且垂直于I 时取最值(23BM+MN)min=3第30问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D M 为直线y =33x 3上的点,求21BM+OM 的最小值 过点B 作I:y =3x -33,MH ⊥I,∠MBH=300,MH=21BH,21BH+OM=MH+OM,当Q 、M 、H共线且垂直于I 时取最值(21BM+MN )min=233xy EBCAOPxy BCA O MN H第31问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D M 为直线y =33x 3上的点,求22BM+OM 的最小值 过点B 作I,I 与直线MN 夹角450,MH ⊥I,∠MBH=450,MH=22BM,22BM+OM=MH+OM,当Q 、M 、H 共线且垂直于I 时取最值两着色三角形相似,得cos150=426,(21BM +MN)min=423-63第32问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D在AB 上是否存在点M,使CM+21BM 取最小值. 过点B 作I,I 与x 轴夹角为300,MH=21BM,21BM+CM=MH+CM,当C 、M 、H 共线且垂直于I 时取最值(21BM+CM)min=2333+第33问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为Dxy BCAMO Hxy BCAMOHxy BCAO M EHM 是抛物线上一点,作MH ⊥x 轴,交BC 于点E,当ME:EH=3:2时,求M 点的横坐标, 设M(m,-m 2+2m+3),则E(m,3-m),ME=-m 2+2m+3-(3-m),EH=3-m,ME:EH=3:2 即有-m 2+2m+3-(3-m)=23(3-m) m=23第34问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于顶点为D P 是抛物线上一点,且∠PAB=2CBD,求P 点坐标. tan ∠CBD=31,tan ∠PAB=tan2∠CBD=43(12345模型) 设P(m,-m 2+2m+3)(1)tan ∠PAB=1322+++-m m m =43,m=49,P(49,1639)(2)tan ∠PAB=1322+--m m m =43,m=415,P(415,1657)第35问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为DF(1,415)直线y =417,(1)证明:M 上任意一点到直线y =417距离等于到F 点的距离, M(m,-m 2+2m+3),MH=417-(-m 2+2m+3)=m 2-2m+45MF=222)41532()1(-++-+-m m m =m 2-2m+45,故MH=MF xyEBCAOMHxy BCAODPP第36问:如图,抛物线与x 轴交于、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为DF(1,415)直线y =417,(2)证明:N(2,-1)M 为抛物线上一点,求NM+MF 的最小值 由(1)可知MF=MH,故NM+MF=MN+MH,(NM+MF)min=421第37问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D ∠BAC 的角平分线交y 轴于点M,绕点M 作直线I,与x 轴交于点E,与A 交于点F,求证:AE 1+AF 1为定值 过点M 、F 、C 作x 轴的平行线,交AC 于点G,交AM 于点H 、I ,易知:∆AEM~∆HFM,∆AFH~∆ACI,AO GM =AC CG ,CI GM =AC AG ,相加得AO GM +CI GM =AC CG +ACAG=1 即有AO 1+AC 1=GM 1,同理可得AE 1+AF 1=GM1=1+1010第38问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D P 为第四象限抛物线上一点,且tan ∠APC=21,求出点P 的坐标; 过点C 作CE ⊥AC,取一点E 使CE=2AC,过点C 作MN||x 轴,作A M ⊥MN 、EN ⊥MN,易知∆ACM~∆CEN,CN=6,EN=2,E(6,1),P 为以AE 为直径的圆与抛物线的交点AE 的中点F,F(25,21) xy BCOFMHxy BCNOFMHA过点易知AE HF AFACGM AO =CG AC ,GM CI =AGAC,GM AO +GM CI =CG AC +AGAC =1即有1AO +1AC =1GM,同1AE +1AF =1GM =11010xy H G FEMBCOIPF=225,设P(m,-m 2+2m+3),PF 2=(m -25)2+(-m 2+2m+325)2=225m=255,y =2531--,P(255,2531--)第39问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 直线y =x -3与抛物线交于点P,在x 轴正半轴上找一点E,使tan(∠PBO+∠PEO)=25 在x 轴上找一点F,使tan ∠HPF=25,∠HPF=450+∠BPH=∠PBO+∠PEO=450+∠PEO, 故∠BPF=∠PEO,故∆BEP~∆BPF,BP BE =BF BP ,即253-m =21525,m -3=320,m=329故E(329,0)第40问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 对称轴与BC 交于点E,在直线BC 上找一点P,使∆ABP 与∆DEB 相似,∠BED=1350=∠ABP,故P 在CB 的延长线上,DE=2,BE=22,AB=3,1.当∆EDB~∆BAP,AB DE =BP EB ,即42=BP22,BP=42,P(7,-4) 2.∆EDB~∆BPA 时,BP=22,P(5,-2)AxyN MPFEBCOAH PE FAxyIHEBCODP 1P 2。
中考数学解答题压轴题突破 重难点突破七 二次函数综合题 类型四:二次函数与特殊四边形问题

Ⅰ)如答图①,连接AC,分别过点A,B作对边的平行线交于 点F. 在▱ ACBF中,∵C(0,-5)向右平移1个单位长度,再向上平 移5个单位长度得到A(1,0), ∴B(5,0)按照相同的平移方式得到F(6,5);
解:设点Q的坐标为(a,b),过点Q作QM∥x轴,过点B作BM∥y轴,交QM 于点M,过点F作FN∥y轴交QM于点N,过点E作EK∥x轴交BM于点K, ∴△BMQ≌△QNF≌△EKB, ∴NF=KB=MQ=|a+2|,QN=EK=BM=|b|, ∴点F的坐标为 (a-b,a+b+2), 点E的坐标为 (-2-b,a+2),
Ⅱ)如答图②,分别过点A,C作BC,AB的平行线交于点 F,在▱ ABCF中,∵B(5,0)向左平移5个单位长度,再向 下平移5个单位长度得到C(0,-5), ∴A(1,0)按照相同的平移方式得到F(-4,-5);
Ⅲ)如答图③,连接AC,分别过点B,C作对边的平行线交 于点F.在▱ ACFB中,∵A(1,0)向左平移1个单位长度,再 向下平移5个单位长度得到C(0,-5), ∴B(5,0)按照相同的平移方式得到F(4,-5); 综上所述,满足条件的点F分别为(6,5),(-4,-5)或 (4,-5).
(1)求抛物线的函数解析式; (2)把抛物线 y=x2+bx+c 平移,使得新抛物线的顶点 为点 P(2,-4).M 是新抛物线上一点,N 是新抛物线对 称轴上一点,直接写出所有使得以点 A,B,M,N 为顶点 的四边形是平行四边形的点 M 的坐标,并把求其中一个 点 M 的坐标的过程写出来.
解:(1)该抛物线的函数解析式为y=x2-72x-1. (2)满足条件的点M的坐标为 (2,-4),(6,12),(-2,12). 由题意可知,平移后抛物线的函数解析式为 y=x2-4x, 对称轴为直线x=2,如答图.
二次函数中考压轴题四边形的存在性问题解析
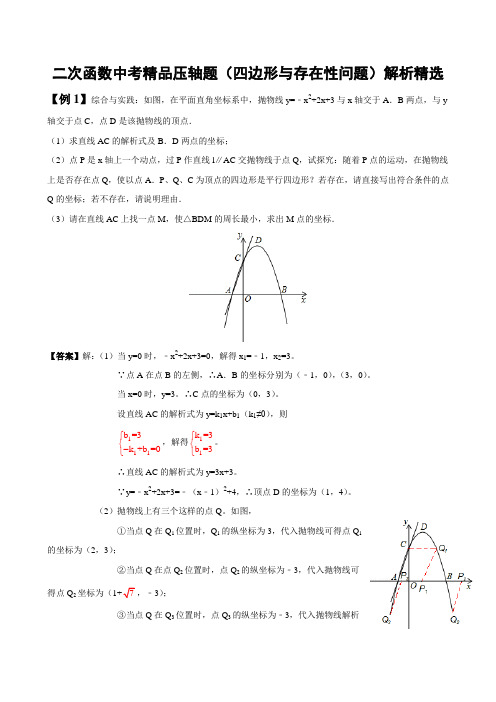
二次函数中考精品压轴题(四边形与存在性问题)解析精选【例1】综合与实践:如图,在平面直角坐标系中,抛物线y=﹣x 2+2x+3与x 轴交于A .B 两点,与y 轴交于点C ,点D 是该抛物线的顶点.(1)求直线AC 的解析式及B .D 两点的坐标;(2)点P 是x 轴上一个动点,过P 作直线l ∥AC 交抛物线于点Q ,试探究:随着P 点的运动,在抛物线上是否存在点Q ,使以点A .P 、Q 、C 为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q 的坐标;若不存在,请说明理由.(3)请在直线AC 上找一点M ,使△BDM 的周长最小,求出M 点的坐标.【答案】解:(1)当y=0时,﹣x 2+2x+3=0,解得x 1=﹣1,x 2=3。
∵点A 在点B 的左侧,∴A .B 的坐标分别为(﹣1,0),(3,0)。
当x=0时,y=3。
∴C 点的坐标为(0,3)。
设直线AC 的解析式为y=k 1x+b 1(k 1≠0),则111b =3k +b =0⎧⎨-⎩,解得11k =3b =3⎧⎨⎩。
∴直线AC 的解析式为y=3x+3。
∵y=﹣x 2+2x+3=﹣(x ﹣1)2+4,∴顶点D 的坐标为(1,4)。
(2)抛物线上有三个这样的点Q 。
如图,①当点Q 在Q 1位置时,Q 1的纵坐标为3,代入抛物线可得点Q 1的坐标为(2,3);②当点Q 在点Q 2位置时,点Q 2的纵坐标为﹣3,代入抛物线可得点Q 2坐标为(1+7,﹣3);③当点Q 在Q 3位置时,点Q 3的纵坐标为﹣3,代入抛物线解析式可得,点Q 3的坐标为(1﹣7,﹣3)。
综上可得满足题意的点Q 有三个,分别为:Q 1(2,3),Q 2(1+7,﹣3),Q 3(1﹣7,﹣3)。
(3)点B 作BB′⊥AC 于点F ,使B′F=BF ,则B′为点B 关于直线AC 的对称点.连接B′D 交直线AC 与点M ,则点M 为所求。
过点B′作B′E ⊥x 轴于点E 。
中考数学专题-四边形存在性问题解析

中考数学专题四边形存在性问题解析1.如图,在平面直角坐标系中,直角梯形OABC的边OC、OA分别与x轴、y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,BC=122,点C的坐标为(-18,0)。
(1)求点B的坐标;(2)若直线DE交梯形对角线BO于点D,交y轴于点E,且OE=4,OD=2BD,求直线DE的解析式;(3)若点P是(2)中直线DE上的一个动点,在坐标平面内是否存在点Q,使以O、E、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由。
2.如图,四边形ABCD为矩形,C点在x轴上,A点在y轴上,D点坐标是(0,0),B点坐标是(3,4),矩形ABCD沿直线EF折叠,点A落在BC边上的G处,E、F分别在AD、AB上,且F点的坐标是(2,4).(1)求G点坐标;(2)求直线EF解析式;(3)点N在x轴上,直线EF上是否存在点M,使以M、N、F、G为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.3.如图,在平面直角坐标系中,已知Rt△AOB的两条直角边0A、08分别在y轴和x轴上,并且OA、OB的长分别是方程x2—7x+12=0的两根(OA<0B),动点P从点A开始在线段AO上以每秒l个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.(1)求A、B两点的坐标。
(2)求当t为何值时,△APQ与△AOB相似,并直接写出此时点Q的坐标.(3)当t=2时,在坐标平面内,是否存在点M,使以A、P、Q、M为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.4.如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.(1)求AD的长及抛物线的解析式;(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似?(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.5.已知二次函数y=x 2﹣(m 2﹣2)x ﹣2m 的图象与x 轴交于点A (x 1,0)和点B (x 2,0),x 1<x 2,与y 轴交于点C ,且满足12111+=x x 2. (1)求这个二次函数的解析式;(2)探究:在直线y=x+3上是否存在一点P ,使四边形PACB为平行四边形?如果有,求出点P 的坐标;如果没有,请说明理由.6.已知抛物线y=41x 2 + 1(如图所示). (1)填空:抛物线的顶点坐标是(______,______),对称轴是_____;(2)已知y 轴上一点A(0,2),点P 在抛物线上,过点P 作PB ⊥x 轴,垂足为B .若△PAB 是等边三角 形,求点P 的坐标;(3)在(2)的条件下,点M 在直线..AP 上.在平面内是否存在点N ,使四边形OAMN 为菱形?若存在,直接写出所有..满足条件的点N 的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系中,O 为原点,平行四边形ABCD 的边BC 在x 轴上,D 点在y 轴上,C点坐标为(2,0),BC=6,60BCD ∠=︒,点E 是AB 边上一点,AE=3EB ,⊙P 过D 、O 、C 三点,抛物线2y ax bx c =++过点D 、B 、C 三点。
中考数学“特殊四边形的存在性问题”题型解析

中考数学“特殊四边形的存在性问题”题型解析由抛物线上的点构成特殊四边形的问题,需要根据特殊四边形的性质与判定去确定点的坐标,然后求解 . 具体而言,解该类题时,我们要根据题目中的条件,科学地进行分类,然后画出图形,再根据这个四边形的性质或判定求出这点的坐标,若这一点是根据特殊四边形的特性得到的坐标,我们还应将这一点代入到抛物线的解析式中去验证是否是抛物线上的点 .本节主要来讨论下特殊四边形:平行四边形、菱形、矩形的存在性问题 .类型一:平行四边形问题【例题1】如图,抛物线y = 1/2 x^2 + bx + c 经过点A(-1,0)和点B(3,0),同时交y 轴于点C .(1)求抛物线的解析式;(2)若点Q 在y 轴上,点P 在抛物线上,且以A , B , Q , P 为顶点的四边形是平行四边形,求满足条件的点P 的坐标 .【分析】(1)根据抛物线经过A , B 两点即可求得b , c 的值,可解题;(2)以A , B , Q , P 为顶点的四边形是平行四边形,则点P 横坐标为4 或- 4,将x = 4 或- 4 代入抛物线解析式即可求得y 的值,即可解题 .【解析】(1)把A(-1,0),B(3,0)代入y = 1/2 x^2 + bx + c 中,∴抛物线的解析式是y = 1/2 x^2 - x - 3/2 .(2)①当AB 为边时,只要PQ∥AB 且PQ = AB = 4 即可 .又知点Q 在y 轴上,∴点P 的横坐标为4 或- 4 ,这时符合条件的点P 有两个,分别记为P1 , P2,把x = 4 代入y = 1/2 x^2 - x - 3/2 ,得y = 5/2 ,把x = - 4 代入y = 1/2 x^2 - x - 3/2 ,得y = 21/2 ,此时P1(4 , 5/2),P2(- 4 , 21/2);②当AB 为对角线时,只要线段PQ 与线段AB 互相平分即可 .又知点Q 在y 轴上,且线段AB 中点的横坐标为1,∴点P 的横坐标为2,这时符合条件的P 只有一个记为P3 ,而且当x = 2 时,y = - 3/2 ,此时P3(2,- 3/2),综上,满足条件的P 为P1(4 , 5/2),P2(- 4 , 21/2),P3(2,-3/2).类型二:菱形问题【例题2】如图,在平面直角坐标系中,点O 为坐标原点,直线y = -x + b 与坐标轴交于C,D 两点,直线AB 与坐标轴交于A , B 两点,线段OA , OC 的长是方程x^2 - 3x + 2 = 0 的两个根(OA > OC).(1)求点A , C 的坐标;(2)直线AB 与直线CD 交于点E,若点E 是线段AB 的中点,反比例函数y = k/x (k ≠0 )的图象的一个分支经过点E,求k 的值;(3)在(2)的条件下,点M 在直线CD 上,坐标平面内是否存在点N,使以点B , E , M , N 为顶点的四边形是菱形?若存在,请直接写出满足条件的点N 的坐标;若不存在,请说明理由 .【分析】(1)利用分解因式法解一元二次方程x^2 - 3x + 2 = 0 即可得出OA , OC 的值,再根据点所在的位置即可得出A , C 的坐标;(2)根据点C 的坐标利用待定系数法即可求出直线CD 的解析式,根据点A , B 的横坐标结合点E 为线段AB 的中点即可得出点E 的横坐标,将其代入直线CD 的解析式中即可求出点E 的坐标,再利用待定系数法即可求出k 的值;(3)假设存在,设点M 的坐标为(m , - m + 1), 分别以BE 为边、BE 为对角线来考虑 .根据菱形的性质找出关于m 的方程,解方程即可得出点M 的坐标,再结合点B , E 的坐标即可得出点N 的坐标 .【解析】(1)x^2 - 3x + 2 = (x - 1)(x - 2)= 0 ,∴x1 = 1 , x2 = 2 ,∵OA > OC ,∴OA = 2 , OC = 1 ,∴A(-2,0),C(1,0);(2)将C(1,0)代入y = - x + b 中,得0 = - 1 + b , 解得b = 1 ,∴直线CD 的解析式为y = - x + 1 .∵点E 为线段AB 的中点,A(-2,0),B 的横坐标为0 ,∴点E 的横坐标为- 1 .∵点E 为直线CD 上一点,∴E(-1,2).将点E(-1,2)代入y = k/x (k ≠0 )中,得2 = k / -1 , 解得k = -2 ;(3)假设存在,设点M 的坐标为(m , - m + 1),以点B , E , M , N 为顶点的四边形是菱形分两种情况(如上图所示)类型三:矩形问题【例题3】【解题策略】这三道例题分别呈现了运动变化过程中的平行四边形、菱形、矩形的存在性问题,三道例题的思路都是要依据特殊四边形的性质构图并建立方程求点的坐标 .特别地,由于菱形任意三个顶点组成的三角形都是等腰三角形,因此可将菱形问题转化为等腰三角形的存在性问题;而矩形问题则可转化为直角三角形的问题,要注意体会相关知识之间的联系 .。
2020年中考数学压轴题专题之抛物线上的特殊平行四边形问题探究

抛物线上的特殊平行四边形问题探究专题导入导图:给出两点确定平行四边形关系如下图:导例如图1,在平面直角坐标系中,已知抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.(1)求抛物线的解析式;(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△MAB的面积为S,求S关于m的函数关系式,并求出S的最大值;(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.图1 图2思路点拨1.求抛物线的解析式,设交点式比较简便.2.把△MAB分割为共底MD的两个三角形,高的和为定值O A.3.当PQ与OB平行且相等时,以点P、Q、B、O为顶点的四边形是平行四边形,按照P、Q 的上下位置关系,分两种情况列方程.答案:(1) 因为抛物线与x轴交于A(-4,0)、C(2,0)两点,设y=a(x+4)(x-2).代入点B(0,-4),求得12a =.所以抛物线的解析式为211(4)(2)422y x x x x =+-=+-. (2)如图2,直线AB 的解析式为y =-x -4.过点M 作x 轴的垂线交AB 于D ,那么2211(4)(4)222MD m m m m m =---+-=--.所以2142MDA MDB S S S MD OA m m ∆∆=+=⋅=--2(2)4m =-++.因此当2m =-时,S 取得最大值,最大值为4.(3) 如果以点P 、Q 、B 、O 为顶点的四边形是平行四边形,那么PQ //OB ,PQ =OB =4. 设点Q 的坐标为(,)x x -,点P 的坐标为21(,4)2x x x +-. ①当点P 在点Q 上方时,21(4)()42x x x +---=.解得225x =-±.此时点Q 的坐标为(225,225)-+-(如图3),或(225,225)--+(如图4). ②当点Q 在点P 上方时,21()(4)42x x x --+-=.解得4x =-或0x =(与点O 重合,舍去).此时点Q 的坐标为(-4,4) (如图5).图3 图4 图5典例类型一:已知“两点”判断平行四边形存在性问题例1、如图,在平面直角坐标系中,抛物线y =x 2+mx +n 经过点A (3,0)、B (0,﹣3),点P 是直线AB 上的动点,过点P 作x 轴的垂线交抛物线于点M ,设点P 的横坐标为t . (1)分别求出直线AB 和这条抛物线的解析式.(2)若点P 在第四象限,连接AM 、BM ,当线段PM 最长时,求△ABM 的面积.(3)是否存在这样的点P ,使得以点P 、M 、B 、O 为顶点的四边形为平行四边形?若存在,请直接写出点P 的横坐标;若不存在,请说明理由.【分析】:(1)分别利用待定系数法求两函数的解析式:把A(3,0)B(0,﹣3)分别代入y=x2+mx+n 与y=kx+b,得到关于m、n的两个方程组,解方程组即可;(2)设点P的坐标是(t,t﹣3),则M(t,t2﹣2t﹣3),用P点的纵坐标减去M的纵坐标得到PM 的长,即PM=(t﹣3)﹣(t2﹣2t﹣3)=﹣t2+3t,然后根据二次函数的最值得到当t=﹣=32时,PM最长为=94,再利用三角形的面积公式利用S△ABM=S△BPM+S△APM计算即可;(3)由PM∥OB,根据平行四边形的判定得到当PM=OB时,点P、M、B、O为顶点的四边形为平行四边形,然后讨论:当P在第四象限:PM=OB=3,PM最长时只有,所以不可能;当P在第一象限:PM=OB=3,(t2﹣2t﹣3)﹣(t﹣3)=3;当P在第三象限:PM=OB=3,t2﹣3t=3,分别解一元二次方程即可得到满足条件的t的值.类型二:菱形的存在性问题例2 如图2所示,直线y=x+c与x轴交于点A(-4,0),与y轴交于点C,抛物线y=-x2+bx+c 经过点A,C.(1)求抛物线的解析式;(2)点E在抛物线的对称轴上,求CE+OE的最小值;(3)如图2所示,点M是线段OA上的一个动点,过点M作垂直于x轴的直线与直线AC和抛物线分别交于点P,N.若点P恰好是线段MN的中点,点F是直线AC上一个动点,在坐标平面内是否存在点D,使以点D,F,P,M为顶点的四边形是菱形?若存在,请直接写出点D的坐标;若不存在,请说明理由.注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣,)【分析】(1)把已知点坐标代入解析式;(2)取点C关于抛物线的对称轴直线l的对称点C′,由两点之间线段最短,最小值可得;(3)①由已知,注意相似三角形的分类讨论.②设出M坐标,求点P坐标.注意菱形是由等腰三角形以底边所在直线为对称轴对称得到的.本题即为研究△CPN为等腰三角形的情况.类型三:正方形的存在性问题例3如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.(1)求该抛物线的解析式;(2)P 是抛物线上一动点(不与点A 、B 重合),①如图2,若点P 在直线AB 上方,连接OP 交AB 于点D ,求的最大值;②如图3,若点P 在x 轴的上方,连接PC ,以PC 为边作正方形CPEF ,随着点P 的运动,正方形的大小、位置也随之改变.当顶点E 或F 恰好落在y 轴上,直接写出对应的点P 的坐标.【分析】(1)利用直线解析式求出点A 、B 的坐标,再利用待定系数法求二次函数解析式解答; (2)作PF ∥BO 交AB 于点F ,证△PFD ∽△OBD ,得比例线段,则PF 取最大值时,求得的最大值;(3)(i )点F 在y 轴上时,P 在第一象限或第二象限,如图2,3,过点P 作PH ⊥x 轴于H ,根据正方形的性质可证明△CPH ≌△FCO ,根据全等三角形对应边相等可得PH =CO =2,然后利用二次函数解析式求解即可;(ii )点E 在y 轴上时,过点PK ⊥x 轴于K ,作PS ⊥y 轴于S ,同理可证得△EPS ≌△CPK ,可得PS =PK ,则P 点的横纵坐标互为相反数,可求出P 点坐标;点E 在y 轴上时,过点PM ⊥x 轴于M ,作PN ⊥y 轴于N ,同理可证得△PEN ≌△PCM ,可得PN =PM ,则P 点的横纵坐标相等,可求出P 点坐标.由此即可解决问题. 专题突破1、如图,抛物线2y x bx c =-++与直线122y x =+交于,C D 两点,其中点C 在y 轴上,点D 的坐标为7(3,)2。
专题08 二次函数中特殊四边形存在性问题的四种考法(解析版)-2024年常考压轴题攻略(9上人教版)

专题08二次函数中特殊四边形存在性问题的四种考法类型一、平行四边形存在性问题(1)求抛物线的表达式;(2)如图1,连接BC ,PB ,PC ,设PBC 的面积为①求S 关于t 的函数表达式;②求P 点到直线BC 的距离的最大值,并求出此时点(3)如图2,设抛物线的对称轴为l ,l 与x 轴的交点为边形CDPM 是平行四边形?若存在,直接写出点【答案】(1)22y x=-(2)①23922S t t =-+;②点P 到直线BC 的距离的最大值为(3)存在,()1,6M 【分析】(1)待定系数法求解析式即可求解;(2)①在图1中,过点P 作PF y ∥轴,交BC 于点P 的坐标为()2,23t t t -++,则点F 的坐标为(t 2139222S PF OB t t =⋅=-+;②根据二次函数的性质得出当32t =时,S 取最大值,最大值为面积法求得点P 到直线BC 的距离,进而得出P (3)如图2,连接PC ,交抛物线对称轴l 于点设直线BC 的解析式为将()3,0B 、()0,3C 代入30,3m n n +=⎧⎨=⎩,解得:∴直线BC 的解析式为∵点P 的坐标为(,t t -∴点F 的坐标为(,t -∴(223PF t t =-++-∴1322S PF OB =⋅=-②12S PF OB =⋅=-∵302-<,∴当32t =时,S 取最大值,最大值为抛物线2y x bx =-++∴抛物线的对称轴为直线 1D C x x -=,∴1P M x x -=,∴2P x =,()2,3P ∴,在223y x x =-++中,当()0,3C ∴,∴3C D y y -=,∴3M P y y -=,∴6M y =,∴点M 的坐标为()1,6;当2P x ¹时,不存在,理由如下,若四边形CDPM 是平行四边形,则 点C 的横坐标为0,点∴点P 的横坐标12t =⨯又 2P x ¹,(1)求点C 的坐标;(2)点P 为直线AC 下方抛物线上一点,过点此时点P 的坐标;(3)抛物线顶点为M ,在平面内是否存在点若存在请求出N 点坐标并在备用图中画出图形;若不存在,请说明理由.【答案】(1)()4,5C (2)315,24P ⎛⎫- ⎪⎝⎭(3)存在,点N 的坐标为:()154N -,,【详解】(1)解:在2=23y x x --中,令解得:11x =-,23x =,()()1,0,3,0A B ∴-,直线y x m =+经过点()1,0A -,∴01m =-+,解得:1m =,∴直线AC 的解析式为1y x =+,联立方程组,得2123y x y x x =+⎧⎨=--⎩,解得:1110x y =-⎧⎨=⎩,2245x y =⎧⎨=⎩()4,5C ∴;(2)如图1,设点2(,23)P n n n --,则点∴2212334()PE n n n n n =+---=-++ 10-<,∴当32n =时,PE 取得最大值254,此时,(3) 2223(1)4y x x x =--=--,∴抛物线顶点为()14M -,,如图2,点,,,A B M N 为顶点的四边形是平行四边形时,设①BM 为对角线时,AN 的中点与BM ∴(1)3122m +-+=,04022n +-+=,解得:∴()154N -,,②AM 为对角线时,BN 的中点与AM ∴31122m +-+=,04022n +-+=,解得:(1)求此拋物线的解析式;(2)在抛物线的对称轴上有一点P ,使得PA PC +值最小,求最小值;(3)点M 为x 轴上一动点,在拋物线上是否存在一点N ,使以边形为平行四边形?若存在,直接写出点N 的坐标;若不存在,请说明理由.【答案】(1)215222y x x =--(2)552(3)54,2⎛⎫- ⎪⎝⎭,5214,2⎛⎫+ ⎪⎝⎭,5214,2⎛⎫- ⎪⎝⎭【分析】(1)把()1,0A -,()5,0B 两点代入求出a 、b 的值即可;(2)因为点A 关于对称轴对称的点B 的坐标为()5,0,连接BC 点坐标即可;(3)分点N 在x 轴下方或上方两种情况进行讨论.拋物线的解析式为212y x =-∴其对称轴为直线2b x a =-=-当0x =时,52y =-,50,2C ⎛⎫∴- ⎪⎝⎭,又()5,0B ,∴设BC 的解析式为(y kx b =+5052k b b +=⎧⎪∴⎨=-⎪⎩,解得:12k =,52b =-,∴BC 的解析式为1522y x =-,当2x =时,1532222y =⨯-=-,①当点N 在x 轴下方时,抛物线的对称轴为2x =,0,C ⎛- ⎝154,2N ⎛⎫∴- ⎪⎝⎭,②当点N 在x 轴上方时,如图,过点在2AN D △和2M CO △中,22N AD AN N DA ∠⎧⎪⎨⎪∠⎩252N D OC ∴==,即2N 点的纵坐标为21552222x x ∴--=,解得:2x =+25214,2N ⎛⎫∴+ ⎪⎝⎭,35214,2N ⎛⎫- ⎪⎝⎭综上所述符合条件的N 的坐标有⎛ ⎝【点睛】本题考查的是二次函数综合题,式、平行四边的判定与性质、全等三角形等知识,两点间距离的求解,在解答(意进行分类讨论.(1)求抛物线的解析式:(2)在抛物线的对称轴上是否存在点P ,使PCD 是以CD 为腰的等腰三角形?如果存在,求出点P 的坐标;如果不存在,请说明理由;(3)点E 在x 轴上运动,点F 在抛物线上运动,当以点B ,C ,E ,F 为顶点的四边形是平行四边形,直接写出点E 的坐标.【答案】(1)213222y x x =-++(2)存在,3,42⎛⎫ ⎪⎝⎭或35,22⎛⎫ ⎪⎝⎭或35,22⎛⎫- ⎪⎝⎭(3)541,02⎛⎫-+ ⎪ ⎪⎝⎭或541,02⎛⎫-- ⎪ ⎪⎝⎭或(7,0)或(1,0)【分析】(1)用待定系数法即可求解;(2)分两种情况:以C 为顶点,即CP CD =;以D 为顶点,即CD =等腰三角形的定义建立方程即可完成;(3)分三种情况:当BC 是对角线时;当BE 是对角线时;当BF 是对角线时;分别设点与F 的坐标,利用中点坐标公式即可求解.【详解】(1)解:∵点B 的坐标是(40),,点C 的坐标是(02),,∴16602a c c ++=⎧⎨=⎩,解得:122a c ⎧=-⎪⎨⎪=⎩,∴所求抛物线解析式为213222y x x =-++;(2)解:存在(1)求抛物线的表达式;(2)若点E 在第一象限内对称右侧的抛物线上,四边形ODEB 的面积为(3)在(2)的条件下,若点F 是对称轴上一点,点H 是坐标平面内一点,在对称轴右侧的抛物线上是否存在点G ,使以E ,F ,G ,H 为顶点的四边形是菱形,且存在,请直接写出点G 的坐标;如果不存在,请说明理由.【答案】(1)232333y x x =-++(2)()2,33E 2039⎫⎪⎭或532,339⎛⎫⎪⎝⎭)根据待定系数法求解即可;∵232333y x x =-++()23143x =--+,∴()1,43D .令232333y x x =-++中0y =,则解得=1x -或3x =,抛物线的对称轴与x轴交于点M,过点∵四边形EFGH 是菱形,EFG ∠∴EF FG GH EG ===,∵60EFG ∠=︒,∴EFG 是等边三角形.∴60FEG EF FG ∠=︒=,,∵()2,33E ,()0,33C ,(1,4D ∴2CE CD ==,()24333-+同理可证: EFG 是等边三角形,∵CF FE =,=GE FE ,∴DG ∴CDG CEG ∆∆≌.∴DCG ∠=∴直线CG 的表达式为:33y =与抛物线表达式联立得33y y ⎧=⎪⎨⎪=-(1)求抛物线的表达式;(2)若点D 是直线AC 上方拋物线上一动点,连接BC ,AD ADM △的面积为1S ,BCM 的面积为2S ,当121S S -=时,求点(3)如图2,若点P 是抛物线上一动点,过点P 作PQ x ⊥轴交直线上是否存在点E ,使以P ,Q ,E ,C 为顶点的四边形是菱形,若存在,请直接写出点坐标;若不存在,请说明理由【答案】(1)223y x x =-++(2)271,22⎛⎫+ ⎪ ⎪⎝⎭或271,22⎛⎫- ⎪ ⎪⎝⎭.(3)符合条件的点E 有三个,坐标为:()0,1E ,(10,132E -【分析】(1)把点()30A ,和()10B -,代入解析式求解即可;(2)由121S S -=得121S S =+从而121ABM ABM S S S S +=++ 程求解即可;(3)分类当CQ 为对角线和菱形边时,利用直线AC 与x 轴成标的方程,进而求出点的坐标.【详解】(1)把点()3,0A 和()1,0B -代入得:93330a b a b ++=⎧⎨-+=⎩解得:12a b =-⎧⎨=⎩,∴抛物线的解析式为223y x x =-++;(2)设(),D x y ,对于抛物线223y x x =-++,令0x =,则()0,3C ∴.121S S -= ,121S S ∴=+.∵()30A ,,()0,3C ,∴3OA OB ==,45OCA ∴∠=︒,此时四边形CEQP 是正方形.PQ EQ ∴=.设()2,23P m m m -++,则23PQ m m =-+,23m m m ∴-+=,解得m =此时32OE OC m =-=-=②当CQ 为菱形的边时,如图设()2,23P m m m -++,则∴HQ m =,2PQ m =-+作QH OC ⊥于点H ,45OCA ∠︒= ,∴22CQ HQ m ==.∴23CE PQ m m ==-+=解得:132m =-,23m =()323213OE =+-=+()10,132E ∴-,(20,1E +综上所述,符合条件的点【点睛】本题考查待定系数法求函数的解析式,二次函数的性质,二次函数与几何综合,数形结合是解题的关键.【变式训练2】如图1,在平面直角坐标系中,点(点A 在点B 左侧),与(1)求ABC 的面积;(3)解:∵抛物线212y x x =--∴()211942212y x x x =--+=-2++∵将抛物线2142y x x =--+沿着水平方向向右平移∴新抛物线为:()112y x =--2+∴原抛物线与新抛物线的交点,∴()()1111992222x x -=--22+++,∴解得:0x =,【点睛】本题考查了二次函数的图象及性质,二次函数与特殊图形,二次函数的平移规律,掌握二次函数与特殊图形的位置关系是解题的关键.类型三、矩形存在性问题(1)求抛物线的解析式;(2)如图,点P 是抛物线上位于直线直线AC 于点D ,交x 轴于点E ,(3)在抛物线上是否存在点M ,对于平面内任意点一条边的四边形为矩形,若存在,请直接写出【答案】(1)2142y x x =--(2)335,28P ⎛⎫- ⎪⎝⎭;254(3)()4,8M -、()8,4N -【分析】(1)把点()4,0A 和点B a 、b 的值;(2)先用待定系数法求出直线2211,422D t t t t ⎛⎫--- ⎪⎝⎭,然后求出最大值时t 的值,即可求出点P (3)假设抛物线上是存在点M ,一条边的四边形为矩形,过点O 点A 且与OH 平行的直线解析式,经计算验证可得过点立方程可求得M 的坐标,通过平移即可求得点【详解】(1)解:把点()4,0A 和点∵()4,0A ,()0,4C -,∴OAC 为等腰直角三角形,∴点H 为AC 的中点,即(H 则OH 所在的直线方程为y =∵四边形AMNC 为矩形,∴过A 与直线AC 相垂直的直线函数解析式中的∴设AM 所在的直线解析式为∵点A 在直线AM 上,(1)求点A 、B 、C 的坐标;(2)将抛物线L 向右平移1个单位,得到新抛物线对称轴l 上是否存在点D ,使得以点D 的坐标;若不存在,请说明理由.【答案】(1)()1,0A -,()3,0B (2)存在,点D 的坐标为()2,1或【分析】(1)分别令0y =和x (2)先求得平移后的抛物线L 角线时,根据矩形的性质求解即可.【详解】(1)解:令0y =,则解得11x =-,23x =,当AD 为对角线时,连接AC ,过点 ()1,0A -,()0,1C -,∴1OA OC ==,∴45OCA ∠=︒∴45OCG ∠=︒∴1OG OC ==,∴()1,0G .设CG 所在直线解析式为y kx =+将()0,1C -,()1,0G 代入得,⎧⎨⎩解得11k b =⎧⎨=-⎩,∴CG 所在直线解析式为1y x =-当2x =时,1211y x =-=-=.∴()2,1D .当AD 为边时,同理过点A 作AC 易得AH 所在直线解析式为y =当AC 为对角线时,DE 也为对角线,∴此种情况不存在.(1)求抛物线的表达式;(2)若点P 为第一象限内抛物线上的一点,设PBC 的面积为S ,求S 坐标;(3)已知M 是抛物线对称轴上一点,在平面内是否存在点N ,使以B 的四边形是矩形?若存在,直接写出N 点坐标;若不存在,请说明理由.【答案】(1)22+3y x x =-+(2)S 最大值为278,315(,)24P (3)存在,点1(2,(317))2N +或1(2,(317))2-或(2,1)-或(4,1).【分析】(1)运用抛物线交点式解析式求解,设抛物线(1)(y a x x =+解;(2)如图,过点P 作PD AC ⊥,垂足为点D ,交BC 于点E ,设(,P m 的解析式3y x =-+,于是23PE m m =-+,从而13(22S PE OC m ==- 时,S 最大值为278,进而求得315(,)24P ;设2(,23)P m m m -++设直线BC 的解析式为y kx =033k hh =+⎧⎨=⎩,解得13k h =-⎧⎨=⎩∴3y x =-+则点(,3)E m m -+,2PE m =-∴2113(22S PE OC m ==´-+ ∴当32m =时,S 最大值为2782915233344m m -++=-++=∴315(,)24P ;(3)存在.设(1,)M p ,如图,223BC =222(13)(0)CM p p =-+-=如图,当BM 为对角线时,∠222BM CM BC =+,即26p p -+01330n p q +=+⎧⎨+=+⎩解得21n q =-⎧⎨=⎩∴点(2,1)N -如图,当CM 为对角线时,MBC ∠222BM BC CM +=,即26p p -+(1)求抛物线的对称轴方程;(2)若点P 满足PAB PBA ∠=∠,求点P 的坐标;(3)设M 是抛物线的对称轴上一点,N 是坐标平面内一点,正方形的面积.【答案】(1)32x =-(2)()51,51P --+(3)正方形AMPN 的面积为172或372【分析】(1)由4y x =+可知()4,0A -,()0,4B ,进而求得抛物线解析式为即可得抛物线的对称轴方程;(2)由题意可知PAB PBA ∠=∠,可知PA PB =,进而值OP 其与AB 交于点Q ,可得()2,2Q -,可求得OP 的解析式为则90PDM ACM ∠=∠=︒∴DPM PMD PMD ∠+∠=∠∴(AAS PDM MCA △≌△∴PD MC =,MD AC =,∵()4,0A -,3,02C ⎛⎫- ⎪⎝⎭,∴35422MD AC ==-=,则90PEM ACM ∠=∠=︒∴EPM PME PME ∠+∠=∠∴(AAS PEM MCA △≌△∴PE MC =,ME AC =,∵()4,0A -,3,02C ⎛⎫- ⎪⎝⎭,∴35422ME AC ==-=,则P y CE MC ME ==+=即:32P x m =-,P y m =-(1)求A ,B ,C 三点的坐标,并直接写出直线(2)在点P 的运动过程中,求使四边形(3)点N 为平面内任意一点,在(2N 为顶点的四边形是正方形?若存在,请直接写出点【答案】(1)()1,0A -,()3,0B ,C (2)32m =-(3)()1221,2Q +,2252,2Q ⎛+ ⎝【分析】(1)分别令0y =,0x =,可求出点∵()3,0B ,()0,3C ,∴3OB OC ==,∴BOC 是等腰直角三角形,∴点()221,2Q +,∴()22132322EQ =+--=-∴PE EQ =,此时点()221,2Q +使得以P ,E 如图,过点E 作EQ PM ⊥于点Q ,过点由(2)得:45BED ∠=︒,∵PM BC ∥,∴45BED DPQ ∠=∠=︒,∴PEQ ,PSQ 是等腰直角三角形,∴此时点Q 使得以P ,E ,Q ,N 为顶点的四边形是正方形;∴132222PS SE PE -===,∴点5232,12S ⎛⎫-- ⎪ ⎪⎝⎭,对于321y x =-++,当5212y =-时,222x =+,(1)求抛物线的解析式;(2)点E 在第一象限内,过点E 作EF y ∥轴,交BC 于点F ,作EH 点H 在点E 的左侧,以线段,EF EH 为邻边作矩形EFGH ,当矩形求线段EH 的长;(3)点M 在直线AC 上,点N 在平面内,当四边形OENM 是正方形时,请直接写出点标.【答案】(1)抛物线的解析式为2142y x x =-++;(2)4EH =;(3)点N 的坐标为()44,或7322⎛⎫- ⎪⎝⎭,.【分析】(1)利用待定系数法即可求解;(2)先求得直线BC 的解析式为4y x =-+,设2142x E x x ⎛ ⎝-++,对称性质求得21422H x x x ⎛⎫- ⎪+⎝-+⎭,,推出2122GH EF x -=-+矩形周长公式列一元二次方程计算即可求解;(3)先求得直线AC 的解析式为24y x =+,分别过点M 、E 作90OPE MQO ∠=∠=︒,90OEP ∠=︒∴OEP MOQ ≌△△,∴PE OQ =,PO MQ =,设2142m E m m ⎛⎫ ⎪⎝-++⎭,,∴PE OQ m ==-,12P m O M Q ==-∵点M 在直线AC 上,∴244212m m m -⎛⎫=+ ⎪⎝⎭-,解得m =当4m =时,()04M ,,()40E ,,即点M 与点C 重合,点E 与点B 重合时,四边形当1m =-时,512M ⎛⎫-- ⎪⎝⎭,,512E ⎛- ⎝,点O 向左平移52个单位,再向下平移则点E 向左平移52个单位,再向下平移∴551122N ⎛⎫--- ⎪⎝⎭,,即7322N ⎛⎫- ⎪⎝⎭,.课后训练(1)求抛物线的解析式;(2)如图2,点P 、Q 为直线BC 下方抛物线上的两点,点Q 的横坐标比点过点P 作PM y ∥轴交BC 于点M ,过点Q 作QN y ∥轴交BC 于点N ,求值及此时点Q 的坐标;(3)如图3,将抛物线()230y ax bx a =+-≠先向右平移1个单位长度,再向下平移长度得到新的抛物线y ',在y '的对称轴上有一点D ,坐标平面内有一点E D 、E 为顶点的四边形是矩形,请直接写出所有满足条件的点E 的坐标.【答案】(1)抛物线的解析式为2=23y x x --(2)当1a =时,max ()4PM QN +=,()2,3Q -(3)()1,2E --或()5,2-或3171,2⎛⎫-- ⎪ ⎪⎝⎭或3171,2⎛⎫-+ ⎪ ⎪⎝⎭【分析】(1)直接运用待定系数法即可解答;(2)设()2,23P a a a --,则()21,4Q a a +-,进而得到(),3M a a -,(N 出222422(1)4PM QN a a a +=-++=--+,最后根据二次函数的性质即可解答;(3)分以BC 为矩形一边和对角线两种情况,分别根据等腰直角三角形的性质、平移和矩形的判定定理解答即可.【详解】(1)解:把()1,0A -和()3,0B 代入()230y ax bx a =+-≠,得309330a b a b --=⎧⎨+-=⎩,解得1a =,2b =-∴222422(1)4PM QN a a a +=-++=--+∴当1a =时,max ()4PM QN +=∴()2,3Q -.(3)解:由题意可得:()()()222=1213152x y x x x x --'---=---=-,∴y '的对称轴为2x =∵抛物线()230y ax bx a =+-≠与y 轴交于点C .∴()0,3C -,∵()3,0B ,∴3OC OB ==,45BCO CBO ∠=∠=︒;如图:当BC 为矩形一边时,且点D 在x 轴的下方,过D 作DF y ⊥轴,∵D 在y '的对称轴为2x =,∴2FD =,∴2CF FD ==,325OF =+=,即点()2,5D -,∴点C 向右平移2个单位、向下平移3个单位可得到点D ,则点B 向右平移2个单位、向下平移3个单位可得到()5,3E -;如图:当BC 为矩形一边时,且点D 在x 轴的上方,y '的对称轴为2x =与x 轴交于F ,∵D 在y '的对称轴为2x =,∴2FO =,∴321BF =-=,∵45CBO ∠=︒,即45DBO ∠=︒,∴321BF FD ==-=,即点()2,1D ,∴点B 向左平移1个单位、向上平移1个单位可得到点D ,则点C 向左平移1个单位、向上平移1个单位可得到点()1,2E --;如图:当BC 为矩形对角线时,设∴BC 的中点F 的坐标为32⎛ ⎝∴2322322m d n +⎧=⎪⎪⎨+⎪=⎪⎩,解得:m d =⎧⎨+⎩又∵DE BC =,∴()()22222133d n -+-=+联立173d n d n ⎧-=±⎪⎨+=⎪⎩,解得:∴点E 的坐标为3171,2⎛-- ⎝综上,存在()1,2E --或(5,的四边形是矩形.【点睛】本题主要考查了运用待定系数法求解析式、与几何的综合等知识点,掌握二次函数的性质和矩形的判定定理是解答本题的关键.2.如图,在平面直角坐标系中,抛物线与y 轴交于点C ,点P 为抛物线上的动点.(1)求该抛物线的函数表达式;(2)点D 为直线y x =上的动点,当点P 在第四象限时,求四边形PBDC 面积的最大值及此时点P 的坐标;(3)已知点E 为x 轴上一动点,点Q 为平面内任意一点,是否存在以点P ,C ,E ,Q 为顶点的四边形是以PC 为对角线的正方形,若存在,请直接写出点Q 的坐标,若不存在,请说明理由.【答案】(1)2=23y x x --(2)278,315,24P ⎛⎫- ⎪⎝⎭(3)3333,2⎛⎫+- ⎪ ⎪⎝⎭;3333,2⎛⎫-- ⎪ ⎪⎝⎭;(3,3)-;(3,2)【分析】(1)用待定系数法求函数的解析式即可;(2)作直线BC ,过P 作PH x ⊥轴于点G ,交BC 于点H .设()2,23P m m m --,则(,3)H m m -,23PH m m =-+,则2139()228BPC S t ∆=--+,当32t =时,BPC △的面积最大值为从而求出此时四边形PBDC 面积的最大值,P 点坐标;(3)设()2,23P m m m --,(,0)E n ,分四种情况画出图形,利用正方形性质求解即可.【详解】(1)解:将(1,0)A -,(3,0)B 代入23y ax bx =+-中,得309330a b a b --=⎧⎨+--⎩,解得12a b =⎧⎨=-⎩.∴该抛物线的函数表达式为2=23y x x --.(2)解:作直线BC ,过P 作PH x ⊥轴于点G ,交BC 于点H .设直线BC 的表达式为:y kx =+得303k n n +=⎧⎨=-⎩,解得13k n =⎧⎨=-⎩,3y x ∴=-.设()2,23P m m m --,则(,H m m ∵BPC CPH BPHS S S =+△△△∴1122BPC S PH OG PH BG =⋅+⋅△∴(21322BPC S PH OB m =⨯=-+△∴28323272BPC S m ⎛⎫=-+ ⎪⎝-⎭△,∴当32m =时,BPC △面积的最大值为BC 与直线y x =平行,1122DBC OBC S S OB OC ∴==⋅=△△∴四边形PBDC 面积的最大值为当32m =时,2332322y ⎛⎫-⨯- ⎪⎝⎭=315,24P ⎛⎫∴- ⎪⎝⎭(3)解:设()2,23P m m m --,I.如图,当点E 在原点时,即点∵四边形PECQ 为正方形,∴点3(3,)Q -,II.如解图3-2,当四边形PECQ 作PI x ⊥轴,垂足为I ,作QH ⊥又∵90CEO OCE ∠+∠=︒,∴OCE PEO ∠=∠,∴(ASA)OCE PEI ≅ △∴3CO IE ==,22EO IP m ==-同理可得:3QH CO IE ===,∴3OE OI IE m =+=+,HO IO=∴2323m m m +=--,解得:m ∴3332HO IO +==,∴点)33(3,32Q +-,同理可得:PI OE CH ==,IE QH =∴3OE IE IO m =-=+,∴2233m m m =---,解得:m =∴3332HO IO -+==,∴点3,(Q -IV.如解图3-4,当四边形PECQ 为正方形时,同理可得:PI OE CH ==,EI HQ =∴2323m m m -=--,解得:m =∴2HO IO ==,∴点(3,2)Q ,综上所述:点Q 坐标为3333,2⎛+- ⎝【点睛】此题重点考查二次函数的图象与性质、数解析式、正方形性质、全等三角形的判定与性质、一元二次方程的解法、数形结合与分类讨论数学思想的运用等知识与方法,此题综合性强,难度较大,属于考试压轴题.3.如图,抛物线212y x bx c =++与物线交于A 、D 两点,与y 轴交于点综上所述,341,22N ⎛⎫+ ⎪ ⎪⎝⎭或341,22N ⎛- ⎝【点睛】本题考查了待定系数法求解析式,面积问题,平行四边形的性质,熟练掌握是二次函数的性质解题的关键.4.在平面直角坐标系中,抛物线2y ax =(1)求抛物线的表达式;(2)若直线x m =与x 轴交于点求出抛物线上点M 的坐标;(3)若点P 为抛物线y ax =位长度后,Q 为平移后抛物线上一动点,在(构成平行四边形?若能构成,求出【答案】(1)223y x x =-++(2)315,24⎛⎫ ⎪⎝⎭(3)1(2-,15)4或3(2-,7)4或【分析】(1)利用待定系数法,即可求出抛物线的表达式;(2)由“直线x m =与x 轴交于点的坐标,进而可得出AN 再利用二次函数的性质,即可求出(3)利用平移的性质,可得出平移后抛物线的表达式为点的坐标特征,可求出点点P 的坐标为(1,)m ,点Q 线三种情况考虑,由平行四边形的对角线互相平分,可得出关于得出n 值,再将其代入点【详解】(1)解:将(1,0)-09303a b c a b c c -+=⎧⎪++=⎨⎪=⎩,解得:∴抛物线的表达式为y =-(2) 直线x m =与x 轴交于点∴点M 的坐标为2(,m m -。
专题05 二次函数中特殊平行四边形存在性问题(原卷版)--2023 年中考数学压轴真题汇编

挑战2023年中考数学解答题压轴真题汇编专题05二次函数中特殊平行四边形存在性问题一.平行四边形的存在性1.(2022•重庆)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于点A(4,0),与y轴交于点B(0,3).(1)求抛物线的函数表达式;(2)点P为直线AB上方抛物线上一动点,过点P作PQ⊥x轴于点Q,交AB于点M,求PM+AM的最大值及此时点P的坐标;(3)在(2)的条件下,点P′与点P关于抛物线y=﹣x2+bx+c的对称轴对称.将抛物线y=﹣x2+bx+c向右平移,使新抛物线的对称轴l经过点A.点C在新抛物线上,点D在l上,直接写出所有使得以点A、P′、C、D为顶点的四边形是平行四边形的点D的坐标,并把求其中一个点D的坐标的过程写出来.2.(2022•郴州)已知抛物线y=x2+bx+c与x轴相交于点A(﹣1,0),B(3,0),与y轴相交于点C.(1)求抛物线的表达式;(2)如图1,将直线BC向上平移,得到过原点O的直线MN.点D是直线MN上任意一点.①当点D在抛物线的对称轴l上时,连接CD,与x轴相交于点E,求线段OE的长;②如图2,在抛物线的对称轴l上是否存在点F,使得以B,C,D,F为顶点的四边形是平行四边形?若存在,求出点F与点D的坐标;若不存在,请说明理由.3.(2022•攀枝花)如图,二次函数y=ax2+bx+c的图象与x轴交于O(O为坐标原点),A两点,且二次函数的最小值为﹣1,点M(1,m)是其对称轴上一点,y轴上一点B(0,1).(1)求二次函数的表达式;(2)二次函数在第四象限的图象上有一点P,连结PA,PB,设点P的横坐标为t,△PAB的面积为S,求S与t的函数关系式;(3)在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点N的坐标,若不存在,请说明理由.4.(2022•内蒙古)如图,抛物线y=ax2+x+c经过B(3,0),D(﹣2,﹣)两点,与x轴的另一个交点为A,与y轴相交于点C.(1)求抛物线的解析式和点C的坐标;(2)若点M在直线BC上方的抛物线上运动(与点B,C不重合),求使△MBC面积最大时M点的坐标,并求最大面积;(请在图1中探索)(3)设点Q在y轴上,点P在抛物线上,要使以点A,B,P,Q为顶点的四边形是平行四边形,求所有满足条件的点P的坐标.(请在图2中探索)5.(2022•资阳)已知二次函数图象的顶点坐标为A(1,4),且与x轴交于点B (﹣1,0).(1)求二次函数的表达式;(2)如图,将二次函数图象绕x轴的正半轴上一点P(m,0)旋转180°,此时点A、B的对应点分别为点C、D.①连结AB、BC、CD、DA,当四边形ABCD为矩形时,求m的值;②在①的条件下,若点M是直线x=m上一点,原二次函数图象上是否存在一点Q,使得以点B、C、M、Q为顶点的四边形为平行四边形,若存在,求出点Q的坐标;若不存在,请说明理由.二.矩形的存在性6.(2022•泸州)如图,在平面直角坐标系xOy中,已知抛物线y=ax2+x+c经过A(﹣2,0),B(0,4)两点,直线x=3与x轴交于点C.(1)求a,c的值;(2)经过点O的直线分别与线段AB,直线x=3交于点D,E,且△BDO与△OCE的面积相等,求直线DE的解析式;(3)P是抛物线上位于第一象限的一个动点,在线段OC和直线x=3上是否分别存在点F,G,使B,F,G,P为顶点的四边形是以BF为一边的矩形?若存在,求出点F的坐标;若不存在,请说明理由.8.(2021•齐齐哈尔)综合与探究如图,在平面直角坐标系中,抛物线y=ax2+2x+c(a≠0)与x轴交于点A、B,与y轴交于点C,连接BC,OA=1,对称轴为直线x=2,点D为此抛物线的顶点.(1)求抛物线的解析式;(2)抛物线上C、D两点之间的距离是2;(3)点E是第一象限内抛物线上的动点,连接BE和CE,求△BCE面积的最大值;(4)点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.9.(2022•随州)如图1,平面直角坐标系xOy中,抛物线y=ax2+bx+c(a<0)与x轴分别交于点A和点B(1,0),与y轴交于点C,对称轴为直线x=﹣1,且OA=OC,P为抛物线上一动点.(1)直接写出抛物线的解析式;(2)如图2,连接AC,当点P在直线AC上方时,求四边形P ABC面积的最大值,并求出此时P点的坐标;(3)设M为抛物线对称轴上一动点,当P,M运动时,在坐标轴上是否存在点N,使四边形PMCN为矩形?若存在,直接写出点P及其对应点N的坐标;若不存在,请说明理由.10.(2023•秦都区校级二模)如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0)、B两点(点B在点A的右侧),与y轴交于点C,且OC=3OA,点D为抛物线的对称轴与x轴的交点,连接CD.(1)求抛物线的函数表达式;(2)点F为坐标平面内一点,在第一象限的抛物线上是否存在点E,使得以点C、D、E、F为顶点的四边形是以CD为边的矩形?若存在,请求出符合条件的点E的横坐标;若不存在,请说明理由.7.(2022•元宝区校级二模)如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A、B,与y轴交于点C,连接BC,OA=1,对称轴为直线x=2,点D为此抛物线的顶点.(1)求抛物线的解析式;(2)抛物线上C、D两点之间的距离是11;(3)点E是第一象限内抛物线上的动点,连接BE和CE,求△BCE面积的最大值;(4)点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.8.(2022•鱼峰区模拟)如图,在平面直角坐标系中,抛物线y=x2+bx+c与坐标轴交于A(0,﹣2),B(4,0)两点,直线BC:y=﹣2x+8交y轴于点C.(1)求该抛物线的解析式;(2)在第二象限内是否存在一点M,使得四边形ABCM为矩形?如果存在,求出点M的坐标;如果不存在,请说明理由.三.菱形的存在性9.(2022•朝阳)如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴分别交于点A(1,0)和点B,与y轴交于点C(0,﹣3),连接BC.(1)求抛物线的解析式及点B的坐标.(2)如图,点P为线段BC上的一个动点(点P不与点B,C重合),过点P 作y轴的平行线交抛物线于点Q,求线段PQ长度的最大值.(3)动点P以每秒个单位长度的速度在线段BC上由点C向点B运动,同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动,在平面内是否存在点N,使得以点P,M,B,N为顶点的四边形是菱形?若存在,请直接写出符合条件的点N的坐标;若不存在,请说明理由.10.(2021•湘潭)如图,一次函数y=x﹣图象与坐标轴交于点A、B,二次函数y=x2+bx+c图象过A、B两点.(1)求二次函数解析式;(2)点B关于抛物线对称轴的对称点为点C,点P是对称轴上一动点,在抛物线上是否存在点Q,使得以B、C、P、Q为顶点的四边形是菱形?若存在,求出Q点坐标;若不存在,请说明理由.11.(2021•鄂尔多斯)如图,抛物线y=x2+2x﹣8与x轴交于A,B两点(点A 在点B左侧),与y轴交于点C.(1)求A,B,C三点的坐标;(2)连接AC,直线x=m(﹣4<m<0)与该抛物线交于点E,与AC交于点D,连接OD.当OD⊥AC时,求线段DE的长;(3)点M在y轴上,点N在直线AC上,点P为抛物线对称轴上一点,是否存在点M,使得以C、M、N、P为顶点的四边形是菱形?若存在,请直接写出点M的坐标;若不存在,请说明理由.12.(2021•通辽)如图,抛物线y=ax2+bx+3交x轴于A(3,0),B(﹣1,0)两点,交y轴于点C,动点P在抛物线的对称轴上.(1)求抛物线的解析式;(2)当以P,B,C为顶点的三角形周长最小时,求点P的坐标及△PBC的周长;(3)若点Q是平面直角坐标系内的任意一点,是否存在点Q,使得以A,C,P,Q为顶点的四边形是菱形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.13.(2021•娄底)如图,在直角坐标系中,二次函数y=x2+bx+c的图象与x轴相交于点A(﹣1,0)和点B(3,0),与y轴交于点C.(1)求b、c的值;(2)点P(m,n)为抛物线上的动点,过P作x轴的垂线交直线l:y=x于点Q.①当0<m<3时,求当P点到直线l:y=x的距离最大时m的值;②是否存在m,使得以点O、C、P、Q为顶点的四边形是菱形,若不存在,请说明理由;若存在,请求出m的值.14.(2021•山西)综合与探究如图,抛物线y=x2+2x﹣6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC.(1)求A、B,C三点的坐标并直接写出直线AC,BC的函数表达式.(2)点P是直线AC下方抛物线上的一个动点,过点P作BC的平行线l,交线段AC于点D.①试探究:在直线l上是否存在点E,使得以点D,C,B,E为顶点的四边形为菱形,若存在,求出点E的坐标,若不存在,请说明理由;②设抛物线的对称轴与直线l交于点M,与直线AC交于点N.当S△DMN=S△AOC时,请直接写出DM的长.15.(2020•阜新)如图,二次函数y=x2+bx+c的图象交x轴于点A(﹣3,0),B(1,0),交y轴于点C.点P(m,0)是x轴上的一动点,PM⊥x轴,交直线AC于点M,交抛物线于点N.(1)求这个二次函数的表达式;(2)①若点P仅在线段AO上运动,如图,求线段MN的最大值;②若点P在x轴上运动,则在y轴上是否存在点Q,使以M,N,C,Q为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.。
专题03 特殊平行四边形中的三种几何动点问题(原卷版)-2024年常考压轴题攻略(9年级上册人教版)

专题03特殊平行四边形中的三种几何动点问题类型一、面积问题例.如图,在四边形ABCD 中,AB CD ∥,90BCD ∠= ,10cm AB AD ==,=8cm BC .点P 从点A 出发,以每秒3cm 的速度沿折线ABC 方向运动,点Q 从点D 出发,以每秒2cm 的速度沿线段DC 方向向点C 运动.已知动点P ,Q 同时发,当点Q 运动到点C 时,P ,Q 运动停止,设运动时间为t .(1)直接写出CD 的长(cm );(2)当四边形PBQD 为平行四边形时,直接写出四边形PBQD 的周长(cm );(3)在点P 、点Q 的运动过程中,是否存在某一时刻,使得BPQ V 的面积为215cm ?若存在,请求出所有满足条件的t 的值;若不存在,请说明理由.【变式训练1】如图,在四边形ABCD 中,,90,120,12cm,15cm AD BC A B ADC AD BC ∠=∠=︒∠=︒==∥,点P 自点A 沿折线AD DC -以1cm/s 的速度运动,点Q 自点C 沿向CB BA -以1cm/s 的速度运动.点P ,Q 同时出发,其中一个点到达终点,另一个点也停止运动.设运动时间为(s)t .(1)当P 在AD 边上,点Q 在BC 边上时,如图1.①用含t 的代数式表示:DP =___________,BQ =___________;②若四边形APQB 是平行四边形,求t 的值?(2)求BPQ V 的面积S 与运动时间t 之间的数量关系式,并写出t 的取值范围.【变式训练2】如图,在矩形ABCD 中,AB =12,BC =18,点P 从点A 出发,以每秒2个单位长度的速度沿类型二、几何图形存在性问题长的速度向点A 匀速运动,同时点E 从点A 出发沿AB 方向以每秒1个单位长的速度向点B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D E ,运动的时间是t 秒()0t >.过点D 作DF BC ⊥于点F ,连接DE ,EF .(1)求AB AC ,的长;(2)求证:AE DF =;(3)当t 为何值时,DEF 为直角三角形?请说明理由.例2.如图,已知正方形ABCD 的边长为4cm ,动点P 从点B 出发,以2cm /s 的速度沿B C D →→方向向点D 运动,动点Q 从点A 出发,以1cm /s 的速度沿A B →方向向点B 运动,若P 、Q 两点同时出发运动时间为s t .(1)连接PD 、PQ 、DQ ,求当t 为何值时,PQD △的面积为27cm ?(2)当点P 在BC 上运动时,是否存在这样的t 使得PQD △是以PD 为一腰的等腰三角形?若存在,请求出符合条件的t 的值;若不存在,请说明理由.例3.如图,在四边形ABCD 中,AD ∥BC ,∠B =90°,AB =8cm ,AD =12cm ,BC =18cm ,点P 从点A 出发以1cm/s 的速度向点D 运动;点Q 从点C 同时出发,以2cm/s 的速度向点B 运动,当点Q 到达点B 时,(1)填空:AB =;菱形ABCD 的面积S =;菱形的高h =.(2)若点M 的速度为每秒1个单位,点N 的速度为每秒a 个单位(其中52a <),当4t =时在平面内存在点得以A ,M ,N ,E 为顶点的四边形为菱形,请求出所有满足条件的a 的值.类型三、直线位置关系问题例1.如图,在Rt ABC △中,90ABC ∠=︒,5AC =,4BC =,点D 是边AB 的中点,动点P 从点A 出发(1)直接写出AB的长.(2)当点Q落在AB边上时,用含t的代数式表示(1)分别求BD和BE的长度;(2)连接PQ,当95t=时,判断PQ与AD是否垂直,并说明理由;(3)试判断是否存在t的值,使得以P,Q,C,DC 点以1cm /s 的速度运动,动点Q 从点B 开始沿BA 向A 点以3cm /s 的速度运动,P ,Q 分别从点D ,B 同时出发,当其中一点到达终点时,另一点也随之停止运动,运动的时间为t 秒.(1)t 为何值时,四边形DPQA 为矩形?(2)t 为何值时,四边形PQBC 为平行四边形?2.如图,在ABC 中,6cm AC =,=8cm BC ,点O 以每秒1cm 的速度由点A 向点C 运动(不与点C 重合),过点O 作直线MN BC ∥,BCA ∠的外角平分线CF 于点F ,ACB ∠的平分线CE 于点.E 设运动时间为t 秒.发现:(1)在点O 的运动过程中,OE 与OF 的关系是______,请写出理由.(2)当=2t 时,=EF ______cm .探究:当=t ______时,四边形AECF 是矩形,并证明你的结论.拓展:若点O 在运动过程中,能使四边形AECF 是正方形,试写出线段AB 的长度.(直接写出结论即可)3.已知正方形ABCD 中,8AB BC CD DA ====,90A B C D ∠=∠=∠=∠=︒.动点P 以每秒2个单位速度从点B 出发沿线段BC 方向运动,动点Q 同时以每秒8个单位速度从B 点出发沿正方形的边(1)当运动时间为秒时,点P与点Q相遇;∥时,求线段DQ的长度;(2)当BQ PD全等时,求t的值.(3)连接PA,当PAB和QAD(1)CB的长为______.(2)用含t的代数式表示线段QB的长.(3)连接PQ,=;(1)求证:PE DQ(1)=a______cm,b=______cm;(2)t为何值时,EP把四边形BCDE的周长平分?(1)当2t =时,BP =___________cm ;(2)当t 为何值时,连接,,CP DP CDP △是等腰三角形;(3)Q 为AD 边上的点,且6DQ =,P 与Q 不重合,当t 为何值时,以长方形的两个顶点及点P 为顶点的三角形与DCQ 全等.。
压轴题06二次函数与特殊四边形存在性问题(四大类型)-2023年中考数学压轴题专项训练(全
2023年中考数学压轴题专项训练压轴题06二次函数与特殊四边形存在性问题(四大类型)题型一:二次函数与平行四边形存在性问题例1.(2023•泽州县一模)综合与探究.如图1,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与直线l交于B,C 两点,其中点A的坐标为(﹣2,0),点C的坐标为(﹣1,﹣4).(1)求二次函数的表达式和点B的坐标.(2)若P为直线l上一点,Q为抛物线上一点,当四边形OBPQ为平行四边形时,求点P的坐标.(3)如图2,若抛物线与y轴交于点D,连接AD,BD,在抛物线上是否存在点M,使∠MAB=∠ADB?若存在,请直接写出点M的坐标;若不存在,请说明理由.题型二:二次函数与矩形存在性问题例2.(2023•歙县校级模拟)如图,若二次函数y=ax2+bx+4的图象与x轴交于点A(﹣1,0)、B(4,0),与y轴交于点C,连接BC.(1)求该二次函数的解析式;(2)若点Q是抛物线上一动点,在平面内是否存在点K,使以点B、C、Q、K为顶点,BC为边的四边形是矩形?若存在请求出点K的坐标;若不存在,请说明理由.题型三: 二次函数与菱形存在性问题例3.(2023春•沙坪坝区校级月考)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c经过A(0,1),B (4,﹣1).直线AB交x轴于点C,P是直线AB上方且在对称轴右侧的一个动点,过P作PD⊥AB,垂足为D,E为点P关于抛物线的对称轴的对应点.(1)求抛物线的函数表达式;(2)当√5PD+PE的最大值时,求此时点P的坐标和√5PD+PE的最大值;(3)将抛物线y关于直线x=3作对称后得新抛物线y',新抛物线与原抛物线相交于点F,M是新抛物线对称轴上一点,N是平面中任意一点,是否存在点N,使得以C,F,M,N为顶点的四边形是菱形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.题型四: 二次函数与正方形存在性问题例4.(2023•前郭县一模)如图,在平面直角坐标系中,抛物线y=x2﹣4x+c与y轴相交于点A(0,2).(1)求c的值;(2)点B为y轴上一点,其纵坐标为m(m≠2),连接AB,以AB为边向右作正方形ABCD.①设抛物线的顶点为P,当点P在BC上时,求m的值;②当点C在抛物线上时,求m的值;③当抛物线与正方形ABCD有两个交点时,直接写出m的取值范围.一.解答题(共20小题)1.(2023春•兴化市月考)已知:二次函数y=ax2+2ax﹣8a(a为常数,且a>0)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,顶点为点D.(1)分别求点A、B的坐标;(2)若△ABC是直角三角形,求该二次函数相应的表达式;(3)当a=12时,一次函数y=12x+b的图象过B点,与二次函数的对称轴交于Q点,N为一次函数图象上一点,过N点作y的平行线交二次函数图象于M点,当D、M、N、Q四点组成的四边形是平行四边形时,求N点的坐标.2.(2023春•沙坪坝区校级月考)如图1,在平面直角坐标系中,抛物线y=ax2+bx+8(a≠0)与x轴交于点B(﹣4,0),点C(8,0),与y轴交于点A.点D的坐标为(0,4).(1)求二次函数的解析式及点C的坐标.(2)如图1,点F为该抛物线在第一象限内的一动点,过E作FE∥CD,交CD于点F,求EF+√55DF的最大值及此时点E的坐标.(3)如图2,在(2)的情况下,将原抛物线绕点D旋转180°得到新抛物线y',点N是新抛物线y'上一点,在新抛物线上的对称轴上是否存在一点M,使得点D,E,M,N为顶点的四边形为平行四边形,若存在,请直接写出点M的坐标,并写出其中一个点M的求解过程.3.(2023•武清区校级模拟)在平面直角坐标系中,二次函数y=ax2+bx+3的图象与x轴交于A(﹣4,0),B(2,0)两点,与y轴交于点C.(1)求这个二次函数的解析式;(2)抛物线上是否存在点Q,且满足AB平分∠CAQ,若存在,求出Q点坐标;若不存在,说明理由;(3)点N为x轴上一动点,在抛物线上是否存在点M,使以B,C,M,N为顶点的四边形是平行四边形?若存在,直接写出点M的坐标;若不存在,说明理由.4.(2023春•承德县月考)已知二次函数y=14x2−32x−4与x数轴交于点A、B(A在B的左侧),与y轴交于点C,连接BC.发现:点A的坐标为,求出直线BC的解析式;拓展:如图1,点P是直线BC下方抛物线上一点,连接PB、PC,当△PBC面积最大时,求出P点的坐标;探究:如图2,抛物线顶点为D,抛物线对称轴交BC于点E,M是线段BC上一动点(M不与B、C两点重合),连接PM,设M点的横坐标为m(0<m<8),当m为何值时,四边形PMED为平行四边形?5.(2023春•梅江区校级月考)如图,在平面直角坐标系中,△AOC绕原点O逆时针旋转90°得到△DOB,其中OA=1,OC=3.(1)若二次函数经过A、B、C三点,求该二次函数的解析式;(2)在(1)条件下,在二次函数的对称轴l上是否存在一点P,使得P A+PC最小?若P点存在,求出P点坐标;若P点不存在,请说明理由.(3)在(1)条件下,若E为x轴上一个动点,F为抛物线上的一个动点,使得B、C、E、F构成平行四边形时,求E点坐标.6.(2022秋•云州区期末)综合与探究如图,二次函数y=ax2+bx+4的图象经过x轴上的点A(6,0)和y轴上的点B,且对称轴为直线x=7 2.(1)求二次函数的解析式.(2)点E位于抛物线第四象限内的图象上,以OE,AE为边作平行四边形OEAF,当平行四边形OEAF 为菱形时,求点F的坐标与菱形OEAF的面积.(3)连接AB,在直线AB上是否存在一点P,使得△AOP与△AOB相似,若存在,请直接写出点P坐标,若不存在,请说明理由.7.(2023春•开福区校级月考)【定义】对于函数图象上的任意一点P(x,y),我们把x+y称为该点的“雅和”,把函数图象上所有点的“雅和”的最小值称为该函数的“礼值”.根据定义回答问题:(1)①点P(9,10)的“雅和”为;(直接写出答案)②一次函数y=3x+2(﹣1≤x≤3)的“礼值”为;(直接写出答案)(2)二次函数y=x2﹣bx+c(bc≠0)(3≤x≤5)交x轴于点A,交y轴于点B,点A与点B的“雅和”相等,若此二次函数的“礼值”为1﹣b,求b,c的值;(3)如图所示,二次函数y=x2﹣px+q的图象顶点在“雅和”为0的一次函数的图象上,四边形OABC 是矩形,点B的坐标为(5,﹣3),点O为坐标原点,点C在x轴上,当二次函数y=x2﹣px+q的图象与矩形的边有四个交点时,求p的取值范围.8.(2023春•无锡月考)在平面直角坐标系中,O为坐标原点,二次函数y=ax2﹣2ax﹣3a(a>0)的图象分别与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,过点B作BC的垂线交对称轴于点M,以BM、BC为邻边作矩形BMNC.(1)求A、B的坐标;(2)当点N恰好落在函数图象上时,求二次函数的表达式;(3)作点N关于MC的对称点N',则点N'能否落在函数图象的对称轴上,若能,请求出二次函数的表达式;若不能,请说明理由.9.(2022秋•开福区校级期末)若凸四边形的两条对角线所夹锐角为60°,我们称这样的凸四边形为“美丽四边形”.(1)①在“平行四边形、矩形、菱形、正方形”中,一定不是“美丽四边形”的有;②若矩形ABCD是“美丽四边形”,且AB=1,则BC=;(2)如图1,“美丽四边形”ABCD内接于⊙O,AC与BD相交于点P,且对角线AC,为直径,AP=2,PC=8,求另一条对角线BD的长;(3)如图2,平面直角坐标系中,已知“美丽四边形”ABCD的四个顶点A(﹣2,0),C(1,0),B在第三象限,D在第一象限,AC与BD交于点O,且四边形ABCD的面积为6√3,若二次函数y=ax2+bx+c (a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.10.(2022秋•南关区校级期末)在平面直角坐标系中,二次函数y=x2﹣2x+n(x>0)的图象记为G1,将G1绕坐标原点旋转180°得到图象G2,图象G1和G2合起来记为图象G.(1)若点P(﹣2,3)在图象G上,求n的值.(2)当n=﹣1时.①若O(t,1)在图象G上,求t的值.②当k≤x≤3(k<3)时,图象G对应函数的最大值为2,最小值为﹣2,直接写出k的取值范围.(3)当以A(﹣2,2),B(﹣2,﹣1),C(1,﹣1),D(1,2)为顶点的矩形ABCD的边与图象G有且只有3个公共点时,直接写出n的取值范围.11.(2022•株洲)已知二次函数y=ax2+bx+c(a>0).(1)若a=1,b=3,且该二次函数的图象过点(1,1),求c的值;(2)如图所示,在平面直角坐标系xOy中,该二次函数的图象与x轴相交于不同的两点A(x1,0)、B (x2,0),其中x1<0<x2、|x1|>|x2|,且该二次函数的图象的顶点在矩形ABFE的边EF上,其对称轴与x轴、BE分别交于点M、N,BE与y轴相交于点P,且满足tan∠ABE=3 4.①求关于x的一元二次方程ax2+bx+c=0的根的判别式的值;②若NP=2BP,令T=1a2+165c,求T的最小值.阅读材料:十六世纪的法国数学家弗朗索瓦•韦达发现了一元二次方程的根与系数之间的关系,可表述为“当判别式Δ≥0时,关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根x1、x2有如下关系:x1+x2=−b a,x1x2=ca”.此关系通常被称为“韦达定理”.12.(2023春•南关区月考)已知抛物线y=−12x2+bx+c(b、c是常数)的顶点B坐标为(﹣1,2),抛物线的对称轴为直线l,点A为抛物线与x轴的右交点,作直线AB.点P是抛物线上的任意一点,其横坐标为m,过点P作x轴的垂线交直线AB于点Q,过点P作PN⊥l于点N,以PQ、PN为边作矩形PQMN.(1)b=,c=.(2)当点Q在线段AB上(点Q不与A、B重合)时,求PQ的长度d与m的函数关系式,并直接写出d的最大值.(3)当抛物线被矩形PQMN截得的部分图象的最高点纵坐标与最低点纵坐标的距离为2时,求点P的坐标.13.(2023春•南关区校级月考)在平面直角坐标系中,抛物线y =﹣x 2+bx +c (b 、c 是常数)经过点A (﹣1,0)和点B (3,0).点P 在抛物线上,且点P 的横坐标为m . (1)求b 、c 的值;(2)当△P AB 的面积为8时,求m 的值;(3)当点P 在点A 的右侧时,抛物线在点P 与点A 之间的部分(包含端点)记为图象G ,设G 的最高点与最低点的纵坐标之差为h ,求h 与m 之间的函数关系式;(4)点Q 的横坐标为1﹣3m ,纵坐标为m +1,以PQ 为对角线构造矩形,且矩形的边与坐标轴平行.当抛物线在矩形内部的点的纵坐标y 随x 的增大而增大或y 随x 的增大而减小时,直接写出m 的取值范围.14.(2023•九台区校级一模)在平面直角坐标系中,已知抛物线y =x 2﹣2ax ﹣a (a 为常数). (1)若点(2,﹣1)在抛物线上. ①求抛物线的表达式;②当x 为何值时y 随x 的增大而减小?(2)若x ≤2a ,当抛物线的最低点到x 轴的距离恰好是1时,求a 的值;(3)已知A (﹣1,1)、B(−1,2a −12),连结AB .当抛物线与线段AB 有交点时,该交点为P (点P 不与A 、B 重合),将线段PB 绕点P 顺时针旋转90°得到线段PM ,以PM 、P A 为邻边构造矩形PMQA .当抛物线在矩形PMQA 内部(包含边界)图象所对应的函数的最大值与最小值的差为32时,直接写出a 的值.15.(2023•靖江市校级模拟)如图,在平面直角坐标系中,抛物线y=−12x2+bx+32与x轴正半轴交于点A,且点A的坐标为(3,0),过点A作垂直于x轴的直线l.P是该抛物线上的任意一点,其横坐标为m,过点P作PQ⊥l于点Q,M是直线l上的一点,其纵坐标为﹣m+32,以PQ、QM为边作矩形PQMN.(1)求b的值.(2)当点Q与点M重合时,求m的值.(3)当矩形PQMN是正方形,且抛物线的顶点在该正方形内部时,求m的值.(4)当抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而减小时.直接写出m的取值范围.16.(2022秋•临朐县期末)如图,在平面直角坐标系中,O是坐标原点,菱形OABC的顶点A(3,4),C 在x轴的负半轴,抛物线y=ax2+bx+c的对称轴x=2,且过点O,A.(1)求抛物线y=ax2+bx+c的解析式;(2)若在线段OA上方的抛物线上有一点P,求△P AO面积的最大值,并求出此时P点的坐标;(3)若把抛物线y=ax2+bx+c沿x轴向左平移m个单位长度,使得平移后的抛物线经过菱形OABC的顶点B.直接写出平移后的抛物线解析式.17.(2023•道外区一模)如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2ax+c经过点A (﹣4,0),点C(0,6),与x轴交于另一点B.(1)求抛物线的解析式;(2)点D为第一象限抛物线上一点,连接AD,BD,设点D的横坐标为t,△ABD的面积为S,求S关于t的函数解析式(不要求写出自变量t的取值范围);(3)在(2)的条件下,点P为第四象限抛物线上一点,连接P A交y轴于点E,点F在线段BC上,点G在直线AD上,若tan∠BAD=12,四边形BEFG为菱形,求点P的坐标.18.(2023春•九龙坡区校级月考)如图,在平面直角坐标系中,抛物线y=12x2+bx+c与x轴交于A(﹣1,0),B(4,0),与y轴于点C,连接BC,D为抛物线的顶点.(1)求该抛物线的解析式;(2)点P为直线BC下方抛物线上的一动点,过P作PE⊥BC于点E,过P作PF⊥x轴于点F,交直线BC于点G,求PE+PG的最大值,以及此时点P的坐标;(3)将抛物线y=12x2+bx+c沿射线CB方向平移,平移后的图象经过点H(2,﹣1),点M为D的对应点,平移后的抛物线与y轴交于点N,点Q为平移后的抛物线对称轴上的一点,且点Q在第一象限.在平面直角坐标系中确定点R,使得以点M,N,Q,R为顶点的四边形为菱形,请写出所有符合条件的点R的坐标,并写出求解点R的坐标的其中一种情况的过程.19.(2023•安徽一模)如图,在平面直角坐标系中,抛物线C 1:y =−14x 2+bx +c 的图象与坐标轴交于A 、B 、C 三点,其中点A 的坐标为(0,8),点B 的坐标为(﹣4,0),点D 的坐标为(0,4).(1)求该二次函数的表达式及点C 的坐标;(2)若点F 为该抛物线在第一象限内的一动点,求△FCD 面积的最大值;(3)如图2,将抛物线C 1向右平移2个单位,向下平移5个单位得到抛物线C 2,M 为抛物线C 2上一动点,N 为平面内一动点,问是否存在这样的点M 、N ,使得四边形DMCN 为菱形,若存在,请直接写出点N 的坐标;若不存在,请说明理由.20.(2023•九台区一模)在平面直角坐标系中,抛物线y =x 2+bx +c (b 、c 是常数)经过点(﹣2,﹣1),点(1,2).点A 在抛物线上,且点A 的横坐标为m (m ≠0).以点A 为中心,构造正方形POMN ,PQ =2|m |,且PQ ⊥x 轴.(1)求该抛物线对应的函数表达式;(2)若点B 是抛物线上一点,且在抛物线对称轴右侧.过点B 作x 轴的平行线交抛物线于另一点C ,连接BC .当BC =6时,求点B 的坐标;(3)若m <0,当抛物线在正方形内部的点的纵坐标y 随x 的增大而增大或y 随x 的增大而减小时,求m 的取值范围;(4)当抛物线与正方形PQMN 的边只有2个交点,且交点的纵坐标之差为34时,直接写出m 的值.。
特殊平行四边形动点及存在性问题(压轴题)

特殊平行四边形动点及存在性问题(压轴题)例1】在正方形ABCD中,DM=2,N是AC上的动点,求使得DN+MN最小的N点坐标。
解:由于正方形对称性,不妨设N在AC上且AN=x,则NC=8-x,由勾股定理得DN=sqrt(x^2+4),MN=sqrt((8-x)^2+4),因此DN+MN=sqrt(x^2+4)+sqrt((8-x)^2+4),对XXX求导得到x=2,即N点坐标为(2,6)。
练1】在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点。
1)若E为边OA上的一个动点,求使得△CDE周长最小的E点坐标。
解:由于矩形OACB的对称性,不妨设E在OA上且AE=x,则OE=3-x,CE=4-x,DE=sqrt((3-x)^2+x^2),CD=sqrt((4-x)^2+9),因此△CDE周长为sqrt((3-x)^2+x^2)+sqrt((4-x)^2+9),对其求导得到x=1/2,即E点坐标为(1/2,3/2)。
2)若E、F为边OA上的两个动点,且EF=2,求使得四边形CDEF周长最小的E、F点坐标。
解:同样设AE=x,则EF=2,AF=3-x,OE=3-x/2,OF=2-x/2,CE=4-x,CF=5/2-x/2,DE=sqrt((3-x/2)^2+x^2),DF=sqrt((2-x/2)^2+(5/2-x/2)^2),因此四边形CDEF的周长为sqrt((3-x/2)^2+x^2)+sqrt((2-x/2)^2+(5/2-x/2)^2)+2,对其求导得到x=1/2,即E、F点坐标分别为(1/2,3/2)和(2,1/2)。
例2】在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P 在BC上运动,当三角形△ODP是腰长为5的等腰三角形时,求P点坐标。
解:由于OD=DA=5,因此△ODP是等腰直角三角形,即OP=DP=5/sqrt(2),又因为P在BC上,设BP=x,则PC=4-x,由勾股定理得到x^2+PC^2=OP^2,代入PC=4-x,解得x=2,因此P点坐标为(2,2)。
中考数学专题复习课件:特殊四边形存在性问题

典例精析
例 如图,抛物线y=x2+6x+5与x轴交于A,B 两点(点A在点B的左侧),与y轴交于点C,顶点为 M,对称轴l与x轴交于点D,与直线AC交于点E.
例题图
(1)设点N是抛物线上一点,点S是x轴上一点,是否存在点N,使得以A, E,N,S为顶点的四边形是平行四边形?若存在,求出点N的坐标;若 不存在,请说明理由;
x1 y1
2 3
x2 y2
5 0
例题解图④
∵△AP1Q1是等腰直角三角形,Q1是x轴上一点,∴Q1(1,0);当点P在x轴上
例题解图④
③当∠AQP=90°时,∠QAP=45°,∴点P的情况与②相同,如解图④,过 (1,0)或(5,0)或(-2,0)或(0,0).
例题解图④
针对训练
1.如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),点B(-3,0),且 OB=OC.(1)求抛物线的解析式;
或(-3- ,-2); 6
6
6
6
2
2
∟
NG 例题图
(2)设点G是抛物线的对称轴上一点,K是坐标平面内一点,是否存在点 G,使得A,C,G,K为顶点的四边形是矩形?若存在,求出点G的坐标; 若不存在,请说明理由;
【思维教练】要使以A,C,G,K为顶点的四边 形是矩形,只需△ACG是直角三角形即可,可分 为①∠ACG=90°,②∠CAG=90°,③∠CGA =90°三种情况,分别利用勾股定理列方程即可 求解.
,t4=
∴P3(
9 ,33
4
),9 4 33
P4(-
I
将点I的坐标代入,可得t=-1,∴直线OI的解析式为y=-x,
联立
y
中考数学微专题7 四边形存在性问题

(3)存在.如图 2,分两种情况:点 Q 在 x 轴上方或点 Q 在 x 轴下方. ①当点 Q 在 x 轴上方时,P 与 Q 纵坐标相等, ∴-x2-2x+3=145,
解得:x1=-12,x2=-32(舍去),
∴Q1-12,145, ②当点 Q 在 x 轴下方时,P 与 Q 纵坐标互为相反数,
∴-x2-2x+3=-145,
问题3:如图直角坐标系中有一点B,C为x轴上一点, 坐标平面内是否存在点D,使以A,B,C,D为顶点 的四边形为矩形?
①画出所有可能存在的点C的位置,使用的方法为以O, B,C三点做直角三角形的方法,即两线一圆.
②代数法 以其中一个情况为例,如图, 当我们确定 O,B,C 的位置后,可以以 OC、OB 为邻边做出矩形 OCDB,该四边形可以看作是 以 OC 为对角线的平行四边形,则可以用平行四边形存在性的方法列出两个方程,而由于矩形对 角线相等,再用两点间距离公式加入一个 OC=BD 的方程即可求解 xO+xC=xB+xD,yO+yC=yB+yD, (xO-xC)2+(yO-yC)2= (xD-xB)2+(yD-yB)2.
∴12(-4m-8)(-2-m)=12×6×6, 整理得:m2+4m-5=0,解得:m1=-5,m2=1(舍去), ∴点 D 的坐标为(-5,-1),∴点 M 的坐标为(-2,8), ∴DM= (-2+5)2+(8+1)2=3 10, 答:dm 的长为 3 10.
解法总结
1.平行四边形的存在性问题 类型一:“三定一动”型 问题:如图,已知三点A,B,C,找一点D,使以A,B,C, D为顶点的四边形为平行四边形. 作法:连接AB,AC,BC,分别过点A,B,C作对边的平行 线,三条平行线的交点即为所求点D.我们通常用直尺来代替 线段进行平移,很容易就能判断出是否存在这样的D点. 类型二:“两定两动”型
2014中考压轴题全面突破之五:四边形的存在性

中考数学压轴题全面突破•四边形的存在性
题型特点
四边形的存在性问题是一类考查是否存在点,使其能构成某种特殊四边形的问题,如:平行四边形、菱形、梯形的存在性等,往往结合动点、函数与几何,考查分类讨论、画图及建等式计算等.
解题思路
①寻找定量,结合特殊四边形判定确定分类;
②转化四边形的存在性为点的存在性或三角形的存在性;
③借助几何特征建等式.
难点拆解
①平行四边形存在性,由定线分别作边、对角线分类,通过平移或旋转
画图,借助坐标间关系及中点坐标公式建等式求解.
②菱形存在性可转化为等腰三角形存在性处理.
③等腰梯形存在性通常直接表达两腰长,利用两腰相等建等式;两腰不
易表达,借助对称性和中点坐标公式联立求解.
④直角梯形存在性关键是利用好直角.。
2019甘肃中考数学专题训练特殊四边形存在性问题

探究特殊四边形存在性问题1.如图,抛物线y =x 2-2x -3经过点A (2,-3),与x 轴负半轴交于点B ,与y 轴交于点C ,且OC =3OB .(1)求点B ,C 的坐标;(2)若点D 在y 轴上,且∠BDO =∠BAC ,求点D 的坐标;(3)若点M 为抛物线上一点,点N 在抛物线的对称轴上,是否存在以点A 、B 、M 、N 为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M 的坐标,若不存在,请说明理由.第1题图解:(1)令x =0得y =-3,∴C (0,-3),∴OC =3,∵OC =3OB ,∴OB =1,∴B (-1,0),把A (2,-3),B (-1,0)分别代入y =ax 2+bx -3得:⎩⎪⎨⎪⎧a -b -3=04a +2b -3=-3,解得⎩⎪⎨⎪⎧a =1b =-2, ∴抛物线的解析式为y =x 2-2x -3;(2)如解图①,过点B 作BE ⊥ AC ,交AC 延长线于点E .第1题解图①∵C (0,-3),A (2,-3),∴AC ∥x 轴,∴BE =3,又∵OB=1,∴AE=3,∴AE=BE,∴∠BAE=45°,∵∠BDO=∠BAC=45°,∴OB=OD,∴D点的坐标为(0,1)或(0,-1),(3)存在.如解图②.第2题解图②当AB∥MN时,由AB=MN=32,可知点M与对称轴的距离为3,由y=x2-2x-3可得对称轴为直线x=1,∴点M的横坐标为4或-2,把x=4和-2分别代入y=x2-2x-3可得点M坐标,把x=-2代入y=x2-2x-3得y=4+4-3=5,∴M1(-2,5).把x=4代入y=x2-2x-3得y=16-8-3=5,∴M2(4,5),当MN与AB互相平分时,四边形AMBN是平行四边形,由AC=BN=2,可知点M与点C重合,∴点M3坐标为(0,-3),∴M的坐标为(-2,5)或(0,-3)或(4,5).2.如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.(1)求抛物线的解析式;(2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标;(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E,是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.第2题图解:(1)设抛物线解析式为:y=a(x-1)2+4(a≠0).∵抛物线过点C(0,3),∴a+4=3,∴a=-1.∴y =-(x -1)2+4=-x 2+2x +3;(2)由(1)得,抛物线的解析式为y =-x 2+2x +3,令y =0,解得x 1=-1,x 2=3,∴A (-1,0),B (3,0),∵C (0,3),∴直线BC 的解析式为y =-x +3,∵S △BCP =S △BCQ ,∴点P 、Q 到BC 的距离相等.①当点P 、Q 位于BC 的同侧时,如解图①,过点P 作PQ ∥BC 交抛物线于Q ,又∵P (1,4),∴直线PQ 的解析式为y =-x +5,联立⎩⎪⎨⎪⎧y =-x +5,y =-x 2+2x +3.解得⎩⎪⎨⎪⎧x 1=1y 1=4(舍去),⎩⎪⎨⎪⎧x 2=2y 2=3, ∴Q 1(2,3).第2题解图①②当点P 、Q 位于BC 的异侧时,设抛物线的对称轴交BC 于点G ,交x 轴于点H ,∴G (1,2), ∵此时点P 、H 到BC 的距离相等,∴H (1,0),∴PG =GH =2,如解图①,过点H 作Q 2Q 3∥BC 交抛物线于点Q 2,Q 3.直线Q 2Q 3的解析式为y =-x +1,联立⎩⎪⎨⎪⎧y =-x +1,y =-x 2+2x +3. 解得⎩⎪⎨⎪⎧x 1=3+172y 1=-1-172,⎩⎪⎨⎪⎧x 2=3-172y 2=-1+172, ∴Q 2(3-172,-1+172),Q 3(3+172,-1-172).综上所述,满足条件的点Q 的坐标为(2,3)或(3-172,-1+172)或(3+172,-1-172);第2题解图②(3)存在满足条件的M ,N .如解图②,过点M 作MF ∥y 轴,过点N 作NF ∥x 轴交MF 于点F ,过点N 作NH ∥y 轴交BC 于点H .则△MNF 与△NEH 都是等腰直角三角形.设M (x 1,y 1),N (x 2,y 2),直线MN 的解析式为y =-x +b .∵⎩⎪⎨⎪⎧y =-x +b ,y =-x 2+2x +3, ∴x 2-3x +(b -3)=0.∴NF 2=|x 1-x 2|2=(x 1+x 2)2-4x 1x 2=21-4b .∵△MNF 为等腰直角三角形,∴MN 2=2NF 2=42-8b .∵直线MN 与y 轴交点(0,b )到点C (0,3)的距离为|b -3|,∴NH 2=(b -3)2,∵NE =22NH , ∴NE 2=12(b -3)2. 如果四边形MNED 为正方形,∴NE 2=MN 2, ∴42-8b =12(b 2-6b +9). ∴b 2+10b -75=0,∴b 1=-15,b 2=5.∵正方形边长为MN =42-8b ,∴MN =92或2,∴正方形MNED 的边长为92或 2.。
存在性问题系列: 特殊四边形的存在性问题 2023年九年级数学中考复习

存在性问题系列:特殊四边形的存在性问题 2023九年级数学中考复习1.如图,在平面直角坐标系中,直线8=-+分别交两轴于点A、B,点C的横坐标为4,点D在线段OAy x上,且7AD=.(1)求点D的坐标;(2)求直线CD的解析式;(3)在平面内是否存在这样的点F,使以A、C、D、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,不必说明理由.2.如图,在平面直角坐标系中,函数28=+的图象分别交x轴、y轴于A、B两点,过y x点A的直线交y轴正半轴于点M,且点M为线段OB的中点.(1)求直线AM的函数解析式.(2)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、B、M、H为顶点的四边形是平行四边形?若存在,请直接写出所有点H的坐标;若不存在,请说明理由.3.如图1,已知直线y mx =分别与双曲线8y x =,(0)k y x x =>交于P ,Q 两点,且2OP OQ =, (1)求k 的值;(2)如图2,若A 是双曲线8y x =上的动点,//AB x 轴,//AC y 轴,分别交双曲线(0)k y x x => 于B ,C ,连接BC ,设A 点的横坐标为t .当2m =时,D 为直线2y x =上的一点,若以A , B ,C ,D 为顶点的四边形是平行四边形,求A 点坐标.4.如图,在平面直角坐标系中,直线:4l y =+与y 轴、x 轴分别交于点E 、F ,边长为的等边ABC ∆,边BC 在x 轴上,将此三角形沿着x 轴的正方向平移,在平移过程 中,得到△111A B C ,当点1B 与原点重合时,解答下列问题:(1)求出点1A 的坐标,并判断点1A 是否在直线l 上;(2)求出边11A C 所在直线的解析式;(3)在坐标平面内找一点P ,使得以P 、1A 、1C 、F 为顶点的四边形是平行四边形,请直接写出P 点坐标.5.如图1,直线11:6y +与x 轴,y 轴分别交于B ,A 两点,过点A 做AC AB ⊥交x 轴于点C ,将直线1l 沿着x 轴正方向平移m 个单位得到直线2l 交直线AC 于点D ,交x 轴于点E ,将CDE ∆沿直线2l 翻折得到点F .(1)若m =E ;(2)若BCF ∆的面积等于2l 的解析式;(3)在(1)的条件下,将ABO ∆绕点C 旋转60︒得到△111A B O ,点R 是直线2l 上一点,在直角坐标系中是否存在点S ,使得以点1A 、1B 、R 、S 为顶点的四边形是矩形?若存在,求出点S 的坐标;若不存在,请说明理由.6.如图,平面直角坐标系中,直线483y x=-+分别交x轴、y轴于点B、点A,点D从点A出发沿射线AB方向以每秒1个单位长的速度匀速运动,同时点E从点B出发沿射线BC方向以每秒35个单位长的速度匀速运动.设点D、E运动的时间是t秒(0)t>.过点D作DF AO⊥于点F,连接DE、EF,是否存在这样一个时刻,此时以点D、F、E、B为顶点的四边形是菱形?如果存在,求出相应的t的值;如果不存在,请说明理由.7.如图,直线y kx bb+.=+与x轴,y轴分别交于A,B两点,且经过点(4,3)(1)求k的值;(2)若2=+,AB OB①求b的值;②点M为x轴上一动点,点N为坐标平面内另一点.若以A,B,M,N为顶点的四边形是菱形,请直接写出所有符合条件的点N的坐标.8.如图,在平面直角坐标系xOy内,AOBC的顶点A、O、B、C的坐标分别为(0,1)、(0,0)、(1,0)、(1、1),过点B的直线MN与OC平行,AC的延长线交MN于点D,点P 是直线MN上的一个动点,//CQ OP交MN于点Q.当四边形OPQC为菱形时,①请求出点P的坐标;②请求出POC的度数.9.如图,在平面直角坐标系xOy 中,梯形ABCD 的四个顶点的坐标分别是(1,0)A -、(4,0)B 、(3C ,5)(0D ,5),直线3y x b =-+平分梯形ABCD 的面积,且与线段CD 、AB 交于点E ,F .(1)求b 的值;(2)设点P 是直线EF 上一点,点Q 在第四象限,且以点A 、B 、P 、Q 为顶点的四边形是菱形,请直接写出所有满足条件的点Q 的坐标.。
中考数学:以四边形为载体的几何压轴问题真题+模拟(原卷版北京专用)

中考数学以四边形为载体的几何压轴问题【方法归纳】北京市中考数学倒数第二道压轴题会以四边形为载体的几何压轴题出现,要求学生理解和掌握平行四边形、矩形、菱形、正方形的性质定理和判定定理,会画出四边形全等变换后的图形,并会结合其他知识解答一些有探索性、开放性的问题,提高解决问题的能力.解决此类问题的关键是要牢牢把握四边形的性质与特征,挖掘相关图形之间的联系,利用所给图形及图形之间形状、大小、位置关系,进行观察、实验、比较、联想、类比、分析、综合等.常用到的矩形、菱形、正方形的解题策略有:(1)对于矩形:①判定四边形是矩形,一般先判定是平行四边形,然后再判定是矩形;②矩形的内角是直角和对角线相等,相对于平行四边形来说是矩形特殊的性质;③利用矩形的性质计算或证明时,常常运用勾股定理,锐角三角函数或相似三角形求解.(2)对于菱形:①判定四边形是菱形,一般先判定是平行四边形,然后再判定是菱形;②菱形的邻边相等和对角线垂直,相对于平行四边形来说是菱形特殊的性质;③利用菱形的性质计算或证明时,常常运用勾股定理,锐角三角函数或相似三角形求解;④求线段和的最小值时,往往运用菱形的轴对称的性质转化为求线段的长度.(3)对于正方形:①判定四边形是正方形,一般先判定是平行四边形,然后再判定是矩形或菱形,最后判定这个四边形是正方形;②正方形是最特殊的四边形,在正方形的计算或证明时,要特别注意线段或角的等量转化.【典例剖析】【例1】(2018·北京·中考真题)如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.(1)求证:GF=GC;(2)用等式表示线段BH与AE的数量关系,并证明.【真题再现】1.(2014·北京·中考真题)在正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E,连接BE,DE,其中DE交直线AP于点F.(1)依题意补全图1.(2)若∠PAB=20°,求∠ADF的度数.(3)如图2,若45°<∠PAB<∠90°,用等式表示线段AB,FE,FD之间的数量关系,并证明.2.(2015·北京·中考真题)在正方形ABCD中,BD是一条对角线.点P在射线CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于点H,连接AH、PH.(1)若点P在线CD上,如图1,①依题意补全图1;②判断AH与PH的数量关系与位置关系并加以证明;(2)若点P在线CD的延长线上,且∠AHQ=152°,正方形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果)3.(2013·北京·中考真题)请阅读下列材料:小明遇到这样一个问题:如图1,在边长为a(a>2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现,分别延长QE,MF,NG,PH交F A,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2) .请回答:(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙不重叠),则这个新正方形的边长为_________;(2)求正方形MNPQ的面积;(3)参考小明思考问题的方法,解决问题:如图3,在等边△ABC各边上分别截取AD=BE=CF,,求AD的再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ.若S△RPQ=√33长.4.(2016·北京·中考真题)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.(1)求证:BM=MN;(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.【模拟精练】1.(2022·北京昌平·模拟预测)两张宽度均为4的矩形纸片按如图所示方式放置(1)如图①,求证:四边形ABCD是菱形.(2)如图②,点P在BC上,PF⊥AD于F,若S四边形ABCD=16√2,PB=2,①求∠BAD的度数;②求DF的长.2.(2021·北京四中模拟预测)如图所示,四边形ABCD为菱形,AB=2,∠ABC=60°,点E为边BC上动点(不含端点),点B关于直线AE的对称点为点F,点G为DF中点,连接AG.(1)依题意,补全图形;(2)点E运动过程中,是否可能EF∥AG?若可能,求BE长;若不可能,请说明理由;(3)连接CG,点E运动过程中,直接写出CG的最小值.3.(2021·北京门头沟·一模)在正方形ABCD中,将边AD绕点A逆时针旋转a(0°<a<90°)得到线段AE,AE与CD延长线相交于点F,过B作BG//AF交CF于点G,连接BE.(1)如图1,求证:∠BGC=2∠AEB;(2)当(45°<a<90°)时,依题意补全图2,用等式表示线段AH,EF,DG之间的数量关系,并证明.4.(2020·北京亦庄实验中学二模)如图,在正方形ABCD中,E是边BC上一动点(不与点B,C重合),连接DE,点C关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,过点D作DF AP于F.(1)求∠FDP的度数;(2)连接BP,请用等式表示线段BP与线段AF之间的数量关系,并证明.(3)连接PC,若正方形的边长为√2,直接写出△BCP面积的最大值.5.(2020·北京四中模拟预测)在△ABC中,点D在AB边上(不与点B重合),DE⊥BC,垂足为点E,如果以DE为对角线的正方形上的所有点都在△ABC的内部或边上,则称该正方形为△ABC的内正方形.(1)如图,在△ABC中,AB=4,∠B=30°,点D是AB的中点,画出△ABC的内正方形,直接写出此时内正方形的面积;t,0).(2)在平面直角坐标系xOy中,点A(t,2),B(0,0),C(32①若t=2,求△ABC的内正方形的顶点E的横坐标的取值范围;②若对于任意的点D,△ABC的内正方形总是存在,直接写出t的取值范围.6.(2020·北京延庆·一模)四边形ABCD 中,∠A=∠B= 90°,点E在边AB上,点F在AD的延长线上,且点E与点F关于直线CD对称,过点E作EG∥AF交CD于点G,连接FG,DE.(1)求证:四边形DEGF 是菱形;(2)若AB=10,AF=BC=8,求四边形DEGF 的面积.7.(2019·北京·一模)如图1,正方形ABCD中,AB=5,点E为BC边上一动点,连接AE,以AE为边,在线段AE右侧作正方形AEFG,连接CF、DF.设BE=x.(当点E与点B重合时,x的值为0),DF=y,CF=y2.小明根据学习函数的经验,对函数y1、y2随自变量1x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整:(1)通过取点、画图、测量、观察、计算,得到了x与y1、y2的几组对应值;(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x , y1) , (x , y2),并画出函数y1,y2的图象;(3)结合函数图象2,解决问题:当△CDF为等腰三角形时,BE的长度约为cm.8.(2017·北京顺义·一模)在正方形ABCD和正方形DEFG中,顶点B、D、F在同一直线上,H是BF的中点.(1)如图1,若AB=1,DG=2,求BH的长;(2)如图2,连接AH,GH.小宇观察图2,提出猜想:AH=GH,AH⊥GH.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:想法1:延长AH交EF于点M,连接AG,GM,要证明结论成立只需证△GAM是等腰直角三角形;想法2:连接AC,GE分别交BF于点M,N,要证明结论成立只需证△AMH≌△HNG.…请你参考上面的想法,帮助小宇证明AH=GH,AH⊥GH.(一种方法即可)9.(2018·北京顺义·一模)如图1,在长方形ABCD中,AB=12cm,BC=10cm,点P从A出发,沿A→B→C→D的路线运动,到D停止;点Q从D点出发,沿D→C→B→A路线运动,到A点停止.若P、Q两点同时出发,速度分别为每秒1cm、2cm,a秒时P、Qcm(P、Q两点速度改变后一直保持此速度,直到两点同时改变速度,分别变为每秒2cm、54停止),如图2是ΔAPD的面积s(cm2)和运动时间x(秒)的图象.(1)求出a值;(2)设点P已行的路程为y1(cm),点Q还剩的路程为y2(cm),请分别求出改变速度后,y1,y2和运动时间x(秒)的关系式;(3)求P、Q两点都在BC边上,x为何值时P,Q两点相距3cm?10.(2021·北京四中模拟预测)在平面直角坐标系xOy中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y=x上,那么称该菱形为点A,C的“极好菱形”.如图为点A,C的“极好菱形”的一个示意图.已知点M的坐标为(1,1),点P的坐标为(3,3).(1)点E(2,1),F(1,3),G(4,0)中,能够成为点M,P的“极好菱形”的顶点的是;(2)如果四边形MNPQ是点M,P的“极好菱形”.①当点N的坐标为(3,1)时,求四边形MNPQ的面积;②当四边形MNPQ的面积为8,且与直线y=x+b有公共点时,写出b的取值范围.11.(2021·北京四中九年级开学考试)定义:如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为平面图形的一条面积等分线.(1)如图1,已知△ABC,请用尺规作出△ABC的一条面积等分线.(2)已知:如图2,在平面直角坐标系xOy中,矩形OABC的边OA在x轴的正半轴上、OC在y轴的正半轴上,OA=6,OC=4.①请判断直线y=43x−83是否为矩形OABC的面积等分线,并说明理由;②若矩形OABC的面积等分线与坐标轴所围成的三角形面积为4,请直接写出此面积等分线的函数表达式.(3)如图3,在△ABC中,点A的坐标为(−2,0),点B的坐标为(4,3),点C的坐标为(2,0),点D的坐标(0,−2),求过点D的一条△ABC的面积等分线的解析式.(4)在△ABC中点A的坐标为(−1,0),点B的坐标为(1,0),点C的坐标为(0,1),直线y= ax+b(a>0)是△ABC的一条面积等分线,请直接写出b的取值范围.12.(2021·北京·九年级专题练习)如图,在四边形ABCD中,∠ACB=∠CAD=90°,点E在BC上,AE//DC,EF⊥AB,垂足为F.(1)求证:四边形AECD是平行四边形;(2)若AE平分∠BAC,BE=5,cosB=45,求BF和AD的长.13.(2021·北京·九年级专题练习)如图,在正方形ABCD中,AB=3,M是CD边上一动点(不与D点重合),点D与点E关于AM所在的直线对称,连接AE,ME,延长CB到点F,使得BF=DM,连接EF,AF.(1)依题意补全图1;(2)若DM=1,求线段EF的长;(3)当点M在CD边上运动时,能使△AEF为等腰三角形,直接写出此时tan∠DAM的值.14.(2021·北京石景山·九年级期末)已知矩形MBCD的顶点M是线段AB上一动点,AB=BC,矩形MBCD的对角线交于点O,连接MO,BO.点P为射线OB上一动点(与点B不重合),连接PM,作PN⊥PM交射线CB于点N.(1)如图1,当点M与点A重合时,且点P在线段OB上.①依题意补全图1;②写出线段PM与PN的数量关系并证明.(2)如图2,若∠OMB=α,当点P在OB的延长线上时,请补全图形并直接写出PM与PN的数量关系.15.(2020·北京·北师大实验中学九年级开学考试)如图,在正方形ABCD中,AB=6,M是CD边上一动点(不与D点重合),点D与点E关于AM所在的直线对称,连接AE,ME,延长CB 到点F,使得BF=DM,连接EF,AF.(1)当DM=2时,依题意补全图1;(2)在(1)的条件下,求线段EF的长;(3)当点M在CD边上运动时,能使△AEF为等腰三角形,请直接写出此时DM与AD的数量关系________.16.(2017·全国·九年级专题练习)猜想与证明:如图①摆放矩形纸片ABCD与矩形纸片ECGF,使B,C,G三点在一条直线上,CE在边CD上.连结AF,若M为AF的中点,连结DM,ME,试猜想DM与ME的数量关系,并证明你的结论.拓展与延伸:(1)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为__________________;(2)如图②摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.[提示:直角三角形斜边上的中线等于斜边的一半]①②17.(2020·北京通州·一模)已知线段AB,过点A的射线l⊥AB.在射线l上截取线段AC=AB,连接BC,点M为BC的中点,点P为AB边上一动点,点N为线段BM上一动点.以点P为旋转中心,将△BPN逆时针旋转90°得到△DPE,B的对应点为D,N的对应点为E.(1)当点N与点M重合,且点P不是AB中点时,①据题意在图中补全图形;②证明:以A,M,E,D为顶点的四边形是矩形.(2)连接EM,若AB=4,从下列3个条件中选择1个:①BP=1,②PN=1,③BN=√2,当条件______(填入序号)满足时,一定有EM=EA,并证明这个结论.18.(2020·北京一七一中九年级阶段练习)在四边形ABCD中,∠B+∠D=180°,对角线AC 平分∠BAD.(1)如图1,若∠DAB=120°,且∠B=90°,直接写出线段AD、AB、AC的数量关系.(2)如图2,若将(1)中的条件“∠B=90°”去掉,求边AD、AB与对角线AC的数量关系.请证明.(3)如图3,若∠DAB=2αAD、AB与对角线AC的数量关系(用α来表示)19.(2020·北京四中九年级阶段练习)在菱形ABCD中,∠BAD=60°.(1)如图1,点E为线段AB的中点,连接DE,CE.若AB=4,求线段EC的长.(2)如图2,M为线段AC上一点(不与A,C重合),以AM为边向上构造等边三角形△AMN,线段AN与AD交于点G,连接NC,DM,Q为线段NC的中点.连接DQ,MQ,判断DM与DQ的数量关系,并证明你的结论.(3)在(2)的条件下,若AC=√3,请你直接写出DM+CN的最小值.20.(2020·北京顺义·九年级期末)已知:如图,在正方形ABCD中,点E在AD边上运动,从点A出发向点D运动,到达D点停止运动.作射线CE,并将射线CE绕着点C逆时针旋转45°,旋转后的射线与AB边交于点F,连接EF(1)依题意补全图形;(2)猜想线段DE,EF,BF的数量关系并证明;(3)过点C作CG⊥EF,垂足为点G,若正方形ABCD的边长是4,请直接写出点G运动的路线长.21.(2022·北京·九年级单元测试)图1,菱形ABCD的顶点A,D在直线上,∠BAD=60°,以点A为旋转中心将菱形ABCD顺时针旋转α(0°<α<30°),得到菱形AB′C′D′,B′C′交对角线AC于点M,C′D′交直线l于点N,连接MN.(1)当MN∥B′D′时,求α的大小.(2)如图2,对角线B′D′交AC于点H,交直线l与点G,延长C′B′交AB于点E,连接EH.当△HEB′的周长为2时,求菱形ABCD的周长.22.(2022·北京·九年级单元测试)综合与实践动手操作:第一步:如图1,正方形纸片ABCD沿对角线AC所在直线折叠,展开铺平.在沿过点C的直线折叠,使点B,点D都落在对角线AC上.此时,点B与点D重合,记为点N,且点E,点N,点F三点在同一直线上,折痕分别为CE,CF.如图2.第二步:再沿AC所在的直线折叠,△ACE与△ACF重合,得到图3第三步:在图3的基础上继续折叠,使点C与点F重合,如图4,展开铺平,连接EF,FG,GM,ME,如图5,图中的虚线为折痕.问题解决:(1)在图5中,∠BEC的度数是,AE的值是;BE(2)在图5中,请判断四边形EMGF的形状,并说明理由;(3)在不增加字母的条件下,请你以图中5中的字母表示的点为顶点,动手画出一个菱形(正方形除外),并写出这个菱形:.23.(2019·北京·101中学九年级阶段练习)在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作射线EF,(1)若∠DAB=60°,EF∥AB交BC于点H,请在图1中补全图形,并直接写出四边形ABHE 的形状;(2)如图2,若∠DAB=90°,EF与AB相交,在EF上取一点G,使得∠EGB=∠EAB,连接AG.请在图2中补全图形,并证明点A,E,B,G在同一个圆上;(3)如图3,若∠DAB=α(0°<α<90°),EF与AB相交,在EF上取一点G,使得∠EGB=∠EAB,连接AG.请在图3中补全图形(要求:尺规作图,保留作图痕迹),并求出线段EG、AG、BG 之间的数量关系(用含α的式子表示);24.(2022·北京朝阳·二模)在正方形ABCD中,E为BC上一点,点M在AB上,点N在DC上,且MN⊥DE,垂足为点F.(1)如图1,当点N与点C重合时,求证:MN=DE;(2)将图1中的MN向上平移,使得F为DE的中点,此时MN与AC相交于点H,①依题意补全图2;②用等式表示线段MH、HF,FN之间的数量关系,并证明.25.(2022·北京四中模拟预测)已知,点B是射线AP上一动点,以AB为边作△ABC,∠BCA= 90°,∠A=60°,将射线BC绕点B顺时针旋转120°,得到射线BD,点E在射线BD上,BE+BC= m.(1)如图1,若BE=BC,求CE的长(用含m的式子表示);(2)如图2,点F在线段AB上,连接CF、EF.添加一个条件:AF、BC、BE满足的等量关系为______,使得EF=CF成立,补全图形并证明.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⎪⎪
⎩⎩
探究特殊四边形存在性问题
1.如图,抛物线y=x2-2x-3经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
(1)求点B,C的坐标;
(2)若点D在y轴上,且∠BDO=∠BAC,求点D的坐标;
(3)若点M为抛物线上一点,点N在抛物线的对称轴上,是否存在以点A、B、M、N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标,若不存在,请说明理由.
第1题图
解:(1)令x=0得y=-3,
∴C(0,-3),
∴OC=3,
∵OC=3OB,
∴OB=1,
∴B(-1,0),
把A(2,-3),B(-1,0)分别代入y=ax2+bx-3得:
⎧a-b-3=0⎧a=1
⎨,解得⎨,
⎪4a+2b-3=-3⎪b=-2
∴抛物线的解析式为y=x2-2x-3;
(2)如解图①,过点B作BE⊥AC,交AC延长线于点E.
第1题解图①
∵C(0,-3),A(2,-3),
∴AC∥x轴,
∴BE=3,
又∵OB=1,
∴AE=3,∴AE=BE,
∴∠BAE=45°,
∵∠BDO=∠BAC=45°,
∴OB=OD,
∴D点的坐标为(0,1)或(0,-1),
(3)存在.如解图②.
第2题解图②
当AB∥MN时,由AB=MN=32,可知点M与对称轴的距离为3,由y=x2-2x-3可得对称轴为直线x=1,
∴点M的横坐标为4或-2,把x=4和-2分别代入y=x2-2x-3可得点M坐标,
把x=-2代入y=x2-2x-3得y=4+4-3=5,
(-2,5).
∴M
1
把x=4代入y=x2-2x-3得y=16-8-3=5,
(4,5),
∴M
2
当MN与AB互相平分时,四边形AMBN是平行四边形,由AC=BN=2,可知点M与点C重合,∴点M3坐标为(0,-3),
∴M的坐标为(-2,5)或(0,-3)或(4,5).
2.如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.
(1)求抛物线的解析式;
(2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标;
(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E,是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.
第2题图
解:(1)设抛物线解析式为:y=a(x-1)2+4(a≠0).
∵抛物线过点C(0,3),
∴a+4=3,∴a=-1.
∴y=-(x-1)2+4=-x2+2x+3;
(2)由(1)得,抛物线的解析式为y=-x2+2x+3,
⎧⎪x1=1⎧⎪x2=2
⎩
⎩⎩
⎩
⎧x=3+17⎧x=3-17
解得
⎨,⎨
⎪⎩y=-1-17⎪⎩y=-1
+17
2
2
∴Q
2
(,),Q
3
(,).
综上所述,满足条件的点Q的坐标为(2,3)或(,)或(,);令y=0,解得x1=-1,x2=3,
∴A(-1,0),B(3,0),
∵C(0,3),∴直线BC的解析式为y=-x+3,
∵△S
BCP
=△S
BCQ
,
∴点P、Q到BC的距离相等.
①当点P、Q位于BC的同侧时,如解图①,过点P作PQ∥BC交抛物线于Q,
又∵P(1,4),
∴直线PQ的解析式为y=-x+5,
⎧⎪
y=-x+5,
联立⎨
⎪y=-x2+2x+3.
解得⎨(舍去),⎨,
⎪y1=4⎪y2=3
∴Q
1
(2,3).
第2题解图①
②当点P、Q位于BC的异侧时,设抛物线的对称轴交BC于点G,交x轴于点H,∴G(1,2),∵此时点P、H到BC的距离相等,∴H(1,0),
∴PG=GH=2,
如解图①,过点H作Q2Q3∥BC交抛物线于点Q2,Q3.
直线Q2Q3的解析式为
y=-x+1,
⎧⎪
y=-x+1,
联立⎨
⎪y=-x2+2x+3.
1
22
122
,
3-17-1+173+17-1-17
2222
3-17-1+173+17-1-17
2222
∵NE = 2
NH ,
∴NE 2= (b -3)2.
∴42-8b = (b 2-6b +9).
⎩
第 2 题解图②
(3)存在满足条件的 M ,N .
如解图②,过点 M 作 MF ∥y 轴,过点 N 作 NF ∥x 轴交 MF 于点 F ,过点 N 作 NH ∥y 轴交 BC 于点 H . 则△MNF 与△NEH 都是等腰直角三角形.
设 M (x 1,y 1),N (x 2,y 2),直线 MN 的解析式为 y =-x +b .
⎧⎪y =-x +b ,
∵⎨ ⎪y =-x 2+2x +3,
∴x 2-3x +(b -3)=0.
∴NF 2=|x 1-x 2|2=(x 1+x 2)2-4x 1x 2=21-4b .
∵△MNF 为等腰直角三角形,
∴MN 2=2NF 2=42-8b .
∵直线 MN 与 y 轴交点(0,b )到点 C (0,3)的距离为|b -3|,
∴NH 2=(b -3)2,
2
1 2 如果四边形 MNED 为正方形,
∴NE 2=MN 2,
1
2 ∴b 2+10b -75=0,
∴b 1=-15,b 2=5.
∵正方形边长为 MN = 42-8b ,
∴MN =9 2或 2,
∴正方形 MNED 的边长为 9 2或 2.。
