中考数学压轴题解题策略(3)直角三角形的存在性问题解题策略(最新整理)
直角三角形的存在性问题解题策略

03
CATALOGUE
直角三角形的存在性问题分类
直角在三角形内部
总结词
当直角位于三角形内部时,可以通过构建直角三角形并利用勾股定理解决。
详细描述
首先,根据题目条件,确定直角的位置和已知条件。然后,利用勾股定理计算直 角三角形的斜边长度。接着,根据三角形的性质和已知条件,判断是否能够构成 三角形。如果可以,则存在满足条件的直角三角形;否则,不存在。
在题目中,有时候会隐含一些关于三角形或 角度的条件,需要仔细审题并挖掘。
举例说明
在求解三角形边长的问题时,需要注意隐含 的等腰或等边条件,这些条件可能会影响三 角形的形状和存在性。
掌握常见题型和解题方法
01
02
03
常见题型
直角三角形存在性问题的 常见题型包括角度问题、 边长问题、高的长度问题 等。
直角在三角形外部
总结词
当直角位于三角形外部时,可以通过构建直角三角形并利用勾股定理解决。
详细描述
首先,根据题目条件,确定直角的位置和已知条件。然后,利用勾股定理计算直角三角形的斜边长度。接着,根 据三角形的性质和已知条件,判断是否能够构成三角形。如果可以,则存在满足条件的直角三角形;否则,不存 在。
建立方程
根据题目条件,可以建立关于未知数 (如角度、边长等)的方程,然后求 解该方程。
解方程
解方程的方法有很多种,如代数法、 三角函数法等,选择合适的方法求解 方程。
利用数形结合思想
数形结合
将题目中的条件和图形结合起来,通过 观察图形和计算数据,找到解决问题的 线索。
VS
综合分析
综合运用数学知识和图形分析,逐步推导 和验证,最终得出结论。
解题方法
针对不同的问题类型,需 要掌握相应的解题方法, 如利用三角函数、勾股定 理、相似三角形等。
初三直角三角形的存在性问题

xyABC O1、 知识内容:在以函数为背景的此类压轴题中,坐标轴作为一个“天然”的直角存在,在解题时经常会用到,作出垂直于坐标轴的直线来构造直角。
另外,较困难的情况则需要用到全等/相似或者勾股定理的计算来确定直角三角形. 2、 解题思路:(1) 按三个角分别可能是直角的情况进行讨论; (2) 计算出相应的边长等信息;(3) 根据边长与已知点的坐标,计算出相应的点的坐标.【例1】 如图,抛物线233384y x x =--+与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C .(1)求点A 、B 的坐标;(2)若直线l 过点E (4,0),M 为直线l 上的动点,当以A 、B 、M 为顶点所作的直 角三角形有且只有三个时,求直线l 的解析式.直角三角形的存在性问题一:以函数为背景的直角三角形问题【例2】 在平面直角坐标平面内,O 为原点,二次函数2y x bx c =-++的图像经过点A (1-,0)和点B (0,3),顶点为P . (1)求二次函数解析式及点P 的坐标;(2)如果点Q 是x 轴上一点,以点A 、P 、Q 为顶点的三角形是直角三角形,求点Q 的坐标.ABCDOPxy ABCDE1、 解题思路:(1) 按三个角分别可能是直角的情况进行讨论;(2) 运用相似/全等、勾股定理等方法,计算出相应的边长.【例3】 如图,在平面直角坐标系中,矩形OABC 的两边OA 、OC 分别在x 轴、y 轴的正半轴上,OA = 4,OC = 2.点P 从点O 出发,沿x 轴以每秒1个单位长的速度向点A 匀速运动,当点P 到达点A 时停止运动,设点P 运动的时间是t 秒.将线段CP 的中点绕点P 按顺时针方向旋转90°得点D ,点D 随点P 的运动而运动,连接DP 、DA . (1)请用含t 的代数式表示出点D 的坐标;(2)在点P 从O 向A 运动的过程中,DPA ∆能否成为直角三角形?若能,求t 的值.若 不能,请说明理由.【例4】 如图,在ABC ∆中,CA = CB ,AB = 8,4cos 5A ∠=.点D 是AB 边上的一个动点,点E 与点A 关于直线CD 对称,联结CE 、DE . (1)求底边AB 上的高;(2)设CE 与AB 交于点F ,当ACF ∆为直角三角形时,求AD 的长; (3)联结AE ,当ADE ∆是直角三角形时,求AD 的长.二:以几何为背景的直角三角形问题AB CDEFGP【例5】 如图,已知ABC ∆为等边三角形,AB = 6,点P 是AB 上的一个动点(与A 、B 不重合),过点P 作AB 的垂线与BC 交于点D ,以点D 为正方形的一个顶点,在ABC ∆内作正方形DEFG ,其中D 、E 在BC 上,F 在AC 上.(1)设BP 的长为x ,正方形DEFG 的边长为y ,写出y 与x 的函数关系式及定义域; (2)当BP = 2时,求CF 的长;(3)GDP ∆是否可能成为直角三角形?若能,求出BP 的长;若不能,请说明理由.ABCDEP Q 【例6】 如图,在ABC ∆中,90C ∠=︒,AC = 4 cm ,BC = 5 cm ,点D 在BC 上,并且CD =3 cm .现有两个动点P 、Q 分别从点A 、B 同时出发,其中点P 以1cm/s 的速度,沿AC 向终点C 移动;点Q 以1.25 cm/s 的速度沿BC 向终点C 移动.过点P 作PE // BC 交AD 于点E ,联结EQ .设动点运动时间为x (s ). (1)用含x 的代数式表示AE 、DE 的长度; (2)当x 为何值时,EDQ ∆为直角三角形.。
初中数学中考专题2:直角三角形的存在性问题探究

中考专题(二) 直角三角形的存在性问题探究一、专题攻略1、解直角三角形存在性问题,一般分三步,第一步寻找分类标准,第二步列方程,第三步解方程并验根.2、一般情况下,按照直角顶点或者斜边分类,然后按照三角比或勾股定理列方程.3、有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便.4、解直角三角形的问题,常常和相似三角形、三角比的问题联系在一起.5、如果直角边与坐标轴不平行,那么过三个顶点作与坐标轴平行的直线,可以构造两个新的相似直角三角形,这样列比例方程比较简便.6、在平面直角坐标系中,两点间的距离公式常常用到.7、怎样画直角三角形的示意图呢?如果已知直角边,那么过直角边的两个端点画垂线,第三个顶点在垂线上;如果已知斜边,那么以斜边为直径画圆,直角顶点在圆上(不含直径的两个端点).二、例题解析例1:(可以按照直角的顶点分类)如图,在△ABC 中,AB =AC =10,cos ∠B =45.D 、E 为线段BC 上的两个动点,且DE =3(E 在D 右边),运动初始时D 和B 重合,当E 和C 重合时运动停止.过E 作EF //AC 交AB 于F ,连结DF .设BD =x ,如果△BDF 为直角三角形,求x 的值.例2: (可以按照斜边分类)如图,已知A 、B 是线段MN 上的两点,,,.以A 为中心顺时针旋转点M ,以B 为中心逆时针旋转点N ,使M 、N 两点重合成一点C ,构成△ABC ,设AB =x ,若△ABC 为直角三角形,求x 的值.4=MN 1=MA 1>MB例3:(以线段AB 为分类标准)如图,已知在平面直角坐标系中,点A 的坐标为(-2, 0),点B 是点A 关于原点的对称点,P 是函数)0(2>=x xy 图象上的一点,且△ABP 是直角三角形,求点P 的坐标.练习1、如图,已知直线y =kx -6经过点A (1,-4),与x 轴相交于点B .若点Q 是y 轴上一点,且△ABQ 为直角三角形,求点Q 的坐标.练习2、如图,抛物线233384y x x =--+与x 轴交于A 、B 两点(点A 在点B 的左侧).若直线l 过点 E (4, 0),M 为直线l 上的动点,当以A 、B 、M 为顶点所作的直角三角形有且只有....三个时,求直线l 的解析式.练习3、如图,在△ABC 中,CA =CB ,AB =8,4cos 5A ∠=.点D 是AB 边上的一个动点,点E 与点A 关于直线CD 对称,连结CE 、DE .(1)求底边AB 上的高;(2)设CE 与AB 交于点F ,当△ACF 为直角三角形时,求AD 的长;(3)连结AE ,当△ADE 是直角三角形时,求AD 的长.练习4:如图,抛物线()2230y mx mx m m =-->与x 轴交于A B 、两点,与y 轴交于C 点. (1)请求出抛物线顶点M 的坐标(用含m 的代数式表示),A B 、两点的坐标;(2)经探究可知,BCM △与ABC △的面积比不变,试求出这个比值;(3)是否存在使BCM △为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.练习5:在平面直角坐标系中,现将一块等腰直角三角板ABC 放在第二象限,斜靠在两坐标轴上,点C为 (-1,0) .如图所示,B 点在抛物线y =12x 2+12x -2图象上,过点B 作BD ⊥x 轴,垂足为D ,且B 点横坐标为-3.(1)求证:△BDC ≌△COA ;(2)求BC 所在直线的函数关系式;(3)抛物线的对称轴上是否存在点P ,使△ACP 是以AC 为直角边的直角三角形?若存在,求出所有点P 的坐标;若不存在,请说明理由.。
中考数学专题讲解:直角三角形的存在性问题
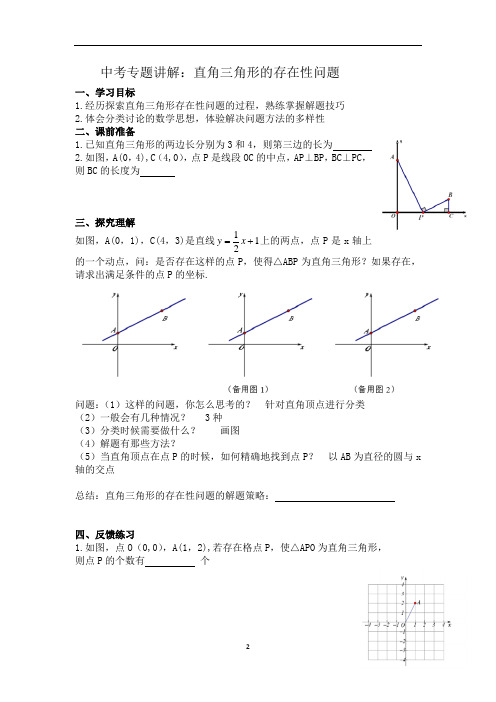
中考专题讲解:直角三角形的存在性问题 一、学习目标1.经历探索直角三角形存在性问题的过程,熟练掌握解题技巧2.体会分类讨论的数学思想,体验解决问题方法的多样性二、课前准备1.已知直角三角形的两边长分别为3和4,则第三边的长为2.如图,A(0,4),C (4,0),点P 是线段OC 的中点,AP ⊥BP ,BC ⊥PC ,则BC 的长度为三、探究理解如图,A(0,1),C(4,3)是直线121+=x y 上的两点,点P 是x 轴上的一个动点,问:是否存在这样的点P ,使得△ABP 为直角三角形?如果存在,请求出满足条件的点P 的坐标.问题:(1)这样的问题,你怎么思考的? 针对直角顶点进行分类(2)一般会有几种情况? 3种(3)分类时候需要做什么? 画图(4)解题有那些方法?(5)当直角顶点在点P 的时候,如何精确地找到点P ? 以AB 为直径的圆与x 轴的交点总结:直角三角形的存在性问题的解题策略:四、反馈练习1.如图,点O (0,0),A(1,2),若存在格点P ,使△APO 为直角三角形, 则点P 的个数有 个2.在△ABC 中,∠C=900,AC=8 cm,BC=6 cm ,动点P 、Q 分别同时从点A 、B 出发,其中点P 在线段AB 上向点B 移动,速度是2 cm/s,点Q 在线段BC上向点C 运动,速度为1cm/s ,设运动时间为t s,当t= 时,△BPQ 是直角三角形.3.如图,已知A 、B 是线段MN 上的两点,MN=4,MA=1,MB>1,以A 为中心顺时针旋转点M ,以B 为中心逆时针旋转点N ,使M 、N 两点重合成一点C ,构成△ABC ,设AB=x.若△ABC 为直角三角形,(1)求x 的值.(2)x 的取值是多少.五、链接中考如图,矩形OABC 中,点O 为原点,点A 的坐标为(0,8),点C 的坐标为(6,0).抛物线834942++-=x x y 经过A 、C 两点,与AB 边交于点D ,Q 是AC 上一点,且AQ=5.请问在抛物线对称轴l 上是否存在点F ,使得△FDQ 为直角三角形?若存在,请直接写出所有符合条件的点F 的坐标,若不存在,请说明理由六、课堂小结直角三角形的存在性问题解题策略分类画图(1)角:构造相似三角形解题 (2) 边:勾股定理(3)函数:k 1·k 2=-1六、课后练习在平面直角坐标系中,现将一块等腰直角三角板ABC 放在第二象限,斜靠在两坐标轴上,点C 为(-1,0),如图所示,B 点在抛物线221212-+=x x y 图像上,过点B 作BD ⊥X 轴,垂足为D ,且B 点的横坐标为-3.(1)求证:△BDC ≌△COA(2)求BC 所在直线的函数关系式(3)抛物线的对称轴上是否存在点P ,使△ACP 是以AC为直角边的直角三角形?若存在,求出所有点P 的坐标;若不存在,请说明理由。
中考数学直角三角形的存在性问题解题策略

直角三角形的存在性问题解题策略专题攻略解直角三角形的存在性问题,一般分三步走,第一步寻找分类标准,第二步列方程,第三步解方程并验根. 一般情况下,按照直角顶点或者斜边分类,然后按照三角比或勾股定理列方程. 有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便.解直角三角形的问题,常常和相似三角形、三角比的问题联系在一起.如果直角边与坐标轴不平行,那么过三个顶点作与坐标轴平行的直线,可以构造两个新的相似直角三角形,这样列比例方程比较简便.在平面直角坐标系中,两点间的距离公式常常用到.怎样画直角三角形的示意图呢?如果已知直角边,那么过直角边的两个端点画垂线,第三个顶点在垂线上;如果已知斜边,那么以斜边为直径画圆,直角顶点在圆上(不含直径的两个端点).例题解析例1、 如图1-1,在△ABC 中,AB =AC =10,cos ∠B =45.D 、E 为线段BC 上的两个动点,且DE =3(E 在D 右边),运动初始时D 和B 重合,当E 和C 重合时运动停止.过E 作EF //AC 交AB 于F ,连结DF .设BD =x ,如果△BDF 为直角三角形,求x 的值.图1-1【解析】△BDF 中,∠B 是确定的锐角,那么按照直角顶点分类,直角三角形BDF 存在两种情况.如果把夹∠B 的两条边用含有x 的式子表示出来,分两种情况列方程就可以了. 如图1-2,作AH ⊥BC ,垂足为H ,那么H 是BC 的中点.在Rt △ABH 中,AB =10,cos ∠B =45,所以BH =8.所以BC =16. 由EF //AC ,得BF BE BA BC =,即31016BF x +=.所以BF =5(3)8x +.图1-2 图1-3 图1-4①如图1-3,当∠BDF =90°时,由4cos 5BD B BF ∠==,得45BD BF =. 解方程45(3)58x x =⨯+,得x =3.②如图1-4,当∠BFD =90°时,由4cos 5BF B BD ∠==,得45BF BD =. 解方程5154885x x +=,得757x =. 我们看到,在画示意图时,无须受到△ABC 的“限制”,只需要取其确定的∠B . 例2、 如图2-1,已知A 、B 是线段MN 上的两点,4=MN ,1=MA ,1>MB .以A 为中心顺时针旋转点M ,以B 为中心逆时针旋转点N ,使M 、N 两点重合成一点C ,构成 △ABC ,设AB =x ,若△ABC 为直角三角形,求x 的值.图2-1【解析】△ABC 的三边长都可以表示出来,AC =1,AB =x ,BC =3-x . 如果用斜边进行分类,每条边都可能成为斜边,分三种情况:①若AC 为斜边,则22)3(1x x -+=,即0432=+-x x ,此方程无实根.②若AB 为斜边,则1)3(22+-=x x ,解得35=x (如图2-2). ③若BC 为斜边,则221)3(x x +=-,解得34=x (如图2-3). 因此当35=x 或34=x 时,△ABC 是直角三角形.图2-2 图2-3例3、 如图3-1,已知在平面直角坐标系中,点A 的坐标为(-2, 0),点B 是点A 关于原点的对称点,P 是函数)0(2>=x xy 图象上的一点,且△ABP 是直角三角形,求点P 的坐标.图3-1【解析】A 、B 两点是确定的,以线段AB 为分类标准,分三种情况.如果线段AB 为直角边,那么过点A 画AB 的垂线,与第一象限内的一支双曲线没有交点;过点B 画AB 的垂线,有1个交点.以AB 为直径画圆,圆与双曲线有没有交点呢?先假如有交点,再列方程,方程有解那么就有交点.如果是一元二次方程,那么可能是一个交点,也可能是两个交点.由题意,得点B 的坐标为(2,0),且∠BAP 不可能成为直角.①如图3-2,当∠ABP =90°时,点P 的坐标为(2,1).②方法一:如图3-3,当∠APB =90°时,OP 是Rt △APB 的斜边上的中线,OP =2.设P 2(,)x x ,由OP 2=4,得2244x x+=.解得x =P (2,2).图3-2 图3-3 方法二:由勾股定理,得P A 2+PB 2=AB 2.解方程2222222(2)()(2)()4x x x x+++++=,得x = 方法三:如图3-4,由△AHP ∽△PHB ,得PH 2=AH ·BH .解方程22()(2)(2)x x x=+-,得x =图3-4 图3-5这三种解法的方程貌似差异很大,转化为整式方程之后都是(x 2-2)2=0.这个四次方程的解是x 1=x 2=2,x 3=x 4=它的几何意义就是以AB 为直径的圆与双曲线相切于P 、P ′两点(如图3-5).例4、 如图4-1,已知直线y =kx -6经过点A (1,-4),与x 轴相交于点B .若点Q 是y 轴上一点,且△ABQ 为直角三角形,求点Q 的坐标.图4-1【解析】和例题3一样,过A 、B 两点分别画AB 的垂线,各有1个点Q .和例题3不同,以AB 为直径画圆,圆与y 轴有没有交点,一目了然.而圆与双曲线有没有交点,是徒手画双曲线无法肯定的.将A (1,-4)代入y =kx -6,可得k =2.所以y =2x -6,B (3,0).设OQ 的长为m .分三种情况讨论直角三角形ABQ :①如图4-2,当∠AQB =90°时,△BOQ ∽△QHA ,BO QH OQ HA =.所以341m m -=. 解得m =1或m =3.所以Q (0,-1)或(0,-3).②如图4-3,当∠BAQ =90°时,△QHA ∽△AGB ,QH AG HA GB =.所以4214m -=. 解得72m =.此时7(0,)2Q -. ③如图4-4,当∠ABQ =90°时,△AGB ∽△BMQ ,AG BM GB MQ =.所以243m =. 解得32m =.此时3(0,)2Q .图4-2 图4-3 图4-4三种情况的直角三角形ABQ ,直角边都不与坐标轴平行,我们以直角顶点为公共顶点,构造两个相似的直角三角形,这样列比例方程比较简便.已知A (1,-4)、B (3,0),设Q (0, n ),那么根据两点间的距离公式可以表示出AB 2,AQ 2和BQ 2,再按照斜边为分类标准列方程,就不用画图进行“盲解”了.例5、 如图5-1,抛物线233384y x x =--+与x 轴交于A 、B 两点(点A 在点B 的左侧).若直线l 过点E (4, 0),M 为直线l 上的动点,当以A 、B 、M 为顶点所作的直角三角形有且只...有.三个时,求直线l 的解析式.图5-1【解析】有且只有三个直角三角形ABM 是什么意思呢?过A 、B 两点分别画AB 的垂线,与直线l 各有一个交点,那么第三个直角顶点M 在哪里?以AB 为直径的⊙G 与直线l 相切于点M 啊! 由23333(4)(2)848y x x x x =--+=-+-,得A (-4, 0)、B (2, 0),直径AB =6. 如图5-2,连结GM ,那么GM ⊥l .在Rt △EGM 中,GM =3,GE =5,所以EM =4.因此3tan 4GEM ∠=. 设直线l 与y 轴交于点C ,那么OC =3.所以直线l (直线EC )为334y x =-+. 根据对称性,直线l 还可以是334y x =-.图5-2例6、 如图6-1,在△ABC 中,CA =CB ,AB =8,4cos 5A ∠=.点D 是AB 边上的一个动点,点E 与点A 关于直线CD 对称,连结CE 、DE .(1)求底边AB 上的高;(2)设CE 与AB 交于点F ,当△ACF 为直角三角形时,求AD 的长;(3)连结AE ,当△ADE 是直角三角形时,求AD 的长.图6-1【解析】这道题目画示意图有技巧的,如果将点D 看作主动点,那么CE 就是从动线段.反过来画图,点E 在以CA 为半径的⊙C 上,如果把点E 看作主动点,再画∠ACE 的平分线就产生点D 了.(1)如图6-2,设AB 边上的高为CH ,那么A H =BH =4.在Rt △ACH 中,AH =4,4cos 5A ∠=,所以AC =5,CH =3. (2)①如图6-3,当∠AFC =90°时,F 是AB 的中点,AF =4,CF =3. 在Rt △DEF 中,EF =CE -CF =2,4cos 5E ∠=,所以52DE =.此时52AD DE ==. ②如图6-4,当∠ACF =90°时,∠ACD =45°,那么△ACD 的条件符合“角边角”. 作DG ⊥AC ,垂足为G .设DG =CG =3m ,那么AD =5m ,AG =4m .由CA =5,得7m =5.解得57m =.此时2557AD m ==.图6-2 图6-3 图6-4 (3)因为DA=DE,所以只存在∠ADE=90°的情况.①如图6-5,当E在AB下方时,根据对称性,知∠CDA=∠CDE=135°,此时△CDH 是等腰直角三角形,DH=CH=3.所以AD=AH-DH=1.②如图6-6,当E在AB上方时,根据对称性,知∠CDA=∠CDE=45°,此时△CDH 是等腰直角三角形,DH=CH=3.所以AD=AH+DH=7.图6-5 图6-6。
中考 压轴题一:两招破解因动点产生直角三角形难题 压轴题二:因动点产生平行四边形的存在性问题解题新策略

压轴题一:两招破解因动点产生的的直角三角形难题一、问题导读因动点产生的直角三角形问题是中考试卷的考查热点,解决这类问题时,我们常常需要分情况讨论,即究竟哪个角是直角。
具体解题策略分类说明如下。
二、典例精析类型1.两动点或三动点形成的直角三角形重要策略:分角讨论法:讨论直角三角形的时候,如果能设出或明确出三角形三个顶点坐标,可利用两点间距离公式分别求出三角形三边长,如果两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
涉及到的知识点有:全等;相似倒角;函数交点;两一次函数斜率之积为-1等知识求解;例1.(2018秋梁子湖区期末)如图,已知直线y=﹣x+4分别交x轴、y轴于点A、B,抛物线过y=ax2+bx+c经过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.(1)若抛物线的解析式为y=﹣1/2x2+x+4,设其顶点为M,其对称轴交AB于点N.①求点M、N的坐标;②是否存在点P,使四边形MNPD为菱形?并说明理由;(2)当点P的横坐标为2时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形是直角三角形?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.【分析】(1)①把二次函数表达式化为顶点式表达式,即可求解;②不存在.理由如下:设点P 的坐标为(m,﹣m+4),则D(m,﹣1/2m2+m+4),PD=﹣1/2m2+m+4﹣(﹣m+4)=﹣1/2m2+2m,当四边形MNPD为平行四边形,则:1/2m2+2m=3/2,解得:m=1,则:点P(3,1),由N(1,3),则由两点间距离公式可得:PN=2√2≠MN,即可求解;(2)分∠BDP=90°或∠PBD=90°两种情况,求解即可.【解答】(1)①y=﹣1/2x2+x+4=﹣1/2(x﹣1)2+9/2,∴顶点M的坐标为(1,9/2),当x=1时,y=﹣1+4=3,∴点N的坐标为(1,3);②不存在.理由如下:MN=9/2﹣3=3/2,设点P 的坐标为(m,﹣m+4),则D(m,﹣1/2m2+m+4),PD=﹣1/2m2+m+4﹣(﹣m+4)=﹣1/2m2+2m,∵PD∥MN.∴当PD=MN时,四边形MNPD为平行四边形,即﹣1/2m2+2m=3/2,解得:m=1或3(m=1舍去),∴点P(3,1),由N(1,3),∴则由两点间距离公式可得PN=2√2≠MN,∴平行四边形MNPD不是菱形,即:不存在点P,使四边形MNPD为菱形;(2)①当∠BDP=90°时,点P(2,2),则四边形BOCD为矩形,∴D(2,4),又A(4,0),B(0,4),∴抛物线的表达式为:y=﹣1/2x2+x+4;②当∠PBD=90°时,△PBD为等腰直角三角形,则PD=2xP=4,∴D(2,6),又A(4,0),B(0,4),把A、B、D坐标代入二次函数表达式得:16a+4b+c=0, c=4, 4a+2b+c=6,解得:a=-1,b=3,c=4,故:二次函数表达式为:y=﹣x2+3x+4.。
中考数学几何压轴题解题技巧

中考数学几何压轴题解题技巧
中考数学几何压轴题通常比较难,需要有一定的数学基础和思维能力。
以下是一些中考数学几何压轴题解题技巧:
1. 熟悉几何图形的特性:在解决几何压轴题时,要对一些特殊的形状和性质进行记忆和识别,例如平行线的性质、垂直线的性质、三角形的判定和性质等。
2. 理解空间观念:几何压轴题通常涉及到空间问题,因此要具备良好的空间观念,例如理解向量的概念、理解点、线、面之间的关系等。
3. 运用基本定理:解决几何压轴题时,需要运用一些基本定理,
例如相似三角形定理、勾股定理、三角函数等。
4. 化简和化归:在解决几何压轴题时,常常需要进行化简和化归,将复杂的问题转化为更简单的形式,从而更容易解决问题。
5. 寻找关键信息:几何压轴题通常需要寻找一些关键信息,例如对称性、三角形的重心、垂心、内心、外心等。
6. 画图辅助思考:在解决几何压轴题时,画图可以更加直观地理
解问题,帮助你找到解决问题的方法。
7. 多练习:最后,多练习是必要的。
通过大量的练习,你可以加深对几何图形的理解和记忆,提高解决问题的能力。
总之,几何压轴题需要理解和掌握几何图形的特性、运用基本定理、化简和化归、寻找关键信息、画图辅助思考以及多练习等方法,才能有效地解决问题。
中考专题讲解:直角三角形的存在性问题解题策略

中考专题讲解:直角三角形的存在性问题解题策略有关直角三角形的存在性问题,一般都是放在平面直角坐标系中和抛物线结合起来考察,这种题的解法套路一般都是固定的,在学习的过程中只需要牢固掌握直角三角形存在的基本模型:两线一圆,多加练习,这类问题就可以轻松掌握。
一、模型讲解“两线一圆”模型:在平面直角坐标系中遇到直角三角形的相关问题时,通常是以直角顶点作为分类标准,如下图,分别以点A、点B、点M为直角定点来构造直角三角形,然后根据相关条件来进行求解即可。
已知:定点A(2,1)、B(6,4)和动点M(m,0),存在直角三角形。
具体有以下三种情况:(1)过点A作直线AM垂直AB,交x轴于点M;(2)过点B作直线BM垂直AB,交x轴于点M;(3)根据直径所对的圆周角为90度,以AB为直径作圆,交x轴的点即为满足条件的点M(一般情况下有两个交点,特殊情况下只有一个交点),然后根据相关条件来进行求解即可。
作出图形后,具体求解方法有三种:方法一:“K型”图(有的叫“一线三等角”),三角形相似易得△ACM∽△BEA,求得CM,从而求出点M的坐标。
易得△AEB ∽△BFM求得BF,从而得M的坐标方法二:勾股定理∵BH²=BG²-GH² ∵AC²+CM²=AM²BH²=BM²-HM² MD²+BD²=BM²∴BG²-GH² =BM²-HM² AM²+BM²=AB²∴AC²+CM²+MD²+BD²=AB²方法三:解析法(来源于高中的解析几何,虽然有点超纲,但是很多老师都教学生这种方法)K AB ·K AM =-1,直线BM 与x 轴的交点即为M 。
K AB ·K BM =-1,直线A 与x 轴的交点即为M 。
3-直角三角形的存在性问题解题策略

中考数学压轴题解题策略 3直角三角形的存在性问题解题策略挑战压轴题·中考数学 的作者 海 马学斌专题攻略解直角 角形的存在性问题 一般 走 第一 寻找 类标准 第二 列方程 第 解方程并验根一般情况 按照直角顶点或者斜边 类 然后按照 角比或勾股定理列方程有时根据直角 角形斜边 的中线等于斜边的一半列方程更简便解直角 角形的问题 常常和相似 角形、 角比的问题联系在一起如果直角边 坐标轴 平行 那 过 个顶点作 坐标轴平行的直线 可以构造两个新的相似直角 角形 样列比例方程比较简便在平面直角坐标系中 两点间的距离公式常常用到怎样画直角 角形的示意图呢?如果已知直角边 那 过直角边的两个端点画垂线 第 个顶点在垂线 如果已知斜边 那 以斜边 直径画圆 直角顶点在圆 含直径的两个端点例题解析例❶ 如图1-1 在△ABC中 AB=AC=10 cos∠B=45D、E 线段BC 的两个动点 且DE=3 E在D右边 运动初始时D和B 合 当E和C 合时运动停止 过E 作EF//AC交AB于F 连结DF 设BD=x 如果△BDF 直角 角形 求x的值图1-1解析 △BDF中 ∠B是确定的锐角 那 按照直角顶点 类 直角 角形BDF存在两种情况 如果把夹∠B的两条边用含有x的式子表示出来 两种情况列方程就可以了 如图1-2 作AH⊥BC 垂足 H 那 H是BC的中点在Rt△ABH中 AB=10 cos∠B=45所以BH=8 所以BC=16由EF//AC 得BF BEBA BC= 即31016BF x+= 所以BF=5(3)8x+图1-2 图1-3 图1-4如图1-3 当∠BDF =90°时 由4cos 5BD B BF ∠== 得45BD BF = 解方程45(3)58x x =×+ 得x =3 如图1-4 当∠BFD =90°时 由4cos 5BF B BD ∠== 得45BF BD = 解方程5154885x x += 得757x = 们看到 在画示意图时 无 到△ABC 的 限制 只需要 其确定的∠B 例❷ 如图2-1 已知A 、B 是线段MN 的两点 以A 中心 时针旋转点M 以B 中心逆时针旋转点N 使M 、N 两点 合 一点C 构 △ABC 设AB =x 若△ABC 直角 角形 求x 的值图2-1解析 △ABC 的 边长都可以表示出来 AC =1 AB =x BC =3 x如果用斜边进行 类 条边都可能 斜边 种情况若AC 斜边 则22)3(1x x −+= 即0432=+−x x 方程无实根若AB 斜边 则1)3(22+−=x x 解得35=x 如图2-2 若BC 斜边 则221)3(x x +=− 解得34=x 如图2-3 因 当35=x 或34=x 时 △ABC 是直角 角形图2-2 图2-3例❸ 如图3-1 已知在平面直角坐标系中 点A 的坐标 -2, 0 点B 是点A 关于原点的对称点 P 是函数)0(2>=x xy 图象 的一点 且△ABP 是直角 角形 求点P 的坐标图3-1解析 A 、B 两点是确定的 以线段AB 类标准 种情况4=MN 1=MA 1>MB如果线段AB 直角边 那 过点A 画AB 的垂线 第一象限内的一支 曲线没有交点 过点B 画AB 的垂线 有1个交点以AB 直径画圆 圆 曲线有没有交点呢?先假如有交点 再列方程 方程有解那 就有交点 如果是一元二次方程 那 可能是一个交点 也可能是两个交点由题意 得点B 的坐标 2 0 且∠BAP 可能 直角如图3-2 当∠ABP =90°时 点P 的坐标 2 1方法一 如图3-3 当∠APB =90°时 OP 是Rt △APB 的斜边 的中线 OP =2设P 2(,x x 由OP 2=4 得2244x x += 解得x = 时P (2,2)图3-2 图3-3方法二 由勾股定理 得PA 2 PB 2=AB 2解方程2222222(2)()(2)()4x x x x +++++= 得x =方法 如图3-4 由△AHP ∽△PHB 得PH 2=AH ·BH解方程22((2)(2)x x x =+− 得x =图3-4 图3-5种解法的方程貌似差异很大 转化 整式方程之后都是(x 2 2)2=0 个四次方程的解是x 1=x 2=2 x 3=x 4= 它的几何意 就是以AB 直径的圆 曲线相 于P 、P ′两点 如图3-5例❹ 如图4-1 已知直线y =kx 6 过点A (1, 4) x 轴相交于点B 若点Q 是y 轴 一点 且△ABQ 直角 角形 求点Q 的坐标图4-1解析 和例题3一样 过A 、B 两点 别画AB 的垂线 各有1个点Q 和例题3 同 以AB 直径画圆 圆 y 轴有没有交点 一目了然 而圆 曲线有没有交点 是徒手画 曲线无法肯定的将A (1, 4)代入y =kx 6 可得k =2 所以y =2x 6 B (3,0)设OQ 的长 m 种情况讨论直角 角形ABQ如图4-2 当∠AQB =90°时 △BOQ ∽△QHABO QH OQ HA = 所以341m m −= 解得m =1或m =3 所以Q (0, 1)或(0, 3)如图4-3 当∠BAQ =90°时 △QHA ∽△AGBQH AG HA GB = 所以4214m −= 解得72m = 时7(0,2Q − 如图4-4 当∠ABQ =90°时 △AGB ∽△BMQ AG BM GB MQ= 所以243m = 解得32m = 时3(0,)2Q图4-2 图4-3 图4-4种情况的直角 角形ABQ 直角边都 坐标轴平行 们以直角顶点 公共顶点 构造两个相似的直角 角形 样列比例方程比较简便已知A (1, 4)、B (3,0) 设Q (0, n ) 那 根据两点间的距离公式可以表示出AB 2 AQ 2和BQ 2 再按照斜边 类标准列方程 就 用画图进行 盲解 了例❺ 如图5-1 抛物线233384y x x =−−+ x 轴交于A 、B 两点 点A 在点B 的 侧 若直线l 过点E (4, 0) M 直线l 的动点 当以A 、B 、M 顶点所作的直角 角形有且只 有个时 求直线l 的解析式图5-1解析 有且只有 个直角 角形ABM 是什 意思呢?过A 、B 两点 别画AB 的垂线 直线l 各有一个交点 那 第 个直角顶点M 在哪 ?以AB 直径的⊙G 直线l 相 于点M 啊! 由23333(4)(2)848y x x x x =−−+=−+− 得A ( 4, 0)、B (2, 0) 直径AB =6 如图5-2 连结GM 那 GM ⊥l在Rt △EGM 中 GM =3 GE =5 所以EM =4 因 3tan 4GEM ∠=设直线l y 轴交于点C 那 OC =3 所以直线l 直线EC 334y x =−+ 根据对称性 直线l 可以是334y x =−图5-2例❻ 如图6-1 在△ABC 中 CA =CB AB =8 4cos 5A ∠=点D 是AB 边 的一个动点 点E 点A 关于直线CD 对称 连结CE 、DE1 求底边AB 的高2 设CE AB 交于点F 当△ACF 直角 角形时 求AD 的长3 连结AE 当△ADE 是直角 角形时 求AD 的长图6-1解析 道题目画示意图有技 的 如果将点D 看作 动点 那 CE 就是从动线段 过来画图 点E 在以CA 半径的⊙C 如果把点E 看作 动点 再画∠ACE 的平 线就产生点D 了1 如图6-2 设AB 边 的高 CH 那 AH =BH =4在Rt △ACH 中 AH =4 4cos 5A ∠= 所以AC =5 CH =3 2 如图6-3 当∠AFC =90°时 F 是AB 的中点 AF =4 CF =3 在Rt △DEF 中 EF =CE CF =2 4cos 5E ∠= 所以52DE = 时52AD DE ==如图6-4 当∠ACF=90°时 ∠ACD=45° 那 △ACD的条件符合 角边角 作DG⊥AC 垂足 G 设DG=CG=3m 那 AD=5m AG=4m由CA=5 得7m=5 解得57m= 时2557AD m==图6-2 图6-3 图6-43 因 DA=DE 所以只存在∠ADE=90°的情况如图6-5 当E在AB 方时 根据对称性 知∠CDA=∠CDE=135° 时△CDH 是等腰直角 角形 DH=CH=3 所以AD=AH DH=1如图6-6 当E在AB 方时 根据对称性 知∠CDA=∠CDE=45° 时△CDH 是等腰直角 角形 DH=CH=3 所以AD=AH DH=7图6-5 图6-6。
专题三直角三角形的存在性问题解题策略

授课题目专题三直角三角形的存在性问题解题策略授课日期2015年3月14日教师柳娜授课学时 1 时 00 分学生课型复习课学科组长柳娜师生活动一、要点归纳直角三角形的存在性问题是苏州中考数学的热点问题.解直角三角形的存在性问题,一般分三步走,第一步寻找分类标准,第二步列方程,第三步解方程并验根。
解直角三角形的问题,常常和相似三角形、三角比的问题联系在一起.二、课前热身已知直角三角形的两条边长为6和8,那么第三边的长为多少?怎样画出这个直角三角形?三、例题讲解1.如图1,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x.(1)求x的取值范围;(2)若△ABC为直角三角形,求x的值;图12.如图,已知在平面直角坐标系中,点A 的坐标为(-2,0),点B 是点A 关于原点的对称点,P 是函数图像上的一点,且△ABP 是直角三角形.求点P 的坐标;3.如图1,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0). (1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M 运动t 秒, 在运动过程中,当△MON 为直角三角形时,求t 的值.图14.如图1,在平面直角坐标系中,O 是坐标原点,点A 的坐标为(-4,0),点B 的坐标为(0,b )(b >0).P是直线AB 上的一个动点,作PC ⊥x 轴,垂足为C .记点P 关于y 轴的对称点为P ′(点P ′不在y 轴上),联结PP ′、P ′A 、P ′C .设点P 的横坐标为a .问是否同时存在a 、b ,使△P ′CA 为等腰直角三角形?若存在,请求出所有满足要求的a 、b 的值;若不存在,请说明理由.图15.已知点P 是函数x y 21=(x >0)图像上一点,P A ⊥x 轴于点A ,交函数xy 1=(x >0)图像于点M ,PB ⊥y 轴于点B ,交函数xy 1=(x >0)图像于点N (点M 、N 不重合).(1)当点P 的横坐标为2时,求△PMN 的面积; (2)证明:MN ‖AB (如图1);(3)试问:△OMN 能否为直角三角形?若能,请求出此时点P 的坐标;若不能,请说明理由.图1 备用图6.已知: 在直角坐标系xOy 中,将直线y =kx 沿y 轴向下平移3个单位长度后恰好经过点B (-3,0)及y 轴上的点C .若抛物线y =-x 2+bx +c 与x 轴交于A ,B 两点(点A 在点B 的右侧),且经过点C .(1)求直线BC 及抛物线的解析式;(2)设抛物线的顶点为D ,点P 在抛物线的对称轴上,且∠APD =∠ACB ,求点P 的坐标.专项训练1.如图1,已知抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.(1)求抛物线的函数表达式;(2)求直线BC的函数表达式;(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.①当线段34PQ AB=时,求tan∠CED的值;②当以C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.温馨提示:考生可以根据第(3)问的题意,在图中补出图形,以便作答.图12.设直线l1:y=k1x+b1与l2:y=k2x+b2,若l1⊥l2,垂足为H,则称直线l1与l2是点H的直角线.(1)已知直线①122y x=-+;②2y x=+;③22y x=+;④24y x=+和点C(0,2),则直线_______和_______是点C的直角线(填序号即可);(2)如图,在平面直角坐标系中,直角梯形OABC的顶点A(3,0)、B(2,7)、C(0,7),P为线段OC上一点,设过B、P两点的直线为l1,过A、P两点的直线为l2,若l1与l2是点P的直角线,求直线l1与l2的解析式.图13.在平面直角坐标系xOy 中,抛物线22153244m my x x m m -=-++-+与x 轴的交点分别为原点O 和点A ,点B (2,n )在这条抛物线上.(1)求点B 的坐标;(2)点P 在线段OA 上,从点O 出发向点A 运动,过点P 作x 轴的垂线,与直线OB 交于点E ,延长PE 到点D ,使得ED =PE ,以PD 为斜边,在PD 右侧作等腰直角三角形PCD (当点P 运动时,点C 、D 也随之运动).①当等腰直角三角形PCD 的顶点C 落在此抛物线上时,求OP 的长;②若点P 从点O 出发向点A 作匀速运动,速度为每秒1个单位,同时线段OA 上另一个点Q 从点A 出发向点O 作匀速运动,速度为每秒2个单位(当点Q 到达点O 时停止运动,点P 也停止运动).过Q 作x 轴的垂线,与直线AB 交于点F ,延长QF 到点M ,使得FM =QF ,以QM 为斜边,在QM 的左侧作等腰直角三角形QMN (当点Q 运动时,点M 、N 也随之运动).若点P 运动到t 秒时,两个等腰直角三角形分别有一条边恰好落在同一条直线上,求此刻t 的值.图14.如图1,已知A 、B 是线段MN 上的两点,4=MN ,1=MA ,1>MB .以A 为中心顺时针旋转点M ,以B 为中心逆时针旋转点N ,使M 、N 两点重合成一点C ,构成△ABC ,设x AB =.(1)求x 的取值范围;(2)若△ABC 为直角三角形,求x 的值; (3)探究:△ABC 的最大面积?图15.如图1,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0). (1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M 运动t 秒时,△MON 的面积为S .① 求S 与t 的函数关系式;② 设点M 在线段OB 上运动时,是否存在S =4的情形?若存在,求出对应的t 值;若不存在请说明理由;③在运动过程中,当△MON 为直角三角形时,求t 的值.图16.已知Rt △ABC 中,︒=∠90ACB ,CB CA =,有一个圆心角为︒45,半径的长等于CA 的扇形CEF 绕点C 旋转,且直线CE ,CF 分别与直线AB 交于点M ,N .(1)当扇形CEF 绕点C 在ACB ∠的内部旋转时,如图1,求证:222BN AM MN +=;思路点拨:考虑222BN AM MN +=符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM 沿直线CE 对折,得△DCM ,连DN ,只需证BN DN =,︒=∠90MDN 就可以了.请你完成证明过程.(2)当扇形CEF 绕点C 旋转至图2的位置时,关系式222BN AM MN +=是否仍然成立?若成立,请证明;若不成立,请说明理由.图1 图2学科组长审核签字:。
存在型问题——直角三角形问题

中考数学压轴题解题策略直角三角形的存在性问题解题策略专题攻略解直角三角形的存在性问题,一般分三步走,第一步寻找分类标准,第二步列方程,第三步解方程并验根. 一般情况下,按照直角顶点或者斜边分类,然后按照三角比或勾股定理列方程. 有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便.解直角三角形的问题,常常和相似三角形、三角比的问题联系在一起.如果直角边与坐标轴不平行,那么过三个顶点作与坐标轴平行的直线,可以构造两个新的相似直角三角形,这样列比例方程比较简便.在平面直角坐标系中,两点间的距离公式常常用到.怎样画直角三角形的示意图呢?如果已知直角边,那么过直角边的两个端点画垂线,第三个顶点在垂线上;如果已知斜边,那么以斜边为直径画圆,直角顶点在圆上(不含直径的两个端点).例题解析例❶ 如图1-1,在△ABC 中,AB =AC =10,cos ∠B =45.D 、E 为线段BC 上的两个动点,且DE =3(E 在D 右边),运动初始时D 和B 重合,当E 和C 重合时运动停止.过E 作EF //AC 交AB 于F ,连结DF .设BD =x ,如果△BDF 为直角三角形,求x 的值.图1-1【解析】△BDF 中,∠B 是确定的锐角,那么按照直角顶点分类,直角三角形BDF 存在两种情况.如果把夹∠B 的两条边用含有x 的式子表示出来,分两种情况列方程就可以了.如图1-2,作AH ⊥BC ,垂足为H ,那么H 是BC 的中点.在Rt △ABH 中,AB =10,cos ∠B =45,所以BH =8.所以BC =16. 由EF //AC ,得BF BE BA BC =,即31016BF x +=.所以BF =5(3)8x +.图1-2 图1-3 图1-4①如图1-3,当∠BDF =90°时,由4cos 5BD B BF ∠==,得45BD BF =.解方程45(3)58x x =⨯+,得x =3. ②如图1-4,当∠BFD =90°时,由4cos 5BF B BD ∠==,得45BF BD =. 解方程5154885x x +=,得757x =. 我们看到,在画示意图时,无须受到△ABC 的“限制”,只需要取其确定的∠B .例❷ 如图2-1,已知在平面直角坐标系中,点A 的坐标为(-2, 0),点B 是点A 关于原点的对称点,P 是函数)0(2>=x xy 图象上的一点,且△ABP 是直角三角形,求点P 的坐标.图2-1【解析】A 、B 两点是确定的,以线段AB 为分类标准,分三种情况.如果线段AB 为直角边,那么过点A 画AB 的垂线,与第一象限内的一支双曲线没有交点;过点B 画AB 的垂线,有1个交点.以AB 为直径画圆,圆与双曲线有没有交点呢?先假如有交点,再列方程,方程有解那么就有交点.如果是一元二次方程,那么可能是一个交点,也可能是两个交点.由题意,得点B 的坐标为(2,0),且∠BAP 不可能成为直角.① 图2-2,当∠ABP =90°时,点P 的坐标为(2,1).② 方法一:如图2-3,当∠APB =90°时,OP 是Rt △APB 的斜边上的中线,OP =2.设P 2(,)x x ,由OP 2=4,得2244x x+=.解得x =P (2,2).图2-2 图2-3 方法二:由勾股定理,得P A 2+PB 2=AB 2.解方程2222222(2)()(2)()4x x x x+++++=,得x = 方法三:如图3-4,由△AHP ∽△PHB ,得PH 2=AH ·BH .解方程22()(2)(2)x x x=+-,得x =图2-4 图2-5这三种解法的方程貌似差异很大,转化为整式方程之后都是(x2-2)2=0.这个四次方程的解是x1=x2=2,x3=x4=它的几何意义就是以AB为直径的圆与双曲线相切于P、P′两点(如图2-5).例❸如图3-1,已知直线y=kx-6经过点A(1,-4),与x轴相交于点B.若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标.图3-1【解析】和例题3一样,过A、B两点分别画AB的垂线,各有1个点Q.和例题2不同,以AB为直径画圆,圆与y轴有没有交点,一目了然.而圆与双曲线有没有交点,是徒手画双曲线无法肯定的.将A(1,-4)代入y=kx-6,可得k=2.所以y=2x-6,B(3,0).设OQ的长为m.分三种情况讨论直角三角形ABQ:①图3-2,当∠AQB=90°时,△BOQ∽△QHA,BO QHOQ HA=.所以341mm-=.解得m=1或m=3.所以Q(0,-1)或(0,-3).②如图3-3,当∠BAQ=90°时,△QHA∽△AGB,QH AGHA GB=.所以4214m-=.解得72m=.此时7(0,)2Q-.②图3-4,当∠ABQ=90°时,△AGB∽△BMQ,AG BMGB MQ=.所以243m=.解得32m=.此时3(0,)2Q.图4-2 图4-3 图4-4三种情况的直角三角形ABQ ,直角边都不与坐标轴平行,我们以直角顶点为公共顶点,构造两个相似的直角三角形,这样列比例方程比较简便.已知A (1,-4)、B (3,0),设Q (0, n ),那么根据两点间的距离公式可以表示出AB 2,AQ 2和BQ 2,再按照斜边为分类标准列方程,就不用画图进行“盲解”了.(难)例❹ 如图4-1,抛物线233384y x x =--+与x 轴交于A 、B 两点(点A 在点B 的左侧).若直线l 过点E (4, 0),M 为直线l 上的动点,当以A 、B 、M 为顶点所作的直角三角形有且只有....三个时,求直线l 的解析式.图4-1【解析】有且只有三个直角三角形ABM 是什么意思呢?过A 、B 两点分别画AB 的垂线,与直线l 各有一个交点,那么第三个直角顶点M 在哪里?以AB 为直径的⊙G 与直线l 相切于点M 啊! 由23333(4)(2)848y x x x x =--+=-+-,得A (-4, 0)、B (2, 0),直径AB =6. 如图5-2,连结GM ,那么GM ⊥l .在Rt △EGM 中,GM =3,GE =5,所以EM =4.因此3tan 4GEM ∠=. 设直线l 与y 轴交于点C ,那么OC =3.所以直线l (直线EC )为334y x =-+. 根据对称性,直线l 还可以是334y x =-.图4-2例❺如图5-1,在△ABC中,CA=CB,AB=8,4cos5A∠=.点D是AB边上的一个动点,点E与点A关于直线CD对称,连结CE、DE.(1)求底边AB上的高;(2)设CE与AB交于点F,当△ACF为直角三角形时,求AD的长;(3)连结AE,当△ADE是直角三角形时,求AD的长.图5-1【解析】这道题目画示意图有技巧的,如果将点D看作主动点,那么CE就是从动线段.反过来画图,点E在以CA为半径的⊙C上,如果把点E看作主动点,再画∠ACE的平分线就产生点D了.(1)如图5-2,设AB边上的高为CH,那么A H=BH=4.在Rt△ACH中,AH=4,4cos5A∠=,所以AC=5,CH=3.(2)①如图5-3,当∠AFC=90°时,F是AB的中点,AF=4,CF=3.在Rt△DEF中,EF=CE-CF=2,4cos5E∠=,所以52DE=.此时52AD DE==.②如图5-4,当∠ACF=90°时,∠ACD=45°,那么△ACD的条件符合“角边角”.作DG⊥AC,垂足为G.设DG=CG=3m,那么AD=5m,AG=4m.由CA=5,得7m=5.解得57m=.此时2557AD m==.图5-2 图5-3 图5-4(3)因为DA=DE,所以只存在∠ADE=90°的情况.①如图5-5,当E在AB下方时,根据对称性,知∠CDA=∠CDE=135°,此时△CDH 是等腰直角三角形,DH=CH=3.所以AD=AH-DH=1.③图5-6,当E在AB上方时,根据对称性,知∠CDA=∠CDE=45°,此时△CDH是等腰直角三角形,DH=CH=3.所以AD=AH+DH=7.图5-5 图5-6。
[中考数学压轴题的解题策略12讲之三]直角三角形的存在性问题解题策略
![[中考数学压轴题的解题策略12讲之三]直角三角形的存在性问题解题策略](https://img.taocdn.com/s3/m/8b53e4fb04a1b0717fd5ddc0.png)
1 所以OE � OA � 1 2
于是EB � 3, EC � 1.5
所以OC � 2.5, C (2.5,0)
三部曲:
——
先找分类标准; 再画示意图;
②当∠EAD=90°
那么△AOE∽△BOA
后计算.
OA OB 因此 � �2 OE OA 1 所以OE � OA � 1 2
于是EB � 5, EC � 2.5
①C为直角顶点
后计算.
A(1.5,0),B(4,0),C(0,-3)
1 2 11 y � � x � x�3 2 4
1 2 11 设P( x,� x � x � 3) 2 4 1 2 11 那么x � 2( x � x) 2 4 13 解得x1 � 0, x2 � 2
三部曲:
——
先找分类标准; 再画示意图;
②Q为直角顶点 的Rt△QCP有2个
三部曲:
——
先找分类标准; 再画示意图;
后计算.
①C为直角顶点
NC OA 1 于是 � � NP OC 2
那么△AOC∽△CNP
因此NP � 2 NC
数形结合, xP � 2( yC � y N )
三部曲:
——
先找分类标准; 再画示意图;
数形结合, xP � 2( yC � y N )
①C为直角顶点
后计算.
13 解得x1 � 0, x2 � 2
x1 � 0的几何意义就是点 C
13 x2 � 的几何意义就是点 P 2
三部曲:
——
先找分类标准; 再画示意图;
后计算.
②Q为直角顶点
MP' OB' 1 于是 � � MB OB 2
数形结合, xB � xP ' � 2 yP '
直角三角形存在性问题专题攻略

一、专题攻略1、解直角三角形的存在性问题,一般分三个步骤第一步寻找分类标准,第二步列方程,第三步解方程并验根。
2、解直角三角形的问题,常常和相似三角形、三角比的问题联系在一起。
3、一般情况下,按照直角顶点或者斜边分类,然后按照三角比或勾股定理列方程。
4、在平面直角坐标系中,两点间的距离公式常常用得到。
5、有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便。
二、典型例题例、如图,在直角坐标平面内,O为原点,二次函数y=-x2十2x+ 3的图象与,轴交于点A,与y 轴交于点B,顶点为P.如果点Q是x轴上一点,以点A、P、Q为顶点的三角形是直角三角形,求点Q的坐标三、针对训练1.如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC.设AB=x,若△ABC 为直角三角形,求x的值.【考点】旋转的性质;勾股定理的逆定理.【专题】分类讨论.【分析】根据三角形的三边关系:两边之和大于第三边,即可得到关于x的不等式组,求出x的取值范围,再根据勾股定理,即可列方程求解.【解答】解:∵在△ABC中,AC=1,AB=x,BC=3﹣x.∴,解得1<x<2;①若AC为斜边,则1=x2+(3﹣x)2,即x2﹣3x+4=0,无解,②若AB为斜边,则x2=(3﹣x)2+1,解得x=,满足1<x<2,③若BC为斜边,则(3﹣x)2=1+x2,解得x=,满足1<x<2,故x的值为:或.故答案为:或.【点评】本题主要考查了三角形的三边关系以及勾股定理,正确理解分类讨论是解题的关键.2.如图,已知在平面直角坐标系中,点A的坐标为(﹣2,0),点B是点A关于原点的对称点,P是函数图象上的一点,且△ABP是直角三角形.(1)求点P的坐标;(2)如果二次函数的图象经过A、B、P三点,求这个二次函数的解析式;(3)如果第(2)小题中求得的二次函数图象与y轴交于点C,过该函数图象上的点C,点P的直线与x轴交于点D,试比较∠BPD与∠BAP的大小,并说明理由.【考点】二次函数综合题.【专题】综合题.【分析】(1)先求得B点坐标,再分析△ABP满足是直角三角形时P点的情况,可分为AB为直角边和AB为斜边两种情况作答.(2)对(1)求得的P点坐标分别讨论是否满足二次函数抛物线,求得二次函数的解析式.(3)由点的坐标可证得△PBD∽△APD,则∠BPD与∠BAP满足相等.【解答】解:(1)由题意,得点B的坐标为(2,0).设点P的坐标为(x,y),由题意可知∠ABP=90°或∠APB=90°.(i)当∠ABP=90°时,x=2,y=1,∴点P坐标是(2,1);(ii)当∠APB=90°时,PA2+PB2=AB2,即(x+2)2+y2+(x﹣2)2+y2=16①.又由,可得y2=,代入①解得:(负值不合题意,舍去).当时,.∴点P点坐标是(,).综上所述,点P坐标是(2,1)或(,).(2)设所求的二次函数的解析式为y=ax2+bx+c(a≠0),(i)当点P的坐标为(2,1)时,点A、B、P不可能在同一个二次函数图象上;(ii)当点P的坐标为(,)时,代入A、B、P三点的坐标,解得:∴所求的二次函数解析式为.(3)∠BPD=∠BAP.证明如下:∵点C坐标为(0,),∴直线PC的表达式为.∴点D坐标为(,0).∴PD=2,BD=,AD=.,∴.∵∠PDB=∠ADP,∴△PBD∽△APD.∴∠BPD=∠BAP.【点评】本题考查了二次函数的综合应用,重点是求解函数的解析式.3.如图,抛物线y=ax2+bx﹣3与x轴交于两点A(1,0)、B(3,0),与y轴交于点D.(1)求抛物线的解析式;(2)在抛物线是否存在一点P,使得△BDP是以BD为斜边的直角三角形,若存在,请求出点P 的坐标;若不存在,请说明理由;(3)在x轴下方的抛物线上是否存在点M,过M作MN⊥x轴于点N,使以A、M、N为顶点的三角形与△BCD相似?若存在,则求出点M的坐标;若不存在,请说明理由.【考点】二次函数综合题.【专题】压轴题.【分析】(1)利用待定系数法求出二次函数解析式即可;(2)过P作x轴的平行线交Y轴于E点,过B点作X轴的垂线交EP的延长线于F点,利用三角形相似得出P点的坐标;(3)利用△AMN∽△CDB,当N在A点左边时,当N在A点右边时,当N在A点右边时,当N在A点左边时分别得出即可.【解答】解:(1)∵抛物线y=ax2+bx﹣3与x轴交于两点A(1,0)、B(3,0),∴0=a+b﹣3,0=9a+3b﹣3,解得:a=﹣1,b=4,∴y=﹣x2+4x﹣3;(2)如图1,过P作x轴的平行线交Y轴于E点,过B点作X轴的垂线交EP的延长线于F点,设P(t,﹣t2+4t﹣3),当P点在第一象限时,则DE=﹣t2+4t,PF=3﹣t,PE=t,BF=﹣t2+4t﹣3,可证△DEP∽△PFB,,,可求得,所以P(,),同理,当P点在第四象限时,可求得P(,);(3)如图2,设N(m,0)则M(m,﹣m2+4m﹣3),MN=m2﹣4m+3若△AMN∽△CDB,,当N在A点左边时AN=1﹣m,,m=0或m=1(舍),所以M(0,﹣3),当N在A点右边时AN=m﹣1,,m=6或m=1(舍),所以M(6,﹣15),若△MAN∽△CDB,,当N在A点左边时AN=1﹣m,,m=(舍)或m=1(舍),所以此时M不存在,当N在A点右边时AN=m﹣1,,m=或m=1(舍),所以M(,),综上M1(0,﹣3)M2(6,﹣15)M3(,).【点评】此题主要考查了二次函数的综合应用,(2)(3)小题中,都用到了分类讨论的数学思想,难点在于考虑问题要全面,做到不重不漏.四、三年真题4.(15宜宾24)如图,抛物线y=﹣x2+bx+c与x轴分别相交于点A(﹣2,0),B(4,0),与y轴交于点C,顶点为点P.(1)求抛物线的解析式;(2)动点M、N从点O同时出发,都以每秒1个单位长度的速度分别在线段OB、OC上向点B、C方向运动,过点M作x轴的垂线交BC于点F,交抛物线于点H.①当四边形OMHN为矩形时,求点H的坐标;②是否存在这样的点F,使△PFB为直角三角形?若存在,求出点F的坐标;若不存在,请说明理由.【考点】二次函数综合题.【专题】压轴题.【分析】(1)把A(﹣2,0),B(4,0),代入抛物线y=﹣x2+bx+c,求出b、c即可;(2)①表示出ON、MH,运用ON=MH,列方程求解即可;②存在,先求出BC的解析式,根据互相垂直的直线一次项系数积等于﹣1,直线经过点P,待定系数法求出直线PF的解析式,求直线BC与直线PF的交点坐标即可.【解答】解:(1)把A(﹣2,0),B(4,0),代入抛物线y=﹣x2+bx+c得:解得:b=1,c=4,∴y=﹣x2+x+4;(2)点C的坐标为(0,4),B(4,0)∴直线BC的解析式为y=﹣x+4,①根据题意,ON=OM=t,MH=﹣t2+t+4∵ON∥MH∴当ON=MH时,四边形OMHN为矩形,即t=﹣t2+t+4解得:t=2或t=﹣2(不合题意舍去)把t=2代入y=﹣t2+t+4得:y=2∴H(2,2);②存在,当PF⊥BC时,∵直线BC的解析式为y=﹣x+4,∴设PF的解析式为y=x+b,又点P(1,)代入求得b=,∴根据题意列方程组:解得:∴F(,)当PF⊥BP时,∵点P(1,),B(4,0),∴直线BP的解析式为:y=﹣x+6,∴设PF的解析式为y=x+b,又点P(1,)代入求得b=,∴根据题意列方程组:解得:∴F(,),综上所述:△PFB为直角三角形时,点F的坐标为(,)或(,).【点评】本题考查了待定系数法求直线和抛物线解析式,求顶点坐标,矩形的判定与性质以及两直线互相垂直的性质,本题有一定的综合性,难度不大,关键是掌握两直线互相垂直的性质.5.(16白银张掖28)如图,已知抛物线y=﹣x2+bx+c经过A(3,0),B(0,3)两点.(1)求此抛物线的解析式和直线AB的解析式;(2)如图①,动点E从O点出发,沿着OA方向以1个单位/秒的速度向终点A匀速运动,同时,动点F从A点出发,沿着AB方向以个单位/秒的速度向终点B匀速运动,当E,F中任意一点到达终点时另一点也随之停止运动,连接EF,设运动时间为t秒,当t为何值时,△AEF为直角三角形?(3)如图②,取一根橡皮筋,两端点分别固定在A,B处,用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P与A,B两点构成无数个三角形,在这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时点P的坐标;如果不存在,请简要说明理由.【考点】二次函数综合题.【分析】(1)用待定系数法求出抛物线,直线解析式;(2)分两种情况进行计算即可;(3)确定出面积达到最大时,直线PC和抛物线相交于唯一点,从而确定出直线PC解析式为y=﹣x+,根据锐角三角函数求出BD,计算即可.【解答】解:(1)∵抛物线y=﹣x2+bx+c经过A(3,0),B(0,3)两点,∴,∴,∴y=﹣x2+2x+3,设直线AB的解析式为y=kx+n,∴,∴,∴y=﹣x+3;(2)由运动得,OE=t,AF=t,∴AE=OA﹣OE=3﹣t,∵△AEF为直角三角形,∴①△AOB∽△AEF,∴,∴,∴t=,②△AOB∽△AFE,∴,∴,∴t=1;(3)如图,存在,过点P作PC∥AB交y轴于C,∵直线AB解析式为y=﹣x+3,∴设直线PC解析式为y=﹣x+b,联立,∴﹣x+b=﹣x2+2x+3,∴x2﹣3x+b﹣3=0∴△=9﹣4(b﹣3)=0∴b=,∴BC=﹣3=,x=,∴P(,).过点B作BD⊥PC,∴直线BD解析式为y=x+3,∴BD=,∴BD=,∵AB=3S最大=AB×BD=×3×=.即:存在面积最大,最大是,此时点P(,).【点评】此题是二次函数综合题,主要考查了待定系数法求函数解析式,相似三角形的性质和判定,平行线的解析式的确定方法,互相垂直的直线解析式的确定方法,解本题的关键是确定出△PAB面积最大时点P的特点.6.(16重庆B卷26)如图1,二次函数y=x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.(1)求直线AB和直线BC的解析式;(2)点P是线段AB上一点,点D是线段BC上一点,PD∥x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F.当PF与PE的乘积最大时,在线段AB上找一点H (不与点A,点B重合),使GH+BH的值最小,求点H的坐标和GH+BH的最小值;(3)如图2,直线AB上有一点K(3,4),将二次函数y=x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K是直角三角形时,求t的值.【考点】二次函数综合题.【分析】(1)根据S△AMO:S四边形AONB=1:48,求出三角形相似的相似比为1:7,从而求出BN,继而求出点B的坐标,用待定系数法求出直线解析式.(2)先判断出PE×PF最大时,PE×PD也最大,再求出PE×PF最大时G(5,),再简单的计算即可;(3)由平移的特点及坐标系中,两点间的距离公式得A′C′2=8,A′K2=5m2﹣18m+18,C′K2=5m2﹣22m+26,最后分三种情况计算即可.【解答】解:(1)∵点C是二次函数y=x2﹣2x+1图象的顶点,∴C(2,﹣1),∵PE⊥x轴,BN⊥x轴,∴△MAO∽△MBN,∵S△AMO:S四边形AONB=1:48,∴S△AMO:S△BMN=1:49,∴OA:BN=1:7,∵OA=1∴BN=7,把y=7代入二次函数解析式y=x2﹣2x+1中,可得7=x2﹣2x+1,∴x1=﹣2(舍),x2=6∴B(6,7),∵A的坐标为(0,1),∴直线AB解析式为y=x+1,∵C(2,﹣1),B(6,7),∴直线BC解析式为y=2x﹣5.(2)如图1,设点P(x0,x0+1),∴D(,x0+1),∴PE=x0+1,PD=3﹣x0,∵∠DPF固定不变,∴PF:PD的值固定,∴PE×PF最大时,PE×PD也最大,PE×PD=(x0+1)(3﹣x0)=﹣x02+x0+3,∴当x0=时,PE×PD最大,即:PE×PF最大.此时G(5,)∵△MNB是等腰直角三角形,过B作x轴的平行线,∴BH=B1H,GH+BH的最小值转化为求GH+HB1的最小值,∴当GH和HB1在一条直线上时,GH+HB1的值最小,此时H(5,6),最小值为7﹣=(3)令直线BC与x轴交于点I,∴I(,0)∴IN=,IN:BN=1:2,∴沿直线BC平移时,横坐标平移m时,纵坐标则平移2m,平移后A′(m,1+2m),C′(2+m,﹣1+2m),∴A′C′2=8,A′K2=5m2﹣18m+18,C′K2=5m2﹣22m+26,当∠A′KC′=90°时,A′K2+KC′2=A′C′2,解得m=,此时t=m=2±;当∠KC′A′=90°时,KC′2+A′C′2=A′K2,解得m=4,此时t=m=4;当∠KA′C′=90°时,A′C′2+A′K2=KC′2,解得m=0,此时t=0.【点评】此题是二次函数综合题,主要考查了相似三角形的性质,待定系数法求函数解析式,两点间的距离公式,解本题的关键是相似三角形的性质的运用.7.(14年福州21)如图1,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.(1)当t=秒时,则OP=,S△ABP=;(2)当△ABP是直角三角形时,求t的值;(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求证:AQ•BP=3.【考点】相似形综合题.【专题】几何动点问题;压轴题.【分析】(1)如答图1所示,作辅助线,利用三角函数或勾股定理求解;(2)当△ABP是直角三角形时,有三种情形,需要分类讨论;(3)如答图4所示,作辅助线,构造一对相似三角形△OAQ∽△PBO,利用相似关系证明结论.【解答】(1)解:当t=秒时,OP=2t=2×=1.如答图1,过点P作PD⊥AB于点D.在Rt△POD中,PD=OP•sin60°=1×=,∴S△ABP=AB•PD=×(2+1)×=.(2)解:当△ABP是直角三角形时,①若∠A=90°.∵∠BOC=60°且∠BOC>∠A,∴∠A≠90°,故此种情形不存在;②若∠B=90°,如答图2所示:∵∠BOC=60°,∴∠BPO=30°,∴OP=2OB=2,又OP=2t,∴t=1;③若∠APB=90°,如答图3所示:过点P作PD⊥AB于点D,则OD=OP•sin30°=t,PD=OP•sin60°=t,∴AD=OA+OD=2+t,BD=OB﹣OD=1﹣t.在Rt△ABP中,由勾股定理得:PA2+PB2=AB2∴(AD2+PD2)+(BD2+PD2)=AB2,即[(2+t)2+(t)2]+[(1﹣t)2+(t)2]=32解方程得:t=或t=(负值舍去),∴t=.综上所述,当△ABP是直角三角形时,t=1或t=.(3)证明:如答图4,过点O作OE∥AP,交PB于点E,则有,∴PE=PB.∵AP=AB,∴∠APB=∠B,∵OE∥AP,∴∠OEB=∠APB,∴∠OEB=∠B,∴OE=OB=1,∠3+∠B=180°.∵AQ∥PB,∴∠OAQ+∠B=180°,∴∠OAQ=∠3;∵∠AOP=∠1+∠QOP=∠2+∠B,∠QOP=∠B,∴∠1=∠2;∴△OAQ∽△PEO,∴,即,化简得:AQ•PB=3.【点评】本题是运动型综合题,考查了相似三角形的判定与性质、解直角三角形、勾股定理、一元二次方程等多个知识点.第(2)问中,解题关键在于分类讨论思想的运用;第(3)问中,解题关键是构造相似三角形,本问有多种解法,可探究尝试.五、两年模拟8.(2015年曲靖麒麟区中考模拟第24题)如图,过点C(0,2)的抛物线与直线AD交于A(﹣1,0),D(3,2)两点.(1)求直线AD和抛物线的解析式;(2)点M为抛物线对称轴上一点,求MA+MC最小时点M的坐标;(3)在y轴上是否存在点P使△PAD是直角三形?若存在,求出点P坐标;若不存在,说明理由.【考点】二次函数综合题.【分析】(1)设出一次函数、二次函数解析式分别为y=kx+b,y=ax2+bx+c,将函数图象上的点代入,即可求函数解析式;(2)连接BC,与对称轴交于M,此时MA+MC最小.求出BC解析式,将M点横坐标代入即可求出其纵坐标;(3)分四种情况讨论:①当∠AP1D=90°时,△DCP1∽△P1OA;②∠AP2D=90°时,△AOP2∽△P2CD;③设AP3解析式为y=﹣2x+s,将A(﹣1,0)分别代入解析式,求出s的值;④设AP4解析式为y=﹣2x+t,将A(3,2)分别代入解析式得,t=8.【解答】解:(1)设AD的解析式为y=kx+b,将A(﹣1,0),D(3,2)分别代入解析式得,,解得,∴AD的解析式为y=x+.设抛物线的解析式为y=ax2+bx+c,将A(﹣1,0),C(0,2),D(3,2)分别代入解析式得,解得,,函数解析式为y=﹣x2+x+2.(2)如图1,连接BC,与对称轴交于M,此时MA+MC最小.设BC解析式为y=ax+b,把B(4,0),C(0,2)代入解析式得,,解得,则y=﹣x+2,当x=﹣=时,y=﹣×+2=,∴M(,).(3)①当∠AP1D=90°时,△DCP1∽△P1OA,∴=,即=,∴P1C2+2P1C=3,解得,P1C=1,P1C=﹣3(舍去).∴P1O=3,∴P1(0,3).②∠AP2D=90°时,△AOP2∽△P2CD,∴=,即=,∴P2O2+2P2O=3,解得,P2O=1,P2O=﹣3(舍去).∴P2O=3,∴P2(0,﹣3).③如图3,∵AP3⊥AD,DP4⊥AD,且AD解析式为y=x+,设AP3解析式为y=﹣2x+s,将A(﹣1,0)分别代入解析式得,s=﹣2,解析式为y=﹣2x﹣2,当x=0时,y=﹣2,则得P3(0,﹣2),④设AP4解析式为y=﹣2x+t,将A(3,2)分别代入解析式得,t=8,解析式为y=﹣2x+8,当x=0时,y=8,则得P4(0,8).【点评】本题考查了二次函数综合题,涉及待定系数法求二次函数解析式和一次函数解析式、轴对称最短路径问题、存在性问题和相似三角形的判定与性质,难度较大.9.(2016年汕头潮阳区中考模拟第25题)如图所示,在平面直角坐标系xOy中,Rt△AOB的直角边OB,OA分别在x轴上和y轴上,其中OA=2,OB=4,现将Rt△AOB绕着直角顶点O按逆时针方向旋转90°得到△COD,已知一抛物线经过C、D、B三点.(1)该抛物线的解析式为;(2)设点E是抛物线上位于第一象限的动点,过点E作EF⊥x轴于点F,并交直线AB于N,过点E再作EM⊥AB于点M,求△EMN周长的最大值;(3)当△EMN的周长最大时,在直线EF上是否存在点Q,使得△QCD是以CD为直角边的直角三角形?若存在请求出点Q的坐标,若不存在,请说明理由.【考点】二次函数综合题.【分析】(1)设抛物线的解析式为y=ax2+bx+c.由线段OA、OB的长度可得出点A、B的坐标,再由旋转的特性可得出点C、D的坐标,由点B、C、D三点的坐标利用待定系数法即可求出抛物线的解析式;(2)在Rt△AOB中,找出∠ABO的正弦余弦值,再根据相似三角形的判定定理找出△EMN∽△BFN,从而得出∠MEN=∠FBN,用EN的长度来表示出EM和MN的长度,由点A、B的坐标利用待定系数法求出直线AB的函数解析式,设出点E的坐标为(t,﹣+t+4)(0<t<4),即可找出点N的坐标为(t,﹣t+2),从而得出线段EN的长度,将EN、MN、EM相加即可得出△EMN的周长,根据二次函数的性质可求出EN的最大值,由此即可得出结论;(3)结合(2)的结论可知直线EF的解析式为x=,分∠QDC=90°和∠DCQ=90°两种情况来考虑,利用相似三角形的性质找出相似边的比例关系来找出线段的长度,再根据点与点间的数量关系即可找出点Q的坐标.【解答】解:(1)设抛物线的解析式为y=ax2+bx+c.∵OA=2,OB=4,∴点A(0,2),点B(4,0),由旋转的特性可知:点C(﹣2,0),点D(0,4).将点B(4,0)、点C(﹣2,0)、点D(0,4)代入到抛物线解析式得:,解得:.∴该抛物线的解析式为y=﹣+x+4.故答案为:y=﹣+x+4.(2)依照题意画出图形,如图1所示.在Rt△AOB中,OA=2,OB=4,∴AB===2,∴sin∠ABO=,cos∠ABO=.∵EM⊥AB,EF⊥OB,∴∠EMN=∠BFN=90°.∵∠BNF=∠ENM,∴△EMN∽△BFN,∴∠MEN=∠FBN.在Rt△EMN中,sin∠MEN=,cos∠MEN=,∴MN=EN•sin∠MEN=EN•sin∠ABO=EN,EM=EN•cos∠MEN=EN•cos∠ABO=EN.∴C△EMN=EM+MN+EN=EN+EN+EN=EN.由(1)知A(0,2)、B(4,0),设直线AB的解析式为:y=kx+2,∴4k+2=0,解得:k=﹣,∴直线AB的解析式为:y=﹣x+2.设抛物线上点E的坐标为(t,﹣+t+4)(0<t<4),∵EF⊥OB,∴令y=﹣x+2中x=t,y=﹣t+2,∴点N的坐标为(t,﹣t+2),∴EN=﹣+t+4﹣(﹣t+2)=﹣+t+2.∴C△EMN=(﹣+t+2)=﹣+t+(0<t<4).∴当t=﹣=时,EN最大,此时C△EMN最大,∴C△EMN最大为:[﹣+2]=.(3)由(2)知,当C△EMN取最大值时,EF的解析式为:x=.①若∠QDC=90°,过点Q作QG⊥y轴于点G,如图2所示.∵EF的解析式为:x=,∴QG=,∵∠QDG+∠DQG=90°,∠CDO+∠QDG=90°,∴∠DGQ=∠CDO,又∵∠QGD=∠DOC=90°,∴△QDG∽△DCO,∴,∴DG=2×=.∴OG=OD﹣DG=4﹣=,∴点Q的坐标为(,);②若∠DCQ=90°,如图3所示.CF=﹣(﹣2)=,∵∠QCF+∠OCD=90°,∠CDO+∠OCD=90°,∴∠QCF=∠CDO,又∵∠CFQ=∠DOC=90°,∴△COD∽△QFC,∴,即,∴FQ=,∴点Q的坐标为(,﹣).综上所述,当点Q的坐标为(,)或(,﹣)时,使得△QCD是以CD为直角边的直角三角形.【点评】本题考查了二次函数的性质、待定系数法求函数解析式、相似三角形的判定及性质以及三角形的周长,解题的关键是:(1)求出点B、C、D的坐标;(2)用线段EN的长度来表示△EMN 的周长;(3)分两种情况考虑.本题属于中档题,难道不大,但非常繁琐,解决该题型题目时,依据题意作出图形,利用数形结合来解决问题是关键。
直角三角形的性质及解题方法

直角三角形的性质及解题方法直角三角形是我们在初中数学中学习的一个重要概念。
它不仅有着特殊的性质,而且在解题中也有着独特的方法。
本文将探讨直角三角形的性质以及解题方法。
首先,我们来了解直角三角形的基本定义。
直角三角形是指其中一个角为90度的三角形。
在直角三角形中,我们通常将直角所在的边称为斜边,而与直角相邻的两条边分别称为直角边。
根据勾股定理,直角三角形的斜边的平方等于两个直角边的平方和。
这是直角三角形的基本性质之一。
除了勾股定理,直角三角形还有许多其他重要的性质。
首先,直角三角形的两个直角边互为补角。
也就是说,它们的两个角的和等于90度。
这个性质在解题中经常被用到。
其次,直角三角形的两个直角边的比例关系也很重要。
我们可以利用这个比例关系来求解各种与直角三角形有关的问题。
在解题中,我们经常需要利用直角三角形的性质来求解各种未知量。
其中最常见的问题是求解直角三角形的边长。
根据勾股定理,我们可以通过已知的两个边长来求解第三个边长。
例如,如果我们已知一个直角三角形的一个直角边长为3,斜边长为5,那么我们可以利用勾股定理求解另一个直角边的长度。
根据勾股定理,我们有3的平方加上另一个直角边的平方等于5的平方。
解方程得到另一个直角边的长度为4。
除了求解边长,我们还可以利用直角三角形的性质来求解角度。
例如,如果我们已知一个直角三角形的两个直角边的长度,我们可以通过求解三角函数来求解角度。
三角函数是一组与三角形的边长和角度之间的关系相关的函数。
其中最常见的三角函数有正弦、余弦和正切。
通过利用这些三角函数,我们可以求解直角三角形中各个角的大小。
除了以上的解题方法,我们还可以利用直角三角形的相似性质来求解各种问题。
直角三角形的相似性质是指如果两个直角三角形的对应角相等,那么它们的对应边的比例也相等。
这个性质在解题中经常被用到。
例如,如果我们已知一个直角三角形的两个角度,我们可以通过相似性质来求解其他边的长度。
总之,直角三角形是数学中一个重要的概念。
中考数学压轴题专题直角三角形的存在性
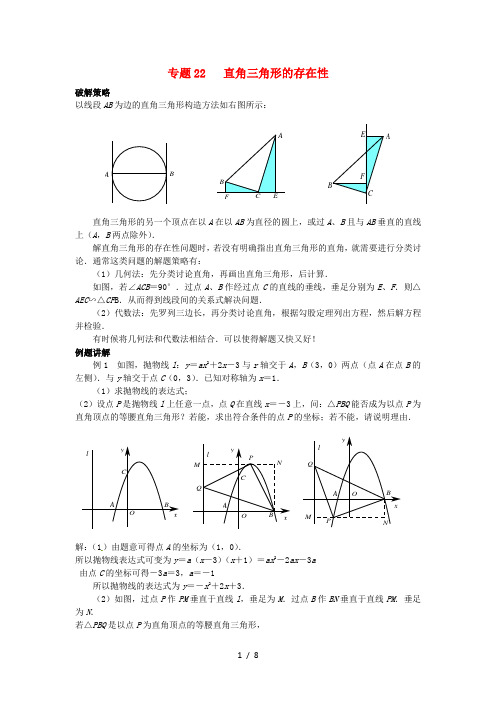
专题22 直角三角形的存在性破解策略以线段AB 为边的直角三角形构造方法如右图所示:A BAB ECFEFABC直角三角形的另一个顶点在以A 在以AB 为直径的圆上,或过A 、B 且与AB 垂直的直线上(A ,B 两点除外).解直角三角形的存在性问题时,若没有明确指出直角三角形的直角,就需要进行分类讨论.通常这类问题的解题策略有:(1)几何法:先分类讨论直角,再画出直角三角形,后计算.如图,若∠ACB =90°.过点A 、B 作经过点C 的直线的垂线,垂足分别为E 、F .则△AEC ∽△CF B .从而得到线段间的关系式解决问题.(2)代数法:先罗列三边长,再分类讨论直角,根据勾股定理列出方程,然后解方程并检验.有时候将几何法和代数法相结合.可以使得解题又快又好! 例题讲解例1 如图,抛物线l :y =ax 2+2x -3与r 轴交于A ,B (3,0)两点(点A 在点B 的左侧).与y 轴交于点C (0,3).已知对称轴为x =1. (1)求抛物线的表达式;(2)设点P 是抛物线l 上任意一点,点Q 在直线x =-3上,问:△PBQ 能否成为以点P 为直角顶点的等腰直角三角形?若能,求出符合条件的点P 的坐标;若不能,请说明理由.xy CB AOlxyCMNABOQlP xylQA O NB PM解:(1)由题意可得点A 的坐标为(1,0).所以抛物线表达式可变为y =a (x -3)(x +1)=ax 2-2ax -3a 由点C 的坐标可得-3a =3,a =-1所以抛物线的表达式为y =-x 2+2x +3.(2)如图,过点P 作PM 垂直于直线l ,垂足为M .过点B 作BN 垂直于直线PM .垂足为N .若△PBQ 是以点P 为直角顶点的等腰直角三角形,无论点P 在BQ 的上方或下方,由“弦图模型”均可得△PQM ∽△BPN . 所以PM =BN .设点P 的坐标为(m ,H ,-m 2+2m +3).则PM =|m +3|,BN =|-m 2+2m +3|,所以|m +3|=|-m 2+2m +3|.解得m 1=0,m 2=1,m 3=3+332,m 4=3332- 所以点P 的坐标为(0,3),(1,4),(3+132,332-9-),(3332-,32+3-9)例2 如图,一次函数y =-2x +10的图象与反比例函数y =kx(k >0)的图象相交于A 、B两点(点A 在点B 的右侧),分别交x 轴.y 轴于点E ,F .若点A 的坐标为(4,2).问:反比例函数图象的另一支上是否存在一点P .使△PAB 是以AB 为直角边的直角三角形?若存在,求出所有符合条件的点P 的坐标;若不存在,请说明理由,xy B AFPO Exy OPEBFA解:将点A (4,2)代入反比例函数表达式,得k =8, 所以反比例函数为y =8x, 联立方程纽组8210y x y x ⎧=⎪⎨⎪=-+⎩ , 解得1142x y =⎧⎨=⎩,2218x y =⎧⎨=⎩ 所以点B 的坐标为(1,8).由题意可得点E .F 的坐标分剐为(5,0),(0,10), 以AB 为直角迎的直角三角形有两种情况:如图1,当∠PAB =90°时,连结OA ,则OA 2242+25而AE 2212+5,OE =5,所以OA 2+AE 2=OE 2, 即OA ⊥A B .所以A ,O ,P 三点共线. 由O 、A 两点的坐标可得直线AP 的表达式为y =12x . 联立方程组812y xy x ⎧=⎪⎪⎨⎪=⎪⎩解得1142x y =⎧⎨=⎩,2242x y =-⎧⎨=-⎩所以点P的坐标为(-4,-2).②如图2,当∠PBA=90°时,记BP与y轴的交点为G.易证△FBC∽△FOE,所以FB FO FG FE=,而FO=10.FEFB可求得FG=52,所以点G的坐标为(0,152).由B,G两点的坐标可得直线BP的表达式为y=12x+152,联立方程组115228y xyx⎧⎪⎪⎨⎪⎪⎩=+,=,解得1118xy⎧⎨⎩=,=;221612xy⎧⎪⎨⎪⎩=-,=-.所以点P的坐标为(-16,-12);综上可得,满足条件的点P坐标为(-4,-2)或(-16,-12).图2例3 如图,抛物线C1:y=a(x-2)2-5的顶点为P,与x轴相交于A,B两点(点A 在点B的左侧),点A的横坐标是-1.D是x轴负半轴上的一个动点,将抛物线C1绕点D旋转180°后得到抛物线C2.抛物线C2的顶点为Q,与x轴相交于E,F两点(点E在点F的左侧).当以点P,Q,E为顶点的三角形是直角三角形时,求顶点Q的坐标.C解 由题意可得点A (-1,0),P (2,-5),B (5,0).设点D 的坐标为(m ,0),则点Q 的坐标为(2m -2,5),E 的坐标为(2m -5,0),所以PQ 2=(2m -4)2 +102,PE 2=(2m -7)2+52,EQ 2=32+52=34. △PQE 为直角三角形有三种情况:①当∠PQE = 90°时,有PE 2=PQ 2+ EQ 2,即(2m -7)2+52=(2m -4)2+102+34,解得m =-193,所以点Q 的坐标为(-443,5);②当∠QEP =90°时,有PQ 2=PE 2 +EQ 2,即(2m -4)2+102=(2m -7)2+52+34,解得m =-23,所以点Q 的坐标为(-103,5);③当∠QPE = 90°时,有EQ 2=PE 2 + PQ 2,即(2m -7)2+52+(2m -4)2+102=34,方程无解,所以此种情况不成立,综上可得,当△PQE 为直角三角形时,顶点Q 的坐标为(-443,5)或(-103,5). 例4 如图.在直角梯形ABCD 中,AD ∥BC ,∠B = 90°,AD =2,BC =6,AB =3.E 为BC 边上一点,当BE =2时,以BE 为边作正方形BEFG ,使正方形BEFG 和梯形ABCD 在BC 的同侧.当正方形BEFG 沿BC 向右平移,记平移中的正方形BEFG 为正方形B ′EFG ,当点E 与点C 重合时停止平移.设平移的距离为t ,正方形B 'EFG 的边EF 与AC 交于点M ,连结B ′D ,B 'M ,DM .问:是否存在这样的t ,使△B 'DM 是直角三角形,若存在,求出t 的值;若不存在,请说明理由.EB'MFGCD AB解 存在满足条件的t .理由如下:如图,过点D 作DH ⊥ BC 于点H ,过点M 作MN ⊥DH 于点N , 则BH =AD =2,DH =AB =3.所以BB ′=HE =t ,HB ′=|t -2|,EC =4-t . 易证△MEC ∽△ABC , 可得ME AB =EC BC ,即3ME =46t -,所以ME =2-12t . 在Rt △B ′ME 中,有B ′M 2=ME 2+B ′E 2=14t 2-2t +8. 在Rt △DHB ′中,有B ′D 2=DH 2+B ′H 2=t 2-4t +13. 在Rt △DMN 中,DN =DH -NH =12t +1. 则DM 2=DN 2+MN 2=54t 2+t +1. ①若∠DB'M =90°,则DM 2=B'M 2+B'D 2,即54t 2+t +1=(14t 2-2t +8)+(t 2-4t +13), 解得t 1=207; ②若∠B'MD =90°,则B'D 2=B'M 2+DM 2,即t 2-4t +13=(14t 2-2t +8)+(54t 2+t +1), 解得t 2=-3+17,t 3=-3-17(舍);③若∠B'DM =90°,则B'M 2=B 'D 2+DM 2,即14t 2-2t +8=(t 2-4t +13)+(54t 2+t +1), 此方程无解. 综上所得,当t =207或-3+17时,△B'DM 是直角三角形. NHBAD CGFM B'E进阶训练1.如图,在平面直角坐标系xOy 中,Rt △OAB 的直角顶点A 在x 轴上,OA =4,AB =3.动点M 从点A 出发,以每秒1个单位长度的速度,沿AO 向终点O 移动;同时点N 从点O 出发,以每秒1.25个单位长度的速度,沿OB 向终点B 移动.当两个动点运动了x (0<x <4)时,解答下列问题:(1)求点N 的坐标(用含x 的代数式表示);(2)在两个动点运动过程中,是否存在某一时刻,使△OMN 是直角三角形?若存在,求出x 的值;若不存在,请说明理由.yMN O解:(1)N (x ,34x ); (2)当△OMN 是直角三角形时,x 的值为2或6441. 【提示】(1)过点N 作NP ⊥OA 于点P ,由△PON ∽△AOB 即可求得; (2)分类讨论,通过△OMN 和△OAB 相似即可列出等式求得x 的值.POBA N M xy2.如图,在平面直角坐标xOy 中,直线y =kx -3与双曲线y =4x的两个交点为A ,B .其中A (-1,a ).若M 为x 轴上的一个动点,且△AMB 为直角三角形,求满足条件的点M 的坐标.AxyBO解:满足条件的点M 的坐标为(-5,0),(5,0),(3412-,0)或(3412+,0). 【提示】先求出点A ,B 的坐标,再设点M 的坐标,从而用待定字母表示AM 2,BM 2,AB 2.然后讨论直角,根据勾股定理列方程即可.3.如图,抛物线233384yx x 与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C .(1)求点A ,B 的坐标; (2)若直线l 过点E (4,0),M 为直线l 上的一个动点,当以A ,B ,M 为顶点所作的直角三角形有且只有三个时,求直线l 的表达式.OCBAy xD EM 3M 2M 1OCBAyx解:(1)A (﹣4,0),B (2,0);(2)直线l 的表达式为334yx 或334y x . 【提示】(2)若△ABM 是直角三角形,则点M 在以AB 为直径的圆上,或过A ,B 且与AB 垂直的直线上(A ,B 两点除外).由题意可得直线l 与以AB 为直径的圆相切(如图),点M 1,M 2,M 3即为满足条件的三个点,此时直线l :334yx ;根据对称性,直线l 还可以为334yx4,如图,顶点为P (4,﹣4)的二次函数图象经过原点O (0,0),点A 在该图象上, OA 交其对称轴l 于点M ,点M ,N 关于点P 对称,连结AN ,ON . (1)求该二次函数的表达式;(2)当点A 在对称轴l 右侧的二次函数图象上运动时,请回答下列问题: ①证明:∠ANM =∠ONM ;②△ANO 能否为直角三角形?如果能,请求出所有符合条件的点A 的坐标;如果不能,请说明理由.解:(1)2124y x x ;(2)①略;②△ANO 能为直角三角形,符合条件的点A 的坐标为(442,4)【提示】(2)①过点A 作AH ⊥l 于点H ,令l 与x 轴的交点为D .设点A (m ,2124m m ),则直线AO 的表达式为1(2)4ym x ,从而求得点M 的坐标为(4,m -8),N 的坐标为(4,﹣m ),只需证明tan∠ANH =tan∠OND 即可;②分类讨论:当∠ANO =90°时,∠ANM =∠ONM =45°,点N 与点P 重合,点M 与点D 重合,不满足M ,N 关于点P 对称,故此时不存在这样的点A ; 当∠NOA =90°时,有12OP MN ,求得满足条件的点A (442,4);当∠NAO =90°时,有12APMN ,即22221(4)(24)(4)4m m m m ,解得m =4,此时点A ,P 重合,不满足题意.5.抛物线y =﹣x 2+2x +3的顶点为C ,点A 的坐标为(﹣1,4),其对称轴l 上是否存在点M ,使线段MA 绕点M 逆时针旋转90°得到线段MB ,且点B 恰好落在抛物线上?若存在,求出点M 的坐标;若不存在,请说明理由. 解:存在,点M 的坐标为(1,2)或(1,5).【提示】如图,连结AC ,则AC ⊥l ,作BD ⊥l 于点D ,则△MCA ≌△BDM ,从而MD =AC =2,BD =M C .无论点A ,B 在l 同侧还是异侧,设点M (1,m ),都可得B (m -3,m -2),代入抛物线表达式即可求得m =2或5,从而点M 的坐标为(1,2)或(1,5).B 2M 2M 1D 2D 1OC B 1Al yx。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学压轴题解题策略(3)直角三角形的存在性问题解题策略《挑战压轴题·中考数学》的作者 上海 马学斌专题攻略解直角三角形的存在性问题,一般分三步走,第一步寻找分类标准,第二步列方程,第三步解方程并验根.一般情况下,按照直角顶点或者斜边分类,然后按照三角比或勾股定理列方程.有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便.解直角三角形的问题,常常和相似三角形、三角比的问题联系在一起.如果直角边与坐标轴不平行,那么过三个顶点作与坐标轴平行的直线,可以构造两个新的相似直角三角形,这样列比例方程比较简便.在平面直角坐标系中,两点间的距离公式常常用到.怎样画直角三角形的示意图呢?如果已知直角边,那么过直角边的两个端点画垂线,第三个顶点在垂线上;如果已知斜边,那么以斜边为直径画圆,直角顶点在圆上(不含直径的两个端点).例题解析例❶ 如图1-1,在△ABC 中,AB =AC =10,cos ∠B =.D 、E 为线段BC 上的两个45动点,且DE =3(E 在D 右边),运动初始时D 和B 重合,当E 和C 重合时运动停止.过E作EF //AC 交AB 于F ,连结DF .设BD =x ,如果△BDF 为直角三角形,求x 的值.图1-1【解析】△BDF 中,∠B 是确定的锐角,那么按照直角顶点分类,直角三角形BDF 存在两种情况.如果把夹∠B 的两条边用含有x 的式子表示出来,分两种情况列方程就可以了.如图1-2,作AH ⊥BC ,垂足为H ,那么H 是BC 的中点.在Rt △ABH 中,AB =10,cos ∠B =,所以BH =8.所以BC =16.45由EF //AC ,得,即.所以BF =.BF BE BA BC =31016BF x +=5(3)8x +图1-2 图1-3 图1-4①如图1-3,当∠BDF =90°时,由,得.4cos 5BD B BF ∠==45BD BF =解方程,得x =3.45(3)58x x =⨯+②如图1-4,当∠BFD =90°时,由,得.4cos 5BF B BD ∠==45BF BD =解方程,得.5154885x x +=757x =我们看到,在画示意图时,无须受到△ABC 的“限制”,只需要取其确定的∠B .例❷ 如图2-1,已知A 、B 是线段MN 上的两点,4=MN ,1=MA ,1>MB .以A 为中心顺时针旋转点M ,以B 为中心逆时针旋转点N ,使M 、N 两点重合成一点C ,构成△ABC ,设AB =x ,若△ABC 为直角三角形,求x 的值.图2-1【解析】△ABC 的三边长都可以表示出来,AC =1,AB =x ,BC =3-x .如果用斜边进行分类,每条边都可能成为斜边,分三种情况:①若AC 为斜边,则,即,此方程无实根.22)3(1x x -+=0432=+-x x ②若AB 为斜边,则,解得(如图2-2).1)3(22+-=x x 35=x ③若BC 为斜边,则,解得(如图2-3).221)3(x x +=-34=x 因此当或时,△ABC 是直角三角形.35=x 34=x图2-2 图2-3例❸ 如图3-1,已知在平面直角坐标系中,点A 的坐标为(-2, 0),点B 是点A 关于原点的对称点,P 是函数图象上的一点,且△ABP 是直角三角形,求点P 的坐)0(2>=x xy 标.图3-1【解析】A 、B 两点是确定的,以线段AB 为分类标准,分三种情况.如果线段AB 为直角边,那么过点A 画AB 的垂线,与第一象限内的一支双曲线没有交点;过点B 画AB 的垂线,有1个交点.以AB 为直径画圆,圆与双曲线有没有交点呢?先假如有交点,再列方程,方程有解那么就有交点.如果是一元二次方程,那么可能是一个交点,也可能是两个交点.由题意,得点B 的坐标为(2,0),且∠BAP 不可能成为直角.①如图3-2,当∠ABP =90°时,点P 的坐标为(2,1).②方法一:如图3-3,当∠APB =90°时,OP 是Rt △APB 的斜边上的中线,OP =2.设P ,由OP 2=4,得.解得.此时P (,).2(,)x x 2244x x +=x =22图3-2图3-3方法二:由勾股定理,得PA 2+PB 2=AB 2.解方程,得.2222222(2)()(2)()4x x x x +++++=x =方法三:如图3-4,由△AHP ∽△PHB ,得PH 2=AH ·BH .解方程,得.22((2)(2)x x x =+-x =图3-4 图3-5这三种解法的方程貌似差异很大,转化为整式方程之后都是(x 2-2)2=0.这个四次方程的解是x 1=x 2=,x 3=x 4=,它的几何意义就是以AB 为直径的圆与双曲线相切于P 、2P ′两点(如图3-5).例❹ 如图4-1,已知直线y =kx -6经过点A (1,-4),与x 轴相交于点B .若点Q 是y轴上一点,且△ABQ 为直角三角形,求点Q 的坐标.图4-1【解析】和例题3一样,过A 、B 两点分别画AB 的垂线,各有1个点Q .和例题3不同,以AB 为直径画圆,圆与y 轴有没有交点,一目了然.而圆与双曲线有没有交点,是徒手画双曲线无法肯定的.将A (1,-4)代入y =kx -6,可得k =2.所以y =2x -6,B (3,0).设OQ 的长为m .分三种情况讨论直角三角形ABQ :①如图4-2,当∠AQB =90°时,△BOQ ∽△QHA ,.所以.BO QH OQ HA =341m m -=解得m =1或m =3.所以Q (0,-1)或(0,-3).②如图4-3,当∠BAQ =90°时,△QHA ∽△AGB ,.所以.QH AG HA GB =4214m -=解得.此时.72m =7(0,2Q -③如图4-4,当∠ABQ =90°时,△AGB ∽△BMQ ,.所以.AG BM GB MQ =243m =解得.此时.32m =3(0,)2Q图4-2 图4-3 图4-4三种情况的直角三角形ABQ ,直角边都不与坐标轴平行,我们以直角顶点为公共顶点,构造两个相似的直角三角形,这样列比例方程比较简便.已知A (1,-4)、B (3,0),设Q (0, n ),那么根据两点间的距离公式可以表示出AB 2,AQ 2和BQ 2,再按照斜边为分类标准列方程,就不用画图进行“盲解”了.例❺ 如图5-1,抛物线与x 轴交于A 、B 两点(点A 在点B 的左233384y x x =--+侧).若直线l 过点E (4, 0),M 为直线l 上的动点,当以A 、B 、M 为顶点所作的直角三角形有且只有三个时,求直线l 的解析式.图5-1【解析】有且只有三个直角三角形ABM 是什么意思呢?过A 、B 两点分别画AB 的垂线,与直线l 各有一个交点,那么第三个直角顶点M 在哪里?以AB 为直径的⊙G 与直线l 相切于点M 啊!由,得A (-4, 0)、B (2, 0),直径AB =6.23333(4)(2)848y x x x x =--+=-+-如图5-2,连结GM ,那么GM ⊥l .在Rt △EGM 中,GM =3,GE =5,所以EM =4.因此.3tan 4GEM ∠=设直线l 与y 轴交于点C ,那么OC =3.所以直线l (直线EC )为.334y x =-+根据对称性,直线l 还可以是.334y x =-图5-2例❻ 如图6-1,在△ABC 中,CA =CB ,AB =8,.点D 是AB 边上的一个4cos 5A ∠=动点,点E 与点A 关于直线CD 对称,连结CE 、DE .(1)求底边AB 上的高;(2)设CE 与AB 交于点F ,当△ACF 为直角三角形时,求AD 的长;(3)连结AE ,当△ADE 是直角三角形时,求AD 的长.图6-1【解析】这道题目画示意图有技巧的,如果将点D 看作主动点,那么CE 就是从动线段.反过来画图,点E 在以CA 为半径的⊙C 上,如果把点E 看作主动点,再画∠ACE 的平分线就产生点D 了.(1)如图6-2,设AB 边上的高为CH ,那么AH =BH =4.在Rt △ACH 中,AH =4,,所以AC =5,CH =3.4cos 5A ∠=(2)①如图6-3,当∠AFC =90°时,F 是AB 的中点,AF =4,CF =3.在Rt △DEF 中,EF =CE -CF =2,,所以.此时.4cos 5E ∠=52DE =52AD DE ==②如图6-4,当∠ACF =90°时,∠ACD =45°,那么△ACD 的条件符合“角边角”.作DG ⊥AC ,垂足为G .设DG =CG =3m ,那么AD =5m ,AG =4m .由CA =5,得7m =5.解得.此时.57m =2557AD m ==图6-2 图6-3 图6-4(3)因为DA =DE ,所以只存在∠ADE =90°的情况.①如图6-5,当E 在AB 下方时,根据对称性,知∠CDA =∠CDE =135°,此时△CDH是等腰直角三角形,DH =CH =3.所以AD =AH -DH =1.②如图6-6,当E 在AB 上方时,根据对称性,知∠CDA =∠CDE =45°,此时△CDH是等腰直角三角形,DH =CH =3.所以AD =AH +DH =7.图6-5 图6-6“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
