求二面角平面角的方法
(完整版)二面角求解方法

二面角的作与求求角是每年高考必考内容之一,可以做为选择题,也可作为填空题,时常作为解答题形式出现,重点把握好二面角,它一般出现在解答题中。
下面就对求二面角的方法总结如下:1、定义法:在棱上任取一点,过这点在两个面内分别引棱的垂线,这两条射线所成的角就是二面角的平面角。
2、三垂线定理及逆定理法:自二面角的一个面上的一点向另一个面引垂线,再由垂足向棱作垂线得到棱上的点。
斜足与面上一点连线,和斜足与垂足连线所夹的角即为二面角的平面角。
3、作棱的垂面法:自空间一点作与棱垂直的平面,截二面角的两条射线所成的角就是二面角的平面角。
4、投影法:利用s投影面=s被投影面θcos 这个公式对于斜面三角形,任意多边形都成立,是求二面角的好方法。
尤其对无棱问题5异面直线距离法: EF 2=m 2+n 2+d 2-2mn θcos例1:若p 是ABC ∆所在平面外一点,而PBC ∆和ABC ∆都是边长为2的正三角形,PA=6,求二面角P-BC-A 的大小。
分析:由于这两个三角形是全等的三角形, 故采用定义法解:取BC 的中点E ,连接AE 、PEAC=AB ,PB=PC ∴AE ⊥ BC ,PE ⊥BC∴PEA ∠为二面角P-BC-A 的平面角在PAE ∆中AE=PE=3,PA=6PCBAE∴PEA ∠=900∴二面角P-BC-A 的平面角为900。
例2:已知ABC ∆是正三角形,⊥PA 平面ABC 且PA=AB=a,求二面角A-PC-B 的大小。
[思维]二面角的大小是由二面角的平面角 来度量的,本题可利用三垂线定理(逆)来作 平面角,还可以用射影面积公式或异面直线上两点 间距离公式求二面角的平面角。
解1:(三垂线定理法)取AC 的中点E ,连接BE ,过E 做EF ⊥PC,连接BF ⊥PA 平面ABC ,PA ⊂平面PAC∴平面PAC ⊥平面ABC, 平面PAC 平面ABC=AC∴BE ⊥平面PAC由三垂线定理知BF ⊥PC∴BFE ∠为二面角A-PC-B 的平面角设PA=1,E 为AC 的中点,BE=23,EF=42∴tan BFE ∠=6=EFBE∴BFE ∠=arctan 6解2:(三垂线定理法)取BC 的中点E ,连接AE ,PE 过A 做AF ⊥PE, FM ⊥PC,连接FMAB=AC,PB=PC ∴AE ⊥BC,PE ⊥BC∴ BC ⊥平面PAE,BC ⊂平面PBC∴平面PAE ⊥平面PBC, 平面PAE 平面PBC=PE由三垂线定理知AM ⊥PCPC BAEF MEPCBAF图1图2∴FMA ∠为二面角A-PC-B 的平面角设PA=1,AM=22,AF=721.=PE AE AP∴sin FMA ∠=742=AM AF ∴FMA ∠=argsin742解3:(投影法)过B 作BE ⊥AC 于E,连结PE ⊥PA 平面ABC ,PA ⊂平面PAC∴平面PAC ⊥平面ABC, 平面PAC 平面ABC=AC∴BE ⊥平面PAC∴PEC ∆是PBC ∆在平面PAC 上的射影设PA=1,则PB=PC=2,AB=141=∆PEC S ,47=∆PBC S由射影面积公式得,77cosarg ,77=∴==∆∆θθPBC PEC S S COS , 解4:(异面直线距离法)过A 作AD ⊥PC,BE ⊥PC 交PC 分别于D 、E 设PA=1,则AD=22,PB=PC=2 ∴BE=PC S PBC 21∆=414,CE=42,DE=42由异面直线两点间距离公式得 AB 2=AD 2+BE 2+DE 2-2ADBE θCOS ,θCOS =77cos arg ,77=∴θ [点评]本题给出了求平面角的几种方法,应很好掌握。
二面角的求法公式

二面角的求法公式
二面角的求法有多种,以下是其中的一些:
1. 一般求法:先找到二面角的平面角,然后用量角器直接测量。
2. 法向量法:利用向量的数量积来求二面角。
设两个法向量分别为
$\mathbf{a}$ 和 $\mathbf{b}$,则二面角的大小为
$\arccos(\frac{\mathbf{a} \cdot \mathbf{b}}{\mathbf{a} \times
\mathbf{b}})$。
3. 平行向量法:利用向量的平行性质来求二面角。
设两个平行的向量分别为$\mathbf{a}$ 和 $\mathbf{b}$,则二面角的大小为
$\arccos(\frac{\mathbf{a} \cdot \mathbf{b}}{\mathbf{a} \times
\mathbf{b}})$。
4. 方程方法:利用空间几何的知识,建立二面角的方程,然后求解。
这些方法各有优缺点,具体使用哪种方法需要根据具体的情况来决定。
二面角求法总结

二面角求法总结一、定义法定义法是求二面角的基本方法,它通过定义二面角的平面角来求解。
具体来说,如果两个平面相交,那么它们会在交线上形成一个角,这个角就是二面角的平面角。
通过找到这个角的两边,我们可以使用三角函数来求解这个角的大小。
二、垂线法垂线法是一种常用的求二面角的方法,它通过找到一个垂直于两个平面的交线的直线,并将这个直线延长到一个已知点,然后使用三角函数来求解这个角的大小。
这个方法的关键在于找到正确的垂线,并且这个垂线应该是垂直于交线的。
三、射影面积法射影面积法是一种利用射影面积定理求解二面角的方法。
通过找到两个平面上的两条射线和它们之间的夹角,我们可以使用射影面积定理来求解这个角的大小。
这种方法需要先找到正确的射线和夹角,然后使用射影面积定理来计算结果。
四、三垂线定理法三垂线定理法是一种利用三垂线定理来求解二面角的方法。
如果一个平面内的直线与另一个平面垂直,那么这个直线与第一个平面的交点与第二个平面的交点的连线与原直线的夹角就是要求的二面角。
这种方法的关键在于找到正确的三垂线定理的应用条件,并且正确地应用三垂线定理来计算结果。
五、角平分线法角平分线法是一种利用角平分线定理来求解二面角的方法。
如果一个平面内的角平分线与另一个平面垂直,那么角平分线与原直线的夹角就是要求的二面角。
这种方法的关键在于找到正确的角平分线的应用条件,并且正确地应用角平分线定理来计算结果。
六、向量法向量法是一种利用向量的数量积和向量积来求解二面角的方法。
通过找到两个平面上的两个向量,我们可以使用向量的数量积和向量积来计算这两个向量的夹角,这个夹角就是要求的二面角。
这种方法的关键在于正确地找到两个向量,并且正确地应用向量的数量积和向量积来计算结果。
七、坐标法坐标法是一种利用坐标系来求解二面角的方法。
通过建立适当的坐标系,我们可以将二面角的问题转化为求解一个几何量的值的问题。
这种方法的关键在于建立正确的坐标系,并且正确地使用代数方法来计算结果。
二面角的计算方法

图1二面角计算一 、直接法:即先作出二面角的平面角,再利用解三角形知识求解之。
通常作二面角的平面角的途径有:⑴定义法:在二面角的棱上取一个特殊点,由此点出发在二面角的两个面内分别作棱的垂线;⑵三垂线法:如图1,C 是二面角βα--AB 的面β内的一个点,CO ⊥平面α于O ,只需作OD⊥AB 于D ,连接CD ,用三垂线定理可证明∠CDO 就是 所求二面角的平面角。
⑶垂面法:即在二面角的棱上取一点,过此点作平面γ,使γ垂直于二面角的棱,则γ 与二面角的两个面的交线所成的角就是该二面角的平面角。
例1 如图2,在四棱锥V-ABCD 中,底面ABCD 是正方形,侧面VAD 是正三角形, 平面VAD⊥底面ABCD . (1)证明AB⊥平面VAD ;(2)求面VAD 与面VDB 所成的二面角的大小. 解:(1)证明:VAD ABCD AB AD AB VADAB ABCD AD VAD ABCD ⊥⎫⎪⊥⎪⇒⊥⎬⊂⎪⎪=⎭平面平面平面平面平面平面 (2)解:取VD 的中点E ,连结AF ,BE , ∵△VAD 是正三形,四边形ABCD 为正方形, ∴由勾股定理可知,BD VB,===∴AE⊥VD,BE⊥VD,∴∠AEB 就是所求二面角的平面角. 又在Rt△ABE 中,∠BAE=90°,AB ,因此,tan∠AEB=.332=AE AB 即得所求二面角的大小为.332arctan例2 如图3,AB⊥平面BCD ,DC⊥CB,AD 与平面BCD成30°的角,且AB=BC.(1)求AD 与平面ABC 所成的角的大小; (2)求二面角C-AD-B 的大小;(3)若AB=2,求点B 到平面ACD 的距离。
解:(1) ∵AB⊥平面BCD ,∴∠ADB 就是AD 与平面BCD 所成的角,即∠ADB=300,且CD⊥AB, 又∵DC⊥BC,ABBC B =,∴ CD⊥平面ABC ,∴ AD 与平面ABC 所成的角为∠DAC ,设AB=BC=a,则AC=a 2, BD=acot300=a 3,AD=2a, a BC BD CD 222=-=,∴ tan∠DAC=122==aa CDAC , ∴ 045=∠DAC ,即,AD 与平面ABC 所成的角为450. (2)作CE⊥BD 于E ,取AD 的中点F ,连CF , ∵ AB⊥面BCD ,ABD AB ⊂面, ∴ 面ABD⊥面BCD , 又∵ 面ABD面BCD=BD ,BCD CE ⊂面,CE⊥BD,∴ CE⊥面ABD ,又∵AC=BC=a 2,AF=FD ,∴AD⊥EF,有三垂线定理的逆定理可知,∠CFE 就是所求二面角的平面角.计算可知, BC CD CE BD ⋅=,2AD a,=12CF AD a ==,∴ CE sin CFE CF ∠==故,所求的二面角为3.略例3如图4,P 是边长为1的正六边形ABCDEF 所在平面外一点,1PA =,P 在平面ABC 内的射影为BF 的中点O.(1)证明PA ⊥BF ;(2)求面APB 与面DPB 所成二面角的大小。
二面角8种求法

二面角求法正方体是研究立体几何概念的一个重要模型,中学立体几何教学中,求平面与平面所成的二面角是转化为平面角来度量的,也可采用一些特殊的方法求二面角,而正方体也是探讨求二面角大小方法的典型几何体。
笔者通过探求正方体中有关二面角,分析求二面角大小的八种方法:(1)平面角定义法;(2)三垂线定理法;(3)线面垂直法;(4)判定垂面法;(5)异面直线上两点间距离公式法;(6)平行移动法;(7)投影面积法;(8)棱锥体积法。
一、平面角定义法此法是根据二面角的平面角定义,直接寻求二面角的大小。
以所求二面角棱上任意一点为端点,在二面角两个平面内分别作垂直于棱的两条射线所成角就是二面角的平面角,如图二面角α-l-β中,在棱l上取一点O,分别在α、β两个平面内作AO⊥l,BO⊥l,∠AOB即是所求二面角的平面角。
例题1:已知正方体ABCD-A1B1C1D1中,O、O1是上下底面正方形的中心,求二面角O1-BC-O的大小。
例题2:已知正方体ABCD-A1B1C1D1中,E、F为A1D1、C1D1的中点,求平面EFCA与底面ABCD所成的二面角。
二、 利用三垂线定理法此方法是在二面角的一个平面内过一点作另一个面的垂线,再由垂足(或仍是该点)作棱的垂线,连接该点和棱上的垂足(或连两垂足)两点线,即可得二面角的平面角。
如图二面角α-l-β中,在平面α内取一点A ,过A 作AB ⊥平面β,B 是垂足, 由B (或A )作BO (或AO )⊥l ,连接AO (或BO )即得AO 是平面β的斜线, BO 是AO 在平面β中的射影,根据三垂线定理(或逆定理)即得AO ⊥l ,BO ⊥l , 即∠AOB 是α-l-β的平面角。
例题3:已知正方体ABCD-A 1B 1C 1D 1中,求二面角B-AC-B 1的大小。
例题4:已知正方体ABCD-A 1B 1C 1D 1中,求平面ACD 1与平面BDC 1所成的二面角。
三、 线面垂直法此法利用直线垂直平面即该直线垂直平面内任何直线的性质来寻求二面角的平面角。
找面角的平面角的方法汇总

找二面角的平面角的方法汇总二面角是高中立体几何中的一个重要内容,也是一个难点.对于二面角方面的问题,学生往往无从下手,他们并不是不会构造三角形或解三角形,而是没有掌握寻找二面角的平面角的方法.我们试将寻找二面角的平面角的方法归纳为以下六种类型. 一、根据平面角的定义找出二面角的平面角例 1 在60的二面角βα--a 的两个面内,分别有A 和B 两点.已知A 和B 到棱的距离分别为2和4,且线段10=AB ,试求:(1)直线AB 与棱a 所构成的角的正弦值;(2)直线AB 与平面α所构成的角的正弦值.分析:求解这道题,首先得找出二面角的平面角,也就是找出 60角在哪儿.如果解决了这个问题,这道题也就解决了一半.根据题意,在平面β内作a AD ⊥;在平面α内作α⊥BE ,EB CD //,连结BC 、AC .可以证明a CD ⊥,则由二面角的平面角的定义,可知ADC ∠为二面角βα--a 的平面角.以下求解略. 二、根据三垂线定理找出二面角的平面角例2 如图,在平面β内有一条直线AC 与平面α成 30,AC 与棱BD 成 45,求平面α与平面β的二面角的大小.分析:找二面角的平面角,可过A 作BD AF ⊥;⊥AE 平面α,连结FE .由三垂线定理可证EF BD ⊥,则AFE ∠为二面角的平面角.总结:(1)如果两个平面相交,有过一个平面内的一点与另一个平面垂直的垂线,可过这一点向棱作垂线,连结两个垂足.应用三垂线定理可证明两个垂足的连线与棱垂直,那么就可以找到二面角的平面角.(2)在应用三垂线定理寻找二面角的平面角时,注意“作”、“连”、“证”,即“作BD AF ⊥”、“连结EF ”、“证明BD EF ⊥”. 三、作二面角棱的垂面,垂面与二面角的两个面的两条交线所构成的角,即为二面角的平面角例3 如图1,已知P 为βα--CD 内的一点,α⊥PA 于A 点,β⊥PB 于B 点,如果n APB =∠,试求二面角βα--CD 的平面角. 分析:⊥⇒⊥⇒⊥⊥⇒⊥CD CDPB PB CD PA PA βα平面PAB . 因此只要把平面PAB 与平面α、β的交线画出来即可.证明AEB ∠为βα--CD 的平面角, n AEB -=∠180(如图2).注意:这种类型的题,如果过A 作CD AE ⊥,垂足为E ,连结EB ,我们还必须证明CD EB ⊥,及AEBP 为平面图形,这样做起来比较麻烦.图1 图2例4 已知斜三棱柱111-C B A ABC 中,平面1AB 与平面1AC 构成的二面角的平面角为 30,平面1AB 与平面1BC 构成的二面角为 70.试求平面1AC 与平面1BC 构成的二面角的大小.分析:作三棱柱的直截面,可得△DEF ,其三个内角分别为斜三棱柱的三个侧面两两构成的二面角的平面角.总结:对棱柱而言,其直截面与各个侧棱的交点所形成的多边形的各个内角,分别为棱柱相邻侧面构成的二面角的平面角. 四、平移平面法例 5 如图,正方体1111-D C B A ABCD 中,E 为1AA 的中点,H 为1CC 上的点,且211::=H C CH .设正方体的棱长为a ,求平面EH D 1与底面1111D C B A 构成的锐角的正切. 分析:本题中,仅仅知道二面角棱上的一点1D ,在这种情况下,寻找二面角的平面角较困难.根据平面平移不改变它与另一个平面构成的角的大小的原理,如果能把二面角中的一个平面平移,找出辅助平面与另一个平面的交线,就可以作出二面角的平面角.有了平面角之后,只需要进行常规构造三角形和解三角形的计算,就可以解决问题了.如图,过点E 作11//D A EM 与D D 1相交于M 点,过M 点作11D C MN ⊥,与H D 1相交于N 点.可证平面//EMN 平面1111D C B A .这样,求平面EH D 1与平面1111D C B A 的二面角的平面角就转化为求平面EH D 1与平面EMN 的二面角的平面角.显然EN 为这两个平面的交线,过点M 作EN MF ⊥,F 为垂足,连结F D 1,可证EN F D ⊥1.则FM D 1∠为本题要寻找的二面角. 五、找垂面,作垂线例6 如图,正方体1111-D C B A ABCD 中,M 为棱AD 的中点,求平面CB C B 11和平面M BC 1所构成的锐二面角的正切.分析:平面AC 与二面角C BC M --1的一个面C B 1垂直,与另一个平面1C MB 相交,过M 点作BC MP ⊥,垂足为P ,过P 作BC PN ⊥,交1C B于N 点,连结MN ,由三垂线定理可证1BC MN ⊥,则MNP ∠为二面角C BC M --1的平面角.总结:当一个平面与二面角的一个平面垂直,与另一个平面相交时,往往过这个面上的一点作这两个垂直平面交线的垂线,再过垂足作二面角棱的垂线.根据三垂线定理即可证明,并找出二面角的平面角.再如图,要找βα--a 所构成的二面角的平面角,可找平面βγ⊥,且b =αγ ,l =βγ ,过b 上任何一点A 作l AB ⊥,垂足为B ,过B 作α⊥BC ,垂足为C ,连结AC ,可证ACB ∠为βα--a 的平面角. 六、根据特殊图形的性质找二面角的平面角1.三线合一例7 如图,空间四边形ABCD 中,3==AD AB ,4==CD BC ,2=BD ,5=AC .试求C BD A --二面角的余弦值.分析:如图1,AD AB =,CD BC =,则△ABD 和△BDC 为等腰三角形.过A 作BD AE ⊥,垂足为E ,连结CE .根据三线合一,且E 为BD 中点,可证BD CE ⊥,则AEC ∠为二面角C BD A --的平面角.2.全等三角形例8 如图,已知空间四边形ABCD ,6==BC AB ,4==DC AD ,8=BD ,6=AC .试求C BD A --的余弦值.分析:过A 作BD AE ⊥,垂足为E ,连结CE .根据已知条件,△AED 和△CED 全等,可证BD CE ⊥,则AEC ∠为二面角C BD A --的平面角.3.二面角的棱蜕化成一点例9 如图,四棱锥BCED A -中,DB 和EC 与面ABC 垂直,△ABC 为正三角形.(1)若BD EC BC ==时,求面ADE 与面ABC 的夹角;(2)若BD EC BC 2==时,求面ADE 与面ABC 的夹角.分析:如图,面ADE 与面ABC 的交线蜕化成一点,但面ADE 与面ABC 与面DC 相交.如果三个平面两两相交,它们可能有三种情况:(1)交线为一点;(2)一条交线;(3)三条交线互相平行.在图1中,两条交线BC 与DE 互相平行,所以肯定有过A 且平行于DE 的一条交线.可过A 作DE AM //,平面ADE 与平面ABC 的交线即为AM .过A 作DE AN ⊥于N ,过A 作BC AF ⊥于F .可证AM AN ⊥,AM AF ⊥,则NAF ∠为面ADE 与面ABC 的夹角.如图,DE 与C B 不平行且相交.根据三个平面两两相交可能出现的三种情况,这三个面的交线为一点.延长ED 、CB 相交于G 点,连结AG .AG 即为平面ADE 与平面ABC的交线,通过一些关系可证CAE ∠为平面ADE 与平面ABC 的夹角.通过以上分析和举例说明,寻找二面角的平面角的方法就比较容易了.只要我们勤动脑,善观察,多总结,抓住问题的特征,找出适当的方法,关于二面角的平面角的问题就会迎刃而解.。
二面角的平面角的求法

★二面角的平面角的求法:⒈定义法:在二面角的棱上找一点(特殊点),在两个半平面内分别作垂直与棱的射线。
如图,在二面角βα--a 的棱a 上任取一点O ,在平面α内过点O 作a OA ⊥,在平面β内过点O 作a BO ⊥,则AOB ∠为二面角βα--a 的平面角。
⒉垂面法:过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条射线所成的角,即为二面角的平面角。
如图,已知二面角-αβ-l ,过棱上一点O 作一平面γ,使l γ⊥,.,OB OA =⋂=⋂βγβγOB l OA l OB OA ⊥⊥⊆⊆,,,γγ ∴ AOB ∠为二面角βα--l 的平面角。
⒊垂线法:※ 该法也就是利用三垂线定理或逆定理来寻找二面角的平面角,是最常用的一种方法。
由一个半平面内异与棱上的点A 向另一个半平面作垂线,垂足为B ,由点B 向二面角的棱作垂线,垂足为O ,连结AO ,则AOB ∠为二面角的平面角。
如图,已知二面角βα--l ,自平面α内一点A 作AB β⊥于B ,由点B 作BO l ⊥于O ,连结AOAO 为平面β的斜线,BO 为AO 在平面β内的射影∴ AO ,l ⊥∴ AOB ∠为二面角l -α-β的平面角。
⒋射影法: 被投影面投影面S S =θcos⒌向量法:(1)⑴AB,CD 分别是二面角βα--l 的两个面内与棱AC 垂直的异面直线,则二面角的大小为CD AB .[(2)平面α与β相交于直线l ,平面α的法向量为n 1,平面β的法向量为n 2,<n 1,n 2>=θ,则二面角α-l -β为θ或π-θ.设二面角大小为φ,则|cos φ|=|cos θ|=|n 1·n 2||n 1|·|n 2|. ★★利用二面角的两个面的法向量求解※ 法向量的夹角与二面角的大小相等或互补①当法向量21n n 与的方向分别指向二面角的内侧与外侧时,二面角的大小等于法向量夹角②当法向量1n 与2n 方向同时指向二面角的内侧或外侧时,二面角的大小等于法向量夹角的补角,1.二面角的棱上有A 、B 两点,直线AC 、BD 分别在这个二面角的两个半平面内,且都垂直于AB .已知AB =4,AC =6,BD =8,CD =217,则该二面角的大小为( )A .150°B .45°C .60°D .1202.如图,四棱锥S -ABCD 的底面是边长为1的正方形,SD ⊥底面ABCD ,SB =3,求平面ASD 与平面BSC 所成二面角的大小.3.如图,在四棱锥P-ABCD中,底面ABCD是矩形,P A⊥平面ABCD,AP=AB=2,BC=22,E,F分别是AD,PC的中点.(1)证明:PC⊥平面BEF.(2)求平面BEF与平面BAP夹角的大小.4.如图,在长方体ABCD—A1B1C1D1中,E、F分别是棱BC,CC1上的点,CF=AB=2CE,AB∶AD∶AA1=1∶2∶4.(1)求异面直线EF与A1D所成角的余弦值;(2)证明AF⊥平面A1ED;(3)求二面角A1-ED-F的正弦值.5.如图所示,在正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为22a,D是棱A1C1的中点.(1)求证:BC1∥平面AB1D;(2)求二面角A1-AB1-D的大小;6.(12分)在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°且异面直线A1B与B1C1所成的角等于60°,设AA1=a.(1)求a的值;(2)求平面A1BC1与平面B1BC1所成的锐二面角的大小.7..如图,已知正方形ABCD 和梯形ACEF 所在平面互相垂直,AB =2,AF =22,CF ∥AF ,AC ⊥CE ,ME →=2FM →,(1)求证:CM ∥平面BDF ;(2)求异面直线CM 与FD 所成角的余弦值的大小;(3)求二面角A -DF -B 的大小.8. (2010·湖北)如图所示,在四面体A -BOC 中,OC ⊥OA ,OC⊥OB ,∠AOB =120°,且OA =OB =OC =1.(1)设P 为AC 的中点,证明:在AB 上存在一点Q ,使PQ ⊥OA ,并计算AB AQ的值; (2)求二面角O -AC -B 的平面角的余弦值.9.(14分)已知四棱锥S -ABCD 的底面ABCD 是正方形,SA ⊥底面ABCD ,E 是SC 上的任意一点.(1)求证:平面EBD ⊥平面SAC ;(2)当SA AB的值为多少时,二面角B -SC -D 的大小为120°.。
二面角的求法---三垂线法

”三垂线法作二面角的平面角的技巧求二面角的大小是考试中经常出现的问题,而用三垂线法作二面角的平面角是求二面角大小的一个重要方法,许多同学在解题过程中由于没有有效地利用三垂线定理(或逆定理)作出二面角的平面角,使得解题受阻.我们把用三垂线定理(或逆定理)作二面角的平面角的方法称为三垂线法,其作图模型为:如图1,在二面角α—l一β中,过平面α内一点A作AO⊥平面β,垂足为O,过点O作OB⊥l于B(过A点作AB⊥于B),连结AB(或OB),由三垂线定理(或逆定理)知AB⊥l(或OB⊥l),则∠ABO为二面角。
α—l—β的平面角.作图过程中,作出了两条垂线AO与OB(或AB),后连结AB两点(或OB两点),这一过程可简记为“两垂一连,其中AO为“第一垂线.“第一垂线”能否顺利找到或恰当作出是用三垂线法作二面角的平面角的关键,在具体解题过程中要注意以下几点:1.善于利用图中已有的“第一垂线”例1已知斜三棱柱ABC—A1B1C1中,∠BCA=90°,AC=BC,A1在底面ABC的射影恰为AC的中点M,又知AA1与底面ABC所成的角为60°.(1)求证:BC⊥平面AA1CC1;(2)求二面角B一AA1—C的大小.-可编辑修改-的平面角.设 AC =BC = ,正△a AA 1C 的边长为 a ,所以 CN =3a ,在 Rt△” ” 剖析:注意该题的第(1)问,事实上本题已经暗示了 BC 就是我们要寻求的“第一垂线.略解 2 A 1A 与底面 AB 成的角为 60°,所以∠A 1AC =60°,又 M 是 AC中点,所以 △AA 1C 是正三角形,作 CN ⊥AA 1 于 N ,点 N 为 A 1A 的中点,连结 BN ,由 BC ⊥平面 AA 1CC 1,BN ⊥AA 1,则∠BNC 为二面角 B 一 AA 1 一 C2BNC 中,tan∠BNC = BC = a = 2 3 ,即∠BNC = arctan 2 3 .NCa 3 332例 2如图 3,在底面是直角梯形的四棱锥 S —ABCD 中,∠ABC =90°,SA ⊥面 ABCD ,SA =AB =BC =1,AD = 12(1)求四棱锥 S —ABCD 的体积;(2)求面 SCD 与面 SBA 所成的二面角的正切值.剖析:由 SA ⊥面 ABCD 及∠ABC =90°,不难发现,BC 即为“第一垂线,但是,本题要作二面角的平面角,还需首先作出二面角的棱.略解 2 延长 BA 、CD 相交于点 E ,连结 SE ,则 SE 是所求二面角的棱,因为 AD ∥BC ,BC =2AD ,所以 EA =AB =SA ,所以 SE ⊥SB ,因为 SA ⊥面 ABCD ,得面 SEB ⊥面 EBC ,EB 是交线,又 BC ⊥EB ,所以 BC ⊥面 SEB ,故 SB 是CS 在面 SEB 上的射影,所以 CS ⊥SE ,所以∠BSC 是所求二面角的平面角,因为 SB = SA 2+ AB 2= 2 ,BC =1,BC ⊥SB ,因为 tan∠BSC = = BC = 2,即所SB2求二面角的正切值为 2 .2-可编辑修改-例3如图4,正三棱柱ABC—A1B1C1的底边长为a,侧棱长为2a,DF⊥面A1AB1,即DF为我们要作的“第一垂线.因为D是A1C1中点,A1B1=a,所以B1F=3a,DF=3a,在Rt△DFG,可2.借助第三个平面,作“第一垂线”2若经过对角线AB1且与对角线BC1平行的平面交上底面一边A1C1于点D.(1)确定点D的位置,并证明你的结论;(2)求二面角A1—AB1—D的大小.剖析:由线面平行的性质定理及三角形中位线性质,易知D是A1C1中点.二面角A1—AB1一D的放置属于非常规位置的图形,但是,容易发现,平面A1B1C1过点D且与平面A1AB1垂直,这样的平面相对于二面角的两个平面而言,我们称为第三个平面.过D作DF⊥A1B1,由面面垂直的性质知,”略解2在平面A1B1C1内,作CF⊥A1B1于F,连DC,由三垂线定理可证AB1⊥DG,∠DGF就是二面角A1—AB1一D的平面角,在正△A1B1C1中,44求得∠DCF=45°.3.利用特殊图形的定义、性质作“第一垂线”-可编辑修改-例4已知:△Rt ABC的斜边BC在平面α内,AB、AC分别与平面。
二面角的定义

,12 PB=1,PE
,22 PO
1 2
3 2
∴ tanPEO 2
2
∴所求的二面角P-AB-C 的正切值为
2 2
P
E
B
O
C P
E
O
例5 已知:Rt△ABC中,AB=AC=a,AD是斜边BC上的
高,以AD为折痕使∠BDC成直角。
求证:① 平面ABD⊥平面BDC,平面ACD⊥平面BDC
②
∠
BAC
=
D 在Rt△PBE中,BE ,PB=1,PE
1
求(1)平面C BD与平面 1 ∵直线B1C与平面ABC成300角,∴B1CB=300,B1C=2,Rt△B1AC中,由勾股定理得AC= ,∴AQ=1。
C1
∵AB=AC=a,∠BAC=90。
P
ABCD所成角的大小; A 此法得出的平面角在任意三角形中,所以不好计算,不是我们首选的方法。
的大小。 BD=DC=BC/2=2/2
例4.如图,三棱锥P-ABC的顶点P在底面ABC上的射影是底面Rt△ABC斜边AC的中点O,若PB=AB=1,BC= ,求二面角P-AB-C的正
切值。 已知三个侧面的顶角,求相邻两个侧面所成的角
D
C
面分别相交于射线PA、PB
取AB 的中点为E,连PE,OE ∴∠P= 60º ∴∠AOB=120º
已知三个侧面的顶角,求相邻两个侧面所成的角
⑴定义法是选择一个平面内的一点(一般为这个面的一个顶点)向棱作垂线,再由垂足在另一个面内作棱的垂线。
ABCD-A B C D 中, ∵AB=AC=a,∠BAC=90。
1 ∠COD是二面角α-AB-β的平面角
求(1)平面C1BD与平面
二面角的平面角的四种求解策略
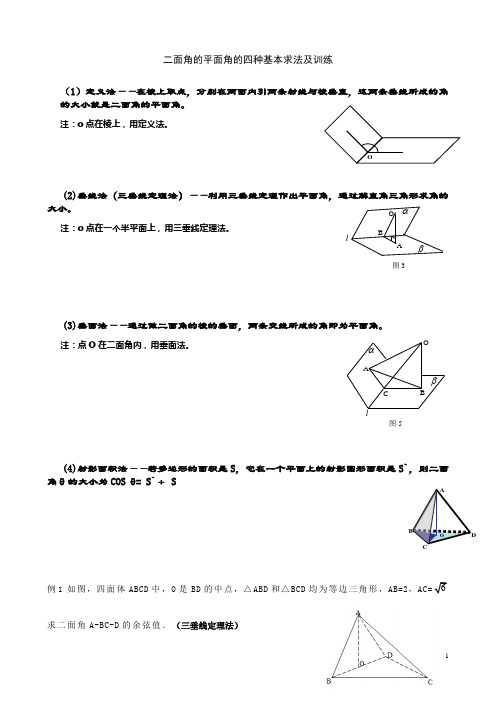
二面角的平面角的四种基本求法及训练(1)定义法——在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。
注:o 点在棱上,用定义法。
(2)垂线法(三垂线定理法)——利用三垂线定理作出平面角,通过解直角三角形求角的大小。
注:o 点在一个半平面上,用三垂线定理法。
(3)垂面法——通过做二面角的棱的垂面,两条交线所成的角即为平面角。
注:点O 在二面角内,用垂面法。
(4)射影面积法——若多边形的面积是S ,它在一个平面上的射影图形面积是S`,则二面角θ的大小为COS θ= S`÷ S例求二面角A-BC-D 的余弦值.(三垂线定理法)A 图3αβO BlO图5βαlCBAD例2 在60°二面角M -a -N 内有一点P ,P 到平面M 、平面N 的距离分别为1和2,求点P 到直线a 的距离。
(垂面法)例3 如图在三棱锥 S-ABC 中,SA ⊥底面ABC ,AB ⊥BC ,DE 垂直平分SC ,且分别交 AC 、SC 于D 、E ,又SA =AB ,BS =BC , 求以BD 为棱,BDE 与BDC 为面的二面角的度数。
(定义法)例4如图△ABC 与△BCD 所在平面垂直,且AB =BC =BD ,∠ABC =∠DBC =120,求二面角 A-BD-C 的余弦值。
(补棱法和射影面积法)AC例5.在四棱锥P-ABCD 中,ABCD 为正方形,PA ⊥平面ABCD ,PA =AB =a ,求平面PBA 与平面PDC 所成二面角的大小。
(补棱法和射影面积法)练习题1.如图,二面角α-l-β的大小是60°,线段AB ⊂α.B ∈l ,AB 与l 所成的角为30°.则AB 与平面β所成的角的正弦值是2.山坡与水平面成30︒角,坡面上有一条与坡角水平线成30︒角的直线小路,某人沿小路上坡走了一段路程后升高了100米,则此人行走的路程为 3.在一个二面角的一个面内有一个点,它到棱的距离等于到另一个面的距离的2倍,则二面角的度数为 。
求二面角的基本方法

解题宝典二面角是立体几何的重要内容,也是各类试题考查的重点内容.求二面角问题主要考查作二面角的平面角的方法以及同学们的空间想象能力.本文重点介绍求二面角的三种基本方法:定义法、三垂线法、公垂面法.一、定义法从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱.以二面角棱上的任意一点O 为端点,在两个半平面内分别作垂直于棱的两条射线OA 、OB ,则∠AOB 就是此二面角的平面角.二面角的大小可以用它的平面角来度量.在求二面角的大小时,我们只要根据二面角的平面角的定义作出平面角,通过解三角形,即可求得平面角的大小.例1.已知二面角α-a -β等于120°,PA ⊥α,A∈α,PB ⊥β,B ∈β,求∠APB 的大小.分析:本题可运用定义法求解,首先需要根据二面角的定义作出二面角的平面角.为了求得∠APB ,可过A 作二面角棱的垂线交棱于O 点,连接OB ,使APBO 在同一平面内,这样便可运用四边形的内角和为360o的定理求得结果.解:如图1,过A 作二面角棱的垂线交棱于O 点,连接OB ,∵PA ⊥α,a ⊂α,∴PA ⊥a ,同理PB ⊥a ,∴a ⊥平面PAB 又∵OA ⊂平面PAB ,∴a ⊥OA ,且O 、P 、A 、B 四点共面,同理a ⊥OB ,∴∠AOB 是二面角α-a -β的平面角.在四边形PAOB 中,∠AOB =120°,∠PAO =∠POB =90°,∴∠APB =60°.图3图1图2二、三垂线法三垂线法是指运用三垂线定理求二面角的方法.我们首先要找到一个平面的垂线,再过垂足作棱的垂线,连结两个垂足即得到二面角的平面角.在运用三垂线法解题时,只需要构造出三条垂线,便可利用三垂线定理来证明所作的角为二面角的平面角.例2.如图2,ABCD -A 1B 1C 1D 1是长方体,侧棱AA 1长为1,底面为正方体且边长为2,E 是棱BC 的中点,求二面角C 1-DE -C 的正切值.解:过点C 1作C 1O ⊥DE ,连接CO ,由三垂线定理可得CO ⊥DE ,∴∠C 1OC 为二面角C 1-DE -C 的平面角,又∵ABCD 是边长为2的正方形,∴CD =2,CE =1,DE =5,在RtΔADE 中,S ΔCDE =12CD ∙CE =12DE ∙CO ,∴CO =,又∵CC 1=1,tan ∠C 1OC =CC1CO.该解法主要运用了三垂线法作出了二面角的平面角,然后在直角三角形C 1OC 中,根据正弦函数的定义求得二面角C 1-DE -C 的平面角∠C 1OC 的正切值.三、公垂面法公垂面法是指作一个与棱垂直的平面,使该垂面与二面角的两半平面相交,得到的交线所成的角即为二面角的平面角.公垂面法的适用范围较小,一般只适用于方便求作两个半平面的公垂面的问题.例3.如图3,已知PA 与正方形ABCD 所在的平面垂直,且AB =PA ,求平面PAB 与平面PCD 所成的二面角的大小.分析:该二面角的平面角很难作出来,由图可知平面PAD 为平面PAB 与平面PCD 的公垂面,可运用公垂面法求解,寻找出它们的交线便可找出二面角的平面角,由已知的边角关系即可求得二面角的大小.解:∵PA ⊥平面ABCD ,∴PA ⊥CD ,又∵CD ⊥AD ,∴CD ⊥平面PAD ,而CD ⊂平面PCD ,∴平面PCD ⊥平面PAD ,同理可证,平面PAB ⊥平面PAD ,∵平面PCD ∩平面PAD =PD ,平面PAB ∩平面PAD =PA ,∴PA ,PD 与所求二面角的棱均垂直,∴∠APD 为所求二面角的平面角,且∠APD =45°.定义法、三垂线法、公垂面法三种方法都是求二面角的常用方法,但其适用的情形各不相同.定义法适用于解答可直接利用定义作出二面角的问题;三垂线法适用于解答垂直关系较多的问题;公垂面法适用于解答方便求作两个半平面的公垂面的问题.(作者单位:山东省无棣县第三高级中学)刘阳43。
求解二面角问题的基本方法
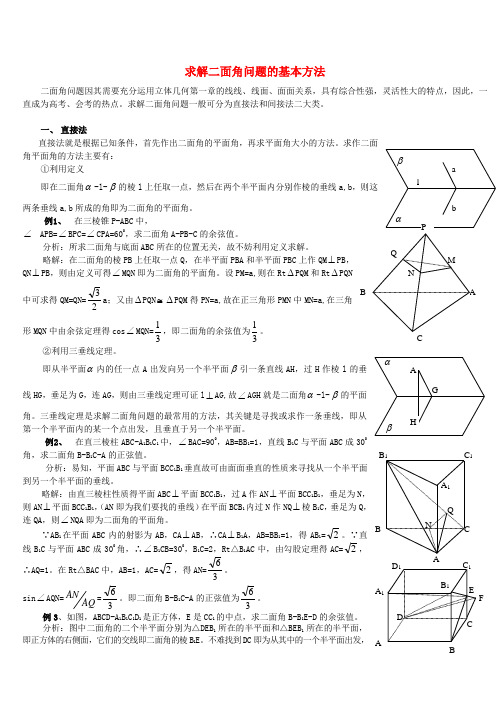
求解二面角问题的基本方法二面角问题因其需要充分运用立体几何第一章的线线、线面、面面关系,具有综合性强,灵活性大的特点,因此,一直成为高考、会考的热点。
求解二面角问题一般可分为直接法和间接法二大类。
一、 直接法角平面角的方法主要有:①利用定义即在二面角α-l-β的棱l 上任取一点,然后在两个半平面内分别作棱的垂线a,b 两条垂线a,b 所成的角即为二面角的平面角。
例1、 在三棱锥P-ABC 中,∠ APB=∠BPC=∠CPA=600,求二面角A-PB-C 的余弦值。
分析:所求二面角与底面ABC 所在的位置无关,故不妨利用定义求解。
略解:在二面角的棱PB 上任取一点Q ,在半平面PBA 和半平面PBC 上作QM ⊥PB ,QN ⊥PB ,则由定义可得∠MQN 即为二面角的平面角。
设PM=a,则在Rt ∆PQM 和Rt ∆PQN 中可求得QM=QN=23a ;又由∆PQN ≅∆PQM 得PN=a,故在正三角形PMN 中MN=a,在三角形MQN 中由余弦定理得cos ∠MQN=31,即二面角的余弦值为31。
②利用三垂线定理。
即从半平面α内的任一点A 出发向另一个半平面β引一条直线AH ,过H 作棱l 的垂线HG ,垂足为G ,连AG ,则由三垂线定理可证l ⊥AG,故∠AGH 就是二面角α-l-β的平面角。
三垂线定理是求解二面角问题的最常用的方法,其关键是寻找或求作一条垂线,即从第一个半平面内的某一个点出发,且垂直于另一个半平面。
例2、 在直三棱柱ABC-A 1B 1C 1中,∠BAC=900,AB=BB 1=1,直线B 1C 与平面ABC 成30角,求二面角B-B 1C-A 的正弦值。
分析:易知,平面ABC 与平面BCC 1B 1垂直故可由面面垂直的性质来寻找从一个半平面到另一个半平面的垂线。
略解:由直三棱柱性质得平面ABC ⊥平面BCC 1B 1,过A 作AN ⊥平面BCC 1B 1,垂足为N ,则AN ⊥平面BCC 1B 1,(AN 即为我们要找的垂线)在平面BCB 1内过N 作NQ ⊥棱B 1C ,垂足为Q ,连QA ,则∠NQA 即为二面角的平面角。
求二面角的方法

解题宝典空间角主要包括异面直线所成的角、直线与平面所成的角、二面角.二面角是指从一条直线出发的两个半平面所组成的图形.求二面角的大小是一类常见的问题.本文重点介绍求二面角大小的四种方法:定义法、向量法、面积投影法、三垂线定理法.一、定义法过二面角棱上的任一点,在两个半平面内分别作与棱垂直的射线,则两射线所成的角叫做二面角的平面角.一般地,要求得二面角的大小只需要求出二面角的平面角的大小即可.在求二面角的大小时,我们可以根据二面角的平面角的定义来求解.首先在二面角的棱上选取一点,在两个面内作棱的垂线,则两条垂线的夹角,即为二面角的平面角,求得平面角的大小即可得到二面角的大小.例题:如图1,在长方体ABCD-A1B1C1D1中,底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明:BE⊥EB1C1;(2)若AE=A1E,求二面角B-EC-C1正弦值.图1图2解:(1)略;(2)由(1)知∠BEB1=90°.由题设知Rt△ABE≌Rt△A1B1E,所以∠AEB=45°,故AE=AB,AA1=2AB.如图2所示,在平面BCE内过B点作BM⊥CE于点M,取棱CC1的中点N,连结MN,EN.因为EC1=EC,所以EN⊥CC1,所以ΔCEN为直角三角形.因为BC⊥BE,所以ΔCEB为直角三角形.令AB=1,则BC=NC=1,BE=EN=2,CE=3,所以RtΔBEC≌RtΔNEC,所以MN⊥EC,则∠BMN即为二面角B-EC-C1的平面角.在RtΔBEC中,sin∠BCE=BE CE=BM BC,所以BM=,MN.在ΔBMN中,cos∠BMN=BM2+MN2-BN22BM∙MN=-12,则sin∠BMN=,故二面角B-EC-C1正弦值.利用定义法求二面角的大小的关键是作出二面角的平面角.在作图的过程中要充分利用题目条件中隐含的垂直关系,如等腰三角形三线合一的性质、菱形或正方形的对角线相互垂直、直角三角形中勾股定理及其逆定理等.另外在构造二面角的平面角时,常用的方法还有垂面法,即经过两个面的垂线的平面与两个平面的交线所夹的角即为二面角的平面角.二、三垂线法三垂线法是指利用三垂线定理求作二面角的平面角,求得二面角大小的方法.在求作二面角的平面角时,需过其中一个面内的一点作另一个面的垂线,再经过垂足作棱的垂线,连接该点与棱上的垂足,进而构造出与二面角的平面角相关的角,再结合图形中的垂直关系求得二面角的大小.以上述例题为例.解:如图3,连接BD,AC,交点为O,过点O作CE的垂线,垂足为P,连接BP.由三垂线定理可知BP垂直于CE,所以∠BPO即为所求二面角平面角的补角.设AB=1,由(1)可知AE=1,所以BE=2,CE=3.因为BC⊥BE,所以ΔBCE为直角三角形,所以RtΔBCP∽RtΔBCE.陈秀林图342解题宝典所以BP.在Rt△BOP 中,sin ∠BPO =BC BP=,即所求二面角正弦值为.此法与定义法的不同之处是将所求二面角的相关角置于直角三角形中,从而使解题的过程更加简洁.三、向量法向量法是通过空间向量的坐标运算,将所求的二面角转化为两个平面的法向量的夹角的方法.解题的思路是通过建立空间直角坐标系,求出两个平面的法向量,根据向量的数量积公式求出夹角,再利用法向量的夹角与二面角的关系来确定二面角的大小.值得说明的是,二面角的平面角与法向量的夹角的关系是相等或互补.以上述例题为例.解:(2)由(1)知∠BEB 1=90°.由题设知Rt△ABE ≌Rt△A 1B 1E ,所以∠AEB =45°,故AE =AB ,AA 1=2AB .以D 为坐标原点,建立如图4所示的空间直角坐标系D -xyz ,则C (0,1,0),B (1,1,0),C 1(0,1,2),E (1,0,1),所以 CB =(1,0,0),CE =(1,-1,1),CC 1=(0,0,2).设平面BCE 的法向量为n =(x ,y ,z ),则ìíî CB ∙n =0,CE ∙n =0,即{x =0,x -y +z =0,令y =-1,得n =(0,-1,-1).设平面ECC 1的法向量为m =(x ,y ,z ),则ìíî CC 1∙m =0,CE ∙m =0,即{2z =0,x -y +z =0,令x =1得m=(1,1,0).于是cos m,n =m ∙n |m |∙|n |=-12.所以二面角B -EC-C 1平面角正弦值为.向量的引入降低了立体几何问题的难度,但对同学们的运算能力提出了更高的要求.求法向量的原则是先找后求,即如果存在一条已知的直线与二面角的某一个平面垂直,则该直线的方向向量即可视为此平面的法向量.四、投影法投影法,即为构造出二面角的两个平面中的一个平面在另外一个平面内的投影,从而利用此平面与其投影的夹角θ来判断所求二面角的大小的方法.若该平面与其投影的面积分别为S 1,S 2,则cos θ=S 1S 2.θ与所求二面角的关系有两种,即相等或互补.以上述例题为例.解:如图5,连接BD 交AC 于点O ,连接EO .因为四边形ABCD 为正方形,所以BD ⊥AC ,所以点B 在面C 1CE 内的投影,三角形EOC 为ECB 的投影.设棱AB =1,由(1)可知AE =1,则AC =BE =2,EC =3,所以三角形OCE 的面积为S 1=12∙OC ∙AE =12,三角形BCE 的面积为S 2=12BC ∙BE =12×1×2.所以S 2S 1=42=12.所以面BCE 与面ECC 1所成锐二面角的余弦值为12,故二面角的正弦值为.在本题中,三角形ECB 与其在面ECC 1上的投影EOC 的夹角即为所求二面角的补角,而两角互补,则其正弦值相等,所以可直接利用投影法来求解.一般地,求二面角的问题主要有两类,即求有棱二面角的大小和无棱二面角的大小,虽然图形有所不同,但解题的方法基本上一致.同学们在解题的过程中要注意仔细审题,择优而用.(作者单位:江苏省大丰高级中学)图5图443。
二面角的平面角及求法

二面角的平面角及求法1、半平面的定义:一条直线把平面分成两个部分,每一部分都叫做半平面.2、二面角的定义:从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面。
3、二面角的平面角的概念:以二面角的棱上任意一点为顶点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫二面角的平面角。
一个平面角的大小可用它的平面的大小来衡量,二面角的平面角是多少度,就说这个二面角是多少度。
二面角大小的取值范围是[0,180°]。
4、直二面角:平面角是直角的二面角叫直二面角。
两相交平面如果所组成的二面角是直二面角,那么这两个平面垂直;反过来,如果两个平面垂直,那么所成的二面角为直二面角。
5、二面角的平面角具有下列性质:a.二面角的棱垂直于它的平面角所在的平面,即l⊥平面AOB.b.从二面角的平面角的一边上任意一点(异于角的顶点)作另一面的垂线,垂足必在平面角的另一边(或其反向延长线)上.c.二面角的平面角所在的平面与二面角的两个面都垂直,即平面AOB⊥α,平面AOB⊥α.6、求二面角的平面角的方法:(1)定义法:通过二面角的平面角来求;找出或作出二面角的平面角;证明其符合定义;通过解三角形,计算出二面角的平面角.上述过程可概括为一作(找)、二证、三计算”.(2)三垂线法:已知二面角其中一个面内一点到另一个面的垂线,用三垂线定理或其逆定理作出平面角.(3)垂面法:已知二面角内一点到两个面的垂线时,过两垂线作平面与两个半平面的交线所成的角即为平面角,由此可知,二面角的平面角所在的平面与棱垂直.(4)射影法:利用面积射影定理求二面角的大小;其中S为二面角一个面内平面图形的面积,S′是这个平面图形在另一个面上的射影图形的面积,α为二面角的大小.(5)向量法:设二面角的平面角为θ.①如果那么②设向量m、n分别为平面α和平面β的法向量是相等还是互补,根据具体图形判断。
二面角的平面角的求法

二面角的平面角的求法知识点拨1、二面角的定义以一条直线出发的两个半平面所成的图形叫做二面角,记作:二面角α—l —β。
二面角出现的状态形式有:竖立式、横卧式、倒向式2、二面角的平面角的定义以二面角的顶点任意一点为端点,在两个面内分别作垂直于边的两条射线,这两条射线所成的角叫做二面角的平面角。
二面角的平面角的定义要注意三个重要的词组:“棱上”、“面上”、“垂直”, 事实上, 二面角的平面角具有三个要素:(1)过棱上任意一点;(2)分别在两个面内引射线;(3)射线垂直于棱。
其中(1)(2)决定了平面角的两边是在同一平面内。
所以才有“平面角”之称, (3)是决定了平面角的数值的唯一性。
由二面角的平面角的定义可知: 二面角的棱垂直于二面角的平面角所在平面。
平面角是直角的二面角叫做直二面角.3、二面角大小求法的要领二面角的大小,可以用它的平面角来度量,二面角的平面角是几度,就说这个二面角是几度.( 也可转化为求三角形内角问题)4、求二面角大小的基本方法我们总结一下作二面角平面角的几种基本方法. (1)定义法;(2)垂面法;(3)三垂线法;(4)面积法cos θ=S 射影多边形/S 多边形(射影面积公式)。
(1)如何利用定义作二面角的平面角呢?在二面角的棱a 上任意取一点O 为端点,在面α,β内分别引垂直于棱a 的两条射线OA ,OB ,则∠AOB 为该二面角的平面角.(2)如何利用三垂线定理(或其逆定理)作二面角的平面角呢?在二面角α-a-β的面α上任取一点A ,过A 分别作棱a 和另一面β的垂线AO 和AB(O ,B 分别是垂足),连BO ;或者过A 作面β的垂线AB ,又过垂足B 引棱a 的垂线BO ,连AO ;则∠AOB 为该二面角的平面角.(3)如何用作垂面的办法作二面角的平面角呢?过二面角的棱a上任一点O,作平面γ与该棱垂直(作棱的垂面),平面γ与α,β分别交于OA,OB,则可用∠AOB来度量二面角α-a-β的大小.(4)射影面积公式用此方法可避免寻找二面角的平面角的繁琐步骤。
立体几何中二面角8个常用求法

⽴体⼏何中⼆⾯⾓8个常⽤求法
⼆⾯⾓定义的回顾:
⼆⾯⾓的通常求法
1、由定义作出⼆⾯⾓的平⾯⾓;
2、利⽤三垂线定理(逆定理)作出⼆⾯⾓的平⾯⾓;
3、作⼆⾯⾓棱的垂⾯,则垂⾯与⼆⾯⾓两个⾯的交线所成的⾓就是⼆⾯⾓的平⾯⾓。
4、空间坐标法求⼆⾯⾓的⼤⼩
5、平移或延长(展)线(⾯)法
6、射影公式S射影=S斜⾯cosθ
7、化归为分别垂直于⼆⾯⾓的两个⾯的两条直线所成的⾓
⼀、利⽤定义作出⼆⾯⾓的平⾯⾓,并设法求出其⼤⼩。
⼆、三垂线定理(逆定理)法
由⼆⾯⾓的⼀个⾯上的斜线(或它的射影)与⼆⾯⾓的棱垂直,推得它位于⼆⾯⾓的另⼀的⾯上的射影(或斜线)也与⼆⾯⾓的棱垂直,从⽽确定⼆⾯⾓的平⾯⾓。
四、找(作)公垂⾯法
由⼆⾯⾓的平⾯⾓的定义可知两个⾯的公垂⾯与棱垂直,因此公垂⾯与两个⾯的交线所成的⾓,就是⼆⾯⾓的平⾯⾓。
五、平移或延长(展)线(⾯)法
将图形中有关线段或平⾯进⾏平移或延长(展),以其得到⼆⾯⾓的两个平⾯的交线。
图⼆:
六、射影公式
由公式S射影=S斜⾯cosθ,作出⼆⾯⾓的平⾯⾓直接求出。
运⽤这⼀⽅法的关键是从图中找出斜⾯多边形和它在有关平⾯上的射影,⽽且它们的⾯积容易求得。
图⼆:
七、化归为分别垂直于⼆⾯⾓的两个⾯的两条直线所成的⾓
图⼆:
图三:
⼋、空间向量求解⼆⾯⾓
求解⼆⾯⾓⼤⼩的⽅法很多,诸如定义法、三垂线法、垂⾯法、射影法、向量法等若⼲种。
⽽这些⽅法中最简单易学的就是向量法。
图⼆:
图四:
图五:
图六:
图七:
图⼋:
图九:
图⼗:。
二面角的定义

二面角
一、二面角的定义
从空间一直线出发的 两个半平面所组成的 图形叫做二面角。
α
ι
β
二面角
二面角的平面角
一个平面垂直于二面角
的棱,并与两半平
面 分 别 相 交 于 射 线 PA 、 P B 垂足为P,则∠APB叫做二面
γ
角 的平面角
ι
β
P
B
A
α
二面角的求法
二、二面角的求法
解:由直三棱柱性质得平面ABC ⊥平面BCC1B1, 过A作AN ⊥平面BCC1B1,垂足为N,则AN ⊥平 面BCC1B1,(AN即为我们要找的垂线)在平面 BCB1内过N作NQ棱B1C,垂足为Q,连QA,则 NQA即为二面角的平面角。
∵AB1在平面ABC内的射影为AB,CAAB, ∴CAB1A,AB=BB1=1,得AB1= 2。∵直线B1C与 平面ABC成300角,∴B1CB=300,B1C=2, Rt△B1AC中,由勾股定理得AC= 2 ,∴AQ=1。 在Rt△BAC中,AB=1,AC=,得AN= 6 。
于P到棱的距离的一半,则这个二
面角的度数是多少? 60º
O
Aα
ι
二面角
一、二面角的定义
α
从空间一直线出发的两个半 平面所组成的图形叫做二面角
ι
β
二、二面角的平面角
小 1、定义 2、求二面角的平面角方法
ι αβ
γP
B A
结
①点P在棱上 —定义法 ②点P在一个半平面上 —三垂线定理法
③点P在二面角内 —垂面法
∵O为 AC 中点, ∠ABC=90º
∴OE∥BC且 OE BC1
OE⊥AB ,因此 PE⊥A2B ∴∠PEO为二面角P-AB-C 的平面角
求二面角平面角的常用六法

姨 2 a袁又 疫AB彝BC袁亦AC= 姨 3 a袁在 Rt吟SAC 中袁tan蚁ACS=
SA AC
=
1 姨3
=
姨3 3
,
亦蚁ACS=30莓遥 又 疫DE彝SC袁亦蚁EDC=60莓袁 即所求二面角
的平面角的大小为 60莓遥
四尧延伸法院针对无棱问题遥 若所求二面角的两个面只有一
个公共点是已知的袁则可把两个面延伸而得到二面角的棱袁然后
教学信息
求二面角平面角的常用六法
吴焕群 渊河北省唐山市第十二高级中学 河北 唐山 063000冤
揖摘要铱二面角是每年高考必考内容袁求解过程中要做到野一作尧二证尧三算冶的统一遥 现介绍几种常见求法院一尧定义法;二尧垂线法;
三尧垂面法;四尧延伸法;五尧射影面积法;六尧公式法遥
揖关键词铱二面角平面角 曰 常见几法
CD2=CE2+DE2= AC2+AE2-2AC窑AEcos 蚁CAE +DE2, 即 CD2=
AC2+BD2-2AC窑BDcos蚁CAE+AB2,亦cos蚁CAE=
62 +242 +82-渊2姨133 2伊6伊24
冤2
=
1 2
袁亦蚁CAE=60莓遥
2015 年第 2 期
245
ABC遥 亦 平 面 PAB 彝 平 面 ABC袁
CD 彝 平 面 PAB袁 连 接 PD袁 则 吟PBD 为吟PBC 在平面 PAB 内
的射影遥
易知
S = 吟PBD
1 2
S = 吟PBD
1 2
窑a窑
姨2 2
a
=
姨2 4
2
a
袁S = 吟PCB
1 2
(完整版)找二面角的平面角的方法汇总

找二面角的平面角的方法汇总二面角是高中立体几何中的一个重要内容,也是一个难点.对于二面角方面的问题,学生往往无从下手,他们并不是不会构造三角形或解三角形,而是没有掌握寻找二面角的平面角的方法.我们试将寻找二面角的平面角的方法归纳为以下六种类型. 一、根据平面角的定义找出二面角的平面角 例1 在60的二面角βα--a 的两个面内,分别有A 和B 两点.已知A 和B 到棱的距离分别为2和4,且线段10=AB ,试求:(1)直线AB 与棱a 所构成的角的正弦值;(2)直线AB 与平面α所构成的角的正弦值. 分析:求解这道题,首先得找出二面角的平面角,也就是找出 60角在哪儿.如果解决了这个问题,这道题也就解决了一半.根据题意,在平面β内作a AD ⊥;在平面α内作α⊥BE ,EB CD //,连结BC 、AC .可以证明a CD ⊥,则由二面角的平面角的定义,可知ADC ∠为二面角βα--a 的平面角.以下求解略.二、根据三垂线定理找出二面角的平面角例2 如图,在平面β内有一条直线AC 与平面α成 30,AC 与棱BD 成 45,求平面α与平面β的二面角的大小.分析:找二面角的平面角,可过A 作BD AF ⊥;⊥AE 平面α,连结FE .由三垂线定理可证EF BD ⊥,则AFE ∠为二面角的平面角.总结:(1)如果两个平面相交,有过一个平面内的一点与另一个平面垂直的垂线,可过这一点向棱作垂线,连结两个垂足.应用三垂线定理可证明两个垂足的连线与棱垂直,那么就可以找到二面角的平面角.(2)在应用三垂线定理寻找二面角的平面角时,注意“作”、“连”、“证”,即“作BD AF ⊥”、“连结EF ”、“证明BD EF ⊥”. 三、作二面角棱的垂面,垂面与二面角的两个面的两条交线所构成的角,即为二面角的平面角例3 如图1,已知P 为βα--CD 内的一点,α⊥PA 于A 点,β⊥PB 于B 点,如果n APB =∠,试求二面角βα--CD 的平面角.图1 图2分析:⊥⇒⊥⇒⊥⊥⇒⊥CD CDPB PB CDPA PA βα平面PAB . 因此只要把平面PAB 与平面α、β的交线画出来即可.证明AEB ∠为βα--CD 的平面角, n AEB -=∠180(如图2).注意:这种类型的题,如果过A 作CD AE ⊥,垂足为E ,连结EB ,我们还必须证明CD EB ⊥,及AEBP 为平面图形,这样做起来比较麻烦.例4 已知斜三棱柱111-C B A ABC 中,平面1AB 与平面1AC 构成的二面角的平面角为 30,平面1AB 与平面1BC 构成的二面角为 70.试求平面1AC 与平面1BC 构成的二面角的大小.分析:作三棱柱的直截面,可得△DEF ,其三个内角分别为斜三棱柱的三个侧面两两构成的二面角的平面角.总结:对棱柱而言,其直截面与各个侧棱的交点所形成的多边形的各个内角,分别为棱柱相邻侧面构成的二面角的平面角.四、平移平面法例5 如图,正方体1111-D C B A ABCD 中,E 为1AA 的中点,H 为1CC 上的点,且211::=H C CH .设正方体的棱长为a ,求平面EH D 1与底面1111D C B A 构成的锐角的正切.分析:本题中,仅仅知道二面角棱上的一点1D ,在这种情况下,寻找二面角的平面角较困难.根据平面平移不改变它与另一个平面构成的角的大小的原理,如果能把二面角中的一个平面平移,找出辅助平面与另一个平面的交线,就可以作出二面角的平面角.有了平面角之后,只需要进行常规构造三角形和解三角形的计算,就可以解决问题了.如图,过点E 作11//D A EM 与D D 1相交于M 点,过M 点作11D C MN ⊥,与H D 1相交于N 点.可证平面//EMN 平面1111D C B A .这样,求平面EH D 1与平面1111D C B A 的二面角的平面角就转化为求平面EH D 1与平面EMN 的二面角的平面角.显然EN 为这两个平面的交线,过点M 作EN MF ⊥,F 为垂足,连结F D 1,可证EN F D ⊥1.则FM D 1∠为本题要寻找的二面角.五、找垂面,作垂线例6 如图,正方体1111-D C B A ABCD 中,M 为棱AD 的中点,求平面CB C B 11和平面M BC 1所构成的锐二面角的正切.分析:平面AC 与二面角C BC M --1的一个面C B 1垂直,与另一个平面1C MB 相交,过M 点作BC MP ⊥,垂足为P ,过P 作BC PN ⊥,交1C B于N 点,连结MN ,由三垂线定理可证1BC MN ⊥,则MNP ∠为二面角C BC M --1的平面角.总结:当一个平面与二面角的一个平面垂直,与另一个平面相交时,往往过这个面上的一点作这两个垂直平面交线的垂线,再过垂足作二面角棱的垂线.根据三垂线定理即可证明,并找出二面角的平面角.再如图,要找βα--a 所构成的二面角的平面角,可找平面βγ⊥,且b =αγ ,l =βγ ,过b 上任何一点A 作l AB ⊥,垂足为B ,过B 作α⊥BC ,垂足为C ,连结AC ,可证ACB ∠为βα--a 的平面角. 六、根据特殊图形的性质找二面角的平面角 1.三线合一 例7 如图,空间四边形ABCD 中,3==AD AB ,4==CD BC ,2=BD ,5=AC .试求C BD A --二面角的余弦值.分析:如图1,AD AB =,CD BC =,则△ABD 和△BDC 为等腰三角形.过A 作BD AE ⊥,垂足为E ,连结CE .根据三线合一,且E 为BD中点,可证BD CE ⊥,则AEC ∠为二面角C BD A --的平面角.2.全等三角形例8 如图,已知空间四边形ABCD ,6==BC AB ,4==DC AD ,8=BD ,6=AC .试求C BD A --的余弦值.分析:过A 作BD AE ⊥,垂足为E ,连结CE .根据已知条件,△AED 和△CED 全等,可证BD CE ⊥,则AEC ∠为二面角C BD A --的平面角.3.二面角的棱蜕化成一点例9 如图,四棱锥BCED A -中,DB 和EC 与面ABC 垂直,△ABC 为正三角形.(1)若BD EC BC ==时,求面ADE 与面ABC 的夹角;(2)若BD EC BC 2==时,求面ADE 与面ABC 的夹角.分析:如图,面ADE 与面ABC 的交线蜕化成一点,但面ADE 与面ABC 与面DC 相交.如果三个平面两两相交,它们可能有三种情况:(1)交线为一点;(2)一条交线;(3)三条交线互相平行.在图1中,两条交线BC 与DE 互相平行,所以肯定有过A 且平行于DE 的一条交线.可过A 作DE AM //,平面ADE 与平面ABC 的交线即为AM .过A 作DE AN ⊥于N ,过A 作BC AF ⊥于F .可证AM AN ⊥,AM AF ⊥,则NAF ∠为面ADE 与面ABC 的夹角.如图,DE 与C B 不平行且相交.根据三个平面两两相交可能出现的三种情况,这三个面的交线为一点.延长ED 、CB 相交于G 点,连结AG .AG 即为平面ADE 与平面ABC 的交线,通过一些关系可证CAE ∠为平面ADE 与平面ABC 的夹角.通过以上分析和举例说明,寻找二面角的平面角的方法就比较容易了.只要我们勤动脑,善观察,多总结,抓住问题的特征,找出适当的方法,关于二面角的平面角的问题就会迎刃而解.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
寻找二面角的平面角的方法面角是高中立体几何中的一个重要内容,也是一个难点•对于二面角方面的问题,学生往往无从下手,他们并不是不会构造三角形或解三角形,而是没有掌握寻找二面角的平面角的方法.我们试将寻找二面角的平面角的方法归纳为以下六种类型.1.1二面角的相关概念新教材⑴在二面角中给出的定义如下:从一条直线出发的两个半平面所组成的图形叫做二面角定义只给出二面角的定性描述,关于二面角的定量刻画还必须放到二面角的平面角中去研究•教材如下给出了二面角的平面角的概念:二面角的平面角是指在二面角:的棱上任取一点 0,分别在两个半平面内作射线AO _ I, BO _丨,则.AOB为二面角〉-丨- 一:的平面角•2.二面角的求解方法对二面角的求解通常是先定位二面角的平面角,从而将三维空间中的求角问题转化为二维空间并可以通过三角形的边角问题加以解决•定位出二面角为解题的关键环节,下面就二面角求解的步骤做初步介绍:一、“找”:找出图形中二面角,若不能直接找到可以通过作辅助线补全图形定位二面角的平面角二、“证”:证明所找出的二面角就是该二面角的平面角三、“算”:计算出该平面角由于定位二面角的难度较大,对于求解二面角还有一种思路就是绕开定位二面角这一环节,通过一些等价的结论或公式或用空间向量等方法来直接求出二面角的大小.本文将根据这两种解题思路对二面角的解题方法做一一介绍•2.1定位二面角的平面角,求解二面角二面角常见题型中根据所求两面是否有公共棱可分为两类:有棱二面角、无棱二面角.对于前者的二面角的定位通常采用找点、连线或平移等手段来定位出二面角的平面角;而对于无棱二面角我们还必须通过构造图形如延展平面或找公垂面等方法使其有“无棱”而“现棱”再进一步定位二面角的平面角一、根据平面角的定义找出二面角的平面角例1 在60的二面角:-a -■的两个面内,分别有A和B两点•已知A和B到棱的距离分别为2和4,且线段AB =10,试求:(1 )直线AB与棱a所构成的角的正弦值; (2)直线AB与平面〉所构成的角的正弦值.分析:求解这道题,首先得找出二面角的平面角,也就是找出60角在哪儿•如果解决了这个问题,这道题也就解决了一半.根据题意,在平面1内作AD — a ;在平面〉内作BE —〉, CD/EB ,连结B CAC•可以证明CD— a,则由二面角的平面角的定义,可知∙ADC为二面角:-a-'EI巳22i23BG =iT 蔦;的平面角•以下求解略∙例1 正方体 ABCD-A1B1C1D1 中,求二面角 A-BD-CI 的大小为 例2(2006年江苏试题)如图2(1),在正三角形 ABC 中,E 、F 、P 分别是AB 、AC 、BC 上的点,满足 AE : EB=CF : FA=CP : BP=I : 2•如图 2(2),将厶 AEF 折起 到厶A1EF 的位置,使二面角 AI-EF-B 成直二面角,连 接 A1B 、A1P.(I )与(∏ )略;(川)求二面角B-AIP-F 的余弦值 tan ∠ COC i = . 2分析与略解:在例1中,图形的对称和谐状态对解题产生了很好的启迪作用,在这里更离不开图形的这种对称 和谐性 若取BP 的中点Q ,连接EQ ,则在正三角形 ABC 中,很容易证得△ BEQPEQ ^△ PEF ^△ AEF ,那么在图 2(2)中,有 A i Q=A i F 作 FM 丄 A i P 于 M ,连接 QH 、QF ,则易得△ A i QP ^^ A i FP , △ QMP ◎△ FMP ,所以∠ PMQ= ∠ PMF=90o ,∠ QMF 为二面角 B-A I P-F 的平面角,使题解取得了突破性的进展 .设正三角形的边长为 3,依次可求得 2 ; 5"7A i P= .5 , QM=FM=—,在△ QMF 中,由余弦定理得 cos ∠ QMF= - - O _820II 广东高考理i8.(本小题满分I3分)如图5.在锥体P-ABCD 中,ABCD 是边长为I 的菱形, 且∠ DAB=60 , PA =PD = ,PB =2, E,F 分别是 BC,PC 的中点. (I)证明:AD —平面DEF; (2)求二面角P-AD-B 的余弦值.解:(2)由(I )知/PGB 为二面角P - AD - B 的平面角, 在 Rt PGA 中,PG222 (I )27“2 -(2八4在 PGB 中,CoS PGB HPG 2BG 2- PB 22PG BG.2i 7例 2 在如图 3 所示的三棱锥 P-ABC 中,AB=AC=PB=PC=2,BC=、2 ,PA= ■ 2 .求二面角 P-BC-A 的大小.解:作 BC 中点 D,连接 PD,AD.因 PB=PC=AB=A )C 知 PQBC,AdBC, 又有面 PBC 与面 ABC 共棱可得∠ PDA 为二面角P-BC-A 的平面角.而 AB=2,BC=2 . 2 ,易知 AD=PD= 2 ,在 RT?PAD 中,CoS PDA =PD 2AD 2-PA 22PD AD所以二面角P-BC-A 的大小为60图3分析与略解:所求二面角的棱为 AB ,不像图3的那样一看就明白的状态,但本质却是一样的,对本质的观察 能力反映的是思维的深刻性作A i E⊥ AB i 于AB i 于E,则可证 A i E 丄平面 AB i B.过E 作EF 丄AB 交AB 于F,连接 A i F,则得 A i F 丄AB , ∙∙∙∠ A i FE 就是所求二面角的平面角•依次可求得 ABI =BI B=転 A I B= √3 , A i E=乎,AI F 吟,则在 Rt△ AI EF中, sin∠ A I F E=A|=普例2.(2009山东卷理)如图,在直四棱柱 ABCD-A 1B 1C 1D 1中,底面ABCD 为等腰梯形,AB//CD , AB=4, BC=CD=2, AA I =2, E 、E 1、F 分别是棱 AD 、AA I 、AB 的中点。
(1) 证明:直线EE 1//平面FCC 1 ; (2) 求二面角B-FC I -C 的余弦值。
证(1)略解(2)因为AB=4, BC=CD=2,、F 是棱AB 的中点,所以BF=BC=CF,△ BCF 为正三角形,取CF 的中点O,则OB 丄CF,又因为直四棱柱 ABCD-A 1B 1C 1D 1中,CC i 丄平面ABCD,所以CC i 丄BO,所以OB 丄平 面CC i FM O 在平面CC i F 内作OP 丄C i F,垂足为P 连接BP,则∠ OPB第3页共15页二、根据三垂线定理找出二面角的平面角此法最基本的一个模型为:如图3 ,设锐二面角〉J - ',过面〉内一点P 作PA 丄〉于A ,作AB ⊥于B ,连接PB ,由三垂线定理得 PB ⊥,则∠PBA 为二面角〉J - 1的平面角,故称此法为三垂线法.例2如图,在平面:内有一条直线AC与平面〉成30 ,AC与棱BD 成45 ,求平面〉与平面:的二面角的大小.分析:找二面角的平面角,可过 A 作AF _ BD ; AE _平面〉,连结FE .由三垂 线定理可证BD _ EF ,则一 AFE 为二面角的平面角.总结:(1)如果两个平面相交,有过一个平面内的一点与另一个平面垂直的垂线,可过这一点向棱作垂线,连结两个垂足.应用三垂线定理可证明两个垂足的连线与棱垂直,那么就可以找到二面角的平面角(2)在应用三垂线定理寻找二面角的平面角时,注意“作” 、“连”’“证”即“作AF 丄BD ” “连结EF ” “证明例3(2006年陕西试题)如图4,平面〉丄平面1 ,〉∩ '■ =l , A ∈ :■ , B ∈ 直线I 上的射影为 A ι,点B 在I 的射影为B i ,已知AB=2 , AA ι=1 , BB i = 2,(I )略;(∏ )二面角A i -AB — B i 的大小.[,点A 在 A iB,B i为二面角B-FC I -C 的一个平面角,在厶BCF 为正三角形中,OBi3,在Rt △ CC i F 中,△ OPFs^ CC i F,τOPOF2=22,在 Rt△ OPFCG 一GF '面角B-FC ι-C 的余弦值为练习2 (2008天津)如图,在四棱锥 P- ABCD 中,底面ABCD 是矩形• 已知 AB =3, AD =2, PA =2, PD =2、2,. PAB = 60 . (I )证明AD _平面PAB ;(∏)求异面直线 PC 与AD 所成的角的大小; (川)求二面角 P-BD-A 的大小.分析:本题是一道典型的利用三垂线定理求二面角问题, 在证明AD 丄平面PAB 后,容易发现平面 PABL 平面ABCD 点P 就是二面角P-BD-A 的半平面上的一个点,于是可过点P 作棱BD 的垂线,再作平面 ABCD 勺垂线,于是可形成垂线定理中的斜线与射影内容,从而可得本解法。
J 39(答案:二面角 P- BD- A 的大小为arctan ----- )4例3在正方体 ABCD-A 1B 1C 1D 1中,O 1为面A 1B 1C 1D 1中心,求二面角 O 1-AC 1-D 1的大小. 解:在正方体 ABCD - A 1B 1C 1D 1 中 B 1D 1 — A1C 1,且 A 1C 1 — B 1D 1, B 1D 1 —面 A 1B 1C 1D 1,故 B 1D 1- AC 1, B 1 D 1 _ A 1C 1又 A 1C 1, AC^-面 AC 1A 1,可知 B ∙J D ∙∣ — AC 1A过D 1作D 1M _ AG 于M ,连接O 1 M 则由三垂线(逆)定理可知D 1MO 1为二面角O 1-AC 1-D 1的平面角.不妨令AA^= 2 ,*于是,有 D 1M = 2.6 , OO 12 , OM-,可得 33CoS D 1MO 1 =°M=1D 1M2所以二面角 O 1 - AC 1 -D 1的大小为60三、作二面角棱的垂面,垂面与二面角的两个面的 两条交线所构成的角,即为二面角的平面角CoSEOPB =OP BP14,所以二Pn图5B例3如图 1 ,已知P 为—CD -:内的一点,PA_:•于A 点,PB —'于B 点,如果∙ APB = n ,试PA . : = PA _ CD求二面角I-CD- L的平面角•分析:PB- U PB- CD因此只要把平面PAB 与平面〉、:的交线画出来即可•证明∙ AEB 为:-CD^的平面角,■ AEB =18O - n (如图 2) •注意:这种类型的题,如果过A 作AE 一 CD ,垂足为E ,连结EB ,我们还必须证明EB 一 CD ,及AEBP 为 平面图形,这样做起来比较麻烦.例4已知斜三棱柱ABC -A I B I C I中,平面AB I与平面AC I构成的二面角的平面角为30 ,平面AB I与平 面BC I构成的二面角为70 •试求平面AC I与平面BC I构成的二面角的大小.分析:作三棱柱的直截面,可得△ DEF ,其三个内角分别为斜三棱柱的三个侧面两 两构成的二面角的平面角.总结:对棱柱而言,其直截面与各个侧棱的交点所形成的多边形的各个内角,分别 为棱柱相邻侧面构成的二面角的平面角.例4空间的点P 到二面角〉-丨- 一:的面〉、■-及棱I 的距离分别 为4、3、2- 39,求二面角. -I--的大小.3分析与略解:如图 5 ,分别作PA 丄〉于A , PB⊥ [于B ,则易知 I 丄平面PAB ,设I ∩平面PAB=C ,连接PC,贝U I ⊥ PC.2%/39213分别在 Rt△ PAC> Rt△ PBC 中,PC=, PA=4, PB=3 ,贝U AC=—3 3因为P 、A 、C 、B 四点共圆,且 PC 为直径,设PC=2R,二面角〉-丨-:的大小为 X 分别在△ PAB、△ ABC 中,由余弦定理得2 2 2 2 2AB =AC +BC -2 ∙ AC ∙ BCCoSh =PA +PB -2 ∙ PA ∙ PBeoS ( ),1则可解得CoST=,r =120O, 二面角二-I -F 的大小为120o.2例5如图7,在正三棱柱 ABC -A i B i C i 中,截面A i EC —侧面AC i ,若AA i — Ai B i ,求平面A i EC 与平面A l BQ i 所成二面角(锐角)的大小 •解:设A i C AC i =G .因为面A i C i G 与面AC i 重合,由题意面A iB i=CD -平面PABB222A 1C 1G _面A 1EC ,而A 1为面A 1EC 与面A 1B 1C 1相交于棱上一点且 A 1 面AC I G ,所以面A 1C 1G 为所求二面角的一垂面,.GA 1C 1为所求二面角的平面角•在正三棱柱 ABC-A 1B 1C 1 中,AA 1 =A 1B 1,可知.GA 1C 1 = 45 故所求二面角的大小为 45 . 四、平移平面法(无棱的一种) 例5如图,正方体ABCD -A I B lG D I 中,E 为AA I 的中点,H 为CC I 上的点,且CH : C I H 二1:2 .设正方体的棱长为a ,求平面D I EH 与底面A I B I C I D I构成的锐角的正切. 分析:本题中,仅仅知道二面角棱上的一点 D I,在这种情况下,寻找二面角 的平面角较困难.根据平面平移不改变它与另一个平面构成的角的大小的原理,如果 能把二面角中的一个平面平移,找出辅助平面与另一个平面的交线,就可以作出二面 角的平面角•有了平面角之后,只需要进行常规构造三角形和解三角形的计算,就可以解决问题了. 如图,过点E 作EM 〃 A l D I与D I D 相交于M 点,过M 点作MN 一 C I D I ,与D I H 相交于N 点.可证平面 EMN〃平面^B I C I D I •这样,求平面D I EH 与平面^B I C I D I的二面角的平面角就转化 为求平面D I EH 与平面EMN 的二面角的平面角.显然EN 为这两个平面的交线,过点M 作MF 一 EN , F 为垂足,连结D IF ,可证D IF-EN .则.D IFM 为本题要寻找的二面角. 例6 (本题关键在利用平移棱的垂线进行解题) 在正三棱柱ABC - A 1B 1C 1中,D 是AC 的中点, AB 1 _ BC 1,求二面角 D- BC 1 -C 的大小• 解:作AE _ BC 于E 且交BD 于F,则Al 平面BB 1C 1C , 连接B 1E , C 1B ,并记它们的交点为O 连接OF,由 AAOE OB 1 BE EF=EF,知 OF//B 1A . B 1C 1 FA 图8因此由 AB 1-BC 1 知 OF-BC 1QE.BC I ,而 BB 1E =×z CBC 1 =90 - BEO ,RT? BB 1E -RTP BCC 1, BB 1 BCBE CC 1BE B 1B故有BB 1二 BC BE 二BC2 2 2B 1E =B 1B BE叵(匹)2=%C 24可得.EOF = . EB 1A = 45故二面角D - BC 1 -C 的大小为45 . 例7 在棱长为1的正方体 ABCD-A 1B 1C 1D 1中,E 是BC 的中点,试求面B*D 与平面ABB 1A 1所成二面角的大小• 解:取A 1D 1中点F 连FD,FB; 取AD 中点K 连接A*,BK,A 応.显然,DE 応F 为平行四边形.因为 A?K//FD,KB 〃DE,知平面 AXB// 平面 DEBFO 取A?3中点0,连接OK,OA, 由 A?K=BK,AA=BA 知, OK_A?3,0A_A?3故∠ AoK 为二面角的平面角. OA 2 =OB 2 =1,0K 2 = BK 2 _OB 2 =32 4 .6 可得 cos _AOK =3 C 1故平面B 1ED 与平面ABB 1A 1所成二面角的大小为 46arccos . 3五、找垂面,作垂线 例6如图,正方体ABCD - A I B I C I D I中,M 为棱AD 的中点,求平面B IC I CB 和平面BC I M 所构成的锐二面角的正切. 分析:平面AC 与二面角M - BC I -C 的一个面B I C垂直,与另一个平面 B 1MBC I 相交,过M 点作MP 一 BC ,垂足为P ,过P 作PN 一 BC ,交BC I于N 点,连结MN ,由三垂线定理可 证MN 一 BG ,则.MNP 为二面角M -BC I -C的平面角. 总结:当一个平面与二面角的一个平面垂直,与另一个平面相交时,往往过这个面上的一点作这两个垂直平面交线的垂线,再过垂足作二面角棱的垂线•根据三垂线定理即可证明,并找出二面角的平面角. 再如图,要找:-a-所构成的二面角的平面角,可找平面一 一,且:=b, 一“,过b上任何一点A 作AB-I ,垂足为B ,过B 作BC _〉,垂足为C ,连结AC ,可证∙ A C B为'-a- -的平面角.六、根据特殊图形的性质找二面角的平面角 1 •三线合一1可过A 作AM〃DE ,平面ADE 与平面ABC的交线即为AM .过A 作AN 丄DE 于N ,过A 作AF 丄BC于F .可证AN — AM , AF _ AM ,则NAF 为面ADE 与面ABC 的夹角.如图,DE 与BC 不平行且相交.根据三个平面两两相交可能出现的三种情况,这三个面的交线为一点.延长 ED、CB 相交于G 点,连结AG .AG即为平面ADE与平面ABC的交线,通过一些 关系可证∙CAE为平面ADE 与平面ABC的夹角.通过以上分析和举例说明,寻找二面角的平面角的方法就比较容易了.只要我们勤 动脑,善观察,多总结,抓住问题的特征,找出适当的方法,关于二面角的平面角的问例 7 如图,空间四边形 ABCD 中,AB=AD= 3 , BC=CD= 4, BD = 2, A C = 5 .试求 A - BD -C面角的余弦值•分析:如图1, AB=AD , BC=CD ,则厶ABD 和厶BDC为等腰三角形.过A 作AE _ BD ,垂足为E ,连结CE .根据三线合一,且E 为BD 中点,可证CE 一BD2 .全等三角形 例8如图,已知空间四边形ABCD, A B =BC BD =:8 , AC =:6 .试求A-BD-C的余弦值. B分析:过A 作AE 一 BD ,垂足为E ,连结CE•根据已知条件,△ AED 和△CED 全等,可证CE —BD ,则.AEC 为二面角A- BD-C 的平面角. 3 .二面角的棱蜕化成一点 例9如图,四棱锥A-BCED 中,DB 和EC 与面ABC 垂直,△ ABC为正三角形. (1) 若BC =EC =BD 时,求面ADE 与面ABC 的夹角; (2) 若 BC =E C =2BD 时,求面ADE 与面A BC 的夹角. 分析:如图,面ADE 与面ABC 的交线蜕化成一点,但面ADE 与面ABC 与面DC 相交.如果三个平面两两相交,它们可能有三种情况: (1)交线为一点;(2) 一条交线;(3)三条交线互相平行.在图1中,两条交线BC 与DE互相平行,所以肯定有过 A 且平行于DE的一条交线.例4. (2008北京理)如图,在三棱锥 P-ABC 中,AC =BC =:2 , Z ACB =90:,AP=BPrAB , PC _ AC . (I)求证:PC _ AB ;(∏)求二面角 B - AP -C 的大小;题就会迎刃而解.七、面积法(不作二面角求法)CO 如图i ,设二面角 C-BD-C i 的大小为 二,则在 Rt △ COC i 中,cos-C i O -CO BD 2 _________ 1 C i o BD2-S CB D ,在某些情S'.C i BD况下用此法特别方便•6,平面〉夕卜的△ A i B i C i 在〉内的射影是边长为 i 的正三角形 求厶A iB iC i 所在的平面与平面:■所成锐二面角的大小• 问题的情境很容易使人想到用面积法,分别在 BB i 、 例5如图BB i =3, CC i =4,分析与略解: BD=CE=AA 1,则厶 A i B i C i ^△ A i DE ,可求得 A i B=. 2 , A i C i = ∙.. 5 , B i C i = 2 ,所以等腰△A iB iC i 的面积为i5 4又正△ ABC 的面积为•设所求二面角的大小为J5V ,贝U COSV =-C i,且ABC A i AA 1=2 , BCC iB 图6H 工 M1第11页共i5页图5分析:本题要求二面角 B —AP —C 的大小,如果利用射影面积法解题,不难想到在平面 对原图形与射影图形并分别求出 S 原与S 射 于是得到下面解法。
