全等三角形SAS练习题(基础)

合集下载

三角形全等的判定(二)SAS判定方法专题训练

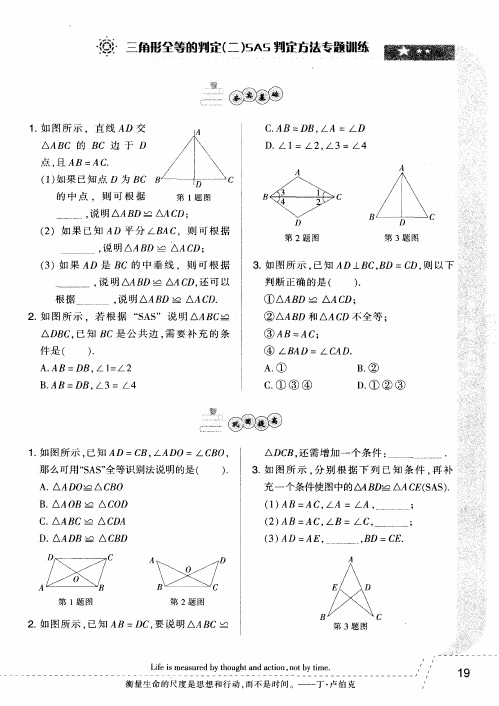
（３）如果／４Ｄ是ＢＣ的中垂线，则可根据
，
说明 △ＡＢＤＡＡＣＤ，还可以
判断正确的是（
）．
根据
，说明ＡＡＢＤ △ＡＣＤ．
①ＡＡＢＤＡＡＣＤ； ②ＡＡＢＤ和△ＡＣＤ不全等；
的中线，延长ＡＥ到点Ｆ，使ＥＦ＝ＡＥ，连接
ＤＦ，你能说明４Ｅ＝１Ａｃ吗？
，、
／
Ｆ
Ｃ
第７题图
８．如图，（１）ＡＡＢＣ和ＡＡＤＥ中，已知ＡＢ＝
４Ｃ，ＡＤ＝ＡＥ，且／ＣＡＢ＝ＥＡＤ．
三角形仝等的判定（－）ＳＡＳ定方法专题训练
１．如图所示，直线ＡＤ交
△ＡＢＣ的ＢＣ边于Ｄ
Ｃ．ＡＢ：ＤＢ．Ａ＝／Ｄ
点．且ＡＢ＝ＡＣ．
／／／Ａ＼
／
第１题图
Ｄ．／１＝２．／３＝／４
）．
充一个条件使图中的△４ＤＡＡＣＥ（ＳＡＳ）．
（１）ＡＢ＝ＡＣ，／４＝／＿Ａ， … 一 … 一一一；
（２）ＡＢ＝ＡＣ，＝／Ｃ，
一 …
Ｂ． △ ０Ｂ
Ｃ． △ＡＣ
△ Ｃ０Ｄ
△（４
Ｄ． △／４ＤＢ
（１）如果已知点Ｄ为ＢＣＢ的中点，则可根据
，
＼＼＼
ＣＣＤ
ＪＤ
说明ＡＡＢＤＡＡＣＤ：Ｃ，则可根据

全等三角形的判定(2)SAS练习

11.2 全等三角形的判定（2） SAS1.如图，AB=AC ，AD=AE ，欲证△ABD ≌△ACE ，可补充条件( ) A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD2.能判定△ABC ≌△A ′B ′C ′的条件是（）(A ．AB=A ′B ′，AC=A ′C ′，∠C=∠C ′ B. AB=A ′B ′， ∠A=∠A ′，BC=B ′C ′ C. AC=A ′C ′， ∠A=∠A ′，BC=B ′C D. AC=A ′C ′， ∠C=∠C ′，BC=B ′C3.如图，AB 与CD 交于点O ，OA=OC ，OD=OB ，∠AOD= ，根据_________可得到△AOD ≌△COB ，从而可以得到AD=_________．4.如图，已知BD=CD ，要根据“SAS”判定△ABD ≌△ACD ，则还需添加的条件是。

5.如图，AD=BC ，要根据“SAS”判定△ABD ≌△BAC ，则还需添加的条件是 7.如图，AC 与BD 相交于点O ，已知OA=OC ，OB=OD ，求证:△AOB ≌△COD8.已知：如图，AB=CB ，∠1=∠2 ,△ABD 和△CBD 全等吗？说明理由。

9. 已知：如图，△ABC 中， AD ⊥BC 于D ，AD=BD ， DC=DE ， ∠C=50°。

求∠ EBD 的度数。

10.已知：如图，AB=AC ，AD=AE ，∠1 =∠2 。

试说明：△ABD ≌△ACE 。

11、（能力提升）如图，在△ABC 和△DEF 中，B 、E 、F 、C ，在同一直线上，下面有4个条件，请你在其中选3个作为题设，余下的一个作为结论，写一个真命题，并加以证明. ①AB=DE ； ②AC=DF ； ③∠ABC=∠DEF ； ④BE=CF.。

《用“SAS”证三角形全等》练习题

＝∠E.
解： ∵C 是线段 AB 的中点， ∴AC＝CB， ∵CD∥BE， ∴∠ACD＝∠B， AC＝CB，在△ACD 和△CBE 中，∠ACD＝∠B，∴△ACD≌△CBE(SAS)，∴∠D＝ CD＝BE， ∠E
6．如图，AB＝AD，AC＝AE，∠1＝∠2，求证：
(1)△ABC≌△ADE； (2)CB＝ED. 解：(1)∵∠1＝∠2，∴∠1＋∠EAC＝∠2＋∠EAC，即∠BAC＝∠DAE，又∵AB＝AD，AC＝AE，∴△ABC≌△ADE(SAS) (2)∵△ABC≌△ADE，∴CB＝ED
) D
不一定 2．有两边和其中一边的对角分别相等的两个三角形_____________ 全等．
知识点1：用“SAS”判定两个三角形全等 1．下图中全等的三角形有( D ) A．图1和图2 B．图2和图3
C．图2和图4 D．图1和图3
2．(易错题) 的条件是( D
如图，AB＝DB，BC＝BE，欲使△ABC≌△DBE，需要增加 )
13．某大学计划为新生配备如图1所示的折叠凳．图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计)，其中凳腿AB和CD的长相等，O是它们的中cm，则由以上信息可推得CB的长度是多少？
解： ∵O 是 AB， CD 的中点， ∴OA＝OB， OD＝OC，在△AOD 和△BOC OA＝OB，中， ∴CB＝AD.∵AD＝30 cm， ∠AOD＝∠BOC，∴△AOD≌△BOC(SAS)， OD＝OC， ∴CB＝30 cm
9．如图，AB＝AC，AD＝AE，若要得到“△ABD≌△ACE”，必须添加一个条件，则下列所添条件不成立的是( B )
A．BD＝CE B．∠ABD＝∠ACE C．∠BAD＝∠CAE D．∠BAC＝∠DAE

八年级数学—全等三角形判定一(SSS,SAS)(基础)巩固练习【名校试题+详细解答】

【巩固练习】一、选择题1. △ABC 和△'''A B C 中，若AB ＝''A B ，BC ＝''B C ，AC ＝''A C .则（）A.△ABC ≌△'''A C BB. △ABC ≌△'''A B CC. △ABC ≌△'''C A BD. △ABC ≌△'''C B A2. 如图，已知AB ＝CD ，AD ＝BC ，则下列结论中错误的是（）A.AB ∥DCB.∠B ＝∠DC.∠A ＝∠CD.AB ＝BC3. 下列判断正确的是（）A.两个等边三角形全等B.三个对应角相等的两个三角形全等C.腰长对应相等的两个等腰三角形全等D.直角三角形与锐角三角形不全等4. 如图，AB 、CD 、EF 相交于O ，且被O 点平分，DF ＝CE ，BF ＝AE ，则图中全等三角形的对数共有（）A. 1对B. 2对C. 3对D. 4对5. 如图，将两根钢条'AA ，'BB 的中点O 连在一起，使'AA ，'BB 可以绕着点O 自由转动，就做成了一个测量工件，则''A B 的长等于内槽宽AB ，那么判定△OAB ≌△''OA B 的理由是( )A.边角边B.角边角C.边边边D.角角边6. 如图，已知AB ⊥BD 于B ，ED ⊥BD 于D ，AB ＝CD ，BC ＝ED ，以下结论不正确的是（）A.EC ⊥ACB.EC ＝ACC.ED ＋AB ＝DBD.DC ＝CB二、填空题7. 如图，AB ＝CD ，AC ＝DB ，∠ABD ＝25°，∠AOB ＝82°，则∠DCB ＝_________.8. 如图，在四边形ABCD中，对角线AC、BD互相平分，则图中全等三角形共有_____对.9. 如图，在△ABC和△EFD中，AD＝FC，AB＝FE，当添加条件_______时，就可得△ABC≌△EFD（SSS）10. 如图，AC＝AD，CB＝DB，∠2＝30°，∠3＝26°，则∠CBE＝_______.11. 如图，点D在AB上，点E在AC上，CD与BE相交于点O，且AD＝AE，AB＝AC，若∠B ＝20°，则∠C＝_______．12. 已知，如图，AB＝CD，AC＝BD，则△ABC≌，△ADC≌ .三、解答题13. 已知：如图，四边形ABCD中，对角线AC、BD相交于O，∠ADC＝∠BCD，AD＝BC，求证：CO＝DO．14. 已知：如图，AB ∥CD ，AB ＝CD ．求证：AD ∥BC ．分析：要证AD ∥BC ，只要证∠______＝∠______，又需证______≌______．证明：∵ AB ∥CD （），∴ ∠______＝∠______ （），在△______和△______中，⎪⎩⎪⎨⎧===),______(______),______(______),______(______ ∴ Δ______≌Δ______ （）．∴ ∠______＝∠______ （）．∴ ______∥______（）．15. 如图，已知AB ＝DC ，AC ＝DB ，BE ＝CE 求证：AE ＝DE.【答案与解析】一.选择题1. 【答案】B ；【解析】注意对应顶点写在相应的位置.2. 【答案】D ；【解析】连接AC 或BD 证全等.3. 【答案】D ；4. 【答案】C ；【解析】△DOF ≌△COE ，△BOF ≌△AOE ，△DOB ≌△COA.5. 【答案】A ；【解析】将两根钢条'AA ，'BB 的中点O 连在一起，说明OA ＝'OA ，OB ＝'OB ，再由对顶角相等可证.6. 【答案】D ；【解析】△ABC ≌△EDC ，∠ECD ＋∠ACB ＝∠CAB ＋∠ACB ＝90°，所以EC ⊥AC ，ED ＋AB ＝BC ＋CD ＝DB.二.填空题7. 【答案】66°；【解析】可由SSS 证明△ABC ≌△DCB ，∠OBC ＝∠OCB ＝82412︒=︒，所以∠DCB ＝ ∠ABC ＝25°＋41°＝66°8. 【答案】4；【解析】△AOD ≌△COB ，△AOB ≌△COD ，△ABD ≌△CDB ，△ABC ≌△CDA.9. 【答案】BC ＝ED ；10.【答案】56°；【解析】∠CBE ＝26°＋30°＝56°.11.【答案】20°；【解析】△ABE ≌△ACD （SAS ）12.【答案】△DCB ，△DAB ；【解析】注意对应顶点写在相应的位置上.三.解答题13.【解析】证明：在△ADC 与△BCD 中，,,,DC CD ADC BCD AD BC =⎧⎪∠=∠⎨⎪=⎩()...ADC BCD SAS ACD BDC OC OD ∠=∠=∴△≌△∴∴14. 【解析】3，4；ABD ，CDB ；已知；1，2；两直线平行，内错角相等；ABD ，CDB ；AB ，CD ，已知；∠1＝∠2，已证；BD ＝DB ，公共边；ABD ，CDB ，SAS ；3，4，全等三角形对应角相等；AD ，BC ，内错角相等，两直线平行.15.【解析】证明：在△ABC 和△DCB 中D C BAAB DC AC DB BC =CB ⎧⎪⎨⎪⎩＝＝∴△ABC ≌△DCB （SSS ） ∴∠ABC ＝∠DCB ，在△ABE 和△DCE 中ABC DCB AB DC BE CE =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△DCE （SAS ） ∴AE ＝DE.。

全等三角形判定一(SSS,SAS)(基础)巩固练习

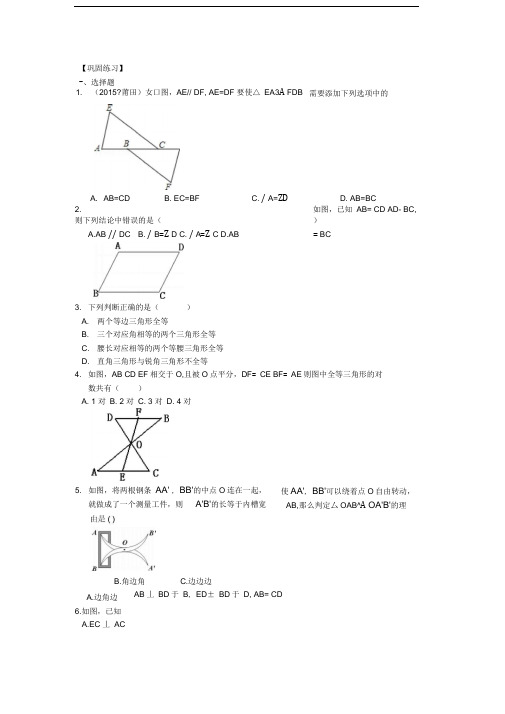
【巩固练习】-、选择题2.如图，已知AB= CD AD- BC,则下列结论中错误的是（）A.AB // DCB. / B=Z DC. / A=Z CD.AB = BC3. 下列判断正确的是（）A. 两个等边三角形全等B. 三个对应角相等的两个三角形全等C. 腰长对应相等的两个等腰三角形全等D. 直角三角形与锐角三角形不全等4. 如图，AB CD EF相交于O,且被O点平分，DF= CE BF= AE则图中全等三角形的对数共有（）A. 1 对B. 2 对C. 3 对D. 4 对B.角边角C.边边边AB丄BD于B, ED± BD于D, AB= CD1. （2015?莆田）女口图，AE// DF, AE=DF 要使△ EA3A FDB 需要添加下列选项中的B. EC=BFC. / A=ZDD. AB=BC5. 如图，将两根钢条AA' , BB'的中点O连在一起，就做成了一个测量工件，则A'B'的长等于内槽宽使AA', BB'可以绕着点O自由转动，AB,那么判定厶OAB^A OA'B'的理A.边角边6.如图，已知A.EC 丄ACA. AB=CDB.EC = ACC.ED + AB = DBD.角角边BC= ED,以下结论不正确的是（D.DC = CB12.、填空题如图，AB= CD AC= DB,Z ABD= 25°,/ AOB= 82°，则/ DCB=点D在AB上，点E在AC上, CD与BE相交于点0,且AD= AE, AB= AC,若/ B = 贝y C= .,△ AD®7.AC BD互相平分，则图中全等三角形共有（2015?虎林市校级二模）如图，已知BD=AC，那么添加一个条件后，能得11.8.9.，/ 3= 26°，则/ CBBAC= ABC^如图,20°,12.三、解答题13. （2014春?章丘市校级期中）如图A B两点分别位于一座小山脚的两端，小明想要测量A、B两点间的距离，请你帮他设计一个测量方案，测出AB的距离.并说明其中的道理.14•已知：如图，AB // CD , AB = CD .求证：AD // BC .分析：要证AD// BC只要证/ ________ =Z __________ ,又需证______ 也_______ .证明：••• AB // CD ( ),二 / ________ =/ _________ ( ),在厶 ______ 和厶_____ 中，_____ 二____ ( ),< _____ = _____ (),、---- = -------- ()‘•••△_______ A___________ ( ).二 / ________ =/ ______ ( ).•- _____ // ______ ( ).15.如图，已知AB= DC AC= DB, BE= CE求证：AE= DE.【答案与解析】一. 选择题1. 【答案】A；【解析】解：••• AE// FD,•••/ A=Z D,•/ AB=CD•AC=BD在厶AEC和厶DFB中，f AE=DF-ZA=ZD,AC=DBk•△EAC^A FDB( SAS ,故选：A.2. 【答案】D;【解析】连接AC或BD证全等.3. 【答案】D;4. 【答案】C;【解析】△ DOF^A COE △ BOF^A AOE △ DOB^A COA.5. 【答案】A;【解析】将两根钢条AA' , BB'的中点O连在一起，说明OA= OA', OB= OB'，再由对顶角相等可证•6. 【答案】D;【解析】△ ABC^^ EDC Z ECD^Z ACB=Z CA聊/ ACB= 90°，所以ECL AC, ED + AB = BC+ CD= DB.二. 填空题7. 【答案】66°;82 °【解析】可由SSS证明厶ABC^A DCB Z OBC=Z OCB= 41 , 所以Z DCB=2Z ABC= 25°+ 41 °= 66°8. 【答案】4;【解析】△ AOD^A COB △ AOB^A COD △ ABD^A CDB △ ABC^A CDA.9. 【答案】BC=AD ;【解析】解：添加BC=AD ,r AC=BD•••在△ ABC 和厶BAD 中」BC=AD ,i AB 二AB•△ ABC ◎△ BAD ( SSS),故答案为：BC=AD .10. 【答案】56°;【解析】Z CBE= 26°+ 30°= 56° .11. 【答案】20°;【解析】△ ABE^A ACD( SAS12. 【答案】△ DCB △ DAB【解析】注意对应顶点写在相应的位置上.三. 解答题13. 【解析】解：如图所示：在AB下方找一点O,连接BO并延长使BO=B O,连接AQ并延长使AO=A O,在厶AOB和厶A OB中：f AO=OA?“ ZAOB=ZA V0B y，QB 二OB'•••△AOB2A A OB ( SAS, ••• AB=A B ,量出A B'的长即可.14. 【解析】3, 4;ABD CDB已知；1, 2;两直线平行，内错角相等；ABD CDBAB, CD已知；/ 1 = 7 2,已证；BD= DB公共边；ABD CDB SAS3 , 4,全等三角形对应角相等；AD, BC内错角相等，两直线平行15. 【解析】证明：在厶ABC^n^ DCB中AB = DCAC = DBBC =CB• △ABC^A DCB(SSS•••7 ABC=7 DCB 在厶ABE和△ DCE中AB = DCABC = DCBBE =CE•••△ ABE^A DCE( SAS ••• AE= DE.。

三角形全等SAS课后练习

O D C B AP E D C BA 11.2三角形全等的判定（二）课后练习设计：吉裕艳夏晓芳审核：冒光明班级______姓名_________学号____得分_______1.△ABC 和△Ａ′B ′C ′中若AB=Ａ′B ′,B C = B ′C ′ ,则补充条件 ________________可得到△ABC ≌△Ａ′B ′C ′. 2.如图，AB 、CD 相交于O ，且AO =OB 观察图形，图中已具备的另一个相等的条件是，联想SAS 公理，只需补充条件，则有△AOC ≌△BOD 。

第2题图3.下列条件中，能让△ABC ≌△DFE 的条件是（）A. AB=DE ，∠A=∠D ， BC=EFB. AB=BC ，∠B=∠E ， BE=EFC. AB=EF ，∠A=∠D ， AC=DFD. BC=EF ，∠C=∠F ， AC=DF4.下面命题错误的是（）A .边长相等的两个等边三角形全等B .两条直角边对应相等的两个直角三角形全等C .有两条边对应相等的两个等腰三角形全等D .形状和大小完全相同的两个三角形全等5.如图所示，△ABD 和△CBD 都是等边三角形，AC 与BD 交于点O ，图中全等三角形的对数有（） A.2对 B.4对 C.6对 D.8对第5题图第6题图6.如图所示，已知AB=AC ，PB=PC ，下面结论：（1）EB=EC ；（1）AD ⊥BC ；（3）AE 平分∠BEC ；（4）∠PBC =∠PCB ，其中正确的是（）A.1个B.2个C.3个D.4个7.如图，∠DAB =∠CAE ，AB =AE ，AD =AC ，求证:BC =DE.ODC B A ED CB A21C B AE DF E D C B A 8.已知，如图所示，BE=DF ，AE=CF ，AE ∥CF ，求证:AD ∥BC9.已知如图所示，AB=AD ，BC=DE ∠1=∠2，求证：（1）AC=AE （2）∠CAE =∠CDE10．如图，△ABC 为等边三角形，点M 、N 分别在BC 、AC 上，且BM=CN ，AM 与BN 交于Q 点，当点M 在BC 上移动时，∠AQN 的的大小是否变化？证明你的结论。

三角形全等的判定(SSS,SAS)同步训练

1、如图，AB=AC ，BD=CD ，求证：∠1=∠2．
2.如图, DA DB = ,AC BC =。

求证：DAC
DBC ∆≅∆
3、如图，已知AB=CD ，AC=BD ，求证：∠A=∠D ．
4、如图，AC与BD交于点O，AD=CB，E、F是BD上两点，且AE=CF，DE=BF.请推导下列结论：⑴∠D=∠B；⑵AE∥CF．
5.如图，点E，F在BD上，且AB＝CD，BF＝DE，AE＝CF，AC与BD相交于点O.求证：AE∥CF.
6、已知如图，A、E、F、C四点共线，BF=DE，AB=CD.
⑴请你添加一个条件，使△DEC≌△BFA；
⑵在⑴的基础上，求证：DE∥BF.
C B A 7、如图6，已知AB=A
D ，AC=A
E ，∠1=∠2，求证∠ADE=∠B.
8、如图，已知AB=AD ，若AC 平分∠BAD ，问AC 是否平分∠BCD ？为什么？
9．如图，已知在ABC △中，AB AC =，12∠=∠．
求证：AD BC ⊥，BD DC =．
A C
2 1
3 4
10. 如图，CF BE =, DC AB =, C B ∠=∠ ,求证：DCE ABF ∆≅∆
11.如图，点C 是BD 的中点 ,EC AC =, , ECB ACD ∠=∠ ,求证：EDC ABC ∆≅∆
12.如图，点M ，N 在线段AC 上，AM ＝CN ，AB ∥CD ，AB ＝CD.求证：∠1＝∠2.。

13.2三角形全等的判定(SAS)练习

例1
已知：如图， AB=CB ，∠ ABD= ∠ CBD △ ABD 和△ CBD 全等吗？
A
分析: △ ABD ≌△ CBD
边: AB=CB(已知) (SAS)
B
D
角: ∠ABD= ∠CBD(已知) 边:
C
？
现在例1的已知条件不改变,而问题改变成:
问AD=CD，BD平分∠ADC吗？
例题推广
C
D
BC=EF
E
F
如图AC与BD相交于点O，已知 OA=OC，OB=OD，说明 △AOB≌△COD的理由。
A
B
O
D C
解：在△AOB和△COD中 ∵ OA=OC（已知） ∠AOB=∠COD(对顶角） OB=OD(已知) ∴ △AOB≌△COD(SAS)
例1
已知：如图,AB=CB,∠1=∠2 ,
△ABD 和△CBD 全等吗？为什么? A

2.如图，已知AB＝AC，AD＝AE。
求证：△ABD≌△ACE 证明：在△ABD和△ACE中 E AB＝AC（已知） B A＝A（公共角） AD＝AE（已知） A ∴△ABD≌△ACE（SAS）
DE B A
D
C A
C
已知:如图，AB=AC,AD=AE. 求证: △ABE≌△ACD 证明：在△ABE和△ACD中∵ AB=AC（已知）
证明的书写步骤：
1.准备条件：证全等时要用的条件要先证好； 2.三角形全等书写三步骤： ①写出在哪两个三角形中 ②摆出三个条件(注意:按定理名称的顺序书写) ③写出全等结论
巩固练习
若∠BAD= ∠CAD,则添加什么条件可使ΔABD≌ΔACD?
A
ΔABD≌ΔACD S A S

全等三角形SAS专题练习知识分享

全等三角形S A S专题练习全等三角形的判定方法SAS专题练习1.如图，AB=AC，AD=AE，欲证△ABD≌△ACE，可补充条件( )A.∠1=∠2B.∠B=∠CC.∠D=∠ED.∠BAE=∠CAD2.能判定△ABC≌△A′B′C′的条件是（）A．AB=A′B′，AC=A′C′，∠C=∠C′B. AB=A′B′，∠A=∠A′，BC=B′C′C. AC=A′C′，∠A=∠A′，BC=B′CD. AC=A′C′，∠C=∠C′，BC=B′C3.如图，AB与CD交于点O，OA=OC，OD=OB，∠AOD= ，根据_________可得到△AOD≌△COB，从而可以得到AD=_________．4.如图，已知BD=CD，要根据“SAS”判定△ABD≌△ACD，则还需添加的条件是。

5.如图，AD=BC，要根据“SAS”判定△ABD≌△BAC，则还需添加的条件是6.如图，已知△ABC中，AB=AC，AD平分∠BAC，请补充完整过程说明△ABD≌△ACD的理由．解：∵AD平分∠BAC，∴∠________=∠_________(角平分线的定义).在△ABD和△ACD中，∵∴△ABD≌△ACD（）7.如图，AC与BD相交于点O，已知OA=OC，OB=OD，第1题第3题第4题第6题第5题求证:△AOB≌△COD证明：在△AOB和△COD中∵∴△AOB≌△COD( )8.已知：如图，AB=CB，∠1=∠2 △ABD 和△CBD 全等吗？9.已知：如图，AB=AC，AD=AE ，∠1 =∠2 。

试说明：△ABD ≌△ACE 。

10.已知：如图，△ABC中， AD⊥BC 于D，AD=BD， DC=DE，∠C=50°。

求∠ EBD的度数。

第7题【经典练习】1．在△ABC 和△C B A '''中，若AB=B A ''，AC=C A ''，还要加一个角的条件，使△ABC ≌△C B A '''，那么你加的条件是（）A ．∠A=∠A ' B.∠B=∠B ' C.∠C=∠C ' D.∠A=∠B '2．下列各组条件中，能判断△ABC ≌△DEF 的是（） A ．AB=DE ，BC=EF ；CA=CD B.CA=CD ；∠C=∠F ；AC=EFC ．CA=CD ；∠B=∠E D.AB=DE ；BC=EF ，两个三角形周长相等 3．已知△ABC 的6个元素，则下面甲乙丙三个三角形中，和△ABC 全等的图形是（）A.甲和乙B. 乙和丙C. 没有乙D. 没有甲4．如图工作师傅做门时，常用木条EF 固定矩形门框ABCD ，使其不变形这种做法根据是（）.A 、两点之间线段最短B 、矩形的对称性C 、矩形的四个角都是直角D 、三角形的稳定性5．如果△ABC ≌△DEF ，且△ABC 的周长95cm ，A 、B 分别与D 、E 对应并且AB=30cm ，DF=25 cm ，那么BC 的长等于（）A ．40cmB ．35cmC ．30cmD ．25cm 6．如图，AB ∥DE ，CD=BF ，若△ABC ≌△DEF ，还需要补充的条件可以是（）A ．AC=EFB ．AB=DEC ．∠B=∠ED ．不用补充 7.如图，∠CAB ＝∠DBA ，AC=BD ，则下列结论中，不正确的是（）A 、BC=ADB 、CO=DOC 、∠C ＝∠D D 、∠AOB=∠C ＋∠DAC B 50°50°72° a bcab c 甲D A C A D FE8．如图，AB=AC ，若AD 平分∠BAC ，则AD 与BC9．阅读理解题：如图：已知AC ，BD 相交于O，OA=OB ，OC=OD. 那么△ABC 与△BAD 全等吗？请说明理由.△ABC 与△BAD 全等吗？请说明理由.小明的解答： 21∠=∠AOD ≌△BOC而BAD=△AOD+△ADB △ABC=△BOC+△AOB所以△ABC ≌△BAD（1）你认为小明的解答有无错误；（2）如有错误给出正确解答；10．如图，点C 是AB 中点，CD ∥BE ，且CD=BE ，试探究11．如图，AE 是，BAC 的平分线∠AB=AC（1）若D 是AE 上任意一点，则△ABD ≌△ACD （2）若D 是AEBCDOA=OOD=OD12．如图，已知AB=AC ，EB=EC ，请说明BD=CD 的理由13. 如图，△ABC ，△BDF 为等腰直角三角形。

11.2 三角形全等的判定(SAS)(课时练含答案)

11.2 三角形全等的判定（SAS）◆课堂测控测试点 SAS1．如图，∠1=∠2，若用“SAS”证明△ACB≌△BDA，还需要加上条件（）A．AD=BC B．BD=AC C．∠D=∠C D．OA=OB2．不能判定△ABC≌△A′B′C′的条件是（）A．AB=A′B′，BC=B′C′，∠B=∠B′B．∠B=135°，∠C′=135°，AB=B′C′，BC=C′A′C．AB=BC=CA，A′B′=B′C′=C′A′，∠A=∠A′D．AB=A′B′，AC=A′C′，∠A=∠A′=135°3．如图，点D在AB上，点E在AC上，且AD=AE，AB=AC，•若∠B=•20•°，•则∠C=_____．4．如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C，求证：AF=DE．◆课后测控5．如图，∠1=∠2，BC=EF，那么需要补充一个直接条件________（•写出一个即可），才能使△ABC≌△DEF．(第5题) (第6题) (第7题)6．如图，已知AB=AE，AC=AD，只要找出∠____=∠_____或∠____=∠____，就可证得△_____≌△______．7．如图，AD=AE，BE=CD，∠1=∠2，则∠B=_____，图中有____对三角形全等，请写出来_______．8．如图，已知AB⊥BD于B，ED⊥BD于D，点C在BD上，AB=CD，BC=ED，则∠ACE=_______．9．如图，已知AB=AC，AD=AE，欲证△ABD≌△ACE，须补充的条件是（）A．∠B=∠C B．∠D=∠E C．∠1=∠2 D．∠CAD=∠DAC10．如图，已知AD是△ABC的中线，在AD及其延长线上截取DE=DF，•连结CE，BF。

求证：BF∥CE．11．已知：如图，OP是∠AOC和∠BOD的平分线，OA=OC，OB=OD，•求证：AB=CD．12．已知：如图，AE=CF，AD∥BC，AD=CB，求证：△ADF≌△CBE．◆拓展测控13．（变式题）如图（1），A，B，C，D在同一直线上，AB=CD，DE∥AF，且DE=AF．•由上题结论可知：△AFC≌△DEB．探究：如果将BD沿着AD边的方向平行移动，如图（2），（3）时，•其余条件不变，结论是否成立，如果成立，请选择其中一个图形予以证明；如果不成立，•请说明理由．答案：1．B （点拨：夹∠1，∠2的另一边分别为AC 和BD ） 2．C （点拨：没有对应边相等）3．20° （点拨：根据已知条件可得△ABE ≌△ACD ，有∠B=∠C ） 4．证明：∵BE=CF ，∴BE+EF=CF+EF ，即BF=CE ．在△ABF 和△DCE 中，,,AB DC B C BF CE =⎧⎪∠=∠⎨⎪=⎩∴△ABF ≌△DCE （SAS ），∴AF=DE ．[总结反思]两边及其夹角对应相等的两个三角形全等． 5．AC=DF （点拨：根据夹角选择边）6．EAD BAC BAE CAD AED ABC （点拨：依据两边找夹角） 7．∠C 两 △ABD ≌△ACE △ABE ≌△ACD（点拨：可直接得△ABD ≌△ACE ，从而∠B=∠C ，AB=AC ，进而由SAS 可得△ABE•≌△ACD ） 8．90° （点拨：易知△ABC ≌△CDE ，有∠A=∠DCE ，因为∠A+∠ACB=90°，•所以∠DCE+∠ACB=90°，故∠ACE=90°）9．C （点拨：由∠1=∠2得∠BAD=∠CAE ，即可运用SAS ，同时注意有两边和其中一边的对角对应相等的两个三角形不一定全等） 10．证明：∵AD 为中线，∴BD=CD ，在△BDF 和△CDE 中，,,,BD CD BDF CDE DF DE =⎧⎪∠=∠⎨⎪=⎩∴△BDF ≌△CDE （SAS ）． ∴∠F=∠CED ，∴BF ∥CE ．[解题规律]直接运用SAS 可证△BDF ≌△CDE ，注意隐含条件对顶角相等的运用． 11．证明：∵OP 是∠AOC 和∠BOD 的平分线， ∴∠AOP=∠COP ，∠BOP=∠DOP ． ∴∠AOB=∠COD ．在△AOB 和△COD 中，,,.OA OC AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩∴△AOB ≌△COD （SAS ），∴AB=CD ．[解题技巧]运用等式性质得夹角∠AOB=∠COD 是证明的关键． 12．∵AE=CF ，∴AE-EF=CF-EF ，即AF=CE ．又∵AD ∥CB （已知），∴∠A=∠C ．在△ADF 和△CBE 中，,,,AD CB A C AF CE =⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△CBE （SAS ），[解题规律]间接的已知条件必须进行加工，如本题中AE=CF 不能直接用，•可运用等式性质加工成AF=CE ．13．解：（2），（3）中结论依然成立，选择（3）证明． ∵AB=CD ，∴AB+BC=CD+BC ，即AC=DB ． ∵DE ∥AF ，∴∠A=∠D ．在△AFC 和△DEB 中，,,AF DE A D AC DB =⎧⎪∠=∠⎨⎪=⎩∴△AFC ≌△DEB （SAS ）．[解题方法]对于探究结论的题可解题方法是：（1）图形在运动过程中，•哪些量发生了变化，哪些量是没有变化，原来的等线段，等角还是否存在，是解题关键；（2）几种变化得到的之间存在必然的内在联系，证明的方法必然相似．。

14.2.1 用“SAS”判定两三角形全等(基础达标提升训练解析答案)

沪科版数学八年级上册第14章全等三角形14.2三角形全等的判定第1课时用“SAS”判定两三角形全等基础达标提升训练1. 如图所示，图中全等的三角形有()甲乙丙丁A. 甲和乙B. 乙和丙C. 乙和丁D. 甲和丙2. 如图，已知点A，D，C，F在同一直线上，且AB=DE，BC=EF，要使△ABC≌△DEF，还需要添加的一个条件是()A. ∠B=∠EB. ∠A=∠EDFC. ∠BCA=∠FD. BC∥EF第2题第3题3. 如图，AB平分∠CAD，E为AB上一点，若AC=AD，则下列结论错误的是()A. BC=BDB. CE=DEC. BA平分∠CBDD. 图中有两对全等三角形4. 小明用同种材料制成的金属框架如图所示，已知∠B=∠E，AB=DE，BF=EC，其中框架△ABC 的质量为840克，CF的质量为106克，则整个金属框架的质量为()A. 734克B. 946克C. 1052克D. 1574克第4题第5题5. 如图，已知AB=AC，AD=AE，∠BAC=∠DAE，下列结论不正确的是()A. ∠BAD=∠CAEB. △ABD≌△ACEC. AB=BCD. BD=CE6. 下列叙述正确的是()A. 两边和角对应相等的两个三角形全等B. 有一腰相等的两等腰三角形全等C. 有一角为80°且腰长为3 cm的两等腰三角形全等D. 有一个角为100°且腰长为3 cm的两等腰三角形全等7. 如图，AD和CB相交于点E，BE=DE，请添加一个条件，使△ABE≌△CDE(只添一个即可)，你所添加的条件是.第7题第8题8. 如图，一块三角形玻璃裂成①②两块，现需配一块同样的玻璃，为方便起见，只需带上碎片即可.9. 把两根钢条AA′，BB′的中点连在一起，可以做成一个测量工件内槽宽的工具(卡钳).如图所示，若测得AB=8 cm，则内槽宽为cm.第9题第10题10. 如图，点E在AB上，点F在AC上，且AE=AF，AB=AC，BF=8，DE=2，则DC的长为.11. 如图，△ABC，△ADE均为等腰直角三角形，∠ACB=∠DCE=90°，点E在AB上.求证：△CDA≌△CEB.12. 如图所示，A，B，C，D四点在一直线上，且EA⊥AD，FD⊥AD，AE=DF，AB=DC.求证：∠ACE=∠DBF.13. 如图，已知点B，E，C，F在一条直线上，AB=DF，AC=DE，∠A=∠D.(1)求证：AC∥DE；(2)若BF=13，EC=5，求BC的长.14. 如图所示，C是线段AB中点，CD平分∠ACE，CE平分∠BCD，CD=CE.(1)求证：△ACD≌△BCE；(2)若∠D=50°，求∠B的度数.15. 如图，A，B两点分别位于池塘两侧，池塘旁边有一水房D，在BD中点C处有一棵树，小明从点A出发，沿AC走到E点(A，C，E在一条直线上)，并使CE=CA，量出E到水房D的距离就是A，B的距离.(1)你能说出小明这样做的道理吗?(2)若已知CD=140 m，AC=100 m，你能确定AB的长度范围吗?拓展探究综合训练16. 如图，在△ABC中，∠BAC=∠B=60°，AB=AC，点D，E分别是边BC，AB所在直线上的动点，且BD=AE，AD与EC交于点F.当点D，E在边BC，AB上运动时，∠DFC的度数是否发生变化?若不变，求出其度数，若变化，写出其变化规律.。

12.2 三角形全等的判定第2课时用“SAS”判定三角形全等同步练习试题(含答案)

第2课时用“SAS ”判定三角形全等01 基础题知识点1 用“SAS ”判定三角形全等 1．下图中全等的三角形有(D )图1 图2 图3 图4A ．图1和图2B ．图2和图3C ．图2和图4D ．图1和图32．如图所示，在△ABD 和△ACE 中，AB ＝AC ，AD ＝AE ，要证△ABD ≌△ACE ，需补充的条件是(C )A ．∠B ＝∠C B ．∠D ＝∠E C ．∠DAE ＝∠BAC ；D ．∠CAD ＝∠DAC 3．已知：如图，OA ＝OB ，OC 平分∠AOB ，求证：△AOC ≌△BO C.证明：∵OC 平分∠AOB ， ∴∠AOC ＝∠BO C. 在△AOC 和△BOC 中，⎩⎨⎧OA ＝OB ，∠AOC ＝∠BOC ，OC ＝OC ，∴△AOC ≌△BOC (SAS )．4．如图，已知B ，E ，F ，C 四个点在同一条直线上，AB ＝CD ，BE ＝CF ，∠B ＝∠C ，求证：△ABF ≌△DCE .证明：∵BE ＝CF ，∴BE ＋EF ＝CF ＋EF ，即BF ＝CE . 在△ABF 和△DCE 中，⎩⎨⎧AB ＝DC ，∠B ＝∠C ，BF ＝CE ，∴△ABF ≌△DCE (SAS )．知识点2 全等三角形的判定与性质的综合5．(泸州中考)如图，C 是线段AB 的中点，CD ＝BE ，CD ∥BE .求证：∠D ＝∠E .证明：∵C 是线段AB 的中点， ∴AC ＝C B.∵CD ∥BE ，∴∠ACD ＝∠CBE . 在△ACD 和△CBE 中，⎩⎨⎧AC ＝CB ，∠ACD ＝∠CBE ，CD ＝BE ，∴△ACD ≌△CBE . ∴∠D ＝∠E .6．如图，已知△ABC 和△DAE ，D 是AC 上一点，AD ＝AB ，DE ∥AB ，DE ＝A C.求证：AE ＝B C.证明：∵DE ∥AB ，∴∠ADE ＝∠BA C.在△ADE 和△BAC 中，⎩⎨⎧AD ＝BA ，∠ADE ＝∠BAC ，DE ＝AC ，∴△ADE ≌△BAC (SAS )． ∴AE ＝B C.知识点3 利用“SAS ”判定三角形全等解决实际问题7．如图，将两根钢条AA ′，BB ′的中点O 连在一起，使AA ′，BB ′可以绕着点O 自由转动，就做成了一个测量工件，则AB 的长等于内槽宽A ′B ′，那么判定△AOB ≌△A ′OB ′的理由是(A )A ．边角边B ．角边角C ．边边边D ．角角边8．如图所示，有一块三角形镜子，小明不小心将它打破成1、2两块，现需配成同样大小的一面镜子．为了方便起见，需带上1块，其理由是两边及其夹角分别相等的两个三角形全等．02 中档题9．如图，已知AB ＝AC ，AD ＝AE ，若要得到“△ABD ≌△ACE ”，必须添加一个条件，则下列所添条件不成立的是(B )A ．BD ＝CEB ．∠ABD ＝∠ACEC ．∠BAD ＝∠CAE D ．∠BAC ＝∠DAE10．(陕西中考)如图，在四边形ABCD 中，AB ＝AD ，CB ＝CD ，若连接AC 、BD 相交于点O ，则图中全等三角形共有(C )A ．1对B ．2对C ．3对D ．4对11．如图，点A 在BE 上，AD ＝AE ，AB ＝AC ，∠1＝∠2＝30°，则∠3的度数为30°．12．如图所示，A ，B ，C ，D 是四个村庄，B ，D ，C 在一条东西走向公路的沿线上，BD ＝1 km ，DC ＝1 km ，村庄AC ，AD 间也有公路相连，且公路AD 是南北走向，AC ＝3 km ，只有AB 之间由于间隔了一个小湖，所以无直接相连的公路．现决定在湖面上造一座斜拉桥，测得AE ＝1.2 km ，BF ＝0.7 km ，则建造的斜拉桥长至少有1.1km .13．(曲靖中考)如图，已知点B ，E ，C ，F 在一条直线上，AB ＝DF ，AC ＝DE ，∠A ＝∠D.(1)求证：AC ∥DE ；(2)若BF ＝13，EC ＝5，求BC 的长．解：(1)证明：在△ABC 和△DFE 中，⎩⎨⎧AB ＝DF ，∠A ＝∠D ，AC ＝DE ，∴△ABC ≌△DFE (SAS )． ∴∠ACE ＝∠DEF . ∴AC ∥DE .(2)∵△ABC ≌△DFE ， ∴BC ＝EF .∴CB－EC＝EF－EC，即EB＝CF.∵BF＝13，EC＝5，∴EB＝13－52＝4.∴CB＝4＋5＝9.14．如图所示，A，F，C，D四点同在一直线上，AF＝CD，AB∥DE，且AB＝DE.求证：(1)△ABC≌△DEF；(2)∠CBF＝∠FE C.证明：(1)∵AB∥DE，∴∠A＝∠D.又∵AF＝CD，∴AF＋FC＝CD＋F C.∴AC＝DF.∵AB＝DE，∴△ABC≌△DEF(SAS)．(2)∵△ABC≌△DEF，∴BC＝EF，∠ACB＝∠DFE.∵FC＝CF，∴△FBC≌△CEF(SAS)．∴∠CBF＝∠FE C.03综合题15．如图，在四边形ABCD中，∠A＝∠BCD＝90°，BC＝D C.延长AD到E点，使DE＝A B.求证：(1)∠ABC＝∠EDC；(2)△ABC≌△ED C.证明：(1)在四边形ABCD 中， ∵∠BAD ＝∠BCD ＝90°， ∴∠B ＋∠ADC ＝180°. 又∵∠CDE ＋∠ADC ＝180°. ∴∠ABC ＝∠ED C. (2)连接A C.在△ABC 和△EDC 中，⎩⎨⎧AB ＝ED ，∠ABC ＝∠EDC ，CB ＝CD ，∴△ABC ≌△EDC (SAS )．。

12.2三角形全等的判定(二)(“SAS”)练习题人教版八年级数学上册

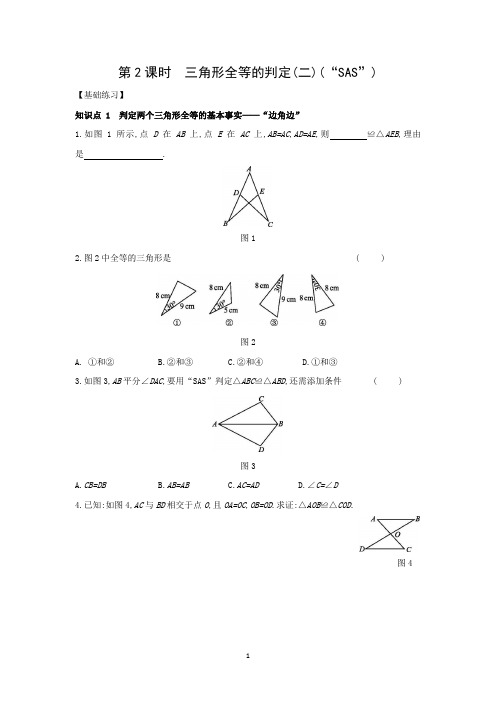
第2课时三角形全等的判定(二)(“SAS”)【基础练习】知识点 1 判定两个三角形全等的基本事实——“边角边”1.如图1所示,点D在AB上,点E在AC上,AB=AC,AD=AE,则≌△AEB,理由是.图12.图2中全等的三角形是 ()图2A.①和②B.②和③C.②和④D.①和③3.如图3,AB平分∠DAC,要用“SAS”判定△ABC≌△ABD,还需添加条件 ( )图3A.CB=DBB.AB=ABC.AC=ADD.∠C=∠D4.已知:如图4,AC与BD相交于点O,且OA=OC,OB=OD.求证:△AOB≌△COD.图45.如图5所示,CD=CA,∠1=∠2,EC=BC.求证:△ABC≌△DEC.图56.如图6所示,AD=BE,AC=DF,AC∥DF.求证:△ABC≌△DEF.图6知识点 2 全等三角形的判定(SAS)的简单应用7.如图7所示,AA',BB'表示两根长度相同的木条.若O是AA',BB'的中点,经测量AB=9 cm,则容器的内径A'B'为 ( )图7A.8 cmB.9 cmC.10 cmD.11 cm8.[2020·镇江]如图8,AC是四边形ABCD的对角线,∠1=∠B,点E,F分别在AB,BC 上,BE=CD,BF=CA,连接EF.(1)求证:∠D=∠2;(2)若EF∥AC,∠D=78°,求∠BAC的度数.图8【能力提升】9.如图9所示,在△ABC和△ADC中,有下列三个论断:①AB=AD;②∠BAC=∠DAC;③BC=DC.将其中的两个论断作为条件,另一个论断作为结论写出一个真命题为.(写成“如果 ,那么 ”的形式,写一个即可)图910.[2020·江西]如图10,CA平分∠DCB,CB=CD,DA的延长线交BC于点E.若∠EAC=49°,则∠BAE的度数为.图1011.如图11,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.有下列说法:①CE=BF;②△ABD≌△ACD;③BF∥CE;④△BDF和△CDE的面积相等.其中正确的是.(填序号)图1112.:[2020·宜宾]如图12,在△ABC中,D是边BC的中点,连接AD并延长到点E,使DE=AD,连接CE.(1)求证:△ABD≌△ECD;(2)若△ABD的面积为5,求△ACE的面积.图12 变式:在△ABC中,AB=7,AC=3,AD是中线,求AD的取值范围.第2课时三角形全等的判定(二)(“SAS ”)1.△ADC SAS2.D [解析] 从图中可以看到①和③符合“SAS ”.3.C [解析] 由题意可得,在△ABC 和△ABD 中,{AC =AD,∠CAB =∠DAB,AB =AB,∴△ABC ≌△ABD (SAS).选项C 正确,其余选项都不正确. 4.证明:在△AOB 和△COD 中,{OA =OC,∠AOB =∠COD,OB =OD,∴△AOB ≌△COD (SAS).5.证明:∵∠1=∠2,∴∠1+∠ECA=∠2+∠ECA ,即∠ACB=∠DCE.在△ABC 和△DEC 中,{CA =CD,∠ACB =∠DCE,BC =EC,∴△ABC ≌△DEC (SAS).6.证明:∵AD=BE ,∴AB+BD=DE+BD ,即AB=DE.∵AC ∥DF ,∴∠A=∠FDE.在△ABC 和△DEF 中,{AB =DE,∠A =∠FDE,AC =DF,∴△ABC ≌△DEF (SAS).7.B8.解:(1)证明:在△BEF 和△CDA 中,{BE =CD,∠B =∠1,BF =CA,∴△BEF ≌△CDA (SAS).∴∠D=∠2.(2)∵∠D=∠2,∴∠2=78°.∵EF∥AC,∴∠BAC=∠2=78°.9.答案不唯一,如:如果①②,那么③(或如果①③,那么②)[解析] (1)已知AB=AD,∠BAC=∠DAC,AC=AC,可得△ABC≌△ADC(SAS),所以BC=DC;(2)已知AB=AD,BC=DC,AC=AC,可得△ABC≌△ADC(SSS),所以∠BAC=∠DAC.10.82°[解析] ∵CA平分∠DCB,∴∠BCA=∠DCA.又∵CB=CD,AC=AC,∴△ABC≌△ADC(SAS).∴∠B=∠D.∴∠B+∠ACB=∠D+∠ACD.∵∠CAE=∠D+∠ACD=49°,∴∠B+∠ACB=49°.∴∠BAE=180°-∠B-∠ACB-∠CAE=82°.故答案为82°.11.①③④[解析] ∵AD是△ABC的中线,∴BD=CD.又∠CDE=∠BDF,DE=DF,∴△BDF≌△CDE,故④正确;由△BDF≌△CDE,可知CE=BF,故①正确;∵AD是△ABC的中线,∴△ABD和△ACD等底同高,∴△ABD和△ACD的面积相等,但不一定全等,故②错误;由△BDF≌△CDE,可知∠FBD=∠ECD,∴BF∥CE,故③正确.故答案为①③④.12.解:(1)证明:∵D是边BC的中点,∴BD=CD.在△ABD 和△ECD 中,{BD =CD,∠ADB =∠EDC,AD =ED,∴△ABD ≌△ECD (SAS).(2)∵在△ABC 中,D 是边BC 的中点,∴S △ABD =S △ACD .∵△ABD ≌△ECD ,∴S △ABD =S △ECD . ∵S △ABD =5,∴S △ACE =S △ACD +S △ECD =5+5=10,即△ACE 的面积为10.变式:解:如图,延长AD 到点E ,使ED=AD ,连接BE.∵AD 是△ABC 的中线,∴BD=CD.又ED=AD ,∠ADC=∠EDB ,∴△BED ≌△CAD (SAS). ∴BE=AC=3. ∵DE=AD ,∴AE=2AD.在△ABE 中,AB-BE<AE<AB+BE , 即AB-BE<2AD<AB+BE ,∴7-3<2AD<7+3. ∴2<AD<5.。

全等三角形的判定(一)SAS

对：如图所示：已知，AB=AD,AC＝AE，应 ∠1 = ∠2. 练习求证： BC=DE
证明:
∵ ∠1 = ∠2.
B
∴ ∠1 + ∠EAC = ∠2+ ∠EAC. E ∴ ∠BAC＝∠DAE
在△ABC与△ADE中， C D
1 A 2
∵
AB＝AD， (已知) ∠BAC＝∠DAE， (已证) AC＝AE， (已知)
B
C
结论：
实践与探索
在两个三角形中,如果有两条边及它们的夹角对应相等，那么这两个三角形全等（简记为 “边角边”或“SAS”)
A A’
B AB= A′B′
C BC＝B′C′
B’
C’
∠B = ∠ B′
△ABC≌ △ A′B′C′
1.在下列图中找出全等三角形
Ⅰ Ⅱ
Ⅲ
30º
30º
Ⅴ
Ⅵ Ⅲ
Ⅶ
2.在下列推理中填写需要补充的条件，使结论成立：
Ｂ
Ｃ
A’Ｂ’
Ｃ’
B’
在△ABC与△A’B’C’中， ∵ AB＝A’B’ ∠B ＝∠B’， AC＝A’C’，
M
∴
△ ABC≌ △A’B’C’（ＳＡＳ）
新知运用：
例 1: 如图 19.2.4 ，在 △ ABC 中， AB ＝ AC ， AD平分∠BAC，求证： △ABD≌△ACD．
证明: ∵ AD平分∠BAC，
小明不小心打翻了墨水，将自己所画的三角形涂黑了，你能帮小明想想办法，画一个与原来完全一样的三角形吗？
ＡＢ'
Ａ'
Ｂ
Ｃ
Ｃ'
实践与探索
A
⑴
a a