最新全等三角形判定(92道基础证明题)
全等三角形证明题专项练习

全全全全全全全全一、解答题1.如图,已知AB=ED,AD=EC,点D是BC的中点,试说明:△ABD≌△EDC.2.如图,已知AD=BC,OD=OC,O为AB的中点,说出∠C=∠D的理由.3.如图,已知AD=BC,BD=AC.试说明:∠ADB=∠BCA.4.如图,点A、E、F、B在同一条直线上,CA⊥AB,DB⊥AB,AE=FB,CF=DE.求证:∠AFC=∠DEB.5.如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB同侧,连接BE.求证:△DEB≌△ABC.6.如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.求证:BE=CE.7.已知:如图,AD=BC,AC=BD.求证:(1)∠C=∠D;(2)AO=BO.8.如图,已知AB=DE,AC=DF,BF=EC.(1)说明△ABC与△DEF全等的理由;(2)如果AC=CF,∠1=30°,∠D=105°,求∠AFC的度数.9.如图,已知AB=AE,AB∥DE,∠ECB+∠D=180°.求证:AD=BC.10.如图,已知∠1=∠2,AO=BO,求证:△AOP≌△BOP.11.如图,已知∠BDC=∠CEB=90°,BE,CD交于点O,且AO平分∠BAC,试说明:(1)△ADO≌△AEO;(2)△BDO≌△CEO.12.如图,四边形ABCD的对角线交于点O,AB // CD,O是BD的中点.(1)说明:△ABO≌△CDO;(2)若BC=AC=4,BD=6,求△BOC的周长.13.如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.(1)求证:AC=CD;(2)若AC=AE,求∠DEC的度数.14.如图,A、F、E、B四点共线,AC CE,BD DF,AE=BF,AC=BD.求证:△ACF≌△BDE.15.如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:(1)EC=BF;(2)EC⊥BF.16.如图,已知AD为△ABC的中线,延长AD,分别过点B,C作BE⊥AD,CF⊥AD.(1)求证:△BED≌△CFD.(2)若∠EAC=45°,AF=12,DC=13,求EF的长.17.如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.(1)若CD=3,则求CE的长;(2)求证:BF⊥AE.18.已知:如图,CB⊥AD,AE⊥DC,垂足分别B、E,AE、BC相交于点F,且AB=BC.求证:△ABF≌△CBD.19.如图,在△ABC中,点D,E分别在边AC,AB上,BD,CE交于点P,且∠A.∠PBC=∠PCB=12(1)探究∠AEP与∠ADP的数量关系,并证明之;(2)求证BE=CD.20.在△ABC和△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.(1)求证:△ABC≌△DCB;(2)当∠AEB=50°时,求∠EBC的度数.21.如图1,在△ABC中,AE⊥BC于点E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.(1)试判断BD与AC的位置关系和数量关系,并说明理由;(2)如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;(3)如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变.试猜想BD与AC的数量关系,并说明理由;你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角(锐角)的度数;如果不能,请说明理由.22.问题背景:如图(1),在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F 分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是________;探索延伸:如图(2),若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,∠BAD,上述结论是否仍然成立,并说明理由.CD上的点,且∠EAF=1223.已知,△ABC是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.(1)如图1所示,若A的坐标是(-3,0),点B的坐标是(0,1),求点C的坐标;(2)如图2,过点C作CD⊥y轴于D,请直接写出线段OA,OD,CD之间等量关系;(3)如图3,若x轴恰好平分∠BAC,BC与x轴交于点E,过点C作CF⊥x轴于F,问CF与AE有怎样的数量关系?并说明理由.24.已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D,点M是AB边上的点,点N是射线CB上的点,且MC=MN.(1)如图1,求证:∠MCD=∠BMN.(2)如图2,当点M在∠ACD的平分线上时,请在图2中补全图,猜想线段AM 与BN有什么数量关系,并证明;(3)如图3,过点M作ME∥BC,交CD与点E,求证:EM=BN.25.定义:如果一个三角形的一个内角等于另一个内角的两倍,则称这样的三角形为“倍角三角形”.(1)如图,△ABC中,AB=AC,∠A=36∘,求证:△ABC是倍角三角形;(2)如图,△ABC的外角平分线AD与CB的延长线相交于点D,延长CA到点E,使得AE=AB,连接DE,若AB+AC=BD,请你找出图中的倍角三角形,并进行证明.26.在△ABC中,∠ACB=90∘,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)当直线MN绕点C旋转到图的位置时,求证:DE=AD+BE;(2)当直线MN绕点C旋转到图的位置时,求证:DE=AD-BE;(3)当直线MN绕点C旋转到图的位置时,试问:DE、AD、BE有怎样的数量关系?请直接写出这个数量关系,不用证明.27.(1)如图,△ABC中,BC=AC,△CDE中,CE=CD,现把两个三角形的C点重合,且∠BCA=∠ECD,连接BE,AD,求证:BE=AD;(2)若将△DEC绕点C旋转至图所示的情况,其余条件不变,BE与AD还相等吗?利用图说明理由.28.在△ABC中,∠A=60°,BD,CE是△ABC的两条角平分线,且BD,CE交于点F.(1)如图1,用等式表示BE,BC,CD这三条线段之间的数量关系,并证明你的结论;小东通过观察、实验,提出猜想:BE+CD=BC.他发现先在BC上截取BM,使BM=BE,连接FM,再利用三角形全等的判定和性质证明CM=CD即可.①下面是小东证明该猜想的部分思路,请补充完整:ⅰ)在BC上截取BM,使BM=BE,连接FM,则可以证明△BEF与______全等,判定它们全等的依据是______;ⅱ)由∠A=60°,BD,CE是△ABC的两条角平分线,可以得出∠EFB=______°;…②请直接利用ⅰ),ⅱ)已得到的结论,完成证明猜想BE+CD=BC的过程.(2)如图2,若∠ABC=40°,求证:BF=CA.一、常见模型 1.K 字型2.手拉手模型3.4.普通旋转型二、常见辅助线 1.角平分线相关辅助线2. 中点相关的辅助线ECABDBC DBEAAEBDC AEBDC三、典型例题 1.【一线三等角】例1 (1)如图,等腰直角三角形ABC 的直角顶点在直线m 上,过点B 作BE ⊥m 于点E ,过点C 作CD ⊥m 于点D ,说明线段BE ,CD ,DE 的数量关系,并证明.(2)将(1)中等腰Rt △ABC 绕直角顶点A 旋转,使B ,C 分别位于直线m 的两侧,过点B 作BE⊥m 于点E ,过点C 作CD ⊥m 于点D ,说明线段BE ,CD ,DE 的数量关系,并证明.2.【普通旋转型】例2. 如图,正三角形ABC内有一点D,BD延长线上取一点E,使∠ABD=∠ACE,∠BAD=∠CAE.(1)求证:△ABD≌△ACE;(2)求证:△ADE是正三角形.【练习】1. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,∠EDF=90°.求证:①△BDE≌△ADF;②AE=CF;③△DEF是等腰直角三角形.3.【手拉手模型】例3 如图,A,B,E三点在同一直线上,△ABC,△CDE都是等边三角形,连接AD,BE,OC.(1)求证:△ACD≌△BCE;(2)求证:△CPQ是等边三角形;(3)求证:OC平分∠AOE.【练习】1. 如图,PA=PB,PC=PD,∠APB=∠CPD,线段AC,BD交于点O.求证:(1)求证:△ACP≌△BPD;(2)求证:∠APB=∠AOB;(3)求证:OP平分∠AO D.A4.【截长补短】例4已知:如图,△ABC中,∠C=2∠B,AD平分∠BA C.求证:AB=AC+C D.A【练习】1.如图,在△ABC 中,∠BAC =60°,AD 是∠BAC 的平分线,且AC =AB +BD 。
全等三角形证明题

全等三角形证明1、已知:如图,OP 是AOC ∠和BOD ∠的平分线,OA OC OB OD ==,. 求证:AB CD =.2、如图,将一等腰直角三角形ABC (AC=BC )的直角顶点置于直线l 上,且过A 、B 两点分别作直线l 的垂线,垂足分别为D 、E .请你仔细观察后,在图中找出一对全等三角形,并写出说明它们全等的过程.3、如图,已知AB ∥CD ,AB=CD ,O 为AC 中点,过点O 的直线交DA 延长线和BC 延长线于E 、F ,求证:OE=OF.4、如图,C 是线段AB 上的一点ACD 和BCE于点G ,BD 交CE 于点H ,求证GC=HC.B A COD P A lBA5、如图:AC=DF ,AD=BE ,BC=EF 。
求证:∠C=∠F 。
6、如图:AD 是△ABC 的高,E 为AC 上一点,BE 交AD 于F ,且有BF=AC ,FD=CD 。
求证:BE ⊥AC 。
7、如图:E 是∠AOB 的平分线上一点,EC ⊥OA ,ED ⊥OB ,垂足为C ,D 。
求证:(1)OC=OD ,(2)DF=CF 。
8、如图:在△ABC ,AB=AC ,BD ⊥AC 于D ,CE ⊥AB 于E ,BD 、CE 相交于F 。
求证:AF 平分∠BAC 。
C FEB D ACFEBDA CF E B DAOFEDCBA9、如图:在△ABC 中,BE 、CF 分别是AC 、AB 两边上的高,在BE 上截取BD=AC ,在CF 的延长线上截取CG=AB ,连结AD 、AG 。
求证:(1)AD=AG ,(2)AD 与AG 的位置关系如何。
10、如图:在△ABC 中,∠C=90°,AC=BC ,过点C 在△ABC 外作直线MN ,AM ⊥MN 于M ,BN ⊥MN 于N 。
(1)求证:MN=AM+BN 。
(2)若过点C 在△ABC 内作直线MN ,AM ⊥MN 于M ,BN ⊥MN 于N ,则AM 、BN 与MN 之 间有什么关系?请说明理由。
全等三角形证明题及答案道共35页

41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间,才能认识自 己。——德国
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。ቤተ መጻሕፍቲ ባይዱ—贝多芬
45、自己的饭量自己知道。——苏联
全等三角形证明题及答案道
21、没有人陪你走一辈子,所以你要 适应孤 独,没 有人会 帮你一 辈子, 所以你 要奋斗 一生。 22、当眼泪流尽的时候,留下的应该 是坚强 。 23、要改变命运,首先改变自己。
24、勇气很有理由被当作人类德性之 首,因 为这种 德性保 证了所 有其余 的德性 。--温 斯顿. 丘吉尔 。 25、梯子的梯阶从来不是用来搁脚的 ,它只 是让人 们的脚 放上一 段时间 ,以便 让别一 只脚能 够再往 上登。
全等三角形的判定证明题asa-aas-hl

全等三角形判定练习(ASA、AAS、HL) 判定定理3、有两角及其夹边对应相等的两个三角形全等(ASA)在△ABC和△DFE中∠A=∠D (已知)AB=DE(已知)∠B=∠E(已知)∴△ABC≌△DEF(ASA)判定定理4、有两角及一角的对边对应相等的两个三角形全等(AAS)在△ABC和△DFE中∠A=∠D ,∠C=∠FAB=DE∴△ABC≌△DFE(AAS)判定定理5、直角三角形全等条件有:斜边及一直角边对应相等的两个直角三角形全等(HL) 在Rt△ABC和Rt△A′B′C′中AB=AB (直角边)BC = B′C′(斜边)∴Rt△ABC≌Rt△A′B′C′(HL)1 如图,∠E=∠B,∠1=∠2,EC=BC,求证:DE=AB。
2 已知:如图点C是AB的中点,CD∥BE,且∠D=∠E.求证:. CD=BE3 如图,DC=BC,∠B=∠D=90°,求证:AB=AD.ACB ED4 如图,AC⊥OB,BD⊥OA,AC与BD交于E点(1)如果OC=OD,求证:∠A=∠B。
(2)如果∠A=∠B ,OC=OD,求证:AC=BD。
(3)如果AO=BO,OC=OD,求证:∠A=∠B。
OBACDE5 如图.已知AC∥DF,且BE=CF、(1)请你只添加一个条件,使△ABC≌△DEF,你添加的条件是;..(2)添加条件后,证明△ABC≌△DEF.6 如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.请从下列三个条件中选择一个合适....的条件...,添加到已知条件中,使AB∥ED成立,并给出证明.供选择的三个条件(请从其中选择一个):①AB=ED;②BC=EF;③∠ACB=∠DFE.7 如图,∠A=∠D,AB=CD,则△≌△,请证明8如图,O为AC中点,AB∥CD,证明AB=CDDOC BAAB EFC9 在ABC △中,D 是AB 上一点,DF 交AC 于点E ,DE FE =,AE CE =,AB 与CF 有什么位置关系?证明你的结论10 已知:如图∠B=∠E=90°AC=DF FB=EC ,证明:AB=DEAD BCFE11如图,已知AB=AC,AD=AE,BE与CD相交于O,证明:(1)ΔABE≌ΔACD(2)ΔDOB≌ΔEOC (3)ΔDBC≌ΔECB12 正方形ABCD 中, F 分别是AB 和AD 上的点,已知CE ⊥BF ,垂足为M ,证明BE=AFDMFEA。
全等三角形证明题集锦
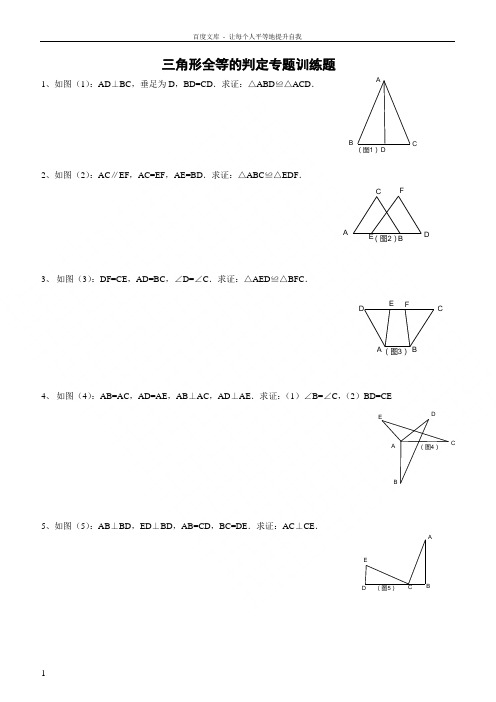
三角形全等的判定专题训练题1、如图(1):AD ⊥BC ,垂足为D ,BD=CD .求证:△ABD ≌△ACD .2、如图(2):AC ∥EF ,AC=EF ,AE=BD .求证:△ABC ≌△EDF .3、 如图(3):DF=CE ,AD=BC ,∠D=∠C .求证:△AED ≌△BFC .4、 如图(4):AB=AC ,AD=AE ,AB ⊥AC ,AD ⊥AE .求证:(1)∠B=∠C ,(2)BD=CE5、如图(5):AB ⊥BD ,ED ⊥BD ,AB=CD ,BC=DE .求证:AC ⊥CE .(图1)D CB AF E D C B A F E (图3)DC BA E(图4)D CBA EDBA6、如图(6):CG=CF ,BC=DC ,AB=ED ,点A 、B 、C 、D 、E 在同一直线上. 求证:(1)AF=EG ,(2)BF ∥DG .7、如图(7):AC ⊥BC ,BM 平分∠ABC 且交AC 于点M 、N 是AB 的中点且BN=BC . 求证:(1)MN 平分∠AMB ,(2)∠A=∠CBM .8、如图(8):A 、B 、C 、D 四点在同一直线上,AC=DB ,BE ∥CF ,AE ∥DF .求证:△ABE ≌△DCF .9、如图(9)AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF .求证:AM 是△ABC 的中线.10、如图(10)∠BAC=∠DAE ,∠ABD=∠ACE ,BD=CE . 求证:AB=AC .GF E(图6)D CBA NM(图7)CBA F E (图8)D CBA MF E(图9)C BAE (图10)DC B A11、如图(11)在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是BC上任一点.求证:PA=PD.12、如图(12)AB∥CD,OA=OD,点F、D、O、A、E在同一直线上,AE=DF.求证:EB∥CF.13、如图(13)△ABC≌△EDC.求证:BE=AD.14、如图(14)在△ABC中,∠ACB=90°,AC=BC,AE是BC的中线,过点C作CF⊥AE于F,过B作BD⊥CB交CF的延长线于点D.(1)求证:AE=CD,(2)若BD=5㎝,求AC的长.15、如图15△ABC中,AB=2AC,∠BAC=90°,延长BA到D,使AD=12AB,延长AC到E,使CE=AC.求证:△ABC≌△AED.P4321(图11)DBAOFE(图12)DCBAE(图13)DCBAFE(图14)DC BAE16、如图(16)AD ∥BC ,AD=BC ,AE=CF .求证:(1)DE=DF ,(2)AB ∥CD .17、如图:在△ABC 中,AD ⊥BC 于D ,AD=BD ,CD=DE ,E 是AD 上一点,连结BE 并延长交AC 于点F . 求证:(1)BE=AC ,(2)BF ⊥AC .18、如图:在△ABC 中,∠ACB=90°,AC=BC ,D 是AB 上一点,AE ⊥GD 于E ,BF ⊥CD 交CD 的延长线于F .求证:AE=EF+BF .19、如图:AB=DC ,BE=DF ,AF=DE .求证:△ABE ≌△DCF .20、如图;AB=AC ,BF=CF .求证:∠B=∠C . F (图16)EDCB A F (图17)E DCB AF(图18)EDC BA F(图19)E DC BA FE D C BA21、如图:AB ∥CD ,∠B=∠D ,求证:AD ∥BC .22、如图:AB=CD ,AE=DF ,CE=FB .求证:AF=DE .23、如图:AB=DC ,∠A=∠D .求证:∠B=∠C .24、如图:AD=BC ,DE ⊥AC 于E ,BF ⊥AC 于F ,DE=BF .求证:(1)AF=CE ,(2)AB ∥CD .25、如图:CD ⊥AB 于D ,BE ⊥AC 于E ,OD=OE . 求证:AB=AC .(图21)D CBAF(图22)E D CB A (图23)D CB AF(图24)E D C BA O (图25)ED C BA26、如图:在△ABC 中,AB=AC ,AD 和BE 都是高,它们相交于点H ,且AH=2BD . 求证:AE=BE .27、如图:在△ABC 中,BE 、CF 分别是AC 、AB 两边上的高,在BE 上截取BD=AC ,在CF 的延长线上截取CG=AB ,连结AD 、AG . 求证:(1)AD=AG ,(2)AD ⊥AG .28、如图:AB=AC ,EB=EC ,AE 的延长线交BC 于D .求证:BD=DC .29、如图:△ABC 和△DBC 的顶点A 和D 在BC 的同旁,AB=DC ,AC=DB ,AC 和DB 相交于O . 求证:OA=OD .H(图26)EDC B A GHF(图27)E D C B AED C BAO DC B A30、如图:AB=AC ,DB=DC ,F 是AD 的延长线上的一点.求证:BF=CF .31、如图:AB=AC ,AD=AE ,AB 、DC 相交于点M ,AC 、BE 相交于点N ,∠DAC=∠EAC . 求证:AM=AN .32、如图:AD=CB ,AE ⊥BD ,CF ⊥BD ,E 、F 是垂足,AE=CF .求证:AB=CD .33、如图:在△ABC 中,AD 是它的角平分线,且BD=CD ,DE ,DF 分别垂直AB ,AC ,垂足为E ,F .求证:EB=FC .34、如图:CD ⊥AB ,BE ⊥AC ,垂足分别为D 、E ,BE ,CD 相交于点O . 求证:(1)当∠1=∠2时,OB=OC .(2)当OB=OC 时,∠1=∠2. FD C BAN M ED CBAFED C B AFE DC B AE D A35、如图:在△ABC 中,∠BAC=90°,∠ABD=12∠ABC ,BC ⊥DF ,垂足为F ,AF 交BD 于E .求证:AE=EF .36、如图:在△ABC 中,,O 是∠ABC 与∠ACB 的平分线的交点.求证:点O 在∠A 的平分线上.37、如图:在△ABC 中,∠B ,∠C 相邻的外角的平分线交于点D .求证:点D 在∠A 的平分线上.38、如图:AD 是△ABC 中∠BAC 的平分线,过AD 的中点E 作EF ⊥AD 交BC 的延长线于F ,连结AF .求证:∠B=∠CAF .39、如图:AD 是△ABC 的中线,DE ⊥AC 于E ,DF ⊥AB 于F ,且BF=CE ,点P 是AD 上一点,PM ⊥AC于M ,PN ⊥AB 于N . 求证:(1)DE=DF ,(2)PM=PN .FED C B AO C BA D CB A FE DC B AA40、如图:在△ABC 中,∠A=60°,∠B ,∠C 的平分线BE ,CF 相交于点O . 求证:OE=OF .41、如图:E 是∠AOB 的平分线上一点,EC ⊥OA ,ED ⊥OB ,垂足为C ,D . 求证:(1)OC=OD ,(2)DF=CF .42、如图:在△ABC 中,∠C=90°,AC=BC ,D 是AC 上一点,AE ⊥BD 交BD 的延长线于E ,且AE=12BD ,DF ⊥AB 于F .求证:CD=DF .43、如图:AB=FE ,BD=EC ,AB ∥EF .求证:(1)AC=FD ,(2)AC ∥EF ,(3)∠ADC=∠FCD .FOECB AOFEDCBAF ED CB AE D C B A44、如图:AD=AE ,∠DAB=∠EAC ,AM=AN .求证:AB=AC .45、如图:AB=AC ,BD=CE .求证:OA 平分∠BAC .46、如图:AD 是△ABC 的BC 边上的中线,BE 是AC 边上的高,OC 平分∠ACB ,OB=OC .求证:△ABC 是等边三角形.47、如图△ABC 中,∠C=90°,AC=BC ,过点C 在△ABC 外作直线MN ,AM ⊥MN 于M ,BN ⊥MN 于N .(1)求证:MN=AM+BN .(2)若过点C 在△ABC 内作直线MN ,AM ⊥MN 于M ,BN ⊥MN 于N ,则AM 、BN 与MN 之间有什么关系?请说明理由. NM ED C BAO ED CBAO ED C B AN MCBA NMCBA。
全等三角形证明题练习

全等三角形证明题练习姓名:班级:一、准备0个条件1、如图,已知:AB=CD,AC=BD,求证:AC∥BD.二、准备1个条件2、如图,已知:AB=DE,BE=CF,AC=DF,求证:AB∥DE.3、如图,已知:∠1=∠2,∠A=∠C,AB=CD,求证:OC=OB.三、准备2个条件4、如图,已知:AB⊥BD,ED⊥BD,AC⊥CE,AC=CE,求证:BD=AB+BC.四、准备3个条件5、如图,已知:AD是△ABC的角平分线和中线,且DE⊥AB,DF⊥AC.求证:BE=CF.五、二次全等6、如图,已知:PA⊥OA,PB⊥OB,PA=PB,PM=PN,(1)证明:△APM≌△BPN,(2 证明:△APO≌△BP0,(3)证明:OM=ON.六、添加辅助线7、如图,已知:AC=AD,BC=BD.求证:∠C=∠D.8、如图,已知:AB=AC.求证:∠B=∠C.9、如图,已知:∠1+∠2=180°,QM=QN,求证:AP平分∠BAC.七、三角形及全等三角形重要公式1、三角形内角和180°,直角三角形两锐角互余。
2、三角形的一个外角等于不相邻的两个内角之和。
3、三角形的三条角平分线交于一点(内心),三角形的任意两个外角平分线交于一点(旁心)4、到三角形三边距离相等的点只有一个,即内心,到三角形三边所在直线距离相等的点有 四个,一个内心,三个旁心。
5、多边形内角和公式(n-2)180°,6、n 边形外角和360°。
7、正多边形内角公式n1802-n ︒∙)( 8、判断一个正多边形能否进行镶嵌的方法n1802-n ︒∙)(x=360°,是否存在正整数解。
6、判断两种正多边形能否进行镶嵌的公式n 1802-n ︒∙)(x+m1802-m ︒∙)(y=360°7、全等三角形的性质对应边相等,对应角相等。
8、全等三角形的判定SSS,SAS,ASA,AAS,9、直角三角形的特殊判定定理:斜边直角边(HL )10、全等三角形判定中常用隐含条件公共边,公共角,对顶角11、全等三角形判定中,经常涉及的转化根据等式性质,进行线段或角的加减,等量代换12、全等三角形的证明题(1)方法:因果分析法,综合分析法(2)思路:用定义证明,或者全等的性质,转化思想等(3)。
(完整版)全等三角形证明经典30题

全等三角形经典题目精选1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CAD BCB ACDF21 ECD B A6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE7. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
8.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C9.已知:AB=CD ,∠A=∠D ,求证:∠B=∠C10.P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB11.已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE12.已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DCDC B A F E A B C DPD A CB13.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .14.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA15.如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .PED CB A16.如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠BD C B A17.如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,F A E DCBAF =CE ,BD 交AC 于点M .(1)求证:MB =MD ,ME =MF (2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.18.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点,(1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):O E DC B A19.如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .FEDC B A20、如图:DF=CE ,AD=BC ,∠D=∠C 。
七年级全等三角形的证明110道经典练习题附带答案
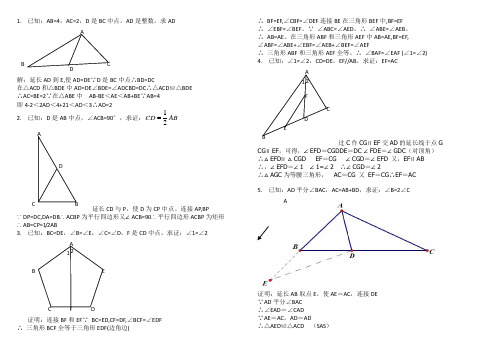
1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE ∠BDE=∠ADCBD=DC ∴△ACD ≌△BDE ∴AC=BE=2∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4 即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP ,BP∵DP=DC,DA=DB ∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF 连接BE 在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2) 4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC ∠FDE =∠GDC (对顶角) ∴△EFD ≌△CGD EF =CG ∠CGD =∠EFD 又,EF ∥AB ∴,∠EFD =∠1 ∠1=∠2 ∴∠CGD =∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:延长AB 取点E ,使AE =AC ,连接DE ∵AD 平分∠BAC ∴∠EAD =∠CAD ∵AE =AC ,AD =AD∴△AED ≌△ACD (SAS )A BC DEF 21 ADBCDABCBA CDF2 1 EA∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF ∴AE=AF+FE=AD+BE12. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形的判定 1.已知AD是⊿ABC的中线,BE⊥AD,CF⊥AD,问BE=CF吗?说明理由。
2.已知AC=BD,AE=CF,BE=DF,问AE∥CF吗? 3.已知AB=CD,BE=DF,AE=CF,问AB∥CD吗? 4.已知在四边形ABCD中,AB=CD,AD=CB,问AB∥CD吗?说明理由。 5.已知∠BAC=∠DAE,∠1=∠2,BD=CE,问ABD≌⊿ACE.吗?为什么?
6.已知CD∥AB,DF∥EB,DF=EB,问AF=CE吗?说明理由。 7.已知BE=CF,AB=CD, ∠B=∠C.问AF=DE吗? 8.已知AD=CB, ∠A=∠C,AE=CF,问EB∥DF吗?说明理由。 9.已知,M是AB的中点,∠1=∠2,MC=MD,问∠C=∠D吗?说明理由。
A B C D
F
E
A C B
D
E F
D C F E A B
A B C D
A D E
B C
1 2
A D C E F B A C D B E F
B A D F E
C
M A B C D 1 2 10.已知,AE=DF,BF=CE,AE∥DF,问AB=CD吗?说明理由。 11.已知∠1=∠2,∠3=∠4,问AC=AD吗?说明理由。 12.已知∠E=∠F,∠1=∠2,AB=CD,问AE=DF吗?说明理由。 13.已知ED⊥AB,EF⊥BC,BD=EF,问BM=ME吗?说明理由。 14.在⊿ABC中,高AD与BE相交于点H,且AD=BD,问⊿BHD≌⊿ACD,为什么? 15.已知∠A=∠D,AC∥FD,AC=FD,问AB∥DE吗?说明理由。 16.已知AC=AB,AE=AD, ∠1=∠2,问∠3=∠4吗? 17.已知EF∥BC,AF=CD,AB⊥BC,DE⊥EF,问⊿ABC≌⊿DEF吗?说明理由。 18.已知AD=AE,∠B=∠C,问AC=AB吗?说明理由。
A C
D B 1 2 3
4
A B C
D
E F 1 2
A B C E H
D
A C M
E
F B D
A B C E
F
D
A B C
E D F
A D E B C
1 2 3 4
D C F E A B 19.已知AD⊥BC,BD=CD,问AB=AC吗?
20.已知∠1=∠2,BC=AD,问⊿ABC≌⊿BAD吗?
21.已知AB=AC, ∠1=∠2,AD=AE,问⊿ABD≌⊿ACE.说明理由。 22.已知BE∥DF,AD∥BC,AE=CF,问⊿AFD≌⊿CEB吗? 23.已知AD=AE,BD=CE,∠1=∠2,问⊿ABD≌⊿ACE吗? 24.已知AB=AC,AD=AE,∠1=∠2,问CE=BD吗?
25.已知CE⊥AB,DF⊥AB,AC∥DB,AC=BD,问CE=DF吗?说明理由。 26.如图,AD=BC,AE=BE,问∠C=∠D吗? C
A E
B F
D
A D E
B C
A
B C D
A B C D O 1 2
B A D F E
C A
B C D E
1 2
A C D
B E F
G 1
2
A C D E B
A D B
E
C 1 2 27.已知∠1=∠2,AC=BD,E,F,A,B在同一直线上,问∠3=∠4吗? 28.已知DO⊥BC,OC=OA,OB=OD,问CD=AB吗? 29.已知CE=DF,AE=BF,AE⊥AD,FD⊥AD,问⊿EAB≌⊿FDC吗?
30.已知AB与CD相交于点E,EA=EC,ED=EB,问⊿AED≌⊿CEB吗? 31.已知AB=AC,D,E分别是AB,AC的中点。问BE=CD吗?说明理由。 32.已知DE=FE,FC∥AB,问AE=CE吗? 33.已知CE⊥AB,DF⊥AB,CE=DF,AE=BF,问⊿CEB≌⊿DFA吗?说明理由。
34.如图,D,E,F,B在一条直线上,AB=CD,∠B=∠D,BF=DE,问(1)AE=CF(2)AE∥CF。 35.已知,点C是AB的中点,CD∥BE,且CD=BE,问∠D=∠E吗?说明理由。
A E D C B O
C D A E F B
2 1
3 4
B A C D E F
C D E F A B
D A
E C B
1
2
A C B
D
E
C A E
B F
D
A D B
E F
C
A C B E D 36.已知,E、F是AB上的两点,AE=BF,又AC∥DB,AC=DB,问CF=DE吗?说明理由。 37.已知,AC⊥CE,AC=CE, ∠ABC=∠DEC=900,问BD=AB+ED吗? 38.⊿ABC≌⊿A′B′C′,AD与A′D′分别是中线,问AD=A′D′吗? 39. 已知:如图 , E, B, F, C四点在同一直线上, ∠A=∠D=90° , BE=FC, AB=DF. 求证:∠E=∠C
40.已知:如图 , DN=EM , 且DNAB于D , EMAC于E , BM=CN.求证:∠B=∠C.
41.已知:如图 , AE , FC都垂直于BD , 垂足为E、F , AD=BC , BE=DF.求证:OA=OC. 42. 已知:如图 , AB=CD , D、B到AC的距离DE=BF.求证:AB∥CD. 43. 已知:如图 , OC=OD , ADOB于D , BCOA于C,求证:EA=EB.
A B C
D
E
A B C D
A′ B′ C′ D′
B A
D
F
E
C 44.如图 , 已知:∠ACB和∠ADB都是直角 , BC=BD , E是AB上任一点 ,求证:CE=DE.
45.已知:如图,∠A=∠D=90°,AC,BD交于O,AC=BD,求证:OB=OC. 46、如图(1):AD⊥BC,垂足为D,BD=CD。求证:△ABD≌△ACD。 47、如图(2):AC∥EF,AC=EF,AE=BD。求证:△ABC≌△EDF。 48、如图(3):DF=CE,AD=BC,∠D=∠C。求证:△AED≌△BFC。 49、如图(4):AB=AC,AD=AE,AB⊥AC,AD⊥AE。求证:(1)∠B=∠C,(2)BD=CE
50、如图(5):AB⊥BD,ED⊥BD,AB=CD,BC=DE。求证:AC⊥CE 51、如图(6):CG=CF,BC=DC,AB=ED,点A、B、C、D、E在同一直线上。 求证:(1)AF=EG,(2)BF∥DG。
(图1)DCBAFE(图2)
D
CBAFE
(图3)DC
BAE
(图4)D
C
BA
E(图5)D
C
B
A
GFE(图6)D
C
BA 52、如图(7):AC⊥BC,BM平分∠ABC且交AC于点M、N是AB的中点且BN=BC。求证:(1)MN平分∠AMB,(2)∠A=∠CBM。
53、如图(8):A、B、C、D四点在同一直线上,AC=DB,BE∥CF,AE∥DF。 求证:△ABE≌△DCF。
54、如图(9)AE、BC交于点M,F点在AM上,BE∥CF,BE=CF。 求证:AM是△ABC的中线。
55、如图(10)∠BAC=∠DAE,∠ABD=∠ACE,BD=CE。 求证:AB=AC。 56、如图(11)在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是BC上任一点。 求证:PA=PD。
57、如图(12)AB∥CD,OA=OD,点F、D、O、A、E在同一直线上,AE=DF。 求证:EB∥CF。
58、如图(13)△ABC≌△EDC。求证:BE=AD。
NM(图7)CBA
F
E(图8)D
C
BA
MFE(图9)CB
A
E(图10)DCB
A
P43
21(图11)DC
BA
OF
E(图12)DC
BAE
(图13)DC
B
A
