瑞利信道Matlab仿真程序
瑞利信道仿真

瑞利分布信道M A T L A B仿真一、瑞利衰败原理在陆地挪动通讯中,挪动台常常遇到各样阻碍物和其余挪动体的影响,致使抵达挪动台的信号是来自不一样流传路径的信号之和。
而描绘这样一种信道的常用信道模型即是瑞利衰败信道。
定义 : 因为信号进行多径流传达到接收点处的场强来自不一样流传的路径,各条路径延不时间是不一样的,而各个方向重量波的叠加,又产生了驻波场强,进而形成信号快衰败称为瑞利衰败。
瑞利衰败信道( Rayleighfadingchannel )是一种无线电信号流传环境的统计模型。
这类模型假定信号经过无线信道以后,其信号幅度是随机的,表现为“衰败”特征,而且多径衰败的信号包络听从瑞利散布。
由此,这类多径衰败也称为瑞利衰败。
这一信道模型能够描绘由电离层和对流层反射的短波信道,以及建筑物密集的城市环境。
瑞利衰败只合用于从发射机到接收机不存在直射信号的情况,不然应使用莱斯衰败信道作为信道模型。
假定经反射(或散射)抵达接收天线的信号为 N 个幅值和相位均随机的且统计独立的信号之和。
信号振幅为 r, 相位为 , 则其包络概率密度函数为r r 2P(r)= 2 e 22 (r 0)相位概率密度函数为:P( )=1/2(02)二、仿真原理( 1)瑞利散布剖析环境条件:往常在离基站较远、反射物许多的地域,发射机和接收机之间没有直射波路径(如视距流传路径),且存在大批反射波,抵达接收天线的方向角随机的(( 0~2π)平均散布),各反射波的幅度和相位都统计独立。
幅度与相位的散布特征:包络 r 听从瑞利散布,θ 在 0~2π内听从平均散布。
瑞利散布的概率散布密度如图 1 所示:0.90.80.70.60.50.40.30.20.100.51 1.52 2.5 3图1 瑞利散布的概率散布密度(2)多径衰败信道基本模型失散多径衰败信道模型为N ( t )% %k )y ( t ) r k ( t ) x (tk 1 (1)此中 , r k(t )复路径衰败,听从瑞利散布 ; k 是多径时延。
matlab信道仿真经典源程序

%
% Rayleigh Fading Channel Signal Generator
% Using the Dent Model (a modification to the Jakes Model)
%
% Last Mouthor: Avetis Ioannisyan (avetis@)
% Number of oscillators
N0 = NumAngles/4;
% Maximum Doppler shift of carrier at some wavelength
omega_m = (2*pi) * fm(Velocity, carrierFreq);
% specify variance of the Rayleigh channel
%
% Usage Examples:
% [omega_mTau, Tk] = ai_RayCh(2^7, 2^18, 64, 2, 900, 100)
%
% where
%
% NumAngles=2^7, Length=2^18, symbolRate=64, NumWaveforms=2, carrierFreq=900, Velocity=100
% use this for *constant* variange - requires changing other params in prog
sigma2 = 10;
% make sigma2 a gaussian RV around u = sigma2 and var = sigma2/5
%
%
% Usage:
% [omega_mTau, Tk] =
% ai_RayCh(NumAngles, Length, SymbolRate, NumWaveforms, CarrierFreq, Velocity)
课程设计报告——matlab瑞利衰落信道仿真

目录摘要 (1)1、设计原理 (2)1.1设计目的 (2)1.2仿真原理 (2)1.2.1瑞利分布简介 (2)1.2.2多径衰落信道基本模型 (2)1.2.3产生服从瑞利分布的路径衰落r(t) (3)1.2.4产生多径延时 (4)1.3仿真框架 (4)2、设计任务 (4)2.1设计任务要求 (4)2.2 MATLAB 仿真程序要求 (4)3、DSB调制解调分析的MATLAB实现 (5)3.1 DSB调制解调的MA TLAB实现 (5)3.2瑞利衰落信道的MA TLAB实现 (6)4、模拟仿真及结果分析 (7)4.1模拟仿真 (7)4.1.1多普勒滤波器的频响 (7)4.1.2多普勒滤波器的统计特性 (7)4.1.3信道的时域输入/输出波形 (8)4.2仿真结果分析 (8)4.2.1时域输入/输出波形分析 (8)4.2.2频域波形分析 (8)4.2.3多普勒滤波器的统计特性分析 (9)5、小结与体会 (9)6、参考文献 (9)MATLAB 通信仿真设计摘要主要运用MATLAB进行编程,实现采用对输入信号进行抑制载波的双边带调幅;而后将调幅波输入信道,研究多径信道的特性对通信质量的影响;最后将信道内输出的条幅波进行同步解调,解调出与输入信号波形相类似的波形,观测两者差别。
同时输出多普勒滤波器的统计特性图及信号时域和频域的输入、输出波形。
关键字:双边带调幅瑞利衰落相干解调MATLAB121、设计原理 1.1设计目的由于多径和移动台运动等影响因素,使得移动信道对传输信号在时间、频率和角度上造成了色散,如时间色散、频率色散、角度色散等等,因此多径信道的特性对通信质量有着至关重要的影响,而多径信道的包络统计特性成为我们研究的焦点。
根据不同无线环境,接收信号包络一般服从几种典型分布,如瑞利分布、莱斯分布和Nakagami-m 分布。
在设计中,专门针对服从瑞利分布的多径信道进行模拟仿真,进一步加深对多径信道特性的了解。
matlab信道仿真经典源程序

matlab信道仿真经典源程序% %% Rayleigh Fading Channel Signal Generator% Using the Dent Model (a modification to the Jakes Model) %% Last Modified 10/18/05 %% Author: Avetis Ioannisyan (avetis@) % %% Usage:% [omega_mTau, Tk] =% ai_RayCh(NumAngles, Length, SymbolRate, NumWaveforms, CarrierFreq, Velocity) %% Where the output omega_mTau is a time scaling factor for plotting% normalized correlations. The LAGS value output by [C,LAGS] = XCORR(...) % should be multiplied by the omega_mTau scaling factor to properly display % axis. Tk is a two dimensional vector [M, N] = SIZE(Tk) with% M=numWaverorms and N=Length specified in the RayCh(...) function call %% And the input variables are: %% NumAngles - scalar power of 2, NumAngles > 2^7 is used to specify the % number of equally strong rays arriving at the receiver. It used to% compute the number of oscillators in the Dent model with N0 =numAngles/4 %% Length - scalar preferably power of 2 for faster computation, Length >2^17 % is used to specify the length of the generated sequence. Lengths near1E6 % are close to realistic signals %% SymbolRate - scalar power of 2 and is in kilo-symbols-per-sec is usedto % specify what should be the transmission data rate. Slower rates will % provide slowly fading channels. Normal voice and soem data rates are % 64-256 ksps %% NumWaveforms - scalar used to specify how many 'k' waveforms to generate % in the model. NumWaveforms > 2 to properly display plots %% CarrierFreq - scalar expressed in MHz is the carrier frequency of the % tranmitter. Normally 800 or 1900 MHz for mobile comms %% Velocity - scalar expressed in km/hr is the speed of the receiver. % 100 km/hr = 65 mi/hr. Normal values are 20-130 km/hr %% Usage Examples:% [omega_mTau, Tk] = ai_RayCh(2^7, 2^18, 64, 2, 900, 100) %% where %% NumAngles=2^7, Length=2^18, symbolRate=64, NumWaveforms=2,carrierFreq=900, Velocity=100% [omega_mTau, Tk] = RayCh(NumAngles, Length, symbolRate, NumWaveforms, % carrierFreq, Velocity); % %function [omega_mTau, Tk] = ai_RayCh(NumAngles, Length, symbolRate, NumWaveforms, carrierFreq, Velocity)% Number of oscillators N0 = NumAngles/4;% Maximum Doppler shift of carrier at some wavelength omega_m = (2*pi) * fm(Velocity, carrierFreq); % specify variance of the Rayleigh channel% use this for *constant* variange - requires changing other params in prog sigma2 = 10;% make sigma2 a gaussian RV around u = sigma2 and var = sigma2/5% use for *non constant* variaance - requires changing other params in prog sigma2 = sigma2 + sqrt(sigma2/5) .* randn(1,NumWaveforms); % Initialize phasesalpha_n = []; beta_n = []; theta_nk = []; % make a hadamard matrix Ak = hadamard(N0);% determine phase values 'alpha' and 'beta' n=[1:N0];alpha_n = 2*pi*n/NumAngles - pi/NumAngles; beta_n = pi*n/N0;% convert to time scale using 'fs' sampling frequencyt=[1/(symbolRate*1000):1/(symbolRate*1000):1/(symbolRate*1000) * Length];Tk = [];for q = 1 : NumWaveformsrand('state',sum(100*clock)) % reset randomizertheta_nk = rand(1,length(n)) * 2 *pi; % create uniform random phasein range [0,2pi]sumRes = 0; for i = 1 : N0term1 = Ak(NumWaveforms,i);term2 = cos(beta_n(i)) + j*sin(beta_n(i));term3 = cos(omega_m .* t .* cos(alpha_n(i)) + theta_nk(i)); sumRes = sumRes + (term1 .* term2 .* term3); endTk(q,:) = sqrt(2/N0) .* sumRes;% use line below to apply *non-constant* varianceTk(q,:) = repmat(10.^(sigma2(q)/20),1, Length) .* Tk(q,:); %apply variable in dB end% apply *constant* variance unilaterly in dB % Tk = repmat(10^(sigma2/20), k, Length) .* Tk;% plot resultsfigure(20); subplot(3,1,1); semilogy(t,abs(Tk(1,:))); xlabel('Time (sec)'); ylabel('Signal Strength (dB)');title(['Received Envelope, Symbol Rate = ', num2str(symbolRate), ',Carrier = ', num2str(carrierFreq), ', Velocity = ', num2str(Velocity)]); % computeauto and cross correlations and plot themomega_mTau = (1/(symbolRate*1000)) * (omega_m/(2*pi)); % computeomega_m * tau scaling[C1, Lags] = crosscorr(Tk(1,:), Tk(2,:), 20000); [C2, Lags2] =autocorr(Tk(1,:), 20000);figure(20); subplot(3,1,3); plot(Lags * omega_mTau, C1);xlabel('Normalized Time Delay'); ylabel('Normalized Crosscorrelation'); title('Crosscorrelation between waveforms k=1 and k=2'); figure(20);subplot(3,1,2); plot(Lags2 * omega_mTau, C2);xlabel('Normalized Time Delay'); ylabel('Normalized Autocorrelation'); title('Autocorrelation of the first waveform k=1');感谢您的阅读,祝您生活愉快。
信道接收机matlab仿真

信道接收机matlab仿真1.信道化接收机MATLAB仿真代码:clc;clear;f1=2000;f2=5000;%测频范围f=input('输入待测频率 (MHz) ');if f>=f1&&f<=f2m1=4;m2=4;m3=4;%各分路器均设为5,分路器结构u=(f2-f1)/(m1*m2*m3);%频率分辨力ur=[0,0,0];%为各分路器中放带宽提供缓存ur(1)=(f2-f1)/m1; %写入各分路器中放带宽ur(2)=(f2-f1)/(m1*m2);ur(3)=(f2-f1)/(m1*m2*m3);fi=[0,0,0];%为各分路器中频频率提供缓存fi(1)=ceil(((f2-f1)/2)*1.2);%写入各分路中频频率fi(2)=ceil((ur(1)/2)*1.2);fi(3)=ceil((ur(2)/2)*1.6);fl=zeros(3,4);for j=1:1:4fl(1,j)=f1-fi(1)+(j-0.5)*ur(1);%第一本振组fl(2,j)=(fi(1)-ur(1)/2)-fi(2)+(j-0.5)*ur(2);%第二本振组fl(3,j)=(fi(2)-ur(2)/2)-fi(3)+(j-0.5)*ur(3);%第三本振组end num=zeros(1,3);%为每层的信道提供缓存for k=1:3j=1;while j<=4if f-fl(k,j)>=fi(k)-ur(k)/2&&f-fl(k,j)<=fi(k)+ur(k)/2 f=f-fl(k,j); num(k)=j-1;break;else j=j+1;endendendf=f1+num(1)*ur(1)+num(2)*ur(2)+num(3)*ur(3)+u/2;%进行频率估计fprintf('估计频率为 %f MHz\n',f);else disp('不在测频范围内 ');end仿真结果:。
Rayleigh无线衰落信道的MATLAB仿真

通信原理课程设计汇报书课题名称Rayleigh 无线衰落信道的MATLAB 仿真姓 名学 号 学 院 专 业 通信工程指导教师年 月 日※※※※※※※※※ ※※ ※※ ※※ ※※※※※※※※※通信工程专业 通信原理课程设计Rayleigh无线衰落信道的MATLAB仿真1 设计目的〔1〕对瑞利信道的数学分析,得出瑞利信道的数学模型。
〔2〕利用MATLAB对瑞利无线衰落信道进行编程。
〔3〕针对服从瑞利分布的多径信道进行模拟仿真,加深对多径信道特性的了解。
〔4〕对仿真后的结果进行分析,得出瑞利无线衰落信道的特性。
2 设计思路无线衰落信道的MATLAB仿真:〔1〕分析出无线信道符合瑞利概率密度分布函数,写出数学表达式。
〔2〕建立多径衰落信道的根本模型。
〔3〕对符合瑞利信道的路径衰落进行分析,并利用MATLAB进行仿真。
3 设计过程3.1 方案论证3.1.1.瑞利信道环境与数学模型瑞利衰落信道〔Rayleigh fading channel〕是一种无线电信号传播环境的统计模型。
这种模型假设信号通过无线信道之后,其信号幅度是随机的,即“衰落〞,并且其包含服从瑞利分布。
瑞利衰落属于小尺寸的衰落效应,它总是叠加于如阴影、衰减等大尺度衰落效应上。
信道衰落的快慢与开展端和接收端的相对运动速度的大小有关,相对运动对导致接受信号的多普勒频移,一固定信号通过单径的瑞利衰落信道后,在1秒内的能量波动,这一瑞利衰落信道的多普勒频移最大分别为10Hz和100Hz,在GSM1800MHz的载波频率上,其相应的移动速度分别为约6千米每小时和60千米每小时。
特别需要注意的事信号“深衰落〞现象,此时信号能量的衰减到达数千倍,即30到40分贝。
瑞利衰落模型适用于描述建筑物密集的城镇中心地带的无线信道。
密集的建筑和其他物体使得无线设备的发射机和接收机之间没有直射路径,而且使得无线信号被衰减、反射、折射、衍射。
在曼哈顿的实验证明,当地的无线信道环境实在接近于瑞利衰落。
Rayleigh无线衰落信道的MATLAB仿真

通信原理课程设计报告书课题名称 Rayleigh 无线衰落 信道的MATLAB 仿真姓 名学 号 学 院 专 业 通信工程指导教师※※※※※※※※※ ※※ ※※ ※※通信工程专业 通信原理课程设计年月日Rayleigh无线衰落信道的MATLAB仿真1 设计目的(1)对瑞利信道的数学分析,得出瑞利信道的数学模型。
(2)利用MATLAB对瑞利无线衰落信道进行编程。
(3)针对服从瑞利分布的多径信道进行模拟仿真,加深对多径信道特性的了解。
(4)对仿真后的结果进行分析,得出瑞利无线衰落信道的特性。
2 设计思路无线衰落信道的MATLAB仿真:(1)分析出无线信道符合瑞利概率密度分布函数,写出数学表达式。
(2)建立多径衰落信道的基本模型。
(3)对符合瑞利信道的路径衰落进行分析,并利用MATLAB进行仿真。
3 设计过程3.1 方案论证3.1.1.瑞利信道环境与数学模型瑞利衰落信道(Rayleigh fading channel)是一种无线电信号传播环境的统计模型。
这种模型假设信号通过无线信道之后,其信号幅度是随机的,即“衰落”,并且其包括服从瑞利分布。
瑞利衰落属于小尺寸的衰落效应,它总是叠加于如阴影、衰减等大尺度衰落效应上。
信道衰落的快慢与发展端和接收端的相对运动速度的大小有关,相对运动对导致接受信号的多普勒频移,一固定信号通过单径的瑞利衰落信道后,在1秒内的能量波动,这一瑞利衰落信道的多普勒频移最大分别为10Hz和100Hz,在GSM1800MHz的载波频率上,其相应的移动速度分别为约6千米每小时和60千米每小时。
特别需要注意的事信号“深衰落”现象,此时信号能量的衰减达到数千倍,即30到40分贝。
瑞利衰落模型适用于描述建筑物密集的城镇中心地带的无线信道。
密集的建筑和其他物体使得无线设备的发射机和接收机之间没有直射路径,而且使得无线信号被衰减、反射、折射、衍射。
在曼哈顿的实验证明,当地的无线信道环境确实接近于瑞利衰落。
Matlab下多径衰落信道的仿真代码

%区别个条路径的均匀分布随机相位
theta=2*pi*rand(1,1)-pi;
for ii=1i*ii-pi+theta)/N;
N=40;
wm=2*pi*fd;
%每象限的入射波数目即振荡器数目
N0=N/4;
%信道函数的实部
Tc=zeros(1,length(t));
%信道函数的虚部
Ts=zeros(1,length(t));
%归一化功率系数
function [h]=rayleigh(fd,t)
%改进的jakes模型来产生单径的平坦型瑞利衰落信道
%输入变量说明:
% fd:信道的最大多普勒频移 单位Hz
% t :信号的抽样时间序列,抽样间隔单位s
% h为输出的瑞利信道函数,是一个时间函数复序列
%假设的入射波数目
衰落信道参数包括多径扩展和多普勒扩展。时不变的多径扩展相当于一个延时抽头滤波器,而多普勒扩展要注意多普勒功率谱密度,通常使用Jakes功率谱、高斯、均匀功率谱。
多径衰落信道由单径信道叠加而成,而单径信道中最重要的就是瑞利(Rayleigh)平坦衰落信道。
下面给出瑞利平坦衰落信道的改进Jakes模型的实现:
chan=rayleighchan(ts,fd);
y=filter(chan,x);%过信道
此内置函数可以直接生成一个频率选择多径衰落信道,每径为一个瑞利衰落过程。
chan=rayleighchan(ts,fd,tau,pdb);
%tau为每径相对时延向量
%pdb为每径相对增益
%对每个子载波而言在(-pi,pi)之间均匀分布的随机相位
QPSK通过Rayleigh信道多径衰落的Matlab仿真

QPSK通过Rayleigh信道多径衰落的Matlab仿真参照《通信系统仿真原理与无线应用》351页例14-1在这个例子里,我们对有3条固定路径的AWGN多径信道中的QPSK系统进行BER性能仿真,并与在理想的AWGN信道(没有多径)中同样系统地BER性能进行比较……书上有比较详细的数学推导,不抄了。
这个例子似乎没有考虑多普勒频移。
待我继续学习下一个例子,这个也没太看懂。
下面是该例子的源程序,P0、P1、P2分别是LOS路径和两条延迟瑞利分量的相对功率级。
当p0=0且delay!=0时为瑞利频率选择性衰落,delay==0时为瑞利平坦衰落。
主程序scriptfile:% 两径瑞利衰落信道仿真% 设定默认参数NN=256; % 传输符号个数tb=0.5; % 一比特时间fs=10; % 每符号采样数ebn0db=[1:2:15]; % 设定Eb/N0% 建立QPSK信号x=random_binary(NN,fs)+i*random_binary(NN,fs); % x为QPSK信号% 输入功率和延迟p0=0; % 视距LOS分量p1=20; % 第一路径分量p2=1; % 第二路径分量delay=1; % 按照每符号采样数决定的延迟delay0=0;delay1=0;delay2=delay;% 设定复高斯(瑞利)衰减gain1=sqrt(p1)*abs(randn(1,NN)+i*randn(1,NN));gain2=sqrt(p2)*abs(randn(1,NN)+i*randn(1,NN));for k=1:NNfor kk=1:fsindex=(k-1)*fs+kk;ggain1(1,index)=gain1(1,k);ggain2(1,index)=gain2(1,k);endendy1=x;for k=1:delay2y2(1,k)=y1(1,k)*sqrt(p0);endfor k=(delay2+1):(NN*fs)y2(1,k)=y1(1,k)*sqrt(p0)+y1(1,k-delay1)*ggain1(1,k)+y1(1,k-delay2)*ggain2(1,k);end% 匹配滤波器b=-ones(1,fs);b=b/fs;a=1;y=filter(b,a,y2);% 仿真结束% Use the semianalytic BER estimator . The following sets up the semi% analytic estimator . Find the maximun magnitude of the cross correlation % and the corresponding lag .[cor lags]=vxcorr(x,y);cmax=max(max(abs(cor)));nmax=find(abs(cor)==cmax);timelag=lags(nmax);corrmag=cmax;theta=angle(cor(nmax));y=y*exp(-i*theta); % derotate% Noise BW calibrationhh=impz(b,a);ts=1/16;nbw=(fs/2)*sum(hh.^2);% Delay the input ,and do BER estimation on the last 128 bits . Use middle % sample .Make sure the index does not exceed number of input points .Eb % should be computed at the receiver input .index=(10*fs+8:fs:(NN-10)*fs+8);xx=x(index);yy=y(index-timelag+1);[n1 n2]=size(y2);ny2=n1*n2;eb=tb*sum(sum(abs(y2).^2))/ny2;eb=eb/2;[peideal,pesystem]=qpsk_berest(xx,yy,ebn0db,eb,tb,nbw);figuresemilogy(ebn0db,peideal,'b*-',ebn0db,pesystem,'r+-')xlabel('Eb/N0 (db)');ylabel('Probability of Error');grid onaxis([0 14 10^(-10) 1]);% End of script file.相关的一些调用程序(4个):[1] vxcorr.mfunction [c,lags]=vxcorr(a,b)% This function calculates the unscaled cross-correlation of 2 vectors of% the same length . The output length(c) is length(a)+length(b)-1. It is a% simplified function of xcorr function in matlabR12 using the definition: % c(m)=E[a(n+m)*conj(b(n))]=E[a(n)*conj(b(n-m))] a=a(:); % convert a to column vectorb=b(:); % convert b to column vectorM=length(a); % same as length(b)maxlag=M-1; % maximum value of laglags=[-maxlag:maxlag]';A=fft(a,2^nextpow2(2*M-1)); % fft of AB=fft(b,2^nextpow2(2*M-1)); % fft of Bc=ifft(A.*conj(B)); % corsscorrelation% Move negative lags before positive lags.c=[c(end-maxlag+1:end,1);c(1:maxlag+1,1)];% Return row vector if a,b are row vectors.[nr nc]=size(a);if(nr>nc)c=c.';lags=lags.';end% End of function file.[2] random_binary.mfunction [x,bits]=random_binary(nbits,nsamples)% This function generates a random binary waveform of length nbits% sampled at a rate of nsamples/bit.x=zeros(1,nbits*nsamples);bits=round(rand(1,nbits));for m=1:nbitsfor n=1:nsamplesindex=(m-1)*nsamples+n;x(1,index)=(-1)^bits(m);endend% End of function file.[3] qpsk_berest.m% File: psk_berest.mfunction[peideal,pesystem]=psk_berest(xx,yy,ebn0db,eb,tb,nbw) % ebn0db is an array of Eb/No values in db (specified at the receiver%input); tb is the bit duration and nbw is the noise BW% xx is the reference (ideal) input; yy is the filtered output;nx=length(xx);% For comparision purposes , set the noise BW of the ideal receiver% (integrate and dump) to be equal to rs/2.nbwideal=1/(2*tb); % noise bandwidthfor m=1:length(ebn0db)peideal(m)=0.0; pesystem(m)=0.0; %initialize% find n0 and the variance of the noise.ebn0(m)=10^(ebn0db(m)/10); % dB to linearn0=eb/ebn0(m); % noise powersigma=sqrt(n0*nbw*2); %variancesigma1=sqrt(n0*nbwideal*2);%% Multiply the input constellation/signal by a scale factor so that input% constellation and the constellations/signal at the input to receive % filter have the same ave power a=sqrt(2*eb/(2*tb)).b=sqrt(2*eb/tb)/sqrt(sum(abs(xx).^2)/nx);d1=b*abs(xx);d3=abs(yy);peideal(m)=sum(q(d1/sigma1));pesystem(m)=sum(q(d3/sigma));endpeideal=peideal/nx;pesystem=pesystem/nx; % End of function file.[4] q.m% File: q.mfunction out=q(x)out=0.5*erfc(x/sqrt(2)); % End of function file。
瑞利衰落信道的matlab仿真【开题报告】

开题报告通信工程瑞利衰落信道的matlab仿真一、课题研究意义及现状随着科学技术的不断提高,无线通信系统不断更新还代,无线通信走入各家各户,它带来的便利深入人心。
无线移动通信自诞生以来,其发展速度令人惊叹。
经历第二代和第三代移动通信的快速发展,下一代即后三代(Beyond 3G)或第四代移动通信系统(4G)的研究工作已经开始展开。
移动信道的研究与应用为移动通信开辟更为广阔的前景,认识移动信道本身的特性是解决移动通信中关键技术的前提.瑞利衰落信道是一种无线电信号传播环境的统计模型。
这种模型假设信号通过无线信道之后,其信号幅度是随机的,即“衰落”,并且其包络服从瑞利分布。
在无线通信中,信号通过无线信道后,由于基站周围反光物体或者其它障碍物的阻塞,经过多种路径的反射、折射,导致信号幅度随机化,使信号的干扰增大,给接受信号带来很大不便。
而第四代移动通信技术要普及,就要研发出瑞利衰落信道的解决方法,所以研究瑞利衰落信道具有很大的意义。
在MIMO中,传统的多天线被用来增加分集度从而克服信道衰落。
具有相同信息的信号通过不同的路径被发送出去,在接收机端可以获得数据符号多个独立衰落的复制品,从而获得更高的接收可靠性。
要克服瑞利衰落信道带来的不便,就要先研究它的特性。
当在实际电子通信系统中进行试验研究比较困难或更本无法实现时,仿真技术就成为必然选择。
我的研究课题就是利用Matlab仿真对瑞利衰落信道进行模拟仿真,对产生的各种符合瑞利分布的信道系数画出曲线图,并进行分析研究。
二、课题研究的主要内容和预期目标课题研究的主要内容1.先掌握matlab程序设计;2.通过资料了解瑞利衰落信道的原理;3.通过m语言编程建立瑞利衰落信道模型;4.在完善的信道模型基础上进行Matlab仿真;课题的预期目标:1.要求根据瑞利衰落信道模型,能产生符合瑞利分布的信道系数;2.再根据这些信道系数画出相应的曲线图;3.课题的验收成果包括瑞利衰落信道仿真的matlab源程序以及相应的说明书。
matlab实现频域瑞利(Rayleigh)信道仿真

plot(GaussN2);
title('频域复数高斯信号2');
xlabel('实部');
ylabel('虚部');
grid;
figure(5)
subplot(2,1,1)
plot(sqrt(SEf).*GaussN1);
title('高斯噪声与多普勒功率谱相乘1');
plot(Gauss_time2);
title('时域高斯信号2');
xlabel('N');
ylabel('V');
grid;
subplot(2,2,3)
plot(GaussN1);
title('频域复数高斯信号1');
xlabel('实部');
ylabel('虚部');
grid;
GaussN2=fft(Gauss_time2);
% 产生瑞利衰落信道
x = ifft(sqrt(SEf).*GaussN1);
y = ifft(sqrt(SEf).*GaussN2);
rayleigh_amp = sqrt(abs(x).^2+abs(y).^2);
rayleigh_db = 20*log10(rayleigh_amp); %用dB表示瑞利信号
figure(2);
plot(rayleigh_db);
% axis([0 140 -100 20]);
title('瑞利信号衰落');
matlab瑞利衰落信道仿真
瑞利分布信道MATLAB仿真1、引言由于多径效应和移动台运动等影响因素,使得移动信道对传输信号在时间、频率和角度上造成了色散,即时间色散、频率色散、角度色散等等,因此多径信道的特性对通信质量有着重要的影响,而多径信道的包络统计特性则是我们研究的焦点。
根据不同无线环境,接收信号包络一般服从几种典型分布,如瑞利分布、莱斯分布等。
在此专门针对服从瑞利分布的多径信道进行模拟仿真,进一步加深对多径信道特性的了解。
2、仿真原理(1)瑞利分布分析环境条件:通常在离基站较远、反射物较多的地区,发射机和接收机之间没有直射波路径(如视距传播路径),且存在大量反射波,到达接收天线的方向角随机的((0~2π)均匀分布),各反射波的幅度和相位都统计独立。
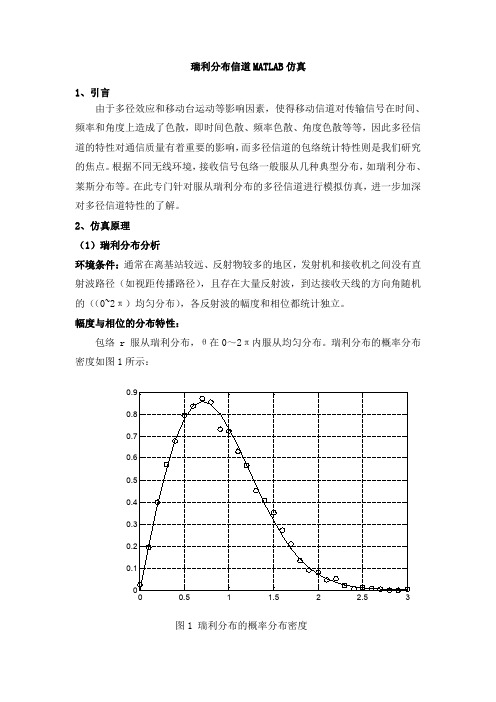
幅度与相位的分布特性:包络r服从瑞利分布,θ在0~2π内服从均匀分布。
瑞利分布的概率分布密度如图1所示:图1瑞利分布的概率分布密度(2)多径衰落信道基本模型离散多径衰落信道模型为()1()()()N t k k k yt r t x t τ==-∑ (1)其中,()k r t 复路径衰落,服从瑞利分布;k τ是多径时延。
多径衰落信道模型框图如图2所示:图2多径衰落信道模型框图(3)产生服从瑞利分布的路径衰落r(t)利用窄带高斯过程的特性,其振幅服从瑞利分布,即()r t =(2)上式中()()c s n t n t 、,分别为窄带高斯过程的同相和正交支路的基带信号。
3、仿真框架根据多径衰落信道模型(见图2),利用瑞利分布的路径衰落r(t)和多径延时参数k τ,我们可以得到多径信道的仿真框图,如图3所示;图3多径信道的仿真框图4、仿真结果(1)(1)多普勒滤波器的频响图4多普勒滤波器的频响(2)多普勒滤波器的统计特性图5多普勒滤波器的统计特性(3)信道的时域输入/输出波形图6信道的时域输入/输出波形5、仿真结果(2)(1)当终端移动速度为30km/h时,瑞利分布的包络如下图所示(2)当终端移动速度为100km/h时,瑞利分布的包络如下图所示三、仿真代码%main.mclc;LengthOfSignal=10240;%信号长度(最好大于两倍fc)fm=512;%最大多普勒频移fc=5120;%载波频率t=1:LengthOfSignal;%SignalInput=sin(t/100);SignalInput=sin(t/100)+cos(t/65);%信号输入delay=[03171109173251];power=[0-1-9-10-15-20];%dBy_in=[zeros(1,delay(6))SignalInput];%为时移补零y_out=zeros(1,LengthOfSignal);%用于信号输出for i=1:6Rayl;y_out=y_out+r.*y_in(delay(6)+1-delay(i):delay(6)+LengthOfSignal-delay (i))*10^(power(i)/20);end;figure(1);subplot(2,1,1);plot(SignalInput(delay(6)+1:LengthOfSignal));%去除时延造成的空白信号title('Signal Input');subplot(2,1,2);plot(y_out(delay(6)+1:LengthOfSignal));%去除时延造成的空白信号title('Signal Output');figure(2);subplot(2,1,1);hist(r,256);title('Amplitude Distribution Of Rayleigh Signal')subplot(2,1,2);hist(angle(r0));title('Angle Distribution Of Rayleigh Signal');figure(3);plot(Sf1);title('The Frequency Response of Doppler Filter');%Rayl.mf=1:2*fm-1;%通频带长度y=0.5./((1-((f-fm)/fm).^2).^(1/2))/pi;%多普勒功率谱(基带)Sf=zeros(1,LengthOfSignal);Sf1=y;%多普勒滤波器的频响Sf(fc-fm+1:fc+fm-1)=y;%(把基带映射到载波频率)x1=randn(1,LengthOfSignal);x2=randn(1,LengthOfSignal);nc=ifft(fft(x1+i*x2).*sqrt(Sf));%同相分量x3=randn(1,LengthOfSignal);x4=randn(1,LengthOfSignal);ns=ifft(fft(x3+i*x4).*sqrt(Sf));%正交分量r0=(real(nc)+j*real(ns));%瑞利信号r=abs(r0);%瑞利信号幅值。
瑞利信道仿真

瑞利分布信道MATLAB 仿真一、瑞利衰落原理在陆地移动通信中,移动台往往受到各种障碍物和其他移动体的影响,以致到达移动台的信号是来自不同传播路径的信号之和。
而描述这样一种信道的常用信道模型便是瑞利衰落信道。
定义:由于信号进行多径传播达到接收点处的场强来自不同传播的路径,各条路径延时时间是不同的,而各个方向分量波的叠加,又产生了驻波场强,从而形成信号快衰落称为瑞利衰落。
瑞利衰落信道(Rayleigh fading channel )是一种无线电信号传播环境的统计模型。
这种模型假设信号通过无线信道之后,其信号幅度是随机的,表现为“衰落”特性,并且多径衰落的信号包络服从瑞利分布。
由此,这种多径衰落也称为瑞利衰落。
这一信道模型能够描述由电离层和对流层反射的短波信道,以及建筑物密集的城市环境。
瑞利衰落只适用于从发射机到接收机不存在直射信号的情况,否则应使用莱斯衰落信道作为信道模型。
假设经反射(或散射)到达接收天线的信号为N 个幅值和相位均随机的且统计独立的信号之和。
信号振幅为r,相位为θ,则其包络概率密度函数为 P(r)=2222r σσr e - (r ≥0)相位概率密度函数为:P(θ)=1/2π (πθ20≤≤)二、仿真原理(1)瑞利分布分析环境条件:通常在离基站较远、反射物较多的地区,发射机和接收机之间没有直射波路径(如视距传播路径),且存在大量反射波,到达接收天线的方向角随机的((0~2π)均匀分布),各反射波的幅度和相位都统计独立。
幅度与相位的分布特性:包络 r 服从瑞利分布,θ在0~2π内服从均匀分布。
瑞利分布的概率分布密度如图1所示:00.51 1.52 2.5300.10.20.30.40.50.60.70.80.9图1 瑞利分布的概率分布密度(2)多径衰落信道基本模型离散多径衰落信道模型为()1()()()N t k k k y t r t x t τ==-∑%% (1)其中,()k r t 复路径衰落,服从瑞利分布; k τ是多径时延。
瑞利信道仿真[特辑]
![瑞利信道仿真[特辑]](https://img.taocdn.com/s3/m/7c3f35f1a48da0116c175f0e7cd184254b351b6a.png)
瑞利信道仿真[特辑]瑞利衰落信道的matlab仿真瑞利衰落信道(Rayleigh fading channel)是一种无线电信号传播环境的统计模型。
这种模型假设信号通过无线信道之后,其信号幅度是随机的,即“衰落”,并且其包络服从瑞利分布。
模型的适用瑞利衰落模型适用于描述建筑物密集的城镇中心地带的无线信道。
密集的建筑和其他物体使得无线设备的发射机和接收机之间没有直射路径,而且使得无线信号被衰减、反射、折射、衍射。
在曼哈顿的实验证明,当地的无线信道环境确实接[3]近于瑞利衰落。
通过电离层和对流层反射的无线电信道也可以用瑞利衰落来描述,因为大气中存在的各种粒子能够将无线信号大量散射。
瑞利衰落属于小尺度的衰落效应,它总是叠加于如阴影、衰减等大尺度衰落效应上。
信道衰落的快慢与发射端和接收端的相对运动速度的大小有关。
相对运对导致接收信号的多普勒频移。
图中所示即为一固定信号通过单径的瑞利衰落信道后,在1秒内的能量波动,这一瑞利衰落信道的多普勒频移最大分别为10Hz和100Hz,在GSM1800MHz的载波频率上,其相应的移动速度分别为约6千米每小时和60千米每小时。
特别需要注意的是信号的“深衰落”现象,此时信号能量的衰减达到数千倍,即30,40分贝。
性质多普勒功率普密度,瑞利衰落信道的仿真根据上文所述,瑞利衰落信道可以通过发生实部和虚部都服从独立的高斯分布变量来仿真生成。
不过,在有些情况下,研究者只对幅度的波动感兴趣。
针对这种情况,有两种方法可以仿真产生瑞利衰落信道。
这两种方法的目的是产生一个信号,有着上文所示的多普勒功率谱或者等效的自相关函数。
这个信号就是瑞利衰落信道的冲激响应。
Jakes模型和clark模型本次只以下图所示的模型来仿真单路信号的产生。
课本上也有相关的分析。
仿真结果如下:当终端移动速度为30km/h时,瑞利分布的包络为: 当终端移动速度为100km/h时,瑞利分布的包络为:瑞利分布的概率密度函数为:0.90.80.70.60.50.40.30.20.1000.511.522.53与书上相符,因标准化时令r’=r/sqrt(2),故上图下标正确。
瑞利信道Matlab仿真程序

瑞利信道Matlab仿真程序%%File_C7:Jakes.m%本程序将一随机信号通过瑞利信道产生输出%%clear;clc;Ts=0.02;fmax=2;%最大多普勒频移Nt=400;%采样序列的长度sig=j*ones(1,Nt);%信号t=[0:Nt];%设定信道仿真参数N0=25;D=1;[u]=jakes_single_rayleigh(N0,D,fmax,Nt,Ts);%生成瑞利信道RecSignal=u.*sig;plot(20*log10(RecSignal));%JakesRayleigh.m%本函数用Jakes方法产生单径的符合瑞利分布的复随机过程%%%%%%%%%%%%%%%%%%%%%%%%%%% function [u]=jakes_single_rayleigh(N0,D,fmax,M,Ts,Tc) % 输入参数:% N0 频率不重叠的正弦波个数% D 方差,可由输入功率得到% fmax 最大多普勒频移% M 码片数%输出参数%u 输出复信号%u1 输出信号的实部%u2 输出信号的虚部%%%%%%%%%%%%%%%%%%%%%%%%%%%%%N=4*N0+2;%Jakes仿真叠加正弦波的总个数%计算Jakes仿真中的离散多普勒频率fi,nf=zeros(1,N0+1);for n=1:N0f(n)=fmax*cos(2*pi*n/N);endf(N0+1)=fmax;%计算多普勒增益ci,n%同向分量增益c1,nc1=zeros(1,N0+1);for n=1:N0c1(n)=D*(2/sqrt(N))*2*cos(pi*n/N0); endc1(N0+1)=D*(2/sqrt(N))*sqrt(2)*cos(pi/4); %正交分量增益c2,nc2=zeros(1,N0+1);for n=1:N0c2(n)=D*(2/sqrt(N))*2*sin(pi*n/N0); endc2(N0+1)=D*(2/sqrt(N))*sqrt(2)*sin(pi/4); %插入随机相移ph_i,解决Jakes方法的广义平稳问题n=(1:N0+1);U=rand(size(n));[x,k]=sort(U);ph_i=2*pi*n(k)/(N0+1);%计算复包络u1=zeros(1,M);%Rc(t)u2=zeros(1,M);%Rs(t)u=zeros(1,M);%R(t)k=0;%计算Rc(t)k=0;for t=0:Ts:(M-1)*Ts;w2=cos(2*pi*f*t+ph_i); ut2=c2*w2.';k=k+1;u2(k)=ut2;end%计算u(t)k=0;for t=0:Ts:(M-1)*Tsk=k+1;u(k)=u1(k)-j*u2(k); end%程序结束。
Matlab瑞利信道仿真

Matlab瑞利信道仿真转眼间三⽉都已经过去⼀半,⼀直找不到有什么可以写的,⼀直想等⾃⼰把LTE仿真平台搭好后,再以连载的形式记录下来。
但是,后来⼀想,我必须先做好充分的铺垫,在这过程中也遇到了很多问题,及时留下点什么,也是好的。
即便以后回过头来再看这些⽂章,可能会有些许惊讶,惊讶于当时的⽆知或是稚嫩。
不得不说,时间真的是⼀把杀猪⼑,猪没少杀,更可怕的是扼杀了许多⼈的梦想。
今天没有去实验室,我觉得在忙了⼀周后,应该停下来歇歇,有时候的驻⾜观望或许是为了更好的前⾏。
⾔归正传,今天想记录的是⾃⼰在仿真中遇到的⼀个问题,那就是信道模型的仿真。
对于⽆线通信来说,最常见的就是瑞利衰落+多径+多普勒的模型了。
具体分析如下:瑞利衰落:就是有很多独⽴的⼩径的叠加,根据中⼼极限定理,知道这样的分布满⾜的是2个⾃由度的chi-square分布,也就是功率满⾜指数分布,幅度的分布就叫做瑞利分布。
它表明的是信道h的幅度和相位变化情况,幅度满⾜瑞利分布的变化,相位满⾜[0,2pi]上均匀分布的变化。
可以参考博⽂:多径效应:谈到多径效应,我们就应该想到频率选择性这个概念。
简单地说,就是延时的径在频域相当于相位搬移,每个径我们都可以看做是⼀个⽮量,幅度是由它们各⾃的功率决定,⾓度(相位)就是由每径延时决定。
然后,我们就做⽮量相加,最后得到的就是⼀个旋转⽮量,它对每个频率的响应都不同。
第⼆个概念就是,相⼲带宽:既然信道响应在各个频率点处的不同,那么我们关⼼的⼀个问题是,在多⼤的频率间隔上,它的响应是呈现⼀定的相关性(也就是说,在这个频率间隔上的响应变化⾮常慢,可以认为是相同的)。
这就很⾃然的过渡到功率延迟分布图上了,信道响应的频域(相关性)⽅⾯实质上是由信道时域的功率延迟分布做傅⽴叶变换得到的(功率与⾃相关函数的关系)。
功率延迟分布图是⼀个很有⽤的⼯具,我们能从中得到Trms(信道平均延迟,⽤功率去对延时加权)和Tmax(信道最⼤延时)等。
matlab多径瑞利衰落信道

matlab多径瑞利衰落信道【原创实用版】目录1.多径瑞利衰落信道的概念和背景2.Matlab 在多径瑞利衰落信道仿真中的应用3.多径瑞利衰落信道仿真的重要性和挑战4.如何在 Matlab 中实现多径瑞利衰落信道的仿真5.总结与展望正文一、多径瑞利衰落信道的概念和背景多径瑞利衰落信道是一种无线通信信道模型,它描述了无线信号在传输过程中由于多径效应和瑞利衰落所引起的信号衰减和失真。
在城市密集区域、建筑物内部等环境中,无线信号会受到反射、折射、衍射等影响,导致信号强度的快速衰减和信道质量的恶化。
因此,研究多径瑞利衰落信道对于无线通信系统的设计和优化具有重要意义。
二、Matlab 在多径瑞利衰落信道仿真中的应用Matlab 是一种广泛应用于科学计算和工程设计的软件,其强大的数值计算和数据分析功能为多径瑞利衰落信道的仿真提供了便利。
在Matlab 中,可以通过编写自定义函数或使用现有的工具箱(如Communication Toolbox)来实现多径瑞利衰落信道的仿真。
三、多径瑞利衰落信道仿真的重要性和挑战多径瑞利衰落信道仿真对于无线通信系统的设计和优化具有重要意义,因为它可以帮助工程师了解系统在不同信道条件下的性能,从而指导系统参数的调整和优化。
然而,多径瑞利衰落信道仿真也面临着一些挑战,如信号模型的复杂性、参数设置的合理性、计算资源的需求等。
四、如何在 Matlab 中实现多径瑞利衰落信道的仿真在 Matlab 中实现多径瑞利衰落信道的仿真,可以采用如下步骤:1.创建信号模型:首先需要建立一个信号模型,描述信号在多径瑞利衰落信道中的传播过程。
这可以通过编写自定义函数或使用现有的工具箱来实现。
2.设置系统参数:在进行仿真之前,需要设置一些系统参数,如信号的调制方式、传输速率、信道带宽等。
这些参数的设置会影响到仿真结果的准确性和可靠性。
3.编写仿真代码:根据信号模型和系统参数,可以编写 Matlab 代码来实现多径瑞利衰落信道的仿真。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
%%File_C7:
%本程序将一随机信号通过瑞利信道产生输出
%%
clear;
clc;
Ts=;
fmax=2;%最大多普勒频移
Nt=400;%采样序列的长度
(
sig=j*ones(1,Nt);%信号
t=[0:Nt];
%设定信道仿真参数
N0=25;
D=1;
[u]=jakes_single_rayleigh(N0,D,fmax,Nt,Ts);%生成瑞利信道RecSignal=u.*sig;
?
plot(20*log10(RecSignal));
%
%本函数用Jakes方法产生单径的符合瑞利分布的复随机过程%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [u]=jakes_single_rayleigh(N0,D,fmax,M,Ts,Tc)
% 输入参数:
% N0 频率不重叠的正弦波个数
{
% D 方差,可由输入功率得到
% fmax 最大多普勒频移
% M 码片数
%输出参数
%u 输出复信号
%u1 输出信号的实部
%u2 输出信号的虚部
%%
、
%%%%%%%%%%%%%%%%%%%%%%%%%%%
N=4*N0+2;%Jakes仿真叠加正弦波的总个数
%计算Jakes仿真中的离散多普勒频率fi,n
f=zeros(1,N0+1);
for n=1:N0
f(n)=fmax*cos(2*pi*n/N);
~
f(N0+1)=fmax;
%计算多普勒增益ci,n
%同向分量增益c1,n
c1=zeros(1,N0+1);
for n=1:N0
c1(n)=D*(2/sqrt(N))*2*cos(pi*n/N0);
end
c1(N0+1)=D*(2/sqrt(N))*sqrt(2)*cos(pi/4);
《
%正交分量增益c2,n
c2=zeros(1,N0+1);
for n=1:N0
c2(n)=D*(2/sqrt(N))*2*sin(pi*n/N0);
end
c2(N0+1)=D*(2/sqrt(N))*sqrt(2)*sin(pi/4);
%插入随机相移ph_i,解决Jakes方法的广义平稳问题n=(1:N0+1);
\
U=rand(size(n));
[x,k]=sort(U);
ph_i=2*pi*n(k)/(N0+1);
%计算复包络
u1=zeros(1,M);%Rc(t)
u2=zeros(1,M);%Rs(t)
u=zeros(1,M);%R(t)
k=0;
&
%计算Rc(t)
k=0;
for t=0:Ts:(M-1)*Ts;
w2=cos(2*pi*f*t+ph_i);
ut2=c2*w2.';
k=k+1;
u2(k)=ut2;
end
%计算u(t)
k=0;
for t=0:Ts:(M-1)*Ts
k=k+1;
u(k)=u1(k)-j*u2(k);
end
%程序结束。
