初中数学面积法
初中求面积的常用方法

初中求面积的常用方法
1. 直接计算法:对于简单的图形,可以直接根据公式计算面积,如长方形的面积为长乘以宽,正方形的面积为边长的平方,三角形的面积为底边乘以高再除以2等。
2. 分割法:对于复杂的图形,可以将其分割为若干个简单的图形,计算出每个简单图形的面积,然后将它们相加即可得到整个图形的面积。
例如,对于一个不规则的多边形,可以将它分割为多个三角形,计算每个三角形的面积再相加。
3. 同等面积法:若两个图形有相等的面积,可以利用较简单的图形计算出面积,然后利用两个图形的面积相等的性质,直接得到另一个图形的面积。
例如,一个不规则的四边形和一个已知面积的矩形相等,可以通过计算矩形面积知道四边形的面积。
4. 数学推导法:通过利用几何概念和数学推导,可以得到一些特殊图形的面积公式。
例如,圆的面积公式为πr²,其中r为
半径。
这种方法通常要求对相关的数学知识有一定的掌握。
以上是初中常用的求面积方法,但实际上还有很多其他的方法,具体使用哪种方法取决于图形的形状和题目要求。
完整版初中数学面积公式总结.doc

四边形的面积公式长方形:S=ab{长方形面积=长×宽}正方形:S=a^2{正方形面积=边长×边长}平行四边形:S=ah{平行四边形面积=底×高}梯形:S=(a+b)×h÷2{梯形面积=(上底+下底)×高÷2}三角形的面积公式三角形:S=ah÷2{三角形面积=底×高÷2}圆的面积公式圆形(正圆):S=πr^2{圆形(正圆)面积=圆周率×半径×半径}圆环:S=(R^2-r^2)×π{圆形(外环)面积={圆周率×(外环半径^2-内环半径^2)}扇形:S=πr^2×n/360{圆形(扇形)面积=圆周率×半径×半径×扇形角度/360}椭圆S=π(圆周率)×a×b(其中a,b分别是椭圆的长半轴,短半轴的长).半圆半圆形的面积公式=圆周率×半径的平方÷2用字母公式表示是:S半=Πr^2÷2立方体的面积公式长方体表面积:S=2(ab+ac+bc){长方体表面积=(长×宽+长×高+宽×高)×2}正方体表面积:S=6a^2{正方体表面积=棱长×棱长×6}球体(正球)表面积:S=4πr^2{球体(正球)表面积=圆周率×半径×半径×4}2018中考数学复习快速记忆的6个技巧日期:2018-06-27 来源:中考网责编:樊亚蕾1、归类记忆法就是根据识记材料的性质、特征及其内在联系,进行归纳分类,以便帮助学生记忆大量的知识。
比如,学完计量单位后,可以把学过的所有内容归纳为五类:长度单位;面积单位;体积和容积单位;重量单位;时间单位。
这样归类,能够把纷纭复杂的事物系统化、条理化,易于记忆。
2、歌诀记忆法就是把要记忆的数学知识编成歌谣、口诀或顺口溜,从而便于记忆。
初中数学几何图形面积求法最全总结

初中数学几何图形面积求法最全总结
几何问题一直都是中学数学阶段的一大重点,不仅仅在初中,在高中数学学习中也占有很大比例,所以要学好几何,基础很重要。
在初中数学几何问题中,有时候图形是不规则的,它是由一些基本图形组合、拼凑而成的,对于这类不规则图形,考试经常考的就是求该图形的面积或阴影部分的面积。
公式法
这是最简单,最基础的一种方法,当所求图形是我们常规的几何图形,例如三角形、正方形等。
此时直接运用公式即可。
例如:
和差法
和差法比公式法略微复杂,需要学生进行简单的判断,不过一般难度不大,只需学生用两个或多个常见的几何图形面积进行加减。
1.直接和差法
2.构造和差法
在构造和差法中,通常需要学生构建自己的数学图形转化思维,学会通过添加辅助线求解。
割补法
割补法,是学生拥有比较强的转化能力后才能轻松运用的,否则学生看到这样的题目还是会无从下手。
尤其适用于直接求面积较复杂或无法计算时,通过对图形的平移、旋转、割补等,为利用公式法或和差法求解创造条件。
1.全等法
2.对称法
3.平移法
4.旋转法
当然在实际问题中,解决方法可能不止这一种,有时我们碰到的问题还需要多种方法结合,这就需要我们熟练掌握多种方法,活学活用。
初中数学面积和分割法教案

初中数学面积和分割法教案一、教学目标1. 让学生掌握面积法的概念及应用,能够运用面积法解决几何问题。
2. 让学生理解分割法的原理,学会运用分割法求解几何图形的面积。
3. 培养学生的逻辑思维能力,提高学生解决几何问题的技巧。
二、教学内容1. 面积法的概念及应用2. 分割法的原理及应用三、教学重点与难点1. 面积法的运用2. 分割法的运用四、教学过程1. 导入:通过一个实际问题引出面积法与分割法的重要性。
2. 面积法的讲解:(1)介绍面积法的概念,让学生理解面积法的基本原理。
(2)讲解面积法的应用,如证明线段相等、角相等、不等关系等。
(3)举例说明面积法在解决几何问题中的优势。
3. 分割法的讲解:(1)介绍分割法的原理,让学生理解分割法的基本思路。
(2)讲解分割法的应用,如求解几何图形的面积。
(3)举例说明分割法在解决几何问题中的优势。
4. 课堂练习:让学生运用面积法与分割法解决实际问题,巩固所学知识。
5. 总结与拓展:总结面积法与分割法的运用,引导学生思考如何灵活运用这两种方法解决更复杂的问题。
五、教学策略1. 采用直观演示、讲解、练习相结合的方式,让学生充分理解面积法与分割法的原理及应用。
2. 通过举例分析,让学生感受面积法与分割法在解决几何问题中的优势。
3. 注重学生的主体地位,鼓励学生积极参与课堂讨论,提高学生的逻辑思维能力。
4. 布置适量的课堂练习,让学生在实践中巩固所学知识。
六、教学评价1. 课堂讲解:评价学生对面积法与分割法的理解程度。
2. 课堂练习:评价学生运用面积法与分割法解决实际问题的能力。
3. 课后作业:评价学生对课堂所学知识的巩固程度。
4. 学生反馈:了解学生在学习过程中遇到的问题,及时调整教学方法。
七、教学反思在教学过程中,要注意引导学生理解面积法与分割法的本质,培养学生灵活运用这两种方法解决几何问题的能力。
同时,要关注学生在学习过程中的反馈,及时调整教学策略,提高教学效果。
初中数学等面积法公式

初中数学等面积法公式在咱们初中数学的世界里,等面积法公式可是个相当实用的“宝贝”。
先来说说啥是等面积法。
简单来讲,就是在一个图形中,通过不同的方法计算面积,最后得到相同的结果。
就像你有两条路可以走到同一个目的地,不管走哪条,目的地是不变的。
举个例子,比如一个三角形,我们可以用底乘以高除以2 来算面积,也可以用两边及其夹角的正弦值乘积的一半来算。
这两种方法,只要条件给足了,算出来的面积肯定是一样的。
记得有一次,我在给学生讲这部分内容的时候,有个同学特别较真儿。
那是一道关于菱形的题目,已知菱形的两条对角线长度,让用等面积法求菱形的面积。
这同学怎么都理解不了为啥两种方法算出来的结果必须一样。
我就耐心地给他画了好几遍图,一点点解释,从菱形的特性到公式的推导。
最后这同学恍然大悟,那表情就像是发现了新大陆一样,兴奋得不行。
等面积法的公式在解决很多问题的时候都能派上用场。
比如求三角形的高,如果知道了三角形的面积和底边长,用面积乘以 2 再除以底边长度,就能求出高。
还有在证明一些几何定理的时候,等面积法也能助我们一臂之力。
比如证明勾股定理,就可以通过构造直角三角形,利用等面积法巧妙地得出结论。
在实际应用中,等面积法可以帮我们求出很多看似复杂的图形中的未知量。
像那种给出了一堆线段长度和角度,但就是不知道怎么下手的题目,往往用等面积法就能找到突破口。
而且等面积法不仅仅局限于三角形、四边形这些常见图形,在一些不规则的图形中,我们也可以通过巧妙地分割和组合,运用等面积法来解决问题。
总之,初中数学里的等面积法公式就像是一把万能钥匙,能帮我们打开很多几何难题的大门。
同学们可得把它牢牢掌握在手里,让它成为我们解题的好帮手!只要多做练习,多思考,等面积法一定会在数学学习中发挥出巨大的作用。
相信大家都能在数学的海洋里畅游,用等面积法攻克一个又一个难题!。
八年级数学竞赛例题专题讲解:面积法

八年级数学竞赛例题专题讲解:面积法阅读与思考平面几何学的产生源于人们测量土地面积的需要,面积关联着几何图形的重要元素边与角.所谓面积法是指借助面积有关的知识来解决一些直接或间接与面积问题有关的数学问题的一种方法.有许多数学问题,虽然题目中没有直接涉及面积,但由于面积联系着几何图形的重要元素,所以借助于有关面积的知识求解,常常简捷明快.用面积法解题的基本思路是:对某一平面图形面积,采用不同方法或从不同角度去计算,就可得到一个含边或角的关系式,化简这个面积关系式就可得到求解或求证的结果.下列情况可以考虑用面积法:(1)涉及三角形的高、垂线等问题;(2)涉及角平分线的问题.例题与求解【例1】如图,从等边三角形内一点向三边作垂线,已知这三条垂线段的长分别为1,3,5,则这个等边三角形的边长为______________.(全国初中数学联赛试题) 解题思路:从寻求三条垂线段与等边三角形的高的关系入手.等腰三角形底边上任一点到两腰距离之和等于一腰上的高,那么等边三角形呢?等腰梯形呢?【例2】如图,△AOB中,∠O=,OA=OB,正方形CDEF的顶点C在DA上,点D在OB上,点F在AB上,如果正方形CDEF的面积是△AOB的面积的,则OC:OD等于( )A.3:1 B.2:1C.3:2 D.5:3解题思路:由面积关系,可能想到边、角之间的关系,这时通过设元,即可把几何问题代数化来解决.【例3】如图,在□ABCD中,E为AD上一点,F为AB上一点,且BE=DF,BE与DF交于G,求证:∠BGC=∠DGC.(长春市竞赛试题)解题思路:要证∠BGC=∠DGC,即证CG为∠BGD的平分线,不妨用面积法寻找证题的突破口.【例4】如图,设P为△ABC内任意一点,直线AP,BP,CP交BC,CA,AB于点D、E、F.求证:(1);(2).(南京市竞赛试题)解题思路:过P点作平行线,产生比例线段.【例5】如图,在△ABC中,E,F,P分别在BC,CA,AB上,已知AE,BF,CP相交于一点D,且,求的值.解题思路:利用上例的结论,通过代数恒等变形求值.(黄冈市竞赛试题)【例6】如图,设点E,F,G,H分别在面积为1的四边形ABCD的边AB,BC,CD,DA上,且(是正数),求四边形EFGH的面积.(河北省竞赛试题)解题思路:连对角线,把四边形分割成三角形,将线段的比转化为三角形的面积比.线段比与面积比的相互转化,是解面积问题的常用技巧.转化的基本知识有:(1) 等高三角形面积比,等于它们的底之比;(2) 等底三角形面积比,等于它们的高之比;(3) 相似三角形面积比,等于它们相似比的平方.能力训练1.如图,正方形ABCD的边长为4cm,E是AD的中点,BM⊥EC,垂足为M,则BM=______.(福建省中考试题)2.如图,矩形ABCD中,P为AB上一点,AP=2BP,CE⊥DP于E,AD=,AB=,则CE=__________.(南宁市中考试题)第1题图第2题图第3题图3.如图,已知八边形ABCDEFGH中四个正方形的面积分别为25,48,121,114,PR=13,则该八边形的面积为____________.(江苏省竞赛试题) 4. 在△ABC中,三边长为,,,表示边上的高的长,,的意义类似,则(++)的值为____________. (上海市竞赛试题)5.如图,△ABC的边AB=2,AC=3,Ⅰ,Ⅱ,Ⅲ分别表示以AB,BC,CA为边的正方形,则图中三个阴影部分的面积之和的最大值是__________.(全国竞赛试题) 6.如图,过等边△ABC内一点P向三边作垂线,PQ=6,PR=8,PS=10,则△ABC的面积是 ( ).A. B.C.D.(湖北省黄冈市竞赛试题)第5题图第6题图第7题图7.如图,点D是△ABC的边BC上一点,若∠CAD=∠DAB=,AC=3,AB=6,则AD的长是( ).A.2 B. C.3 D.8.如图,在四边形ABCD中,M,N分别是AB,CD的中点,AN,BN,DM,CM划分四边形所成的7个区域的面积分别为,,,,,,,那么恒成立的关系式是( ).A.+=B.+=C.+= D.+=9.已知等边△ABC和点P,设点P到△ABC三边AB,AC,BC的距离分别为,,,△ABC的高为.若点P在一边BC上(如图1),此时,可得结论:++=.请直接用上述信息解决下列问题:当点P在△ABC内(如图2)、点P在△ABC外(如图3)这两种情况时,上述结论是否还成立?若成立.请给予证明;若不成立,,,与之间又有怎样的关系?请写出你的猜想,不需证明.(黑龙江省中考试题)10.如图,已知D,E,F分别是锐角△ABC的三边BC,CA,AB上的点,且AD、BE、CF相交于P点,AP=BP=CP=6,设PD=,PE=,PF=,若,求的值.(“希望杯”邀请赛试题)11.如图,在凸五边形ABCDE中,已知AB∥CE,BC∥AD,BE∥CD,DE∥AC,求证:AE∥BD.(加拿大数学奥林匹克试题)12.如图,在锐角△ABC中,D,E,F分别是AB,BC,CA边上的三等分点. P,Q,R分别是△ADF,△BDE,△CEF的三条中线的交点.(1) 求△DEF与△ABC的面积比;(2) 求△PDF与△ADF的面积比;(3) 求多边形PDQERF与△ABC的面积比.13.如图,依次延长四边形ABCD的边AB,BC,CD,DA至E,F,G,H,使,若,求的值.(上海市竞赛试题)14.如图,一直线截△ABC的边AB,AC及BC的延长线分别交于F,E,D三点,求证:.(梅涅劳斯定理)15.如图,在△ABC中,已知,求的值.(“华罗庚金杯”少年数学邀请赛试题)。
数学方法篇:面积法

数学方法篇三:面积法用面积法解几何问题是一种重要的数学方法,在初中数学中有着广泛的应用,这种方法有时显得特别简捷,有出奇制胜、事半功倍之效。
(一)怎样证明面积相等。
以下是常用的理论依据1.三角形的中线把三角形分成两个面积相等的部分。
2.同底同高或等底等高的两个三角形面积相等。
3.平行四边形的对角线把其分成两个面积相等的部分。
4.同底(等底)的两个三角形面积的比等于高的比。
同高(或等高)的两个三角形面积的比等于底的比。
5.三角形的面积等于等底等高的平行四边形的面积的一半。
6.三角形的中位线截三角形所得的三角形的面积等于原三角形面积的417.三角形三边中点的连线所成的三角形的面积等于原三角形面积的418.有一个角相等或互补的两个三角形的面积的比等于夹角的两边的乘积的比。
(二)用面积法解几何问题(常用的解题思路)1.分解法:通常把一个复杂的图形,分解成几个三角形。
2.作平行线法:通过平行线找出同高(或等高)的三角形。
3.利用有关性质法:比如利用中点、中位线等的性质。
4.还可以利用面积解决其它问题。
【范例讲析】一、怎样证明面积问题1. 分解法例1. 从△ABC的各顶点作三条平行线AD、BE、CF,各与对边或延长线交于D、E、F,求证:△DEF的面积=2△ABC的面积。
2. 作平行线法例2. 已知:在梯形ABCD中,DC//AB,M为腰BC上的中点,二、用面积法解几何问题1. 用面积法证线段相等例1. 已知:如图,AD是△ABC的中线,CF⊥AD于F,BE⊥AD交AD的延长线于E。
求证:CF=BE。
2. 用面积法证两角相等例2. 如图,C是线段AB上的一点,△ACD、△BCE都是等边三角形,AE、BD相交于O。
求证:∠AOC=∠BOC 。
3. 用面积法证线段不等例3. 如图,在△ABC中,已知AB>AC,∠A的平分线交BC于D。
求证:BD>CD。
4. 用面积法证线段的和差例4. 已知:如图,设等边△ABC一边上的高为h,P为等边△ABC内的任意一点,PD⊥BC于D,PE⊥AC于E,PF⊥AB于F。
浅谈初中数学面积法在解题中的应用

浅谈初中数学面积法在解题中的应用[论文摘要]随着新课程改革的不断深入,这几年我市初中数学教材也在不断更新与完善。
教材的变化带来的是中考题型的变化,但是这里解决数学问题的思想方法却是没有改变的。
笔者根据近几年的中考和日常的教学实际情况总结一下一种重要的数学方法—面积法。
一、直接运用公式法和割补法:对于三角形或者特殊四边形的面积,可以直接运用面积公式求解;对于不规则的几何图形的面积,可以运用割补法求解。
(一)规则图形面积有关的公式(二)不规则的图形可以通过割补法转化为规则图形二、运用转化法求解图形的面积:此法就是通过等积变换、平移、旋转等方法将不规则的图形转化成面积相等的规则图形,再利用规则图形的面积公式,计算出所求的不规则图形的面积。
(一)等积变换:同底等高,等底同高(二)通过平移变换求解面积(三)通过旋转变换求解面积随着新课程改革的不断深入,这几年我市初中数学教材也在不断更新与完善。
教材的变化带来的是中考题型的变化,但是这里解决数学问题的思想方法却是没有改变的。
笔者根据近几年的中考和日常的教学实际情况总结一下一种重要的数学方法—面积法。
所谓面积法,就是利用面积相等或者成比例,来证明其他的线段相等或成比例的方法。
它在初中数学中有着广泛的应用,这种方法有时显得特别简捷,有出奇制胜、事半功倍之效。
许多数学问题,表面上看来似与面积无关,但灵活运用面积法,往往能使问题顺利获解。
下面列举几个例子说说面积法在解题中的应用。
一、直接运用公式法和割补法 :对于三角形或者特殊四边形的 面积,可以直接运用面积公式求解;对于不规则的几何图形的面积,可以运用割补法求解。
(一)规则图形面积有关的公式1、三角形的面积公式:ah S 21=2、矩形的面积公式:S=长⨯宽3、平行四边形面积公式: S=底⨯高4、梯形面积公式: S=21⨯(上底+下底)⨯高 对于这些规则图形直接运用面积公式计算即可。
(二)不规则的图形可以通过割补法转化为规则图形1、 作对角线,化四边形为三角形例1. 如图1所示,凸四边形ABCD 的四边AB 、BC 、CD 和DA 的长分别是3、4、12和3,,求四边形ABCD 的面积。
面积法在初中数学解题中的应用

师生园地2022年4月下半月㊀㊀㊀面积法在初中数学解题中的应用◉辽宁省大连市第五十一中学㊀穆永强1引言面积法解题的基本思想是以 面积 当作思维起点,将题目中的已知量与未知量通过面积公式联系起来,这样显得更为简洁与直观,有助于学生快速理清思路,使其充分体会到面积法的妙用与价值.2应用面积法证明线段相等问题证明线段相等是一类较为常见的平面几何类问题,虽然运用常规方法能够证明,但有时,过程较为繁琐㊁步骤较多,有时学生容易陷入到思维障碍当中,影响他们的解题自信.对此,教师可以指导学生应用面积法证明线段相等的问题,使其转变解题思路,帮助他们找到正确的证明流程与方法.图1例1㊀如图1,已知在等腰三角形A B C 中,A B 和A C 相等,点D 在B C 边上,其中D B 的长度与D C 相等,D E 垂直于A B ,垂点是E ,D F 垂直于A C ,垂点为F ,请尝试证明D E 与D F 相等.分析:学生通过初步审题与观察图形,发现虽然题设中给出的条件较多,也极具条理性,不过他们一时间难以想到用何种方法来证明这两条线段相等,以至于陷入到困境当中.教师可提示学生应用面积法进行证明.具体证明方法如下:因为B D =C D ,所以әA B D 的面积同әA C D 的面积相等,得出12A B D E =12A C D E ,又因为AB =AC ,所以DE =DF .虽然本题可以使用全等三角形的相关知识进行证明,不过采用面积法思路更为简洁,既可以培养学生一题多解的意识,还能够让他们感受到面积法的优势,扩充认知范围.3应用面积法准确求出线段长度求线段长度是数学解题训练中的惯设题目,贯穿于小学㊁初中㊁高中整个教学阶段,虽然这类题目大多数难度都不是特别大,不过部分题目中给出的隐藏条件难以发现,影响解题的正常进行.此时,教师在教学中,应指引学生尝试应用面积法来处理此类题目,使其通过面积的拆分准确求出线段长度,帮助他们建立解题自信.图2例2㊀如图2所示,在三角形A B C 中,B C =90c m ,A D 为高,A D =60c m ,正方形P Q MN 的顶点Q ,M 在BC 边上,顶点P ,N 分别在边A B ,A C 上,其中AD 垂直于B C ,垂点是D ,同正方形的边P N 相交于点E ,那么正方形P Q MN 的边长是多少?分析:学生读完题目后,发现题目中给出的具体数据仅限于三角形,似乎与正方形的关系不大,所以他们很难找准切入点,极易遇到解题障碍,所以教师可引导学生应用面积法,并结合方程相关知识求解.设正方形的边长是x c m ,因为12ˑB C ˑA D =12ˑP N ˑA E +12ˑB Q ˑP Q +12ˑC M ˑMN +P Q 2,代入相关数据可得,12ˑ90ˑ60=x 2ˑ(60-x )+12ˑP Q (B Q +C M )+P Q 2,由此得12ˑ90ˑ60=x2ˑ(60-x )+x 2ˑ(90-x )+x 2,将这个方程化简,解得的x 值即为正方形的边长.在本例中,常规解法是用相似三角形的相似比等于对应高线的比列出比例式求得结果,这里用面积的拆分求解有异曲同工之妙,可以有效活化学生的解题思路.4应用面积法求得线段长度的和不少平面几何类问题都与线段有一定的联系,除09Copyright ©博看网. All Rights Reserved.2022年4月下半月㊀师生园地㊀㊀㊀㊀求一条线段的长度以外,还会求几条线段的总长,这类题目难度通常较大,学生处理起来颇费周折.为此,教师在教学中,可以引导学生尝试应用面积法求几条线段长度的和,使其通过拆分面积及面积公式顺利求得正确答案.图3例3㊀如图3所示,已知梯形A B C D 中,A D ʊB C ,A B =D C ,对角线A C 与B D 相交于点O ,E 为B C 上的一个动点(E 不与B ,C 两点重合),在点E 运动过程中,如果点E 到A C ,B D 的垂线段分别是E Q ,E P ,而B C =8,B D =6,梯形的高DF 的长度是3,求E P +E Q 的和.分析:本题涉及的元素较多,线段较为复杂,还存在一个动点,结果要求两条线段之和,对学生来说难度相对较大,不易找到突破口.应用面积法的解答方法如下:因为四边形A B C D 是一个等腰梯形,对角线A C 与B D 相交于点O ,据此能证明әO B C 是一个等腰三角形,又因为点E 是梯形下底上的一个动点,点E 到A C ,B D 的垂线段分别是E Q ,E P ,作辅助线延长B D 至H ,与C H 垂直,再根据等腰三角形底边上一点到两腰的距离之和等于一腰上的高这一性质,得出E P +E Q =C H .因为S әD B C =12B C D F =12B DC H ,由已知条件,求得C H =4,E P +E Q 的和是4.本案例,由于点E 是动点学生觉得无从下手,只要证明定理 等腰三角形底边上一点到两腰的距离之和等于一腰上的高 ,再结合同一个三角形面积的不同表示问题就轻松解决.5应用面积法求证线段比例等式求证线段比例也是初中数学解题教学中的一类常见题型,由于涉及到比例难度相对较大,对学生的解题能力与思维水平要求较高,通常要用到代数方面的知识,他们很难轻松证明.教师可引领学生巧妙采用面积法证明线段的比例等式,主要通过构建面积这一载体 ,证明几何图形的线段比例等式关系,显得清晰又直观.例4㊀已知在әA B C 中,D 是B C 上的一点,设点E 是A D 的中点,连接B E ,并延长与A C 交于点F ,假设B D ʒC D =2ʒ1,求证A F ʒF C =2ʒ3.分析:首先,根据题意画出图形,如图4,把点C 与点E 连接起来.设әC E D 的面积是x ,因为A E =D E ,所以әA E C 的面积也是x .又因为B D ʒC D =2ʒ1,图4可得әB E D 的面积是2x ,又因A E =D E ,可得әA E B 的面积也是2x .设әE F C 的面积为y ,则A F F C =S әA B F S әB F C =3x -y3x +y①A F F C =S әA E F S әE F C =x -yy②由式①㊁②式联立,可得x =53y .所以A F F C =S әA E F S әE F C =x -y y =53y -y y =23yy=23,即A F ʒF C =2ʒ3成立.本题采用面积法证明线段的比例等式十分巧妙,借助面积这一纽带,清楚地证明几何图形中线段比例的等式关系,使学生的解题思路变得愈加开阔.6应用面积法有效解决函数问题在求解初中函数类试题时,除运用待定系数法之外,还经常用到数形结合法,而面积法就属于数形结合思想的一种.有时,借助面积法也可以有效解决函数问题.例5㊀如果一次函数y =4x +b 的图象与两个坐标轴之间围成一个面积为8的三角形,求该一次函数的解析式.图5分析:本题虽然是一道代数题,但其求解过程要利用三角形的面积.为此,利用函数式找出两直角边的长即可.如图5所示.列出算式12ˑ|b |ˑ|b |4=8,解之得b =8,或b =-8,所以该一次函数的解析式为y =4x +8,或y =4x -8.本例结合面积法处理代数中的一次函数类题目,其实是对数形结合思想的巧妙应用,以此增进数与形之间的关系,使其掌握更多解题方法,优化他们的解题思路.总的来说,在初中数学解题教学活动中,教师很有必要把面积法的思想融会贯通至解题实践中,引领学生学会转变解题思路,思维变得发散与开阔起来,使其通过面积法的有效应用,将一些比较抽象㊁难懂㊁复杂的数学试题变得直观㊁易懂与简单,这对培养学生的解题能力㊁数学思想等均有着相当积极的意义.Z 19Copyright ©博看网. All Rights Reserved.。
初中数学重点梳理:面积问题与面积方法(二)
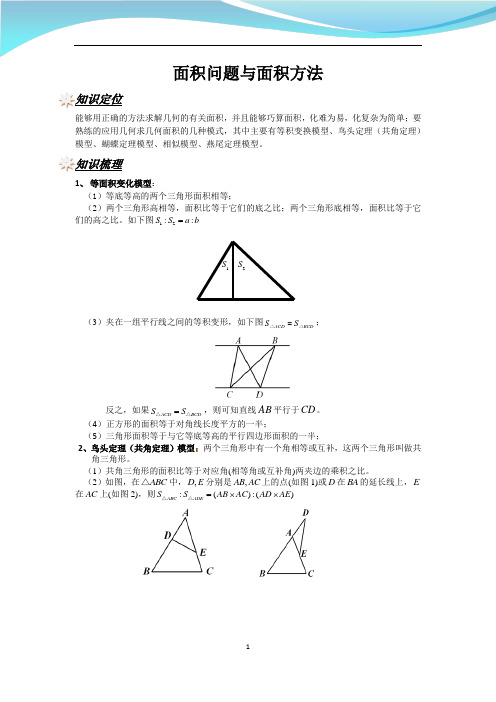
面积问题与面积方法知识定位能够用正确的方法求解几何的有关面积,并且能够巧算面积,化难为易,化复杂为简单;要熟练的应用几何求几何面积的几种模式,其中主要有等积变换模型、鸟头定理(共角定理)模型、蝴蝶定理模型、相似模型、燕尾定理模型。
知识梳理1、 等面积变化模型:(1)等底等高的两个三角形面积相等;(2)两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如下图12::S S a b =(3)夹在一组平行线之间的等积变形,如下图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD 。
(4)正方形的面积等于对角线长度平方的一半;(5)三角形面积等于与它等底等高的平行四边形面积的一半;2、鸟头定理(共角定理)模型:两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
(1)共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
(2)如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△1S 2S3、蝴蝶定理模型:任意四边形中的比例关系。
蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
① 1243::S S S S =1324S S S S ⨯=⨯ ② ()()1243::AO OC S S S S =++ 4、相似模型:相似三角形:相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:(1)相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; (2)相似三角形的面积比等于它们相似比的平方。
初中数学面积法总结归纳

初中数学面积法总结归纳面积是数学中一个重要的概念,它在初中数学中有着广泛的应用。
通过计算几何图形的面积,我们可以解决很多实际问题。
本文将对初中数学中常用的面积法进行总结和归纳。
1. 矩形和正方形的面积计算方法矩形和正方形都是常见的几何图形,计算它们的面积非常简单。
矩形的面积公式是“面积 = 长 ×宽”,即A = l × w;正方形的面积公式是“面积 = 边长 ×边长”,即A = s × s。
其中,A表示面积,l表示矩形的长,w表示矩形的宽,s表示正方形的边长。
2. 三角形的面积计算方法三角形是初中数学中研究得较多的几何图形之一,计算其面积有多种方法。
常用的方法有以下两种:a) 高 ×底边法:三角形的面积可以通过底边和高的乘积的一半来计算。
即A = 1/2 ×底边 ×高。
其中A表示三角形的面积,底边表示三角形的底边长度,高表示从顶点往底边所画的垂直线段的长度。
b) 海伦公式:对于已知三边长度的三角形,可以使用海伦公式计算其面积。
公式为A = √[s(s-a)(s-b)(s-c)],其中A表示三角形的面积,s 表示三角形的半周长,a、b、c表示三角形的三边长度。
3. 平行四边形的面积计算方法平行四边形是一种既有特殊性又常见的四边形,计算其面积有特定的方法。
平行四边形的面积等于底边长度与高的乘积,即A = 底边 ×高。
其中A表示平行四边形的面积,底边表示平行四边形的底边长度,高表示从底边上某一点到与之平行的另一边的垂直距离。
4. 梯形的面积计算方法梯形也是常见的四边形,在计算其面积时需要使用特定的公式。
梯形的面积等于上底和下底长度之和的一半乘以高,即A = 1/2 ×(上底 + 下底) ×高。
其中A表示梯形的面积,上底和下底分别表示两边平行的底边长度,高表示两底边之间的垂直距离。
通过以上总结归纳,我们掌握了初中数学中常用的面积计算方法,包括矩形和正方形的计算、三角形的高×底边法和海伦公式、平行四边形的计算以及梯形的计算。
初中数学-面积问题与面积方法

即 的边BE上的高等于 的边CF上的高
∴
评注:解决本题的关键是运用“平行得等积”。
例2(2003年德国数学竞赛)在平行四边形ABCD中,M、N分别在AB、BC上,且M、N不与端点重合, 。设AN与CM相交于点Q。求证:DQ平分 。
证明:设点Q到AB、BC、CD、DA的距离分别为a、b、c、d
2. 中,设 为a边上的高,R、r分别为 外接圆、内切圆的半径, ,则
三角形的面积公式形式多样,注意根据问题需要灵活选取。
3.(1)相似三角形面积的比等于相似比的平方;
(2)等底(或等高)的三角形的面积比等于其所对应的高(或底)的比。
4.共角定理
若 与 相等或互补,则 。
5.共边定理
如图,若直线AB与PQ相交于M,则 。
又
∴
又∵
∴
∴
评注:本题涉及到圆内接四边形,其另一种解法是运用托勒密定理,请参考本章超级训练第3题。
例6(2000年全国高中数学联赛)如图,在锐角三角形ABC的BC边上有两点E、F,满足∠BAE=∠CAF,作FM⊥AB,FN⊥AC(M、N为垂足),延长AE交三角形ABC的外接圆于D点。证明:四边形AMDN与三角形ABC的面积相等。
作 和 的平分线,且交于点M。于是,BM是AK的中垂线,DM是EK的中垂线。特别地,有 ,即M是 的外心。
因为
所以,
所以 ,即
又因为 ,
所以
故AE是 的斜边,即M是AE的中点。
因为 , ,
所以
评注:巧妙地构造K点,采用“割补法”求解。
例8(2004年首届中国东南地区数学奥林匹克)设点D为等腰 的底边BC上一点,F为过A、D、C三点的圆在 内的弧上一点,过B、D、F三点的圆与边AB交于点E。求证: 。
初中数学竞赛:面积问题与面积方法

(4)梯形ABCD中,AB∥CD,对角线AC与BD相交于O.若S△ABO=p2,S△CDO=q2,则SABCD=____.
△ABC=40.若BE,CD相交于F,则S△DEF=______.
所以
同理可得
从①,②,③中可以解得
所以
例5在一个面积为1的正方形中构造一个如图2-131所示的正方形:将单位正方形的每一条边n等分,然后将每个顶点和它相对的顶点最接近的分点连接起来.如果小正方形(图中阴影部分)的面积恰
解如图2-131,过F作BC的平行线交BG于H,则∠GHF=∠CED,∠FGH=∠DCE=90°,故
证首先,同例2类似,容易证明
说明本例的结论很重要,在处理三角形内三条线交于一点的问题时,常常可以用这一结论去解决.
例8如图2-134,已知D,E,F分别是锐角三角形ABC的三边BC,CA,AB上的点,且AD,BE,CF相交于点P,AP=BP=CP=6,设PD=x,PE=y,PF=z,若xy+yz+zx=28,求xyz的值.
5.在直角三角形ABC中,∠A=90°,AD,AE分别是高和角平分线,且△ABE,△AED的面积分别为S1=30,S2=6,求△ADC的面积S.
6.设P是△ABC内一点,AD,BE,CF过点P并且交边BC,CA,AB于点D,E,F.求证:
7.已知△ABC中,DE∥BC交AB于D,交AC于E,AM为BC边上的中线,与DE相交于N,求证:DN=NE.
初中数学竞赛:面积问题与面积方法
几何学的产生,源于人们测量土地面积的需要.面积不仅是几何学研究的一个重要内容,而且也是用来研究几何学的一个有力工具.
初中等面积法经典例题

初中等面积法经典例题初中数学中的等面积法是一种常用的解题方法,通过找到合适的几何形状,使其面积等于题目中给出的条件,从而求解出问题中未知的数值。
下面将介绍几个经典的等面积法例题。
例题1:一个矩形的长是5cm,宽是3cm,求其周长。
解析:已知矩形的长和宽,我们可以直接使用周长的公式进行计算:周长=2(长+宽)=2(5cm+3cm)=16cm。
例题2:一个长方形底面积是10cm²,高是2cm,求其体积。
解析:已知长方形的底面积和高,我们可以利用体积的公式进行计算:体积=底面积×高=10cm²×2cm=20cm³。
例题3:一个正方形的面积是64cm²,求它的边长。
解析:已知正方形的面积,我们可以使用面积的公式进行计算:面积=边长²=64cm²。
两边开平方即可得到边长:边长=√64cm=8cm。
例题4:一个圆的面积是12.56cm²,求其半径。
解析:已知圆的面积,我们可以使用面积的公式进行计算:面积=π×半径²=12.56cm²。
解方程得到半径的值:半径=√(12.56cm²/π)≈2cm。
例题5:一个梯形的底边长是4cm,上底长是8cm,高是6cm,求其面积。
解析:已知梯形的底边长、上底长和高,我们可以使用面积的公式进行计算:面积=(底边长+上底长)×高÷2=(4cm+8cm)×6cm÷2=36cm²。
通过以上例题可以看出,等面积法解题时可以根据已知条件选择适当的几何形状,并利用对应的公式去计算未知的数值。
在解题过程中,我们还需要熟练掌握各类几何形状的面积和周长公式,以及一些常见的数学运算规律,比如开平方、解方程等。
除了以上给出的例题,还有许多其他类型的等面积法题目,比如三角形、平行四边形、菱形等等。
解题时我们需要根据题目给出的条件和要求,找到适合的几何形状,并运用相应的公式求解。
初中数学几何模型(九)面积模型
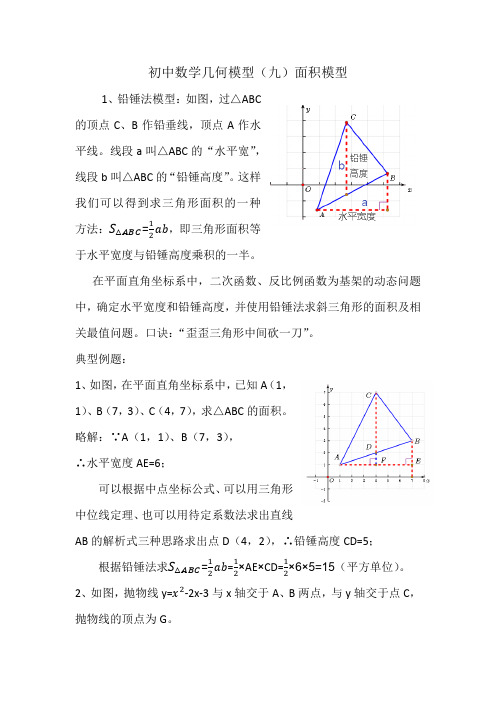
初中数学几何模型(九)面积模型1、铅锤法模型:如图,过△ABC的顶点C、B作铅垂线,顶点A作水平线。
线段a叫△ABC的“水平宽”,线段b叫△ABC的“铅锤高度”。
这样我们可以得到求三角形面积的一种方法:S△ABC=12ab,即三角形面积等于水平宽度与铅锤高度乘积的一半。
在平面直角坐标系中,二次函数、反比例函数为基架的动态问题中,确定水平宽度和铅锤高度,并使用铅锤法求斜三角形的面积及相关最值问题。
口诀:“歪歪三角形中间砍一刀”。
典型例题:1、如图,在平面直角坐标系中,已知A(1,1)、B(7,3)、C(4,7),求△ABC的面积。
略解:∵A(1,1)、B(7,3),∴水平宽度AE=6;可以根据中点坐标公式、可以用三角形中位线定理、也可以用待定系数法求出直线AB的解析式三种思路求出点D(4,2),∴铅锤高度CD=5;根据铅锤法求S△ABC=12ab=12×AE×CD=12×6×5=15(平方单位)。
2、如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C,抛物线的顶点为G。
(1)求△ABC和△BCG的面积;(2)若点D在直线BC下方抛物线上运动,求△BCD面积的最大值。
(3)若点D在直线BC下方抛物线上运动,求四边形ACDB面积的最大值。
2、等积模型:用不同方法表示同一个图形的面积,结果相等。
(1)当所表示的图形是“规则”图形时,不同的方法指的是:①直接用面积公式表示;②用其他图形面积的和或差表示。
(2)当所表示的图形是“不规则”的图形时,不同方法指的是:用割补法来表示。
典型例题:1、在Rt△ABC中,∠C=90°,CD是斜边上的高,用直角三角形的三边表示斜边上的高CD。
解:∵S △ABC =12ch ,S △ABC =12ab ,∴12ch =12ab ,∴h=ab c。
结论:直角三角形斜边上的高等于两直角边的乘积除以斜边。
2、(1)如图①,已知△ABC 中,AB=AC ,点P 是BC 上的一点,PN ⊥AC 于点N ,PM ⊥AB 于点M ,CG ⊥AB 于点G ,求证:CG=PM+PN 。
初中数学面积法的个口诀大全

初中数学面积法的个口诀大全在初中数学学习中,掌握和运用面积计算方法是非常重要的一项基础技能。
为了帮助同学们更好地记忆和理解面积计算方法,今天我给大家整理了一份初中数学面积法的个口诀大全。
希望通过这些简单易记的口诀,同学们可以在数学学习中取得更好的成绩。
一、平行四边形的面积计算口诀口诀:底乘高就能解难题,顶行底斜不亏损。
解释:平行四边形的面积等于底边乘以高,顶边跟底边不影响面积。
二、三角形的面积计算口诀口诀:底高除以二,三角形叼起来。
解释:三角形的面积等于底边乘以高再除以2。
三、长方形的面积计算口诀口诀:长乘以宽,长方形牛。
解释:长方形的面积等于长乘以宽。
四、正方形的面积计算口诀口诀:边长平方,正方形香。
解释:正方形的面积等于边长的平方。
五、梯形的面积计算口诀口诀:上下底相加 × 高除以二,梯形面积好搞定。
解释:梯形的面积等于上底加下底的和乘以高再除以2。
六、圆的面积计算口诀口诀:半径平方× π,圆面积该死简单。
解释:圆的面积等于半径的平方乘以π。
七、扇形的面积计算口诀口诀:扇形面积等于弓形(弧)面积除以360度。
解释:扇形的面积等于弧形的面积除以360度。
八、正多边形的面积计算口诀口诀:正多边形的面积等于边长的平方乘以边数除以4乘以tan(180度除以边数)。
解释:正多边形的面积可以通过边长的平方乘以边数除以4乘以tan(180度除以边数)来计算。
九、不规则图形的面积计算口诀口诀:通过拆分成各种可以计算的图形,再进行面积计算。
解释:对于不规则图形,可以通过将其拆分成各种可以计算的图形(如矩形、三角形等),然后计算各个形状的面积,最后将各个形状的面积相加得到整个不规则图形的面积。
通过以上口诀,相信同学们对初中数学面积计算方法有了更深的理解。
掌握这些口诀后,同学们在解题过程中可以更加迅速准确地计算出不同形状图形的面积。
在平时的数学学习中,同学们也要多加练习,熟练掌握不同图形的面积计算方法,提高自己的运算能力。
初中数学重点梳理:面积问题的解决方法
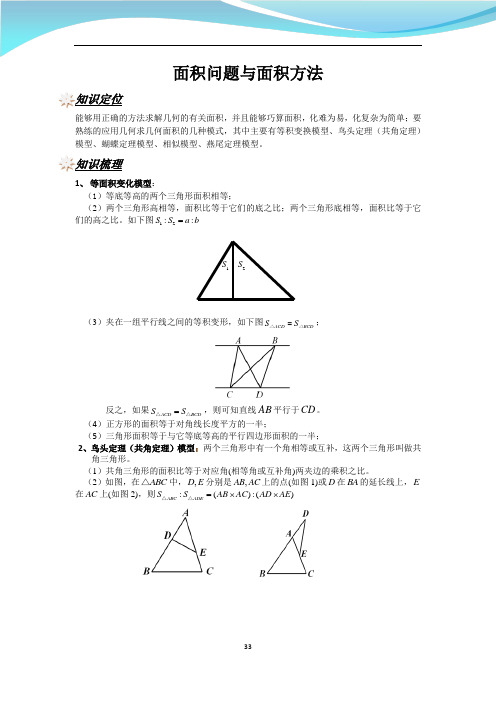
面积问题与面积方法知识定位能够用正确的方法求解几何的有关面积,并且能够巧算面积,化难为易,化复杂为简单;要熟练的应用几何求几何面积的几种模式,其中主要有等积变换模型、鸟头定理(共角定理)模型、蝴蝶定理模型、相似模型、燕尾定理模型。
知识梳理1、 等面积变化模型:(1)等底等高的两个三角形面积相等;(2)两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如下图12::S S a b =(3)夹在一组平行线之间的等积变形,如下图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD 。
(4)正方形的面积等于对角线长度平方的一半;(5)三角形面积等于与它等底等高的平行四边形面积的一半;2、鸟头定理(共角定理)模型:两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
(1)共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
(2)如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△1S 2S3、蝴蝶定理模型:任意四边形中的比例关系。
蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
① 1243::S S S S =1324S S S S ⨯=⨯ ② ()()1243::AO OC S S S S =++ 4、相似模型:相似三角形:相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:(1)相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; (2)相似三角形的面积比等于它们相似比的平方。
初中数学-面积问题与面积方法

面积问题与面积方法[赛点突破]1.利用面积关系解决几何问题,古已有之,最典型的例子就是勾股定理的许多采用面积割补的证明。
在数学竞赛中,有些问题是要求出指定图形的面积,也有些问题从表面上看似乎不直接涉及到面积,但若用等积变换与面积法去解答,往往会收到事半功倍的效果。
在运用等积变换与面积法时,常常用到以下的公式和定理。
2.ABC ∆中,设a h 为a 边上的高,R 、r 分别为ABC ∆外接圆、内切圆的半径,1()2p a b c ,则11sin 22ABCa Sah ab C ()()()rp p p a p b p c22sin sin sin 4abcR A B CR三角形的面积公式形式多样,注意根据问题需要灵活选取。
3.(1)相似三角形面积的比等于相似比的平方;(2)等底(或等高)的三角形的面积比等于其所对应的高(或底)的比。
4.共角定理若ABC 与'''A B C 相等或互补,则'''''''ABC A B C S AB BCS A B B C 。
5.共边定理如图,若直线AB 与PQ 相交于M ,则PAB QABS PMSQM。
ABPQMABPM Q[范例解密]例1 已知:如图,P 是△ABC 中BAC 平分线上的任一点,过C 作CE ∥PB 交AB 的延长线于E ,过B 作BF ∥PC 交AC 的延长线于F.求证:BECF 。
分析:利用角平分线性质得到距离相等,结合等底等高的两个三角形面积相等,将问题转化为等积问题。
证明:连结PE 、PF ∵ CE ∥PB,BF ∥PC ∴ ,= =PBEPBCPCFPBCS S SS∴ =PBE PCFSS又∵ P 是BAC 平分线上的点∴ P 到BE 及CF 的距离相等即PBE 的边BE 上的高等于PCF 的边CF 上的高∴ BE CF评注:解决本题的关键是运用“平行得等积”。
初中数学面积计算口诀

初中数学面积计算口诀一.求几何图形的面积有“三板斧”(1)直接用三角形,特殊四边形,圆,扇形的面积公式来求。
(2)间接割补法,把不规则图形面积通过割补、运动、变形转化为规则易求图形面积的和或差。
(3)特殊求法,即利用相似图形的面积比等于相似比的平方,等底(等高)的三角形面积比等于高(底)比的性质来解。
其次有些乘法公式、勾股定理、三角形的一边平行四边形的比例式等性质,也可用面积法来推导。
二.面积法是什么?运用面积关系解决平面几何体的方法,称为面积法。
它是几何中常用的一种方法。
特点是把已知和未知各量用面积公式联系起来,通过运算达到求证的结果。
所以用面积法来解几何题,几何元素之间关系会变成数量之间的关系。
这个时候,问题就化繁为简了,只需要计算,有事甚至可以不添置补助线就迎刃而解了!此外,用面积法还可以用来求线段长,证明线段相等(不等),角相等,比例式或等积式,求线段比等。
虽然这些几乎都可以用其他方法来解决,但是面积法无疑是一种更直接、简易、有效的方法。
三.面积法的常用理论口诀1.三角形的中线把三角形分成两个面积相等的部分。
2.同底同高或等底等高的两个三角形面积相等。
3.平行四边形的对角线把其分成两个面积相等的部分。
4.同底(等底)的两个三角形面积的比等于高的比。
同高(或等高)的两个三角形面积的比等于底的比。
5.三角形的面积等于等底等高的平行四边形的面积的一半。
6.三角形的中位线截三角形所得的三角形的面积等于原三角形面积的1/47.三角形三边中点的连线所成的三角形的面积等于原三角形面积的1/48.有一个角相等或互补的两个三角形的面积的比等于夹角的两边的乘积的比。
四.面积法的常用解题思路1.分解法:通常把一个复杂的图形,分解成几个三角形。
2.作平行线法:通过平行线找出同高(或等高)的三角形。
3.利用有关性质法:比如利用中点、中位线等的性质。
4.还可以利用面积解决其它问题。
初中数学几何图形面积计算的方法与练习

初中数学几何图形面积计算的方法与练习在初中数学的学习中,几何图形面积的计算是一个重要的部分。
它不仅是考试中的常见考点,更是培养我们逻辑思维和空间想象能力的有效途径。
接下来,让我们一起深入探讨一下初中数学中几何图形面积计算的方法,并通过一些练习来巩固所学。
一、常见几何图形面积计算公式1、三角形三角形的面积计算公式为:面积=底×高÷2。
这里的底和高是相互对应的,需要注意的是,同一个三角形可以有不同的底和高,选择不同的底和高计算时,要确保底和高的对应关系正确。
2、矩形(长方形)矩形的面积等于长乘以宽。
3、正方形正方形的面积等于边长的平方。
4、平行四边形平行四边形的面积等于底乘以高。
5、梯形梯形的面积=(上底+下底)×高÷2 。
6、圆形圆的面积=π×半径的平方。
其中,π通常取 314。
二、面积计算方法1、直接运用公式法这是最基本也是最常见的方法。
当我们遇到规则的几何图形,如矩形、正方形、三角形等,且已知相关的边长、底、高等数据时,直接代入相应的公式即可求出面积。
例如:一个矩形的长为 5 厘米,宽为 3 厘米,其面积为 5×3 = 15平方厘米。
2、割补法对于一些不规则的几何图形,我们可以通过割补的方法,将其转化为我们熟悉的规则图形,然后再计算面积。
比如,一个不规则的四边形,我们可以通过添加辅助线,将其分割成两个三角形或一个三角形和一个梯形,分别计算出各部分的面积,再相加得到整个四边形的面积。
3、等积变形法利用图形的面积不变性质,通过对图形的平移、旋转、对称等变换,将图形转化为易于计算面积的形式。
例如,两个三角形等底等高,则它们的面积相等。
我们可以利用这一性质,对图形进行变形,从而更方便地计算面积。
4、整体减部分法当一个图形由几个部分组成时,我们可以先求出整体的面积,再减去不需要的部分的面积,从而得到所求图形的面积。
比如,一个大正方形中包含一个小正方形,求阴影部分的面积,就可以用大正方形的面积减去小正方形的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F GE 图 2ACBD 面积法1、常见规则图形的面积公式;2、等积定理;3、面积比定理。
A 卷1、如图1,凸四边形ABCD 的四边AB 、BC 、CD 、DA 的长分别是3、4、12、13,︒=∠90ABC ,则四边形ABCD 的面积为 .答案:36考点:勾股定理;勾股定理的逆定理。
分析:连接AC ,在ABC Rt ∆中,已知AB 、BC 根据勾股定理可以求得5=AC ,在ACD ∆中,222AD CD AC =+,根据勾股定理的逆定理确定ACD ∆为直角三角形,四边形ABCD 的面积为ACD ∆和ABC Rt ∆面积之和。
解答:连接AC ,在ABC Rt ∆中,3=AB ,4=BC ,则 522=+=BC AB AC又∵222AD CD AC =+ ∴ACD ∆为直角三角形∴ABC Rt ∆的面积为64321=⨯⨯,ACD Rt ∆的面积为3012521=⨯⨯∴四边形ABCD 的面积为ACD ∆和ABC Rt ∆面积之和,36630=+=S 故答案为 36.点评:本题考查了勾股定理在直角三角形中的运用,考查了直角三角形面积的计算,本题中判定ACD ∆为直角三角形是解题的关键。
2、如图2,已知ABC ∆中,D 、E 、F 、G 均为BC 边上的点,且CG BD =,BD GF DE 21==, DE EF 3=,若1=∆ABC S ,则图中所有三角形的面积之和为 .答案:7考点:三角形面积与底的正比关系。
分析:如图所示的所有三角形都具有相等的高,于是可将计算所有三角形面积之和的问题转化为计算BC 上所有线段长度之和的问题。
解答:因为所有线段长之和是BC 的n 倍 ∴图中所有三角形面积之和就是ABC S ∆的n 倍 设1==GF DE ,则2==CG BD ,3=EF ,9=BC ∴图中共有1554321=++++个三角形 则它们在线段BC 上的底边之和为:图 1ACBDF E图 3ACBDECFA BD()()()()[]()()[]EF FG DF EG DE DG GC BG FC BF EC BE DC BD BC ++++++++++++++ 6333559=+⨯+⨯=由此可知BC 上所有线段之和63是BC =9的7倍 ∴图中所有三角形面积之和等于ABC S ∆的7倍. 已知1=∆ABC S ,故图中所有三角形的面积之和为7. 故答案为:7点评:此题主要考查学生对三角形面积的理解和掌握,解答此题的关键是图中所有三角形都具有相等的高,通过转化的思想,找出解决问题的捷径。
3、如图3,□ABCD 的面积是m ,点E 、F 分别平分AB 、BC ,则_______=∆DEF S .答案:m 83解答:不妨设□ABCD 为长方形,如图,则有m BC AD ==,1==CD AB∴m m m m m S S S S S DCF BEF ADE ABCD DEF 83484=---=---=∆∆∆∆四边形 4、如图4,已知边长为a 的正方形ABCD ,E 为AD 的中点,P 为CE 的中点,那么BPD ∆的面积的值是 .答案:281a考点:正方形的性质;三角形的面积;勾股定理。
分析:观察图形可以发现BCP CDP BCD BPD S S S S ∆∆∆∆--=,所以要求BPD ∆的面积分别计算BPD S ∆、BCD S ∆、CDP S ∆、BCP S ∆即可。
解答:过P 作CD PF ⊥,BC PG ⊥,则AD PF //,CG PF =,CF PG = 观察图形可以发现BCP CDP BCD BPD S S S S ∆∆∆∆--= ∴22121a CD BC S BCD=⋅=∆ 28121a PF CD S CDP =⋅=∆ 24121a PG BC S BCP =⋅=∆ ∴2281418121a a S BPD =⎪⎭⎫⎝⎛--=∆点评:本题考查了正方形各边长相等、各内角为直角的性质,考查了三角形面积的计算,本题中正确计算BPD S ∆、BCD S ∆、CDP S ∆、BCP S ∆是解题的关键。
G FPE 图 4A C BDO图 5ACD5、如图5,四边形ABCD 的对角线AC 和BD 相交于O 点,如果5=∆ABD S ,6=∆ABC S ,10=∆BCD S ,那么_________=∆OBC S .答案:4考点:三角形的面积。
分析:先设出一个三角形的面积:AOB ∆的面积是x s =1,再用代数式表示出图中其它三角形的面积,利用中间桥OCOA得出方程,进一步求出结果。
解答:设AOB ∆的面积是x s =1,则ADO ∆的面积是x s -=52,BOC ∆的面积是x s -=63,DOC ∆的面积是()x x s +=--=46104∵ABO ∆的边OA 上和BOC ∆的边上的高相等 ∴OC OA s s =31,同理OCOA s s =42 ∴4231s s s s = 即xxx x +-=-456,解得:2=x ∴426=-=∆OBC S点评:解此题的关键是灵活运用三角形的面积公式,等高时面积比等于边之比,从而转化成解方程,求出未知数的值。
6、(第5届“希望杯”邀请赛题)在ABC ∆的三边AB 、BC 、CA 上,分别取AD 、BE 、CF ,使AB AD 41=,BC BE 41=,AC CF 41=,则DEF ∆的面积是ABC ∆的面积的( ) A 、41 B 、83 C 、85 D 、167 答案:A考点:三角形的面积。
分析:连接AE .根据三角形的面积公式求得BDE ∆和ABE ∆的面积比,ABE ∆和ABC ∆的面积比,进而求得BDE ∆和ABC ∆的面积比,同理求得ECF ∆、ADF ∆和ABC ∆的面积比,最后求解。
解答:如图,连接AE ∵AB AD 41=,BC BE 41= ∴ABE BDE S S ∆∆=43,ABC ABE S S ∆∆=41∴ABC BDE S S ∆∆=163同理可得:ABC CEF S S ∆∆=163,ABC ADF S S ∆∆=163所以ABC DEF S S ∆∆=167F E CABDS 2 图 6A CBS 1 S 4S 3 甲DAC BE 乙DACBEGF 丙DACB EGF 丁D ACBEG F 戊D ACBE点评:此题考查了根据三角形的面积公式求三角形的面积比的方法。
7、(2004年第15届“希望杯”初二年级竞赛题)如图6,在直角扇形ABC 内,分别以AB 和AC 为直径作半圆,两条半圆弧相交于点D ,整个图形被分成S 1,S 2,S 3,S 4四部分,则S 2和S 4的大小关系是( )A 、42S SB 、42S S =C 、42S SD 、无法确定 答案:B考点:扇形面积的计算。
分析:设a AC AB 2==,由42S S S S S AC AB ACB +--=半圆半圆扇形S2=S ,根据扇形和圆的面积公式分别计算出它们的面积就可得到2S 和4S 的大小关系。
解答:设a AC AB 2==,根据题意得: 42S S S S S AC AB ACB +--=半圆半圆扇形()4422212360290S S a a =+⨯⨯⨯-⨯=ππ故42S S = 故选B .点评:本题考查了扇形的面积公式:3602R n S π=,其中n 为扇形的圆心角的度数,R 为圆的半径),或R S 21=, 为扇形的弧长,R 为半径。
8、在矩形ABCD 中,2=AB ,1=BC ,则矩形的内接三角形的面积总比数( )小或相等。
A 、74 B 、1 C 、82 D 、81 答案:B解答:需分类讨论,如图,显然图(甲)及图(乙)中内接三角形面积为1,如图(丙)、(丁)、(戊)中EFG ∆的面积显然小于1,综上所述,故选B .B 卷9、(第11届“希望杯”邀请赛)在正方形ABCD 中,3=AB ,点E 、F 分别在BC 、CD 上,且︒=∠30BAE ,︒=∠15DAF ,则AEF ∆的面积为 .答案:33-考点:正方形的性质;全等三角形的判定与性质;旋转的性质。
分析:将ADF ∆绕A 点顺时针方向旋转90°到ABG ∆的位置,得到ABG ∆,得≅∆AEF AEG ∆,要求AEF ∆的面积求AEG ∆即可,且AB 为底边上的高,EG 为底边。
解答:将ADF ∆绕A 点顺时针方向旋转90°到ABG ∆的位置∴AF AG =,︒=∠=∠15FAD GAB ,︒=︒+︒=∠453015GAE ,()︒=︒+︒-︒=∠45153090EAF ∴FAE GAE ∠=∠ 又AE AE = ∴AEG AEF ∆≅∆∴EG EF =,︒=∠=∠60AEG AEF 在ABE Rt ∆中,3=AB ,︒=∠30BAE ∴︒=∠60AEB ,130tan =︒=AB BE在EFC Rt ∆中,()︒=︒+︒-︒=∠606060180FEC ,13-=-=BE BC EC ,()132-=EF ∴()132-=EG ,3321-=⋅=∆AB EG S AEG ∴33-==∆∆AEG AEF S S点评:本题考查了全等三角形的证明,考查了正方形各边各内角均相等的性质,解本题的关键是巧妙地构建ABG ∆,并且求证AEG AEF ∆≅∆.10、(2005年第16届“希望杯”初二年级竞赛题)已知ABC ∆三条高的比是5:4:3,且三条边的长均为整数,则ABC ∆的一条边长可能是( )A 、10B 、12C 、14D 、16 答案:B考点:约数与倍数;三角形的面积。
专题:推理填空题。
分析:根据题意,设三边为X ,Y ,Z ,运用三角形面积公式得到321212121Za Ya Xa ==,据给出的已知条件得出三边之比,既而得出答案。
解答:解:设三边为X ,Y ,Z 三条对应的高为1a ,2a ,3a 可得:321212121Za Ya Xa == GFCD E 图 11AB已知5:4:3::321=a a a 可得12:15:20::=Z Y X 因为三边均为整数又4个答案分别是10,12,14,16 所以答案应该是12 故选B .点评:此题考查了学生对公倍数和三角形面积的理解和掌握。
关键是运用三角形面积公式得到321212121Za Ya Xa ==,据给出的已知条件得出三边之比。
11、(第14届“希望杯“邀请赛)如图7,将ABC ∆的三边AB ,BC ,CA 分别延长至B ',C ',A ',且使AB B B =',BC C C 2=',AC A A 3=',若1=∆ABC S ,那么C B A S '''∆是( )A 、15B 、16C 、17D 、18 答案:D考点:三角形的面积。
