第10章 弹性力学轴对称问题的有限元法简介
三维问题有限元分析(包括轴对称问题)

建立每个有限元的平衡方程,通过求解这些方程来得到近似解。
离散化
将连续的问题离散化,将整个求解域划分为有限个小的子域(称为有限元),每个子域上定义节点。
有限元方法的基本原理
解方程
通过求解整体矩阵的方程,得到各个节点的值,从整体矩阵,用于表示整个求解域上的问题。
详细描述
三维弹性力学问题的有限元分析
总结词
详细描述了三维热传导问题有限元分析的基本原理、方法和应用。
详细描述
三维热传导问题是有限元分析的另一个重要领域,主要研究热量在物体中的传递和分布。通过将连续的物体离散化为有限个小的单元,可以建立单元之间的热量传递关系,从而得到整个物体的温度分布。这种方法广泛应用于工程领域,如传热学、热能工程等。
边界条件处理
轴对称问题的有限元方法
轴对称问题有限元分析的实现流程
建立系统方程
根据有限元近似解法,将微分方程转化为离散化的系统方程。
划分网格
根据问题的几何形状和特点,将求解区域划分为一系列离散的网格单元。
建立数学模型
根据实际问题,建立相应的数学模型,包括物理方程、边界条件和初始条件。
求解系统方程
采用适当的数值方法(如直接法、迭代法等),求解离散化的系统方程,得到每个离散单元上的近似解。
轴对称问题具有旋转对称性,即其解在绕对称轴旋转时保持不变。
轴对称问题的定义和特性
特性
定义
将连续的物理问题离散化为有限个离散的单元,每个单元具有特定的形状和大小。
离散化
在每个离散单元上,使用近似函数来逼近真实解。常用的近似函数包括多项式、样条函数等。
近似解法
对于轴对称问题,边界条件通常与对称轴相关。需要对边界条件进行特殊处理,以确保离散化后的系统方程满足原始问题的约束。
弹性有限元法及应用

Ty Tz
,所受的面积力
Tx Tx T y Ty T z T z
设应力边界的外法线为N,其方向余弦为 l m n ,则:
Tx l x s m xy n xz s s Ty l yx s m y s n yz s T l m n zx s zy s z s z
29
1 有限元法的基础
V wj
V wj
权函数
就可得到近似的积分形式
w A( Na )d w B( Na )d 0
T j T j j
T
w Rd w Rd 0
j
T
重庆大学材料学院
30
1 有限元法的基础
w A( Na )d w1 B( Na )d 0
28
1 有限元法的基础
(2)等效积分形式的近似:加权余量法
对于微分方程和边界条件所表达的物理问题,未知场函 数可以采用试探函数来表示,去求近似解。
u u N i ai Na
i 1
n
N是已知函数,a是待定系数
显然
A( Na ) R B( Na ) R
残差也称为余量
重庆大学材料学院
以矩阵形式表示为:
L σ f 0
T
应
力
外
力
重庆大学材料学院
18
1 有限元法的基础
其中,
x 0 0 L y 0 z 0 0 z 0 y x
力的平衡描述
方程:(针对微体dxdydz) 物理本构方程
力的平衡描述
4 弹性力学轴对称问题的有限元法

4. 彈性力學軸對稱問題的有限元法本章包括以下內容:4.1用虛功方程建立有限元方程 4.2三結點單元位移函數 4.3三結點單元剛度矩陣 4.4載荷移置4.5軸對稱分析舉例4.1用虛功方程建立有限元方程物體的幾何形狀、約束情況及所受的外力都對稱於空間的某一根軸,因此在物體中通過該軸的任何平面都是對稱面,所有應力、應變和位移也對稱於該軸,這類問題稱為軸對稱問題。
研究軸對稱問題時通常採用圓柱坐標系(r ,θ,z ),以z 軸為對稱軸。
圖4.1受均布內壓作用的長圓筒如圖4.1所示的受均布內壓作用的長圓筒,通過Z 軸的一個縱截面就是對稱面。
由於對稱性,軸對問題共有4個應力分量:⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=zrz r τσσσσθ}{ (4-1)其中r σ表示沿半徑方向的正應力,稱為徑向應力;θσ表示沿θ方向的正應力,稱為環向應力或切向應力;z σ表示沿z 方向的正應力,稱為軸向應力;zr τ表示在圓柱面上沿z 方向作用的剪應力。
同樣,軸對稱問題共有4個應變分量:⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=zrz r γεεεεθ}{ (4-2)其中r ε表示沿半徑方向的正應變,稱為徑向正應變;θε表示沿θ方向的正應變,稱為環向正應變或切向正應變;z ε表示沿z 方向的正應變,稱為軸向正應變;zrγ表示沿r 和z方向的剪應變。
在軸對稱問題中,彈性體內任意一點上,不存在切向位移,只存在徑向位移u 和軸向位移w ,兩個位移分量表示為,⎭⎬⎫⎩⎨⎧=w u f }{(4-3)在討論彈性力學平面問題的有限元法時,我們先由將彈性體劃分為有限個單元的組合體,由虛功方程得到單元剛度矩陣,集成後得到整體剛度矩陣。
在這裏,我們用虛功方程直接得到軸對稱問題的有限元列式。
由虛功方程可得,外力虛功等於內力虛功或虛應變能, ds p f dxdydz F f dxdydz TsTT}{}{}{}{}{}{***⎰⎰⎰⎰⎰⎰⎰⎰+=σε(4-4)其中{F}為體力,{p}為面力。
弹性力学问题的有限元法_轴对称问题

A
Wi U j W j U m Wm
S
T
2 r p 0
2013-7-24
11
Ni e R 2π A 0
0 Ni
Nj 0
0 Nj
Nm 0
0 2r rdrdz Nm 0
T
使用
Ni Li (i, j, m) r Lr L r L r i i j j m m , 得到 2 A ! ! ! Li L j Lmdrdz z ! A
Ri
当
e
0 πA 2ri rj rm 6
(i, j, m)
rc ri r j rm, 则有
1 Wi W j Wm 2πArc 3
2013-7-24 13
面积力 沿单元的jm面
Ni e R 2π A 0 0 Ni Nj 0 0 Nj Nm 0
L j q q 0
0 L j q rdS Nm 0
T
z
m
j i r 2013-7-24
q
14
在 jm面 ,
z
m j i r q
整合,
Ni 0, N j L j , N m Lm r L j rj Lm rm ! ! l Li L j dS l 1!
(i, j , m)
u f N e N i I 2 w
N j I2
N m I 2
e
备注:
平面三角形单元 轴对称三角形单元
x, y
r, z
4
有限元法PPT课件

如何克服局限性
改进模型
通过更精确地描述实际 结构,减少模型简化带
来的误差。
优化网格生成
采用先进的网格生成技 术,提高网格质量,降
低计算误差。
采用高效算法
采用并行计算、稀疏矩 阵技术等高效算法,提
高计算效率。
误差分析和验证
对有限元法的结果进行误 差分析和验证,确保结果
的准确性和可靠性。
05 有限元法的应用实例
有限元法ppt课件
目 录
• 引言 • 有限元法的基本原理 • 有限元法的实现过程 • 有限元法的优势与局限性 • 有限元法的应用实例 • 有限元法的前沿技术与发展趋势 • 结论
01 引言
有限元法的定义
01
有限元法是一种数值分析方法, 通过将复杂的结构或系统离散化 为有限个简单元(或称为元素) 的组合,来模拟和分析其行为。
有限元法在流体动力学分析中能够处理复杂的流体流动和 压力分布。
详细描述
通过将流体域离散化为有限个小的单元,有限元法能够模 拟流体的流动、压力、速度等状态,广泛应用于航空、航 天、船舶等领域。
实例
分析飞机机翼在不同飞行状态下的气动性能,优化机翼设 计。
热传导分析
总结词
有限元法在热传导分析中能够处理复杂的热传递过程。
实例
分析复杂电磁设备的电磁干扰问题,优化设备性能。
06 有限元法的前沿技术与发 展趋势
多物理场耦合的有限元法
总结词
多物理场耦合的有限元法是当前有限元法的重要发展方向, 它能够模拟多个物理场之间的相互作用,为复杂工程问题提 供更精确的解决方案。
详细描述
多物理场耦合的有限元法涉及到流体力学、热力学、电磁学 等多个物理场的耦合,通过建立统一的数学模型,能够更准 确地模拟多物理场之间的相互作用。这种方法在航空航天、 能源、环境等领域具有广泛的应用前景。
有限元分析理论(弹性力学)

3)可以适应不连续的边界条件和载荷条件。 4)各单元的计算程式都相同,便于实现规范化和在计算机上统一编程,容易将程序编成模 块式结构。 5)有限元法最后得到的大型联立方程组的系数是一个稀疏矩阵,其中所有元素都分布在矩 阵的主对角线附近,且是对称的正定矩阵,方程间的联系较弱。这种方程计算工作量小,稳定 性好,便于求解,占用的计算机内存也少。 有限元法的这些特点,正好可以克服工程科学计算中所遇到的许多困难。对于已有方程的 物理问题,主要是因为集合形状复杂、边界条件复杂、本构关系复杂而解不出来。利用有限元 法离散化的手段,用各种小单元来适应这些复杂多变的因素,用分块近似插值函数来逼近全域 上的连续函数,问题就变得容易了。
目前,有限元法以远远超出了原有的应用范畴,已从弹性力学扩展到了弹塑性力学、岩石 力学、地质力学、流体力学、传热学、气动力学、计算物理学、海洋工程、大气污染等各种学 科和应用领域,取得了出人意料的成功。
在机械工程领域内,可以用有限元法解决的问题有: 1)包括杆、梁、板、壳、三维块体、二维平面、管道等各种单元的各种复杂结构的静力分 析。 2)各种复杂结构的动力分析,包括频率、振型和动力响应计算。 3)整机(如水压机、汽车、发电机、泵、机床)的静、动力分析。 4)工程结构和机械零部件的弹塑性应力分析及大变形分析。 5)工程结构和机械零件的热弹性蠕变、粘弹性、粘塑性分析。 6)大型工程机械轴承油膜计算等。
弹性力学空间轴对称问题有限元法

7.1 弹性力学空间轴对称问题的描述
一、柱坐标系
由于轴对称性质,采用柱坐标系( r、θ、z ) 分析轴对称问题
w r
u z
• 尽管点的位移发生在平面内,但是,对于垂直于 平面的线元素却存在着伸缩的可能,因此,轴对 称问题的环向应变不为零。
2)几何方程
• 对于周向应变,尽管不存在周向位移,但由于A点 发生径向位移后,它与轴的距离变为,从而导致 产生周向的变形,如图所示,则产生周向应变为
(r u)d rd rd
Ke
B
eT
e
DB
dv
Ve
Fbe NeTf dv
Ve
Fqe NeT f dS Se
Fe 0
BeT0 dv
Ve
Fe 0
BeTD0 dv
Ve
Ke 2
BeT
e
DB
rdrdz
e
Fbe 2 NeTf rdrdz e
Fqe 2 NeT f rds Se
Fe 0
2
BeT0 rdrdz
u r
u
r
z
r u r w
rz
z
w
u
r z
7.1 弹性力学空间轴对称问题的描述 三、基本方程
(2)应力应变关系 —物理方程
1
1 1
0
r
σ
z rz
E 1 1 1
2
1 1
1
1
1
1
有限元法简介.ppt

四边形单元
u4 v4
4 u1
v1
1
u2 v2 2
(82)
u3
v3 3
u2 v2
2
2节点
2×3
3个节点自由度
用处:平面刚架
3节点
3×2
2个节点自由度
用处:平面应力
4节点 2个节点自由度
4×2
用处:平面应力
轴对承单元
板单元 (板弯曲)
三维
三棱柱 (四面体单元)
节点数:3
处理问题对象:
uv1 1
节点自由度:2 轴对承问题
...... ......
......
......
......
......
...... ...... ...... ......
......
......
...... ...... ...... ......
......
0
...... 0
...... [K63]4
1
常数项
xy x2 xy y2
一次项 二次项
x3 x2 y xy2 y3 三次项
x4 x3 y x2 y 2 xy3 y 4 四次项
实例分析 对单元1进行分析
取位移模式 u=α 0+ α 1x 1点: x=0 u=u1 2点: x=l1 u=u2
l1
l2
P
A1
A2
1
2
1
2
3
划分单元
uu12
0 0
ANSYS
预备知识:
1.线性代数(矩阵加、减、乘、除、秩、逆、 分块等)
2.弹性力学
轴对称问题的有限元分析

第1节基本知识本节的有限元对象为轴对称问题,目的是学习将3D问题转化为2D问题分析的轴对称方法,涉及如何选取轴对称单元、建模规律、载荷的施加方法和后处理技术。
一、轴对称问题的定义轴对称问题是指受力体的几何形状、约束状态,以及其它外在因素都对称于某一根轴(过该轴的任一平面都是对称面)。
轴对称受力体的所有应力、应变和位移均对称于这根轴。
二、用ANSYS解决2D轴对称问题的规定用ANSYS解决2D轴对称问题时,轴对称模型必须在总体坐标系XOY平面的第一象限中创建,并且Y轴为轴旋转的对称轴。
求解时,施加自由约束、压力载荷、温度载荷和Y方向的加速度可以像其它非轴对称模型一样进行施加,但集中载荷有特殊的含义,它表示的是力或力矩在360°范围内的合力,即输入的是整个圆周上的总的载荷大小。
同理,在求解完毕后进行后处理时,轴对称模型输出的反作用力结果也是整个圆周上的合力输出,即力和力矩按总载荷大小输出。
在ANSYS中,X方向是径向,Z方向是环向,受力体承载后的环向位移为零,环向应力和应变不为零。
常用的2D轴对称单元类型和用途见表11-1。
表11-1 2D轴对称常用结构单元列表的高阶单的高阶单在利用ANSYS进行有限元分析时,将这些单元定义为新的单元后,设置单元配置项KEYOPT(3)为Axisymmetric(Shell51和Shell61单元本身就是轴对称单元,不用设置该项),单元将被指定按轴对称模型进行计算。
后处理时,可观察径向和环向应力,它对应的是SX与SZ应力分量,并且在直角坐标系下观察即可。
可以通过轴对称扩展设置将截面结果扩展成任意扇型区域大小的模型,以便更加真实地观察总体模型的各项结果。
轴对称问题有限元分析实例 2D节2第p=1000 N/mF2y611xO61211-1 圆柱筒壳示意图图——圆柱筒的静力分析一、案例1问题,直0.1 m1000 N/m的压力作用,其厚度为如图11-1所示,圆柱筒材质为A3钢,受,并且圆柱筒壳的下部轴线方向固定,其它方向自由,试计算其变形、mm,高度为16 径12径向应力和轴向应力。
弹性力学轴对称问题的有限元法

4. 弹性力学轴对称问题的有限元法本章包括以下内容:4.1用虚功方程建立有限元方程 4.2三结点单元位移函数 4.3三结点单元刚度矩阵 4.4载荷移置4.5轴对称分析举例4.1用虚功方程建立有限元方程物体的几何形状、约束情况及所受的外力都对称于空间的某一根轴,因此在物体中通过该轴的任何平面都是对称面,所有应力、应变和位移也对称于该轴,这类问题称为轴对称问题。
研究轴对称问题时通常采用圆柱坐标系(r ,θ,z ),以z 轴为对称轴。
图4.1受均布内压作用的长圆筒如图4.1所示的受均布内压作用的长圆筒,通过Z 轴的一个纵截面就是对称面。
由于对称性,轴对问题共有4个应力分量:⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=zr z r τσσσσθ}{(4-1)其中r σ表示沿半径方向的正应力,称为径向应力;θσ表示沿θ方向的正应力,称为环向应力或切向应力;z σ表示沿z 方向的正应力,称为轴向应力;zr τ表示在圆柱面上沿z 方向作用的剪应力。
同样,轴对称问题共有4个应变分量:⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=zr z r γεεεεθ}{(4-2)其中r ε表示沿半径方向的正应变,称为径向正应变;θε表示沿θ方向的正应变,称为环向正应变或切向正应变;z ε表示沿z 方向的正应变,称为轴向正应变;zr γ表示沿r 和z 方向的剪应变。
在轴对称问题中,弹性体内任意一点上,不存在切向位移,只存在径向位移u 和轴向位移w ,两个位移分量表示为,⎭⎬⎫⎩⎨⎧=w u f }{(4-3)在讨论弹性力学平面问题的有限元法时,我们先由将弹性体划分为有限个单元的组合体,由虚功方程得到单元刚度矩阵,集成后得到整体刚度矩阵。
在这里,我们用虚功方程直接得到轴对称问题的有限元列式。
由虚功方程可得,外力虚功等于内力虚功或虚应变能, ds p f dxdydz F f dxdydz T sT T }{}{}{}{}{}{***⎰⎰⎰⎰⎰⎰⎰⎰+=σε(4-4)其中{F}为体力,{p}为面力。
弹性力学及其有限元法

弹性力学及有限元分析1、 设试件两定点之间的长度为L 0,其截面积为F 0,加上拉力P 后,L 0 伸长了△L 。
我们把P/ F 0 称为拉伸应力(σ),△L/ L 0 称为拉伸应变(ε),于是有σ=P/ F 0 ,ε= △L/ L 0某种材料的拉伸应力和拉伸应变的比,称为该材料的杨氏模量或弹性模量(E),即 LF PL E ∆==00εσ,弹性模量E 表征了材料的物理性质。
2、 根据力学特性,固体通常分为韧性固体和脆性固体。
首先分析韧性材料,材料在受力变形过程中,明显地有四个特性点划分三各阶段。
a. 弹性阶段,这一阶段的明显特征是,当外力逐渐去掉时,变形也逐渐消失,物体能够恢复到原来的形状,物体的这种性质称为弹性,存在一个应力极限称为弹性极限。
随着外力的消失而消失的变形称为弹性变形;去掉外力后仍然保留的变形称为残余变形或永久变形。
弹性阶段另一个明显特征是,应力与应变保持线性关系。
设受力方向为x 方向,x xE εσ=,这就是简单拉伸时的虎克定律,弹性模量E 为常数,表示应力与应变成正比例。
通常把弹性极限和比例极限规定为一个值。
b. 塑性阶段,超过弹性极限后,材料开始失去弹性,进入塑性阶段,这时产生较大的永久变形,应力应变关系不再是线性的。
当曲线超过s 点(屈服极限)后,材料开始屈服,即在应力几乎不增加的情况下,应变会不断的增加,称s 点为屈服极限;当变形大到一定程度后,材料开始强化,要继续增加变形必须再增加外力,到达b 点后产生颈缩。
从弹性极限到b 的变形范围统称为塑性阶段,属于塑性力学的研究范畴。
c. 断裂阶段,试件产生颈缩后,开始失去抵抗外力的能力,最后发生断裂,相对于b点的应力称为强度极限。
脆性材料:它的拉伸曲线图没有明显的三个阶段之分,也没有明显的屈服应力点,材料亦不再满足虎克定律。
为了分析上的需要,往往以切线斜率作为弹性模量,即εσd d E =。
如果对脆性固体材料加载,应力应变曲线将沿着OA 上升,若到A 点后即行卸载,应力应变曲线并不沿着原来的途径回复到原点,而是沿着直线AB 下降,当全部载荷卸去之后,试件中尚残存一部分永久变形''ε。
弹性力学有限元法详解

x
4
i1 4
Ni ( ,)xi
y
i1
Ni ( ,) yi
总体坐标系适用于整体结构,局部坐标系只适用于具体某个 单元。
常用的对于平面问题还有八节点等参元,空间问题有八节 点空间等参元,二十节点等参元等 。
第18页,共40页。
3.2 连续体离散化
5.轴对称单元
对于回转结构,如果约束条件和载荷都对称于回转轴,其 应力、应变和位移也都对称于回转轴线,这类应力应变问题称 为轴对称问题 ,通常用柱坐标来描述应力、应变和位移,单元 为实心圆环体,仅截面不同
1
2
ai
(1
0
)
ai (1 0 ) ai (1 0 )
1
2
ai
(1
0
)
(i, j,l,m)
对于平面应变问题:
E
E 1 2
1
第29页,共40页。
3.3 单元分析
2. 单元分析
由虚功原理得:
Fe
K e BT DBdxdyt A
BT DBdxdyt δe
A
Fe Keδe
单元刚度矩阵可分块表示为:
第10页,共40页。
3.2 连续体离散化
3. 薄板弯曲单元和薄板单元
A. 薄板弯曲单元
l
θxi
i
θyi
wi
m
j
四边形弯 曲单元
四边形单元有四个节点,每个节点有三个自由度,主要承 受横向载荷和绕水平轴的弯矩。
第11页,共40页。
3.2 连续体离散化
3.薄板弯曲单元和薄板单元
A. 薄板弯曲单元
m
θxi
对于平面应变问题:
E
E 1 2
轴对称问题有限元法
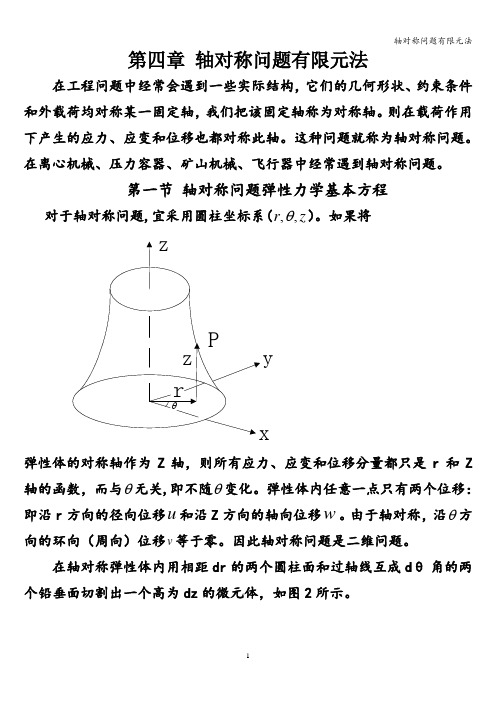
第四章 轴对称问题有限元法在工程问题中经常会遇到一些实际结构,它们的几何形状、约束条件和外载荷均对称某一固定轴,我们把该固定轴称为对称轴。
则在载荷作用下产生的应力、应变和位移也都对称此轴。
这种问题就称为轴对称问题。
在离心机械、压力容器、矿山机械、飞行器中经常遇到轴对称问题。
第一节 轴对称问题弹性力学基本方程对于轴对称问题,宜采用圆柱坐标系(,,r z θ)。
如果将y弹性体的对称轴作为Z 轴,则所有应力、应变和位移分量都只是r 和Z 轴的函数,而与θ无关,即不随θ变化。
弹性体内任意一点只有两个位移:即沿r 方向的径向位移u 和沿Z 方向的轴向位移w 。
由于轴对称,沿θ方向的环向(周向)位移v 等于零。
因此轴对称问题是二维问题。
在轴对称弹性体内用相距dr 的两个圆柱面和过轴线互成d θ角的两个铅垂面切割出一个高为dz 的微元体,如图2所示。
(a )σ(b)沿r 方向作用的正应力r σ称为径向应力 沿θ方向作用的正应力θσ称为环向应力 沿z 方向作用的正应力z σ称为轴向应力 rz 面内的剪应力 zr τ=rz τ 故轴对称弹性体内任意一点的应力分量{}[]Tr z rz θσσσστ=对应的轴对称弹性体内任意一点的应变分量{}[]Tr z rz θεεεεγ=其中r ε ———-—- 沿r 方向径向线应变θε —----— 沿θ方向环向线应变 z ε ---—-- 沿z 方向轴向线应变rz γ-—---— rz 面内的剪应变与平面问题相比,轴对称问题多了一个环向应变θε。
弹性体受载时,点(,,r z θ)产生径向位移u ,使过点(,,r z θ)的周长增加了2()2r u r ππ+-,因而产生相对伸长,即环向应变:2()22r u r u r rθππεπ+-==轴对称问题的几何方程(应变与位移之间的关系)为,,,r z zr u u w w ur r z r zθεεεγ∂∂∂∂====+∂∂∂∂写成矩阵形式{}r z rz u r u rw z u w z r θεεεεγ⎧⎫⎪⎪⎪⎪⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪⎨⎬⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭⎪⎪⎪⎪⎩⎭==∂∂∂∂∂∂+∂∂根据虎克定律,应力与应变的关系为1()r r z Eθεσμσσ⎡⎤⎣⎦=-+ 1()z r Eθθεσμσσ⎡⎤⎣⎦=-+ 1()z z r Eθεσμσσ⎡⎤⎣⎦=-+ 12(1)rz rz rz r G Eμττ+==由上式得[]10111011(1)(1)(12)101112002(1)r z zr r z rz E θθσσσστμμμμεμμεμμμμμεμμμμγμμ⎧⎫⎪⎪⎪⎪=⎨⎬⎪⎪⎪⎪⎩⎭⎡⎤⎢⎥--⎢⎥⎧⎫⎢⎥⎪⎪⎢⎥---⎪⎪⎢⎥⎨⎬+-⎢⎥⎪⎪⎢⎥⎪⎪--⎩⎭⎢⎥-⎢⎥⎢⎥-⎣⎦=(4—2)这里弹性矩阵[D]为[D ]=10111011(1)(1)(12)101112002(1)E μμμμμμμμμμμμμμμμμ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦-----+-----第二节 三角形截面环单元一、 结构离散化离散化轴对称体时,采用的单元是一些圆环。
弹性力学中的有限元法

弹性力学中的有限元法FINITE ELEMENT METHOD同济大学土木工程学院第章第一章弹性力学与有限元弹性力学的任务弹性力学的求解体系弹性力学的解析求解实际科学和工程求解的需求有限单元法弹性力学的求解体系=任意弹性问15个()i i ij u u ,,,1+=ε0,+i j ij X σ题均应满足右边的控制j j j j 2ijij kk ij μεδλεσ2+=方程弹性力学问题的求解困难存在15个未知量,相应地建立了15个基本方程,好像已经完成了弹性力学的任务?!但是,进一步应用就会发现,时至今日,这15个微分方程组的求解在数学上的遇到困难也是非常巨大的。
在随后的100多年的时间里,数学、力学家们为了弹性力学的求解付出了艰苦的劳动和努力。
弹性力学问题的解析求解平面问题的应力函数解法:寻找一个满足双调和方程的应力函数U(亦称Airy应力函数)。
则其应力解答为该应力解答还必须满足应力及位移边界条件。
弹性力学问题的解析求解扭转问题的扭转函数解法:寻找满足泊松方程的扭转函数F(x,y),其应力解为其应力解还必须满足力的边界条件:弹性力学问题的解析求解空间轴对称问题的Love位移函数解法:寻找满足双调和方程的Love位移函数Ψ(r,z),其位移解为该位移解还必须满足边界条件薄板问题的挠曲函数解法:弹性力学问题的解析求解寻找一个满足双调和方程的挠曲函数w 。
则其应力解答为……该应力解答还必须满足应力及位移边界条件。
最小势能原理及近似解法最小势能原理:在满足位移边界条件(约束所允许的)一切位移中,真实的位移使弹性体的总势能取极值(极小值)。
近似解法:根据最小势能原理与弹性力学求解体系的等价性,可以提出弹性力学的近似解法求解微分方程求泛函的极值瑞利李兹近似解法瑞利-李兹近似解法选择一组满足位移边界条件的试探函数u (x ,y ,z ):将上述位移函数u (x ,y ,z )代入几何方程求出应变εij 、代入物理方程求出应力σij ,进而可以求得分析物体的总势能Π()m m m C B A f V U ,,=+=∏瑞利李兹近似解法瑞利-李兹近似解法利用最小势能原理,对总势能取极值:可以得到一组以Am 、Bm、Cm为未知系数的代数方程组。
有限元法PPT课件

Motorola– Drop Test Fujitsu-Computers Intel –Chip Integrity
电子
Baxter - Equipment J&J – Stents Medtronic - Pacemakers
医疗
Principia-spain Arup-U.K. T.Y. Lin - Bridge
有限元法
左图所示,为分析齿轮上一个齿内的应力分布,可分析图中所示的一个平面截面内位移分布.作为近似解,可以先求出图中各三角形顶点的位移.这里的 三角形就是单元,其顶点就是节点。
从物理角度理解, 可把一个连续的齿形截面单元之间在节点处以铰链相链接,由单元组合而成的结构近似代替原连续结构,在一定的约束条件下,在给定的载荷作用下,就可以求出各节点的位移,进而求出应力.
一.Abaqus公司简介
公司
’00 ’01 ’02 ’03 ’04 ‘05 ’06 ‘07
18%
18%
20%
SIMULIA公司(原ABAQUS公司)成立于1978年,全球超过600名员工,100% 专注于有限元分析领域。 全球28个办事处和9个代表处 业务迅速稳定增长,是当前有限元软件行业中唯一保持两位数增长率的公司。 2005年5月ABAQUS加入DS集团,将共同成为全球PLM的领导者
Where :
Displacement interpolation functions (位移插值函数)
13.3 Approximating Functions for Two-Dimensional Linear Triangular Elements (二维线性三角形单元的近似函数)
node (节点)
element(单元)
有限元法介绍 PPT

与CAD软件的无缝集成
当今有限元分析系统的另一个特点是与通用CAD 软件的集成使用, 即:在用CAD软件完成部件和零件 的造型设计后,自动生成有限元网格并进行计算,如 果分析的结果不符合设计要求则重新进行造型和计算, 直到满意为止,从而极大地提高了设计水平和效率。 当今所有的商业化有限元系统商都开发了和著名的 CAD软件( 例如Pro/ENGINEER 、Unigraphics 、 SolidEdge 、SolidWorks 、IDEAS 、Bentley 和 AutoCAD 等) 的接口。
3、增强可视化的前置建模和后置数据处理功 能
➢随着数值分析方法的逐步完善,尤其是计算机 运算速度的飞速发展,整个计算系统用于求解 运算的时间越来越少,而数据准备和运算结果 的表现问题却日益突出。
➢在现在的工程工作站上,求解一个包含10万个 方程的有限元模型只需要用几十分钟。工程师 在分析计算一个工程问题时有80%以上的精力 都花在数据准备和结果分析上。
取决于材料性质、形状、尺寸
节点位移
ui
v
i
e
u v
j j
u
m
v m
节点力
U i
V
i
F
e
U
V
j j
U
m
V m
FeKee
– 选择位移模式:在反映力和位移的关系式中,依据那一 个量是未知量,可建立不同的模型。
➢ 位移法:选择节点位移作为基本未知F量e称为K位e移法e ;
➢ 力法:选择节点力作为基本未知量时称为力法; ➢ 混合法:取一部分节点力和一部分节点位移作为基
本未知量时称为混合法。 位移法易于实现计算自动化,所以,在有限单元法 中位移法应用范围最广。
弹性力学第十章空间问题的解答PPT

z
z
ρ
dφ
dρ
dφ
φ
φ
ρ
ρ
z
dρ
ρ
φ
应变分量:
径向正应变 剪应变:
•球对称问题的几何方程为:
环向正应变 •描述空间轴对称问题的应力、形变、位移宜用柱坐标
•通过与平面问题及极坐标中同样的分析,由径向位移引起的形变分量为:
•5 无限体内一点受集中力作用
•从轴对称物体中取出图示的单元体
•可见中的前二式自然满足,而第三式成为
亥姆霍兹(Helmholtz)定理:一个任意的位 •能直接利用拉梅应变势求解的问题极少。
•轴对称问题的弹性体的形状一般为圆柱体或半空间体。 •可见中的前二式自然满足,而第三式成为
移场 U总可以分解为两部分,一部分代表 •根据连续性假设,微元体的正面相对负面其应力分量都有微小增量。
•代入式(10-18)得 •解: 由于体力不计,球对称问题的微分方程简化为
显然,球对称问题只可能发生于空心或实心的圆球 体中。
•x
•y •z
一 平衡微分方程
取微元体。用相距 dr的 两个圆球面和两两互成d 角 的两对径向平面,从弹性体 割取一个微小六面体。由于 球对称,各面上只有正应力, 其应力情况如图所示。
由于对称性,微元体只 有径向体积力K r。由径向平 衡,并考虑到 sind d ,再
z
z
z
径向正应力,
φρ
沿ρ方向的正应力
dφ dρ
z
环向正应力,沿方向的正应力 轴向正应力,沿z方向的正应力
z z
z 作用在圆柱面上而沿z方向作用的剪应力
z 作用在水平面上而沿ρ方向作用的剪应力
由于对称性,
有限元法的理论基础

有限元法的理论基础-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN有限元法的理论基础有限元法是一种离散化的数值计算方法,对于结构分析而言,它的理论基础是能量原理。
能量原理表明,在外力作用下,弹性体的变形、应力和外力之间的关系受能量原理的支配,能量原理与微分方程和定解条件是等价的。
下面介绍有限元法中经常使用的虚位移原理和最小势能原理。
1.虚位移原理虚位移原理又称虚功原理,可以叙述如下:如果物体在发生虚位移之前所受的力系是平衡的(物体内部满足平衡微分方程,物体边界上满足力学边界条件),那么在发生虚位移时,外力在虚位移上所做的虚功等于虚应变能(物体内部应力在虚应变上所做的虚功)。
反之,如果物体所受的力系在虚位移(及虚应变)上所做的虚功相等,则它们一定是平衡的。
可以看出,虚位移原理等价于平衡微分方程与力学边界条件。
所以虚位移原理表述了力系平衡的必要而充分的条件。
虚位移原理不仅可以应用于弹性性力学问题,还可以应用于非线性弹性以及弹塑性等非线性问题。
2.最小势能原理最小势能原理可以叙述为:弹性体受到外力作用时,在所有满足位移边界条件和变形协调条件的可以位移中,真实位移使系统的总势能取驻值,且为最小值。
根据最小势能原理,要求弹性体在外力作用下的位移,可以满足几何方程和位移边界条件且使物体总势能取最小值的条件去寻求答案。
最小势能原理仅适用于弹性力学问题。
有限元法求解问题的基本步骤弹性力学中的有限元法是一种数值计算方法,对于不同物理性质和数学模型的问题,有限元法的基本步骤是相同的,只是具体方式推导和运算求解不同,有限元求解问题的基本步骤如下。
2.2.1问题的分类求解问题的第一步就是对它进行识别分析,它包含的更深层次的物理问题是什么比如是静力学还是动力学,是否包含非线性,是否需要迭代求解,要从分析中得等到什么结果等。
对这些问题的回答会加深对问题的认识与理解,直接影响到以后的建模与求解方法的选取等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、轴对称问题的定义 (1)几何形状轴对称:要求结构是相对对称轴的受到的载荷和位移约束条件具 有轴对称性。 (3)材料轴对称要求:结构的材料特性具有轴对称性。
二、 轴对称问题基本方程
轴对称问题的特点是结构的位移、应变和应力都呈轴对称分布。 (l) 柱坐标系(r, θ, z) (u, v, w) 有许多实际工程问题,其几何形状、约束条件以及载荷 都对称于某一固定轴,这类问题为轴对称问题。 (2)基本变量 对于轴对称问题,在柱坐标中的三大 类力学变量为: 位移: ur , wz , (vθ=0)
(下标i, j, m轮换)
用矩阵表示的单元位移为
u Ni w 0
0 Ni
Nj 0
0 Nj
Nm 0
ui w i 0 u j N m w j um wm
四、 三结点单元刚度矩阵
轴对称问题的几何方程:
u a1 a 2 r a 3 z w a4 a5 r a6 z
该模式与平面问题三节点三角形单元相同,由节点条件可以推出相同的形 状函数矩阵,即
Ni N 0
定义形态函数为
Ni
0 Ni
Nj 0
0 Nj
Nm 0
0 Nm
1 (ai bi r ci z ) 2
bj 0 fj 0 0 cj cj bj
式中
ai ci z f i bi r r
{ } [ B] { }e
(i , j, m )
B B( r , z )
用几何矩阵表示单元的应变
[ B] [ Bi
Bj
Bm ]
bi 1 fi [ Bi ] 2 0 ci
0 0 ci bi
由轴对称问题的物理方程,得到弹性矩阵
1 E (1 ) 1 [ D] (1 )(1 2 ) 1 0
1 1
1
1 0
1 0
1
0 0 1 2 2(1 ) 0
单元刚度矩阵为
[ K ]e 2 [ B ]T [ D][ B ]rdrdz
由于几何矩阵中的元素不是常量,单元刚度矩阵需要通过积分得到。
第11章 等参单元
由于实际问题的复杂性,需要使用一些几何形状不太 规整的单元来逼近原问题,特别是在一些复杂的边界上, 有时只能采用不规整单元;但直接研究这些不规整单元则 比较困难,如何利用规整单元(如三角形单元、矩形单元、 正六面体单元)的原理来研究所对应的不规整单元的表达 式? 这将涉及到几何形状映射、坐标系变换(等参变换、 非等参变换)等问题。
应变: 应力: 由于是轴对称问题,所以以上力学参量 只是r和z的函数,与θ无关.
(3) 基本方程
①平衡方程
②几何方程
③物理方程
三、 三结点单元位移函数
轴对称问题分析中所使用的三结点单元,在对称面上是三角形,在整 个弹性体中是三棱圆环,各单元中圆环形铰相联接。参照平面问题的三 角形单元位移函数,轴对称问题的三结点三角形单元位移函数取为
u r bi 0 r u 1 fi 0 r w z 2 0 c i zr z c i bi u w z r ui bm 0 w i f m 0 u j 0 c m w j c m bm um wm
等参单元的基本概念
局部坐标系中的正方形单元称为基本单元。
整体坐标系中的任意四边形单元看作由基本单元通过坐 标变换得来的,称为实际单元。 单元几何形状和单元内的未知量采用相同数目的结点参 数以及相同的插值函数进行变换,称为等参变换。采用等 参变换的单元,称为等参单元。
