等积变形专项练习

合集下载

等积变形专项练习

等积变形专项练习
1。

在一个底面积是31.4平方厘米的长方体玻璃容器中，有一个底面半径是1厘米的圆锥形铝块完全浸在水中,当从水中取出铝块时,容器的水面下降了0。

2厘米。

这个圆锥形铝块高多少厘米？
2。

用半径10cm高7cm的圆柱形泥巴揉成半径一样大的圆锥形，圆锥的高是多少厘米呢？
3.一个圆柱形的水桶，内部的底面半径是20厘米，高是45厘米，里面盛有30厘米深的水。

将一个底面半径是15厘米的圆锥形铁块完全沉进水里，水不溢出，水面上升了3厘米，圆锥形铁块的高是多少？
4.有一段钢可做一个底面直径8厘米，高9厘米的圆柱形零件.如果把它改制成高是12厘米的圆锥形零件，零件的底面积是多少平方厘米？
5。

一个圆柱形容器的底面半径是4分米,高6分米，里面盛满水,把水倒在棱长是8分米的正方体容器中，水深多少分米？
6.将一个底面直径是20厘米、高是9厘米的金属圆锥，全部浸没在直径是40厘米的圆柱形水槽中且水未溢出。

水槽中的水面会升高多少厘米?
7。

把一个长2米的圆柱截去4分米后,原来的表面积就减少了25.12平方分米，原来圆柱的体积是多少立方分米?
8。

在一个底面是边长为2分米的正方形的长方形水槽中，放入一块青铜（完全浸没在水中），水面上升1分米且水未溢出.(水槽厚度忽略不计）
（1)求这块青铜的体积.
(2)如果把这块青铜铸成一个底面直径是2分米的圆柱,它的高是多少？(得数保留一位小数）
9.(拓展)在一个圆柱形储水桶里，把一段半径是5cm的圆钢全部放入水中,水面就上升9cm；把圆钢竖着拉出水面8cm长后，水面就下降4cm。

求圆钢的体积。

六年级体育等积变形练习题15道(动作)

六年级体育等积变形练习题15道(动作)题目一请用两个动作表示以下变形：- 将手臂从胸前伸直到头顶，并保持5秒钟- 将手臂从胸前伸直到向上侧伸直，同时向侧面弯曲，并保持5秒钟题目二请用动作演示以下变形：- 双脚并拢站立- 双脚并拢跳起并向前跳一小步，同时将双手向下伸直题目三请用动作表示以下变形：- 将右手抬起过头并向后伸直，并保持5秒钟- 将右手向上侧伸直并同时向左侧弯曲，并保持5秒钟题目四请用动作演示以下变形：- 腿部打开并跨出一小步- 腿部打开并向前跨出一小步，同时将双手向上伸直题目五请用动作表示以下变形：- 将头向右侧转动，使下巴尽量靠近右肩，并保持5秒钟- 将头向右侧倾斜，使右耳朵尽量靠近右肩，并保持5秒钟题目六请用动作演示以下变形：- 双脚分开站立- 双脚分开并向前跳开一小步，同时将双手向前伸直题目七请用动作表示以下变形：- 将左腿弯曲向胸部靠拢，并保持5秒钟- 将左腿向上侧伸直并同时向左侧弯曲，并保持5秒钟题目八请用动作演示以下变形：- 双脚并拢站立- 双脚并拢跳起并向后跳一小步，同时将双手向下伸直题目九请用动作表示以下变形：- 将头向左侧转动，使下巴尽量靠近左肩，并保持5秒钟- 将头向左侧倾斜，使左耳朵尽量靠近左肩，并保持5秒钟题目十请用动作演示以下变形：- 双手提起过头并向后伸直，并保持5秒钟- 双手向上侧伸直并同时向右侧弯曲，并保持5秒钟题目十一请用动作表示以下变形：- 将右腿弯曲向胸部靠拢，并保持5秒钟- 将右腿向上侧伸直并同时向右侧弯曲，并保持5秒钟题目十二请用动作演示以下变形：- 左脚向左侧迈出一小步- 左脚向前迈出一小步，同时将双手向上伸直题目十三请用动作表示以下变形：- 将左手抬起过头并向后伸直，并保持5秒钟- 将左手向上侧伸直并同时向左侧弯曲，并保持5秒钟题目十四请用动作演示以下变形：- 腿部分开并向右迈出一小步- 腿部分开并向前跨出一小步，同时将双手向前伸直题目十五请用动作表示以下变形：- 将头向右侧转动，使下巴尽量靠近右肩，并保持5秒钟- 将头向右侧倾斜，使右耳朵尽量靠近右肩，并保持5秒钟以上是15道六年级体育等积变形练习题(动作)。

【小升初专项训练】04 等积变形

第5讲等积变形第一关三角形的等积变形【例1】如图，在等腰直角三角形ABC中，已知AB的长是7厘米，那么这个直角三角形的面积为　平方厘米。

【答案】12.25【例2】如图，E、F分别是梯形ABCD两腰上的中点，已知阴影部分的面积是43c㎡，那么梯形ABCD 的面积是多少？【答案】172【例3】如图：三条直线互相平行，l1与l3之间的距离是7厘米，l2上AB=4厘米．求阴影部分三角形的面积是多少平方厘米？　【答案】14【例4】你能看出下面两个阴影部分A与B面积的大小关系吗？（两个长方形面积相等）【答案】A与B的面积相等【例5】如图，在斜边长为20cm的直角三角形ABC中去掉一个正方形EDFB，留下两个阴影部分直角三角形AED和DFC．若AD=8cm，CD=12cm，则阴影部分面积为多少？给出答案并说明你的计算依据．【答案】48【例6】如图，在直角三角形中有一个正方形，已知BD=10厘米，DC=7厘米，阴影部分的面积是多少？【答案】35平方厘米【例7】如图，梯形ABCD的面积是36，下底长是上底长的2倍，阴影三角形的面积是多少？【答案】16【例8】下图中阴影部分甲的面积与阴影部分乙的面积哪个大？【答案】图中甲乙的面积相等【例9】如图，在三角形ABC中，D是BC上靠近C的三等分点，E是AD中点，已知三角形ABC的面积为1，那么图中两个阴影三角形面积之和是多少？【答案】0.4【例10】已知△ABC面积为5，且BD=2DC，AE=ED，求阴影部分面积．要求写出关键的解题推理过程．【答案】2【例11】如图，将一个梯形分成四个三角形，其中两个三角形的面积分别为10与12．已知梯形的上底长度是下底的．请问：阴影部分的总面积是多少？【答案】23【例12】如图，已知梯形ABCD中，CD=10，梯形ABCD的高是4，那么阴影部分的面积是多少。

【答案】20【例13】（1）如图1，阴影部分的面积是多少？（2）如图2，一个长方形长4厘米，宽3厘米．A为长方形内的任意一点，阴影部分的面积是多少？【答案】（1）100；（2）6【例14】如图，在图中△ABE、ADF和四边形AECF面积相等．阴影部分的面积是多少？【答案】15【例15】如图，两个正方形（单位：厘米）中阴影部分的面积是多少平方厘米？【答案】8【例16】由面积为1，2，3，4的矩形拼成如图的长方形，图中阴影部分的面积为多少？【答案】【例17】如图所示，正方形ABCD的对角线BD长20厘米，BDFE是长方形．那么，五边形ABEFD的面积是多少平方厘米。

小学数学《三角形的等积变形》练习题(含答案)

小学数学《三角形的等积变形》练习题（含答案）
内容概述
我们已经知道三角形面积的计算公式：三角形面积=底×高÷2
从这个公式我们可以发现：三角形面积的大小，取决于三角形底和高的乘积．
如果三角形的底不变，高越大（小），三角形面积也就越大（小）；
如果三角形的高不变，底越大（小），三角形面积也就越大（小）；
这说明当三角形的面积变化时，它的底和高之中至少有一个要发生变化．但是，当三角形的底和高同时发生变化时，三角形的面积不一定变化．比如当高变为原来的3倍，底变为原来的1/3，则三角形面积与原来的一样。这就是说：一个三角形的面积变化与否取决于它的高和底的乘积，而不仅仅取决于高或底的变化．同时也告诉我们：一个三角形在面积不改变的情况下，可以有无数多个不同的形状．
于是：三角形ABD的面积=12×高÷2=6×高
三角形ABC的面积=（12+4）×高÷2=8×高
三角形ADC的面积=4×高÷2=2×高
所以，三角形ABC的面积是三角形ABD面积的4/3倍；三角形ABD的面积是三角形ADC面积的3倍。
巩固理解结论：两个三角形等高时，面积的倍数=底的倍数
【例2】如右图，E在AD上，AD垂直BC，AD=12厘米，DE=3厘米。
【例6】如右图所示，在平行四边形ABCD中，E为AB的中点，AF=2CF，三角形AFE(图中阴影部分)的面积为8平方厘米．平行四边形的面积是多少平方厘米?
【例7】图中△AOB的面积为15cm2，线段OB的长度为OD的3倍，求梯形ABCD的面积.
【例8】（北京市第一届“迎春杯”刊赛）如右图.将三角形ABC的BA边延长1倍到D，CB边延长2倍到E，AC边延长3倍到F.如果三角形ABC的面积等于l，那么三角形DEF的面积是？
例题精讲

专项练习—等积变形

专项练习—等积变形1. 已知直角三角形的两条直角边长分别是21和28，求这个三角形内的最大正方形的边长？2. 如图，四边形ABCD 是等腰梯形，ADBE 是平行四边形，面积等于8，还知道三角形BCE 的面积是2，那么三角形CDE 的面积是多少？3. 开发商准备在一块地面上盖商品房，这块长方形地形情况如图，甲处比乙处高50厘米．现在要把这块地推平整，要从甲处取下多少厘米厚的土填在乙处上？ED CBA50厘米100米60米30米乙甲4. 如图，折线A ﹣B ﹣C ﹣D 的每一条线段都平行于矩形的边，它把矩形分成面积相等的两部分．点E 在矩形的边上，使得线段AE 也平分矩形的面积．已知线段AB ＝30，BC ＝24，CD ＝10，求DE 的长．5. 如图是直角三角形中有一个内接正方形，求图中阴影部分的面积．单位：厘米．提示：分拆图形时常用“分割、填补、组合、旋转”等方法．6. 雨哗哗地不停地下着．如果在雨地放一个如图1那样的长方体的容器（单位：厘米），雨水将它灌满要用1小时．雨水灌满图2容器各需多长时间？E D CBA图2图1107. 把一个底面直径是4厘米的圆柱底面分成许多相等的扇形，然后沿着直径切开，拼成一个和它体积相等的长方体，这个长方体的表面积比原来圆柱的表面积增加了20平方厘米，这个长方体的体积是多少立方厘米？8. 如图，O 是半圆的圆心，AC ＝BC ，CD ＝DB ，AB ＝12厘米，求阴影部分的面积．9. 如图，直角梯形ABCD 中，AB ＝12，BC ＝8，CD ＝9，且三角形AED 、三角形FCD 和四边形EBFD 的面积相等，求三角形DEF 的面积．BAFEDCBA10.边长分别为8cm和6cm的两个正方形ABCD与BEFG如图并排放在一起．连接DE交BG于P，则图中阴影部分APEG的面积是多少？11.有一个长方体铁块，长8分米，宽4分米，高3分米．把它完全铸成一个圆柱，圆柱的底面半径是5分米，高是多少分米？（保留一位小数）12.有两个高度相等的容器A和B，已知A容器半径是6厘米，B容器的半径是8厘米，现在把A容器装满水，然后全部倒入B容器中，测得B容器中的水深比A容器高的3 4低了3厘米．求A、B两个容器的高是多少厘米？E13. 如图，正方形ABCD 的边长为4cm ，则图中阴影部分的面积为多少平方厘米？14. 如图，有边长分别是15分米和20分米的两个正方形，一条直线把这两个相连的正方形分成甲、乙、丙、丁四部分．甲三角形的面积比丙三角形的面积大多少平方分米？15. 如图，ABCD 是等腰梯形，上底和下底分别是16厘米和24厘米，高是12厘米．阴影部分的面积是多少？丁丙乙甲CD。

等积变形应用题练习

10 10 10 分析：等量关系是变形前后周长相等 6 6 10
பைடு நூலகம்
？
答案：小影所钉长方形的长是16厘米，宽是10厘米。
4、小明的爸爸想用10米铁丝网把墙当一长边围成一个鸡棚，使长比宽大4 米，问小明的爸爸围成的鸡棚的长和宽各是多少呢？
墙面
x
铁线
X+4
5、一个长方形的养鸡场的长边靠墙，墙长14 米，其他三边用竹篱笆围成，现有长为35米的竹篱笆，小王打算用它围成一个鸡场，其中长比宽多5米；小赵也打算用它围成一个鸡场，其中长比宽多2米.你认为谁的设计符合实际？按照他的设计，鸡场的面积是多少？
相等关系：水面增高体积=长方体体积解：设水面增高 x 厘米. 则
4 x 5 3 3
2
解得： x
45 0 .9 16
因此，水面增高约为0.9厘米.
3、墙上钉着用一根彩绳围成的梯形形状的装饰物，小颖将梯形下底的钉子去掉，并将这条彩绳钉成一个长方形，那么，小颖所钉长方形的长和宽各为多少厘米？
5.3 练习题
1、将一个底面直径为10厘米、高为36厘米的“瘦长”形圆柱锻压成底面直径为20厘米的“矮胖”形的圆柱,高变成了多少？
想什么发生了变化？一想
什么没有发生变化？答案：高变成了9厘米。
2、把一块长、宽、高分别为5cm、3cm、3cm的长方体木块，浸入半径为4cm的圆柱形玻璃杯中（盛有水），水面大约增高多少？（水不外溢，结果近似到0.1cm）
墙壁篱笆
6、在一个底面直径为3cm，高为22cm的量筒内装满水，再将筒内的水到入底面直径为7cm，高为9cm的烧杯内，能否完全装下？若装不下，筒内水还剩多高？若能装下，求杯内水面的高度。

小学数学《三角形的等积变形》练习题(含答案)

分析：图中，三角形AEC与三角形ABC的高相等，而BE=1/3BC，于是EC=2/3BC，
又由于三角形AED与三角形AEC的高相等，而CD=1/4AC,于是AD=3/4AC,
所以，三角形AED的面积=3/4×三角形AEC的面积
=
.
=
【附4】（北京市第四届“迎春杯”刊赛）下图中三角形ABC的面积为1，其中AE=3AB，BD=2BC，那么三角形BED的面积是________.
分析：连接辅C助线E.
(三角形BCE的面积)︰(三角形DCE的面积)=BC﹕CD=1﹕1，
所以三角形BCE的面积等.于三角形DCE的面积.
又因为(三角形BCE的面积)︰l=BE﹕AB=2﹕1，
所以三角形BCE的面积等于2.
因此三角形BDE的面积等于2+2=4.
【附5】（第四届《小数报》数学竞赛初赛）如图，梯形ABCD被它的一条对角线BD分成了两部分．三角形BDC的面积比三角形ABD的面积大l0平方分米．已知梯形的上底与下底的长度之和是15分米，它们的差是5分米．求梯形ABCD的面积．
【例6】如右图所示，在平行四边形ABCD中，E为AB的中点，AF=2CF，三角形AFE(图中阴影部分)的面积为8平方厘米．平行四边形的面积是多少平方厘米?
【例7】图中△AOB的面积为15cm2，线段OB的长度为OD的3倍，求梯形ABCD的面积.
【例8】（北京市第一届“迎春杯”刊赛）如右图.将三角形ABC的BA边延长1倍到D，CB边延长2倍到E，AC边延长3倍到F.如果三角形ABC的面积等于l，那么三角形DEF的面积是？
【附2】如图，在△ABC中，DC=3BD，DE=EA，若△ABC面积是2，则阴影部分的面积是多少？
分析：连结FD，由AE=ED可知：S△AFE=S△EFD，S△AEC＝S△DCE

六年级科学等积变形练习题15道(实验)

六年级科学等积变形练习题15道(实验)
实验介绍
本实验旨在让六年级学生通过等积变形练题的实践操作，加深对科学概念的理解和应用能力。

实验中，学生将进行一系列关于等积变形的练题，通过操作和观察，探索物体的形状和容量的变化规律。

实验材料
- 不同形状的塑料（如圆柱形、长方形、三角形等）
- 水
- 尺子
- 计时器
实验步骤
1. 准备不同形状的塑料，如圆柱形、长方形、三角形等。

2. 用尺子测量每个的长度、宽度、高度，并记录在实验记录表中。

3. 填充每个的水，使水位分别达到的一半、三分之一、四分之一位置，记录中的水量。

4. 使用计时器，分别记录每个形状中的水从一半、三分之一、四分之一位置流出所需的时间。

5. 根据实验数据和观察结果，回答练题中的问题。

实验问题示例
1. 当形状相同时，水的容量变化是否会影响水的流出速度？
2. 当水的容量相同时，不同形状的水的流出速度是否一样？
3. 当形状相同时，水的容量变化是否会影响水的流出时间？
实验结论
根据实验结果，我们可以得出以下结论：
1. 当形状相同时，水的容量变化会影响水的流出速度。

2. 当水的容量相同时，不同形状的水的流出速度不一样。

3. 当形状相同时，水的容量变化会影响水的流出时间。

总结
通过这次实验，六年级学生通过实践操作发现了等积变形的一些规律。

他们通过观察和记录实验数据，了解了不同形状和容量的对水流出速度和时间的影响。

这对他们的科学研究和应用能力有着积极的促进作用。

参考资料
[1] XX实验教材
[2] XX科学学习网站。

小学五年级数学思维专题训练—等积变形(含答案解析)

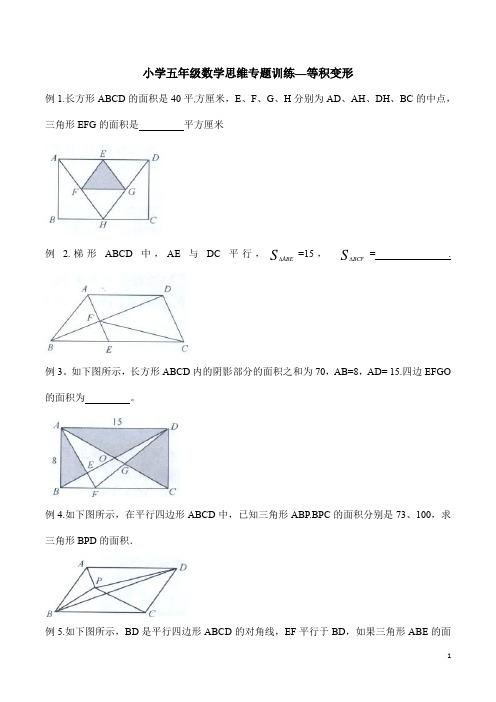
小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米，E、F、G、H分别为AD、AH、DH、BC的中点，三角形EFG的面积是平方厘米例 2.梯形ABCD中，AE与DC平行，S ABE∆=15，S BCF∆= .例3。

如下图所示，长方形ABCD内的阴影部分的面积之和为70，AB=8，AD= 15.四边EFGO 的面积为。

例4.如下图所示，在平行四边形ABCD中，已知三角形ABP.BPC的面积分别是73、100，求三角形BPD的面积．例5.如下图所示，BD是平行四边形ABCD的对角线，EF平行于BD，如果三角形ABE的面积是12平方厘米，那么三角形AFD的面积是平方厘米。

例6.如下图所示，已知AE=EC，CD=DB，S ABC =60，求四边形FDCE的面积．例7.如右图所示，正方形ABC D和正方形ECGF并排放置，BF与CD相交于点H,已知AB=6厘米，则阴影部分的面积是平方厘米．例8.如下图所示，E、F、G、H分别是四边形ABCD各边的中点，EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积．试比较S1+S3与S2+S4的大小．例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份，长方形内任意一点与分点及顶点连结，如右图所示，则阴影部分的面积是平方厘米．例10.右图所示ABCD 是个直角梯形（∠DAB=∠ABC= 900），以， AD 为一边向外作长方形ADEF ，其面积为6.36平方厘米，连接BE 交AD 于P ，再连接PC ．则图中阴影部分的面积是平方厘米。

A.6.36B.3.18C.2.12D.1.59例11.如下图所示，平行四边形内有两个大小一样的正六边形，那么阴影部分的面积占平行四边形面积的。

A ．21B ．32C ．52D ．125例12.如下图所示，矩形ABCD 的面积是24平方厘米，三角形ADM 与三角形BCN 的面积之和是7.8平方厘米，则四边形PMON 的面积是平方厘米．例13.一个矩形分成4个不同的三角形（如下图），绿色三角形面积占矩形面积的15%，黄色三角形的面积是21平方厘米．问：矩形的面积是多少平方厘米？例14.如下图所示，正方形每条边上的三个点（端点除外）都是这条边的四等分点，则阴影部分的面积是正方形面积的。

五年级数学思维《等积变形》专题训练

五年级数学思维《等积变形》专题训练一、填空题（每小题6分，共60分）1 如图，三角形ABC被ED分成甲、乙两部分，BD=DC=4，BE=3，AE=6，那么乙部分面积是甲部分而积的倍．2 如图，BD是梯形ABCD的一条对角线，线段AE与梯形的腰DC平行，AE与BD柜交于O点已知三角形BOE的面积比三角形AOD的BC,那么梯形ABCD的面积是面积大4平方厘米，并且EC=38平方厘米.3 如图，已知平行四边形ABCD中，BC=3厘米，BC边上的高AE是2厘米，那么△ACD的面积是平方厘米.4 如图，平行匹边形MNOP中，Q是OP上任意一点，则S△MRQS△NRO，S△MRN S△QRO.（填“大于”、“＜”或“=”）5 如图，平行四边形ABCD中，E、F分别为AD、CD的中点，那么与△BFC面积相等的三角形有个．6 如图，△ABC中，D为BC中点，且DE=2AD，那么△ABC的面积等5于△CDE面积的倍．7 如图，AC=4AD,三角形CDE的面积是三角形ABC面积的一半，那么BE的长等于 BC.8 如图，△ABC与△BCD 中AD与BC交于点E, AE=ED,且AD⊥BC，把BC八等分，点F为第一个八等分点，E恰为第二个八等分点，各等分点分别与A、D连线，那么与△ABF面积相等的三角形个．9 如图，已知BC是5，其他数据如图所示，那么阴影部分的两个三角形的面积之和是 .10 如图，大正六边形的面积是24平方厘米，共中放了三个一样的小正六边形，那么阴影部分的面积是平方厘米．二、解答题（每小题12分，共60分）11 如图，梯形ABCD的上底AD是12厘米，高BD是18厘米，BE=2DE，那么下底BC是多少厘米？12 如图，平行四边形ABCD 的边BC是10厘米，直角三角形ECB的直角边EC是8厘米，已知阴影部分的总面积比△EFG的面积大10平方厘米，那么平行四边形ABCD的面积是多少平方厘米？13 如图，△ABC的面积是180平方厘米，D是BC的中点，AD=3AE,EF=3BF，求△AEF的面积．14 如图，正方形ABCD的边长为12，P是AB边上任意一点，M、N、I、H分别是BC 、AD的三等分点，E、F、G分别是边CD的四等分点，求图中阴影部分的面积．15 如图，BD、CF将长方形ABCD分成四块，红色三角形面积是4平方厘米，黄色三角形面积是6平方厘米，问：绿色四边形面积是多少平方厘米？。

等积变形(思维拓展专项练习)六年级下册小升初数学专项培优(通用版)含参考答案

等积变形(思维拓展提高卷)一．选择题(共9小题)1我国古代数学家刘徽利用“出入相补”原理计算平面图形的面积，其原理是：把一个图形分割、移补，而面积保持不变。

下面没有用到这个原理的是()A. B. C. D.2把割补成后，面积()A.不变B.变大了C.变小了D.无法判断3一个圆柱形橡皮泥，底面积是12.56cm2，高是6cm，如果把它捏成同样底面积大小的圆锥，这个圆锥的高是( )cm．A.2B.3C.18D.364如图，长方形的面积与圆的面积相等，已知阴影部分的面积是84.78cm2，圆的周长是( )cm．A.18.84B.75.36C.37.685如果图中每个小方格代表1cm2，那么大长方形的面积是( )cm2．A.56B.60C.58D.666轧钢厂要把一种底面直径6厘米，长1米的圆柱形钢锭，轧制成内径(内侧直径)为10厘米，外径(外侧直径)为30厘米的无缝钢管，如果不计加工过程中的损耗，则这种无缝钢管的长是()A.4.25厘米B.5厘米C.4厘米D.4.5厘米7把圆柱的底面平均分成若干等份，切开后，拼成一个长方体，这个长方体与圆柱相比()A.体积不变，表面积也不变B.体积不变，表面积变大C.体积变大，面积不变8以下是四位同学运用转化的策略将左边的图形转化成右边的图形解决问题，其中做对的有( )位．A.1B.2C.3D.49如图的等腰梯形中，甲三角形的面积( )乙三角形的面积。

A.大于B.等于C.小于D.无法判断二．填空题(共25小题)10(如图)运用了数学思想方法是，你还知道哪些数学思想方法？再列举一个。

11如图，大正方形ABCD的边长是10cm，小正方形CGFE的边长是6cm，那么图中阴影部分的面积是cm2。

12将一底面半径为2分米的圆柱的底面平均分成若干个扇形，截开拼成一个和它等底等高的长方体后，表面积增加16平方分米，圆柱的体积是．13把一个底面半径2厘米、高1.5厘米的圆柱形钢锭，铸成底面积大小不变的圆锥形钢锭，圆柱的高和圆锥的高的比是．14有一种饮料瓶的容积是50立方厘米，瓶身呈圆柱形(不包括瓶颈)．现在瓶中装有一些饮料，正放时饮料高度为20厘米，倒放时空余部分的高度为5厘米．瓶内现有饮料立方厘米．15如图，外侧大正方形的边长是10厘米，图中阴影部分的面积是27.5平方厘米，那么圆内的大正方形面积是小正方形面积的倍．16用6米、8米、10米、16米、20米、28米分别作为如图的6条边的边长，当这个图形的面积最大时，过A点画一条直线把图形分成面积相等的两部分，这条直线与边界的交点为K，从A点沿边界走到K点，较短的路线是米．17如图所示，梯形下底是上底的1.5倍，梯形中阴影面积等于空白面积，三角形OBC的面积是12，那么三角形AOD的面积是．18如图，ABCDEF为正六边形，P为其内部任意一点，若△PBC、△PEF的面积分别为3和12，则正六边形ABCDEF的面积是．19每块砖0.6元，修补好下图中的墙体上的漏洞需要砖钱元．20图中阴影部分的面积是．(图中的三角形是等腰直角三角形，π=3.14)21如图，E，F，G，H是边长为2的正方形ABCD各边的中点，则图中阴影部分的面积等于．22如图，三个大小相同的正方形重叠地放在一个大的正方形ABCD内，已知能看见的部分Ⅰ、Ⅱ、Ⅲ的面积分别是64平方厘米、38平方厘米、34平方厘米．那么正方形ABCD的边长是厘米．23如图中E、F、G、H分别是边AB、BC、CD、DA上的三等分点，如果阴影部分面积为10平方厘米，则四边形ABCD的面积等于平方厘米．24如图所示，有一张四边形纸片ABCD，其中AD=2，AB=4，CD=5，把这张四边形纸片如图所示折叠，点A落在点E处，点E到点C的最短距离为．25一张长方形铁皮长32厘米，宽10厘米，把它围成一个圆柱体，做底面周长，做高，所围成的圆柱体的体积最大．长方形围圆柱体有两种围法，但所围成的圆柱体没变．26一级台阶的长10米、宽0.8米、高0.5米，从一楼到二楼有12级台阶，二楼到六楼每层有18级台阶，台阶的表面积平方米．27用一块正方形玻璃来修补窗户，需要在相邻的两边分别划掉5厘米和2厘米，共划掉298平方厘米，原来正方形玻璃的面积是平方厘米，剩下部分的面积是平方厘米．28如图，图中的小正方形完全一样，大长方形的周长是56厘米．这个大长方形的面积是平方厘米．29长方形的广告牌长为15米，宽为10米，A、B、C、D分别在四条边上，并且C比A低4米，D在B 的右边7米，则四边形ABCD的面积是平方米．30如图所示，一种饮料瓶，容积是200ml，瓶身是圆柱形．将该瓶正放时饮料高20cm，倒放时余部分高5cm，瓶内的饮料是ml．31数学小组将一圆柱按左图切割开，然后拼为右图，观察填空．拼出的右图是一个近似的体，它的高与圆柱的高，是；它的底面积与圆柱的底面积，是；拼出图形的体积是，圆柱的体积与它，所以圆柱的体积是．32右图中，四边形ABCD都是边长为1的正方形，E、F、G、H分别是AB、BC、CD、DA的中点，左图中阴影部分是右图中阴影部分的面积%．33一个圆柱铅块和一个圆锥铅块等底等高，它们可以熔铸成一个长8厘米、宽3厘米、厚2厘米的长方体，那么圆柱的体积是立方厘米，它们的体积相差立方厘米．34如图所示，把底面直径4厘米、高10厘米的圆柱切成若干等份，拼成一个近似的长方体．这个长方体的体积是立方厘米，表面积是平方厘米．三．应用题(共2小题)35如图所示，S A=32dm2，S B=8dm2，h=5dm．现在要把A处的铁块熔到B处．使A、B处同样高，这时B处比原来升高了多少分米？36如图，一瓶营养液的瓶底直径是12厘米，瓶高30厘米，液面高20厘米，倒置后，液面高25厘米．这个瓶子的容积是多少？等积变形(思维拓展提高卷)参考答案与试题解析一．选择题(共9小题)1【答案】A【分析】根据题意，我国古代数学家刘徽利用“出入相补”原理来计算平面图形的面积，根据数学常识即可完成判断。

等积变形练习题

等积变形练习题
1、用一块体积是2000立方厘米的钢块锻造成一根横截面面积是20平方厘米长方体方
钢，这根长方体方钢长多少?
2、将体积是360立方厘米的块油泥捏成一个长是10厘米,宽5厘米的
长方体油泥,能
• 3、将一块棱长0.8分米的正方体油泥捏成一个横截面面积是0.16平方分米的长方体,能捏多长?
• 10、一个长方体玻璃缸,底面是2分米的正方形,向容器内倒入5.4升水, 再把一个梨子放入水中,量得水深 1.5分米,这个梨子的体积有多大?
• 11、一个长方体玻璃缸，底面积是 200平方厘米，高是8厘米，里面盛有4厘米深的水，现在将一块石头放入水中，水面升高2厘米。这块石头的体积是多少立方厘米？
•
• 7、一个货车的车厢是棱长4米,宽 2.5米,高1.5米的长方体,将它装满石子,铺在一个长20米,宽5米的路上,能铺多厚?
• 8、一个棱长5分米的玻璃缸内有水100升,将一个石块投入缸内,水面上升了1厘米,这个石块的体积是多少?
• 9、一个长8分米,宽5分米,高6分米的玻璃缸内有2分米的水,将一个石块放入水中,水面上升到2.5分米,这个石块的体积有多大?
• 4、将一块棱长0.8米的正方体钢块,熔铸成一个横截面是边长2分米的正方形的长方体钢材,熔铸成和长方体钢材有多长?
• 5、将30升水倒入一个棱长是5分米的正方体体玻璃缸内,水深多少分米?
• 6、两个容器，甲正方体（棱长6分米），乙长方体（长8分米、宽和高都是6分米），将甲容器的水装满倒入乙容器，乙容器水面有多高？
• 12、一个长方5升水，在把一个苹果浸没在水中，这时容器内的水深是1.5分米。这个苹果的体积是多少？
• 13、在一个长25厘米、宽12厘米、高20厘米的长方体玻璃容缸中放入一个棱长9厘米的正方体铁块，然后在玻璃缸中加入一些水，使铁块完全浸没在水中。当铁块从水中取出时，玻璃缸中的水会下降多少厘米？

43 等积变形(一)

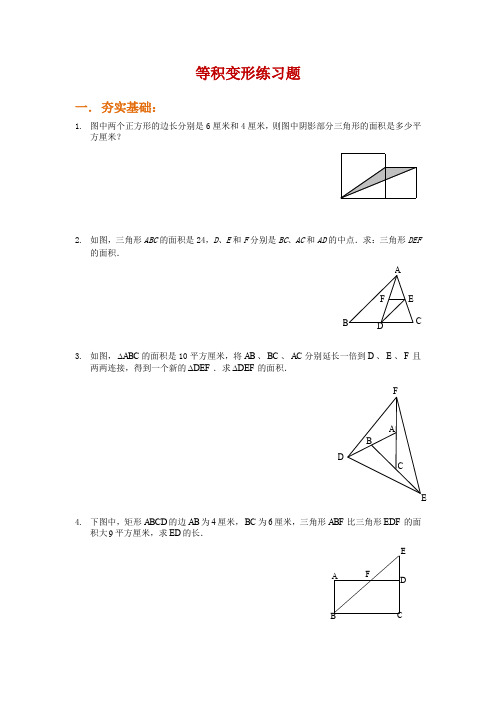
等积变形练习题一．夯实基础：1. 图中两个正方形的边长分别是6厘米和4厘米，则图中阴影部分三角形的面积是多少平方厘米？2. 如图，三角形ABC 的面积是24，D 、E 和F 分别是BC 、AC 和AD 的中点．求：三角形DEF的面积．3. 如图，ABC ∆的面积是10平方厘米，将AB 、BC 、AC 分别延长一倍到D 、E 、F 且两两连接，得到一个新的DEF ∆．求DEF ∆的面积．4. 下图中，矩形ABCD 的边AB 为4厘米，BC 为6厘米，三角形ABF 比三角形EDF 的面积大9平方厘米，求ED 的长．B ACDEFFE DCBA FEDCBA5. 图中4CA AB ==厘米，三角形ABE 比三角形CDE 的面积大2平方厘米，求CD 的长．二．拓展提高：6. 在图中，平行四边形ABCD 的边BC 长10厘米，直角三角形ECB 的直角边EC 长8厘米．已知阴影部分的总面积比三角形EFG 的面积大10平方厘米，求平行四边形ABCD 的面积．7. 如图，ABCD 是边长为8厘米的正方形，梯形AEBD 的对角线相交于O ，三角形AOE 的面积比三角形BOD 的面积小16平方厘米，则梯形AEBD 的面积是多少平方厘米？AB CDEO8. 如图，在长方形ABCD 中，Y 是BD 的中点，Z 是DY 的中点，如果24AB =厘米，8BC =厘米，求三角形ZCY 的面积．EDCB AYZ DCBA9. 如图所示，在平行四边形ABCD 中，E 为AB 的中点，2AF CF =，三角形AFE (图中阴影部分)的面积为8 平方厘米．平行四边形的面积是多少平方厘米？10. 如图，ABCD 与AEFG 均为正方形，三角形ABH 的面积为6平方厘米，图中阴影部分的面积为多少平方厘米？三. 超常挑战11. 如图，O 是长方形ABCD 内一点，已知OBC 的面积是52cm ，OAB 的面积是22cm ，求OBD 的面积是多少？12. 如下图，过平行四边形ABCD 内的一点P 作边的平行线EF 、GH ，若PBD ∆的面积为8平方分米，求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米？13. 如图，长方形ABCD 的面积是56平方厘米，点E 、F 、G 分别是长方形ABCD 边上的中点，H 为AD 边上的任意一点，求阴影部分的面积．FCH14. 如图所示，ABC ∆中，90ABC ∠=︒，3AB =，5BC =，以AC 为一边向ABC ∆外作正方形ACDE ，中心为O ，求OBC ∆的面积．四．杯赛演练：15. (《小数报》数学竞赛)如图，梯形ABCD 被它的一条对角线BD 分成了两部分．三角形BDC的面积比三角形ABD 的面积大10平方分米．已知梯形的上底与下底的长度之和是15分米，它们的差是5分米．求梯形ABCD 的面积．16. (西城某重点中学小升初分班考题)下图是由大、小两个正方形组成的，小正方形的边长是4厘米，求三角形ABC 的面积．EDCBAFED CBA答案：1. 4428⨯÷=．2. 三角形ADC 的面积是三角形ABC 面积的一半24212÷=，三角形ADE 又是三角形ADC 面积的一半1226÷=．三角形FED 的面积是三角形ADE 面积的一半，所以三角形FED 的面积623=÷=．3. 根据题意可知，2ADF ABC S S ∆∆=，同理可知2BDE CEF ABC S S S ∆∆∆==，于是(123)771070DEF ABCABCS SS∆=+⨯==⨯=平方厘米．4. (469)6241⨯-÷⨯-=（厘米）5. 连结CB ．三角形DCB 的面积为44226⨯÷-=（平方厘米），6423CD =÷⨯=（厘米）．6. 因为阴影部分比三角形EFG 的面积大10平方厘米，都加上梯形FGCB 后，根据差不变性质，所得的两个新图形的面积差不变，即平行四边形ABCD 比直角三角形ECB 的面积大10平方厘米,所以平行四边形ABCD 的面积等于10821050⨯÷+=平方厘米．7. 题目中出现了两个三角形面积之差16，若将AOD ∆作为公共部分分别加给这两个三角形后，根据差不变原理可知，AED ∆的面积比BAD ∆的面积小16平方厘米,而BAD ∆正好是正方形面积的一半即88232⨯÷=(平方厘米)，从而AED ∆的面积为321616-=（平方厘米）．作为梯形的另一部分，EBD ∆的面积与BAD ∆面积相等（同底等高）．可见，梯形的面积=163248+=(平方厘米).8. ∵Y 是BD 的中点，Z 是DY 的中点224ZCY DCB ZY DB S S ∴=÷÷=÷，又∵ABCD 是长方形，∴42424ZCYDCBABCD SSS =÷=÷÷=长方形(平方厘米)．9. 连接FB ．三角形AFB 面积是三角形CFB 面积的2倍，而三角形AFB 面积是三角形AEF面积的2倍，所以三角形ABC 面积是三角形AEF 面积的3倍；又因为平行四边形的面积是三角形ABC 面积的2倍，所以平行四边形的面积是三角形AFE 面积的326⨯=（）倍．因此，平行四边形的面积为8648⨯=(平方厘米)．10. 如图，连接AF ，比较ABF ∆与ADF ∆，由于AB AD =，FG FE =，即ABF ∆与ADF ∆的底与高分别相等，所以ABF ∆与ADF ∆的面积相等，那么阴影部分面积与ABH ∆的面积相等，为6平方厘米．F11. 设AODSX =，因为12AOBDOCAODBOCABCD SSSSS +=+=所以可得：25DOC S X +=+，即3DOC S X =+ 另有253102ABCD AOB DOC AOD BOC S S S S S X X X =+++=++++=+（）所以152ABD ABCD S S X ==+,可得523OBD ABD AOB AOD S S S S X X =--=+--=(2cm )．12. 根据差不变原理，要求平行四边形PHCF 的面积与平行四边形PGAE 的面积差，相当于求平行四边形BCFE 的面积与平行四边形ABHG 的面积差．如下图，连接CP 、AP ．由于12BCP ADP ABP BDP ADP ABCD S S S S S S ∆∆∆∆∆+=++=，所以BCP ABP BDP S S S ∆∆∆-=．而12BCP BCFE S S ∆=，12ABP ABHG S S ∆=，所以()2216BCFE ABHG BCP ABP BDP S S S S S ∆∆∆-=-==(平方分米)．13. 本题是等底等高的两个三角形面积相等的应用．连接BH 、CH ． ∵AE EB =， ∴S S AEH BEH =．同理，S S BFH CFH =，S =S CGH DGH ，∴11S S 562822==⨯=阴影长方形ABCD （平方厘米）．14. 如图，将OAB ∆沿着O 点顺时针旋转90︒，到达OCF ∆的位置．由于90ABC ∠=︒，90AOC ∠=︒，所以180OAB OCB ∠+∠=︒．而OCF OAB ∠=∠，所以180OCF OCB ∠+∠=︒，那么B 、C 、F 三点在一条直线上．由于OB OF =，90BOF AOC ∠=∠=︒，所以BOF ∆是等腰直角三角形，且斜边BF 为538+=，所以它的面积为218164⨯=．CH E BA根据面积比例模型，OBC ∆的面积为516108⨯=．15. 方法一：如右图，作AB 的平行线DE ．三角形BDE 的面积与三角形ABD 的面积相等，三角形DEC 的面积就是三角形BDC 与三角形ABD 的面积差(10平方分米)．从而，可求出梯形高(三角形DEC 的高)是：21054⨯÷=(分米)，梯形面积是：154230⨯÷=(平方分米)．方法二：10330⨯=(平方分米)．16. 连结AD (见右上图)，可以看出，三角形ABD 与三角形ACD 的底都等于小正方形的边长，高都等于大正方形的边长，所以面积相等．因为三角形AFD 是三角形ABD 与三角形ACD 的公共部分，所以去掉这个公共部分，根据差不变性质，剩下的两个部分，即三角形ABF 与三角形FCD 面积仍然相等．根据等量代换，求三角形ABC 的面积等于求三角形BCD 的面积，等于4428⨯÷=（平方厘米）．ABCDEF。

五年级等积变形题

五年级等积变形题一、等积变形题目。

1. 一个长方体水箱，从里面量长6分米，宽5分米，高4分米。

先倒入82升水，再浸入一块棱长2分米的正方体铁块，这时水面离水箱口1分米。

求水箱的容积是多少升？- 解析：正方体铁块体积为2×2×2 = 8立方分米，因为1立方分米= 1升，所以8立方分米= 8升。

倒入水的体积是82升，此时水和铁块总体积为82+8=90升。

水面离水箱口1分米，则此时水和铁块占水箱的高度是4 - 1=3分米。

水箱底面积为6×5 = 30平方分米，根据长方体体积公式V=Sh（S是底面积，h是高），那么3分米高的水和铁块的体积对应的水箱容积部分为30×3 = 90升，所以水箱容积为90÷3×4 = 120升。

2. 有一个底面积是300平方厘米、高10厘米的长方体，里面盛有5厘米深的水。

现在把一块石头浸没到水里，水面上升2厘米。

这块石头的体积是多少立方厘米？- 解析：因为石头浸没到水中，水面上升的体积就是石头的体积。

长方体底面积是300平方厘米，水面上升了2厘米，根据长方体体积公式V = Sh，石头体积为300×2=600立方厘米。

3. 一个正方体容器棱长为6分米，里面装满水。

现将水倒入一个长0.8米、宽0.6米的长方体容器中，水面高多少分米？- 解析：首先统一单位，0.8米= 8分米，0.6米= 6分米。

正方体容器棱长6分米，则水的体积为6×6×6 = 216立方分米。

将水倒入长方体容器中，长方体容器底面积为8×6 = 48平方分米，根据h=(V)/(S)（h是高，V是体积，S是底面积），水面高度为216÷48 = 4.5分米。

4. 把一块棱长12厘米的正方体铁块熔铸成一个底面积是144平方厘米的长方体铁块，这个长方体铁块的高是多少厘米？- 解析：正方体铁块体积为12×12×12 = 1728立方厘米。

小学数学几何问题之等积变形问题完整版题型训练 PPT带答案带练习

练习6
6、右图ADEF为正方形,BD的长为9,FC的长为4,求右图沿阴影长方形的四周作四个正方形,四个正方形的面积之和为68平方厘米,其阴影的长方形的周长是16厘米,求阴影部分的面积。
设正方形ADEF边长为a 4×9=36=6×6 a=6 三角形ABC面积=（6+9）×（6+4）÷2=75
练习7 7、右图沿阴影长方形的四周作四个正方形,四个正方形的面积之和为68平方厘米,其阴影的长方形的周长是16厘米,求阴影部分的面积
设阴影长方形长与宽分别为a,b a×a+b×b=130÷2=65 a+b=22÷2=11 经尝试a,b分别为4,7 阴影长方形面积=4×7=28（平方厘米）
ห้องสมุดไป่ตู้
课后作业
练习1
1、如图,图形甲与乙的面积差又可以看做是长方形 ABCD与（三角形）的差
ABF
练习2
2、将右图通过平移的方法变成一个长方形
小学数学几何问题之等积变形
例1 下图(单位:厘米)是两个相同的直角梯形重叠在一起: 求阴影部分的面积
20-5=15(厘米) (15+20)×8÷2=140(平方厘米)
例2
下图中,矩形ABCD的边AB为4厘米,BC为6厘米,三角形ABF比三角形EDF的面积大9平方厘米，求ED的长。
4×6-9=15（平方厘米） EC=15×2÷6=5（厘米） ED=5-4=1（厘米）
设阴影长方形长与宽分别为a,b a×a+b×b=68÷2=34 A+b=16÷2=8 经尝试长与宽分别为5,3 阴影面积=3×5=15（平方厘米）
平行四边形ABCD面积--三角形BCE面积=10（平方厘米）三角形BCE面积=10×8÷2=40（平方厘米）平行四边形ABCD面积=40+10=50（平方厘米）

五年级数学(下)长方体正方体等积变形有关题型专项练习

五年级数学（下）长方体正方体等积变形有关题型专项练习
1）体育场用 37.5 立方米的煤渣铺在一条长100米、宽7.5米的直跑道上。

煤渣可以铺多厚？
2）有一块棱长是80厘米的正方体的铁块，现在要把它溶铸成一个横截面积是20平方厘米的长方体，这个长方体的长是多少厘米？
3）学校运来7.6立方米的沙子，铺在一个宽5米，厚40厘米的沙坑里，可以铺多少米长？
4)一辆货车的车厢是长方体的，长4米，宽2米，高1.8米，里面装满了沙子。

把这些沙子铺到长30米，宽4米的公路上，可以铺多少厘米厚？
5)有一个正方体橡皮泥棱长6厘米。

现在把这块橡皮泥捏成一个长为8 cm，宽为3cm的长方体，这个长方体的高是多少厘米?
6）有一个正方体铝块，棱长是6cm。

如果把它锻造成长为9cm，宽为8cm（锻造过程中的损耗忽略不计）的长方体，长方体的高是多少厘米?
7）学校把 8m的黄沙填入沙坑，已知沙坑长5m，宽36 dm。

如果沙坑中至少需要填 40cm深的黄沙，这些黄沙够用吗?
8）如右图：一个长方体封闭容器长20厘米，宽15厘米，高
35厘米，里面装有25厘米高的水。

如果把这封闭容器如图放
倒，这时容器里面的水高是多少厘米？。