(完整版)将军饮马系列最值问题-教师版
将军饮马(最完整讲义)
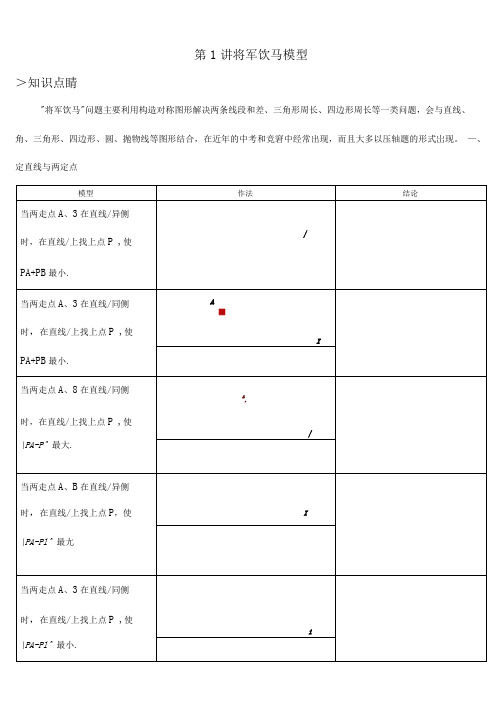
第1讲将军饮马模型>知识点睛"将军饮马"问题主要利用构造对称图形解决两条线段和差、三角形周长、四边形周长等一类问题,会与直线、角、三角形、四边形、圆、抛物线等图形结合,在近年的中考和竞窘中经常出现,而且大多以压轴题的形式岀现。
—、定直线与两定点>精讲精练例1 :如图,点P是乙AOB内任意一点f"O於30° r OP=8,点〃和点AZ分别是射线Q4和射线OB上的动点,贝ZPMN周长的最小值・例2 :如图,正方形ABCD 的边长是4 , 〃在DC 上,且DM", /V 是力0边上的一动点,贝4DMN 周长的最小 值.例3 :如图,在R2ABO 中.zO 必=90° " ( 4,4 ),点。
在边ABA L ^AC.CB^.3,点Z?为OB 的中点,点P 为边OA 上的动点,当点P 在OA 上移动时,使四边形PWU 周长最小的点P 的坐标为( )例4 :如图,在汀中r AC=BC^ACB=^ .点D 在BC 上f BD=3 . DC=\ ,点Q 是力0上的动点,则PC+PD 的最小值为()A.4例5 :如图,在等边卫力中,AB=6 , /V 为AB±-点且BN=2AN t 的高线力。
交EC 于点D t 〃是AD±_的动点■连结BM. MN.则3/W+/14/V 的最小值是 ______________ .A ・(2,2)D M8. 3>/3 C. 2>/6 0・ 4.5例6 :如图,在R2ABD 中,力於6 , z24Q=30° , zZ?=90° r /V 为力0上一点且BN=2AN. 〃是力。
上的动点, 连结BM t MN.则劭升/14/V 的最小值・例7 :如图,在 ^ABC 中,z/l«=90°, AC=6・力於12 r 力。
平分z04/点尸是力。
的中点,点F 是AD±_的 动点,则QF+FF 的最小值为()例8 :如图,在锐角三角形力中,BC=4 t z/I^C=60° , BD 平分zABC,交MU 于点D, M 、/V 分别是BD, BC 上的动点,则CM+ MN 的最小值是()A ・ VJB . 2C. 2 JID . 4例9 :如图,在菱形ABCD 中r AC= 6^2 , BD=6 , F 是BC 的中点,P 、M 分别是AC^力0上的动点,连接PE 、如,则PF+加的最小值是()B ・ 4 D ・ 2s/3第7题图 第8题图例10 :如图r矩形ABOC的顶点力的坐标为(45 ) , Q是03的中点,F是OC上的一点,当出力%的周长最小时,点F的坐标是(4A ・(0.-)B • 2>/10例12:如图f ABCD中/於10/U5,点£ F、G、〃分别在矩形力02各边上,旦AE=CG, BF=DH,则四边形"6片周长的最小值为()力.5>/5 B ・C・ 10j亍 D • \5長例13 :如图,zMO於60° f点P是乙AOB内的走点且OP= 73 ,若点M、/V分别是射线04 03上异于点O的动点,贝ZPMN周长的最小值是(力•迹B•巫2 2)C. 6D. 3C • (0,2) D.(O.y) 例11 :如图,在矩形ABCD中z AB=6 , AD=3 .动点P满足片刑第10题图例14 :如图,乙AOB的边02与"轴正半轴重合点P是04上的一动点,点/V( 3,0 )是03上的一定点,点M 是O/V的中点,zAO8=30°.要使PW+P/V最小,则点P的坐标为________________________ .例15 :如图,已知正比例函数y=kx( £>0 )的图像与x轴相交所成的锐角为70°,走点力的坐标为(0,4) , P 为F轴上的f 动点,M、/V为函数y^kx ( k>0 )的图像上的两个动点r则AM±MP+PN的最小值为第15题图例16 :如图,在平面直角坐标系中,矩形ABCD的顶点B在原点,点4 U在坐楙由上r点Z?的坐标为(6,4), F为CO的中点,点只Q为边上两个动点,且Pg2 ,要使四边形APQE的周长最小r则点P的坐示应为例17 :如图,矩形ABCD中,A»2 t AB=4 , MU为对角线,E、F分别为边AB、CQ上的动点,且EFrAC于点连接CF,求AF+CE的最小值.例18 :如图,正方形ABCD的面积是12 r心ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,求PD + PE的最小值。
(完整word版)将军饮马问题的11个模型及例题

将军饮马问题问题概述路径最短、线段和最小、线段差最大、周长最小等一系列最值问题方法原理1.两点之间,线段最短;2.三角形两边之和大于第三边,两边之差小于第三边;3.中垂线上的点到线段两端点的距离相等;4.垂线段最短.基本模型1.已知:如图,定点A、B分布在定直线l两侧;要求:在直线l上找一点P,使PA+PB的值最小解:连接AB交直线l于点P,点P即为所求,PA+PB的最小值即为线段AB的长度理由:在l上任取异于点P的一点P´,连接AP´、BP´,在△ABP’中,AP´+BP´>AB,即AP´+BP´>AP+BP∴P为直线AB与直线l的交点时,PA+PB最小.2.已知:如图,定点A和定点B在定直线l的同侧要求:在直线l上找一点P,使得PA+PB值最小(或△ABP的周长最小)解:作点A关于直线l的对称点A´,连接A´B交l于P,点P即为所求;理由:根据轴对称的性质知直线l为线段AA´的中垂线,由中垂线的性质得:PA=PA´,要使PA+PB最小,则需PA´+PB值最小,从而转化为模型1.3.已知:如图,定点A、B分布在定直线l的同侧(A、B两点到l的距离不相等)要求:在直线l上找一点P,使︱PA-PB︱的值最大解:连接BA并延长,交直线l于点P,点P即为所求;理由:此时︱PA-PB︱=AB,在l上任取异于点P的一点P´,连接AP´、BP´,由三角形的三边关系知︱P´A-P´B︱<AB,即︱P´A-P´B︱<︱PA-PB︱4. 已知:如图,定点A、B分布在定直线l的两侧(A、B两点到l的距离不相等)要求:在直线l上找一点P,使︱PA-PB︱的值最大解:作点B关于直线l的对称点B´,连接B´A并延长交于点P,点P即为所求;理由:根据对称的性质知l为线段BB´的中垂线,由中垂线的性质得:PB=PB´,要使︱PA-PB︱最大,则需︱PA-PB´︱值最大,从而转化为模型3.典型例题1-1如图,直线y=2x+4与x轴、y轴分别交于点A和点B,点C、D分3别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为_________,此时PC+PD的最小值为_________.【分析】符合基本模型2的特征,作点D关于x轴的对称点D',连接CD'交x轴于点P,此时PC+PD值最小,由条件知CD为△BAO的中位线,OP为△CDD'的中位线,易求OP长,从而求出P点坐标;PC+PD的最小值即CD'长,可用勾股定理(或两点之间的距离公式,实质相同)计算.【解答】连接CD,作点D关于x轴的对称点D′,连接CD′交x轴于点P ,此时PC+PD 值最小.令y=23x+4中x=0,则y=4, ∴点B 坐标(0,4);令y=23x+4中y=0,则23x+4=0,解得:x=﹣6,∴点A 的坐标为(﹣6,0).∵点C 、D 分别为线段AB 、OB 的中点,∴CD 为△BAO 的中位线, ∴CD ∥x 轴,且CD=21AO=3,∵点D ′和点D 关于x 轴对称,∴O 为DD ′的中点,D ′(0,-1),∴OP 为△CDD ′的中位线,∴OP=21CD=23,∴点P 的坐标为(﹣32,0).在Rt △CDD ′中,CD ′=22D D CD '+=2243+=5,即PC+PD 的最小值为5.【小结】还可用中点坐标公式先后求出点C 、点P 坐标;若题型变化,C 、D 不是AB 和OB 中点时,则先求直线CD ′的解析式,再求其与x 轴的交点P 的坐标.典型例题1-2如图,在平面直角坐标系中,已知点A 的坐标为(0,1),点B的坐标为(32,﹣2),点P 在直线y=﹣x 上运动,当|PA ﹣PB|最 大时点P 的坐标为_________,|PA ﹣PB|的最大值是_________.【分析】符合基本模型4的特征,作A 关于直线y=﹣x 对称点C ,连接BC ,可得直线BC 的方程;求得BC 与直线y=﹣x 的交点P 的坐标;此时|PA ﹣PB|=|PC ﹣PB|=BC 取得最大值,再用两点之间的距离公式求此最大值.【解答】作A 关于直线y=﹣x 对称点C ,易得C 的坐标为(﹣1,0);连接BC ,可得直线BC的方程为y=﹣54x ﹣54,与直线y=﹣x 联立解得交点坐标P 为(4,﹣4);此时|PA﹣PB|=|PC ﹣PB|=BC 取得最大值,最大值BC=2223)2()1(-++=241;【小结】“两点一线”大多考查基本模型2和4,需作一次对称点,连线得交点.变式训练1-1已知菱形OABC 在平面直角坐标系的位置如图所示,顶点A (5,0),OB=4√5,点P 是对角线OB 上的一个动点,D (0,1),当CP+DP 最短时,点P 的坐标为( )A .(0,0)B .(1,12)C .(65,35)D .(107,57)变式训练1-2如图,菱形ABCD 中,对角线AC 和BD 交于点O ,AC=2,BD=2√3,E 为AB 的中点,P 为对角线AC 上一动点,则PE+PB 的最小值为__________.变式训练1-3如图,已知直线y=12x+1与y 轴交于点A ,与x 轴交于点D ,抛物线y=12x 2+bx+c 与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为(1,0).(1)求该抛物线的解析式;(2)在抛物线的对称轴上找一点M ,使|AM ﹣MC|的值最大,求出点M 的坐标.拓展模型1. 已知:如图,A 为锐角∠MON 外一定点;要求:在射线OM 上找一点P ,在射线ON 上找一点Q ,使AP+PQ 的值最小.解:过点A 作AQ ⊥ON 于点Q ,AQ 与OM 相交于点P ,此时,AP+PQ 最小;理由:AP+PQ ≧AQ ,当且仅当A 、P 、Q 三点共线时,AP+PQ 取得最小值AQ ,根据垂线段最短,当AQ ⊥ON 时,AQ 最小.2. 已知:如图,A 为锐角∠MON 内一定点;要求:在射线OM 上找一点P ,在射线ON 上找一点Q ,使AP+PQ 的值最小.解:作点A关于OM的对称点A′,过点A′作AQ⊥ON于点Q,A′Q交OM于点P,此时AP+PQ最小;理由:由轴对称的性质知AP=A′P,要使AP+PQ最小,只需A′P+PQ最小,从而转化为拓展模型13.已知:如图,A为锐角∠MON内一定点;要求:在射线OM上找一点P,在射线ON上找一点Q,使△APQ的周长最小解:分别作A点关于直线OM的对称点A1,关于ON的对称点A 2,连接 A1A2交OM于点P,交ON于点Q,点P和点Q即为所求,此时△APQ周长最小,最小值即为线段A1A2的长度;理由:由轴对称的性质知AP=A1P,AQ=A2Q,△APQ的周长AP+PQ+AQ=A1P+PQ+A2Q,当A1、P、Q、A2四点共线时,其值最小.4. 已知:如图,A、B为锐角∠MON内两个定点;要求:在OM上找一点P,在ON上找一点Q,使四边形APQB的周长最小解:作点A关于直线OM的对称点A´,作点B关于直线ON的对称点B´,连接A´B´交OM于P,交ON于Q,则点P、点Q即为所求,此时四边形APQB周长的最小值即为线段AB和A´B´的长度之和;理由:AB长为定值,由基本模型将PA转化为PA´,将QB转化为QB´,当A´、P、Q、B´四点共线时,PA´+PQ+ QB´的值最小,即PA+PQ+ QB的值最小.5.搭桥模型已知:如图,直线m∥n,A、B分别为m上方和n下方的定点,(直线AB不与m垂直)要求:在m、n之间求作垂线段PQ,使得AP+PQ+BQ最小.分析:PQ为定值,只需AP+BQ最小,可通过平移,使P、Q“接头”,转化为基本模型解:如图,将点A沿着平行于PQ的方向,向下平移至点A′,使得AA′=PQ,连接A′B交直线n于点Q,过点Q作PQ⊥n,交直线m于点P,线段PQ即为所求,此时AP+PQ+BQ最小.理由:易知四边形QPAA′为平行四边形,则QA′=PA,当B、Q、A′三点共线时,QA′+BQ最小,即AP+BQ最小,PQ长为定值,此时AP+PQ+BQ最小.6.已知:如图,定点A、B分布于直线l两侧,长度为a(a为定值)的线段PQ在l上移动(P在Q左边)要求:确定PQ的位置,使得AP+PQ+QB最小分析:PQ为定值,只需AP+QB的值最小,可通过平移,使P、Q“接头”,转化为基本模型解:将点A沿着平行于l的方向,向右移至A´,使AA´=PQ=a,连接A´B交直线l于点Q,在l上截取PQ=a(P在Q左边),则线段PQ即为所求,此时AP+PQ+QB的最小值为A´B+PQ,即A´B+a理由:易知四边形APQA´为平行四边形,则PA=QA´,当A´、Q、B三点共线时,QA´+QB最小,即PA+QB最小,又PQ长为定值此时PA+PQ+QB值最小.7.已知:如图,定点A、B分布于直线l的同侧,长度a(a为定值)的线段PQ在l上移动(P在Q左边)要求:确定PQ 的位置,使得四边形APQB 周长最小分析:AB 长度确定,只需AP+PQ+QB 最小,通过作A 点关于l 的对称点,转化为上述模型3解:作A 点关于l 的对称点A ´,将点A ´沿着平行于l的方向,向右移至A ´´,使A ´A ´´=PQ=a ,连接A ´´B交l 于Q ,在l 上截取QP=a (P 在Q 左边),线段PQ 即为所求,此时四边形APQB 周长的最小值为A ´´B+AB+PQ ,即A ´´B+AB+a典型例题2-1如图,在矩形ABCD 中,AB=10,BC=5,若点M 、N 分别是线段AC 、AB 上的两个动点,则BM+MN 的最小值为 .【分析】符合拓展模型2的特征,作点B 关于AC 的对称点E ,再过点E 作AB 的垂线段,该垂线段的长即BM+MN 的最小值,借助等面积法和相似可求其长度.【解答】作点B 关于AC 的对称点E ,再过点E 作EN ⊥AB 于N ,则BM+MN=EM+MN ,其最小值即EN 长;∵AB=10,BC=5,∴AC=22BC AB +=55,等面积法求得AC 边上的高为55510⨯=25,∴BE=45, 易知△ABC ∽△ENB ,∴,代入数据解得EN=8. 即BM+MN 的最小值为8.【小结】该类题的思路是通过作对称,将线段转化,再根据定理、公理连线或作垂线;可作定点或动点关于定直线的对称点,有些题作定点的对称点易解,有些题则作动点的对称点易解.典型例题2-2如图,∠AOB=60°,点P 是∠AOB 内的定点且OP=,点M 、N 分别是射线OA 、OB 上异于点O 的动点,则△PMN 周长的最小值是( )A .B .C .6D .3【分析】符合拓展模型3的特征;作P点分别关于OA、OB的对称点C、D,连接CD分别交OA、OB于M、N,此时△PMN周长最小,其值为CD长;根据对称性连接OC、OD,分析条件知△OCD是顶角为120°的等腰三角形,作底边上高,易求底边CD. 【解答】作P点分别关于OA、OB的对称点C、D,连接CD分别交OA、OB于M、N,如图,则MP=MC,NP=ND,OP=OD=OC=,∠BOP=∠BOD,∠AOP=∠AOC,∴PN+PM+MN=ND+MN+NC=DC,∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB=120°,∴此时△PMN周长最小,作OH⊥CD于H,则CH=DH,∵∠OCH=30°,∴OH=OC=,CH=OH=,∴CD=2CH=3.即△PMN周长的最小值是3;故选:D.【小结】根据对称的性质,发现△OCD是顶角为120°的等腰三角形,是解题的关键,也是难点.典型例题2-3如图,已知平行四边形ABCO,以点O为原点,OC所在的直线为x轴,建立直角坐标系,AB交y轴于点D,AD=2,OC=6,∠A=60°,线段EF所在的直线为OD的垂直平分线,点P为线段EF上的动点,PM⊥x轴于点M点,点E与E′关于x轴对称,连接BP、E′M.(1)请直接写出点A坐标为,点B坐标为;(2)当BP+PM+ME′的长度最小时,请求出点P的坐标.【分析】(1)解直角三角形求出OD,BD的长即可解决;(2)符合“搭桥模型”的特征;首先证明四边形OPME′是平行四边形,可得OP=EM,PM是定值,PB+ME′=OP+PB的值最小时,BP+PM+ME′的长度最小,此时P点为直线OB与EF的交点,结合OB的解析式可得P点坐标;【解答】(1)在Rt△ADO中,∵∠A=60°,AD=2,∴OD=2•tan60°=2,∴A(﹣2,2),∵四边形ABCO是平行四边形,∴AB=OC=6,∴DB=6﹣2=4,∴B(4,2)(2)如图,连接OP.∵EF垂直平分线段OD,PM⊥OC,∴∠PEO=∠EOM=∠PMO=90°,∴四边形OMPE是矩形,∴PM=OE=,∵OE=OE′,∴PM=OE′,PM∥OE′,∴四边形OPME′是平行四边形,∴OP=EM,∵PM是定值,∴PB+ME′=OP+PB的值最小时,BP+PM+ME′的长度最小,∴当O、P、B共线时,BP+PM+ME′的长度最小,∵直线OB的解析式为y=x,∴P(2,).【小结】求没有公共端点的两条线段之和的最小值,一般通过作对称和平移(构造平行四边形)的方法,转化为基本模型.典型例题2-4如图所示,在平面直角坐标系中,Rt△AOB的顶点坐标分别为A(﹣2,0),O(0,0),B(0,4),把△AOB绕点O按顺时针方向旋转90°,得到△COD.(1)求C、D两点的坐标;(2)求经过A、B、D三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上取两点E、F(点E在点F的上方),且EF=1,使四边形ACEF的周长最小,求出E、F两点的坐标.【分析】符合拓展模型7的特征,通过作对称、平移、连线,可找出E、F点,结合直线的解析式和抛物线的对称轴可解出E、F坐标.【解答】(1)由旋转的性质可知:OC=OA=2,OD=OB=4,∴C点的坐标是(0,2),D点的坐标是(4,0),(2)设所求抛物线的解析式为y=ax2+bx+c,4a-2b+c=0由题意,得 16a+4b+c=0c=4解得a=-12,b=1,c=4,∴所求抛物线的解析式为y=-12x²+x+4;(3)只需AF+CE最短,抛物线y=-12x²+x+4的对称轴为x=1,将点A向上平移至A1(﹣2,1),则AF=A1E,作A1关于对称轴x=1的对称点A2(4,1),连接A2C,A2C与对称轴交于点E,E为所求,可求得A2C的解析式为y=-14x+2,当x=1时,y=74,∴点E的坐标为(1,74),点F的坐标为(1,34).【小结】解决此类题的套路是“对称、平移、连线”;其中,作对称和平移的顺序可互换.变式训练2-1几何模型:条件:如图1,A,B是直线l同旁的两个定点.问题:在直线l上确定一点P,使PA+PB的值最小.方法:作点A关于直线l的对称点A’,连接A’B交l于点P,即为所求.(不必证明)模型应用:(1)如图2,已知平面直角坐标系中两定点A(0,﹣1)和B(2,﹣1),P为x轴上一动点,则当PA+PB的值最小是点P的横坐标是,此时PA+PB= .(2)如图3,正方形ABCD的边长为4,E为AB的中点,P是AC上一动点,连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是.(3)如图4,在菱形ABCD中,AB=10,∠DAB=60°,P是对角线AC上一动点,E,F分别是线段AB和BC上的动点,则PE+PF的最小值是.(4)如图5,在菱形ABCD中,AB=6,∠B=60°,点G是边CD边的中点,点E.F分别是AG,AD上的两个动点,则EF+ED的最小值是.变式训练2-2如图,矩形ABCD中,AD=15,AB=10,E为AB边上一点,且DE=2AE,连接CE与对角线BD交于F;若P、Q分别为AB边和BC边上的动点,连接EP、PQ和QF;则四边形EPQF周长的最小值是___________.变式训练2-3如图,已知直线l 1∥l2,l1、l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ=4,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ最小,此时PA+BQ= .变式训练2-4如图,已知在平面直角坐标系xOy中,直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于点E和F.(1)求经过A、B、C三点的抛物线的解析式;(2)当BE经过(1)中抛物线的顶点时,求CF的长;(3)在抛物线的对称轴上取两点P、Q(点Q在点P的上方),且PQ=1,要使四边形BCPQ 的周长最小,求出P、Q两点的坐标.中考真题1.要在街道旁建奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使A、B到它的距离之和最短?小聪以街道为x轴,建立了如图所示的平面直角坐标系,A点坐标为(0,3),B点坐标为(6,5),则A、B两点到奶站距离之和的最小值是.2.如图,矩形ABOC的顶点A的坐标为(﹣4,5),D是OB的中点,E是OC上的一点,当△ADE的周长最小时,点E的坐标是()A .(0,)B .(0,)C .(0,2)D .(0,)3.如图,在矩形ABCD 中,AB=5,AD=3,动点P 满足S △PAB =31S 矩形ABCD ,则点P 到A 、B 两点距离之和PA+PB 的最小值为( )A .B .C .5D .4.已知抛物线y=x 2+1具有如下性质:该抛物线上任意一点到定点F (0,2)的距离与到x轴的距离始终相等,如图,点M 的坐标为(,3),P 是抛物线y=x 2+1上一个动点,则△PMF 周长的最小值是( )A .3B .4C .5D .65.如图,点A (a ,3),B (b ,1)都在双曲线y=上,点C ,D ,分别是x 轴,y 轴上的动点,则四边形ABCD 周长的最小值为( )A .B .C .D .6.如图,在Rt △ABC 中,∠C=90°,AC=3,BC=4,D 、E 分别是AB 、BC 边上的动点,则AE+DE 的最小值为( )A .B .C .5D .7.如图,Rt △ABC 中,∠BAC=90°,AB=3,AC=6,点D ,E 分别是边BC ,AC 上的动点,则DA+DE 的最小值为 .8.如图,等腰△ABC 的底边BC=20,面积为120,点F 在边BC 上,且BF=3FC ,EG 是腰AC 的垂直平分线,若点D 在EG 上运动,则△CDF 周长的最小值为 .9.如图,菱形ABCD 的边长为6,∠ABC=120°,M 是BC 边的一个三等分点,P 是对角线AC 上的动点,当PB+PM 的值最小时,PM 的长是( )A.B.C.D.10.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为()A.B.C.D.611.如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN 的最小值是()A.6B.10 C.2D.212.如图,△ABC中,AC=BC=2,AB=1,将它沿AB翻折得到△ABD,则四边形ADBC的形状是形,P、E、F分别为线段AB、AD、DB上的任意点,则PE+PF的最小值是.13.如图,已知抛物线y=x2+bx+c与直线y=x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).(1)求此抛物线的解析式;(2)在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P,使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.14.如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD.(1)用尺规作∠ADC的平分线DE,交BC于点E,连接AE(保留作图痕迹,不写作法);(2)在(1)的条件下,①证明:AE⊥DE;②若CD=2,AB=4,点M,N分别是AE,AB上的动点,求BM+MN的最小值.15.如图,抛物线y=ax2+bx+c(a≠0)经过点A(﹣1,0),B(3,0),C(0,3)三点.(1)求抛物线的解析式及顶点M的坐标;(2)连接AC、BC,N为抛物线上的点且在第四象限,当S△NBC=S△ABC时,求N点的坐标;(3)在(2)问的条件下,过点C作直线l∥x轴,动点P(m,3)在直线l上,动点Q(m,0)在x轴上,连接PM、PQ、NQ,当m为何值时,PM+PQ+QN的和最小,并求出 PM+PQ+QN 和的最小值.16.如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.(1)求二次函数的表达式;(2)连接BC,点N是线段BC上的动点,作ND⊥x轴交二次函数的图象于点D,求线段ND 长度的最大值;(3)若点H为二次函数y=ax2+4x+c图象的顶点,点M(4,m)是该二次函数图象上一点,在x轴、y轴上分别找点F,E,使四边形HEFM的周长最小,求出点F,E的坐标.17.如图1,已知抛物线y=(x﹣2)(x+a)(a>0)与x轴从左至右交于A,B两点,与y轴交于点C.(1)若抛物线过点T(1,﹣),求抛物线的解析式;(2)在第二象限内的抛物线上是否存在点D,使得以A、B、D三点为顶点的三角形与△ABC相似?若存在,求a的值;若不存在,请说明理由.(3)如图2,在(1)的条件下,点P的坐标为(﹣1,1),点Q(6,t)是抛物线上的点,在x轴上,从左至右有M、N两点,且MN=2,问MN在x轴上移动到何处时,四边形PQNM 的周长最小?请直接写出符合条件的点M的坐标.18.如图,对称轴为直线x=2的抛物线经过A(﹣1,0),C(0,5)两点,与x轴另一交点为B.已知M(0,1),E(a,0),F(a+1,0),P是第一象限内抛物线上的动点.(1)求此抛物线的解析式;(2)当a=1时,求四边形MEFP的面积的最大值,并求此时点P的坐标;(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.19.探究:小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用图1得到结论:P1P2=他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x=,y=.(1)请你帮小明写出中点坐标公式的证明过程;运用:(2)①已知点M(2,﹣1),N(﹣3,5),则线段MN长度为;②直接写出以点A(2,2),B(﹣2,0),C(3,﹣1),D为顶点的平行四边形顶点D的坐标:;拓展:(3)如图3,点P(2,n)在函数y=x(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.20.如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C.(1)求直线y=kx+b的函数解析式;(2)若点P(x,y)是抛物线y=﹣x2+2x+1上的任意一点,设点P到直线AB的距离为d,求d关于x的函数解析式,并求d取最小值时点P的坐标;(3)若点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,求CE+EF的最小值.21.如图①,在平面直角坐标系中,OA=6,以OA为边长作等边三角形ABC,使得BC∥OA,且点B、C落在过原点且开口向下的抛物线上.(1)求这条抛物线的解析式;(2)在图①中,假设一动点P从点B出发,沿折线BAC的方向以每秒2个单位的速度运动,同时另一动点Q从O点出发,沿x轴的负半轴方向以每秒1个单位的速度运动,当点P 运动到A点时,P、Q都同时停止运动,在P、Q的运动过程中,是否存在时间t,使得PQ⊥AB,若存在,求出t的值,若不存在,请说明理由;(3)在BC边上取两点E、F,使BE=EF=1个单位,试在AB边上找一点G,在抛物线的对称轴上找一点H,使得四边形EGHF的周长最小,并求出周长的最小值.本人所著《初中几何模型与解题通法》已发行,可在当当、淘宝和京东搜索购买特色:1.由一线名师编写,更专业权威,各地历年中考压轴题几乎都能在书中找到对应的模型和方法,甚至出现大量高度类似题。
(完整版)将军饮马系列最值问题-教师版

1.两点之间,线段最短.2.点到直线的距离,垂线段最短.3.三角形两边之和大于第三边,两边之差小鱼第三边.4.A B 、分别为同一圆心O 半径不等的两个圆上的一点,R r AB R r -≤≤+ 当且仅当A B O 、、三点共线时能取等号.古希腊亚里山大里亚城有一位久负盛名的学者,名叫海伦.有一天,有位将军不远千里专程前来向海伦求教一个百思不得其解的问题:如图,将军从A 出发到河边饮马,然后再到B 地军营视察,显然有许多走法.问怎样走路线最短呢?精通数理的海伦稍加思索,便作了完善的回答.这个问题后来被人们称作“将军饮马”问题.下面我们来看看数学家是怎样解决的.海伦发现这是一个求折线和最短的数学问题. 根据公理:连接两点的所有线中,线段最短.若A B 、在河流的异侧,直接连接AB ,AB 与l 的交点即为所求. 若A B 、在河流的同侧,根据两点间线段最短,那么显然要把折线变成直线再解.“将军饮马”系列最值问题知识回顾知识讲解海伦解决本问题时,是利用作对称点把折线问题转化成直线现在人们把凡是用对称点来实现解题的思想方法叫对称原理,即轴对称思想轴对称及其性质:把一个图形沿某一条直线折叠,如果直线两旁的部分能够互相重合,那么这个图形就叫做轴对称图形.这条直线就是它的对称轴.这时我们就说这个图形关于这条直线(或轴)对称.如等腰ABC ∆是轴对称图形.把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就是说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.如下图,ABC ∆与'''A B C ∆关于直线l 对称,l 叫做对称轴.A 和'A ,B 和'B ,C 和'C 是对称点.轴对称的两个图形有如下性质:①关于某条直线对称的两个图形是全等形; ②对称轴是任何一对对应点所连线的垂直平分线;③两个图形关于某条直线对称,如果他们的对应线段或延长线相交,那么交点在对称轴上.线段垂直平分线:垂直平分线上点到线段两个端点的距离相等;到线段两个端点距离相等的点在线段的垂直平分线上.当已知条件出现了等腰三角形、角平分线、高,或者求几条折线段的最小值等情况,通常考虑作轴对称变换,以“补齐”图形,集中条件。
专题六—线段最值问题之将军饮马问题.doc

学员编号: 学员姓名:
授课 类型 授课日 期时段
T (同步知识主题)
辅导讲义
小初高中精品学科讲义
年 级:初三 辅导科目:数学
课 时 数:3 学科教师:
C (专题方法主题)
T (学法与能力主题)
线段最值问题—将军饮马问题
唐朝诗人李欣的诗《古从军行》开头两句说:"白日登山望烽火,黄昏饮马傍交河."诗中隐含着一个有趣的 数学问题.如图所示,诗中将军在观望烽火之后从山脚下的 A 点出发,走到河边饮马后再到 B 点宿营.请问怎样 走才能使总的路程最短?
落在 AB 边上的点 E 处,若点 P 是直线 AD 上的动点,则△ PEB 的周长的最小值是
.
5、如图,在锐角△ ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交 BC 于点 D,M、N 分别是 AD 和 AB 上的动
初中数学—最全将军饮马问题(最值问题)

初中数学—最全将军饮马问题(最值问题)(word电⼦资料⽂末领取)唐朝诗⼈李颀的诗《古从军⾏》开头两句说:'⽩⽇登⼭望烽⽕,黄昏饮马傍交河。
'诗中隐含着⼀个有趣的数学问题。
传说亚历⼭⼤城有⼀位精通数学和物理的学者,名叫海伦。
⼀天,⼀位罗马将军专程去拜访他,向他请教⼀个百思不得其解的问题。
将军每天从军营A出发,先到河边饮(yìn)马,然后再去河岸同侧的B地开会,应该怎样⾛才能使路程最短?从此,这个被称为'将军饮马'的问题⼴泛流传。
这个问题的解决并不难,据说海伦略加思索就解决了它。
抽象为数学模型:直线l同侧有两个定点A、B,请在直线l上找⼀点C,使AC+BC最⼩。
假设点A、B在直线l的⼀侧就好了,这样我们就可以利⽤【点到点最值模型:两点之间线段最短】找到点C的位置了。
即连接AB交直线l于点C。
因此,我们可以找点A关于直线l的对称点,再连接A’B交直线l于点C,点C即为所求!如果将军在河边的另外任⼀点C'饮马,所⾛的路程就是AC'+C'B但是,AC'+C'B=A'C'+C'B>A'B=A'C+CB=AC+CB.故在点C处饮马,路程最短。
掌握了这个“将军饮马模型”的原理和结论后,我们来具体挑战⼀下吧!第⼀关:⾓中应⽤1、如图,已知两点P、Q在锐⾓∠AOB内,分别在OA、OB上求点M、N,使PM+MN+NQ最短.解析:如图,分别作点P、点Q关于OA、OB的对称点P’,Q’,分别交OA、OB于点M、点N。
PM+MN+NQ=P’M+MN+N’Q,当点Q’,P’,M,N共线时,最⼩为P’Q’。
第⼆关:三⾓形中应⽤2、已知,如图△ABC为等边三⾓形,⾼AH=10cm,P为AH上⼀动点,D为AB的中点,则PD+PB的最⼩值为______cm.解析:连接PC,∵△ABC为等边三⾓形,D为AB的中点,∴PD+PB的最⼩值为:PD+PB=PC+PD=CD=AH=10cm.第三关:四边形中应⽤3、如图,正⽅形ABCD的边长为8,M在DC上,且DM=2,N是AC上⼀动点,则DN+MN的最⼩值为解析:如图,连接BM,∵点B和点D关于直线AC对称,∴NB=ND,则BM就是DN+MN的最⼩值,∵正⽅形ABCD的边长是8,DM=2,∴CM=6,∴由勾股定理得BM=10,∴DN+MN的最⼩值是10.第四关:圆中应⽤4、如图,MN是O的直径,MN=2,点A在O上,∠AMN=30∘,B为弧AN的中点,P是直径MN上⼀动点,则PA+PB的最⼩值为___.解析:作点B关于MN的对称点C,连接AC交MN于点P,则P点就是所求作的点。
2022年中考数学二次函数压轴突破 专题02 将军饮马模型(教师版含解析)

将军饮马模型考情分析:通过全国中考试题分析来看,将军饮马的模型多出现在中考二次函数压轴题第二问中出现,难度不大,但需要注意对称点的选择,动点通常在对称轴上,而且已知定点中往往有一个与x 轴的交点.考法主要有以下几种:1.求取最小值时动点坐标2.求最小值.3.求三角形或四边形周长最小值.模型一:两定点一动点如图,A,B 为定点,P 为l 上动点,求AP+BP 最小值解析:作点A 关于直线的对称点A',连接P A',则P A '=P A ,所以P A +PB =P A '+PB当A'、P 、B 三点共线的时候,P A'+PB =A'B ,此时为最小值(两点之间线段最短)PBAA 'ABP 折点端点A 'P BA如图,P 为定点,M 、N 分别为OA 和OB 上的动点,求△PMN 周长最小值解析:分别作点P 关于OA 、OB 的对称点,则△PMN 的周长为PM +MN +NP =P'M +MN +NP '',当P '、M 、N 、P ''共线时,△PMN 周长最小.模型三:两定点两动点如图,P 、Q 为两定点,M 、N 分别为OA 、OB 上的动点,求四边形PQMN 的最小值.解析:∵PQ 是条定线段,∴只需考虑PM +MN +NQ 最小值即可, 分别作点P 、Q 关于OA 、OB 对称, PM +MN +NQ =P 'M +MN +NQ ',当P '、M 、N 、Q '共线时,四边形PMNQ 的周长最小。
BBBB如图,P 为定点,M 、N 分别为OA 、OB 上的动点,求PM +MN 最小值。
解析:作点P 关于OA 对称的点P ',PM +MN =P 'M +MN ,过点P '作OB 垂线分别交OA 、OB 于点M 、N , 得PM +MN 最小值(点到直线的连线中,垂线段最短)模型五:将军饮马有距离例一、如图,A 、D 为定点,B 、C 为直线l 上两动点,BC 为定值,求AB+BC+CD 最小值?解析:BC 为定值,只需求AB+CD 最小即可;平移AB 至CE ,则变成求CE+CD 的最小值,基本将军饮马的模型例二、如图,A 、D 为定点,B 、C 为直线l 1 、l 2上两动点,BC ⊥l 1,求AB+BC+CD 最小值?解析:BC 为定值,只需求AB+CD 最小即可;BB平移CD至BE,则变成求AB+BE最小,基本将军饮马.经典例题剖析:例一:如图1(注:与图2完全相同),在直角坐标系中,抛物线经过点(1,0)A、(5,0)B、(0,4)C三点.(1)求抛物线的解析式和对称轴;(2)P是抛物线对称轴上的一点,求满足PA PC+的值为最小的点P坐标(请在图1中探索);【分析】(1)将点A、B的坐标代入二次函数表达式得:2(1)(5)(65)y a x x a x x=--=-+,即可求解;(2)连接B、C交对称轴于点P,此时PA PC+的值为最小,即可求解;【解答】解:(1)将点A、B的坐标代入二次函数表达式得:2(1)(5)(65)y a x x a x x=--=-+,则54a=,解得:45a=,抛物线的表达式为:224424(65)4555y x x x x=-+=-+,函数的对称轴为:3x=,顶点坐标为16(3,)5-;(2)连接B、C交对称轴于点P,此时PA PC+的值为最小,将点B、C的坐标代入一次函数表达式:y kx b=+得:054k bb=+⎧⎨=⎩,解得:454kb⎧=-⎪⎨⎪=⎩,直线BC的表达式为:445y x=-+,当3x =时,85y =, 故点8(3,)5P ;例二:如图,直线3y x =-+与x 轴、y 轴分别交于B 、C 两点,抛物线2y x bx c =-++经过点B 、C ,与x 轴另一交点为A ,顶点为D .(1)求抛物线的解析式;(2)在x 轴上找一点E ,使EC ED +的值最小,求EC ED +的最小值;【分析】(1)直线3y x =-+与x 轴、y 轴分别交于B 、C 两点,则点B 、C 的坐标分别为(3,0)、(0,3),将点B 、C 的坐标代入二次函数表达式,即可求解;(2)如图1,作点C 关于x 轴的对称点C ',连接CD '交x 轴于点E ,则此时EC ED +为最小,即可求解; 【解答】解:(1)直线3y x =-+与x 轴、y 轴分别交于B 、C 两点,则点B 、C 的坐标分别为(3,0)、(0,3), 将点B 、C 的坐标代入二次函数表达式得:9303b c c -++=⎧⎨=⎩,解得:23b c =⎧⎨=⎩,故函数的表达式为:223y x x =-++,令0y =,则1x =-或3,故点(1,0)A -; (2)如图1,作点C 关于x 轴的对称点C ',连接CD '交x 轴于点E ,则此时EC ED +为最小,函数顶点D 坐标为(1,4),点(0,3)C '-,将C '、D 的坐标代入一次函数表达式并解得: 直线C D '的表达式为:73y x =-, 当0y =时,37x =, 故点3(7E ,0),则EC ED +的最小值为DC '=例三:如图,以D 为顶点的抛物线2y x bx c =-++交x 轴于A 、B 两点,交y 轴于点C ,直线BC 的表达式为3y x =-+. (1)求抛物线的表达式;(2)在直线BC 上有一点P ,使PO PA +的值最小,求点P 的坐标;【分析】(1)先求得点B 和点C 的坐标,然后将点B 和点C 的坐标代入抛物线的解析式得到关于b 、c 的方程,从而可求得b 、c 的值;(2)作点O 关于BC 的对称点O ',则(3,3)O ',则OP AP +的最小值为AO '的长,然后求得AO '的解析式,最后可求得点P 的坐标;【解答】解:(1)把0x =代入3y x =-+,得:3y =,(0,3)C ∴. 把0y =代入3y x =-+得:3x =,(3,0)B ∴,将(0,3)C 、(3,0)B 代入2y x bx c =-++得:9303b c c -++=⎧⎨=⎩,解得2b =,3c =.∴抛物线的解析式为223y x x =-++.(2)如图所示:作点O 关于BC 的对称点O ',则(3,3)O '. O '与O 关于BC 对称,PO PO ∴='.OP AP O P AP AO ∴+='+'.∴当A 、P 、O '在一条直线上时,OP AP +有最小值.设AP 的解析式为y kx b =+,则033k b k b -+=⎧⎨+=⎩,解得:34k =,34b =.AP ∴的解析式为3344y x =+. 将3344y x =+与3y x =-+联立,解得:127y =,97x =,∴点P 的坐标为9(7,12)7.例四:如图,抛物线2y ax bx c =++的图象过点(1,0)A -、(3,0)B 、(0,3)C .(1)求抛物线的解析式;(2)在抛物线的对称轴上是否存在一点P ,使得PAC ∆的周长最小,若存在,请求出点P 的坐标及PAC ∆的周长;若不存在,请说明理由;【分析】(1)由于条件给出抛物线与x 轴的交点(1,0)A -、(3,0)B ,故可设交点式(1)(3)y a x x =+-,把点C 代入即求得a 的值,减小计算量.(2)由于点A 、B 关于对称轴:直线1x =对称,故有PA PB =,则PAC C AC PC PA AC PC PB ∆=++=++,所以当C 、P 、B 在同一直线上时,PAC C AC CB ∆=+最小.利用点A 、B 、C 的坐标求AC 、CB 的长,求直线BC 解析式,把1x =代入即求得点P 纵坐标.【解答】解:(1)抛物线与x 轴交于点(1,0)A -、(3,0)B ∴可设交点式(1)(3)y a x x =+- 把点(0,3)C 代入得:33a -=1a ∴=-2(1)(3)23y x x x x ∴=-+-=-++∴抛物线解析式为223y x x =-++(2)在抛物线的对称轴上存在一点P ,使得PAC ∆的周长最小. 如图1,连接PB 、BC点P 在抛物线对称轴直线1x =上,点A 、B 关于对称轴对称PA PB ∴=PAC C AC PC PA AC PC PB ∆∴=++=++当C 、P 、B 在同一直线上时,PC PB CB +=最小 (1,0)A -、(3,0)B 、(0,3)C221310AC ∴=+=,223332BC =+=1032PAC C AC CB ∆∴=+=+最小设直线BC 解析式为3y kx =+把点B 代入得:330k +=,解得:1k =-∴直线:3BC y x =-+132P y ∴=-+=∴点(1,2)P 使PAC ∆的周长最小,最小值为1032+专题训练1.(2020秋•马山县期中)如图,抛物线2(0)y ax bx c a =++≠与x 轴交于点A 、(1,0)B ,与y 轴交于点C ,直线122y x =-经过点A 、C .抛物线的顶点为D ,对称轴为直线l . (1)求抛物线的解析式;(2)设点G 是y 轴上一点,是否存在点G ,使得GD GB +的值最小,若存在,求出点G 的坐标;若不存在,请说明理由.【分析】(1)利用一次函数的性质求得点A 、C 的坐标,然后把点A 、B 、C 的坐标分别代入二次函数解析式,利用待定系数法求得二次函数解析式;(2)利用轴对称-最短路径方法得点G ,先计算B D '的解析式,令0x =可得点G 的坐标. 【解答】解:(1)如图1,对于直线122y x =-,令0y =,得4x =,令0x =,得2y =-,∴点(4,0)A ,点(0,2)C -,将(4,0)A ,(1,0)B ,(0,2)C -代入抛物线解析式得:164002a b c a b c c ++=⎧⎪++=⎨⎪=-⎩,解得:12522a b c ⎧=-⎪⎪⎪=⎨⎪=-⎪⎪⎩,∴抛物线解析式为215222y x x =-+-;(2)存在.如图3,取点B 关于y 轴的对称点B ',则点B '的坐标为(1,0)-,连接B D ',直线B D '与y 轴的交点G 即为所求的点.22151592()22228y x x x =-+-=--+,∴顶点5(2D ,9)8,设直线B D '的解析式为(0)y kx d k =+≠, 则05928k d k d -+=⎧⎪⎨+=⎪⎩,解得:928928k b ⎧=⎪⎪⎨⎪=⎪⎩,∴直线B D '的解析式为992828y x =+, 当0x =时,928y =, ∴点G 的坐标为9(0,)28. 2.(2019•遵义)如图,抛物线21:2C y x x =-与抛物线22:C y ax bx =+开口大小相同、方向相反,它们相交于O ,C 两点,且分别与x 轴的正半轴交于点B ,点A ,2OA OB =.(1)求抛物线2C 的解析式;(2)在抛物线2C 的对称轴上是否存在点P ,使PA PC +的值最小?若存在,求出点P 的坐标,若不存在,说明理由;【分析】(1)1C 、22:C y ax bx =+开口大小相同、方向相反,则1a =-,将点A 的坐标代入2C 的表达式,即可求解;(2)作点C 关于1C 对称轴的对称点(1,3)C '-,连接AC '交函数2C 的对称轴于点P ,此时PA PC +的值最小,即可求解;【解答】解:(1)令:220y x x =-=,则0x =或2,即点(2,0)B ,1C 、22:C y ax bx =+开口大小相同、方向相反,则1a =-,则点(4,0)A ,将点A 的坐标代入2C 的表达式得:0164b =-+,解得:4b =,故抛物线2C 的解析式为:24y x x =-+;(2)联立1C 、2C 表达式并解得:0x =或3,故点(3,3)C ,作点C 关于2C 对称轴的对称点(1,3)C ',连接AC '交函数2C 的对称轴于点P ,此时PA PC +的值最小为:线段AC '的长度=此时点(2,2)P ;3.(2020秋•金乡县期中)如图,在平面直角坐标系中,二次函数2y x bx c =++的图象与x 轴交于A ,B 两点,与y 轴交于点(0,3)C -,A 点的坐标为(1,0)-.(1)求二次函数的解析式;(2)若Q 为抛物线对称轴上一动点,当Q 在什么位置时QA QC +最小,求出Q 点的坐标,并求出此时QAC ∆的周长.【分析】(1)用待定系数法即可求解;(2)点A 关于函数对称轴的对称点为点B ,连接BC 交函数对称轴于点Q ,连接AQ ,则此时QAC ∆的周长最小,进而求解.【解答】解:(1)(1,0)A -,(0,3)C -在2y x bx c =++上, 则103b c c -+=⎧⎨=-⎩,解得23b c =-⎧⎨=-⎩, ∴二次函数的解析式为223y x x =--;(2)点A 关于函数对称轴的对称点为点B ,连接BC 交函数对称轴于点Q ,连接AQ ,则此时QAC ∆的周长最小,理由:QAC ∆的周长AC AQ QC AB AQ QC BC CQ =++=++=+为最小,由点B 、C 的坐标得,直线BC 的表达式为3y x =-,当1x =时,32y x =-=-,即点(1,2)Q -,则QAC ∆的周长最小值BC AC =+==.4.(2020秋•房县期中)如图,抛物线213y x mx n =-+与x 轴交于A 、B 两点,与y 轴交于点(0,1)C -,且对称轴1x =.(1)求出抛物线的解析式及A ,B 两点的坐标;(2)在对称轴上方是否存在点D ,使三角形ADC 的周长最小?若存在,求出点D 的坐标;若不存在.说明理由(使用图1);【分析】(1)用待定系数法即可求解;(2)连接CB 交对称轴于点D ,此时三角形DAC 周长最小,进而求解;【解答】解:(1)抛物线与y 轴交于点(0,1)C -,且对称轴x l =, 则11231m n -⎧-=⎪⎪⨯⎨⎪=-⎪⎩,解得231m n ⎧=⎪⎨⎪=-⎩, ∴抛物线解析式为212133y x x =--, 令2121033y x x =--=,得:11x =-,23x =, (1,0)A ∴-,(3,0)B ;(2)在对称轴上存在D 使三角形形DAC 的周长最小,连接CB 交对称轴于点D ,此时三角形DAC 周长最小.设BC 的解析式为y kx b =+,把(3,0)B 、(0,1)C -分别代入上式得:130b k b =-⎧⎨+=⎩,解得131k b ⎧=⎪⎨⎪=-⎩, 故直线BC 的解析式为113y x =-, 当1x =时,23y =-, 所以点D 的坐标为2(1,)3-; 5.(2020秋•青羊区校级期中)如图,抛物线25()2y a x h =-+经过点(1,0)A ,(0,3)C . (1)求抛物线与x 轴的另一个交点B 的坐标;(2)如图①,在抛物线的对称轴上是否存在点P ,使得四边形PAOC 的周长最小?若存在,求出此时P 点坐标;若不存在,请说明理由;【分析】(1)根据函数的对称性即可求解;(2)A、B两点关于对称轴对称,连接BC交对称轴于点P,则P点即为所求,进而求解;【解答】解:(1)由抛物线表达式知,函数的对称轴为52x=,而点(1,0)A,根据点的对称性,则512(1)42xB=+⨯-=,故点B的坐标为(4,0);(2)存在,理由:抛物线经过点(1,0)A,(4,0)B,A∴、B关于对称轴对称,如图1,连接BC,BC ∴与对称轴的交点即为所求的点P ,此时PA PC BC +=,∴四边形PAOC 的周长最小值为:OC OA BC ++,(1,0)A ,(4,0)B ,(0,3)C ,设直线BC 解析式为y kx n =+,把B 、C 两点坐标代入可得403k n n +=⎧⎨=⎩,解得343k n ⎧=-⎪⎨⎪=⎩, ∴直线BC 的解析式为334y x =-+, 由抛物线的表达式知,抛物线的对称轴为52x =, 当52x =时,39348y x =-+=, 故点P 的坐标为5(2,9)8; 6.(2019•柳州)如图,直线3y x =-交x 轴于点A ,交y 轴于点C ,点B 的坐标为(1,0),抛物线2(0)y ax bx c a =++≠经过A ,B ,C 三点,抛物线的顶点为点D ,对称轴与x 轴的交点为点E ,点E 关于原点的对称点为F ,连接CE ,以点F 为圆心,12CE 的长为半径作圆,点P 为直线3y x =-上的一个动点. (1)求抛物线的解析式;(2)求BDP ∆周长的最小值;【分析】(1)直线3y x =-,令0x =,则3y =-,令0y =,则3x =,故点A 、C 的坐标为(3,0)、(0,3)-,即可求解;(2)过点B 作直线3y x =-的对称点B ',连接BD 交直线3y x =-于点P ,直线B B '交函数对称轴与点G ,则此时BDP ∆周长BD PB PD BD B B =++=+'为最小值,即可求解;【解答】解:(1)直线3y x =-,令0x =,则3y =-,令0y =,则3x =,故点A 、C 的坐标为(3,0)、(0,3)-,则抛物线的表达式为:2(3)(1)(43)y a x x a x x =--=-+,则33a =-,解得:1a =-,故抛物线的表达式为:243y x x =-+-⋯①;(2)连接DB '交于直线于P ;此时三角形BDP 周长BD PB PD BD DB =++=+'为最小值,(2,1)D ,则点(2,1)G -,即:BG EG =,即点G 是BB '的中点,过点(3,2)B '-,BDP ∆周长最小值BD B D =+'7.(2019•荆州)如图,在平面直角坐标系中,平行四边形OABC 的顶点A ,C 的坐标分别为(6,0),(4,3),经过B ,C 两点的抛物线与x 轴的一个交点D 的坐标为(1,0).(1)求该抛物线的解析式;(2)若AOC ∠的平分线交BC 于点E ,交抛物线的对称轴于点F ,点P 是x 轴上一动点,当PE PF +的值最小时,求点P 的坐标;【分析】(1)由平行四边形OABC 的性质求点B 坐标,根据抛物线经过点B 、C 、D 用待定系数法求解析式.(2)由OE 平分AOC ∠易证得COE AOE OEC ∠=∠=∠,故有CE OC =,求得点E 坐标,进而求得直线OE 解析式.求抛物线对称轴为直线7x =,即求得点F 坐标.作点E 关于x 轴的对称点点E ',由于点P 在x 轴上运动,故有PE PE '=,所以当点F 、P 、E '在同一直线上时,PE PF PE PF FE ''+=+=最小.用待定系数法求直线E F '解析式,即求得E F '与x 轴交点P 的坐标.【解答】解:(1)平行四边形OABC 中,(6,0)A ,(4,3)C6BC OA ∴==,//BC x 轴610B C x x ∴=+=,3B C y y ==,即(10,3)B设抛物线2y ax bx c =++经过点B 、C 、(1,0)D∴10010316430a b c a b c a b c ++=⎧⎪++=⎨⎪++=⎩ 解得:19149139a b c ⎧=-⎪⎪⎪=⎨⎪⎪=-⎪⎩∴抛物线解析式为211413999y x x =-+-(2)如图1,作点E 关于x 轴的对称点E ',连接E F '交x 轴于点P (4,3)C5OC ∴= //BC OAOEC AOE ∴∠=∠ OE 平分AOC ∠AOE COE ∴∠=∠OEC COE ∴∠=∠5CE OC ∴==59E C x x ∴=+=,即(9,3)E∴直线OE 解析式为13y x = 直线OE 交抛物线对称轴于点F ,对称轴为直线:149712()9x =-=⨯-7(7,)3F ∴点E 与点E '关于x 轴对称,点P 在x 轴上 (9,3)E '∴-,PE PE '= ∴当点F 、P 、E '在同一直线上时,PE PF PE PF FE ''+=+=最小 设直线E F '解析式为y kx h =+ ∴93773k h k h +=-⎧⎪⎨+=⎪⎩解得:8321k h ⎧=-⎪⎨⎪=⎩ ∴直线8:213E F y x '=-+ 当82103x -+=时,解得:638x = ∴当PE PF +的值最小时,点P 坐标为63(8,0).。
最短路径(将军饮马)问题(知识梳理与考点分类讲解)(人教版)(教师版) 24-25学年八年级数学上册

专题13.10最短路径(将军饮马)问题(知识梳理与考点分类讲解)第一部分【知识点归纳】【模型一:两定交点型】如图1,直线l和l的异侧两点A.B,在直线l上求作一点P,使PA+PB 最小;图1【模型二:两定一动型】如图2,直线l和l的同侧两点A.B,在直线l上求作一点P,使PA+PB 最小(同侧转化为异侧);图2【模型三:一定两动型】如图3,点P是∠MON内的一点,分别在OM,ON上作点A,B。
使△PAB的周长最小。
图3【模型四:两定两动型】如图4,点P,Q为∠MON内的两点,分别在OM,ON上作点A,B。
使四边形PAQB的周长最小。
图4【模型五:一定两动(垂线段最短)型】如图5,点A是∠MON外的一点,在射线ON上作点P,使PA与点P到射线OM的距离之和最小。
图5【模型六:一定两动,找(作)对称点转化型】如图6,点A是∠MON内的一点,在射线ON 上作点P,使PA与点P到射线OM的距离之和最小。
图6【考点1】两定一动型;【考点2】一定两动(两点之间线段最短)型;【考点3】一定两动(垂线段最短)型;【考点4】两定两动型;【考点5】一定两动(等线段)转化型;.第二部分【题型展示与方法点拨】【考点1】两定一动型;【例1】(23-24八年级上·全国·课后作业)如图,在ABC ∆中,3,4AB AC ==,EF 垂直平分BC ,交AC 于点D ,则ABP 周长的最小值是()A .12B .6C .7D .8【答案】C 【分析】本题主要考查了,轴对称﹣最短路线问题的应用,解此题的关键是找出P 的位置.凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,根据题意知点B 关于直线EF 的对称点为点C ,故当点P 与点D 重合时,AP BP +的值最小,即可得到ABP 周长最小.解:∵EF 垂直平分BC ,∴点B ,C 关于EF 对称.∴当点P 和点D 重合时,AP BP +的值最小.此时AP BP AC +=,∵3,4AB AC ==,ABP ∴ 周长的最小值是347AP BP AB AB AC ++=+=+=,故选:C .【变式】(23-24八年级上·广东广州·期中)如图,在ABC V 中,1216AB AC ==,,20BC =.将ABC V 沿射线BM 折叠,使点A 与BC 边上的点D 重合,E 为射线BM 上的一个动点,则CDE 周长的最小值.【答案】24【详解】设BM 与AC 的交点为点F ,连接AE ,DF 先根据折叠的性质可得12BD AB ==,DF AF =,DE AE =,BDF BAF ∠=∠,再根据两点之间线段最短可得当点E 与点F 重合时,CDE 周长最小,进而求解即可.解:如图,设BM 与AC 的交点为点F ,连接AE ,DF ,由折叠的性质得:12BD AB ==,DF AF =,DE AE =,BDF BAF ∠=∠,20128CD BC BD ∴=-=-=,CDE ∴ 周长8CD DE CE AE CE =++=++,要使CDE 周长最小,只需AE CE +最小,由两点之间线段最短可知,当点E 与点F 重合时,最小值为AC ,∴CDE 周长为:681624AC +=+=.故答案为:24.【点拨】本题考查了折叠的性质等知识点,熟练掌握折叠的性质是解题关键.【考点2】一定两动(两点之间线段最短)型;【例2】(23-24八年级上·湖北省直辖县级单位·期末)如图,45MON ∠=︒,P 为MON ∠内一点,A 为OM 上一点,B 为ON 上一点,当PAB 的周长取最小值时,APB ∠的度数为()A .45︒B .90︒C .100︒D .135︒【答案】B 【分析】本题主要考查了最短路线问题、四边形的内角和定理、轴对称的性质等知识点,掌握两点之间线段最短的知识画出图形是解题的关键.如图:作P 点关于OM ON 、的对称点A B ''、,连接A B '',此时PAB 的周长最小为A B '',求出A B ''即可.解:如图:作P 点关于OM ON 、的对称点A B ''、,然后连接A B '',∵点A '与点P 关于直线OM 对称,点B '与点P 关于ON 对称,∴A P OM B P ON A A AP B B BP ''''⊥⊥==,,,,∴A APA B BPB ''''∠=∠∠=∠,,∵A P OM B P ON ''⊥⊥,,∴180MON A PB ''∠+∠=︒,∴18045135A PB ''∠=︒-︒=︒,在A B P ''△中,由三角形的内角和定理可知:18013545A B ''∠+∠=︒-︒=︒,∴45A PA BPB ''∠+∠=︒,∴1354590APB ∠=︒-︒=︒.故选:B .【变式】(23-24八年级上·江苏无锡·期中)如图,45AOB ∠=︒,点M N 、分别在射线OA OB 、上,5MN =,15OMN S = ,点P 是直线MN 上的一个动点,点P 关于OA 的对称点为1P ,点P 关于OB 的对称点为2P ,连接1OP 、2OP 、12PP ,当点P 在直线MN 上运动时,则12OPP 面积的最小值是.【考点3】一定两动型(垂线段最短);【例3】(22-23八年级上·湖北武汉·期末)如图,在ABC V 中,3AB =,4BC =,5AC =,AB BC ⊥,点P 、Q 分别是边BC 、AC 上的动点,则AP PQ +的最小值等于()A .4B .245C .5D .275【答案】B 【分析】作A 过于BC 的对称点A ',过点A '作A Q AC '⊥,交AC 于点Q ,交BC 于点P ,根据对称可得:AP PQ A P PQ A Q ''+=+≥,得到当,,A P Q '三点共线时,AP PQ +最小,再根据垂线段最短,得到A Q AC '⊥时,A Q '最小,进行求解即可.解:作A 过于BC 的对称点A ',过点A '作A Q AC '⊥,交AC 于点Q ,交BC 于点P ,【变式】(23-24七年级下·陕西西安·阶段练习)如图,在Rt ABC △中,90ACB ∠=︒,3AC =,4BC =,5AB =,AD 是ABC V 的角平分线,若P Q 、分别是AD 和AC 边上的动点,则PC PQ +的最小值是.AD 是BAC ∠的平分线,1QAD Q AD∴∠=∠在AQD 与1AQ D 中【考点4】两定两动型;【例4】如图,已知24AOB ∠=︒,OP 平分AOB ∠,1OP =,C 在OA 上,D 在OB 上,E 在OP 上.当CP CD DE ++取最小值时,此时PCD ∠的度数为()A .36︒B .48︒C .60︒D .72︒【答案】D 【分析】作点P 关于OA 的对称点P',作点E 关于OB 的对称点'E ,连接'OP 、'PP 、'OE 、'EE 、''P E ,则由轴对称知识可知=''CP CD DE CP CD DE ++++,所以依据垂线段最短知:当''P C D E 、、、在一条直线上,且'''P E OE ⊥时,CP CD DE ++取最小值,根据直角三角形的两锐角互余及三角形外角的性质可以'P C PC =,'E D ED =,'1OP OP ==,=''CP CD DE CP CD DE ++++,'P OE ∠''P C D E 、、、在一条直线上,且''P E ''=9048=42OP E ∠︒-︒︒,'='''=7842CP P OP P OP E ∠∠-∠︒-︒=【答案】44βα-=︒【分析】本题考查轴对称—最短问题、三角形的内角和定理.三角形的外角的性质等知识,解题的关键是灵活运用所学知识解决问题.OQM OQM NQP '∴∠=∠=∠,OPQ ∠∴1(180)2PQN AOB α∠=︒-=∠+∠44βα∴-=︒,故答案为:44βα-=︒.【考点5】一定两动(等线段)转化型;【例5】(20-21八年级上·湖北鄂州·期中)如图,AD 为等腰△ABC 的高,其中∠ACB =50°,AC =BC ,E ,F 分别为线段AD ,AC 上的动点,且AE =CF ,当BF +CE 取最小值时,∠AFB 的度数为()A .75°B .90°C .95°D .105°【答案】C 【分析】先构造△CFH 全等于△AEC ,得到△BCH 是等腰直角三角形且FH=CE ,当FH+BF 最小时,即是BF+CE 最小时,此时求出∠AFB 的度数即可.解:如图,作CH ⊥BC ,且CH=BC ,连接HB ,交AC 于F ,此时△BCH 是等腰直角三角形且FH+BF 最小,∵AC=BC ,∴CH=AC ,∵∠HCB=90°,AD ⊥BC ,∴AD//CH ,∵∠ACB=50°,∴∠ACH=∠CAE=40°,∴△CFH ≌△AEC ,∴FH=CE ,∴FH+BF=CE+BF 最小,此时∠AFB=∠ACB+∠HBC=50°+45°=95°.故选:C .【点拨】本题考查全等三角形的性质和判定、等腰三角形的性质、最短路径问题,关键是作出辅助线,有一定难度.【变式】(23-24七年级下·四川宜宾·期末)在ABC V 中,80CAB ∠=︒,2AB =,3AC =,点E 是边AB 的中点,CAB ∠的角平分线交BC 于点D .作直线AD ,在直线AD 上有一点P ,连结PC 、PE ,则PC PE -的最大值是.∵CAB ∠的角平分线交∴FAP ∠∠=∵AP AP =,∴APF APE ≌∴PF PE =,第三部分【中考链接与拓展延伸】1、直通中考【例1】(2020·湖北·中考真题)如图,D 是等边三角形ABC 外一点.若8,6BD CD ==,连接AD ,则AD 的最大值与最小值的差为.【答案】12【分析】以CD 为边向外作等边三角形CDE ,连接BE ,可证得△ECB ≌△DCA 从而得到BE=AD ,再根据三角形的三边关系即可得出结论.解:如图1,以CD 为边向外作等边三角形CDE ,连接BE ,∵CE=CD ,CB=CA ,∠ECD=∠BCA=60°,∴∠ECB=∠DCA ,∴△ECB ≌△DCA (SAS ),∴BE=AD ,∵DE=CD=6,BD=8,∴8-6<BE<8+6,∴2<BE<14,∴2<AD<14.∴则AD 的最大值与最小值的差为12.故答案为:12【点拨】本题考查三角形全等与三角形的三边关系,解题关键在于添加辅助线构建全等三角形把AD 转化为BE 从而求解,是一道较好的中考题.【例2】(2020·新疆·中考真题)如图,在ABC V 中,90,60,4A B AB ∠=∠=︒=︒,若D 是BC 边上的动点,则2AD DC +的最小值为.在Rt DFC △中,30DCF ∠=︒,12DF DC ∴=,122()2AD DC AD DC +=+2()AD DF =+,∴当A ,D ,F 在同一直线上,即此时,60B ADB ∠=∠=︒,2、拓展延伸【例1】(23-24八年级上·江苏镇江·阶段练习)如图,AC 、BD 在AB 的同侧,点M 为线段AB 中点,2AC =,8BD =,8AB =,若120CMD ∠=︒,则CD 的最大值为()A .18B .16C .14D .12【答案】C 【分析】本题考查等边三角形的判定和性质,两点之间线段最短,解题的关键是学会添加常用辅助线,学会利用两点之间线段最短解决最值问题.如图,作点A 关于CM 的对称点A ',点B 关于DM 的对称点B ',证明'' A MB 为等边三角形,即可解决问题.解:如图,作点A 关于CM 的对称点A ',点B 关于DM 的对称点B ',∵120CMD ∠=︒,∴60∠+∠=︒AMC DMB ,∴60''∠+∠=︒CMA DMB ,∴60''∠=︒A MB ,∵MA MB MA MB ''===,∴'' A MB 为等边三角形∵14CD CA A B B D CA AM BD ''''<++=++=,∴CD 的最大值为14,故选:C .【例2】(22-23八年级上·湖北武汉·期末)如图,锐角ABC V 中,302A BC ∠=︒=,,ABC V 的面积是6,D 、E 、F 分别是三边上的动点,则DEF 周长的最小值是()A .3B .4C .6D .7∴AM AE AN ==,MF =∵BAC BAD DAC ∠=∠+∠∴MAN MAB BAD ∠=∠+∠∴(2MAN BAE EAC ∠=∠+∠。
微专题3:圆锥曲线中的将军饮马问题教师版

微专题:圆锥曲线中的将军饮马问题
一动点M 与两定点A ,B 的距离之和MA MB +(差的绝对值||MA MB -)的最小(大)值问题,如果设动点M 坐标,转化为求函数最值,不易求解,常用方法:数形结合;解题关键:转化.
MA MB AB +≥,当且仅当动点M 在线段AB 上时取“=”
,||MA MB AB -≤,当且仅当动点M 在线段AB 或BA 的延长线上时取“=”.否则,转化!若动点在定直线上则对称转化,若动点在圆锥曲线上则定义转化.
1.已知F 是双曲线C :2
218
y x -=的右焦点,P 是C 的左支上任一点.
(1)若点A ,则PA PF +的最小值为 ;17
(2)若点(4,1)A -,则3PA PF +的最小值为 .13
2.已知F 是椭圆C :22
195
x y +=的右焦点,P 是C 上任一点,(1,1)A ,则
(1)PA PF +的最小值为 ;6(2)23PA PF +的最小值为 .7
3.(1)已知F 是抛物线C :22y x =的焦点,P 是C 上任一点,(2,1)A ,则PA PF +的最小值
为 ;52
(2)已知P 是抛物线C :22y x =上动点,点P 在y 轴上的射影是M ,点7(,4)2
A ,则P A P M + 的最小值为 .92
4.若P 是圆O :229x y +=上任一点,点(5,0)A -,(B -,则35
P A P B +的最小值为 .135。
2024年浙教版八年级上册数学期末培优复习第6招“将军饮马”求最值

返回
1
2
3
4
分类训练
【解】如图,作点 D 关于 AB 的对称点 G ,关于 AC 的对
称点 H ,连结 GH ,分别交 AB , AC 于点 E , F ,连结
CH ,此时△ DEF 的周长最小,最小周长为 GH 的长度.
∵∠ ABC =90°,点 D 与点 G 关于 AB 对称,
∴在Rt△ BHA2中, BA2= + = + =
.
∴ AC + BD 的最小值为 .
返回
1
2
3
4
BD 上的动点,已知△ ABC 的面积是12 cm2, BC 的长是
8 cm,则 AF + EF 的最小值是
3 cm.
返回
1
2
3
4
分类训练
2. 如图,∠ AOB =30°,点 P 为∠ AOB 内一点, OP =8.
点 M , N 分别在射线 OA , OB 上.当△ PMN 的周长最小
时,下列结论:
120°, P1 P2= OP1= OP =8.
∴△ PMN 周长的最小值为8.∴①④正确.
返回
1
2
3
4
分类训练
3. [2024·杭州拱墅区期中]如图,在等腰直角三角形 ABC
中, AB = BC =4,点 D 在边 BC 上且 CD =1,点 E , F
分别为边 AB , AC 上的动点,连结 DE , EF , DF 得到
平移和对称的性质得 AC = A2 D ,连结 BA2.
∵ BD + A2 D ≥ BA2,
∴线段 BA2的长即为 AC + BD 的最小值.
返回
1
2
专题02 二次函数与将军饮马最值问题(知识解读)(老师版)

专题02二次函数与将军饮马最值问题(知识解读)【专题说明】“将军饮马”问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题,会与直线、角、三角形、四边形、圆、抛物线等图形结合,在近年的中考和竞赛中经常出现,而且大多以压轴题的形式出现。
【知识点梳理】考点1:两条线段和最小值问题一)、已知两个定点一个动点:(对称轴为:动点所在的直线上)1、在一条直线m上,求一点P,使PA+PB最小;(1)点A、B在直线m两侧:(2)点A、B在直线同侧:A,A’是关于直线m的对称点。
考点2:三条线段和最小值问题在直线m、n上分别找两点P、Q,使PA+PQ+QB最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:(4)、台球两次碰壁模型变式一:已知点A、B位于直线m,n的内侧,在直线n、m分别上求点D、E点,使得围成的四边形ADEB 周长最短.变式二:已知点A位于直线m,n的内侧,在直线m、n分别上求点P、Q点PA+PQ+QA周长最短.考点3:两条线段差最大值问题求两线段差的最大值问题(运用三角形两边之差小于第三边)基本图形解析:1、在一条直线m上,求一点P,使PA与PB的差最大;(1)点A、B在直线m同侧:解析:延长AB交直线m于点P,根据三角形两边之差小于第三边,P’A—P’B<AB,而PA—PB=AB此时最大,因此点P为所求的点。
(2)点A、B在直线m异侧:解析:过B作关于直线m的对称点B’,连接AB’交点直线m于P,此时PB=PB’,PA-PB最大值为AB’【考点1两条线段和最小值问题】【典例1】(2019秋•东莞市校级期末)已知,抛物线y=ax2+bx+c,过A(﹣1,0)、B(3,0)、C(0,﹣3),M为顶点.(1)求抛物线的解析式;(2)在该抛物线的对称轴上找一点P,使得PA+PC的值最小,并求出P的坐标;【解答】解:(1)设抛物线解析式为y=a(x+1)(x﹣3),把C(0,﹣3)代入得a×(0+1)×(0﹣3)=﹣3,解得a=1,∴抛物线解析式为y=(x+1)(x﹣3),即y=x2﹣2x﹣3;(2)抛物线的对称轴为直线x=1,点A与点B关于直线x=1对称,连接BC交直线x=1于P点,则PA=PB,∵PA+PC=PB+PC=BC,∴此时PA+PC的值最小,设直线BC的解析式为y=mx+n,把B(3,0),C(0,﹣3)代入得,解得,∴直线BC的解析式为y=x﹣3,当x=1时,y=x﹣3=﹣2,则满足条件的P点坐标为(1,﹣2);【变式1】(2019•赤峰)如图,直线y=﹣x+3与x轴、y轴分别交于B、C两点,抛物线y=﹣x2+bx+c经过点B、C,与x轴另一交点为A,顶点为D.(1)求抛物线的解析式;(2)在x轴上找一点E,使EC+ED的值最小,求EC+ED的最小值;【解答】解:(1)直线y=﹣x+3与x轴、y轴分别交于B、C两点,则点B、C的坐标分别为(3,0)、(0,3),将点B、C的坐标代入二次函数表达式得:,解得:,故函数的表达式为:y=﹣x2+2x+3,令y=0,则x=﹣1或3,故点A(﹣1,0);(2)如图1中,作点C关于x轴的对称点C′,连接CD′交x轴于点E,则此时EC+ED为最小,函数顶点D坐标为(1,4),点C′(0,﹣3),将C′、D的坐标代入一次函数表达式并解得:直线C′D的表达式为:y=7x﹣3,当y=0时,x=,故点E(,0),则EC+ED的最小值为DC′=;【考点2两条线段和最小值问题】【典例2】(2022•恩施州模拟)如图1,已知抛物线.点A(﹣1,2)在抛物线的对称轴上,是抛物线与y轴的交点,D为抛物线上一动点,过点D作x轴的垂线,垂足为点C.(1)直接写出h,k的值;(2)如图1,若点D的坐标为(3,m),点Q为y轴上一动点,直线QK与抛物线对称轴垂直,垂足为点K.探求DK+KQ+QC的值是否存在最小值,若存在,求出这个最小值及点Q的坐标;若不存在,请说明理由;【解答】解:(1)∵点A(﹣1,2)在抛物线的对称轴上,∴抛物线的对称轴为直线x=﹣1,∴h=1,∴y=(x+1)2+k,∵是抛物线与y轴的交点,∴+k=,∴k=1;(2)存在最小值,理由如下:由(1)可知y=(x+1)2+1,由对称性可知C'K=CQ,∴CQ+KQ+KD=C'K+KD+KQ≥C'D+KQ,当C'、K、D三点共线时,CQ+KQ+KD的值最小,∵抛物线的对称轴为直线x=﹣1,∴KQ=1,∵D(3,5),CD⊥x轴,∵C(3,0),∴C'(﹣4,0),∴C'D=,∴CQ+KQ+KD的最小值为+1,设直线C'D的解析式为y=kx+b,∴,解得,∴y=x+,【变式2】(2022•桂林)如图,抛物线y=﹣x2+3x+4与x轴交于A,B两点(点A位于点B的左侧),与y 轴交于C点,抛物线的对称轴l与x轴交于点N,长为1的线段PQ(点P位于点Q的上方)在x轴上方的抛物线对称轴上运动.(1)直接写出A,B,C三点的坐标;(2)求CP+PQ+QB的最小值;【解答】解:(1)在y=﹣x2+3x+4中,令x=0得y=4,令y=0得x=﹣1或x=4,∴A(﹣1,0),B(4,0),C(0,4);(2)将C(0,4)向下平移至C',使CC'=PQ,连接BC'交抛物线的对称轴l于Q,如图:∵CC'=PQ,CC'∥PQ,∴四边形CC'QP是平行四边形,∴CP=C'Q,∴CP+PQ+BQ=C'Q+PQ+BQ=BC'+PQ,∵B,Q,C'共线,∴此时CP+PQ+BQ最小,最小值为BC'+PQ的值,∵C(0,4),CC'=PQ=1,∴C'(0,3),∵B(4,0),∴BC'==5,∴BC'+PQ=5+1=6,∴CP+PQ+BQ最小值为6【考点3两条线段差最大值问题】【典例3】(2020秋•椒江区校级月考)如图,已知抛物线y=ax2+bx+3(a≠0)经过点A(1,0)和点B(3,0),与y轴交于点C.(1)求此抛物线的解析式;(2)若点T为对称轴直线x=2上一点,则TC﹣TB的最大值为多少?【解答】解:(1)设抛物线的表达式为y=a(x﹣x1)(x﹣x2)=a(x﹣1)(x﹣3)=a(x2﹣4x+3)=ax2+bx+3,解得a=1,故抛物线的表达式为y=x2﹣4x+3①;(2)点B关于函数对称轴的对称点为点A,连接CA交函数对称轴于点T,则点T为所求点,则TC﹣TB=TC﹣TA=AC为最大,故TC﹣TB的最大值为AC==,故答案为;【变式1】(2020•连云港)在平面直角坐标系xOy中,把与x轴交点相同的二次函数图象称为“共根抛物线”.如图,抛物线L1:y=x2﹣x﹣2的顶点为D,交x轴于点A、B(点A在点B左侧),交y轴于点C.抛物线L2与L1是“共根抛物线”,其顶点为P.(1)若抛物线L2经过点(2,﹣12),求L2对应的函数表达式;(2)当BP﹣CP的值最大时,求点P的坐标;【解答】解:(1)当y=0时,x2﹣x﹣2=0,解得x=﹣1或4,∴A(﹣1,0),B(4,0),C(0,﹣2),由题意设抛物线L2的解析式为y=a(x+1)(x﹣4),把(2,﹣12)代入y=a(x+1)(x﹣4),﹣12=﹣6a,解得a=2,∴抛物线的解析式为y=2(x+1)(x﹣4)=2x2﹣6x﹣8.(2)∵抛物线L2与L1是“共根抛物线”,A(﹣1,0),B(4,0),∴抛物线L1,L2的对称轴是直线x=,∴点P在直线x=上,∴BP=AP,如图1中,当A,C,P共线时,BP﹣PC的值最大,此时点P为直线AC与直线x=的交点,∵直线AC的解析式为y=﹣2x﹣2,∴P(,﹣5).。
轴对称及将军饮马问题.教师版

轴对称及“将军饮马”问题知识点睛轴对称图形:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.这条直线就是它的对称轴.这时我们就说这个图形关于这条直线(或轴)对称.如下图,ABC 是轴对称图形.两个图形轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就是说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.如下图,ABC 与'''A B C 关于直线l 对称,l 叫做对称轴.A 和'A ,B 和'B ,C 和'C 是对称点.轴对称图形和两个图形轴对称的区别和联系:对称轴的性质:对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段.即:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.类似地,轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.线段的垂直平分线:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.如图,直线l 经过线段AB 的中点O ,并且垂直于线段AB ,则直线l 就是线段AB 的垂直平分线.线段垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等.轴对称图形两个图形轴对称区别图形的个数1个图形2个图形对称轴的条数一条或多条只有1条联系二者都的关于对称轴对称的如图,点P是线段AB垂直平分线上的点,则PA PB.线段垂直平分线的判定:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.成轴对称的两个图形的对称轴的画法:如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.因此,我们只要找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.成轴对称的两个图形的主要性质:①成轴对称的两个图形全等②如果两个图形关于某条直线对称,那么对称轴是任何一对对应点连线的垂直平分线轴对称变换的方法应用:轴对称变换是通过作图形关于一直线的对称图形的手段,把图形中的某一图形对称地移动到一个新的位置上,使图形中的分散条件和结论有机地联系起来.常用的辅助线有角平分线条件时的各种辅助线,本质上都是对称变换的思想.轴对称变换应用时有下面两种情况:⑴图形中有轴对称图形条件时,可考虑用此变换;⑵图形中有垂线条件时,可考虑用此变换.重、难点重点:理解轴对称的概念,并且熟悉掌握轴对称的性质以及作图,同时理解轴对称变换的概念,能很好的做出轴对称变换的图形,并能很好的利用轴对称的知识来解决题目难点:运用轴对称变换来解决实际题目,以及轴对称的生活中的实际运用例题精讲板块一、轴对称与轴对称图形的认识【例1】下列”QQ表情”中属于轴对称图形的是( )A.B.C.D.【解析】C【巩固】(08年广东省)下列图形中是轴对称图形的是 ( )【解析】C【例2】(09湖南株洲)下列四个图形中,不是轴对称图形的是( )A.B.C.D.【解析】D【巩固】(2004泸州)下列各种图形不是轴对称图形的是( )【解析】C.【巩固】(2003吉林)下面四个图形中,从几何图形的性质考虑,哪一个与其他三个不同?请指出这个图形,并简述你的理由.答:图形__________;理由是__________.【解析】②;四个图形中,只有图②不是轴对称图形.【例3】如图,它们都是对称图形,请观察并指出哪些是轴对称图形,哪些图形成轴对称.【解析】轴对称图形:1,3,4,6,8,10成轴对称的图形有:2,5,7,9【例4】(09黑龙江哈尔滨)下列图形中,既是轴对称图形,又是中心对称图形的是( )【解析】D【巩固】(2004北京)下列图形中,既是轴对称图形又是中心对称图形的是( )A.等腰三角形B.等腰梯形C.正方形D.平行四边形【解析】C【例5】(2003四川)我国主要银行的商标设计基本上都融入了中国古代钱币的图案,下列我国四大银行的商标图案中是轴对称图形而不是中心对称图形的是( )【解析】C【例6】(2003北京市海淀区)羊年话”羊”字象征着美好和吉祥,?下列图案都与”羊”字有关,其中是轴对称图形的个数是( )A.1;B.2;B.3;D.4【解析】B【巩固】⑴(08山东省青岛市)下列图形中,轴对称图形的个数是( )A.1B.2C.3D.4⑵如图所示的图案是我国几家银行标志,其中轴对称图形有( )A.1个B.2个C.3个D.4个【解析】⑴B;⑵C【例7】(上海)正六边形是轴对称图形,它有条对称轴.【解析】6.点拨:可以画出例图进行分析,明确正n边形有n条对称轴.【巩固】(2003河北省)下列图案中,有且只有三条对称轴的是( )【解析】D【巩固】⑴(08苏州)下列图形中,轴对称图形.....的是⑵下列图形中对称轴最多的是( )A.圆B.正方形C.等腰三角形D.线段【解析】⑴D;⑵A【例8】作出下图所示的图形的对称轴:【解析】答案见右上图.【巩固】作出下图所示的成轴对称图形的对称轴:【解析】答案见右上图.【例9】求作线段AB的垂直平分线BA【解析】略【例10】已知:如图,ABC及两点M、N.求作:点P,使得PM PN,且P点到ABC两边所在的直线的距离相等.NM CB A【解析】因为是两边所在的直线,所以有两个答案.答案一:ABC 内角平分线与线段MN 的垂直平分线的交点PNMCBA答案二:ABC 外角平分线与线段MN 的垂直平分线的交点CPBANM【例11】(2003长沙)如图,请根据小文在镜中的像写出他的运动衣上的实际号码:_______.【解析】108【例12】(2004河南)如图,直线l 是四边形ABCD 的对称轴,若AB CD ,有下面的结论:①AB CD ∥②AC BD ③AO OC ④AB BC ,其中正确的结论有_______.lODCBA【解析】①②③【巩固】(2003安徽)如图,l 是四边形ABCD 的对称轴,如果AD BC ∥,有下列结论:①AB CD ∥②ABBC③AB BC ④AO OC .其中正确的结论是_________.(?把你认为正确的结论的序号都填上)l ODCBA【解析】①、②、④【例13】(2003南宁市)尺规:把右图(实线部分)补成以虚线L 为对称轴的轴对称图形,你会得到一只美丽蝴蝶的图案(不用写作法、保留作图痕迹).【解析】答案见右上图.板块二、轴对称的应用【例14】如图,ABC 和'''A B C 关于直线l 对称,且90B ,''6cm A B ,求'B 的度数和AB 的长.LC'B'A'CBA【解析】∵ABC 和'''A B C 关于直线l 成轴对称∴'B B ,''AB A B ;又∵90B ,''6cm A B ∴'90B ,6cm AB .【例15】如图,有一块三角形田地,10cm ABAC,作AB 的垂直平分线ED 交AC 于D ,交AB 于E ,量得BDC 的周长为17m ,请你替测量人员计算BC 的长.【解析】∵ED 垂直平分AB∴DA DB ,∵17m BD DC BC ,∴17mAD DCBC ∵10m AC ,∴7m BC.【巩固】如图,ABC 中,BC 边的垂直平分线DE 交BC 于D ,交AC 于E ,5BE 厘米,BCE 的周长是18厘米,则BC 等于多少厘米?EDCBA【解析】∵ED 垂直平分BC∴EB EC ,∵BEC 的周长为18cm ∴8cm BC .【例16】如图,已知40AOB,CD为OA的垂直平分线,求ACB的度数.O DC BA【解析】∵CD垂直平分OA∴CO CA∴O A∵40O∴40A∴80ACB A O.【例17】(2004陕西)已知:如图,在ABC中,2AB BC,120ABC,BC平行于x轴,点B?的坐标是(3,1).⑴画出ABC关于y轴对称的'''A B C;⑵求以点A、B、'B、'A为顶点的四边形的面积.【解析】⑴画图正确⑵过A点作AD BC,交BC的延长线于点D,则18060ABD ABC,在Rt ABD中,BD=AB·cos∠ABD=2×12=1AD =AB ·sin ∠ABD =2×32=3又知点B 的坐标为(-3,1) 可得点A 的坐标为413,∵'AA y 轴,'BB y 轴∴''AA BB ∥∵AB 与''A B 不平行∴以点''A B B A ,,,为顶点的四边形是等腰梯形由点A 、B 的坐标可求得'248'236AA BB ,∴梯形''ABB A 的面积=12(AA ′+BB ′)·AD =12×(8+6)×3=73.板块三、轴对称在几何最值问题中的应用【例18】已知点A 在直线l 外,点P 为直线l 上的一个动点,探究是否存在一个定点B ,当点P 在直线l 上运动时,点P 与A 、B 两点的距离总相等,如果存在,请作出定点B ;若不存在,请说明理由.【解析】点B 与点A 重合,或者点B 是点A 关于直线l 的对称点.【例19】如图,在公路a 的同旁有两个仓库A 、B ,现需要建一货物中转站,要求到A 、B 两仓库的距离和最短,这个中转站M 应建在公路旁的哪个位置比较合理?aBA【解析】答案见右上图.【巩固】若此题改成,在a 上找到M 、N 两点,且10MN ,M 在N 的左边,使四边形ABMN 的周长最短.aBABNMB''AaB ‘【解析】见右上图.【例20】(”五羊杯”邀请赛试题)如图,45AOB ,角内有点P ,在角的两边有两点Q 、R (均不同于O点),求作Q 、R ,使得PQR 的周长的最小.POBARQPOBA【解析】见右上图.【巩固】如图,M 、N 为ABC 的边AC 、BC 上的两个定点,在AB 上求一点P ,使PMN 的周长最短.NMCBA【解析】见右上图.【例21】(2000年全国数学联赛)如图,设正ABC 的边长为2,M 是AB 边上的中点,P 是BC 边上的任意一点,PAPM 的最大值和最小值分别记为s 和t .求22st 的值.MPCBAM'MPCBA【解析】作点M 关于BC 的对称点'M ,连接'AM 、'PM .由点M 、'M 关于BC 对称可知,'PM PM .故''PA PM PA PM AM ≥当且仅当A 、P 、'M 共线时,等号成立,故22(')7tAM .另外两个临界位置在点B 和点C 处.当点P 位于点C 处时,23PA PMAC CM ;当点P 位于点B 处时,3PA PMAB BM.故22(23)743s,2243st.本题也可作点A 关于BC 的对称点'A ,连接'A M 、'PA .【例22】已知如图,点M 在锐角AOB 的内部,在OB 边上求作一点P ,使点P 到点M 的距离与点P 到OA的边的距离和最小.PM'MOBAM OBA【解析】见右上图.【例23】已知:A 、B 两点在直线l 的同侧,在l 上求作一点M ,使得||AMBM 最小.【解析】见右上图.【巩固】已知:A 、B 两点在直线l 的同侧,在l 上求作一点M ,使得||BM AM最大.【解析】见右上图.【例24】(07年三帆中学期中试题)如图,正方形ABCD 中,8AB,M 是DC 上的一点,且2DM,N 是AC 上的一动点,求DNMN 的最小值与最大值.NMDC B ANMD CB A【解析】找点D 关于AC 的对称点,由正方形的性质可知,B 就是点D 关于AC 的对称点,连接BN 、BM ,由DN MN BN MN BM 可知,当且仅当B 、N 、M 三点共线时,DN MN 的值最小,该最小值为226810.当点N 在AC 上移动时,有三个特殊的位置我们要考察:BM 与AC 的交点,即DN MN 取最小值时;当点N 位于点A 时,8217DN MNADAM;当点N 位于点C 时,8614DNMN CD CM .故DN MN 的最大值为8217.【巩固】例题中的条件不变,求DN MN 的最小值与最大值.【解析】当DNMN 时,DNMN 有最小值为0,此时点N 位于DM 的垂直平分线与AC 的交点处.2DNMNDM,当点N 与点C 重合时,等号成立,此时有最大值2.【巩固】(黑龙江省中考题)如图,已知正方形ABCD 的边长为8,M 在DC 上,且2DM ,N 是AC 上的一个动点,则DN MN 的最小值是MD CBA【解析】连接BM 交AC 于N ,此点即为所求.所以根据勾股定理,10DN MN.【例25】(2004郸县改编)某供电部门准备在输电主干线l 上连接一个分支线路同时向新落成的A 、B 两个居民小区送电,分支点为M ,已知居民小区A 、B 到主干线l 的距离分别为12AA 千米,12BB 千米,且114A B 千米.⑴居民小区A 、B 在主干线l 的两旁如图⑴所示,那么分支点M 在什么地方时总线路最短?最短线路的长度是多少千米?⑵如果居民小区A 、B 在主干线l 的同旁,如图⑵所示,那么分支点M 在什么地方时总线路最短?此时分支点M 与1A 距离多少千米?l (1)ABA 1B 1l (2)ABA 1B 1Ml A 1ABB 1Ml AB A 1B 1B 2【解析】⑴连结AB ,AB 与l 的交点就是所求的分支点M ,分支点开在此处总线路最短,如图,因为1190BB M AA M ,11BMB AMA .所以11B BM A AM ≌.所以12A M.由勾股定理,得22AMBM,42ABAMBM,所以分支点M 在线段11A B 上距A 点22千米处,最短线段的长度为42千米;⑵如图,作B 点关于直线l 的对称点2B ,连结2AB 交直线l 于点M ,此处即为分支点,由图可知,1A M 的长度为2千米.点拨:在解本题时,应注意线段最短,在第⑵问中也可以先画A 点的对称点A 2.【例26】(09山东临沂)如图,A ,B 是公路l (l 为东西走向)两旁的两个村庄,A 村到公路l 的距离1km AC ,B 村到公路l 的距离2km BD ,B 村在A 村的南偏东45方向上.⑴求出A ,B 两村之间的距离;⑵为方便村民出行,计划在公路边新建一个公共汽车站P ,要求该站到两村的距离相等,请用尺规在图中作出点P 的位置(保留清晰的作图痕迹,简明书写作法).【解析】⑴方法一:设AB 与CD 的交点为O ,根据题意可得45A B .∴ACO 和BDO 都是等腰直角三角形.∴2AO,22BO.∴A B ,两村的距离为22232kmABAOBO方法二:过点B 作直线l 的平行线交AC 的延长线于E .易证四边形CDBE 是矩形,∴2CE BD .在Rt AEB 中,由45A ,可得3BE EA .323332kmAB ∴A B ,两村的距离为32km .⑵作图正确,痕迹清晰.作法:①分别以点A B ,为圆心,以大于12AB 的长为半径作弧,两弧交于两点M ,N ,作直线MN ;②直线MN 交l 于点P ,点P 即为所求.家庭作业【习题1】(08苏州)下列图形中,轴对称图形.....的是BACDlN MOP北东BACDl【解析】D【习题2】⑴(09湖南株洲)下列四个图形中,不是轴对称图形的是( )A.B.C.D.⑵(08山东烟台)下列交通标志中,不是轴对称图形的是( )⑶(08年广东省)下列图形中是轴对称图形的是 ( )【解析】⑴D;⑵C;⑶C.【习题3】如图,ABC中,90A,BD为ABC的平分线,DE BC,E是BC的中点,求C的度数.ED CBA【解析】∵BD平分ABC∴ABD EBD∵DE垂直平分BC∴BD CD,DBE C∴ABD DBE C∵90A∴30ABD DBE C.【习题4】(四川省竞赛题)如图,在等腰Rt ABC中,3CA CB,E的BC上一点,满足2BE,在斜边AB 上求作一点P使得PC PE长度之和最小.PE'ECBAE PC BA【解析】见右上图.【习题5】在正方形ABCD 中,E 在BC 上,2BE,1CE ,P 在BD 上,求PE 和PC 的长度之和的最小值.E PDC B AE ‘E PDCB A【解析】当'E 、P 、C 三点共线时,PE PC 有最小值13.备选【备选1】(2004天津)在下列图形中,既是轴对称图形,又是中心对称图形的是( )【解析】C【备选2】判断下列图形(图)是否为轴对称图形?如果是,说出它有几条对称轴.⑴⑵⑶⑷⑸⑹⑺⑻⑼【解析】是轴对称图形的有:⑵,⑷,⑹,⑺,⑼;分别有1条,1条,4条,1条,2条对称轴.【备选3】(2008年荆门市中考题)如图,菱形ABCD 的两条对角线分别长6和8,点M 、N 分别是变AB 、BC的中点,在对角线AC 求作一点P 使得PM PN 的值最小.PNMDCBAN'ABC DMNP【解析】见右上图.。
第11讲 “将军饮马”问题探究(教师版)
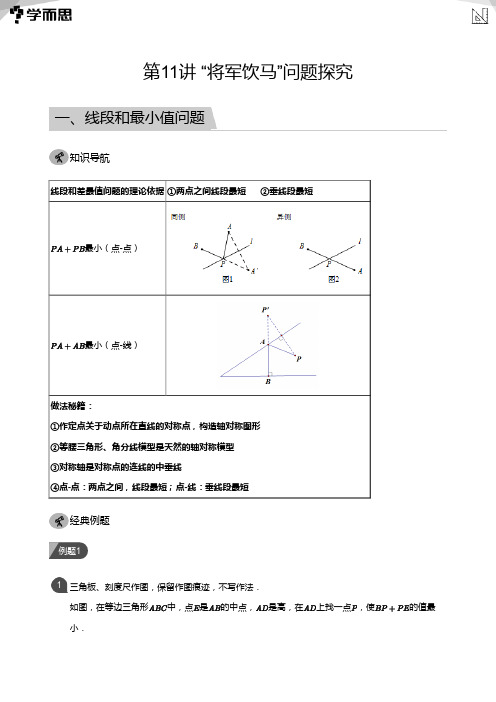
等于多少度?如果
,
又等于多少?
的周长取最
答案 当
的周长取最小值时,
.
时,
.
解析 如下图所示:连 、 .
∵点 与点 关于直线 对称,点 与点 关于
对称,
∴
,
,
,
.
∴
,
,
∵
,
,
∴
,
∴
,
在
中,由三角形的内角和定理可知:
.
∴
,
∴
,
如果
,则
.
在
中,由三角形的内角和定理可知:
.
∴
,
∴
.
标注 三角形 > 三角形及多边形 > 与三角形有关的角 > 题型:三角形内角的应用
天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题。
将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的B地开会,应该怎样走才能使路程最
短?
从此,这个被称为“将军饮马”的问题广泛流传.这个问题的解决并不难,据说海伦略加思索就解
决了它.如图所示,从 出发向河岸引垂线,垂足为 ,在 的延长线上取 关于河岸的对称点 ,连
于,
∵是
的平分线,
且
,
∴
,
,
∴
,
当 、 、 共线且
时,
最小,
过作
于,
则
,
,
∴
,
∴
.
标注 三角形 > 全等三角形 > 角平分线 > 题型:角分线性质应用
二、三角形、四边形周长最小
知识导航
经典例题
例题5
1 三角板、刻度尺作图,保留作图痕迹,不写作法:
第11讲 “将军饮马”问题探究(教师版)

知识导航
①作定点关于动点所在直线的对称点,构造轴对称图形
②等腰三角形、角分线模型是天然的轴对称模型
经典例题
1
三角板、刻度尺作图,保留作图痕迹,不写作法.
2
如图,正方形
3
如图,正方形4
在
直线、射线、线段问题>题型:动点与线段-无数轴1
三角板、刻度尺作图,保留作图痕迹,不写作法:
2
如图,在
3
如图,在知识导航
经典例题1
如图,直线2
如图,
知识导航
经典例题
1
如图,在一组平行线
2
如图,直线
3
如图,在正方形
设汽车行驶到公路上点的位置时,距离村庄最近,行驶到点的位置时,距离村庄上分别画出、的位置;
行驶时,在公路的哪一段上距离、两村都越来越近?在哪一段两村都越来越
关于直
三角形
>等腰三角形>等腰等边综合如图,四边形中,。
(完整版)将军饮马问题的11个模型及例题

5.搭桥模型 已知:如图,直线m∥n,A、B分别为m上方和n下方的定
点,(直线AB不与m垂直)
要求:在m、n之间求作垂线段PQ,使得AP+PQ+BQ最小.
分析:PQ为定值,只需AP+BQ最小,可通过平移,使
P、Q“接头”,转化为基本模型
解:如图,将点A沿着平行于PQ的方向,向下平移至
【小结】“两点一线”大多考查基本模型2和4,需作一次对称点,连线得交点.
变式训练1-1
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),
OB=4 ,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短
时,点P的坐标为( )
A.(0,0)B.(1, )C.( , )D.( , )
要求:确定PQ的位置,使得四边形APQB周长最小
分析:AB长度确定,只需AP+PQ+QB最小,通过作A点
关于l的对称点,转化为上述模型3
解:作A点关于l的对称点A´,将点A´沿着平行于l
的方向,向右移至A´´,使A´A´´=PQ=a,连接A´´B
交l于Q,在l上截取QP=a(P在Q左边),线段
PQ即为所求,此时四边形APQB周长的最小值为
点到l的距离不相等)
要求:在直线l上找一点P,使︱PA-PB︱的值最大
解:作点B关于直线l的对称点B´,连接B´A并延长交
于点P,点P即为所求;
理由:根据对称的性质知l为线段BB´的中垂线,由中垂
线的性质得:PB=PB´,要使︱PA-PB︱最大,则需
︱PA-PB´︱值最大 ,从而转化为模型3.
二次函数中最值问题(教师版)

二次函数与几何综合专题----线段最值问题将军饮马:这个将军饮的不是马,是数学!原理:两点间线段最短;点到直线的垂直距离最短;对称(翻折)、平移.策略:对称(翻折)→化同为异、化异为同;化折为直.两村一路(异侧)和最小两村一路(同侧)和最小两路一村和最小两村两路和最小两村一路和最小两村一路(同侧)差最大两村一路(异侧)差最大例:如图,在平面直角坐标系xOy 中,抛物线2y x bx c =++与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,3OA OC ==,顶点为D ,对称轴交x 轴于点E . (1)求抛物线的解析式、对称轴及顶点D 的坐标.PN y轴交AC于N,求线段PN的最大值及此时点P (2)直线AC下方的抛物线上有一动点P,过点P作//的坐标.于H,求线段PH的最大值及此时点P的坐标.(3)直线AC下方的抛物线上有一动点P,过点P作PH AC(4)直线AC 下方的抛物线上有一动点P ,过点P 作//PN y 轴交AC 于N ,过点P 作PH AC 于H ,求PNH △周长的最大值及此时点P 的坐标.(5)在抛物线对称轴上找一点N ,使得BCN △的周长最小,求BCN △周长的最小值及此时点N 的坐标.⊥交AC于点M,求CM的最小值.(6)在线段OA上找一点N,连接NC,作NM NCMN=,求四边形BNMC周长的最小值及(7)在抛物线对称轴上有两动点N、M(点N在点M上方),且1此时M的坐标.(8)在对称轴上找一点N ,使得NA NC -最大,求点N 的坐标.【答案】(1)223y x x =+-,对称轴为:直线x =-1,顶点坐标为:D (-1,-4);(2)PN 的最大值为94,此时P (-32,154-);(3)当PN 最大为94时,PH 92P (-32,154-);(4)当PNH △周9294,此时P (-32,154-);(5)1032N (-1,-2);(6)1262-(7)6105(8)10131,M (713-,-);(9)N 的坐标为:(-1,-6). 【详解】(1)解:∵3OA OC ==, ∴A (-3,0),C (0,-3),∴()20333b c c ⎧=--+⎪⎨-=⎪⎩,解得:23b c =⎧⎨=-⎩,∴抛物线的解析式为:223y x x =+-,对称轴为:直线x =-1,顶点坐标为:D (-1,-4). (2)解:设P (x ,223x x +-),则N (x ,-x -3),∴PN =-x -3-(223x x +-)=23x x --=23924x ⎛⎫-++ ⎪⎝⎭,∴当x =-32时,PN 的最大值为94,此时P (-32,154-).(3)解:过点P 作PN ∥y 轴,交AC 于点N , ∵OA =OC =3, ∴∠ACO =45°, ∵PN ∥y 轴,∴∠PNH =45°,即:PNH 是等腰直角三角形,∴PH 2PN , 设P (x ,223x x +-),则N (x ,-x -3),∴PN =-x -3-(223x x +-)=23x x --=23924x ⎛⎫-++ ⎪⎝⎭,∴当x =-32时,PN 的最大值为94,∴当PN 最大为94时,PH 最大值=94×22=928,此时P (-32,154-).(4)解:∵OA =OC =3, ∴∠ACO =45°, ∵PN ∥y 轴,∴∠PNH =45°,即:PNH 是等腰直角三角形, ∴PH =NH 2, ∴PNH △周长= PH +NH +PN 22PN 22PN + PN =(21)PN , 设P (x ,223x x +-),则N (x ,-x -3),∴PN =-x -3-(223x x +-)=23x x --=23924x ⎛⎫-++ ⎪⎝⎭,∴当x =-32时,PN 的最大值为94,∴当PN 最大为94时,PNH △周长最大值=94×)219294,此时P (-32,154-).(5)解:连接AC 交对称轴于点N ′,∵A、B关于对称轴对称,∴AN′=BN′∴BCN△的周长=BC+CN′+BN′=BC+CN′+AN′=BC+AC,∴此时BCN△的周长最小值=BCN'的周长=BC+AC222213331032++∵直线AC的解析式为:y=-x-3,∴当x=-1时,y=-2,即N(-1,-2).(6)解:由题意得:点N在以CM为直径的圆上,设CM的中点为E,连接EN,则当圆E与x轴相切时,即:EN⊥x轴时,EN最小,此时CM=2EN最小,设M(x,-x-3),则E(622x x--,),∴EN=62x+,CM()222332x x x+--+=∴2×62x +22x 662x =-62x =+, ∴M (662-629), ∴CM ()()2266262931262-+-+-(7)解:过点N 作作NQ ∥MC 交y 轴于点Q ,连接AQ 交DE 于点N ′,连接BN ′,则Q (-2,0),∵NQ ∥MC ,MN ∥CQ , ∴四边形MNQC 是平行四边形, ∴CM =QN ,∴四边形BNMC 的周长=BC +BN +MN +CM =BC +BN +1+QN 101+BN +QN , ∵B 、A 关于DE 对称, ∴AN ′=BN ′,∴四边形BNMC 101+BN ′+QN ′101+AN ′+QN 101+AQ 101+222310131+,∵直线AQ 的解析式为:223y x =--,∴N ′(413-,-),∴此时M (713-,-).(8)解:连接BC ,并延长交ED 于点N ′,连接BN ,∵A 、B 关于DE 对称, ∴AN =BN ,∴NA NC -=NB NC -≤BC =N B N C ''-, ∵B (1,0),C (0,-3), ∴直线BC 的解析式为:33y x =-, 令x =-1代入33y x =-得:y =-6, ∴N ′(-1,-6),∴NA NC -最大时,N 的坐标为:(-1,-6).二次函数与几何综合专题---- 胡不归和阿氏圆问题【胡不归最值问题】 求BC +kAC 的最小值.解决思路:构造射线AD 使得sin ∠DAN=k ,即CHk AC,CH=kAC .将问题转化为求BC+CH 最小值,过B 点作BH ⊥AD 交MN 于点C ,交AD 于H 点,此时BC+CH 取到最小值,即BC+kAC 最小.1.已知抛物线y =ax 2+bx +c 与x 轴交于A (﹣1,0),B (5,0)两点,C 为抛物线的顶点,抛物线的对称轴交x 轴于点D ,连结BC ,且tan ∠CBD =43,如图所示. (1)求抛物线的解析式;(2)设P 是抛物线的对称轴上的一个动点.①过点P 作x 轴的平行线交线段BC 于点E ,过点E 作EF ⊥PE 交抛物线于点F ,连结FB 、FC ,求△BCF 的面积的最大值;②连结PB ,求35PC +PB 的最小值.CH=kACsin α=CH AC=kHDαA BCM MCBAαDH2.在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(﹣3,0)、B(1,0),交y轴于点N,点M 为抛物线的顶点,对称轴与x轴交于点C.(1)求抛物线的解析式;(2)如图1,连接AM,点E是线段AM上方抛物线上一动点,EF⊥AM于点F,过点E作EH⊥x轴于点H,交AM于点D.点P是y轴上一动点,当EF取最大值时:①求PD+PC的最小值;②如图2,Q点为y轴上一动点,请直接写出DQ+14OQ的最小值.3.如图,抛物线y =ax 2﹣2ax +c 的图象经过点C (0,﹣2),顶点D 的坐标为(1,−83),与x 轴交于A 、B 两点.(1)求抛物线的解析式.(2)连接AC ,E 为直线AC 上一点,当△AOC ∽△AEB 时,求点E 的坐标和AE AB的值.(3)在(2)的条件下,点F (0,y )是y 轴上一动点,当y 为何值时,√55FC +BF 的值最小.并求出这个最小值.(4)点C 关于x 轴的对称点为H ,当√55FC +BF 取最小值时,在抛物线的对称轴上是否存在点Q ,使△QHF 是直角三角形?若存在,请求出点Q 的坐标;若不存在,请说明理由.4.如图1,抛物线y=x2+(m﹣2)x﹣2m(m>0)与x轴交于A,B两点(A在B左边),与y轴交于点C.连接AC,BC.且△ABC的面积为8.(1)求m的值;(2)在(1)的条件下,在第一象限内抛物线上有一点T,T的横坐标为t,使∠ATC=60°.求(t﹣1)2的值.(3)如图2,点P为y轴上一个动点,连接AP,求CP+AP的最小值,并求出此时点P的坐标.【阿氏圆最值问题】计算PA k PB +的最小值时,利用两边成比例且夹角相等构造母子型相似三角形问题:在圆上找一点P 使得PA k PB +的值最小,解决步骤具体如下: ①如图,将系数不为1的线段两端点与圆心相连即OP ,OB ②计算出这两条线段的长度比OPk OB= ③在OB 上取一点C ,使得OC k OP =,即构造△POM ∽△BOP ,则PCk PB=,PC k PB = ④则=PA k PB PA PC AC ++≥,当A 、P 、C 三点共线时可得最小值1.如图,抛物线2y ax bx c =++与x 轴交于(3A 0),B 两点(点B 在点A 的左侧),与y 轴交于点C ,且33OB OA OC ==,OAC ∠的平分线AD 交y 轴于点D ,过点A 且垂直于AD 的直线l 交y 轴于点E ,点P 是x 轴下方抛物线上的一个动点,过点P 作PF x ⊥轴,垂足为F ,交直线AD 于点H . (1)求抛物线的解析式;(2)设点P 的横坐标为m ,当FH HP =时,求m 的值; (3)当直线PF 为抛物线的对称轴时,以点H 为圆心,12HC 为半径作H ,点Q 为H 上的一个动点,求14AQ EQ +的最小值.2.如图1,抛物线y=ax2+bx+c与x轴正半轴交于点A,点B(点A在点B的左侧),与y轴交于点C.若线段AB绕点A逆时针旋转120°,点B刚好与点C重合,点B的坐标为(3,0).(1)求抛物线的表达式;(2)抛物线的对称轴上是否存在一点P,使△ACP为直角三角形?若存在,请求出点P的坐标,若不存在,请说明理由;(3)如图2,以点B为圆心,以1为半径画圆,若点Q为⊙B上的一个动点,连接AQ,CQ,求AQ+CQ 的最小值.3.如图,已知抛物线y=﹣x2+2x+3与x轴交于点A,B(点A在点B的右侧),与y轴交于点C.(1)如图①,若点D为抛物线的顶点,以点B为圆心,3为半径作⊙B.点E为⊙B上的动点,连接A,DE,求DE+AE的最小值.(2)如图②,若点H是直线AC与抛物线对称轴的交点,以点H为圆心,1为半径作⊙H,点Q是⊙H 上一动点,连接OQ,AQ,求OQ+AQ的最小值;(3)如图③,点D是抛物线上横坐标为2的点,过点D作DE⊥x轴于点E,点P是以O为圆心,1为半径的⊙O上的动点,连接CD,DP,PE,求PD﹣PE的最大值.4.如图1,抛物线y=ax2+bx﹣4与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(﹣1,0),抛物线的对称轴是直线x=.(1)求抛物线的解析式;(2)若点P是直线BC下方的抛物线上一个动点,是否存在点P使四边形ABPC的面积为16,若存在,求出点P的坐标若不存在,请说明理由;(3)如图2,过点B作BF⊥BC交抛物线的对称轴于点F,以点C为圆心,2为半径作⊙C,点Q为⊙C 上的一个动点,求BQ+FQ的最小值.【课后训练】1.如图,直线y=x+2与抛物线y=x2﹣2mx+m2+m交于A、B两点(A在B的左侧),与y轴交于点C,抛物线的顶点为D,抛物线的对称轴与直线AB交于点M.(1)当四边形CODM是菱形时,求点D的坐标;(2)若点P为直线OD上一动点,求△APB的面积;′(3)作点B关于直线MD的对称点B',以点M为圆心,MD为半径作⊙M,点Q是⊙M上一动点,求QB'+QB的最小值.2.如图,已知二次函数y=ax2+bx+c的图象经过点C(2,﹣3),且与x轴交于原点及点B(8,0),点A为抛物线的顶点.(1)求二次函数的表达式;(2)在抛物线的对称轴上是否存在点M,使△ABM是等腰三角形?如果存在,请求出点M的坐标.如果不存在,请说明理由;(3)若点P为⊙O上的动点,且⊙O的半径为,求的最小值.3.抛物线y=ax2+bx﹣5的图象与x轴交于A、B两点,与y轴交于点C,其中点A坐标为(﹣1,0),一次函数y=x+k的图象经过点B、C.(1)试求二次函数及一次函数的解析式;(2)如图1,点D(2,0)为x轴上一点,P为抛物线上的动点,过点P、D作直线PD交线段CB于点Q,连接PC、DC,若S△CPD=3S△CQD,求点P的坐标;(3)如图2,点E为抛物线位于直线BC下方图象上的一个动点,过点E作直线EG⊥x轴于点G,交直线BC于点F,当EF+√22CF的值最大时,求点E的坐标.4.如图①,直线y=﹣x﹣3分别与x轴、y轴交于点B,C,抛物线y=ax2+bx+c经过B,C两点,且与x轴的另一交点为A(1,0).(1)求抛物线的函数解析式;(2)如图①,点P在第三象限内的抛物线上.①连接AC,PB,PC,当四边形ABPC的面积最大时,求点P的坐标;②在①的条件下,G为x轴上一点,当PG+√55AG取得最小值时,求点G的坐标;(3)如图②,Q为x轴下方抛物线上任意一点,D是抛物线的对称轴与x轴的交点,直线AQ,BQ分别交抛物线的对称轴于点M,N.问:DM+DN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.21Math唐老师22。
(完整版)将军饮马问题的11个模型及例题

如图,菱形ABCD中,对角线AC和BD交于点O,AC=2,
BD=2 ,E为AB的中点,P为对角线AC上一动点,则PE+PB的
最小值为__________.
变式训练1-3
如图,已知直线y= x+1与y轴交于点A,与x轴交于点D,抛物线y= x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
点到l的距离不相等)
要求:在直线l上找一点P,使︱PA-PB︱的值最大
解:作点B关于直线l的对称点B´,连接B´A并延长交
于点P,点P即为所求;
理由:根据对称的性质知l为线段BB´的中垂线,由中垂
线的性质得:PB=PB´,要使︱PA-PB︱最大,则需
︱PA-PB´︱值最大 ,从而转化为模型3.
典型例题1-1
【解答】作P点分别关于OA、OB的对称点C、D,连接CD分别交OA、OB于M、N,如图,
则MP=MC,NP=ND,OP=OD=OC= ,∠BOP=∠BOD,∠AOP=∠AOC,
∴PN+PM+MN=ND+MN+NC=DC,∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB=120°,
∴此时△PMN周长最小,作OH⊥CD于H,
如图,直线y= x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为_________,此时PC+PD的最小值为_________.
【分析】符合基本模型2的特征,作点D关于x轴的对称点D',连接CD'交x轴于点P,此时PC+PD值最小,由条件知CD为△BAO的中位线,OP为 △CDD'的中位线,易求OP长,从而求出P点坐标;PC+PD的最小值即CD'长,可用勾股定理(或两点之间的距离公式,实质相同)计算.
2021年中考数学几何专项复习 专题12 几何最值之将军饮马巩固练习(提优)(教师版含解析)

几何最值之将军饮马巩固练习(提优)1.如图所示,在四边形ABCD中,∠A=90º,∠C=90º,∠D=60º,AD=3,AB=,若点M、N 分别为边CD,AD上的动点,则△BMN的周长最小值为( )A. B. C. 6 D. 3【解答】C【解析】作点B关于CD、AD的对称点分别为点B'和点B'',连接B'B''交DC和AD于点M和点N,连接MB、NB;再DC和AD上分别取一动点M’和N’(不同于点M和N),连接M'B,M'B',N’B和N'B'',如图1所示:∵B'B''<M'B'+M'N'+N'B",B'M'=BM',B"N'=BN',∴BM'+M'N'+BN'>B'B",又∵B'B"=B'M+MN+NB",MB=MB',NB=NB'',∴NB+NM +BM<BM'+M’N'+BN'NB+NM+BM时周长最小;连接DB,过点B'作B'H⊥DB''于B’’D的延长线于点H,如图示2所示:在Rt△ABD中,AD=3,AB=,,∴∠2=30º,∴∠5=30º,DB=DB'',又∵∠ADC=∠1+∠2=60º,∴∠1=30º,∴∠7=30º,DB'=DB,∴∠B'DB''=∠1+∠2+∠5+∠7=120º,DB'=DB''=DB又∵∠B'DB"+∠6=180º,∴∠6=60º,∴HD,HB'=3,在Rt△B'HB''中,由勾股定理得:B'B"=,NB+NM+BM=6,故选C.2.如图,在四边形ABCD中,DA⊥AB,DA=6,∠B+∠C=150º,CD与BA的延长线交于E点,A 刚好是EB中点,P、Q分别是线段CE、BE上的动点,则BP+PQ最小值是( )A. 12B. 15C. 16D. 18【解答】D【解析】如图,作点B关于CE的对称点F,连接BF,EF,则EB=EF,∵∠B+∠C=150º,∴∠BEC=30º,∴∠BEF=60º,∴△BEF是等边三角形,连接BP,PF,PQ,则BP=FP,∴BP+QP=FP+PQ,当F,P,Q在同一直线上且FQ⊥EB时,BP+PQ的最小值为FQ的长,此时,Q为EB的中点,故与A重合,∵DA⊥AB.DA=6,∴AE ,∴Rt△QEF中,FQ=AE=18,∴BP+PQ最小值值为18,故选D.3.如图,等边△ABC中,AD为BC边上的高,点M、N分别在AD、AC上,且AM=CN,连接BM、BN,当BM+BN最小时,∠MBN=度.【解答】30º【解析】作CH⊥BC,使得CH=BC,连接NH,BH,如图所示:∵△ABC是等边三角形,AD⊥BC,CH⊥BC,∴∠DAC=∠DAB=30º,AD∥CH,∴∠HCN=∠CAD=∠BAM=30º,∵AM=CN,AB=BC=CH,∴△ABM≌△CHN(SAS),∴BM=HN,∵BN+HN≥BH,∴B,N,H共线时,BM+BN=NH+BN的值最小,当B,N,H共线时,如图所示:∵△ABM≌△CHN,∴∠ABM=∠CHB=∠CBH=45º,∵∠ABD=60º,∴∠DBM=15º,∴∠MBN=45º-15º=30º,当BM+BN的值最小时,∠MBN=30º.4.如图,矩形ABCD中,AB=4,BC=6,点P是矩形ABCD PC+PD的最小值为.【解析】如图,作PM⊥AD于M,作点D关于直线PM的对称点E,连接PE,EC.设AM=,∵四边形ABC都是矩形,AB//CD,AB=CD=4,BC=AD=6,∴,∴=2,∴AM=2,DM=EM=4,在Rt△ECD中,,∵PM垂直平分线段DE,∴PD=PE,∴PC+PD=PC+PE≥EC,∴PD+PC,∴PD+PC.5.如图,在△ABC中,∠ACB=90º,点D是直线BC上一点.(1)如图1,若AC=BC=2,点D是BC边的中点,点M是线段AB上一动点,求△CMD周长的最小值;(2)如图2,若AC=4,BC=8,是否存在点D,使以A,D,B为顶点的三角形是等腰三角形,若存在,请直按写出线段CD的长度;若不存在,请说明理由.【解答】(1)△CMD周长的最小值为;(2)存在,详细见解析【解析】(1)如图,作C关于AB的对称点E,连接DE交AB于M,此时,△CMD周长的值最小,∵AC=BC,∠ACB=90º,∴∠BCE=45º,连接BE,∴BC=BE=2,△CBE是等腰直角三角形,,∴△CMD周长的最小值=;(2)存在,∵AC=4,BC=8,,当AD1=AB时,△AD1B的等腰三角形,∵AC⊥BC,∴CD1=BC=8当BD2=AB=时,△AD2B是等腰三角形,,当AD3=D3B时,△AD3B的等腰三角形,∴BD3=8-CD3,=3,解得CD当BD4=AB=时,△AD4B的等腰三角形,∴CD4=8+,综上所述,以A,D,B为顶点的三角形是等腰三角形,线段CD的长度为8-8或3+8.6.如图,在锐角三角形ABC中,BC=4 ,∠ABC=45º,BD平分∠ABC,M、N分别是BD、BC 上的动点,试求CM+MN的最小值.【解答】4【解析】如图所示,过点C作CE⊥AB于点E,交BD于点M',过点M'作M'N'⊥BC于N',则CE即为CM +MN的最小值.∵BC,∠ABC=45º,BD平分∠ABC,∴△BCE是等腰直角三角形,,故CM+MN的最小值为4.7.如图,在平行四边形ABCD中,BD是对角线,∠ADB=90º,E、F分别为边AB、CD的中点.(1)求证:四边形DEBF是菱形;(2)若BE=4,∠DEB=120º,点M为BF的中点,当点P在BD边上运动时,求PF+PM的最小值.【解答】(1)见解析;【解析】(1)证明:∵平行四边形ABCD中,AD∥BC,∴∠DBC=∠ADB=90º,∵△ABD中,∠ADB=90º,E时AB的中点,∴DE=AB=AE=BE,同理,BF=DF,∵平行四边形ABCD中,AB=CD,∴DE=BE=BF=DF,∴四边形DEBF是菱形;(2)连接BF,如图所示:∵菱形DEBF中,∠DEB=120º,∴∠EBF=60º,∴△BEF是等边三角形,∵M是BF的中点,∴EM⊥BF,,即PF+PM.8.已知:矩形ABCD中,AD=2AB,AB=6,E为AD中点,M为CD上一点,PE⊥EM交CB于点P,EN平分∠PEM交BC于点N.(1)求证:PE=EM;(2)用等式表示BP2、PN2、NC2三者的数量关系,并加以证明;(3)过点P作PG⊥EN于点G,K为EM中点,连接DK、KG,求DK+KG+PG的最小值.【解答】(1)见解析;(2)BP2+NC2=PN2;(3)【解析】(1)证明:过P作PQ⊥AD于Q,则PQ=AB,如图所示:∵AD=2AB,E为AD中点,∴AD=2DE,∴PQ=DE,∵PE⊥EM,∴∠PQE=∠D=∠PEM=90º,∴∠QPE+∠PEQ=∠PEQ+∠DEM=90º,∴∠QPE=∠DEM,∴△PQE≌△EDM(ASA),∴PE=EM;(2)三者的数量关系是:BP2+NC2=PN2①点N与点C重合时,P为BC的中点,显然BP2+NC2=PN2成立;②点P与点B重合时,N为BC的中点,显然BP2+NC2=PN2成立;③证明:连接BE、CE,如图所示:∵四边形ABCD为矩形,AD=2AB,E为AD中点,∴∠A=∠ABC=90º,AB=CD=AE=DE,∴∠AEB=45º,∠DEC=45º,在△ABE和△DCE中,,∴△ABE≌△DCE(SAS),∠BEC=90º,∴BE=CE,∴∠EBC=∠ECB=45º,∴∠EBC=∠ECD,又∵∠BEC=∠PEM=90º,∴∠BEP=∠MEC,∠EBP=∠ECM在△BEP和△CEM中,,∴△BEP≌△CEM(ASA),∴BP=MC,PE=ME,∵EN平分∠PEM,∴∠PEN=∠MEN=45º,在△EPN和△EMN中,,∴△EPN≌△EMN(SAS),∴PN=MN,在Rt△MNC中有:MC2+NC2=MN2,∴BP2+NC2=PN2;(3)连接PM,如图所示:由(2),可得PN =MN,PE=ME,∴EN垂直平分PM,PG⊥EN,∴P、G、M三点共线,且G为PM的中点,∵K为EM中点,又∵∠D=90º,,由(2),可得△PEM为等腰直角三角形,根据勾股定理,可得,∴当ME取得最小值时,DK+GK+PG取得最小值,即当ME=DE=6时,DK+GK+PG有最小值,最小值为.。
《将军饮马——最值为王》+课件-2025学年人教版八年级数学上册+

P
l 3.形成的线段长即为最短(三点共线)
探究二
求出最短值
A
A
P l
B
A'
将最短线段构造在直角三角形中, 利用勾股定理求具体值
B
l P
例题讲解
如图所示,AM⊥EF,BN⊥EF,垂足为M,N,MN=12m,
AM=5m,BN=4m,P是EF上任意一点,则PA+PB的最小
值是多少m? 15m
A B
E MP N
且A,B,C三点不在同一条直线上,当△ABC的
周长最小时点C的坐标是( A )
A.(0,3)
B.(0,2)
C′
C.(0,1)
D.(0,0)
B′
解析:作B点关于y轴对称点B′,连接AB′,
E
交y轴于点C′,此时△ABC的周长最小,
然后依据点A与点B′的坐标可得到BE、
AE的长,然后证明△B′C′O为等腰直角三
(2)如图②,在∠AOB内部有一点P,是否在OA、OB上分别存
在点E、F,使得E、F、P三点组成的三角形的周长最短,找出E、
F两点,并说明理由.
(3)如图③,在∠AOB内部有两点M、N,是否在OA、OB上分
别存在点E、F,使得E、F、M、N,四点组成的四边形的周长最
短,找出E、F两点,并说明理由.
D
A.7.5
B.5
C.4
D.不能确定
课堂检测
1. 如图,已知点D、点E分别是等边三角形ABC中
BC、AB边的中点,AD=5,点F是AD边上的动点,
则BF+EF的最小值为( B )
A.7.5
B.5
C.4
D.不能确定
解析:△ABC为等边三角形,点D是BC边的中点,即点B与点 C关于直线AD对称.∵点F在AD上,故BF=CF.即BF+EF的最小 值可转化为求CF+EF的最小值,故连接CE即可,线段CE的长 即为BF+EF的最小值.
专题04 利用将军饮马模型解决特殊平行四边形中的最值问题的五种考法(老师版)

利用将军饮马模型解决特殊平行四边形中的最值问题的五种考法目录解题知识必备 (1)压轴题型讲练 (4)模型一、求两条线段和的最小值(将军饮马模型) (4)模型二、平移型将军饮马(将军过桥模型) (9)模型三、修桥选址模型(将军遛马模型) (14)模型四、求多条线段和(周长)最小值 (19)模型五、求两条线段差最大值 (27)压轴能力测评(10题) (34)模型一、求两条线段和的最小值(将军饮马模型)【模型解读】在一条直线m上,求一点P,使PA+PB最小;(1)点A、B在直线m两侧:(2)点A、B在直线同侧:【最值原理】两点之间线段最短.上图中A’是A关于直线m的对称点.模型二、平移型将军饮马(将军过桥模型)【模型解读】已知,如图1将军在图中点A处,现要过河去往B点的军营,桥必须垂直于河岸建造,问:桥建在何处能使路程最短?考虑MN长度恒定,只要求AM+NB最小值即可.问题在于AM、NB彼此分离,所以首先通过平移,使AM与NB 连在一起,将AM向下平移使得M、N重合,此时A点落在A’位置(图2).问题化为求A’N+NB最小值,显然,当共线时,值最小,并得出桥应建的位置(图3).图1图2图3【最值原理】两点之间线段最短.模型三、修桥选址模型(将军遛马模型)【模型解读】已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA +PQ +QB 的值最小.(原理用平移知识解)(1)点A 、B 在直线m 两侧:(2)点A 、B 在直线m 同侧:如图1如图2(1)如图1,过A 点作AC ∥m ,且AC 长等于PQ 长,连接BC ,交直线m 于Q ,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点.(2)如图2,过A 点作AE ∥m ,且AE 长等于PQ 长,作B 关于m 的对称点B ’,连接B ’E ,交直线m 于Q ,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点.【最值原理】两点之间线段最短.模型四、求多条线段和(周长)最小值【模型解读】在直线m 、n 上分别找两点P 、Q ,使PA +PQ +QB 最小.(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:(4)台球两次碰壁模型1)已知点A、B位于直线m,n的内侧,在直线n、m分别上求点D、E点,使得围成的四边形ADEB周长最短.2)已知点A位于直线m,n的内侧,在直线m、n分别上求点P、Q点PA+PQ+QA周长最短.【最值原理】两点之间线段最短.模型五、求两条线段差最大值【模型解读】在一条直线m上,求一点P,使PA与PB的差最大;(1)点A、B在直线m同侧:延长AB交直线m于点P,根据三角形两边之差小于第三边,P’A-P’B<AB,而PA-PB=AB此时最大,因此点P为所求的点.(2)点A、B在直线m异侧:【最值原理】三角形两边之差小于第三边.模型一、求两条线段和的最小值(将军饮马模型)【模型解读】在一条直线m 上,求一点P ,使PA +PB 最小;(1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:【最值原理】两点之间线段最短.上图中A’是A 关于直线m 的对称点.例题:(23-24八年级下·云南昭通·阶段练习)如图,正方形ABCD 的边长为4,点M 在DC 上,且1DM =,点N 是AC 上一动点,则DN MN +的最小值为()A .4B .5C .42D .8【答案】B 【分析】本题考查的是轴对称﹣最短路线问题及正方形的性质,由正方形的对称性可知点B 与D 关于直线AC 对称,连接BM 交AC 于N '点,N '即为所求,在Rt BCM △中利用勾股定理即可求出BM 的长即可.【详解】解:∵四边形ABCD 是正方形,∴点B 与D 关于直线AC 对称,即AC 是线段BD 的垂直平分线,连接BD ,BM ,BM 交AC 于N ',连接DN ',N '即为所求的点,根据对称有:BN DN ''=,即BN N M DN N M ''''+=+,当点B 、N '、M 三点共线时,BN MN ''+最小,则BM 的长即为DN MN +的最小值,∵413CM CD DM =-=-=,∴在Rt BCM △中,2222345BM CM BC =+=+=,故DN MN +的最小值是5.故选:B .【变式训练1】(23-24八年级下·河北沧州·期末)如图,在菱形ABCD 中,135D ∠=︒,AD =32,2CE =,点P 是线段AC 上一动点,点F 是线段AB 上一动点,则PE PF +的最小值.【答案】10【分析】本题考查了菱形的性质与轴对称的性质,勾股定理.先作点E 关于AC 的对称点点G ,再连接BG ,过点B 作BH CD ⊥于H ,运用勾股定理求得BH 和GH 的长,最后在Rt BHG 中,运用勾股定理求得BG 的长,即为PE PF +的最小值.【详解】解:作点E 关于AC 的对称点点G ,连接PG 、PE ,则PE PG =,2CE CG ==,连接BG ,过点B 作BH CD ⊥于H ,则45BCH CBH ∠=∠=︒,四边形ABCD 是菱形,32,AD =∴32,BC AD ==Rt BHC ∴中,BH CH ==2sin sin 453232BC BCH BC ⋅=⋅︒=⨯=∠∠,321HG HC GC ∴=-=-=,Rt BHG ∴中,BG =2222=31=10BH HG ++,当点F 与点B 重合时,PE PF PG PB BG +=+=(最短),PE PF ∴+的最小值是10.故答案为:10.点F 、P 为BC AC 、边上的动点,则PE PF +的最小值为.【答案】4.8【分析】先根据菱形的性质求出其边长,再作E 关于AC 的对称点E ',过E '作AD 的垂线交BC 于点F ',则E F ''的长度即为PE PF +的最小值,最后根据菱形的面积求出E F ''的长度即可.【详解】解:∵四边形ABCD 是菱形,对角线6,8AC BD ==,∴22345=+=AD ,作E 关于AC 的对称点E ',过E '作AD 的垂线交BC 于点F ',则E F ''的长度即为PE PF +的最小值,∵12ABCD S AC BD =⋅=菱形∴2AC BD AD E F ⋅=⋅''即68225AC BD E F AD ⋅⨯''==⨯分别过点B 、C 作AC 与BD 的平行线相交于点E .点G 在直线AC 上运动,则BG EG +的最小值为.OB OD ∴=,AC BD ⊥,四边形BOCE 是矩形,3BE OC EBO ∴==∠=,作B 点关于AC 的对称点,即BG DG ∴=,足为点M ,连接CM ,若3AM =,则CM AD +的最小值为.故答案为:41.【变式训练5】(23-24八年级下E 是AD 上一点,且5AD DE =,点F 是DH 的中点,点P 是线段BD 上一动点.点P 在运动过程中,PE PF +的最小值为.Rt 222125FI FD DI ⎛⎫=+= ⎪⎝⎭∴PE PF PF PI FI +=+³最小值为135.模型二、平移型将军饮马(将军过桥模型)【模型解读】已知,如图1将军在图中点A 处,现要过河去往B 点的军营,桥必须垂直于河岸建造,问:桥建在何处能使路程最短?考虑MN 长度恒定,只要求AM +NB 最小值即可.问题在于AM 、NB 彼此分离,所以首先通过平移,使AM 与NB 连在一起,将AM 向下平移使得M 、N 重合,此时A 点落在A ’位置(图2).问题化为求A ’N +NB 最小值,显然,当共线时,值最小,并得出桥应建的位置(图3).图1图2图3【最值原理】两点之间线段最短.例题:(2024·四川泸州·一模)如图,在直角坐标系中,()2,0A -,()0,2B ,C 是OB 的中点,点D 在第二象限,且四边形AOCD 为矩形,P 是CD 上一个动点,过点P 作PH OA ⊥于H ,Q 是点B 关于点A 的对称点,则BP PH HQ ++的最小值为.【答案】6【分析】本题考查了一次函数点的坐标的求法、三角形面积的求法和三点共线及最值,综合性强,是中考常见题型.连接CH ,根据A 、B 的坐标先确定OA 和OB 的长,证明四边形PHOC 是矩形,得1PH OC BC ===,再证明四边形PBCH 是平行四边形,则BP CH =,在BP PH HQ ++中,1PH =是定值,所以只要CH HQ +的值最小就可以,当C 、H 、Q 在同一直线上时,CH HQ +的值最小,利用平行四边形的性质求出即可.【详解】解:如图,连接CH ,(2,0)A -,(0,2)B ,2OB ∴=,2OA =,C 是OB 的中点,1BC OC ∴==,90PHO COH DCO ∠=∠=∠=︒,∴四边形PHOC 是矩形,1PH OC BC ∴===,PH BC ∥,∴四边形PBCH 是平行四边形,BP CH ∴=,1BP PH HQ CH HQ ∴++=++,要使CH HQ +的值最小,只需C 、H 、Q 三点共线即可,点Q 是点B 关于点A 的对称点,(4,2)Q ∴--,又点(0,1)C ,根据勾股定理可得()()2204125CQ =+++=,此时,1516BP PH HQ CH HQ PH CQ ++=++=+=+=,即BP PH HQ ++的最小值,6;故答案为:6【变式训练1】(23-24八年级下·浙江金华·期末)如图,正方形ABCD 的边长为3,点E 在CD 上且1CE =,点F P 、分别为线段BC AD 、上的动点,连接BE ,BP ,FP ,EF .若在点F P 、的运动过程中始终满足PF BE ⊥,则BP EF +的最小值为()A .B .C .D .【变式训练2】(2024移得到A B C '''(点A '在线段AC 上),连接A B '',A D ',B D '.在平移过程中,(1)若四边形A B CD ''是矩形,则=AA ';(2)A D B D ''+的最小值为.∵在菱形ABCD 中,4AB =∴BD AC ⊥,ABD CBD ∠=∠∴30BAO ∠=︒,∵将ABC 向右平移得到A B ''∴AB A B ''∥,AB A B ''=,∴A BD B '''是平行四边形,∴A B B D '''=,∵在菱形ABCD 中,由菱形对称性得到【点睛】本题考查了平移的性质,菱形的性质,矩形的性质,含30︒角的直角三角形的三边关系,等边三角形的判定与性质,解题关键是合理添加辅助线构造直角三角形,求线段长,添加辅助线构造平行四边形,使得求A D B D ''+最小值转化求B D B D '''+的最小值.模型三、修桥选址模型(将军遛马模型)【模型解读】已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA +PQ +QB 的值最小.(原理用平移知识解)(1)点A 、B 在直线m 两侧:(2)点A 、B 在直线m 同侧:如图1如图2(1)如图1,过A 点作AC ∥m ,且AC 长等于PQ 长,连接BC ,交直线m 于Q ,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点.(2)如图2,过A 点作AE ∥m ,且AE 长等于PQ 长,作B 关于m 的对称点B ’,连接B ’E ,交直线m 于Q ,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点.【最值原理】两点之间线段最短.例题:(23-24八年级下·北京·期中)如图,在矩形ABCD 中,6AB =,5AD =,点P 在AD 上,点Q 在BC 上,且AP BQ =,连接CP 、QA ,则PC QA +)A .10B .11C .12D .13【答案】D 【分析】本题考查的是最短路径问题,勾股定理,矩形的性质,平行四边形的判定与性质,中垂线的性质,熟知两点之间线段最短的知识是解答此题的关键.连接BP ,PQ ,在BA 的延长线上截取6AE AB ==,连接PE ,CE ,PC QD PC PB +=+,则PC QD +的最小值转化为PC PB +的最小值,则PC QD PC PB PC PE CE +=+=+≥,根据勾股定理可得结果.【详解】解:如图,连接BP ,PQ ,在矩形ABCD 中,AD BC ∥,∴AP BQ ∥,∵AP BQ =,∴四边形ABQP 是平行四边形,∴四边形ABQP 是矩形,则PC QA PC PB+=+,则PC 在BA的延长线上截取AE AB=∵PA BE⊥,【变式训练1】如图,AC是矩形ABCD的对角线,点M,N是AC上两点且14MN AC=,已知4=AD,30ACD∠=︒,则+DM BN的最小值为()A.6B.5C.D.4∥,DP MN=,DP MN∴四边形DPNM为平行四边形,∴=,PN DM∴+=+=,DM BN PN BN PB∴此时+DM BN的值最小,过P点作PH AB⊥于H点,PH交F是AD边上的动点,且EF=2,则四边形BEFC周长的最小值为.AD ∴BE+EF+FC+BC=B″F+EF+FC+BC=B″C+EF+BC BB'=2,∠ABC=60°,∴B'B″经过点A ∵BC=12,∴B'C=10,∴B″C=237,【变式训练3】(23-24九年级上·陕西榆林如图1,已知正方形ABCD 的边长为3,点E 是边AB 上的一点,把ADE V 沿直线DE 对折后,点A 落在点F 处.【问题探究】(1)如图2,当1AE =时,正方形的对角线AC 与DE 相交于点M ,与正方形另一条对角线BD 相交于点O ,连接OF 并延长,交线段AB 于点G .①求AM MC的值,并说明点M 是OA 的中点;②试探究OG 与DE 有怎样的位置关系,并说明理由.【拓展延伸】(2)如图3,点H 是线段DF 上的一点,且1DH =,连接BF 、CH .在点E 从点A 运动到点B 的过程中,求BF CH +的最小值.由折叠可知DE 垂直平分点M 是OA 的中点,MN ∴是AFO V 的中位线,MN OF ∴,即OG ∥(2)如图3,在DC DP DH FDP CDH DF DC =⎧⎪∠=∠⎨⎪=⎩,(SAS DPF DHC ∴≌PF CH ∴=,BF CH BF FP ∴+=+模型四、求多条线段和(周长)最小值【模型解读】在直线m 、n 上分别找两点P 、Q ,使PA +PQ +QB 最小.(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:(4)台球两次碰壁模型1)已知点A 、B 位于直线m ,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.2)已知点A 位于直线m ,n 的内侧,在直线m 、n 分别上求点P 、Q 点PA +PQ +QA 周长最短.【最值原理】两点之间线段最短.例题:如图,菱形ABCD 的BC 边在x 轴上,顶点C 坐标为()3,0-,顶点D 坐标为()0,4,点E 在y 轴上,线段EF x ∥轴,且点F 坐标为()8,6,若菱形ABCD 沿x 轴左右运动,连接AE 、DF ,则运动过程中,四边形ADFE 周长的最小值是.【答案】18【分析】在EF 上截取ET ,使得ET AD =,作点T 关于直线AD 的对称点T ',连接FT '交直线AD 于D ¢,即为CD ∵()0,4D ,()3,0C -∴3OC =,4OD =222234CD OC OD ∴=+=+∵四边形ABCD 是菱形∴5AD CD ==,AD BC∥线AC 和边CD 上的动点,且AE CF =,则BE BF +的最小值是.MG【点睛】本题考查矩形的性质,勾股定理,等边三角形的判定和性质,全等三角形的判定和性质,30︒角的直角三角形,三角形三边关系,两点之间线段最短等知识点,通过作辅助线构造全等三角形的是解题的关键.【变式训练2】(23-24八年级下·四川成都·期中)已知矩形ABCD 中,3AB =,4BC =,点E 为BC 延长线上一点,若1CE =,连接DE ,M 为DE 的中点,P 、Q 为AD 边上两个动点,且52PQ =,连接P 、B 、M 、Q ,则四边形PBMQ 周长的最小值为.过点Q 作QG BP 交BC 于G ,作点当点G ',Q ,M 在同一条线上时,QM ∴此时,四边形PBMQ 周长最小,QG PB ,PQ BG ,在Rt BCD 中,CD 5BD ∴=,∵1CE =5BE ∴=,5BE BD ∴==∵M 为DE 的中点,1,2BM DE HM ∴⊥=【点睛】此题是四边形综合题,主要考查了矩形的性质,勾股定理,等腰三角形的性质,对称性,确定出DA 上的点,依次连接它们得到四边形EFGH ,探究四边形EFGH 周长的最小值.探究:(1)如图1,H F ,分别是边AD 和BC 上点,在边CD 上作一点G ,使得GH GF +的值最小,并证明DGH CGF ∠=∠(用没有刻度的直尺和圆规作图,保留作图痕迹,不要求写作法).(2)如图2,求证;当四边形EFGH 的周长最小时,它是平行四边形.(3)如图2,若矩形ABCD 中,8AB =,6AD =,求四边形EFGH 周长的最小值.拓展:如图3,四边形ABCD 中,AB AD =,CB CD =,AB CB ⊥,AD CD ⊥,8AC =,6BD =,直接写出四边形ABCD 的内接四边形EFGH 周长的最小值.(2)过点H 作,AB CD 如图:则12311,,H E HE H G HG H G GF G F ====,记四边形∴311C HG GF FE EH H G G F FE =+++=++当点113,,,H F G H 共线时,周长最小且为H 由对称得12∠=∠,而13∠=∠,∴设123α∠=∠=∠=,∴1802HEF α∠=︒-,∵四边形ABCD 是矩形,∴90B Ð=°,∴3490∠+∠=°,由对称得:1223,,2AH AH DH DH H H DC ===∵四边形ABCD 是矩形,∴290BCD ADC DCM H DC ∠=∠=∠=∠=︒,∴四边形2DH MC 是矩形,∴12390H H H ∠=︒,∵8AB =,6AD =,由对称得1112,,EF EF FG FG FG GH ===∴四边形EFGH 的周长EF FG GH =++当点312,,,,G H E F G 共线时,四边形EFGH 图:同(1)得四边形EFGH 周长取得最小值,此时点E 由对称得:1EF EF =,32∠=∠,3DG DG =,BF ∴124∠=∠=∠,∴3=4∠∠,∴23FG G G ∥,∴3DFG DNG ∠=∠,∵3NDG FDG ∠=∠,3DG DG =,模型五、求两条线段差最大值【模型解读】在一条直线m 上,求一点P ,使PA 与PB 的差最大;(1)点A 、B 在直线m 同侧:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P’A -P’B <AB ,而PA -PB =AB 此时最大,因此点P 为所求的点.(2)点A 、B 在直线m 异侧:过B 作关于直线m 的对称点B’,连接AB’交点直线m 于P ,此时PB =PB’,PA -PB 最大值为AB’【最值原理】三角形两边之差小于第三边.例题:(2024·陕西西安·二模)如图,在菱形ABCD 中,8AB =,60B ∠=,AE BC ⊥于点E ,点M 在边AB 上,且2AM =,N 是CD 的中点,P 是AE 上的动点,连接PM PN 、.则PN PM -的最大值为.【答案】27【分析】先根据菱形性质得出8AB CB ==,结合直角三角形的性质,得出1903042BAE ABE BE AB ∠=︒-∠=︒==,,分析出当11N M P ,,三点共线,则PN PM -有最大值,且为1111N P MP N M -=,再运用勾股定理列式,计算出1HN ,最后把数值代入2211N M HN HM =+进行计算,即可作答.【详解】解:∵在菱形ABCD 中,8AB =,∴8AB CB ==,∵60B ∠=,AE BC ⊥于点E ,∴在Rt ABE △中,1903042BAE ABE BE AB ∠=︒-∠=︒==,,∴84CE BE =-=,则CE BE=作线段DC 关于AE 所在直线的对称线段1BD ,此时点N 的对应点为1N ,连接1N M ,并延长交AE 于一点,即为1P ,如图:当11N M P ,,三点共线,则PN PM -有最大值,且为1111N P MP N M-=∴111608D AB ABE AD AD D B ∠=∠=︒===,'-'的最大值是.点P为直线DE上一点,点P与点P'关于AC对称,F为BC中点,连接P F'、P A',则P F P AP 所在直线上一动点,已知8AB =,2DF =,且60ABC ∠=︒,则PF PE -的最大值为.【答案】23【分析】本题考查菱形的性质,轴对称中最值问题,勾股定理.取AD 的中点G ,连接PG ,易得PG PE =,故PF PE PF PG FG -=-≤,即当,,F G P 共线时,PF PE FG -=最大,作PH AD ⊥于H ,先后求出,,H D H F G H ,最后用勾股定理求FG 即可.【详解】解:如图,取AD 的中点G ,连接PG ,四边形ABCD 是菱形,A G A E G A P E A P∴=∠=∠在APG 和APE V 中AG AE GAP EAP AP AP =⎧⎪∠=∠⎨⎪=⎩(SA S)A PG A PE ∴≌PG PE∴=连接FG∴PF PE PF PG FG-=-≤当,,F G P 共线时,PF PE FG -=最大,图中P '处作PH AD ⊥于H60D B ∠=∠=︒30DFH ∴∠=︒112H D D F ∴==22213FH ∴=-=142G D A D ==413G H ∴=-=2223FG G H FH ∴=+=.即PF PE -的最大值为23.的中点,PQ 是对角线AC 上的一条动线段,若BP EQ -5PQ 的长为.【答案】1【分析】本题考查正方形的性质,线段最值问题等知识点,正确作辅助线是解题关键.过Q 点作BP 的平行线,过B 点作PQ 的平行线,两平行线交于点B ',取E 关于AC 的对称点E ',连接B E '',QE ',B Q ',根据三角形两边之查小于第三边即可得到5B E ''=,在Rt B BE ''中,利用勾股定理即可求得答案.【详解】解:如图,过Q 点作BP 的平行线,过B 点作PQ 的平行线,两平行线交于点B ',取E 关于AC 的对称点E ',连接B E '',QE ',B Q ',∵BB PQ '∥,QB PB '∥,∴四边形BB QP '是平行四边形,∴BP B Q '=,BB PQ '=,∵E 关于AC 的对称点是E ',E 是OD 的中点,∴E '是OB 的中点,即EQ E Q'=在B E Q ''中,B Q E Q B E ''''-<,∴BP E Q B E '''-<,当Q 点运动到与点B ',E '在一条直线上的时候BP E Q B E '''-=,即BP EQ -取到最大值5,即5B E ''=,∵BB AC '∥,AC BD ⊥,∴BB BD '⊥,∴在Rt B BE ''中,11142222BE OB OD '===⨯=,∴()2222521BB B E BE ''''=-=-=,∴1PQ BB '==.故答案为:1.连接BD ,交AC 于O 点,E 点在OD 上,且2DE OE =,F 是BC 的中点,P 是AC 上的一个动点,则PF PE -的最大值为.【答案】3【分析】由折叠可证四边形ABCD 为菱形,BO 是AC 边上的中线,如图,连接AE AF PM 、、,交BD 于M ,AF 是BC 边上的中线,BAC ∠的角平分线,则2BM OM =,2AM MF =,30CAF ∠=︒,由2DE OE =,可得OM OE =,则PE PM =,AE AM =,PF PE PF PM -=-,可知当点P 运动到点A 时,PF PE -最大,最大为FM ,勾股定理求2233AF AC CF =-=,则13FM AF =,计算求解即可.【详解】解:ABC 为等边三角形,6AB =,6AB AC BC ∴===,将ABC 沿AC 翻折,得到ADC △,6AD CD BC AB ∴====,∴四边形ABCD 为菱形,∴DO BO =,3AO CO ==,BD AC ⊥,∴BO 是AC 边上的中线,如图,连接AE AF PM 、、,交BD 于M ,∵F 是BC 的中点,∴AF 是BC 边上的中线,BAC ∠的角平分线,∴2BM OM =,2AM MF =,30CAF ∠=︒,∵2DE OE =,∴OM OE =,∵BD AC ⊥,∴PE PM =,AE AM =,∴PF PE PF PM -=-,∴当点P 运动到点A 时,PF PE -最大,最大为FM ,∵30CAF ∠=︒,∴3CF =,由勾股定理得,2233AF AC CF =-=,一、单选题1.(23-24八年级下·云南昭通·阶段练习)如图,正方形ABCD 的边长为4,点M 在DC 上,且1DM =,点N 是AC 上一动点,则DN MN +的最小值为()A .4B .5C .D .8∵CM CD DM =-=∴在Rt BCM △中,故DN MN +的最小值是2.(23-24八年级下·广东广州·期中)如图,在矩形ABCD 中,5AB =,3AD =,点P 满足13PAB ABCD SS =矩形,则点P 到A ,B 两点距离之和PA PB +的最小值为()A 29B 34C .52D 41【答案】D【分析】首先由13PAB ABCDS S =矩形,得出动点在与平行且与的距离是2的直线上,作点A 关于直线l 的对称点E ,连结AE ,BE ,则BE 的长就是所求的最短距离,然后勾股定理求得BE 的长,即得答案.【详解】设AB 边上的高是h ,13PAB ABCDS S =矩形,1123AB h AB AD ∴⋅=⋅,223h AD ∴==,∴动点P 在与AB 平行且与AB 的距离是2的直线l 上,如图,作点A 关于直线l 的对称点E ,连结AE ,BE ,则BE 的长就是所求的最短距离,在Rt ABE 中,5AB =,224AE =+=,22225441BE AB AE ∴=+=+=,即PA PB +的最小值为41.故选D .【点睛】本题考查了最短路线问题,轴对称的性质,矩形的性质,勾股定理,两点之间线段最短的性质,作点A 关于直线l 的对称点E ,并得到BE 的长就是所求的最短距离是解题的关键.ABCD ,AB DC ,,EF ED BF 若EF BC ∥,6,4AB AD ==,则四边形BFDE 的周长的最小值是()A .23B .16C .22D .15【分析】本题考查矩形的判定和性质,全等三角形的判定和性质,勾股定理,延长∴,,AD BC AB CD A ∠=∥∥∴四边形AEFD 和四边形EBCF ∴AE DF =,EAD FDM =∠∠AD DM =,()SAS ADE DMF ∴≌,4.(2024·安徽六安·一模)如图,AC 是菱形ABCD 的对角线,120ABC ∠=︒,点E ,F 是AC 上的动点,且14EF AC =,若4=AD ,则DE BF +的最小值为()AB C .4D【答案】D 【分析】本题考查了轴对称-最短路线问题,熟练运用轴对称的性质和平行四边形的性质以及勾股定理是解题的关键.连接BD 交AC 于O ,以EF ,BF 为邻边作平行四边形BFEG ,则EF BG =,BF GE =,所以DE BF DE EG DG +=+≥,即DE BF +的最小值.【详解】解:如图所示,∴120ABC ∠=︒,4=AD ,60DAB ∴∠=︒,2423,,,OD BD OA ∴===1143344EF AC ∴==⨯=二、填空题5.(23-24八年级下·湖北武汉·期中)如图,在矩形ABCD 中,6,10,AB AD E ==为CD 的中点,若P Q 、为BC 边上的两个动点,且2PQ =,则线段AP QE +的最小值为.∵E 为CD 边的中点,∴11322DE EC CD AB ====F 点与点G 关于BC 对称,BC ∴垂直平分FG ,162CH GF AB ∴===,∴10GH DF AD AF ==-=-三模)如图,正方形取BE 中点F ,连CF ,则DE CF +最小值为.∵正方形ABCD 边长为4BE CB ===∴AB ,∵F 是BE 中点,2BF BG ∴==,在BCF △和BEG 中,BC BE CBF EBG BF BG =⎧⎪∠=∠⎨⎪=⎩,(SAS)BCF BEG ∴≌,CF EG ∴=,DE CF DE EG ∴+=+4CD =,2CG =,222DG CD CG ∴=+=DE CF ∴+的最小值为2故答案为:25.7.(23-24八年级下·四川泸州别过点C ,D 作BD AC ,的平行线相交于点E ,点F 是CD 的中点,点G ,H 分别是四边形OCED 的边DE CE ,上的动点,则FG FH +的最小值是.∵在矩形ABCD 中,∴90ABC BCD BD OD OC ∠=∠=︒==,AC ,∵6AB =,12AC BD ==,∴30ACB ∠=︒,∴903060ACD ∠=︒-︒=︒,于点E,F是OA的中点,P是AB边上的一个动点,则PE﹣PF的最大值是.∵四边形ABCD是菱形,∴AD=AB=CD=BC=8∵∠ABC=60°,∴AC=AD=CD=8,OA三、解答题Y中,E、F分别为边AB、CD的中点,BD是对角线,过A 9.(22-23八年级下·四川广安·期中)如图,在ABCD∥交CB的延长线于点G.点作AG DB(1)求证:DE BF ∥;(2)若90G ∠=︒,求证四边形DEBF 是菱形;(3)请利用备用图分析,在(2)的条件下,若4BE =,120DEB ∠=︒,点M 为BF 的中点,当点P 在BD 边上运动时,求PF PM +的最小值,并求出此时线段BP 的长.【答案】(1)见解析(2)见解析(3)PF PM +的最小值为23,433BP =【分析】(1)根据平行四边形的性质得到DF BE =,ABCD ,根据平行四边形的判定定理证明四边形DEBF 是平行四边形,根据平行四边形的性质证明结论;(2)根据平行四边形的性质及矩形的判定定理得到四边形ADBG 是矩形,根据直角三角形斜边的中线等于斜边的一半得到DE BE =,即可得出四边形DEBF 是菱形;(3)连接EM 交BD 于P ,根据轴对称的性质证明此时PF PM +的值最小,根据等边三角形的性质计算即可得出最小值,最后根据三角形的重心即可得出BP 的值.【详解】(1)证明:∵四边形ABCD 是平行四边形,∴AB CD =,AB CD ,∵E 、F 分别为边AB 、CD 的中点,∴DF BE =,又AB CD ,∴四边形DEBF 是平行四边形,∴DE BF ∥;(2)四边形ABCD 是平行四边形,AD BC∴∥即AD BG∥AG DB∥∴四边形ADBG 是平行四边形,又90G ∠=︒∴四边形ADBG 是矩形,90ADB ∴∠=︒E 为边AB 的中点,DE BE ∴=∵四边形DEBF是菱形,∴点E和点F关于BD轴对称,此时∠∵四边形DEBF是菱形,DEB∴60∠=︒,EBF∴BEF△是等边三角形,∴∠=︒BEM30条件:如图1,A、B是直线l同旁的两个顶点.问题:在直线l上确定一点P,使PA PB+的值最小.+=的值最小(不必证明)方法:作点A关于直线l的对称点A',连接A B'交l于点P,则PA PB A B'模型应用:(1)如图2,已知平面直角坐标系中两定点()01A -,和()21B -,,P 为x 轴上一动点,则当PA PB +的值最小时,点P 的横坐标是___________,此时PA PB +=___________.(2)如图3,正方形ABCD 的边长为2,E 为AB 的中点,P 是AC 上一动点,连接BD ,由正方形对称性可知,B 与D 关于直线AC 对称,则PB PE +的最小值是___________.(3)如图4,正方形ABCD 的面积为12,ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一动点P ,则PD PE +的最小值为___________.(4)如图5,在菱形ABCD 中,8AB =,=60B ∠︒,点G 是边CD 边的中点,点E ,F 分别是AG ,AD 上的两个动点,则EF ED +的最小值是___________.【答案】(1)1;22(2)5(3)23(4)43【分析】(1)取点A 关于x 轴对称的点A ',连接A B ',交x 轴于点P ,作BH x ⊥轴于H ,则此时PA PB +的值最小,根据点的坐标,得出1OA OA '==,1BH =,2OH =,进而得出2AA OA OA ''=+=,1OA BH '==,再根据“角角边”,得出A OP BHP '≌,再根据全等三角形的性质,得出112OP HP OH ===,进而得出点P 的横坐标,再根据平行线间的距离相等,得出2AB OH ==,再根据勾股定理,计算即可得出答案;(2)根据对称性和线段最短,得出PB PE +的最小值是DE 的长,再根据中点的定义,得出1AE =,再根据勾股定理,计算出5DE =,进而即可得出PB PE +的最小值;(3)设BE 与AC 交于点P ',连接BD ,BP ,根据对称性,得出PD PB =,再根据线段最短,得出当点P 运动至点P '时,PD PE +的最小值,此时最小值为BE 的长,再根据正方形的面积,结合算术平方根的定义,得出23AB =,再根据等边三角形的性质,得出23BE AB ==,进而得出PD PE +的最小值;(4)作DH AC ⊥垂足为H 与AG 交于点E ,根据菱形的性质,得出8AB AD CD BC ====,60ADC B ∠=∠=︒,是等边三角形,再根据三线合一的性质,得出的最小,最小值为则此时PA PB +的值最小,∵()01A -,和()21B -,,∴1OA OA '==,1BH =,∴2AA OA OA ''=+=,OA ∵OPA HPB '∠=∠,A OP '∠∵点B 与D 关于直线AC ∴PD PB =,∴当点P 运动至点P '时,∵正方形ABCD 的面积为∴23AB =,又∵ABE 是等边三角形,∵四边形ABCD 是菱形,∴8AB AD CD BC ====,∵=60B ∠︒,∴60ADC B ∠=∠=︒,∴ADC △是等边三角形,【点睛】本题考查了坐标与图形、轴对称—最短路径问题、全等三角形的判定与性质、正方形的性质、菱形的性质、等边三角形的判定与性质、含30 角的直角三角形的性质,熟练掌握轴对称—最短路径的确定方法、并灵活运用勾股定理是解本题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
同步课程˙“将军饮马”系列最值问题将军饮马”系列最值问题1. 两点之间,线段最短.2. 点到直线的距离,垂线段最短.3. 三角形两边之和大于第三边,两边之差小鱼第三边.4. A 、B 分别为同一圆心 O 半径不等的两个圆上的一点,当且仅当 A 、B 、O 三点共线时能取等号古希腊亚里山大里亚城有一位久负盛名的学者,名叫海伦.有一天, 有位将军不远千里专程前来向海伦求教一个百思不得其解的问题: 如图,将军从 A 出发到河边 饮马,然后再到 B 地军营视察, 显然有许多走法. 问怎样走路线最短呢?精通数理的海伦稍加思索, 便 作了完善的回答.这个问题后来被人们称作“将军饮马”问题.下面我们来看看数学家是怎样解决的.海伦发现这是一个求折线和最短的数学问题. 根据公理:连接两点的所有线中,线段最短.若 A 、B 在河流的异侧,直接连接 AB , AB 与 l 的交点即为所求.知识回顾R r AB R若A 、B 在河流的同侧,根据两点间线段最短,那么显然要把折线变成直线再解.海伦解决本问题时,是利用作对称点把折线问题转化成直线现在人们把凡是用对称点来实现解题的思想方法叫对称原理,即轴对称思想 轴对称及其性质:把一个图形沿某一条直线折叠, 如果直线两旁的部分能够互相重合, 形.这条直线就是它的对称轴.这时我们就说这个图形关于这条直线 称图形.把一个图形沿着某一条直线折叠, 如果它能够与另一个图形重合, 直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点. 如下图, ABC 与 A' B' C '关于直线 l 对称, l 叫做对称轴. A 和A',B 和B',C 和C'是对称点.轴对称的两个图形有如下性质:① 关于某条直线对称的两个图形是全等形; ② 对称轴是任何一对对应点所连线的垂直平分线;③两个图形关于某条直线对称,如果他们的对应线段或延长线相交,那么交点在对称轴上.那么这个图形就叫做轴对称图 (或轴)对称.如等腰 ABC 是轴对那么就是说这两个图形关于这条同步课程˙“将军饮马”系列最值问题线段垂直平分线:垂直平分线上点到线段两个端点的距离相等;到线段两个端点距离相等的点在线段的垂直平分线上.当已知条件出现了等腰三角形、 角平分线、高,或者求几条折线段的最小值等情况, 对称变换,以“补齐”图形,集中条件。
所有的轴对称图形(角、线、等腰三角形、等边三角形、标轴),都可以考察“将军饮马”问题。
题考查。
PA PB ⋯BC常见模型:1) PA PB 最小通常考虑作轴 菱形、矩形、正方形、等腰梯形、圆、坐 考察知识点: 两点之间线段最短” ,“垂线段最短” ,“点关于线对称” ,“线段的平移” 。
解题总思路: 找点关于线的对称点实现“折”转“直” ,近两年出现“三折线”转“直”等变式问构建“对称模型” 实现转化PMBCMPACA BCA同步课程˙“将军饮马”系列最值问题同侧异侧2)① PA PB 最小同侧异侧② PA同侧lAPB 最大异侧A变形】异侧时,也可以问:在直线l 上是否存在一点P 使的直线l为APB 的角平分线3)周长最短类型一类型类型三BACA'4)“过河”最短距离类型一类型同步课程˙“将军饮马”系列最值问题BE APE= BPEB' B MNBAlNMMA' AB'EEl2l2AAFFBAA'A'AAEBBP A'A'5)线段和最小6)在直角坐标系里的运用B l1MNl1BFB'同步练习同步课程˙“将军饮马”系列最值问题【例1】尺规作图,作线段AB 的垂直平分线,作COD 的角平分线.解析】用尺规作图画角平分线和垂直平分线.变式练习】已知:如图,ABC及两点M 、N .求作:点P,使得PM PN,且P点到ABC两边所在的直线的距离相等.解析】用尺规作图画角平分线和垂直平分线.因为是两边所在的直线,所以有两个答案:ABC 内角平分线与线段MN 的垂直平分线的交点P1;ABC 外角平分线与线段MN 的垂直平分线的交点P2.例2】已知点A 在直线l 外,点P 为直线l 上的一个动点,探究是否存在一个定点B ,当点P 在直线l上运动时,点P与A、B 两点的距离总相等,如果存在,请作出定点B ;若不存在,请说明理由.同步课程˙“将军饮马”系列最值问题解析】作 A 点关于直线 l 的对称点,即为 B 点.例3】如图,在公路 a 的同旁有两个仓库 A 、 B ,现需要建一货物中转站,要求到 A 、 B 两仓库的距离和最短,这个中转站 M 应建在公路旁的哪个位置比较合理?长最短.解析】如图,作对称再连接. 这题实质还是 “将军饮马 之和最小.巩固】若此题改成,在 a 上找到 M 、 N 两点,且 MN最短.解析】作 A 点关于直线a 的对称点 A',在连接变式练习】如图,N 为 ABC 的边 AC 、BC 上的两个定点,在 AB 上求一点 P ,使 PMN 的周问题,在 AB 上找一点 P ,使得 PM PN10,M 在 N 的左边,使四边形 ABMN 的周长BA'B 于直线 a的交点即为 M 点. EA''【解析】作A点AA'∥a ,AA' MN 10,作A'点关于直线a的对称点A'',连接BA''与直线a的交点即为所求N 点,再向左平移10 个单位即为所求M 点.例4】(”五羊杯”邀请赛试题)如图,AOB 45 ,角内有点P ,在角的两边有两点Q、R(均不同于O 点),求作Q 、R ,使得PQR 的周长的最小.解析】如图,作对称再连接.例5】已知:如图,C、D分别是AOB内两点,OC OD,(1)分别在角两边各取两点E、F ,使得△CEF 周长l1 (2)分别在角两边各取两点M、N,使得△DMN周长l2最小(3)l1、l 2是否相等,若相等,请证明;若不相等,请说明原因.同步课程˙“将军饮马”系列最值问题解析】如图 ,分别做对称再连接.△CEF 周长l 1最小 PQ , △DMN 周长 l 2最小GHl 1 l 2, △GOH ≌△ POQ , PQ GH如图,在 POQ 内部有 M 点和 N 点,同时能使 MOP NOQ ,这时在直线 OP 上再取 A 点,例 6】 使从A 点到 M 点及 N 点的距离和为最小;在直线 OQ 上也取 B 点,使从 B 点到 M 点和 N 点 的距离和也最小.证明: AM AN BMBN .解析】如图, M 1点与 M 点关于射线 OP 成对称, 而 N 1点与 N 点关于射线 OQ 对称,这是 A 点和 B 点分别位于线段 NM 1 和线段 N 1M 上, OMOM 1, ON ON 1 , N 1OM 2 NOQNOM ,NOM 1 2 MOP NOM ,∵ MOPNOQ ,∴ N 1OMNOM 1 ,易证 △N 1OM ≌△NOM 1, ∴N 1M NM 1, ∴ N 1B BMNA AM 1,即 BN BM AN AM .例 7】 已知如图, 点 M 在锐角 A OB 的内部, 在OB 边上求作一点 P ,使点 P 到点 M 的距离与点 P 到OA 的边的距离和最小. 同步课程˙“将军饮马”系列最值问题HQ解析】如图,作 M 点关于 OB 的对称点 N ,再过 N 点作OA 的垂线 OA 于H .例8】(2000 年全国数学联赛 )如图,设正 ABC 的边长为 2,M 是 AB 边上的中点, P 是BC 边上的 任意一点, PA PM 的最大值和最小值分别记为 s 和t .求 s 2t 2的值.解析】作点 M 关于 BC 的对称点 M',连接 AM'、 PM '.由点M 、M'关于 BC 对称可知, PM PM'. 故 PA PM PA PM ' ≥ AM '当且仅当 A 、P 、 M '共线时,等号成立,故 t 2(AM')27 另外两个临界位置在点 B 和点 C 处.当点 P 位于点 C 处时, PA PM AC CM 2 3 ; 当点 P 位于点 B 处时, PA PM AB BM 3 . 故 s 2(2 3)27 4 3 , s 2t 24 3.在 l 上求作一点 M ,使得 | AM BM |最小值和最大值.例9】已知: A 、B 两点在直线 l 的同侧, ABM'AN 是 AC 上的一动点.求( 1) DN MN 的最小值与最大值.2) DN MN 的最小值与最大值.解析】(1)找点 D 关于 AC 的对称点,解析】作 AB 的垂直平分线于直线 l 的交点处可取得最小值,MA MB ,MA MB 0;连接 BA 并延长 BA 于直线 l 的交点处处可取得最大值,| AM BM |=AB 0剟|AM BM | AB变式练习】 (07 年三帆中学期中试题 ) 如图,正方形 ABCD 中,AB 8 ,M 是DC 上的一点,且 DM 2,lA MA D MC BD MCA由正方形的性质可知,B就是点D关于AC 的对称点,连接BN 、BM ,由DN MN BN MN BM 可知,当且仅当B 、N 、M 三点共线时,DN MN 的值最小,该最小值为62 82 10 .当点N在AC上移动时,有三个特殊的位置我们要考察:同步课程˙“将军饮马”系列最值问题BM 与 AC 的交点,即 DN MN 取最小值时;当点 N 位于点 A 时, DN MN AD AM 8 2 17 ;当且仅当 D 、M 、N 三点共线时,位于 C 点时, DN MN 可取的最大值为 DM 2 ;0剟 DN MN 2例10】如图1,已知等边 △ABC 的边长为 1, D 、E 、F 分别是 AB 、BC 、AC 边上的点(均不与点A 、B 、C 重合),记 △ DEF 的周长为 p.(1)若 D 、E 、F 分别是 AB 、BC 、AC 边上的中点,则 p = __ ;(2)若 D 、E 、F 分别是 AB 、BC 、AC 边上任意点,则 p的取值范围是 ___ .小亮和小明对第( 2)问中的最小值进行了讨论,小亮先提出了自己的想法:将 △ABC 以 AC 边为轴翻折一次得 △AB 1C ,再将△ AB 1C 以B 1C 为轴翻折一次得 △ A 1B 1C ,如图 2所示. 则由轴对 称的性质可知, DF FE 1 E 1D 2 p ,根据两点之间线段最短, 可得 p DD 2. 老师听了后说: “你 的想法很好,但 DD2的长度会因点 D 的位置变化而变化,所以还得不出我们想要的结果 . ”小明接过老师的话说:“那我们继续再翻折 3次就可以了” . 请参考他们的想法,写出你的答案.3解析】(1) p= 3232 ) 3剟p 32当点 N 位于点 C 时,DN MN CD CM10 剟DN MN 8 2 172) N 位于 DM 的垂直平分线于 AC 的交点处,8 6 14 .故 DN MN 的最大值为 8 2 17 .DN MN可取的最小值为 0 ;图1图2A例11】如图△ABC ,D 、E 、F 分别是AB 、BC 、AC边上的点(均不与点A、B 、C重合),记△DEF 的周长为p ,请作出周长最小的△DEF .A【解析】如图,过 A 作AE BC 于E ,在分别作 E 点关于 AB 、AC 的对称点 M 、N ,连接 MN 分别交AB 、AC 于D 、F ,连接 DE 、EF ,所得△DEF 即为周长最小.例 12】如图,当点 A 与l 1 、l 2 、l 3 连续相撞时,假设入射角等于反射角,求作出点最短路程.解析】四个对称轴,作出对称点,连线A 向点B 运动时的解析】利用三条对称轴作出对称点,然后根据两点之间线段最短例13】如图,矩形台球桌 ABCD 上有两个球 P 、Q ,求作一击球路线, 使 P 球顺次撞击球桌四边后再撞击 Q 球(球撞击桌边的入射角等于反射角)PQ例14】点M 是四边形 ABCD 的边 BC 的中点,AMD 120 ,证明: AB 1BC CD AD .2ADQ'1AB BC CD AD ”非常有特点,即为21什么会出现 1BC ,同时还是证明不等关系,只有我们在接触最短路程,已经三角形三边关系2的时候做过类似的问题.答案】作点 B 关于 AM 的对称点 E ,连接 AE 、 EM ,作点C 关于 MD 的对称点 F ,连接 DF 、 MF 、 EF当 AMD 150 时,他们又有什么关系呢?解析】( 1)当 AMD 135 时连接 DF 、 MF 、 EF∴AB AE , BM ME , CD DF , MC MF 易证 ABM ≌ AEM , MCD≌ MFDBMAEMA , CMD FMDEMF AMD AMB DMC 90∴ EMF 是等腰直角三角形.解析】本题是典型轴对称变换,条件非常少,不过结论“∴AB AE , BM ME ,CD DF ,MC MF 易证 ABM ≌ AEM , MCD≌ MFDBMAEMA , CMD FMD∴ EMF AMD AMB DMC 60 ∴ EMF 是等边三角形 ∴EF EM 1BC ,∵ AE EF FD AD2∴AB 1BC CD AD2变式练习】 点M 是四边形 ABCD 的边 BC 的中点,AMD 135 ,证明: AB2BC CD AD .2作点 B 关于 AM 的对称点 E ,连接 AE 、 EM, 作点 C 关于 MD 的对称点 F ,∴EF= 2 BC2,∵AE EF FD AD ∴AB 22BC CD AD2 )当AMD 150 时,同理可推出EMF 是一个顶角为120 等腰三角形.∴EF= 3EM3 BC ,∵ AE EF FD AD2∴AB3 BC CD AD2例15】已知:如图,在直角坐标系中,点A 在x 轴上,点D 在y轴上,等腰△ABD ,BA BD .1)作出△ABD关于y轴的对称图形△CMD .2)若BAC 2 ACB ,求证ABC 3 CBD解析】(1)根据轴对称的性质,作出对称图形△CMD. 2 )依题可知,BA BD MD MD,MB∥AC ,BAC MCA 2 ACBMCB ACB= MBC ,MC MB MD BD△MBD 为等边三角形BAC 2 ACB设CBD x°,则MBD BCA (60 x)BAC 120 2x ,ABC 3xABC 3 CBD课后练习习题1】如图,在等腰Rt ABC中,CA CB 3,E的BC上一点,满足BE 2,在斜边AB上求作一点P使得PC PE 长度之和最小.习题2】如图,菱形ABCD的两条对角线分别长6和8,点M N 分别是变AB 、BC 的中点,在对角线AC 求作一点P使得PM PN的值最小.习题3】如图,在锐角△ABC中,AB 4 2 ,BAC 45?°,BAC 的平分线交BC于点D ,M、N 分别是AD 和AB 上的动点,则BM MN 的最小值是B B答案】 A习题 7】如图,在平面直角坐标系中,直线 l 是第一、三象限的角平分线.【答案】 4习题 4】已知⊙ O 的直径 CD 为 4, AOD 的度数为 60 °,点 B 是的中点,在直径 CD 上找一点 P ,使BP AP 的值最小,并求 BP AP 的最小值.答案】 4 2习题 5】如图,点 P 关于 OA 、 OB 的对称点分别为 C 、 D ,连接 CD ,交 OA 于M ,交OB 于 N ,若CD 18cm ,则△PMN 的周长为答案】 18习题 6】如图所示,正方形 ABCD 的面积为 12, △ABE 是等边三角形,点 E 在正方形 ABCD 内,在对角线 AC 上有一点 P ,使 PD PE 的和最小,则这个最小值为(A . 2 3 C . 3 DB .2 6CD . 6C21 / 19实验与探究:1)由图观察易知 A2,0 关于直线l 的对称点 A'的坐标为 2,0 ,请在图中分别标B 5 ,3 、C 2 ,5 关于直线 l 的对称点 B' 、C '的位置,并写出它们的坐标: B' C'归纳与发现:( 2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点 P a ,b 关于第一、三象限的角平分线 l 的对称点 P'的坐标为 __ (不必证明) ;运用与拓广:(3)已知两点 D1,3 、E 1,4 ,试在直线 l 上找一点 Q ,使点Q 到D 、E 两点的距离之和最 小. 答案】( 1) B' 3 ,5 C' 5 , 2( 2) P' b ,a(3)作对称在连接习题 8】在平面直角坐标系中,点 P 2 ,3 、Q 3 ,2 ,请在 x 轴和 y轴上分别找到 M 点和 N 点,(1)请在 x 轴和 y 轴上分别找到 M 点和 N 点使四边形 PQMN 周长最小,作出 M 点和N 点. (2)请在 x 轴上找到一点 E ,使得 PE PQ 最大,作出 E点.22 / 19答案】(1)作对称再连接.(2)连接 PQ 与 x的交点即为 E . 习题 9】已知:如图,四边形 ABCD 中, A B 90°,∠ C =60°, CD 2AD , AB 4.(1)在 AB 边上求作点 P ,使 PC PD 最小;(2)求出( 1)中 PC PD 的最小值答案】(1)作对称再连接,如图所示.2) PC PD 的最小值为 DE ,在 Rt△DEH 中, DH 4, EH 4 3 , DE 8 .依题可知 △BCD 为等边三角形, BE BCBD CD 4 3,。
