第六章 整数规划
合集下载
运筹学课件 第六章-整数规划3
物品 1 2 3 4 5 6 7 8 9 10
体积 200 350 500 430 320 120 700 420 250 100
价格 15 45 100 70 50 75 200 90 20 30
设变量xij为第i个物品是否放在第j个包裹中
xij 1,0; i 1,2...,17, j 1,2,3
• 保证需求约束
x11 + x21 + x31 = 450 x12 + x22 + x32 = 275 x13 + x23 + x33 = 300 x14 + x24 + x34 = 350
} 项目1 } 项目2 } 项目3 } 项目4
最大供应量 525 450 550
约束条件：
厂家1一旦向某项目供应水泥，其至少供应量为150。 厂家2对单个项目供应量超过200吨的项目数不大于1。总产量=450 厂家3仅接受 200, 400, 和 550 吨这三个规格的货单。
1 中锋 1.93 2 中锋 1.91 3 前锋 1.87 4 前锋 1.86 5 后卫 1.80 6 后卫 1.85
配送计划模型
• 某建筑公司为完成4个工程项目，需要从3个厂家购买水泥，有关成
本如下
厂家1 厂家2 厂家3 需求量(吨)
项目1 $120 $100 $140 450
水泥的吨运费
项目2 $115 $150 $95 275
xi
0, 不携带第i件物品 1, 携带第i件物品 (i
1,2,, m)
m
max z ci xi i 1
m
ai xi
a
st.
i 1 m
bi
《运筹学》第6章 整数规划
整数规划（Integer Programming，简称IP），是 要求全部或部分决策变量为整数的规划。整数规 划分为线性整数规划和非线性整数规划。本章只 介绍线性整数规划，简称为整数规划。
整数规划分为两大类：一般整数规划与0-1整数规 划（Binary Integer Programming，简称BIP）。
6.3 0-1整数规划
例6.2 分公司选址问题。某销售公司打算通过在武汉 或长春设立分公司（也可以在两个城市都设分公司） 以增加市场份额，管理层同时也在考虑建立一个配送 中心（也可以不建配送中心），但配送中心地点限制 在新设分公司的城市。
经过计算，每种选择使公司收益的净现值和所需费 用如表6-2所示。总的预算费用不得超过1000万元。目 标是在满足以上约束的条件下使总的净现值最大。
100万元 500万元
2
大型飞机
500万元 5000万元 没有限制
可获得的总资金 1亿元
6.1 整数规划基本概念、分类与解的特点
解：
(1)决策变量
设小型飞机与大型飞机的购买 数量分别为x1、x2(架)。 (2)目标函数
目标是年总净利润最大。
M ax z x1 5 x2
(3) 约束条件 ① 资金限制 ② 小型飞机数量限制（最多
在长春设立分公司 在武汉设立分公司 在长春建配送中心 在武汉建配送中心
净现值（万元） 800 500 600 400
所需资金（万元） 600 300 500 200
6.3 0-1整数规划
解：
（1）决策变量
本题的决策变量是是非决策的0-1决策变量，每一个决策只有 两种选择，是或者否，1表示对于这个决策选择“是”，0表 示对于这个决策选择“否” 。
是非决策问题
整数规划分为两大类：一般整数规划与0-1整数规 划（Binary Integer Programming，简称BIP）。
6.3 0-1整数规划
例6.2 分公司选址问题。某销售公司打算通过在武汉 或长春设立分公司（也可以在两个城市都设分公司） 以增加市场份额，管理层同时也在考虑建立一个配送 中心（也可以不建配送中心），但配送中心地点限制 在新设分公司的城市。
经过计算，每种选择使公司收益的净现值和所需费 用如表6-2所示。总的预算费用不得超过1000万元。目 标是在满足以上约束的条件下使总的净现值最大。
100万元 500万元
2
大型飞机
500万元 5000万元 没有限制
可获得的总资金 1亿元
6.1 整数规划基本概念、分类与解的特点
解：
(1)决策变量
设小型飞机与大型飞机的购买 数量分别为x1、x2(架)。 (2)目标函数
目标是年总净利润最大。
M ax z x1 5 x2
(3) 约束条件 ① 资金限制 ② 小型飞机数量限制（最多
在长春设立分公司 在武汉设立分公司 在长春建配送中心 在武汉建配送中心
净现值（万元） 800 500 600 400
所需资金（万元） 600 300 500 200
6.3 0-1整数规划
解：
（1）决策变量
本题的决策变量是是非决策的0-1决策变量，每一个决策只有 两种选择，是或者否，1表示对于这个决策选择“是”，0表 示对于这个决策选择“否” 。
是非决策问题
第六章 整数规划(应用运筹学)
x2≥3
线性规划B6 Z5=6 x1=0 , x2=3
z6
z 6
§3 0—1规划Binary integer programming
当我面临是与非两种选择时，我们可以用决策变量取0或1值来表示 这样的决策，这样，地j个是非决策问题可以表示成
if decision j is yes, 1 如果决策是 xj if decision j is no 0 如果决策是非
x2 3 2 1 2x1+3x2 =6 o 1 2 3 4 x1 2x1+3x2 =14 2x1+3x2 =14.66
得到线性规划的最优解为x1=2.44, x2=3.26,目标函数值为14.66。 由图表可看出，整数规划的最优解为x1=4, x2=2,目标函数值为14。
性质1：任何求最大目标函数值的纯整数规划或混合整数规划的最大目
B0
max z =x1+2x2 s.t. 2x1+5x2 ≤ 15 2x1－2x2 ≤5 x1 , x2≥0
x2为整数的限制条件，得规 划B0对应的最优解与最优 值如下，而 X=(0，0)为A0 3 的可行解 B0 13 3 T 11 X (3 ,1 ) , z 6 14 7 14
2x1＋5x2=15
(1)每求出一次符合整数的解，都要考虑修改下界
函数值最大者为新的下界 (2)修改
z
，选整数解的目标
z
0
z ，找出所有未 分枝问题目标函数值最大者，为新的上界 z 当改变完上、下界 z ，z 后，若 z ＝ z，则所有分枝均已查明，得到 A
的最优解， 若
z＞ z
，则说明仍有分枝未查明，返回到第四步
分枝定界法
分枝定界法步骤
6第六章 整数规划(3-4节)
max z 7 x1 9 x 2 6 x1 3 x 2 x 3 x 4 35 7 x1 x 2 x 、x 0， 整 数 1 2
x 3 6 x1 3 x 2 x 4 35 7 x1 x 2
第36页
将上式代入割平面约束：
优解为止。
第2页
一、割平面的概念
通过举例来阐述割平面的概念 。
例：
maxz 7 x1 9 x 2 x1 3 x 2 6 7 x1 x 2 35 x 、x 0， 整 数 1 2
第3页
x1
C 3
2 D
B A 4
5
7
x2
可行域：ABCD
1 1 最优解：C点，其坐标为 ( x1 , x2 ) (4 ,3 ) 2 2
第27页
解：（1）利用单纯型法求解原问题的松弛问题 B ：
cj
CB XB b
7
x1
9
x2
0
x3
0
x4
θi
9
7
x2
x1
7/2
9/2
0
1
1
0
7/22
-1/22
1/22
3/22
c j– z j
0
0
-28/11 -15/11
第28页
（2）构造割平面约束 x1 = 9/2 = 4 + 1/2 x2 = 7/2 = 3 + 1/2
N
4
5
7
x2 Q
割去的部分 EFGCE 中不包含任何整数解。
第6页
新增加的线性约束条件切割掉了原问题可行域的一
部分，但该可行域内不包含任何整数可行解，所有
运筹学 第六章 整数规划 第一讲 整数规划数学模型与纯整数规划的求解
项目 所需资金（万元） 收益期望值（万元）
A B C D E
6 4 2 4 5
10 8 7 6 9
A，B，C，D，E 之间的关系是： ① A、C、E 三项中需且只能选一项； ② B、D 两项中需且只能选一项； ③ 选 C 必须先选 D 。 问题：如何选择投资决策，使总投资期望值最大？
6.1 整数规划的数学模型 Mathematical Model of IP
① 求解LP : 如果LP无最优解, 则IP无最优解;
设LP的最优解为x , 最优值为z , 则IP的最优值z * 满足 :
z z* z
其中 z 为IP在任何一个可行解处的目标值.
② 检验与分支：
如果x 满足IP的整数要求, 则x为IP的最优解：z* z . 否则 考虑一个不满足整数要求的xr , 将约束
示不安排第i人去做 j工 作。逻辑变量也是只允许取整数值的一类变量。
整数线性规划数学模型的一般形式：
max Z (或 min Z ) c j x j
j 1 n
要求一部分或全部决策变量取整数值
n a ij x j bi ( i 1.2 m ) j 1 x j 0 (j 1.2n) 且 部 分 或 全 部 为 整 数
xr xr 和
xr xr 1
分别加入LP形成两个子问题 a] ([
不超过a的最大整数)
6.2 纯整数规划的求解 Solving Pure Integer Programming
Ch6 整数规划 Integer Programming
n
max
z cj xj
j 1
ij j
不考虑整数条件，由余下的目标函数和 约束条件构成的规划问题称为该整数规 划问题的松弛问题。
A B C D E
6 4 2 4 5
10 8 7 6 9
A，B，C，D，E 之间的关系是： ① A、C、E 三项中需且只能选一项； ② B、D 两项中需且只能选一项； ③ 选 C 必须先选 D 。 问题：如何选择投资决策，使总投资期望值最大？
6.1 整数规划的数学模型 Mathematical Model of IP
① 求解LP : 如果LP无最优解, 则IP无最优解;
设LP的最优解为x , 最优值为z , 则IP的最优值z * 满足 :
z z* z
其中 z 为IP在任何一个可行解处的目标值.
② 检验与分支：
如果x 满足IP的整数要求, 则x为IP的最优解：z* z . 否则 考虑一个不满足整数要求的xr , 将约束
示不安排第i人去做 j工 作。逻辑变量也是只允许取整数值的一类变量。
整数线性规划数学模型的一般形式：
max Z (或 min Z ) c j x j
j 1 n
要求一部分或全部决策变量取整数值
n a ij x j bi ( i 1.2 m ) j 1 x j 0 (j 1.2n) 且 部 分 或 全 部 为 整 数
xr xr 和
xr xr 1
分别加入LP形成两个子问题 a] ([
不超过a的最大整数)
6.2 纯整数规划的求解 Solving Pure Integer Programming
Ch6 整数规划 Integer Programming
n
max
z cj xj
j 1
ij j
不考虑整数条件，由余下的目标函数和 约束条件构成的规划问题称为该整数规 划问题的松弛问题。
第六章 整数规划(2012)
割平面法cutting plane approach 构造切割方程的步骤： 2、将（2 式）代入（1 式）得： xi + ∑ Nik xk - Ni = fi - ∑ fik xk ……………………（3 式） 3、提出变量为整（当然含非负）的条件： 由于（3 式）中等式左边需整，而 0 ＜ fi ＜ 1 ，故有 fi - ∑ fik xk ≤ 0 ……………………（4 式） 此即为所需切割方程。
16
第三节 割平面法
割平面法cutting plane approach 构造切割方程的步骤： （1）切割方程 fi - ∑ fik xk ≤ 0 真正进行了切割，至少把非整数最优 解这一点切割掉了。 证明：（反证法）假设松驰问题的最优解 X* 未被切割掉，则由 fi - ∑ fik x*k ≤ 0， 又因为 x*k = 0，（因 x*k 为非基变量） 有 fi ≤ 0 ，这与 fi ＞ 0 矛盾。 （2）不会切割掉任何整数解，因为切割方程是由变量为整的条件 提出的。
该整数规划松弛问题的解为： （X1 ，X2 ）= （3/2 ，10/3） Z1 = 29/6
7
第二节 分支定界法
分支定界法图解整数规划
（3/2 ，10/3） Z1 = 29/6 B1：解 （2，23/9 ） Z11 = 41/9 B2 Max 松弛问题 Max Z = X1 + X2 14X1 + 9X2 ≤ 51 - 6X1 + 3X2 ≤ 1 X1 ， X2 ≥ 0 B1 Max Z = X 1 + X2 14X1 + 9X2 ≤ 51 - 6X1 + 3X2 ≤ 1 X1 ≥2 X1 ， X2 ≥ 0 Z = X 1 + X2 14X1 + 9X2 ≤ 51 - 6X1 + 3X2 ≤ 1 X1 ≤1 X1 ， X2 ≥ 0
16
第三节 割平面法
割平面法cutting plane approach 构造切割方程的步骤： （1）切割方程 fi - ∑ fik xk ≤ 0 真正进行了切割，至少把非整数最优 解这一点切割掉了。 证明：（反证法）假设松驰问题的最优解 X* 未被切割掉，则由 fi - ∑ fik x*k ≤ 0， 又因为 x*k = 0，（因 x*k 为非基变量） 有 fi ≤ 0 ，这与 fi ＞ 0 矛盾。 （2）不会切割掉任何整数解，因为切割方程是由变量为整的条件 提出的。
该整数规划松弛问题的解为： （X1 ，X2 ）= （3/2 ，10/3） Z1 = 29/6
7
第二节 分支定界法
分支定界法图解整数规划
（3/2 ，10/3） Z1 = 29/6 B1：解 （2，23/9 ） Z11 = 41/9 B2 Max 松弛问题 Max Z = X1 + X2 14X1 + 9X2 ≤ 51 - 6X1 + 3X2 ≤ 1 X1 ， X2 ≥ 0 B1 Max Z = X 1 + X2 14X1 + 9X2 ≤ 51 - 6X1 + 3X2 ≤ 1 X1 ≥2 X1 ， X2 ≥ 0 Z = X 1 + X2 14X1 + 9X2 ≤ 51 - 6X1 + 3X2 ≤ 1 X1 ≤1 X1 ， X2 ≥ 0
整数规划(数据模型与决策)
0-1型整数线性规划：决策变量只能取值0或1的整数线性 规划。
整数规划的特点及应用
Page 4
例:指派问题或分配问题。人事部门欲安排四人到四个不同岗 位工作，每个岗位一个人。经考核四人在不同岗位的成绩 （百分制）如表所示，如何安排他们的工作使总成绩最好。
工作
人员 甲 乙 丙 丁
A 85 95 82 86
1 x ij 0
指派第 i个 人 做 第 j件 事 ( i , j 1,2,..., n) 不指派第 i个 人 做 第 j件 事
分配问题与匈牙利法
指派问题的数学模型为：
Page 8
min Z
c
i 1 j 1
n
n
ij
x ij
n x ij 1 ( i 1.2. .n) j 1 n x ij 1 ( j 1.2. .n) i 1 x ij 取0或1(i , j 1.2. .n)
Page 19
0 13 7 0 6 0 6 9 0 5 3 2 0 1 0 0
0 Ø 6 0 ◎ Ø 0
13 7 ◎ 0 ◎ 0 6 9 5 3 2 1 ◎ 0 Ø 0
独立0元素的个数为4 , 指派问题的最优指 派方案即为甲负责D工作，乙负责B工作， 丙负责A工作，丁负责C工作。这样安排 能使总的工作时间最少，为4＋4＋9＋11 ＝28。
2）试指派（找独立0元素）
Page 22
2 2 4 4 0
0 4 2 4 5 0 3 0 1 0 1 3 0 3 5 1 2 3 0 5
2 2 4 4 ◎ 0
◎ 0
5 1 0 Ø 2
4 2 4 0 3 ◎ 0 Ø ◎ 0 1 3 3 5 1 3 Ø 0 5
整数规划_精品文档
整数规划引言：整数规划是一类特殊的数学优化问题，其中一部份或者全部变量被限制为整数。
整数规划问题在许多领域都有广泛的应用，如物流、生产计划、金融投资等。
随着科技的不断发展，整数规划的应用场景和求解方法也在不断扩展和深化。
一、整数规划的定义与分类定义：整数规划是一种特殊的数学优化问题，其目标是最小化或者最大化一个数学表达式（目标函数），同时满足一系列约束条件，且一部份或者全部决策变量被限制为整数。
分类：根据问题的特性，整数规划可以分为以下几种类型：0-1背包问题：决策变量只能取0或者1。
彻底背包问题：决策变量可以取任意非负整数。
整数线性规划：线性规划的变种，要求部份或者全部决策变量为整数。
二次整数规划：目标函数或者约束条件包含二次项。
二、整数规划的应用场景生产计划：在创造业中，整数规划可以用于优化生产流程、物料需求计划等。
物流优化：通过整数规划可以解决货物配送路线、车辆调度等问题。
金融投资：整数规划在投资组合优化、风险管理等领域有广泛应用。
资源分配：整数规划可用于解决资源分配问题，如人员调度、设备配置等。
组合优化：如旅行商问题（TSP）、装箱问题等，都是整数规划的典型应用场景。
三、整数规划的求解算法穷举法：通过逐个测试所有可能的解来找到最优解，但只适合于小规模问题。
分支定界法：一种基于树结构的搜索算法，能够处理较大规模的问题。
遗传算法：摹拟生物进化过程的优化算法，适合处理大规模问题。
摹拟退火算法：借鉴物理中退火过程的优化算法，具有避免陷入局部最优解的能力。
蚁群算法：摹拟蚂蚁觅食行为的优化算法，适合于求解具有离散变量的优化问题。
元胞遗传算法：将遗传算法和元胞自动机结合，能够处理更复杂的问题。
粒子群算法：摹拟鸟群觅食行为的优化算法，具有简单易实现的特点。
深度学习算法：利用神经网络进行求解，特别在处理大规模、高维度的问题时表现出色。
四、整数规划软件介绍CPLEX：由IBM开辟的商业优化软件，支持整数规划、线性规划、混合整数规划等多种优化问题。
第六章 运筹学 整数规划案例
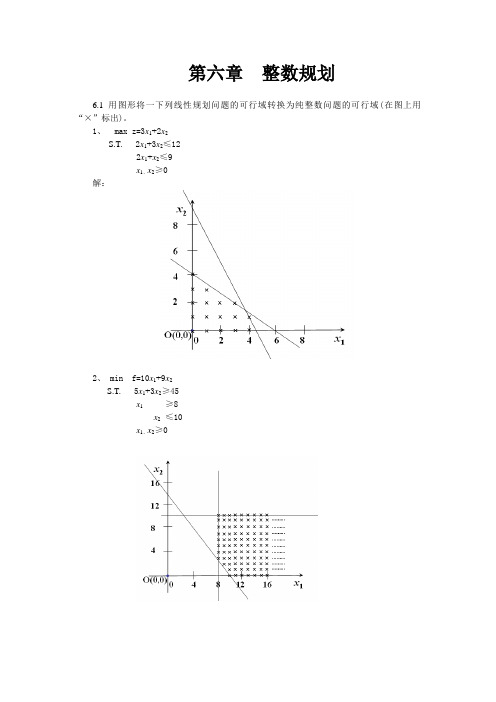
第六章整数规划6.1 用图形将一下列线性规划问题的可行域转换为纯整数问题的可行域(在图上用“×”标出)。
1、 max z=3x1+2x2S.T. 2x1+3x2≤122x1+x2≤9x1、x2≥0解：2、 min f=10x1+9x2S.T. 5x1+3x2≥45x1≥8x2≤10x1、x2≥06.2 求解下列整数规划问题1、 min f=4x1+3x2+2x3S.T. 2x1-5x2+3x3≤44x1+x2+3x3≥3x2+x3≥1x1、x2、x3=0或1解：最优解（0，0，1），最优值：22、 min f=2x1+5x2+3x3+4x3S.T. -4x1+x2+x3+x4≥2-2x1+4x2+2x2+4x2≥4x1+x2-x2+x2≥3x1、x2、x3、x3=0或1解：此模型没有可行解。
3、max Z=2x1+3x2+5x3+6x4S.T. 5x1+3x2+3x3+x4≤302x1+5x2-x2+3x2≤20-x1+3x2+5x2+3x2≤403x1-x2+3x2+5x2≤25x1、x2、x3、x3=正整数解：最优解（0，3，4，3），最优值：474、min z =8x1 +4 x2+3 x3+5 x4+2 x5＋3 x6＋4 x7＋3 x8+4 x9+9 x10+7 x11+5 x12 +10 x13+4 x14+2 x15+175 x16+300 x17+375 x18 +500 x19约束条件x1 + x2+x3≤30x4+ x5＋x6-10 x16≤0x7+ x8＋x9-20 x17≤0x10+ x11＋x12-30 x18≤0x13+ x14＋x15-40 x19≤0x1 + x4+ x7+x10+ x13＝30x2 + x5+ x8+x11+ x14＝20x3 + x6+ x9+x12+ x15＝20x i为非负数（i=1,2…..8）x i为非负整数（i=9,10…..15）x i为为0－1变量（i=16,17…..19）解：最优解（30，0，0，0，0，0，0，0，0，0，0，0，0，20，20，0，0，0，1），最优值：8606.3 一餐饮企业准备在全市范围内扩展业务，将从已拟定的14个点中确定8个点建立分店，由于地理位置、环境条件不同，建每个分店所用的费用将有所不同，现拟定的14个店的费用情况如下表：公司办公会决定选择原则如下：（1）B5、B3和B7只能选择一个。
第六章 整数规划
原来的上界 .
在分枝定界法的整个求解过程中,上界的值在不断减小.
问题 B5
max f 20 x1 10 x2
问题 B6
max f 20 x1 10 x2
5 x1 8 x2 60 x1 8 x2 4 s.t x1 6 x2 3 x ,x 0 1 2
第六章 整数规划
整数规划模型
分支定界法
割平面法 0-1整数规划问题
指派问题
整数规划模型
在许多线性规划问题中,要求最优解必须取整数.例如 所求的解是机器的台数、人数、车辆船只数等.如果所得的 解中决策变量为分数或小数则不符合实际问题的要求. 对于一个规划问题,如果要求全部决策变量都取整数, 称为纯(或全)整数规划;如果仅要求部分决策变量取整数, 称为混合整数规划问题.有的问题要求决策变量仅取0或l两
解 设计划甲种宿舍建 x1 幢,乙种宿舍建 x2 幢,则本题数学 模型为 :
max Z 20 x1 10 x2
0.25 x1 0.4 x2 3 x1 8 s.t x2 4 x1 , x2 0, 取整数
这是一个纯整数规划问题,称为问题 A0 。
（1）
作出问题 A1 , A2 的伴随规划 B1 , B2 , 则问题 B1 , B2 , 的可行 域为 K1 , K 2 , 见图2(b). 以下我们将由同一问题分解出的两 个分枝问题称为"一对分枝".
x2
4
3
x2
2 1
O
2
4
6
8
x1
O
1
2
4
6
8
x1
(a)
(b)
(第五、六章 目标规划和整数规划
1
x 1、 x2 、 x3分别为采用3条生产线时的产量
50x3 +1000，若x 3 ＞0 C 3(x 3 )＝ 0，若x 3 ＝0
目标函数：min z=C 1(x 1)+C 2(x 2)+C3(x 3)
可变成本（吨/元） 固定成本（元）
1,当采用第j条生产线时，即当xj＞0 令y j = 0,当不采用第j条生产线时，即当xj＝0
建立0－1整数规划模型
引入0-1变量,令
Xi= 1,当Ai点被选用 0,当Ai点没被选用
7
于是: max z= ∑ ci xi i =1 7 s.t. ∑ bi xi ≤ Β,
x1 + x 2 + x3 ≤ 2, ( xi = 0 / 1 x 4 + x5 ≥ 1, x6 + x7 ≥ 1,
i =1
则：C 1(x 1)＝ 20x 1 +1500 y1 C 2(x 2)＝ 30x 2 +1200 y2 C 3 (x 3 ) ＝ 50x 2 +1000 y3 0≤x 1≤5000y 1 0≤x2 ≤5000y 2 0≤x 3 ≤5000y 3
场所选择
某公司拟在市东、西、南三区建立门市部, 拟议中有7个位置Ai（i=1,2, …7）可供选择, 规定:在东区,由A1,A2,A3三个点中至多选两个; 在西区,由A4,A5两个点中至少选一个;在南区, 由A6,A7两个点中至少选一个.如选用Ai点设备 投资估计为bi元,每年可获利润估计为ci元,公 司投资总额不能超过B元。如何选择使年利润 最大?
单纯形法
由于目标规划的目标函数中含有优先因 子，所以在单纯形表中，将检验数行按 优先因子的个数分成k行 用单纯形法求解(同前) 例如：前面第一个目标规划模型
x 1、 x2 、 x3分别为采用3条生产线时的产量
50x3 +1000，若x 3 ＞0 C 3(x 3 )＝ 0，若x 3 ＝0
目标函数：min z=C 1(x 1)+C 2(x 2)+C3(x 3)
可变成本（吨/元） 固定成本（元）
1,当采用第j条生产线时，即当xj＞0 令y j = 0,当不采用第j条生产线时，即当xj＝0
建立0－1整数规划模型
引入0-1变量,令
Xi= 1,当Ai点被选用 0,当Ai点没被选用
7
于是: max z= ∑ ci xi i =1 7 s.t. ∑ bi xi ≤ Β,
x1 + x 2 + x3 ≤ 2, ( xi = 0 / 1 x 4 + x5 ≥ 1, x6 + x7 ≥ 1,
i =1
则：C 1(x 1)＝ 20x 1 +1500 y1 C 2(x 2)＝ 30x 2 +1200 y2 C 3 (x 3 ) ＝ 50x 2 +1000 y3 0≤x 1≤5000y 1 0≤x2 ≤5000y 2 0≤x 3 ≤5000y 3
场所选择
某公司拟在市东、西、南三区建立门市部, 拟议中有7个位置Ai（i=1,2, …7）可供选择, 规定:在东区,由A1,A2,A3三个点中至多选两个; 在西区,由A4,A5两个点中至少选一个;在南区, 由A6,A7两个点中至少选一个.如选用Ai点设备 投资估计为bi元,每年可获利润估计为ci元,公 司投资总额不能超过B元。如何选择使年利润 最大?
单纯形法
由于目标规划的目标函数中含有优先因 子，所以在单纯形表中，将检验数行按 优先因子的个数分成k行 用单纯形法求解(同前) 例如：前面第一个目标规划模型
北交大交通运输学院《管理运筹学》知识点总结与例题讲解第6章 整数规划
解为：
表 6-1 问题 B1 z1 = 349 x1 = 4.00 x2 = 2.10
问题 B2 z2 = 341 x1 = 5.00 x2 = 1.57
显然没有得到全部变量是整数的解。现存在两个打开节点 B1 和 B2，因 z1 > z2 ，故将 z 改 为 349，那么必存在最优整数解，得到 z* ，并且
3．定界与剪枝：通过不断的分枝和求解各个子问题，分枝定界法不断修正其上下界的 过程称为定界。上界通常由各打开节点中最大的目标函数值确定，下界则由已经找到的最好 的整数解来确定。求解任何一个子问题都有以下三种可能的结果。
(1)子问题无可行解。此时无需继续向下分枝，该节点因不可行而被关闭。因为与父节 点相比，子节点是一个约束得更紧得的问题（比父节点多一个约束）。如果父节点不可行，
z3 = z = z* = 340 问题 B3 得解 x1 = 4.00 ， x2 = 2.00 为最优整数解。
问题 B
x1=4.81 x2=1.82 z0=356
z=0, z=356
x1 4
问题 B1
明显减少搜索的计算量。所有节点的被关闭表明搜索已经完成。如果此时没有找到任何整数
解，则该问题没有整数解；否则搜索过程中得到的最好的整数解就是该问题的最优解。
6.2.2 分枝定界算法
下面结合一具体例子来说明分枝定界法是如何工作的。
例 2 求解 A
max z = 40x1 + 90x2
①
⎧⎪⎪⎨⎪79xx11x++1,27x02xx2≥2≤0≤5760
0 ≤ z* ≤ 349 继续对问题 B1 和 B2 进行分解，因 z1 > z2 ，故先分解 B1 为两支。增加条件 x2 ≤ 2 者，称为问 题 B3 ；增加条件 x2 ≥ 3 者称为问题 B4 。在图 1-4 中再舍去 x2 > 2 与 x3 < 3 之间的可行域，再 进行第二次迭代。解题过程的结果都列在图 1-5 中。可见问题 B3 的解已都是整数，它的目 标函数值 z3 = 340 ，可取为 z ，而它大于 z4 = 327 。所以再分解 B4 已无必要。而问题 B2 的 z2 = 341，所以 z* 可能在 340 ≤ z* ≤ 341 之间有整数解。于是对 B2 分解，得问题 B5 ，既非整 数解，且 z5 = 308 < z3 ，问题 B6 为无可行解。于是可以断定
第六章 整数规划
第一节 整数规划实例与模型
点
(0,0) (0,1) (0,2)
条件
可行解
Z值
0 10 20
(1,0)
(1,1) (1,2) (2,0) (2,1) (2,2) (3,0) (3,1) (3,2) (4,0) (4,1) (4,2)
① √ √ √ √ √ √ √ √ √ √ √ √ √ √
② √ √ √ √ √ √ √ √ √ √ √ √
b1x1+b2x2+b3x3+…b7x7≤B
1，表示Ai点被选用 Xi= 0，表示Ai点没被选用
第二节
0－1整数规划的建模方法
max Z=c1x1+c2x2+c3x3+…+c7x7 s.t. b1x1+b2x2+b3x3+…b7x7≤B X1+x2+x3≤2 X4+x5 ≥1 X6+x7 ≥1 Xi=0或＝1 i=1,2…7
第一节 整数规划实例与模型
所以选址模型为： min TC= TC1+TC2 s.t．x11+x12+x13≤10y1 x21+x22+x23≤20y2 x31+x32+x33≤30y3 x41+x42+x43≤40y4 x51+x52+x53≤30 x11+x21+x31+x41+x51=30 x12+x22+x32+x42+x52=20 x13+x23+x33+x43+x53=20
第二节
扩建厂房
0－1整数规划的建模方法
项目（千元） 扩建仓库 更新机器 新产品研制 40 10 37 总可用成本 10 10 15 40 15 10 50 20 10 40 5 4 10 35
整数规划教学课件
PuLP和Pyomo都支持多种线 性规划求解器，如GLPK、CBC 等，能够方便地求解大规模的 整数规划问题。
Part
05
整数规划案例分析
生产计划问题
总结词
生产计划问题是一个经典的整数规划 问题，旨在确定在满足市场需求的同 时，如何优化生产过程，降低生产成 本。
详细描述
生产计划问题需要考虑多个因素，如 市场需求、生产成本、生产能力等。 整数规划可以用来确定最佳的生产计 划，使得总成本最低，同时满足市场 需求。
投资组合优化问题
总结词
投资组合优化问题是一个重要的整数规划问 题，旨在确定在风险和收益之间取得平衡的 最佳投资组合。
详细描述
投资组合优化问题需要考虑多个资产的风险 和收益，以及投资者对风险和收益的需求。 整数规划可以用来确定最佳的投资组合，使 得在满足投资者需求的同时，风险最小。
路径规划问题
总结词
详细描述
遗传算法的基本思想是通过模拟生物进化过程中的基因遗传和变异过程来寻找最优解。 在算法执行过程中，会随机生成一组初始解，然后通过选择、交叉和变异等操作不断优 化解的质量。遗传算法具有较强的鲁棒性和全局搜索能力，能够处理复杂的整数规划问
题。
模拟退火算法
总结词
模拟退火算法是一种启发式搜索算法， 通过模拟物理退火过程来寻找最优解。
一种迭代算法，通过添加割平面来排 除不可行解，并缩小可行解的范围。 适用于大规模问题。
分支定界法
一种迭代算法，通过不断分割可行解 空间并排除不可能的解来逼近最优解 。适用于中等规模到大规模问题。
Part
02
整数规划的数学模型
线性整数规划
总结词
线性整数规划是整数规划的一种，其目标函数和约束条件均为线性函数，决策变量为整 数。
第六章 整数规划
5
衣服
4
5
15
解：Xi为是否带第 i 种物品
maxZ=20X1 + 30X2 +10X3+18X4 +15X5
5X1+3X2 +X3 +2X4 +4X5 8 2X1+X2 +4X3 +3X4 +5X5 10 Xi为0, 1
一般形式：
max Z
C
i 1
n
i
Xi
n ai X i b i 1 X 0 ,且为整数 i
当100个0－1变量，几亿年
(二) 常用方法 • 分枝定界法
• 割平面法
• 隐枚举法 • 匈牙利法
(三) 分枝定界法
基本思路 maxZ=CX maxZ=CX (B) AX=b X 0
AX=b
(A) X 0
X 0且为整数 (B)为(A)的松弛问题。
i+1
Xj*
i
X*
(B1)
(B) Xj i+1 (B2)
maxZ = 20 X1 + 10 X2
5X1+4X2 24 2X1+5X2 13 X1 , X2 0 X1 , X2为整数
例2、背包问题
背包可再装入8单位重量，10单位体积物品 物品 1 2 3 4 名称 书 摄像机 枕头 休闲食品 重量 5 3 1 2 体积 2 1 4 3 价值 20 30 10 18
优点： (1) 任何模型均可用；
(2) 思路简单、灵活；
(3) 速度快； (4) 适合上机。
分枝变量选择原则 ① 按目标函数系数：选系数绝对值最大者变
量先(分对目标值升降影响最大)。
第6章 python 整数规划与非线性规划
目前，没有一种方法可以有效求解一切整数规划。常见的整数规划求解 算法有：
（1）分枝定界法：可求纯或混合整数线性规划； （2）割平面法：可求纯或混合整数线性规划； （3）隐枚举法：用于求解0 1整数规划，有过滤隐枚举法和分枝隐枚 举法； （4）匈牙利法：解决指派问题（0 1整数规划特殊情形）； （5）蒙特卡罗法：求解各种类型规划。
i1
xij
0或1,
i, j 1,2,
, n,
第 13 页
（6.1）
第6章
6.1整数规划
第 14 页
这是一个纯0 1整数规划模型。 若将模型（6.1）中的cij组成一个n阶方阵C (cij )nn，则称C 为效率矩阵。 这样，标准指派问题中的工作效率就可以很方便地用矩阵C 来表示，并且效 率矩阵C 与标准指派问题一一对应。同样地，模型（6.1）的最优解也可以用 n阶方阵 X *的形式来表示，我们称之为指派问题的最优解方阵。由于标准指 派问题要求“每项工作需且仅需一个人去完成，每个人需完成且仅需完成一 项工作”，故最优解方阵一定是一个置换矩阵，即矩阵的每一行、每一列都 恰好有一个“1”，其余元素均为 0。
标准指派问题的一般提法是：拟分派n个人 A1, A2 , , An去完成n项工作 B1, B2 , , Bn，要求每项工作需且仅需一个人去完成，每个人需完成且仅需完 成一项工作。已知人 Ai 完成工作Bj的时间或费用等成本型指标值为cij，则应 如何指派才能使总的工作效率最高？
第6章
6.1整数规划
第6章
6.1整数规划
第 15 页
标准指派问题的数学模型表现为0 1整数规划的形式，当然可以通过整 数规划的分支定界法或0 1整数规划的隐枚举法来求得最优解。但标准指派 问题的数学模型具有独特的结构，因此，为提高求解的效率，1955 年美国 数学家 H. W. Kuhn 根据匈牙利数学家 D. König 关于矩阵中独立零元素定 理，提出了一个求解标准指派模型的有效算法—匈牙利算法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
纯整数规划的可行解就是可行域中的整 数点
非整数点不是可行解，对于求解没有意 义，故切割掉可行域中的非可行解，不 妨碍整数规划问题的优化
IP问题的最优解不优于LP问题的最优解
OR3
5
6.2 分枝定界法
思路：切割可行域，去掉非整数点。一次分枝 变成两个可行域，分别求最优解
例1. maxZ=2000x1+1000x2
第五步 造0——直线未覆盖的元素，减
去其最小值，交叉点上加最小元素，产
生新的0元素，Go to 2
0 6 2 1 -1 5 1 0 0 4 0
Cij= 0 5 3 1 -1 0 4 2 0 3 1 0
0001
1 0 1
2 0 2
1320
2 3 2 2 2 1
+1
最优解：x13=1,x21=1,x32=1,x44=1 Z=15
继续分解，Go to 3
（例题2讲解）
OR3
9
6.3 0—1规划问题
某些特殊问题，只做是非选择，故变量设置简 化为0或1，1代表选择，0代表不选择。
例4. 600万元投资5个项目，求利润最大的方案？
项目 投资额 项目收益 约束条件
210 160
中选1项
300 210
ቤተ መጻሕፍቲ ባይዱ
之中选1项
150 60
5x1+4x2≤24
2x1+5x2 ≤13
x1.x2 ≥0且为整数 解此LP问题，得：X1=4.8，X2=0 显然不是可行解
OR3
3
整数规划图解法
x2
3
2
1
B
A
1 2 3 4 5 6 7 x1
OR3
4
图解法的启示
A（4.8，0）点是LP问题的可行解，不 是IP问题的可行解，B（4，1）才是IP的 最优解
原问题分解为两个
maxZ=2000x1+1000x2
maxZ=2000x1+1000x2
5x1+4x2≤24
5x1+4x2≤24
2x1+5x2 ≤13 ( IP1 ) 2x1+5x2 ≤13 (IP2)
x1 ≤4
x1 ≥5
x1.x2 ≥0且为整数
x1.x2 ≥0且为整数
OR3
7
分枝定界法（续）
不考虑整数要求，解相应LP问题。
ABCBD
1
1
2
1
3
1
41
5
1
OR3
17
（1，0，0，1，1）
………..
Z值
240
X
X
X
X
X
X
X
X
X
X
420
OR3
12
6.4 指派问题
例8 甲乙丙丁四个人，A、B、D四项任 务，不同的人做不同的工作效率不同， 如何指派不同的人去做不同的工作使效 率最高？
数模： minZ=ΣΣcijxij Σxij=1 i=1,…,n Σxij=1 j=1,…,n Xij=0或1
专门方法：分枝定界法、割平面法、隐 枚举法、匈牙利法
OR3
2
问题举例
某集装箱运输公司，箱型标准体积24m3，重量 13T,现有两种货物可以装运，甲货物体积5m3、 重量2T、每件利润2000元；乙货物体积4m3、 重量5T、每件利润1000元，如何装运获利最 多？
maxZ=2000x1+1000x2
选必先选
130 80
260 180
OR3
10
求解0—1规划的隐枚举法
例4解：
0 当项目未被选中
建模：设xj= 1 当项目被选中
max Z=160x1+210x2+60x3+80x4+180x5
210x1+300x2+150x3+130x4+260x5 ≤ 600
X1+x2+x3=1
X3+x4=1
3 3 4 4 -3 0 0 1 1 0 0 1
4 6 6 3 -3 1 3 3 0 1 3 2
-1
第二步 圈0——寻找不同行不同列的0元素，
圈之。 所在行和列其它0元素划掉
第三步 打——无的行打，打行上0列打
，打列上行打，打行上0列打 …
OR3
14
指派问题解法—匈牙利法（续）
第四步 划线——无行、打列划线
OR3
15
相关问题：
非标准型的转化
（1）maxZ= ΣΣcijxij minZ’= ΣΣ(-cij)xij minZ’’= ΣΣ(M-cij)xij = ΣΣbijxij
M是足够大的常数， 新问题的最优解 就是原问题的最优解 （2）整数规划的计算机求解
OR3
16
整数规划习题课
P222——6.11
第六章 整数规划
本章要求 理解整数规划的含义 掌握分枝定界法的思想和方法 掌握0-1变量的含义和用法 掌握指派问题的算法 微机求解
OR3
1
6.1 整数规划问题的提出
决策问题中经常有整数要求，如人数、 件数、机器台数、货物箱数……如何解 决？四舍五入不行，枚举法太慢
问题分类：纯整数规划、混合整数规划、 0-1整数规划
5x1+4x2≤24
2x1+5x2 ≤13 x1.x2 ≥0且为整数 解：先不考虑整数要求，解相应的LP问题，得： x1=4.8 x2=0 Z=9600 不是可行解 Z=9600是IP问题的上界，记为：Z=9600
OR3
6
分枝定界法（续）
X1=4.8不符合要求，切掉4—5之间的可行域， 可行域变成两块，即原有约束条件再分别附加 约束条件x1 ≤4和x1 ≥5
x5 ≤ x1
Xj=0或1 j=1，2,…,5
增加过滤条件：160x1+210x2+60x3+80x4+180x5 ≥ 240
OR3
11
用隐枚举法解例4：
(x1,x2,x3,x4,x5）
（1，0，0，1，0） （1，1，1，1，1） （1，1，1，1，0） （1，1，1，0，1） （1，1，1，0，0） （1，1，0，1，1） （1，1，0，1，0） （1，1，0，0，1） （1，1，0，0，0） （1，0，1，1，1） （1，0，1，1，0）
任务 人 时间
甲 乙 丙 丁
ABC D 4 10 7 5 2763 3344 4663
OR3
13
指派问题解法—匈牙利法
解：类似运输问题的最小元素法
第一步 造0——各行各列减其最小元素
4 10 7 5 -4 0 6 3 1 6 2 1
Cij= 2 7 6 3 -2 0 5 4 1 0 5 3 1
2、检查是否符合整数要求，是，则得最 优解，完毕。否则，转下步
3、任取一个非整数变量xi=bi，构造两个 新的约束条件：xi ≤[bi] ,xi ≥ [bi]+1,分别 加入到上一个LP问题，形成两个新的分 枝问题。
4、不考虑整数要求，解分枝问题。若整
数解的Z值>所有分枝末梢的Z值，则得最
优解。否则， 取Z值最大的非整数解，
解IP1得：x1=4 ,x2=1 z=9000
解IP2得：无可行解
此时可以断定IP问题的下界为9000，记 为Z=9000
٭由于目前的分枝末梢最大值是9000，故
IP问题的上界便是9000。由于Z=Z，此 时已得IP问题的最优解，即
x1=4,x2=1,Z=9000
OR3
8
分枝定界法的解题步骤
1、不考虑整数约束，解相应LP问题
非整数点不是可行解，对于求解没有意 义，故切割掉可行域中的非可行解，不 妨碍整数规划问题的优化
IP问题的最优解不优于LP问题的最优解
OR3
5
6.2 分枝定界法
思路：切割可行域，去掉非整数点。一次分枝 变成两个可行域，分别求最优解
例1. maxZ=2000x1+1000x2
第五步 造0——直线未覆盖的元素，减
去其最小值，交叉点上加最小元素，产
生新的0元素，Go to 2
0 6 2 1 -1 5 1 0 0 4 0
Cij= 0 5 3 1 -1 0 4 2 0 3 1 0
0001
1 0 1
2 0 2
1320
2 3 2 2 2 1
+1
最优解：x13=1,x21=1,x32=1,x44=1 Z=15
继续分解，Go to 3
（例题2讲解）
OR3
9
6.3 0—1规划问题
某些特殊问题，只做是非选择，故变量设置简 化为0或1，1代表选择，0代表不选择。
例4. 600万元投资5个项目，求利润最大的方案？
项目 投资额 项目收益 约束条件
210 160
中选1项
300 210
ቤተ መጻሕፍቲ ባይዱ
之中选1项
150 60
5x1+4x2≤24
2x1+5x2 ≤13
x1.x2 ≥0且为整数 解此LP问题，得：X1=4.8，X2=0 显然不是可行解
OR3
3
整数规划图解法
x2
3
2
1
B
A
1 2 3 4 5 6 7 x1
OR3
4
图解法的启示
A（4.8，0）点是LP问题的可行解，不 是IP问题的可行解，B（4，1）才是IP的 最优解
原问题分解为两个
maxZ=2000x1+1000x2
maxZ=2000x1+1000x2
5x1+4x2≤24
5x1+4x2≤24
2x1+5x2 ≤13 ( IP1 ) 2x1+5x2 ≤13 (IP2)
x1 ≤4
x1 ≥5
x1.x2 ≥0且为整数
x1.x2 ≥0且为整数
OR3
7
分枝定界法（续）
不考虑整数要求，解相应LP问题。
ABCBD
1
1
2
1
3
1
41
5
1
OR3
17
（1，0，0，1，1）
………..
Z值
240
X
X
X
X
X
X
X
X
X
X
420
OR3
12
6.4 指派问题
例8 甲乙丙丁四个人，A、B、D四项任 务，不同的人做不同的工作效率不同， 如何指派不同的人去做不同的工作使效 率最高？
数模： minZ=ΣΣcijxij Σxij=1 i=1,…,n Σxij=1 j=1,…,n Xij=0或1
专门方法：分枝定界法、割平面法、隐 枚举法、匈牙利法
OR3
2
问题举例
某集装箱运输公司，箱型标准体积24m3，重量 13T,现有两种货物可以装运，甲货物体积5m3、 重量2T、每件利润2000元；乙货物体积4m3、 重量5T、每件利润1000元，如何装运获利最 多？
maxZ=2000x1+1000x2
选必先选
130 80
260 180
OR3
10
求解0—1规划的隐枚举法
例4解：
0 当项目未被选中
建模：设xj= 1 当项目被选中
max Z=160x1+210x2+60x3+80x4+180x5
210x1+300x2+150x3+130x4+260x5 ≤ 600
X1+x2+x3=1
X3+x4=1
3 3 4 4 -3 0 0 1 1 0 0 1
4 6 6 3 -3 1 3 3 0 1 3 2
-1
第二步 圈0——寻找不同行不同列的0元素，
圈之。 所在行和列其它0元素划掉
第三步 打——无的行打，打行上0列打
，打列上行打，打行上0列打 …
OR3
14
指派问题解法—匈牙利法（续）
第四步 划线——无行、打列划线
OR3
15
相关问题：
非标准型的转化
（1）maxZ= ΣΣcijxij minZ’= ΣΣ(-cij)xij minZ’’= ΣΣ(M-cij)xij = ΣΣbijxij
M是足够大的常数， 新问题的最优解 就是原问题的最优解 （2）整数规划的计算机求解
OR3
16
整数规划习题课
P222——6.11
第六章 整数规划
本章要求 理解整数规划的含义 掌握分枝定界法的思想和方法 掌握0-1变量的含义和用法 掌握指派问题的算法 微机求解
OR3
1
6.1 整数规划问题的提出
决策问题中经常有整数要求，如人数、 件数、机器台数、货物箱数……如何解 决？四舍五入不行，枚举法太慢
问题分类：纯整数规划、混合整数规划、 0-1整数规划
5x1+4x2≤24
2x1+5x2 ≤13 x1.x2 ≥0且为整数 解：先不考虑整数要求，解相应的LP问题，得： x1=4.8 x2=0 Z=9600 不是可行解 Z=9600是IP问题的上界，记为：Z=9600
OR3
6
分枝定界法（续）
X1=4.8不符合要求，切掉4—5之间的可行域， 可行域变成两块，即原有约束条件再分别附加 约束条件x1 ≤4和x1 ≥5
x5 ≤ x1
Xj=0或1 j=1，2,…,5
增加过滤条件：160x1+210x2+60x3+80x4+180x5 ≥ 240
OR3
11
用隐枚举法解例4：
(x1,x2,x3,x4,x5）
（1，0，0，1，0） （1，1，1，1，1） （1，1，1，1，0） （1，1，1，0，1） （1，1，1，0，0） （1，1，0，1，1） （1，1，0，1，0） （1，1，0，0，1） （1，1，0，0，0） （1，0，1，1，1） （1，0，1，1，0）
任务 人 时间
甲 乙 丙 丁
ABC D 4 10 7 5 2763 3344 4663
OR3
13
指派问题解法—匈牙利法
解：类似运输问题的最小元素法
第一步 造0——各行各列减其最小元素
4 10 7 5 -4 0 6 3 1 6 2 1
Cij= 2 7 6 3 -2 0 5 4 1 0 5 3 1
2、检查是否符合整数要求，是，则得最 优解，完毕。否则，转下步
3、任取一个非整数变量xi=bi，构造两个 新的约束条件：xi ≤[bi] ,xi ≥ [bi]+1,分别 加入到上一个LP问题，形成两个新的分 枝问题。
4、不考虑整数要求，解分枝问题。若整
数解的Z值>所有分枝末梢的Z值，则得最
优解。否则， 取Z值最大的非整数解，
解IP1得：x1=4 ,x2=1 z=9000
解IP2得：无可行解
此时可以断定IP问题的下界为9000，记 为Z=9000
٭由于目前的分枝末梢最大值是9000，故
IP问题的上界便是9000。由于Z=Z，此 时已得IP问题的最优解，即
x1=4,x2=1,Z=9000
OR3
8
分枝定界法的解题步骤
1、不考虑整数约束，解相应LP问题