2009初中数学竞赛试题与答案
2009年初中数学联赛(四川)初赛试题5的探究

同 , 专D+ 理r ( c 一
分线 上去 . 过研究 , 通 笔者得 到 了如下 几个 结论 :
D —C , A A)r:÷ ( DC+DB—c . B)于是 ,+ r r
B, C所对 的 边 分 别 为 口, , ,D 为 斜 边 AB bCC 上 的 中线 , 别 用 r r ,。表 示 AAB AA D, 分 ,。 r C, C
( ) .
19
c a+ b+ c 。 n+ b+ c ( ) C( )
解法 2比解 法 1更 具 一般 性 , 是这 种 解 法 正 启 发 了笔 者对 上述 问题 进 一 步 的 探 究 , 到 如 下 得
的结论 :
结论 1 在 Rt AAB 中 , C 一 9 。 A, C 0,
r + r — r ; + 一 一 2. i c
r1 r2 r
( 0 9 全 国初 中数 学联 赛 四川省初 赛题 ) 20 年 经 过仔 细 的斟 酌 , 者 发 现此 题 有 进 一 步 探 笔 究 的价 值.
2 问 题 的 探 究
解 法 1 参 考答 案 ) 由勾股 定 理得 A 一 5 ( B , 由面积 关系 得 c : , Rt BC 的 内切 圆半 D = : 则 AA
2 1 年 第 9期 01
中学 数学 月刊
・4 l・
20 初 中数 学 联 赛( 川) 赛试 题 5的探 究 0 9年 四 初
王伯龙 ( 宁夏 彭阳县 第三 中学 7 6 0 ) 5 5 0
1 提 出 问 题
堂:
一 -
堡垒 :
一堡 垒
C。
题目 在 R AA C 中 , D 为斜边 AB上 的 t B C 高 , C一 3 B : , A , C= 4 分别 用 rr , 示 AA = , r 表 BC, AAC A B D 内切 圆 的 半 径 , r r + r = D, C 则 + = =
历届(第1-23届)希望杯数学竞赛初一七年级真题及答案

“希望杯”全国数学竞赛(第1-23届)初一年级/七年级第一/二试题目录1.希望杯第一届(1990年)初中一年级第一试试题......................003-0052.希望杯第一届(1990年)初中一年级第二试试题......................010-0123.希望杯第二届(1991年)初中一年级第一试试题...... 0错误!未定义书签。
-0204.希望杯第二届(1991年)初中一年级第二试试题...... 0错误!未定义书签。
-0265.希望杯第三届(1992年)初中一年级第一试试题...... 0错误!未定义书签。
-0326.希望杯第三届(1992年)初中一年级第二试试题...... 0错误!未定义书签。
-0407.希望杯第四届(1993年)初中一年级第一试试题...... 0错误!未定义书签。
-0508.希望杯第四届(1993年)初中一年级第二试试题...... 0错误!未定义书签。
-0589.希望杯第五届(1994年)初中一年级第一试试题...... 0错误!未定义书签。
-06610.希望杯第五届(1994年)初中一年级第二试试题..... 0错误!未定义书签。
-07311.希望杯第六届(1995年)初中一年级第一试试题..... 0错误!未定义书签。
-080 12希望杯第六届(1995年)初中一年级第二试试题..... 0错误!未定义书签。
-08713.希望杯第七届(1996年)初中一年级第一试试题..... 0错误!未定义书签。
-09814.希望杯第七届(1996年)初中一年级第二试试题....... 错误!未定义书签。
-10515.希望杯第八届(1997年)初中一年级第一试试题....... 错误!未定义书签。
-11316.希望杯第八届(1997年)初中一年级第二试试题....... 错误!未定义书签。
-12017.希望杯第九届(1998年)初中一年级第一试试题....... 错误!未定义书签。
2009上海大同杯(原新知杯)数学竞赛试题

EP
值为
。
CF
A
第五题图
1
2009 年新知杯上海市初中数学竞赛试题
6、设a,b是方程 x2 68x 1 0 的两个根,c,d是方程 x2 86x 1 0 的
两个根,则(a+ c)( b + c)( a − d)( b − d)的值
。
7在平面直角坐标系中有两点P(-1,1) , Q (2,2),函数y=kx−1 的图像与 线段PQ 延长线相交(交点不包括Q),则实数k的取值范围是 。
4、已知关于x的方程 x4 2x3 (3 k )x2 (2 k )x 2k 0 有实根,并且所有实根
的乘积为−2,则所有实根的平方和为
。
【答案】5 B
EP
CF
A
第五题图
5、如图,直角三角形ABC中, AC=1,BC=2,P为斜边AB上一动点。PE⊥BC,
PF⊥CA,则线段EF长的最小值为
98 x
1
,
y
20 x
25
,
y
30 25
因此
abcd
9801,
2025, 3025
。
四、(本题15分)正整数n满足以下条件:任意n个大于1且不超过2009的两两互 素的正整数中,至少有一个素数,求最小的n。 解:由于 22 , 32 , 52 , 72 ,112 ,132 ,172 ,192 , 232 , 292 , 312 , 372 , 412 , 432 这14个合数都小于
b
3
2009 年新知杯上海市初中数学竞赛试题
2009年新知杯上海市初中数学竞赛
参考解答
历届(1-23)希望杯数学竞赛初一七年级真题及答案(最新整理WORD版)

“希望杯”全国数学竞赛(第1-23届)初一年级/七年级第一/二试题第 1 页共277 页目录1.希望杯第一届(1990年)初中一年级第一试试题............................................. 003-0052.希望杯第一届(1990年)初中一年级第二试试题............................................. 010-0123.希望杯第二届(1991年)初中一年级第一试试题............................................. 016-0204.希望杯第二届(1991年)初中一年级第二试试题............................................. 022-0265.希望杯第三届(1992年)初中一年级第一试试题............................................. 029-0326.希望杯第三届(1992年)初中一年级第二试试题............................................. 034-0407.希望杯第四届(1993年)初中一年级第一试试题............................................. 044-0508.希望杯第四届(1993年)初中一年级第二试试题............................................. 051-0589.希望杯第五届(1994年)初中一年级第一试试题............................................. 058-06610.希望杯第五届(1994年)初中一年级第二试试题 .......................................... 065-07311.希望杯第六届(1995年)初中一年级第一试试题 ........................................... 072-080 12希望杯第六届(1995年)初中一年级第二试试题........................................... 079-08713.希望杯第七届(1996年)初中一年级第一试试题........................................... 089-09814.希望杯第七届(1996年)初中一年级第二试试题............................................. 95-10515.希望杯第八届(1997年)初中一年级第一试试题........................................... 103-11316.希望杯第八届(1997年)初中一年级第二试试题........................................... 110-12017.希望杯第九届(1998年)初中一年级第一试试题........................................... 119-12918.希望杯第九届(1998年)初中一年级第二试试题........................................... 128-13819.希望杯第十届(1999年)初中一年级第二试试题........................................... 135-14720.希望杯第十届(1999年)初中一年级第一试试题........................................... 148-15121.希望杯第十一届(2000年)初中一年级第一试试题....................................... 148-16122.希望杯第十一届(2000年)初中一年级第二试试题....................................... 155-16923.希望杯第十二届(2001年)初中一年级第一试试题....................................... 159-17424.希望杯第十二届(2001年)初中一年级第二试试题....................................... 163-17825.希望杯第十三届(2002年)初中一年级第一试试题....................................... 169-18426.希望杯第十三届(2001年)初中一年级第二试试题....................................... 173-18927.希望杯第十四届(2003年)初中一年级第一试试题....................................... 180-19628.希望杯第十四届(2003年)初中一年级第二试试题....................................... 184-200第 2 页共277 页29.希望杯第十五届(2004年)初中一年级第一试试题 (188)30.希望杯第十五届(2004年)初中一年级第二试试题 (189)31.希望杯第十六届(2005年)初中一年级第一试试题....................................... 213-21832.希望杯第十六届(2005年)初中一年级第二试试题 (189)33.希望杯第十七届(2006年)初中一年级第一试试题....................................... 228-23334.希望杯第十七届(2006年)初中一年级第二试试题....................................... 234-23835.希望杯第十八届(2007年)初中一年级第一试试题....................................... 242-246 26.希望杯第十八届(2007年)初中一年级第二试试题....................................... 248-25137.希望杯第十九届(2008年)初中一年级第一试试题....................................... 252-25638.希望杯第十九届(2008年)初中一年级第二试试题....................................... 257-26239.希望杯第二十届(2009年)初中一年级第一试试题....................................... 263-26620.希望杯第二十届(2009年)初中一年级第二试试题....................................... 267-27121.希望杯第二十一届(2010年)初中一年级第一试试题 ................................... 274-27622.希望杯第二十二届(2011年)初中一年级第二试试题 ................................... 285-28823.希望杯第二十三届(2012年)初中一年级第二试试题 ................................... 288-301第 3 页共277 页第 4 页 共 277 页希望杯第一届(1990年)初中一年级第1试试题一、选择题(每题1分,共10分)1.如果a ,b 都代表有理数,并且a +b=0,那么 ( )A .a ,b 都是0.B .a ,b 之一是0.C .a ,b 互为相反数.D .a ,b 互为倒数.2.下面的说法中正确的是 ( )A .单项式与单项式的和是单项式.B .单项式与单项式的和是多项式.C .多项式与多项式的和是多项式.D .整式与整式的和是整式.3.下面说法中不正确的是 ( )A. 有最小的自然数. B .没有最小的正有理数.C .没有最大的负整数.D .没有最大的非负数.4.如果a ,b 代表有理数,并且a +b 的值大于a -b 的值,那么( ) A .a ,b 同号. B .a ,b 异号.C .a >0. D .b >0.5.大于-π并且不是自然数的整数有( ) A .2个. B .3个.C .4个. D .无数个.6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身.这四种说法中,不正确的说法的个数是 ( )A .0个.B .1个.C .2个.D .3个.7.a 代表有理数,那么,a 和-a 的大小关系是 ( )A .a 大于-a .B .a 小于-a .C .a 大于-a 或a 小于-a .D .a 不一定大于-a .8.在解方程的过程中,为了使得到的方程和原方程同解,可以在原方程的两边( )A .乘以同一个数.B .乘以同一个整式.C .加上同一个代数式.D .都加上1.9.杯子中有大半杯水,第二天较第一天减少了10%,第三天又较第二天增加了10%,那么,第三天杯中的水量与第一天杯中的水量相比的结果是( )A .一样多.B .多了.C .少了.D .多少都可能.10.轮船往返于一条河的两码头之间,如果船本身在静水中的速度是固定的,那么,当这条河的水流速度增大时,船往返一次所用的时间将( )A .增多.B .减少.C .不变.D .增多、减少都有可能.二、填空题(每题1分,共10分)1. 21115160.01253(87.5)(2)4571615⨯-⨯-÷⨯+--= ______. 2.198919902-198919892=______.第 5 页 共 277 页 3.2481632(21)(21)(21)(21)(21)21+++++-=________. 4. 关于x 的方程12148x x +--=的解是_________. 5.1-2+3-4+5-6+7-8+…+4999-5000=______.6.当x=-24125时,代数式(3x 3-5x 2+6x -1)-(x 3-2x 2+x -2)+(-2x 3+3x 2+1)的值是____. 7.当a=-0.2,b=0.04时,代数式272711()(0.16)()73724a b b a a b --++-+的值是______. 8.含盐30%的盐水有60千克,放在秤上蒸发,当盐水变为含盐40%时,秤得盐水的重是______克.9.制造一批零件,按计划18天可以完成它的13.如果工作4天后,工作效率提高了15,那么完成这批零件的一半,一共需要______天.10.现在4点5分,再过______分钟,分针和时针第一次重合.答案与提示一、选择题1.C 2.D 3.C 4.D 5.C 6.B 7.D 8.D 9.C 10.A提示:1.令a=2,b=-2,满足2+(-2)=0,由此2.x2,2x2,x3都是单项式.两个单项式x3,x2之和为x3+x2是多项式,排除A.两个单项式x2,2x2之和为3x2是单项式,排除B.两个多项式x3+x2与x3-x2之和为2x3是个单项式,排除C,因此选D.3.1是最小的自然数,A正确.可以找到正所以C“没有最大的负整数”的说法不正确.写出扩大自然数列,0,1,2,3,…,n,…,易知无最大非负数,D正确.所以不正确的说法应选C.5.在数轴上容易看出:在-π右边0的左边(包括0在内)的整数只有-3,-2,-1,0共4个.选C.6.由12=1,13=1可知甲、乙两种说法是正确的.由(-1)3=-1,可知丁也是正确的说法.而负数的平方均为正数,即负数的平方一定大于它本身,所以“负数平方不一定大于它本身”的说法不正确.即丙不正确.在甲、乙、丙、丁四个说法中,只有丙1个说法不正确.所以选B.7.令a=0,马上可以排除A、B、C,应选D.8.对方程同解变形,要求方程两边同乘不等于0的数.所以排除A.我们考察方程x-2=0,易知其根为x=2.若该方程两边同乘以一个整式x-1,得(x-1)(x -2)=0,其根为x=1及x=2,不与原方程同解,排除B.若在方程x-2=0两边加上同一个代数式去了原方程x=2的根.所以应排除C.事实上方程两边同时加上一个常数,新方程与原方程同解,对D,这里所加常数为1,因此选D.9.设杯中原有水量为a,依题意可得,第二天杯中水量为a×(1-10%)=0.9a;第 6 页共277 页第三天杯中水量为(0.9a)×(1+10%)=0.9×1.1×a;第三天杯中水量与第一天杯中水量之比为所以第三天杯中水量比第一天杯中水量少了,选C.10.设两码头之间距离为s,船在静水中速度为a,水速为v0,则往返一次所用时间为设河水速度增大后为v,(v>v0)则往返一次所用时间为由于v-v0>0,a+v0>a-v0,a+v>a-v所以(a+v0)(a+v)>(a-v0)(a-v)∴t0-t<0,即t0<t.因此河水速增大所用时间将增多,选A.二、填空题第7 页共277 页提示:2.198919902-198919892=(19891990+19891989)×(19891990-19891989)=(19891990+19891989)×1=39783979.3.由于(2+1)(22+1)(24+1)(28+1)(216+1)=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)=(22-1)(22+1)(24+1)(28+1)(216+1)=(24-1)(24+1)(28+1)(216+1)=(28-1)(28+1)(216+1)=(216-1)(216+1)=232-1.2(1+x)-(x-2)=8,2+2x-x+2=8解得;x=45.1-2+3-4+5-6+7-8+…+4999-50005000)=(1-2)+(3-4)+(5-6)+(7-8)+…+(4999-=-2500.+1)=5x+26.(3x3-5x2+6x-1)-(x3-2x2+x-2)+(-2x3+3x27.注意到:当a=-0.2,b=0.04时,a2-b=(-0.2)2-0.04=0,b+a+0.16=0.04-0.2+0.16=0.第8 页共277 页8.食盐30%的盐水60千克中含盐60×30%(千克)设蒸发变成含盐为40%的水重x克,即0.001x千克,此时,60×30%=(0.001x)×40%解得:x=45000(克).10.在4时整,时针与分针针夹角为120°即第9 页共277 页希望杯第一届(1990年)初中一年级第2试试题一、选择题(每题1分,共5分)以下每个题目里给出的A,B,C,D四个结论中有且仅有一个是正确的.请你在括号填上你认为是正确的那个结论的英文字母代号.1.某工厂去年的生产总值比前年增长a%,则前年比去年少的百分数是( )A.a%.B.(1+a)%. C.1100aa+D.100aa+2.甲杯中盛有2m毫升红墨水,乙杯中盛有m毫升蓝墨水,从甲杯倒出a毫升到乙杯里, 0<a<m,搅匀后,又从乙杯倒出a毫升到甲杯里,则这时( )A.甲杯中混入的蓝墨水比乙杯中混入的红墨水少.B.甲杯中混入的蓝墨水比乙杯中混入的红墨水多.C.甲杯中混入的蓝墨水和乙杯中混入的红墨水相同.D.甲杯中混入的蓝墨水与乙杯中混入的红墨水多少关系不定.3.已知数x=100,则( )A.x是完全平方数.B.(x-50)是完全平方数.C.(x-25)是完全平方数.D.(x+50)是完全平方数.4.观察图1中的数轴:用字母a,b,c依次表示点A,B,C对应的数,则111,,ab b a c-的大小关系是( )A.111ab b a c<<-; B.1b a-<1ab<1c; C.1c<1b a-<1ab; D.1c<1ab<1b a-.5.x=9,y=-4是二元二次方程2x2+5xy+3y2=30的一组整数解,这个方程的不同的整数解共有( )A.2组.B.6组.C.12组.D.16组.二、填空题(每题1分,共5分)1.方程|1990x-1990|=1990的根是______.2.对于任意有理数x,y,定义一种运算*,规定x*y=ax+by-cxy,其中的a,b,c表示已知数,等式右边是通常的加、减、乘运算.又知道1*2=3,2*3=4,x*m=x(m≠0),则m 的数值是______.3.新上任的宿舍管理员拿到20把钥匙去开20个房间的门,他知道每把钥匙只能开其中第10 页共277 页的一个门,但不知道每把钥匙是开哪一个门的钥匙,现在要打开所有关闭着的20个房间,他最多要试开______次.4.当m=______时,二元二次六项式6x2+mxy-4y2-x+17y-15可以分解为两个关于x,y 的二元一次三项式的乘积.5.三个连续自然数的平方和(填“是”或“不是”或“可能是”)______某个自然数的平方.三、解答题(写出推理、运算的过程及最后结果.每题5分,共15分)1.两辆汽车从同一地点同时出发,沿同一方向同速直线行驶,每车最多只能带24桶汽油,途中不能用别的油,每桶油可使一辆车前进60公里,两车都必须返回出发地点,但是可以不同时返回,两车相互可借用对方的油.为了使其中一辆车尽可能地远离出发地点,另一辆车应当在离出发地点多少公里的地方返回?离出发地点最远的那辆车一共行驶了多少公里?2.如图2,纸上画了四个大小一样的圆,圆心分别是A,B,C,D,直线m通过A,B,直线n通过C,D,用S表示一个圆的面积,如果四个圆在纸上盖住的总面积是5(S-1),直线m,n之间被圆盖住的面积是8,阴影部分的面积S1,S2,S3满足关系式S3=13S1=13S2,求S.3.求方程11156x y z++=的正整数解.第11 页共277 页答案与提示一、选择题1.D 2.C 3.C 4.C 5.D提示:1.设前年的生产总值是m ,则去年的生产总值是前年比去年少这个产值差占去年的应选D.2.从甲杯倒出a毫升红墨水到乙杯中以后:再从乙杯倒出a毫升混合墨水到甲杯中以后:乙杯中含有的红墨水的数量是①乙杯中减少的蓝墨水的数量是②∵①=②∴选C.∴x-25=(10n+2+5)2可知应当选C.4.由所给出的数轴表示(如图3):可以看出第12 页共277 页∴①<②<③,∴选C.5.方程2x2+5xy+3y2=30可以变形为(2x+3y)(x+y)=1·2·3·5∵x,y是整数,∴2x+3y,x+y也是整数.由下面的表可以知道共有16个二元一次方程组,每组的解都是整数,所以有16组整数组,应选D.二、填空题提示:1.原方程可以变形为|x-1|=1,即x-1=1或-1,∴x=2或0.2.由题设的等式x*y=ax+by-cxy及x*m=x(m≠0)得a·0+bm-c·0·m=0,∴bm=0.∵m≠0,∴b=0.∴等式改为x*y=ax-cxy.∵1*2=3,2*3=4,解得a=5,c=1.∴题设的等式即x*y=5x-xy.在这个等式中,令x=1,y=m,得5-m=1,∴m=4.第13 页共277 页3.∵打开所有关闭着的20个房间,∴最多要试开4.利用“十字相乘法”分解二次三项式的知识,可以判定给出的二元二次六项式6x2+mxy-4y2-x+17y-15中划波浪线的三项应当这样分解:3x -52x +3现在要考虑y,只须先改写作然后根据-4y2,17y这两项式,即可断定是:由于(3x+4y-5)(2x-y+3)=6x2+5xy-4y2-x+17y-15就是原六项式,所以m=5.5.设三个连续自然数是a-1,a,a+1,则它们的平方和是(a-1)2+a2+(a+1)2=3a2+2,显然,这个和被3除时必得余数2.另一方面,自然数被3除时,余数只能是0或1或2,于是它们可以表示成3b,3b+1,3b+2(b是自然数)中的一个,但是它们的平方(3b)2=9b2(3b+1)2=9b2+6b+1,(3b+2)2=9b2+12b+4=(9b2+12b+3)+1被3除时,余数要么是0,要么是1,不能是2,所以三个连续自然数平方和不是某个自然数的平方.三、解答题1.设两辆汽车一为甲一为乙,并且甲用了x升汽油时即回返,留下返程需的x桶汽油,将多余的(24-2x)桶汽油给乙.让乙继续前行,这时,乙有(24-2x)+(24-x)=48-3x桶汽油,依题意,应当有48-3x≤24,∴x≥8.甲、乙分手后,乙继续前行的路程是这个结果中的代数式30(48-4x)表明,当x的值愈小时,代数式的值愈大,因为x≥8,所以当x=8时,得最大值30(48-4·8)=480(公里),因此,乙车行驶的路程一共是2(60·8+480)=1920(公里).2.由题设可得第14 页共277 页即2S-5S3=8……②∴x,y,z都>1,因此,当1<x≤y≤z时,解(x,y,z)共(2,4,12),(2,6,6),(3,3,6),(3,4,4)四组.由于x,y,z在方程中地位平等.所以可得如下表所列的15组解.第15 页共277 页希望杯第二届(1991年)初中一年级第1试试题一、选择题(每题1分,共15分)以下每个题目的A,B,C,D四个结论中,仅有一个是正确的,请在括号内填上正确的那个结论的英文字母代号.1.数1是( )A.最小整数.B.最小正数.C.最小自然数.D.最小有理数.2.若a>b,则( )A.11a b; B.-a<-b.C.|a|>|b|.D.a2>b2.3.a为有理数,则一定成立的关系式是( )A.7a>a.B.7+a>a.C.7+a>7.D.|a|≥7.4.图中表示阴影部分面积的代数式是( )A.ad+bc.B.c(b-d)+d(a-c).C.ad+c(b-d).D.ab-cd.5.以下的运算的结果中,最大的一个数是( )A.(-13579)+0.2468; B.(-13579)+12468;C.(-13579)×12468; D.(-13579)÷124686.3.1416×7.5944+3.1416×(-5.5944)的值是( ) A.6.1632. B.6.2832.C.6.5132.D.5.3692.7.如果四个数的和的14是8,其中三个数分别是-6,11,12,则笫四个数是( )A.16. B.15. C.14. D.13.8.下列分数中,大于-13且小于-14的是( )A.-1120; B.-413; C.-316; D.-617.9.方程甲:34(x-4)=3x与方程乙:x-4=4x同解,其根据是( )A.甲方程的两边都加上了同一个整式x.B.甲方程的两边都乘以43x;C. 甲方程的两边都乘以43; D. 甲方程的两边都乘以34.第16 页共277 页第 17 页 共 277 页10.如图: ,数轴上标出了有理数a ,b ,c 的位置,其中O是原点,则111,,a b c的大小关系是( ) A.111a b c>>; B.1b >1c >1a ; C. 1b >1a >1c ; D. 1c >1a >1b .11.方程522.2 3.7x =的根是( ) A .27. B .28. C .29. D .30. 12.当x=12,y=-2时,代数式42x y xy -的值是( )A .-6.B .-2.C .2.D .6.13.在-4,-1,-2.5,-0.01与-15这五个数中,最大的数与绝对值最大的那个数的乘积是( )A .225.B .0.15.C .0.0001.D .1.14.不等式124816x x x xx ++++>的解集是( ) A .x <16. B .x >16.C .x <1. D.x>-116. 15.浓度为p%的盐水m 公斤与浓度为q%的盐水n 公斤混合后的溶液浓度是 ( )A.%2p q +;B.()%mp nq +;C.()%mp nq p q ++;D.()%mp nq m n++. 二、填空题(每题1分,共15分)1. 计算:(-1)+(-1)-(-1)×(-1)÷(-1)=______. 2. 计算:-32÷6×16=_______. 3. 计算:(63)36162-⨯=__________.4. 求值:(-1991)-|3-|-31||=______. 5. 计算:1111112612203042-----=_________. 6.n 为正整数,1990n-1991的末四位数字由千位、百位、十位、个位、依次排列组成的四位数是8009.则n 的最小值等于______.7. 计算:19191919199191919191⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=_______.8. 计算:15[(-1989)+(-1990)+(-1991)+(-1992)+(-1993)]=________.9.在(-2)5,(-3)5,512⎛⎫-⎪⎝⎭,513⎛⎫-⎪⎝⎭中,最大的那个数是________.10.不超过(-1.7)2的最大整数是______.11.解方程21101211,_____. 3124x x xx-++-=-=12.求值:355355113113355113⎛⎫---⎪⎝⎭⎛⎫- ⎪⎝⎭=_________.13.一个质数是两位数,它的个位数字与十位数字的差是7,则这个质数是______.14.一个数的相反数的负倒数是119,则这个数是_______.15.如图11,a,b,c,d,e,f均为有理数.图中各行,各列、两条对角线上三个数之和都相等,则ab cd efa b c d e f+++++++=____.第18 页共277 页答案与提示一、选择题1.C 2.B 3.B 4.C 5.C 6.B 7.B 8.B 9.C 10.B 11.D 12.A 13.B 1 4.A 15.D提示:1.整数无最小数,排除A;正数无最小数,排除B;有理数无最小数,排除D.1是最小自然数.选C.有|2|<|-3|,排除C;若2>-3有22<(-3)2,排除D;事实上,a>b必有-a<-b.选B.3.若a=0,7×0=0排除A;7+0=7排除C|0|<7排除D,事实上因为7>0,必有7+a>0+a=a.选B.4.把图形补成一个大矩形,则阴影部分面积等于ab-(a-c)(b-d)=ab-[ab-ad-c(b-d)]=ab-ab+ad+c(b-d)=ad+c(b-d).选C.5.运算结果对负数来说绝对值越小其值越大。
余杭区2009年“假日杯”初中数学竞赛试卷
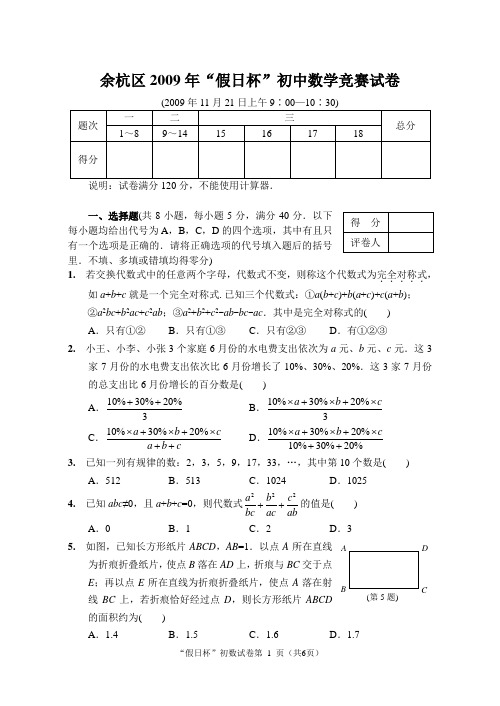
余杭区2009年“假日杯”初中数学竞赛试卷说明:试卷满分120分,不能使用计算器.一、选择题(共8小题,每小题5分,满分40分.以下每小题均给出代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的.请将正确选项的代号填入题后的括号里.不填、多填或错填均得零分)1. 若交换代数式中的任意两个字母,代数式不变,则称这个代数式为完全对称式.....,如a +b +c 就是一个完全对称式.已知三个代数式:①a (b +c )+b (a +c )+c (a +b ); ②a 2bc +b 2ac +c 2ab ;③a 2+b 2+c 2-ab -bc -ac .其中是完全对称式的( ) A .只有①②B .只有①③C .只有②③D .有①②③2. 小王、小李、小张3个家庭6月份的水电费支出依次为a 元、b 元、c 元.这3家7月份的水电费支出依次比6月份增长了10%、30%、20%.这3家7月份的总支出比6月份增长的百分数是( ) A .10%30%20%3++B .10%30%20%3a b c⨯+⨯+⨯C .10%30%20%a b ca b c⨯+⨯+⨯++D .10%30%20%10%30%20%a b c⨯+⨯+⨯++3. 已知一列有规律的数:2,3,5,9,17,33,…,其中第10个数是( )A .512B .513C .1024D .10254. 已知abc ≠0,且a +b +c =0,则代数式222a b c bc ac ab++的值是( )A .0B .1C .2D .35. 如图,已知长方形纸片ABCD ,AB =1.以点A 所在直线为折痕折叠纸片,使点B 落在AD 上,折痕与BC 交于点E ;再以点E 所在直线为折痕折叠纸片,使点A 落在射线BC 上,若折痕恰好经过点D ,则长方形纸片ABCD 的面积约为( ) A .1.4B .1.5C .1.6D .1.7ABCD(第5题)6. 如图,D ,E ,F 分别是等边三角形ABC 的边AB ,BC ,AC 上的点,且DE ⊥BC ,EF ⊥AC ,FD ⊥AB ,则△DEF 的面积与△ABC 的面积之比等于( ) A .1∶3 B .2∶3 C .2∶5D .3∶57. 从甲地到乙地有a ,b ,c 三条道路可走,小王、小李、小张都任选一条道路从甲地到乙地.则恰有两人走同一条a 道路的概率是( )A .23 B .13C .29D .198. 如图,已知△ABC 中,∠ABC =90°,AB =BC ,AC =C ,A ,B 依次在相互平行的三条直线l 1,l 2,l 3上,且l 2,l 3之间的距离 为7 ,那么 l 1,l 2之间的距离为( ) A .5 B .4 C .3D .2二、填空题(共6小题,每小题5分,满分30分)9. 在△ABC 中,AB =AC ,∠BAC =40°,以AB 为边作等腰直角三角形ABD ,使∠BAD =90°,连结DC .则∠BDC 的度数为 . 10. 已知5个数据:8,8,x ,10,10.如果这组数据的某个众数与平均数相等,那么这组数据的中位数是 .11. 已知方程组1122,a x y c a x y c +=⎧⎨+=⎩的解是,,x n y m =⎧⎨=⎩则关于x ,y 的方程组111222,a x y a c a x y a c -=+⎧⎨-=+⎩的解是 (解中不含a 1,c 1,a 2,c 2).12. 侧棱长为15cm的直三棱柱的三个侧面面积分别为2、2和2,则该棱柱上底面的面积为 cm 2.(第6题)E CFDAB(第8题)l 1l 2 l 3ACB13. 一个几何体的三视图如图所示(图中的a ,b ,c 为相应的线段长度),则这个几何体的体积 是 .14. 小王和小李都生于某年的1月份,他们的出生日不是同一天,但都出生于星期日,且小王比小李早出生.两人出生日期之和是30,那么小李的出生日期是1月份的 .三、解答题(共4题,分值依次为12分、12分、12分和14分,满分50分)15. 如图,直四棱柱侧棱长为4cm ,底面是长为5cm 宽为3cm 的长方形.一只蚂蚁从顶点A 出发沿棱柱的表面爬到顶点B .求:(1) 蚂蚁经过的最短路程;(2) 蚂蚁沿着棱爬行(不能重复爬行同一条棱)的最长路程.(第13题)主视图 左视图俯视图ab cB16. 如图,AD 是等边三角形ABC 的高,点E 在AB 上,EF ⊥BC于F ,EG ⊥AC 于G .请判断EF +EG 与AD 的大小,并说明理由.ABC DE GF17. 已知22a ab b=+,222233a b ab b+=+,其中ab·(a-b)≠0,求11a b+的值.路公交车,每隔3分钟从迎面驶来一辆5路公交车.假设每辆5路公交车行驶速度相同,而且公交车终点站每隔固定时间发一辆5路公交车.试求5路公交车发车的间隔时间.。
“《数学周报》杯”2009年全国初中数学竞赛(辽宁赛区北师大版九年级)初赛试题及参考答案

、
选择题 ( 下列每 小题的选项 中 ,
( <2或 >4 A)
3
5 若 函数 y = +6与 y = 的 图 . 1 z
象 如 图 1 示 ,则 有 ( 所
、
只有 一 个 是 正确 的 ,请 将 正 确 选 项 的代 号 填 入 题 号 后 的 括 号 内.本 大题 共 8道 小
4 8
ll 2 28 0
23 2 13 9 15 6 4 2
C
B
图 2
( A) 10 2。 ( C)1 0 5。
( ) 1 5 B 3。 ( D)1 5 2o
[ 0 , 1 0 ) 1 0 50 3 [ o ,l 0 ) 1 o 0 5 7 [ 0 ,l 0 ) 1 0 0 7 9
塑
D A
频率
的 ,还有 捐 5 和 10元 的.如 图 6所 结果如表 2所示 : 0元 0 示的统计 图反映 了不 同捐款 的人数 比例 , 那 么该班学生平均每人捐款
5元
表2
分组 频数
[0 ,9 0 50 0 )
[0 90,110) 0 [ 0 ,1 0 ) 1 o 0 1 3
点 G, F AC于点 F 上 ;过点 曰作 B L H_ AC
于 点 H.
C
的平 分线 ,设 B C=0 ,AC=b E=d ,A , B e E= '则有,=、 一 . E= ,c , / 如
证 明 :如 图 l ,延 长 C O E交 △A C B
的 外 接 圆 于点 D,连接 A . D
显 然 , 当 =9 。 , 此 公 式 即 f= 0时
—
则 者 ・ 有
又 =d e,
历届(1-23)希望杯数学竞赛初一七年级真题及答案(最新整理WORD版)

“希望杯”全国数学竞赛(第1-23届)初一年级/七年级第一/二试题目录1.希望杯第一届(1990年)初中一年级第一试试题............................................. 003-0052.希望杯第一届(1990年)初中一年级第二试试题............................................. 010-0123.希望杯第二届(1991年)初中一年级第一试试题............................................. 016-0204.希望杯第二届(1991年)初中一年级第二试试题............................................. 022-0265.希望杯第三届(1992年)初中一年级第一试试题............................................. 029-0326.希望杯第三届(1992年)初中一年级第二试试题............................................. 034-0407.希望杯第四届(1993年)初中一年级第一试试题............................................. 043-0508.希望杯第四届(1993年)初中一年级第二试试题............................................. 050-0589.希望杯第五届(1994年)初中一年级第一试试题............................................. 057-06610.希望杯第五届(1994年)初中一年级第二试试题 .......................................... 063-07311.希望杯第六届(1995年)初中一年级第一试试题 ........................................... 070-080 12希望杯第六届(1995年)初中一年级第二试试题........................................... 077-08713.希望杯第七届(1996年)初中一年级第一试试题........................................... 086-09814.希望杯第七届(1996年)初中一年级第二试试题............................................. 91-10515.希望杯第八届(1997年)初中一年级第一试试题............................................. 99-11316.希望杯第八届(1997年)初中一年级第二试试题........................................... 106-12017.希望杯第九届(1998年)初中一年级第一试试题........................................... 114-12918.希望杯第九届(1998年)初中一年级第二试试题........................................... 123-13819.希望杯第十届(1999年)初中一年级第二试试题........................................... 130-14720.希望杯第十届(1999年)初中一年级第一试试题........................................... 148-15121.希望杯第十一届(2000年)初中一年级第一试试题....................................... 143-16122.希望杯第十一届(2000年)初中一年级第二试试题....................................... 150-16923.希望杯第十二届(2001年)初中一年级第一试试题....................................... 154-17424.希望杯第十二届(2001年)初中一年级第二试试题....................................... 158-17825.希望杯第十三届(2002年)初中一年级第一试试题....................................... 164-18426.希望杯第十三届(2001年)初中一年级第二试试题....................................... 168-18927.希望杯第十四届(2003年)初中一年级第一试试题....................................... 175-19628.希望杯第十四届(2003年)初中一年级第二试试题....................................... 179-20029.希望杯第十五届(2004年)初中一年级第一试试题 (183)30.希望杯第十五届(2004年)初中一年级第二试试题 (184)31.希望杯第十六届(2005年)初中一年级第一试试题....................................... 213-21832.希望杯第十六届(2005年)初中一年级第二试试题 (184)33.希望杯第十七届(2006年)初中一年级第一试试题....................................... 228-23334.希望杯第十七届(2006年)初中一年级第二试试题....................................... 234-23835.希望杯第十八届(2007年)初中一年级第一试试题....................................... 242-246 26.希望杯第十八届(2007年)初中一年级第二试试题....................................... 248-25137.希望杯第十九届(2008年)初中一年级第一试试题....................................... 252-25638.希望杯第十九届(2008年)初中一年级第二试试题....................................... 257-26239.希望杯第二十届(2009年)初中一年级第一试试题....................................... 263-26620.希望杯第二十届(2009年)初中一年级第二试试题....................................... 267-27121.希望杯第二十一届(2010年)初中一年级第一试试题 ................................... 274-27622.希望杯第二十二届(2011年)初中一年级第二试试题 ................................... 285-28823.希望杯第二十三届(2012年)初中一年级第二试试题 ................................... 288-301希望杯第一届(1990年)初中一年级第1试试题一、选择题(每题1分,共10分)1.如果a ,b 都代表有理数,并且a +b=0,那么 ( )A .a ,b 都是0.B .a ,b 之一是0.C .a ,b 互为相反数.D .a ,b 互为倒数.2.下面的说法中正确的是 ( )A .单项式与单项式的和是单项式.B .单项式与单项式的和是多项式.C .多项式与多项式的和是多项式.D .整式与整式的和是整式.3.下面说法中不正确的是 ( )A. 有最小的自然数. B .没有最小的正有理数.C .没有最大的负整数.D .没有最大的非负数.4.如果a ,b 代表有理数,并且a +b 的值大于a -b 的值,那么( ) A .a ,b 同号. B .a ,b 异号.C .a >0. D .b >0.5.大于-π并且不是自然数的整数有( ) A .2个. B .3个.C .4个. D .无数个.6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身.这四种说法中,不正确的说法的个数是 ( )A .0个.B .1个.C .2个.D .3个.7.a 代表有理数,那么,a 和-a 的大小关系是 ( )A .a 大于-a .B .a 小于-a .C .a 大于-a 或a 小于-a .D .a 不一定大于-a .8.在解方程的过程中,为了使得到的方程和原方程同解,可以在原方程的两边( )A .乘以同一个数.B .乘以同一个整式.C .加上同一个代数式.D .都加上1.9.杯子中有大半杯水,第二天较第一天减少了10%,第三天又较第二天增加了10%,那么,第三天杯中的水量与第一天杯中的水量相比的结果是( )A .一样多.B .多了.C .少了.D .多少都可能.10.轮船往返于一条河的两码头之间,如果船本身在静水中的速度是固定的,那么,当这条河的水流速度增大时,船往返一次所用的时间将( )A .增多.B .减少.C .不变.D .增多、减少都有可能.二、填空题(每题1分,共10分)1. 21115160.01253(87.5)(2)4571615⨯-⨯-÷⨯+--= ______. 2.198919902-198919892=______.3.2481632(21)(21)(21)(21)(21)21+++++-=________. 4. 关于x 的方程12148x x +--=的解是_________. 5.1-2+3-4+5-6+7-8+…+4999-5000=______.6.当x=-24125时,代数式(3x 3-5x 2+6x -1)-(x 3-2x 2+x -2)+(-2x 3+3x 2+1)的值是____. 7.当a=-0.2,b=0.04时,代数式272711()(0.16)()73724a b b a a b --++-+的值是______. 8.含盐30%的盐水有60千克,放在秤上蒸发,当盐水变为含盐40%时,秤得盐水的重是______克.9.制造一批零件,按计划18天可以完成它的13.如果工作4天后,工作效率提高了15,那么完成这批零件的一半,一共需要______天.10.现在4点5分,再过______分钟,分针和时针第一次重合.答案与提示一、选择题1.C 2.D 3.C 4.D 5.C 6.B 7.D 8.D 9.C 10.A提示:1.令a=2,b=-2,满足2+(-2)=0,由此2.x2,2x2,x3都是单项式.两个单项式x3,x2之和为x3+x2是多项式,排除A.两个单项式x2,2x2之和为3x2是单项式,排除B.两个多项式x3+x2与x3-x2之和为2x3是个单项式,排除C,因此选D.3.1是最小的自然数,A正确.可以找到正所以C“没有最大的负整数”的说法不正确.写出扩大自然数列,0,1,2,3,…,n,…,易知无最大非负数,D正确.所以不正确的说法应选C.5.在数轴上容易看出:在-π右边0的左边(包括0在内)的整数只有-3,-2,-1,0共4个.选C.6.由12=1,13=1可知甲、乙两种说法是正确的.由(-1)3=-1,可知丁也是正确的说法.而负数的平方均为正数,即负数的平方一定大于它本身,所以“负数平方不一定大于它本身”的说法不正确.即丙不正确.在甲、乙、丙、丁四个说法中,只有丙1个说法不正确.所以选B.7.令a=0,马上可以排除A、B、C,应选D.8.对方程同解变形,要求方程两边同乘不等于0的数.所以排除A.我们考察方程x-2=0,易知其根为x=2.若该方程两边同乘以一个整式x-1,得(x-1)(x -2)=0,其根为x=1及x=2,不与原方程同解,排除B.若在方程x-2=0两边加上同一个代数式去了原方程x=2的根.所以应排除C.事实上方程两边同时加上一个常数,新方程与原方程同解,对D,这里所加常数为1,因此选D.9.设杯中原有水量为a,依题意可得,第二天杯中水量为a×(1-10%)=0.9a;第三天杯中水量为(0.9a)×(1+10%)=0.9×1.1×a;第三天杯中水量与第一天杯中水量之比为所以第三天杯中水量比第一天杯中水量少了,选C.10.设两码头之间距离为s,船在静水中速度为a,水速为v0,则往返一次所用时间为设河水速度增大后为v,(v>v0)则往返一次所用时间为由于v-v0>0,a+v0>a-v0,a+v>a-v所以(a+v0)(a+v)>(a-v0)(a-v)∴t0-t<0,即t0<t.因此河水速增大所用时间将增多,选A.二、填空题提示:2.198919902-198919892=(19891990+19891989)×(19891990-19891989)=(19891990+19891989)×1=39783979.3.由于(2+1)(22+1)(24+1)(28+1)(216+1)=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)=(22-1)(22+1)(24+1)(28+1)(216+1)=(24-1)(24+1)(28+1)(216+1)=(28-1)(28+1)(216+1)=(216-1)(216+1)=232-1.2(1+x)-(x-2)=8,2+2x-x+2=8解得;x=45.1-2+3-4+5-6+7-8+…+4999-5000=(1-2)+(3-4)+(5-6)+(7-8)+…+(4999-5000)=-2500.6.(3x3-5x2+6x-1)-(x3-2x2+x-2)+(-2x3+3x2+1)=5x+27.注意到:当a=-0.2,b=0.04时,a2-b=(-0.2)2-0.04=0,b+a+0.16=0.04-0.2+0.16=0.8.食盐30%的盐水60千克中含盐60×30%(千克)设蒸发变成含盐为40%的水重x克,即0.001x千克,此时,60×30%=(0.001x)×40%解得:x=45000(克).10.在4时整,时针与分针针夹角为120°即希望杯第一届(1990年)初中一年级第2试试题一、选择题(每题1分,共5分)以下每个题目里给出的A,B,C,D四个结论中有且仅有一个是正确的.请你在括号填上你认为是正确的那个结论的英文字母代号.1.某工厂去年的生产总值比前年增长a%,则前年比去年少的百分数是( )A.a%.B.(1+a)%. C.1100aa+D.100aa+2.甲杯中盛有2m毫升红墨水,乙杯中盛有m毫升蓝墨水,从甲杯倒出a毫升到乙杯里, 0<a<m,搅匀后,又从乙杯倒出a毫升到甲杯里,则这时( )A.甲杯中混入的蓝墨水比乙杯中混入的红墨水少.B.甲杯中混入的蓝墨水比乙杯中混入的红墨水多.C.甲杯中混入的蓝墨水和乙杯中混入的红墨水相同.D.甲杯中混入的蓝墨水与乙杯中混入的红墨水多少关系不定.3.已知数x=100,则( )A.x是完全平方数.B.(x-50)是完全平方数.C.(x-25)是完全平方数.D.(x+50)是完全平方数.4.观察图1中的数轴:用字母a,b,c依次表示点A,B,C对应的数,则111,,ab b a c-的大小关系是( )A.111ab b a c<<-; B.1b a-<1ab<1c; C.1c<1b a-<1ab; D.1c<1ab<1b a-.5.x=9,y=-4是二元二次方程2x2+5xy+3y2=30的一组整数解,这个方程的不同的整数解共有( )A.2组.B.6组.C.12组.D.16组.二、填空题(每题1分,共5分)1.方程|1990x-1990|=1990的根是______.2.对于任意有理数x,y,定义一种运算*,规定x*y=ax+by-cxy,其中的a,b,c表示已知数,等式右边是通常的加、减、乘运算.又知道1*2=3,2*3=4,x*m=x(m≠0),则m 的数值是______.3.新上任的宿舍管理员拿到20把钥匙去开20个房间的门,他知道每把钥匙只能开其中的一个门,但不知道每把钥匙是开哪一个门的钥匙,现在要打开所有关闭着的20个房间,他最多要试开______次.4.当m=______时,二元二次六项式6x2+mxy-4y2-x+17y-15可以分解为两个关于x,y 的二元一次三项式的乘积.5.三个连续自然数的平方和(填“是”或“不是”或“可能是”)______某个自然数的平方.三、解答题(写出推理、运算的过程及最后结果.每题5分,共15分)1.两辆汽车从同一地点同时出发,沿同一方向同速直线行驶,每车最多只能带24桶汽油,途中不能用别的油,每桶油可使一辆车前进60公里,两车都必须返回出发地点,但是可以不同时返回,两车相互可借用对方的油.为了使其中一辆车尽可能地远离出发地点,另一辆车应当在离出发地点多少公里的地方返回?离出发地点最远的那辆车一共行驶了多少公里?2.如图2,纸上画了四个大小一样的圆,圆心分别是A,B,C,D,直线m通过A,B,直线n通过C,D,用S表示一个圆的面积,如果四个圆在纸上盖住的总面积是5(S-1),直线m,n之间被圆盖住的面积是8,阴影部分的面积S1,S2,S3满足关系式S3=13S1=13S2,求S.3.求方程11156x y z++=的正整数解.答案与提示一、选择题1.D 2.C 3.C 4.C 5.D提示:1.设前年的生产总值是m,则去年的生产总值是前年比去年少这个产值差占去年的应选D.2.从甲杯倒出a毫升红墨水到乙杯中以后:再从乙杯倒出a毫升混合墨水到甲杯中以后:乙杯中含有的红墨水的数量是①乙杯中减少的蓝墨水的数量是②∵①=②∴选C.∴x-25=(10n+2+5)2可知应当选C.4.由所给出的数轴表示(如图3):可以看出∴①<②<③,∴选C.5.方程2x2+5xy+3y2=30可以变形为(2x+3y)(x+y)=1·2·3·5∵x,y是整数,∴2x+3y,x+y也是整数.由下面的表可以知道共有16个二元一次方程组,每组的解都是整数,所以有16组整数组,应选D.二、填空题提示:1.原方程可以变形为|x-1|=1,即x-1=1或-1,∴x=2或0.2.由题设的等式x*y=ax+by-cxy及x*m=x(m≠0)得a·0+bm-c·0·m=0,∴bm=0.∵m≠0,∴b=0.∴等式改为x*y=ax-cxy.∵1*2=3,2*3=4,解得a=5,c=1.∴题设的等式即x*y=5x-xy.在这个等式中,令x=1,y=m,得5-m=1,∴m=4.3.∵打开所有关闭着的20个房间,∴最多要试开4.利用“十字相乘法”分解二次三项式的知识,可以判定给出的二元二次六项式6x2+mxy-4y2-x+17y-15中划波浪线的三项应当这样分解:3x -52x +3现在要考虑y,只须先改写作然后根据-4y2,17y这两项式,即可断定是:由于(3x+4y-5)(2x-y+3)=6x2+5xy-4y2-x+17y-15就是原六项式,所以m=5.5.设三个连续自然数是a-1,a,a+1,则它们的平方和是(a-1)2+a2+(a+1)2=3a2+2,显然,这个和被3除时必得余数2.另一方面,自然数被3除时,余数只能是0或1或2,于是它们可以表示成3b,3b+1,3b+2(b是自然数)中的一个,但是它们的平方(3b)2=9b2(3b+1)2=9b2+6b+1,(3b+2)2=9b2+12b+4=(9b2+12b+3)+1被3除时,余数要么是0,要么是1,不能是2,所以三个连续自然数平方和不是某个自然数的平方.三、解答题1.设两辆汽车一为甲一为乙,并且甲用了x升汽油时即回返,留下返程需的x桶汽油,将多余的(24-2x)桶汽油给乙.让乙继续前行,这时,乙有(24-2x)+(24-x)=48-3x桶汽油,依题意,应当有48-3x≤24,∴x≥8.甲、乙分手后,乙继续前行的路程是这个结果中的代数式30(48-4x)表明,当x的值愈小时,代数式的值愈大,因为x≥8,所以当x=8时,得最大值30(48-4·8)=480(公里),因此,乙车行驶的路程一共是2(60·8+480)=1920(公里).2.由题设可得即2S-5S3=8……②∴x,y,z都>1,因此,当1<x≤y≤z时,解(x,y,z)共(2,4,12),(2,6,6),(3,3,6),(3,4,4)四组.由于x,y,z在方程中地位平等.所以可得如下表所列的15组解.希望杯第二届(1991年)初中一年级第1试试题一、选择题(每题1分,共15分)以下每个题目的A,B,C,D四个结论中,仅有一个是正确的,请在括号内填上正确的那个结论的英文字母代号.1.数1是( )A.最小整数.B.最小正数.C.最小自然数.D.最小有理数.2.若a>b,则( )A.11a b; B.-a<-b.C.|a|>|b|.D.a2>b2.3.a为有理数,则一定成立的关系式是( )A.7a>a.B.7+a>a.C.7+a>7.D.|a|≥7.4.图中表示阴影部分面积的代数式是( )A.ad+bc.B.c(b-d)+d(a-c).C.ad+c(b-d).D.ab-cd.5.以下的运算的结果中,最大的一个数是( )A.(-13579)+0.2468; B.(-13579)+12468;C.(-13579)×12468; D.(-13579)÷124686.3.1416×7.5944+3.1416×(-5.5944)的值是( ) A.6.1632. B.6.2832.C.6.5132.D.5.3692.7.如果四个数的和的14是8,其中三个数分别是-6,11,12,则笫四个数是( )A.16. B.15. C.14. D.13.8.下列分数中,大于-13且小于-14的是( )A.-1120; B.-413; C.-316; D.-617.9.方程甲:34(x-4)=3x与方程乙:x-4=4x同解,其根据是( )A.甲方程的两边都加上了同一个整式x.B.甲方程的两边都乘以43x;C. 甲方程的两边都乘以43; D. 甲方程的两边都乘以34.10.如图: ,数轴上标出了有理数a,b,c的位置,其中O是原点,则111,,a b c的大小关系是( ) A.111a b c>>; B.1b >1c >1a ; C. 1b >1a >1c ; D. 1c >1a >1b .11.方程522.2 3.7x =的根是( ) A .27. B .28. C .29. D .30. 12.当x=12,y=-2时,代数式42x y xy -的值是( )A .-6.B .-2.C .2.D .6.13.在-4,-1,-2.5,-0.01与-15这五个数中,最大的数与绝对值最大的那个数的乘积是( )A .225.B .0.15.C .0.0001.D .1.14.不等式124816x x x xx ++++>的解集是( ) A .x <16. B .x >16.C .x <1. D.x>-116. 15.浓度为p%的盐水m 公斤与浓度为q%的盐水n 公斤混合后的溶液浓度是 ( ) A.%2p q +; B.()%mp nq +; C.()%mp nq p q ++;D.()%mp nq m n++.二、填空题(每题1分,共15分)1. 计算:(-1)+(-1)-(-1)×(-1)÷(-1)=______. 2. 计算:-32÷6×16=_______. 3. 计算:(63)36162-⨯=__________.4. 求值:(-1991)-|3-|-31||=______. 5. 计算:1111112612203042-----=_________. 6.n 为正整数,1990n -1991的末四位数字由千位、百位、十位、个位、依次排列组成的四位数是8009.则n 的最小值等于______.7. 计算:19191919199191919191⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=_______.8. 计算:15[(-1989)+(-1990)+(-1991)+(-1992)+(-1993)]=________.9.在(-2)5,(-3)5,512⎛⎫-⎪⎝⎭,513⎛⎫-⎪⎝⎭中,最大的那个数是________.10.不超过(-1.7)2的最大整数是______.11.解方程21101211,_____. 3124x x xx-++-=-=12.求值:355355113113355113⎛⎫---⎪⎝⎭⎛⎫- ⎪⎝⎭=_________.13.一个质数是两位数,它的个位数字与十位数字的差是7,则这个质数是______.14.一个数的相反数的负倒数是119,则这个数是_______.15.如图11,a,b,c,d,e,f均为有理数.图中各行,各列、两条对角线上三个数之和都相等,则ab cd efa b c d e f+++++++=____.答案与提示一、选择题1.C 2.B 3.B 4.C 5.C 6.B 7.B 8.B 9.C 10.B 11.D 12.A 13.B 1 4.A 15.D提示:1.整数无最小数,排除A;正数无最小数,排除B;有理数无最小数,排除D.1是最小自然数.选C.有|2|<|-3|,排除C;若2>-3有22<(-3)2,排除D;事实上,a>b必有-a<-b.选B.3.若a=0,7×0=0排除A;7+0=7排除C|0|<7排除D,事实上因为7>0,必有7+a>0+a=a.选B.4.把图形补成一个大矩形,则阴影部分面积等于ab-(a-c)(b-d)=ab-[ab-ad-c(b-d)]=ab-ab+ad+c(b-d)=ad+c(b-d).选C.5.运算结果对负数来说绝对值越小其值越大。
2009年全国 初中数学联赛(含答案)

12009年全国初中数学联合竞赛试题参考答案第一试一、选择题(本题满分42分,每小题7分)1.设71a =,则32312612a a a +--=( )A .24B .25C .4710D .4712【解析】 A .由()217a +=,有2226,62a a a a +==-.于是32312612a a a +--()()3621262612a a a a =-+---()2261212621224a a a a =+-=+-=2.在ABC △中,最大角A ∠是最小角C ∠的两倍,且7AB =,8AC =,则BC =( )A .2B .10C 105D .73【解析】 C .做A ∠的角平分线交BC 边于D .于是78AB BD AC DC ==.不妨设7,8BD x DC x ==,由BAD BAC △∽△,有BD AB AB BC =,即77715x x =,于是715x ,15105BC x =3.用[]x 表示不大于x 的最大整数,则方程[]2230x x --=的解的个数为( )2A .1B .2C .3D .4【解析】 C .原问题等价于函数23y x =-与函数[]2y x =的图像的交点个数问题.观察出交点个数为3个.方程的解分别为2,3x x =-=,另一个位于2,3之间.4.设正方形ABCD 的中点为点O ,在以五个数A 、B 、C 、D 、O 为顶点所构成的所有三角形中任意取出两个,它们的面积相等的概率为( )A .314B .37C .12D .47【解析】 B .不妨设三角形边长为1,则三角形的面积有两种,一种是14,形如ABO △,有4个;一种是12,形如ABD △,有4个.于是对于这8个三角形,先选出任意一个,再选出其余7个三角形中面积和它相等的三角形(共3个)中的一个,概率为37.5.如图,在矩形ABCD 中,3AB =,2BC =,以BC 为直径在矩形内作半圆, 自点A 作半圆的切线AE ,则sin CBE ∠=( )A 6B .23C .13D 103ECBDA【解析】 D .取BC 中点F ,连接AF ,则CBE BAF ∠=∠,于是2210sin sin 13CBE BAF ∠=∠==+6.设n 是大于1909的正整数,使得19092009n n--为完全平方数的n 的个数是( )A .3B .4C .5D .6【解析】 B .由1909100120092009n n n -=-+--,而1002009n-可能取整数2,5,4,10,25,50,100.若10012009n --为完全平方数,则有1002,5,10,502009n=-.于是这样的n 有4个.二、填空题(本题满分28分,每小题7分)1.已知t 是实数,若a ,b 是关于x 的一元二次方程2210x x t -+-=的两个非负实根,则()()2211a b --的最小值是 .【解析】3-.2,1a b ab t +==-,又由0∆≥知2t 1≤≤.于是()()()222222111a b a b a b --=+-+424t =-.于是当1t =时代数式有最小值3-.2.设D 是ABC △ 的边AB 上的一点,作DE BC ∥交AC 于点E ,作DF AC ∥交BC 于点F ,已知ADE △、DBF △的面积分别为m 和n ,则四边形DECF 的面积为 .【解析】 2mn ADE BDF △∽△,相似比为ADDB.观察到DEF △的面积等于m 和n 的等比中项,所以所求答案为2mn3.如果实数a ,b 满足条件221a b +=,221221a b a b a -+++=-,则a b += .【解析】 1-.分情况讨论,可得221221a b a b a -+++=-或22(12)21a b a b a --+++=-.如果是第一种,则222b b a +=-,消去a 可得2230b b --=,可得1b =-或32.经检验,1,0b a =-=符合,所求结果为1-;如果是第二种,则224a b b a -=-.因为去绝对值符号的时候有120a b -+≤,即21a b +≥,而10b +≥,则设法凑出含有1b +的形式.因为2240a a b b +--=,所以2222114()22a ab b a b +--++=,即22238(1)4a a b a +=+≤,所以8a ≥或0a ≤,因此只能有0a =,和第一种情况是同一个解.4.已知a ,b 是正整数,且满足15152a b 是整数,则这样的有序数对()a b ,共有 对.5【解析】 7.显然两个根式的值都是有理数(否则把它平方即可发现).穷举,可能是1+1,112+, 1122+,1144+,1136+,考虑顺序,共7种.第二试(A )一、(本题满分20分)已知二次函数()20y x bx c c =++<的图象与x 轴的交点分别为A 、B ,与y 轴的交点为C .设ABC △的外接圆的圆心为点P .⑴ 证明:P ⊙与y 轴的另一个交点为定点.⑵ 如果AB 恰好为P ⊙的直径且2ABC S =△,求b 和c 的值. 【解析】 ⑴ 易求得点C 的坐标为()0c ,, 设()10A x ,,()20B x ,,则12x x b +=-,12x x c =. 设P ⊙与y 轴的另一个交点为D ,由于AB 、CD 是P ⊙的两条相交弦,它们的交点为点O ,所以OA OB OC OD ⨯=⨯则121x x c OA OB OD OC c c⨯====. 因为0c <,所以点C 在y 轴的负半轴上,从而点D 在y 轴的正半轴上,旗开得胜6所以点D 为定点,它的坐标为()01,. ⑵ 因为AB CD ⊥,如果AB 恰好为P ⊙的直径,则C 、D 关于点O 对称,所以点C 的坐标为()01-,, 即1c =-.又()()222121212444AB x x x x x x b c b =-+---+所以21141222ABC S AB OC b =⋅+⋅△, 解得23b =±.二、(本题满分25分)设CD 是直角三角形ABC 的斜边AD 上的高,1I 、2I 分别是ADC △、BDC △的内心,3AC =,4BC =,求12I I .I 2I 1CABBACE DFI 1I 2【解析】 作1I E AB ⊥于E ,2I F AB ⊥于F .旗开得胜7在直角三角形ABC 中,3AC =,4BC =,225AB AC BC +=.又CD AB ⊥,由射影定理可得295AC AD AB ==, 故165BD AB AD =-=,22125CD AC AD -. 因为1I E 为直角三角形ACD 的内切圆的半径,所以()11325I E AD CD AC =+-=. 连接1DI 、2DI ,则1DI 、2DI 分别是ADC ∠和BDC ∠的平分线,所以112245I DC I DA I DC I DB ∠=∠=∠=∠=o,故1290I DI ∠=o,所以12I D I D ⊥,1113325sin sin 45I E DI ADI ===∠o . 同量,可求得245I F =,242DI . 所以2212122I I DI DI +三、(本题满分25分)已知a ,b ,c 为正数,满足如下两个条件:32a b c ++= ①14b c a c a b a b c bc ca ab +-+-+-++= ②旗开得胜8a b c【解析】证法1:将①②两式相乘,得()8b c a c a b a b c a b c bcca ab +-+-+-⎛⎫++++= ⎪⎝⎭,即()()()2222228b c a c a b a b c bccaab+-+-+-++=,即()()()222222440b c a c a b a b c bccaab+-+-+--+-+=,即()()()2222220b c a c a b a b c bccaab----+-++=,即()()()()()()0b c a b c a c a b c a b a b c a b c bccaab-+---+--+++-++=,即()()()()0b c a ab c a b c a b c a b c abc-+----++++=⎡⎤⎣⎦,即()22220b c a ab a b c abc-+⎡⎤--+=⎣⎦,即()()220b c a c a b abc-+⎡⎤--=⎣⎦,即()()()0b c a c a b c a b abc-++--+=,所以0b c a -+=或0c a b +-=或0c a b -+=,即b a c +=或c a b +=或c b a +=.a b c9证法2:结合①式,由②式可得32232232214a b c bc ca ab ---++=, 变形,得()2221102424a b c abc -++=③又由①式得()21024a b c ++=,即()22210242a b c ab bc ca ++=-++,代入③式,得()110242102424ab bc ca abc --++=⎡⎤⎣⎦, 即()164096abc ab bc ca =++-.()()()()()331616161625616409625632160a b c abc ab bc ca a b c ---=-+++++-=-+⨯-=,所以16a =或16b =或16c =.结合①式可得b a c +=或c a b +=或c b a +=.a b c第二试(B )一、(本题满分20分)已知二次函数()20y x bx c c =++<的图象与x 轴的交点分别为A 、B ,与y 轴的交点为C .设ABC △的外接圆的圆心为点P .10⑴ 证明:P ⊙与y 轴的另一个交点为定点.⑵ 如果AB 恰好为P ⊙的直径且2ABC S =△,求b 和c 的值. 【解析】 ⑴ 易求得点C 的坐标为()0c ,, 设()10A x ,,()20B x ,,则12x x b +=-,12x x c =. 设P ⊙与y 轴的另一个交点为D ,由于AB 、CD 是P ⊙的两条相交弦,它们的交点为点O ,所以OA OB OC OD ⨯=⨯则121x x c OA OB OD OC c c⨯====. 因为0c <,所以点C 在y 轴的负半轴上,从而点D 在y 轴的正半轴上, 所以点D 为定点,它的坐标为()01,. ⑵ 因为AB CD ⊥,如果AB 恰好为P ⊙的直径,则C 、D 关于点O 对称,所以点C 的坐标为()01-,, 即1c =-.又()()222121212444AB x x x x x x b c b =-+---+所以21141222ABC S AB OC b =⋅+⋅△, 解得23b =±.旗开得胜11二、(本题满分25分)已知ABC △中,90ACB ∠=o ,AB 边上的高线CH 与ABC △的两条内角平分线AM 、BN 分别交于P 、Q 两点PM 、QN 的中点分别为E 、F .求证:DE AB ∥.ACBHNMF P EQQEP F MNHBCA【解析】 因为BN 是ABC ∠的平分线,所以ABN CBN ∠=∠.又因为CH AB ⊥,所以9090CQN BQH ABN CBN CNB ∠=∠=-∠=-∠=∠o o ,因此CQ NC =.又F 是QN 的中点,所以CF QN ⊥,所以90CFB CHB ∠==∠o ,因此C 、F 、H 、B 四点共圆.又FBH FBC ∠=∠,所以FC FH =,故点F 在CH 的中垂线上.、同理可证,点E 在CH 的中垂线上.旗开得胜12因此EF CH ⊥,又AB CH ⊥,所以EF AB ∥.三、(本题满分25分)已知a ,b ,c 为正数,满足如下两个条件:32a b c ++= ①14b c a c a b a b c bc ca ab +-+-+-++= ②a b c【解析】证法1:将①②两式相乘,得()8b c a c a b a b c a b c bc ca ab +-+-+-⎛⎫++++= ⎪⎝⎭, 即()()()2222228b c a c a b a b c bccaab+-+-+-++=,即()()()222222440b c a c a b a b c bccaab+-+-+--+-+=,即()()()2222220b c a c a b a b c bccaab----+-++=,即()()()()()()0b c a b c a c a b c a b a b c a b c bccaab-+---+--+++-++=,13即()()()()0b c a ab c a b c a b c a b c abc-+----++++=⎡⎤⎣⎦,即()22220b c a ab a b c abc-+⎡⎤--+=⎣⎦,即()()220b c a c a b abc-+⎡⎤--=⎣⎦,即()()()0b c a c a b c a b abc-++--+=,所以0b c a -+=或0c a b +-=或0c a b -+=,即b a c +=或c a b +=或c b a +=.a b c证法2:结合①式,由②式可得32232232214a b c bc ca ab ---++=, 变形,得()2221102424a b c abc -++=③又由①式得()21024a b c ++=,即()22210242a b c ab bc ca ++=-++,代入③式,得()110242102424ab bc ca abc --++=⎡⎤⎣⎦, 即()164096abc ab bc ca =++-.()()()()()331616161625616409625632160a b c abc ab bc ca a b c ---=-+++++-=-+⨯-=,所以16a =或16b =或16c =.结合①式可得b a c +=或c a b +=或c b a +=.a b c第二试(C)一、(本题满分20分)△的已知二次函数()20y x bx c c=++<的图象与x轴的交点分别为A、B,与y轴的交点为C.设ABC 外接圆的圆心为点P.⊙与y轴的另一个交点为定点.⑴ 证明:P1415⑵ 如果AB 恰好为P ⊙的直径且2ABC S =△,求b 和c 的值. 【解析】 ⑴ 易求得点C 的坐标为()0c ,, 设()10A x ,,()20B x ,,则12x x b +=-,12x x c =. 设P ⊙与y 轴的另一个交点为D ,由于AB 、CD 是P ⊙的两条相交弦,它们的交点为点O ,所以OA OB OC OD ⨯=⨯则121x x c OA OB OD OC c c⨯====. 因为0c <,所以点C 在y 轴的负半轴上,从而点D 在y 轴的正半轴上, 所以点D 为定点,它的坐标为()01,. ⑵ 因为AB CD ⊥,如果AB 恰好为P ⊙的直径,则C 、D 关于点O 对称,所以点C 的坐标为()01-,, 即1c =-.又()()222121212444AB x x x x x x b c b =-+---+所以21141222ABC S AB OC b =⋅+⋅△, 解得23b =±.16二、(本题满分25分)已知ABC △中,90ACB ∠=o ,AB 边上的高线CH 与ABC △的两条内角平分线AM 、BN 分别交于P 、Q 两点PM 、QN 的中点分别为E 、F .求证:DE AB ∥.ACBHNMF P EQQEP F MNHBCA【解析】 因为BN 是ABC ∠的平分线,所以ABN CBN ∠=∠.又因为CH AB ⊥,所以9090CQN BQH ABN CBN CNB ∠=∠=-∠=-∠=∠o o ,因此CQ NC =.又F 是QN 的中点,所以CF QN ⊥,所以90CFB CHB ∠==∠o ,因此C 、F 、H 、B 四点共圆.又FBH FBC ∠=∠,所以FC FH =,故点F 在CH 的中垂线上.、同理可证,点E 在CH 的中垂线上.因此EF CH ⊥,又AB CH ⊥,所以EF AB ∥.17三、(本题满分25分)已知a ,b ,c 为正数,满足如下两个条件:32a b c ++= ①14b c a c a b a b c bc ca ab +-+-+-++= ②a b c【解析】解法1:将①②两式相乘,得()8b c a c a b a b c a b c bc ca ab +-+-+-⎛⎫++++= ⎪⎝⎭, 即()()()2222228b c a c a b a b c bccaab+-+-+-++=,即()()()222222440b c a c a b a b c bccaab+-+-+--+-+=,即()()()2222220b c a c a b a b c bccaab----+-++=,即()()()()()()0b c a b c a c a b c a b a b c a b c bccaab-+---+--+++-++=,即()()()()0b c a ab c a b c a b c a b c abc-+----++++=⎡⎤⎣⎦,18即()22220b c a ab a b c abc-+⎡⎤--+=⎣⎦,即()()220b c a c a b abc-+⎡⎤--=⎣⎦, 即()()()0b c a c a b c a b abc-++--+=,所以0b c a -+=或0c a b +-=或0c a b -+=,即b a c +=或c a b +=或c b a +=.a b c 90o .解法2:结合①式,由②式可得32232232214a b c bc ca ab ---++=, 变形,得()2221102424a b c abc -++=③又由①式得()21024a b c ++=,即()22210242a b c ab bc ca ++=-++,代入③式,得()110242102424ab bc ca abc --++=⎡⎤⎣⎦, 即()164096abc ab bc ca =++-.()()()()()331616161625616409625632160a b c abc ab bc ca a b c ---=-+++++-=-+⨯-=,所以16a =或16b =或16c =.结合①式可得b a c +=或c a b +=或c b a +=.a b c 90o .19。
2009年全国初中数学竞赛武汉赛区预赛试题

2
一
竞赛 全国初中数学
)
武 汉 赛 区预 赛试 题
7 .如 图3 所示 , AAE 是 以正方 形A D的 对角线 为边 的等 C BC
边 三 角 形 , 上A曰 交 且 曰的 延 长 线 于 点 F,则 8 瑚
、
选择 题 ( 小题6 , 吩 ) 每 分 共3
1 一个正数 . 的两个平方根分别是叶l 与 , 的值为 ( 则n
A > 2 B <2 . C. > 2 -
)
1 已 知方 程 +础 一 l O m是 整数 ) 两 个 不相 等 的正 Q :, m+ - ( 有 整 数根 , 则m= .
D.x - < 2
二 、 空题 ( 填 每小题 6 , 0 ) 分 共3分
6 对 于任意 实数 。 , , , , c d 规定 了一种 运算
则 { 5 l2时 ,= 当3 _= 5 I 4 2
58
重 蕊
编 者 语 :亲 爱 的 同 学 们 本 刊 2 0 0 9 年 第 1 1 期 数 独 游
,
戏 正 在 火 热 进 行 中 速 速 挑 战 有精 美礼 品 等 着你 哦 !
, ,
数 独
3
(s u d 0 ㈨
.
第
,
A B
,
-
90
F
,
它 的 内切 圆 分 别
,
( 1 ) 求s 的最 小 值
与边B
C CA A B
,
,
一
相 切 于 点D E
, ,
,
连 结A D 且 A D 与 内
,
( 2 ) 若 对 任何 实 数z y都有 s
,
≥
全国初中数学竞赛(联赛)分类题型详解-几何

历年(95-10)年全国数学竞赛(联赛)分类题型详解 - 几何(1)选择题(30道题)1. 如果边长顺次为25、39、52与60的四边形内接于一圆,那么此圆的周长为[ ]A.62πB.63π C.64πD.65π1995年全国初中数学联赛试题答案: D详解:四个选择支表明,圆的周长存在且唯一,从而直径也存在且唯一.又由AB2+AD2 =252+602 =52×(52+122)=52×132=(32+42)×132 =392+522 =BC2+CD2故可取BD=65为直径,得周长为65π,选D.2. 设AB是⊙O的一条弦,CD是⊙O的直径,且与弦AB相交,记M=|S△CAB-S△DAB|,N=2S△OAB,则[ ]A.M>N B.M=N C.M<N D.M、N的大小关系不确定1995年全国初中数学联赛试题答案: B详解1: 不失一般性,设CE≥ED,在CE上取CF=ED,则有OF=OE,且S△ACE-S△ADE=S△AEF=2S△AOE.同理,S△BCE-S△BDE=2S△BOE.相加,得S△ABC-S△DAB=2S△OAB,即M=N.选B.详解2: 若过C、D、O分别作AB的垂线(图3),CE⊥AB、DF⊥AB、OL⊥AB,垂足分别为E、F、L.连CF、DE,可得梯形CEDF.又由垂径分弦定理,知L是EF的中点.根据课本上做过的一道作业:梯形对角线中点的连线平行底边,并且等于两底差的一半,有|CE-DF|=2OL.即M=N.选B.3.如图,A是半径为1的圆O外的一点,OA=2,AB是圆O的切线,B是切点,弦BC∥OA,连结AC,则阴影部分的面积等于[ ]1996年全国初中数学联赛试题答案: B4.如果一个三角形的面积和周长都被一直线所平分,那么该直线必通过这个三角形的[ ]A.内心B.外心C.重心D.垂心1996年全国初中数学联赛试题答案: A5.如果20个点将某圆周20等分,那么顶点只能在这20个点中选取的正多边形的个数有[ ]A.4个B.8个 C.12个 D.24个1996年全国初中数学联赛试题答案: C6. 在△ABC中,已知BD和CE分别是两边上的中线,并且BD⊥CE,BD=4,CE=6,那么△ABC的面积等于()(A)12(B)14(C)16(D)181998年全国数学联赛试卷答案: C详解: 连ED,则又因为DE是△ABC两边中点连线,所以故选C.7.一个凸n边形的内角和小于1999°,那么n的最大值是().A.11 B.12 C.13 D.141999年全国初中数学竞赛答案: C8.在三角形ABC 中,D 是边BC 上的一点,已知AC=5,AD=6,BD=10,CD=5,那么三角形ABC 的面积是( ).A .30B .36C .72D .1251999年全国初中数学竞赛答案: B9.在正五边形ABCDE 所在的平面内能找到点P ,使得△PCD 与△BCD 的面积相等,并且△ABP 为等腰三角形,这样的不同的点P 的个数为( ).A .2B .3C .4D .51999年全国初中数学竞赛答案: D10. 设a ,b ,c 分别是△ABC 的三边的长,且cb a ba b a +++=,则它的内角∠A 、∠B 的关系是( )。
初二数学竞赛试题7套整理版(含答案)

1 2009年初中数学(初二组)初赛试卷 01一、选择题(本大题满分42分,每小题7分)1、下列名人中:①比尔·盖茨②高斯③袁隆平④诺贝尔⑤陈景润⑥华罗庚⑦高尔基⑧爱因斯坦,其中是数学家的是()A .①④⑦B.③④⑧C.②⑥⑧D.②⑤⑥2、已知111,,bc a a b c a b c +=+=+¹¹则a 2b 2c 2=( )A.5B.3.5C.1D.0.53、在直角坐标系中,若一点的纵横坐标都是整数,则称该点为整点。
设k 为整数,当直线2y x =-与y kx k =+的交点为整点时,的交点为整点时,k k 的值可以取()A .4个 B.5个 C.6个 D.7个4、如图,边长为1的正方形ABCD 绕A 逆时针旋转300到正方形AB ‘C ’D ‘,图中阴影部分的面积为()A.331-B.33C.341-D.125、已知()421M p p q =+,其中,p q 为质数,且满足29q p -=,则M =()A.2009B.2005C.2003D.2000(第4题图)(第6题图)6、四边形ABCD 中0060,90,DAB B D Ð=Ð=Ð=1,2BC CD ==,则对角线AC 的长为()A.21B.213 C.2213 D.5213二、填空题(本大题满分28分,每小题7分)1、如果有2009名学生排成一列,按1、2、3、4、5、4、3、2、1、2、3、4、5、4、3、2、1的规律报数,那么第2009名学生所报的数是。
2、已知,,a b c 满足()222242322a b a b a c ac -+++-++=+,则a b c -+的值为______ 3、已知如图,在矩形ABCD 中,AE BD ^,垂足为E ,030ADB Ð=且43BC =,则ECD 的面积为_____ (第3题图)(第4题图)DA B CKC BAB ′C ′DD ′E ABCDEF ABCD2x2xx xx4、有一等腰钝角三角形纸片,若能从一个顶点出发,将其剪成两个等腰三角形纸片,则等腰三角形纸片的顶角为_______度。
历届(1-24)希望杯数学竞赛初一七年级真题及答案

“希望杯”全国数学竞赛(第1-24届)初一年级/七年级第一/二试题目录1.希望杯第一届(1990年)初中一年级第一试试题............................................. 003-0052.希望杯第一届(1990年)初中一年级第二试试题............................................. 010-0123.希望杯第二届(1991年)初中一年级第一试试题............................................. 015-0204.希望杯第二届(1991年)初中一年级第二试试题............................................. 021-0265.希望杯第三届(1992年)初中一年级第一试试题............................................. 028-0326.希望杯第三届(1992年)初中一年级第二试试题............................................. 033-0407.希望杯第四届(1993年)初中一年级第一试试题............................................. 042-0508.希望杯第四届(1993年)初中一年级第二试试题............................................. 049-0589.希望杯第五届(1994年)初中一年级第一试试题............................................. 056-06610.希望杯第五届(1994年)初中一年级第二试试题 .......................................... 062-07311.希望杯第六届(1995年)初中一年级第一试试题 ........................................... 069-080 12希望杯第六届(1995年)初中一年级第二试试题........................................... 076-08713.希望杯第七届(1996年)初中一年级第一试试题........................................... 085-09814.希望杯第七届(1996年)初中一年级第二试试题............................................. 90-10515.希望杯第八届(1997年)初中一年级第一试试题............................................. 98-11316.希望杯第八届(1997年)初中一年级第二试试题........................................... 105-12017.希望杯第九届(1998年)初中一年级第一试试题........................................... 113-12918.希望杯第九届(1998年)初中一年级第二试试题........................................... 122-13819.希望杯第十届(1999年)初中一年级第二试试题........................................... 129-14720.希望杯第十届(1999年)初中一年级第一试试题........................................... 148-15121.希望杯第十一届(2000年)初中一年级第一试试题....................................... 142-16122.希望杯第十一届(2000年)初中一年级第二试试题....................................... 149-16923.希望杯第十二届(2001年)初中一年级第一试试题....................................... 153-17424.希望杯第十二届(2001年)初中一年级第二试试题....................................... 157-17825.希望杯第十三届(2002年)初中一年级第一试试题....................................... 163-18426.希望杯第十三届(2001年)初中一年级第二试试题....................................... 167-18927.希望杯第十四届(2003年)初中一年级第一试试题....................................... 174-19628.希望杯第十四届(2003年)初中一年级第二试试题....................................... 178-20029.希望杯第十五届(2004年)初中一年级第一试试题 (182)30.希望杯第十五届(2004年)初中一年级第二试试题 (183)31.希望杯第十六届(2005年)初中一年级第一试试题....................................... 213-21832.希望杯第十六届(2005年)初中一年级第二试试题 (183)33.希望杯第十七届(2006年)初中一年级第一试试题....................................... 228-23334.希望杯第十七届(2006年)初中一年级第二试试题....................................... 234-23835.希望杯第十八届(2007年)初中一年级第一试试题....................................... 242-246 26.希望杯第十八届(2007年)初中一年级第二试试题....................................... 248-25137.希望杯第十九届(2008年)初中一年级第一试试题....................................... 252-25638.希望杯第十九届(2008年)初中一年级第二试试题....................................... 257-26239.希望杯第二十届(2009年)初中一年级第一试试题....................................... 263-26620.希望杯第二十届(2009年)初中一年级第二试试题....................................... 267-27121.希望杯第二十一届(2010年)初中一年级第一试试题 ................................... 274-27622.希望杯第二十二届(2011年)初中一年级第二试试题 ................................... 270-27323.希望杯第二十三届(2012年)初中一年级第二试试题 ................................... 270-273 23.希望杯第二十四届(2013年)初中一年级第二试试题 ................................... 274-281 23.希望杯第二十四届(2013年)初中一年级第二试试题 ................................... 274-281希望杯第一届(1990年)初中一年级第1试试题一、选择题(每题1分,共10分)1.如果a ,b 都代表有理数,并且a +b=0,那么 ( )A .a ,b 都是0.B .a ,b 之一是0.C .a ,b 互为相反数.D .a ,b 互为倒数.2.下面的说法中正确的是 ( )A .单项式与单项式的和是单项式.B .单项式与单项式的和是多项式.C .多项式与多项式的和是多项式.D .整式与整式的和是整式.3.下面说法中不正确的是 ( )A. 有最小的自然数. B .没有最小的正有理数.C .没有最大的负整数.D .没有最大的非负数.4.如果a ,b 代表有理数,并且a +b 的值大于a -b 的值,那么( ) A .a ,b 同号. B .a ,b 异号.C .a >0. D .b >0.5.大于-π并且不是自然数的整数有( ) A .2个. B .3个.C .4个. D .无数个.6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身.这四种说法中,不正确的说法的个数是 ( )A .0个.B .1个.C .2个.D .3个.7.a 代表有理数,那么,a 和-a 的大小关系是 ( )A .a 大于-a .B .a 小于-a .C .a 大于-a 或a 小于-a .D .a 不一定大于-a .8.在解方程的过程中,为了使得到的方程和原方程同解,可以在原方程的两边( )A .乘以同一个数.B .乘以同一个整式.C .加上同一个代数式.D .都加上1.9.杯子中有大半杯水,第二天较第一天减少了10%,第三天又较第二天增加了10%,那么,第三天杯中的水量与第一天杯中的水量相比的结果是( )A .一样多.B .多了.C .少了.D .多少都可能.10.轮船往返于一条河的两码头之间,如果船本身在静水中的速度是固定的,那么,当这条河的水流速度增大时,船往返一次所用的时间将( )A .增多.B .减少.C .不变.D .增多、减少都有可能.二、填空题(每题1分,共10分)1. 21115160.01253(87.5)(2)4571615⨯-⨯-÷⨯+--= ______. 2.198919902-198919892=______.3.2481632(21)(21)(21)(21)(21)21+++++-=________. 4. 关于x 的方程12148x x +--=的解是_________. 5.1-2+3-4+5-6+7-8+…+4999-5000=______.6.当x=-24125时,代数式(3x 3-5x 2+6x -1)-(x 3-2x 2+x -2)+(-2x 3+3x 2+1)的值是____. 7.当a=-0.2,b=0.04时,代数式272711()(0.16)()73724a b b a a b --++-+的值是______.8.含盐30%的盐水有60千克,放在秤上蒸发,当盐水变为含盐40%时,秤得盐水的重是______克.9.制造一批零件,按计划18天可以完成它的13.如果工作4天后,工作效率提高了15,那么完成这批零件的一半,一共需要______天.10.现在4点5分,再过______分钟,分针和时针第一次重合.答案与提示一、选择题1.C 2.D 3.C 4.D 5.C 6.B 7.D 8.D 9.C 10.A提示:1.令a=2,b=-2,满足2+(-2)=0,由此2.x2,2x2,x3都是单项式.两个单项式x3,x2之和为x3+x2是多项式,排除A.两个单项式x2,2x2之和为3x2是单项式,排除B.两个多项式x3+x2与x3-x2之和为2x3是个单项式,排除C,因此选D.3.1是最小的自然数,A正确.可以找到正所以C“没有最大的负整数”的说法不正确.写出扩大自然数列,0,1,2,3,…,n,…,易知无最大非负数,D正确.所以不正确的说法应选C.5.在数轴上容易看出:在-π右边0的左边(包括0在内)的整数只有-3,-2,-1,0共4个.选C.6.由12=1,13=1可知甲、乙两种说法是正确的.由(-1)3=-1,可知丁也是正确的说法.而负数的平方均为正数,即负数的平方一定大于它本身,所以“负数平方不一定大于它本身”的说法不正确.即丙不正确.在甲、乙、丙、丁四个说法中,只有丙1个说法不正确.所以选B.7.令a=0,马上可以排除A、B、C,应选D.8.对方程同解变形,要求方程两边同乘不等于0的数.所以排除A.我们考察方程x-2=0,易知其根为x=2.若该方程两边同乘以一个整式x-1,得(x-1)(x -2)=0,其根为x=1及x=2,不与原方程同解,排除B.若在方程x-2=0两边加上同一个代数式去了原方程x=2的根.所以应排除C.事实上方程两边同时加上一个常数,新方程与原方程同解,对D,这里所加常数为1,因此选D.9.设杯中原有水量为a,依题意可得,第二天杯中水量为a×(1-10%)=0.9a;第三天杯中水量为(0.9a)×(1+10%)=0.9×1.1×a;第三天杯中水量与第一天杯中水量之比为所以第三天杯中水量比第一天杯中水量少了,选C.10.设两码头之间距离为s,船在静水中速度为a,水速为v0,则往返一次所用时间为设河水速度增大后为v,(v>v0)则往返一次所用时间为由于v-v0>0,a+v0>a-v0,a+v>a-v所以(a+v0)(a+v)>(a-v0)(a-v)∴t0-t<0,即t0<t.因此河水速增大所用时间将增多,选A.二、填空题提示:2.198919902-198919892=(19891990+19891989)×(19891990-19891989)=(19891990+19891989)×1=39783979.3.由于(2+1)(22+1)(24+1)(28+1)(216+1)=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)=(22-1)(22+1)(24+1)(28+1)(216+1)=(24-1)(24+1)(28+1)(216+1)=(28-1)(28+1)(216+1)=(216-1)(216+1)=232-1.2(1+x)-(x-2)=8,2+2x-x+2=8解得;x=45.1-2+3-4+5-6+7-8+…+4999-5000=(1-2)+(3-4)+(5-6)+(7-8)+…+(4999-5000)=-2500.6.(3x3-5x2+6x-1)-(x3-2x2+x-2)+(-2x3+3x2+1)=5x+27.注意到:当a=-0.2,b=0.04时,a2-b=(-0.2)2-0.04=0,b+a+0.16=0.04-0.2+0.16=0.8.食盐30%的盐水60千克中含盐60×30%(千克)设蒸发变成含盐为40%的水重x克,即0.001x千克,此时,60×30%=(0.001x)×40%解得:x=45000(克).10.在4时整,时针与分针针夹角为120°即希望杯第一届(1990年)初中一年级第2试试题一、选择题(每题1分,共5分)以下每个题目里给出的A,B,C,D四个结论中有且仅有一个是正确的.请你在括号填上你认为是正确的那个结论的英文字母代号.1.某工厂去年的生产总值比前年增长a%,则前年比去年少的百分数是( )A.a%.B.(1+a)%. C.1100aa+D.100aa+2.甲杯中盛有2m毫升红墨水,乙杯中盛有m毫升蓝墨水,从甲杯倒出a毫升到乙杯里, 0<a<m,搅匀后,又从乙杯倒出a毫升到甲杯里,则这时( )A.甲杯中混入的蓝墨水比乙杯中混入的红墨水少.B.甲杯中混入的蓝墨水比乙杯中混入的红墨水多.C.甲杯中混入的蓝墨水和乙杯中混入的红墨水相同.D.甲杯中混入的蓝墨水与乙杯中混入的红墨水多少关系不定.3.已知数x=100,则( )A.x是完全平方数.B.(x-50)是完全平方数.C.(x-25)是完全平方数.D.(x+50)是完全平方数.4.观察图1中的数轴:用字母a,b,c依次表示点A,B,C对应的数,则111,,ab b a c-的大小关系是( )A.111ab b a c<<-; B.1b a-<1ab<1c; C.1c<1b a-<1ab; D.1c<1ab<1b a-.5.x=9,y=-4是二元二次方程2x2+5xy+3y2=30的一组整数解,这个方程的不同的整数解共有( )A.2组.B.6组.C.12组.D.16组.二、填空题(每题1分,共5分)1.方程|1990x-1990|=1990的根是______.2.对于任意有理数x,y,定义一种运算*,规定x*y=ax+by-cxy,其中的a,b,c表示已知数,等式右边是通常的加、减、乘运算.又知道1*2=3,2*3=4,x*m=x(m≠0),则m 的数值是______.3.新上任的宿舍管理员拿到20把钥匙去开20个房间的门,他知道每把钥匙只能开其中的一个门,但不知道每把钥匙是开哪一个门的钥匙,现在要打开所有关闭着的20个房间,他最多要试开______次.4.当m=______时,二元二次六项式6x2+mxy-4y2-x+17y-15可以分解为两个关于x,y 的二元一次三项式的乘积.5.三个连续自然数的平方和(填“是”或“不是”或“可能是”)______某个自然数的平方.三、解答题(写出推理、运算的过程及最后结果.每题5分,共15分)1.两辆汽车从同一地点同时出发,沿同一方向同速直线行驶,每车最多只能带24桶汽油,途中不能用别的油,每桶油可使一辆车前进60公里,两车都必须返回出发地点,但是可以不同时返回,两车相互可借用对方的油.为了使其中一辆车尽可能地远离出发地点,另一辆车应当在离出发地点多少公里的地方返回?离出发地点最远的那辆车一共行驶了多少公里?2.如图2,纸上画了四个大小一样的圆,圆心分别是A,B,C,D,直线m通过A,B,直线n通过C,D,用S表示一个圆的面积,如果四个圆在纸上盖住的总面积是5(S-1),直线m,n之间被圆盖住的面积是8,阴影部分的面积S1,S2,S3满足关系式S3=13S1=13S2,求S.3.求方程11156x y z++=的正整数解.答案与提示一、选择题1.D 2.C 3.C 4.C 5.D提示:1.设前年的生产总值是m,则去年的生产总值是前年比去年少这个产值差占去年的应选D.2.从甲杯倒出a毫升红墨水到乙杯中以后:再从乙杯倒出a毫升混合墨水到甲杯中以后:乙杯中含有的红墨水的数量是①乙杯中减少的蓝墨水的数量是②∵①=②∴选C.∴x-25=(10n+2+5)2可知应当选C.4.由所给出的数轴表示(如图3):可以看出∴①<②<③,∴选C.5.方程2x2+5xy+3y2=30可以变形为(2x+3y)(x+y)=1·2·3·5∵x,y是整数,∴2x+3y,x+y也是整数.由下面的表可以知道共有16个二元一次方程组,每组的解都是整数,所以有16组整数组,应选D.二、填空题提示:1.原方程可以变形为|x-1|=1,即x-1=1或-1,∴x=2或0.2.由题设的等式x*y=ax+by-cxy及x*m=x(m≠0)得a·0+bm-c·0·m=0,∴bm=0.∵m≠0,∴b=0.∴等式改为x*y=ax-cxy.∵1*2=3,2*3=4,解得a=5,c=1.∴题设的等式即x*y=5x-xy.在这个等式中,令x=1,y=m,得5-m=1,∴m=4.3.∵打开所有关闭着的20个房间,∴最多要试开4.利用“十字相乘法”分解二次三项式的知识,可以判定给出的二元二次六项式6x2+mxy-4y2-x+17y-15中划波浪线的三项应当这样分解:3x -52x +3现在要考虑y,只须先改写作然后根据-4y2,17y这两项式,即可断定是:由于(3x+4y-5)(2x-y+3)=6x2+5xy-4y2-x+17y-15就是原六项式,所以m=5.5.设三个连续自然数是a-1,a,a+1,则它们的平方和是(a-1)2+a2+(a+1)2=3a2+2,显然,这个和被3除时必得余数2.另一方面,自然数被3除时,余数只能是0或1或2,于是它们可以表示成3b,3b+1,3b+2(b是自然数)中的一个,但是它们的平方(3b)2=9b2(3b+1)2=9b2+6b+1,(3b+2)2=9b2+12b+4=(9b2+12b+3)+1被3除时,余数要么是0,要么是1,不能是2,所以三个连续自然数平方和不是某个自然数的平方.三、解答题1.设两辆汽车一为甲一为乙,并且甲用了x升汽油时即回返,留下返程需的x桶汽油,将多余的(24-2x)桶汽油给乙.让乙继续前行,这时,乙有(24-2x)+(24-x)=48-3x桶汽油,依题意,应当有48-3x≤24,∴x≥8.甲、乙分手后,乙继续前行的路程是这个结果中的代数式30(48-4x)表明,当x的值愈小时,代数式的值愈大,因为x≥8,所以当x=8时,得最大值30(48-4·8)=480(公里),因此,乙车行驶的路程一共是2(60·8+480)=1920(公里).2.由题设可得即2S-5S3=8……②∴x,y,z都>1,因此,当1<x≤y≤z时,解(x,y,z)共(2,4,12),(2,6,6),(3,3,6),(3,4,4)四组.由于x,y,z在方程中地位平等.所以可得如下表所列的15组解.希望杯第二届(1991年)初中一年级第1试试题一、选择题(每题1分,共15分)以下每个题目的A,B,C,D四个结论中,仅有一个是正确的,请在括号内填上正确的那个结论的英文字母代号.1.数1是( )A.最小整数.B.最小正数.C.最小自然数.D.最小有理数.2.若a>b,则( )A.11a b; B.-a<-b.C.|a|>|b|.D.a2>b2.3.a为有理数,则一定成立的关系式是( )A.7a>a.B.7+a>a.C.7+a>7.D.|a|≥7.4.图中表示阴影部分面积的代数式是( )A.ad+bc.B.c(b-d)+d(a-c).C.ad+c(b-d).D.ab-cd.5.以下的运算的结果中,最大的一个数是( )A.(-13579)+0.2468; B.(-13579)+1 2468;C.(-13579)×12468; D.(-13579)÷124686.3.1416×7.5944+3.1416×(-5.5944)的值是( ) A.6.1632. B.6.2832.C.6.5132.D.5.3692.7.如果四个数的和的14是8,其中三个数分别是-6,11,12,则笫四个数是( )A.16. B.15. C.14. D.13.8.下列分数中,大于-13且小于-14的是( )A.-1120; B.-413; C.-316; D.-617.9.方程甲:34(x-4)=3x与方程乙:x-4=4x同解,其根据是( )A.甲方程的两边都加上了同一个整式x.B.甲方程的两边都乘以43x;C. 甲方程的两边都乘以43; D. 甲方程的两边都乘以34.10.如图: ,数轴上标出了有理数a,b,c的位置,其中O是原点,则111,,a b c的大小关系是( ) A.111a b c>>; B.1b >1c >1a ; C. 1b >1a >1c ; D. 1c >1a >1b .11.方程522.2 3.7x =的根是( ) A .27. B .28. C .29. D .30. 12.当x=12,y=-2时,代数式42x y xy -的值是( )A .-6.B .-2.C .2.D .6.13.在-4,-1,-2.5,-0.01与-15这五个数中,最大的数与绝对值最大的那个数的乘积是( )A .225.B .0.15.C .0.0001.D .1.14.不等式124816x x x xx ++++>的解集是( ) A .x <16. B .x >16.C .x <1. D.x>-116. 15.浓度为p%的盐水m 公斤与浓度为q%的盐水n 公斤混合后的溶液浓度是 ( ) A.%2p q +; B.()%mp nq +; C.()%mp nq p q ++;D.()%mp nq m n++.二、填空题(每题1分,共15分)1. 计算:(-1)+(-1)-(-1)×(-1)÷(-1)=______. 2. 计算:-32÷6×16=_______. 3. 计算:(63)36162-⨯=__________.4. 求值:(-1991)-|3-|-31||=______. 5. 计算:1111112612203042-----=_________. 6.n 为正整数,1990n -1991的末四位数字由千位、百位、十位、个位、依次排列组成的四位数是8009.则n 的最小值等于______.7. 计算:19191919199191919191⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=_______.8. 计算:15[(-1989)+(-1990)+(-1991)+(-1992)+(-1993)]=________.9.在(-2)5,(-3)5,512⎛⎫-⎪⎝⎭,513⎛⎫-⎪⎝⎭中,最大的那个数是________.10.不超过(-1.7)2的最大整数是______.11.解方程21101211,_____. 3124x x xx-++-=-=12.求值:355355113113355113⎛⎫---⎪⎝⎭⎛⎫- ⎪⎝⎭=_________.13.一个质数是两位数,它的个位数字与十位数字的差是7,则这个质数是______.14.一个数的相反数的负倒数是119,则这个数是_______.15.如图11,a,b,c,d,e,f均为有理数.图中各行,各列、两条对角线上三个数之和都相等,则ab cd efa b c d e f+++++++=____.答案与提示一、选择题1.C 2.B 3.B 4.C 5.C 6.B 7.B 8.B 9.C 10.B 11.D 12.A 13.B 1 4.A 15.D提示:1.整数无最小数,排除A;正数无最小数,排除B;有理数无最小数,排除D.1是最小自然数.选C.有|2|<|-3|,排除C;若2>-3有22<(-3)2,排除D;事实上,a>b必有-a<-b.选B.3.若a=0,7×0=0排除A;7+0=7排除C|0|<7排除D,事实上因为7>0,必有7+a>0+a=a.选B.4.把图形补成一个大矩形,则阴影部分面积等于ab-(a-c)(b-d)=ab-[ab-ad-c(b-d)]=ab-ab+ad+c(b-d)=ad+c(b-d).选C.5.运算结果对负数来说绝对值越小其值越大。
2009年全国初中数学竞赛试题及答案

2009年全国初中数学竞赛试题参考答案一、选择题(共5小题,每小题7分,共35分. 以下每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.已知非零实数a ,b 满足24242a b a -+++=,则a b +等于( ). (A )-1 (B )0 (C )1 (D )2 【答】C . 解:由题设知a ≥3,所以,题设的等式为20b ++=,于是32a b ==-,,从而a b +=1.2.如图,菱形ABCD 的边长为a ,点O 是对角线AC 上的一点,且OA =a ,OB =OC =OD =1,则a 等于( ). (A2(B2(C )1 (D )2【答】A . 解:因为△BOC ∽ △ABC ,所以B O BC A BA C=,即11a aa =+,所以,2a 由0a >,解得2a =.3.将一枚六个面编号分别为1,2,3,4,5,6后投掷两次,记第一次掷出的点数为a ,第二次掷出的点数为b ,则使关于x ,y 的方程组322ax by x y +=⎧⎨+=⎩,只有正数解的概率为( ). (A )121 (B )92 (C )185 (D )3613【答】D .解:当20a b -=时,方程组无解.当02≠-b a 时,方程组的解为62,223.2b x a ba y ab -⎧=⎪⎪-⎨-⎪=⎪-⎩由已知,得⎪⎪⎩⎪⎪⎨⎧>-->--,0232,0226b a a ba b即⎪⎪⎩⎪⎪⎨⎧<>>-,3,23,02b a b a 或⎪⎪⎩⎪⎪⎨⎧><<-.3,23,02b a b a 由a ,b 的实际意义为1,2,3,4,5,6,可得2345612a b =⎧⎨=⎩,,,,,,,共有 5×2=10种情况;或1456a b =⎧⎨=⎩,,,,共3种情况. 又掷两次骰子出现的基本事件共6×6=36种情况,故所求的概率为3613.4.如图1所示,在直角梯形ABCD 中,AB ∥DC ,90B ∠=︒. 动点P 从点 B 出发,沿梯形的边由B →C →D →A 运动. 设点P 运动的路程为x ,△ABP 的面积为y . 把y 看作x 的函数,函数的图像如图2所示,则△ABC 的面积为( ).(A )10 (B )16 (C )18 (D )32【答】B .解:根据图像可得BC 5,AB △ABC =12×8×4=16.5.关于x ,y 的方程22x y =x ,y ). (A )2组 (B )3组 ( (D )无穷多组【答】C .解:可将原方程视为关于x 的二次方程,将其变形为22(229)0x yx y ++-=. 由于该方程有整数根,则判别式∆≥0,且是完全平方数.由2224(229)7116y y y ∆=--=-+≥0,解得 2y ≤11616.57≈.于是显然,只有216y =时,4∆=是完全平方数,符合要求.当4y =时,原方程为2430x x ++=,此时121,3x x =-=-; 当y =-4时,原方程为2430x x -+=,此时341,3x x == .所 以,原方程的整数解为111,4;x y =-⎧⎨=⎩ 223,4;x y =-⎧⎨=⎩ 331,4;x y =⎧⎨=-⎩ 443,4.x y =⎧⎨=-⎩二、填空题(共5小题,每小题7分,共35分)6.一个自行车轮胎,若把它安装在前轮,则自行车行驶5000 km 后报废;若把它安装在后轮,则自行车行驶 3000 km 后报废,行驶一定路程后可以交换前、后轮胎.如果交换前、后轮胎,要使一辆自行车的一对新轮胎同时报废,那么这辆车将能行驶 km .【答】3750.解:设每个新轮胎报废时的总磨损量为k ,则安装在前轮的轮胎每行驶1 km 磨损量为5000k ,安装在后轮的轮胎每行驶1km 的磨损量为3000k .又设一对新轮胎交换位置前走了x km ,交换位置后走了y km .分别以一个轮胎的总磨损量为等量关系列方程,有,50003000,50003000kxky k ky kx k ⎧+=⎪⎪⎨⎪+=⎪⎩ 两式相加,得 ()()250003000k x y k xy k +++=, 则 237501150003000x y +==+.7.已知线段AB 的中点为C ,以点A 为圆心,AB 的长为半径作圆,在线段AB 的延长线上取点D ,使得BD =AC ;再以点D 为圆心,DA 的长为半径作圆,与⊙A 分别相交于F ,G 两点,连接FG 交AB 于点H ,则AH AB的值为 .解:如图,延长AD 与⊙D 交于点E ,连接AF ,EF . 由题设知13A C A D =,13A B A E =,在△FHA 和△EF A 中,EFA ∠=∠FAH EAF ∠=∠ 所以Rt △FHA ∽Rt △EF A ,A H A F A FA E=. 而A F A B =以AH AB13=.8.已知12345a a a a a ,,,,是满足条件123459a a a a a ++++=的五个不同的整数,若b 是关于x 的方程()()()()()123452009x a x a x a x a x a -----=的整数根,则b 的值为 .【答】 10. 解:因为()()()()()123452009b a b a b a b a b a -----=,且12345a a a a a ,,,,是五个不同的整数,所有12345b a b a b a b a b a -----,,,,也是五个不同的整数.又因为()()2009117741=⨯-⨯⨯-⨯,所以1234541b a b a b a b a b a -+-+-+-+-=. 由123459a a a a a ++++=,可得10b =.9.如图,在△ABC 中,CD 是高,CE 为ACB ∠的平分线.若AC =15,BC =20,CD =12,则CE 的长等于 .【答】7.解:如图,由勾股定理知AD =9,BD =16,所以AB =AD +BD =25 . 故由勾股定理逆定理知△ACB且90ACB ∠=︒.作EF ⊥BC,垂足为F .设EF =x ,由12E CF ∠=CF =x ,于是BF =20-x .由于EF ∥AC ,所以E F B F A CB C=,即15x =解得607x =.所以7C E ==.10.10个人围成一个圆圈做游戏.游戏的规则是:每个人心里都想好一个数,并把自己想好的数如实地告诉他两旁的两个人,然后每个人将他两旁的两个人告诉他的数的平均数报出来.若报出来的数如图所示,则报3的人心里想的数是 .【答】2-. 解:设报3的人心里想的数是x ,则报5于是报7的人心里想的数是 12(8)4x x --=+,报9数是16(4)12x x -+=-,报1的人心里想的数是 20(12)8x x --=+是4(8)4x x -+=--.所以4x x =--,解得2x =-.三、解答题(共4题,每题20分,共80分)11.已知抛物线2y x =与动直线c x t y --=)12(有公共点),(11y x ,),(22y x ,且3222221-+=+t t x x .(1)求实数t 的取值范围;(2)当t 为何值时,c 取到最小值,并求出c 的最小值.解:1.联立2y x =与c x t y --=)12(,消去y 得二次方程2(21)0x t x c --+= ①有实数根1x ,2x ,则121221,x x t x x c +=-=.所以2221212121[()()]2c x x x x x x ==+-+=221[(21)(23)]2t t t --+-=21(364)2t t -+. ②………………5分把②式代入方程①得221(21)(364)02x t x t t --+-+=. ③………………10分t 的取值应满足2221223t t x x +-=+≥0, ④且使方程③有实数根,即22(21)2(364)t t t ∆=---+=2287t t -+-≥0,⑤解不等式④得 t ≤-3或t ≥1,解不等式⑤得 22-≤t ≤22+.所以,t 的取值范围为22-≤t ≤22+. ⑥………………15分(2) 由②式知22131(364)(1)222c t t t =-+=-+.由于231(1)22c t =-+在22-≤t ≤22+时是递增的,所以,当22t =-时,2m in 3111(21)2224c -=--+=. ………………20分12.已知正整数a 满足3192191a +,且2009a <,求满足条件的所有可能的正整数a 的和.解:由3192191a +可得31921a -.619232=⨯,且()[]311(1)1(1)(1)(1)a a a a a a a a -=-++=-++-. ………………5分因为()11a a ++是奇数,所以6321a -等价于621a -,又因为3(1)(1)a a a -+,所以331a -等价于31a -.因此有1921a -,于是可得1921a k =+.………………15分又02009a <<,所以0110k = ,,,.因此,满足条件的所有可能的正整数a 的和为11+192(1+2+…+10)=10571. ………………20分 13.已知A B 为⊙O 的直径,弦//DC AB ,连接DO .过点D 作DO 的垂线,与B A 的延长线交于点E ,过点E 作AC 的平行线交CD 于点F ,过点D 作AC 的平行线交B F 于点G .求证:AG BG ⊥.(第13题)证明:连接AD ,BC ,因为四边形AEFC 是平行四边形,所以AE FC =. 由于AD CB DAE BCF =∠=∠,,因此有D AE ∆≌BCF ∆,于是可得 ADE CBF ∠=∠. ………………10分又因为D E 与⊙O 相切于点D ,所以DCA ADE ∠=∠.结合//DG AC ,可得 GDC DCA ADE GBC ∠=∠=∠=∠,于是D B C G ,,,四点共圆.因此点G 在⊙O 上,从而有AG BG ⊥.……………20分14.n 个正整数12n a a a ,,,满足如下条件:1212009n a a a =<<<= ; 且12n a a a ,,,中任意n -1个不同的数的算术平均数都是正整数.求n 的最大值.解:设12n a a a ,,,中去掉i a 后剩下的n -1个数的算术平均数为正整数i b ,12i n = ,,,.即 12()1n ii a a a a b n +++-=- .于是,对于任意的1≤i j <≤n ,都有1j i i j a a b b n --=-,从而 1()j i n a a --. ………………5分 由于 11200811n n a a b b n n --==--是正整数,故312251n -⨯. ………………10分由()()()112211n n n n n a a a a a a a ----=-+-++- ≥()()()2111(1)n n n n -+-++-=- ,所以,2(1)n -≤2008,于是n ≤45. 结合312251n -⨯,所以,n ≤9. ……15分 另一方面,令123801,811,821a a a =⨯+=⨯+=⨯+,…,8871a =⨯+,982511a =⨯+,则这9个数满足题设要求.综上所述,n 的最大值为9. ………20分。
全国初中数学联赛试题及答案(2009年).doc

2009年全国初中数学联合竞赛试题参考答案第一试一、选择题(本题满分42分,每小题7分) 1.设1a =,则32312612a a a +--= ( A )A.24.B. 25.C. 10.D. 12.2.在△ABC 中,最大角∠A 是最小角∠C 的两倍,且AB =7,AC =8,则BC = ( C )A. B. 10.C.D.3.用[]x 表示不大于x 的最大整数,则方程22[]30x x --=的解的个数为 ( C ) A.1. B. 2. C. 3. D. 4.4.设正方形ABCD 的中心为点O ,在以五个点A 、B 、C 、D 、O 为顶点所构成的所有三角形中任意取出两个,它们的面积相等的概率为 ( B ) A.314. B. 37. C. 12. D. 47.5.如图,在矩形ABCD 中,AB =3,BC =2,以BC 为直径在矩形内作半圆,自点A 作半圆的切线AE ,则sin ∠CBE = ( D )B. 23. C. 13.D. .6.设n 是大于1909的正整数,使得19092009n n--为完全平方数的n 的个数是 ( B )A.3.B. 4.C. 5.D. 6.二、填空题(本题满分28分,每小题7分)1.已知t 是实数,若,a b 是关于x 的一元二次方程2210x x t -+-=的两个非负实根,则22(1)(1)a b --的最小值是_____3-_______.2. 设D 是△ABC 的边AB 上的一点,作DE//BC 交AC 于点E ,作DF//AC 交BC 于点F ,已知△ADE 、△DBF 的面积分别为m 和n ,则四边形DECF 的面积为______.3.如果实数,a b 满足条件221a b +=,22|12|21a b a b a -+++=-,则a b +=__1-____.4.已知,a b是正整数,且满足是整数,则这样的有序数对(,)a b 共有___7__对. DC第二试 (A )一.(本题满分20分)已知二次函数2(0)y x bx c c =++<的图象与x 轴的交点分别为A 、B ,与y 轴的交点为C.设△ABC 的外接圆的圆心为点P.(1)证明:⊙P 与y 轴的另一个交点为定点.(2)如果AB 恰好为⊙P 的直径且2ABC S △=,求b 和c 的值.解 (1)易求得点C 的坐标为(0,)c ,设1A(,0)x ,2B(,0)x ,则12x x b +=-,12x x c =.设⊙P 与y 轴的另一个交点为D ,由于AB 、CD 是⊙P 的两条相交弦,它们的交点为点O ,所以O A ×OB =O C×OD ,则121x x c OA OB OD OC c c⨯====.因为0c <,所以点C 在y 轴的负半轴上,从而点D 在y 轴的正半轴上,所以点D 为定点,它的坐标为(0,1). (2)因为AB ⊥C D ,如果AB 恰好为⊙P 的直径,则C 、D 关于点O 对称,所以点C 的坐标为(0,1)-, 即1c =-.又12AB x x =-===1122ABC S AB OC =⋅==△,解得b =±.二.(本题满分25分)设CD 是直角三角形ABC 的斜边AD 上的高,1I 、2I 分别是△ADC 、△BDC 的内心,AC =3,BC =4,求1I 2I .解 作1I E ⊥AB 于E ,2I F ⊥AB 于F.在直角三角形ABC 中,AC =3,BC =4,AB =5=.又C D ⊥AB ,由射影定理可得2AC 9A D =AB 5=,故16BD =AB AD 5-=,12CD =5=. 因为1I E 为直角三角形ACD 的内切圆的半径,所以1I E =13(AD CD AC)25+-=. 连接D 1I 、D 2I ,则D 1I 、D 2I 分别是∠ADC 和∠BDC 的平分线,所以∠1I DC =∠1I DA =∠2I DC =∠2I DB=45°,故∠1I D 2I =90°,所以1I D ⊥2I D,1113I E 5DI sin ADI sin 455===∠︒.同理,可求得24I F 5=,2D I =所以1I 2I=.C三.(本题满分25分)已知,,a b c 为正数,满足如下两个条件:32a b c ++= ①14b c a c a b a b c bc ca ab +-+-+-++= ②. 证法1 将①②两式相乘,得()()8b c a c a b a b ca b c bc ca ab+-+-+-++++=, 即222222()()()8b c a c a b a b c bc ca ab +-+-+-++=, 即222222()()()440b c a c a b a b c bc ca ab +-+-+--+-+=, 即222222()()()0b c a c a b a b c bc ca ab----+-++=, 即()()()()()()0b c a b c a c a b c a b a b c a b c bc ca ab-+---+--+++-++=,即()[()()()]0b c a a b c a b c a b c a b c abc -+----++++=,即222()[2]0b c a ab a b c abc -+--+=,即22()[()]0b c a c a b abc -+--=,即()()()0b c a c a b c a b abc-++--+=,所以0b c a -+=或0c a b +-=或0c a b -+=,即b a c +=或c a b +=或c b a +=..证法2 结合①式,由②式可得32232232214a b c bc ca ab ---++=, 变形,得222110242()4a b c abc -++= ③又由①式得2()1024a b c ++=,即22210242()a b c ab bc ca ++=-++, 代入③式,得110242[10242()]4ab bc ca abc --++=,即16()4096abc ab bc ca =++-. 3(16)(16)(16)16()256()16a b c abc ab bc ca a b c ---=-+++++-3409625632160=-+⨯-=,所以16a =或16b =或16c =.结合①式可得b a c +=或c a b +=或c b a +=..第二试 (B )一.(本题满分20分)题目和解答与(A )卷第一题相同.二. (本题满分25分) 已知△ABC 中,∠ACB =90°,AB 边上的高线CH 与△ABC 的两条内角平分线 AM 、BN 分别交于P 、Q 两点.PM 、QN 的中点分别为E 、F.求证:EF ∥AB.解 因为BN 是∠ABC 的平分线,所以ABN CBN ∠=∠. 又因为C H ⊥AB ,所以CQN BQH 90ABN 90CBN CNB ∠=∠=︒-∠=︒-∠=∠,因此CQ NC =.又F 是QN 的中点,所以C F ⊥QN ,所以CFB 90CHB ∠=︒=∠,因此C 、F 、H 、B 四点共圆. 又FBH =FBC ∠∠,所以FC =FH ,故点F 在CH 的中垂线上. 同理可证,点E 在CH 的中垂线上.因此E F ⊥CH.又AB ⊥CH ,所以EF ∥AB.三.(本题满分25分)题目和解答与(A )卷第三题相同.第二试 (C )一.(本题满分20分)题目和解答与(A )卷第一题相同. 二.(本题满分25分)题目和解答与(B )卷第二题相同.三.(本题满分25分)已知,,a b c 为正数,满足如下两个条件:32a b c ++= ①14b c a c a b a b c bc ca ab +-+-+-++= ②. 解法1 将①②两式相乘,得()()8b c a c a b a b ca b c bc ca ab+-+-+-++++=, 即222222()()()8b c a c a b a b c bc ca ab +-+-+-++=, 即222222()()()440b c a c a b a b c bc ca ab +-+-+--+-+=, 即222222()()()0b c a c a b a b c bc ca ab----+-++=, 即()()()()()()0b c a b c a c a b c a b a b c a b c bc ca ab-+---+--+++-++=,即()[()()()]0b c a a b c a b c a b c a b c abc-+----++++=,NB即222()[2]0b c a ab a b c abc -+--+=,即22()[()]0b c a c a b abc -+--=,即()()()0b c a c a b c a b abc-++--+=,所以0b c a -+=或0c a b +-=或0c a b -+=,即b a c +=或c a b +=或c b a +=.90°.解法2 结合①式,由②式可得32232232214a b c bc ca ab ---++=, 变形,得222110242()4a b c abc -++= ③又由①式得2()1024a b c ++=,即22210242()a b c ab bc ca ++=-++, 代入③式,得110242[10242()]4ab bc ca abc --++=,即16()4096abc ab bc ca =++-. 3(16)(16)(16)16()256()16a b c abc ab bc ca a b c ---=-+++++-3409625632160=-+⨯-=,所以16a =或16b =或16c =.结合①式可得b a c +=或c a b +=或c b a +=.90°.。
2009年全国初中数学联赛试题及解答

2009年全国初中数学联合竞赛试题第一试一、选择题1.设1a =−,则32312612a a a +−−=( )A.24.B. 25.C. 10+.D. 12+.2.在△ABC 中,最大角∠A 是最小角∠C 的两倍,且AB =7,AC =8,则BC =( )A..B. 10.C..D. 3.用[]x 表示不大于x 的最大整数,则方程22[]30x x −−=的解的个数为( ) A.1. B. 2. C. 3. D. 4.4.设正方形ABCD 的中心为点O ,在以五个点A 、B 、C 、D 、O 为顶点所构成的所有三角形中任意取出两个,它们的面积相等的概率为( )A.314. B. 37. C. 12. D. 47. DC5.如图,在矩形ABCD 中,AB =3,BC =2,以BC 为直径在矩形内作半圆,自点A 作半圆的切线AE ,则CBE =()sin ∠A.3. B. 23. C. 13.D. 10.6.设是大于1909的正整数,使得n 19092009n n−−为完全平方数的n 的个数是( )A.3.B. 4.C. 5.D. 6.二、填空题(本题满分28分,每小题7分)1.已知是实数,若是关于t ,a b x 的一元二次方程221x x t 0−+−=的两个非负实根,则(1的最小值是____________.22)(1)a b −−22|21a b a b a 2. 设D 是△ABC 的边AB 上的一点,作DE//BC 交AC 于点E ,作DF//AC 交BC 于点F ,已知△ADE 、△DBF 的面积分别为和,则四边形DECF 的面积为______.m n 3.如果实数满足条件,|1,a b 221a b +=2−+++=−,则a b +=______. 4.已知是正整数,且满足,a b 是整数,则这样的有序数对共有 对. (,)a b第二试 (A)一.已知二次函数的图象与2(0y x bx c c =++<)x 轴的交点分别为A 、B ,与轴的交点为C.设△ABC 的外接圆的圆心为点P.y (1)证明:⊙P 与轴的另一个交点为定点.y (2)如果AB 恰好为⊙P 的直径且,求和的值.2ABC S △=b c 二.设CD 是直角三角形ABC 的斜边AD 上的高,I 、I 分别是△ADC 、△BDC 的内心,AC =3,BC =4,求I .1212I 三.已知为正数,满足如下两个条件:,,a b c 32a b c ++= ①14b c a c a b a b c bc ca ab+−+−+−++= ②.第二试 (B)一.题目和解答与(A )卷第一题相同.NB二.已知△ABC 中,∠ACB =90°,AB 边上的高线CH 与△ABC 的两条内角平分线 AM 、BN 分别交于P 、Q 两点.PM 、QN 的中点分别为E 、F.求证:EF ∥AB.三.题目和解答与(A )卷第三题相同.第二试 (C)一.题目和解答与(A )卷第一题相同. 二.题目和解答与(B )卷第二题相同. 三.已知为正数,满足如下两个条件:,,a b c 32a b c ++= ①14b c a c a b a b c bc ca ab +−+−+−++=② .2009年全国初中数学联合竞赛试题参考答案第一试一、选择题 1.A 2.C 3.C 4.B 5.D 6.B 二、填空题 1. 3−2. 3. 1−4.7第二试 (A)一.解 (1)易求得点的坐标为,设,,则C (0,)c 1A(,0)x 2B(,0)x 12x x b +=−,12x x c =.设P ⊙与轴的另一个交点为D ,由于AB 、CD 是P ⊙的两条相交弦,它们的交点为点O ,所以OA×OB =OC×OD ,则y 121x x c OA OB OD OC c c×====. 因为,所以点C 在轴的负半轴上,从而点D 在轴的正半轴上,所以点D 为定点,它的坐标为(0,1).0c <y y (2)因为AB CD ⊥,如果AB 恰好为P ⊙的直径,则C 、D 关于点O 对称,所以点的坐标为,即.C (0,1)−1c =−又12AB x x =−===,所以12ABC S ==△,解得b =±.二.解 作E ⊥AB 于E ,F ⊥AB 于F.1I 2I 在直角三角形ABC 中,AC =3,BC =4,AB =5=.又CD ⊥AB ,由射影定理可得2AC 9A D =AB 5=,故16BD =AB AD 5−=,12CD =5=.C 因为E 为直角三角形ACD 的内切圆的半径,所以I =1I 1E 13(AD CD AC)25+−=. 连接D 、D 2,则D 1I 、2I 分别是ADC ∠和∠BDC 的平分线,所1I DC =∠A =∠2I DC =∠2I DB 45°∠1I D 2I =90°,所以1ID 2D ,1I I D 以∠D =,故⊥1I I 1I E 1135DI sin ADI sin 45===5∠°.同理,可求得24I F 5=,2D I 5=. 所以1I 2I =. 三.证法1 将①②两式相乘,得()b c a c a b a b ca b c bc ca ab+−+−+−()8++++=, 即222222()()()8b c a c a b a b c bc ca ab +−+−+−++=, 即222222()()()44b c a c a b a b c bc ca ab +−+−+−−+−+=0, 即222222()()()0b c a c a b a b c bc ca ab−−−−+−++=, 即()()()()()()0b c a b c a c a b c a b a b c a b c bc ca ab −+−−−+−−+++−++=,即()[()()()]0b c a a b c a b c a b c a b c abc−+−−−−++++=,即222()[2]0b c a ab a b c abc −+−−+=,即22()[()]b c a c a b abc 0−+−−=,即()()()b c a c a b c a b abc−++−−+=0,所以或或,即0b c a −+=0c a b +−=0c a b −+=b a c +=或c a b +=或. c b a +=.证法2 结合①式,由②式可得32232232214a b c bc ca ab −−−++=, 变形,得222110242()4a b c abc −++=③ 又由①式得,即, 2()1024a b c ++=22210242()a b c ab bc ca ++=−++代入③式,得110242[10242()]4ab bc ca abc −−++=,即 16()4096abc ab bc ca =++−.3(16)(16)(16)16()256()16a b c abc ab bc ca a b c −−−=−+++++−3409625632160=−+×−=,所以或或16a =16b =16c =.结合①式可得b a 或或c b .c +=c a b +=a +=.第二试 (B)二.证明 因为BN 是∠ABC 的平分线,所以ABN CBN ∠=∠.又因为CH ⊥AB ,所以, CQN BQH 90ABN 90CBN CNB ∠=∠=°−∠=°−∠=∠因此.CQ NC =又F 是QN 的中点,所以CF ⊥QN ,所以CFB 90CHB ∠=°=∠,因此C 、F 、H 、B 四点共圆.又,所以FC =FH ,故点F 在CH 的中垂线上.FBH =FBC ∠∠N B同理可证,点E 在CH 的中垂线上. 因此EF CH.⊥又AB CH ⊥,所以EF AB. ∥第二试 (C)三. 解法1 将①②两式相乘,得()b c a c a b a b ca b c bc ca ab+−+−+−++++()8=, 即222222()()()8b c a c a b a b c bc ca ab +−+−+−++=, 即222222()()()44b c a c a b a b c bc ca ab +−+−+−−+−+=0, 即222222()()()0b c a c a b a b c bc ca ab −−−−+−++=, 即()()()()()()0b c a b c a c a b c a b a b c a b c bc ca ab −+−−−+−−+++−++=,即()[()()()]0b c a a b c a b c a b c a b c abc−+−−−−++++=, 即222()[2]0b c a ab a b c abc −+−−+=,即22()[()]b c a c a b abc 0−+−−=, 即()()()b c a c a b c a b abc−++−−+=0, 所以或0b c a −+=0c a b +−=或0c a b−+=,即b ac +=或c a b +=或.c b a +=90°. 解法2 结合①式,由②式可得32232232214a b c bc ca ab −−−++=, 变形,得22211024 ③ 2()4a b c abc −++=又由①式得,即, 2()1024a b c ++=22210242()a b c ab bc ca ++=−++代入③式,得110242[10242()]4ab bc ca abc −−++=,即 16()4096abc ab bc ca =++−.3(16)(16)(16)16()256()16a b c abc ab bc ca a b c −−−=−+++++−3409625632160=−+×−=,所以或或.16a =16b =16c =结合①式可得b a 或c a 或c b c +=b +=a +=.90°.。
2009年全国初中数学竞赛试题

报 出 来 若 报 出 来 的 数 如 图所 示 则 报
.
,
3
的人
一
心 里 想 的数是
参考 答 案
、
.
选择 题
,
1 10
1
2 3
.
由题设 知 口 ≥ 3
=
所 以 题设 的 等式可 化 为
于是
a
=
/ f b + 2 f + 、瓦二巧矿
a +
o
,
3 ,6 —
2
,
从而
9
b 1
=
.
选C
I~
}
.
8
、
6
r
4 5
-
:
,
2 64
9
;
=
㈣
,
;
fx 3
心 里 想 的数应是 8 吨
.
=
2 544
,
fx 4
;
-
2 364
于 是报 7 的人 心 里 想 的
【3 6 0 1 7 2 0 9 y
=
【4 6 0 1 7 2 0 9 y
=
.
数是
16
一
12
一
(8 吨 ) 4 帆
=
=
,
报
9
的 人 心 里 想 的数 是
20
一
(4 慨 )
2
.
A B OC
—
A ABC
,
所以
器器即
=
,
上
=
』
,
所以 扛
0
—
1= 0
.
第1 0 题 图
副
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009年全国初中数学联合竞赛试题与解答第一试一、选择题(本题满分42分,每小题7分)1.设1a =,则32312612a a a +--=( )A.24.B. 25.C. 10.D. 12.2.在△ABC 中,最大角∠A 是最小角∠C 的两倍,且AB =7,AC =8,则BC =( )A..B. 10.C.D. 3.用[]x 表示不大于x 的最大整数,则方程22[]30x x --=的解的个数为( )A.1.B. 2.C. 3.D. 4.4.设正方形ABCD 的中心为点O ,在以五个点A 、B 、C 、D 、O 为顶点所构成的所有三角形中任意取出两个,它们的面积相等的概率为( )A.314. B. 37. C. 12. D. 47. 5.如图,在矩形ABCD 中,AB =3,BC =2,以BC 为直径在矩形内作半圆,自点A 作半圆的切线AE ,则sin ∠CBE = ( )A.3B. 23.C. 13.D. 10.6.设n 是大于1909的正整数,使得19092009n n--为完全平方数的n 的个数是 ( )A.3.B. 4.C. 5.D. 6.二、填空题(本题满分28分,每小题7分)1.已知t 是实数,若,a b 是关于x 的一元二次方程2210x x t -+-=的两个非负实根,则22(1)(1)a b --的最小值是____________.2. 设D 是△ABC 的边AB 上的一点,作DE//BC 交AC 于点E ,作DF//AC 交BC 于点F ,已知△ADE 、△DBF 的面积分别为m 和n ,则四边形DECF 的面积为______.3.如果实数,a b 满足条件221a b +=,22|12|21a b a b a -+++=-,则a b +=______.4.已知,a b是正整数,且满足是整数,则这样的有序数对(,)a b 共有_____对. 第二试 (A )DC一.(本题满分20分)已知二次函数2(0)y x bx c c =++<的图象与x 轴的交点分别为A 、B ,与y 轴的交点为C.设△ABC 的外接圆的圆心为点P.(1)证明:⊙P 与y 轴的另一个交点为定点.(2)如果AB 恰好为⊙P 的直径且2ABC S △=,求b 和c 的值.二.(本题满分25分)设CD 是直角三角形ABC 的斜边AD 上的高,1I 、2I 分别是△ADC 、△BDC 的内心,AC =3,BC =4,求1I 2I .三.(本题满分25分)已知,,a b c 为正数,满足如下两个条件:32a b c ++= ①14b c a c a b a b c bc ca ab +-+-+-++= ②为三边长可构成一个直角三角形.第二试 (B )一.(本题满分20分)题目和解答与(A )卷第一题相同.二. (本题满分25分) 已知△ABC 中,∠ACB =90°,AB 边上的高线CH 与△ABC 的两条内角平分线 AM 、BN 分别交于P 、Q 两点.PM 、QN 的中点分别为E 、F.求证:EF ∥AB.三.(本题满分25分)题目和解答与(A )卷第三题相同.第二试 (C )一.(本题满分20分)题目和解答与(A )卷第一题相同.二.(本题满分25分)题目和解答与(B )卷第二题相同.三.(本题满分25分)已知,,a b c 为正数,满足如下两个条件:32a b c ++= ①14b c a c a b a b c bc ca ab +-+-+-++= ②.参考答案 第一试一、 选择题1、 A2、 C3、 C4、 B5、 D6、 B 二、 填空题 1、3- 2、NB3、1-4、7第二试 (A )二.(本题满分25分)解: (1)易求得点C 的坐标为(0,)c ,设1A(,0)x ,2B(,0)x ,则12x x b +=-,12x x c =.设⊙P 与y 轴的另一个交点为D ,由于AB 、CD 是⊙P 的两条相交弦,它们的交点为点O ,所以O A ×OB =O C ×OD ,则121x x c OA OB OD OC c c⨯====.因为0c <,所以点C 在y 轴的负半轴上,从而点D 在y 轴的正半轴上,所以点D 为定点,它的坐标为(0,1). (2)因为AB ⊥C D ,如果AB 恰好为⊙P 的直径,则C 、D 关于点O 对称,所以点C 的坐标为(0,1)-, 即1c =-.又12AB x x =-===1122ABC S AB OC =⋅==△,解得b =±. 二.(本题满分25分)解: 作1I E ⊥AB 于E ,2I F ⊥AB 于F.在直角三角形ABC 中,AC =3,BC =4,AB =5=.又C D ⊥AB ,由射影定理可得2AC 9A D =AB 5=,故16BD =AB AD 5-=,12CD =5=. 因为1I E 为直角三角形ACD 的内切圆的半径,所以1I E =13(AD CD AC)25+-=. 连接D 1I 、D 2I ,则D 1I 、D 2I 分别是∠ADC 和∠BDC 的平分线,所以∠1I DC =∠1I DA =∠2I DC =∠2I DB=45°,故∠1I D 2I =90°,所以1I D ⊥2I D,1113I E 5DI sin ADI sin 45===∠︒.同理,可求得24I F 5=,2D I 5=. 所以1I 2I=三.(本题满分25分)证法1 将①②两式相乘,得()()8b c a c a b a b ca b c bc ca ab+-+-+-++++=, 即222222()()()8b c a c a b a b c bc ca ab+-+-+-++=,C即222222()()()440b c a c a b a b c bc ca ab +-+-+--+-+=, 即222222()()()0b c a c a b a b c bc ca ab----+-++=, 即()()()()()()0b c a b c a c a b c a b a b c a b c bc ca ab-+---+--+++-++=,即()[()()()]0b c a a b c a b c a b c a b c abc -+----++++=,即222()[2]0b c a ab a b c abc -+--+=,即22()[()]0b c a c a b abc -+--=,即()()()0b c a c a b c a b abc-++--+=,所以0b c a -+=或0c a b +-=或0c a b -+=,即b a c +=或c a b +=或c b a +=.为三边长可构成一个直角三角形.证法2 结合①式,由②式可得32232232214a b c bc ca ab ---++=, 变形,得222110242()4a b c abc -++= ③又由①式得2()1024a b c ++=,即22210242()a b c ab bc ca ++=-++, 代入③式,得110242[10242()]4ab bc ca abc --++=,即16()4096abc ab bc ca =++-. 3(16)(16)(16)16()256()16a b c abc ab bc ca a b c ---=-+++++-3409625632160=-+⨯-=,所以16a =或16b =或16c =.结合①式可得b a c +=或c a b +=或c b a +=..第二试 (B )二. (本题满分25分)解 因为BN 是∠ABC 的平分线,所以ABN CBN ∠=∠. 又因为C H ⊥AB ,所以CQN BQH 90ABN 90CBN CNB ∠=∠=︒-∠=︒-∠=∠,因此CQ NC =.又F 是QN 的中点,所以C F ⊥QN ,所以CFB 90CHB ∠=︒=∠,因此C 、F 、H 、B 四点共圆. 又FBH =FBC ∠∠,所以FC =FH ,故点F 在CH 的中垂线上. 同理可证,点E 在CH 的中垂线上.因此E F ⊥CH.又AB ⊥CH ,所以EF ∥AB. 三.(本题满分25分)解法1 将①②两式相乘,得()()8b c a c a b a b ca b c bc ca ab+-+-+-++++=, 即222222()()()8b c a c a b a b c bc ca ab +-+-+-++=, 即222222()()()440b c a c a b a b c bc ca ab +-+-+--+-+=, 即222222()()()0b c a c a b a b c bc ca ab----+-++=, 即()()()()()()0b c a b c a c a b c a b a b c a b c bc ca ab-+---+--+++-++=,即()[()()()]0b c a a b c a b c a b c a b c abc -+----++++=,即222()[2]0b c a ab a b c abc -+--+=,即22()[()]0b c a c a b abc -+--=,即()()()0b c a c a b c a b abc-++--+=,所以0b c a -+=或0c a b +-=或0c a b -+=,即b a c +=或c a b +=或c b a +=.为三边长可构成一个直角三角形,它的最大内角为90°.解法2 结合①式,由②式可得32232232214a b c bc ca ab ---++=, 变形,得222110242()4a b c abc -++= ③又由①式得2()1024a b c ++=,即22210242()a b c ab bc ca ++=-++, 代入③式,得110242[10242()]4ab bc ca abc --++=,即16()4096abc ab bc ca =++-. 3(16)(16)(16)16()256()16a b c abc ab bc ca a b c ---=-+++++-3409625632160=-+⨯-=,所以16a =或16b =或16c =.结合①式可得b a c +=或c a b +=或c b a +=.为三边长可构成一个直角三角形,它的最大内角为90°.。
