整式的加减(4课时) (共55张PPT)
合集下载
《整式的加减 》课件

根据乘法分配律,将代数式中 的每一项分别乘以另一个代数 式中的每一项,再将结果相加 。
整式的除法运算
转化为乘法运算,再按照乘法 运算法则进行计算。
整式的混合运算实例
整式加法实例
$2x^2y + 3xy^2 + 4xz$
整式乘法实例
$(x + y)^2 times (x - y)^3$
整式减法实例
$5x^3 - 3x^2y + 4y^2 - 2y^3$
整式的分类
单项式
只包含一个项的整式,如: 3x^2y、4a。
多项式
包含多个项的整式,如:x^2 3x + 2、a^3 - 2a^2 + a。
整式的加减运算规则
同类项合并
幂次不变
同类项是指具有相同变量和幂次的项 ,同类项可以合并,如:2x^2 + 3x^2 = 5x^2。
在进行加减运算时,变量的幂次保持 不变,如:x^2 + x = x^2 + x。
整式除法实例
$frac{x^4 - y^4}{x + y}$
04
CATALOGUE
整式的加减在实际问题中的应用
整式的加减在数学问题中的应用
01
02
03
代数方程求解
通过整式的加减运算,可 以求解代数方程,如一元 一次方程、二元一次方程 等。
函数图像变换
整式的加减可以用于函数 图像的平移、伸缩等变换 ,有助于理解函数的性质 和变化规律。
几何图形面积计算
在几何图形中,整式的加 减可以用于计算图形的面 积和周长,如矩形、三角 形等。
整式的加减在实际生活中的应用
购物计算
在购物时,整式的加减可以用于 计算折扣、找零等,方便快捷。
整式的除法运算
转化为乘法运算,再按照乘法 运算法则进行计算。
整式的混合运算实例
整式加法实例
$2x^2y + 3xy^2 + 4xz$
整式乘法实例
$(x + y)^2 times (x - y)^3$
整式减法实例
$5x^3 - 3x^2y + 4y^2 - 2y^3$
整式的分类
单项式
只包含一个项的整式,如: 3x^2y、4a。
多项式
包含多个项的整式,如:x^2 3x + 2、a^3 - 2a^2 + a。
整式的加减运算规则
同类项合并
幂次不变
同类项是指具有相同变量和幂次的项 ,同类项可以合并,如:2x^2 + 3x^2 = 5x^2。
在进行加减运算时,变量的幂次保持 不变,如:x^2 + x = x^2 + x。
整式除法实例
$frac{x^4 - y^4}{x + y}$
04
CATALOGUE
整式的加减在实际问题中的应用
整式的加减在数学问题中的应用
01
02
03
代数方程求解
通过整式的加减运算,可 以求解代数方程,如一元 一次方程、二元一次方程 等。
函数图像变换
整式的加减可以用于函数 图像的平移、伸缩等变换 ,有助于理解函数的性质 和变化规律。
几何图形面积计算
在几何图形中,整式的加 减可以用于计算图形的面 积和周长,如矩形、三角 形等。
整式的加减在实际生活中的应用
购物计算
在购物时,整式的加减可以用于 计算折扣、找零等,方便快捷。
整式的加减的ppt课件

多项式
由多个单项式组成的整式,如:x + 2y、3x^2 - 4x + 5等。
整式的加减运算规则
01
02
03
合并同类项
将相同变数的项合并,如 :3x + 5x = 8x。
系数相加减
将同类项的系数进行相加 或相减,如:3x + (-2x) = x。
变数和常数相加减
在整式的加减中,变数和 常数可以相加减,如:x + 5 = x + 5。
电磁学问题
在电磁学中,电流、电压、电阻等物 理量的计算也需要使用到整式的加减 。通过整式的加减,我们可以得到更 加准确的物理量值。
整式的加减在化学问题中的应用
化学反应方程式
在化学反应方程式中,整式的加减可 以帮助我们理解反应物和生成物之间 的关系。例如,通过比较反应前后的 质量变化,我们可以计算出反应的能 量变化。
整式的加减在实际问题中的应用
整式的加减在数学问题中的应用
代数方程的求解
整式的加减在代数方程求解中有 着广泛的应用,例如线性方程、 二次方程等。通过合并同类项、 移项等整式加减运算,可以简化
方程,找到解。
函数图像的处理
在函数的学习中,整式的加减可 以帮助我们处理函数图像,例如 通过平移、伸缩等变换,使图像
利用分配律简化计算
分配律是整式加减运算的基础,灵活运用分 配律可以简化计算。
灵活运用交换律和结合律
交换律和结合律可以用来调整项的顺序,便 于计算。
合并同类项时注意符号
在合并同类项时,要注意各项的符号,正负 号要正确处理。
化简时注意化到最简形式
在化简整式时,应尽可能化到最简形式,避 免复杂计算。
整式的加减运算实例
由多个单项式组成的整式,如:x + 2y、3x^2 - 4x + 5等。
整式的加减运算规则
01
02
03
合并同类项
将相同变数的项合并,如 :3x + 5x = 8x。
系数相加减
将同类项的系数进行相加 或相减,如:3x + (-2x) = x。
变数和常数相加减
在整式的加减中,变数和 常数可以相加减,如:x + 5 = x + 5。
电磁学问题
在电磁学中,电流、电压、电阻等物 理量的计算也需要使用到整式的加减 。通过整式的加减,我们可以得到更 加准确的物理量值。
整式的加减在化学问题中的应用
化学反应方程式
在化学反应方程式中,整式的加减可 以帮助我们理解反应物和生成物之间 的关系。例如,通过比较反应前后的 质量变化,我们可以计算出反应的能 量变化。
整式的加减在实际问题中的应用
整式的加减在数学问题中的应用
代数方程的求解
整式的加减在代数方程求解中有 着广泛的应用,例如线性方程、 二次方程等。通过合并同类项、 移项等整式加减运算,可以简化
方程,找到解。
函数图像的处理
在函数的学习中,整式的加减可 以帮助我们处理函数图像,例如 通过平移、伸缩等变换,使图像
利用分配律简化计算
分配律是整式加减运算的基础,灵活运用分 配律可以简化计算。
灵活运用交换律和结合律
交换律和结合律可以用来调整项的顺序,便 于计算。
合并同类项时注意符号
在合并同类项时,要注意各项的符号,正负 号要正确处理。
化简时注意化到最简形式
在化简整式时,应尽可能化到最简形式,避 免复杂计算。
整式的加减运算实例
整式的加减(公开课) ppt课件
ppt课件
6
整式的加减 去括号
ppt课件
7
知识结构:
整式的概念 整式的加减
整式的计算
单项式 多项式
系数
次数 项,项数,常数项, 最高次项 次数
同类项与合并同类项 去括号 化简求值
用字母来表示生活中的量
ppt课件
8
如何进行整式的加减呢? 八字诀
去括号、合并同类项
ppt课件
9
口诀: 去括号,看符号: 是“+”号,不变号; 是“-”号,全变号.
整式的加减整式的加减整式的整式的概念整式的整式的计算单项式单项式多项式多项式系数系数次数次数项项数常数项项项数常数项最高次项最高次项次数次数同类项与合并同类项与合并同类项去括号去括号化简求值化简求值用字母来表示生活中的量用字母来表示生活中的量10例如
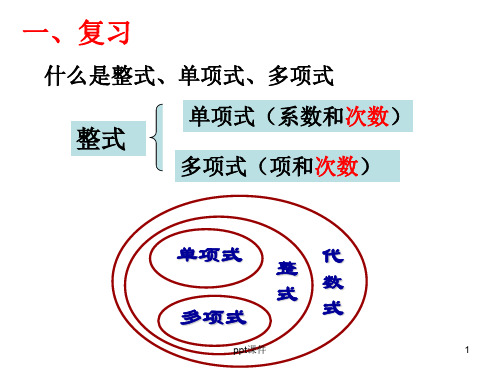
一、复习
什么是整式、单项式、多项式
整式
单项式(系数和次数) 多项式(项和次数)
合并同类项概念: _把__多__项_式__中__的__同__类_项__合__并__成__一_项_.
合并同类项法则: 1.__系_数___相加减;
2._字__母__和__字_母__的__指__数___不变。
ppt课件
5
1.下列各式中,是同类项的是:__③__⑤_⑥______
① 2x2 y3 与 x3 y2 ② x2 yz 与 x2 y
思维分析:把多项式看作一个整体,并用括号
括起来。 见多必括
解 (2x2 -3x + 1)+( -3x2 + 5x-7) = 2x2 -3x + 1 -3x2 + 5x-7
= (2x2 -3x2 )+(-3x + 5x)+(1-7)
数学七上4.4《整式的加减》ppt课件

(3)如果6a-2=16,那么6a=18,即 a=3.所以,当a=3时,这个长方形的周长是16.
有这样一道题:”已知A=2a2+2b2-3c2 ,B=3a2-b2-2c2,C=c2+2a2-3b2,当a=1,b=2,c=3时,求A-B+C的值.”有一学生说,题中给出b=2,c=3是多余的,他说的有道理吗?为什么?
观察与思考:
“求整式2a2 +a b+3b2与a2 -2a b+b2的差”
解:(2a2 +a b+3b2 )-( a2 -2a b+b2 ) = 2a2 +a b+3b2 - a2 +2a b-b2 = a2 +3a b+2b2
因此,整式加减运算的过程与步骤,包含以下两个运算:
冲刺:
(1)一个多项式加上2x2-x3-5-3x4得 3x4-5x3-3,求这个多项式。
(2)已知A+B=3x2-5x+1,A-C=-2x+3x2-5, 当x=2时,求B+C的值。
冲刺:
代数式(x2+ax-2y+7)-(bx2-2x+9y-1)的值与字母x的取值无关,求a、b的值。
3. (1)已知某多项式与3x2-6x+5的差是4x2+7x-6,求此多项式.
解: (3x2- 6x+5) + ( 4x2+7x - 6)
=2x2 +xy + 3y2 –x2 +xy
=x2+2xy+3y2
4.计算:(1) 2x2y3 + (- 4x2) - (- 3x2y3) - ( - xy3 -5x2)(2) (8xy - 3y2) -5xy -2( 3xy -2x2)
有这样一道题:”已知A=2a2+2b2-3c2 ,B=3a2-b2-2c2,C=c2+2a2-3b2,当a=1,b=2,c=3时,求A-B+C的值.”有一学生说,题中给出b=2,c=3是多余的,他说的有道理吗?为什么?
观察与思考:
“求整式2a2 +a b+3b2与a2 -2a b+b2的差”
解:(2a2 +a b+3b2 )-( a2 -2a b+b2 ) = 2a2 +a b+3b2 - a2 +2a b-b2 = a2 +3a b+2b2
因此,整式加减运算的过程与步骤,包含以下两个运算:
冲刺:
(1)一个多项式加上2x2-x3-5-3x4得 3x4-5x3-3,求这个多项式。
(2)已知A+B=3x2-5x+1,A-C=-2x+3x2-5, 当x=2时,求B+C的值。
冲刺:
代数式(x2+ax-2y+7)-(bx2-2x+9y-1)的值与字母x的取值无关,求a、b的值。
3. (1)已知某多项式与3x2-6x+5的差是4x2+7x-6,求此多项式.
解: (3x2- 6x+5) + ( 4x2+7x - 6)
=2x2 +xy + 3y2 –x2 +xy
=x2+2xy+3y2
4.计算:(1) 2x2y3 + (- 4x2) - (- 3x2y3) - ( - xy3 -5x2)(2) (8xy - 3y2) -5xy -2( 3xy -2x2)
《整式的加减》PPT课件(华师大版)

去括号法则:
(1)括号前是“+”号,把括号和它前
No 面的“+”号去掉,括号里各项都不变
号;
Image (2)括号前是“-”号,把括号和它前
面的“-”号去掉,括号里各项都改变符 号;
一、 去括号合并同类项
a (b c) a (b c) a (b c) a (b c)
(x y z) (x y z) (x y z)
二、指出下列各式是否正确?如果错误,请指 出原因.
(1) a-(b-c+d) = a-b+c+d (2) -(a-b)+(-c+d)= a+b-c-d (3) a-3(b-2c)=a-3b+2c x-2(-y-3z+1)=x-2y+6z
例6 计算:
(1)(2x-3y)+ (5x+4y) (2)(8a-7b)- (4a-5b)
分析:第(1)题求多项式2x-3y与5x+4y的和 第(2) 题求多项式8a-7b与4a-5b的差
解:
(1)(2x-3y)+ (5x+4y) = 2x-3y+ 5x+4y =7x+y
(2)(8a-7b)- (4a-5b) = 8a-7b- 4a+5b =4a-2b
(1)整式的加减实际上就是合并同类项; (2)一般步骤是先去括号,再合并同类项: (3)整式加减的结果还是整式.
注意:几个整式相加减,通常先用括号把 每一个整式括起来,再用加减号连接;然 后去括号,合项式加上2x2-x3-5-3x4得3x4-5x3-3,求这 个多项式.
例7:一种笔记本的单价是x元,圆珠笔的单 价是y元,小红买这种笔记本3个,买圆珠笔2 支;小明买这种笔记本4个,买圆珠笔3支.买 这些笔记本和圆珠笔,小红和小明一共花费 多少元?
(1)括号前是“+”号,把括号和它前
No 面的“+”号去掉,括号里各项都不变
号;
Image (2)括号前是“-”号,把括号和它前
面的“-”号去掉,括号里各项都改变符 号;
一、 去括号合并同类项
a (b c) a (b c) a (b c) a (b c)
(x y z) (x y z) (x y z)
二、指出下列各式是否正确?如果错误,请指 出原因.
(1) a-(b-c+d) = a-b+c+d (2) -(a-b)+(-c+d)= a+b-c-d (3) a-3(b-2c)=a-3b+2c x-2(-y-3z+1)=x-2y+6z
例6 计算:
(1)(2x-3y)+ (5x+4y) (2)(8a-7b)- (4a-5b)
分析:第(1)题求多项式2x-3y与5x+4y的和 第(2) 题求多项式8a-7b与4a-5b的差
解:
(1)(2x-3y)+ (5x+4y) = 2x-3y+ 5x+4y =7x+y
(2)(8a-7b)- (4a-5b) = 8a-7b- 4a+5b =4a-2b
(1)整式的加减实际上就是合并同类项; (2)一般步骤是先去括号,再合并同类项: (3)整式加减的结果还是整式.
注意:几个整式相加减,通常先用括号把 每一个整式括起来,再用加减号连接;然 后去括号,合项式加上2x2-x3-5-3x4得3x4-5x3-3,求这 个多项式.
例7:一种笔记本的单价是x元,圆珠笔的单 价是y元,小红买这种笔记本3个,买圆珠笔2 支;小明买这种笔记本4个,买圆珠笔3支.买 这些笔记本和圆珠笔,小红和小明一共花费 多少元?
《整式的加减》课件

整式的分类
01
02
03
单项式
只包含一个项的整式,例 如:$x^2$、$5a$。
多项式
包含多个项的整式,例如 :$x^2 - 3x + 2$。
整式的次数
一个整式中,所有字母的 指数之和称为该整式的次 数,例如:$x^2$的次数 为2。
整式的加减运算规则
同类项合并
同类项是指具有相同字母和相同 指数的项,同类项可以合并,例 如:$2x^2 + 3x^2 = 5x^2$。
去括号法则
总结词
去括号法则是整式加减运算中的一项重要法则,用于消除括号并简化整式的形式。
详细描述
去括号法则包括两个步骤,一是消除括号前的正号或负号,二是将括号内的各项分别与括号前的符号相乘或相除 。例如,在整式2(x + 3y) - (2x - y)中,根据去括号法则,首先消除括号前的正号,得到2x + 6y - 2x + y,然后 分别将括号内的各项与括号前的符号相乘或相除,得到最终结果-5y。
移项法则
总结词
移项法则是整式加减运算中的另一项重要法则,用于将整式中的项从一边移动到另一边 。
详细描述
移项法则包括两个步骤,一是将整式中的项从一边移动到另一边,二是根据移动的方向 改变该项的符号。例如,在整式6x - 5 = 2x + 1中,要将-5移到等号的另一边,根据 移项法则,首先将-5从等号的左边移动到右边,并改变其符号得到+5,得到新的等式
05
练习与巩固
基础练习题
总结词
帮助学生掌握整式加减的基本概 念和运算规则。
详细描述
设计一些简单的整式加减题目, 如合并同类项、去括号等,让学 生通过练习加深对整式加减基本 概念和运算规则的理解。
《整式的加减》PPT课件

(3) 3x2 2x2 __(3_+_2_) __ x2 __5____ x2;
(4) 3ab2 4ab2 _(_3-_4_)_ ab2 __-1__ ab2 _-_ ab2.
问题2:怎么样的多项式才 能进行化简?前面的3a+2b
能不能再化简呢?
观察上面的运算,请思考两个问题:
问题3:上述化简的方法是什么? (对比原式和结果,系数发生了 什么变化?字母和它的指数呢?)
归纳1: 同类项的定义:
所含字母相同,并且相同字母的指数也相同 的项,叫做同类项.几个常数项也是同类项.
归纳2:
(1)合并同类项的定义: 把多项式中的同类项合并成一项,叫做合并同类项.
(2)合并同类项的法则:
①系数是合并前各同类项的系数的和; ②字母和字母的指数不变.
三.基础训练,巩固新知
练习1 判断下列说法是否正确,正确的在括号里打“√”,错误的“×”. (1) 3x 与 3mx 是同类项;( × ) (2) 2ab 与 5ab是同类项;( √ ) (3) 3xy2 与 1 y2x是同类项;( √ )
3
3
6
解: 3a abc 1 c2 3a 1 c2
3
3
(3 3)a ( 1 1)c2 abc 33
abc.
当a 1 ,b 2, c 3时,原式 ( 1) 2( 3) 1.
6
6
思考:当a=0.2,b=0.3时,你能迅速求出下列多项式的值吗?
102ab33a2b3 2ab33a2b3 2
解: 上下两面面积和 2 1.5a 2b 6ab 左右两面面积和 2 2b 2c 8bc 前后两面面积和 2 2c 1.5a 6ca
大纸盒的表面积是(6ab 8bc 6ca )cm2
(4) 3ab2 4ab2 _(_3-_4_)_ ab2 __-1__ ab2 _-_ ab2.
问题2:怎么样的多项式才 能进行化简?前面的3a+2b
能不能再化简呢?
观察上面的运算,请思考两个问题:
问题3:上述化简的方法是什么? (对比原式和结果,系数发生了 什么变化?字母和它的指数呢?)
归纳1: 同类项的定义:
所含字母相同,并且相同字母的指数也相同 的项,叫做同类项.几个常数项也是同类项.
归纳2:
(1)合并同类项的定义: 把多项式中的同类项合并成一项,叫做合并同类项.
(2)合并同类项的法则:
①系数是合并前各同类项的系数的和; ②字母和字母的指数不变.
三.基础训练,巩固新知
练习1 判断下列说法是否正确,正确的在括号里打“√”,错误的“×”. (1) 3x 与 3mx 是同类项;( × ) (2) 2ab 与 5ab是同类项;( √ ) (3) 3xy2 与 1 y2x是同类项;( √ )
3
3
6
解: 3a abc 1 c2 3a 1 c2
3
3
(3 3)a ( 1 1)c2 abc 33
abc.
当a 1 ,b 2, c 3时,原式 ( 1) 2( 3) 1.
6
6
思考:当a=0.2,b=0.3时,你能迅速求出下列多项式的值吗?
102ab33a2b3 2ab33a2b3 2
解: 上下两面面积和 2 1.5a 2b 6ab 左右两面面积和 2 2b 2c 8bc 前后两面面积和 2 2c 1.5a 6ca
大纸盒的表面积是(6ab 8bc 6ca )cm2
整式的加减ppt课件

解:(4 5x2 3x) (2x 7x2 3)
有括号要先去括号
4 5x2 3x 2x 7x2 3
(5x2 7x2 ) (3x 2x) (4 3)
有同类项再合并同类项
2x2 x 1.
结果中不能再有同类项
练一练:求上述两多项式的差. 答案:− 12x2 + 5x + 7. 提示:对于运算结果,常将多项式按某个字母(如 x )的_降__幂__(___升__幂__)___排__列___.
本,买圆珠笔 2 支;小明买这种笔记本 4 本,买圆珠笔 3 支. 买这些笔
记本和圆珠笔,小红和小明一共花费多少钱?
思考3:小红买笔记本和圆珠笔共花费___________,小明买笔记本和圆珠笔共 花费 __________元.
思考4:小红和小明买笔记本共花费 _________元,买圆珠笔共花费 _________元.
A. 2
B.7a + 3b
C.10a + 10b
与多项式
D.12a + 8b 的和不含二次项,则
B. -2
C. 4
D.-4
4. 已知 A = 3a2 -2a + 1,B = 5a2 - 3a + 2,则2A-3B=_-_9_a_2_+__5_a_-_4__.
5. 若 mn = m + 3,则 2mn + 3m - 5mn + 10 =__1___.
2. 去括号、合并同类项; 3. 得出最后结果.
学习探究 ➢【自学】 完成《学习任务单》例4(3分钟).
例4
求
1 2
x
2
x
1 3
y2
3 2
x
1 3
《整式的加减》ppt实用课件

(2) 3x2 y 2x2 y 3xy2 2xy2
3 2 x2 y 3 2 xy2
x2 y xy2
(3) 4a2 3b2 2ab 4a2 4b2
4a2 4a2 3b2 4b2 2ab
4 4 a2 3 4b2 2ab
2
2
2
2019/5/5
13
似曾相识
若单项式2ab 与 m3 a2nb2 是同类项,则 m , n
的值分别为( A )
A. m 1 , n 12Βιβλιοθήκη C. m 5 , n 0
B. m 1 , n 1
2
D. m 1, n 0
2019/5/5
14
掂量掂量
下列说法正确的是( D ) A.单项式与单项式的和是单项式 B.单项式与单项式的和是多项式 C.多项式与多项式的和是多项式 D.整式与整式的和是整式
9、成功的道路上,肯定会有失败;对于失败,我们要正确地看待和对待,不怕失败者,则必成功;怕失败者,则一无是处,会更5、别着急要结果,先问自己够不够格,付出要配得上结果,工夫到位了,结果自然就出来了。 6、你没那么多观众,别那么累。做一个简单的人,踏实而务实。不沉溺幻想,更不庸人自扰。
7、别人对你好,你要争气,图日后有能力有所报答,别人对你不好,你更要争气望有朝一日,能够扬眉吐气。 8、奋斗的路上,时间总是过得很快,目前的困难和麻烦是很多,但是只要不忘初心,脚踏实地一步一步的朝着目标前进,最后的结局交给时间来定夺。 9、运气是努力的附属品。没有经过实力的原始积累,给你运气你也抓不住。上天给予每个人的都一样,但每个人的准备却不一样。不要羡慕那些总能撞大运的人,你必须很努力,才能遇上好运气。
整式的加减ppt35(5份) 人教版4

的取值无关, ∴1-b=0,a+2=0,解得a=-2 ,b=1. 答:a=-2 ,b=1.
9
1.计算3x2-2x+1-(3+x+3x2).
解:原式=3x2-2x+1-3-x-3x2 =3x2-3x2-2x-x+1-3=-3x-2.
2.计算(3a2+2a+1)-(2a2+3a-5)的结果是( D )
11
方法二:巧用相反数 当x=-3时,原式=a(-3)5+b(-3)3+c(-3)-5
=-35a-33b-3c-5
=7, ∴-35a-33b-3c=12, ∵(35a+33b+3c)+(-35a-33b-3c)=0, ∴(35a+33b+3c)与(-35a-33b-3c)互为相反数,
∴35a+33b+3c=-12,
2 ( 1 4 a b2 6 b c1 8 a c ) c m .
6
(2)做大纸盒比做小纸盒多用料:
( 1 2 a b 1 6 a c 2 4 b c ) ( 2 a b 2 b c 2 a c )
1 2 a b 1 6 a c 2 4 b c 2 a b 2 b c 2 a c 2 ( 1 0 a b 1 4 a c2 2 b c ) c m
大纸盒的表面积是: ( 22 a3 b 22 a4 c 2 3 b4 c )
2 ( 1 2 a b 1 6 a c 2 4 b c ) c m
(1)做这两个纸盒共用料:
( 2 a b2 b c2 a c ) ( 1 2 a b1 6 a c2 4 b c )
9
1.计算3x2-2x+1-(3+x+3x2).
解:原式=3x2-2x+1-3-x-3x2 =3x2-3x2-2x-x+1-3=-3x-2.
2.计算(3a2+2a+1)-(2a2+3a-5)的结果是( D )
11
方法二:巧用相反数 当x=-3时,原式=a(-3)5+b(-3)3+c(-3)-5
=-35a-33b-3c-5
=7, ∴-35a-33b-3c=12, ∵(35a+33b+3c)+(-35a-33b-3c)=0, ∴(35a+33b+3c)与(-35a-33b-3c)互为相反数,
∴35a+33b+3c=-12,
2 ( 1 4 a b2 6 b c1 8 a c ) c m .
6
(2)做大纸盒比做小纸盒多用料:
( 1 2 a b 1 6 a c 2 4 b c ) ( 2 a b 2 b c 2 a c )
1 2 a b 1 6 a c 2 4 b c 2 a b 2 b c 2 a c 2 ( 1 0 a b 1 4 a c2 2 b c ) c m
大纸盒的表面积是: ( 22 a3 b 22 a4 c 2 3 b4 c )
2 ( 1 2 a b 1 6 a c 2 4 b c ) c m
(1)做这两个纸盒共用料:
( 2 a b2 b c2 a c ) ( 1 2 a b1 6 a c2 4 b c )
七年级2.2整式的加减(共4课时75张ppt)

解:原式=(2-10.3)x =-8.3x
( 2) 3x x 5 x 解:原式=3 1 5x 3x
b 0.6b 2.6b ( 3)
解:原式=1 0.6 2.6b 3b
mn mn ( 4)
2
2
解:原式=(m+m)+(-n2-n2) =(1+1)m+[(-1)+(-1)]n2 =2m-2n2
2
2
y 2x y 3xy 2xy
2 2
2
2 2 ( 3 2 ) x y ( 3 2 ) xy 解: 原式=
= x y xy
2
2
2 2 2 2 4 a 3 b 2 ab 4 a 4 b ; (3 )
解: 原式= 4 a 4a 3b 4b 2ab 2 2 2ab ( 3 4 ) b = (4 4)a 2 2ab b =
即:合并同类项后,所得项的系 数是合并前各同类项的系数的 和,且字母连同它的指数不变.
例1、4 x 2 2 x 7 3 x 8 x 2 2 找出多项式中的同类项并进行合并。 思考下面问题: 每一步运算的依据是什么? 注意什么?
2 2 例1 、 4x 2x 7 3x 8x 2
3、乘法分配律(用字母表示)
a(b+c)=ab+ac
思考:反过来相等吗?
ab+ac=a(b+c)
2.2 整式的加减 合作探究
(1)运用有理数的运算律计算:
100×2+252×2=______________ (100+252)×2 =________ 352×2 =______ 704 ; 100×(-2)+252×(-2)=________________________ = (100+252)×(-2) 352×(-2) =________ -704 _____________ ; (2)根据(1)中的方法完成下面的运算,并说明其中的道理: (100+252)t =______ 352t ,根据:分配律。 100t+252t=______________
( 2) 3x x 5 x 解:原式=3 1 5x 3x
b 0.6b 2.6b ( 3)
解:原式=1 0.6 2.6b 3b
mn mn ( 4)
2
2
解:原式=(m+m)+(-n2-n2) =(1+1)m+[(-1)+(-1)]n2 =2m-2n2
2
2
y 2x y 3xy 2xy
2 2
2
2 2 ( 3 2 ) x y ( 3 2 ) xy 解: 原式=
= x y xy
2
2
2 2 2 2 4 a 3 b 2 ab 4 a 4 b ; (3 )
解: 原式= 4 a 4a 3b 4b 2ab 2 2 2ab ( 3 4 ) b = (4 4)a 2 2ab b =
即:合并同类项后,所得项的系 数是合并前各同类项的系数的 和,且字母连同它的指数不变.
例1、4 x 2 2 x 7 3 x 8 x 2 2 找出多项式中的同类项并进行合并。 思考下面问题: 每一步运算的依据是什么? 注意什么?
2 2 例1 、 4x 2x 7 3x 8x 2
3、乘法分配律(用字母表示)
a(b+c)=ab+ac
思考:反过来相等吗?
ab+ac=a(b+c)
2.2 整式的加减 合作探究
(1)运用有理数的运算律计算:
100×2+252×2=______________ (100+252)×2 =________ 352×2 =______ 704 ; 100×(-2)+252×(-2)=________________________ = (100+252)×(-2) 352×(-2) =________ -704 _____________ ; (2)根据(1)中的方法完成下面的运算,并说明其中的道理: (100+252)t =______ 352t ,根据:分配律。 100t+252t=______________
人教版七年级数学上册《整式》整式的加减PPT精品课件

解:(1) ∵25>10,
∴购买25个排球应付25a×0.8=20a(b元; ②当b>10时,应付0.8ab元.
2.1 整式
第2课时
复习导入
1.什么是单项式?单项式的系数和次数? 表示数或字母的积的式子叫做单项式.
注意:单独的一个数或一个字母也是单项式. 一个单项式中,所有字母的指数的和,叫做这
⑥x2+√13x.
其中属于多项式的有( C )
A.2 个 B.3 个 C.4 个 D.5 个
2.多项式2x4+5x2-6的项是____2_x_4_,___5_x_2__,_-_,6 常数项是 ______-. 6
课堂小结
(1)利用定义判定多项式,其关键是看式子是否是单项式的和,是 哪几个单项式的和; (2)多项式是由单项式组成的,但不能说多项式包含单项式,它们 是两个不同的概念,没有从属关系.
属于单项式的是___①__②___⑤__⑦________(填序号). 属于多项式的是____④__⑥___⑧_________(填序号). 属于整式的是_①___②___④__⑤___⑥__⑦___⑧___(填序号).
课堂小结
1.几个单项式的和叫做多项式 2.在多项式中,每个单项式叫做多项式的项 3.不含字母的项叫做常数项 4.多项式里次数最高项的次数就是多项式的次数
=392.5 这个圆环的面积是392.5 cm2.
应用提高
如图,文化广场上摆了一些桌子,若并排摆n张桌 子,可同时容纳多少人?当n=20时,可同时容纳多
少人?
……
1张桌子
2张桌子
3张桌子
解:并排摆n张桌子,可同时容纳(4n+2)人. 当n=20时, 4n+2=4×20+2=82
此时,可同时容纳82人.
∴购买25个排球应付25a×0.8=20a(b元; ②当b>10时,应付0.8ab元.
2.1 整式
第2课时
复习导入
1.什么是单项式?单项式的系数和次数? 表示数或字母的积的式子叫做单项式.
注意:单独的一个数或一个字母也是单项式. 一个单项式中,所有字母的指数的和,叫做这
⑥x2+√13x.
其中属于多项式的有( C )
A.2 个 B.3 个 C.4 个 D.5 个
2.多项式2x4+5x2-6的项是____2_x_4_,___5_x_2__,_-_,6 常数项是 ______-. 6
课堂小结
(1)利用定义判定多项式,其关键是看式子是否是单项式的和,是 哪几个单项式的和; (2)多项式是由单项式组成的,但不能说多项式包含单项式,它们 是两个不同的概念,没有从属关系.
属于单项式的是___①__②___⑤__⑦________(填序号). 属于多项式的是____④__⑥___⑧_________(填序号). 属于整式的是_①___②___④__⑤___⑥__⑦___⑧___(填序号).
课堂小结
1.几个单项式的和叫做多项式 2.在多项式中,每个单项式叫做多项式的项 3.不含字母的项叫做常数项 4.多项式里次数最高项的次数就是多项式的次数
=392.5 这个圆环的面积是392.5 cm2.
应用提高
如图,文化广场上摆了一些桌子,若并排摆n张桌 子,可同时容纳多少人?当n=20时,可同时容纳多
少人?
……
1张桌子
2张桌子
3张桌子
解:并排摆n张桌子,可同时容纳(4n+2)人. 当n=20时, 4n+2=4×20+2=82
此时,可同时容纳82人.
整式的加减课件PPT

1、下列各式中,与-3 x 2 y 是同类项的是
(c )
A.xy 2 B.2xy C. x2 y D.3x2 y 2
2、如果 3x k y 与 x 2 y 是同类项, 则 k= 2 .
把多项式中的__同__类__项____合并成一项, 叫做合并同类项.如
4x2 2x 7 3x2 8x 2
=( 4-4 ) a 2 +( 3-4 ) b 2 + 2ab
= -b2+2ab .
计算:
(1)12x 20x
解:原式=(12-20)x =-8x
(2) x 7x 5x
解:原式=(1+7-5)x=3x
(3) 5a 0.3a 2.7a 解:原式=(-5+0.3-2.7)a=-7.4a
(4) 1 y 2 y 2y 33
-2a+0.5a=-1.5a(cm) 所以,这两天水位总的变化情况为 下降了-1.5a .
(2)某商店原有5袋大米,每袋大米为 xkg , 上午卖出3袋,下午又购进同样包装的大米4袋. 进货后这个商店有大米多少千克?
解:(2) 把进货的数量记为正,售出的数量记 为负.
商店原有大米量为_____千克;售出大米量 为_____千克,
(2) 3x2 y 2x2 y 3xy 2 2xy 2 解:原式=(-3+2 )x 2 y +( 3-2 )xy 2
=___x__2 y___x _y_2 __________.
(3) 4a2 3b2 2ab 4a2 4b2
解:原式=( 4a2-4a2 )+( 3b2-4b2 )+ 2ab
3、合并同类项可简记为:系数 相加 ,字母 连同它的指数 不变 .
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题讲解
例7 笔记本的单价是x元,圆珠笔的单价是
y元.小红买3本笔记本,2支圆珠笔;小明买 4本笔记本,3支圆珠笔.买这些笔记本和圆珠
笔,小红和小明一共花费多少钱? 解法1:小红花 (3x+2y)元,小明花 (4x+3y)元, 一共花 (7x+5y)元. 解法2:买笔记本花费 (3x+4x) 元,买圆珠笔 花费(2y+3y) 元,一共花费 (7x+5y) 元.
(3)原式 7a2b 4a2b 5ab2 4a2b 6ab2
7a2b ab2.
第二章 整式的加减 2.2 整式的加减
第4课时 整式的加减
创设情境
1.某学生合唱团出场时第一排站了n人,从第 二排起每一排都比前面一排多1人,一共站了 四排,则该合唱团一共有多少名学生参加?
答案:[n+(n+1)+(n+2)+(n+3)].
x5
(3)-5a (3a 2) (3a 7) 5a 5
(4) 1 (9 y 3) 2( y 1) 3
5y 1
2.飞机的无风航速为a km/h,风速为 20 km/h.飞机顺风飞行4 h的行程是多少? 飞机逆风飞行3 h的行程是多少?两个行程 相差多少? 解:顺风航速=无风航速_+__风速=(_x_+_2_0_)_k__m_/_h_. 逆风航速=无风航速_-__风速=_(_x_-_2_0_)__km/_h_. 飞机顺风飞行4 h的行程是 4(x+20)=(4x+80)km. 飞机逆风飞行3 h的行程是 3(x-20)=(3x-60)km. 两个行程相差(4x+80)-(3x-60)= (x+140)km.
能进一步 化简吗?
4n+6
实际应用
例8 做大小两个长方体纸盒,尺寸如下(单
位:cm):
长
宽
1.5a 2b
2c
(1)做这两个纸盒共用料多少平方厘米? (2)做大纸盒比做小纸盒多用料多少平方厘米?
实际应用
解:小纸盒的表面积是(2ab+2bc+2ac)cm², 大纸盒的表面积是(6ab+8bc+6ca)cm². (1)做这两个纸盒共用料(单位:cm²) (2ab+2bc+2ac)+(6ab+8bc+6ca)=8ab+10bc+8ca. (2)做大纸盒比做小纸盒多用料(单位:cm²) (6ab+8bc+6ca)-(2ab+2bc+2ca)=(4ab+6bc+4ca).
23
解:5(3a2b ab2 ) (ab2 3a2b)
15a2b 5ab2 ab2 - 3a2b
12a2b - 6ab2.
当a 1 , b 1 时,
2
3
原式
12
1 2
2
1 3
-6
1 3
2
1 2
2. 3
课堂小结
整式加减的一般步骤:
(1)如果有括号,那么先去括号; (2)观察有无同类项; (3)利用加法的交换律和结合律,分组同类项; (4)合并同类项.
课堂练习 1.计算:
(1)3xy 4xy (2xy); (2) 1 ab 1 a2 1 a2 ( 2 ab).
343
3
解:(1)3xy 4xy (2xy)
3xy 4xy 2xy
xy.
(2) 1 ab 1 a 2 1 a 2 ( 2 ab)
3
4
3
3
1 ab 1 a 2 1 a 2 2 ab
特别地,对于形如+(10a+b),-(10a
+b)的式子,可以将因数看作1,-1.
运用法则
例4 化简下列各式:
(1)8a+2b+(5a-b);(2)(5a-3b)-3(a2-2b).
解(1)8a+2b+(5a-b) =8a+2b+5a-b =13a+b;
(2)(5a-3b)-3(a2-2b) =(5a-3b)-(3a2-6b) =5a-3b-3a2+6b =-3a2+5a+3b.
x y z.
(2)a2 2ab b2 (a2 2ab b2 );
(2)原式 a2 2ab b2 a2 2ab-b2
4ab.
(3)3(2x2 y2 ) 2(3y2 2x2 ).
(3)原式 6 x2 3 y 2 6 y 2 4 x2
10 x2 9 y 2
课堂练习4.化简:
简单地讲就是:去括号、合并同类项.
注意:整式加减运算的结果仍然是整式.
练习
如图的长方体盒子,长、宽、高分别是a, b,c.如果用如图的两种方法捆绑起来,哪种 方法用的绳子长?
4a+6b+2c
2a+6b+4c
若a>c,则第一种方法用的绳子长;
若a<c,则第二种方法用的绳子长.
例9 求 1 x 2(x 1 y2 ) ( 3 x 1 y2 )
2
的值,其中
3 x 2, y
(2)(8a-7b)-(4a-5b).
解:(1)( 2x-3y)+(5x+4y)
=2x-3y+5x+4y 去括号
=2x+5x-3y+4y
找同类项
=7x+y.
合并同类项
例题讲解
(2)(8a-7b)-(4a-5b)
=8a-7b-4a+5b
去括号
=8a-4a-7b+5b
加法交换律
=4a-2b.
合并同类项
课堂小结
如果括号外的因数是正数,去括号后 原括号内各项的符号与原来的符号相同;
如果括号外的因数是负数,去括号后 原括号内各项的符号与原来的符号相反.
第二章 整式的加减 2.2 整式的加减
第3课时 去括号法则的应用
复习提问 ①合并同类项法则的内容是什么? ②去括号法则的内容是什么?
例题讲解
例6 (1)(2x-3y)+(5x+4y);
2.
2
3
3
解:1 x 2(x 1 y2 ) ( 3 x 1 y2 )
2
3
23
1 x 2x 2 y2 3 x 1 y2
2
3 23
去括号
3x y2.
合并同类项
当x 2, y 2 时
3
原式
(3) (2)
2 3
2
6
4 9
6
4. 9
课堂练习
1.先化简下式,再求值:
5(3a2b ab2 ) (ab2 3a2b), 其中a 1 ,b 1 .
解:(1) 2 h后两船相距(单位:km) 2(50+a)+2(50-a) =100+2a+100-2a =200.
(2) 2 h后甲船比乙船多航行(单位:km) 2(50+a)-2(50-a)
=100+2a-100+2a =4a.
巩固练习
1.化简:
(1)12(x 0.5)
12x 6
(2) 5(1 1 x) 5
例5 两船从同一港口同时出发反向而
行,甲船顺水,乙船逆水,两船在静水中的
速度都是50 km/h,水流速度是a km/h. (1) 2 h后两船相距多远? (2) 2 h后甲船比乙船多航行多少千米? 想一想:顺水航速、逆水航速与船速、水速
之间有什么关系? 顺水航速=船速十水速=(50+a) km/h 逆水航速=船速-水速=(50-a) km/h
100u-120(u-0.5) =100u-(120u-60) =100u-120u+60 =-20u+60.
观察以上各式,在去括号的过程中你发 现有什么规律?
归纳去括号法则
如果括号外的因数是正数,去括号 后原括号内各项的符号与原来的符号相 同;如果括号外的因数是负数,去括号 后原括号内各项的符号与原来的符号相 反.
(2)(3a2 ab 7) 4a2 2ab 7
3a2 ab 7 4a2 2ab-7 7a2 3ab.
课堂练习 3.先去括号,再合并同类项.
(1)(x y z) (x y z) (x y z);
解:(1)原式 x y z x y z x y z
3
4
3
3
1 a 2 1 ab.
12
3
课堂练习 2.计算: (1)(x 2x2 5) (4x2 3 6x);
(2)(3a2 ab 7) 4a2 2ab 7 .
解:(1)(x 2x2 5) (4x2 3 6x) x 2x2 5 4x2 3 6x 6x2 7 x 2.
差是10b+a-(10a+b) 和是10b+a+(10a+b)
=10b+a-10a-b
=10b+a+10a+b
=9b-9a.
=11a+11b.
化简:100u+120(u-0.5) 100u-120(u-0.5)
解:100u+120(u-0.5) =100u+(120u-60) =100u+120u-60 =220u-60.
第二章 整式的加减 2.2 整式的加减
第2课时 去括号法则
创设情境
数学爱好者发现了一个非常有趣的现象, 将一个两位数的个位和十位对调得到一个新 的两位数以后,这两个数的差能被9整除,和 能被11整除.这是为什么呢?
如果设这个两位数的个位数字是a,十位 数字是b,如何表示这个两位数呢?
创设情境
原数是10b+a 新数10a+b
