高中计算能力提升专项练习
高中提高计算能力的好题

解不等式:1. 2. 3.(x+3)(1﹣x )≥04. 5.6.7.8. 9.10. 11.12.11023x x ⎛⎫⎛⎫--> ⎪⎪⎝⎭⎝⎭()12303x x ⎛⎫+-≤ ⎪⎝⎭512x >+2340x x -++<()()230x x -->3121x x ≤+x(1-2x)>013. 14. 15.﹣2x2﹣x+6≥0 16. 17.18.19. 20. 21、30 2xx-≥-22、2113xx->+23.3113xx+>--24.2112xx->-+2230x x--+≤211x<+132xx+≥-25.解不等式. 26.解关于的不等式:,.27.若不等式的解集为,则的值是28.不等式的解集为,则不等式的解集为29.已知关于x 的不等式ax 2+bx+c >0的解集为{x|1<x <2},则不等式cx 2﹣bx+a >0的解集为 .30.解已知关于x 的不等式 x 2﹣(a 2+3a+2)x+3a (a 2+2)<0(a ∈R ).31.已知函数, ()2220x ax a a R --≤∈x 2104ax x --≥0a ≠220ax bx ++>11{|}23x x -<<a b +220ax bx ++>{|12}x x -<<220x bx a ++<()()2228,2416f x x x g x x x =--=--(1)求不等式的解集;(2)若对一切,均有成立,求实数的取值范围.32.解关于x 的不等式33.已知不等式.(1)若,解该不等式;(2)讨论下,该不等式的解集.34.已知函数(). (1)若不等式的解集为,求的取值范围;(2)当时,解不等式;35.已知,解不等式;()0g x <5x >()()215f x m x m ≥+--m ()()()20.x a x a a R --<∈()()2110ax a x a R x -++>∈2a =-a R ∈()()211f x m x mx m =+-+-m R ∈()0f x <∅m 2m >-()f x m ≥()31f x x x =-++()6f x ≥36.已知函数的一个零点为2.求不等式的解集;37.已知关于的不等式(其中).当时,求不等式的解集;38.已知函数,解不等式;39.已知函数.求不等式的解集;()()130f x x a x a =-+--≠()2f x ≤x 2211log x x a +--≤0a >4a =()231f x x x =++-()4f x >()2221f x x x =-++()7f x >。
高中数学计算题专项练习一

高中数学计算题专项练习一高中数学计算题专项练习一一.解答题(共30小题)1.(Ⅰ)求值:;(Ⅰ)解关于x的方程.2.(1)若=3,求的值;(2)计算的值.3.已知,b=(log43+log83)(log32+log92),求a+2b的值.4.化简或计算:(1)()﹣[3×()0]﹣1﹣[81﹣0.25+(3)]﹣10×0.027;(2).5.计算的值.6.求下列各式的值.(1)(2)已知x+x﹣1=3,求式子x2+x﹣2的值.7.(文)(1)若﹣2x2+5x﹣2>0,化简:(2)求关于x的不等式(k2﹣2k+)x<(k2﹣2k+)1ˉx的解集.8.化简或求值:(1)3a b(﹣4a b)÷(﹣3a b);(2).9.计算:(1);(2)(lg8+lg1000)lg5+3(lg2)2+lg6﹣1+lg0.006.10.计算(1)(2).11.计算(1)(2).12.解方程:log2(x﹣3)﹣=2.13.计算下列各式(Ⅰ)lg24﹣(lg3+lg4)+lg5(Ⅰ).14.求下列各式的值:(1)(2).15.(1)计算(2)若xlog34=1,求4x+4﹣x的值.16.求值:.17.计算下列各式的值(1)0.064﹣(﹣)0+160.75+0.25(2)lg25+lg5•lg4+lg22.18.求值:+.19.(1)已知a>b>1且,求log a b﹣log b a的值.(2)求的值.20.计算(1)(2)(lg5)2+lg2×lg50 21.不用计算器计算:.22.计算下列各题(1);(2).23.解下列方程:(1)lg(x﹣1)+lg(x﹣2)=lg(x+2);(2)2•(log3x)2﹣log3x﹣1=0.24.求值:(1)(2)2log525﹣3log264.25.化简、求值下列各式:(1)•(﹣3)÷;(2)(注:lg2+lg5=1).26.计算下列各式(1);(2).27.(1)计算;(2)设log23=a,用a表示log49﹣3log26.28.计算下列各题:(1);(2)lg25+lg2lg50.29.计算:(1)lg25+lg2•lg50;(2)30++32×34﹣(32)3.30.(1)计算:;(2)解关于x的方程:.高中数学计算题专项练习一参考答案与试题解析一.解答题(共30小题)1.(Ⅰ)求值:;(Ⅰ)解关于x的方程.考点:有理数指数幂的化简求值.专题:计算题.分析:(Ⅰ)利用对数与指数的运算法则,化简求值即可.(Ⅰ)先利用换元法把问题转化为二次方程的求解,解方程后,再代入换元过程即可.解答:(本小题满分13分)解:(Ⅰ)原式=﹣1++log2=﹣1﹣1+23=﹣1+8+=10.…(6分)(Ⅰ)设t=log2x,则原方程可化为t2﹣2t﹣3=0…(8分)即(t﹣3)(t+1)=0,解得t=3或t=﹣1…(10分)Ⅰlog2x=3或log2x=﹣1Ⅰx=8或x=…(13分)点评:本题考查有理指数幂的化简求值以及换元法解方程,是基础题.要求对基础知识熟练掌握.2.(1)若=3,求的值;(2)计算的值.考点:有理数指数幂的化简求值.专题:计算题.分析:(1)利用已知表达式,通过平方和与立方差公式,求出所求表达式的分子与分母的值,即可求解.(2)直接利用指数与对数的运算性质求解即可.解答:解:(1)因为=3,所以x+x﹣1=7,所以x2+x﹣2=47,=()(x+x﹣1﹣1)=3×(7﹣1)=18.所以==.(2)=3﹣3log22+(4﹣2)×=.故所求结果分别为:,点评:本题考查有理数指数幂的化简求值,立方差公式的应用,考查计算能力.3.已知,b=(log43+log83)(log32+log92),求a+2b的值.考点:有理数指数幂的化简求值;对数的运算性质.专题:计算题.分析:直接利用有理指数幂的运算求出a,对数运算法则求出b,然后求解a+2b的值解答:解:==.b=(log43+log83)(log32+log92)=(log23+log23)(log32+log32)==,Ⅰ,,Ⅰa+2b=3.点评:本题考查指数与对数的运算法则的应用,考查计算能力.4.化简或计算:(1)()﹣[3×()0]﹣1﹣[81﹣0.25+(3)]﹣10×0.027;(2).考点:有理数指数幂的化简求值.专题:计算题.分析:根据有理数指数幂的运算法则进行化简求值即可.解答:解:(1)原式=﹣(3×1)﹣1﹣﹣10×=﹣﹣1﹣3=﹣1.(2)原式=+﹣2=+﹣2=﹣2+﹣2.点评:本题考查有理数指数幂的运算法则,考查学生的运算能力,属基础题,熟记有关运算法则是解决问题的基础.5.计算的值.考点:有理数指数幂的化简求值.专题:计算题.分析:根据分数指数幂运算法则进行化简即可.解答:解:原式===.点评:本题主要考查用分数指数幂的运算法则进行化简,要求熟练掌握分数指数幂的运算法则.6.求下列各式的值.(1)(2)已知x+x﹣1=3,求式子x2+x﹣2的值.考点:有理数指数幂的化简求值.专题:计算题.分析:(1)直接利用有理指数幂的运算性质和对数的运算性质化简求值.(2)把已知的等式两边平方即可求得x2+x﹣2的值.解答:解:(1)==;(2)由x+x﹣1=3,两边平方得x2+2+x﹣2=9,所以x2+x﹣2=7.点评:本题考查了有理指数幂的化简求值,考查了对数的运算性质,是基础的计算题.7.(文)(1)若﹣2x2+5x﹣2>0,化简:(2)求关于x的不等式(k2﹣2k+)x<(k2﹣2k+)1ˉx的解集.考点:指数函数的单调性与特殊点;方根与根式及根式的化简运算.专题:计算题;转化思想.分析:(1)由﹣2x2+5x﹣2>0,解出x的取值范围,判断根号下与绝对值中数的符号,进行化简.(2)先判断底数的取值范围,由于底数大于1,根据指数函数的单调性将不等式进行转化一次不等式,求解即可.解答:解:(1)Ⅰ﹣2x2+5x﹣2>0Ⅰ,Ⅰ原式===(8分)(2)Ⅰ,Ⅰ原不等式等价于x<1﹣x,Ⅰ此不等式的解集为(12分)点评:本题考查指数函数的单调性与特殊点,求解本题的关键是判断底数的符号,以确定函数的单调性,熟练掌握指数函数的单调性是正确转化的根本.8.化简或求值:(1)3a b(﹣4a b)÷(﹣3a b);(2).考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)利用分数指数幂的运算法则即可得出;(2)利用对数的运算法则和lg2+lg5=1即可得出.解答:解:(1)原式==4a.(2)原式=+50×1=lg102+50=52.点评:本题考查了分数指数幂的运算法则、对数的运算法则和lg2+lg5=1等基础知识与基本技能方法,属于基础题.9.计算:(1);(2)(lg8+lg1000)lg5+3(lg2)2+lg6﹣1+lg0.006.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)先将每一个数化简为最简分数指数幂的形式,再利用运算性质化简.(2)先将每一个对数式化简,再利用对数运算性质化简.解答:解:(1)===﹣45;(2)(lg8+lg1000)lg5+3(lg2)2+lg6﹣1+lg0.006=(3lg2+3)•lg5+3(lg2)2﹣lg6+(lg6﹣3)=3lg2•lg5+3lg5+3(lg2)2﹣3=3lg2(lg5+lg2)+3lg5﹣3=3lg2+3lg5﹣3=3﹣3=0.点评:本题考察运算性质,做这类题目最关键的是平时练习时要细心、耐心、不怕麻烦,考场上才能熟练应对!10.计算(1)(2).考点:对数的运算性质;有理数指数幂的化简求值.专题:函数的性质及应用.分析:(1)利用指数幂的运算性质即可得出;(2)利用对数函数的运算性质即可得出.解答:解:(1)原式=|2﹣e|﹣+﹣=e﹣2﹣+=e﹣2﹣e+=﹣2.(2)原式=+3=﹣4+3=2﹣4+3=1.点评:熟练掌握指数幂的运算性质、对数函数的运算性质是解题的关键.11.计算(1)(2).考点:对数的运算性质;有理数指数幂的运算性质.专题:计算题.分析:(1)直接利用对数的运算法则求解即可.(2)直接利用有理指数幂的运算法则求解即可.解答:解:(1)==(2)==9×8﹣27﹣1=44.点评:本题考查对数的运算法则、有理指数幂的运算法则的应用,考查计算能力.12.解方程:log2(x﹣3)﹣=2.考点:对数的运算性质.专题:计算题.分析:由已知中log2(x﹣3)﹣=2,由对数的运算性质,我们可得x2﹣3x﹣4=0,解方程后,检验即可得到答案.解答:解:若log2(x﹣3)﹣=2.则x2﹣3x﹣4=0,…(4分)解得x=4,或x=﹣1(5分)经检验:方程的解为x=4.…(6分)点评:本题考查的知识点是对数的运算性质,其中利用对数的运算性质,将已知中的方程转化为整式方程是解答醒的关键,解答时,易忽略对数的真数部分大于0,而错解为4,或﹣1.13.计算下列各式(Ⅰ)lg24﹣(lg3+lg4)+lg5(Ⅰ).考点:对数的运算性质;根式与分数指数幂的互化及其化简运算.专题:计算题.分析:(Ⅰ)利用对数的运算的性质可得结果;(Ⅰ)利用指数幂的运算性质可得结果;解答:解:(Ⅰ)lg24﹣(lg3+lg4)+lg5=lg24﹣lg12+lg5=lg=lg10=1;(Ⅰ)=×+﹣﹣1=32×23+3﹣2﹣1=72.点评:本题考查对数的运算性质、指数幂的运算性质,考查学生的运算能力,属基础题.14.求下列各式的值:(1)(2).考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:根据对数和指数的运算法则进行求解即可.解答:解:(1)原式==log﹣9=log39﹣9=2﹣9=﹣7.(2)原式=== =.点评:本题主要考查对数和指数幂的计算,要求熟练掌握对数和指数幂的运算法则.15.(1)计算(2)若xlog34=1,求4x+4﹣x的值.考点:对数的运算性质;根式与分数指数幂的互化及其化简运算.分析:(1)利用指数幂的运算性质即可;(2)利用指数式和对数式的互化和运算性质即可.解答:解:(1)原式===3.(2)由xlog34=1,得x=log43,Ⅰ4x=3,,Ⅰ4x+4﹣x==.点评:熟练掌握对数和指数幂的运算性质是解题的关键.16.求值:.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:根据有理数指数幂的定义,及对数的运算性质,即可求出的值.解答:解:原式…(4分)…(3分)=…(1分)点评:本题考查的知识点是对数的运算性质,有理数指数幂的化简求值,其中掌握指数的运算性质和对数的运算性质,是解答本题的关键.17.计算下列各式的值(1)0.064﹣(﹣)0+160.75+0.25(2)lg25+lg5•lg4+lg22.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)利用指数幂的运算性质可求;(2)利用对数运算性质可求;解答:解:(1)原式==0.4﹣1+8+=;(2)原式=lg25+2lg5•lg2+lg22=(lg5+lg2)2=(lg10)2=1点评:本题考查对数的运算性质、有理数指数幂的运算,属基础题,熟记有关运算性质是解题基础.18.求值:+.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:直接利用对数的运算法则,求出表达式的值即可.解答:解:原式==3+9+2000+1=2013.点评:本题考查对数的运算法则的应用,基本知识的考查.19.(1)已知a>b>1且,求log a b﹣log b a的值.(2)求的值.考点:对数的运算性质.专题:计算题.分析:(1)通过a>b>1利用,平方,然后配出log a b﹣log b a的表达式,求解即可.(2)直接利用对数的运算性质求解的值解答:解:(1)因为a>b>1,,所以,可得,a>b>1,所以log a b﹣log b a<0.所以log a b﹣log b a=﹣(2)==﹣4.点评:本题考查对数与指数的运算性质的应用,整体思想的应用,考查计算能力.20.计算(1)(2)(lg5)2+lg2×lg50考点:对数的运算性质;根式与分数指数幂的互化及其化简运算;有理数指数幂的化简求值.专题:计算题.分析:(1)把根式转化成指数式,然后利用分数指数幂的运算法则进行计算.(2)先把lg50转化成lg5+1,然后利用对数的运算法则进行计算.解答:解:(1)===(6分)(2)(lg5)2+lg2×lg50=(lg5)2+lg2×(lg5+lg10)=(lg5)2+lg2×lg5+lg2=lg5(lg5+lg2)+lg2=lg5+lg2=1(12分)点评:本题考查对数的运算法则和根式与分数指数幂的互化,解题时要注意合理地进行等价转化.21.不用计算器计算:.考点:对数的运算性质.专题:计算题.分析:,lg25+lg4=lg100=2,,(﹣9.8)0=1,由此可以求出的值.解答:解:原式=(4分)=(8分)=(12分)点评:本题考查对数的运算性质,解题时要认真审题,注意公式的灵活运用.22.计算下列各题(1);(2).考点:对数的运算性质.专题:计算题.分析:(1)直接利用对数的运算性质求解表达式的值.(2)利用指数的运算性质求解表达式的值即可.解答:解:(1)==9+﹣1=(2)===﹣45.点评:本题考查指数与对数的运算性质的应用,考查计算能力.23.解下列方程:(1)lg(x﹣1)+lg(x﹣2)=lg(x+2);(2)2•(log3x)2﹣log3x﹣1=0.考点:对数的运算性质.专题:计算题.分析:(1)先根据对数运算性质求出x,再根据对数的真数一定大于0检验即可.(2)设log3x=y,得出2y2﹣y﹣1=0,求出y的值,再由对数的定义求出x的值即可.解答:解:(1)原方程可化为lg(x﹣1)(x﹣2)=lg(x+2)所以(x﹣1)(x﹣2)=x+2即x2﹣4x=0,解得x=0或x=4经检验,x=0是增解,x=4是原方程的解.所以原方程的解为x=4(2)设log3x=y,代入原方程得2y2﹣y﹣1=0.解得y1=1,.log3x=1,得x1=3;由,得.经检验,x1=3,都是原方程的解.点评:本题主要考查对数的运算性质和对数函数的定义域问题.属基础题.24.求值:(1)(2)2log525﹣3log264.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)首先变根式为分数指数幂,然后拆开运算即可.(2)直接利用对数式的运算性质化简求值.解答:解:(1)====.(2)2log525﹣3log264==4﹣3×6=﹣14.点评:本题考查了对数式的运算性质,考查了有理指数幂的化简求值,解答的关键是熟记有关性质,是基础题.25.化简、求值下列各式:(1)•(﹣3)÷;(2)(注:lg2+lg5=1).考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)利用指数幂的运算性质化简即可;(2)利用对数的运算性质化简即可.解答:解:(1)原式=﹣b﹣3÷(4)…..3分=﹣…..7分(2)解原式=…..2分=…..4分=…..6分=….7分.点评:本题考查对数的运算性质,考查有理数指数幂的化简求值,熟练掌握其运算性质是化简的基础,属于基础题.26.计算下列各式(1);(2).考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)利用指数幂的运算法则即可得出;(2)利用对数的运算法则和换底公式即可得出.解答:解:(1)原式=﹣1﹣+=.(2)原式=+lg(25×4)+2+1==.点评:本题考查了指数幂的运算法则、对数的运算法则和换底公式,属于基础题.27.(1)计算;(2)设log23=a,用a表示log49﹣3log26.考点:对数的运算性质;根式与分数指数幂的互化及其化简运算.专题:计算题.分析:(1)把第一、三项的底数写成平方、立方的形式即变成幂的乘方运算,第二项不等于0根据零指数的法则等于1,化简求值即可;(2)把第一项利用换底公式换成以2为底的对数,第二项利用对数函数的运算性质化简,log23整体换成a即可.解答:解:(1)原式=+1+=+1+=4;(2)原式=﹣3log22×3=log23﹣3(1+log23)=a﹣3(1+a)=﹣2a﹣3.点评:本题是一道计算题,要求学生会进行根式与分数指数幂的互化及其运算,会利用换底公式及对数的运算性质化简求值.做题时注意底数变乘方要用到一些技巧.28.计算下列各题:(1);(2)lg25+lg2lg50.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)利用指数的运算法则,直接求解表达式的值即可.(2)利用对数的运算性质,直接化简求解即可.解答:解:(1)原式===.(5分)(2)原式lg25+lg2lg50=lg25+2lg2lg5+lg25=(lg2+lg5)2=1 (5分)点评:本题考查对数的运算性质,有理数指数幂的化简求值,考查计算能力.29.计算:(1)lg25+lg2•lg50;(2)30++32×34﹣(32)3.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题;函数的性质及应用.分析:(1)直接利用对数的运算性质即可求解(2)直接根据指数的运算性质即可求解解答:解:(1)原式=lg25+lg2(1+lg5)=lg25+lg2lg5+lg2=lg5(lg5+lg2)+lg2=lg5+lg2=1(2)原式=1+3+36﹣36=4.…(14分)点评:本题主要考查了对数的运算性质及指数的运算性质的简单应,属于基础试题30.(1)计算:;(2)解关于x的方程:.考点:对数的运算性质;有理数指数幂的运算性质;有理数指数幂的化简求值;函数的零点.专题:计算题.分析:(1)根据分数指数幂运算法则进行化简即可.(2)利用对数函数的性质和对数的运算法则进行计算即可.解答:解:(1)原式==﹣3;(2)原方程化为log5(x+1)+log5(x﹣3)=log55,从而(x+1)(x﹣3)=5,解得x=﹣2或x=4,经检验,x=﹣2不合题意,故方程的解为x=4.点评:本题主要考查分数指数幂和对数的运算,要求熟练掌握分数指数幂和对数的运算法则.。
(完整word版)高中数学计算题专项练习一(3)

高中数学计算题专项练习一高中数学计算题专项练习一一.解答题(共30小题)1.(Ⅰ)求值:;(Ⅰ)解关于x的方程.2.(1)若=3,求的值;(2)计算的值.3.已知,b=(log43+log83)(log32+log92),求a+2b的值.4.化简或计算:(1)()﹣[3×()0]﹣1﹣[81﹣0.25+(3)]﹣10×0.027;(2).5.计算的值.6.求下列各式的值.(1)(2)已知x+x﹣1=3,求式子x2+x﹣2的值.7.(文)(1)若﹣2x2+5x﹣2>0,化简:(2)求关于x的不等式(k2﹣2k+)x<(k2﹣2k+)1ˉx的解集.8.化简或求值:(1)3a b(﹣4a b)÷(﹣3a b);(2).9.计算:(1);(2)(lg8+lg1000)lg5+3(lg2)2+lg6﹣1+lg0.006.10.计算(1)(2).11.计算(1)(2).12.解方程:log2(x﹣3)﹣=2.13.计算下列各式(Ⅰ)lg24﹣(lg3+lg4)+lg5(Ⅰ).14.求下列各式的值:(1)(2).15.(1)计算(2)若xlog34=1,求4x+4﹣x的值.16.求值:.17.计算下列各式的值(1)0.064﹣(﹣)0+160.75+0.25(2)lg25+lg5•lg4+lg22.18.求值:+.19.(1)已知a>b>1且,求log a b﹣log b a的值.(2)求的值.20.计算(1)(2)(lg5)2+lg2×lg50 21.不用计算器计算:.22.计算下列各题(1);(2).23.解下列方程:(1)lg(x﹣1)+lg(x﹣2)=lg(x+2);(2)2•(log3x)2﹣log3x﹣1=0.24.求值:(1)(2)2log525﹣3log264.25.化简、求值下列各式:(1)•(﹣3)÷;(2)(注:lg2+lg5=1).26.计算下列各式(1);(2).27.(1)计算;(2)设log23=a,用a表示log49﹣3log26.28.计算下列各题:(1);(2)lg25+lg2lg50.29.计算:(1)lg25+lg2•lg50;(2)30++32×34﹣(32)3.30.(1)计算:;(2)解关于x的方程:.高中数学计算题专项练习一参考答案与试题解析一.解答题(共30小题)1.(Ⅰ)求值:;(Ⅰ)解关于x的方程.考点:有理数指数幂的化简求值.专题:计算题.分析:(Ⅰ)利用对数与指数的运算法则,化简求值即可.(Ⅰ)先利用换元法把问题转化为二次方程的求解,解方程后,再代入换元过程即可.解答:(本小题满分13分)解:(Ⅰ)原式=﹣1++log2=﹣1﹣1+23=﹣1+8+=10.…(6分)(Ⅰ)设t=log2x,则原方程可化为t2﹣2t﹣3=0…(8分)即(t﹣3)(t+1)=0,解得t=3或t=﹣1…(10分)Ⅰlog2x=3或log2x=﹣1Ⅰx=8或x=…(13分)点评:本题考查有理指数幂的化简求值以及换元法解方程,是基础题.要求对基础知识熟练掌握.2.(1)若=3,求的值;(2)计算的值.考点:有理数指数幂的化简求值.专题:计算题.分析:(1)利用已知表达式,通过平方和与立方差公式,求出所求表达式的分子与分母的值,即可求解.(2)直接利用指数与对数的运算性质求解即可.解答:解:(1)因为=3,所以x+x﹣1=7,所以x2+x﹣2=47,=()(x+x﹣1﹣1)=3×(7﹣1)=18.所以==.(2)=3﹣3log22+(4﹣2)×=.故所求结果分别为:,点评:本题考查有理数指数幂的化简求值,立方差公式的应用,考查计算能力.3.已知,b=(log43+log83)(log32+log92),求a+2b的值.考点:有理数指数幂的化简求值;对数的运算性质.专题:计算题.分析:直接利用有理指数幂的运算求出a,对数运算法则求出b,然后求解a+2b的值解答:解:==.b=(log43+log83)(log32+log92)=(log23+log23)(log32+log32)==,Ⅰ,,Ⅰa+2b=3.点评:本题考查指数与对数的运算法则的应用,考查计算能力.4.化简或计算:(1)()﹣[3×()0]﹣1﹣[81﹣0.25+(3)]﹣10×0.027;(2).考点:有理数指数幂的化简求值.专题:计算题.分析:根据有理数指数幂的运算法则进行化简求值即可.解答:解:(1)原式=﹣(3×1)﹣1﹣﹣10×=﹣﹣1﹣3=﹣1.(2)原式=+﹣2=+﹣2=﹣2+﹣2.点评:本题考查有理数指数幂的运算法则,考查学生的运算能力,属基础题,熟记有关运算法则是解决问题的基础.5.计算的值.考点:有理数指数幂的化简求值.专题:计算题.分析:根据分数指数幂运算法则进行化简即可.解答:解:原式===.点评:本题主要考查用分数指数幂的运算法则进行化简,要求熟练掌握分数指数幂的运算法则.6.求下列各式的值.(1)(2)已知x+x﹣1=3,求式子x2+x﹣2的值.考点:有理数指数幂的化简求值.专题:计算题.分析:(1)直接利用有理指数幂的运算性质和对数的运算性质化简求值.(2)把已知的等式两边平方即可求得x2+x﹣2的值.解答:解:(1)==;(2)由x+x﹣1=3,两边平方得x2+2+x﹣2=9,所以x2+x﹣2=7.点评:本题考查了有理指数幂的化简求值,考查了对数的运算性质,是基础的计算题.7.(文)(1)若﹣2x2+5x﹣2>0,化简:(2)求关于x的不等式(k2﹣2k+)x<(k2﹣2k+)1ˉx的解集.考点:指数函数的单调性与特殊点;方根与根式及根式的化简运算.专题:计算题;转化思想.分析:(1)由﹣2x2+5x﹣2>0,解出x的取值范围,判断根号下与绝对值中数的符号,进行化简.(2)先判断底数的取值范围,由于底数大于1,根据指数函数的单调性将不等式进行转化一次不等式,求解即可.解答:解:(1)Ⅰ﹣2x2+5x﹣2>0Ⅰ,Ⅰ原式===(8分)(2)Ⅰ,Ⅰ原不等式等价于x<1﹣x,Ⅰ此不等式的解集为(12分)点评:本题考查指数函数的单调性与特殊点,求解本题的关键是判断底数的符号,以确定函数的单调性,熟练掌握指数函数的单调性是正确转化的根本.8.化简或求值:(1)3a b(﹣4a b)÷(﹣3a b);(2).考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)利用分数指数幂的运算法则即可得出;(2)利用对数的运算法则和lg2+lg5=1即可得出.解答:解:(1)原式==4a.(2)原式=+50×1=lg102+50=52.点评:本题考查了分数指数幂的运算法则、对数的运算法则和lg2+lg5=1等基础知识与基本技能方法,属于基础题.9.计算:(1);(2)(lg8+lg1000)lg5+3(lg2)2+lg6﹣1+lg0.006.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)先将每一个数化简为最简分数指数幂的形式,再利用运算性质化简.(2)先将每一个对数式化简,再利用对数运算性质化简.解答:解:(1)===﹣45;(2)(lg8+lg1000)lg5+3(lg2)2+lg6﹣1+lg0.006=(3lg2+3)•lg5+3(lg2)2﹣lg6+(lg6﹣3)=3lg2•lg5+3lg5+3(lg2)2﹣3=3lg2(lg5+lg2)+3lg5﹣3=3lg2+3lg5﹣3=3﹣3=0.点评:本题考察运算性质,做这类题目最关键的是平时练习时要细心、耐心、不怕麻烦,考场上才能熟练应对!10.计算(1)(2).考点:对数的运算性质;有理数指数幂的化简求值.专题:函数的性质及应用.分析:(1)利用指数幂的运算性质即可得出;(2)利用对数函数的运算性质即可得出.解答:解:(1)原式=|2﹣e|﹣+﹣=e﹣2﹣+=e﹣2﹣e+=﹣2.(2)原式=+3=﹣4+3=2﹣4+3=1.点评:熟练掌握指数幂的运算性质、对数函数的运算性质是解题的关键.11.计算(1)(2).考点:对数的运算性质;有理数指数幂的运算性质.专题:计算题.分析:(1)直接利用对数的运算法则求解即可.(2)直接利用有理指数幂的运算法则求解即可.解答:解:(1)==(2)==9×8﹣27﹣1=44.点评:本题考查对数的运算法则、有理指数幂的运算法则的应用,考查计算能力.12.解方程:log2(x﹣3)﹣=2.考点:对数的运算性质.专题:计算题.分析:由已知中log2(x﹣3)﹣=2,由对数的运算性质,我们可得x2﹣3x﹣4=0,解方程后,检验即可得到答案.解答:解:若log2(x﹣3)﹣=2.则x2﹣3x﹣4=0,…(4分)解得x=4,或x=﹣1(5分)经检验:方程的解为x=4.…(6分)点评:本题考查的知识点是对数的运算性质,其中利用对数的运算性质,将已知中的方程转化为整式方程是解答醒的关键,解答时,易忽略对数的真数部分大于0,而错解为4,或﹣1.13.计算下列各式(Ⅰ)lg24﹣(lg3+lg4)+lg5(Ⅰ).考点:对数的运算性质;根式与分数指数幂的互化及其化简运算.专题:计算题.分析:(Ⅰ)利用对数的运算的性质可得结果;(Ⅰ)利用指数幂的运算性质可得结果;解答:解:(Ⅰ)lg24﹣(lg3+lg4)+lg5=lg24﹣lg12+lg5=lg=lg10=1;(Ⅰ)=×+﹣﹣1=32×23+3﹣2﹣1=72.点评:本题考查对数的运算性质、指数幂的运算性质,考查学生的运算能力,属基础题.14.求下列各式的值:(1)(2).考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:根据对数和指数的运算法则进行求解即可.解答:解:(1)原式==log﹣9=log39﹣9=2﹣9=﹣7.(2)原式=== =.点评:本题主要考查对数和指数幂的计算,要求熟练掌握对数和指数幂的运算法则.15.(1)计算(2)若xlog34=1,求4x+4﹣x的值.考点:对数的运算性质;根式与分数指数幂的互化及其化简运算.分析:(1)利用指数幂的运算性质即可;(2)利用指数式和对数式的互化和运算性质即可.解答:解:(1)原式===3.(2)由xlog34=1,得x=log43,Ⅰ4x=3,,Ⅰ4x+4﹣x==.点评:熟练掌握对数和指数幂的运算性质是解题的关键.16.求值:.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:根据有理数指数幂的定义,及对数的运算性质,即可求出的值.解答:解:原式…(4分)…(3分)=…(1分)点评:本题考查的知识点是对数的运算性质,有理数指数幂的化简求值,其中掌握指数的运算性质和对数的运算性质,是解答本题的关键.17.计算下列各式的值(1)0.064﹣(﹣)0+160.75+0.25(2)lg25+lg5•lg4+lg22.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)利用指数幂的运算性质可求;(2)利用对数运算性质可求;解答:解:(1)原式==0.4﹣1+8+=;(2)原式=lg25+2lg5•lg2+lg22=(lg5+lg2)2=(lg10)2=1点评:本题考查对数的运算性质、有理数指数幂的运算,属基础题,熟记有关运算性质是解题基础.18.求值:+.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:直接利用对数的运算法则,求出表达式的值即可.解答:解:原式==3+9+2000+1=2013.点评:本题考查对数的运算法则的应用,基本知识的考查.19.(1)已知a>b>1且,求log a b﹣log b a的值.(2)求的值.考点:对数的运算性质.专题:计算题.分析:(1)通过a>b>1利用,平方,然后配出log a b﹣log b a的表达式,求解即可.(2)直接利用对数的运算性质求解的值解答:解:(1)因为a>b>1,,所以,可得,a>b>1,所以log a b﹣log b a<0.所以log a b﹣log b a=﹣(2)==﹣4.点评:本题考查对数与指数的运算性质的应用,整体思想的应用,考查计算能力.20.计算(1)(2)(lg5)2+lg2×lg50考点:对数的运算性质;根式与分数指数幂的互化及其化简运算;有理数指数幂的化简求值.专题:计算题.分析:(1)把根式转化成指数式,然后利用分数指数幂的运算法则进行计算.(2)先把lg50转化成lg5+1,然后利用对数的运算法则进行计算.解答:解:(1)===(6分)(2)(lg5)2+lg2×lg50=(lg5)2+lg2×(lg5+lg10)=(lg5)2+lg2×lg5+lg2=lg5(lg5+lg2)+lg2=lg5+lg2=1(12分)点评:本题考查对数的运算法则和根式与分数指数幂的互化,解题时要注意合理地进行等价转化.21.不用计算器计算:.考点:对数的运算性质.专题:计算题.分析:,lg25+lg4=lg100=2,,(﹣9.8)0=1,由此可以求出的值.解答:解:原式=(4分)=(8分)=(12分)点评:本题考查对数的运算性质,解题时要认真审题,注意公式的灵活运用.22.计算下列各题(1);(2).考点:对数的运算性质.专题:计算题.分析:(1)直接利用对数的运算性质求解表达式的值.(2)利用指数的运算性质求解表达式的值即可.解答:解:(1)==9+﹣1=(2)===﹣45.点评:本题考查指数与对数的运算性质的应用,考查计算能力.23.解下列方程:(1)lg(x﹣1)+lg(x﹣2)=lg(x+2);(2)2•(log3x)2﹣log3x﹣1=0.考点:对数的运算性质.专题:计算题.分析:(1)先根据对数运算性质求出x,再根据对数的真数一定大于0检验即可.(2)设log3x=y,得出2y2﹣y﹣1=0,求出y的值,再由对数的定义求出x的值即可.解答:解:(1)原方程可化为lg(x﹣1)(x﹣2)=lg(x+2)所以(x﹣1)(x﹣2)=x+2即x2﹣4x=0,解得x=0或x=4经检验,x=0是增解,x=4是原方程的解.所以原方程的解为x=4(2)设log3x=y,代入原方程得2y2﹣y﹣1=0.解得y1=1,.log3x=1,得x1=3;由,得.经检验,x1=3,都是原方程的解.点评:本题主要考查对数的运算性质和对数函数的定义域问题.属基础题.24.求值:(1)(2)2log525﹣3log264.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)首先变根式为分数指数幂,然后拆开运算即可.(2)直接利用对数式的运算性质化简求值.解答:解:(1)====.(2)2log525﹣3log264==4﹣3×6=﹣14.点评:本题考查了对数式的运算性质,考查了有理指数幂的化简求值,解答的关键是熟记有关性质,是基础题.25.化简、求值下列各式:(1)•(﹣3)÷;(2)(注:lg2+lg5=1).考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)利用指数幂的运算性质化简即可;(2)利用对数的运算性质化简即可.解答:解:(1)原式=﹣b﹣3÷(4)…..3分=﹣…..7分(2)解原式=…..2分=…..4分=…..6分=….7分.点评:本题考查对数的运算性质,考查有理数指数幂的化简求值,熟练掌握其运算性质是化简的基础,属于基础题.26.计算下列各式(1);(2).考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)利用指数幂的运算法则即可得出;(2)利用对数的运算法则和换底公式即可得出.解答:解:(1)原式=﹣1﹣+=.(2)原式=+lg(25×4)+2+1==.点评:本题考查了指数幂的运算法则、对数的运算法则和换底公式,属于基础题.27.(1)计算;(2)设log23=a,用a表示log49﹣3log26.考点:对数的运算性质;根式与分数指数幂的互化及其化简运算.专题:计算题.分析:(1)把第一、三项的底数写成平方、立方的形式即变成幂的乘方运算,第二项不等于0根据零指数的法则等于1,化简求值即可;(2)把第一项利用换底公式换成以2为底的对数,第二项利用对数函数的运算性质化简,log23整体换成a即可.解答:解:(1)原式=+1+=+1+=4;(2)原式=﹣3log22×3=log23﹣3(1+log23)=a﹣3(1+a)=﹣2a﹣3.点评:本题是一道计算题,要求学生会进行根式与分数指数幂的互化及其运算,会利用换底公式及对数的运算性质化简求值.做题时注意底数变乘方要用到一些技巧.28.计算下列各题:(1);(2)lg25+lg2lg50.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)利用指数的运算法则,直接求解表达式的值即可.(2)利用对数的运算性质,直接化简求解即可.解答:解:(1)原式===.(5分)(2)原式lg25+lg2lg50=lg25+2lg2lg5+lg25=(lg2+lg5)2=1 (5分)点评:本题考查对数的运算性质,有理数指数幂的化简求值,考查计算能力.29.计算:(1)lg25+lg2•lg50;(2)30++32×34﹣(32)3.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题;函数的性质及应用.分析:(1)直接利用对数的运算性质即可求解(2)直接根据指数的运算性质即可求解解答:解:(1)原式=lg25+lg2(1+lg5)=lg25+lg2lg5+lg2=lg5(lg5+lg2)+lg2=lg5+lg2=1(2)原式=1+3+36﹣36=4.…(14分)点评:本题主要考查了对数的运算性质及指数的运算性质的简单应,属于基础试题30.(1)计算:;(2)解关于x的方程:.考点:对数的运算性质;有理数指数幂的运算性质;有理数指数幂的化简求值;函数的零点.专题:计算题.分析:(1)根据分数指数幂运算法则进行化简即可.(2)利用对数函数的性质和对数的运算法则进行计算即可.解答:解:(1)原式==﹣3;(2)原方程化为log5(x+1)+log5(x﹣3)=log55,从而(x+1)(x﹣3)=5,解得x=﹣2或x=4,经检验,x=﹣2不合题意,故方程的解为x=4.点评:本题主要考查分数指数幂和对数的运算,要求熟练掌握分数指数幂和对数的运算法则.。
高中数学人教A版必修三课下能力提升:(一)含解析

下能力提高(一 )[ 学水平达]1算法的含及特点1.以下对于算法的法的是()A.一个算法的步是可逆的B.描绘算法能够有不一样的方式C.算法要本着方便的原D.一个算法不可以够无止境地运算下去2.以下句表达的是算法的有()① 当地的程: 1 提起筒; 2 号; 3 等通信号; 4 开始通或挂机;5束通;②利用公式V= Sh 算底面3,高 4 的三棱柱的体;③x2- 2x- 3= 0;④求全部能被 3 整除的正数,即3,6,9,12,⋯ .A .①②B .①②③C.①②④ D .①②③④3.以下各式中S 的不可以够用算法求解的是()A.S=1+2+3+4B.S= 12+ 22+ 32+⋯+ 100211C.S= 1+2+⋯+10 000D. S= 1+ 2+ 3+ 4+⋯2算法4.出下边一个算法:第一步,出三个数x, y,z.第二步,算M= x+ y+ z.1第三步,算N=3M.第四步,得出每次算果.上述算法是()A .乞降B.求余数C.求均匀数D.先乞降再求均匀数5. (2016 · 高一 )一个算法步以下:S1, S 取 0, i 取 1;S2,假如 i ≤ 10,行S3,否行S6;S3,计算 S+ i 并将结果取代S;S4,用 i+ 2 的值取代i ;S5,转去履行S2;S6,输出 S.运转以上步骤后输出的结果S=()A.16B. 25C.36 D .以上均不对6.给出下边的算法,它解决的是()第一步,输入 x.第二步,假如x<0,则 y=x2;不然履行下一步.第三步,假如x=0,则 y=2;不然 y=- x2.第四步,输出 y.A .求函数 y=x2 x< 0 ,的函数值- x2 x≥ 0x2 x<0 ,B.求函数 y= 2 x= 0 ,的函数值- x2 x> 0x2 x>0 ,C.求函数 y= 2 x= 0 ,的函数值- x2 x< 0D.以上都不正确7.试设计一个判断圆(x- a)2+ (y- b)2= r2和直线 Ax+ By+ C= 0 地点关系的算法.8.某商场举办优惠促销活动.若购物金额在800 元以上 (不含 800 元 ),打 7 折;若购物金额在400 元以上 (不含 400 元 )800 元以下 (含 800 元),打 8 折;不然,不打折.请为商场收银员设计一个算法,要求输入购物金额x,输出实质交款额y.题组 3算法的实质应用9.国际奥委会宣告2020 年夏天奥运会主办城市为日本的东京.据《中国体育报》报导:对参加竞选的 5 个夏天奥林匹克运动会申办城市进行表决的操作程序是:第一进行第一轮投票,假如有一个城市得票数超出总票数的一半,那么该城市将获取举办权;假如全部申办城市得票数都不超出总票数的一半,则将得票最少的城市裁减,而后进行第二轮投票;假如第二轮投票仍没选出主办城市,将进行第三轮投票,这样重复投票,直到选出一个主办城市为止,写出投票过程的算法.[ 能力提高综合练]1.小明正午下学回家自己煮面条吃,有下边几道工序:①洗锅、盛水 2 分钟;②洗菜6 分钟;③准备面条及佐料 2 分钟;④用锅把水烧开10 分钟;⑤煮面条和菜共 3 分钟.以上各道工序,除了④以外,一次只好进行一道工序.小明要将面条煮好,最少要用() A.13 分钟B. 14 分钟C.15 分钟D. 23 分钟2.在用二分法求方程零点的算法中,以下说法正确的选项是()A.这个算法能够求方程全部的零点B.这个算法能够求任何方程的零点C.这个算法能求方程全部的近似零点D.这个算法其实不必定能求方程全部的近似零点3. (2016 青·岛质检 )联合下边的算法:第一步,输入x.第二步,判断x 能否小于 0,假如,则输出x+2,不然履行第三步.第三步,输出x-1.当输入的 x 的值为- 1,0,1 时,输出的结果分别为()A .- 1,0,1B.- 1,1,0C.1,- 1,0D. 0,- 1,14.有以下算法:第一步,输入不小于 2 的正整数n.第二步,判断n 能否为 2.若 n= 2,则 n 知足条件;若n>2,则履行第三步.第三步,挨次从 2 到 n-1 查验能不可以整除n,若不可以整除,则n 知足条件.则上述算法知足条件的n 是 ()A .质数B.奇数C.偶数D.合数5. (2016 ·南检测济 )输入一个x 值,利用y= |x- 1|求函数值的算法以下,请将所缺部分增补完好:第一步:输入x;第二步: ________;第三步:当x<1 时,计算 y= 1- x;第四步:输出y.6.已知一个算法以下:第一步,令m= a.第二步,假如b< m,则 m= b.第三步,假如c<m,则 m=c.第四步,输出m.假如 a= 3, b=6, c= 2,则履行这个算法的结果是________.7.下边给出了一个问题的算法:第一步,输入 a.第二步,假如a≥ 4,则 y=2a- 1;不然, y=a2-2a+ 3.第三步,输出y 的值.问: (1)这个算法解决的是什么问题?(2)当输入的 a 的值为多少时,输出的数值最小?最小值是多少?8.“韩信点兵”问题:韩信是汉高祖手下的大将,他勇敢善战,谋略超群,为汉朝的成立立下了不朽功绩.听说他在一次点兵的时候,为保住军事奥密,不让仇敌知道自己队伍的军事实力,采纳下述点兵方法:①先令士兵从1~ 3 报数,结果最后一个士兵报2;②又令士兵从1~ 5 报数,结果最后一个士兵报3;③又令士兵从1~ 7 报数,结果最后一个士兵报 4.这样韩信很快算出自己队伍里士兵的总数.请设计一个算法,求出士兵起码有多少人.答案[ 学业水平达标练]1.分析:选A由算法定义可知 B 、C、D 对, A 错.2.分析:选 A 算法往常是指依据必定规则解决某一类问题的明确和有限的步骤.①②都各表达了一种算法;③不过一个纯数学识题,不是一个明确步骤;④的步骤是无量的,与算法的有穷性矛盾.3.分析:选 D D 中的乞降不切合算法步骤的有限性,因此它不可以够用算法求解,故选 D.4.分析:选 D 由算法过程知, M 为三数之和, N 为这三数的均匀数.5.分析:选 B 由以上计算可知: S= 1+3+ 5+ 7+ 9= 25,答案为 B.6.分析:选B由算法知,当x< 0 时, y= x2;当 x=0 时, y= 2;当 x> 0 时, y=-x2.应选 B.7.解:算法步骤以下:第一步,输入圆心的坐标(a,b)、半径 r 和直线方程的系数A、 B、C.第二步,计算z1= Aa+ Bb+ C.第三步,计算z2= A2+B2.|z1|第四步,计算d=.z2第五步,假如d>r ,则输出“相离”;假如 d=r ,则输出“相切”;假如 d<r,则输出“订交”.8.解:算法步骤以下:第一步,输入购物金额 x(x> 0).第二步,判断“ x> 800”能否成立,假如,则 y= 0.7x,转第四步;不然,履行第三步.第三步,判断“x> 400”能否成立,假如,则 y= 0.8x;不然, y= x.第四步,输出y,结束算法.9.解:算法以下:第一步,投票.第二步,统计票数,假如一个城市得票数超出总票数的一半,那么该城市就获取主办权,不然裁减得票数最少的城市并转第一步.第三步,宣告主办城市.[ 能力提高综合练]1.分析:选C①洗锅、盛水 2 分钟+④用锅把水烧开10 分钟 (同时②洗菜 6 分钟+③准备面条及佐料 2 分钟 )+⑤煮面条和菜共 3 分钟= 15 分钟.解决一个问题的算法不是唯一的,但在设计时要综合考虑各个方面的要素,选择一种较好的算法.2.分析:选D二分法求方程零点的算法中,仅能求方程的一些特别的近似零点(知足函数零点存在性定理的条件),故 D 正确.3.分析:选 C 依据 x 值与 0 的关系选择履行不一样的步骤.4.分析:选 A 依据质数、奇数、偶数、合数的定义可知,知足条件的n 是质数.5.分析:以 x-1 与 0 的大小关系为分类准则知第二步应填当x≥1 时,计算 y= x- 1.答案:当 x≥ 1 时,计算 y=x- 16.分析:这个算法是求 a, b, c 三个数中的最小值,故这个算法的结果是 2.答案: 27.解: (1) 这个算法解决的是求分段函数2a-1, a≥ 4,y=的函数的.a2- 2a+ 3, a<4(2)当 a≥ 4 , y= 2a-1≥ 7;当 a<4 , y= a2-2a+ 3= (a- 1)2+ 2≥ 2,∵当 a= 1 , y 获得最小 2.∴当入的 a1 ,出的数最小 2.8. 解:第一步,第一确立最小的足除以 3 余 2 的正整数: 2.第二步,挨次加 3 就获取全部除以 3 余 2的正整数: 2,5,8,11,14,17,20,⋯ .第三步,在上列数中确立最小的足除以5余 3的正整数: 8.第四步,而后在自然数内在8 的基上挨次加上15,获取 8,23,38,53,⋯ .第五步,在上列数中确立最小的足除以7余 4的正整数: 53.即士兵起码有 53 人.。
人教版高中数学必修三 课下能力提升:(一)

课下能力提升(一)[学业水平达标练]题组1 算法的含义及特征1.下列关于算法的说法错误的是( )A .一个算法的步骤是可逆的B .描述算法可以有不同的方式C .设计算法要本着简单方便的原则D .一个算法不可以无止境地运算下去2.下列语句表达的是算法的有( )①拨本地电话的过程为:1提起话筒;2拨号;3等通话信号;4开始通话或挂机;5结束通话;②利用公式V =Sh 计算底面积为3,高为4的三棱柱的体积;③x 2-2x -3=0;④求所有能被3整除的正数,即3,6,9,12,….A .①②B .①②③C .①②④D .①②③④3.下列各式中S 的值不可以用算法求解的是( )A .S =1+2+3+4B .S =12+22+32+…+1002C .S =1+12+…+110 000D .S =1+2+3+4+…题组2 算法设计4.给出下面一个算法:第一步,给出三个数x ,y ,z .第二步,计算M =x +y +z .第三步,计算N =13M . 第四步,得出每次计算结果.则上述算法是( )A .求和B .求余数C .求平均数D .先求和再求平均数5.(2016·东营高一检测)一个算法步骤如下:S 1,S 取值0,i 取值1;S 2,如果i ≤10,则执行S 3,否则执行S 6;S 3,计算S +i 并将结果代替S ;S 4,用i +2的值代替i ;S 5,转去执行S 2;S 6,输出S .运行以上步骤后输出的结果S =( )A .16B .25C .36D .以上均不对6.给出下面的算法,它解决的是( )第一步,输入x .第二步,如果x <0,则y =x 2;否则执行下一步.第三步,如果x =0,则y =2;否则y =-x 2.第四步,输出y .A .求函数y =⎩⎪⎨⎪⎧ x 2x <,-x 2x 的函数值B .求函数y =⎩⎪⎨⎪⎧ x 2x <,x =,-x 2x >的函数值C .求函数y =⎩⎪⎨⎪⎧ x 2x >,x =,-x 2x <的函数值D .以上都不正确 7.试设计一个判断圆(x -a )2+(y -b )2=r 2和直线Ax +By +C =0位置关系的算法.8.某商场举办优惠促销活动.若购物金额在800元以上(不含800元),打7折;若购物金额在400元以上(不含400元)800元以下(含800元),打8折;否则,不打折.请为商场收银员设计一个算法,要求输入购物金额x ,输出实际交款额y .题组3 算法的实际应用9.国际奥委会宣布2020年夏季奥运会主办城市为日本的东京.据《中国体育报》报道:对参与竞选的5个夏季奥林匹克运动会申办城市进行表决的操作程序是:首先进行第一轮投票,如果有一个城市得票数超过总票数的一半,那么该城市将获得举办权;如果所有申办城市得票数都不超过总票数的一半,则将得票最少的城市淘汰,然后进行第二轮投票;如果第二轮投票仍没选出主办城市,将进行第三轮投票,如此重复投票,直到选出一个主办城市为止,写出投票过程的算法.[能力提升综合练]1.小明中午放学回家自己煮面条吃,有下面几道工序:①洗锅、盛水2分钟;②洗菜6分钟;③准备面条及佐料2分钟;④用锅把水烧开10分钟;⑤煮面条和菜共3分钟.以上各道工序,除了④之外,一次只能进行一道工序.小明要将面条煮好,最少要用() A.13分钟B.14分钟C.15分钟D.23分钟2.在用二分法求方程零点的算法中,下列说法正确的是()A.这个算法可以求方程所有的零点B.这个算法可以求任何方程的零点C.这个算法能求方程所有的近似零点D.这个算法并不一定能求方程所有的近似零点3.(2016·青岛质检)结合下面的算法:第一步,输入x.第二步,判断x是否小于0,若是,则输出x+2,否则执行第三步.第三步,输出x-1.当输入的x的值为-1,0,1时,输出的结果分别为()A.-1,0,1 B.-1,1,0C.1,-1,0 D.0,-1,14.有如下算法:第一步,输入不小于2的正整数n.第二步,判断n是否为2.若n=2,则n满足条件;若n>2,则执行第三步.第三步,依次从2到n-1检验能不能整除n,若不能整除,则n满足条件.则上述算法满足条件的n是()A.质数B.奇数C.偶数D.合数5.(2016·济南检测)输入一个x值,利用y=|x-1|求函数值的算法如下,请将所缺部分补充完整:第一步:输入x;第二步:________;第三步:当x<1时,计算y=1-x;第四步:输出y.6.已知一个算法如下:第一步,令m=a.第二步,如果b<m,则m=b.第三步,如果c<m,则m=c.第四步,输出m.如果a=3,b=6,c=2,则执行这个算法的结果是________.7.下面给出了一个问题的算法:第一步,输入a.第二步,如果a≥4,则y=2a-1;否则,y=a2-2a+3.第三步,输出y的值.问:(1)这个算法解决的是什么问题?(2)当输入的a的值为多少时,输出的数值最小?最小值是多少?8.“韩信点兵”问题:韩信是汉高祖手下的大将,他英勇善战,谋略超群,为汉朝的建立立下了不朽功勋.据说他在一次点兵的时候,为保住军事秘密,不让敌人知道自己部队的军事实力,采用下述点兵方法:①先令士兵从1~3报数,结果最后一个士兵报2;②又令士兵从1~5报数,结果最后一个士兵报3;③又令士兵从1~7报数,结果最后一个士兵报4.这样韩信很快算出自己部队里士兵的总数.请设计一个算法,求出士兵至少有多少人.答案[学业水平达标练]1. 解析:选A由算法定义可知B、C、D对,A错.2. 解析:选A算法通常是指按照一定规则解决某一类问题的明确和有限的步骤.①②都各表达了一种算法;③只是一个纯数学问题,不是一个明确步骤;④的步骤是无穷的,与算法的有穷性矛盾.3. 解析:选D D中的求和不符合算法步骤的有限性,所以它不可以用算法求解,故选D.4. 解析:选D由算法过程知,M为三数之和,N为这三数的平均数.5. 解析:选B由以上计算可知:S=1+3+5+7+9=25,答案为B.6. 解析:选B由算法知,当x<0时,y=x2;当x=0时,y=2;当x>0时,y=-x2.故选B.7. 解:算法步骤如下:第一步,输入圆心的坐标(a,b)、半径r和直线方程的系数A、B、C.第二步,计算z1=Aa+Bb+C.第三步,计算z2=A2+B2.第四步,计算d=|z1| z2.第五步,如果d>r,则输出“相离”;如果d=r,则输出“相切”;如果d<r,则输出“相交”.8. 解:算法步骤如下:第一步,输入购物金额x(x>0).第二步,判断“x >800”是否成立,若是,则y =0.7x ,转第四步;否则,执行第三步. 第三步,判断“x >400”是否成立,若是,则y =0.8x ;否则,y =x .第四步,输出y ,结束算法.9. 解:算法如下:第一步,投票.第二步,统计票数,如果一个城市得票数超过总票数的一半,那么该城市就获得主办权,否则淘汰得票数最少的城市并转第一步.第三步,宣布主办城市.[能力提升综合练]1. 解析:选C ①洗锅、盛水2分钟+④用锅把水烧开10分钟(同时②洗菜6分钟+③准备面条及佐料2分钟)+⑤煮面条和菜共3分钟=15分钟.解决一个问题的算法不是唯一的,但在设计时要综合考虑各个方面的因素,选择一种较好的算法.2. 解析:选D 二分法求方程零点的算法中,仅能求方程的一些特殊的近似零点(满足函数零点存在性定理的条件),故D 正确.3. 解析:选C 根据x 值与0的关系选择执行不同的步骤.4. 解析:选A 根据质数、奇数、偶数、合数的定义可知,满足条件的n 是质数.5. 解析:以x -1与0的大小关系为分类准则知第二步应填当x ≥1时,计算y =x -1. 答案:当x ≥1时,计算y =x -16. 解析:这个算法是求a ,b ,c 三个数中的最小值,故这个算法的结果是2.答案:27. 解:(1)这个算法解决的是求分段函数y =⎩⎪⎨⎪⎧2a -1,a ≥4,a 2-2a +3,a <4的函数值的问题. (2)当a ≥4时,y =2a -1≥7;当a <4时,y =a 2-2a +3=(a -1)2+2≥2,∵当a =1时,y 取得最小值2.∴当输入的a 值为1时,输出的数值最小为2.8. 解:第一步,首先确定最小的满足除以3余2的正整数:2.第二步,依次加3就得到所有除以3余2的正整数:2,5,8,11,14,17,20,….第三步,在上列数中确定最小的满足除以5余3的正整数:8.第四步,然后在自然数内在8的基础上依次加上15,得到8,23,38,53,….第五步,在上列数中确定最小的满足除以7余4的正整数:53.即士兵至少有53人.。
高中数学苏教版必修三 能力提升习题:(七) 算法案例含答案

课下能力提升(七) 算法案例一、填空题1.用辗转相除法求294和84的最大公约数时,需要做除法的次数是________.2.下列伪代码运行的一个结果是________.m←2While Mod(m,4)≠2 orMod(m,5)≠3 orMod(m,7)≠3m←m+1End WhilePrint m________.4.84和32的最小公倍数是________.5.下列伪代码的运行结果是________.a←120b←252While a≠bIf a>ba←a-bElseb←b-aEnd IfEnd WhilePrint a二、解答题6.已知如图所示的流程图(其中的m、n为正整数):(1)这个算法的功能是什么?(2)当m =286,n =91时,运行的结果是什么?7.试写出用二分法求方程x 3+x 2-1=0在[0,1]上的近似解的伪代码(精确度为0.01).8.有一堆围棋子,5个5个地数余2,7个7个地数余3,9个9个地数余4,请画出求这堆围棋子共有多少个的流程图,并写出伪代码.答案1.解析:294=84×3+42,84=42×2,故需要做2次. 答案:22.解析:此伪代码的功能是求⎩⎪⎨⎪⎧m =4x +2,m =5x +3,m =7x +3的最小正整数∴m =38. 答案: 383.解析:由86>68得a =18,b =68,由68>18得b =50,a =18;由50>18得b =32,a =18;由32>18得b=14,a=18;由18>14得a=4,b=14;由14>4得b=10,a=4;由10>4得b=6,a=4;由6>4得b=2,a=4;由4>2得a=2,b=2.满足a=b,输出2.答案:24.解析:先求84和32的最大公约数.84=32×2+2032=20+1220=12+812=8+48=4×2.故84和32的最大公约数是4.所以84和32的最小公倍数为84×32÷4=672.答案:6725.解析:此伪代码的功能是求两个正整数的最大公约数.a,b的值依次是:(120,252)→(120,132)→(120,12)→(108,12)→(96,12)→(84,12)→(72,12)→(60,12)→(48,1 2)→(36,12)→(24,12)→(12,12),∴输出12.答案:126.解:(1)这个算法的功能是用辗转相除法求两个正整数的最大公约数.(2)∵286=91×3+13,91=13×7,∴286与91的最大公约数是13.故运行结果为13.7.解:伪代码如下:b←1ε←0.01Dox0←(a+b)/2f(a)←a3+a2-1f(x0)←x30+x20-1If f(x0)=0 Then Exit DoIf f(a)f(x0)>0 Thena←x0Elseb←x0End IfUntil |a-b|<εEnd DoPrint x0伪代码:。
高中数学 课下能力提升(一)新人教A版必修3

课下能力提升(一)[学业水平达标练]题组1 算法的含义及特征1.下列关于算法的说法错误的是( )A .一个算法的步骤是可逆的B .描述算法可以有不同的方式C .设计算法要本着简单方便的原则D .一个算法不可以无止境地运算下去2.下列语句表达的是算法的有( )①拨本地电话的过程为:1提起话筒;2拨号;3等通话信号;4开始通话或挂机;5结束通话;②利用公式V =Sh 计算底面积为3,高为4的三棱柱的体积;③x 2-2x -3=0;④求所有能被3整除的正数,即3,6,9,12,….A .①②B .①②③C .①②④D .①②③④3.下列各式中S 的值不可以用算法求解的是( )A .S =1+2+3+4B .S =12+22+32+…+1002C .S =1+12+…+110 000D .S =1+2+3+4+…题组2 算法设计4.给出下面一个算法:第一步,给出三个数x ,y ,z .第二步,计算M =x +y +z .第三步,计算N =13M . 第四步,得出每次计算结果.则上述算法是( )A .求和B .求余数C .求平均数D .先求和再求平均数5.(2016·东营高一检测)一个算法步骤如下: S 1,S 取值0,i 取值1;S 2,如果i ≤10,则执行S 3,否则执行S 6;S 3,计算S +i 并将结果代替S ;S 4,用i +2的值代替i ;S 5,转去执行S 2;S 6,输出S .运行以上步骤后输出的结果S =( )A .16B .25C .36D .以上均不对6.给出下面的算法,它解决的是( )第一步,输入x .第二步,如果x <0,则y =x 2;否则执行下一步.第三步,如果x =0,则y =2;否则y =-x 2.第四步,输出y .A .求函数y =⎩⎪⎨⎪⎧ x 2x <,-x 2x的函数值 B .求函数y =⎩⎪⎨⎪⎧ x 2x <,x =,-x 2x >的函数值C .求函数y =⎩⎪⎨⎪⎧ x 2x >,x =,-x 2x <的函数值D .以上都不正确 7.试设计一个判断圆(x -a )2+(y -b )2=r 2和直线Ax +By +C =0位置关系的算法.8.某商场举办优惠促销活动.若购物金额在800元以上(不含800元),打7折;若购物金额在400元以上(不含400元)800元以下(含800元),打8折;否则,不打折.请为商场收银员设计一个算法,要求输入购物金额x ,输出实际交款额y .题组3 算法的实际应用9.国际奥委会宣布2020年夏季奥运会主办城市为日本的东京.据《中国体育报》报道:对参与竞选的5个夏季奥林匹克运动会申办城市进行表决的操作程序是:首先进行第一轮投票,如果有一个城市得票数超过总票数的一半,那么该城市将获得举办权;如果所有申办城市得票数都不超过总票数的一半,则将得票最少的城市淘汰,然后进行第二轮投票;如果第二轮投票仍没选出主办城市,将进行第三轮投票,如此重复投票,直到选出一个主办城市为止,写出投票过程的算法.[能力提升综合练]1.小明中午放学回家自己煮面条吃,有下面几道工序:①洗锅、盛水2分钟;②洗菜6分钟;③准备面条及佐料2分钟;④用锅把水烧开10分钟;⑤煮面条和菜共3分钟.以上各道工序,除了④之外,一次只能进行一道工序.小明要将面条煮好,最少要用( ) A.13分钟 B.14分钟C.15分钟 D.23分钟2.在用二分法求方程零点的算法中,下列说法正确的是( )A.这个算法可以求方程所有的零点B.这个算法可以求任何方程的零点C.这个算法能求方程所有的近似零点D.这个算法并不一定能求方程所有的近似零点3.(2016·青岛质检)结合下面的算法:第一步,输入x.第二步,判断x是否小于0,若是,则输出x+2,否则执行第三步.第三步,输出x-1.当输入的x的值为-1,0,1时,输出的结果分别为( )A.-1,0,1 B.-1,1,0C.1,-1,0 D.0,-1,14.有如下算法:第一步,输入不小于2的正整数n.第二步,判断n是否为2.若n=2,则n满足条件;若n>2,则执行第三步.第三步,依次从2到n-1检验能不能整除n,若不能整除,则n满足条件.则上述算法满足条件的n是( )A.质数 B.奇数C.偶数 D.合数5.(2016·济南检测)输入一个x值,利用y=|x-1|求函数值的算法如下,请将所缺部分补充完整:第一步:输入x;第二步:________;第三步:当x<1时,计算y=1-x;第四步:输出y.6.已知一个算法如下:第一步,令m=a.第二步,如果b<m,则m=b.第三步,如果c<m,则m=c.第四步,输出m .如果a =3,b =6,c =2,则执行这个算法的结果是________.7.下面给出了一个问题的算法:第一步,输入a .第二步,如果a ≥4,则y =2a -1;否则,y =a 2-2a +3.第三步,输出y 的值.问:(1)这个算法解决的是什么问题?(2)当输入的a 的值为多少时,输出的数值最小?最小值是多少?8.“韩信点兵”问题:韩信是汉高祖手下的大将,他英勇善战,谋略超群,为汉朝的建立立下了不朽功勋.据说他在一次点兵的时候,为保住军事秘密,不让敌人知道自己部队的军事实力,采用下述点兵方法:①先令士兵从1~3报数,结果最后一个士兵报2;②又令士兵从1~5报数,结果最后一个士兵报3;③又令士兵从1~7报数,结果最后一个士兵报4.这样韩信很快算出自己部队里士兵的总数.请设计一个算法,求出士兵至少有多少人.答 案[学业水平达标练]1. 解析:选A 由算法定义可知B 、C 、D 对,A 错.2. 解析:选A 算法通常是指按照一定规则解决某一类问题的明确和有限的步骤.①②都各表达了一种算法;③只是一个纯数学问题,不是一个明确步骤;④的步骤是无穷的,与算法的有穷性矛盾.3. 解析:选D D 中的求和不符合算法步骤的有限性,所以它不可以用算法求解,故选D.4. 解析:选D 由算法过程知,M 为三数之和,N 为这三数的平均数.5. 解析:选B 由以上计算可知:S =1+3+5+7+9=25,答案为B.6. 解析:选B 由算法知,当x <0时,y =x 2;当x =0时,y =2;当x >0时,y =-x 2.故选B.7. 解:算法步骤如下:第一步,输入圆心的坐标(a ,b )、半径r 和直线方程的系数A 、B 、C .第二步,计算z 1=Aa +Bb +C .第三步,计算z 2=A 2+B 2.第四步,计算d =|z 1|z 2. 第五步,如果d >r ,则输出“相离”;如果d =r ,则输出“相切”;如果d <r ,则输出“相交”.8. 解:算法步骤如下:第一步,输入购物金额x (x >0).第二步,判断“x >800”是否成立,若是,则y =0.7x ,转第四步;否则,执行第三步. 第三步,判断“x >400”是否成立,若是,则y =0.8x ;否则,y =x .第四步,输出y ,结束算法.9. 解:算法如下:第一步,投票.第二步,统计票数,如果一个城市得票数超过总票数的一半,那么该城市就获得主办权,否则淘汰得票数最少的城市并转第一步.第三步,宣布主办城市.[能力提升综合练]1. 解析:选C ①洗锅、盛水2分钟+④用锅把水烧开10分钟(同时②洗菜6分钟+③准备面条及佐料2分钟)+⑤煮面条和菜共3分钟=15分钟.解决一个问题的算法不是唯一的,但在设计时要综合考虑各个方面的因素,选择一种较好的算法.2. 解析:选D 二分法求方程零点的算法中,仅能求方程的一些特殊的近似零点(满足函数零点存在性定理的条件),故D 正确.3. 解析:选C 根据x 值与0的关系选择执行不同的步骤.4. 解析:选A 根据质数、奇数、偶数、合数的定义可知,满足条件的n 是质数.5. 解析:以x -1与0的大小关系为分类准则知第二步应填当x ≥1时,计算y =x -1. 答案:当x ≥1时,计算y =x -16. 解析:这个算法是求a ,b ,c 三个数中的最小值,故这个算法的结果是2.答案:27. 解:(1)这个算法解决的是求分段函数y =⎩⎪⎨⎪⎧ 2a -1,a ≥4,a 2-2a +3,a <4的函数值的问题.(2)当a ≥4时,y =2a -1≥7;当a <4时,y =a 2-2a +3=(a -1)2+2≥2,∵当a =1时,y 取得最小值2.∴当输入的a 值为1时,输出的数值最小为2.8. 解:第一步,首先确定最小的满足除以3余2的正整数:2.第二步,依次加3就得到所有除以3余2的正整数:2,5,8,11,14,17,20,….第三步,在上列数中确定最小的满足除以5余3的正整数:8.第四步,然后在自然数内在8的基础上依次加上15,得到8,23,38,53,….第五步,在上列数中确定最小的满足除以7余4的正整数:53.即士兵至少有53人.。
高中数学人教A版必修三课下能力提升:(八)含解析

课下能力提升(八)[学业水平达标练]题组1辗转相除法与更相减损术1.下列关于利用更相减损术求156和72的最大公约数的说法中正确的是()A.都是偶数必须约简B.可以约简,也可以不约简C.第一步作差为156-72=84;第二步作差为72-84=-12D.以上都不对2.用更相减损术求294和84的最大公约数时,需做减法运算的次数是()A.2 B.3 C.4 D.53.1 624与899的最大公约数是________.4.用两种方法求210与98的最大公约数.题组2秦九韶算法5.用秦九韶算法求多项式f(x)=7x6+6x5+3x2+2当x=4时的值时,先算的是() A.4×4=16 B.7×4=28C.4×4×4=64 D.7×4+6=346.用秦九韶算法计算多项式f(x)=3x6+4x5+5x4+6x3+7x2+8x+1当x=0.4时的值时,需要做乘法和加法的次数分别是()A.6,6 B.5,6C.5,5 D.6,57.利用秦九韶算法求多项式f(x)=3x6+12x5+8x4-3.5x3+7.2x2+5x-13当x=6时的值,写出详细步骤.题组3进位制及其转化8.以下各数有可能是五进制数的是()A.15 B.106C.731 D.21 3409.完成下列进位制之间的转化.(1)1 034(7)=________(10);(2)119(10)=________(6).10.若k进制数123(k)与十进制数38相等,则k=________.11.若1 0b1(2)=a02(3),求数字a,b的值及与此相等的十进制数.[能力提升综合练]1.用秦九韶算法求多项式f(x)=x3-3x2+2x-11当x=x0时的值时,应把f(x)变形为()A.x3-(3x-2)x-11B.(x-3)x2+(2x-11)C.(x-1)(x-2)x-11D.((x-3)x+2)x-112.45和150的最大公约数和最小公倍数分别是()A.5,150 B.15,450C.450,15 D.15,1503.下列各数中,最小的是()A.101 010(2)B.111(5)C.32(8)D.54(6)4.(2016·福州高一检测)三进制数2 022(3)化为六进制数为abc(6),则a+b+c=________.5.用秦九韶算法求多项式f(x)=1-5x-8x2+10x3+6x4+12x5+3x6当x=-4时的值时,v0,v1,v2,v3,v4中最大值与最小值的差是________.6.有甲、乙、丙三种溶液分别重147 g、343 g、133 g,现要将它们分别全部装入小瓶中,每个小瓶装入液体的质量相同,问每瓶最多装多少?7.古时候,当边境有敌人来犯时,守边的官兵通过在烽火台上举火向国内报告,如图,烽火台上点火,表示数字1,不点火表示数字0,约定二进制数对应的十进制的单位是1 000,请你计算一下,这组烽火台表示约有多少敌人入侵?答案[学业水平达标练]1. 解析:选B约简是为了使运算更加简捷,故不一定要约简,A错.C中第二步应为84-72=12,故选B.2. 解析:选C294-84=210,210-84=126,126-84=42,84-42=42,共做4次减法运算.3. 解析:1 624=899×1+725,899=725×1+174,725=174×4+29,174=29×6,故1 624与899的最大公约数是29.答案:294. 解:用辗转相除法:210=98×2+14,98=14×7.∴210与98的最大公约数为14.用更相减损术:∵210与98都是偶数,用2约简得105和49,105-49=56,56-49=7,49-7=42,42-7=35,35-7=28,28-7=21,21-7=14,14-7=7.∴210与98的最大公约数为2×7=14.5. 解析:选D因为f(x)=a n x n+a n-1x n-1+…+a1x+a0=(…((a n x+a n-1)x+a n-2)x+…+a1)x+a0,所以用秦九韶算法求多项式f(x)=7x6+6x5+3x2+2当x=4的值时,先算的是7×4+6=34.6. 答案:A7. 解:f(x)=(((((3x+12)x+8)x-3.5)x+7.2)x+5)x-13.v0=3,v1=v0×6+12=30,v2=v1×6+8=188,v3=v2×6-3.5=1 124.5,v4=v3×6+7.2=6 754.2,v5=v4×6+5=40 530.2,v6=v5×6-13=243 168.2.所以f(6)=243 168.2.8. 解析:选D五进制数中各个数字均是小于5的自然数,故选D.9. 解析:(1)1 034(7)=1×73+0×72+3×7+4×70=368.(2)∴119(10)=315(6).答案:(1)368(2)31510. 解析:由k进制数123可知k≥4.下面可用验证法:若k=4,则38(10)=212(4),不合题意;若k=5,则38(10)=123(5)成立,所以k=5.答案:511. 解:∵1 0b1(2)=a02(3),∴1×23+b×2+1=a×32+2,且a只能取1,2,b只能取0,1.整理得9a-2b=7.当b=0时,a=79(不合要求,舍去);当b=1时,a=1.∴a=b=1.∴102(3)=1 011(2),转化为十进制数为1×32+2=11.[能力提升综合练]1. 解析:选D f(x)=x3-3x2+2x-11=(x2-3x+2)x-11=((x-3)x+2)x-11,故选D.2. 解析:选B利用辗转相除法求45和150的最大公约数:150=45×3+15,45=15×3,45和150的最大公约数为15.45和150的最小公倍数为15×(45÷15)×(150÷15)=450,故选B.3. 解析:选C101 010(2)=1×25+0×24+1×23+0×22+1×21+0×20=42,111(5)=1×52+1×51+1×50=31,32(8)=3×81+2×80=26,54(6)=5×61+4×60=34.又42>34>31>26,故最小的是32(8).4. 解析:2 022(3)=2×33+0×32+2×31+2×30=62.三进制数2 022(3)化为六进制数为142(6),∴a+b+c=7.答案:75. 解析:多项式变形为f(x)=3x6+12x5+6x4+10x3-8x2-5x+1=(((((3x+12)x+6)x+10)x-8)x-5)x+1,v0=3,v1=3×(-4)+12=0,v2=0×(-4)+6=6,v3=6×(-4)+10=-14,v4=-14×(-4)-8=48,所以v4最大,v3最小,所以v4-v3=48+14=62.答案:626. 解:先求147与343的最大公约数.343-147=196,196-147=49,147-49=98,98-49=49.所以147与343的最大公约数是49.再求49与133的最大公约数.133-49=84,84-49=35,49-35=14,35-14=21,21-14=7,14-7=7.所以147,343,133的最大公约数为7.所以每瓶最多装7 g.7. 解:由图可知从左到右的五个烽火台,表示二进制数的自左到右五个数位,依题意知这组烽火台表示的二进制数是11 011,改写为十进制为:11 011(2)=1×24+1×23+0×22+1×21+1×20=16+8+2+1=27(10).又27×1 000=27 000,所以这组烽火台表示边境约有27 000个敌人来犯.。
高中生数学计算能力提升专练-含答案

高中生数学计算能力提升专练-含答案介绍数学计算是高中学习过程中必不可少的一部分。
精确而迅速地计算对于理解数学概念和解决实际问题至关重要。
为了帮助高中生提升数学计算能力,本专练提供了一系列练习题,涵盖了高中数学中常见的计算技巧和方法。
专练内容1. 整数运算练习题1:计算:(-14) + (-12) - (-5) - 8 + 3 * 2答案:-14 + (-12) - (-5) - 8 + 3 * 2 = -14 + (-12) + 5 - 8 + 6 = -23练习题2:计算:2^3 - 2^(2-3) + 8 / 4 * 2 - 6答案:2^3 - 2^(2-3) + 8 / 4 * 2 - 6 = 8 - 2^(-1) + 4 * 2 - 6 = 8 - 0.5 + 8 - 6 = 9.52. 代数式化简练习题1:化简代数式:x^2 + 3x - 4 + 2x^2 - 5(x + 2)答案:x^2 + 3x - 4 + 2x^2 - 5(x + 2) = 3x^2 + 3x - 4 - 5x - 10 = 3x^2 - 2x -14练习题2:化简代数式:3(2x - 4) - (x + 2) (4 - 2x)答案:3(2x - 4) - (x + 2) (4 - 2x) = 6x - 12 - (4 - 2x)(x + 2) = 6x - 12 - 4(x + 2) + 2x(x + 2) = 6x - 12 - 4x - 8 + 2x^2 + 4x = 2x^2 + 6x - 203. 方程求解练习题1:解方程:3x - 5 = 7答案:3x - 5 = 73x = 7 + 53x = 12x = 12 / 3x = 4练习题2:解方程:2x^2 + 5x - 3 = 0答案:2x^2 + 5x - 3 = 0(2x - 1)(x + 3) = 02x - 1 = 0 或者 x + 3 = 0 2x = 1 或者 x = -3x = 1/2 或者 x = -34. 几何计算练习题1:已知正方形的边长为5cm,求其面积和周长。
初升高计算能力训练题答案

初升高计算能力训练题答案一、选择题1. A2. C3. B4. D5. A二、填空题1. 2x + 3y = 72. (a + b)^2 = a^2 + 2ab + b^23. √34. 55. 1/4三、计算题1. 解:(2x + 3)(2x - 3) = 4x^2 - 92. 解:(x - 2)^2 = x^2 - 4x + 43. 解:(3x + 2) / (x - 1) = 3 + 5/(x - 1)4. 解:√(4x^2 + 9) = √(4(x^2 + 9/4)) = 2|x + 3/2|5. 解:(3x - 2) / (x + 1) = 3 - 5/(x + 1)四、应用题1. 解:设甲班有x人,乙班有y人。
根据题意,我们有以下方程组:x + y = 100x - y = 8解得:x = 54,y = 46答:甲班有54人,乙班有46人。
2. 解:设原计划每天生产x件产品,实际每天生产y件产品。
根据题意,我们有以下方程:x * 30 = y * 25 + 100解得:y = 4x - 4答:实际每天生产的产品数量是原计划的4倍减去4件。
五、综合题1. 解:设A点到B点的距离为d,速度为v。
根据题意,我们有以下方程:d = v * t其中,t为时间。
解得:t = d/v答:从A点到B点所需的时间为d/v。
2. 解:设x年后,小明的年龄是小红的2倍。
根据题意,我们有以下方程:x + 5 = 2 * (x + 3)解得:x = 1答:1年后,小明的年龄将是小红的2倍。
本套训练题旨在帮助学生巩固计算能力,提高解题技巧,为初升高的数学考试做好准备。
希望同学们能够认真练习,查漏补缺,不断提高自己的数学水平。
高中数学苏教版必修三 能力提升习题:(五) 条 件 语 句含答案

课下能力提升(五) 条件语句一、填空题1.下面是一个算法的伪代码.如果输出的y的值是20,则输入的x的值是________.2.下面程序的运行结果是________.A←100B←90If A<B ThenT←A A←B B←TElseA←A-BEnd IfPrint A4|+1的函数值,则横线处应为________.3.求函数y=|x-Read xIf x≤0Thenf(x)←4xElsef(x)←2xEnd IfPrint f(x)根据以上算法,可求得f(-3)+f(2)的值为________.5.下列伪代码运行结果是________.X←0If X>0 ThenX←X+1ElseX←X-1End IfIf X>0 ThenY←XElse If X=0 ThenY←1ElseY←3-XEnd IfEnd IfPrint Y二、解答题6.已知算法:Read a,b,cm←aIf b>m Thenm←bEnd IfIf c>m Thenm←cEnd IfPrint m若输入10、12、8,求输出的结果.7.用算法语句表示下列过程,输入一个学生的成绩S,根据该成绩的不同值作以下输出:若S<60,则输出“不及格”;若60≤S≤90,则输出“及格”;若S>90,则输出“优秀”.8.某商场为迎接店庆举办促销活动,活动规定:购物额在100元及以内不予优惠;在100~300元之间(含300元)优惠货款的5%;超过300元之后,超过部分优惠8%,原优惠条件仍然有效.用伪代码写出根据输入购物额能输出应付货款的算法,并画出流程图.答案1.解析:由10x=20,得x=2.由2.5x+5=20,得x=6.答案:2或62.解析:由题意可知:A=100-90=10.答案: 103.解析:当x<4时,y=4-x+1=5-x,故横线处应填y←5-x.答案:y←5-x4.解析:由题意知f(-3)=-12,f(2)=4,∴f(-3)+f(2)=-12+4=-8.答案:-85.解析:当X=0时,将X-1的值赋给X,此时X为-1,当X=-1时,将3-X的值赋给Y,则Y=3-(-1)=4.答案: 46.解:∵12>10,∴m=12,又8>12不成立.∴输出m为12.7.解:伪代码如下:Read SIf S <60 ThenPrint“不及格”ElseIf S ≥60 And S ≤90 ThenPrint“及格”ElseP rint“优秀”End IfEnd If8.解:设购物额为x 元时,实付金额为y 元,由题意得y =⎩⎪⎨⎪⎧ x , x ≤100,0.95x , 100<x ≤300,285+x -300×0.92, x >300伪代码如下:Read xIf x ≤100 Theny ←xElseIf x ≤300 Theny ←0.95xElsey ←285+(x -300)×0.92End IfEnd IfPrint y。
高中数学 课下能力提升(十二)北师大版必修3
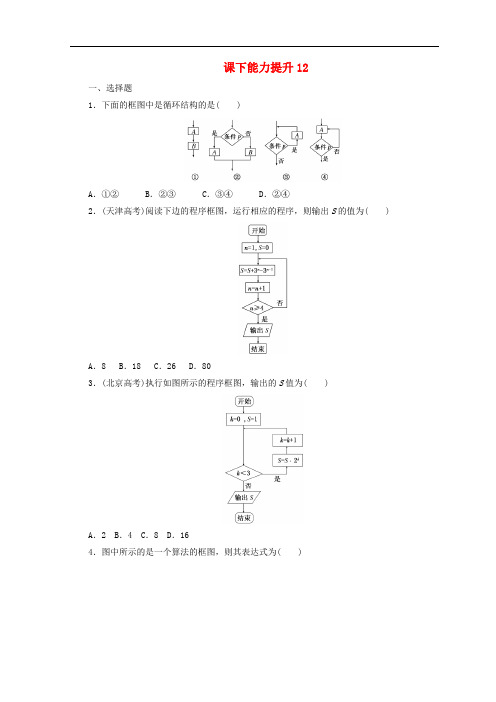
课下能力提升12一、选择题1.下面的框图中是循环结构的是( )A.①②B.②③C.③④D.②④2.(天津高考)阅读下边的程序框图,运行相应的程序,则输出S的值为( )A.8 B.18 C.26 D.803.(北京高考)执行如图所示的程序框图,输出的S值为( )A.2 B.4 C.8 D.164.图中所示的是一个算法的框图,则其表达式为( )A.11+2+3+…+99 B.11+2+3+…+100 C.199 D.11005.(天津高考)阅读如图所示的算法框图, 运行相应的算法.若输入x 的值为1, 则输出S 的值为( )A .64B .73C .512D .585二、填空题6.阅读如图所示的框图,若输入m =4,n =3,则输出a =________,i =________.7.(江西高考)下图是某算法的程序框图,则程序运行后输出的结果是________.8.若算法框图所给的程序运行的结果为S =90,那么判断框中应填入的关于k 的判断条件是________.三、解答题9.设计求1+4+7+10+…+40的一个算法,并画出相应的算法框图.10.以下是某次考试中某班15名同学的数学成绩:72, 91, 58, 63, 84, 88, 90, 55, 61, 73, 64, 77, 82, 94, 60.要求将80分以上的同学的平均分求出来,画出算法框图.答 案1. 解析:选C ①是顺序结构,②是选择结构,③④是循环结构.2. 解析:选C 程序执行情况为S =31-30=2,n =2;S =2+32-31=8,n =3;S =8+33-32=26,n =4≥4,跳出循环.故输出26.3. 解析:选C 框图的功能为计算S =1·20·21·22的值,计算结果为8. 4. 解析:选 A 依题意当i ≤99时,S =1+2+…+99,当i =100时,S =11+2+3+…+99.5. 解析:选B 第1次循环,S =1,不满足判断框内的条件,x =2;第2次循环,S =9,不满足判断框内的条件,x =4;第3次循环,S =73,满足判断框内的条件,跳出循环,输出S =73.6. 解析:由算法框图可知,当a =m ×i =4×i 能被n =3整除时输出a 和i 并结束程序.显然,当i =3时,a 可以被3整除,故i =3,此时a =4×3=12.答案:12 37. 解析:此框图依次执行如下循环:第一次:T =0,k =1,sin π2>sin 0成立,a =1,T =T +a =1,k =2,2<6,继续循环;第二次:sin π>sin π2不成立,a =0,T =T +a =1,k =3,3<6,继续循环;第三次:sin 3π2>sin π不成立,a =0,T =T +a =1,k =4,4<6,继续循环;第四次:sin 2π>sin 3π2成立,a =1,T =T +a =2,k =5,5<6,继续循环;第五次:sin 5π2>sin 2π成立,a =1,T =T +a =3,k =6,跳出循环,输出的结果是3.答案:38. 解析:由算法框图可知其作用是计算S=1×10×9×…,当运行结果为S=90时,应有S =1×10×9,∴当k=8时应符合条件且k>8不符合条件,∴条件应为k≤8或k<9.答案:k≤8或k<99. 解:算法:1.令S=0,i=1.2.S=S+i.3.i=i+3.4.若i≤40,返回第2步;重新执行第2、3、4步;若i>40,执行第5步.5.输出S的值.算法框图如图所示:法一:法二:10. 解:算法框图如下所示:。
高中数学课下能力提升十四北师大版

课下能力提升14 一、选择题1.以下程序S=0For x=-1 To 11S=x*xNext输出S.该程序输出结果是( )A.-1 B.11 C.100 D.1212.下列程序的运行结果为( )i=0S=0Doi=i+1S=S+iLoop While S<=20输出i.A.5 B.6 C.7 D.83.下列程序中的For语句终止循环时,S等于( )S=1For M=1 To 13 Step 3S=S+MNext输出S.A.1 B.5 C.10 D.354.下列算法的运行结果是( )S=0For i=1 To 5S=S+1/iNext输出S.A.13760B.160C.13060D.35.下列算法运行后的输出结果为( ) i=1Doi=i+2S=3+2*ii=i+1Loop While i<=8输出S.A.17B.19C.21D.23二、填空题6.S=0For i=0 To 10 000 Step 2S=S+iNext输出S.则循环10次的结果是________.7.S=0For i=1 To 100S=S+i*iNext输出S则该语句的算法功能为______________.8.把求11×4+12×5+13×6+…+150×53的值的下列程序补充完整,则(1)____________;(2)____________.i=1S=0Doi=i+1Loop While __(2)__输出S.三、解答题9.据下列框图写出对应算法语句.10.猴子第一天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了一个,第二天又将剩下的桃子吃掉一半,又多吃了一个,以后每天早上都吃前一天剩下的一半零一个,到第五天早上想吃时,见只剩一个桃子了,求第一天共摘了多少桃子?画出算法框图,并用语句描述.答 案1. 解析:选D 由For 语句的算法特点可知,S =11×11=121.2. 解析:选B 由于0+1+2+3+4+5=15,0+1+2+3+4+5+6=21,∴i =6.3. 解析:选D S =1+4+7+10+13=35.4. 解析:选 A 本算法是求1+12+13+14+15的和. 5. 解析:选C 这是用Do Loop 语句编写的算法,按Do Loop 语句的运行程序可知最后一次执行循环体时S =3+2×(7+2)=21.6. 解析:算法程序实际是在计算S =0+2+4+…+10 000,如果循环10次,则有S =0+2+4+6+8+…+18=90.答案:907. 解析:S =12+22+…+1002.答案:计算12+22+…+1002的值8. 答案:(1)S =S +1/i *(i +3)(2)i <=509. 解: S =0i =1DoS =S +ii =i +1Loop While i <=1 000输出S.10. 解:算法框图如图所示.程序如下:S=1For i=1 To 4S=2*(S+1)Next输出S.。
高中数学 课下能力提升(一)新人教A版必修3

课下能力提升(一)[学业水平达标练]题组1 算法的含义及特征1.下列关于算法的说法错误的是( )A .一个算法的步骤是可逆的B .描述算法可以有不同的方式C .设计算法要本着简单方便的原则D .一个算法不可以无止境地运算下去2.下列语句表达的是算法的有( )①拨本地电话的过程为:1提起话筒;2拨号;3等通话信号;4开始通话或挂机;5结束通话;②利用公式V =Sh 计算底面积为3,高为4的三棱柱的体积;③x 2-2x -3=0;④求所有能被3整除的正数,即3,6,9,12,….A .①②B .①②③C .①②④D .①②③④3.下列各式中S 的值不可以用算法求解的是( )A .S =1+2+3+4B .S =12+22+32+…+1002C .S =1+12+…+110 000D .S =1+2+3+4+…题组2 算法设计4.给出下面一个算法:第一步,给出三个数x ,y ,z .第二步,计算M =x +y +z .第三步,计算N =13M . 第四步,得出每次计算结果.则上述算法是( )A .求和B .求余数C .求平均数D .先求和再求平均数5.(2016·东营高一检测)一个算法步骤如下: S 1,S 取值0,i 取值1;S 2,如果i ≤10,则执行S 3,否则执行S 6;S 3,计算S +i 并将结果代替S ;S 4,用i +2的值代替i ;S 5,转去执行S 2;S 6,输出S .运行以上步骤后输出的结果S =( )A .16B .25C .36D .以上均不对6.给出下面的算法,它解决的是( )第一步,输入x .第二步,如果x <0,则y =x 2;否则执行下一步.第三步,如果x =0,则y =2;否则y =-x 2.第四步,输出y .A .求函数y =⎩⎪⎨⎪⎧ x 2x <,-x 2x的函数值 B .求函数y =⎩⎪⎨⎪⎧ x 2x <,x =,-x 2x >的函数值C .求函数y =⎩⎪⎨⎪⎧ x 2x >,x =,-x 2x <的函数值D .以上都不正确 7.试设计一个判断圆(x -a )2+(y -b )2=r 2和直线Ax +By +C =0位置关系的算法.8.某商场举办优惠促销活动.若购物金额在800元以上(不含800元),打7折;若购物金额在400元以上(不含400元)800元以下(含800元),打8折;否则,不打折.请为商场收银员设计一个算法,要求输入购物金额x ,输出实际交款额y .题组3 算法的实际应用9.国际奥委会宣布2020年夏季奥运会主办城市为日本的东京.据《中国体育报》报道:对参与竞选的5个夏季奥林匹克运动会申办城市进行表决的操作程序是:首先进行第一轮投票,如果有一个城市得票数超过总票数的一半,那么该城市将获得举办权;如果所有申办城市得票数都不超过总票数的一半,则将得票最少的城市淘汰,然后进行第二轮投票;如果第二轮投票仍没选出主办城市,将进行第三轮投票,如此重复投票,直到选出一个主办城市为止,写出投票过程的算法.[能力提升综合练]1.小明中午放学回家自己煮面条吃,有下面几道工序:①洗锅、盛水2分钟;②洗菜6分钟;③准备面条及佐料2分钟;④用锅把水烧开10分钟;⑤煮面条和菜共3分钟.以上各道工序,除了④之外,一次只能进行一道工序.小明要将面条煮好,最少要用( ) A.13分钟 B.14分钟C.15分钟 D.23分钟2.在用二分法求方程零点的算法中,下列说法正确的是( )A.这个算法可以求方程所有的零点B.这个算法可以求任何方程的零点C.这个算法能求方程所有的近似零点D.这个算法并不一定能求方程所有的近似零点3.(2016·青岛质检)结合下面的算法:第一步,输入x.第二步,判断x是否小于0,若是,则输出x+2,否则执行第三步.第三步,输出x-1.当输入的x的值为-1,0,1时,输出的结果分别为( )A.-1,0,1 B.-1,1,0C.1,-1,0 D.0,-1,14.有如下算法:第一步,输入不小于2的正整数n.第二步,判断n是否为2.若n=2,则n满足条件;若n>2,则执行第三步.第三步,依次从2到n-1检验能不能整除n,若不能整除,则n满足条件.则上述算法满足条件的n是( )A.质数 B.奇数C.偶数 D.合数5.(2016·济南检测)输入一个x值,利用y=|x-1|求函数值的算法如下,请将所缺部分补充完整:第一步:输入x;第二步:________;第三步:当x<1时,计算y=1-x;第四步:输出y.6.已知一个算法如下:第一步,令m=a.第二步,如果b<m,则m=b.第三步,如果c<m,则m=c.第四步,输出m .如果a =3,b =6,c =2,则执行这个算法的结果是________.7.下面给出了一个问题的算法:第一步,输入a .第二步,如果a ≥4,则y =2a -1;否则,y =a 2-2a +3.第三步,输出y 的值.问:(1)这个算法解决的是什么问题?(2)当输入的a 的值为多少时,输出的数值最小?最小值是多少?8.“韩信点兵”问题:韩信是汉高祖手下的大将,他英勇善战,谋略超群,为汉朝的建立立下了不朽功勋.据说他在一次点兵的时候,为保住军事秘密,不让敌人知道自己部队的军事实力,采用下述点兵方法:①先令士兵从1~3报数,结果最后一个士兵报2;②又令士兵从1~5报数,结果最后一个士兵报3;③又令士兵从1~7报数,结果最后一个士兵报4.这样韩信很快算出自己部队里士兵的总数.请设计一个算法,求出士兵至少有多少人.答 案[学业水平达标练]1. 解析:选A 由算法定义可知B 、C 、D 对,A 错.2. 解析:选A 算法通常是指按照一定规则解决某一类问题的明确和有限的步骤.①②都各表达了一种算法;③只是一个纯数学问题,不是一个明确步骤;④的步骤是无穷的,与算法的有穷性矛盾.3. 解析:选D D 中的求和不符合算法步骤的有限性,所以它不可以用算法求解,故选D.4. 解析:选D 由算法过程知,M 为三数之和,N 为这三数的平均数.5. 解析:选B 由以上计算可知:S =1+3+5+7+9=25,答案为B.6. 解析:选B 由算法知,当x <0时,y =x 2;当x =0时,y =2;当x >0时,y =-x 2.故选B.7. 解:算法步骤如下:第一步,输入圆心的坐标(a ,b )、半径r 和直线方程的系数A 、B 、C .第二步,计算z 1=Aa +Bb +C .第三步,计算z 2=A 2+B 2.第四步,计算d =|z 1|z 2. 第五步,如果d >r ,则输出“相离”;如果d =r ,则输出“相切”;如果d <r ,则输出“相交”.8. 解:算法步骤如下:第一步,输入购物金额x (x >0).第二步,判断“x >800”是否成立,若是,则y =0.7x ,转第四步;否则,执行第三步. 第三步,判断“x >400”是否成立,若是,则y =0.8x ;否则,y =x .第四步,输出y ,结束算法.9. 解:算法如下:第一步,投票.第二步,统计票数,如果一个城市得票数超过总票数的一半,那么该城市就获得主办权,否则淘汰得票数最少的城市并转第一步.第三步,宣布主办城市.[能力提升综合练]1. 解析:选C ①洗锅、盛水2分钟+④用锅把水烧开10分钟(同时②洗菜6分钟+③准备面条及佐料2分钟)+⑤煮面条和菜共3分钟=15分钟.解决一个问题的算法不是唯一的,但在设计时要综合考虑各个方面的因素,选择一种较好的算法.2. 解析:选D 二分法求方程零点的算法中,仅能求方程的一些特殊的近似零点(满足函数零点存在性定理的条件),故D 正确.3. 解析:选C 根据x 值与0的关系选择执行不同的步骤.4. 解析:选A 根据质数、奇数、偶数、合数的定义可知,满足条件的n 是质数.5. 解析:以x -1与0的大小关系为分类准则知第二步应填当x ≥1时,计算y =x -1. 答案:当x ≥1时,计算y =x -16. 解析:这个算法是求a ,b ,c 三个数中的最小值,故这个算法的结果是2.答案:27. 解:(1)这个算法解决的是求分段函数y =⎩⎪⎨⎪⎧ 2a -1,a ≥4,a 2-2a +3,a <4的函数值的问题.(2)当a ≥4时,y =2a -1≥7;当a <4时,y =a 2-2a +3=(a -1)2+2≥2,∵当a =1时,y 取得最小值2.∴当输入的a 值为1时,输出的数值最小为2.8. 解:第一步,首先确定最小的满足除以3余2的正整数:2.第二步,依次加3就得到所有除以3余2的正整数:2,5,8,11,14,17,20,….第三步,在上列数中确定最小的满足除以5余3的正整数:8.第四步,然后在自然数内在8的基础上依次加上15,得到8,23,38,53,….第五步,在上列数中确定最小的满足除以7余4的正整数:53.即士兵至少有53人.。
高中数学人教A版必修三课下能力提升:(二)含解析

课下能力提高(二 )[ 学业水平达标练]题组 1程序框图1.在程序框图中,一个算法步骤到另一个算法步骤的连结用()A .连结点B .判断框C.流程线D.办理框2.a 表示“办理框”, b 表示“输入、输出框”, c 表示“起止框”, d 表示“判断框”,以下四个图形挨次为()A . abcd B. dcab C. bacd D. cbad3.假如输入n= 2,那么履行以下算法的结果是()第一步,输入n.第二步, n= n+1.第三步, n= n+2.第四步,输出n.A.输出 3B.输出 4C.输出 5 D .程序犯错题组 2次序构造4.以下图的程序框图表示的算法意义是()A .边长为3,4,5 的直角三角形面积B.边长为3,4,5 的直角三角形内切圆面积C.边长为3,4,5 的直角三角形外接圆面积D.以 3,4,5 为弦的圆面积5. (2016 东·营高一检测 )给出以下图的程序框图:若输出的结果为2,则①处的履行框内应填的是()A . x= 2B. b= 2C.x= 1D. a= 56.写出以下图程序框图的运转结果:S=________.7.已知半径为r 的圆的周长公式为C= 2πr,当 r= 10 时,写出计算圆的周长的一个算法,并画出程序框图.8.已知函数f(x)= x2- 3x-2,求 f(3)+ f(- 5)的值,设计一个算法并画出算法的程序框图.[ 能力提高综合练]1.程序框图符号“”可用于()A .输出 a=10 B.赋值 a= 10C.判断 a= 10D.输入 a= 12. (2016 ·州高一检测广 )如图程序框图的运转结果是()533C.-2D.- 13. (2016 ·州高一检测广 )如图是一个算法的程序框图,已知a1= 3,输出的b= 7,则 a2等于()A.9B. 10C.11D. 124. (2016 ·山高一检测佛)阅读以下图的程序框图,若输出的结果为6,则①处履行框应填的是 ()A . x= 1B. x=2C.b= 1 D .b= 25.依据以下图的程序框图所表示的算法,输出的结果是________.6.计算图甲中空白部分面积的一个程序框图如图乙,则①中应填________.图甲图乙7.在以下图的程序框图中,当输入的x 的值为 0 和 4 时,输出的值相等,依据该图和各小题的条件回答下列问题.(1)该程序框图解决的是一个什么问题?(2)当输入的x 的值为 3 时,求输出的f(x)的值.(3)要想使输出的值最大,求输入的x 的值.8.如图是为解决某个问题而绘制的程序框图,认真剖析各框内的内容及图框之间的关系,回答下边的问题:(1)图框①中x= 2 的含义是什么?(2)图框②中y1=ax+ b 的含义是什么?(3)图框④中y2=ax+ b 的含义是什么?(4)该程序框图解决的是如何的问题?(5)当最后输出的结果是y1= 3, y2=- 2 时,求 y=f(x)的分析式.答案[ 学业水平达标练]1.分析:选 C 流程线的意义是流程进行的方向,一个算法步骤到另一个算法步骤表示的是流程进行的方向,而连结点是当一个框图需要分开来画时,在断开处画上连结点.判断框是依据给定条件进行判断,办理框是赋值、计算、数据办理、结果传递,因此A,B,D 都不对.应选 C.2.答案: D3.答案: C4.分析:选B r=a+ b-c由直角三角形内切圆半径,知选 B.25.分析:选 C ∵b= 2,∴2= a- 3,即 a= 5.∴2x+ 3= 5 时,得 x=1.6.分析: S= log24+ 42= 18.答案: 187.解:算法以下:第一步,令r = 10.第二步,计算C= 2πr.第三步,输出C.程序框图如图:8.解:自然语言算法以下:第一步,求f(3) 的值.第二步,求f(- 5)的值.第三步,将前两步的结果相加,存入y.第四步,输出y.程序框图:[ 能力提高综合练]1.分析:选 B 图形符号“” 是办理框,它的功能是赋值、计算,不是输出、判断和输入,应选 B.2.分析:选Ca b 243由于 a= 2, b=4,因此 S=-=-=-,应选 C.b a 4223.分析:选Ca1+a2的值.由题意知该算法是计算23+ a2∴2= 7,得 a2= 11,应选 C.4.分析:选 B 若 b=6,则 a=7,∴x3- 1= 7,∴x= 2.5.分析:该算法的第 1 步分别将1,2,3 赋值给 X, Y, Z,第 2 步使 X 取 Y 的值,即X 取值变为2,第 3 步使 Y 取 X 的值,即 Y 的值也是2,第 4 步让 Z 取 Y 的值,即 Z 取值也是2,进而第 5 步输出时, Z 的值是 2.答案: 26.分析:图甲空白部分的面积为 a2-16πa2,故图乙①中应填 S= a2-16πa2.2π 2答案: S= a-16a7. 解: (1) 该程序框图解决的是求二次函数f(x)=- x2+ mx 的函数值的问题.(2)当输入的 x 的值为 0 和 4 时,输出的值相等,即f(0)= f(4) .由于 f(0) = 0, f(4)=- 16+4m,因此- 16+ 4m= 0,因此 m= 4.2则 f(3) =- 32+ 4× 3= 3,因此当输入的x 的值为 3 时,输出的f(x)的值为 3.(3)由于 f(x)=- x2+4x=- (x- 2)2+ 4,因此当 x= 2 时, f(x)max= 4,因此要想使输出的值最大,输入的x 的值应为 2.8.解: (1) 图框①中 x=2 表示把 2 赋值给变量 x.(2)图框②中y1=ax+ b 的含义是:该图框在履行①的前提下,即当x=2时,计算ax+b 的值,并把这个值赋给y1.(3)图框④中y2= ax+ b 的含义是:该图框在履行③的前提下,即当x=- 3 时,计算ax +b 的值,并把这个值赋给y2.(4)该程序框图解决的是求函数y= ax+ b 的函数值的问题,此中输入的是自变量x 的值,输出的是对应x 的函数值.(5)y1=3,即 2a+b= 3.⑤y2=- 2,即- 3a+ b=- 2.⑥由⑤⑥,得a=1, b= 1,因此 f(x)= x+ 1.。
