8.4 光的相速度与群速度
光的相速度和群速度

二.群速
E E1 E2 E0 cos(1t k1r ) E0 cos(2t k2r ) 2E0 cos(t kr )cos(0t k0r )
1
2
2
,k
k1
k2 2
,0
1
2
2
,k0
k1
k2 2
E A(r,t )cos(0t k0r )
实部 : n 1
N
(q2 /2m0)(02 (02 2)2 ()2
2
)
.
实部 : n
1
N
(q2 /2m0)(02 (02 2)2 ()2
2
)
.n~
n
i,
虚部 :
N (q2
(02
/2m 0 )( ) 2)2 ()2
在色散介质中测量光速:
1.脉冲,有限长波列,复色光 2.各单色光相速不同,“波包”的传播速度?
二.群速
简化讨论,并不失一般性. 在色散介质中,设有两束频率非常相近、振幅 相同的单色平行光沿r 方向传播.
E E1 E2 E0 cos(1t k1r ) E0 cos(2t k2r )
§7.1.3. 光的相速度和群速度
•“单色平面波”——沿传播方向的无限长波列
E E0 cos(t kr ),
2 ,k 2 2 ,v c c .
T
n n v
n r
n : 介质中波长, v : 位相传播速度 . 一.相速
由: t-kr =常数,即 dt-kdr =0
得
v dr c .
相速度与群速度

§6-4 光的相速度和群速度折射率是光在真空中和介质中传播速度的比值,即v c n /=,通常可以通过测定光线方向的改变并应用折射定律()21sin /sin i i n =来求它,但原则上也可分别实测c 和v 来求它们的比值,用近代实验室方法,不难以任何介质中的光速进行精确的测定,例如水的折射率为,用这两种方法测得的结果是符合的,但对二硫化碳,用光线方向的改变的折射法测得的折射率为,而1885年迈克耳孙用实测光速求得的比值则为,其间差别很大,这绝不是由实验误差所造成的,瑞利找到了这种差别的原因,他对光速概念的复杂性进行了说明,从而引出了相速度和群速度的概念。
按照波动理论,这种通常的光速测定法相当于测定由下列方程所决定的波速的数值: ⎪⎭⎫ ⎝⎛-=v r t A E ωcos 不难看出,这里v 所代表的是单色平面波的一定的位相向前移动的速度,因为位相不变的条件为 常量=-vr t 由此得到 01=-dr vdt 或 dt dr v = (6-1) 所以这个速度称为位相速度(简称相速),这速度的量值可用波长和频率来计算。
波的表达式部是t 和r 的函数,可以写成下列形式:()kr t A E -=ωcos式中v πω2= 和λπ/2=k 都是不随 t 和 r 而改变的量,故位相不变的条件为kr t -ω=常量0=-kdr dt ω由此得或 λωv kv dt dr === (6-2) (6-2)式表示的位相速度乃是严格的单色波地(ω有单一的确定值)所特有的一种速度,单色波以t 和r 的余弦函数表达,ω为常量,这种严格的单色波的空间延续和时间延续都是无穷无尽的余弦(或正弦)波,但是这种波仅是理想的极限情况,实际所到的永远是形式不同的脉动,这种脉动仅在空间某一有限范围内、在一定的时间间隔内发生,在时间和空间上都是有起点和终点的,任何形式的脉动都可看成是由无限多个不同频率、不同振幅的单色正弦波或余弦波叠加而成的,即可将任何脉动写成傅里叶级数或傅里叶积分的形式,在无色散介质中所有这些组成脉动的单色平面波都以同一相速度传播,那么该脉动在传播过程中将永远保持形状不变,整个脉动也永远以这一速度向前传播,但是除真空以外,任何介质通常都具有色散的特征,就是说,各个单色平面波各以不同的相速传播,其大小随频率而变,所以由它们叠加而成的脉动在传播过程中将不断改变其形状,在这种情况下,关于脉动的传播速度问题就变得比较复杂了,观察种脉动时,可以先认定它上面的某一特殊点,例如振幅最在大的一点,而把这一点在空间的传播速度看作是代表整个脉动的传播速度,但是由于脉动形状的改变,所选定的这一特殊点在脉动范围内也将不断改变其位置,因而该点的传播速度和任何一个作为组成部分的单针平面波的相速都将有所不同,按照瑞利的说法,这脉动称为波群,因而脉动的传播速度称为群速度,简称群速,现在仅就一个简化的例子来讨论两种速度的关系。
信号速度,相速度及群速度的区别(论稿)

信号速度,相速度及群速度的区别胡良深圳市宏源清实业有限公司摘要:光子具有波粒二象性,粒子具有波粒二象性,任何孤立量子体系都具有波粒二象性关键词:信号速度,相速度,群速度作者:总工,高工,硕士,副董事长1信号速度的内涵光子具有波粒二象性,粒子具有波粒二象性,任何孤立量子体系都具有波粒二象性;对于光子,粒子及孤立量子体系来说,其内禀的速度可表达为:p E p E k f V n ∂∂=∂∂=∂∂=)/()/( ,其中,n V ,孤立量子体系内禀的一维空间速度,或粒子内禀的一维空间速度或光子内禀的一维空间速度(光速),量纲是,[L^(1)T^(-1)];E ,能量,量纲是,[L^(3)T^(-1)]*[L^(2)T^(-2)];p ,动量,量纲是,[L^(3)T^(-1)]*[L^(1)T^(-1)];,约化普朗克常数(或,固有的普朗克常数),量纲是,[L^(3)T^(0)]*[L^(2)T^(-2)];f ,频率,量纲是,[L^(0)T^(-1)];k ,波数,量纲是,[L^(-1)T^(0)]。
值得一提的是,最大的信号速度是真空中的光速,这意味着超光速通信是不可能实现的。
2群速度的内涵信号速度,相速度及群速度的内涵是有所不同的;但是,在绝对的真空中,则,信号速度,相速度及群速度是不可能区分的。
群速度(与选择的参考系相关),即,波的群速度,是指波振幅外形上的变化(波包)在空间中所传递的速度。
群速度可表达为:k f V g ∂∂= ,其中,g V ,群速度,量纲是,[L^(1)T^(-1)];f ,波的角频率,量纲是,[L^(0)T^(-1)];k ,波数(波矢),量纲是,[L^(-1)T^(0)]。
第一,如果波的角频率(f )正比于波数(k ),即,k V f * =;则群速度等于相速度,波形在传播过程中不会被扭曲。
第二,如果波的角频率(f )与波数(k )体现为线性关系;此时,群速度及相速度不同;波包以群速度传播,而波包里的波峰及波谷以相速度传播。
正常色散介质中群速度与相速度的相对关系

正常色散介质中群速度与相速度的相对关系
光的传播速度在不同介质中会发生改变,这种现象被称为光在介质中的折射,其中光传播的速度,在正常色散介质中群速度与相速度有一定的关系。
在正常色散介质中,介质中的光速度与频率之间呈现线性关系,也就是说在相同介质中,频率越高,光速度也越高。
根据自然的光学原理,光在介质中的传输速度是由群速度和相速度组成的。
群速度和相速度在正常色散介质中是有一定的关系的。
群速度表示的是光信号在介质中整体传播的速度,而相速度则是光的电场和磁场在介质中传播的速度。
在正常的色散介质中,群速度通常要大于相速度,也就是说,在介质中传输光信号的速度整体上要快于电场和磁场的传输速度。
这可以通过正常色散介质中材料的复合折射率来解释。
光的相位速度与群速度之间的差异是由折射率的频率依赖性造成的。
在正常色散材料中,较高频率的光会快速折射并且离开表面,而较低频率的光则会被材料捕获和重新释放,从而形成相对较慢的群速度。
在光纤通讯系统中,光速度和光的传输性能至关重要。
对于正常色散介质,光信号传播的快慢由材料的折射率决定,因此了解群速度和相速度之间的相对关系对于光纤通讯系统的设计和优化非常重要。
总之,在正常色散介质中,群速度和相速度之间存在一定程度的相对关系。
群速度比相速度更高,这是由于复合折射率的频率依赖性造成的。
这种相对关系在光学系统的优化中非常重要,因为光速和光的传输性能通常是光学系统设计和优化的关键因素之一。
§1-8 相速、群体及色散特性

二、色 散 特 性
相速与工作频率的关系称为色散特性。显然,我们更感兴趣的是导波模的色散特性。表示色散 特性的常用方法包括如下几种: (1) β = f (ω)或ω = f (β ) ,见图 1-8-1。图中画出了三个导波模 a、b、c 的色散特性。由§ 1-5 的讨论可知,它们都夹在 (β / ω) = n 1 / c和(β / ω) = n 2 / c 的扇形区域 II 内。其中 b、c 的截 止角频率为 ωcb 和ωcc 。模式 a 的截止频率最低(在本例中为 0),称为基模。当 ω → ∞ 时各模式
−2 −1 2
,或光强角谱 A (u ) 下降
。对 s 上述两种不同 E(r)的计算结果见表 1-10-1。 表 1-10-1 光束的角谱及相关参数
E(r) A(u) ud θd
∞
高斯光束 exp(-r2/w2) exp[-(uw/2)2] 2/w 0.32λ/nw
阶跃光束 1, 0≤r<w 0, r>w 2J1(uw)/uw ≈ exp[-0.14(uw)2] 2.7/w 0.43λ/nw
2 2
(
2 1/ 2
(1-5-13)有该分量应为 [k n
2 0
2
(x ) − β 2 ]1/ 2 。二维限制光波导中,当 n = n (r ) 时,由式(1-5-13)
1/ 2
)
;当折射率为对称渐变分布(图 1-2-4)时,由式(1-2-8)、
2 2 v2 2 有该分量应为 k 0 n (r ) − β − 2 r
2
ˆ (r ) 是空间位置的函数。只要与波长相比,n(r)是空间位置的慢变函数,此近似就 k (r ) = n (r )k 0 k
二、用本地平面波概念确定波导模的本征值
相速度和群速度 (Phase velocity and group velocity )

2. 复色波的速度 该式表明:这个二色波是如图所示的、频率为 、 振幅随时间和空间在 0 到 2E0 之间缓慢变化的光波。 这种复色波可以叫做波群或振幅调制波。 x
振动的合成.exe
2. 复色波的速度
对于上述复色波,其传播速度包含两种含义: 等相位面的传播速度,称为相速度; 等振幅面的传播速度,称为群速度。 形象一点说,你拿电钻在一个很坚固的墙上钻洞, 你会觉得电钻的钻头的螺纹在旋转时似乎以高速前 进,但这只是你的错觉,因为你看到的是螺纹的 “相速度”,虽然很快,但是你的电钻却很慢很慢 地向墙内推进,也就是说电钻的总的向前推进的速 度就是“群速度”。
n
折射率随着波长 增加(或光频率的 减少)而减小的色 散叫正常色散。
由 k=2 / ,有dk=-(2 / 2)d ,可将上式变为
d g = d (77)
d(k ) d g +k dk dk
k=2 / dk=-(2 / 2)d
(76)
2)复色波的群速度
由=c/n,有d =- (c/n2)dn,上式还可表示为
dz m g = = dt km k
EE (z, t )cos (t kz)
E (z,t )=2E0 cos (mt km z)
(73)
m t km z =常数
dz m k m 0 dt dz m dt km
1 1 m = (1 2 )= 2 2 1 1 km = (k1 k2 )= k 2 2 dz m
2. 复色波的速度
2,则 若 E01 E02 E0 且 1 2 1、
EE (z, t )cos (t kz) (73)
式中
E (z ,t )=2E0 cos (m t km z) 1 1 m = (1 2 )= 2 2 1 1 km = (k1 k2 )= k 2 2 1 = (1 2 ) 2 1 k = (k1 k2 ) 2
《相速度和群速度》课件

它并不等于波的能量 或信息传播的速度, 这是群速度的概念。
相速度的物理意义
相速度决定了波在介质中的传 播速度,即波峰和波谷的运动 速度。
它决定了波的相位变化和干涉 、衍射等物理现象的发生。
在某些情况下,相速度可以接 近无穷大,例如在无损介质中 传播的波。
相速度的计算方法
根据波动方程和介质的物理性质,可以求解波的相速度。
影响因素不同
相速度只与介质性质有关,而群速度不仅与介质性质有关,还与频 率有关。
在某些介质中的行为不同
在色散介质中,相速度可以超过光速,而群速度不能超过光速。
相速度与群速度的联系
在某些情况下,两者可能相等
01
在无色散介质中,波的相速度和群速度是相等的。
两者都是描述波动现象的重要参数
02
相速度和群速度分别从不同的角度描述了波动现象,对于理解
展望
未来研究方向
随着科技的发展,相速度和群速 度的研究将更加深入,未来可以 进一步探索其在不同领域的应用
,如量子力学、生物医学等。
技术发展与挑战
随着通信、信号处理等技术的快速 发展,对相速度和群速度的研究将 面临更多挑战,需要不断探索新的 理论和方法。
跨学科合作与交流
相速度和群速度的研究涉及到多个 学科领域,未来需要加强跨学科的 合作与交流,促进相关领域的发展 。
波动现象的本质和传播规律具有重要意义。
两者都是波动方程的解
03
无论是相速度还是群速度,都是波动方程的解,用于描述波动
在介质中的传播行为。
PART 04
相速度和群速度的应用
REPORTING
通信领域的应用
相速度的应用
在通信领域中,相速度控制着信号的相位信息传递。通过调 整相速度,可以实现对信号的相位调制,如调相(PM)和调 频(FM)等,从而实现更高效、更可靠的数据传输。
光速的测定光的相速度和群速度

06 结论
光速测定的重要性和影响
物理学基础
光速是物理学中的一个基本常数,对理解光和物质相互作用、电 磁波传播等基本物理现象具有重要意义。
相对论框架
光速是狭义相对论和广义相对论的基础,对理解时空结构、相对论 效定对光学、激光技术、通信技术等领域的发展和应用 具有重要影响,如光纤通信、卫星导航等。
该实验通过将一束光分成两束,使它们在空间中传播一定距离后相遇,形成干涉条 纹。根据干涉条纹的移动距离和条纹间距,可以计算出光速的大小。
萨格纳克干涉实验的结果也表明,光速是一个恒定的值,不受光源和观察者的相对 运动影响。
其他测定方法
除了迈克尔逊-莫雷实验和萨格纳克干涉实验外,还有许多其他方法可以用来测 定光速,例如利用激光和光学纤维的方法、利用卫星轨道测量和射电望远镜的方 法等。
相速度可以通过光波在介质中的波长和频率计算得出,公式为: v=c/n,其中v为相速度,c为光在真空中的速度,n为介质的折 射率。
也可以通过测量光波在介质中的波长和相位差来计算相速度 。
相速度的物理意义
相速度决定了光波在介质中的传播速 度,是光与物质相互作用的重要参数。
相速度的变化反映了介质对光的折射 效应,是光学研究中的重要概念。
该实验采用了分束器将一束光分为两束,分别沿着地球运 动的方向和垂直于地球运动的方向传播,然后通过干涉仪 观察干涉条纹的变化,从而推算出光速的大小。
迈克尔逊-莫雷实验的结果表明,无论在哪个方向上,光速 都是一样的,这一结果被称为光速的各向同性。
萨格纳克干涉实验
萨格纳克干涉实验是一种利用光的干涉现象测定光速的方法。
05 光速测定在实际中的应用
在物理学研究中的应用
验证光速不变原理
通过精确测定光速,可以验证光速在真空中 恒定的原理,这是爱因斯坦相对论的基本假 设之一。
光的相速和群速
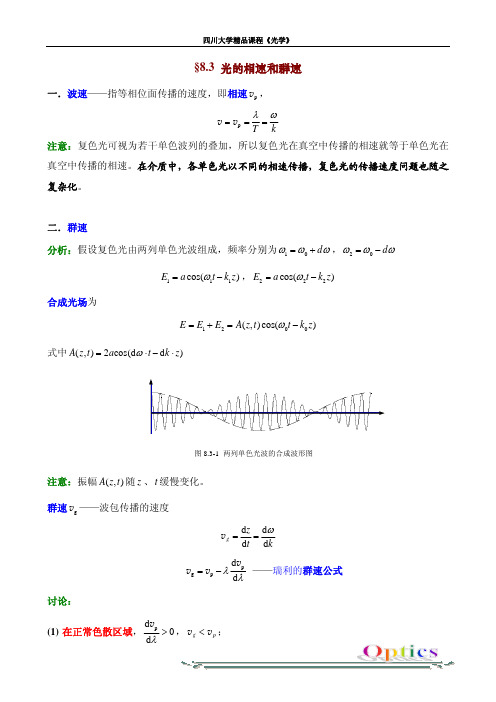
§8.3 光的相速和群速
一.波速——指等相位面传播的速度,即相速p v ,
p T
k
λ
ω
==
=
v v
注意:复色光可视为若干单色波列的叠加,所以复色光在真空中传播的相速就等于单色光在真空中传播的相速。
在介质中,各单色光以不同的相速传播,复色光的传播速度问题也随之复杂化。
二.群速
分析:假设复色光由两列单色光波组成,频率分别为10d ωωω=+,20d ωωω=−
111cos()E a t k z ω=−222cos()E a t k z ,−
=ω合成光场为
1200(,)cos()E E E A z t t k z ω=+=−
式中(,)2cos(d d )A z t a t k z ω=⋅−⋅
注意:振幅(,)A z t 随、t 缓慢变化。
z 群速——波包传播的速度
g v d d d d g z t k
ω
=
=
v p g p d d λ
λ
=−v v v ——瑞利的群速公式
讨论:
(1) 在正常色散区域,
p d 0d λ
>v ,g p <v v ;
(2) 在反常色散区域,
p d 0d λ<v ,g p >v v ;
(3) 在真空中无色散,p d 0d λ
=v ,g p =v v 。
例8.3-1 已知冕玻璃对波长为398.8nm 光的折射率n =1.52546,色散为1410261−−×−=nm .d dn
λ
,求群速和相速。
8.4 光的相速度与群速度

E1
E2
合成波和波包
合成波的速度,即波包上任一点的前移速度,也就是 波包上等振幅面向前推进的速度。它代表着波包具有 的能量传播速度。 物理科学与信息工程学院 6
定义:复色光在色散介质中,整个波包传播的速度, 称为群速度。
振幅不变的条件为:
dt dkr constant
因d,dk都是不随t和r改变的量,微分上式得:
则这两列单色光波可分别表示为:
E1 a cos(1t k1r ) E2 a cos(2t k2 r )
可以推得其合成波为: 其中
E A0 cos(0t k0 r )
A0 2a cos(dt dkr)
即合成波的振幅A0不是常数,而是随r和t缓慢变化 的余弦函数。如图 物理科学与信息工程学院 5
ddt dkdr 0
因此,群速度可表示为:
dr d g dt dk
物理科学与信息工程学院 7
物理科学与信息工程学院 8
三. 群速与相速的关系
d p d d ( p k ) g p k dk dk dk
因
(1)
k
2
2
所以
dk
2
d
d dk 2
随着测定光速方法的改进,问题又复杂化了,1885年 迈克耳逊以较高的精度重复了傅科实验的同时,还测 定了空气和CS2光速之比为1.758,但是用折射法测定 的CS2折射率为1.64,两数相差甚大,这绝非实验误 差所致。 瑞利对光速的概念进行了深入详尽的研究,提出 “群速”的概念之后才解决这个矛盾。
dr p dt k
dt kdr 0
t kr 常数
可见,相速度是严格单色光所特有的一种速度。严格 的单色光在空间延续和时间延续都是无穷无尽的余弦 或正弦波。但这种波是理想的极限情况。 物理科学与信息工程学院 3
相速度与群速度

相速度与群速度群速度和相速度是导波理论中的重要概念,也是导波的主要参数。
群速度(c g )是指脉冲波的包络上具有某种特性(如幅值最大)的点的传播速度,它是波群的能量传播速度。
通俗的说,群速度是关于一族频率相近的波的传播速度。
而相速度(c p )是波上相位固定的一点传播方向的传播速度。
值得注意的是,导波以其群速度向前传播。
Lord Rayleigh 曾说过:“群速度的概念常用下面这个例子说明,即当一族波列到达一个静止水面时,波群的速度比它所包含的每一个子波的速度都要小;这些子波仿佛通过波群前进,当达到其内部极限时而消失。
”群速度和相速度的意义可以通过波的叠加引出。
谐波是最简单的波,一个谐波的振动方程可以表示成式(2.1)的形式。
()t kx Acos u ω-=(2.1)式中: u----质点振动的位移A----振幅k----波数,k=2π/λ,λ为波长 ω---振动的角频率 x----波传播的位置矢量 t----时间变量最简单的分析法是考虑两个振幅相同,频率ω1和ω2略有差异的谐波的传播问题,有)()t x k Acos t x k Acos u 2211ωω-+-=(2.2)式中,k 1=ω1/c 1;k 2=ω2/c 2。
通过三角变换和如下代换 △ω=ω2-ω1 △k=k 2-k 1 ωA V =1/2(ω2+ω1) k A V =1/2(k 2+k 1) c A V =ωA V /k A V则()t x k cos t21kx 212Acos uAV AV ωω-⎪⎭⎫⎝⎛∆-∆=注意到低频项有一传播速度,群速度定义为 C g =△ω/△k 取极限为C g =d ω/dk 。
高频项同样有一传播速度,相速度定义为 C p =ω/k频率相近的一族波的叠加导致了图 2.2中的典型结果。
不同的谐波以不同的相速度C p 传播,但叠加起来之后的波群以群速度C g 传播。
超声导波总是以群速度传播的,但由于实际应用中往往只能得到导波的相速度,群速度C g 可以由相速度C p ,利用公式dkd c g ω=得到,将k=ω/c p 代入上式,得图2-2 群速度、相速度示意图)fd (d dc)fd (c c d dcc c c dc cd d c d d c p2p 2ppp 2p2ppppg -=-=-=⎪⎪⎭⎫ ⎝⎛=ωωωωωωω因此)fd (d dc)fd (c c c p2p 2pg -=(2.3)此时就可以通过式 2.3得到导波的群速度[51]。
相速度与群速度

§6-4 光的相速度和群速度折射率是光在真空中和介质中传播速度的比值,即v c n /=,通常可以通过测定光线方向的改变并应用折射定律()21sin /sin i i n =来求它,但原则上也可分别实测c 和v 来求它们的比值,用近代实验室方法,不难以任何介质中的光速进行精确的测定,例如水的折射率为1.33,用这两种方法测得的结果是符合的,但对二硫化碳,用光线方向的改变的折射法测得的折射率为1.64,而1885年迈克耳孙用实测光速求得的比值则为1.75,其间差别很大,这绝不是由实验误差所造成的,瑞利找到了这种差别的原因,他对光速概念的复杂性进行了说明,从而引出了相速度和群速度的概念。
按照波动理论,这种通常的光速测定法相当于测定由下列方程所决定的波速的数值: ⎪⎭⎫ ⎝⎛-=v r t A E ωcos 不难看出,这里v 所代表的是单色平面波的一定的位相向前移动的速度,因为位相不变的条件为 常量=-vr t 由此得到 01=-dr vdt 或 dt dr v = (6-1) 所以这个速度称为位相速度(简称相速),这速度的量值可用波长和频率来计算。
波的表达式部是t 和r 的函数,可以写成下列形式:()kr t A E -=ωcos式中v πω2= 和λπ/2=k 都是不随 t 和 r 而改变的量,故位相不变的条件为kr t -ω=常量0=-kdr dt ω由此得或 λωv kv dt dr === (6-2) (6-2)式表示的位相速度乃是严格的单色波地(ω有单一的确定值)所特有的一种速度,单色波以t 和r 的余弦函数表达,ω为常量,这种严格的单色波的空间延续和时间延续都是无穷无尽的余弦(或正弦)波,但是这种波仅是理想的极限情况,实际所到的永远是形式不同的脉动,这种脉动仅在空间某一有限范围内、在一定的时间间隔内发生,在时间和空间上都是有起点和终点的,任何形式的脉动都可看成是由无限多个不同频率、不同振幅的单色正弦波或余弦波叠加而成的,即可将任何脉动写成傅里叶级数或傅里叶积分的形式,在无色散介质中所有这些组成脉动的单色平面波都以同一相速度传播,那么该脉动在传播过程中将永远保持形状不变,整个脉动也永远以这一速度向前传播,但是除真空以外,任何介质通常都具有色散的特征,就是说,各个单色平面波各以不同的相速传播,其大小随频率而变,所以由它们叠加而成的脉动在传播过程中将不断改变其形状,在这种情况下,关于脉动的传播速度问题就变得比较复杂了,观察种脉动时,可以先认定它上面的某一特殊点,例如振幅最在大的一点,而把这一点在空间的传播速度看作是代表整个脉动的传播速度,但是由于脉动形状的改变,所选定的这一特殊点在脉动范围内也将不断改变其位置,因而该点的传播速度和任何一个作为组成部分的单针平面波的相速都将有所不同,按照瑞利的说法,这脉动称为波群,因而脉动的传播速度称为群速度,简称群速,现在仅就一个简化的例子来讨论两种速度的关系。
光的相速和群速

作者: 张品
出版物刊名: 昭通学院学报
页码: 47-49页
主题词: 群速;迈克耳孙;折射定律;相速;旋转镜法;折射法;实验误差;瑞利;传播速度;速测
摘要:<正> 介质的折射率一般用两种方法来测定.其一为光速测定法,即折射率是光在真空中和介质中传播速度的比值.其二是折射法,即应用折射定律.这就产生了一个问题:对同一介质,两种方法得出的折射率是否一样?迈克耳孙于1885年用旋转镜法对白光做实验,结果得到:空气中的光速与水中的光速之比值为1.33,光在空气中的速度与在二硫化碳中的速度之比体为1.758.前一数值与由折射法测得的水的折射率相符合,而后一数值与由折射法测得的二硫化碳的折射率1.64相差很大.这绝不是实验误差造成的.瑞利找到了这种差别的原因,他对光速概念的复杂性进行了说明,引出了光的相速和群速的概念.。
光速的测定光的相速度和群速

速
量 技 术
度 和 群 速
第 四 章
的
测
相速度的测量
干涉法
利用光的干涉现象,通过测量干涉条纹的 移动来确定相速度。这种方法需要使用双 缝干涉仪或迈克尔逊干涉仪等实验装置, 并通过精确测量干涉条纹的移动距离和时 间间隔来计算相速度。
VS
相位比较法
通过比较两束光的相位差来确定相速度。 这种方法需要使用相位计或示波器等设备, 测量两束光在传播过程中的相位变化,并 根据相位差与光程差的关系计算相速度。
实验装置
傅科摆实验的装置包括一个光源、一个傅科摆和一个探测器。光源发出的光经过傅科摆后被 探测器接收,探测器记录光的相位变化。
实验结果
傅科摆实验的结果也证实了光速的不变性,为光速的测定提供了一种新的方法。
其他光速测定实验方法
旋转齿轮法
利用高速旋转的齿轮来调制光源发出的光,通过测量调制后的光的频率或周期来计算光速。
感谢您的观看
WATCHING
THANKS FOR
激光干涉法
利用激光的干涉现象来测量光速。将激光分为两路,一路作为参考光路,另一路经过待测距离后返回与参考 光路发生干涉,通过测量干涉条纹的移动来推算光速。
光纤法
利用光纤中光的传输特性来测量光速。将光信号通过光纤传输一段已知距离后,测量其传输时间并计算光速。 这种方法具有高精度和可重复性好的优点。
相
光速测定的历史与意义
历史
自古以来,人们对光速的测定一直充满好奇和探索。从伽利略的首次尝试到迈 克尔逊-莫雷实验的精确测量,光速的测定经历了漫长而曲折的过程。
意义
光速是物理学中的基本常数之一,对于理解光学、电磁学以及相对论等物理理 论具有重要意义。光速的精确测定不仅推动了物理学的发展,也为现代光学、 光通信等领域的应用提供了基础。
微波:波速、相速、群速和能量传输速度的区别与联系_

••••••••••••••当前位置:›微波:波速、相速、群速和能量传输速度的区别与联系微波:波速、相速、群速和能量传输速度的区别与联系波速、相速、群速、能量传输速度1、定义波速(wave celerity):单位时间内波形传播的距离,以波长与波周期之比表示.V=入/T.相速(phase velocity):相速度,单一频率的正弦电磁波波的等相面(例如波峰面或波谷面)在介质中传播的速度v=c/n,c为自由空间中的光速,n为介质对该频率电磁波的折射指数。
在理想介质中,电磁波的相速仅与介质参数有关.群速(group velocity):(1)、波列作为整体的传播速度(2)波群传播的速度。
波的群速度,简称群速,是指波的包络传播的速度。
实际上就是波实际前进的速度。
群速是一个代表能量的传播速度。
概念引入原因:实用系统的信号总是由许多频率分量组成,在色散介质中,各单色分量将以不同的相速传播,因此要确定信号在色散介质中的传播速度就发生困难,为此引入群速的概念,它描述信号的能量传播速度。
能量传播速度:群速是波群的能量传播速度.2、相互关系(1)相关概念非色散介质:无线电波在介质中传播时,介电常数ε与频率无关,波的传播速度也与频率无关的介质;色散介质:与此相反,如果介电常数ε或传播速度v与频率有关的介质.正常色散:一切无色透明介质在可见光区域均表现为正常色散。
特点:波长变大时,由v=λf,频率不变,则V增大。
而n=c/v,则折射率值n变小,角色散率D变小。
反常色散:在某些波段会出现,波长变大时折射率值增大的现象,这称为反常色散。
反常色散同样是物质的普遍性质。
反常色散与选择吸收密切相关,即在发生物质的选择吸收波段附近出现反常色散。
角色散率:由夫琅和费衍射理论知,产生衍射亮条纹的条件(光栅方程):dsinθ=kλ(k= 1, 2,…, n)光栅方程对λ微分,就可得到光栅的角色散率:ψ=Δθ/Δλ=k/dcos.角色散率是光栅、棱镜等分光元件的重要参数,随着k的增大,色散率也就越大。
第七章光的量子性光速的测定光的相速度和群速度

惠斯通(CharlesWheatstone 1802~1875)英国物理学 家、发明家
迈克耳孙,阿尔伯特· 亚伯拉 罕(A.Michelson1852—1931), 德国出生的美国物理学家
随着科学科技的不断发展,人们不断地 改进实验装置和技术,直到1932年用旋转棱 镜测得光速为299774±2公里/秒。20世纪 60年代,激光器的出现,使光速的测定越发 精确,1972年测定的光速值为299792公里/ 秒。目前国际计量委员会承认的光速是 299792458米±1.2米/秒。 从伽利略开始,中间经过斐索和傅科等 人,一直到20世纪80年代,用来测定光速的 实验都是一种定量实验。
激光器的出现把光速的测量推向一个新阶段 。特别是饱和吸收技术的采用,使我们可以得到 频率的稳定性和复现性均十分优良的激光辐射, 并且由于波长可以比原来微波干涉仪法中用的小 三个量级(微米量级),使波长测量的准确度大 为提高,甲烷稳定的3.39μm 氦氖光系统(HeNe:CH4)和碘稳定的633nm氦氖辐射波长的复现 性高百倍以上,比现行的“米”定义86Kr辐射波 长的复现性高百倍以上,因此这不仅是光速的测 量问题了,重新改变“米”的定义问题提上议事 日程。
●迈克耳孙实验的说明
钠黄光测定了液体CS2的折射率;钠黄光包含两条谱线,真空中 波长为:
1 589.0nm
2 589.6nm
两者在色散介质CS2的折射率稍有不同,在折射实验中只涉及光 束的方向,它仅与折射率n1和n2有关,故折射法测量的是折射率 的平均值: n 1.64 而在速度法中测量的是光束的能流,即波拍的群速度vg
*问题的引出 光束在介质表面的折射 折射率n
n2 sin 1 n 1 sin 2 n2 n 1 v1 v2 v
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一. 相速度
迄今为止,对于各向同性介质在提到波速时,都指的是 波面(等位相面)传播的速度,即相速度p,在惠更斯 原理中如此,在波函数的表达式中也如此。
物理科学与信息工程学院 2
理想的单色平面波的波动方程可表示为:
E A cos(t kr)
上式=2,k=2/都是不随t和r改变的量。 因此,相位不变的条件为: 两边微分得: 即
ddt dkdr 0
因此,群速度可表示为:
dr d g dt dk
物理科学与信息工程学院 7
物理科学与信息工程学院 8
三. 群速与相速的关系
d p d d ( p k ) g p k dk dk dk
因
(1)
k
2
2
所以
dk
2
d
d dk 2
dr p dt k
dt kdr 0
t kr 常数
可见,相速度是严格单色光所特有的一种速度。严格 的单色光在空间延续和时间延续都是无穷无尽的余弦 或正弦波。但这种波是理想的极限情况。 物理科学与信息工程学院 3
在真空中所有波长的电磁以同一相速c传播,复色 光可视为若干单色波列的叠加,所以复色光在真 空中传播的相速度就等于单色光在真空中传播的 相速度。
§8.4 光的相速度与群速度
Phase Velocity and Group Velocity
根据光的微粒说,光在两种媒质界面上折射时, sini1/sini2=υ2/υ1,而根据光波动说sini1/sini2=1/2. 傅科做实验测定空气和水中光速之比近于4:3,此数 值与空气到水的折射率相符,从而判定光的波动说 的正确性。 虽然在傅科实验完成之前,光的波动说已为大量事实 (如干涉、衍射、偏振等)所证明,但傅科的实验仍被 认为是对惠斯原理最直接和最有力的支持。 物理科学与信息工程学院 1
在色散介质中,各单色光以不同的相速度传播, 因而,复色光在色散介质中的传播问题也随之复 杂化。
二. 群速度
为简单起见,假设复色光由两列单色光波组成, 其振幅均为a,频率分别为:
1 0 d
2 0 d
物理科学与信息工程学院 4
波数分别为:
k1 k0 dk
k2 k0 dk
则这两列单色光波可分别表示为:
E1 a cos(1t k1r ) E2 a cos(2t k2 r )
可以推得其合成波为: 其中
E A0 cos(0t k0 r )
A0 2a cos(dt dkr)
即合成波的振幅A0不是常数,而是随r和t缓慢变化 的余弦函数。如图 物理科学与信息工程学院 5
2
d p
d p d 2 d p dk d dk 2 d
物理科学与信息工程学院 9
代入(1)式可得:
g p
因为
d p d
——称为瑞利公式
c p n
所以
c c dn g 2 n n d
dn g p (1 ) n d
随着测定光速方法的改进,问题又复杂化了,1885年 迈克耳逊以较高的精度重复了傅科实验的同时,还测 定了空气和CS2光速之比为1.758,但是用折射法测定 的CS2折射率为1.64,两数相差甚大,这绝非实验误 差所致。 瑞利对光速的概念进行了深入详尽的研究,提出 “群速”的概念之后才解决这个矛盾。
也是相速之比 物理科学与信息工程学院 11
通过测量光在不同介质中的速度之比来确定折射率, 不论哪种测量方法,测得的光在介质中的速度实际 上是群速而不是相速。
因为CS2为正常色散,g< p,因而所得折射率n= 1.758大于用折射法测得的结果n=1.64。
第六章结束
物理科学与信息工程学院 12
E1
E2
合成波和波包
合成波的速度,即波包上任一点的前移速度,也就是 波包上等振幅面向前推进的速度。它代表着波包具有 的能量传播速度。 物理科学与信息工程学院 6
定义:复色光在色散介质中,整个波包传播的速度, 称为群速度。
振幅不变的条件为:
dt dkr constant
因d,dk都是不随t和r改变的量,微分上式得:
物理科学与信息工程学院 10讨论: (1)当 (2)当 (3)当
g p
d p d
d p d d p
d d p d
0
时,则
g P
g P g P
正常色散
0 时,则 0 时,则
为相速之比,
反常色散
无色散
c n n
折射定律
sin i1 1 sin i2 2
